Abstract
While studies suggest that peer influence can in some cases encourage adolescent substance use, recent work demonstrates that peer influence may be on average protective for cigarette smoking, raising questions about whether this effect occurs for other substance use behaviors. Herein, we focus on adolescent drinking, which may follow different social dynamics than smoking. We use a data-calibrated Stochastic Actor-Based (SAB) Model of adolescent friendship tie choice and drinking behavior to explore the impact of manipulating the size of peer influence and selection effects on drinking in two school-based networks. We first fit a SAB Model to data on friendship tie choice and adolescent drinking behavior within two large schools (n = 2178 and n = 976) over three time points using data from the National Longitudinal Study of Adolescent to Adult Health. We then alter the size of the peer influence and selection parameters with all other effects fixed at their estimated values and simulate the social systems forward 1000 times under varying conditions. Whereas peer selection appears to contribute to drinking behavior similarity among adolescents, there is no evidence that it leads to higher levels of drinking at the school level. A stronger peer influence effect lowers the overall level of drinking in both schools. There are many similarities in the patterning of findings between this study of drinking and previous work on smoking, suggesting that peer influence and selection may function similarly with respect to these substances.
Keywords: Alcohol use, Stochastic Actor-Based Model, Peer selection and influence, Goodness of fit, Forward simulation
While past research has generally indicated that peer influence is risk promotive with respect to adolescent substance use with some exceptions, recent work suggests that peer influence can be protective for adolescent smoking as an aggregate school level effect (Lakon et al. 2015). This finding raises the question of whether peer influence might have a similarly protective aggregate effect in a school social system for other substances. Though cigarettes and alcohol are sometimes used concurrently or reinforcingly by adolescents (Bailey 1992; Dee 1999; Orlando et al. 2005; Wang et al. 2016b), these substances have different initiation and usage patterns (Kandel and Logan 1984) and thus may be utilized differently in the same social setting. We focus on adolescent drinking behavior and the question of how varying peer influence and selection processes affect drinking prevalence and frequency. To maximize comparability with previous work, we utilize a parallel methodology and the same sample as in Lakon et al. (2015), with drinking behavior as the simulation target. To the extent that the system of peer influence that shapes drinking operates similarly to that which shapes adolescent smoking, we expect to see similar impacts of varying the strength of peer selection and influence on drinking behavior. Observing substantially different results would indicate that these substances operate differently at the individual and aggregate school levels.
Adolescent drinking behavior has been positively related to the drinking behavior of youths’ friends across studies (Ellickson and Hays 1991; Urberg et al. 1997; Ennett et al. 2006). The literature using Stochastic Actor-Based (SAB) Models has focused on differentiating peer influence (i.e., the tendency of youth to adjust their behavior so that it is similar to that of their friends) and peer selection (i.e., the tendency to become friends with those at similar levels of behavior) effects and has shown that peer influence positively relates to adolescent smoking (Mercken et al. 2007; Lakon et al. 2014) and drinking (Pearson et al. 2006; Knecht et al. 2010; Burk et al. 2012; Giletta et al. 2012; Mercken et al. 2012; Mathys et al. 2013; Osgood et al. 2013; Wang et al. 2013, 2015).
The central questions investigated by the above studies are (1) whether individual adolescents’ behaviors are correlated with and (2) whether they will adopt the behaviors of their peers. This foundational question is distinct from the subsequent question of whether such influence is risk promotive or risk protective. The latter question depends not only on influence itself but also on the environment in which it operates. Hence, such an investigation must include other relevant mechanisms like the tendency to select peers based on their own substance use behavior. Peer selection effects might result in the polarization of youth into densely connected clusters in a network based on their drinking status. Such an effect is unlikely to impact the prevalence of drinking in a population per se, unless coupled with a peer influence effect. However, if there is a strong tendency for adolescents to adopt the drinking behavior of their friends (i.e., peer influence effects, Christakis and Fowler 2007, 2008; Fowler and Christakis 2008), this may alter the overall prevalence of drinking in an adolescent population. Such complex interactions cannot be examined by regression-like models, instead requiring simulation studies that directly capture the coevolution of behavior and networks through time.
Herein, we utilize longitudinal network data collected in two high schools from the National Study of Adolescent to Adult Health (Add Health) over three time points to build Stochastic Actor-Based Models of friendship tie choice and drinking behavior dynamics. We manipulate the size of the selection and influence parameters from the models and simulate the networks and behavior over the same time period, allowing us to directly examine the systemic impact of these mechanisms on school drinking prevalence. While conventional thinking on peer influence and substance use might lead one to expect to see an increase in drinking prevalence with higher levels of peer influence, we conjecture that the tendency of peer influence to (on average) suppress deviant behaviors in favor of more conventional ones (see Lakon et al., 2015) will instead lead higher levels of peer influence to result in lower levels of alcohol use. We likewise expect that increases in peer selection on alcohol use will have little direct effect on prevalence, but will instead cluster youth by drinking status.
Methods
Data
We use the two largest schools from the Add Health study saturation sample, a school-based probability sample of adolescents in grades 7–12 (Harris et al. 2009). School-based network nominations and alcohol assessments were collected from all consented students over three waves. Data used in this study come from three adolescent surveys—In-School Survey, wave 1 In-Home Survey, and wave 2 In-Home Survey (1994, 1995, and 1996, respectively)—and one parent survey conducted as part of the wave 1 In-Home Survey (Harris et al. 2009). The two schools had 2178 and 976 students, and have been referred to as “Sunshine High” (Shoham et al. 2012) and “Jefferson High” (Bearman et al. 2004), respectively.
Measures
Friendship Networks
Respondents were asked to list the names of up to five male and five female best friends. The friendship tie choice variable is based on whether a tie was present or absent between any two adolescents. The network descriptive statistics of Sunshine High and Jefferson High are summarized in the upper part of Table 1. For the 2178 respondents in Sunshine High, the number of out-going ties decreased from 5685 during the In-School Survey to 4201 during the wave 1 In-Home Survey and to 2296 during the wave 2 In-Home Survey due to graduation, moving, dropping out, limited nomination (i.e., about 3.49% students in Sunshine High and 4.82% in Jefferson High were limited to only one male and one female friend nomination during the wave 1 In-Home Survey), and attrition/nonresponse/missing network data. A similar pattern is also observed in Jefferson High. Network evolution seemed to be more notable in Sunshine High than in Jefferson High, as indicated by the proportional change of reciprocal ties (from 0.30 to 0.25 in Sunshine High), the transitivity index (from 19 to 14% in Sunshine High), and the Jaccard index (with only 16% of ties persisting over two waves in Sunshine High). Following recent evidence, we use a principled imputation strategy to account for the relatively small amount of missing network data (Hipp et al. 2015; Wang et al. 2016a).
Table 1.
Network and drinking behavior statistics
| Wave 1 | Wave 2 | Wave 3 | |
|---|---|---|---|
| Network statistics | |||
| Sunshine High | |||
| No. of vertices | 2178 | ||
| Out-going ties | 5685 | 4201 | 2296 |
| Reciprocal index | 0.30 | 0.28 | 0.25 |
| Transitive index | 0.19 | 0.19 | 0.14 |
| Jaccard index | 0.16a | 0.16b | |
| Limited nominations (%) | 0 | 3.49 | 1.52 |
| Jefferson High | |||
| No. of vertices | 976 | ||
| Out-going ties | 6063 | 3713 | 2484 |
| Reciprocal index | 0.34 | 0.35 | 0.35 |
| Transitive index | 0.18 | 0.19 | 0.20 |
| Jaccard index | 0.22a | 0.21b | |
| Limited nominations (%) | 0 | 4.82 | 0.41 |
| Drinking level (past year, %) | |||
| Sunshine High | |||
| 0 = never | 44.03 | 51.56 | 53.76 |
| 1 = 1 or 2 days | 26.54 | 19.19 | 14.83 |
| 2 = once a month or less (3–12 times in the past 12 months) | 8.59 | 12.35 | 11.11 |
| 3 = 2 or 3 days a month | 6.66 | 6.06 | 6.80 |
| 4 = more than 1 or 2 days a week | 14.19 | 10.84 | 13.50 |
| Jefferson High | |||
| 0 = never | 30.53 | 34.32 | 37.60 |
| 1 = 1 or 2 days | 23.46 | 19.77 | 13.73 |
| 2 = once a month or less (3–12 times in the past 12 months) | 12.70 | 18.55 | 15.98 |
| 3 = 2 or 3 days a month | 13.63 | 14.34 | 14.04 |
| 4 = more than 1 or 2 days a week | 19.67 | 13.01 | 18.65 |
The reciprocity index is the proportion of ties that were reciprocal. The transitivity index, which captures the tendency for individuals to experience triadic closure, is the proportion of two paths (ties between AB and BC) that were transitive (ties between AB, BC, and AC). The Jaccard index measures the network stability between consecutive waves. The number of vertices is a constant in the Stochastic Actor-Based (SAB) Model for each school (i.e., 2178 in Sunshine High and 976 in Jefferson High). There were 118 and 30 students left Sunshine High and Jefferson High at wave 2 due to graduation, moving, dropping out, and other reasons. The number of students left at wave 3 is 524 for Sunshine High and 150 for Jefferson High. In SAB Models, the leavers are specified as structural zeroes, which means they had no ties to any other students and their drinking behavior at certain wave had no values
waves 1 & 2
waves 2 & 3
Alcohol Use
At wave 1, the item assessing drinking was “During the past twelve months, how often did you drink beer, wine, or liquor?” At waves 2 and 3, the question was “During the past 12 months, on how many days did you drink alcohol?” The respondent answers are recoded to specify nondrinkers (0 = never), casual drinkers (1 = 1 or 2 days per year), light drinkers (2 = once a month or less or 3–12 times in the past 12 months), medium drinkers (3 = 2 or 3 days a month), and heavy drinkers (4 = more than 1 or 2 days a week). As shown in the lower part of Table 1, the percentage of nondrinkers in Sunshine High were relatively constant over the study period, ranging from 44 to 53.8%; the same was true in Jefferson High as it ranged from 30.5 to 37.6%. On average, alcohol use was more prevalent in Jefferson High than in Sunshine High.
The summary statistics of covariates are reported in Table S1 in supplemental materials.
Analytic Methods
The two school-based networks are analyzed with SAB Models (Snijders et al. 2010; Snijders 2011) implemented in the RSiena software package (Ripley et al. 2016). Although the networks and drinking behavior were observed at three discrete time points several months apart, changes in the networks and behavior are considered to be a continuous-time Markov chain. The SAB modeling strategy simultaneously estimates how drinking behavior impacts the evolution of the friendship networks (i.e., peer selection effect) and how the friendship networks impact future drinking behavior (i.e., peer influence effect) in micro steps. The model produces two equations: one in which the outcome variable is the choice of forming or dissolving a tie to another adolescent in the school, and the second in which the outcome is the decision to either increase, stay the same, or decrease one’s level of drinking. The SAB Model assumes that a respondent makes decisions that approximately and myopically optimize his or her desired state—or, objective function1—based on network or alcohol use behavior status. Model parameters are obtained using Methods of Moments (MoM) estimation (Snijders et al. 2010; Snijders 2011).
Network Equation Specification
As shown in Table S2 in supplemental materials, in the network equation predicting friendship tie selection, we include several network structural effects. These are out-degree density and reciprocity to capture tie preference, transitive triplets and three cycles to measure triadic closure, and in-degree popularity and in-in degree assortativity (square root) to differentiate the tendency towards preferential attachment (de Solla Price, 1976; Barabási and Albert 1999) vs. degree assortativity (Newman 2002). The network model also controls effects that might capture homophily along key dimensions (i.e., grade and parental education). Finally, the network model also includes the individual alcohol use which may affect network evolution in three ways: as a main effect on alter attractiveness (drinking alter), as a main effect on network activity of ego (drinking ego), and as a peer selection effect (drinking similarity).
Behavior Equation Specification
The effects included in the drinking behavior equation are shown in Table S3 in supplemental materials. The linear and quadratic shape parameters model the long-term trend in drinking behavior. The peer influence is the focal parameter capturing the tendency for adolescents to change their alcohol use levels to match that of their friends.2 Additional covariates (vi, i.e., gender, depressive symptoms, parental support, parental monitoring, and parental home drinking environment) are controlled to capture drinking behavior changes.
Forward Simulations
The forward simulations consist of setting the peer selection and influence parameters to various values and simulating the model forward over the same time period while leaving the other parameters in the model fixed to the values from the model estimation (Schaefer et al. 2013; Lakon et al. 2015). This allows us to compare the actual network at the final time point with these hypothetical simulated networks. To tune down the peer selection effects, we hold the peer influence and other parameters to the value in the estimated model and manipulated the peer selection parameter for three different scenarios: (1) zero (i.e., selection based on drinking behavior is not present), (2) one half the actual estimated value (i.e., a situation of minimal selection), and (3) the actual value in the observed network. We also set the peer selection parameter to eight larger values to simulate very strong selection effects: 50, 100, 150, 200, 250, 300, 350, and 400% larger than the observed network. We additionally set the peer selection parameter to four negative values: −50, −100, −150, and −200% of the levels in the observed network. We experimentally manipulate the size of the peer selection parameter over a wide range of values to assess how the network behaves at extreme peer selection effects; this allows assessing any possible threshold effects or nonlinearities. In another set of tests, we set the peer influence parameter to the same 15 relative values compared to its value in the observed network. We then manipulate the peer selection and influence parameters simultaneously to values of 0, the observed network estimated value, 100% larger than the estimated value, 200% larger, 300% larger, and 400% larger. This represents a full factorial design with 6 × 6 conditions.
In each scenario, the SAB Model is simulated forward from the first time point to the last, and the network and the drinking behavior of each adolescent are obtained at the end of each of 1000 simulation runs. For the 1000 simulations in each scenario for each school, the average is computed of (1) the percentage of students at each level of drinking behavior, (2) the percentage of drinkers, (3) the percentage who no longer drank, and (4) the percentage who began drinking. We also assess the degree of clustering in the simulated networks based on drinking behavior (network autocorrelation, see Doreian 1989; Steglich et al. 2010) by computing the global Moran’s I value (range from −1 to 1) in the network.
Results
Stochastic Actor-Based Models of Friendship Tie Choice and Drinking Behavior
The results for the SAB Models across the two schools are displayed in Table 2. In both schools, we find evidence of peer selection and influence effects for friendship tie choice and drinking behavior. The peer selection effect can be seen in the drinking similarity variable, which shows effects of .21 (s.e. = 15) and .18 (s.e. = .03) in the bigger and smaller schools, respectively. The peer influence effect can be seen in the drinking behavior peer influence variable, which shows positive effects of .38 (s.e. = .16) and .48 (s.e. = .07).3
Table 2.
Friendship tie choice and drinking behavior models
| Effect name | Sunshine High |
Jefferson High |
||
|---|---|---|---|---|
| Beta | S.E. | Beta | S.E. | |
| Friendship tie choice Constant friendship rate (period 1) |
23.40* | 6.73 | 24.08* | 1.29 |
| Constant friendship rate (period 2) | 9.57* | 0.46 | 15.26* | 0.73 |
| Out-degree (density) | −3.78* | 0.09 | −2.68* | 0.05 |
| Reciprocity | 2.80* | 0.19 | 2.53* | 0.13 |
| Transitive triplets | 0.77* | 0.12 | 0.55* | 0.03 |
| 3 cycles | −0.79* | 0.28 | −0.48* | 0.04 |
| In-degree—popularity | 0.05 | 0.03 | 0.05* | 0.02 |
| In-in degree^(1/2) assortativity | 0.00 | 0.08 | −0.06 | 0.04 |
| Parental education similarity | 0.07 | 0.07 | 0.04* | 0.01 |
| Grade similarity | 0.50* | 0.09 | 0.43* | 0.02 |
| Drinking alter | 0.09 | 0.30 | 0.06* | 0.02 |
| Drinking ego | 0.03 | 0.14 | 0.00 | 0.02 |
| Drinking similarity (peer selection) | 0.21 | 0.15 | 0.18* | 0.03 |
| Limited nomination ego | −0.52* | 0.23 | −0.71* | 0.06 |
| Drinking behavior Rate drinking behavior (period 1) |
15.60* | 1.95 | 9.92* | 0.80 |
| Rate drinking behavior (period 2) | 18.36* | 2.18 | 13.51* | 1.77 |
| Drinking behavior linear shape | −0.63* | 0.03 | −0.25* | 0.03 |
| Drinking behavior quadratic shape | 0.28* | 0.02 | 0.21* | 0.01 |
| Drinking behavior peer influence | 0.38* | 0.16 | 0.48* | 0.07 |
| In-degree | 0.01 | 0.05 | 0.01 | 0.01 |
| Gender (female = 1) | −0.09 | 0.15 | −0.09* | 0.03 |
| Depressive symptoms | 0.09* | 0.03 | 0.07 | 0.04 |
| Parental support | −0.10 | 0.36 | −0.08 | 0.05 |
| Parental monitoring | −0.25 | 0.27 | −0.41* | 0.12 |
| Home drinking environment | 0.07 | 0.04 | 0.07* | 0.02 |
Significance at P < 0.05 level
Results from Forward Simulations
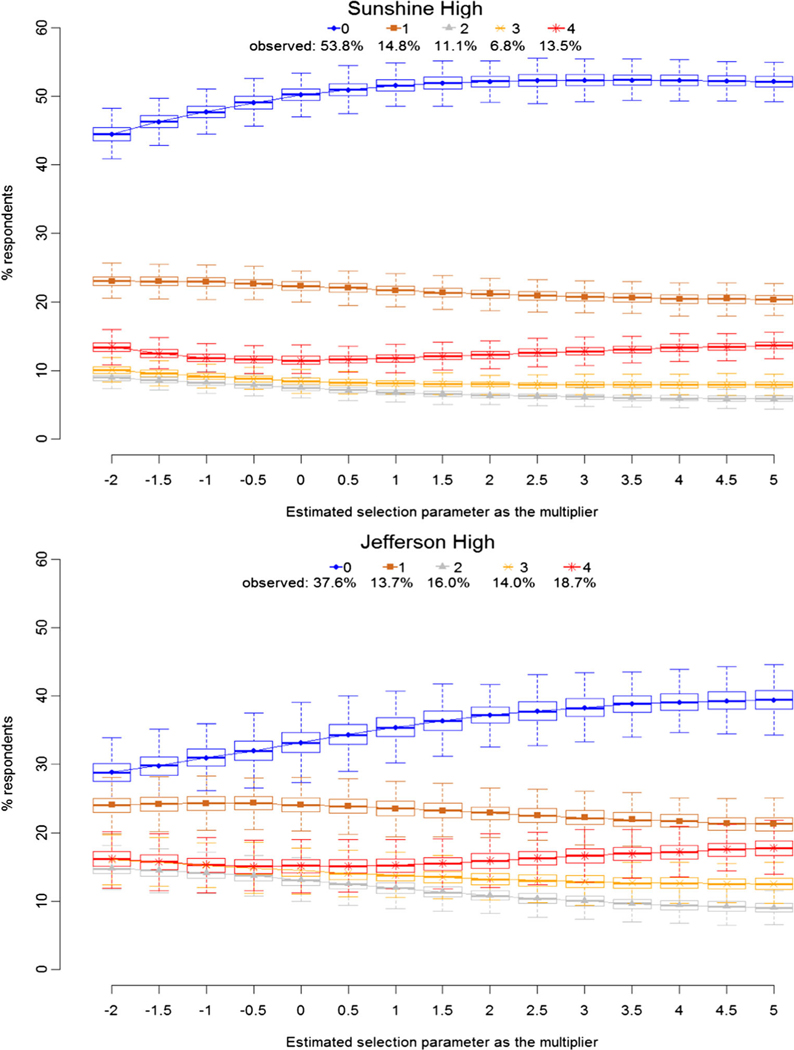
As expected, manipulating the size of the peer selection effect has minimal impact on the number of drinkers at either school. In Sunshine High, there is almost no change in the composition of those who drink at each level, as seen in Fig. 1, even when increasing the peer selection parameter to five times its size in the estimated model. For Sunshine High, the impact of increasing peer selection is quite modest for heavy drinkers, with just a 2 percentage point increase in those drinking more than 1 or 2 days/week in the scenario of very high peer selection effects. It is only in the unlikely scenario of negative selection—students actively seeking to form ties with other students having different drinking behaviors than their own—that we observe a modest drop in the fraction of nondrinkers. In Jefferson High, there is a minimal decrease in the number of nondrinkers when peer selection is not present, and even more when there is negative selection, as seen in the left side of the figure, as nondrinkers fall from 35% in the model with the peer selection parameter at its estimated values to 33% in the no peer selection model. Even after peer selection is increased to very high positive values, the composition of drinkers only changes modestly. In the case of very strong peer selection, the percentage of nondrinkers only increases 4 percentage points. The percentage of those drinking more than 1 or 2 days per week also increases slightly (2.5 percentage points) in the condition of very strong peer selection effects, suggesting a small amount of polarization in the network.
Fig. 1.
Altering selection parameters: percentage of respondents at each drinking level (0 = never; 1 = 1 or 2 days per year; 2 = once a month or less or 3–12 times in the past 12 months; 3 = 2 or 3 days a month; 4 = more than 1 or 2 days a week)
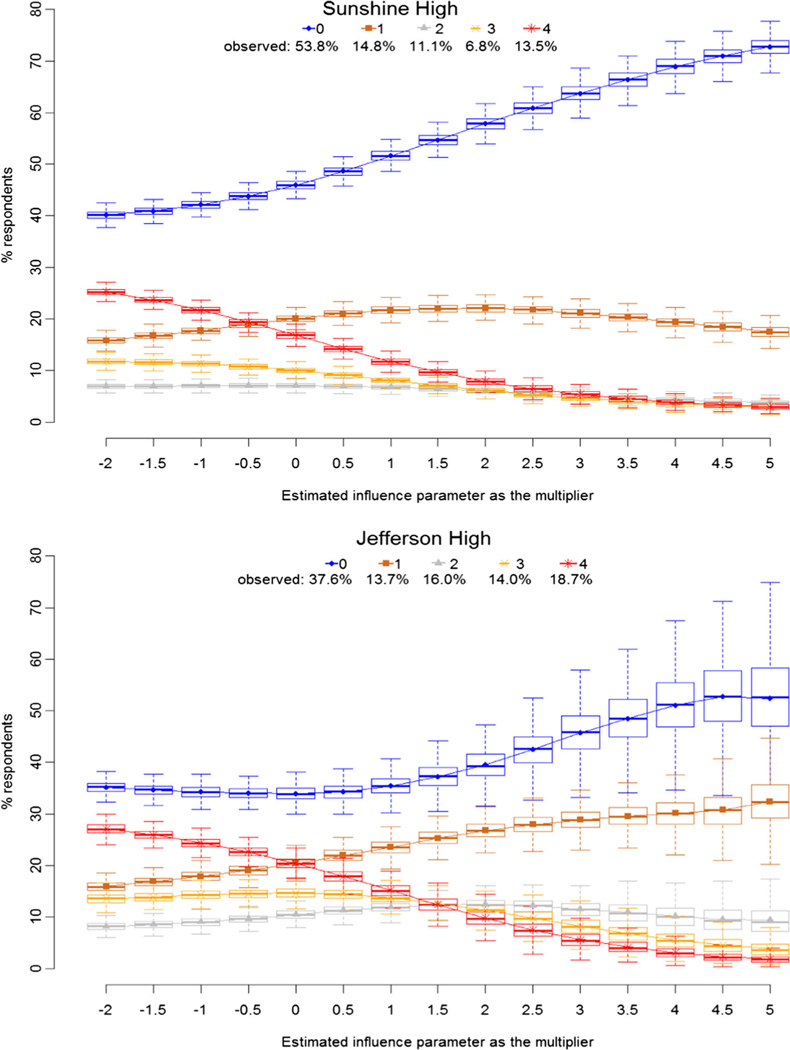
By contrast, manipulating the peer influence parameter more strongly impacts levels of drinking. Fig. 2 shows that increasing the peer influence effect actually has a strong protective effect on drinking behavior. When we simulate the network forward assuming no peer influence effect, the percentage of nondrinkers decreases 5.7 and 1.5 percentage points and the number of those drinking more than 1 or 2 days per week increases 5.1 and 5.2 percentage points in Sunshine High and Jefferson High, respectively, compared to the simulations with an influence effect set to the size observed in these samples. And, in simulations with negative influence, the percentage of heavy smokers increases even more. When we tune up the peer influence parameter to very high level, there are 21.1 and 16.9 percentage points more nondrinkers in Sunshine High and Jefferson High, respectively. There is a decrease in drinking at nearly all levels, especially for those drinking more than 1 or 2 days per week who decline 8.7 and 13.4 percentage points in this condition of very strong peer influence effects. In Jefferson High, the number of those drinking 1 or 2 days per year also increases 8.9 percentage points (along with the increase in non-drinkers) in an environment of very strong peer influence.
Fig. 2.
Altering influence parameters: percentage of respondents at each drinking level (0 = never; 1 = 1 or 2 days per year; 2 = once a month or less or 3–12 times in the past 12 months; 3 = 2 or 3 days a month; 4 = more than 1 or 2 days a week)
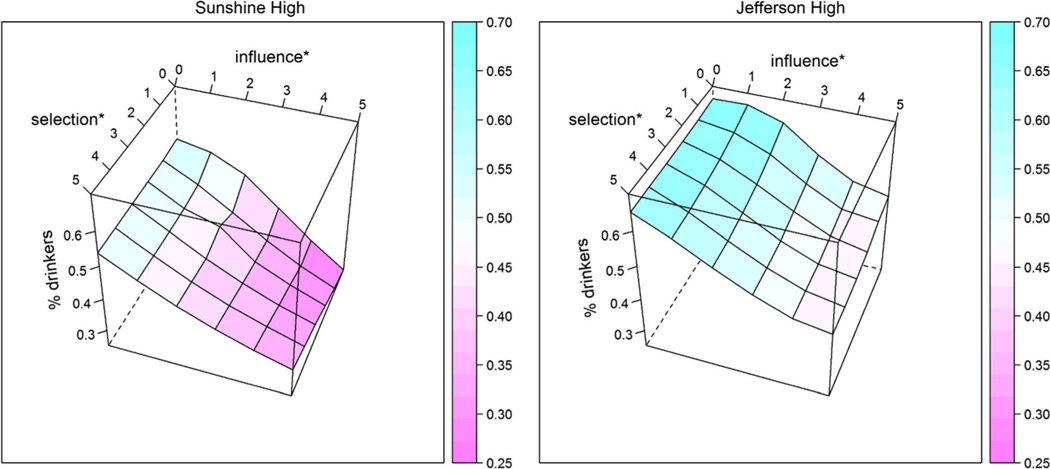
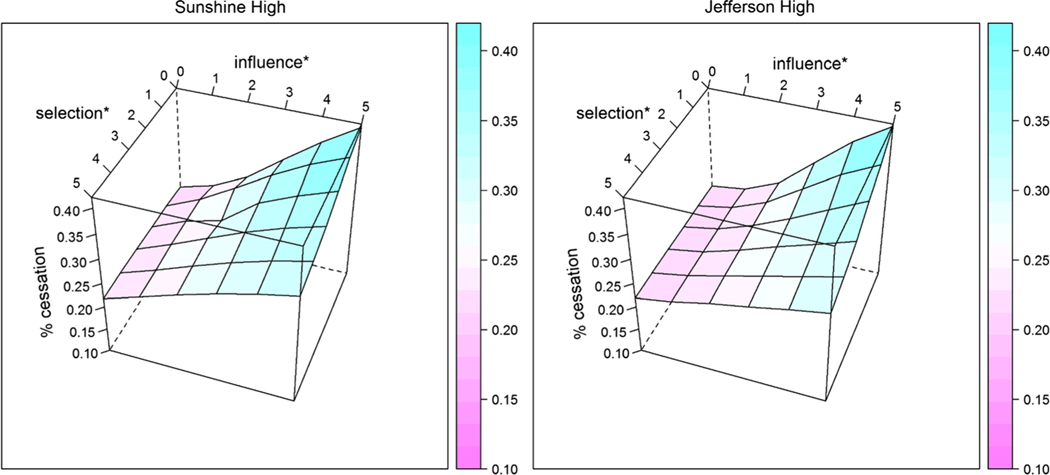
We next simultaneously manipulate the peer selection and influence parameters and assess the percentage of drinkers at the end of each simulation (regardless of the level of drinking). By simultaneously manipulating these parameters, we are capturing interaction effects in which both effects are changing: This form of “interaction” in nonlinear models is distinct from the common approach in linear models in which multiplicative variables are created and included in models to assess how a variable changes in response to the movement of two other variables. Nonetheless, we use the term interaction throughout this section as it is appropriate for nonlinear models. Fig. 3 demonstrates that for both schools, the effect of stronger peer influence overshadows the effect of stronger peer selection. The left axis (y-axis) shows various sizes of peer selection effect, whereas the back axis (x-axis) shows various sizes of peer influence effect. The vertical axis (z-axis) shows the average percentage of drinkers at the end of the simulations for each of the manipulations (the color coding also reflects the percentages, ranging from pink to green). When increasing the level of peer influence (moving from left to right), the percentage of drinkers at the end of the simulation runs consistently falls. For each parameter value of peer influence, the size of peer selection parameter has a modest effect. In Jefferson High, there is only modest evidence that higher peer selection parameter values impact the percentage of drinkers beyond the much stronger effect of peer influence.
Fig. 3.
Jointly manipulating selection and influence parameters: percentage of drinkers
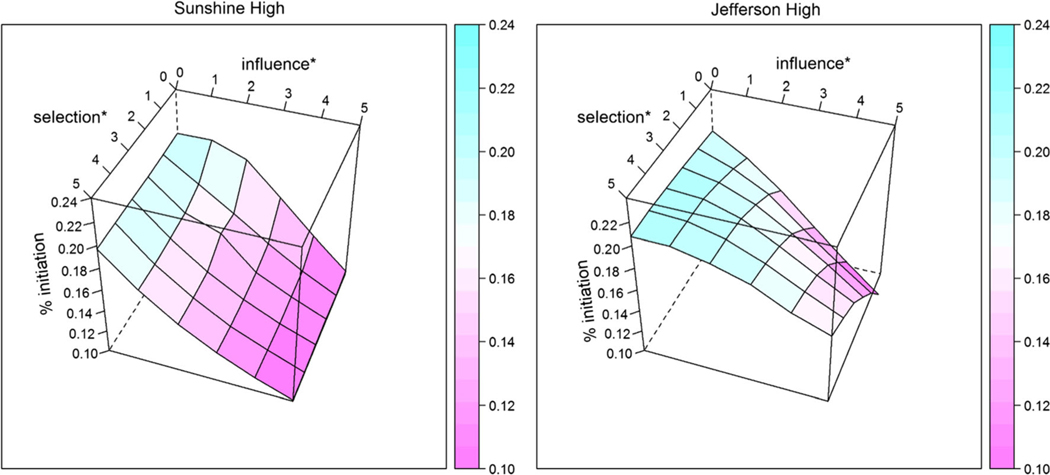
Regarding drinking initiation (Schaefer et al. 2013; Lakon et al. 2015), when the peer influence parameter is manipulated to larger values in Sunshine High with lower levels of drinking behavior overall (based on percent of students who drink at wave 1), the percentage of students that begin drinking steadily decreases, regardless of the size of peer selection parameter (Fig. 4). In Jefferson High, when there are relatively more drinkers available, we detect a modest synergistic effect: Stronger peer influence effects result in a smaller proportion of drinking initiators when accompanied by no peer selection effect. This can be understood as arising from the fact that fewer adolescents are influenced to initiate drinking when everyone frequently interacts with the (more prevalent) nondrinkers.
Fig. 4.
Jointly manipulating selection and influence parameters: new drinkers
For drinking cessation (Schaefer et al. 2013; Lakon et al. 2015), stronger peer influence effects in both schools monotonically increase the number of adolescents who stops drinking (Fig. 5). This positive effect is maximized in the presence of no peer selection effect: Thus, the greatest amount of drinking cessation occurs in a setting with very strong peer influence effect but no peer selection effect. As before, this can be explained by the effect of peer selection on the social interaction of drinking students with nondrinkers; no selection for behaviorally similar peers is needed to increase such mixing, and hence this effect.
Fig. 5.
Jointly manipulating selection and influence parameters: ceasing to drink
Finally, we assess the degree of clustering in the network based on drinking behavior and find that in scenarios with stronger peer selection, the degree of clustering of drinkers in the network increases: Whereas the Moran’s I values for the clustering by drinking behavior were .14 and .16 respectively in the two observed networks, they increase to .42 and .39 when we double the peer selection parameter and increase to .71 and .62 when increasing the peer selection parameter 400%. The changes in clustering are less pronounced when manipulating the peer influence parameter: increasing to .34 and .33 when doubling the peer influence parameter, but just .39 and .29 when increasing the parameter 400%. Therefore, higher levels of peer selection do not impact the overall level of drinking (defined as percent of students who drink), but do increase the similarity in drinking behavior within social groups.
Discussion
Our findings indicate that the consequences of varying peer influence and selection for adolescent drinking in many instances mirror findings of similar work on adolescent smoking (Lakon et al. 2015). However, we do see some differences relating to the nature of the substances involved and the social context of their use. In the current study, the drinking behavior quadratic shape function was not as strong as the same effect for smoking in the previous study, reflecting the relative strength of the drug reinforcing usage of each substance. Another difference is parental support being unrelated to drinking, whereas it was significantly and negatively related to smoking in Sunshine High in the previous study.
It is important to emphasize that we, like others, find a strong peer influence effect for drinking behaviors. As noted above, many studies find a positive relationship between peer influence and adolescent drinking behavior measured at the individual level (Pearson et al. 2006; Knecht et al. 2010; Burk et al. 2012; Giletta et al. 2012; Mercken et al. 2012; Mathys et al. 2013; Osgood et al. 2013; Wang et al. 2013, 2015), collectively establishing that (1) adolescents’ drinking behaviors positively correlate with those of their peers and (2) adolescents adopt the drinking behaviors of their peers. Whereas this prior work has been critical in establishing the existence of the influence mechanism in youth drinking at the individual level, our focus is on understanding the implications of peer influence and selection for overall prevalence, initiation, and cessation of drinking behavior in school network systems. While influence can either increase or decrease drinking (depending upon context), our simulation study demonstrates that stronger peer influence actually reduces overall levels of drinking among the youth in these schools.
Our simulations indicate that increasing the strength of peer influence, when holding constant selection at its observed level, results in fewer adolescents drinking relative to the observed prevalence level, less drinking initiation, and more youth ceasing to drink in both schools. And, reducing peer influence to zero in these networks results in more drinkers than were seen at the observed (positive) level of peer influence. These findings suggest that peer influence will act to reduce drinking prevalence. We interpret this systemic effect as arising from the fact that drinking in these schools is relatively rare, making the overall social impact of nondrinkers on drinkers stronger than the impact of drinkers on nondrinkers. In schools for which drinking is the norm, we would expect the reverse to hold.
Our findings also suggest that peer selection (and its interaction with influence) may vary in effect on different processes with baseline drinking prevalence. In the present study, we observe that peer selection effect on drinking initiation is minimal in a school-based network with a relatively low level of drinking behavior (as in Sunshine High) and modest in the network with more drinking overall (i.e., Jefferson High). For drinking cessation, we find a strong synergistic effect between peer selection and influence in both schools: In the condition of no selection effect, drinkers sometimes select nondrinkers as friends (through this random process) and then are subject to their influence and induced to reduce their drinking behavior. This synergistic effect between peer selection and influence is complex and may depend on other features of these schools, and a larger simulation study varying more background conditions would help further explore how the selection and influence mechanisms might play out in different types of schools. One step in this direction has been taken by Adams and Schaefer (2016), who performed a simulation study to examine how network effects can play out across schools with different levels of smoking behavior. Given our findings regarding the similarities between influence and selection on drinking versus smoking in the two schools examined here, it would be profitable to see if other effects similarly translate from one substance use case to another.
It is notable that parental support is unrelated to drinking, while it was negatively related to smoking in Sunshine High in a previous study (Lakon et al. 2015). It is possible that parent-adolescent communication about cigarette smoking and alcohol use differs, especially if the parent uses one or both of these substances. And, if a parent uses one or both of these substances, this may result in their adolescent child being more likely to use these substances as well (Kandel and Andrews 1987; Jackson et al. 1998).
That peer influence could bring about decreases in alcohol use among an adolescent school-based population suggests potential implications for prevention efforts. Interventions might consider the strategy of enhancing peer influence among the target youth population, using the overall level of alcohol use in a school as a guide. Past studies (Valente et al. 2007; Dishion et al. 1999) have examined amplifying peer influence in naturally existing youth peer networks. While we are not aware of literature that can inform how to directly translate our simulation findings into peer influence interventions, our study provides insight into the consequences of altering peer influence and selection both for the networks and drinking behavior.
Overall, our findings indicate that the social dynamics under study for drinking are similar to those found in previous simulation work on smoking (Lakon et al. 2015). We observe notable similarities in the net impact of peer influence and selection on alcohol versus smoking, suggesting that interventions targeting one substance might also be effective for the other, providing a key insight for interventions targeting both substance use behaviors.
Limitations
Our study has a number of limitations. The SAB Models attempt to detect the continuous time evolution of the network from data collected at three irregularly spaced time points. Our model appears to satisfactorily capture the network and behavior processes in simulation assessments, but caution should nonetheless be exercised. The fact that the survey collects alcohol use behavior in two different settings (in school versus in home) is not ideal. The shape parameters included in the model capture the overall level of drinking and thus to some extent account for possible differences due to elicitation context, but caution is still warranted. We only study two schools, and thus there is uncertainty how generalizable these results will be to other schools. Future data collection efforts are needed to explore this more carefully. Likewise, future simulation research over a set of simulated networks with a range of drinking levels would provide more information on the relationship between the level of drinking in the school and these patterns, analogous to recent research exploring such patterns for smoking behavior (Adams and Schaefer 2016). It would also be useful to have measures of binge drinking (not available in our data set), which would allow us to determine whether it follows similar dynamics to those seen here. Another data-based limitation is that our data do not allow us to distinguish whether the size of the influence parameter differs for drinking uptake versus cessation. Given that adolescent drinking may be relatively more episodic than smoking, we suspect that there is less theoretical reason to expect that drinking uptake and quitting will exhibit very notable differences in parameter values. Nonetheless, this would be a useful direction for future research, which could be pursued given an empirical study with fine-grained time-resolved data on alcohol use. Such data would also be useful for assessing the validity of the dynamic assumptions made by the SAB Models more generally.
Conclusions
Our manipulations and subsequent forward simulations using a SAB modeling strategy have explored the effects of varying peer selection and influence and their consequences for adolescent networks and drinking behavior. This simulation strategy is a cost-effective way to assess a priori what is expected to occur if an intervention brings about a change in the level of peer influence or selection in a network. Whether an intervention can actually achieve such levels of change in the networks is a separate question; nonetheless, this strategy highlights ways that successful interventions may, or may not, substantially change the level of drinking in the network. The forward simulations herein indicate that whereas peer selection is important for bringing about more similarity in the drinking behavior among adolescents, there is little evidence that it results in higher levels of overall drinking in the adolescent population. On the other hand, we find that stronger peer influence effects actually lead to lower levels of overall drinking among adolescents in these schools. Finally, it is the combination of stronger peer influence and no selection effects that leads to more drinking cessation.
Supplementary Material
Funding
This study is funded by Grant no. 1 R21 DA031152-01A1 from National Institute on Drug Abuse (NIDA) Health.
Footnotes
Conflict of Interest The authors declare that they have no conflict of interest.
Ethical Approval All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards. This study was reviewed and granted approval under exempt review by the institutional review board at the University of California, Irvine, on April 12, 2013.
Compliance with Ethical Standards
Informed Consent The secondary data used in this study come from early waves of The National Longitudinal Study of Adolescent to Adult Health (Add Health). Add Health participants provided written informed consent for participation in all aspects of Add Health in accordance with the University of North Carolina School of Public Health Institutional Review Board guidelines that are based on the Code of Federal Regulations on the Protection of Human Subjects 45CFR46: http://www.hhs.gov/ohrp/humansubjects/guidance/45cfr46.html. Written informed consent was given by participants (or next of kin/caregiver) for their answers to be used in this study.
Electronic supplementary material The online version of this article (doi:10.1007/s11121-017-0773-5) contains supplementary material, which is available to authorized users.
The objective function is defined as , where is the log odds multiplier for the kth term in the function of network/behavior and x is the current network/behavioral state. A positive parameter in the objective function implies that the actor prefers options that increase the associated s value, while a negative parameter value implies the avoidance of such changes.
There are three possibilities for changes in adolescent drinking levels—increasing one unit (+1), maintaining the same level (0), or decreasing one unit (−1). In this study, we assume that the utility changes of initiating alcohol use (i.e., 0 vs. +1) and quitting alcohol use (i.e., 0 vs. −1) are the same and thus the peer influence effect in our models is symmetric. In ancillary analyses, we try to decompose the uptake and suppression processes by including separate initiation and quitting effects in the same model. However, model estimation difficulties emerge with unrealistically large parameter estimates and standard errors for the initiation and quitting effects (e.g., >1000). Examining the correlations among the parameter estimates suggests collinearity issues that make it impossible in practice to separate the two effects. Thus, it is not empirically feasible to decompose the suppression and initiation processes in the same model.
The goodness-of-fit for the model is assessed for each school by forward simulation of the model from wave 1 to wave 3 based on the estimated parameters 1000 times and comparing the resulting predicted networks with the actual observed data (see Fig. S1 and Fig. S2 in supplemental materials). Given that the observed network values fall within the range of predicted networks for the distribution of in-degree, out-degree, geodesic distances, and the triadic census, the model does a good job reproducing the network for each school (Lospinoso and Snijders 2011). Furthermore, the number of persons at each level of drinking at each time point in the observed network falls within the range of the simulated networks, and the number of transitions of drinking behavior (i.e., the number of persons beginning drinking and stopping drinking) falls within the range of the predicted networks.
References
- Adams J, & Schaefer DR (2016). How initial prevalence moderates network-based smoking change: Estimating contextual effects with stochastic actor oriented models. Journal of Health and Social Behavior, 57, 22–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailey SL (1992). Adolescents’ multisubstance use patterns: The role of heavy alcohol and cigarette use. American Journal of Public Health, 82, 1220–1224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barabási AL, & Albert R. (1999). Emergence of scaling in random networks. Science, 286, 509–512. [DOI] [PubMed] [Google Scholar]
- Bearman PS, Moody J, & Stovel K. (2004). Chains of affection: The structure of adolescent romantic and sexual networks. American Journal of Sociology, 110, 44–91. [Google Scholar]
- Burk WJ, van der Vorst H, Kerr M, & Sattin H. (2012). Alcohol intoxication frequency and friendship dynamics: Selection and socialization in early, mid- and late adolescent peer networks. Journal of Studies on Alcohol & Drugs, 73, 89–98. [DOI] [PubMed] [Google Scholar]
- Christakis NA, & Fowler JH (2007). The spread of obesity in a large social network over 32 years. The New England Journal of Medicine, 357, 370–379. [DOI] [PubMed] [Google Scholar]
- Christakis NA, & Fowler JH (2008). The collective dynamics of smoking in a large social network. The New England Journal of Medicine, 358, 2249–2258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Solla Price DJ (1976). A general theory of bibliometric and other cumulative advantage processes. Journal of the American Society for Information Science, 27, 292–306. [Google Scholar]
- Dee TS (1999). The complementarity of teen smoking and drinking. Journal of Health Economics, 18, 769–793. [DOI] [PubMed] [Google Scholar]
- Dishion TJ, McCord J, & Poulin F. (1999). When interventions harm: Peer groups and problem behavior. American Psychologist, 54, 755–764. [DOI] [PubMed] [Google Scholar]
- Doreian P. (1989). Network autocorrelation models: Problems and prospects. In Griffith DA(Ed.), Spatial statistics: Past, present, future (pp. 369–389). Ann Arbor, MI: Michigan Document Services. [Google Scholar]
- Ellickson PL, & Hays RD (1991). Antecedents of drinking among young adolescents with different alcohol use histories. Journal of Studies on Alcohol, 52, 398–408. [DOI] [PubMed] [Google Scholar]
- Ennett ST, Bauman KE, Hussong A, Faris R, Foshee VA, Cai L, & DuRant RH (2006). The peer context of adolescent substance use: Findings from social network analysis. Journal of Research on Adolescence, 16, 159–186. [Google Scholar]
- Fowler JH, & Christakis NA (2008). The dynamic spread of happiness in a large social network: Longitudinal analysis over 20 years in the Framingham heart study. British Medical Journal, 337, a2338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giletta M, Scholte RH, Prinstein MJ, Engels RC, Rabaglietti E, & Burk WJ (2012). Friendship context matters: Examining the domain specificity of alcohol and depression socialization among adolescents. Journal of Abnormal Child Psychology, 40, 1027–1043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris KM, Halpern CT, Whitsel E, Hussey J, Tabor J, Entzel P, & Udry JR (2009). The national longitudinal study of adolescent health: Research design. Retrieved from http://www.cpc.unc.edu/projects/AddHealth/design.
- Hipp JR, Wang C, Butts CT, Jose R, & Lakon CM (2015). Research note: The consequences of different methods for handling missing network data in stochastic actor based models. Social Networks, 41, 56–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson J, Henriksen L, & Foshee VA (1998). The authoritative parenting index: Predicting health risk behaviors among children and adolescents. Health Education & Behavior, 25, 319–337. [DOI] [PubMed] [Google Scholar]
- Kandel DB, & Andrews K. (1987). Processes of adolescent socialization by parents and peers. International Journal of the Addictions, 22, 319–342. [DOI] [PubMed] [Google Scholar]
- Kandel DB, & Logan JA (1984). Patterns of drug use from adolescence to young adulthood: Periods of risk for initiation, continued use, and discontinuation. American Journal of Public Health, 74, 660–666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knecht AB, Burk WJ, Weesie J, & Steglich CEG (2010). Friendship and alcohol use in early adolescence: A multilevel social network approach. Journal of Research on Adolescence, 21, 475–487. [Google Scholar]
- Lakon CM, Hipp JR, Wang C, Butts CT, & Jose R. (2015). Simulating dynamic network models and adolescent smoking: The impact of varying peer influence and peer selection. American Journal of Public Health, 105, 2438–2448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakon CM, Wang C, Butts CT, Jose R, Timberlake DS, & Hipp JR (2014). A dynamic model of adolescent friendship networks, parental influences, and smoking. Journal of Youth and Adolescence, 44, 1767–1786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lospinoso JA, & Snijders TAB (2011). Goodness of Fit for Social Network Dynamics. Presentation at the Sunbelt XXXI, St. Pete’s Beach, FL, 2011. Retrieved from http://www.stats.ox.ac.uk/~lospinos/pubs/GOFPresentation.pdf. [Google Scholar]
- Mathys C, Burk WJ, & Cillessen AHN (2013). Popularity as moderator of peer selection and socialization of adolescent alcohol, marijuana, and tobacco use. Journal of Research on Adolescence, 23, 513–523. [Google Scholar]
- Mercken L, Candel M, Willems P, & De Vries H. (2007). Disentangling social selection and social influence effects on adolescent smoking: The importance of reciprocity in friendships. Addiction, 102, 1483–1492. [DOI] [PubMed] [Google Scholar]
- Mercken L, Steglich CEG, Knibbe R, & Vries HD (2012). Dynamics of friendship networks and alcohol use in early and mid-adolescence. Journal of Studies on Alcohol & Drugs, 73, 99–110. [DOI] [PubMed] [Google Scholar]
- Newman MEJ (2002). Assortative mixing in networks. Physical Review Letters, 89, 208701. [DOI] [PubMed] [Google Scholar]
- Orlando M, Tucker JS, Ellickson PL, & Klein DJ (2005). Concurrent use of alcohol and cigarettes from adolescence to young adulthood: An examination of developmental trajectories and outcomes. Substance Use & Misuse, 40, 1051–1069. [DOI] [PubMed] [Google Scholar]
- Osgood DW, Ragan DT, Wallace L, Gest SD, Feinberg ME, & Moody J. (2013). Peers and the emergence of alcohol use: Influence and selection processes in adolescent friendship networks. Journal of Research on Adolescence, 23, 500–512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearson M, Steglich CEG, & Snijders TAB (2006). Homophily and assimilation among sport-active adolescent substance users. Connect, 27, 47–63. [Google Scholar]
- Ripley RM, Snijders TAB, Boda Z, Vörös A, & Preciado P. (2016). Manual for SIENA version 4.0 (version December 16, 2016). Oxford: University of Oxford, Department of Statistics, Nuffield College. Retrieved from http://www.stats.ox.ac.uk/~snijders/siena/RSiena_Manual.pdf. [Google Scholar]
- Schaefer DR, Adams J, & Haas SA (2013). Social networks and smoking: Exploring the effects of peer influence and smoker popularity through simulations. Health Education & Behavior, 40, 24S–32S. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shoham DA, Tong L, Lamberson PJ, Auchincloss AH, Zhang J, Dugas L, Kaufman JS, Cooper RS, & Luke A. (2012). An actor-based model of social network influence on adolescent body size, screen time, and playing sports. PloS One, 7, e39795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snijders TAB (2011). Network dynamics. In Scott J. & Carrington PJ(Eds.), The SAGE handbook of social network analysis (pp. 501–513). Thousand Oaks, CA: Sage. [Google Scholar]
- Snijders TAB, van de Bunt GG, & Steglich CEG (2010). Introduction to stochastic actor-based models for network dynamics. Social Networks, 32, 44–60. [Google Scholar]
- Steglich CEG, Snijders TAB, & Pearson M. (2010). Dynamic networks and behavior: Separating selection from influence. Sociological Methodology, 40, 329–393. [Google Scholar]
- Urberg KA, Degirmencioglu SM, & Pilgram C. (1997). Close friend and group influence on adolescent cigarette smoking and alcohol use. Developmental Psychology, 33, 834–844. [DOI] [PubMed] [Google Scholar]
- Valente TW, Ritt-Olson A, Stacy A, Unger JB, Okamoto J, & Sussman S. (2007). Peer acceleration: Effects of a social network tailored substance abuse prevention program among high-risk adolescents. Addiction, 102, 1804–1815. [DOI] [PubMed] [Google Scholar]
- Wang C, Butts CT, Hipp JR, Jose R, & Lakon CM (2016a). Multiple imputation for missing edge data: A predictive evaluation method with application to add health. Social Networks, 45, 89–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C, Hachen DS,& Lizardo O. (2013). The co-evolution of communication networks and drinking behaviors. AAAI Fall Symposium Series 2013, Social Networks & Social Contagion, 30–36. [Google Scholar]
- Wang C, Hipp JR, Butts CT, Jose R, & Lakon CM (2015). Alcohol use among adolescent youth: The role of friendship networks and family factors in a multi-school study. PloS One, 10, e0119965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C, Hipp JR, Butts CT, Jose R, & Lakon CM (2016b). Coevolution of adolescent friendship networks and smoking and drinking behaviors with consideration of parental influence. Psychology of Addictive Behaviors, 30, 312–324. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.