Cyclodextrins: Establishing building blocks for AI-driven drug design by determining affinity constants in silico

Abstract

Cyclodextrins (CDs) are cyclic carbohydrate polymers that hold significant promise for drug delivery and industrial applications. Their effectiveness depends on their ability to encapsulate target molecules with strong affinity and specificity, but quantifying affinities in these systems accurately is challenging for a variety of reasons. Computational methods represent an exceptional complement to in vitro assays because they can be employed for existing and hypothetical molecules, providing high resolution structures in addition to a mechanistic, dynamic, kinetic, and thermodynamic characterization. Here, we employ potential of mean force (PMF) calculations obtained from guided metadynamics simulations to characterize the 1:1 inclusion complexes between four different modified βCDs, with different type, number, and location of substitutions, and two sterol molecules (cholesterol and 7-ketocholesterol). Our methods, validated for reproducibility through four independent repeated simulations per system and different post processing techniques, offer new insights into the formation and stability of CD-sterol inclusion complexes. A systematic distinct orientation preference where the sterol tail projects from the CD's larger face and significant impacts of CD substitutions on binding are observed. Notably, sampling only the CD cavity's wide face during simulations yielded comparable binding energies to full-cavity sampling, but in less time and with reduced statistical uncertainty, suggesting a more efficient approach. Bridging computational methods with complex molecular interactions, our research enables predictive CD designs for diverse applications. Moreover, the high reproducibility, sensitivity, and cost-effectiveness of the studied methods pave the way for extensive studies of massive CD-ligand combinations, enabling AI algorithm training and automated molecular design.

Graphical Abstract

1. Introduction

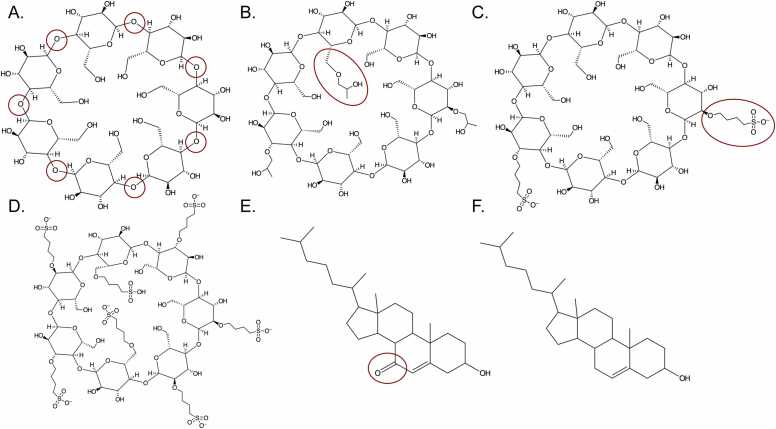
Cyclodextrins (CDs) are cyclic oligosaccharides, usually formed from 6, 7, or 8 glucose units denoted as αCD, βCD, and γCD, respectively. With hydrophilic exteriors and hydrophobic interiors, CDs can encapsulate hydrophobic molecules in soluble inclusion complexes [1], [2], [3]. They can be chemically modified by substituting the hydroxyls with other functional groups, such as methyl, hydroxypropyl (HP), or sulfobutyl (SB). These modifications lead to distributions of structures with different numbers and locations of the substitutions which can improve the solubility of the CD and alter their properties in various ways [1], [4], [5], [6]. The average number of functional groups in the distribution of chemically modified CDs is denoted as the degree of substitution/saturation (DS). These modifications can also modulate the selectivity for the encapsulation of certain molecules as well as their release rate [7], [8], [9], thus opening an opportunity to develop ad hoc applications. In pharmaceuticals, CDs are typically employed to enhance the solubility and stability of drugs, improving delivery and bioavailability [2], [10], [11], [12]. Their applications extend to chemical reactions, environmental uses, food additives, and more [1], [13], [14], [15], [16], [17], [18]. Ongoing research explores novel applications such as for the treatment of atherosclerosis or removal of PFAS (a group of ‘forever’ chemicals linked to health problems) from water [19], [20], showcasing their versatile potential. CD rings with 7 glucopyranoside units, βCDs, are widely used in industrial and drug delivery settings since their cavity is able to effectively host an interesting variety of molecules. In particular, it is known that these medium-sized CDs form water soluble inclusion complexes with sterol molecules, which are related to a variety of health problems [11], [19], [21], [22], [23], [24], [25], [26], [27]. However, actually measuring the affinity constants between CDs and sterols is difficult and unreliable due to solubility problems, stoichiometric considerations, and the presence of a distribution of CD structures in the case of substituted CDs. Therefore, experimental affinity constants are often reported as “apparent” affinity constants, and there is no accepted experimental value for many of these systems, particularly when the guest is poorly soluble, as cholesterol is [19], [28], [29], [30]. Here, we aim to establish an effective and efficient tool for obtaining reliable affinity constants for individual CD inclusion complexes using in silico methods. If this tool was validated, it could enable the automated production of association constants for many CD inclusion complexes. This would open the door for ML training on a system for which we have very little practical control over in vitro, but very precise control over in silico. Such a tool could revolutionize our understanding of CD inclusion complexation.

The development and optimization of applications based on CDs depend on their ability to encapsulate molecules into their hydrophobic cavity. For certain uses, such as the extraction of harmful or undesirable molecules from organisms or from the environment, a high affinity constant and a very low release rate are required to achieve high specificity. A notable example is the use of the engineered sugammadex to capture the neuromuscular blocker rocuronium [31], [32]. In contrast, employing CDs as excipients necessitates a substantial, though comparatively lower, affinity constant, along with lower specificity and a more flexible release rate. This distinction is critical; using a CD with a very high affinity for an active compound can impede its intended function by preventing its release. Therefore, the accurate quantification of CD-target complexation affinity constants and specificity to distinguish targets/off-targets is key for designing and optimizing CD-based applications.

Historically, this has been achieved through a rational approach, assisted by trial-and-error assays. However, AI algorithms represent a family of promising alternative methods for the same aim; the bottleneck of this approach is the availability of a large volume of high-quality data to effectively train models. Acquiring such data for CD systems is challenging due to several factors, including solubility issues of the compounds involved, the potential presence of impurities, and notably, the diversity in the number and location of substitutions in modified CDs, not to mention the difficulties in correctly analyzing measurements from different sources. Recently, a publicly accessible database that compiles affinity constants for the formation of inclusion complexes between relatively small molecules and CDs, gathered from existing literature, has been published [33]. This information has been obtained from different experimental methods published between the years 1963 and 2021 and includes mainly isothermal titration calorimetry (ITC) and various spectroscopic techniques. This publication represents an extraordinary effort to collect affinity data between CDs and ligands, but the sources are highly heterogeneous and difficult to control, reproduce, or scale. Important uncertainties are also present due to the different sources of the samples, experiments, and analysis methods, complicating analysis. Additionally, the employed techniques face challenges both in conducting effective experiments and in analyzing results. This is because complex protocols are often necessary, including competitive experiments with a reference compound, chemical labeling of molecules, or manipulating the solvent.

It is important to keep in mind the fact that none of these methods actually measure affinity constants directly - instead, they rely on the application of thermodynamic models coupled with numerical and statistical calculations. Best practices involve the global fitting of multiple data sets across different concentration ranges, and the employment of advanced mathematical methods, along with estimating reasonable uncertainty values for numerical parameters. The results typically yield apparent values or approaches useful for specific applications within a limited context, rather than direct thermodynamic affinities. Thus, truly direct laboratory measurements of affinity constants remain an unattainable ideal as of yet, but reasonable estimations are possible in many cases by applying robust multidimensional models to multiple experiments [34]. In this context, massive production of many thousand in vitro systems that include a large variety of CDs with specific types, numbers, and locations of substitutions, along with diverse ligands for the purpose of training AI-based algorithms, presents significant challenges in terms of complexity and cost.

The use of computational modeling represents an exceptional and increasingly realistic complement to in vitro assays for characterizing the interaction between molecules - particularly between CDs and small molecules that can potentially be encapsulated in their cavity. These methods can provide important insights into the mechanism of interaction between molecules, saving money, time, and resources by predicting how a molecule might act before synthesizing and/or testing it [35]. Additionally, they can be fully automated and connected to a database which would be fed with the results. The information contained in such a database would be highly uniform and it would be very easy to scale the production to reach many thousand complexes. The database would enable precise control of the CD structures, including the type, number, and location of substitutions, and cover a variety of targets, considering the ionic state of the molecules, the presence of cosolvents, or any other environmental factor. These data could then be easily utilized to train AI algorithms. Employing such a workflow could significantly enhance the design and optimization of CDs for specific applications. The bottleneck to developing a platform based on this computational workflow is, again, just as with in vitro, the availability of accurate and efficient methods to determine the affinity constant of the encapsulation event. Different computational approaches are widely employed for characterizing protein-ligand interactions in both academic research and practical applications, but their use in the characterization of CD systems is quite limited. A reason for this is the lack of specific software available to automatically perform these studies, since the strategies typically employed to build, execute, and analyze simulations of protein systems differ significantly from those that are more suitable for CDs [36], [37], [38], [39], [40]. To take advantage of computational simulations, careful parameterization of the involved molecules, efficient sampling algorithms, and well-designed analysis methods able to provide as much information as possible, are always required. Specifically, while CDs are often depicted as rigid, truncated cone structures, they are actually quite flexible both in solution and in solid form. Capturing this behavior is crucial for accurately describing interactions in computational studies of CD systems [41], [42].

A large variety of computational methods able to provide useful information on inclusion complexes is available. Unbiased molecular dynamics simulations (MD) follow the dynamic behavior of an initial conformation of the studied system. This technique is useful to explore the vicinity of the local minima, but the sampling out of this region is not guaranteed. A number of biased methods have been developed to overcome this limitation, also aiming to determine the free energy profile or Potential of Mean Force (PMF). The PMF is a function of a reduced number of collective variables (CVs) able to describe the process of interest, in this case, the formation of inclusion complexes. From PMF profiles it is possible to obtain the most stable structure of the complex, as well as the standard Gibbs energy (ΔG⁰) corresponding to its formation. Examining PMF functions reveals the energy barriers and wells that contribute to the interaction mechanism. Metadynamics is a biased molecular dynamics method that allows for the incorporation of specific forces into the system, making it possible to observe events that are typically highly improbable; the likeliness of those events can then be rationalized using PMF, based on the amount of energy necessary for the events to occur in the simulation [43], [44]. Metadynamics has already been successfully applied to get PMF profiles of relatively complex CD systems, even considering membranes and higher-order stoichiometries [34], [45].

In this study, we have adapted and tested different approaches based on metadynamics simulations to simulate and evaluate CD-based inclusion complexes. In order to test these methods, 1:1 βCD-sterol systems were employed. Cholesterol (CHOL) and its oxidized form 7-ketocholesterol (7KC) were used as ligands for βCD structures with different type, number and location of substitutions. The position of the substitutions was selected based on steric hindrance and the acidities of the CD OH groups. The difference between 7KC and native CHOL is minuscule: just one additional atom in 7KC, an oxygen forming a keto group at position 7 (Fig. 1). This difference, small as it is, is apparently key to the development of many diseases such as atherosclerosis and Alzheimer’s [46]. Thus, unlike cholesterol, which is essential for various physiological roles including cell membrane composition and hormone precursor functions, 7KC has disastrous effects in living organisms [46]. This is the main reason to look for methods to selectively extract 7KC from cells without significantly affecting the concentration of CHOL. Encapsulation of the oxidized sterol by CDs has been proposed for this end [19].

Fig. 1.

2D structures of the molecules to be simulated. (A) Native βCD (O4 atoms circled in red) (B) DS3 HPβCD (one HP group circled in red) (C) DS2 SBβCD (one SBE group circled in red) (D) DS7 SBβCD (E) 7KC (oxygen at position 7 circled in red) (F) Cholesterol.

In this strategy, specificity for the encapsulation of 7KC over CHOL is crucial. Experimental evidence obtained from turbidity studies suggests that, in contrast to the native βCD, HPβCD exhibits specific behavior to capture 7KC over CHOL [19], [47]. The detailed examination of 1:1 βCD-sterol systems featuring CHOL and 7KC serves as a preliminary model for our broader goal, which is to develop accurate and efficient computational methods that can be implemented in an automated workflow to produce affinity constants for thousands of inclusion complexes. These results enable training machine learning algorithms to design optimal modified CDs for specific purposes.

2. Methods

2.1. Description of the systems

PMF profiles were obtained to characterize the binding of CHOL and 7KC with native βCD, DS3 HPβCD, and SBβCD with DS3 and DS7 (Fig. 1). Regarding the modified CDs, the two DS3 structures, both with HP substitutions and SB substitutions, have these modifications at the exact same positions on the CD molecule.

2.2. System parameters

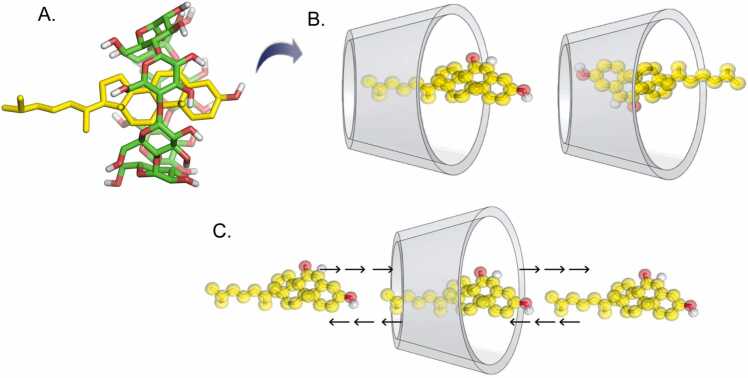
Both the initial coordinates for the βCD and the corresponding topologies were built using our own tools [19]. Initial coordinates and topology files for the target molecules (CHOL and 7KC) were obtained from the ATB server [48]. To ensure consistency with the force field, manual adjustments were made to the parameters, preventing unreasonable interaction constants for bonds and angles. After the βCD and ligand were built and parameterized, the ligand was introduced into the βCD cavity with its principal axis parallel or antiparallel to the symmetry axis of the CD ("up" and "down" orientations, respectively). The up orientation corresponds to the complex with the tail of the sterol molecule pointing to the large face of the βCD while the down orientation corresponds to the tail of the sterol molecule pointing to the small face (Fig. 2). For each of these complexes, twelve different structures, with the position of the ligand incrementally shifted along the symmetry axis of the CD by steps of 1 or 2 Å, both in the positive and in the negative directions, were built. Each of these structures was inserted in a 7x7x7 nm³ dodecahedral simulation box, which was then filled with approximately 7800 SPC waters. The water molecules overlapping the solute molecules were removed and Na⁺ ions were added to neutralize the total charge, when needed. Simulations at constant temperature (298 K) and pressure (1 bar) using the v-rescale thermostat [49] and the Parrinello-Rahman barostat [50] with coupling times of 0.1 ps and 0.5 ps, respectively, were performed in all cases. The long-range interactions were determined using the PME (Particle Mesh Ewald) [51], [52] algorithm with a grid spacing of 0.15 nm and a direct-space cut-off of 1.2 nm. The same cut-off was employed for the short-range interactions. A timestep of 2 fs was employed in all cases using the leap-frog integrator algorithm [53] to integrate the equation of motion. All bonds were constrained using the SETTLE algorithm [54] for water and the LINCS [55] algorithm for the CDs and sterol molecules. These simulations were executed using the GROMACS [56], [57] engine using the GROMOS54a7 forcefield [58] and PLUMED 2.8. [59], [60], [61].

Fig. 2.

(A) 3D molecular structure of the bCD (green carbons) - 7KC (yellow carbons) inclusion complex. (B) Simplified cone representation of the bCD (where the smaller side is the primary face and the larger side is the secondary face) showing the up (left) and down (right) orientations of the inclusion complex. The target is shown in yellow. (C) Illustration of metadynamics simulations, where the target is guided through the cavity of the CD in each direction and in each orientation.

2.3. Metadynamics Simulations

Coupled metadynamics simulations of the twelve slightly different complexes built for each system and relative orientation of the ligand in the CD cavity were executed in parallel. Simulations with the up and down relative orientations of the ligand were conducted separately.

The trajectories were carried out for 300 ns with walls at −2.5 and 2.5 nm between the sterol and the βCD to prevent the sterol from leaving the simulation box and crossing the periodic boundary. The final free energy profile leading to the formation of the complexes, as well as their optimal structure, was obtained by well tempered metadynamics simulations. Many tests were conducted to determine the ideal parameters for the PLUMED metadynamics simulation, and the best are presented here. In these simulations, Gaussian Height = 0.1 kJ/mol, σ = 0.1 nm, biasfactor = 15 at 298 K, and a grid spacing of 0.02 nm between −3.4 and 3.4 nm. The CV was the displacement of the center of mass of the target along the symmetry axis of the CD ($\xi$) which is calculated from the plane formed by the O4 atoms in the CD (Fig. 1A). The following restraints were devised to focus the investigation on inclusion complex structures: permitting the ligand movement solely along the axis perpendicular to the plane of the O4 atoms of the CD and constraining the relative orientation of the ligand to the up or down orientation (Fig. 2). The O4 atoms of the CD were selected as reference points for distance measurements and defining reference planes and axes in the restraints, due to their relatively static nature compared to the other atoms in the CD. All restraints in these simulations were implemented using harmonic potentials with a constant force of 1000 kJ·mol^-1·nm^-2. Each metadynamics simulation was repeated four times with slightly different distributions of the starting positions to check for reproducibility.

2.4. Potential of mean force (PMF)

The PMF profiles were determined from the sum of the gaussian functions generated by the 12 walkers corresponding to each relative orientation of the target molecule with each CD during the metadynamics trajectories, using the sum_hills tool of PLUMED. The resulting PMF profiles were post-processed to determine the corresponding standard binding constant, which for a bimolecular interaction (A+B ↔ AB) can be determined from the partition function of each chemical species ($Z_i$):

$${\mathrm{K}}_{\mathrm{A}}=\frac{Z_{AB}/V}{\left(Z_A/V\right)\left(Z_B/V\right)}$$ (1)

where V is the volume of the simulation box. Neglecting the internal degrees of freedom of A and B, the corresponding Hamiltonian only accounts for the kinetic energy:

$$H_i=\sum _{j=1}^3\frac{p_j^2}{2m_i}$$ (2)

Where p_j is the j component of the linear momentum and m_i is the mass of the molecule i. The partition function corresponding to this Hamiltonian is:

$$Z_i=V{\left(\frac{2\pi ·m_i·K_{B}T}{h^2}\right)}^{3/2}$$ (3)

With $K_B$ representing the Boltzmann constant and h the Plank constant. The Hamiltonian corresponding to the complex would be:

$$H_{\mathit{AB}}=\sum _{j=1}^3\frac{{\left(p_j^{\mathit{com}}\right)}^2}{2\left(m_A+m_B\right)}+\sum _{j=1}^3\frac{{\left(p_j^R\right)}^2}{2\mu }+E(r)$$ (4)

$p_j^{\mathit{com}}$ being the j component of the linear momentum of the center of mass (COM) of the complex, $p_j^R$ the j component of the linear momentum of the relative movement between A and B in the complex, $\mu =\frac{m_A·m_B}{\left(m_A+m_B\right)}$, and $E(r)$ is the potential energy of interaction between A and B as a function of the relative coordinates between both molecules. The corresponding partition function is:

$$Z_{\mathit{AB}}=V{\left(\frac{2\pi \left(m_A+m_B\right)K_{B}T}{h^2}\right)}^{3/2}·{\left(\frac{2\pi \mu K_{B}T}{h^2}\right)}^{3/2}\int e^{-E(r)/\mathit{RT}}\mathit{dv}$$ (5)

where R and T are the gas constant and the temperature, respectively and dv is the volume element expressed in terms of the r coordinates. Replacing (2), (3), (4), (5) in Eq. (1), we obtain:

$${\mathrm{K}}_A=\int e^{-E(r)/\mathit{RT}}\mathit{dv}$$ (6)

Given the symmetry of the CD monomer and the restraints applied to the relative movement of the ligand with respect to the macromolecule, the interaction energy $E(r)$ and the volume element dv are naturally expressed in cylindrical coordinates ($\phi ,\rho$, z). Since the rotations around the CD symmetry axis are not restrained, and the interaction energy is assumed to be independent on the corresponding angle, the volume element can be directly integrated over $\phi$ (from 0 to 2$\pi$). The distance from the ligand to the axis perpendicular to the O4 atoms that pass throughout their COM is restrained with a harmonic potential, so it is not exactly constant, but the PMF is assumed to be independent of this parameter. Thus, the volume element is also integrated over $\rho$ from 0 to the maximum radius of the cylinder where the ligand can move (${\rho }_{\max }$). Importantly, the simulations were not performed in the standard state, so a correction should be performed for this aim. This correction is performed by dividing the volume of each molecule in the simulation box by the volume available for one molecule at 1 M concentration (1660 ų). After simplifying this implies an additional factor of Avogadro’s number (N_A) in the expression for K_A. Taking into account all these approaches and considerations, the final expression for the association constant would be:

$${\mathrm{K}}_{\mathrm{A}}=\mathrm{\pi }{\mathrm{N}}_{\mathrm{A}}{\rho }_{\max }^2\int e^{-E(\xi )/\mathit{RT}}d\xi$$ (7)

where the cylindrical coordinate z was replaced by the collective variable $\xi$ employed in our simulations and $E(\xi )$ can be replaced by the PMF. Using this equation, the binding constant for each system was computed by numerical integration of the PMF along the CV. For our calculations, a constant value of 0.4 nm was taken for ${\rho }_{\max }$. In order to estimate the uncertainty of the K_A values, multiple integrations were considered for each PMF profile, with different integration limits in the unbound region. The values of K_A obtained in this way were then transformed into ΔG⁰ by using the classical relationship: ΔG⁰ = −RT ln(K_A). Then, the ΔG⁰ values obtained in this way for each PMF profile were clusterized with the k-means algorithm with the optimal number of clusters determined using the Silhouette [62] method. The final ΔG⁰ value, together with the corresponding standard errors were taken as the average and standard deviation of the ΔG⁰ values of the most populated cluster. Then, the corresponding association constant was obtained as K_A = exp(−ΔG⁰/RT) and its uncertainty determined by standard error transmission. This procedure allows us to automatically eliminate outliers without any human bias. For the calculation of average values we decided to work in the ΔG space due to the exponential nature of the association constants, whose direct averaging can be heavily skewed by values that differ significantly in magnitude. However, energies are additive, a property that makes it well suited to operations such as summation and averaging. By converting K_A to ΔG⁰ values, one can obtain a more representative average, which can then be transformed back into the K_A space for interpretation. This method ensures that the derived average value is not disproportionately influenced by constants that are significantly larger or smaller than the others, providing a more accurate and meaningful representation of the dataset. This approach resulted in a fully automated PMF method, providing a quantitative approach for obtaining association constants for the formation of 1:1 inclusion complexes using a reasonable amount of computational resources. The final values of K_A and the corresponding ΔG⁰ were obtained using a Python script that uses the pandas, [63], [64] numPy, [65] matplotlib, [66] and kmeans1d [67], [68] libraries.

The PMF calculation was performed two times: once using the entire distribution of the CV (−2 to 2 nm, the “All Method”), and once considering only the wide face of the βCD (CV from 0 to 2 nm only, the “Wide Face Method”). It is expected that the targets will tend to form complexes via the wide face of the βCD, and sampling only half of the βCD will lead to a faster and still accurate result. In addition to association constants, from PMF profiles we can also get the energy wells and barriers of the encapsulation process as a function of the distance between the center of mass of both molecules and the most stable structures for each complex. By using these systems, we hope to gain insight into the effect of each substitution type on the complex.

2.5. Statistical analysis

The ΔG⁰ values obtained from the PMF profiles using both integration methods ("All” and “Wide-Face”) for the four metadynamics simulations of each CD + sterol combination and for both orientations of each system were plotted to check for reproducibility and systematic differences. A total of 128 ΔG⁰ values were collected in this way. Then several statistical tests were applied to check for the normality of the uncertainty distributions (Shapiro-Wilk [69] test) and for significant differences between the values (t-test, Mann-Whitney [70] test, paired t-test, or Wilcoxon [71] test, depending on the case) obtained using different integration methods, considering relative orientations of the ligand in the CD cavity, different ligands for the formation of the complexes, and also to compare the uncertainties obtained using the two integration methods. The average values of the repeats under the same conditions were obtained after removing possible outliers (those with a z-score > 1.5). The standard deviation was taken as a measurement of the reproducibility for these repeats. Bland-Altman [72] plots were also generated to highlight possible trends in the differences of ∆G⁰ value obtained using different integration methods, relative orientations, and ligands.

3. Results

3.1. General description of the PMF profiles

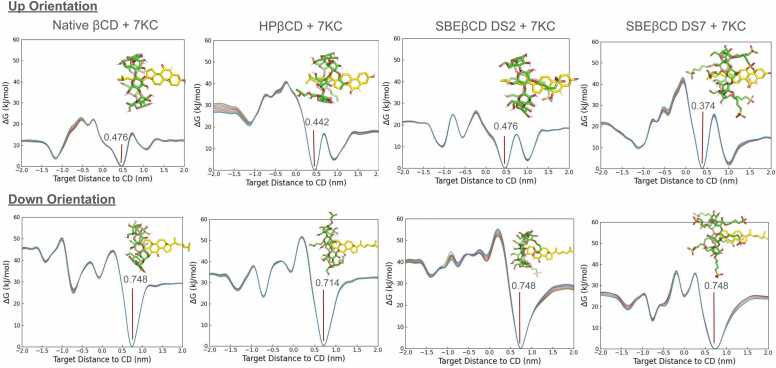
PMF profiles were generated for all systems studied by metadynamics simulationswith 300 ns-long trajectories for each of the 12 walkers to ensure simulation convergence. This convergence is demonstrated by the overlapping curves in the PMF profile evolution over time, as shown in Figs. 3–4 and in the Supplementary Material. The simulations sampled the displacement of the target along the symmetry axis of the CD ring, with restraints on the relative orientation and on the distance to this axis (see Methods for details). Consequently, two regions with negligible interaction in the PMF are expected at both negative and positive long-distance displacements between the CD and the ligand. In these “unbound” regions, the PMF profile should level off, indicating no change in interaction energy. This behavior was observed in most systems, with some exceptions showing significant differences in the height of the PMF at opposite sides of the CD. These discrepancies contribute to the uncertainties in the calculated ΔG⁰ values. Typically, one or more energy barriers are observed for the ligand entry into the CD cavity from the narrower side, presenting a sampling challenge. Conversely, calculating ΔG⁰ values might be simpler when integrating the pathway from the bound to the unbound region via the wider cavity side, usually devoid of significant energy barriers. K_A and corresponding ΔG⁰ values for all systems were calculated using these two approaches, as shown in the Supplementary Material.

Fig. 3.

PMF profiles for the four βCDs with 7KC in the up and down orientations, together with the structures of the complexes and the CV value corresponding to the energy minimum. The K_A and ΔG⁰ values calculated from both the All and Wide Face method, as well as the additional simulation replicates, are available in the Supplementary Material.

Fig. 4.

PMF profiles for the four βCDs with cholesterol in the up and down orientations, together with the structures of the complexes and the CV value corresponding to the energy minimum. The K_A and ΔG⁰ values calculated from both the All and Wide Face method, as well as the additional simulation replicates, are available in the Supplementary Material.

All employed CDs generally exhibit a marked preference, evidenced by more negative ΔG⁰ values, for the down orientation. Specifically, the native βCD monomer shows its lowest energy at exactly 0.748 nm for both sterols in the down orientation, and around 0.4 nm in the up orientation. The positions of these minima are more varied for modified CDs, but they remain fairly consistent for both sterols within each CD and orientation pair, with one notable exception for HPβCD with cholesterol in the up orientation, which shows the absolute minimum at − 1.05 nm and secondary minima at approximately 0.5 and 1 nm. While the PMF profiles for both sterols with a given CD are similar, the presence of two local minima of varying depth for both sterols in the up orientation influences these results. Overall, across all systems, the roughness of the energy profile is much more pronounced in the region corresponding to the narrow face of the CD than the wide face, making the former more challenging to sample than the latter. Additionally, it seems that the larger the number of substitutions the more sophisticated the PMF profile is, with more and higher energy barriers for SBβCD (DS7) than for SBβCD (DS3) and a more complex energy profile for both modified CDs with DS3 than for the native βCD. (Fig. 5).

Fig. 5.

ΔG⁰ values obtained from all the PMF profiles calculated in the present work. For each system and integration method, four independent calculations were conducted, represented by the colors blue, orange, green, and red. The top plot displays results utilizing the entire PMF profile. The middle plot shows the results obtained from the integration from the bound region near the global minimum to the unbound region towards the wide face direction. The bottom plots highlight the differences between the two integration methods for identical simulations. The left column contains the results of simulations where the ligand is in the up orientation, while the results for the down orientation are in the right column.

To facilitate comparison of results from various combinations of employed variables (relative orientation, integration method, and ligand name), the average values for each specific combination, along with their standard deviations, were calculated (Fig. 6 and Table 1). As mentioned above, the outliers (values with z-score > 1.5) were excluded for these calculations (a total of 11 ΔG values). In general, there is a good correlation observed between the two integration methods. Additionally, clear trends are evident in these results, although some are more subtle. A notable example is the difference between the results for the up and down orientations, with the down orientation consistently showing significantly stronger affinity across all CDs. This trend is reproducible with both integration methods. However, the specificity of the CDs for each sterol is less clear. While the native βCD in the up orientation appears to be more specific for CHOL and HPβCD, also in the up orientation, is more specific for 7KC, the overall impact of these differences is limited due to the much lower significance of the up orientation compared to the down orientation. It is important to note that the overall association constant for a given CD is the sum of the association constants from both the up and down orientations. The association constants are proportional to the exponential of ΔG⁰ (K_A = exp(−ΔG⁰/RT)), meaning even small differences in ΔG⁰ can lead to substantial variations in the association constants. Therefore, in all cases, the contribution of the up orientation to the quantification of binding energies is expected to be low when compared to the down orientation. The results corresponding to the down orientation do not exhibit clear specificity for any of the sterol molecules.

Fig. 6.

Average ΔG⁰ values for each group of experiments (n = 4) together with the corresponding standard deviation (error bars). The results using the ‘All’ integration method are in blue and those using the ‘Wide-Face’ method are in orange. Values with z-score > 1 (a total of 11 out of 128 values) were excluded from the calculations.

Table 1.

Average ΔG⁰ values for each group of experiments (n = 4) together with the corresponding standard deviation for the All and the Wide-Face integration methods. Values with z-score > 1 (a total of 11 out of 128 values) were excluded from the calculations.

	up		down
	all	Wide-Face	all	Wide-Face
β-CHOL	−13.53 ± 0.39	−14.2 ± 1.2	−19.5 ± 1.4	−18.40 ± 0.94
β-7KC	−9.5 ± 4.6	−6.5 ± 1.1	−27.1 ± 6.7	−18.83 ± 0.54
HP(3)-CHOL	−7.2 ± 2.5	−7.7 ± 1.0	−23.4 ± 3.9	−22.5 ± 4.0
HP(3)−7KC	−15.9 ± 4.8	−10.05 ± 0.68	−24.80 ± 0.85	−22.4 ± 1.2
SB(3)-CHOL	−11.7 ± 1.7	−10.2 ± 2.5	−29.2 ± 6.5	−22.6 ± 1.1
SB(3)−7KC	−9.6 ± 1.7	−9.6 ± 1.9	−33.6 ± 2.2	−18.33 ± 0.34
SB(7)-CHOL	−7.7 ± 2.1	−7.3 ± 2.0	−12.9 ± 2.1	−15.4 ± 4.4
SB(7)−7KC	−8.6 ± 2.7	−8.6 ± 1.9	−16.4 ± 2.0	−15.5 ± 1.1

A more robust support for this discussion could be provided by applying appropriate statistical tests.

3.2. Statistical results

3.2.1. All vs. Wide-Face methods

To explore the differences in ΔG⁰ values, uncertainties, and reproducibility between the two integration methods (All and Wide-Face) across both up and down orientations, the average values shown in Fig. 6 and in Table 1 were employed. The standard deviation was taken as a measurement of the reproducibility of the ΔG⁰ values in each independent simulation.

The Bland-Altman plots suggest a small bias between the two methods (represented by the red line in Fig. 7). In addition to this visual comparison, a quantitative analysis aimed to assess whether or not both methods are equivalent to each other was performed. The analysis was performed in different ways: (i) ignoring the uncertainties; and (ii) considering the uncertainties to weight the differences in the results obtained from both methods. Note that outliers were excluded from the calculation of the average values. To assess the differences in ΔG⁰ values derived from the two integration methods, both the paired t-test and the Wilcoxon test were utilized. Initial comparisons, which did not account for uncertainties, suggested significant differences between the methods. However, when incorporating the standard deviation of the average values into the analysis, there are no significant differences between the two integration methods (p-value > 0.05) (Table 2).

Fig. 7.

Differences in ΔG⁰ values obtained from the integration of the whole PMF profile and using just the wide face (ΔG⁰_All – ΔG⁰_Wide-Face) as a function of the average of both values (0.5(ΔG⁰_All + ΔG⁰_Wide-Face)). The mean of the difference together with the confidence interval (mean difference ± 1.96 times the standard deviation of the differences) are shown as a dashed red line and dashed green lines, respectively.

Table 2.

Comparison of the average difference in ∆G⁰ values (∆G⁰_all −∆G⁰_wide) obtained from all the PMF plots with different considerations.

Analysis Method	Mean Difference (kJ/mol)	p-value t-test	p-value Wilcoxon
Results using the mean values for each system
Without Uncertainties	−2.67 ± 1.10	0.028	0.0125
With Uncertainties	−1.96 ± 1.04	0.080

The t-test for independent samples and the Mann-Whitney test were employed to check for differences in the uncertainties of both methods. Both tests suggest that the uncertainties are significantly different with p-values of 0.030 and 0.018, respectively. The mean difference of the standard deviations is 1.83 ± 0.49 (larger for the All method). This means that the data obtained using the Wide-Face method is significantly more reproducible than those using the All method, even though the two methods provide equivalent mean values.

3.2.2. Up vs. down orientation

This analysis was performed using the mean values to determine if significant differences exist between the up and down orientations, independent of the reproducibility of repeated experiments for the same system. It was conducted separately for both the All and Wide-Face integration methods.

The Bland-Altman plots show a clear systematic bias between the results provided by both orientations, with a negative excess in the ∆G⁰ value of more than 10 kJ/mol, as shown in Fig. 8. Table 3.

Fig. 8.

Differences in mean ∆G⁰ values obtained for the up and down orientations of each system for the All (left) and Wide-Face (right) integration methods. The mean of the difference together with the confidence interval (mean difference ± 1.96 times the standard deviation of the differences) are shown as a dashed red line and dashed green lines, respectively.

Table 3.

Comparison of the average difference in ∆G⁰ values (∆G⁰_up − ∆G⁰_down) obtained from the mean values of the four PMF replicas obtained for each system and orientation. Both integration methods were employed, providing similar results, as indicated in the Table. The p-values obtained from both the paired t-test and the Wilcoxon tests are lower than 0.05 in all cases, indicating that the difference between ∆G⁰_up and ∆G⁰_down is significant, with lower (more negative) values for ∆G⁰_down.

Analysis Method	Mean Difference (kJ/mol)	p-value t-test	p-value Wilcoxon
Results using the All method with mean values of each system
Without Uncertainties	12.88 ± 2.41	0.0011	0.00781
With Uncertainties	9.79 ± 2.35	0.004
Results using Wide Face method with mean values of each system
Without Uncertainties	9.98 ± 1.26	0.0001	0.00781
With Uncertainties	9.92 ± 118	0.0000

No statistical differences were observed between the uncertainties of the two orientations, the t-test for independent samples, and the Mann-Whitney test providing values of 0.51 and 0.80 for the All method and 0.79 and 0.51 for the Wide-Face method.

3.2.3. Cholesterol vs. 7KC targets

Again, the same analysis as in the previous section was performed, i.e. using the mean values of the four replicas obtained for each system and orientation. Again, the analysis was performed using the two integration methods separately.

The Bland-Altman plots (Fig. 9) suggest systematic bias of different sign, where the All method is positive and the Wide Face method is negative, depending on the employed method to integrate the PMF profiles. The application of statistical tests also provides contradictory results for both integration methods, but with no significant systematic differences between both sterols (Table 4).

Fig. 9.

Differences in mean ∆G⁰ values obtained for cholesterol and 7KC with the different CDs for the All (left) and Wide-Face (right) integration methods. The mean of the difference together with the confidence interval (mean difference ± 1.96 times the standard deviation of the differences) are shown as a dashed red line and dashed green lines, respectively.

Table 4.

Comparison of the average difference in ∆G⁰ values (∆G_cholesterol − ∆G_7KC) obtained from the mean values of the four PMF replicas obtained for each system and orientation.

Analysis Method	Mean Difference (kJ/mol)	p-value t-test	p-value Wilcoxon
Results using the All method with mean values of each system
Without Uncertainties	2.54 ± 1.56	0.148	0.195
With Uncertainties	1.02 ± 1.23	0.433
Results using Wide Face method with mean values of each system
Without Uncertainties	-1.07 ± 1.17	0.931	0.742
With Uncertainties	-1.37 ± 1.21	0.295

Additionally, no statistical differences were observed between the uncertainties of the mean values for both sterols, the t-test for independent samples, and the Mann-Whitney test providing values of 0.53 and 0.51 for the All method and 0.073 and 0.16 for the Wide-Face method.

4. Discussion

The present study provides a comprehensive investigation into the inclusion complexes formed between different βCDs (βCD, HPβCD with DS3, and SBβCD with DS3 and DS7) and sterol molecules, specifically CHOL and 7KC, through guided metadynamics simulations followed by PMF calculations. The research aims to establish robust and efficient methods to characterize the interaction between CDs and small ligands. For this, a relatively large set of trajectories is used to assess the reproducibility in the determination and accuracy of ∆G⁰ values by different approaches. Additionally, the ability of the different CDs to distinguish the two sterols and their relative orientation into the cavity are assessed. Complementarily, the obtained results shed light on the interactions between the molecules employed in our calculations.

All employed CDs display a strong preference for the down orientation, indicated by more negative ΔG⁰ values by ∼10 kJ/mol, compared to the opposite orientation of the sterol in the CD cavity. The positions of all minima (displacement between the CD and the sterol) vary for different CDs, but they are consistent for both sterols within each CD and orientation. SBβCD with DS= 7 is the only exception to this behavior due to the presence of two local minima in the up orientation at similar locations but with different depths for both sterols. This preference could be due to the fact that the hydrophobic headgroup of the sterol is in better contact with the hydrophobic CD cavity, while the hydrophilic tail of the sterol is in better contact with water in this orientation. Subtle differences in sterol specificity among CDs was observed. This could be due to the significant differences in ΔG⁰ values in the up orientation, and the impact of this contribution to the overall association constant is limited due to the much higher significance of the down orientation. Note that the total association constant for the interaction between a given CD-ligand pair results from the sum of the association constants in the two orientations and the transformation from the ΔG⁰ to the K_A space is performed by the exponential function. Thus, relatively small differences in ΔG⁰ are magnified when they are transformed to K_A, as it happens for all the studied systems when combining ΔG⁰ values obtained from both orientations of the sterol in the CD cavity.

The roughness of the energy profile is evident around the narrow face of the CD, in contrast to the wide face, making it harder to sample. The results obtained from the two integration methods (All and Wide-Face) were consistent, with no significant differences between them. However, the Wide-Face method was significantly more reproducible and it is cheaper, from the computational point of view, than the All method, since the former requires the sampling of a much smaller range of the CV used in the metadynamics simulations. This method is expected to be sufficient for randomly substituted or unsubstituted CDs interacting with steroidal target molecules.

The study successfully reveals energy profiles, optimized complex structures, and quantitative estimations of binding affinities for the inclusion complexes between βCDs and sterols. The computed PMF profiles offer a detailed understanding of the energy landscapes governing the association between the host βCDs and the guest sterols. The rationalization of these energy landscapes provides insights into the mechanisms of inclusion, shedding light on the interactions and driving forces governing the formation of inclusion complexes. The employed approach to exploring selective sequestration of specific molecules using modified βCDs opens up possibilities for designing novel molecular systems for targeted drug delivery or other applications. Our study is focused only on 1:1 complexes, but it is worth mentioning that other stoichiometries such as 2:1 (two CD molecules threaded by the same ligand), 1:2 (one CD molecule simultaneously binding 2 sterol molecules), or even aggregates of higher order could significantly contribute to the solubilization of a given ligand by CDs. [24], [27], [73], [74], [75], [76], [77] However, inclusion complexes are of special interest because the interaction mechanism leading to these structures is expected to take advantage of the particular design of the CD molecules to specifically distinguish between different ligands. The CDs employed in this study did not successfully differentiate CHOL from 7KC, but it has been demonstrated, with approaches similar to those employed in the present work, that CD dimers, with the monomers joined by a chemical linker, are indeed able to distinguish these two sterol molecules.

Overall, in addition to the new insight that our calculations provide on the specific interactions between different CDs and the two studied sterol molecules, we propose a protocol that could be employed in massive PMF calculations of CD-ligand systems. This protocol is based on metadynamics simulations that only require the sampling in one dimension (the displacement of the ligand along the symmetry axis of the CD) in the direction of the wide face of the cavity with some restraints (the relative orientation of the ligand with respect to the CD and the distance from the ligand to the symmetry axis of the CD). The ΔG⁰ and association constant values obtained from these calculations were highly reproducible and allowed us to save significant computational resources compared to other methods. We intend to implement this method into an automated workflow for designing modified CDs tailored for specific applications.

5. Conclusion

This study focuses on the computational study of inclusion complexes between multiple βCDs and sterols, using metadynamics simulations and PMF calculations to understand their interactions. The methods reveal that CDs-sterol inclusion complexes are generally preferred in the "down" orientation, with notable differences in binding affinities and energy profiles among different CDs. These differences highlight the impact of number and type of substitution on the characteristics of CD inclusion complexes. The research demonstrates the consistency and efficiency of the Wide-Face integration method in these calculations, offering insights for designing faster, specialized methods to analyze CD-sterol inclusion complexes in silico. These results are significant for various applications, including targeted drug delivery and novel drug design. Finally, the automated techniques presented here showcase the potential of accelerating CD development by creating and using large amounts of data for training AI and ML algorithms. These advancements are poised to not only improve our understanding of CD inclusion complexes, but also open new horizons for a world where tailored, CD-based solutions can be developed more efficiently and effectively than ever before.

CRediT authorship contribution statement

Amelia M. Anderson: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Writing – original draft, Writing – review & editing, Visualization, Project administration. Ángel Piñeiro: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Resources, Writing – original draft, Writing – review & editing, Visualization, Supervision. Rebeca García-Fandiño: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Resources, Writing – original draft, Writing – review & editing, Visualization, Supervision. Matthew S. O’Connor: Conceptualization, Writing – original draft, Writing – review & editing, Supervision, Project administration, Funding acquisition.

Declaration of generative AI and AI-assisted technologies in the writing process During the preparation of this work the author(s) used OpenAI ’s ChatGPT in order to improve the readability and flow of the manuscript. After using this tool/service, the author(s) reviewed and edited the content as needed and take full responsibility for the content of the publication.

Declaration of Competing Interest

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: AMA, RGF, AP, and MSO report financial support was provided by Cyclarity Therapeutics. Inc. AMA, RGF, AP, and MSO report a relationship with Cyclarity Therapeutics Inc that. includes: employment, consultation or advisory, equity or stocks, and travel reimbursement. RGF and AP report a relationship with the company MD.USE that includes: employment. and equity or stocks.

Appendix A. Supplementary material

Supplementary material

.