Quantum Mimicry With Inorganic Chemistry

Abstract

Quantum objects, such as atoms, spins, and subatomic particles, have important properties due to their unique physical properties that could be useful for many different applications, ranging from quantum information processing to magnetic resonance imaging. Molecular species also exhibit quantum properties, and these properties are fundamentally tunable by synthetic design, unlike ions isolated in a quadrupolar trap, for example. In this comment, we collect multiple, distinct, scientific efforts into an emergent field that is devoted to designing molecules that mimic the quantum properties of objects like trapped atoms or defects in solids. Mimicry is endemic in inorganic chemistry and featured heavily in the research interests of groups across the world. We describe a new field of using inorganic chemistry to design molecules that mimic the quantum properties (e.g. the lifetime of spin superpositions, or the resonant frequencies thereof) of other quantum objects, “quantum mimicry.” In this comment, we describe the philosophical design strategies and recent exciting results from application of these strategies.

1. Introduction

Mimicry is ubiquitous in the world, from insects using it to trick predators^{[1, 2]} to popular culture and diabolical (and unfortunately fictitious) “treasure chests” that devour the greedy adventurer.^{[3, 4]} Mimicry is also an important and widespread design principle in molecular inorganic chemistry. Here, the pioneering chemist identifies a property, for example, a specific type of reactivity, in a compound that is unstable, fleeting, or otherwise prevents storage in a bottle on the shelf for future use. The mimicry efforts, then, are to design compounds that have the same (or improved) properties, yet can be bottled, controlled, or otherwise harnessed.

The predominant mimic strategy for molecular inorganic chemists is to identify what aspects of the “to-be-mimicked” species enable its properties, then design an appropriate ligand scaffold to realize that property. There are several prime examples of mimicry using this idea (Fig. 1). In one area, transition metal complexes are developed to mimic the reactivities engineered by nature.^[5–8] The concept of ‘mimicry’ here is far from simple. In-depth spectroscopic and computational studies of active sites in enzymes are often the first, step, revealing the first- and second-coordination shells of the metal ion that produce the desired reactivity.^[9–13] That information will then drive ligand design and metal selection for the molecular mimic. Another example of mimicry is designing earth abundant metals to mimic the properties of expensive precious metals. In these areas, ligand designs focus on making the electronic structures of the earth abundant metals mimic those of precious or rare earth metals, and span many different targeted characteristics, from reactivities^{[14, 15]} to magnetic^[16–19] and photochemical^[20–22] properties.

Fig. 1.

Overview of mimicry efforts in molecular inorganic chemistry.

In this comment, we describe a new type of mimicry in molecular inorganic chemistry, one devoted to understanding how to use synthetic chemistry to mimic the quantum properties of other quantum species in molecules. In several cases, the objects that chemists are trying to mimic with molecules are not molecular at all, such as the mimicry of trapped ions in atomic clocks. In these efforts, just like the examples defined above, the toolkit of the coordination chemist unveils novel insight to instill new properties in molecular metal complexes. In the following section of the review, we define quantum mimicry and detail the need for it, particularly for applications of transition metal complexes in the second quantum revolution.^{[23, 24]} We then describe four specific examples of quantum mimicry in molecules.

2. Deficiencies in all quantum objects and the motivation for a mimicry paradigm.

The viability of a quantum object (defined as a system with two or more discrete quantized states) in next-generation quantum applications depends on whether they meet a set of criteria described by the intended application. The two most common criteria are those of DiVincenzo^[25] for quantum information processing and that of Degen^[26] for quantum sensing. The primary three properties shared by both sets of criteria are the following. First, the quantum system must be scalable, which means that it must be possible to produce many different quantum systems that each possess the same characteristics. This property is most important for computational applications, akin to requiring many identical transistors for a computer chip. Second, the quantum system should be addressable, which means that the state of the quantum system must be able to be read out and controlled. The readout can be by spectroscopy or other techniques, again, akin to how one may readout voltages in a computer chip. Third, the quantum system must be initializable, which means that a user must be able to place a quantum system, or collection of quantum systems, all into the same state. For a computational step, this is like clearing the cache before a calculation, but for a sensing type of application, this initialization maximizes signal to noise in the readout.

The fourth and fifth relevant properties are related to environmental interactions and control. The first of these properties is that the given quantum system must be capable of coupling to the environment. For a quantum computation, this feature requires that quantum bits be coupled for multi-qubit gate operations, like multiple transistors would connect in the chip of a conventional computer. For a quantum sensing application, the quantum system must couple with some aspect of the environment to sense it. The fifth criterion is that the targeted superposition of states produced by a quantum object must be reasonably long lived. The target lifetime highly depends on the application. For a computation application, the lifetime should be ca. 10,000 times the timescale of a single logic operation. This general requirement stems from the necessity of multiple operations in a calculation and to enable error correction.^[27] For a sensing experiment, the lifetime can be lower, indeed, it only needs to be long enough for the superposition to encounter what it is to sense and readout performed. In this light, however, longer lifetimes are still advantageous, as they enable a higher possibility of detecting weaker or more slowly varying environmental effects.

There is, finally, a sixth advantageous criterion worth considering that is not defined in either the DiVincenzo or Degen criteria, which is the tunability of the quantum system. Society does not have universally useful devices for quantum applications, and if we are to find and design those devices, we need to understand how to control the quantum properties of objects to meet the criteria of DiVincenzo and Degen. Tunability is therefore essential to understanding how structural aspects of a given system affect the properties of any produced superpositions.

There are many proposed quantum systems for the above applications: superconducting resonators,^[28] molecules,^{[23, 24]} photons,^[29] topological states,^[30] and more.^{[27, 31]} Importantly, each type of system has certain advantages and disadvantages, such that a given quantum system often only meets some of the criteria described above (Fig. 2). For example, superconducting loops have scalable fabrication, but the superposition state is extremely fragile, requiring extremely low temperatures for function. Trapped atoms can be controlled and exhibit extremely stable superpositions but could never be embedded in a biological system for sensing use. Photons can be controlled, produced in single states at scale and transmitted over very long distances,^[32] but it is challenging to implement multi-qubit gates with them.^[28] The list goes on for every type of quantum system.

Fig. 2.

Overview of common required characteristics of quantum systems and the advantages/disadvantages of four common quantum systems. The asterisk next to “long-lived” in the molecular spins category is because it depends on the type of spin system: nuclear spins exhibit long-lived superpositions, whereas electrons generally do not.

Molecular spins are a promising class of quantum object because they meet many of the above criteria and, on top of that, are tunable in a way that no other type of quantum object is. First, they are scalable with atomic-level precision, and one can in theory produce molar-scale quantities (6.02 × 10²³ objects) or greater of precisely the same unit. Second, molecular spins can be addressed through magnetic resonance: radiowaves and nuclear magnetic resonance, NMR, for magnetic nuclei in a molecule, or microwaves and electron paramagnetic resonance, EPR, for unpaired electrons in a molecule. The largest advantage for molecular spin systems is their chemical tunability with atomic precision. Indeed, one can place atoms at exact positions in space relative to one another through synthetic design, which allows for an immense level of control over the physical and electronic structures of molecules, which impossible in other systems. As a result, the quantum properties of spins in said molecules are incredibly tunable. Despite these advantages, there are some critical challenges in their design. For one, there is an evident competition between the superposition lifetimes of these spin systems and environmental sensitivity. Here, higher sensitivities to local environment produce shorter-lived superpositions. Hence, developing quantum sensors with strong environmental detection capabilities appears to come at the cost of superposition lifetime. Equally upsetting, the ability to couple qubits together in a molecule-scale quantum computer would require a high concentration of nearby spin systems. High densities of spins generally shorten superposition lifetimes.^[33] Hence, that ability in a device would be expected to come at the cost of destabilizing quantum information encoded in its qubits!

In this comment we propose a new paradigm for designing new molecule-based quantum systems based on mimicry, which we here denote as quantum mimicry. Through this paradigm, a molecular chemist identifies a desirable quantum property in a molecular or even a non-molecular quantum system, e.g. a trapped atom or color-center defect, then designs a molecule to mimic that property. In the process, this mimicry will overcome some of the intrinsic disadvantages of molecules in quantum applications, like the superposition lifetime/sensitivity dichotomy. Design strategies for various quantum properties are of interest in many different groups, but the aggregation of these strategies into a conceptual mimicry framework has never been made. As inorganic chemistry has long harnessed different forms of mimicry, like mimicry of active sites,^[5–8] mimicry of precious metals,^[14–22] etc., we propose a new umbrella to unite the quantum-relevant areas of chemical mimicry into one – quantum mimicry.

3. Quantum Mimic Class 1: Unpaired Electrons That Act Like Nuclei

The first class of quantum mimics we cover are those where metal complexes are designed to feature unpaired electrons that respond to low-frequency microwaves (< 1 GHz) or radiowaves at high magnetic field (> 1.5 T). In doing so, these molecules are, in effect, producing electron-spin quantum mimics of magnetic nuclei, which are readily analyzed with radiowaves through NMR spectroscopy.

3.1. Basics of Magnetic Resonance Imaging.

The most pertinent application for an electron spin mimic of a magnetic nucleus is for biological magnetic resonance imaging (MRI). This medical imaging technique, which exploits magnetic nuclei (and, hence, could more accurately be called “nuclear magnetic resonance imaging”), is extremely important for non-invasively identifying tumors and tears in muscles, ligaments, or tendons, among other ailments, while using safe, non-ionizing, radio-frequency radiation.^[34]

There are limitations to biological MRI that paramagnetic molecular quantum mimics may address. For one, while physicians can achieve great anatomical detail from MRI scans of biological systems, there is a lack of sensitivity to local chemistry. Molecular contrast agents, like those based on gadolinium, have made some progress in addressing this challenge, mostly in the form of increasing relaxation rates of protons from the interactions between the electron magnetic moment and the nuclear spin of water molecules.^[35] Yet, the precise physiology, or local biochemistry, is still highly challenging to image via MRI. But, imaging chemistry would be profoundly transformative to treatment technologies! The ability to non-invasively image chemical signatures like pH, local O₂ concentration, or redox stress would improve the diagnostic capabilities for diseases like cancer, hypertension, and sickle cell anemia,^[36–39] as well as provide a new window into studying biological processes.

The inherent insensitivity of MRI may be addressed by combining it with its electron-spin analog, electron paramagnetic resonance imaging (EPRI).^{[35, 40, 41]} Electron spins are orders of magnitude more sensitive than nuclear spins because of the much larger magnetic moment. This difference is reflected in the larger gyromagnetic ratio (28 GHz/T for a free electron, 42.5 MHz/T for a proton), as well as the lowest spin concentrations that can be detected (< 1 nM with EPR, ~0.1 mM with NMR).^[35] As a result of this extraordinary sensitivity, EPRI can non-invasively image pH,^[42–45] redox status,^[46–49] tissue oxygenation,^[50–52] and microviscosity.^{[53, 54]} In principle, one could envision MRI producing a detailed anatomical map with an overlay from EPRI that conveys chemical information, which would be a transformative outcome.

3.2. Need for Design Strategies for Paramagnetic Metal Complexes as Quantum Mimics of Nuclei.

Exogenous paramagnetic molecular probes are needed for EPRI to be viable owing to the brief half-lives of endogenous radicals.^[35] There are many probe systems that have been studied for this purpose, mostly organic radicals.^{[41–50, 55–57]} These systems contain one unpaired electron and are S = ¹/₂. In the high magnetic fields typically used in a clinical MRI scanner (> 1.5 T), the electron spin would need to be addressed with ca. 40 GHz microwaves (Fig. 3).^[57–60] Radiation in this energy regime is readily absorbed by water-rich tissue, resulting in low penetration depth^[61] and microwave-induced heating.^[62] Thus, EPRI utilizing organic radicals is currently not viable in an MRI scanner. The frequency of the EPR transition for an S = ¹/₂ system scales directly with magnetic field, meaning a low (safe) frequency regime can only be achieved at very low magnetic field wherein ¹H MRI resolution would be limited.

Fig 3.

a. Energy diagram of the m_S levels of an S = ¹/₂ radical with increasing magnetic field strength. b. Structures of common radicals for EPRI investigations with their resonant frequency at 1.5 T given. Frequencies were calculated from g-values determined in refs. 57–60. Abbreviations: 3-Carbamoyl-PROXYL = 3-carbamoyl-2,2,5,5-tetramethylpyrrolidine-1-oxyl; ¹³C-dFT = tris-(8-hydroxycarbonyl-2,2,6,6-tetramethyl-(d¹²)-benzo[1,2-d;4,5-d’]bis[1,3]dithiol-4-yl)-methyl¹³C radical; 4-OH-TEMPO = 1-oxyl-2,2,6,6-tetramethyl-4-hydroxypiperidine; MTSL = (1-oxyl-2,2,5,5-tetramethylpyrroline-3-methyl) methanethiosulfonate.

To design a useful probe to merge EPRI and MRI, new frequency dependences need to be discovered that enable low frequency analyses at high field. However, the diagrams of the EPR transitions for all organic radicals look like those in Fig. 3. Hence, organic radicals can only be expected to require high frequency microwaves at higher fields. Thus, new probes built on non-organic radical spin systems need to be developed.

The foregoing discussion highlights the need for a class of quantum mimics: electron-spin systems that can be addressed by low-frequency radiation at high magnetic field, like nuclear spins. One key design strategy here is to target a magnetic interaction that competes with the strength of the Zeeman interaction in a field window near the magnetic field of an MRI scanner. If these interactions engender a crossing of the energies of M_S levels, then the potential for low-frequency EPR transitions at high fields exists.

3.3. Specific Examples.

The first class of quantum mimics in this area stem from paramagnetic metal complexes with S > ¹/₂. As a consequence of the higher spin quantum number and spin-orbit coupling that is present in these complexes, zero-field splitting (ZFS, D) splits the multiple |M_S| levels at zero magnetic field (Fig. 4).^[63–68] Importantly, the presence of ZFS uniquely results in some EPR transitions that decrease in energy with increasing magnetic field. An increasing the magnitude of D will push an EPR signal to occur at higher magnetic fields, and since D can vary 100s of cm⁻¹ in magnitude depending on the molecule,^{[69, 70]} it seems possible to generate low-frequency EPR signals from 0 to 10s, if not 100s of T.

Fig 4.

a. M_S level energies as a function of magnetic field (B) for an S = 1 system with D > 0. b. Example structures of S = 1 molecules with zero-field splittings that produce crossing points at the indicated magnetic field range. c. Common EPR band labels with relevant microwave frequencies. d. First L-band EPR spectrum for Cr³⁺ and corresponding structure of the molecule on which it was recorded. Color code for structures: light green, hot pink, light pink, very light pink, yellow, red, blue, and gray spheres correspond to Ni, Cr, V, B, Cl, O, N and C atoms, respectively. Crystal structures are from refs 65–68. Spectra in d are replotted from ref 68.

Low-frequency EPR analysis of metal complexes first started with L-band (ca. 1–2 GHz) EPR measurements of Mn²⁺ and VO²⁺ aquo complexes by Utsumi et al. in 1992.^[71] The reported L-band spectra showed peaks over a 50 mT window (for Mn²⁺) and a 90 mT window (for VO²⁺). In the Mn²⁺ case, we note that the magnitude of D is typically small, usually less than 0.1 cm⁻¹ for [Mn(H₂O)₆]²⁺.^[72–74] As such, potential low-frequency regimes can only be expected at lower magnetic field strengths, like radicals. For the VO²⁺ system, the compound is S = ¹/₂, so zero-field splitting is impossible. Any levels crossings that occur will do so depending on the hyperfine interaction with ⁵¹V, which is typically small (ca. 0.015 cm⁻¹ or less), and hence any crossing points should be expected to show up only at low field. Indeed, the spectra show evidence of such transitions as low as 5 mT, though precise features akin to the eight-line spectrum of the V⁴⁺ (I = ⁷/₂) ion seen at X-band are not resolvable.

Cu(II) systems, albeit having an electronic spin S = ¹/₂, were the next metal system studied with L-band EPR, likely due to the simplicity of the low-spin system. As with VO²⁺, any crossing points would stem from the hyperfine interaction, which is slightly stronger than VO²⁺ on average. Hence, crossing points can only be expected at low magnetic fields. Indeed, the low-frequency EPR spectra for the selected O- and N-coordinated tetradentate Cu(II) complexes only gave peaks over an 60 mT field range.^{[75, 76]}

In more recent studies, high-spin Co(II) (S = ³/₂) has been examined via low-frequency EPR in both the solid and solution phases. In the first of two publications, the investigated Co(II) ion was substituted in Zn(II) sites in Ba[(Zn_1-yCo_y)_1/3Ta_2/3]O₃.^[77] Similar to in the aforementioned cases with VO²⁺ and Mn²⁺,^[71] the spectra were considerably broad (spanned 60 mT) and few of the hyperfine features are able to be resolved. In a separate study, however, sharp peaks were found from studying Co(EDTA) complexes (EDTA = ethylenediamine tetraacetic acid) in 1 mM frozen solutions by both S-band (3.229 GHz) and L-band EPR.^[78] The improved signal resolution in these two studies is a testament to the advances that have been made in low-frequency EPR instrumentation, which ultimately allow for better detection of S > ¹/₂ metal complexes towards their mimicry of nuclei.

Expanding upon the growing library of metal ions studied with L-band EPR and attempting to solve a major hurdle for metal-based EPRI, we studied a series of S = ³/₂ Cr(III) tris-diamine complexes to elucidate a design strategy for mitigating spectral broadening.^[68] The results of this study suggested that a more distorted coordination sphere produced sharper spectra, which was supported by molecular dynamics simulations demonstrating a smaller variance in Cr–N bond lengths in solution.

Separate work has focused on tuning zero-field splitting in encaged molecules with the goal of knowing how to design the crossing point for low-frequency analyses. Many studies have developed magneto-structural correlations,^{[69, 79–84]} giving chemists tools to tailor molecules for specific D values. The most popular goal for said tailoring efforts is to achieve large D values for designing single molecule magnets. But, D can vary up to 100s of cm⁻¹ for metal ions, which places crossing points only at extremely high magnetic fields relative to the fields of MRI scanners. Hence, figuring out how to design small D values is now a renewed interest! A recent study of ours demonstrated an 11 cm⁻¹ range in D with minor chemical changes to the ligand shell in a series of Ni(II) clathrochelates.^[65] Importantly, this level of tunability allows for an 11 T control of the M_s = 0 and M_s = −1 crossing, and ultimately the field at which L-band EPR resonance would occur.

Another potential route to safe, low-frequency transitions at high magnetic fields can be found in multinuclear complexes with magnetically coupled ions. In an example dinuclear system, two ions can have their magnetic moments aligned together with or against the field (S = 1), or have their moments aligned opposite of each other (S = 0, Fig. 5a). The energy levels at zero-magnetic field are split by the exchange coupling constant J. As a result, levels can potentially cross with increasing magnetic field, analogous to the case with D in the preceding mononuclear examples (Fig. 5).^{[85, 86]} Indeed, the crossing point here also scales with increasing J, also analogous to D. A similar arrangement of levels could also be found in higher nuclearity systems, though the numbers of levels are higher and distribution in energy more complex. Note, however, that EPR transition between crossing M_S levels is a transition between different spin states of the molecule, which is forbidden by the EPR selection rule.

Fig 5.

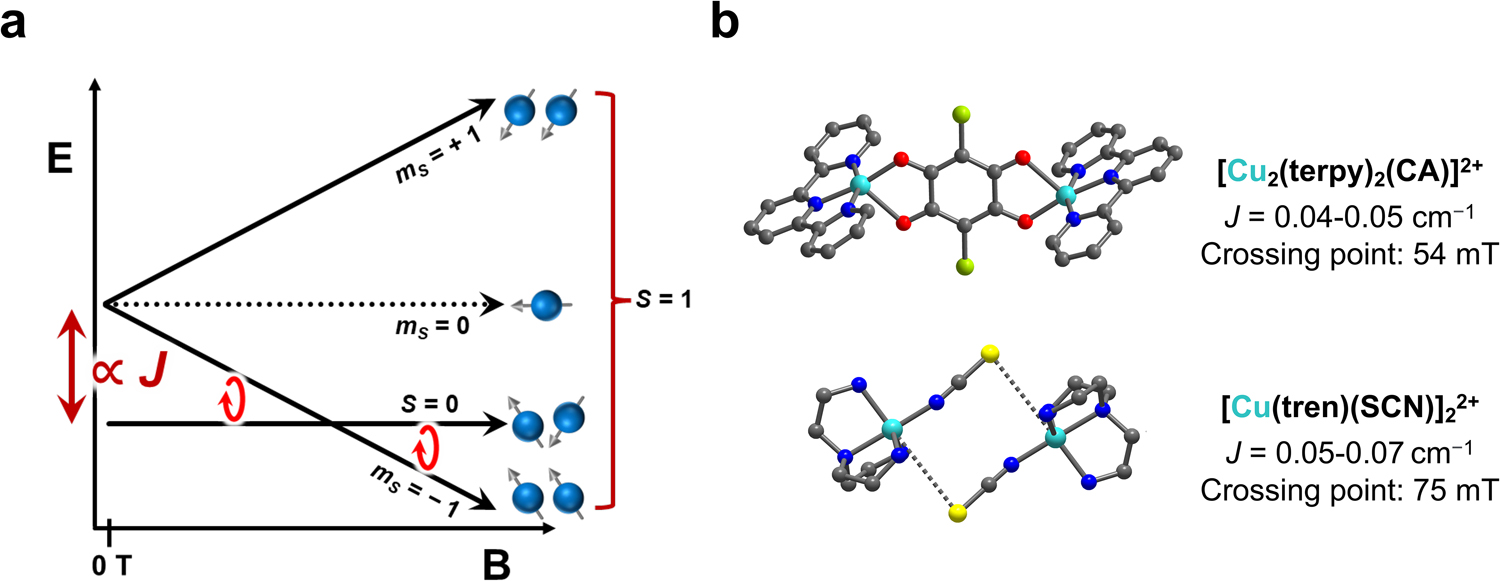
a. Depiction of m_S level energies for an exchange coupled pair of S = ¹/₂ spins and antiferromagnetic coupling. b. Example structures of molecules that exhibit the singlet-to-triplet transition. The crossing point for low-frequency work is highlighted for these species. Color code for the structures: bright blue, yellow, light green, dark blue, red, and gray spheres are Cu, S, Cl, N, O, and C atoms, respectively. Crystal structures from refs 85 and 86.

The first of these forbidden transitions have been observed in weakly coupled dicopper complexes [Cu₂(terpy)₂(CA)](PF₆)₂,^[85] and [Cu(tren)(NCS)]₂(BPh₄)₂.^[86] These systems show those forbidden transition with intensities a fraction of that for the allowed EPR transitions. However, this has only been observed at more conventional (higher) wavebands (X- and Q-band). Indeed, the coupling is so weak that crossing points for these systems do not span out to high field (Fig. 5). It is nevertheless still highly promising that these transitions (which are forbidden) are observed in the first place.

A separate demonstration of a nuclear-spin-like electron spin occurred with a low-frequency analysis of a tetradecanuclear [Cr₁₂Cu₂F₁₆(O₂CCMe₃)₂₆]²⁻ complex (Fig. 6).^[87–89] In the study of this molecule by Prozorov and coworkers, tunnel diode oscillator measurements showed many potential crossing points for low-frequency EPR over a wide, high-field window, from 2.7 to 10 T. The number and dispersion of the crossing points here result from the complexity of the spin system. First, the Cr and Cu ions in these species each possessed their own respective spins (³/₂ and ¹/₂ for Cr and Cu, respectively) and g values (1.98 and 2.1 for Cr and Cu, respectively). Second, there are also several different J values: J_{Cr•••Cr} = 10.8 cm⁻¹, and two distinct J_{Cr•••Cu} values of 39.8 and −14.5 cm⁻¹. These interactions combine to create a very complex M_S-level energy diagram that places low-frequency crossing points over the enormous field range. Note that this specific study probes the Cr₁₂Cu₂ spin system with radiofrequencies (10s of kHz) at high fields. Hence, the exciting result is much closer to a true demonstration of “quantum mimicry” of a nucleus than many of the above-mentioned low-frequency EPR measurements.

Fig. 6.

a. Structure of high-nuclearity complex with 12 Cr(III) S = ³/₂ and 2 Cu(II) S = ¹/₂ spins. Color code for structure: Pink, blue, green, red, and gray spheres are Cr, Cu, F, O, and C atoms respectively. Counterions and t-butyl groups are not shown for clarity. b. The exchange coupling between the many ions produces a complex diagram of M_s levels with many crossing points that span a 14 T window. Radio-frequency spectroscopic measurements revealed these crossing points (bottom panel). Crystal structure is from ref 89. Data is replotted from ref 88.

3.4. Outlook for Low-Frequency EPR of Metal Complexes.

The low-frequency EPR properties of high-spin metal complexes (whether mono or polynuclear) is an almost completely unexplored area of spin physics. Indeed, the foregoing summary of the entire area featured only a handful of metal ions and molecules. We note that in many of the foregoing studies, a persistent challenge toward applicability are the wide linewidths of the low-frequency resonances, which are much wider than radicals^{[68, 90–92]} and diminish possible imaging resolution. Another potential challenge to application could be the lower signal to noise from a smaller EPR gap. Continued innovations in instrumentation will likely allow for higher signal to noise and sharper resolution measurements to overcome these challenges. Indeed, modern low-frequency analyses in some cases provide sharper linewidths than high-frequency EPR.^[93] Hence, we think these complexes exhibit substantial promise as quantum mimics, not only for enabling fundamental studies of the untrodden domain of low-frequency/high field spin physics, but also the development of new biomedical imaging probes and techniques.

4. Quantum Mimic Class 2: Nuclear-Spin Mimics of Electrons

The second class of quantum mimics we cover are those where metal complexes that feature magnetic nuclei (e.g. I = ⁷/₂ ⁵¹V or I = ⁷/₂ ⁵⁹Co) mimic the environmental sensitivity or other magnetic resonance characteristics of unpaired electrons. In doing so, these molecules are, in effect, producing nuclear-spin quantum mimics of electrons.

4.1. Basics of Environmental Sensitivity of Spins.

Environmental sensitivity of the magnetic resonance signals of electrons are generally larger than nuclei for two key reasons (Fig. 7). First, the electron has a relatively large magnetic moment (ca. 3 orders of magnitude larger than a nucleus), which enables the electron to detect magnetic fluctuations further from the location of the electron than a magnetic nucleus. Second, electrons are delocalized over molecules and participate in bonding. Hence, chemical changes on many different sites in a molecule, indeed, any that alter the electronic structure, can be expected to impact the electron over MHz and greater energy scales. In contrast, the nucleus is limited to detecting changes directly in its local chemical space, i.e., the bonds attached to it on Hz energy scales, or through dipolar effects on kHz energy scales.^[94] Finally, again owing to the large magnetic moment, electrons can be manipulated on fast timescales, as demonstrated by π-pulse lengths of 10s to 100s of ns in a conventional pulsed EPR instrument. In contrast, π-pulse lengths for magnetic nuclei are often 10s of μs or more on standard NMR spectrometers.

Fig. 7.

a. Comparison of the advantages of electronic spins (unpaired electrons) versus those of nuclear spins (magnetic nuclei). b. Graphical depiction of dipolar versus the Fermi-contact mechanisms for electronuclear hyperfine coupling.

Nuclear spins interact with nearby electrons through hyperfine interactions (Fig. 7), which can directly affect magnetic resonance signal.^{[95, 96]} The hyperfine interaction predominantly stems from a combination of (1) the isotropic Fermi contact interaction between the electron on a nucleus and that nucleus and (2) the dipolar interaction, which can occur through space. The Fermi contact interaction is prevalent when unpaired electrons are in an s orbital or an orbital mixed with one, because wavefunctions for these orbitals do not have nodes at the nucleus. In contrast, the dipolar interaction can occur between any electron spin/nuclear spin pair.

The hyperfine interaction has two important spectroscopic consequences. First, it governs the energy spacings between the electronuclear, M_S-M_I-coupled levels, which in turn tunes the frequencies that the spin system responds to. The hyperfine interaction also governs the M_S and M_I composition of a given level at a given field and frequency.

The hyperfine interaction may be engineered in molecules by changing oxidation state, geometry, or orbital mixing, which allows for synthetic control.^{[64, 97]} Hence, phenomena that affect an unpaired electron coupled to a nucleus should drive changes to the magnetic resonance properties of the magnetic nucleus. Indeed, it is generally challenging to spectroscopically interrogate magnetic nuclei coupled to unpaired electrons, though as we show, exciting recent results are forcing a revision of that attitude.

4.2. Need for Mimicry of Electrons by Magnetic Nuclei.

Common applications for molecule-based spins are biomedical imaging and quantum computation, and there are serious deficiencies in the use of unpaired electrons in both applications. In imaging-based techniques, we saw in section 3 that undesirable high-frequency microwaves are commonly required for high-field electron magnetic resonance techniques. A second challenge here is that for many species with unpaired electrons, particularly metal ions, relaxation times are extremely fast at high temperature in solution, which broadens spectra and precludes high resolution sensing or otherwise destroys the measurable signal.^[98] In quantum information processing, generally fast relaxation is also a challenge to address because fast relaxation limits the stability of data stored in each spin system. The fast manipulation times of electrons are advantageous in this light because one can utilize more pulses for either more sensitive environmental detection or faster computation in a given period.

Magnetic nuclei are advantageous over electrons for the mentioned applications because they, in contrast, typically have long relaxation times at room temperature, low temperature, and in solution. Furthermore, magnetic nuclei can be addressed by safe, low-frequency radiowaves, which is advantageous for bioimaging. However, the environmental sensitivity of magnetic nuclei is generally weaker than unpaired electrons, which affects their use as spectroscopic readout of local chemistry and produces long manipulation times.

Magnetic nuclei of metal ions are the most promising for designing “electron-spin-like” properties, because many of the same chemically tunable handles applied to electron spins can be applied to metals. For example, “high-spin” isotopes with I > ¹/₂ have the nuclear quadrupolar interaction, which is the nuclear spin analogue to the commonly observed zero-field splitting in S > ¹/₂ metal complexes.^[99] The quadrupolar interaction is absent for commonly investigated, low-mass nuclei because I = ¹/₂ (e.g. ¹H, ¹³C, ¹⁵N, ¹⁹F, ³¹P), whereas I > ¹/₂ states are far more common for metal ions. The quadrupolar interaction importantly controls magnetic resonance relaxation times, frequencies, and is tunable by the geometry of the ligand field, similar to zero-field splitting.

A second way in which metal-ion magnetic nuclei can be viewed as mimics of electron spins is through the direct connection between the chemical shifts and electronic structure. This relationship is captured by Ramsey’s equation for the paramagnetic shift (paradoxically, not requiring actual open-shell ground states).^[97] Hence, variation in ligands can be used to draw linear correlations between chemical shift and electronic structure, as has been done for ⁵⁹Co and ⁵¹V nuclei, among others.^{[100, 101]}

For these and the other reasons above, metal-ion nuclei seem poised for application in many next-generation spin-based applications. Yet, the environmental sensitivities of magnetic nuclei are still relatively small, so understanding how to make the sensitivity more “electron spin like” is an advantage for bioimaging applications.

Importantly, and beyond applications, a fundamentally important goal of this type of quantum mimicry is simply understanding how a strong hyperfine interaction between a nucleus and an electron affects the properties of the nucleus: how fast/slow will electromagnetic radiation flip the spin? Are its properties environmentally sensitive and how so? etc. In this light we have yet to understand what types of mimicry are possible, and even generating proof-of-concept systems is of paramount importance. In the following subsection we describe these systems and how hyperfine interactions directly enable their existence.

4.3. Specific Examples.

The first set of quantum mimics in this class are ⁵⁹Co magnetic nuclei with nuclear magnetic resonance properties that are highly temperature dependent. The possibility of exploiting this sensitivity for noninvasive thermometry was raised decades ago, when Co(III) complexes were identified as having extremely high temperature dependences for their chemical shifts, on the order of 1–3 ppm/°C.^{[102, 103]} This range is orders of magnitude higher than what is typical for other conventional nuclei (e.g ca. 0.01 ppm/°C for ¹H,^[104] 0.05 ppm/°C for ¹⁹F).^[105] Relatively recently, some of us and others have sought to understand how to use molecular design to amplify temperature sensitivity, relying on temperature-dependent structure to drive a temperature sensitivity for the paramagnetic shift. We have made useful connections between molecular structure,^[106–108] vibrational spectra,^[109] and temperature sensitivity. We have also shown that in nearly all cases relaxation times values remain longer (100s of μs and greater) by orders of magnitude compared to electron spins under the same conditions.^[108] But, these specific efforts did not bring the temperature sensitivity to electron spin levels.

We recently demonstrated electron-spin-like temperature sensitivity in a ⁵⁹Co magnetic nucleus using not the paramagnetic shift, but the hyperfine interaction.^[110] The molecules of relevance here are of the formula [(CpCo(OP(OR)₂)₃)₂Co]⁺ (R = Me, Et, t-Bu, see Fig. 8 for one structure).^[111–114] This species contains a ⁵⁹Co nucleus that is NMR active and undergoes spin crossover from an S = 0 to S = 2 state above room temperature. The spin crossover effect is temperature dependent and drives a temperature dependence of the hyperfine interaction, which in turn drives a temperature dependence of the ⁵⁹Co NMR peak, up to 150 ppm/°C depending on the R group. This temperature dependence is significant and eclipses other records for ¹H (14 ppm/°C),^{[115] 31}P (34 ppm/°C),^[116] and ⁵⁹Co systems (3.15 ppm/°C),^[102] indeed, setting a record for all nuclei. If the chemical shift is converted to frequency, then the 18 kHz/°C temperature sensitivity rivals the 74 kHz/°C temperature dependence of the electron paramagnetic resonance signal of the nitrogen vacancy defect – one of the most exciting electron-spin systems proposed for thermometry applications.^{[117, 118]} Hence, this system is a nuclear spin that mimics the temperature response of an electron spin.

Fig. 8.

Molecular structures of notable ⁵⁹Co quantum mimics as determined by single-crystal X-ray diffraction experiments. The complex on the left exhibits one of the highest temperature sensitivities of the chemical shift for all compounds and is on part with the T-dependence of the EPR resonance of the unpaired electron in the nitrogen vacancy defect. The molecule in the middle, Co(acac)₃, held the prior record for ⁵⁹Co NMR thermometry starting in 1980. The molecule on the right has a relatively lower sensitivity but is highly chemically stable, which is an advantage for bioimaging. Crystal structures are from refs 111–113.

Molecular design strategies also recently enabled a nuclear spin to respond to electric fields, analogous to an electron.^{[119, 120]} The key demonstration of this effect was made with a Tb phthalocyanine complex, abbreviated to TbPc_2. TbPc₂ has a J = 6 electronic ground state (note that this J does not refer to the exchange coupling constant, as discussed in section 3.3, but instead the total angular momentum composed of an orbital component L and spin component S) and a nuclear spin of I = ³/₂ from the ¹⁵⁹Tb nucleus. The coupling of these spins and the nuclear quadrupolar coupling produces a multitude of unevenly spaced energy levels that can be addressed. The exciting point, here, is the possibility of controlling the ¹⁵⁹Tb nucleus amongst the m_I levels using an electric field to modulate the hyperfine interaction. Electrons are easily controlled by electric fields, and in a sense, the molecule described here is therefore enabling a nuclear spin to mimic an electron spin’s response to an electric field.

Other lanthanide complexes also show promise as valuable platforms to study magnetic nuclei mimics of electrons. We draw attention to one particular system, Yb(trensal), of the [Ln(trensal)] series (H₃trensal = 2,2’,2’ ’-tris(salicylideneimino)triethylamine).^[121–123] The I = ⁵/₂ ¹⁷³Yb nucleus provides strong hyperfine interaction with the electronic effective spin S = ¹/₂ (here, J = ⁷/₂). An important aspect of this system is that the ¹⁷³Yb nuclear spin in the complex can be addressed directly by NMR – an unusual capability.^[124] The system exhibits superposition lifetimes (T₂) at 1.4 K that are relatively short (ca. 50–60 μs) for nuclei, but relatively long for electrons under these conditions. Importantly, the magnetic nucleus can be controlled extremely fast in this complex. The timescale to control a spin is represented by the amount of time it takes to flip the spin under the action of a π pulse in an NMR or EPR experiment, or the period of the oscillation in a nutation experiment (Fig. 9).^[125–127] For most nuclei, this time length is 10s of μs, while electrons are 10s of ns. Yb(trensal) is therefore remarkable because the hyperfine interactions present in the species produce the remarkable ability to control the magnetic nucleus on a timescale close to what is expected for an electron.

Fig. 9.

a. Crystal structure of TbPc₂ (Pc = phthalocyanine anion/dianion), which was used for the demonstration that one can control the I = ³/₂ ¹⁵⁹Tb nucleus of this complex with electric fields through a hyperfine coupling interaction. b. Crystal structure of Yb(trensal) and the nutation experiment, which demonstrates that a π pulse of the m_I = ¹/₂ to m_I = ³/₂ (high-field labels) transition is possible on a 350 ns timescale, which is closer electron spin timescales (particularly long-pulse experiments) than magnetic nuclei, which are closer to 10s of μs. c. Crystal structure of VO(TPP) (TPP = tetraphenylporphyrin) and an echo decay curve for the m_I = +¹/₂ to m_I = +³/₂ transition for the ⁵¹V nucleus that demonstrates superposition collapse over nearly 100 μs timescale. Inset: The timescale of the echo decay, T₂, increases with increasing magnetic field. These T₂ values are much larger than are typically found for electron spins under the same experimental conditions. Dark purple, dark teal, pink, blue, red, and gray spheres are Tb, Yb, V, N, O, and C atoms, respectively. Crystal structures are from refs 125–127. Data in b and c replotted from refs 124 and 133, respectively.

Attempts to create similar systems out of transition metal nuclei are also underway. Vanadium complexes are of particular interest, as these species are often characterized by S = ¹/₂ (for the V(IV) ion) and the 99.85% natural abundance I = ⁷/₂ ⁵¹V nucleus. The electronic spin is generally characterized by long superposition lifetimes,^{[128, 129]} as is the nuclear spin of the ⁵¹V nucleus, the latter attributable to the generally low nuclear quadrupole coupling of the nucleus.^{[130, 131]}

One system of note here is [VO(TPP)] (vanadyl tetraphenylporphyrinate) and its use in tackling an interesting challenge via quantum mimicry. One of the advantages of the ⁵¹V system is an abundance of m_I levels, which offers the ability for encoding more information per-unit than an I = ¹/₂ system that has only two levels.^[132] However, it is challenging to individually manipulate each pair of these levels in a V(IV) species, as the spacings between all m_I pairs are the same frequency when the quadrupolar interaction is small. This limitation was overcome by taking advantage of the anisotropy of the hyperfine interaction, which then splits the levels by acting as an “effective quadrupolar coupling” that is larger in magnitude than the true one for the ⁵¹V nucleus.^{[133, 134]} Again, this molecule is particularly exciting as the ⁵¹V nucleus of the V(IV) ion is directly addressable with NMR. Furthermore, the ⁵¹V nucleus here displays relatively long superposition lifetimes relative to unpaired electrons, as revealed by Hahn-echo experiments (Fig. 9). Like the Yb example above, we think this system is a promising platform to study the ways in which quantum mimicry manifests.

4.4. Outlook on Electron Spin Mimicry by Nuclei.

Nuclear spins that mimic electron spins are only just now being identified, as exemplified by the summary of the field above including only a handful of different complexes. Yet, the chemical diversity in these systems (transition metal vs. rare earth, spin-crossover vs. open-shell vs. closed shell) suggests that these species are simply the beginning of what will be a large field of quantum mimics, especially if the latter species can be engineered to enable solution-phase analyses.

5. Quantum Mimic Class 3: Molecular Mimics of Color Centers.

The third class of quantum mimics we cover are molecules that mimic the properties of color centers in diamond. Color centers, also referred to as F centers, are defects within a transparent material’s lattice that impart color. In this review, we focus on diamond, but note that color centers exist in many other materials.^[135] The most important ones for this review are the Nitrogen-Vacancy (NV) color centers which are comprised of a Nitrogen atom and an adjacent, absent Carbon (or vacancy) in the diamond lattice (Fig. 10). The NV⁻ defect is the one of primary interest, though other charge states^[136] and chemical compositions^[137] are being actively investigated.

Fig. 10.

(a) Depiction of NV center in the structure of diamond. Note that the V refers to the vacancy center, not a Vanadium atom. (b) Energy level diagram for the NV center and illustration of the spin-selective, two-step relaxation process that leads to buildup of spin polarization in the m_S = 0 level (red arrows) after irradiation with light (green arrows).

5.1. Basics of Color Center Spin Properties.

The exciting properties of the NV center stem from two features related to its ground state spin.^{[33, 138, 139]} The first is the spin state and its magnetic anisotropy. The NV center has two unpaired 2p electrons and a ground state spin of S = 1. The m_S levels of the ground state spin are split by an axial (D) zero-field splitting parameter of ca. 2.9 GHz (0.097 cm⁻¹), generating a zero-magnetic-field energy diagram like in Fig. 10, where the m_S = ±1 levels are higher in energy than the m_S = 0 level.^[140] Because the magnitude of D is small compared to thermal energy above the lowest temperatures (k_BT = 207 cm⁻¹ at room temperature, for example), all three levels have similar population, in other words, the spins of the NV center are not magnetized, polarized, or aligned with the magnetic field to any large degree.

The second important feature of the NV center is its magnetooptical response. The ground state of the NV center is the S = 1 ³A₂ electronic state, and there is a ³E excited state at approximately 1.945 eV (ca. 15,700 cm⁻¹ or 637 nm) higher in energy. With decreasing energy from this ³E excited state, there is a singlet (S = 0) ¹A₁ excited state, followed by a ¹E state, then finally the ³A₂ ground state (Fig. 10). Upon excitation of the ³A₂ to ³E transition, the photoexcited vacancies can fluoresce back to the ground state, but another option is possible: an intersystem crossing to relax to the ¹A₁ state. Once in the ¹A₁ state, the system can relax to the ¹E state, then to the ground ³A₂ state. In this last step, the system must undergo another change in spin, from S = 0 to S = 1. The conservation of angular momentum is preferred for each intersystem crossing step. The decay from ¹A₁ to ³A₂ is therefore notable, because the system preferentially relaxes to the m_S = 0 level of the ground state ³A₂ manifold to conserve angular momentum. If the system is continuously irradiated with light, these spin-selective processes lead to selective population of the m_S = 0 level of the ³A₂, in contrast to the thermally equilibrated situation where all levels nearly equally populated. Hence, this system is spin polarized. The polarization is extremely high (>99.7 %) and can be built up in an extremely short period of time (< ms).^[141] Importantly, the increase of the spin polarization in the m_S = 0 level depletes the photoluminescence of the ³E to ³A₂ ground state. Hence, the spin polarization can be readout by changes in the optical emission. Hence, the NV center exhibits magnetooptical effects, and, excitingly, any environmental and instrumental factors that affect the spin also affect the optical properties.

5.2. Need For Design Strategies of Molecular Mimics of Color Centers.

The color centers of diamond are one of the most exciting systems for quantum applications because of three reasons.^[138] First, the magneto-optical effects enable high sensitivity readout, which means the spins of the individual NV centers can be addressed and controlled as part of a quantum computational scheme. Second, the relaxation times of the spins are long (seconds or longer) in the diamond lattice at high temperature, ensuring that > 10⁵ ns-scale operations are achievable as needed for a computation. Finally, third, environmental factors that affect the spin can be easily readout with high sensitivity optical measurements,^{[142, 143]} which has enabled next-generation quantum sensing applications for, thermometry at the cellular level,^{[128, 129]} nuclear magnetic resonance at the cellular level,^[144] and nanoscale magnetometry on surfaces.^[135]

Molecular mimics of color centers are an exciting area of research because they could be used in the foregoing applications, but with chemical tunability to enable optimization. For example, chemical fine-tuning can be leveraged to understand aspects of the spin polarization build-up and associated relaxation processes to enhance signal-to-noise. At the molecular level, there could be even greater sensitivity to local chemistry than with the NV center of diamond, because of proximity. Indeed, the NV center must be buried 100s of nm deep in the diamond lattice and away from the sensing target to function optimally,^[136] whereas a molecule could potentially approach a sensing target at only Å-level separation. Moreover, the optical properties of molecules are tunable, which would allow for enabling optical readout at different frequencies, or through the low-wavelength window or red that can penetrate the skin to enable bioimaging. This same atomistic level of tuning magnetooptical effects is impossible in the NV center, as the diamond lattice is resistant to chemical change.

Designing a molecular mimic of a color center requires identification of an electronic or molecular structure that enables spin polarization, slow spin relaxation times, or optical addressability. For enabling spin polarization, there should be high-energy states accessible by irradiation that can relax via spin-selective pathways that engender ground-state spin polarization.^[137] For engendering slow spin relaxation, one should design species where there is an avoidance of nuclear spin, as nuclear spins in the ligand shell generally encourage fast relaxation.^{[33, 138]} Finally systems with strong optical excitation/emission are desired, especially those where there are intersystem crossings or other spin-sensitive phenomena.

5.3. Specific Examples of Color Center Mimicry.

In this section, we will cover a handful of selected species spanning inorganic to organic molecular mimics of the nitrogen vacancy center. We will also briefly cover a mimic of Er-based color centers, owing to the importance of this ion in optical communication of quantum information.^[139]

The first molecular quantum mimics of color centers focused mostly on mimicking the slow spin-spin relaxation times, T₂, of the NV center. In these cases, the molecular structures surrounding the metal ions were designed to be analogous to the lattice of diamond. Diamond is composed of carbon, which is 98.84 % naturally abundant in ¹²C, an I = 0 nucleus, and can be isotopically engineered to have even higher abundance of ¹²C.^[140][128] These lattices devoid of spin-having nuclei create a “magnetically quiet” environment that sustains very long (> ms) spin-spin relaxation times for the NV center.^[142] In molecules, relaxation times are in contrast typically < 1 μs, and they are also typically rich in magnetic nuclei such as ¹H (99.97 % natural abundance, I = ¹/₂). Designing molecules without magnetic nuclei, which mimic the diamond lattice, has produced relaxation times that reach orders of magnitude above 1 μs, reaching 100s of μs and approaching ms timescales (Fig. 11).^{[66, 128, 129, 143–146]} In some of these metal complexes, the largest degree of success has deployed a challenging (and odorous) synthetic strategy designing ligand shells composed of C as well as generally nuclear-spin-free S atoms (^32,34,36S, I = 0, 99.2 % natural abundance). Indeed, the current record for spin-spin relaxation times in a metal complex is [V(C₈S₈)₃]²⁻, where T₂ = 0.7 ms. This molecule and others like it are important proofs of concept for how long T₂ can become for metal complexes, but there is clearly more distance to cover to reach those of diamond.

Fig. 11.

a. Structures of color-center mimics composed primarily of nuclear-spin-free elements. Pink, light blue, yellow, dark blue, and gray atoms are V, Cr, S, N, and C atoms respectively; counterions are not depicted for clarity. b. Cr(IV) complexes that exhibit optical spin polarization like the NV color centers. Dark pink, light orange, and gray atoms are Cr, Si, and C, respectively, and hydrogens are not shown for clarity. c. Energy level diagrams for the Cr complexes in b, that demonstrate analogous ground states to the NV center. Useful unit conversion: 10^–5 eV = 2.42 GHz. Crystal structures from top to bottom are from refs 145 and 146 in a, and 62 and 143 in b.

The second set of quantum mimics of color centers focus more on the control of the electronic spin polarization by light. The molecules of primary success here are tetrahedral organometallic complexes of the Cr(IV) ion (Fig 11).^{[66, 144]} The selection of these molecules and this particular ion is a beautiful example of the power of coordination chemistry in quantum mimicry of the NV⁻ center. Cr(IV) has an S = 1 ground state, just like the NV⁻ center. As a result of the strong alkyl σ-donating ligands and a slight compressed tetrahedral distortion, these molecules also have small and positive zero-field splitting values (ca. 2 GHz, or 0.07 cm⁻¹). These zero field splittings are the same sign as the NV⁻ center and closer in magnitude than typical for transition metals, which are often multiple and sometimes 10s to 100s of cm⁻¹ in magnitude.^[99] The small value of the zero-field splitting is important here because it means the compound can be readily analyzed via conventional EPR techniques, and not require challenging high-frequency or high magnetic field instrumentation. Finally, the Cr(IV) complex exhibits a similar electronic structure to the NV⁻ center, with a ground triplet ³A₂ state, an excited triplet ³T₂ state, and an intermediate singlet ¹E state. This arrangement enabled spin polarization to be built up upon shining light upon the compound, the first instance for a transition metal complex.^[66] Beyond this initial discovery, the chemical tunability of these qubits again brought substantial insight into the spin polarization process and how to control the wavelength of the photoluminescence by molecular design.^[144] Other S = 1 complexes of V(III)^[147] and Ni(II)^[148] also show promise for this effect, so these discoveries seem like the opening of a door to a new integrated area of spin and optical spectroscopy.

The third set of quantum mimics center around the optical and spin properties of lanthanide(III) molecular complexes (Fig. 12)^{[149, 150]} Lanthanide defects in ceramics (e.g. Er(III) in Er:Y₂SiO₅, where Er(III) has a J = ¹⁵/₂,)^[151] are an important class of defect because their energy level diagrams can place optical transitions right near 1550 nm, which is the wavelength of low loss for telecommunication across optical fiber. Moreover, the contraction of the 4f orbitals produce generally sharp optical linewidths,^[152] a plethora of energy levels with different J values (again, note that J here denotes the total angular momentum, not exchange coupling), nuclear spins, and in some cases can exhibit long T₂ values (> ms).^{[151, 153]} These color centers are therefore highly promising for enabling quantum information transmission over long distance via photons and interfacing with spin for on-site processing.^[154]

Fig. 12.

a. Crystal structure of a dinuclear Eu complex that exhibits optical polarization of the ground state spin. To the right is the energy level diagram that shows how the excitation proceeds on the ligands (green vertical arrow), which then transfer energy to the Eu ions, and then spin-selective relaxation (red vertical arrow) to the ground state of the spin. b. Crystal structure of mononuclear rare-earth species that follows a similar process to a, but this species builds up a substantial spin polarization of the Eu nuclear spin via spin selective relaxation. Light blue-green, light green, blue, red, and gray atoms are Eu, Cl, N, O, and C atoms, respectively. Crystal structures from top to bottom are from refs 149 and 150.

Recent molecules have been shown to mimic many of the spin-photon interfacial qualities of the lanthanide defects.^{[149, 150]} We highlight two here, a binuclear and mononuclear complex of Eu(III) (Fig. 12). One of the challenges in the photoexcitation of rare-earths is the strong forbiddenness of 4f-4f transitions, and hence, often sensitization via the antenna effect from a ligand is required to effectively photoexcite the rare earth metal. In the binuclear species [Eu₂Cl₆(4-picNO)₄(μ₂-4-picNO)₂]·2H₂O (4-pic-NO = 4-picoline-N-oxide), ligand photoexcitation triggers an intricate cascade of intersystem crossing and energy transfer to promote the Eu(III) ion to the ⁵D₀ state, where it can then relax to the ⁷F₀ state and emit light. This last step to the ⁷F₀ (S = 3, J = 0) ground state of the Eu(III) ion reveals hyperfine structure from electronuclear hyperfine coupling between the Eu(III) electron spin and with the I = ⁵/₂ ¹⁵¹Eu nucleus. What is exciting about this last part is that the transition exhibits spectral hole burning, which indicates that select hyperfine coupled levels are being populated during the decay. Effectively, this result means that pumping light into the ligand shells is producing nuclear spin polarization in the ¹⁵¹Eu nuclei, or that, more simply, ligand photoexcitation is a possible means of controlling the nuclear spin state in a Eu(III) complex.

In the mononuclear complex (pip)[Eu(BA)₄] (BA⁻ = benzoylateonate and pip⁺ = piperidin-1-ium), an extremely sharp optical transition enables complete nuclear spin polarization. This system exhibits the same ⁵D₀ → ⁷F_J transition as the dinuclear species, again driven by sensitization from the nucleus. But here, the linewidth is an incredibly small value: 0.007 nm (compare with 10s of nm or more for transition metals). This linewidth allowed exceptional control of the nuclear spins, enabling optical polarization of the nuclear spins entirely into the m_I = ±¹/₂ levels. As nuclear spins often exhibit extremely slow spin relaxation times (here they even measure these times in the 100 ms range for the ¹⁵¹Eu nucleus), these results are an exciting demonstration of the feasibility of interfacing photons with nuclear spins in tunable molecular species.

5.4. Outlook for Color Center Mimicry.

Defects in diamond and other solids are a popular target for physicists to demonstrate new ideas of spin physics, and in this section we have shown that molecules can mimic many of the quantum properties of the defects. As such, molecular mimics of color centers are a highly promising arena for fundamental studies. However, there are certain aspects of molecules stemming from their chemical tunability that mean many exciting new directions can be envisioned. For example, molecules have chemical sensitivity to changes in pH or changes in redox. The above optical/spin mimicked properties could be harnessed with this reactivity for new biomedical optical imaging techniques based on optically detected magnetic resonance, if the optical responses were tailored to the near-infrared window in biological tissue. Second, we note that the above studies on optical/spin interfacing in molecules do not focus on circularly polarized light. Circularly polarized light is one way of storing quantum information in the polarization of photons. Recently, molecular complexes, some containing rare-earth ions,^[155] have been shown to emit and interact with this light. To what extent this type of polarized light will control the electronic and nuclear spins of the molecules, like the examples above, is an exciting open question.

6. Quantum Mimic Class 4: Molecular Mimics of Atomic Clocks

The final class of quantum mimics we cover are molecules designed to mimic the properties of atomic clocks. Atomic clocks are isolated atoms or ions (via a trap) that possess unpaired electrons and/or magnetic nuclei and are a centrepiece technology in the second quantum revolution (Fig. 13).^[156]

Fig. 13.

a. Depiction of a conventional EPR transition, where the change in the frequency of the transition varies with magnetic field. b. Depiction of a clock-like EPR transition, where the variation in frequency with applied field is zero at the avoided crossing. c. Graphical depiction of the 9.192 GHz hyperfine interaction between the S = ¹/₂ and I = ⁷/₂ spin in the ¹³³Cs atom. d. Picture of the NIST F-2 Cesium fountain atomic clock. Credit: National Institutes of Standards and Technology. e. Calculated M_F level energies as a function of magnetic field for the ¹³³Cs atomic clock, calculated with a g-value of 2.002 and hyperfine coupling value of 2.298157943 GHz (¹/₄ of the 9.192631770 GHz resonant frequency for the ¹³³Cs atomic clock). Blue circles highlight the allowed EPR transitions, and the one that is second from the left is more clock-like than the ones at higher field.

6.1. Basics of Atomic Clock Properties.

The utility of the atomic clocks arises in part because of the unique spectroscopic transition that these species display, which is extraordinarily insensitive to variations in local electric and magnetic fields. As a result, the frequency of the transition is extraordinarily robust, which enables the frequency to be used as a timekeeping element, like the vibrations of quartz that guide the movement of a wristwatch.

The atomic clock transition in trapped atoms and ions arises because of electronuclear hyperfine interactions that create an avoided crossing (Fig. 13). At zero magnetic field, a hyperfine magnetic coupling between the unpaired electrons (or spin, S) of the atom and the nuclear spin of the atom (I) produce a spectrum of coupled states of total angular momentum F (F = S + I, S + I – 1, … , S – I), split in energy by the magnitude of the hyperfine coupling interaction A. Each F state has M_F sublevels, defined by M_F = |F, F – 1, …, –F|. The situation is very similar to the M_S levels for a ground state spin S with multiple coupled electron spins. Under an applied magnetic field, the M_F levels split in energy, and some M_F levels may cross with increasing magnetic field, if the magnetic field stabilizes M_F values that are in contrast destabilized by the hyperfine interaction. At these potential crossing points, levels with the same M_F values do not cross and instead mix, which causes them to bend away from each other near the crossing points.

The avoided crossing imparts a magnetic field insensitivity on the energy difference between the M_F levels because slight variations in the magnetic field do not perturb the ΔE, and hence, the frequency f is field-independent as well. Compare instead to lower or higher magnetic fields, where each M_F level moves substantially with magnetic field, and the gap between the M_F levels varies substantially. This insensitivity of f ensures a clock transition is robust to local fluctuations of magnetic field inside the device.

6.2. Need for Design Strategies for Molecular Mimics of Atomic Clocks.

Molecules that mimic the spectroscopic avoided crossings of atomic clocks in their electron paramagnetic resonance properties have been proposed for applications as molecular qubits in quantum information processing (QIP).^{[138, 157–159]} In QIP, the relevant parameter describing the utility of a qubit is the spin-spin relaxation time, T₂, for the unpaired electrons, which conveys how stable encoded data is. A short T₂ implies that a qubit candidate would only store information for a short an amount of time, potentially too short to perform a calculation. The governing motivation to design atomic-clock analogues for this application is that at the clock transition, the system should be insensitive to local magnetic field fluctuations, which are the primary environmental factor that will shorten T₂ for unpaired electrons.^{[33, 160]} Hence, one might expect that a molecule which mimics the quantum properties of an atomic clock would have a substantially long T₂.

In designing a quantum mimic, all one needs to do is to figure out how to design avoided crossings into the energy level diagrams for their spin systems. The original atomic clocks used hyperfine coupling, however, there are many other magnetic interactions that can afford avoided crossings, including the crystal electric field,^[161] zero-field splitting,^[99] or magnetic exchange coupling.^{[162, 163]} It is for this reason that metals are the most prolific for the demonstration of clock-like properties owing to high natural abundances of isotopes with nuclear spin, prevalence of large-spin ground states, and high spin-orbit coupling constants. We do note a relatively recent acknowledgement that some specific organic species may also be useful quantum mimics of atomic clocks, if they contain N-centered radicals.^{[164, 165]} The main design strategy in all of these cases is that the magnetic interaction has to compete with the energy of the spin’s interaction with an applied magnetic field. In other words, the two interactions must stabilize different ground levels, as this will create crossing points with changing field that turn to avoided crossings.

6.3. Specific Examples of Molecular Mimics of Atomic Clocks.

Hill and coworkers reported the first test of the atomic clock mimicry design principle in the mononuclear holmium complex [Ho(W₅O₁₈)₂]⁹⁻ (Fig 14).^{[166, 167]} In this species, the avoided crossing is engineered through using a crystal electric field. The Ho(III) ion is J = 8 and I = ⁷/₂ (for 100% abundant ¹⁶⁵Ho isotope). The crystal field in the polyoxometalate complex stabilizes the M_J = +/−4 doublet at zero magnetic field, whereas the applied magnetic field stabilizes the M_J = −4 level (and the hyperfine coupled levels stemming from M_J = −4). The avoided crossings of 0.306 cm⁻¹ (or 9.18 GHz) appear at magnetic fields below 1 T, which allowed X-band (ca. 9 GHz) EPR spectroscopy to be used to study the properties of the clock transitions.^{[167, 168]} They found a factor of four enhancement in T₂ (from 2 to 8 μs) near the clock transition. The maximum T₂ value obtained here, though modest contained to record-holding systems (700 μs for [V(C₈S₈)₃]²⁻),^[128] nevertheless was the first demonstration of designing a molecule to mimic the properties of atomic clocks. This singular result inspired many further studies investigating how aspects of molecular structure^[169] and vibrations^[170] control the properties of the mimic, and also deeper investigations of spin relaxation in these unique species.

Fig. 14.

Crystal structures of recent atomic clock mimics. Light green central atoms are the indicated metal. Otherwise, light blue, red, and gray atoms are W, O, and C atoms, respectively. Crystal structures are from refs 166 and 175.

The first molecular system to mimic an atomic clock by creating avoided crossings through the hyperfine interaction was based on the tetracarboxyphenylporphyrin complex of Co(II).^[171] This molecule is a low-spin (S = ¹/₂) square planar cobalt complex, and in the instance where the clock-like behavior was observed, this unit was restrained within the structure of a metal organic framework of the PCN-224^[172] structure type. The species exhibits a uniquely large hyperfine coupling interaction, 1123 MHz,^{[171, 173, 174]} when most transition metal complexes exhibit hyperfine coupling interactions of 100s of MHz. The magnitude of the hyperfine interaction here is driven by 4s-3d_z2 mixing, which enables the unpaired electron to approach closer to the nucleus for stronger coupling. Importantly, the coupling produces an avoided crossing with a gap of ca. 3.6 GHz, allowing for S-band (3–4 GHz) EPR spectroscopy to be applied to study the physics of the clock-like EPR transition in this species. Analyses of this compound showed an increase in T₂ by an order of magnitude (1.9 to 14 μs) relative to the unclock-like transitions, and this species was the first atomic-clock mimic exploiting a transition metal ion.

A later instance of mimicry of an atomic clock in a rare-earth complex came from a remarkable set of Lu(II) complexes (S = ¹/₂, J = ¹/₂),^[175] which possess a single unpaired electron in a 5d¹ electron configuration (Fig. 14). In this species, the geometry of the organometallic compound enables 6s-5d mixing like the Co example above. However, the larger Z_eff of the Lu atom (relative to Co above) enables even stronger hyperfine interactions between the unpaired electron and the ¹⁷⁵Lu nuclear spin (I = ⁷/₂), on the order of 3,500 MHz. The hyperfine coupling in this case generates an avoided crossing addressable by X-band EPR spectroscopy between 300 and 500 mT, which was used to demonstrate that this species exhibited atomic-clock quantum mimicry behavior. T₂ increased from 1 to 3.5 μs near the clock transition, but the unique feature of this particular atomic-clock mimic is that the property was observed in solution – all previous analyses of clock-like EPR properties in molecules had only been done in the crystalline state. The observation in solution therefore opens the door to studying impacts of different solvent environments, frozen glasses, and other local chemical tuning on the clock transition. More broadly, the studied compounds converged two rarely associated fields, synthetic organometallic chemistry, which created the incredibly rare Lu(II) oxidation state, and atomic clock physics, which enabled the lengthening of T₂.

Atomic-clock quantum mimics based on zero-field splitting are relatively less explored than the above hyperfine and crystal field mechanisms. Yet the possibility of creating quantum mimics with this parameter is still clear. At zero-applied magnetic field, the axial zero-field splitting parameter D for a spin S splits values of |M_S| away from one another. For example, the M_S = ±1 levels and M_S = 0 levels are split by D. A second parameter, the transverse zero-field splitting E, mixes, and therefore splits M_S levels with the same |M_S| (i.e. the ±1 pair) away from each other. Near zero magnetic field, these splittings create an avoided crossing. Several S = 1 compounds have been studied to examine whether these zero-field avoided crossings mimic atomic-clock behavior. The first of which was a multinuclear ring-like complex of Cr₇Mn composition with an S = 1 ground state.^[176] In this system, the T₂ climbed from ca. 100 to 400 ns near zero-field where the clock transition (originating from E) occurred. To the best of our knowledge, this is the lone example of using E to create a clock transition in a multinuclear species. However, sizable E values are quite common for S = 1 systems, e.g. Ni(II), and a recent study used heat capacity measurements to identify an avoided crossing,^[177] though the measurement of T₂ has yet to be performed. A recent study by Bayliss and co-workers, however, merged concepts of atomic clock and color-center mimicry into the same molecule, using slight environmental tuning to tweak E and enable a clock-like transition in the optically polarizable color-center mimic Cr(o-tolyl)₄.^[178] In this case, T₂ was increased from 2 to 10 μs as a result of the clock-like transition in a nuclear-spin-rich environment, which represents a substantial increase.

6.4. Outlook for Atomic Clock Mimicry.

The above examples are the only known instances of clock-like transitions in molecules. Hence, there is much that needs to still be understood in these exciting systems, from spin dynamics mechanisms to the consequences of coupling multiple molecular clock mimics together.^[179] Given the prevalence of magnetic interactions that can potentially give rise to avoided crossings, the molecular magnetochemist can foresee see an array of potential molecules that could display even better mimicry capabilities than are reported above. Applications for clock-like spins in molecules may extend even past the relatively focused T₂ engineering, and potentially be harnessed for efficient spin state transitions in photoexcited states^[180] or new electronic spin manipulations.^[181] It is the opinion of the author that we have barely scratched the surface of what is possible with these exciting systems.

7. Final Comments

Molecular inorganic chemistry has harnessed mimicry ideas for decades to enable both fundamental understanding and advance toward new applications. We focus above primarily on magnetic phenomena and how the idea of quantum mimicry can be applied to the control of magnetic properties. In some cases we specifically target species that cannot be isolated in molecular form and instead are part of modern-era quantum devices, e.g. atomic clocks. Yet we think the scope of quantum mimicry can be considerably broader, extending even into biomimetic chemistry! For example, the light harvesting in Photosystem-II has been proposed to harness vibronic coherence, or vibration-based superpositions, to achieve near unity efficiencies.^[182] Recent work on photoactive transition metal complexes is beginning to demonstrate rate controls of photoexcited processes by mimicry of photosystem-II and harnessing molecular design of vibronic coherence.^[183] We anticipate, with excitement, future research efforts in these and others using synthetic design to mimic and harness fundamentally quantum properties.