From big data to big insights: statistical and bioinformatic approaches for exploring the lipidome

Abstract

The goal of lipidomic studies is to provide a broad characterization of cellular lipids present and changing in a sample of interest. Recent lipidomic research has significantly contributed to revealing the multifaceted roles that lipids play in fundamental cellular processes, including signaling, energy storage, and structural support. Furthermore, these findings have shed light on how lipids dynamically respond to various perturbations. Continued advancement in analytical techniques has also led to improved abilities to detect and identify novel lipid species, resulting in increasingly large datasets. Statistical analysis of these datasets can be challenging not only because of their vast size, but also because of the highly correlated data structure that exists due to many lipids belonging to the same metabolic or regulatory pathways. Interpretation of these lipidomic datasets is also hindered by a lack of current biological knowledge for the individual lipids. These limitations can therefore make lipidomic data analysis a daunting task. To address these difficulties and shed light on opportunities and also weaknesses in current tools, we have assembled this review. Here, we illustrate common statistical approaches for finding patterns in lipidomic datasets, including univariate hypothesis testing, unsupervised clustering, supervised classification modeling, and deep learning approaches. We then describe various bioinformatic tools often used to biologically contextualize results of interest. Overall, this review provides a framework for guiding lipidomic data analysis to promote a greater assessment of lipidomic results, while understanding potential advantages and weaknesses along the way.

Introduction

Lipids are an important class of biomolecules that play many essential roles in cellular functions such as acting as the primary constituents of biological membranes and performing various essential processes including signaling and energy storage [1]. Dysregulation of lipid metabolism has therefore been linked to numerous disorders and diseases [2, 3] including cardiovascular disease [4], diabetes [5, 6], cancer [7], and neurological disorders [8]. Among the mechanisms contributing to this dysregulation, the impact of xenobiotic exposure has captured attention within the realm of human health due to its ability to induce significant shifts in lipid homeostasis [9]. Thus, comprehensive lipidomic profiling of chemical exposure and clinically relevant samples has been exploited to assess lipid changes and overall metabolic pathway alterations resulting in disease onset and progression. Ultimately, these studies are elucidating potential lipid biomarkers for the establishment of diagnostic, preventative, and therapeutic initiatives.

While clinical assays often leverage high-throughput techniques to target and quantify a set of known lipid markers, discovery-based lipidomics approaches employ slower untargeted techniques for global lipid profiling. These untargeted approaches, however, are quite complex due to the many possible lipids that exist. Lipids span eight categories and currently the known lipid classes and subclasses result in nearly 50,000 unique lipid species as listed by the LIPID MAPS Structure Database [10]. Comprehensive untargeted lipidomic studies are challenged by this vast number of lipids, as well as their extensive concentration ranges in biological samples and highly isomeric nature [11]. These challenges have therefore driven recent analytical advancements in sample extraction, derivatization, separations (e.g., chromatography and ion mobility spectrometry), mass spectrometry (MS) instrumentation, and data processing software to enable more lipid identifications with greater confidence in complex biomolecular data [12, 13].

As the ability to detect and identify lipids has improved, the statistical challenges associated with these datasets have become apparent [14]. One such challenge is that lipidomic experiments often produce high-dimensional datasets in which the number of lipids (p) exceeds the number of samples (n). This scenario, known as “large p, small n,” is associated with the “curse of dimensionality,” which describes the difficulty of identifying meaningful patterns and relationships in datasets as the number of variables increases [15]. Regression and other commonly used statistical procedures may fail in such cases because no unique solution exists. Moreover, algorithms that handle high-dimensional datasets may become computationally infeasible, as the running time may scale with the number of predictors in a superlinear fashion [16]. In addition to difficulties associated with the size of lipidomic datasets, there are several statistical challenges resulting from the underlying biological patterns in these datasets. Lipid species are often highly correlated, such as those belonging to the same subclass, due to their shared metabolic or regulatory pathways [17]. This multicollinearity can limit the number of appropriate methods, as it violates the assumption that input variables are independent. For example, multicollinearity in regression can yield unstable coefficient estimates and results in reduced statistical power [18]. Furthermore, lipid species vary in abundance across a dataset due to having different levels of expression. This phenomenon is often accompanied by the issue of heteroscedasticity, meaning the variance of a lipid measurement varies with its abundance. This trend may result in inaccurate results for some statistical models.

Beyond the difficulties associated with statistical analysis, biological interpretation of lipidomic data is challenging given the functional diversity and complexity of the lipidome. With thousands of distinct lipid species present in cells, each with unique physical and chemical properties, deciphering their precise roles can be difficult. Lipid composition also varies across organisms, tissues, and cell types, and dynamic fluctuations can occur for each of the different species at various times following perturbation [11]. Furthermore, even with the application of advanced analytical techniques, a significant portion of lipids remains incompletely resolved, leading to a single annotation encompassing multiple isomeric species that share identical chemical compositions but have indiscernible distinctions in fatty acyl sn-positions, double bond locations, or orientations [12]. This complexity has ultimately led to gaps in lipid biology knowledge within pathway databases, as the specific biological functions of individual lipids are largely unknown. For example, the Kyoto Encyclopedia of Genes and Genomes (KEGG) Pathway Database is limited to the pathway analysis of lipid classes rather than lipid species [19]. Thus, while specific lipid annotations may be achieved using modern analytical approaches, this information is lost when only averaged class values are utilized in pathways.

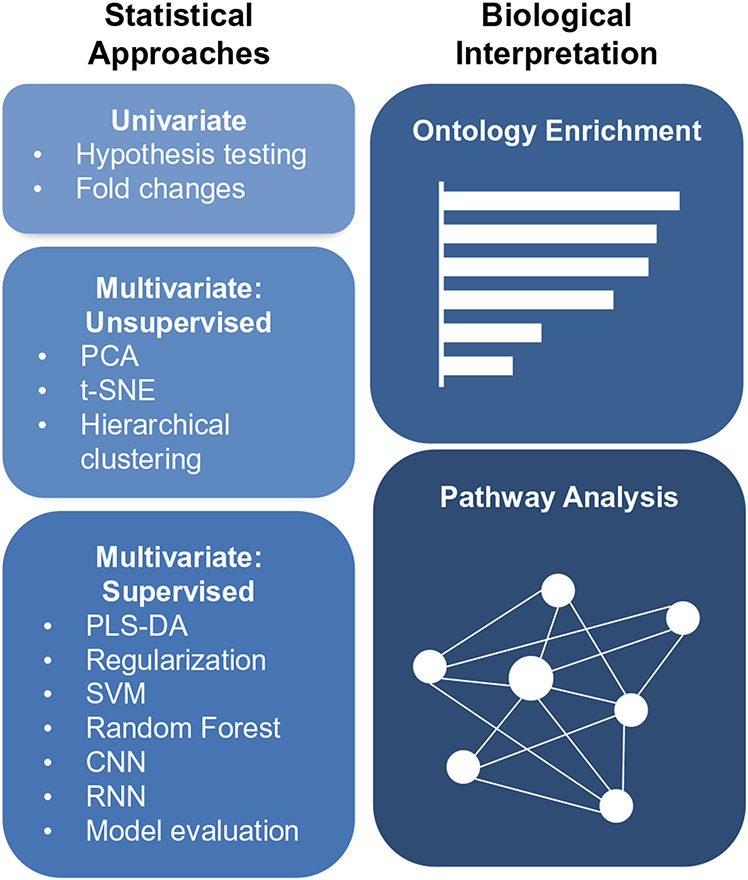
Based on all the described complexities and limitations, it is evident that choosing appropriate statistical methods and tools for biological interpretation is crucial but challenging. This review therefore highlights some of the popular methods used for associating lipid abundances with their phenotypic outcomes and associated assumptions, interpretations, and weaknesses with each. Specifically, we first introduce univariate and multivariate approaches and discuss their differences. Next, we cover univariate hypothesis testing and discuss how to ensure that certain assumptions are met. We then move into multivariate approaches, where we describe the differences between unsupervised and supervised methods, followed by some common examples of each (Fig. 1). Current bioinformatic tools that aid in a biological evaluation of statistical results are then detailed, such as ontology enrichment and pathway analysis. This review thus aims to provide a stronger understanding of these methods so better informed decisions can be made for more reliable and informative analyses, and ultimately a greater understanding of the lipidome.

Fig. 1.

Overview of the analyses covered by this review

Statistical approaches

Preprocessing

Prior to statistical analysis, it may be necessary to preprocess the data in an effort to mitigate impacts of instrumental artifacts or unrelated biological variability. The types of preprocessing steps are often specific to the data collection platforms and/or the experimental design, but may include steps such as noise filtering, correcting for batch effects, or missing value imputation. While the specifics of these approaches are not thoroughly outlined in this review, we direct readers to the work of Sun and Xia for additional information [20].

Univariate versus multivariate approaches

Both univariate and multivariate approaches play integral roles in lipidomic analyses. Univariate methods primarily focus on exploring the connection between a single variable, such as the abundance of a specific lipid, and groups of interest. On the other hand, multivariate methods concurrently examine the relationships among multiple variables, such as the abundances of numerous lipids and associated metadata like age or sex, in relation to the groups of interest [21]. As univariate approaches only consider one variable at a time, they are typically much simpler to implement, much less computationally intensive, and output is often easier to interpret, as they identify individual effects. Furthermore, because univariate methods do not need to estimate the relationship between variables, they generally require fewer samples [22]. On the other hand, multivariate approaches are often preferred because they consider the dependence of numerous input variables, a characteristic that may be particularly useful for lipidomic data due to the highly correlated data structure [18]. By considering this interdependence, multivariate methods are often able to identify groups of variables associated with outcomes that may not be discovered using univariate approaches. However, the output from multivariate approaches is often not as easily interpretable as univariate cases. Thus, researchers may opt for univariate methods when analyzing smaller datasets or to identify individual associations between variables and an outcome. When dealing with high-dimensional data or when the relationships between variables are complex, multivariate methods may be a more appropriate choice. For example, Hines and Xu utilized a univariate method to compare individual phospholipid alterations in wild-type versus knockout Escherichia coli strains [23], whereas Bifarin et al. employed multivariate methods to understand how hundreds of serum lipids changed in an ovarian cancer mouse and identify multiple markers of disease progression [24].

Univariate approaches

Hypothesis testing

In order to identify relationships between individual lipids and groups of interest, the most common statistical approach to employ is hypothesis testing. Hypothesis testing allows for the formal assessment of differences between populations based on studied samples [25]. In these assessments, the null hypothesis typically states that the mean abundance of a given lipid is equal across the groups of interest, and the main result of interest is the p-value, which indicates the probability of seeing the observed or greater difference in abundance given that the null hypothesis is true. Thus, to determine if a result is statistically significant, the p-value is compared to the researcher-chosen alpha level, which gives the probability of rejecting a true null hypothesis. For example, an alpha level of 0.05 means that there is a 5% threshold for considering results as statistically significant. Therefore, if the p-value is less than the alpha level, it suggests that the observed difference in lipid abundance between the groups is unlikely to have occurred by chance under the assumption of the null hypothesis, and the result is considered significant. By default, the alpha level is often set to 0.05, which has become a widely accepted standard in many scientific fields, as it is thought to offer a reasonable balance between the risk of a type I error and a type II error. Here, type I error is defined as the incorrect rejection of a true null hypothesis, resulting in a false positive conclusion that a relationship or effect exists when it does not. A type II error is defined as the failure to reject a false null hypothesis, resulting in the failure to detect a true relationship or effect that exists in the population [26].

Conveniently, most univariate hypothesis tests can be performed in any standard statistical software; however, the challenge of choosing the correct type of test remains. Because each test has underlying assumptions about the input data, application of an inappropriate test may result in incorrect interpretations or reduced statistical power [27]. The choice of test thus relates back to study design characteristics, as well as characteristics of the data. While study design characteristics, such as the number of groups, are usually easy to pinpoint, data characteristics are more difficult to verify, as the underlying distribution of a particular lipid is generally unknown. Therefore, it is common practice to evaluate data within groups either graphically or statistically to assess whether certain assumptions are met. One common assumption in univariate hypothesis tests is the normality of abundances. In lipidomic data, a strong right skew in the raw abundances is often observed due to the presence of a few lipids with exceptionally high concentrations, so it is standard practice to apply data transformations in an attempt to obtain normality. Specifically, raw lipid abundances are often log transformed, and/or normalized, using values such as the total ion current (TIC), median abundance value, or others [28]. To visually assess normality, histograms, probability plots, or Q-Q plots can be used to check if the data follow expected patterns for a normal population. However, as the number of detected lipids in an experiment increases, particularly in untargeted studies, this approach can become quite cumbersome as many plots may need to be examined to assess normality. Formally, normality can be assessed using a number of tests, such as Shapiro-Wilk or Kolmogorov-Smirnov. While these tests may allow for a more rapid assessment of the normality of different lipids, their use has been described as paradoxical, as groups with a low number of samples may not have enough statistical power to detect deviations from normality, while groups with a larger number of samples may be safeguarded from the assumption of normality due to the central limit theorem [29]. Another common assumption is homogeneity of variances, which can be assessed visually with boxplots to assess the distribution of each sample. This approach, similar to visual approaches for normality, may become infeasible as the number of detected lipids increases. Alternatively, statistical methods such as Levene’s and Bartlett’s tests may be used [30], but these may become less reliable when dealing with non-normally distributed data or when the sample sizes in each group are unequal. Thus, the main bottleneck for univariate analyses is the need to verify conditions for potentially hundreds of individual lipids.

Multiple testing correction

As the number of hypothesis tests performed increases, so does the likelihood of a false positive occurring [31]. To address this issue, several methods have been developed to “correct” or adjust p-values post hoc. One of the earliest approaches for multiple testing correction was the Bonferroni procedure, which adjusts the significance threshold by dividing by the number of tests performed [32]. Doing so decreases the family-wise error rate, or the probability of a type I error. Other corrections which control the rate of false positives include Hochberg, Sidak, and Dunnett’s. However, it should be noted that because the threshold for significance becomes increasingly stringent as the number of tests increases, the probability of false negatives (type II errors) increases with corrections, and statistical power consequently decreases. Due to these limitations, methods that control the false discovery rate (FDR), or the expected proportion of false positive findings among all reject hypotheses, may be preferred. Rather than attempting to eliminate all false positives, FDR corrections allow for a controlled proportion of false discoveries while maintaining a higher power to detect true discoveries. The most commonly used FDR method is the Benjamini-Hochberg procedure, which adjusts individual p-values by considering their rank in a sorted list of p-values and the user-chosen allowed FDR [32].

Fold change

While p-values provide information about the statistical significance of differences in lipid abundances between groups, it provides no insight about the magnitude or direction of that difference. This distinction is important because it is possible that the p-value will illustrate a statistically significant result for a particular lipid, but the magnitude of difference may not be biologically relevant. To this end, it has become common practice to combine the results of hypothesis testing with fold change. To calculate fold change, the average abundance of the “case” group is divided by the average abundance of the “control” group to provide a single fold change value for each lipid. The resulting fold changes are then often log transformed, making the values symmetric about zero. A log fold change threshold is then commonly applied to identify lipids of interest, ensuring both significance and effect size have been assessed [33]. In lipidomic studies, log₂ fold changes are commonly used, as they provide a straightforward interpretation of changes in lipid abundance on a binary scale.

Multivariate approaches

Broadly, all multivariate methods can be distinguished as being either unsupervised or supervised with the primary difference being that supervised approaches are trained on a labeled dataset (i.e., each sample has group information), while unsupervised approaches are trained on an unlabeled dataset (i.e., samples do not have group information). Because unsupervised methods do not have access to group labels, their goal is to infer natural patterns present in the data. For this reason, unsupervised approaches are often valuable for exploratory purposes, as they may uncover unexpected relationships for further analysis. Conversely, supervised approaches try to learn relationships between input data and specific outcomes of interest. This makes supervised learning useful for building classification models. However, supervised methods may require a larger sample size than unsupervised methods, as they need enough labeled data to learn relationships between the input features and outcomes of interest [34]. It also may be informative to combine these approaches. For instance, Bifarin et al. utilized unsupervised learning to evaluate sample groupings based on overall lipidome changes and then applied supervised learning to enable classification of double-knock-out versus control mice based on their lipid signatures [24]. Details and specific methods for each approach are further described below.

Unsupervised learning

Principal components analysis

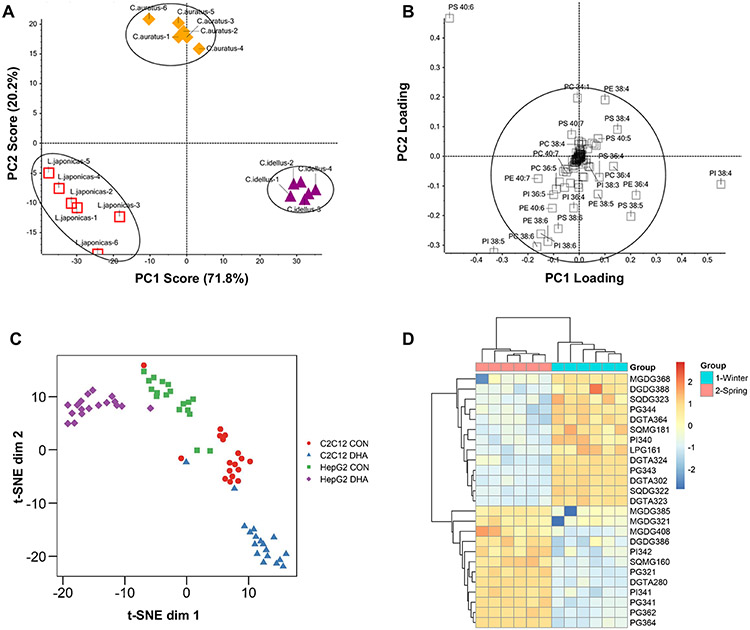
Principal components analysis (PCA) is a widely used method for dimension reduction and exploration of complex, high-dimensional datasets. Its goal is to identify a new, reduced set of variables called principal components that capture a majority of the variability in the original dataset. These components are created as linear combinations of the original variables and are orthogonal, or uncorrelated. This property makes PCA particularly useful for analyzing data with high levels of multicollinearity, a characteristic commonly seen in lipidomic datasets. By plotting data using the top principal components (PCs), patterns and relationships between samples can be visualized, enabling the detection of outliers and other anomalies that may not be apparent in the original high-dimensional space. PCA can also be used for data compression and feature selection, and as a preprocessing step for other multivariate analysis techniques [35, 36]. The most common graphical representation of PCA is a scores plot, where each sample in a dataset is plotted according to its values for the PCs of interest. Generally, this is done using the first two PCs, as they explain the most variance. In these plots, similar samples will appear closely in space, and often the goal is to determine if sample points are separable based on a known group or characteristic [35]. An example PCA is shown in Fig. 2A, where phospholipid differences in viscera from three fish species, Lateolabrax japonicas, Ctenopharyngodon idellus, and Carassius auratus, were evaluated [37]. From the PCA, samples from the different species are separable with 92% of the variance explained by the first two PCs. Following visualization with scores plots, it is often of interest to determine which lipids are contributing considerably to top PCs. To do so, the loadings for each PC can be examined, which indicate the correlation between each original lipid and that PC. Lipids with high absolute loadings contribute most heavily to a PC and are thus considered more important. The loadings for individual phospholipids in the analysis in Fig. 2A are shown in Fig. 2B. Phospholipids with low absolute loadings are concentrated toward the center of the plot, while those with high loadings deviate further out. This plot suggests that PS 40:6, PI 38:4, and PI 38:5 are the phospholipids that contribute most significantly to the separation between the different species seen in Fig. 2A.

Fig. 2.

Unsupervised analysis examples. A PCA score plot showing separation of L. japonicas, C. idellus, and C. auratus fish species using phospholipid data and B loadings for the variables in the first two PCs. C t-SNE scatter plot showing lipidomic single-cell data from C2C12 and HepG2 cell lines grown in both control (CON) and docosahexaenoic acid (DHA)-supplemented media. D A two-dimensional hierarchical clustering heat map of lipid data from Fucus vesiculosus collected in either the winter or spring. The color scale indicates the levels of relative abundance and numbers indicate the fold difference from the mean. The top dendrogram represents clustering of the sample groups into two main clusters: Winter and Spring. Likewise, the left dendrogram illustrates clustering of individual lipid species into two main clusters. A and B were adapted from Shen et al. [37] with permission from ACS, Agriculture and Food Chemistry; C from Hancock et al. [38] with permission from Journal of Lipid Research, American Society for Biochemistry and Molecular Biology; and D from da Costa et al. [39] with permission from MDPI, Marine Drugs

t-distributed stochastic neighbor embedding (t-SNE)

Similar to PCA, t-distributed stochastic neighbor embedding or t-SNE is a dimension reduction technique used for exploring high-dimensional datasets. However, unlike PCA, t-SNE does not assume that the underlying structure of the data can be represented with linear combinations of the original features, and thus, t-SNE may be better suited for datasets with complex, non-linear relationships [40]. t-SNE starts by calculating pairwise similarity between all data points in the original high-dimensional space using a Gaussian kernel. Points close together have a high probability under this distribution, while those further apart have a lower probability. Next, t-SNE randomly projects the data points into a lower-dimensional space (e.g., two-dimensional) and uses gradient descent to iteratively adjust positions of data points to make the pairwise similarities match those in the high-dimensional space as closely as possible. To achieve this, t-SNE employs the t-distribution (Student’s t-distribution) as the probability distribution in the lower-dimensional space. The final result of t-SNE is a scatter plot where the data points are positioned based on their optimized representation in the second dimension. In these plots, similar data points are typically clustered together, while dissimilar points are spread apart [40].

When performing t-SNE, the main decision one must make is what value to use for the perplexity parameter. The perplexity parameter controls the effective number of neighbors each data point considers during optimization. A low perplexity focuses more on local relationships to capture fine-grained structures in the data, while a high perplexity emphasizes global relationships, capturing broader patterns. Selecting the perplexity is critical, as an inappropriate value may obscure patterns in the dataset. In general, this value is set between 5 and 50, and it is common to test different values within this range and assess the resulting visualizations to make the final choice [40]. In lipidomics, t-SNE is commonly employed when analyzing imaging or single-cell data [41]. Hancock et al. used this approach when validating a method they developed for detection and quantification of phosphatidylcholine and sphingomyelin species from single cells [38]. In this analysis, two different cell lines, C2C12 and HepG2, were grown in either control or docosahexaenoic acid (DHA)-supplemented media. Applying t-SNE to the resulting lipidomic datasets demonstrated that cells could be separated based on both their cell line and growth conditions (Fig. 2C).

Hierarchical clustering

Clustering analysis is a common approach for identifying groups, or clusters, of data points with the goal of having highly similar data points in the same cluster and distinct data points in different clusters. In lipidomics, it is common to apply clustering at the sample level to identify samples with similar lipid profiles, and at the lipid level, to identify lipids with similar abundance profiles across the samples in the study [42]. When performing hierarchical clustering, the first step is to calculate the distance, or dissimilarity, between all pairs of data points. There are several equations that can be used to calculate distance, such as Euclidean distance, Manhattan distance, or Mahalanobis distance [43]. After distance is calculated, the next step is to create a proximity matrix, which represents the pairwise distances between all data points. This matrix is then used to iteratively group the data points into clusters using a linkage method, such as single, average, complete, Ward’s method, and/or others [43]. The choice of linkage method is critical and can have a significant impact on the resulting clusters, as each method has different strengths and weaknesses. For example, single linkage can be sensitive to outliers and noise, while complete linkage tends to produce compact clusters [44].

After the linkage process is finished and all data points have been grouped into clusters, the final step is to visualize the results using a dendrogram. In a dendrogram, one axis represents the distance or dissimilarity measure used to create the clustering, and the other axis represents the samples or clusters. Each data point is represented as a leaf node in the diagram, and as the algorithm progresses, these nodes are progressively merged into larger clusters, forming branches in the tree. The dendrogram can be used to visualize the structure of the data, and to identify potential clusters or subgroups within the data. For example, Da Costa et al. performed hierarchical clustering to evaluate lipidomic signatures of Fucus vesiculosus, an edible brown macroalga, during different seasons (Fig. 2D) [39]. In their plot, samples are clustered on the x-axis (top) and individual lipids are clustered on the y-axis, while individual cells represent the relative abundance for a given sample/lipid combination. From the sample clustering, we see that samples cluster perfectly according to their season, suggesting differences in lipid profiles between these two phenotypes. From the lipid clustering, two main groups are present: those that are downregulated in spring and upregulated in winter (top), and those that are upregulated in spring and downregulated in winter (bottom). In these examples, hierarchical clustering demonstrated clear differences at both the sample and lipid levels and allowed for concise visualization.

Supervised learning

Classification modeling

Supervised learning plays a vital role in lipidomics research when the goal is to directly establish associations between input lipid abundances and their corresponding group labels. One of the more popular supervised learning tasks is to create classification models, which aim to predict what group a given sample belongs to based on its lipid data [45]. These models can be created by defining variables of interest and sample outcomes using machine learning libraries or frameworks, such as Scikit-learn, PyTorch, or Caret [46]. Ideally, these models not only accurately capture the relationship between independent and dependent variables in the studied data, but also are general enough to work for unseen datasets, facilitating group identification of unknown samples [47]. Furthermore, by examining the lipids that significantly impact model performance, researchers can also gain valuable insights into the underlying biological mechanisms associated with different phenotypes and identify potential biomarkers.

Modeling workflow

To ensure that a classification model can generalize to new data, it is imperative to test the model on data that it was not trained on. As Mosteller and Tukey stated, “testing the procedure on the data that gave it birth is almost certain to overestimate performance” [48]. Thus, to evaluate a model, one may implement a train-test split. Train-test splits involve dividing the labeled dataset into two distinct subsets: the training set and testing set. The training set is used to build the model, while the testing set is used to independently evaluate its performance. Alternatively, one may perform cross-validation (CV). The most common form of cross-validation is k-fold cross-validation, where the dataset is randomly divided into “k” equally sized groups or folds. The model is then trained on “k-1” folds and evaluated on the remaining fold. This process is repeated “k” times, with each fold acting as the validation set once. The performance metrics (e.g., accuracy) obtained from each iteration are then averaged to provide an overall assessment of the model’s performance. In addition to k-fold cross-validation, there are other variations such as stratified k-fold cross-validation, where the class distribution in each fold is preserved, and leave-one-out cross-validation (LOOCV), where each sample acts as the validation set once [49]. These choices may be useful when classes are imbalanced or when there is a small sample size, respectively.

Popular machine learning models

When developing classification models for lipidomic data, there are numerous machine learning algorithms available, each with their own intricacies. Due to the breadth of options, it is not feasible to provide an exhaustive description of all models. However, here, we offer a brief overview of several popular models commonly used in lipidomics and direct readers to Uddin et al. for more detailed information and additional references [50].

1. Partial least squares-discriminant analysis (PLS-DA): PLS-DA combines PLS regression and linear discriminant analysis (LDA). It uses latent variables to capture the most important relationships between predictor and response variables, making it effective for distinguishing different groups or categories [51]. Examples of lipidomic studies leveraging PLS-DA models include those from Malý et al. to categorize acute coronary syndrome and acute stroke patients [52] and Mi et al. to classify five pork cuts based on their unique lipid profiles [53].

2. Regularization: Regularization is a method used in classification models to avoid overfitting. It adds a penalty term to the model to control its complexity and prevent excessive reliance on less important features. This promotes simplicity and helps the model generalize well to new data. Two common types of regularization are L1 (Lasso) and L2 (Ridge) regularization [54]. For example, Santoro et al. employed the Lasso method to classify breast cancer subtypes and identify their distinct lipid signatures using mass spectrometry imaging data [55].

3. Support Vector Machines (SVM): SVMs are powerful classifiers that can efficiently handle both linearly and non-linearly separable datasets. They find an optimal hyperplane to separate different classes in the feature space. The main goal of SVMs is to maximize the margin between the support vectors, which are the data points closest to the decision boundary. This allows SVMs to achieve effective classification even in complex data scenarios [56]. Huang et al. utilized an SVM algorithm to identify potential plasma lipidomic biomarker candidates for classification of aortic dissection patients, which included one primary and two secondary lysophosphatidylcholine markers [57].

4. Random Forest (RF): RF is an ensemble learning method that combines the predictions of multiple decision trees. It works by training each decision tree on a random subset of the training data, resulting in a diverse set of trees. The final prediction is therefore made by aggregating the predictions of all trees [58]. Using a random forest approach, Phan et al. found that lipidomics could be used to classify wines by origin with 97.5% accuracy, while Chappel et al. used RF to aid in development of a scoring system to identify cancerous tissue phenotypes [59, 60].

Other potential machine learning models that could be considered in lipidomics include logistic regression [61], k-nearest neighbors [62], and other ensemble methods like gradient boosting [63].

Popular deep learning models

Deep learning is a subfield of machine learning that encompasses algorithms that are based on the structure and function of the brain, also known as neural networks [64]. Neural networks consist of layers of interconnected nodes, called artificial neurons or perceptrons. These nodes are organized into three layers: (1) the input layer, which takes in the raw data; (2) hidden layers, where computation is performed on the input data; and (3) the output layer, which yields the network’s prediction. Each connection between nodes is associated with a weight, which determines the strength of the connection. The weighted inputs from one layer are combined and passed through an activation function, which helps the network learn relationships in the data. Thus, deep learning models may be favored over previously mentioned models when dealing with intricate patterns and large unstructured datasets. However, deep learning models may not be suitable when the number of samples is limited or when there is a need to carefully understand the model’s decision-making process [64]. Some commonly used deep learning models are described below.

1. Convolutional Neural Networks (CNNs): CNNs are designed for image and grid-like data. They employ convolutional layers to automatically extract hierarchical features from images, enabling them to perform tasks such as classification and image generation. This approach was employed by Lekadir et al., who trained a CNN on ultrasound image data to identify lipid core and other plaque constituents present in carotid arteries [65].

2. Recurrent Neural Networks (RNNs): RNNs are effective for handling sequential data, such as time series data. By using feedback loops, they retain process information from previous steps, allowing them to capture temporal dependencies within the data. RNNs were used by Cui et al. to predict the risk of dyslipidemia in steel workers using blood samples [66].

Other potential deep learning approaches that may be useful in lipidomics include Generative Adversarial Networks and variational autoencoders [67]. To choose a model, it is necessary to evaluate and compare different models using appropriate evaluation metrics, described below [50].

Model evaluation

The evaluation of classification models is a crucial step in assessing their effectiveness and reliability. One widely used evaluation tool is the confusion matrix, which presents a table as a structured overview of the model’s predictions in relation to the actual labels (e.g., phenotype) [68]. This matrix displays four values: true positives, true negatives, false positives, and false negatives. Examining this table gives a quick overview of the types of errors made by the model and can also be used to calculate specific performance metrics. Most commonly, accuracy, which measures the overall correctness of the model’s predictions, is reported for a given model. However, this metric alone may not tell the full story, as it does not consider group imbalances or give insights into the specific types of errors being made. To alleviate these gaps, it is important to include other metrics that provide a more comprehensive evaluation of the model’s performance. Some of these metrics include precision, recall (or sensitivity), specificity, and F1-score. Precision, which is the ratio of true positive predictions to the total predicted positive instances, indicates how well the model avoids false positives. Recall (sensitivity), on the other hand, measures the ratio of true positive predictions to the total actual positive instances and indicates how well the model avoids false negatives. Specificity is also another critical metric that measures the ratio of true negative predictions to the total actual negative instances, providing insights into the model’s ability to correctly identify true negatives. Finally, the F1-score is a useful combination of precision and recall, considering both false positives and false negatives to make it particularly valuable when class imbalances are present [69].

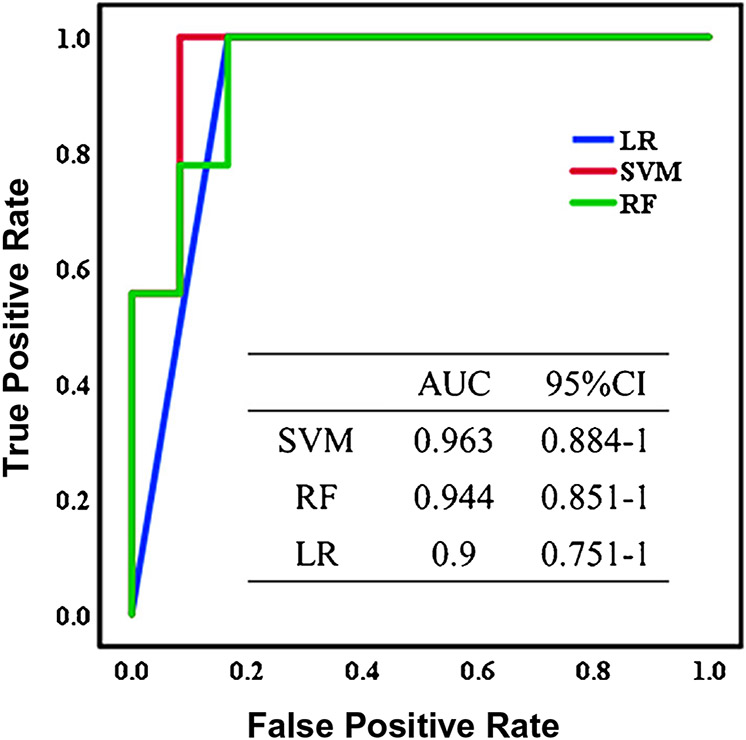
Model performance for binary classification is often visualized graphically using either a receiver operating characteristic (ROC) curve or a precision-recall curve. These curves are constructed by iteratively adjusting the model’s classification threshold (the value used to make decisions about how to classify samples), calculating performance metrics, and then plotting how these metrics vary across the different thresholds. Specifically, ROC curve plots the True Positive Rate (sensitivity) against the False Positive Rate (1 minus specificity), while precision-recall curves plot precision versus recall. In general, precision-recall curves are useful when dealing with imbalanced datasets, as they provide insights into the model’s performance on the minority class, while ROCs summarize model’s overall ability to distinguish between the two classes, regardless of the class distribution [70]. For both types of curves, it is common to calculate the area under the curve (AUC) to quantify the model’s performance, with areas close to 1 indicating strong performance. An example of how this metric is used in shown in Fig. 3, where analysis via AUC-ROC curves was performed in a study by Ye et al. evaluating metabolomic and lipidomic signatures of cerebral infarction [71]. Using their top 10 candidate biomarkers for this condition, they built classification models using SVM, RF, and logistic regression. From the AUC-ROC curves, they concluded that SVM had the best performance due to its high AUC (96.3%), accompanied by high accuracy (95.2%) and sensitivity (91.7%).

Fig. 3.

AUC-ROC curves for cerebral infarction classification for logistic regression, support vector machine, and random forest. Reprinted from da Ye et al. [71] with permission from ACS, Journal of Proteome Research

Implementation

To implement the described methods, a number of statical programming languages, such as R, Python, or SAS, may be used. While these options may be preferred due to their flexibility and ability to perform custom analyses, they do require coding experience to use efficiently. To begin working in these languages, several books and online resources are available to jumpstart the process, such as “R for Data Science” [72] or “Python for Data Analysis” [73]. Alternatively, several online applications exist that have built-in statistical functions and allow for direct upload of lipidomic with the click of a button. Among these tools is MetaboAnalyst [74], LipidSuite [75], and LipidSig [76], which include options such as data normalization, t-tests, PCA, hierarchical clustering, classification modeling, and more.

Biological interpretation

Following statistical analysis, it is important to assess the biological implications of these findings. To overcome the limited knowledge regarding the roles many lipids play, several tools have been developed to assess if significance patterns match expectations and to connect results to previous literature. Below, we discuss a few of these tools and cover analysis types such as ontology enrichment analysis and pathway and network solutions. Additionally, we highlight some new tools and discuss future directions.

Ontology enrichment analysis

Ontology enrichment analysis involves grouping lipids based on shared biological or physical properties such as function, subcellular compartment, class, or degrees of unsaturation. Statistical approaches are then applied to determine if certain ontology terms are enriched, meaning the term is overrepresented compared to a target list or higher ranked by a statistic (e.g., p-value) than expected by chance [77]. These results indicate significant associations and relationships within the lipidomic data, providing insights into the underlying biological mechanisms. For example, ontology enrichment is commonly used to unveil significant associations between specific lipid classes and cellular signaling pathways [13]. Furthermore, because construction of ontologies provides a standard framework for analyzing lipidomic data, their use facilitates data integration and knowledge sharing within the lipidomics community.

Broadly, lipidomic ontology enrichment tools can be broken into two categories: those that utilize a database and those that do not. Notable examples of tools that do not require a database include Lipid Mini-On, LipidSig, and LipidSuite [75, 76, 78]. To obtain ontology terms, Lipid Mini-On and LipidSuite utilize text mining to parse individual lipid species names into structural characteristics such as lipid class, degree of saturation, and carbon chain length. Conveniently, these tools can analyze lipids that do not currently exist in databases, as long as their naming follows the lipid nomenclature established by LIPID MAPS [79]. To obtain the ontology terms for LipidSig, an optional lipid characteristic file may be uploaded by the user. When using Lipid Mini-On, users have two options for analysis. They can either upload a ranked table where each lipid is associated with a statistical measure such as a p-value or fold change, or they can upload a query list containing significant lipids and a universe file comprising all lipids detected in the experiment. After files are uploaded, various statistical tests can be performed and results visualized through bar/pie charts or interactive networks [78]. In contrast with Lipid Mini-On, LipidSig and LipidSuite require differential expression analysis within the software prior to enrichment analysis, rather than directly supplying lipids of interest. Following differential expression analysis, LipidSuite utilizes ranked output and calculates significance using an efficient permutation algorithm that was previously developed for gene set enrichment analysis [75]. For LipidSig, overrepresentation analysis can be conducted on the results of differential expression analysis using Fisher’s exact test, with the outcomes visualized using bar charts [76].

While database-independent ontology enrichment methods primarily focus on structural characteristics, approaches that utilize databases can uncover more biologically contextualized findings. One popular tool for this purpose is LION, which is associated with an ontology database containing over 50,000 lipid species [80]. The LION database is organized into four main branches: lipid classification, chemical and physical properties, function, and subcellular component. For inclusion, a lipid must exist in this database, which represents commonly found lipid species in mammalian systems. For enrichment analysis, LION offers a 1-tailed Fisher’s exact test for comparing query lists to background lists, and a 1-tailed Kolmogorov-Smirnov test for assessing ranked lipid lists. In addition to providing results in enrichment tables/graphs and networks, LION offers a PCA module for comparing datasets with multiple groups. Another potential database-dependent enrichment tool is LipiDisease, which aims to perform disease enrichment analysis based on a set of lipids [81]. To perform these analyses, LipiDisease utilizes the PubMed database, which contains over 26 million biomedical records and their associations with chemicals and diseases. LipiDisease offers two main types of analyses: (1) lipid-set enrichment, which considers sets of lipids collectively for disease enrichment and can be performed with or without ranking statistics, and (2) lipid and disease connections, which examines individual lipids and diseases and identifies associations. Overrepresentation in gene sets compared to PubMed articles is determined using 1-tailed Fisher’s exact tests, and output is ranked based on FDR adjusted p-values. All of the above enrichment tools are freely available online and do not require coding experience to use. An overview of all tools can be found in Table 1.

Table 1.

Summary of lipidomic enrichment tools and their capabilities. Tools that rely on a database mandate that a lipid has been previously reported and described, while those that do not can perform enrichment either by parsing out information from the input name alone or user-input characteristics. A ranked table is a list of all detected lipids and their associated statistical measure, such as p-value, while a universe list is all detected lipids without any statistical measure. A query list includes only lipids (or diseases) that are of specific interest, which is typically based on statistical significance

Tool	Database	Input	Tests	Visualizations
Lipid Mini-On	No	Ranked table or query/universe list	Query/universe: Fisher’s exact, EASE score (DAVID), Binomial, Hypergeometric Ranked: Weighted Kolmogorov-Smirnov	Bar chart, Pie chart, Network
LipidSig	No	Query/universe list	Fisher’s exact	Bar chart
LipidSuite	No	Ranked table	Permutation algorithm	Boxplot
LION	Yes	Ranked table or query/universe list	Query/universe: 1-tailed Fisher’s exact Ranked: 1-tailed Kolmogorov-Smirnov	Bar chart, Network, PCA
LipiDisease	Yes	Query list of lipids or diseases	1-tailed Fisher’s exact	N/A

Pathway and network solutions

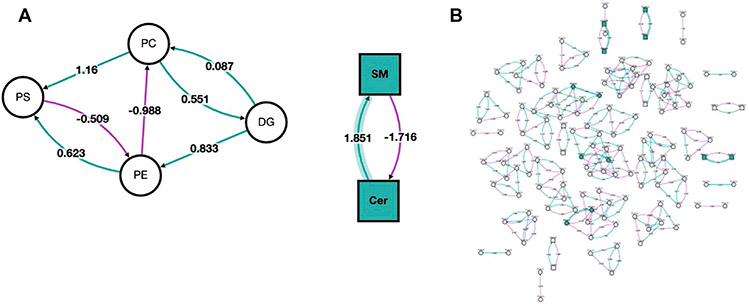
Pathway analysis is a computational approach that connects altered lipids to specific biological pathways or processes, thereby providing insights into functional implications and potential involvement in disease or physiological states. In contrast with enrichment analysis, pathway analysis takes into account the interactions and relationships among different molecules within a pathway, allowing for a more comprehensive understanding of the underlying mechanisms and regulatory networks associated with lipid alterations [82]. In pathway analysis, altered lipids are first compared to pathway databases to determine if certain pathways are overrepresented. Following statistical analysis, results are often visualized using pathway maps or networks to highlight the interconnections between altered lipids and biological pathways. To perform lipid pathway analysis, several tools exist, each of which has slightly different implementations. One popular tool is BioPAN, which is hosted by LIPID MAPS [83]. BioPAN utilizes lipidomic data resulting from experiments with two conditions (e.g., control vs. treated) and identifies pathways that are activated or suppressed between these conditions. These analyses can be performed using lipid classes, subclasses, or individual species. Input lipids are mapped as reactants and products in BioPAN’s manually collated database, which contains biosynthetic pathways from mammalian systems. z-scores are then calculated to assess whether specific reactions show significant changes between the two conditions based on the input lipids. These results can then be visualized in an interactive network. BioPAN also provides a table listing genes that may be involved in the activation or suppression of enzymes catalyzing lipid metabolism in mammalian tissues, providing additional biological insight and generating hypotheses that can be experimentally tested using genomic or proteomic approaches. Pathway analysis with BioPAN was performed by Kipp et al. investigating alterations to the lipidome in obese mice treated with bilirubin nanoparticles [84]. Figure 4A shows their resulting network when analysis was performed at the lipid class level, treatment with bilirubin primarily altered sphingomyelins (SM) and ceramides (Cer). When performed at the individual lipid species level (Fig. 4B), this network is considerably more complex, making it difficult to detect broad trends. However, it identified significant species from classes that were not deemed to be significant when aggregated at the subclass level, such as species from phosphatidylethanolamines (PE) and phosphatidylserines (PS). Additionally, these plots showcase z-score, which indicate the association with bilirubin treatment.

Fig. 4.

Network visualization of altered lipid classes and species in bilirubin nanoparticles and vehicle-treated obese mice. Both A network analysis of lipid classes and B network analysis of lipid species is shown. The nodes’ shapes indicate the lipid type, with circles representing glycerolipids and glycerophospholipids, and squares representing sphingolipids. Node color corresponds to whether the lipid class or species was affected by the bilirubin treatment (green) or remained unchanged (white). Additionally, purple lines represent a negative z-score, green lines indicate a positive z-score, and shaded lines indicate the z-score is associated with a lipid class or species altered by the bilirubin treatment. Reprinted from da Kipp et al. [84] with permission from MDPI, Metabolites

While BioPAN relies on a built-in database, other tools such as PathVisio and Cytoscape allow users to input custom databases [85, 86]. This capability allows researchers to focus on pathways and gene sets that are directly relevant to their research. Additionally, this can be useful when pathways of interest are not adequately covered in standard databases. For instance, many tools’ databases predominantly represent humans and mice, leaving other organisms with limited representation. Thus, curating custom pathway sets can be accomplished by pulling data from existing databases such as WikiPathways, Reactome, KEGG, and Pathway Commons [19, 87-89]. Additionally, researchers can leverage data from in-house lipidomic experiments or publicly available datasets not yet included in databases. Regrettably, lipidomic databases tend to be less developed than databases for other omics, such as transcriptomics and proteomics. This is partially due to the newness of the field of lipidomics, but is also related to the difficulties associated with identifying and characterizing lipid structures, which has resulted in missing or biased biological knowledge in pathway databases. These shortcomings particularly affect complex lipids, such as glycerolipids, glycerophospholipids, and sphingolipids. In order to alleviate these knowledge gaps, it is imperative that researchers make an effort to integrate lipidomic data into publicly available sources. Specifically, we recommend directing new data to LIPID MAPS, which has resources not only for new structures, but also other experimentally and biologically relevant data.

Additional analysis approaches

Beyond the types of analyses previously covered, additional lipidomic data analysis methods exist for various applications. For example, structural-based connectivity and omic phenotype evaluations (SCOPE), a cheminformatics toolbox developed by Odenkirk et al., can be used to cluster lipid species based on structural characteristics and then relate these clusters back to phenotypic observations to provide connections between structure and biological function [90]. Another tool is the LUX score created by Marella et al. which is powerful for determining homology between disparate lipidomes [91]. To aid in the identifications, the global natural products social (GNPS) molecular networking can be used to identify novel lipids following the identification of significant molecular features [92]. Alternatively, region of interest multivariate curve resolution (ROIMCR) methods can be used to determine statistically significant features prior to lipid identification, which may offer a considerable time advantage [93]. A more comprehensive list of potential lipidomic analysis tools and methods can be found at https://github.com/lifs-tools/awesome-lipidomics. In addition to the development of lipid specific tools, improvements in large language models (LLMs), such as ChatGPT, have the potential to aid in lipidomic studies. As accuracy improves, these language models have great potential to assist researchers in deciphering complex lipidomic literature, identifying relevant relationships between lipid structures and biological functions, and even predicting potential interactions within lipidomes. Further, these tools may be useful at automating computational tasks, such as writing code or making plots [94].

Conclusion

Lipidomics has emerged as an exciting yet complex field. This area is challenged not only by difficulties associated with detecting, identifying, and quantifying individual lipid species, but also by the unique data that results from these experiments. In this review, we have covered an array of popular statistical approaches that can be used to make sense of this data, as well as a number of bioinformatic tools that enable biological interpretation following statistical analysis. Ultimately, we believe that the methods and examples outlined in this review will aid lipidomic researchers in their choice of suitable analyses for their given datasets. Furthermore, we anticipate that the capabilities of these computational lipidomic methods will only continue to improve as more well-annotated lipidomic datasets become publicly available, filling current knowledge gaps that are hindering informatic tools.