Investigating zero-state and steady-state performance of MEWMA-CoDa control chart using variable sampling interval

ABSTRACT

Traditional process monitoring control charts (CCs) focused on sampling methods using fixed sampling intervals ( $\mathrm{FSI}$s). The variable sampling intervals ( $\mathrm{VSI}$s) scheme is receiving increasing attention, in which the sampling interval ( $\mathrm{SI}$) length varies according to the process monitoring statistics. A shorter $\mathrm{SI}$ is considered when the process quality indicates the possibility of an out-of-control (OOC) situation; otherwise, a longer $\mathrm{SI}$ is preferred. The $\mathrm{VSI}$ multivariate exponentially moving average for compositional data ( $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$) CC based on a coordinate representation using isometric log-ratio ( $\mathrm{ilr}$) transformation is proposed in this study. A methodology is proposed to obtain the optimal parameters by considering the zero-state ( $\mathrm{ZS}$) average time to signal ( $\mathrm{ZATS}$) and the steady-state (SS) average time to signal ( $\mathrm{SATS}$). The statistical performance of the proposed CC is evaluated based on a continuous-time Markov chain ( $\mathrm{CTMC}$) method for both cases, the $\mathrm{ZS}$ and the SS using a fixed value of in-control (IC) ${\mathrm{ATS}}_0$. Simulation results demonstrate that the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC has significantly decreased the OOC average time to signal ( $\mathrm{ATS}$) than the $\mathrm{FSI}\mathrm{MEWMA}\mathrm{CoDa}$ CC. Moreover, it is found that the number of variables (d) has a negative impact on the $\mathrm{ATS}$ of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC, and the subgroup size (n) has a mildly positive impact on the $\mathrm{ATS}$ of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC. At the same time, the $\mathrm{SATS}$ of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is less than the $\mathrm{ZATS}$ of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC for all the values of n and d. The proposed $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC under steady-State performs effectively compared to its competitors, such as the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC, the $\mathrm{VSI}$- $T^2\mathrm{CoDa}$ CC and the $\mathrm{FSI}$- $T^2\mathrm{CoDa}$ CC. An example of an industrial problem from a plant in Europe is also given to study the statistical significance of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC.

1. Introduction

Monitoring manufacturing processes has become increasingly difficult due to sophisticated consumer demands for quality products. Statistical process monitoring (SPM) is a commonly used statistical approach for quality control in the industrial scenario. Control charts (CCs) are the most widely used tool in SPM. W.A. Shewhart introduced the concept of CCs in 1924. Conventional CCs are simple and sensitive to large process variations but have poor sensitivity to small process variations. Several measurements are required to improve the detection speed for small process shift.

Aitchison defines Compositional data ( $\mathrm{CoDa}$) analysis as an adequate geometry model for the transformation of $\mathrm{CoDa}$ [1]. Since Karl Pearson first emphasized problems in the analysis of $\mathrm{CoDa}$ in 1897. $\mathrm{CoDa}$ has unique numerical characteristics that have significant implications for statistical analysis studied by many researchers (cf. [3,11,37]). Because $\mathrm{CoDa}$ represents parts of a larger whole, they have unique properties. The standard statistical techniques designed for probabilistic random variables that cannot analyze $\mathrm{CoDa}$ in raw form are studied (cf. [15]). In recent years, researchers have started focusing on CCs for $\mathrm{CoDa}$. The First CC for $\mathrm{CoDa}$ was a Chi-square CC, assuming $\mathrm{CoDa}$ follows the properties of Dirichlet distribution. After the d = 3-part $\mathrm{CoDa}$ was analyzed using Hotelling $T^2$ CC to interpret the out-of-control (OOC) signals [59]. The Hotelling $T^2$ CC can also be applied on $\mathrm{CoDa}$ after deleting one component from the $\mathrm{CoDa}$ vector or after applying the isometric log-ratio (ilr) transformation, but the one with transformed values outperforms the other [58]. As these methods deal with d = 3-parts $\mathrm{CoDa}$, a method to deal with high dimensional $\mathrm{CoDa}$ is introduced [60]. After the advancement of Hotelling $T^2$ CC for $\mathrm{CoDa}$, multivariate exponentially moving average (MEWMA) $\mathrm{CoDa}$ CC using ilr transformation [56] and the effect of measurement error on Hotelling $T^2$ CC [62] and MEWMA [63] have been evaluated. The multivariate cumulative sum (MCUSUM) CC for $\mathrm{CoDa}$ has been studied with parameter estimation [17]. Recently, MEWMA CC for $\mathrm{CoDa}$ using variable sampling interval ( $\mathrm{VSI}$) has been studied using zero-state ( $\mathrm{ZS}$) average time to signal for ilr transformed d = 3-part $\mathrm{CoDa}$ using n = 1 subgroup size [35].

A $\mathrm{VSI}$ strategy reduces the detecting time in CCs. A small sampling interval ( $\mathrm{SI}$) is used if there is any signal that the process has changed; if there is no signal, a longer $\mathrm{SI}$ is used. The fixed sampling interval ( $\mathrm{FSI}$) CC is used when the $\mathrm{SI}$ length stays the same through all the samples (please see [64]). The multivariate CC to monitor the mean vector and variance-covariance matrix with $\mathrm{VSI}$ was investigated by Reynolds and Cho [43]. The MEWMA and MEWMA-type CCs were combined to get the best performance of the CC. The variable sampling rate (VSR) scheme has been used to study the increase and decrease in process dispersion in inverse normal transformation [50]. Further, the $\mathrm{VSI}$ CC to monitor the coefficient of variation has been introduced [7]. The CCs with double warning lines are faster at detecting small shifts in the mean vector [22]. The CC with $\mathrm{VSI}$ and variable sample size (VSS) was used to monitor the variance-covariance matrix of a multivariate normally distributed process [23].

Many researchers [4,25,41,61] examined the $\mathrm{VSI}$ and the $\mathrm{FSI}$ features for univariate and multivariate CCs for process monitoring. Simulation is used to investigate the average run length ( $\mathrm{ARL}$) properties of the exponentially weighted moving average (EWMA) CC to effectively detect the small changes in the process's desired value [52]. More recently, the $\mathrm{ARL}$ performance of EWMA techniques based on the $\mathrm{VSI}$ for the monitoring logistic profiles has been proposed [31]. The CUSUM CCs are found to be an effective method for monitoring changes in aquatic toxicity [16]. The robust measures of the location were applied to improve exponential-cum-ratio estimators [14]. The multivariate EWMA ( $\mathrm{MEWMA}$) CCs using unequal sample sizes were studied [20]. Improving the multivariate CUSUM and EWMA CCs for monitoring purposes has focused most research on quality control proposed by Jarrett [18]. Further, MCUSUM CCs using $\mathrm{VSI}$ were used to monitor the ratio when more than two mixture components were considered [33].

The performance of the $\mathrm{MEWMA}$ CC was evaluated using a continuous-time Markov chain ( $\mathrm{CTMC}$) method [39]. Several researchers have attempted to improve the $\mathrm{MEWMA}$ CC's efficiency in identifying shift patterns in the process mean vector through various methods. For example, the $\mathrm{MEWMA}$ CC using sequential sampling [20] and the $\mathrm{MEWMA}$ CC using unequal sample sizes [44]. Changing the $\mathrm{SI}$ value in response to process data is a frequently used technique for increasing the efficiency of CCs [57]. The $\mathrm{VSI}$ scheme has been amalgamated to study the performance of $\overline{X}$ CCs [9], the CUSUM CCs for monitoring process mean [42], double EWMA CCs [49], Hotelling $T^2$ CC for exponentially distributed random variables [12], multivariate Shewhart and $\mathrm{MEWMA}$-type CCs for simultaneously monitoring vectors of means and standard deviations matrix [13]. Further, two $\mathrm{SI}$s were used for designing the optimal process for Taguchi's online monitor and control method with and without misclassification errors [5]. The performance of the $\mathrm{VSI}\mathrm{MEWMA}$ CC was investigated using a proposed $\mathrm{CTMC}$ approach by Sabahno et al. [48]. To study the benefits of using $\mathrm{VSI}$ scheme, the $\mathrm{VSI}$ and the $\mathrm{FSI}\mathrm{MEWMA}$ CC's performance has been compared [34].

In SPM literature, two different types of performance are typically considered: $\mathrm{ZS}$ and steady-state (SS). The term ‘SS performance’ shows the time required for the CC to identify a process shift for control statistics to reach a static distribution. Some processes are initially uncontrollable; the procedure is initiated under control in most realistic scenarios and then changes randomly [40]. When the average number of samples is taken from the start of signal monitoring in an OOC situation, then the CC's performance is evaluated using $\mathrm{ZS}\mathrm{ARL}$ (cf. [8,10]). The comparison between the zero-state average time to signal ( $\mathrm{ZATS}$) symmetric and asymmetric distributions to the steady-state average time to signal ( $\mathrm{SATS}$) using the $\mathrm{CTMC}$ showed the $\mathrm{SATS}$ performed better in terms of $\mathrm{ARL}$ [19]. The $\mathrm{CTMC}$ method is also used to determine the $\mathrm{SS}\mathrm{ARL}$ of the CC [21]. To detect changes in the process mean, the SS properties of synthetic CCs have been examined [10]. The CCs give more significant results by using $\mathrm{SS}\mathrm{ARL}$ to create a CC with m-of-m run rules [24]. Numerous researchers have distinguished between the SS optimal and $\mathrm{ZS}$ optimal $\mathrm{VSI}$ schemes (cf. [53,54]). The CUSUM CC for two possible $\mathrm{SI}$s and probability ratio tests were used to study the SS-optimized $\mathrm{VSI}$ methods [55]. The $\mathrm{VSI}$-based CC scheme is superior to the $\mathrm{FSI}$-based CC scheme in terms of average time to signal ( $\mathrm{ATS}$) performance [29].

As discussed earlier, many researchers are currently working on CC for $\mathrm{CoDa}$, but all the above-mentioned studies deal with the Markov chain model with $\mathrm{ZS}$ ATS to study the CC performance for $\mathrm{CoDa}$. Also, most of the research on $\mathrm{CoDa}$ deals with d = 3-part $\mathrm{CoDa}$. As far as the author knows, till now, the SS ATS performance has not been used for monitoring $\mathrm{CoDa}$. The literature shows the SS ATS performs better than the $\mathrm{ZS}$ ATS (cf. [6,30,51]). Hence to fill this gap, this paper makes an attempt to take SS ATS performance into account. The VSI-MEWMA $\mathrm{CoDa}$ CC has been proposed using ilr transformation to investigate the ATS using the different number of variables p (i.e. d = 3, 5), subgroup sizes n (i.e. n = 1, 3) and the $\mathrm{VSI}h$ (i.e. $h_1,h_2$). The $\mathrm{ZS}$ ATS has also been computed to study the difference between $\mathrm{ZS}$ and SS ATS performances.

The rest of this paper is as follows: Section 2 discusses brief details about how to model and manipulate the $\mathrm{CoDa}$. In Section 3, the model for VSI-MEWMA CC for $\mathrm{CoDa}$ has been presented. Section 4 presents the $\mathrm{CTMC}$ for both $\mathrm{ZS}$ and SS for the $\mathrm{VSI}$ and the $\mathrm{FSI}$. Section 5 gives the CCs performance and compares the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ and the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC. Finally, an illustrative example and conclusions are presented in Sections 6 and 7.

2. Compositional data

A row vector is defined as a $\mathrm{CoDa}$ vector if it belongs to simplex space ${\mathcal{S}}^d$,

$${\mathcal{S}}^d=\{\mathbf{y}=(y_1,y_2,\dots ,y_d)|y_i>0,i=1,2,\dots ,d\mathrm{such}\mathrm{that}\sum _{i=1}^d{y}_i=\kappa \},$$ (1)

where κ is a constant sum of the $\mathrm{CoDa}$ vector. Because of the constraint of constant sum, Euclidean geometry is unsuitable for $\mathrm{CoDa}$. To overcome this problem, J. Aitchison proposed a specific geometry known as Aitchison's geometry [2]. In which advanced operators for sum and multiplications have been defined,

• the perturbation operator for the sum of $\mathrm{CoDa}$ vectors,

  $$\mathbf{y}\oplus \mathbf{z}=\mathcal{C}(y_1{z}_1,y_2{z}_2,\dots ,y_p{z}_d),$$ (2)
• the powering operator for multiplication of $\mathrm{CoDa}$ vector with a constant,

  $$c\odot \mathbf{y}=\mathcal{C}(y_1^c,y_2^c,\dots ,y_d^c).$$ (3)

To overcome the constant sum constraints, $\mathrm{CoDa}$ can be transformed from simplex sample space ${\mathcal{S}}^d$ to real space ${\mathbb{R}}^{d-1}$ using the predefined transformations,

• Centered log-ratio transformation,

  $$\mathrm{clr}(\mathbf{y})=(\ln \frac{y_1}{{\overline{y}}_G},\ln \frac{y_2}{{\overline{y}}_G},\dots ,\ln \frac{y_d}{{\overline{y}}_G}),$$ (4)

  where ${\overline{y}}_G$ is the component-wise geometric mean of $\mathbf{y}$, i.e.

  $${\overline{y}}_G={\left(\prod _{i=1}^p{y}_i\right)}^{\frac{1}{d}}=\exp (\frac{1}{d}\sum _{i=1}^d\ln y_i).$$ (5)
• Isometric log-ratio

  $$\mathrm{ilr}(\mathbf{y})={\mathbf{y}}^{\ast }=\mathrm{clr}(\mathbf{y}){\mathbf{B}}^{⊺},$$ (6)

  where

  $$B_{i,j}=\{\begin{array}{ll}{\displaystyle \sqrt{\frac{1}{(d-i)(d-i+1)}}}& j\le d-i\\ {\displaystyle -\sqrt{\frac{d-i}{d-i+1}}}& j=d-i+1\\ 0& j>d-i+1\end{array}.$$

  To transform the vector from real space to simplex space, we use inverse isometric log-ratio,

  $${\mathrm{ilr}}^{-1}({\mathbf{y}}^{\ast })=\mathbf{y}=\mathcal{C}(\exp ({\mathbf{y}}^{\ast }\mathbf{B})).$$ (7)

There are two ways to deal with $\mathrm{CoDa}$, one is to use $\mathrm{CoDa}$ as it is by using powering and perturbation operator, and the second way is to transform $\mathrm{CoDa}$ into real space by using the above-mentioned log-ratio transformations so that the classical methods can be applied to $\mathrm{CoDa}$ after making some important amendments. For more details about $\mathrm{CoDa}$, the readers can refer to [17].

3. The VSI-MEWMA CoDa chart

Let us assume that there are have n measures ${\mathbf{x}}_{i,1},\dots ,{\mathbf{x}}_{i,n}$ of the quality characteristic ${\mathbf{y}}_i$ at the time $i=1,2,\dots$. ${\mathbf{y}}_i\sim {\mathrm{MNOR}}_{{\mathcal{S}}^d}({\mathit{\mu }}_0,\mathbf{\Sigma })$ when the process is IC, where ${\mathit{\mu }}_0$ is the IC mean vector and ${\mathbf{y}}_i\sim {\mathrm{MNOR}}_{{\mathcal{S}}^d}({\mathit{\mu }}_1,\mathbf{\Sigma })$ when the process is OOC, where ${\mathit{\mu }}_1$ is the OOC mean vector and $\mathbf{\Sigma }$ remain unchanged in both cases. Let ${\overline{\mathbf{x}}}_i^{\ast }=\mathrm{ilr}({\overline{\mathbf{x}}}_i)$ and ${\mathbf{y}}_i^{\ast }\sim {\mathrm{MNOR}}_{{\mathbb{R}}^{d-1}}({\mathit{\mu }}_0^{\ast },{\mathbf{\Sigma }}^{\ast })$, where ${\mathit{\mu }}_0^{\ast }=\mathrm{ilr}({\mathit{\mu }}_0)$ and ${\mathbf{\Sigma }}^{\ast }=\mathrm{ilr}(\mathbf{\Sigma })$. According to [36], x follows a multivariate normal distribution on $S^d$ if the vector of random orthonormal coordinates, $x^{\ast }=\mathrm{ilr}(x)$, follows a multivariate normal distribution on ${\mathbb{R}}^{D-1}$. This paper is an extension of [35] $\mathrm{VSI}-\mathrm{MEWMA}\mathrm{CoDa}$ CC, considering the SS ATS performance analysis. The $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC statistic is,

$${\mathbf{Q}}_i={\mathbf{w}}_i{\mathbf{\Sigma }}_{{\mathbf{w}}_i}^{-1}{\mathbf{w}}_i^{⊺},$$ (8)

with

$${\mathbf{w}}_i=r({\overline{\mathbf{x}}}_i^{\ast }-{\mu }_0^{\ast })+(1-r){\mathbf{w}}_{i-1},$$ (9)

where ${\mathbf{w}}_0=\mathbf{0}$ and $r\in (0,1]$ are smoothing parameters. The $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC shows a signal when

$${\mathbf{Q}}_i={\mathbf{w}}_i{\mathbf{\Sigma }}_{{\mathbf{w}}_i}^{-1}{\mathbf{w}}_i^{⊺}>H,$$ (10)

where H is the upper control limit ( $\mathrm{UCL}$), and ${\mathbf{\Sigma }}_{{\mathbf{w}}_i}$ is the variance-covariance matrix of ${\mathbf{w}}_i$. Here the author used the asymptotic variance-covariance matrix proposed by Lowry et al. [27], i.e.

$${\mathbf{\Sigma }}_{{\mathbf{w}}_i}=\frac{r}{n(2-r)}{\mathbf{\Sigma }}^{\ast }.$$ (11)

Due to the directional invariant property, the $\mathrm{MEWMA}$ CC's $\mathrm{ATS}$ depend on the non-centrality parameter δ [26]. Where the value of δ is,

$$\delta =({\mathit{\mu }}_1^{\ast }-{\mathit{\mu }}_0^{\ast })({\mathbf{\Sigma }}^{\ast }{)}^{-1}({\mathit{\mu }}_1^{\ast }-{\mathit{\mu }}_0^{\ast }{)}^{⊺}.$$ (12)

When the $\mathrm{SI}$ is fixed, the $\mathrm{SI}$ of $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is denoted by $h_0$. But for $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC, the selection of $\mathrm{SI}$ is based on the charting statistics ${\mathbf{Q}}_i$. The time interval between the sample $x_i$ and $x_i+1$ can vary. Using two sampling intervals is reasonable to limit the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC's complexity and achieve the proposed chart's efficacy [46]. Hence following [46], two $\mathrm{SI}$s are used in this paper, $h_1$ and $h_2$, where $h_2$ denotes the small $\mathrm{SI}$ and $h_1$ denotes the long one. For the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC, the $\mathrm{UCL}=H$ is the same as that of $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC. A warning limit (L) is introduced such that 0<L<H and $h_2<h_0<h_1$. The switch between the small and the long $\mathrm{SI}$ depends on the value of the CC parameter ${\mathbf{Q}}_i$. If the CC parameter ${\mathbf{Q}}_i$ lies within the L, a long $\mathrm{SI}{h}_1$ will be used, and if the value of ${\mathbf{Q}}_i$ lies between the L and the H, then the small $\mathrm{SI}{h}_2$ should be used.

4. The average time to signal

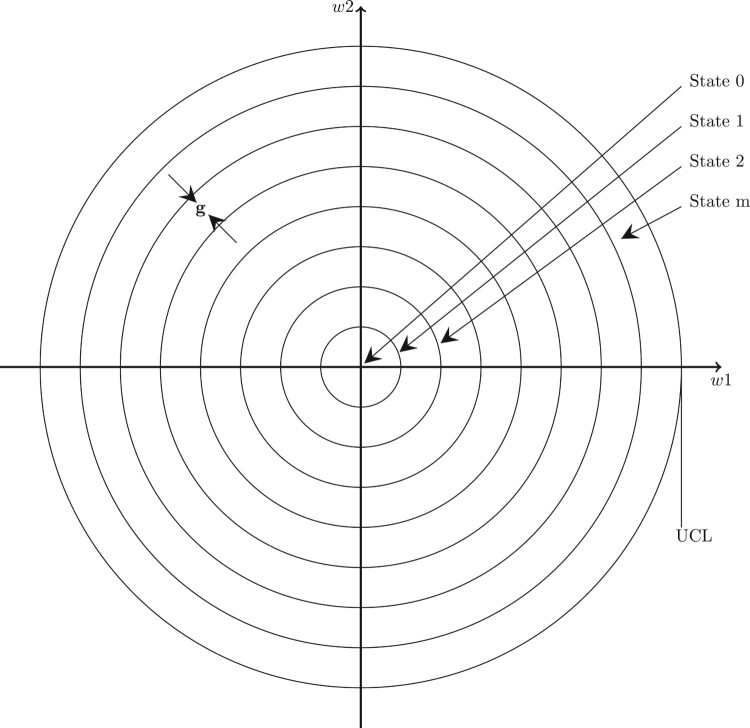
Prabhu and Runger [47] suggested calculating the statistics $q_i=\parallel Y_i{\parallel }_2$ as the standardized form of $Q_i=a\parallel Y_i{\parallel }_2^2$ with $a=\frac{2-r}{r}$ to determine the IC and OOC $\mathrm{ATS}$ of the $\mathrm{MEWMA}$ CC using $\mathrm{CTMC}$ models. For the IC case, one-dimensional $\mathrm{CTMC}$ (i.e. $[0,{\mathrm{UCL}}^{\prime }]$) is used to approximate the $\mathrm{ATS}$ of $q_i$, where ${\mathrm{UCL}}^{\prime }=(H/a{)}^{1/2}$ have m + 1 sub-interval with the length of the first sub-interval g/2 and others g and the width of sub-interval $g=2\mathrm{UCL}/2m+1$. Concerning the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CCs $\mathrm{WL}=(L/a{)}^{1/2}$ is also added to the one-dimensional $\mathrm{CTMC}$ (i.e. $[0,\mathrm{WL},{\mathrm{UCL}}^{\prime }]$). The IC one-dimensional $\mathrm{CTMC}$ is also shown in Figure 1.

Figure 1.

IC $\mathrm{CTMC}$ Distribution for the VSI MEWMA CoDa CC.

The probability of transition for i to j state is,

$$\begin{array}{r}{\mathbf{P}}_1(i,j)=\{\begin{array}{ll}{\displaystyle \mathrm{Pr}({\chi }^2(d-1,c)<{\left(\frac{g}{2r}\right)}^2)}& \mathrm{for}j=0\\ {\displaystyle \mathrm{Pr}({\left(\frac{(j-0.5)g}{r}\right)}^2<{\chi }^2(d-1,c)<{\left(\frac{(j+0.5)g}{r}\right)}^2)}& \mathrm{for}j=1,2,\dots ,m\end{array}\end{array}$$ (13)

where ${\mathbf{P}}_1(i,j)$ follows a non-central chi-square distribution ${\chi }^2(d-1,c)$ with a non-centrality parameter $c=(\frac{(1-r)\mathrm{ig}}{r}{)}^2$ having d−1 degree of freedom.

The $\mathrm{ATS}$ of the VSI- $\mathrm{MEWMA}\mathrm{CoDa}$ CCs for IC case is as follows,

$$\mathrm{ATS}={\mathrm{s}}^{⊺}({\mathbf{I}}_{m+1}-{\mathbf{P}}_1{)}^{-1}{\mathbf{h}}_{m+1},$$ (14)

with ${\mathbf{I}}_{m+1}$ is the identity matrix of size m + 1 and $\mathrm{s}=(1,0,0,\dots ,0{)}^{⊺}$ is the initial probability vector and ${\mathbf{h}}_{m+1}$ is vector of $\mathrm{SI}$. The $\mathrm{SI}$ average for the proposed CC can be written as

$$\overline{h}=\frac{{\mathrm{s}}^{⊺}({\mathbf{I}}_{m+1}-{\mathbf{P}}_1{)}^{-1}{\mathbf{h}}_{m+1}}{{\mathrm{s}}^{⊺}({\mathbf{I}}_{m+1}-{\mathbf{P}}_1{)}^{-1}{\mathbf{1}}_{m+1}}.$$ (15)

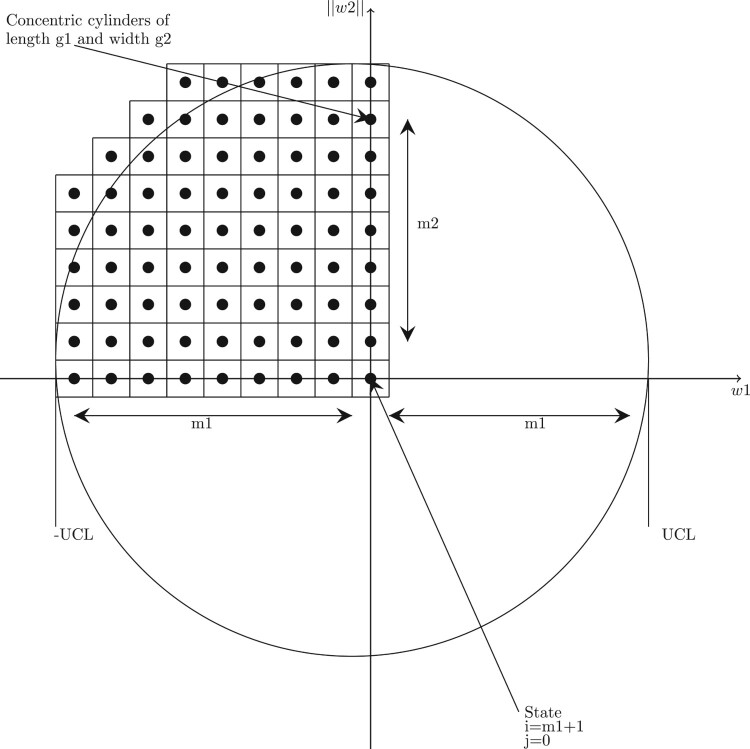
For the OOC case, two-dimensional $\mathrm{CTMC}$ is used to approximate the $\mathrm{ATS}$ of $q_i$ with the partition of ${\mathit{Y}}_i\in {\mathbb{R}}^{d-1}$ into $Y_{i1}\in \mathbb{R}$ and ${\mathit{Y}}_{i2}\in {\mathbb{R}}^{d-2}$ with δ and zero mean, respectively and $||{\mathit{Y}}_i|{|}_2=(Y_{i1}^2+{\mathit{Y}}_{i2}^{⊺}{\mathit{Y}}_{i2}{)}^{\frac{1}{2}}$. A two-dimensional $\mathrm{CTMC}$ can also be used for the $\mathrm{MEWMA}\mathrm{CoDa}$ CC. The approach used to approximate the component $Y_{i1}^2$, and for $||{\mathit{Y}}_{i2}|{|}_2$ is given in [28]; the same method for IC $\mathrm{CTMC}$ is used where d−1 is replaced by d−2. For $Y_{i1}$, the OOC component is analyzed using the transition probability $u(i_1,j_1)$ from state $i_1$ to state $j_1$ with $2m_1+1$ states,i.e.

$$\begin{array}{rl}u(i_1,j_1)& =\mathrm{\Phi }(\frac{-{\mathrm{UCL}}^{\prime }+j_1{g}_1-(1-r)c_i}{r}-\delta )\\ & -\mathrm{\Phi }(\frac{-{\mathrm{UCL}}^{\prime }+(j_1-1)g_1-(1-r)c_i}{r}-\delta ),\end{array}$$ (16)

where Φ is the cumulative standard normal distribution function with $c_i=-{\mathrm{UCL}}^{\prime }+(i-0.5)g_1$ being the midpoint of the state i and $g_1=\frac{2{\mathrm{UCL}}^{\prime }}{2m_1+1}$ be the width of each state. The OOC two-dimensional $\mathrm{CTMC}$ is also shown in Figure 2.

Figure 2.

OOC $\mathrm{CTMC}$ Distribution for the VSI MEWMA CoDa CC.

For ${\mathit{Y}}_{i2}$, the IC component is analyzed using the transition probability $v(i_2,j_2)$ from state $i_2$ to state $j_2$ with $m_2+1$ states. i.e.

$$v(i_2,j_2)=\left\{\begin{array}{l}{\displaystyle \mathrm{Pr}({\chi }^2(d-2,c)<{\left({\displaystyle \frac{g_2}{2r}}\right)}^2)\mathrm{for}{j}_2=0}\\ {\displaystyle \mathrm{Pr}({\left(\frac{(j_2-0.5)g_2}{r}\right)}^2<{\chi }^2(d-2,c)<{\left(\frac{(j_2+0.5)g_2}{r}\right)}^2)}\\ \mathrm{for}{j}_2=1,2,\dots ,m_2\end{array}\right\},$$ (17)

where $c=(\frac{(1-r)i{g}_2}{r}{)}^2$ with width of states $g_2=\frac{2{\mathrm{UCL}}^{\prime }}{2m_2+1}$. All the transient states of $\mathrm{CTMC}$ can be summarized in a transition probability matrix $\mathit{Pr}$. Then,

$$\mathit{Pr}=\mathit{T}(i_1,i_2)⊛{\mathit{P}}_2,$$ (18)

where the symbol ⊛ is used for element-wise matrices multiplication, $\mathit{T}$ is the $(2m_1+1)\times (m_2+1)$ dimensional matrix defined as

$$\mathit{T}(i_1,i_2)=\{\begin{array}{ll}1& \text{if state}(\alpha ,\beta )\text{is a transient state}\\ 0& \text{otherwise}\end{array}$$ (19)

and ${\mathit{P}}_2$ denotes the transition probability matrix of two-dimensional $\mathrm{CTMC}$, $P_2=\mathit{U}\otimes \mathit{V}$, where $\mathit{U}$ and $\mathit{V}$ are the transitional probability matrices of $Y_{i1}$ and $||{\mathit{Y}}_{i2}|{|}_2$ respectively and ⊗ is the Kronecker's matrices product. The $\mathrm{ZS}$ OOC $\mathrm{ATS}$ of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is defined as,

$$\mathrm{ZATS}={\mathrm{s}}^{⊺}({\mathbf{I}}_{m+1}-\mathit{Pr}{)}^{-1}{\mathbf{h}}_{m+1}.$$ (20)

with ${\mathbf{I}}_{m+1}$ is the identity matrix of size m + 1, and $\mathrm{s}$ is the initial probability vector with all components equal to zero except the component corresponding to the state $(\alpha ,\beta )=(m_1+1,0)$ which is equal to one and ${\mathbf{h}}_{m+1}$ is the vector of $\mathrm{SI}$.

The SS OOC $\mathrm{ATS}$ of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is defined as,

$$\mathrm{SATS}={\mathrm{w}}^{⊺}(\mathit{I}-\mathit{Pr}{)}^{-1}\mathit{s}.$$ (21)

where $\mathrm{w}$ is a $(2m+1,m+1)\mathrm{SS}$ vector with ${\mathrm{w}}_i=\frac{{\mathit{s}}_i{\mathit{b}}_i}{\mathit{sb}}$ and $\mathit{s}$ is $(2m+1,m+1)$ vector of $\mathrm{SI}$ with elements $h_1$ if $\sqrt{i_1-(m+1){)}^2\ast g^2+i_2^2{g}^2}<\mathrm{WL}$, $h_2$ if $\mathrm{WL}<\sqrt{i_1-(m+1){)}^2\ast g^2+i_2^2{g}^2}<\mathrm{UCL}$ and zero when the process is OOC. Where b is a SS probability vector obtained by solving the following equation: $\mathit{b}={\mathrm{P}}_1^{⊺}\mathit{b}$ subject to $1^{⊺}\mathit{b}=1$. Where ${\mathrm{P}}_1$ is the transition probability matrix when the process is IC, i.e. $\delta =0$.

The average of $\mathrm{SI}$ for the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC can be written as,

$$\overline{h}=p_1{h}_1+(1-p_1)h_2.$$ (22)

where $p_1$ is the proportion of time to signal. If $h_0=h_1=h_2$ the CC will be the standard $\mathrm{MEWMA}\mathrm{CoDa}$ CC. The number of states greatly impacts the $\mathrm{ATS}$ of the CC. (see [32]), but due to limited resources and time, the author cannot use a large number of m. Following literature reviews, hence $m_1=m_2=30$ will be used. (see [32] or [56]).

5. Comparative analysis of the VSI-MEWMA CoDa chart

This section presents an optimization approach for statistical designing the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC. An optimal $\mathrm{VSI}$ CC can be achieved using two different $\mathrm{SI}$s, with the small $\mathrm{SI}{h}_2$ taken as small as possible and the long $\mathrm{SI}{h}_1$ dependent on δ and $h_2$, where the CC is best for tracking shifts δ. Similar to [38,45], the practitioners need to set the $h_2$ fixed for the minimum interval hmin. The $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is designed by determining the CC parameters (i.e. r, $h_1$, W, and H) that minimize the OOC $\mathrm{ATS}$ aspect to the target value specified for constraints h, $h_2$ = hmin, and ${\mathrm{ATS}}_0$, for the provided values of n, d, and δ. The value of H will be the same for the $\mathrm{FSI}$ and the $\mathrm{VSI}$- $\mathrm{MEWMA}$- $\mathrm{CoDa}$ CCs for given values of r, n, h, and ${\mathrm{ATS}}_0$. The following is the optimized statistical layout process for the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC:

• Specify n, ${\mathrm{ATS}}_0$, d, $h2$, $\overline{h}$ and δ.

• Initialize r as 0.05.

• Initialize $h_1$ as $\overline{h}+0.1$. Set $h_2=0.1$, then find the value of H for the fixed value of IC ${\mathrm{ATS}}_0$, where $h_2<\overline{h}<h_1$. Given δ is calculated, the OOC $\mathrm{ZATS}$ and $\mathrm{SATS}$. Increasing r with a step size of 0.005, iterate Steps 3 to 5.

• The r, $h_1$, W, and H values are used to determine the minimum OOC $\mathrm{ZATS}$ and $\mathrm{SATS}$ for the optimal $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC parameters.

For comparison of the $\mathrm{VSI}$ with the $\mathrm{FSI}$ CC, the average $\mathrm{SI}\overline{h}$ of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is assumed to be the same as the $h_0$ of the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC, i.e. when the process is IC when $\overline{h}=1$. In other words, $\mathrm{SI}$ for the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is chosen to have a similar IC $\mathrm{ATS}$ as the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC; in the specific context, the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC's false alarm rate (i.e. ${\mathrm{ATS}}_0\approx 200$) is the same as the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC.

5.1. ZATS of the VSI-MEWMA CoDa control chart

The values of optimal couples of the $\mathrm{VSI}$ and the $\mathrm{FSI}\mathrm{MEWMA}\mathrm{CoDa}$ CCs under $\mathrm{ZS}$ are presented in Table 1. The OOC $\mathrm{ATS}$ values of the $\mathrm{VSI}$ and the $\mathrm{FSI}\mathrm{MEWMA}\mathrm{CoDa}$ CCs for $\mathrm{ZS}\mathrm{ATS}$ are given in Table 2 when $d\in \{3,5\}$ and $n\in \{1,3\}$. The OOC $\mathrm{ATS}$ values of the $\mathrm{VSI}$ and the $\mathrm{FSI}{T}^2\mathrm{CoDa}$ CCs for the $\mathrm{ZS}$ are also given in Table 2.

Table 1.

$\mathrm{ZS}$ optimum charting parameters for $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ and $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC.

		n = 1		n = 3
		$\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$	$\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$	$\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$	$\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$
δ	p	$(r,H,W,h1,h2)$	$(r,H)$	$(r,H,W,h1,h2)$	$(r,H)$
0.25	3	(0.05, 7.35, 1.74, 1.62, 0.10)	(0.05, 7.35)	(0.05, 7.35, 0.82, 2.70, 0.10)	(0.05, 7.35)
	5	(0.05, 9.46, 2.27, 2.10, 0.10)	(0.05, 9.46)	(0.05, 9.46, 2.30, 2.10, 0.10)	(0.05, 9.46)
0.50	3	(0.05, 7.50, 1.72, 1.65, 0.10)	(0.06, 7.50)	(0.05, 7.50, 1.24, 2.50, 0.10)	(0.06, 7.50)
	5	(0.05, 9.50, 1.73, 2.28, 0.10)	(0.06, 9.50)	(0.05, 9.50, 1.78, 2.28, 0.10)	(0.06, 9.50)
0.75	3	(0.09, 8.51, 1.64, 1.73, 0.10)	(0.09, 8.51)	(0.10, 8.51, 1.48, 2.20, 0.10)	(0.10, 8.51)
	5	(0.08, 10.27, 1.69, 2.09, 0.10)	(0.08, 10.27)	(0.09, 10.27, 1.76, 2.08, 0.10)	(0.08, 10.27)
1.00	3	(0.14, 9.19, 2.90, 1.32, 0.10)	(0.14, 9.19)	(0.15, 9.41, 1.88, 1.89, 0.10)	(0.15, 9.41)
	5	(0.13, 10.71, 1.95, 1.83, 0.10)	(0.13, 10.71)	(0.14, 10.93, 2.05, 1.82, 0.10)	(0.13, 10.93)
1.25	3	(0.19, 9.61, 1.65, 1.82, 0.10)	(0.20, 9.61)	(0.21, 9.77, 2.45, 1.69, 0.10)	(0.20, 9.77)
	5	(0.18, 10.97, 2.45, 1.65, 0.10)	(0.19, 10.97)	(0.20, 11.13, 2.58, 1.64, 0.10)	(0.19, 11.13)
1.50	3	(0.25, 9.91, 3.51, 1.22, 0.10)	(0.25, 9.91)	(0.27, 10.05, 2.86, 1.49, 0.10)	(0.25, 10.05)
	5	(0.24, 11.11, 2.81, 1.46, 0.10)	(0.25, 11.11)	(0.26, 11.25, 2.96, 1.45, 0.10)	(0.25, 11.25)
1.75	3	(0.31, 10.12, 3.72, 1.24, 0.10)	(0.31, 10.12)	(0.34, 10.23, 4.01, 1.28, 0.10)	(0.31, 10.23)
	5	(0.31, 11.16, 3.92, 1.26, 0.10)	(0.31, 11.16)	(0.33, 11.27, 4.09, 1.25, 0.10)	(0.31, 11.27)
2.00	3	(0.37, 10.26, 3.62, 1.25, 0.10)	(0.38, 10.26)	(0.41, 10.36, 4.70, 1.10, 0.10)	(0.38, 10.36)
	5	(0.37, 11.14, 4.57, 1.10, 0.10)	(0.37, 11.14)	(0.40, 11.24, 4.77, 1.10, 0.10)	(0.37, 11.24)

Table 2.

OOC $\mathrm{ZATS}$ of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC.

		n = 1				n = 3
		$\mathrm{MEWMA}\mathrm{CoDa}$		$T^2\mathrm{CoDa}$		$\mathrm{MEWMA}\mathrm{CoDa}$		$T^2\mathrm{CoDa}$
δ	p	$\mathrm{VSI}$	$\mathrm{FSI}$	$\mathrm{VSI}$	$\mathrm{FSI}$	$\mathrm{VSI}$	$\mathrm{FSI}$	$\mathrm{VSI}$	$\mathrm{FSI}$
0.25	3	56.842	64.6	115.528	88.553	48.346	53.980	112.877	85.902
	5	64.362	70.27	120.928	99.909	53.746	59.654	118.277	97.258
0.50	3	19.935	26.4	76.86	51.885	17.731	22.440	75.900	50.925
	5	26.695	31.65	81.86	59.076	22.731	27.686	80.900	58.116
0.75	3	10.441	15.1	55.323	33.367	9.095	12.900	54.784	32.828
	5	15.69	19.72	59.723	38.901	13.495	17.525	59.184	38.362
1.00	3	6.913	9.9	41.916	22.986	5.489	8.440	41.559	22.629
	5	10.748	13.89	45.716	27.482	9.289	12.431	45.359	27.125
1.25	3	4.934	7.1	32.942	16.039	3.885	6.050	32.687	15.784
	5	8.333	10.67	36.342	19.932	7.285	9.623	36.087	19.677
1.50	3	3.728	5.4	26.618	11.744	3.185	4.610	26.425	11.551
	5	6.978	8.55	29.618	15.142	6.185	7.757	29.425	14.948
1.75	3	3.008	4.3	21.984	9.14	2.852	3.680	21.832	8.989
	5	6.075	7.03	24.584	12.088	5.452	6.407	24.432	11.936
2.00	3	2.419	3.5	18.484	7.484	2.246	3.000	18.362	7.362
	5	4.95	5.81	20.684	9.684	4.446	5.306	20.562	9.562

5.1.1. Impact of sampling interval h

Based on Table 2, it can be seen that the $\mathrm{ZATS}$ of the $\mathrm{VSI}$ CC is less than the $\mathrm{ZATS}$ of the $\mathrm{FSI}$ CC. When $\delta =1$, n = 1, d = 3, $h_1=1.90$, $h_2=0.1$ and W = 1.78, the $\mathrm{ZATS}$ for the $\mathrm{FSI}$- $T^2\mathrm{CoDa}$ CC is $\mathrm{ZATS}=41.916$, while for the $\mathrm{VSI}$- $T^2\mathrm{CoDa}$ CC is $\mathrm{ZATS}=22.986$. Similarly, when $\delta =1$, n = 1, d = 3, $h_1=1.90$, $h_2=0.1$, r = 0.14, H = 9.19 and W = 1.78, the $\mathrm{ZATS}$ for the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is $\mathrm{ZATS}=6.98$, while for the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is $\mathrm{ZATS}=9.90$. Hence it is summarized that the $\mathrm{VSI}$ CCs have a greater degree of efficacy than the $\mathrm{FSI}$ CCs for $\mathrm{CoDa}$.

5.1.2. Impact of number of the variables d

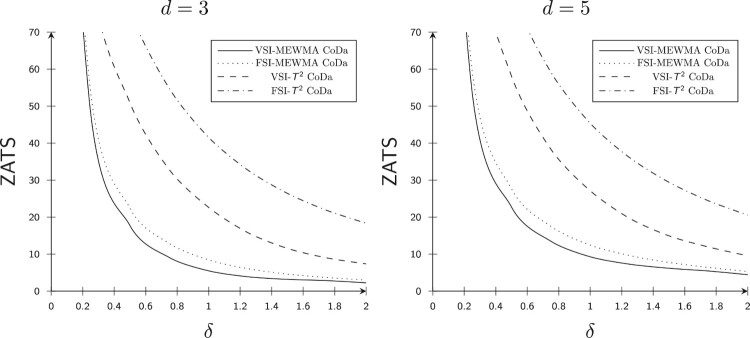
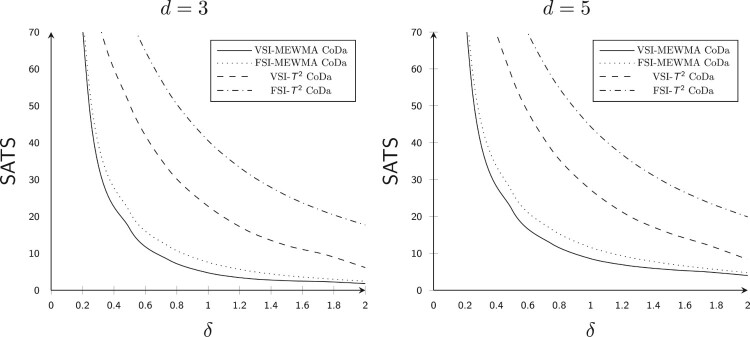
Based on Table 2 and Figure 3, it can be seen that d has a negative effect on the $\mathrm{ZS}\mathrm{ATS}$ of the CC for $\mathrm{CoDa}$; that is, the OOC $\mathrm{ZATS}$ values increase with an increase in the value of d.

Figure 3.

$\mathrm{ZATS}$ Curves for n = 3 and $d\in \{3,5\}$.

When $\delta =1$, n = 1, d = 3, $h_1=1.90$, $h_2=0.1$ and W = 1.78, the $\mathrm{ZATS}$ for the $\mathrm{FSI}$- $T^2\mathrm{CoDa}$ CC is $\mathrm{ZATS}=41.916$ and for the $\mathrm{VSI}$- $T^2\mathrm{CoDa}$ CC is $\mathrm{ZATS}=22.986$. But when the value of d increases to d = 5, the $\mathrm{ZATS}$ for the $\mathrm{FSI}$- $T^2\mathrm{CoDa}$ CC increases to $\mathrm{ZATS}=45.716$ and the $\mathrm{VSI}$- $T^2\mathrm{CoDa}$ CC increases to $\mathrm{ZATS}=27.482$.

Similarly, when $\delta =1$, n = 1, d = 3, $h_1=1.90$, $h_2=0.1$, r = 0.14, H = 9.19 and W = 1.78, the $\mathrm{ZATS}$ for the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is $\mathrm{ZATS}=6.98$, and for the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is $\mathrm{ZATS}=9.90$. But, when the value of d increases to d = 5, the $\mathrm{ZATS}$ for the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC increases to $\mathrm{ZATS}=10.748$ and the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC increases to $\mathrm{ZATS}=13.89$. Figure 3 also shows the impact of the number of variables d on $\mathrm{ZATS}$ of the $T^2\mathrm{CoDa}$ and the $\mathrm{MEWMA}\mathrm{CoDa}$ CC for both the $\mathrm{VSI}$ and the $\mathrm{FSI}$ situations.

Where a solid black line shows the $\mathrm{ZATS}$ of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC, the $\mathrm{ZATS}$ of the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is shown by the dotted line, and the dashed line shows the $\mathrm{ZATS}$ of the $\mathrm{VSI}$- $T^2\mathrm{CoDa}$ CC, the dashed-dotted line shows the $\mathrm{ZATS}$ of the $\mathrm{FSI}$- $T^2\mathrm{CoDa}$ CC. From Figure 3, it is also clearly visible that d has a negative effect on the $\mathrm{ATS}$ of the $\mathrm{VSI}$ and the $\mathrm{FSI}$ CC for $\mathrm{CoDa}$.

5.1.3. Impact of subgroup size n

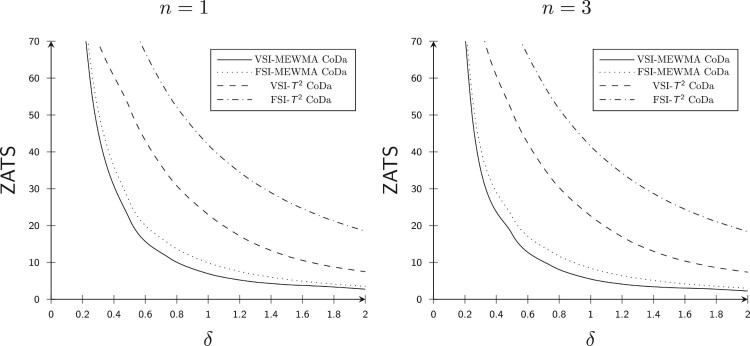
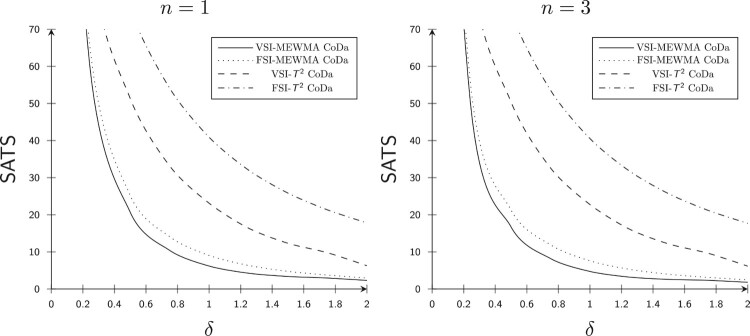
Based on Table 2, it can be seen that n has a mild positive effect on the $\mathrm{ATS}$ of the CC for $\mathrm{CoDa}$; that is, the OOC $\mathrm{ZATS}$ values decrease with an increase in the value of n.

When $\delta =1$, n = 1, d = 3, $h_1=1.90$, $h_2=0.1$ and W = 1.78, the $\mathrm{ZATS}$ for the $\mathrm{FSI}$- $T^2\mathrm{CoDa}$ CC is $\mathrm{ZATS}=41.916$, and for the $\mathrm{VSI}$- $T^2\mathrm{CoDa}$ CC is $\mathrm{ZATS}=22.986$. But when the value of n increases to n = 3, the $\mathrm{ZATS}$ for the $\mathrm{FSI}$- $T^2\mathrm{CoDa}$ CC decreases to $\mathrm{ZATS}=41.559$, and the $\mathrm{VSI}$- $T^2\mathrm{CoDa}$ CC decreases to $\mathrm{ZATS}=22.629$.

Similarly, when $\delta =1$, n = 1, d = 3, $h_1=1.90$, $h_2=0.1$, r = 0.14, H = 9.19 and W = 1.78, the $\mathrm{ZATS}$ for the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is $\mathrm{ZATS}=6.98$ and for the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is $\mathrm{ZATS}=9.90$. But when the value of n increases to n = 3, the $\mathrm{ZATS}$ for the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC decreases to $\mathrm{ZATS}=5.489$, and the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC decreases to $\mathrm{ZATS}=8.44$. Figure 4 also shows the impact of the subgroup size n on $\mathrm{ZATS}$ of the Hotelling $T^2\mathrm{CoDa}$ and the $\mathrm{MEWMA}\mathrm{CoDa}$ CC for both the $\mathrm{VSI}$ and the $\mathrm{FSI}$ situations. From Figure 4, it is also clearly visible that n has a positive effect on the $\mathrm{ATS}$ of the $\mathrm{VSI}$ and the $\mathrm{FSI}$ CC for $\mathrm{CoDa}$.

Figure 4.

$\mathrm{ZATS}$ Curves for d = 3 and $n\in \{1,3\}$.

5.2. SATS of the VSI-MEWMA CoDa control chart

The values of optimal couples of the $\mathrm{VSI}$ and the $\mathrm{FSI}\mathrm{MEWMA}\mathrm{CoDa}$ CCs under SS are presented in Table 3. The OOC $\mathrm{ATS}$ values of the $\mathrm{VSI}$ and the $\mathrm{FSI}\mathrm{MEWMA}\mathrm{CoDa}$ CCs for $\mathrm{SS}\mathrm{ATS}$ are given in Table 4 when $d\in \{3,5\}$ and $n\in \{1,3\}$. The OOC $\mathrm{ATS}$ values of the $\mathrm{VSI}$ and the $\mathrm{FSI}{T}^2\mathrm{CoDa}$ CCs for the SS are also given in Table 4.

Table 3.

SS optimum charting parameters for $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ and $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC.

		n = 1		n = 3
		$\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$	$\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$	$\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$	$\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$
δ	p	$(r,H,W,h1,h2)$	$(r,H)$	$(r,H,W,h1,h2)$	$(r,H)$
0.25	3	(0.05, 7.38, 0.80, 2.50, 0.10)	(0.05, 7.38)	(0.05, 7.38, 0.83, 2.50, 0.10)	(0.05, 7.38)
	5	(0.05, 9.33, 2.25, 1.92, 0.10)	(0.05, 9.33)	(0.05, 9.33, 2.30, 1.91, 0.10)	(0.05, 9.33)
0.50	3	(0.05, 7.53, 1.19, 2.30, 0.10)	(0.05, 7.53)	(0.05, 7.53, 1.24, 2.30, 0.10)	(0.05, 7.53)
	5	(0.05, 9.37, 1.71, 2.09, 0.10)	(0.05, 9.37)	(0.05, 9.37, 1.78, 2.09, 0.10)	(0.05, 9.37)
0.75	3	(0.09, 8.54, 1.42, 2.00, 0.10)	(0.10, 8.54)	(0.10, 8.54, 1.49, 2.00, 0.10)	(0.10, 8.54)
	5	(0.08, 10.14, 1.68, 1.89, 0.10)	(0.09, 10.14)	(0.09, 10.14, 1.77, 1.89, 0.10)	(0.08, 10.14)
1.00	3	(0.14, 9.22, 1.80, 1.70, 0.10)	(0.15, 9.22)	(0.15, 9.44, 1.90, 1.69, 0.10)	(0.15, 9.44)
	5	(0.13, 10.58, 1.95, 1.64, 0.10)	(0.14, 10.58)	(0.14, 10.80, 2.07, 1.63, 0.10)	(0.14, 10.80)
1.25	3	(0.19, 9.64, 2.35, 1.50, 0.10)	(0.20, 9.64)	(0.21, 9.80, 2.47, 1.49, 0.10)	(0.20, 9.80)
	5	(0.19, 10.84, 2.45, 1.46, 0.10)	(0.19, 10.84)	(0.20, 11.00, 2.59, 1.45, 0.10)	(0.19, 11.00)
1.50	3	(0.25, 9.94, 2.74, 1.30, 0.10)	(0.26, 9.94)	(0.27, 10.08, 2.89, 1.29, 0.10)	(0.26, 10.08)
	5	(0.25, 10.98, 2.82, 1.27, 0.10)	(0.25, 10.98)	(0.27, 11.12, 2.99, 1.25, 0.10)	(0.25, 11.12)
1.75	3	(0.31, 10.15, 3.86, 1.10, 0.10)	(0.32, 10.15)	(0.34, 10.26, 4.04, 1.10, 0.10)	(0.32, 10.26)
	5	(0.31, 11.03, 3.94, 1.07, 0.10)	(0.31, 11.03)	(0.33, 11.14, 4.12, 1.10, 0.10)	(0.31, 11.14)
2.00	3	(0.38, 10.29, 4.54, 1.10, 0.10)	(0.38, 10.29)	(0.41, 10.39, 4.74, 1.10, 0.10)	(0.38, 10.39)
	5	(0.37, 11.17, 4.60, 1.08, 0.10)	(0.37, 11.17)	(0.40, 11.27, 4.81, 1.10, 0.10)	(0.37, 11.27)

Table 4.

OOC $\mathrm{SATS}$ of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC.

		n = 1				n = 3
		$\mathrm{MEWMA}\mathrm{CoDa}$		$T^2\mathrm{CoDa}$		$\mathrm{MEWMA}\mathrm{CoDa}$		$T^2\mathrm{CoDa}$
δ	p	$\mathrm{VSI}$	$\mathrm{FSI}$	$\mathrm{VSI}$	$\mathrm{FSI}$	$\mathrm{VSI}$	$\mathrm{FSI}$	$\mathrm{VSI}$	$\mathrm{FSI}$
0.25	3	57.882	63.350	114.028	87.804	47.267	52.740	111.378	85.155
	5	62.882	68.600	119.028	99.900	52.905	58.698	117.129	97.044
0.50	3	20.695	25.250	75.480	51.356	16.732	21.290	74.521	50.398
	5	25.295	30.080	80.080	59.195	21.819	26.642	79.647	57.718
0.75	3	10.410	14.100	54.123	33.169	8.216	11.910	53.586	32.633
	5	14.410	18.300	58.123	39.213	12.662	16.579	58.049	38.194
1.00	3	6.188	9.050	40.896	23.119	4.732	7.590	40.543	22.766
	5	9.588	12.620	44.296	27.986	8.560	11.616	44.380	27.255
1.25	3	4.253	6.350	32.042	16.394	3.209	5.310	31.792	16.144
	5	7.253	9.500	35.042	20.564	6.629	8.899	35.218	20.016
1.50	3	3.378	4.750	25.838	12.320	2.590	3.960	25.652	12.135
	5	5.978	7.480	28.438	15.901	5.606	7.131	28.672	15.509
1.75	3	2.955	3.750	21.324	9.774	2.338	3.130	21.172	9.622
	5	5.155	6.060	23.524	12.524	4.952	5.857	23.772	12.222
2.00	3	2.310	2.950	17.824	6.274	1.806	2.450	17.702	6.152
	5	4.510	5.260	20.024	9.024	4.006	4.756	19.902	8.352

5.2.1. Impact of sampling interval h

Based on Table 4, it can be seen that the $\mathrm{SATS}$ of the $\mathrm{VSI}$ CC is less than the $\mathrm{SATS}$ of the $\mathrm{FSI}$ CC. When $\delta =1$, n = 1, d = 3, $h_1=1.70$, $h_2=0.1$ and W = 1.80, the $\mathrm{SATS}$ for the $\mathrm{FSI}$- $T^2\mathrm{CoDa}$ CC is $\mathrm{SATS}=40.896$, while for the $\mathrm{VSI}$- $T^2\mathrm{CoDa}$ CC is $\mathrm{SATS}=23.119$. Similarly, when $\delta =1$, n = 1, d = 3, $h_1=1.70$, $h_2=0.1$, r = 0.14, H = 9.22 and W = 1.80, the $\mathrm{SATS}$ for the $\mathrm{FSI}\mathrm{MEWMA}\mathrm{CoDa}$ CC is $\mathrm{SATS}=9.05$, while for the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is $\mathrm{SATS}=6.188$. Hence it is summarized that the $\mathrm{VSI}$ CCs have a greater degree of efficacy than the $\mathrm{FSI}$ CCs for $\mathrm{CoDa}$.

5.2.2. Impact of number of the variables d

Based on Table 4, it can be seen that d has a negative effect on the $\mathrm{ATS}$ of the CC for $\mathrm{CoDa}$; that is, the OOC $\mathrm{SATS}$ values increase with an increase in the value of d.

When $\delta =1$, n = 1, d = 3, $h_1=1.70$, $h_2=0.1$ and W = 1.80, the $\mathrm{SATS}$ for the $\mathrm{FSI}$- $T^2\mathrm{CoDa}$ CC is $\mathrm{SATS}=40.896$ and for the $\mathrm{VSI}$- $T^2\mathrm{CoDa}$ CC is $\mathrm{SATS}=23.119$. But when the value of d increases to d = 5, the $\mathrm{SATS}$ for the $\mathrm{FSI}$- $T^2\mathrm{CoDa}$ CC increases to $\mathrm{SATS}=44.296$ and the $\mathrm{VSI}$- $T^2\mathrm{CoDa}$ CC increases to $\mathrm{SATS}=27.986$.

Similarly, when $\delta =1$, n = 1, d = 3, $h_1=1.70$, $h_2=0.1$, r = 0.14, H = 9.22 and W = 1.80, the $\mathrm{SATS}$ for the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is $\mathrm{SATS}=9.05$ and for the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is $\mathrm{SATS}=6.188$. But when the value of d increases to d = 5, the $\mathrm{SATS}$ for the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC increases to $\mathrm{SATS}=12.62$, and the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC increases to $\mathrm{SATS}=9.58$. Figure 5 also shows the impact of the number of variables d on $\mathrm{SATS}$ of the $\mathrm{MEWMA}\mathrm{CoDa}$ CC. From Figure 5, it is also clearly visible that d has a negative effect on the $\mathrm{ATS}$ of the $\mathrm{VSI}$ and the $\mathrm{FSI}$ CC for $\mathrm{CoDa}$.

Figure 5.

$\mathrm{SATS}$ Curves for n = 3 and $d\in \{3,5\}$.

5.2.3. Impact of subgroup size n

Based on Table 4, it can be seen that n has a mild positive effect on the $\mathrm{ATS}$ of the CC for $\mathrm{CoDa}$; that is, the OOC $\mathrm{SATS}$ values decrease with an increase in the value of n.

When $\delta =1$, n = 1, d = 3, $h_1=1.70$, $h_2=0.1$ and W = 1.80, the $\mathrm{SATS}$ for the $\mathrm{FSI}$- $T^2\mathrm{CoDa}$ CC is $\mathrm{SATS}=40.896$ and for the $\mathrm{VSI}$- $T^2\mathrm{CoDa}$ CC is $\mathrm{SATS}=23.119$. But when the value of n increases to n = 3, the $\mathrm{SATS}$ for the $\mathrm{FSI}$- $T^2\mathrm{CoDa}$ CC decreases to $\mathrm{SATS}=40.543$, and the $\mathrm{VSI}$- $T^2\mathrm{CoDa}$ CC decreases to $\mathrm{SATS}=22.766$.

Similarly, when $\delta =1$, n = 1, d = 3, $h_1=1.70$, $h_2=0.1$, r = 0.14, H = 9.22 and W = 1.80, the $\mathrm{SATS}$ for the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is $\mathrm{SATS}=9.05$ and for the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is $\mathrm{SATS}=6.188$. But when the value of n increases to n = 3, the $\mathrm{SATS}$ for the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC decreases to $\mathrm{SATS}=7.59$, and the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC decreases to $\mathrm{SATS}=4.732$. Figure 5 also shows the impact of the subgroup size n on the $\mathrm{SATS}$ of the $\mathrm{MEWMA}\mathrm{CoDa}$ CC. From Figure 6, it is also clearly visible that n has a positive effect on the $\mathrm{ATS}$ of the $\mathrm{VSI}$ and $\mathrm{FSI}$ CC for $\mathrm{CoDa}$.

Figure 6.

$\mathrm{SATS}$ Curves for d = 3 and $n\in \{1,3\}$.

5.3. Comparison of ZATS and SATS of the VSI-MEWMA CoDa control chart

To compare the $\mathrm{ZS}$ and the SS performance of the VSI-MEWMA CoDa CC, all the $\mathrm{ZATS}$ and the $\mathrm{SATS}$ values for different combinations of the involved variables are given in Table 5. It can be seen from Table 5 that the $\mathrm{SATS}$ for both the $\mathrm{FSI}$ and the $\mathrm{VSI}\mathrm{MEWMA}\mathrm{CoDa}$ CC are less than the $\mathrm{ZATS}$ of both the $\mathrm{FSI}$ and the $\mathrm{VSI}\mathrm{MEWMA}\mathrm{CoDa}$ CC.

Table 5.

OOC $\mathrm{ZATS}$ and $\mathrm{SATS}$ of the $\mathrm{FSI}$ and $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC.

	d = 3				d = 5
	n = 1		n = 3		n = 1		n = 3
δ	VSI	FSI	VSI	FSI	VSI	FSI	VSI	FSI
$\mathrm{ZATS}$
0.25	56.842	64.6	48.346	53.98	64.362	70.27	53.746	59.654
0.5	19.935	26.4	17.731	22.44	26.695	31.65	22.731	27.686
0.75	10.441	15.1	9.095	12.9	15.69	19.72	13.495	17.525
1	6.913	9.9	5.489	8.44	10.748	13.89	9.289	12.431
1.25	4.934	7.1	3.885	6.05	8.333	10.67	7.285	9.623
1.5	3.728	5.4	3.185	4.61	6.978	8.55	6.185	7.757
1.75	3.008	4.3	2.852	3.68	6.075	7.03	5.452	6.407
2	2.419	3.5	2.246	3	4.95	5.81	4.446	5.306
$\mathrm{SATS}$
0.25	55.762	63.35	47.267	52.74	62.882	68.6	52.905	58.698
0.5	18.935	25.25	16.732	21.29	25.295	30.08	21.819	26.642
0.75	9.561	14.1	8.216	11.91	14.41	18.3	12.662	16.579
1	6.153	9.05	4.732	7.59	9.588	12.62	8.56	11.616
1.25	4.254	6.35	3.209	5.31	7.253	9.5	6.629	8.899
1.5	3.128	4.75	2.59	3.96	5.978	7.48	5.606	7.131
1.75	2.488	3.75	2.338	3.13	5.155	6.06	4.952	5.857
2	1.979	2.95	1.806	2.45	4.51	5.26	4.006	4.756

When $\delta =1$, n = 1, d = 3, the $\mathrm{ZATS}$ for the $\mathrm{FSI}$ and the $\mathrm{VSI}\mathrm{MEWMA}\mathrm{CoDa}$ CC are $\mathrm{ZATS}=9.90$ and $\mathrm{ZATS}=6.948$ respectively. While the $\mathrm{SATS}$ for the $\mathrm{FSI}$ and the $\mathrm{VSI}\mathrm{MEWMA}\mathrm{CoDa}$ CC are $\mathrm{SATS}=9.05$ and $\mathrm{SATS}=6.188$, respectively, are less than $\mathrm{ZATS}$ for both the $\mathrm{FSI}$ and the $\mathrm{VSI}\mathrm{MEWMA}\mathrm{CoDa}$ CC.

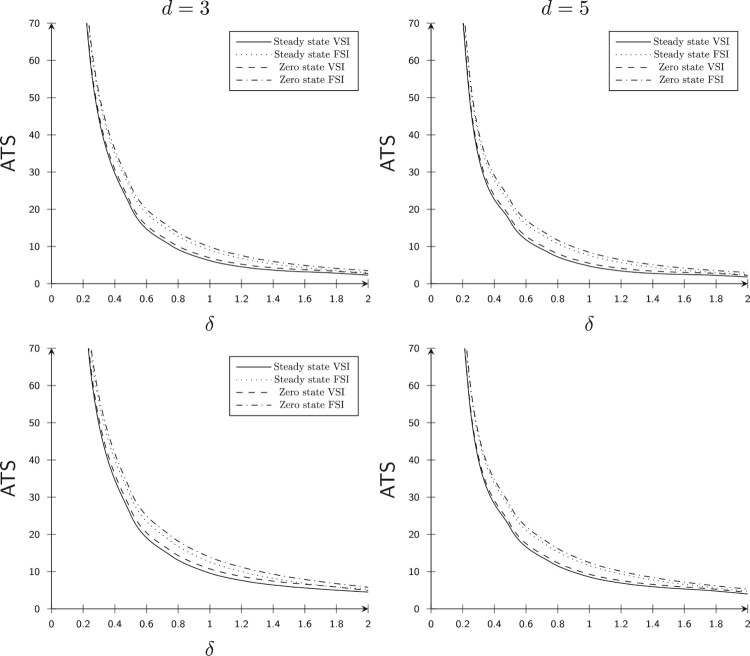
Figure 7 also shows the $\mathrm{ZATS}$ and the $\mathrm{SATS}$ curves for both the $\mathrm{FSI}$ and the $\mathrm{VSI}\mathrm{MEWMA}\mathrm{CoDa}$ CCs. A solid line shows the $\mathrm{SATS}$ of $\mathrm{VSI}$ in all the figures, the $\mathrm{SATS}$ of the $\mathrm{FSI}$ is shown by a dotted line in all the figures, the $\mathrm{ZATS}$ of the $\mathrm{VSI}$ is shown by a dashed line in all the figures, while a dashed-dotted line shows the $\mathrm{ZATS}$ of the $\mathrm{FSI}$ in all the figures. From Figure 7, we can see that the $\mathrm{SATS}$ for both the $\mathrm{FSI}$ and the $\mathrm{VSI}\mathrm{MEWMA}\mathrm{CoDa}$ CC are less than the $\mathrm{ZATS}$ of both the $\mathrm{FSI}$ and the $\mathrm{VSI}\mathrm{MEWMA}\mathrm{CoDa}$ CC.

Figure 7.

$\mathrm{SATS}$ and $\mathrm{ZATS}$ Curves.

Also the out-of-control performances of $\mathrm{VSI}\mathrm{MEWMA}\mathrm{CoDa}$ CC under $\mathrm{ZS}$ and SS can be compared using percentage improvement indicator as,

$$\mathrm{\Delta }=\frac{100({\mathrm{ATS}}_{\mathrm{ZS}}-{\mathrm{ATS}}_{\mathrm{SS}})}{{\mathrm{ATS}}_{\mathrm{ZS}}}$$

Table 6 presents the percentage improvement in terms of out-of-control $\mathrm{ATS}$s under the $\mathrm{ZS}$ and SS of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC for n = 1 and p = 3. The SATS of $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC is always smaller than the ZATS of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC.

Table 6.

Comparison in terms of out-of-control $\mathrm{ATS}$s under the $\mathrm{ZS}$ and SS of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC for n = 1 and p = 3.

δ	$\mathrm{ZATS}$	$\mathrm{SATS}$	Δ
0.25	56.842	55.762	1.90
0.50	19.935	18.935	5.02
0.75	10.441	9.561	8.43
1.00	6.913	6.153	10.99
1.25	4.934	4.254	13.78
1.50	3.728	3.128	16.09
1.75	3.008	2.488	17.29
2.00	2.419	1.979	18.19

In terms of their percentage improvement indicators it can be seen that, depending on the level of shift δ, when n = 1 and p = 3, the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC under SS proposed in this paper is between 2% to 18% more efficient than the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC under $\mathrm{ZS}$ presented in [35].

6. Illustrative example

Similar to [56,58], the example of the particle-size distribution for a plant in Europe is used in this study. According to [58], there were four OOC points in the data (i.e. $(\mathrm{\#}1,\mathrm{\#}26,\mathrm{\#}45,\mathrm{\#}52)$). Following [56], the author removed all the four OOC points described by Vives et al. [58] to get the IC phase I data set. Assume that the author would like to use the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC with r = 0.05 and H = 7.35 to control a process of d = 3-part $\mathrm{CoDa}$. After removing the OOC point, the IC phase-I dataset is given in Table 7. The estimates for the parameters of the multivariate normal distribution of the $\mathrm{ilr}$ transformed mean vector and variance-covariance matrix are given by

$${\mathit{\mu }}_0^{\ast }=\left(\begin{array}{c}1.962\\ 1.184\end{array}\right),$$

and

$${\mathbf{\Sigma }}^{\ast }=\left(\begin{array}{cc}0.099& -0.022\\ -0.022& 0.088\end{array}\right).$$

while the mean of original $\mathrm{CoDa}$ can be written as

$${\mathit{\mu }}_0=\left(\begin{array}{c}0.892\\ 0.056\\ 0.052\end{array}\right),$$

Table 7.

The Phase I dataset from [56].

i	M	L	S	i	M	L	S	i	M	L	S	i	M	L	S
1	92.6	3.2	4.2	14	94.5	2.6	2.9	27	83.6	7.4	9	40	84.5	6.9	8.6
2	91.7	5.2	3.1	15	94.5	2.7	2.8	28	84.8	6.8	8.4	41	84.4	7.4	8.2
3	86.9	3.5	9.6	16	88.7	7.9	3.4	29	87.1	6.3	6.6	42	84.3	8.9	6.8
4	90.4	2.9	6.7	17	84.6	6.6	8.8	30	87.2	6.1	6.7	43	89.8	8.2	2
5	92.1	4.6	3.3	18	90.7	4	5.3	31	87.3	6.6	6.1	44	90.4	6.7	2.9
6	91.5	4.4	4.1	19	90.2	2.5	7.3	32	84.8	6.2	9	45	90.1	5.9	4
7	90.3	5	4.7	20	92.7	3.8	3.5	33	87.4	6.5	6.1	46	83.6	8.7	7.7
8	85.1	8.4	6.5	21	91.5	2.8	5.7	34	86.8	6	7.2	47	88	6.4	5.6
9	89.7	4.2	6.1	22	91.8	2.9	5.3	35	88.8	4.8	6.4	48	84.7	8.4	6.9
10	92.5	3.8	3.7	23	90.6	3.3	6.1	36	89.8	4.9	5.3	49	93	5.1	1.9
11	91.8	4.3	3.9	24	87.3	7.2	5.5	37	86.9	5.8	7.3	50	91.4	5	3.6
12	91.7	3.7	4.6	25	82.6	7	10.4	38	83.8	7.2	9	51	86.2	5	8.8
13	90.3	3.8	5.9	26	83.5	6	10.5	39	89.2	5.6	5.2	52	87.2	5.9	6.9

For the phase II dataset, using simulation, 20 samples of size n = 3 have been generated using ${\mathit{\mu }}_0^{\ast }$. The process is IC up to sample 10, after sample 10, a shift with the assignable cause in the mean vector has been introduced, and the next 10 samples are generated using ${\mathit{\mu }}_1^{\ast }$. Hence the mean vector shifted from

$${\mathit{\mu }}_0^{\ast }=\left(\begin{array}{c}1.962\\ 1.184\end{array}\right),$$

to

$${\mathit{\mu }}_1^{\ast }=\left(\begin{array}{c}2.070\\ 1.15\end{array}\right),$$

or it can be written in original $\mathrm{CoDa}$ as

$${\mathit{\mu }}_1=\left(\begin{array}{c}0.901\\ 0.048\\ 0.051\end{array}\right).$$

Where the shift from ${\mathit{\mu }}_0^{\ast }$ to ${\mathit{\mu }}_1^{\ast }$ equals $\delta =0.34$. But here, the author has used a shift of size $\delta =0.25$ in the mean vector. $\delta =0.25$ is considered enough to detect the shift in ${\mu }^{\ast }$ quickly, as it is interpreted as a signal that something is not right in the process. For this reason, $\delta =0.25$ is used to implement the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC. For n = 1 and $\delta =0.25$, the optimal parameters for the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC are r = 0.05 and H = 7.35 (see Table 2).

Here the author has taken the subgroup of size n = 3 and the IC ${\mathrm{ATS}}_0=200$. Using $h_2=0.1$ and $h_1=2.5$, the author gets a WL of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC W = 0.8 with the SS OOC SATS = 57.882. The next $\mathrm{SI}$ depends on the position of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC; if the CC lies below W, the $\mathrm{SI}$ will be $h_1$, while if the CC lies between W and H, the $\mathrm{SI}$ will be $h_2$. The $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC has a greater degree of efficacy than the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC; as for the same values of r, H, d and n, the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC have the SS OOC SATS = 63.35. For the sake of comparison, the author has used a percentage improvement indicator,

$$\mathrm{\Delta }=\frac{100({\mathrm{ATS}}_{\mathrm{FSI}}-{\mathrm{ATS}}_{\mathrm{VSI}})}{{\mathrm{ATS}}_{\mathrm{FSI}}}.$$

The percentage improvement indicator shows that the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC has almost $8.63\mathrm{\%}$ greater degree of efficacy than the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC in terms of SS OOC SATS. The same is the case with $\mathrm{ZS}$ OOC $\mathrm{ZATS}$, and the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC have an almost $8.73\mathrm{\%}$ greater degree of efficacy than the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC in terms of ZATS.

7. Conclusions

This article has investigated the performance of the $\mathrm{VSI}$ function in the $\mathrm{MEWMA}\mathrm{CoDa}$ CCs using a normal random vector described as the inverse log-ratio of a d-part $\mathrm{CoDa}$ to monitor the mean vector. This article focuses on the $\mathrm{VSI}$s instead of using the $\mathrm{FSI}$-based charting schemes to monitor the shift in the process mean vector. In the $\mathrm{VSI}$ CC, the length of the $\mathrm{SI}$ depends on the charting statistic. A WL was introduced, and the $\mathrm{SI}$ length was divided into two values, $h_1$ for the large $\mathrm{SI}$ and $h_2$ for the small $\mathrm{SI}$. By fixing the small $\mathrm{SI}$ to 0.1, the author can find the values of optimal parameters considering a fixed value of the IC ${\mathrm{ATS}}_0$ for a wide range of shifts in the process mean. If the monitored statistics lie below the WL, then a large $\mathrm{SI}$ has been used. But, when the monitored statistics lie between the warning and the $\mathrm{UCL}$, the small $\mathrm{SI}$ has been used. The proposed study has investigated the $\mathrm{VSI}\mathrm{MEWMA}\mathrm{CoDa}$ CC's performance under zero-state and steady-state properties of the run length using the $\mathrm{CTMC}$ method. The process mean and the variance-covariance matrix is supposed to be known for the $\mathrm{ATS}$ comparative study. Different values of the number of variables d and subgroup size n have been used to investigate the OOC $\mathrm{ATS}$ using a fixed value of IC $\mathrm{ATS}$. The main conclusions of this article are (i). The $\mathrm{ZATS}$ and the $\mathrm{SATS}$ of the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC are greater than the $\mathrm{ZATS}$ and the $\mathrm{SATS}$ of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC; (ii). The $\mathrm{ATS}$ of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC increases with an increase in the d; (iii). The $\mathrm{ATS}$ of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC decreases with an increase in the n; (iv). The $\mathrm{SATS}$ of the proposed CC is less than the $\mathrm{ZATS}$ for all the different combinations of n and d. A comparison of the $\mathrm{VSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC with the $\mathrm{FSI}$- $\mathrm{MEWMA}\mathrm{CoDa}$ CC, the $\mathrm{VSI}$ and the $\mathrm{FSI}$ Hotelling $T^2\mathrm{CoDa}$ CC has also been made to study the statistical sensitivity of the proposed CC. For future research, MCUSUM- $\mathrm{CoDa}$, Hotelling $T^2\mathrm{CoDa}$, for the location mean vector and dispersion matrix, can be designed using $\mathrm{VSI}$.

Funding Statement

This work was supported by National Natural Science Foundation of China [Grant number: 71802110]; Foundation of Nanjing University of Posts and Telecommunications [Grant number: NY222176]; The Excellent Innovation Teams of Philosophy and Social Science in Jiangsu Province [Grant number: 2017ZSTD022]; Key Research Base of Philosophy and Social Sciences in jiangsu Information Industry Integration Innovation and Emergency Management Research Center [Grant number: None]; Humanity and Social Science Foundation of the Ministry of Education of China [Grant number: 19YJA630061].

Disclosure statement

No potential conflict of interest was reported by the author(s).