The optimal CUSUM control chart with a dynamic non-random control limit and a given sampling strategy for small samples sequence

Abstract

This article proposes a performance measure to evaluate the detection performance of a control chart with a given sampling strategy for finite or small samples sequence and prove that the CUSUM control chart with dynamic non-random control limit and a given sampling strategy can be optimal under the measure. Numerical simulations and real data for an earthquake are provided to illustrate that for different sampling strategies, the CUSUM chart will have different monitoring performance in change-point detection. Among the six sampling strategies that take only a part of samples, the numerical comparing results illustrate that the uniform sampling strategy (uniformly dispersed sampling strategy) has the best monitoring effect.

1. Introduction

One of the basic problems of quickest change-point detection is designing an optimal control chart (or sequential test, alarm time, stopping time) to detect possible changes in the statistical behavior of a sequence of observations at some instant in time ( change point). Optimal change-point detection or an optimal control chart for change detection is usually expected to have the smallest average detection delay of all control charts subject to a constraint associated with the cost of false alarms. The need for the quickest detection of change arises in a variety of applications, including quality control [8,14], biomedical signaling and public health [3,17,19], financial markets [3], network monitoring [20], etc.

There are mainly two settings in the optimal change-point detection: one is Bayesian change-point detection in which the distribution of the change-point time is known [10,16,18], another is non-Bayesian or minimax change-point detection in which the change-point time is non-random and unknown [7,9–12]. A recent review of optimal change-point detection theory in both Bayesian and non-Bayesian settings can be found in [6].

Because of sampling constraints or to reduce the sampling cost, we have to consider how to construct an optimal control chart with the best sampling strategy for change detection, which is subject to two constraints: one is on the loss associated with false alarms, another is the cost of observations or sampling restrictions. Premkumar and Kumar [13] formulated the Bayesian change detection problem that minimizes the detection delay for sleeping/waking scheduling in a sensor network. Banerjee and Veeravalli [1,2] investigated the optimal detection problem in both Bayesian and non-Bayesian settings with a constraint on the average energy consumed by the observations. Geng et al. [4] analyzed the Bayesian change detection problem with sampling constraints. Ren et al. [15] studied the optimal detection problem in a non-Bayesian setting with communication rate constraints. All the above work is based on a common assumption that the observation sequence is infinite.

In fact, within a given limited time, people can only observe (or sample) a finite number N of samples. Sometimes we can only obtain dozens or even fewer samples. The following discussion shows that the sequential detection with finite samples can be used for people's special needs. (1) Consider a production line that produces one product per minute one day. Let the production line works 8 hours a day, then the number of sequential observations is N = 480. If someone wants to monitor the product quality of a certain day online, then the task is to design or construct an effect test for monitoring whether the 480 sequential observations ( product quality of 1 day) are abnormal in real time on line. (2) As we know, the securities market trades for 4 hours a day. If we want to monitor online the change of the trading price per minute of a stock 1 day, there are N = 240 sequential trading price data. (3) Silicosis is an occupational disease with the highest incidence rate among workers in cement production enterprises. Usually, the cement production enterprise will arrange physical examination for each employee every year to see if there is silicosis. If an employee works from the age of 20 to the age of 60, there are 40 physical examination data, that is, N = 40. (4) Diabetes is a common disease. Almost every university in Shanghai will arrange physical examinations for teachers every year, one of exam items is to check whether the blood sugar is normal. Usually, the average age of young teachers entering University is 28 and retire at the age of 60. There will be blood glucose physical examination data of 32 years for each teacher, that is, N = 32.

Due to sampling constraints or to reduce sampling costs, people can only get a part of the real samples (data). For example, if one has time only in the morning (or afternoon) to observe the changes in stock prices, he or she may correspondingly adopt the following sampling strategy: the no observed samples in the afternoon (or morning) are replaced by a given number. Therefore, we have only a real trading price data of 2 hours of morning (or afternoon), i.e. 120 real data. If every minute of data needs to pay a certain fee, to save costs and not miss too much information (data), one may take the following sampling strategy: Take a real sample every 2 minutes with replacing the samples not collected between 2 minutes with the given number. In fact, people's different needs can correspond to different sampling strategies. Hence, it is important for us to obtain the optimal control chart with the best sampling strategy in change detection for finite or small samples.

In this paper, we propose a performance measure to evaluate the detection performance of a control chart with a given sampling strategy for finite or small samples sequence and prove that the CUSUM control chart with a dynamic non-random control limit is optimal under this measure when the change point is unknown. Moreover, the numerical comparisons of six kinds of sampling strategies that take only a part of all samples are given to illustrate which sampling strategy has a faster monitoring speed.

The remainder of this paper is organized as follows. Section 2 describes a criterion for the optimal control chart with a given sampling strategy. Section 3 presents mainly the optimal CUSUM control chart. Numerical simulations and a real example for comparing several sampling strategies are given in Sections 4 and 5, respectively. Section 6 provides the conclusion and discussion. The proofs of two theorems are given in Appendix.

2. A criterion of optimal control chart with sampling strategy

Consider finite mutually independent observations, $X_1,X_2,\dots ,X_N$. Without loss of generality, we assume $N\ge 2$. Let τ ( $1\le \tau \le N$) be the unknown change point and the pre-change probability density of $X_1,\dots ,X_{\tau -1}$ is $p_0(x)$ before the change point and after the change point the probability density of $X_{\tau },X_{\tau +1},\dots X_N$ becomes $p_1(x)$ which is also known. Let ${\mathbf{P}}_k$ and ${\mathbf{E}}_k$ be the probability distribution and the expectation of $\{X_k,X_{k+1},\dots X_N\}$ respectively if a change occurs at the change point $\tau =k$. When $\tau >N$, this means that a change does not occur in the observations $X_1,X_2,\dots ,X_N$ and therefore, the probability distribution and the expectation are denoted by ${\mathbf{P}}_0$ and ${\mathbf{E}}_0$ respectively for all observations $X_1,X_2,\dots ,X_N$.

Generally speaking, any control chart (or sequential test) for change-point detection can be modeled as a stopping time or an alarm time $T\ge 1$ adapted to the filtration $\{{\mathfrak{F}}_n{\}}_{n\ge 1}$, where ${\mathfrak{F}}_n=\sigma \{X_k,1\le k\le n\}$ denotes the smallest σ-algebra with respect to which all of the random variables (observations) $X_1\cdots ,X_n$ are measurable. The optimality of the stopping time usually means that the detection delay $(T-\tau {)}^{+}$ measured is in some sense the smallest of all stopping times with a probability of false alarm ${\mathbf{P}}_{\mathrm{\infty }}(T<\tau )$ no greater than a preset level $\alpha \in (0,1)$, or, among all stopping times with a false alarm rate no less than a given value $\gamma >1$, i.e. ${\mathbf{E}}_0(T)\ge \gamma$.

When $N=\mathrm{\infty }$, Moustakides [9] has proved that the following upper-sided CUSUM chart $T_C$:

$$\begin{array}{r}{T}_C=min\{n\ge 1:\underset{1\le j\le n}{max}\{\sum _{k=j}^n\log \mathrm{\Lambda }(X_k)\}\ge \log c\}=min\{n\ge 1:Y_n\ge c\}\end{array}$$

for c>1, is optimal under the following Lorden's measure [6]:

$$\begin{array}{r}\underset{T:{\mathbf{E}}_0(T)\ge \gamma }{inf}{\mathcal{J}}_L(T),\end{array}$$

where $\mathrm{\Lambda }(X_k)=p_1(X_k)/p_0(X_k)$, $Y_k=max\{1,Y_{k-1}\}\mathrm{\Lambda }(X_k)$ with $Y_0=0$ and ${\mathcal{J}}_L(T)$ is the worst average delay, i.e.

$$\begin{array}{r}{\mathcal{J}}_L(T)=\underset{k\ge 1}{sup}\mathrm{ess}\sup \{{\mathbf{E}}_k((T-k+1{)}^{+}|{\mathfrak{F}}_{k-1})\}.\end{array}$$

However, when $N<\mathrm{\infty }$, an example given in [5] has shown that the following upper-sided CUSUM chart $T_C(N):=min\{T_C,N+1\}$ for N observations

$$\begin{array}{r}{T}_C(N)=min\{1\le n\le N+1:Y_n\ge c_n\}\end{array}$$

is not optimal in the Lorden's measure ${\mathcal{J}}_L(min\{T,N+1\})$, where $Y_{N+1}:=Y_N$, $c_{N+1}=0$, $c_n=c$ for $1\le n\le N$ and $\{T=N+1\}:=\{T>N\}=\{Y_n<c\text{for all}1\le n\le N\}\in {\mathfrak{F}}_N$.

Note that Lorden's measure is not easy to calculate. It is natural to ask: can we define a measure that is easy to calculate so that a modified CUSUM chart with a given sampling strategy for finite observations is still optimal under this measure?

Because of sampling constraints or to reduce the sampling cost, we need to choose an appropriate sampling strategy for change-point detection. Let $S=\{S_1,\dots ,S_N\}$ denote a sampling strategy satisfying $S_k\in {\mathfrak{F}}_{k-1}$ for $1\le k\le N$, in which, $S_k=1$ or 0 denote that we will take a sample $X_k$ or not take a sample but replace $X_k$ with a constant $s_0$ at time k, respectively, that is, we have a new series of samples, ${\tilde{X}}_k=S_k{X}_k+(1-S_k)s_0$ for $1\le k\le N$.

Remark 2.1

We know that ${\mu }_0:={\mathbf{E}}_0(\log \mathrm{\Lambda }(X_1))<0$ for $p_1(.)\ne p_0(.)$. Hence, when the substitute sample ${\tilde{X}}_k=s_0$ satisfies ${\mu }_0<\log \mathrm{\Lambda }(s_0)<0$, it implies that the observation sequence may have a small mean shift at time k. If $\log \mathrm{\Lambda }(s_0)\ge 0$ for ${\tilde{X}}_k=s_0$, it implies that there is a possible medium or large change mean shift in the observation sequence at time k.

Next, we will present a measure with a sampling strategy to evaluate the detection performance of a control chart for an unknown change point. Let ${\mathfrak{S}}_N$ denote the set of all sampling strategies. For a given sampling strategy $S\in {\mathfrak{S}}_N$, let ${\mathfrak{T}}_N(S)$ be the set of all control charts, $T(S),$ with the sampling strategy S, which satisfy $1\le T(S)\le N+1$ and $\{T(S)\le n\}\in {\mathfrak{F}}_n(S)=\sigma \{{\tilde{X}}_k:0\le k\le n\}$ for $1\le n\le N$, where $\{T(S)=N+1\}:=\{T(S)>N\}$, ${\tilde{X}}_k=S_k{X}_k+(1-S_k)s_0$ for $1\le k\le N$ and ${\mathfrak{F}}_0(S)=\mathrm{\Omega }$, the sample space.

The upper-sided CUSUM charting statistics for a given sampling strategy S can be written as $Y_k(S)=max\{1,Y_{k-1}(S)\}\mathrm{\Lambda }({\tilde{X}}_k)$ for $1\le k\le N$ with $Y_0(S)=0$. As in [5], we define a measure ${\mathcal{J}}_N(T(S),S)$ for a given sampling strategy S to evaluate the detection performance of a control chart when detecting an upper-sided change by the following:

$$\begin{array}{r}{\mathcal{J}}_N(T(S),S)=\sum _{k=1}^N{\mathbf{E}}_k[(1-Y_{k-1}(S){)}^{+}(T(S)-k{)}^{+}],\end{array}$$ (1)

which is the average total amount of the detection delay, where $x^{+}=max\{x,0\}$ and the random weight, $(1-Y_{k-1}(S){)}^{+}$, of the detection delay $(T(S)-k{)}^{+}$ is determined by the information before the change point k since $(1-Y_{k-1}(S){)}^{+}\in {\mathfrak{F}}_{k-1}(S)$. It can be seen that the smaller ${\mathcal{J}}_N(T(S),S)$, the better $T(S)$ performs.

Remark 2.2

One reason to present the delay measure above is that the charting statistic $Y_{k-1}(S)\ge 1$ can be considered as that there is a false medium or large change before the change point k, and $Y_{k-1}(S)<1$ can denote there being no change or a small false change before the change point k, therefore, taking the weight $(1-Y_{k-1}{)}^{+}$ for the detection delay $(T(S)-k{)}^{+}$ means that if the charting statistic $Y_{k-1}(S)\ge 1$, we do not need to consider the detection delay $(T(S)-k{)}^{+}$, if $Y_{k-1}(S)<1$, we must consider the detection delay $(T(S)-k{)}^{+}$. Another motivation is that, by the definition of the charting statistics, $Y_k(S)=max\{1,Y_{k-1}(S)\}\mathrm{\Lambda }(X_k(S))$ with $Y_0=0$ for $k\ge 1$, we see that $Y_k(S)=\mathrm{\Lambda }(X_k(S))$ when $Y_{k-1}(S)<1$, that is, $Y_{k-1}(S)<1$ means that we can restart monitoring the change from time k.

Remark 2.3

To detect the lower-sided changes, for example, the mean shift from ${\mu }_0$ to ${\mu }_1$, where ${\mu }_1<{\mu }_0$, we can take the weight $(1+Y_{k-1}^{-}(S){)}^{+}$, where $Y_{k-1}^{-}(S)$ is the lower-sided CUSUM charting statistic satisfying $Y_k^{-}(S)=min\{1,Y_{k-1}^{-}(S)\}{p}_1({\tilde{X}}_k)/p_0({\tilde{X}}_k)$ for $1\le k\le N$ with $Y_0^{-}\ge 1$. The corresponding measure, ${\mathcal{J}}_N^{-}(T(S),S)$ can be written as

$$\begin{array}{r}{\mathcal{J}}_N^{-}(T(S),S)=\sum _{k=1}^N{\mathbf{E}}_k[(1+Y_{k-1}^{-}(S){)}^{+}(T(S)-k{)}^{+}],\end{array}$$

which is the total average amount of the detection delay. In this paper, we only consider upper-sided change detection since lower-sided change detection can be dealt with by similar methods.

A criterion for an optimal control chart, $T^{\ast }(S^{\ast }),$ with an optimal sampling strategy $S^{\ast }$ is defined by the following:

$$\begin{array}{rl}& \underset{T(S)\in {\mathfrak{T}}_N(S),S\in {\mathfrak{S}}_N}{min}\{{\mathcal{J}}_N(T(S),S)\}={\mathcal{J}}_N(T^{\ast }(S^{\ast }),S^{\ast })\end{array}$$ (2)

$$\begin{array}{rl}& \text{subject to}{\mathbf{E}}_0(T(S))\ge \gamma ,{\mathbf{E}}_0\left(\sum _{k=1}^N{S}_k\right)\le \beta ,\end{array}$$ (3)

where the two positive constants γ and β denote the lower bound of the false alarm average time for $T(S)$ and the upper bound of the average number of observations, respectively, which satisfy $1<\gamma ,\beta \le N.$ Moreover, the measure ${\mathcal{J}}_N(T(S),S)$ can be regarded as the generalized out-of-control average run length ( $\mathrm{AR}{L}_1$).

3. The optimal CUSUM control chart with sampling strategy

To construct the optimal control chart, we first present a series of nonnegative CUSUM charting statistics, $Y_k(S),1\le k\le N+1,$ for a given sampling strategy $S\in {\mathfrak{S}}_N$ in the following:

$$\begin{array}{rl}{Y}_k(S)& =max\{1,Y_{k-1}(S)\}\mathrm{\Lambda }({\tilde{X}}_k)=[Y_{k-1}(S)+(1-Y_{k-1}(S){)}^{+}]\mathrm{\Lambda }({\tilde{X}}_k)\\ & =\sum _{j=1}^k(1-Y_{j-1}(S){)}^{+}\prod _{i=j}^k\mathrm{\Lambda }({\tilde{X}}_i)\end{array}$$

for $0\le k\le N+1$, where $Y_0(S)=0$ and $Y_{N+1}(S):=Y_N(S)$. It is clear that $Y_k(S)\in {\mathfrak{F}}_k(S)$ for $1\le k\le N$.

As in [5], for a given sampling strategy S, the CUSUM control chart with a nonnegative non-random dynamic control limit, $l_k(S,c)$, is defined by the following:

$$\begin{array}{r}{T}_C(S,c)=min\{1\le k\le N+1,Y_k(S)\ge l_k(S,c)\},\end{array}$$ (4)

where $\{l_k(S,c)\}$ is determined by the following recursive equations:

$$\begin{array}{rl}{l}_{N+1}(S,c)& =0,l_N(S,c)=c{l}_k(S,c)=c+{\mathbf{E}}_0([l_{k+1}(S,c)-Y_{k+1}(S){]}^{+}|{\mathfrak{F}}_k)\end{array}$$

for $0\le k\le N-1$ and c>0, is a constant which can be regarded as an adjustment coefficient for the control limits since $l_k(S,c)$ is increasing in $c\ge 0$ with $l_k(S,0)=0$ and $\underset{c\to \mathrm{\infty }}{lim}{l}_k(S,c)=+\mathrm{\infty }$ for $0\le k\le N$.

The following theorem shows that the CUSUM chart with the dynamic control limit above can be optimal under the measure ${\mathcal{J}}_N(T(S),S)$ for any given sampling strategy $S\in {\mathfrak{S}}_N$.

Theorem 3.1

Let γ be a positive number satisfying $1<\gamma <N$. For a given $S\in {\mathfrak{S}}_N$, there exists a positive number $c_{\gamma }$ such that the CUSUM chart $T^{\ast }(S):=T_C(S,c_{\gamma })$ the dynamic non-random control limit $\{l_k(c_{\gamma })\}$ and ${\mathbf{E}}_0(T^{\ast }(S))=\gamma$, is optimal in the following sense:

$$\begin{array}{r}\underset{T(S)\in {\mathfrak{T}}_N(S),{\mathbf{E}}_0(T(S))\ge \gamma }{inf}\{{\mathcal{J}}_N(T(S),S)\}={\mathcal{J}}_N(T^{\ast }(S),S).\end{array}$$ (5)

Remark 3.1

It can be seen that Theorem 3.1. cannot give the optimal sampling strategy $S^{\ast }$ satisfying the constraint conditions ${\mathbf{E}}_0(T(S^{\ast }))\ge \gamma$ and ${\mathbf{E}}_0\left(\sum _{k=1}^N{S}_k^{\ast }\right)\le \beta$.

Since it is difficult to prove the optimal sampling strategy in theory, we want to find a relatively good sampling scheme by comparing two sampling strategies. To compare two sampling strategies, we present the definition of a relative increasing strategy below. A sampling strategy $S^{\prime }=\{S_1^{\prime },\dots ,S_N^{\prime }\}$ is called a relative increasing strategy by comparison with the sampling strategy $S=\{S_1,\dots ,S_N\}$, if and only if $S_k^{\prime }\ge S_k$ for all $1\le k\le N$, which can be denoted as $S^{\prime }\ge S$. The inequality $S^{\prime }\ge S$ means that strategy $S^{\prime }$ can extract more information (samples) than strategy S.

Theorem 3.2 shows that the more samples (information), the better the performance of the corresponding optimal CUSUM control chart.

Theorem 3.2

Let $s_0$ satisfy

$$\begin{array}{r}\mathrm{\Lambda }(s_0)\ge {\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}max\{p_0(x),p_1(x)\}\mathrm{d}x\end{array}$$ (6)

and both $T^{\ast }(S)$ and $T^{\ast }(S^{\prime })$ be the two optimal CUSUM charts in (5) corresponding to two sampling strategies $S,S^{\prime }\in {\mathfrak{S}}_N$ satisfying $S^{\prime }\ge S$. Then

$$\begin{array}{r}{\mathcal{J}}_N(T^{\ast }(S),S)\ge {\mathcal{J}}_N(T^{\ast }(S^{\prime }),S^{\prime })\end{array}$$ (7)

for ${\mathbf{E}}_0(T^{\ast }(S))\ge {\mathbf{E}}_0(T^{\ast }(S^{\prime }))$, and the optimal CUSUM chart $T^{\ast }(S^{\prime })$ satisfies

$$\begin{array}{rl}& \underset{S\in {\mathfrak{S}}_N,T(S)\in {\mathfrak{T}}_N(S)}{inf}\{{\mathcal{J}}_N(T(S),S)\}={\mathcal{J}}_N(T^{\ast }(S^{\prime }),S^{\prime })\\ & \text{subject to}S\le S^{\prime },{\mathbf{E}}_0(T(S))\ge {\mathbf{E}}_0(T^{\ast }(S^{\prime })).\end{array}$$ (8)

Let $S_a=\{1,1,\dots ,1\}$ denote that we take all N samples. It is clear that any sampling strategy $S\in {\mathfrak{S}}_N$ satisfies $S\le S_a$. Hence, we have the following corollary.

Corollary 3.3

Let the conditions in Theorem 3.2 hold. Then

$$\begin{array}{r}\underset{S\in {\mathfrak{S}}_N,T(S)\in {\mathfrak{T}}_N(S),{\mathbf{E}}_0(T(S))\ge {\mathbf{E}}_0(T^{\ast }(S_a))}{inf}\{{\mathcal{J}}_N(T(S),S)\}={\mathcal{J}}_N(T^{\ast }(S_a),S_a).\end{array}$$ (9)

It can be seen that the optimal CUSUM chart $T^{\ast }(S_a)$ has the best detection performance of all sampling strategies and all control charts subject to a constraint on the false alarm average run length ( $\mathrm{AR}{L}_0$).

Remark 3.2

When the condition (6) does not hold and the two sampling strategies do not meet the relative increase condition, no general theoretical results for the sampling strategies have been obtained, but we will provide numerical simulation results for these cases in the next section.

4. Numerical simulations

By numerical comparisons of the detection performance of the optimal CUSUM chart for seven kinds of sampling strategies in this section, we have two main purposes. One is to see how much the monitoring speed is different between the sampling of all samples and the sampling of missing some samples; the other is see which sampling strategy has a faster monitoring speed among six sampling strategies of missing some samples. The seven sampling strategies $S_a,S_{\mathrm{fir}},S_{\mathrm{las}},S_{\mathrm{uni}},S_{\mathrm{rand}},S_{\mathrm{DE}},{\tilde{S}}_{\mathrm{DE}}$ compared in this section are as follows, β is the number of observations,

• $S_a$ denotes that the observation samples are taken at all times ( $1\le k\le 60$) (full sampling strategy);

• $S_{\mathrm{fir}}$ represents that we take the observation samples only during the first period;

• $S_{\mathrm{las}}$ represents that we take the observation samples only during the last period;

• $S_{\mathrm{uni}}$ denotes that the observation samples are taken evenly and dispersedly (uniformly dispersed sampling strategy);

• $S_{\mathrm{rand}}$ denotes the sampling each time with probability of $\beta /N$;

• $S_{\mathrm{DE}}$ represents the DE-Shiryaev sampling strategy given in [2] (e.g. take a positive constant A which can be called the warning line, it is lower than the constant control line. If the monitoring statistic is lower than the warning line, next sampling is not required but replacing by a given number. If it is higher than the warning line but lower than the control line, next sampling is required). ${\tilde{S}}_{\mathrm{DE}}=\{{\tilde{S}}_{\mathrm{DE},k},1\le k\le N\}$ satisfies

  $$\begin{array}{r}{\mathbf{E}}_0\left(\sum _{k=1}^{T^{\ast }(S_{\mathrm{DE}})}{S}_{\mathrm{DE},k}\right)\approx \beta .\end{array}$$
• ${\tilde{S}}_{\mathrm{DE}}$ denotes that if the monitoring statistic is lower than the warning line (a positive constant A), next sampling is not required but replacing by a given number, if it is higher than the warning line, next sampling is required. $S_{\mathrm{DE}}=\{S_{\mathrm{DE},k},1\le k\le N\}$ satisfies

  $$\begin{array}{r}{\mathbf{E}}_0\left(\sum _{k=1}^N{\tilde{S}}_{\mathrm{DE},k}\right)\approx \beta .\end{array}$$

Let $X_0\sim N(0,1)$ and, after the change point $\tau =1$, $X_k\sim N(1,1)$, $1\le k\le 60$, are mutually independent. It follows that $p_1(X_k)/p_0(X_k)=e^{X_k-1/2}$ for $1\le k\le 60$. We give numerical simulations to compare the detection performance of four non-random sampling strategies $S_a,S_{\mathrm{fir}},S_{\mathrm{las}},S_{\mathrm{uni}}$ and three random sampling strategies $S_{\mathrm{rand}},S_{\mathrm{DE}},{\tilde{S}}_{\mathrm{DE}}$ for N = 60. The substitute $s_0$ for an observation value will be taken as 0, 0.25 and 0.5, respectively.

Consider the three cases for the number of observations $\beta =12,20,30$. As for $S_{\mathrm{uni}}$, if $\beta =30$, we take observations at $1,3,5,2k-1,\dots$. If $\beta =20$, we take observations at $2,5,8,11,\dots$ And if $\beta =12$, we take observations at $3,8,13,18,\dots$

Let $\mathrm{AR}{L}_0={\mathbf{E}}_0(T_C(S,c_{\gamma }))=20,30,40$ for the CUSUM control charts $T_C(S,c_{\gamma })$ with the dynamic control limit $\{l_k(S,c_{\gamma })\}$ and the sampling strategy S considered here. Let the numbers of observations be $\beta =12$, $\beta =20,$ and $\beta =30$, respectively. The simulation results of the adjustment coefficient $c_{\gamma }$, $\mathrm{AR}{L}_0$, the warning line A and the measure ${\mathcal{J}}_N$ are listed in Tables 1–9 respectively for $s_0=0,0.25,$ and 0.5. Note that the sampling strategy $S_{\mathrm{DE}}$ is invalid when $\mathrm{AR}{L}_0\le \beta$.

Table 2.

Comparison of ${\mathcal{J}}_N$ for $\beta =20,s_0=0$ with $\mathrm{AR}{L}_0\approx 20,30,40$.

		Sampling strategies
$\mathrm{AR}{L}_0$		$T^{\ast }(S_a)$	$T^{\ast }(S_{\mathrm{fir}})$	$T^{\ast }(S_{\mathrm{las}})$	$T^{\ast }(S_{\mathrm{uni}})$	$T^{\ast }(S_{\mathrm{rand}})$	$T^{\ast }({\tilde{S}}_{\mathrm{DE}})$	$T^{\ast }(S_{\mathrm{DE}})$
20	$c_{\gamma }$	1.375	1.052	0.4619	0.86	0.862	0.82	–
	$\mathrm{AR}{L}_0$	20.0032	20.0813	19.9731	20.0655	19.9622	20.1297	–
	A	–	–	–	–	–	0.140	–
	${\mathcal{J}}_N$	0.4577	4.6915	3.4111	1.6235	1.9111	8.4980	–
30	$c_{\gamma }$	1.73	1.171	0.4620	0.982	0.995	1.005	1.475
	$\mathrm{AR}{L}_0$	29.9902	29.9951	30.0538	30.0158	30.0262	29.9522	29.9889
	A	–	–	–	–	–	0.140	0.066
	${\mathcal{J}}_N$	0.5426	5.2447	5.4253	1.9208	2.1475	9.1951	3.7056
40	$c_{\gamma }$	2.3	1.355	0.465	1.104	1.135	1.225	1.7
	$\mathrm{AR}{L}_0$	40.1787	39.9391	40.1248	40.0953	40.1222	40.0960	40.0162
	A	–	–	–	–	–	0.140	0.088
	${\mathcal{J}}_N$	0.6734	5.6734	7.4042	2.3050	2.4641	9.6218	5.1029

Table 3.

Comparison of ${\mathcal{J}}_N$ for $\beta =30,s_0=0$ with $\mathrm{AR}{L}_0\approx 20,30,40$.

		Sampling strategies
$\mathrm{AR}{L}_0$		$T^{\ast }(S_a)$	$T^{\ast }(S_{\mathrm{fir}})$	$T^{\ast }(S_{\mathrm{las}})$	$T^{\ast }(S_{\mathrm{uni}})$	$T^{\ast }(S_{\mathrm{rand}})$	$T^{\ast }({\tilde{S}}_{\mathrm{DE}})$	$T^{\ast }(S_{\mathrm{DE}})$
20	$c_{\gamma }$	1.375	1.165	0.4619	0.985	0.987	0.95	–
	$\mathrm{AR}{L}_0$	20.0032	19.9244	20.0507	20.1278	20.1491	20.0527	–
	A	–	–	–	–	–	0.1065	–
	${\mathcal{J}}_N$	0.4577	2.4671	3.4133	1.1217	1.2599	6.5860	–
30	$c_{\gamma }$	1.73	1.34	0.465	1.12	1.14	1.155	–
	$\mathrm{AR}{L}_0$	29.9902	30.0128	30.1108	30.0102	30.0168	30.0487	–
	A	–	–	–	–	–	0.1065	–
	${\mathcal{J}}_N$	0.5426	2.9467	5.4373	1.2505	1.3937	7.4611	–
40	$c_{\gamma }$	2.3	1.625	1.115	1.28	1.33	1.485	2.01
	$\mathrm{AR}{L}_0$	40.1787	40.0563	40.0474	39.9918	40.0423	39.9682	39.9913
	A	–	–	–	–	–	0.1065	0.062
	${\mathcal{J}}_N$	0.6734	3.3345	5.4259	1.4577	1.6134	8.2570	2.8311

Table 4.

Comparison of ${\mathcal{J}}_N$ for $\beta =12,s_0=0.25$ with $\mathrm{AR}{L}_0\approx 20,30,40$.

		Sampling strategies
$\mathrm{AR}{L}_0$		$T^{\ast }(S_a)$	$T^{\ast }(S_{\mathrm{fir}})$	$T^{\ast }(S_{\mathrm{las}})$	$T^{\ast }(S_{\mathrm{uni}})$	$T^{\ast }(S_{\mathrm{rand}})$	$T^{\ast }({\tilde{S}}_{\mathrm{DE}})$	$T^{\ast }(S_{\mathrm{DE}})$
20	$c_{\gamma }$	1.375	0.942	0.53916	0.74	0.715	0.66	1.17
	$\mathrm{AR}{L}_0$	20.0032	20.027	20.0789	20.0286	19.9733	20.1358	20.0195
	A	–	–	–	–	–	0.192	0.065
	${\mathcal{J}}_N$	0.4577	4.2757	2.2781	1.6848	1.8808	6.0869	2.2641
30	$c_{\gamma }$	1.73	1.038	0.53918	0.89	0.88	0.878	1.24
	$\mathrm{AR}{L}_0$	29.9902	30.0239	30.0195	29.9002	29.9605	30.0684	29.9109
	A	–	–	–	–	–	0.192	0.093
	${\mathcal{J}}_N$	0.5426	4.6707	3.4101	1.9928	2.1702	6.3001	3.3299
40	$c_{\gamma }$	2.3	1.16	0.53926	1.035	1.028	1.048	1.363
	$\mathrm{AR}{L}_0$	40.1787	40.0412	40.0162	40.1175	40.1207	40.0229	40.0414
	A	–	–	–	–	–	0.192	0.12
	${\mathcal{J}}_N$	0.6734	4.8850	4.5296	2.3426	2.4499	6.3192	4.4681

Table 5.

Comparison of ${\mathcal{J}}_N$ for $\beta =20,s_0=0.25$ with $\mathrm{AR}{L}_0\approx 20,30,40$.

		Sampling strategies
$\mathrm{AR}{L}_0$		$T^{\ast }(S_a)$	$T^{\ast }(S_{\mathrm{fir}})$	$T^{\ast }(S_{\mathrm{las}})$	$T^{\ast }(S_{\mathrm{uni}})$	$T^{\ast }(S_{\mathrm{rand}})$	$T^{\ast }({\tilde{S}}_{\mathrm{DE}})$	$T^{\ast }(S_{\mathrm{DE}})$
20	$c_{\gamma }$	1.375	1.055	0.53918	0.885	0.88	0.822	–
	$\mathrm{AR}{L}_0$	20.0032	19.9324	20.1048	19.9853	20.0289	20.1873	–
	A	–	–	–	–	–	0.14	–
	${\mathcal{J}}_N$	0.4577	2.9422	2.2650	1.2554	1.4164	5.1551	–
30	$c_{\gamma }$	1.73	1.18	0.53919	1.045	1.04	1.006	1.48
	$\mathrm{AR}{L}_0$	29.9902	30.0336	30.0466	30.1060	30.2288	29.9920	29.9486
	A	–	–	–	–	–	0.14	0.065
	${\mathcal{J}}_N$	0.5426	3.2835	3.3946	1.4230	1.5462	5.5541	2.3093
40	$c_{\gamma }$	2.3	1.377	0.545	1.21	1.215	1.223	1.69
	$\mathrm{AR}{L}_0$	40.1787	40.0162	40.0079	40.0509	39.9874	40.0353	40.0655
	A	–	–	–	–	–	0.14	0.089
	${\mathcal{J}}_N$	0.6734	3.5665	4.4235	1.6069	1.7289	5.7974	3.2478

Table 8.

Comparison of ${\mathcal{J}}_N$ for $\beta =20,s_0=0.5$ with $\mathrm{AR}{L}_0\approx 20,30,40$.

		Sampling strategies
$\mathrm{AR}{L}_0$		$T^{\ast }(S_a)$	$T^{\ast }(S_{\mathrm{fir}})$	$T^{\ast }(S_{\mathrm{las}})$	$T^{\ast }(S_{\mathrm{uni}})$	$T^{\ast }(S_{\mathrm{rand}})$	$T^{\ast }({\tilde{S}}_{\mathrm{DE}})$	$T^{\ast }(S_{\mathrm{DE}})$
20	$c_{\gamma }$	1.375	1.09	0.61708	0.995	0.965	0.825	–
	$\mathrm{AR}{L}_0$	20.0032	20.0708	20.0183	20.0169	20.1259	20.0182	–
	A	–	–	–	–	–	0.14	–
	${\mathcal{J}}_N$	0.4577	0.7132	0.8083	0.7746	0.7863	0.8555	–
30	$c_{\gamma }$	1.73	1.28	0.6174	1.25	1.22	1.008	1.481
	$\mathrm{AR}{L}_0$	29.9902	30.2001	30.1761	29.9333	30.1165	30.1203	29.9841
	A	–	–	–	–	–	0.14	0.065
	${\mathcal{J}}_N$	0.5426	0.7857	0.8699	0.8060	0.8174	0.8736	0.7512
40	$c_{\gamma }$	2.3	1.63	0.628	1.625	1.61	1.22	1.692
	$\mathrm{AR}{L}_0$	40.1787	40.0782	40.0313	39.8233	40.0579	39.9564	40.092
	A	–	–	–	–	–	0.14	0.089
	${\mathcal{J}}_N$	0.6734	0.8831	0.8919	0.8889	0.8984	0.8756	0.8599

Table 1.

Comparison of ${\mathcal{J}}_N$ for $\beta =12,s_0=0$ with $\mathrm{AR}{L}_0\approx 20,30,40$.

		Sampling strategies
$\mathrm{AR}{L}_0$		$T^{\ast }(S_a)$	$T^{\ast }(S_{\mathrm{fir}})$	$T^{\ast }(S_{\mathrm{las}})$	$T^{\ast }(S_{\mathrm{uni}})$	$T^{\ast }(S_{\mathrm{rand}})$	$T^{\ast }({\tilde{S}}_{\mathrm{DE}})$	$T^{\ast }(S_{\mathrm{DE}})$
20	$c_{\gamma }$	1.375	0.938	0.4619	0.735	0.715	0.65	1.171
	$\mathrm{AR}{L}_0$	20.0032	19.9971	20.3822	19.9809	20.0154	20.0674	20.2969
	A	–	–	–	–	–	0.192	0.066
	${\mathcal{J}}_N$	0.4577	6.9661	3.4816	2.3157	2.6917	10.1051	3.4187
30	$c_{\gamma }$	1.73	1.032	0.4620	0.868	0.861	0.88	1.25
	$\mathrm{AR}{L}_0$	29.9902	30.0134	30.1969	30.1281	30.1413	30.1861	30.2598
	A	–	–	–	–	–	0.192	0.093
	${\mathcal{J}}_N$	0.5426	7.6702	5.4208	2.8846	3.2068	10.4783	5.3638
40	$c_{\gamma }$	2.3	1.145	0.4621	0.982	0.985	1.05	1.365
	$\mathrm{AR}{L}_0$	40.1787	39.9446	40.2532	40.0312	40.1859	40.1211	40.1091
	A	–	–	–	–	–	0.192	0.12
	${\mathcal{J}}_N$	0.6734	7.9904	7.3986	3.4693	3.7255	10.7379	7.375

Table 9.

Comparison of ${\mathcal{J}}_N$ for $\beta =30,s_0=0.5$ with $\mathrm{AR}{L}_0\approx 20,30,40$.

		Sampling strategies
$\mathrm{AR}{L}_0$		$T^{\ast }(S_a)$	$T^{\ast }(S_{\mathrm{fir}})$	$T^{\ast }(S_{\mathrm{las}})$	$T^{\ast }(S_{\mathrm{uni}})$	$T^{\ast }(S_{\mathrm{rand}})$	$T^{\ast }({\tilde{S}}_{\mathrm{DE}})$	$T^{\ast }(S_{\mathrm{DE}})$
20	$c_{\gamma }$	1.375	1.205	0.6174	1.14	1.11	0.955	–
	$\mathrm{AR}{L}_0$	20.0032	20.06	29.1920	19.9856	20.0145	20.0150	–
	A	–	–	–	–	–	0.1065	–
	${\mathcal{J}}_N$	0.4577	0.5859	0.8052	0.6780	0.6937	0.7948	–
30	$c_{\gamma }$	1.73	1.44	0.628	1.425	1.39	1.155	–
	$\mathrm{AR}{L}_0$	29.9902	30.1226	30.0324	30.0104	29.9585	30.0487	–
	A	–	–	–	–	–	0.1065	–
	${\mathcal{J}}_N$	0.5426	0.6768	0.8562	0.7345	0.7379	0.8096	–
40	$c_{\gamma }$	2.3	1.85	1.115	1.852	1.85	1.49	2.008
	$\mathrm{AR}{L}_0$	40.1787	40.0221	40.0474	40.0151	40.1107	40.0735	40.0913
	A	–	–	–	–	–	0.1065	0.0618
	${\mathcal{J}}_N$	0.6734	0.7949	0.8599	0.8288	0.8485	0.8322	0.8014

By comparing the measure ${\mathcal{J}}_N$ of the CUSUM charts with the dynamic control limit $\{l_k(S,c_{\gamma })\}$ for seven sampling strategies $S_a$, $S_{\mathrm{fir}}$, $S_{\mathrm{las}}$, $S_{\mathrm{uni}}$, $S_{\mathrm{rand}}$, ${\tilde{S}}_{\mathrm{DE}}$ and $S_{\mathrm{DE}}$ in Tables 1–9, we can make the following five conclusions:

1. For all cases, the full sampling strategy $S_a$ is optimal amongst all seven sampling strategies since its corresponding measure ${\mathcal{J}}_N(T^{\ast }(S_a))$ is the least among all measures ${\mathcal{J}}_N(.)$ for the seven sampling strategies.

2. Excepting the case $s_0=0.5$ in Tables 7–9 and the case $s_0=0.25$ in Table 6 for $\mathrm{AR}{L}_0=40$, the detection performance of the uniformly dispersed sampling strategy $S_{\mathrm{uni}}$ is better than the sampling strategy $S_{\mathrm{rand}}$, the sampling strategy $S_{\mathrm{rand}}$ is better than the sampling strategy $S_{\mathrm{DE}}$, the sampling strategy $S_{\mathrm{DE}}$ is better than $S_{\mathrm{fir}}$ and $S_{\mathrm{las}}$, $S_{\mathrm{fir}}$ and $S_{\mathrm{las}}$ are better than ${\tilde{S}}_{\mathrm{DE}}$. and $S_{\mathrm{DE}}$, since the measure ${\mathcal{J}}_N(T^{\ast }(S_{\mathrm{uni}}))$ of $S_{\mathrm{uni}}$ is smallest. Meanwhile, the detection performance of $S_{\mathrm{rand}}$ and $S_{\mathrm{DE}}$ is better than that of $S_{\mathrm{fir}}$ and  $S_{\mathrm{las}}$.

3. For the case $s_0=0.5$ in Tables 7–9, the detection performance of the six sampling strategies $S_{\mathrm{fir}}$, $S_{\mathrm{las}}$, $S_{\mathrm{uni}}$, $S_{\mathrm{rand}}$, ${\tilde{S}}_{\mathrm{DE}}$ and $S_{\mathrm{DE}}$ is not too different.

4. The adjustment coefficient $c_{\gamma }$ of the dynamic control limit for the sampling strategy $S_a$ is greatest of all adjustment coefficients $c_{\gamma }$ for the six sampling strategies $S_a$, $S_{\mathrm{fir}}$, $S_{\mathrm{las}}$, $S_{\mathrm{uni}}$, ${\tilde{S}}_{\mathrm{DE}}$ and $S_{\mathrm{DE}}$ in all cases.

As a whole, among the six sampling strategies that take only a part of samples, the numerical comparing results illustrate that the uniform sampling strategy $S_{\mathrm{uni}}$ has the best monitoring effect.

Table 7.

Comparison of ${\mathcal{J}}_N$ for $\beta =12,s_0=0.5$ with $\mathrm{AR}{L}_0\approx 20,30,40$.

		Sampling strategies
$\mathrm{AR}{L}_0$		$T^{\ast }(S_a)$	$T^{\ast }(S_{\mathrm{fir}})$	$T^{\ast }(S_{\mathrm{las}})$	$T^{\ast }(S_{\mathrm{uni}})$	$T^{\ast }(S_{\mathrm{rand}})$	$T^{\ast }({\tilde{S}}_{\mathrm{DE}})$	$T^{\ast }(S_{\mathrm{DE}})$
20	$c_{\gamma }$	1.375	0.97	0.61707	0.815	0.76	0.675	1.172
	$\mathrm{AR}{L}_0$	20.0032	19.9630	19.9372	20.1206	19.9615	20.1102	20.0484
	A	–	–	–	–	–	0.192	0.0648
	${\mathcal{J}}_N$	0.4577	0.8079	0.8169	0.8617	0.8239	0.9049	0.8033
30	$c_{\gamma }$	1.73	1.105	0.61709	1.075	1.01	0.885	1.245
	$\mathrm{AR}{L}_0$	29.9902	30.1056	30.1513	30.0324	30.1414	30.0291	30.0813
	A	–	–	–	–	–	0.192	0.093
	${\mathcal{J}}_N$	0.5426	0.8612	0.8837	0.8906	0.8656	0.9221	0.8632
40	$c_{\gamma }$	2.3	1.375	0.61780	1.425	1.325	1.051	1.36
	$\mathrm{AR}{L}_0$	40.1787	40.0447	40.1382	40.2172	39.8161	40.1768	39.9597
	A	–	–	–	–	–	0.192	0.12
	${\mathcal{J}}_N$	0.6734	0.9303	0.9328	0.9501	0.9259	0.9260	0.9269

Table 6.

Comparison of ${\mathcal{J}}_N$ for $\beta =30,s_0=0.25$ with $\mathrm{AR}{L}_0\approx 20,30,40$.

		Sampling strategies
$\mathrm{AR}{L}_0$		$T^{\ast }(S_a)$	$T^{\ast }(S_{\mathrm{fir}})$	$T^{\ast }(S_{\mathrm{las}})$	$T^{\ast }(S_{\mathrm{uni}})$	$T^{\ast }(S_{\mathrm{rand}})$	$T^{\ast }({\tilde{S}}_{\mathrm{DE}})$	$T^{\ast }(S_{\mathrm{DE}})$
20	$c_{\gamma }$	1.375	1.17	0.53919	1.035	1.02	0.952	–
	$\mathrm{AR}{L}_0$	20.0032	19.9407	20.0439	20.0977	20.1199	20.1410	–
	A	–	–	–	–	–	0.1065	–
	${\mathcal{J}}_N$	0.4577	1.6404	2.2613	0.9064	1.0074	4.0474	–
30	$c_{\gamma }$	1.73	1.35	0.545	1.212	1.205	1.156	–
	$\mathrm{AR}{L}_0$	29.9902	30.0331	30.0019	29.9861	30.0344	30.1053	–
	A	–	–	–	–	–	0.1065	–
	${\mathcal{J}}_N$	0.5426	1.9422	3.3056	0.9929	1.0905	4.5446	–
40	$c_{\gamma }$	2.3	1.65	1.115	1.445	1.45	1.488	2.01
	$\mathrm{AR}{L}_0$	40.1787	40.1433	40.0474	40.0477	39.9851	40.0353	40.1093
	A	–	–	–	–	–	0.1065	0.0618
	${\mathcal{J}}_N$	0.6734	2.2098	3.4268	1.1389	1.2404	5.0067	1.8873

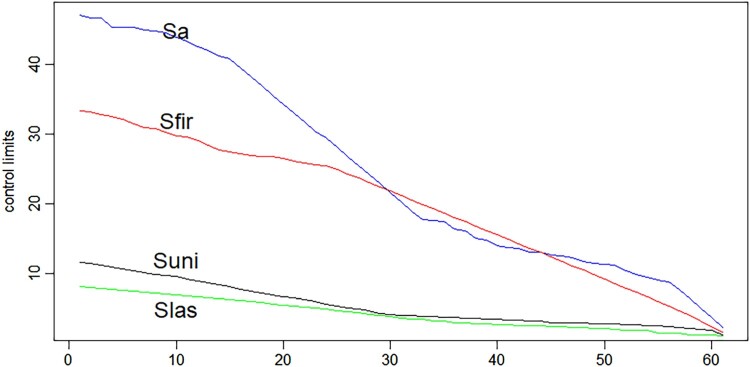
Figure 1 is a diagram of the control limits of four sampling strategies $S_a$, $S_{\mathrm{fir}}$, $S_{\mathrm{las}}$ and $S_{\mathrm{uni}}$ for $s_0=0,\beta =30$ and $\mathrm{AR}{L}_0\approx 40$. It can be seen that the four dynamic control limits all decrease monotonically.

Figure 1.

A diagram of the control limits of different sampling methods.

5. Real data

According to the Chinese earthquake network, on 7 January 2015, in Yilan County, an earthquake measuring 5.2 Richter scale occurred. The data measurements (acceleration in a specific direction) from a sensor are recorded from 12:43:32 to 12:53:32 before and after an earthquake. Since the data are at a relatively high frequency (about 500 Hz), we collect data every 2 microseconds. A simple plot of the measurements against time is shown as follows. There is a significant signal in the middle of Figure 2, which should correspond to the earthquake at 12:48:32. In fact, there is a delay of approximately 0.8 seconds in this data.

Figure 2.

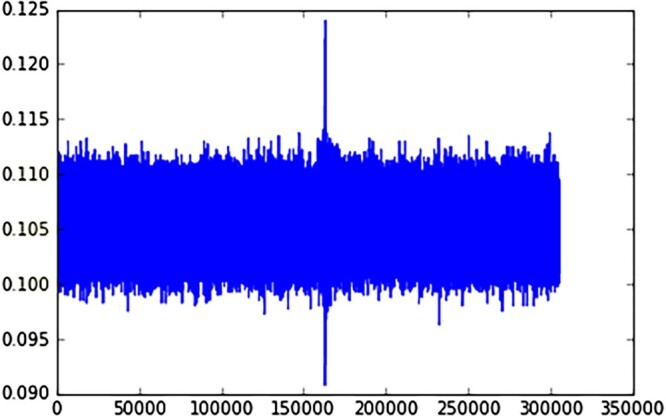
The value of accelerations collected by the sensor in the earthquake.

We know that every seismic sensor has a battery inside. Assuming that the sensor collects one sample every microseconds, the service life of the battery is 1 year. To extend the service life of the battery, at the same time, do not lose too much information (data), we can adjust the sensor so that it collects a sample (data) every 2 microseconds. Based on this consideration, we compare the detection performance of the six sampling strategies $S_a,S_{\mathrm{fir}},S_{\mathrm{both}},S_{\mathrm{uni}}$, $S_{\mathrm{rand}}$ and ${\tilde{S}}_{\mathrm{DE}}$ for N = 60 (60 observations) of seismic sensors to see how much the monitoring speed is different between the sampling of all samples and the sampling of missing some samples. Here, $S_{\mathrm{both}}$ means that we take observations in both the first and last periods. That is, we take observations at $1,2,\dots ,\frac{\beta }{2},N-\frac{\beta }{2}+1,N-\frac{\beta }{2}+2,\dots ,N$.

We first normalize the data by the pre-change mean and variance. Then the pre-change distribution can be approximated as $N(0,1)$ and the post-change distribution as $N(0.4,4^2)$. Accordingly, the likelihood ratio is approximated. The substitute for observation value is $s_0=0.2$. Consider the three cases with numbers of observations $\beta =12,20$ and 30. For $S_{\mathrm{uni}}$, we take observations at $1,3,5,2k-1,\dots$, $2,5,8,11,\dots$ and $3,8,13,18,\dots$, respectively for $\beta =30,20$ and 12.

Let $\mathrm{AR}{L}_0={\mathbf{E}}_0(T(S,c_{\gamma })))=20,30,40$ for the CUSUM control chart $T(S,c_{\gamma }))$ with the dynamic control limit $\{l_k(S,c_{\gamma })\}$ and the sampling strategy S considered here. The simulation results are listed in Tables 10–12 for $\beta =12$, $\beta =20$ and $\beta =30$, respectively.

Table 11.

Comparisons of ${\mathcal{J}}_N$ for $\beta =20$ with $\mathrm{AR}{L}_0\approx 20,30,40$.

		Sampling strategies
$\mathrm{AR}{L}_0$		$T^{\ast }(S_a)$	$T^{\ast }(S_{\mathrm{fir}})$	$T^{\ast }(S_{\mathrm{both}})$	$T^{\ast }(S_{\mathrm{uni}})$	$T^{\ast }(S_{\mathrm{rand}})$	$T^{\ast }({\tilde{S}}_{\mathrm{DE}})$
20	$c_{\gamma }$	0.492	0.436	0.3937	0.385	0.38	0.409
	$\mathrm{AR}{L}_0$	20.1	19.9847	20.0314	20.0119	20.0978	19.9267
	A	–	–	–	–	–	0.9662
	${\mathcal{J}}_N$	0.2131	7.3484	8.8998	1.4004	2.0166	13.7606
30	$c_{\gamma }$	0.57	0.486	0.4358	0.4357	0.4356	0.44
	$\mathrm{AR}{L}_0$	29.9636	29.9018	30.2007	30.1277	30.1620	29.9118
	A	–	–	–	–	–	0.9662
	${\mathcal{J}}_N$	0.2452	8.7327	9.5817	1.5448	2.1545	14.2786
40	$c_{\gamma }$	0.705	0.535	0.489	0.49	0.491	0.505
	$\mathrm{AR}{L}_0$	40.2044	40.2213	39.7759	39.9962	40.1309	40.0014
	A	–	–	–	–	–	0.9662
	${\mathcal{J}}_N$	0.2666	9.4934	10.3945	1.5842	2.1596	14.4995

Table 10.

Comparisons of ${\mathcal{J}}_N$ for $\beta =12$ with $\mathrm{AR}{L}_0\approx 20,30,40$.

		Sampling strategies
$\mathrm{AR}{L}_0$		$T^{\ast }(S_a)$	$T^{\ast }(S_{\mathrm{fir}})$	$T^{\ast }(S_{\mathrm{both}})$	$T^{\ast }(S_{\mathrm{uni}})$	$T^{\ast }(S_{\mathrm{rand}})$	$T^{\ast }({\tilde{S}}_{\mathrm{DE}})$
20	$c_{\gamma }$	0.492	0.4	0.358	0.35	0.341	0.3575
	$\mathrm{AR}{L}_0$	20.1	19.9667	20.3461	19.9128	20.1344	20.9090
	A	–	–	–	–	–	0.975
	${\mathcal{J}}_N$	0.2131	12.0601	14.0645	2.5005	3.4470	17.7804
30	$c_{\gamma }$	0.57	0.436	0.3937	0.3933	0.39299	0.3936
	$\mathrm{AR}{L}_0$	29.9636	30.0716	30.1626	30.0058	29.6563	29.9852
	A	–	–	–	–	–	0.975
	${\mathcal{J}}_N$	0.2452	13.3404	14.2171	2.6707	3.8024	18.0551
40	$c_{\gamma }$	0.705	0.4892	0.4358	0.436	0.4363	0.45
	$\mathrm{AR}{L}_0$	40.2044	40.0470	39.9516	40.0173	40.0552	40.057
	A	–	–	–	–	–	0.975
	${\mathcal{J}}_N$	0.2666	13.9110	14.7122	2.9020	3.8802	18.2491

Table 12.

Comparisons of ${\mathcal{J}}_N$ for $\beta =30$ with $\mathrm{AR}{L}_0\approx 20,30,40$.

		Sampling strategies
$\mathrm{AR}{L}_0$		$T^{\ast }(S_a)$	$T^{\ast }(S_{\mathrm{fir}})$	$T^{\ast }(S_{\mathrm{both}})$	$T^{\ast }(S_{\mathrm{uni}})$	$T^{\ast }(S_{\mathrm{rand}})$	$T^{\ast }({\tilde{S}}_{\mathrm{DE}})$
20	$c_{\gamma }$	0.492	0.4633	0.4353	0.414	0.4135	0.4354
	$\mathrm{AR}{L}_0$	20.1	19.9520	20.1454	20.0048	20.1483	19.9642
	A	–	–	–	–	–	0.959
	${\mathcal{J}}_N$	0.2131	3.4562	5.3101	0.7657	1.1008	9.7635
30	$c_{\gamma }$	0.57	0.515	0.468	0.468	0.467	0.487
	$\mathrm{AR}{L}_0$	29.9636	30.0518	30.0045	29.8777	29.9630	30.0837
	A	–	–	–	–	–	0.959
	${\mathcal{J}}_N$	0.2452	4.54054	5.7852	0.8118	1.1475	10.3039
40	$c_{\gamma }$	0.705	0.6	0.535	0.537	0.54	0.555
	$\mathrm{AR}{L}_0$	40.2044	40.1145	40.1159	39.9882	39.9543	40.062
	A	–	–	–	–	–	0.959
	${\mathcal{J}}_N$	0.2666	5.2234	5.9845	0.8637	1.1861	10.8010

It can be seen from Tables 10–12 that the full sampling strategy, $S_a$, is best, and the uniformly dispersed sampling strategy, $S_{\mathrm{uni}}$, is also good, being better than the sampling strategies $S_{\mathrm{fir}}$, $S_{\mathrm{both}}$, $S_{\mathrm{rand}}$ and ${\tilde{S}}_{\mathrm{DE}}$.

6. Conclusion and discussion

In this paper, for finite or small samples $N(N\ge 2)$ we obtain two theoretical results: one is that for a given sampling strategy S, the CUSUM chart $T^{\ast }(S)$ with the dynamic non-random control limit $\{l_k(c_{\gamma })\}$ is optimal under the measure ${\mathcal{J}}_N(T(S),S)$, and the other is that if $S^{\prime }\ge S$ and condition (10) holds, the optimal CUSUM chart $T^{\ast }(S^{\prime })$ is better than the optimal CUSUM chart $T^{\ast }(S)$, therefore, the optimal CUSUM chart $T^{\ast }(S_a)$ has the best detection performance of all sampling strategies and all control charts subject to a constraint on the false alarm average run length ( $\mathrm{AR}{L}_0$).

The numerical simulations in Tables 1–9 illustrate that when $s_0=0,0.25,0.5$ substitutes for the observation value, which does not satisfy condition (10), the optimal CUSUM chart $T^{\ast }(S_a)$ still has the best detection performance for the number of observations $\beta =12$, $\beta =20$ and $\beta =30$. This leads to the following problem: can the result of Theorem 3.2 still hold for $\log \mathrm{\Lambda }(s_0)\ge {\mu }_0$? Here, ${\mu }_0={\mathbf{E}}_0(\log \mathrm{\Lambda }(X_1))<0$ but the condition (10) implies that $\log \mathrm{\Lambda }(s_0)>0$. In other words, the condition $\log \mathrm{\Lambda }(s_0)\ge {\mu }_0$ is more general than (10).

When the number of samples is restricted, or the number of samples is limited to reduce the cost of sampling, we see from Tables 1–12 that the uniformly dispersed sampling strategy $S_{\mathrm{uni}}$ is better than the sampling strategies $S_{\mathrm{fir}}$, $S_{\mathrm{las}}$, $S_{\mathrm{both}}$, $S_{\mathrm{rand}}$, ${\tilde{S}}_{\mathrm{DE}}$ and $S_{\mathrm{DE}}$ except in the case where $s_0=0.5$. Therefore, we prefer to recommend the use of a uniformly dispersed sampling strategy when the number of samples is less than the total number of samples. Further, this leads to another problem: is the uniformly dispersed sampling strategy $S_{\mathrm{uni}}$ best among all sampling strategies with the same number of samples when ${\mu }_0\le \log \mathrm{\Lambda }(s_0)<0$?

The above two problems are worthy of further study.

Appendix: Proofs of Theorems.

Proof Proof of Theorem 3.1 —

Let $Y_k:=Y_k(S)$ and $T:=T(S)$. We first prove the following equality:

$$\begin{array}{r}{\mathcal{J}}_N(T,S)={\mathbf{E}}_0\left(\sum _{k=1}^T{Y}_{k-1}\right)=\sum _{k=1}^N{\mathbf{E}}_0(Y_{k}I(T\ge k+1)),\end{array}$$ (A1)

where $I(.)$ is the indicator function. Since

$$\begin{array}{r}(T-k{)}^{+}=\sum _{m=k+1}^{N+1}(m-k)[I(T\ge m)-I(T\ge m+1)]=\sum _{m=k+1}^{N+1}I(T\ge m)\end{array}$$

and $T\ge m\in {\mathfrak{F}}_{m-1}(S)$, it follows that

$$\begin{array}{rl}{\mathbf{E}}_k((1-Y_{k-1}{)}^{+}(T-k{)}^{+})& =\sum _{m=k}^{N+1}{\mathbf{E}}_k((1-Y_{k-1}{)}^{+}I(T\ge m))\\ & =\sum _{m=k+1}^{N+1}{\mathbf{E}}_k((1-Y_{k-1}{)}^{+}I(T\ge m)\prod _{j=1}^{k-1}{p}_0({\tilde{X}}_j)\prod _{j=k}^{m-1}{p}_1({\tilde{X}}_j))\\ & =\sum _{m=k+1}^{N+1}{\mathbf{E}}_0((1-Y_{k-1}{)}^{+}I(T\ge m)\frac{\prod _{j=1}^{k-1}{p}_0({\tilde{X}}_j)\prod _{j=k}^{m-1}{p}_1({\tilde{X}}_j)}{\prod _{j=1}^{m-1}{p}_0({\tilde{X}}_j)})\\ & =\sum _{m=k+1}^{N+1}{\mathbf{E}}_0((1-Y_{k-1}{)}^{+}I(T\ge m)\prod _{j=k}^{m-1}\mathrm{\Lambda }({\tilde{X}}_j)).\end{array}$$

Thus

$$\begin{array}{rl}{\mathcal{J}}_N(T,S)& ={\mathbf{E}}_0(\sum _{k=1}^N\sum _{m=k+1}^{N+1}(1-Y_{k-1}{)}^{+}I(T\ge m)\prod _{j=k}^{m-1}\mathrm{\Lambda }({\tilde{X}}_j))\\ & ={\mathbf{E}}_0(\sum _{k=1}^N\sum _{m=k+1}^T(1-Y_{k-1}{)}^{+}\prod _{j=k}^{m-1}\mathrm{\Lambda }({\tilde{X}}_j))\\ & ={\mathbf{E}}_0(\sum _{m=2}^T\sum _{k=1}^m(1-Y_{k-1}{)}^{+}\prod _{j=k}^{m-1}\mathrm{\Lambda }({\tilde{X}}_j))={\mathbf{E}}_0\left(\sum _{m=1}^T{Y}_{m-1}\right),\end{array}$$

since $Y_m=\sum _{k=1}^m(1-Y_{k-1}{)}^{+}\prod _{j=k}^m\mathrm{\Lambda }({\tilde{X}}_j)$ and $Y_0=0$. Note that ${\mathbf{P}}_0(T\ge k+1)=0$ for $k\ge N+1$, we further have

$$\begin{array}{r}{\mathbf{E}}_0\left(\sum _{m=1}^T{Y}_{m-1}\right)={\mathbf{E}}_0(\sum _{k=1}^{N+1}I(T=k)\left(\sum _{m=1}^k{Y}_{m-1}\right))=\sum _{k=1}^N{\mathbf{E}}_0(Y_{k}I(T\ge k+1)).\end{array}$$

This is (A1). Let

$$\begin{array}{r}{\xi }_n=\sum _{k=1}^n{Y}_{k-1}-\mathrm{an}\end{array}$$ (A2)

for $n\ge 1$, be a series of random variables, where a>0 is a constant. It follows from (A1) and (A2) that

$$\begin{array}{r}{\mathbf{E}}_0({\xi }_T)={\mathcal{J}}_N(T,S)-a{\mathbf{E}}_0(T).\end{array}$$ (A3)

Let $T(c):=T_C(S,c)$. By a similar method of proof to Theorems 1 and 3 in [5] we can prove that

$$\begin{array}{r}{\mathbf{E}}_0({\xi }_T)\ge {\mathbf{E}}_0({\xi }_{T(c)})\end{array}$$ (A4)

for every $T\in {\mathfrak{T}}_N(S)$, and that there is a positive constant $c_{\gamma }$ and a dynamic non-random control limit $\{l_k(c_{\gamma })\}$ such that ${\mathbf{E}}_0(T(c_{\gamma }))=\gamma$.

Note that $T^{\ast }(S)=T(c_{\gamma })$. By (A3) and (A4) we have ${\mathcal{J}}_N(T,S)\ge {\mathcal{J}}_N(T^{\ast }(S),S)$ for $T\in {\mathfrak{T}}_N(S)$ as long as ${\mathbf{E}}_0(T)\ge {\mathbf{E}}_0(T(c_{\gamma }))$, which means (5). This completes the proof.

Proof Proof of Theorem 3.2 —

It follows from Theorem 3.1 that

$$\begin{array}{r}{\mathcal{J}}_N(T^{\ast }(S),S^{\prime })\ge {\mathcal{J}}_N(T^{\ast }(S^{\prime }),S^{\prime })\end{array}$$ (A5)

for ${\mathbf{E}}_0(T^{\ast }(S))={\mathbf{E}}_0(T^{\ast }(S^{\prime }))$. Hence, to prove (7), it is only necessary to show

$$\begin{array}{rl}{\mathcal{J}}_N(T^{\ast }(S),S)& =\sum _{k=1}^N{\mathbf{E}}_0(Y_k(S)I(T^{\ast }(S)\ge k+1))\\ & \ge \sum _{k=1}^N{\mathbf{E}}_0(Y_k(S^{\prime })I(T^{\ast }(S)\ge k+1))={\mathcal{J}}_N(T^{\ast }(S),S^{\prime }).\end{array}$$ (A6)

Note that $S_k,S_k^{\prime }\in {\mathfrak{F}}_{m-1}$, ${\mathbf{P}}_0(S_k=1)\le {\mathbf{P}}_0(S_k^{\prime }=1)$, ${\mathbf{P}}_0(S_k=0)\ge {\mathbf{P}}_0(S_k^{\prime }=0)$, $I(T^{\ast }(S)\ge 2)=I(Y_1(S)<l_1(c_{\gamma }))$, $Y_1(S)=S_1\mathrm{\Lambda }(X_1)+(1-S_1)\mathrm{\Lambda }(s_0)$, $Y_1(S^{\prime })=S_1^{\prime }\mathrm{\Lambda }(X_1)+(1-S_1^{\prime })\mathrm{\Lambda }(s_0)$ and $\mathrm{\Lambda }(s_0)\ge 1$. It follows that

$$\begin{array}{rl}& {\mathbf{E}}_0(Y_1(S)I(T^{\ast }(S)\ge 2))-{\mathbf{E}}_0(Y_1(S^{\prime })I(T^{\ast }(S)\ge 2))\\ & =[{\mathbf{P}}_0(S_1^{\prime }=1)-{\mathbf{P}}_0(S_1=1)]{\mathbf{E}}_0([\mathrm{\Lambda }(s_0)-1]I(\mathrm{\Lambda }(s_0)\le l_1(c_{\gamma })))\ge 0\end{array}$$

and furthermore

$$\begin{array}{rl}& {\mathbf{E}}_0([max\{1,Y_1(S)\}-max\{1,Y_1(S^{\prime })\}]I(Y_1(S)\le l_1(c_{\gamma })))\\ & =[{\mathbf{P}}_0(S_1=0)-{\mathbf{P}}_0(S_1^{\prime }=0)][\mathrm{\Lambda }(s_0)-{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}max\{p_0(x),p_1(x)\}\mathrm{d}x]I(\mathrm{\Lambda }(s_0)\le l_1(c_{\gamma }))\ge 0.\end{array}$$

By using $Y_k=max\{1,Y_{k-1}\}\mathrm{\Lambda }({\tilde{X}}_k)$ and mathematical induction, we find that

$$\begin{array}{r}{\mathbf{E}}_0(Y_k(S)I(T^{\ast }(S)\ge k+1))\ge {\mathbf{E}}_0(Y_k(S^{\prime })I(T^{\ast }(S)\ge k+1))\end{array}$$

for $1\le k\le N$, and therefore, (A6) holds. Thus  (7) follows from (A5) and (A6), and (7) implies (8). This completes the proof.

Funding Statement

This work was supported by the National Natural Science Foundation of China (11531001) and RGC Competitive Earmarked Research Grants.

Disclosure statement

No potential conflict of interest was reported by the author(s).