Data of subsurface velocity structures beneath the Japan Islands retrieved from horizontal-to-vertical ratios of earthquake with diffuse field concept

Abstract

The present data are subsurface velocity structures retrieved by applying the theory of diffuse field concept to the strong motion data of earthquakes observed at 1744 sites of K-NET and KiK-net (operated by the National Institute of Earth Science and Disaster Resilience) in Japan. Additionally, the data include peak fundamental and predominant frequencies as identified from the observed and theoretical horizontal-to-vertical spectral ratios for earthquakes (eHVSR). Based on our novel proposed quarter wavelength approach, we could define the effective bedrock depths and correlate them with the corresponding peak frequencies. For better usefulness of the present data, we classify the sites into four categories based on the correlation coefficients and residuals between the observed and theoretical eHVSR. The potentiality of these data could be reused by other researchers to develop new approaches related to the limitations of the established bedrock regressions and the uncertainty associated with the retrieved subsurface velocity structures, particularly at sites with low correlation coefficients and high residuals. Moreover, the data of the subsurface velocity structures could be reused as initial models for future microtremor applications and better enhance the retrieved velocity structures and the associated theoretical eHVSR curves. The data of the present paper is associated with original published article by Thabet et al. [1], which is presented in the Soil Dynamics and Earthquake Engineering under the title “A computational approach for bedrock regressions with diffuse field concept beneath the Japan Islands” [1].

Specifications Table

Subject	Earth and Planetary Sciences •Geophysics •Geotechnical Engineering and Engineering Geology
Specific subject area	Engineering Seismology – seismic site characterization
Data format	Processed, Inverted, Analysed, Classified
Type of data	Graph, Figure, Dataset
Data collection	Earthquake waveforms were acquired from the KiK-net and K-NET (National Research Institute for Earth Science and Disaster Resilience, [2]). Stable and geometrically averaged eHVSR (HVSR for earthquakes) were processed and then inverted using the theory of diffuse field concept for earthquakes to retrieve the subsurface velocity structures at KiK-net and K-NET sites. 291 sites out of the whole 1744 KiK-net and K-NET sites were excluded based on their low correlation coefficients and high residuals to reduce the uncertainty in the further analyses. Fundamental and predominant peak frequencies were correlated with the effective bedrock depths using proposed quarter wavelength approach. The depths to the layers, where shear wave velocities ≥ 800 m/s and ≥ 3000 m/s (i.e. D800 and D3000) are analysed and correlated with the fundamental peak frequencies. Finally, the sites were classified into four categories based on their correlation coefficients and residuals between the observed and theoretical eHVSRs. Thus, reliable and accurate future reuse of these data is potentially beneficial.
Data source location	Disaster Prevention Research Institute (DPRI), Kyoto University, Japan Geology Dept., Faculty of Science, Assiut University, Egypt
Data accessibility	With the article Repository name: Mendeley Data Data identification number: 10.17632/wg6v2v5yrg.1 Direct URL to data: https://data.mendeley.com/datasets/wg6v2v5yrg/1
Related research article	M. Thabet, F. Nagashima, H. Kawase, A computational approach for bedrock regressions with diffuse field concept beneath the Japan Islands, Soil Dynamics and Earthquake Engineering 2024, Volume 177, 108,429, https://doi.org/10.1016/j.soildyn.2023.108429

1. Value of the Data

• •The present data of subsurface velocity structures down to the seismic bedrock in Japan are useful for assessing the site amplification factors since the incident waves at seismic bedrock are not affected by any site amplification.
• •The relationships of fundamental and predominant peak frequencies to the inverted velocity profiles could be used as representative ones valid for the tectonically similar regions.
• •These data could be compared with the well-known velocity structures and site amplification factors provided by J-SHIS (Japan Seismic Hazard Information Station, [3]) for better revealing the precision of different methods.
• •These data of velocity structures could be utilized as initial models in any future microtremor measurements adjacent to K-NET and/or KiK-net sites.
• •The data of fundamental and predominant peak frequencies and subsurface velocity structures could be reused for alternative approaches of detecting the effective bedrock depth other than our novel quarter wavelength approach.
• •The data classification based on their correlation coefficients and residuals between observed and theoretical eHVSR yield significant clues to the distribution of different classes with respect to the prevailing site characterization.

2. Background

K-NET and KiK-net [2] sites in Japan are associated with the measured velocity profiles only down to the very shallow or shallow subsurface velocity structures (i.e. mainly 10 m ∼ 100 m depth). One of the most important obstacles for stable frequency-depth regressions by Thabet [4,5] was the depth limitation, particularly at sites with peak frequencies lower than 1 Hz. Inverting the eHVSR for earthquakes using diffuse field concept [6] at these sites is potentially beneficial to retrieve the detailed subsurface velocity structures down to the seismic bedrock. Above all, obtaining stable and representative eHVSR for earthquakes applying constraint computational approach is crucial input in the consecutive inversion of the eHVSRs. Finally, we could adapt new proposed criteria to estimate the effective bedrock depths responsible for the corresponding fundamental and predominant peak frequencies [1].

Since the seismic waves are not influenced by any site amplification at the seismic bedrock, the generated data in this paper could be useful for future calculations of site amplification factors taking into account velocity structures down to the seismic bedrock. Moreover, these generated data can be useful for other researchers willing to understand and reveal the potentiality whenever possible substituting the fundamental peak frequencies here with the fundamental peak frequencies derived from microtremor measurements as proved earlier by Kawase et al. [7].

3. Data Description

The data of this paper are referenced in [8] and being obtained from linked repository of the Mendeley Data. The data are divided in five excel files and can be found in the address: https://data.mendeley.com/datasets/wg6v2v5yrg/1.

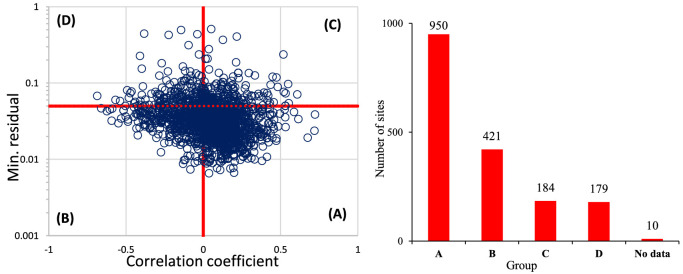
The first excel file “Correlation-vs-Residual” contains the minimum residual and the correlation coefficient calculated between the observed and theoretical eHVSRs of earthquakes at each K-NET and KiK-net site. Moreover, “A, B, C, and D” classification is provided adapting thresholds of 0.05 and 0.0 for the minimum residual and the correlation coefficient, respectively. Some sites are classified as “No data”, because of unavailability or lack of good quality earthquake waveforms.

The second excel file “Physical Properties” contains the P- and S-wave velocities and the thicknesses of the 14-layer model. The seismic bedrock has P- and S-wave velocities of 6000 m/s and 3400 m/s, respectively.

The third excel file “Peak Frequency” contains the peak and trough frequencies and their amplitudes, as derived from both observed and theoretical eHVSRs for earthquakes.

The fourth excel file “No. earthquakes and rho values” contains the number of accepted earthquakes at each site. In addition, median and mean of the $\sigma \left(f\right)$ for each earthquake group (i.e. A through I, as described next), between EW and NS components, and for the overall site.

The fifth excel file “Analyzed Data after exclusion” contains only characterizations of the 1453 included sites. It contains the assigned bedrock characteristics responsible for the fundamental and predominant frequencies according to the quarter wavelength approach. Moreover, we added the characterizations of D₈₀₀ and D₃₀₀₀, V_s30 and, azimuthal angles. In this file, we exclude 291 sites out of the whole 1744 K-NET and KiK-net sites according to systematic sequential steps adapted by Thabet et al. [1].

Detailed identification of each data column is provided and listed inside each data excel file.

4. Experimental Design, Materials and Methods

It is important to emphasize here that our constraint criteria for examining the earthquake waveforms include only the most high-quality waveforms. Thus, these high-quality waveforms enable us to achieve stable and reliable eHVSRs, which are essential for a robust and efficient eHVSR inversion based on the diffuse field concept for earthquakes. The inversions were run assuming one-dimensional horizontal-layered structures at each K-NET and KiK-net site. The following consecutive steps are illustrating the computational approach behind generating the present data.

• •Selecting earthquakes, which we obtained from [2], with magnitudes of M_JMA ≥ 3.0 to take advantage from low noise level at frequencies less than 1 Hz. These selected earthquakes are constrained to peak ground accelerations between ≥ 1.0 cm/s² and ≤ 50.0 cm/s². The high level of noise could be caused by site-specific ground motions or instrumental origin, which is mainly dominate the low frequency bands less than 1 Hz.
• •Correcting the earthquake waveforms by removing the DC offset. It is important to note that we used Fortran routines by Boore [9].
• •Grouping these corrected earthquakes into nine groups (A through I) according to their source distances (< 50 km, ≥ 50 km to ≤ 200 km, and > 200 km) and source depths (< 25 km, ≥ 25 km to ≤ 60 km, and > 60 km), as summarized in Table 1. From each group, we selected 5 to 10 earthquakes for later analyses and fulfilling the criteria of different incidence azimuths and angles according to assumption of the diffuse field concept [6].
• •Picking the S-wave arrivals using the Kurtosis function. Starting from the S-wave arrival, we could limit the analysed time window to 80 s. This time window confirms 10 significant cycles and minimum resolved frequency of interest of 0.125 Hz. Therefore, we could fulfil the reliability condition of ($f_0>10/t_w$), where $f_0$ and $t_w$ are the fundamental frequency of the site and the analysed time window length of 80 s, respectively.
• •Tapering 5 % at both start and end of these time windows.
• •Zero padding, if it is needed, to make the lengths of these time windows unified and suitable for the consequent spectral calculations.
• •Calculating the Fourier acceleration spectra for each independent component (i.e. East-West; EW, North-South; NS, and Up-Down; UD). We also used the Fortran routines by Boore [9].
• •Smoothing the Fourier spectra with Parzen window function of 0.1 Hz bandwidth.
• •Calculating eHVSR curve for each independent earthquake.
• •Geometrically averaging the eHVSRs on the basis of each frequency point with signal-to-noise ratio of ≥ 3.0, so that, we could prevent any source of uncertainty may affect the physical interpretation of the eHVSR.
• •
  Evaluating quantitatively the differences among eHVSRs of the selected earthquakes using (1), (2), (3). The mean of the $\sigma \left(f\right)$ values is adapted.

  $${\mu }_{ln}\left(f\right)=\frac{1}{n}\sum _{i=1}^{n}ln\left[s_i\left(f\right)\right]$$ (1)

  $$\widehat{s}\left(f\right)=exp\left[{\mu }_{ln}\left(f\right)\right]$$ (2)

  $${\sigma }_{ln}\left(f\right)=\sqrt{\frac{1}{n}\sum _{i=1}^n{\left(ln\left[s_i\left(f\right)\right]-ln\left[\widehat{s}\left(f\right)\right]\right)}^2}$$ (3)

where $ln(s_i\left(f\right)$ corresponds to the natural logarithm of eHVSRs of independent earthquakes of $i=1,\dots ,n$.

• •Confirming the stability of eHVSRs for each earthquake, specifically in the low frequency band (i.e. < 1 Hz), through performing spectral selection and removing the spectra that undergo signal-to-noise ratio less than 3 due to possible instrumental noise and/or site-specific ground motion noise. Moreover, we removed the spectra unfulfilling the bell-shaped spectra in this low frequency band (i.e. < 1 Hz). By reaching this step, we could achieve stable and reliable eHVSRs at K-NET and KiK-net sites, consequently, the following steps are describing the robust and efficient eHVSR inversion steps based on the diffuse field concept for earthquakes.
• •Adapting the 14-layer model using the physical properties obtained from [3]. The seismic bedrock is fixed to P- and S-wave velocities of 6000 and 3400 m/sec, respectively.
• •
  Estimating the initial thickness ($h$) for this 14-layer model based on the definition of the minimum wavelengths, as in Eq. (4).

  $$h=\frac{2n+1}{4}\frac{V_S}{f}$$ (4)

where $n$, $f$, $V_S$ correspond to the mode of resonance frequency, maximum frequency resolved in the inversion, which is 20 Hz, and S-wave velocity, respectively. We selected the $n$ value of 2 after many trials of $n$ of 0, 1, 2, 3, and 4.

• •Assigning the P- and S-wave velocity search space between zero and three times higher than the initial values of the 14-layer model and restricting the identified velocities as increasing with depth. The hysteresis damping is 1.1 % assuming linear analyses.
• •
  Assigning unrestricted search space for the thicknesses of the 14 layers, whereas the densities are identified using the S-wave velocity ($V_S$) according to Eq. (5).

  $$\rho =1.4+0.67*V_S^{1/2}$$ (5)
• •Running the one-dimensional inversion using the Fortran code by Nagashima [10], which adapts diffuse field concept for earthquakes. This code adapts hybrid searching algorithm taking advantage of simulated annealing and genetic algorithm. We set the inversion input parameters of initial temperature, crossover, mutation, generations, and populations (i.e. 14-layer models) as 100, 0.7, 0.1, 200, and 400, respectively. The inversions run over frequency bandwidth of 0.2 to 20 and iterate ten times for each K-NET and KiK-net site.
• •
  Selecting the best identified 14-layer model that corresponds to the minimum residual among the ten inversion times, as evaluated in Eq. (6). Because we adapt one-dimensional diffuse field concept, so that, the possible causes of the residual between the observed and theoretical eHVSRs could be due to the three- or two-dimensional medium.

  $$residual=\sum _{i=1}^n{\left[lo{g}_{10}\left(ob{s}_i\right)-lo{g}_{10}\left(in{v}_i\right)\right]}^2$$ (6)
• •
  Assigning the effective bedrock depth ($D_{eff}$) using the quarter wavelength approach. This $D_{eff}$ is responsible for fundamental or predominant peak frequencies ($f$) at the site. We calculate the time-averaged S-wave velocity ($\overline{V_s}$) at each depth in the best identified 14-layer model. Then, we calculate the minimum resolved wavelengths ($\lambda$) using Eq. (7). The assigned $D_{eff}$ has the minimum difference with its corresponding $\lambda$.

  $$\lambda =\overline{V_s}/4*f$$ (7)
• •Establishing frequency-depth regressions.
• •Mapping the D₈₀₀ and D₃₀₀₀ and correlating with the fundamental peak frequency.

Table 1.

The nine groups of the corrected earthquakes.

	Source depth
Source distance	< 25 km	≥ 25 km to ≤ 60 km	> 60 km
< 50 km	A	B	C
≥ 50 km to ≤ 200 km	D	E	F
> 200 km	G	H	I

Limitations

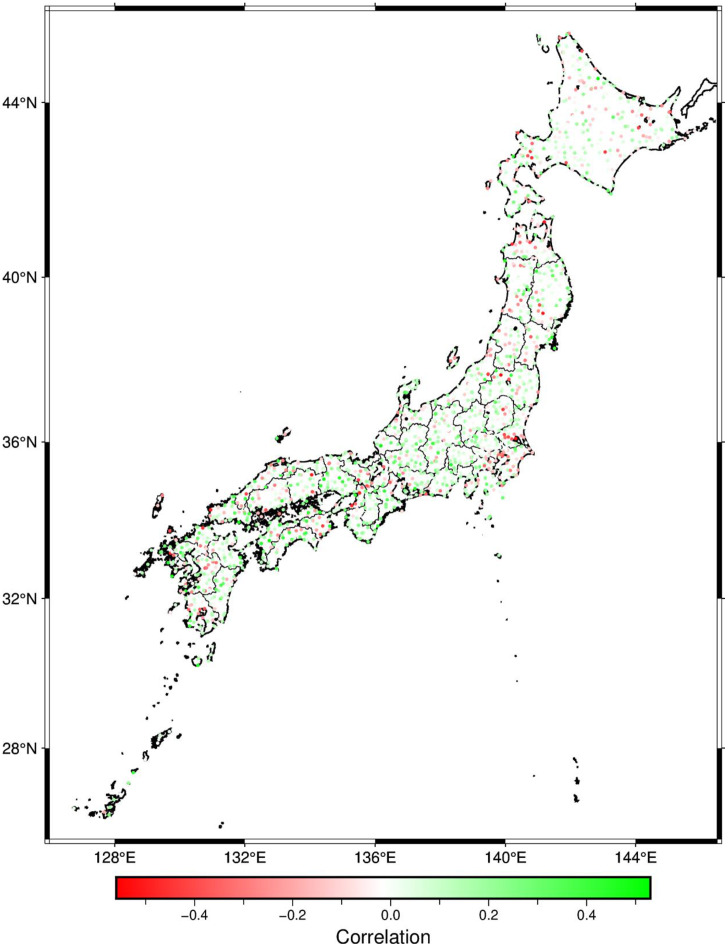
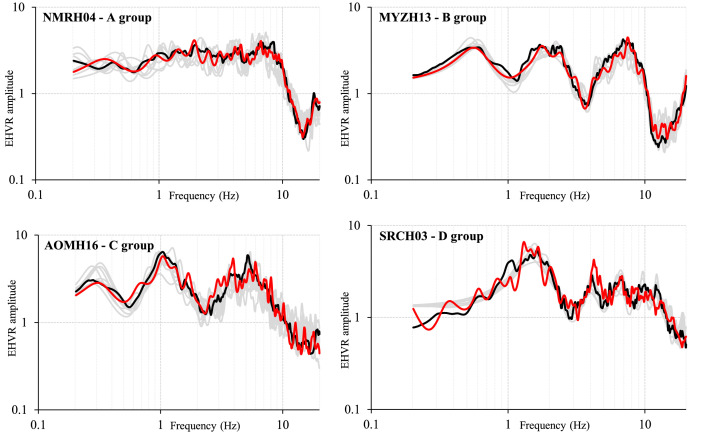
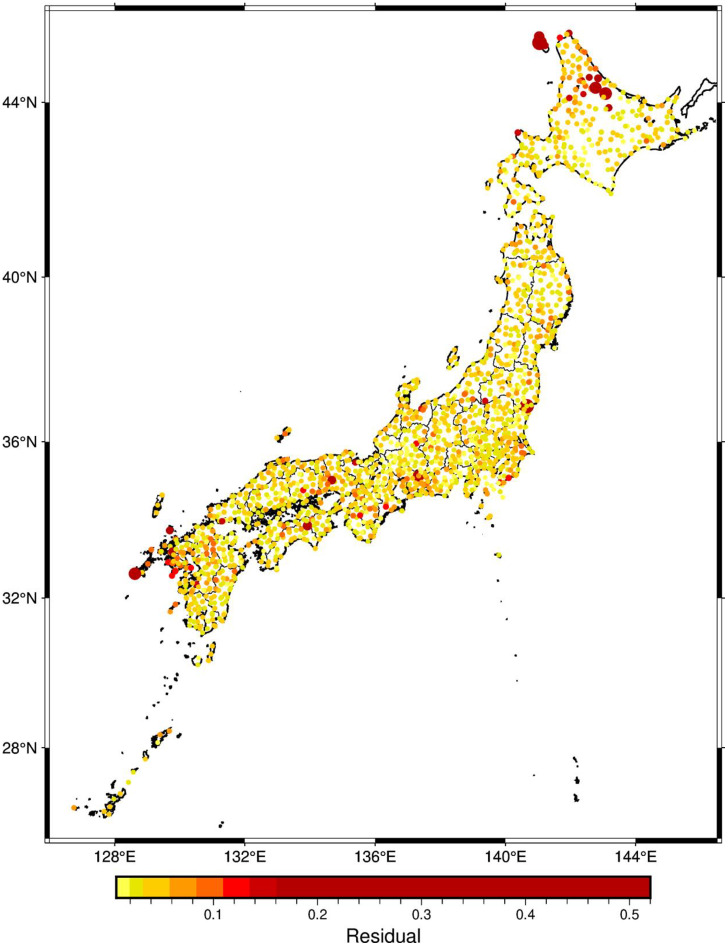
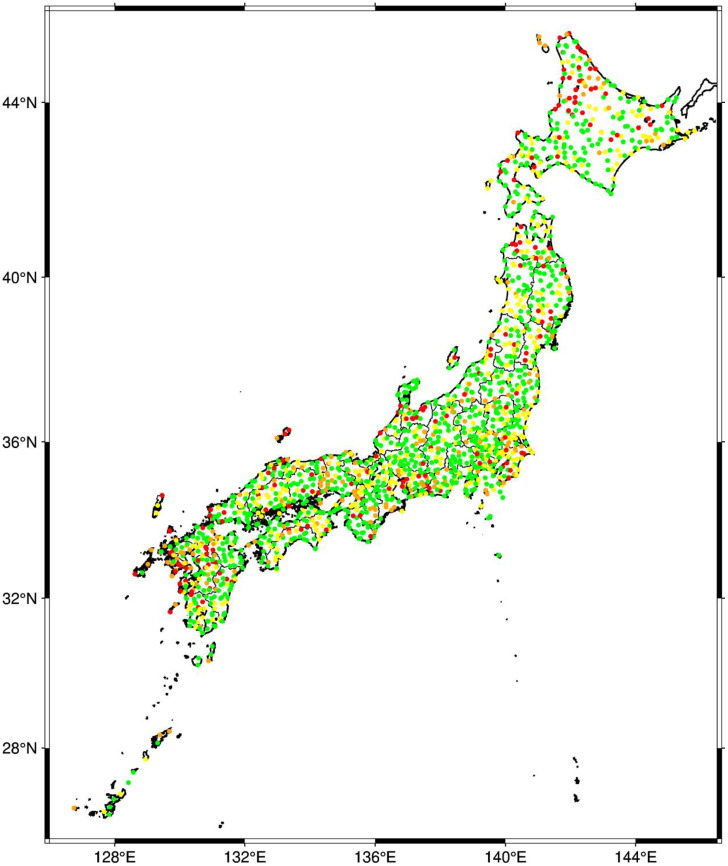
We classified the K-NET and KiK-net sites into four groups according to the quality data. Fig. 1 shows four examples of comparison between observed and theoretical eHVSR curves. This classification is designed using the thresholds of 0.05 and 0.0 for the minimum residual and the correlation coefficient between observed and theoretical eHVSRs for earthquakes, respectively, as shown in Fig. 2. Consequently, group “D” corresponds to low correlation coefficient of ≤ 0.0 and minimum residual of > 0.05, so that, data from these sites should be avoided. Sites of group “D” represent 10 % out of the whole sites. Group “C” corresponds to correlation coefficient of > 0.0 and minimum residual of > 0.05, whereas group “B” corresponds to correlation coefficient of ≤ 0.0 and minimum residual of < 0.05. Thus, data from “B” and “C” groups could be used with proper awareness, and they represent 24 % and 11 %, respectively. Finally, data from group “A” is classified as good quality data and represents the majority with 54 % out of the whole sites. Fig. 3 through Fig. 5 are showing the distribution of residuals, correlation coefficients, and the relevant classification, respectively. There are minor clusters of “D” sites. This could be related to the prevailing site characterizations, and overcoming such a limitation is one of our coming planed research works. All the maps in the present paper are plotted using PyGMT [11].

Fig. 4.

Distribution of correlation coefficients.

Fig. 1.

Examples of observed (black curves) and theoretical (red curves have minimum residual, whereas gray curves are the other nine inversion trials) eHVSRs for the four groups.

Fig. 2.

Minimum residual versus the correlation coefficient showing their thresholds used in the present classification (left panel). Distribution of sites into the four groups (right panel).

Fig. 3.

Distribution of minimum residuals. The sizes of the circles are related to their minimum residual values.

Fig. 5.

Distribution of classes A (green), B (yellow), C (orange), and D (red).

Ethics Statement

All the authors confirm that they have read and follow the ethical requirements for publication in Data in Brief and confirm that this work does not involve the use of human subjects, animal experiment, or any data collected from social media platforms.

CRediT authorship contribution statement

Mostafa Thabet: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Visualization, Writing – original draft, Writing – review & editing. Hiroshi Kawase: Funding acquisition, Supervision, Writing – review & editing. Fumiaki Nagashima: Validation, Formal analysis, Investigation, Project administration, Software, Writing – review & editing.

Data Availability

• Dataset of P- and S-wave Velocity Structures in Japan (Original data) (Mendeley Data).