Abstract
Degradation of insulation paper is a key contributor to the failure of power transformers. Insulation degradation accelerates at elevated temperatures, which highlights the potential for better thermal management to prolong life. While several studies have analyzed the benefits of high thermal conductivity oil for reducing temperatures inside a transformer, this study is an initial assessment of the benefits of high thermal conductivity paper on transformer life. Blending particulates with cellulosic fibers offers a pathway for high thermal conductivity paper (with good dielectric properties), which can reduce internal temperatures. Presently, life extensions that can be achieved by the use of such thermally conducting papers were estimated, with the thermal conductivity of the paper being the key parameter under study. The analytical-numerical thermal model used in this study was validated against experimental measurements in a distribution transformer, adding confidence to the utility of the model. This model was then used to provide estimates of hot-spot temperature reduction resulting from the use of papers with higher thermal conductivity than baseline. Transformer life was predicted conventionally by tracking the degree of polymerization of paper over time, based on an Arrhenius model. Results indicate that increasing the thermal conductivity of paper from 0.2 W/mK (baseline) to 1 W/mK reduces the hot spot temperature by 10 °C. While degradation significantly depends on the moisture and oxygen content, the model shows that such a temperature reduction can increase life for all conditions, by as much as a factor of three.
Keywords: Power transformers, Insulation paper, High thermal conductivity, Thermal modeling, Transformer life model, Paper degradation, Degree of polymerization, Nanoparticles
1. Introduction
Upgrading the electrical grid to accommodate significantly greater contributions from renewables is a national priority for many countries. Next generation electrical grids and equipment will also need to survive harsher operating conditions (e.g., extreme temperature excursions, intermittent operation, and energy spikes). As a key component of the power grid, transformers are widely embedded in all parts of the electricity distribution network [[1], [2], [3]]. Transformer failures can lead to cascading grid-scale issues and affect grid resiliency [4,5]. In the U.S, millions of power and distribution transformers are nearing their end of life and will need to be replaced [6]. Accordingly, the US Department of Energy aims to stimulate key technical advances supporting the doubling of the expected life of transformers [7]. It will also be important for next generation transformers to have low cost and reduced carbon footprint. Furthermore, with the expected widespread adoption of electric vehicles (EV), it is no longer realistic to assume that transformers will run at reduced loads at night, since most EVs will be charged then; this is expected to reduce transformer life [8,9]. These trends underscore the benefit of higher reliability, longer-life transformers.
While transformers fail for many reasons, most failures exhibit as insulation degradation making it an important process for improved understanding [[10], [11], [12], [13], [14]]. A typical transformer consists of laminated steel magnetic cores, primary and secondary windings, and other components like oil, external tank, and cooling system. Tenbohlen et al. [15,16] reported that 49% of faults occurred in windings. Windings need to be electrically insulated; paper or polymer coatings are typically used. Additionally, in oil-filled transformers, windings are immersed in dielectric oil, which provides cooling while enhancing the insulation between windings. Zhang and Gockenbach [17] attributed electrical and thermal faults to weakened insulation components such as paper and oil. According to another field survey by Bartley [18], insulation-related failures (defective installation, insulation degradation and short circuits) are the leading causes of transformer failures. High-voltage impulses may initiate partial discharges (PD) in voids in the paper [19], which can ultimately cause electrical breakdown. While degradation of oil can be remediated by treatment methods or by replacement, there are no straightforward options to remedy or replace paper. The expected life of a transformer is thus directly related to the life of paper [20].
Paper insulation consists of cellulosic fibers containing well-aligned long cellulosic fibrils with each fibril made of hydrogen bonded cellulose chains [13]. The length of the cellulose chains and the hydrogen bonding between cellulosic fibrils give paper its strength [21]. Cellulosic fibers degrade under acidic conditions through hydrolysis reactions which reduce cellulose chain length or degree of polymerization (DP) via cutting of the β-1-4 linkages [22]. The degradation rate increases with temperature and water (H2O) is a key input for the hydrolysis reaction [23]. Degradation can also take place via oxidation of the carbon atoms in the cellulose molecule [21]. Breakdown results in significant increase in local temperature which enhances the oxidation of cellulosic fibers at the breakdown spot to release H2O, CO, CO2 and H2 [23].
A reduction in temperature slows paper degradation, thereby increasing transformer life. Several studies assess the benefits of high thermal conductivity coolants in reducing peak temperatures inside the transformer [10,[24], [25], [26], [27]]. Zhang et al. [26] conducted a computational fluid dynamics (CFD) study and showed a 10 °C reduction in hot-spot temperature inside a transformer upon replacing conventional oil with a nanofluid. Rafiq et al. [24] reported that nanofluids have better dielectric and thermal properties than transformer oils. However, the industry has been slow to capitalize on this because of unresearched downside risks [26]. Santisteban et al. [28] compared the hot-spot temperatures resulting from the use of mineral and ester oils and found that the temperatures are lower with ester oil (higher thermal conductivity). Patel et al. [29] estimated a 9X increase in the life of transformers by using magnetic fluid as a coolant.
While the use of high thermal conductivity fluids for increasing life has been studied, there are far fewer studies on the benefits of enhancing the thermal conductivity of solid insulation. Xiao and Du [30] showed that using BN-filled epoxy composites in cast resin transformers resulted in a more uniform temperature distribution than in conventional transformers. The present work is the first study which predicts the extent to which tuning the thermal conductivity of paper can enhance transformer life.
High thermal conductivity papers have been inspired by significant recent advances in the synthesis of electrically insulating but thermally conducting nanocomposite materials [[31], [32], [33]]. Such papers are synthesized by incorporating high thermal conductivity nanoparticles (e.g., boron nitride) in a cellulosic matrix. Studies [[34], [35], [36]]] have reported in-plane thermal conductivities which are 100X higher than the conductivity of baseline paper (0.2 W/mK); this is primarily a consequence of the very high thermal conductivity of boron nitride (2000 W/mK [34]). Such high values of in-plane thermal conductivity aid in lateral spreading of heat. The enhancement in out-of-plane thermal conductivity is lower than the enhancement in in-plane thermal conductivity. However, the out-of-plane thermal conductivity is still much higher than that of baseline paper (0.2 W/mK). It is noted that very high values of thermal conductivity are achieved using continuous or nearly continuous boron nitride, which will degrade the electrical properties. Therefore, this research focuses on the benefits of modest improvements in thermal conductivity (<10 W/mK), which are more likely to be achievable while maintaining adequate electrical performance.
2. Approach in this study
The benefit of lower temperatures on life enhancement can be quantified by assessing the degree of polymerization (DP) of the paper, which is the average number of glucose molecules in the cellulose chain [4]. DP decreases as the paper degrades. The reduction in DP depends on the temperature and time, and can be quantified using Arrhenius relation (Eqn. (1)) [14,[37], [38], [39]] as:
| (1) |
where is the initial degree of polymerization, is the degree of polymerization at a subsequent time t, R is gas constant and T is temperature. Using this model requires estimates of two kinetics-related parameters A and Ea. Ea is the activation energy of the degradation reaction (oxidation, hydrolysis, pyrolysis) and A is the pre-exponential factor, which determines the rate of reaction for the given activation energy and temperature. Fresh paper is considered in many studies as having a DP value of 1000–2000 [12,38,40]; the paper is considered as having reached end of life when the DP value reaches 200. Equation (1) can be used in conjunction with DP measurements to predict the remaining useful life of the transformer. Another approach to assessing the suitability of paper involves measuring the tensile strength [[41], [42], [43]], which is a parameter related to DP.
There are commercial approaches to assessing and monitoring the health of transformers in situ. Dissolved gas analysis of transformer oil is a commonly used non-destructive method for real-time health monitoring and fault diagnosis [[44], [45], [46], [47]]. Paper degradation can also be tracked via CO2/CO ratio analysis or furan analysis of the oil [39,46]. Yet another approach to track the life of paper is the measurement of partial discharges in the transformer [48]. Importantly, as improved materials including those incorporating nanotechnology and non-mineral oils are adopted, the chemical kinetics change requiring reassessment of the applicability of standard tests used in legacy systems. In this study, DP estimates are used to assess the health of paper, for lack of a more compelling metric.
The present research is a first-ever thermal assessment of the benefits of high thermal conductivity papers on transformer life. To use the published relationship between transformer temperature and life, it is first necessary to determine the influence of the thermal conductivity of the paper on hotspot temperature. This study uses a 3D heat transfer model of a transformer to support this determination. To validate the modeling, temperature predictions from the model are validated by experiments that measure internal temperatures at several points in a single-phase transformer. The validated model is then used to predict the hot spot temperature.
The hot spot temperature is used to estimate transformer life enhancement based on the decay in DP of the paper. This research focuses on the hottest point in the windings where thermal degradation is most rapid. However, the benefits of higher thermal conductivity (and lower internal temperatures) will also be seen in other insulation failure modes, e.g., failure at points of maximum electrical stress. This manuscript does not discuss the composition and processing of nanoparticle-based papers that can achieve the desired thermal conductivity (that development is currently in progress). Rather, the focus is on identifying a target for the novel paper performance by quantifying thermal properties that increase transformer life.
Equation (1) shows that DP reduction (and therefore life) is strongly temperature dependent. There are modeling approaches to predict self-heating and internal temperatures of power transformers under load. The IEEE Loading Guide [12] provides a dynamic semi-empirical model to determine temperature changes in the transformer under daily loading cycles. However, inputs to this model include average winding temperature and top-oil temperature [12], which reduces the model's utility. Thermal hydraulic network models solve heat transfer and fluid flow equations between various points in the transformer using an electrical capacitance-resistance analogy. This method has been used by many researchers due to its simplicity and low computational cost [[49], [50], [51], [52], [53], [54], [55]]. However, this approach, by itself is not sufficient to develop the 3D thermal map of the transformer required for hot spot temperature estimations.
At the more precise end of the computational spectrum, a common approach employs Computational Fluid Dynamics (CFD) models for thermal analysis [50,[56], [57], [58], [59], [60], [61], [62], [63]]. While CFD will support detailed transformer designs which use the novel papers, good estimates of the benefits of thermally conducting papers can be obtained using less detailed modeling. Presently, a CFD-based approach was judged to be unnecessary for assessing the influence of the thermal conductivity of paper on transformer life.
3. Description of thermal model of transformer
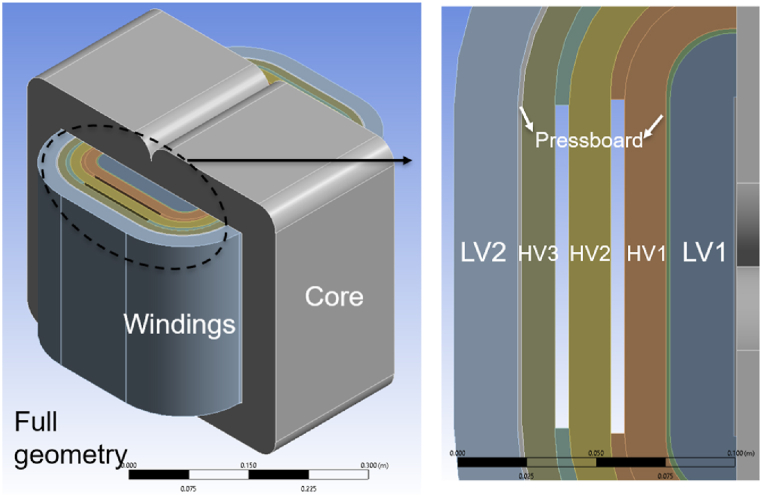
The starting point was the measurement of the geometry of a single-phase 75 kVA, oil-filled transformer. These measurements underpinned a 3D thermal model (Fig. 1) of the transformer interior using the finite element analysis software ANSYS. The key advancement being studied is the impact of high thermal conductivity paper; this was captured via analytical estimates of the thermal resistance of high and low voltage windings (detailed ahead). To reduce the computational cost, a quarter of the full-scale geometry was considered, assuming an axisymmetric temperature distribution. The bulk oil temperature was assumed to be uniform. While this is an approximation, the agreement between the theoretical and experimental measurements shows that the assumption does not likely significantly affect the value of the computed hot spot temperature. A non-uniform oil temperature will significantly influence the hot spot temperature only if there is a significant temperature gradient within the oil, which was not observed experimentally (as detailed ahead).
Fig. 1.
(a) Overview of 3D model of transformer, and (b) schematic depiction of high voltage (HV) and low voltage (LV) windings.
Convective heat transfer correlations were the basis for the model of the heat transfer from the hot surfaces to the oil. Temperature variations within the boundary layer of the fluid side were captured using these convection correlations. Four different correlations were used for the vertical, upper surface (hot side facing up in correlation), lower surface (hot side facing down in correlation), and the narrow vertical duct between the high voltage (HV) windings. All these correlations are provided in the Appendix. Convection coefficients were pre-evaluated for the temperature range of interest and input in the model. Uniform volumetric heat generation was assigned to the windings and core and was calculated from ohmic and core loss measurements of the transformer (stray losses were not included). Total heat generation inside the transformer at full rated load was 887 W, with the ohmic and core losses accounting for 802 W and 85 W, respectively.
High voltage (HV) and low voltage (LV) windings were modeled as bulk materials with an equivalent thermal conductivity (). The LV winding consists of paper-insulated aluminum conductors. The HV winding is a polymer-coated aluminum conductor (magnet wire) and pressboard. Pictures of these layers are included in the Appendix for greater clarity on the thermal modeling approach.
The equivalent thermal resistance of the winding is calculated in both cylindrical and axial directions. The conductor and the insulation layers are connected in series (Eqn. (2)) and parallel (Eqn. (3)) in the cylindrical and axial directions, respectively. The equivalent thermal resistance in each direction is estimated as:
| (2) |
| (3) |
The thermal resistances in radial (Eqn. (4)) and axial directions (Eqn. (5)) are estimated as:
| (4) |
| (5) |
where and are the outer and inner radii of the individual layers, L is the axial length of the layer, and is the thermal conductivity of the layer. A similar equation can be used with total outer and inner radius and to find .
The thicknesses (measured) and thermal conductivities of individual layers are tabulated in Table 1. There are 16 conductors and 17 paper turns in each LV winding (LV1 and LV2). 12 polymer-coated aluminum wire and 13 pressboard turns are used in the HV winding. The HV winding is also divided into 3 concentric sections, which are 0.5 cm apart (see subspace in Appendix). The equivalent thermal conductivity of the magnet wire is calculated as 21.9 W/mK. Using this information, the equivalent thermal conductivity of LV and HV windings in the radial direction was calculated as 0.58 W/mK and 0.54 W/mK, respectively. Similarly, the equivalent thermal conductivity of LV and HV windings in the axial direction was calculated as 156.1 W/mK and 13.5 W/mK, respectively. Based on the above inputs, the model computed the steady-state temperature in the internal regions of the transformer. A mesh independence study verified the adequacy of the selected mesh size.
Table 1.
Key parameters of individual layers in the LV and HV Windings.
| Name | Material | Thickness (mm) | Thermal conductivity (W/mK) |
|---|---|---|---|
| LV paper | Kraft paper | 0.4 | 0.2 |
| LV conductor | Aluminum | 0.8 | 239 |
| HV paper | Pressboard | 1 | 0.2 |
| HV wire conductor | Aluminum | 2.3 | 239 |
| HV wire coating | poly(phenyl sulfone) | 0.1 | 0.35 |
4. Experimental Validation- temperature measurements inside a transformer under load
This section describes experiments conducted to validate the model, which involved temperature measurements inside a transformer under load. K-type twisted-shielded thermocouples (TC) measured the temperature of the top-oil, side-oil, HV and LV windings, core, and casing. Fig. 2 schematically shows the locations of temperature measurements. Preliminary analysis suggested that the hot spot would be within the HV windings.
Fig. 2.
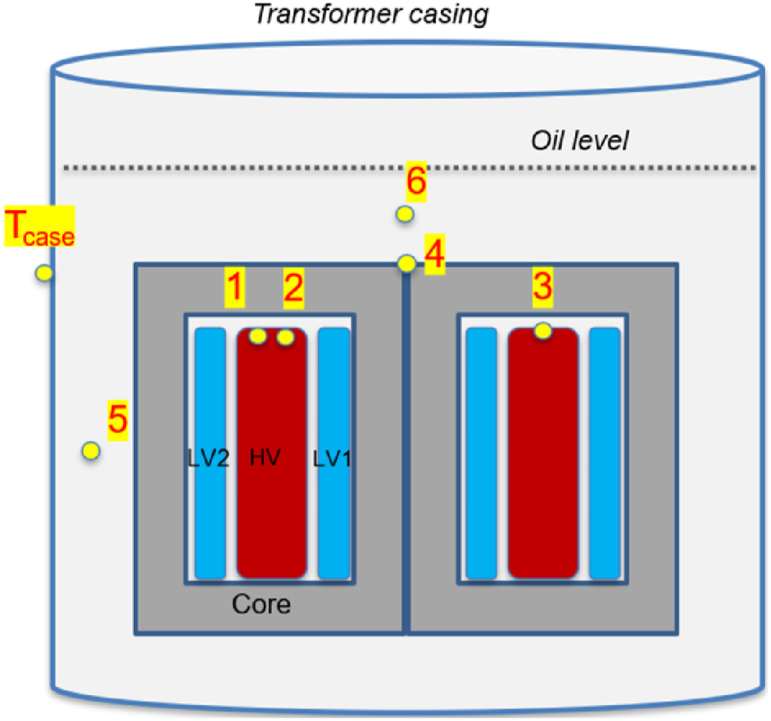
Schematic showing the locations of thermocouples inside the transformer.
Three thermocouples were used for measuring HV winding temperatures, one of which was used to validate the symmetrical condition of the transformer (T3 is at the symmetry location of T2). Thermocouples T4, T5 and T6 were used for core, side-oil, and top-oil temperatures, respectively. All TCs used for winding and core were attached to the surfaces using high thermal conductivity cement. All thermocouple tips were isolated using a thin Kapton tape and oil-resistant heat-shrink tubing to protect the data acquisition system from high voltage. All thermocouples were connected to an HV-rated signal conditioner to improve the signal quality and provide electrical isolation.
The transformer was energized at rated load (75 kW) for 8 h. Heat-run tests to validate transformer performance are typically conducted for 24 h. Eight hours were sufficient to extrapolate for the steady-state temperature since the purpose of the experiment was to validate the applicability of the model and not to provide complete characterization of the transformer. Fans cooled the load resistors to keep the temperatures of the resistors constant. Voltage and current at the secondary and primary side of the transformer was recorded every 30 min to estimate the load and calculate the total loss in the transformer. The real power was calculated by averaging the product of the voltage and current waveforms. Thermocouple readings were sampled every 10 s. For each measurement, 20 data points were collected to assess the precision uncertainty of the measurements. Within the first 10 min after de-energizing the transformer, the resistances of LV and HV windings were measured multiple times.
5. Results and discussion
5.1. Results from experiments
5.1.1. Load profile and loss calculations
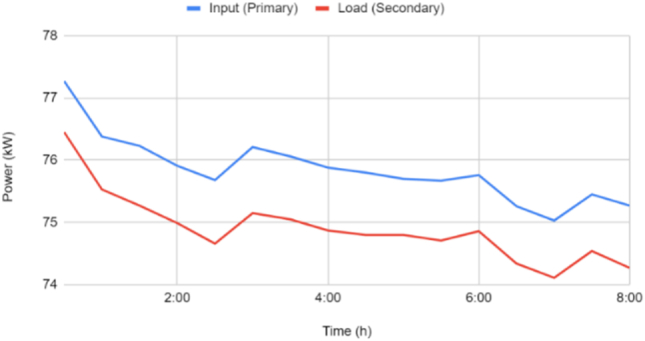
Input and load power profiles during the 8-h experiment are included in the Appendix. On average, the load power was 74.9 kVA, which is near a 100% rating. The power fluctuated due to changes in the temperature of the load resistors and the voltage provided by the grid. The average total loss was calculated to be 950 W; this includes ohmic losses in the windings, core losses, and stray losses. Ohmic losses were calculated based on current and hot wire resistance measurements (i2R). The resistance measurements were extrapolated to the time at shutdown, and were 0.414 Ω, 1.838 mΩ, and 2.187 mΩ for the primary side (HV), first half of the secondary side (LV1), and second half of secondary side (LV2), respectively.
A no-load test was conducted to find the core loss by opening the load side of the transformer. Based on two no-load tests, the core loss was estimated as ∼85W neglecting the no-load ohmic losses. In a transformer with no moving parts, it is reasonable to assume the stray loss to be approximately 0.55 W/kW, which yields ∼41W of stray loss (note that this was not included in the model). All losses are tabulated in Table 2. Total losses add up to 928.1W, which is within 5% of the total measured loss of 950 W.
Table 2.
Decomposition of losses in the transformer.
| Type | Value |
|---|---|
| Ohmic loss, HV | 413.4 W |
| Ohmic loss, LV | 388.7 W |
| Core loss | 85 W |
| Stray loss | 41 W |
| Total loss (calculated) | 928.1 W |
| Total loss (measured) | 950 W |
5.1.2. Temperature measurements
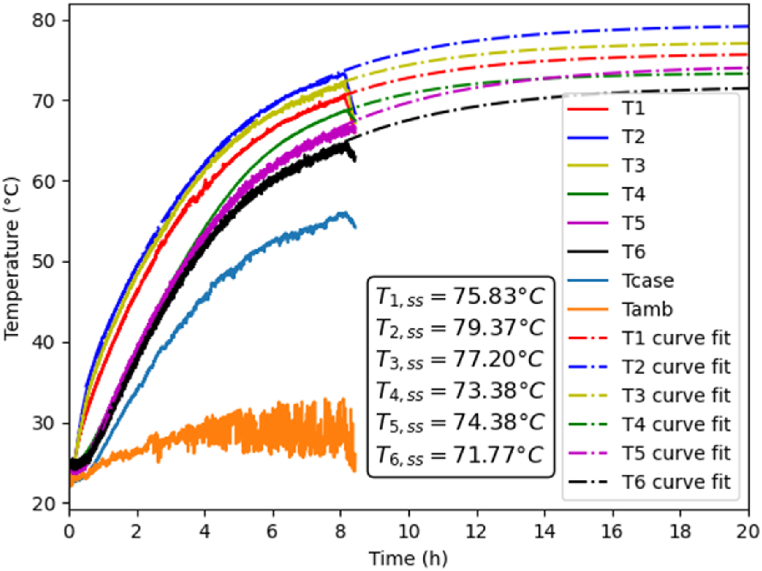
Fig. 3 shows the measured temperatures inside the transformer. The highest temperatures were observed on T2 and T3, which are on the HV winding. Since steady state was not reached in 8 h, the obtained data was extrapolated. A functional form of was used for each temperature profile; this choice is based on the exponential decay in temperature as per the classical lumped capacitance model for transient cooling. Curve fitting was conducted to estimate the constants a, b, c (detailed in Appendix). Although the same functional form is used for all temperatures, values of the constants for each thermocouple were allowed to be different. Note that c is the steady-state temperature. The ambient temperature during the experiment fluctuated from 23 to 28 °C with an average ambient temperature of 23.8 °C. Although the ambient temperature does fluctuate, the thermal inertia of the transformer is large enough to be unaffected by short-term fluctuations. The core temperature was always lower than the winding temperatures, which is expected. T1 and T3 readings were higher than the core and oil temperatures. The difference between T2 and T3 was only 2 °C, which justifies the symmetry assumption of the system. The side oil temperature is 3.5 °C higher than the top oil temperature, which may be due to the side oil sensor being affected by the thermal boundary layer of the hot surface.
Fig. 3.
Temperature-time plots at various locations inside the transformer.
5.2. Modeling results
Results from the modeling are summarized in Table 3, which shows the predicted temperatures at the locations of four of the six thermocouples, along with the measured temperatures. Overall, the predictions and the experiments agree. It is noted that the model solves for the temperature distribution in the interior of the transformer based on a symmetry assumption and uniform oil temperature. There are two choices for the oil temperature to be used in the model. Since the side-oil temperature measurement can be affected by the boundary layer associated with the windings, the measured top-oil temperature was used as the input to the computational model. The model is symmetric, which implies that T2 and T3 will have similar values; this was confirmed by the measurements. The uncertainty of the thermocouples is 1 °C, which means that the difference between the measurements and predictions are within the 2σ uncertainty range. The only exception is the core temperature, which is overestimated by 3.5 °C in the ANSYS model. This discrepancy could be due to the core thermocouple not being intimately attached to the surface and reading a temperature in between that of the surface and the oil. The curve fitting constants for the core temperature curve were also significantly different than the constants for other locations.
Table 3.
Comparison of temperatures predicted by the model with experimental results.
| Data | Location | Results from experiment (°C) | Results from ANSYS modeling (°C) |
|---|---|---|---|
| T1 | HV | 75.8 | 75.8 |
| T2 | HV | 79.4 | 80.6 |
| T3 | HV | 77.2 | 80.6 |
| T4 | Core | 73.9 | 77.2 |
| T5 | Side oil | 74.4 | Not used |
| T6 | Top oil | 71.8 | Input |
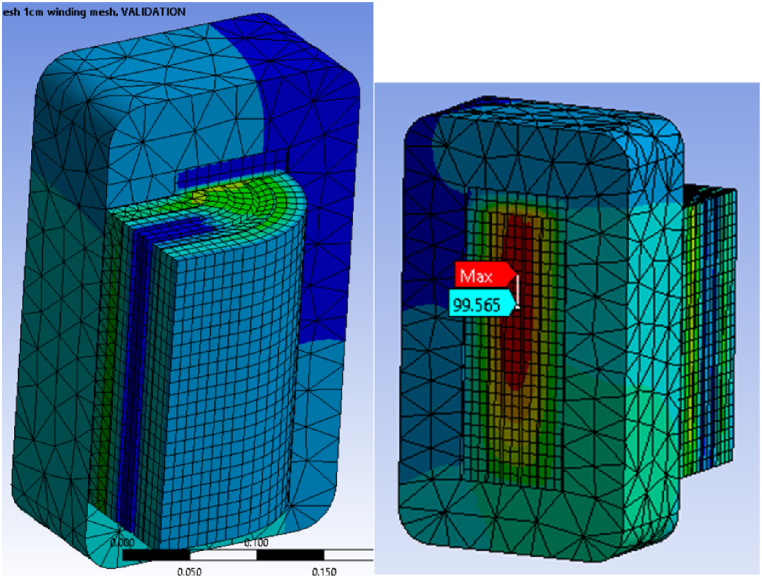
An illustrative temperature contour plot from the simulations is presented in Fig. 4. Temperatures are higher in the inner parts of the HV winding compared to the LV winding or the core. The vertical duct within the HV winding has a cooling effect. A maximum temperature of 99.5 °C was obtained in the HV windings. The location of the hot-spot temperature is indicated in Fig. 4; the hot spot is on the HV winding, where it is between the core region and at the halfway height of the windings. Overall, the experiments validated the model, which was subsequently used to study the impact of the thermal conductivity of paper.
Fig. 4.
(Left) Contour plot showing temperature contours inside the transformer, and (right) location of the hot spot.
5.3. Impact of high thermal conductivity paper
5.3.1. Impact on hot-spot temperature
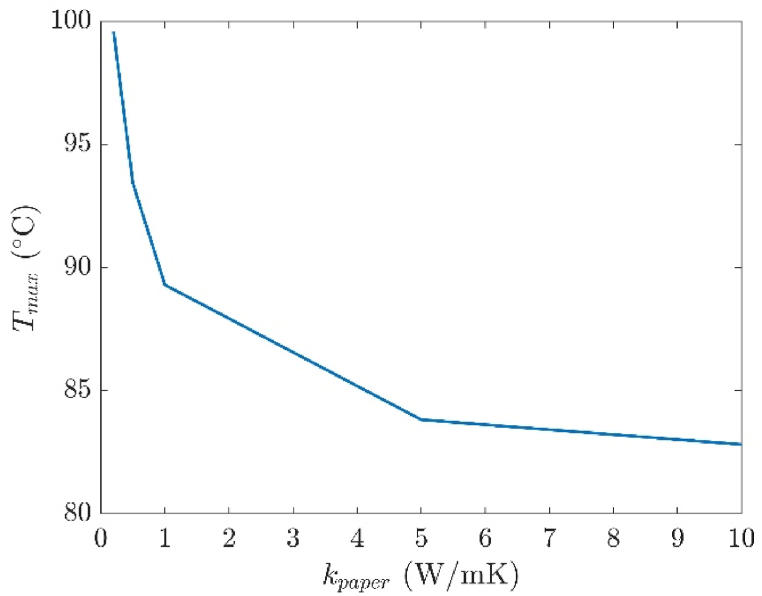
The model was used to predict the hot-spot temperature for assumed values of thermal conductivity of paper (0.5, 1, 5, and 10 W/mK). These are realistic values, as per recent literature [34]. Increasing the thermal conductivity of paper increases the equivalent thermal conductivity of the windings, as tabulated in the Appendix. Fig. 5 shows the change in hot spot temperature as a function of the thermal conductivity of the paper. The hot spot temperature was reduced by 10° for a thermal conductivity increase from 0.2 to 1 W/mK. Importantly, this plot suggests that there are only marginal benefits in increasing the thermal conductivity above 5 W/mK. This is a significant finding and is one of the factors that will determine the loading fraction of nanoparticles in the paper.
Fig. 5.
Dependence of hot-spot temperature inside transformer on thermal conductivity of paper.
5.3.2. Impact on life of paper
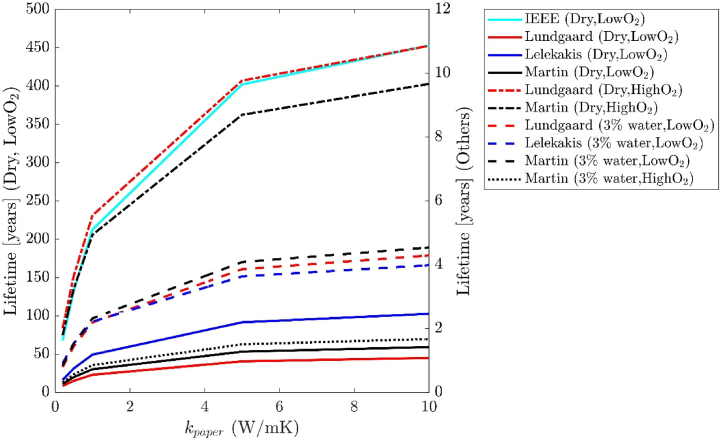
Reduction in hot spot temperature increases the life of the transformer by reducing the rate at which the paper degrades, as tracked by the decrease in the degree of polymerization (DP) of paper, per Equation (1). The hot spot temperature determined by the thermal model was used as the input in Equation (1). Additionally, values for kinetics-related parameters A (pre-exponential factor) and Ea (activation energy) are required to use this model. There are multiple studies that provide values of these parameters; a compilation is provided in Table 4. The values of these parameters are very sensitive to the H2O content of the paper and the oil, and the amount of oxygen in oil.
Table 4.
Summary of parameters and results of the life estimation model.
| Reference | H2O | O2 | Ea (J/mol) | A (1/h) | Lifetime at 110 °C (years) |
|---|---|---|---|---|---|
| IEEE Guide C.57.91–2011 [12] | Dry | Low | 1.25E+05 | 2.26E+09 | 22.57 |
| Lundgaard (2004) [64] | 0.5% wt | Low | 1.11E+05 | 2.00E+08 | 3.14 |
| Lelekakis (2012) [38] | 0.5% wt | Low | 1.21E+05 | 2.58E+09 | 5.63 |
| Martin et.al. (2015) [37] | 0.5% wt | Low | 1.11E+05 | 1.52E+08 | 4.13 |
| Lundgaard (2004) [64] | 0.5% wt | High | 1.11E+05 | 8.30E+08 | 0.76 |
| Martin et.al. (2015) [37] | 0.5% wt | High | 1.11E+05 | 9.32E+08 | 0.67 |
| Lundgaard (2004) [64] | 3–4% wt | Low | 1.11E+05 | 2.10E+09 | 0.3 |
| Lelekakis (2012) [38] | 3% wt | Low | 9.70E+04 | 1.99E+07 | 0.39 |
| Martin et.al. (2015) [37] | 3% wt | Low | 1.11E+05 | 1.98E+09 | 0.32 |
| Martin et.al. (2015) [37] | 3% wt | High | 1.11E+05 | 5.38E+09 | 0.12 |
The last column of Table 4 shows the estimated lifetime as per predictions of the life model, based on and , with a constant hot-spot temperature of 110 °C. One of the key observations from the compilation in Table 4 is the wide discrepancy in predicted life, resulting from the large variation in kinetics parameters reported in literature. The IEEE C57.91 guide [12] is widely used for evaluating the insulation paper lifetime; the expected life is 22.5 years at a hot-spot temperature of 110 °C. However, the kinetics parameters determined via lab experiments by other researchers yield much lower estimates for life (3–6 years) in dry and low oxygen conditions [37,38,64]. Both oxygen and H2O content accelerate degradation of the paper, thereby reducing life. It is seen that the influence of H2O content on degradation is higher than the influence of oxygen. For high O2 and H2O content, the expected life can be as short as 3–4 months. Although transformers are dried and many transformers are sealed during operation, any imperfections in these steps or higher temperatures can result in early insulation failure. While control of moisture (e.g., through desiccant breathers) and oxygen can be challenging, reducing the hot spot temperature is a very attractive option to increase life.
Next, the life prediction model was used with the hot spot temperature predictions of the ANSYS model and the kinetic parameters of Table 4, to quantify the influence of high thermal conductivity paper on life; results are shown in Fig. 6. As expected, the predicted life varies widely based on moisture and oxygen conditions. Lifetime estimations for dry and low oxygen content are plotted on the left axis; estimations for other conditions are plotted on the right axis. It is seen that for all conditions, the life is doubled upon increasing the thermal conductivity of paper from 0.2 to 0.5 W/mK and tripled upon increasing the thermal conductivity to 1 W/mK. In ideal conditions (dry and low oxygen) with W/mK, the life estimate can be as high as 400 and 100 years, based on kinetics parameters reported by IEEE Guide [10] and Lelekakis et al. 6, respectively. It is noted that the increase in life is not very significant after W/mK. While it is not possible to exactly quantify the increase in life (unless the oxygen and moisture content is accurately known), enhancing the thermal conductivity of paper increases the life significantly for all conditions.
Fig. 6.
Dependence of life of transformer on thermal conductivity of paper (for various levels of oxygen and moisture in the environment).
6. Conclusions
Modeling predicts that higher thermal conductivity insulation papers increase transformer life via reduction of hot spot temperatures. Increasing the thermal conductivity from 0.2 W/mK (existing oil-impregnated paper) to 1 W/mK can triple the life under some conditions. A steady-state thermal model was used in this determination of feasibility. This can be extended to a transient model, where the hot-spot fluctuates based on daily loading cycles and ambient temperatures to achieve higher precision in the life estimates.
Transformer life, however, depends critically on the moisture and oxygen content. It is therefore vital to characterize degradation kinetics for the expected operating conditions. It is also noted that degradation kinetics could change for a different type of oil, noting that a transition away from mineral oil to ester-based oils is underway.
While high thermal conductivity of paper is a very beneficial attribute for transformers, such papers also need to have similar or better tensile strength, dielectric strength, relative permittivity, and voltage endurance, compared to conventional papers, and be amenable to large scale processing. Stability and interactions of paper-nanoparticles-fluids at elevated temperatures need to be characterized to ensure reliable predictions of life. Finally, for this concept to make its way to the market, the economics need to be favorable. This study highlights the potential benefits of high thermal conductivity paper, thereby justifying future research on this topic.
CRediT authorship contribution statement
S. Bilyaz: Writing – review & editing, Writing – original draft, Software, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. A. Bhati: Validation, Methodology, Investigation, Formal analysis. M. Hamalian: Investigation. K. Maynor: Investigation. T. Soori: Writing – review & editing, Investigation, Formal analysis. A. Gattozzi: Validation, Supervision, Methodology, Investigation, Formal analysis. C. Penney: Supervision, Methodology, Investigation. D. Weeks: Investigation. Y. Xu: Writing – review & editing, Validation, Formal analysis. L. Hu: Supervision, Funding acquisition. J.Y. Zhu: Validation, Supervision. J.K. Nelson: Writing – review & editing, Writing – original draft, Validation, Methodology, Conceptualization. R. Hebner: Writing – review & editing, Writing – original draft, Validation, Supervision, Project administration, Methodology, Funding acquisition, Conceptualization. V. Bahadur: Writing – review & editing, Writing – original draft, Validation, Supervision, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Conceptualization.
Declaration of competing interest
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests:Robert Hebner reports financial support was provided by ARPA-E.
Acknowledgments
The information, data, or work presented herein was funded in part by the Advanced Research Projects Agency-Energy (ARPA-E, U.S. Department of Energy, under Award Number DE-FOA-0001953. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. The authors would also like to acknowledge personnel at Center for Electromechanics at UT Austin for assistance with experimental characterization and other aspects of this project (John Hahne, Claude Pullen, Shannon Strank). The authors also acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing high performance computing resources that have contributed to the research results reported in this paper.
Footnotes
This work was supported by the Advanced Research Projects Agency-Energy (ARPA-E, U.S. Department of Energyy, under Award Number DE-FOA-0001953.
APPENDIX.
Fig. A1.

Instrumented 75kVA single-phase transformer, prior to experiments.
Fig. A2.
Interior of the 75 kVA transformer..
Fig. A3.

Solid model of the interior of the transformer..
Fig. A4.
Details of winding layers (Left: HV winding, Right: LV winding)..
Fig. A5.
Power at primary and secondary side of transformer during loading..
Table A1.
Constants of the curve fit (c is also the steady-state temperature).
| Data | a | b | c (Tss) [°C] |
|---|---|---|---|
| T1 | 45 | 7.84e-5 | 75.8 |
| T2 | 45 | 7.52e-5 | 79.4 |
| T3 | 44.5 | 8.03e-5 | 77.2 |
| T4 | 8.67 | 8.95e-5 | 73.4 |
| T5 | 45.4 | 7.01e-5 | 74.4 |
| T6 | 43.6 | 7.16e-5 | 71.8 |
Table A2.
Summary of parametric study. the 1st column shows various values of thermal conductivity of paper. The 2nd-5th columns show equivalent thermal conductivities in various parts of the transformer. the last column shows the resulting hot-spot temperatures.
| kpaper (W/mK) | LV keq,r (W/mK) | LV keq,z (W/mK) | HV keq,r (W/mK) | HV keq,z (W/mK) | Tmax (°C) |
|---|---|---|---|---|---|
| 0.2 | 0.58 | 156.1 | 0.54 | 13.5 | 99.5 |
| 0.5 | 1.43 | 156.3 | 1.18 | 13.6 | 93.4 |
| 1 | 2.86 | 156.4 | 1.94 | 13.8 | 89.3 |
| 5 | 13.8 | 157.8 | 4.02 | 15.1 | 83.8 |
| 10 | 26.7 | 159.5 | 4.64 | 16.8 | 82.8 |
-
I
. Convection correlations used in the model
Natural convection from a vertical plate:
Natural convection from a horizontal plate facing up:
Natural convection from a horizontal plate facing down:
In the above correlations, Rayleigh number is defined as:
Natural convection from vertical channel
where S is spacing between plates and L is length of channel. Fluid properties are evaluated at the average of and .
References
- 1.Dumas M., Binita K.C., Cunliff C.I. Oak Ridge National Lab.(ORNL); Oak Ridge, TN (United States): 2019. Extreme Weather and Climate Vulnerabilities of the Electric Grid: A Summary of Environmental Sensitivity Quantification Methods,” No. ORNL/TM-2019/1252. [Google Scholar]
- 2.Panteli M., Mancarella P. Modeling and evaluating the resilience of critical electrical power infrastructure to extreme weather events. IEEE Syst. J. 2015;11(3):1733–1742. doi: 10.1109/JSYST.2015.2389272. [DOI] [Google Scholar]
- 3.Ward D.M. The effect of weather on grid systems and the reliability of electricity supply. Climatic Change. 2013;121(1):103–113. doi: 10.1007/s10584-013-0916-z. [DOI] [Google Scholar]
- 4.Metwally I. Failures, monitoring and new trends of power transformers. IEEE Potentials. May 2011;30(3):36–43. doi: 10.1109/MPOT.2011.940233. [DOI] [Google Scholar]
- 5.Aj C., Salam M.A., Rahman Q.M., Wen F., Ang S.P., Voon W. Causes of transformer failures and diagnostic methods – a review. Renew. Sustain. Energy Rev. Feb. 2018;82:1442–1456. doi: 10.1016/j.rser.2017.05.165. [DOI] [Google Scholar]
- 6.Electric Grid Supply Chain Review: Large Power Transformers and High Voltage Direct Current Systems. USDOE Office of Policy; Feb. 2022. [Google Scholar]
- 7.Nanotechnology-Enabled Transformer Life Extension.” Accessed: Oct. 08, 2022. [Online]. Available: https://arpa-e.energy.gov/technologies/projects/nanotechnology-enabled-transformer-life-extension.
- 8.Uriarte F.M., Toliyat A., Kwasinski A., Hebner R.E. Consumer-data approach to assess the effect of residential grid-tied photovoltaic systems and electric vehicles on distribution transformers. IEEE 5th international symposium on power electronics for distributed generation systems (PEDG), Jun 24. 2014:1–8. 2014. [Google Scholar]
- 9.Gray M.K., Morsi W.G. On the role of prosumers owning rooftop solar photovoltaic in reducing the impact on transformer's aging due to plug-in electric vehicles charging. Elec. Power Syst. Res. 2017 1;143:563–572. [Google Scholar]
- 10.Rafiq M., Shafique M., Azam A., Ateeq M. The impacts of nanotechnology on the improvement of liquid insulation of transformers: emerging trends and challenges. J. Mol. Liq. Mar. 2020;302 doi: 10.1016/j.molliq.2020.112482. [DOI] [Google Scholar]
- 11.McShane C.P., Gauger G.A., Luksich J. Fire resistant natural ester dielectric fluid and novel insulation system for its use. 1999 IEEE Transmission and Distribution Conference (Cat. No. 99CH36333) 1999;2:890–894. [Google Scholar]
- 12.IEEE IEEE Guide for Loading Mineral-Oil-Immersed Transformers and Step-Voltage Regulators. March. 2012;2011:172. [Google Scholar]
- 13.Frimpong G., Oommen T., Asano R. A survey of aging characteristics of cellulose insulation in natural ester and mineral oil. IEEE Electr. Insul. Mag. Sep. 2011;27(5):36–48. doi: 10.1109/MEI.2011.6025367. [DOI] [Google Scholar]
- 14.Ariannik M., Razi-Kazemi A.A., Lehtonen M. An approach on lifetime estimation of distribution transformers based on degree of polymerization. Reliab. Eng. Syst. Saf. June 2019;198 doi: 10.1016/j.ress.2020.106881. 106881–106881, 2020. [DOI] [Google Scholar]
- 15.Transformer reliability survey–interim report. Electra. 2012;261:46–49. [Google Scholar]
- 16.Tenbohlen S., Jagers J., Vahidi F. 2017 International Symposium on Electrical Insulating Materials (ISEIM) Toyohashi; Sep. 2017. Standardized survey of transformer reliability: on behalf of CIGRE WG A2.37; pp. 593–596. [DOI] [Google Scholar]
- 17.Zhang X., Gockenbach E. Asset-management of transformers based on condition monitoring and standard diagnosis [feature article] IEEE Electr. Insul. Mag. Jul. 2008;24(4):26–40. doi: 10.1109/MEI.2008.4581371. [DOI] [Google Scholar]
- 18.Bartley W.H. Annual Conference of International Association of Engineering Insurers--Stockholm; 2003. Analysis of Transformer Failures. presented at the 36th. [Google Scholar]
- 19.Kiiza R., Niasar M., Nikjoo R., Wang X., Edin H. Change in partial discharge activity as related to degradation level in oil-impregnated paper insulation: effect of high voltage impulses. IEEE Trans. Dielectr. Electr. Insul. Jun. 2014;21(3):1243–1250. doi: 10.1109/TDEI.2014.6832271. [DOI] [Google Scholar]
- 20.Medina R.D., Romero A.A., Mombello E.E., Rattá G. Assessing degradation of power transformer solid insulation considering thermal stress and moisture variation. Elec. Power Syst. Res. Oct. 2017;151:1–11. doi: 10.1016/j.epsr.2017.04.006. [DOI] [Google Scholar]
- 21.McShane C.P., Rapp K.J., Corkran J.L., Gauger G.A., Luksich J. Aging of paper insulation in natural ester dielectric fluid. 2001 IEEE/PES Transmission and Distribution Conference and Exposition. Developing New Perspectives (Cat. No. 01CH37294) 2001;2:675–679. [Google Scholar]
- 22.Zhu J., Pan X. Efficient sugar production from plant biomass: current status, challenges, and future directions. Renew. Sustain. Energy Rev. 2022;164 [Google Scholar]
- 23.McNutt W.J. Insulation thermal life considerations for transformer loading guides. IEEE Trans. Power Deliv. Jan. 1992;7(1):392–401. doi: 10.1109/61.108933. [DOI] [Google Scholar]
- 24.Rafiq M., Lv Y., Li C. A review on properties, opportunities, and challenges of transformer oil-based nanofluids. J. Nanomater. 2016;2016 doi: 10.1155/2016/8371560. [DOI] [Google Scholar]
- 25.Amin D., Walvekar R., Khalid M., Vaka M., Mubarak N.M., Gupta T.C.S.M. Recent progress and challenges in transformer oil nanofluid development: a review on thermal and electrical properties. IEEE Access. 2019;7:151422–151438. doi: 10.1109/ACCESS.2019.2946633. [DOI] [Google Scholar]
- 26.Zhang Y., Ho S., Fu W. Heat transfer comparison of nanofluid filled transformer and traditional oil-immersed transformer. AIP Adv. May 2018;8(5) doi: 10.1063/1.5006749. [DOI] [Google Scholar]
- 27.Primo V.A., Garcia B., Albarracin R. Improvement of transformer liquid insulation using nanodielectric fluids: a review. IEEE Electr. Insul. Mag. 2018;34(3):13–26. [Google Scholar]
- 28.Santisteban A., Delgado F., Ortiz A., Fernández I., Renedo C., Ortiz F. Numerical analysis of the hot-spot temperature of a power transformer with alternative dielectric liquids. IEEE Trans. Dielectr. Electr. Insul. 2017;24(5):3226–3235. [Google Scholar]
- 29.Patel J., Parekh K., Upadhyay R. Prevention of hot spot temperature in a distribution transformer using magnetic fluid as a coolant. Int. J. Therm. Sci. 2016;103:35–40. [Google Scholar]
- 30.Xiao M., Du B.X. Review of high thermal conductivity polymer dielectrics for electrical insulation. High Volt. Apr. 2016;1(1):34–42. doi: 10.1049/hve.2016.0008. [DOI] [Google Scholar]
- 31.Nelson J.K., Hu Y. Nanocomposite dielectrics—properties and implications. J. Phys. D Appl. Phys. Jan. 2005;38(2):213–222. doi: 10.1088/0022-3727/38/2/005. [DOI] [Google Scholar]
- 32.Schadler L.S., Nelson J.K., Calebrese C., Travelpiece A., Schweickart D.L. High temperature breakdown strength and voltage endurance characterization of nanofilled polyamideimide. IEEE Trans. Dielectr. Electr. Insul. Dec. 2012;19(6):2090–2101. doi: 10.1109/TDEI.2012.6396969. [DOI] [Google Scholar]
- 33.Lokanathan M., Acharya P.V., Ouroua A., Strank S.M., Hebner R.E., Bahadur V. Review of nanocomposite dielectric materials with high thermal conductivity. Proc. IEEE. Aug. 2021;109(8):1364–1397. doi: 10.1109/JPROC.2021.3085836. [DOI] [Google Scholar]
- 34.Zhu H., Li Y., Fang Z., Xu J., Cao F., Wan J., Preston C., Yang B., Hu L. Highly thermally conductive papers with percolative layered boron nitride nanosheets. ACS Nano. Apr. 2014;8(4):3606–3613. doi: 10.1021/nn500134m. [DOI] [PubMed] [Google Scholar]
- 35.Zhou L., Yang Z., Luo W., Han X., Jang S., Dai J., Yang B., Hu L. Thermally conductive, electrical insulating, optically transparent bi-layer nanopaper. ACS Appl. Mater. Interfaces. 2016;8(42):28838–28843. doi: 10.1021/acsami.6b09471. [DOI] [PubMed] [Google Scholar]
- 36.Yang Z., Zhou L., Luo W., Wan J., Dai J., Han X., Fu K., Henderson D., Yang B., Hu L. Thermally conductive, dielectric PCM–boron nitride nanosheet composites for efficient electronic system thermal management. Nanoscale. 2016;8(46):19326–19333. doi: 10.1039/c6nr07357c. [DOI] [PubMed] [Google Scholar]
- 37.Martin D., Cui Y., Ekanayake C., Ma H., Saha T. An updated model to determine the life remaining of transformer insulation. IEEE Trans. Power Deliv. Feb. 2015;30(1):395–402. doi: 10.1109/TPWRD.2014.2345775. [DOI] [Google Scholar]
- 38.Lelekakis N., Martin D., Wijaya J. Ageing rate of paper insulation used in power transformers Part 1: oil/paper system with low oxygen concentration. IEEE Trans. Dielectr. Electr. Insul. 2012;19(6):1999–2008. doi: 10.1109/TDEI.2012.6396958. [DOI] [Google Scholar]
- 39.Emsley A.M. The kinetics and mechanisms of degradation of cellulosic insulation in power transformers. Polym. Degrad. Stabil. Jan. 1994;44(3):343–349. doi: 10.1016/0141-3910(94)90093-0. [DOI] [Google Scholar]
- 40.Martin D., Cui Y., Saha T., Lelekakis N., Wijaya J. 2013 Australasian Universities Power Engineering Conference (AUPEC) Hobart, Australia; Sep. 2013. Life estimation techniques for transformer insulation; pp. 1–6. [DOI] [Google Scholar]
- 41.Yoshida H., Ishioka Y., Suzuki T., Yanari T., Teranishi T. Degradation of insulating materials of transformers. IEEE Trans. Electr. Insul. 1987;6:795–800. [Google Scholar]
- 42.Emsley A., Heywood R.J., Ali M., Xiao X. Degradation of cellulosic insulation in power transformers. Part 4: effects of ageing on the tensile strength of paper. IEE Proc. Sci. Meas. Technol. 2000;147(6):285–290. [Google Scholar]
- 43.Hill D., Le T., Darveniza M., Saha T. A study of degradation of cellulosic insulation materials in a power transformer. Part 2: tensile strength of cellulose insulation paper. Polym. Degrad. Stabil. 1995;49(3):429–435. [Google Scholar]
- 44.Islam M.M., Lee G., Hettiwatte S.N. A review of condition monitoring techniques and diagnostic tests for lifetime estimation of power transformers. Electr. Eng. 2018;100(2):581–605. doi: 10.1007/s00202-017-0532-4. [DOI] [Google Scholar]
- 45.Bustamante S., Manana M., Arroyo A., Castro P., Laso A., Martinez R. Dissolved gas analysis equipment for online monitoring of transformer oil: a review. Sensors. Sep. 2019;19(19):4057. doi: 10.3390/s19194057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.IEEE Guide for the Interpretation of Gases Generated in Oil-Immersed Transformers,” p. 39.
- 47.Shahsiah A., Degeneff R.C., Nelson J.K. Modeling dynamic propagation of characteristic gases in power transformers oil-paper insulation. IEEE Trans. Dielectr. Electr. Insul. Jun. 2007;14(3):710–717. doi: 10.1109/TDEI.2007.369535. [DOI] [Google Scholar]
- 48.Hussain M.R., Refaat S.S., Abu-Rub H. Overview and partial discharge analysis of power transformers: a literature review. IEEE Access. 2021;9:64587–64605. [Google Scholar]
- 49.Rosillo M.E., Herrera C.A., Jaramillo G. Advanced thermal modeling and experimental performance of oil distribution transformers. IEEE Trans. Power Deliv. Oct. 2012;27(4):1710–1717. doi: 10.1109/TPWRD.2012.2205020. [DOI] [Google Scholar]
- 50.Cotas C., Santos R., Gonçalves N., Quintela M., Couto S., Campelo H., Dias M., Lopes J. Numerical study of transient flow dynamics in a core-type transformer windings. Elec. Power Syst. Res. Oct. 2020;187 doi: 10.1016/j.epsr.2020.106423. [DOI] [Google Scholar]
- 51.Zhang J., Li X. Oil cooling for disk-type transformer windings—Part 1: theory and model development. IEEE Trans. Power Deliv. Jul. 2006;21(3):1318–1325. doi: 10.1109/TPWRD.2006.871019. [DOI] [Google Scholar]
- 52.Zhang J., Li X. Oil cooling for disk-type transformer windings—Part II: parametric studies of design parameters. IEEE Trans. Power Deliv. Jul. 2006;21(3):1326–1332. doi: 10.1109/TPWRD.2006.871018. [DOI] [Google Scholar]
- 53.Zhang J., Li X., Vance M. Experiments and modeling of heat transfer in oil transformer winding with zigzag cooling ducts. Appl. Therm. Eng. Jan. 2008;28(1):36–48. doi: 10.1016/j.applthermaleng.2007.02.012. [DOI] [Google Scholar]
- 54.Susa D., Nordman H. A simple model for calculating transformer hot spot temperature. Power. 2009;24(3):1257–1265. [Google Scholar]
- 55.Susa D., Lehtonen M., Nordman H. Dynamic thermal modelling of power transformers. IEEE Trans. Power Deliv. Jan. 2005;20(1):197–204. doi: 10.1109/TPWRD.2004.835255. [DOI] [Google Scholar]
- 56.Smolka J. CFD-based 3-D optimization of the mutual coil configuration for the effective cooling of an electrical transformer. Appl. Therm. Eng. Jan. 2013;50(1):124–133. doi: 10.1016/j.applthermaleng.2012.06.012. [DOI] [Google Scholar]
- 57.Tenbohlen S., Schmidt N., Breuer C., Khandan S., Lebreton R. Investigation of thermal behavior of an oil-directed cooled transformer winding. IEEE Trans. Power Deliv. Jun. 2018;33(3):1091–1098. doi: 10.1109/TPWRD.2017.2711786. [DOI] [Google Scholar]
- 58.Smolka J., Bíró O., Nowak A.J. Numerical simulation and experimental validation of coupled flow, heat transfer and electromagnetic problems in electrical transformers. Arch. Comput. Methods Eng. Sep. 2009;16(3):319–355. doi: 10.1007/s11831-009-9032-7. [DOI] [Google Scholar]
- 59.Smolka J., Nowak A.J. Experimental validation of the coupled fluid flow, heat transfer and electromagnetic numerical model of the medium-power dry-type electrical transformer. Int. J. Therm. Sci. Oct. 2008;47(10):1393–1410. doi: 10.1016/j.ijthermalsci.2007.11.004. [DOI] [Google Scholar]
- 60.Tian H., Wei Z., Vaisambhayana S., Thevar M., Tripathi A., Kjær P. A coupled, semi-numerical model for thermal analysis of medium frequency transformer. Energies. Jan. 2019;12(2):328. doi: 10.3390/en12020328. [DOI] [Google Scholar]
- 61.Skillen A., Revell A., Iacovides H., Wu W. Numerical prediction of local hot-spot phenomena in transformer windings. Appl. Therm. Eng. Apr. 2012;36:96–105. doi: 10.1016/j.applthermaleng.2011.11.054. [DOI] [Google Scholar]
- 62.Gastelurrutia J., Ramos J.C., Rivas A., Larraona G.S., Izagirre J., del Río L. Zonal thermal model of distribution transformer cooling. Appl. Therm. Eng. Dec. 2011;31(17–18):4024–4035. doi: 10.1016/j.applthermaleng.2011.08.004. [DOI] [Google Scholar]
- 63.Taghikhani M.A., Gholami A. Temperature distribution in ONAN power transformer windings with finite element method. Eur. Trans. Electr. Power. Jul. 2009;19(5):718–730. doi: 10.1002/etep.251. [DOI] [Google Scholar]
- 64.Lundgaard L.E., Hansen W., Linhjell D., Painter T.J. Aging of oil-impregnated paper in power transformers. IEEE Trans. Power Deliv. Jan. 2004;19(1):230–239. doi: 10.1109/TPWRD.2003.820175. [DOI] [Google Scholar]