Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Mar 8;18(11):8029–8037. doi: 10.1021/acsnano.3c11019

Drift of Schottky Barrier Height in Phase Change Materials

Rivka-Galya Nir-Harwood †, Guy Cohen ‡, Amlan Majumdar ‡, Richard Haight ‡, Emanuel Ber †, Lynne Gignac ‡, Efrat Ordan †, Lishai Shoham †, Yair Keller †, Lior Kornblum †, Eilam Yalon †,*
PMCID: PMC10958591  PMID: 38458609

Abstract

graphic file with name nn3c11019_0011.jpg

Phase-change memory (PCM) devices have great potential as multilevel memory cells and artificial synapses for neuromorphic computing hardware. However, their practical use is hampered by resistance drift, a phenomenon commonly attributed to structural relaxation or electronic mechanisms primarily in the context of bulk effects. In this study, we reevaluate the electrical manifestation of resistance drift in sub-100 nm Ge2Sb2Te5 (GST) PCM devices, focusing on the contributions of bulk vs interface effects. We employ a combination of measurement techniques to elucidate the current transport mechanism and the electrical manifestation of resistance drift. Our steady-state temperature-dependent measurements reveal that resistance in these devices is predominantly influenced by their electrical contacts, with conduction occurring through thermionic emission (Schottky) at the contacts. Additionally, temporal current–voltage characterization allows us to link the resistance drift to a time-dependent increase in the Schottky barrier height. These findings provide valuable insights, pinpointing the primary contributor to resistance drift in PCM devices: the Schottky barrier height for hole injection at the interface. This underscores the significance of contacts (interface) in the electrical manifestation of drift in PCM devices.

Keywords: phase change memory, contact resistance, resistance drift, Schottky barrier height, thermionic emission

Phase change memory (PCM) is an excellent candidate for neuromorphic computing hardware because it can exhibit multiple intermediate resistance states,1−7 which is an important requirement for artificial synapses.8−11 Phase change materials, such as Ge2Sb2Te5 (GST), can reversibly switch between two main phases (states): polycrystalline (low resistance) and amorphous (high resistance), as shown schematically in Figure 1a. The phase transition is thermally induced by Joule heating, and the electrical resistance of the cell varies significantly with its phase, encoding the memory state. Yet, a key bottleneck for using PCM with multiple intermediate states for neuromorphic hardware is the increase in resistance with time, namely resistance drift,12,13 which can result in undesired synaptic weight change.14−16 This increase is most significant in the amorphous phase (a-GST), but it is also evident across intermediate states.17

Figure 1.

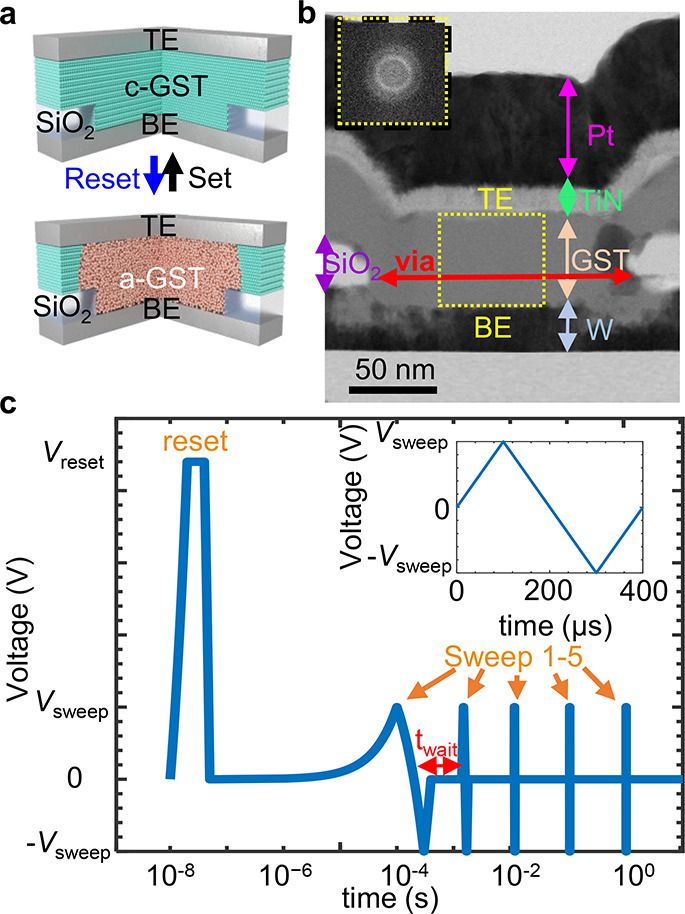
Figure 1

Open in a new tab

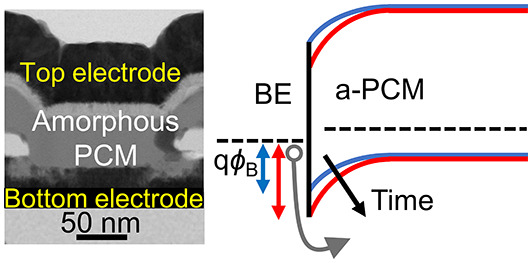
PCM device structure and measurement scheme. (a) Schematic illustration of our confined GST PCM device. (b) Bright field scanning transmission electron microscope (BF-STEM) image of our device in the amorphous phase. Via diameter is ∼150 nm and GST thickness is ∼50 nm. Inset shows a diffractogram from high resolution BF-STEM image of the area between the two electrodes in the amorphous phase. (c) Schematic of the measurement waveform, including a reset pulse followed by multiple read I–V sweeps with time intervals on a logarithmic scale. Inset shows a single sweep in linear scale.

Previous studies have attributed drift in a-GST to either structural relaxation,18−22 or purely electronic mechanisms,23−25 both referring mostly to bulk effects. Typically, the Poole–Frenkel (PF) model is employed to describe charge transport in a-GST.26,27 However, both our current work and previous research,28−31 indicate that electrical contacts dominate the resistance of sub-100 nm-long (lateral) or -thick (vertical) PCM devices. In this study, we employ a combination of techniques, including the transfer length method (TLM), the contact end-resistance method, temperature-dependent current–voltage (I–V ) measurements, and ultraviolet photoelectron spectroscopy (UPS), to determine the dominant current transport mechanism. Our findings reveal that conduction in our a-GST devices is governed by thermionic emission of holes at the contact (p-type). With this understanding, we perform temperature-dependent temporal I–V measurements to analyze resistance drift, focusing on the dominant conduction mechanism: emission over the Schottky barrier. We discover that the drift manifests itself as an increase in the Schottky barrier height (ϕB) with time.

Results and Discussion

Time Dependent I–V

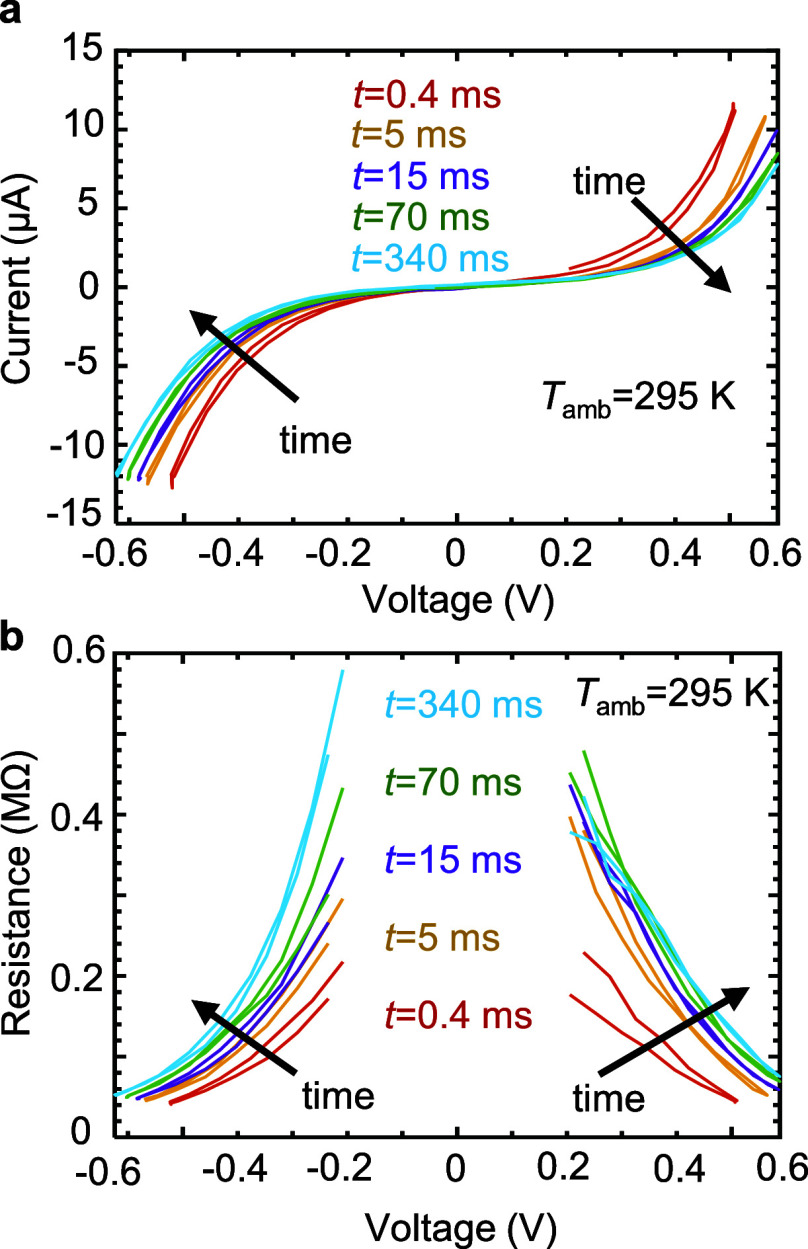
We carried out a systematic study, including fast I–V sweeps to read the PCM resistance vs time following a reset pulse (resistance drift). Typically, PCM resistance is read at a single voltage, but here, we use I–V sweeps to uncover the current transport mechanism and explore the voltage dependence. We studied conventional PCM cells of confined GST (Figure 1a,b), fabricated as outlined in the Methods section, and performed a series of fast I–V sweeps. The sweeps were performed immediately after applying a reset pulse (Figure 1c), separated by time intervals on a logarithmic scale, for different ambient temperatures in the range Tamb = 80–295 K. Figure 2a shows a series of I–V measurements executed at different time intervals from the reset pulse. We observe nonlinear behavior, signifying the non-Ohmic nature of conduction in a-GST devices.18,28,32 In addition, the figure shows that the current at a given voltage decreases with time. Consequently, the resistance, defined as R(t) = V(t)/I(t), increases with time (Figure 2b). We show drift results for a device with via diameter of ∼150 nm and thickness of ∼50 nm at Tamb = 295 K, but other devices exhibited similar behavior in the measured temperature range.

Figure 2.

Figure 2

Open in a new tab

Time dependent I–V measurements. (a) I–V and (b) R–V characteristics in the amorphous phase at Tamb = 295 K, for varying drift time, following a reset pulse. Voltage is applied to the bottom electrode (BE). I–V is nonlinear and shows a drift with time. Resistance is defined by R(t) = V(t)/I(t).

Voltage- and Temperature-Dependent Drift

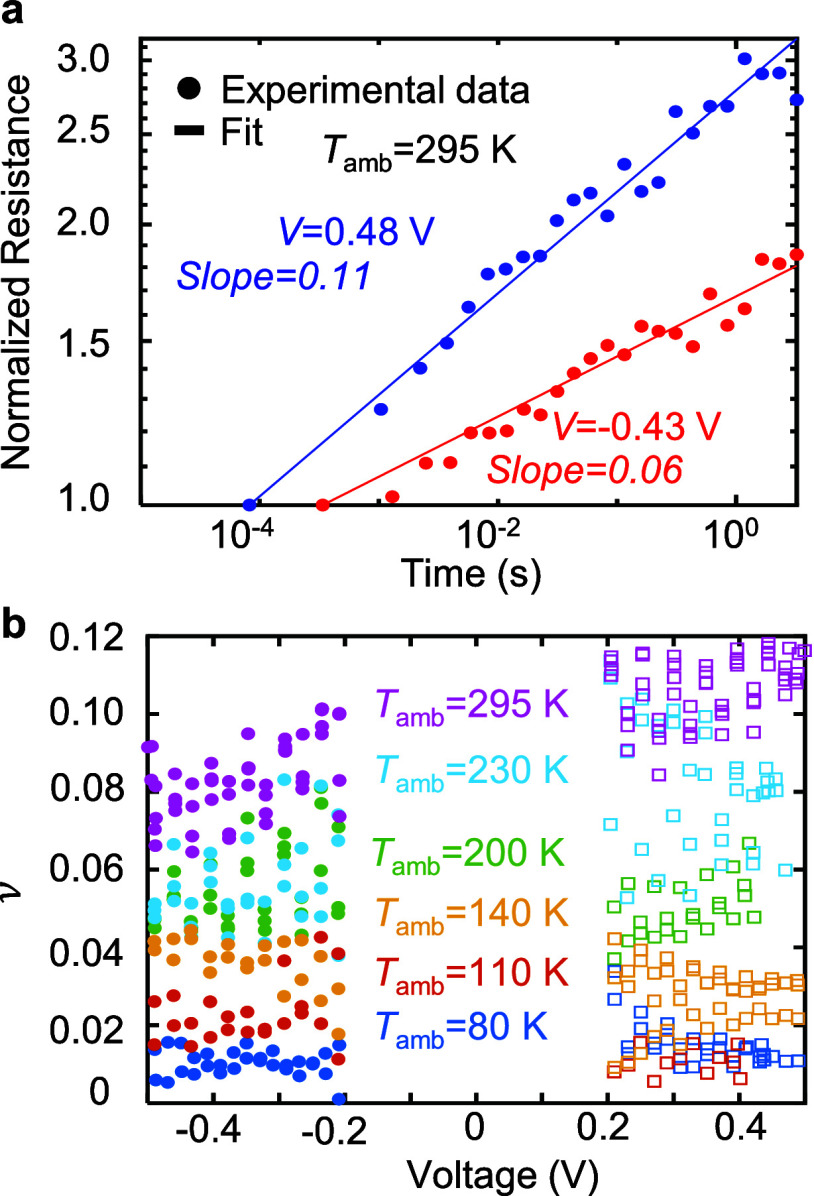
Using the temporal I–V data, we evaluate the resistance drift voltage- and temperature-dependence. We obtain the drift coefficient ν according to the power law:18

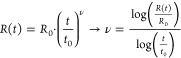graphic file with name nn3c11019_m001.jpg 1

where R0 and t0 are the resistance and time of the first measurement after reset (Figure 3a). Initial resistances were in the range R0 = 100–350 kΩ. Figure 3b shows that the drift coefficient has an appreciable temperature-dependence, increasing as Tamb increases, whereas the voltage-dependence is much less pronounced. This result is consistent with other reports in the literature.33,34 Furthermore, higher initial resistance results in a higher drift coefficient.3,35,36 This helps explain some anomalies in Figure 3b for which the drift coefficient is not higher at higher temperatures. For example, the drift coefficient at 80 K appears to be higher than the coefficient at 110 K for positive bias.

Figure 3.

Figure 3

Open in a new tab

Voltage- and temperature-dependent drift coefficient. (a) Log–log plot of normalized resistance vs time for two representative read voltages (−0.43 V red, 0.48 V blue), to extract drift coefficient, ν (slope) according to R(t)/R0 = (t/t0)ν. (b) Fitted drift coefficient vs read voltage for different temperatures. The drift coefficient has a strong T-dependence and a less pronounced V-dependence.

Contact vs Bulk Resistance

Next, we sought to determine the dominant current transport mechanism in a-GST devices. These mechanisms could be categorized into two main groups: bulk dominated (Poole–Frenkel, hopping, space-charge, etc.) and contact dominated (thermionic emission, tunneling, etc.). Traditionally, the Poole–Frenkel mechanism has been used to describe conduction in a-GST.26,27 However, recent research suggests that contacts may play a more significant role.28−31 In this study our steady-state measurements lead to the conclusion that for sub-100 nm a-GST devices, the conduction is dominated by the contacts, and specifically the thermionic emission (Schottky) mechanism.37 These steady-state measurements were conducted on three different test structures of a-GST. Further details about the methods, sample differences, and limitations can be found in Supporting Information Section S1.

In order to identify whether the conduction is bulk or contact limited, we use the well-known transfer length method.38Figure 4a,b show the test structures for which the contact lengths (Lc) and contact spacings (d) are a few-hundred-nm, fabricated and measured as described in the Methods section. We extract the sheet resistance (slope) and the contact-front resistance (half the ordinate intercept) for both crystalline phase (c-GST) and the amorphous phase (Figure 4c,d), according to38

graphic file with name nn3c11019_m002.jpg 2

where RT is the total resistance, W is the GST width, Rsh is the sheet resistance, and Rcf is the contact-front resistance. For c-GST the sheet resistance is Rsh = 3.0 kΩ/□ (85% confidence intervals: 2.3–5.4 kΩ/□), and for a-GST Rsh = 2.2 MΩ/□ (85% confidence intervals: 0.3–11.8 MΩ/□). In both phases, the contact-front resistance is dominant, signifying the negligible contribution of the sheet resistance compared to the contact resistance. We also used contact-end measurements to evaluate the contact resistivity. Figure 4e,f show the contact-end resistance as a function of the contact length, and the fitted plot, according to38

graphic file with name nn3c11019_m003.jpg 3

Here Rce is the contact-end resistance, ρc is the contact resistivity, and LTk is the transfer length on top of the contacts (LTk = (ρc/Rsk)0.5, where Rsk is the sheet resistance on top of the contacts). For c-GST the contact resistivity is ρc = 1.6 μΩ·cm2 (85% confidence intervals: 1.0–2.4 μΩ·cm2), and for a-GST ρc = 3.3 mΩ·cm2 (85% confidence intervals: 2.0–5.4 mΩ·cm2). A summary of the fitted resistivity values can be found in the first row of Table 1. The contact-front measurements and fits are shown in Supporting Figure S2, and even though they have a higher error, they corroborate the findings from the contact-end measurements, enhancing the robustness of the results. Additional data regarding the TLM measurements can be found in Supporting Information Section S2.

Figure 4.

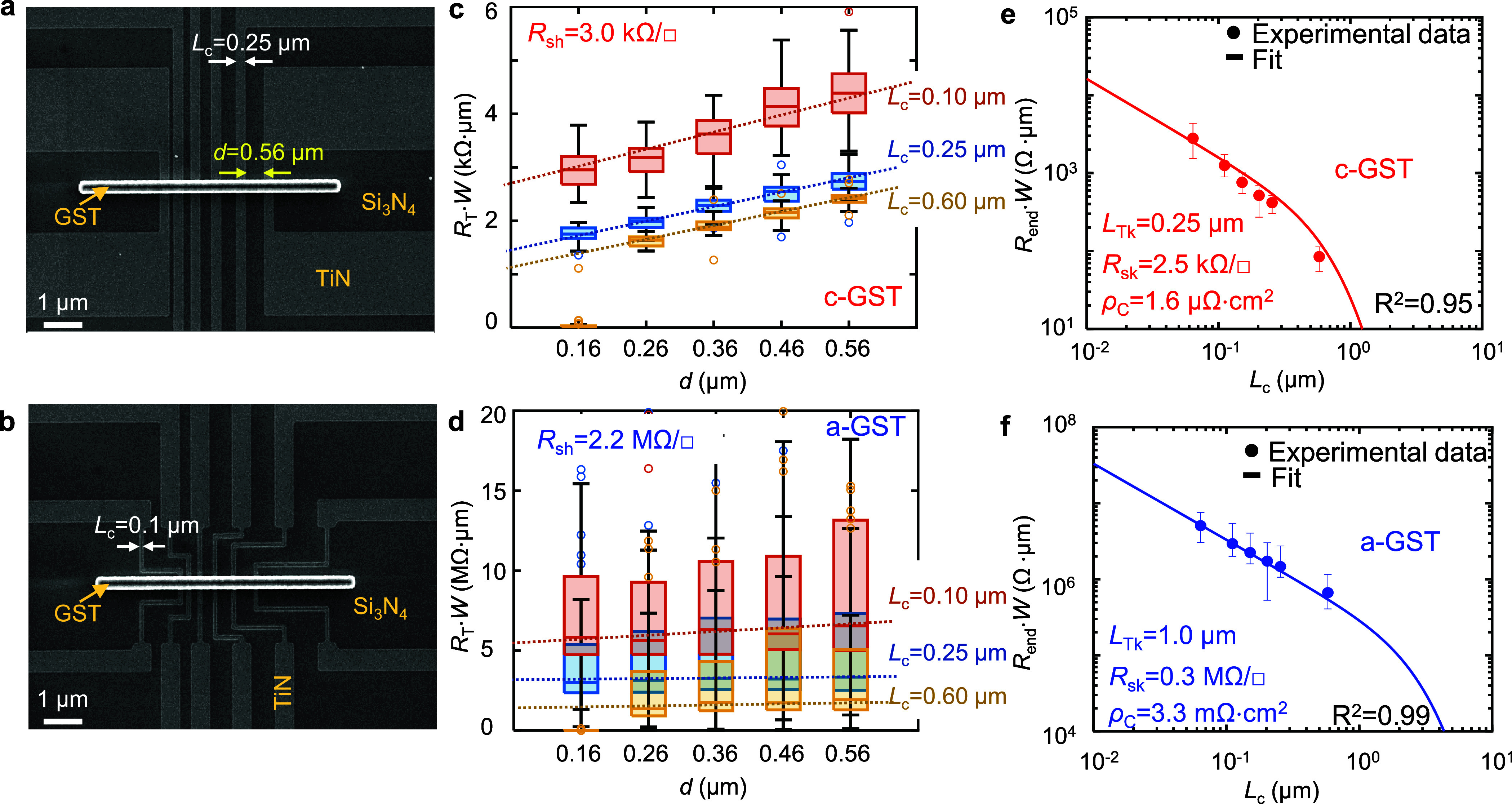
Figure 4

Open in a new tab

Transfer length method (TLM) measurements. Scanning electron microscope (SEM) images of the TLM test structures for contact lengths of (a) Lc = 0.25 μm and (b) Lc = 0.10 μm. Resistance width product (RT·W) as a function of spacing between contacts, d for (c) c-GST, and (d) a-GST. Plots show statistical analysis of 48 measured structures and include dashed lines as a guide for the eye. Contact-end resistance as a function of contact length LC for (e) c-GST, and (f) a-GST. Dots represent median values and error bars the 85% confidence intervals. Results indicate that the resistance in both c-GST and a-GST is dominated by the contacts in sub-100 nm spacing.

Table 1. GST Resistivitya.

contact a-GST measurement strategy a-GST type ρa (mΩ·cm) a-GST bulk resistivity ρc (mΩ·cm) c-GST bulk resistivity ρCa (mΩ·cm2) a-GST contact resistivity ρCc (mΩ·cm2) c-GST contact resistivity γa (μm) ρCa/ρa γc (μm) ρCc/ρc
this work, GST-TiN TLM Ge ion implanted 22 × 103 30 3.3 1.6 × 10–3 1.57 0.53
Savransky,39 GST-metal varying GST thicknesses melt-quenched 10 × 105 20 N/A 0.3 × 10–3 N/A 0.15
Roy,30 GST-TiW cross-bridge Kelvin resistor as-deposited 80.5 × 104 20 95 3.8 × 10–3 1.18 1.90
Huang,28 GST-TiN modified TLM as-deposited 54.5 × 103 34 64 80 × 10–3 11.74 23.52
Shindo,31 GST-W circular TLM as-deposited 22 × 105 48 32 14 × 10–3 0.15 2.91
Adnane,40 GST-W 4-point-probe as-deposited 87 × 104 75 (fcc) N/A N/A N/A N/A
11 (hcp)
Open in a new tab
a

Resistivity of GST ρ, specific contact resistivity ρc, and characteristic length at which bulk resistance equals contact resistance γ, in both crystalline and amorphous phases, compared with those in previous studies. Findings indicate that for 100 nm-long (lateral) or -thick (vertical) devices, in both phases, the resistance is dominated by the contacts.

To assess the contribution of contacts vs bulk to the total resistance, we define a characteristic length (for lateral transport) or thickness (for vertical transport) at which bulk resistance equals contact resistance as γ = ρC/ρ (same as the dominance factor of contact resistivity, in Shindo et al.31). The values obtained from our measurements, along with a comparison to those from previous reports, are summarized in Table 1. As expected, our results are slightly different from previous reports which use as-deposited a-GST and not ion-implantation. However, all findings indicate that for 100 nm-long (lateral) or -thick (vertical) devices, in both phases, the resistance is dominated by the contacts.28−31,39 Our measurements suggest that in thin films, the change in device resistance during switching is primarily attributed to changes in contact resistance, which can differ by more than 3 orders of magnitude (ρCa/ρCc > 103).

Thermionic Emission (Schottky)

With the understanding that the contacts dominate the resistance, we seek to identify the conduction mechanism in the confined a-GST devices (Figure 1a,b). We performed steady state I–V measurements on the confined devices in the amorphous phase, at different ambient temperatures (Figure 5a). The thermionic emission mechanism (i.e., a reversed biased Schottky junction with image force barrier lowering) is the most appropriate contact dominated mechanism to describe our results (Figure 5b,c),41−43 and is given by43

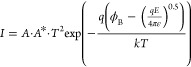graphic file with name nn3c11019_m004.jpg 4

where A is the contact area, A* is the Richardson constant, T is temperature in K, ϕB is the barrier height, E is the electric field, and ε is the dielectric constant. For clarification, in back-to-back Schottky diodes, the polarity of the voltage determines which junction is in reverse bias (top or bottom interface) and limits the conduction, as marked in Figure 5a.

Figure 5.

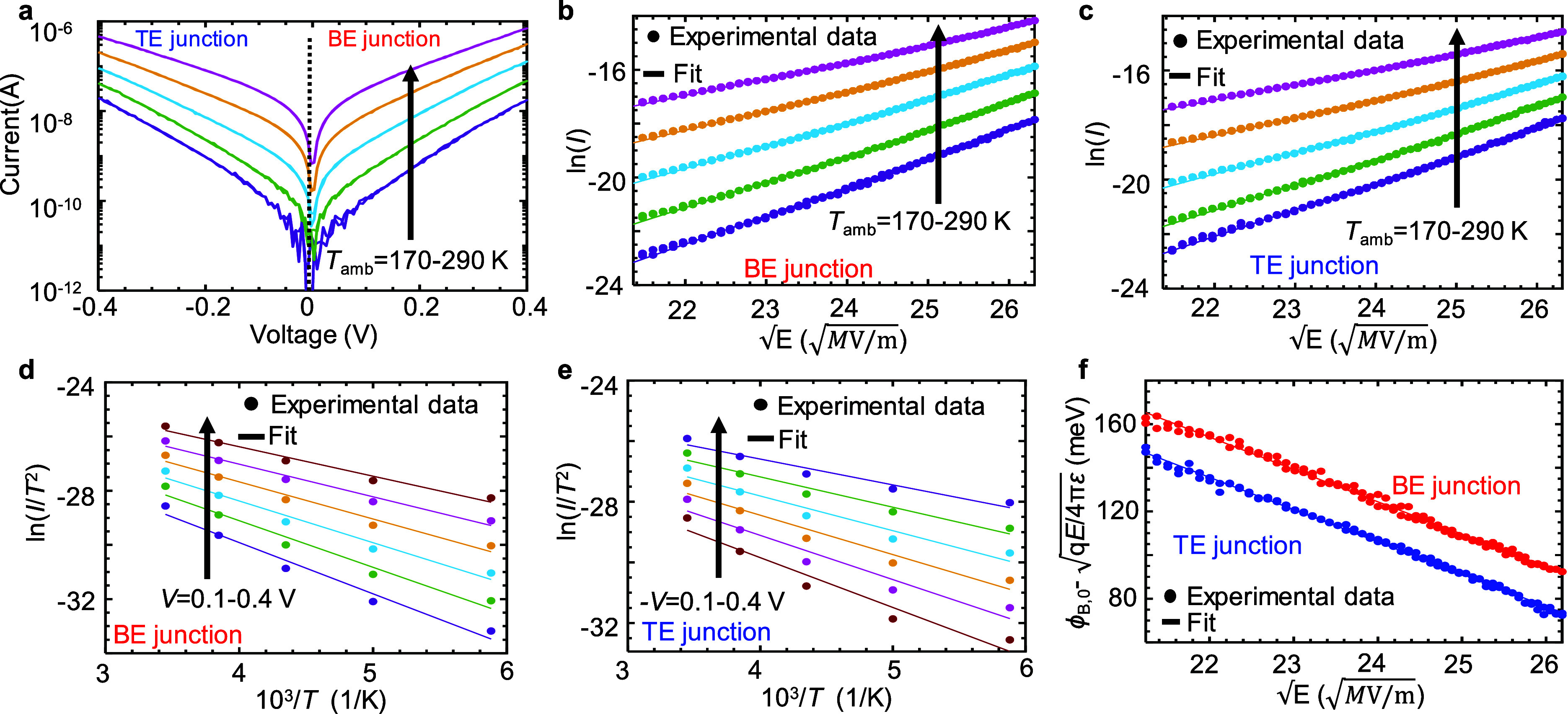
Figure 5

Open in a new tab

Thermionic emission (Schottky) fit. (a) I–V measurements for varying ambient temperatures. Via diameter of the confined area is ∼200 nm. Measured (markers) and fitted thermionic emission expression (lines) ln(I)–E0.5 for varying Tamb at (b) positive and (c) negative bias to bottom electrode (BE). Measured (markers) and fitted (lines): ln(I/T2) vs 103/T for varying read voltages at (d) positive and (e) negative bias to BE. (f) Minimum barrier height extraction. The barrier, ϕB, is obtained from the value at VA = 0 V.

Traditionally, the Poole–Frenkel (PF) conduction mechanism is used to describe the current transport in a-GST,26 due to reasonable I–V fitting and its symmetrical behavior. As both thermionic emission and PF are thermionic effects for which the current is exponentially dependent on E0.5, it could be difficult to distinguish between the two. Therefore, basic I–V analysis is insufficient for pinpointing the conduction mechanism. The TLM results, which show that the contacts dominate the resistance, establish that thermionic emission governs transport in sub-100 nm devices. Furthermore, the symmetrical I–V behavior has led previous work to reject the thermionic emission model.44 Yet, as a-GST has a high impurity density, it is very likely that high density of interface traps dictates the barrier height at the interface (i.e., Fermi level pinning),45 and only a slight dependence on the electrode material work function is expected.46 Consequently, the extracted barrier heights for the TE and BE junctions are similar, as detailed below, and a nearly symmetrical I–V behavior is observed.

We estimate the electric field in the proximity of the interface using the depletion approximation, given by45,47

graphic file with name nn3c11019_m005.jpg 5

where NT is the ionized trap density, VBI is the built-in voltage, and VA is the applied voltage. We do not assume uniform field due to the nonzero built-in field and the nonlinear I–V characteristics.

Using the method described in Yeargan et al.,48 we obtain the plot slopes of ln(I/T2) vs 1/T (Figure 5d,e) and the change in barrier height due to an electric field, known as image force barrier lowering (Figure 5f). The minimum barrier height, extracted from Figure 5f from the value at VA = 0,38 is ∼210 and 190 meV for the tungsten BE contact and TiN TE contact, respectively. More details on the thermionic emission fit are available in Supporting Information Section S3.

Additionally, we performed pump/probe ultraviolet photoelectron spectroscopy (UPS) measurements on as-deposited a-GST. Results show that a-GST behaves as a p-type semiconductor (Figure 6a), in agreement with previous work.40,46,49,50 For a-GST, the built-in voltage, VBI, and the barrier height, ϕB,0, are approximately 130 and 240 meV, respectively (Figure 6b,c). These results are consistent with the steady state I–V measurements and the thermionic emission model. More details of the UPS measurements can be found in Supporting Information Section S4.

Figure 6.

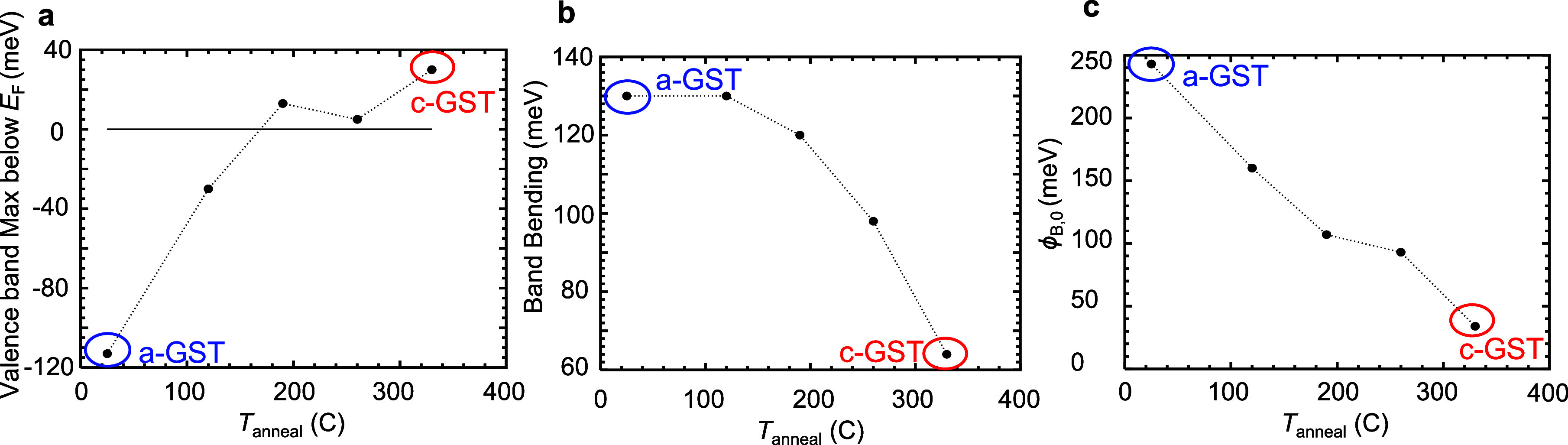
Figure 6

Open in a new tab

Ultraviolet photoelectron spectroscopy (UPS) measurements. (a) Valence band max below EF vs anneal temperature. (b) Band bending vs anneal temperature. (c) Barrier height vs anneal temperature.

For Multilevel PCM implementations, the conventional understanding is that intermediate resistance states could be achieved using varying amorphous volumes.19,51 Our finding that the thermionic emission conduction dominates the resistance in nanoscale devices indicates that we should also consider the varying interface areas of the amorphous material as the source of intermediate resistance states. Both top and bottom interfaces can play a role, and a barrier may exist not only between the metal and a-GST but also between crystalline and amorphous GST.52 The dominant interface depends on the device geometry and the polarity of the applied voltage. More information can be found in Supporting Information Section S5.

Drift in Schottky Barrier Height

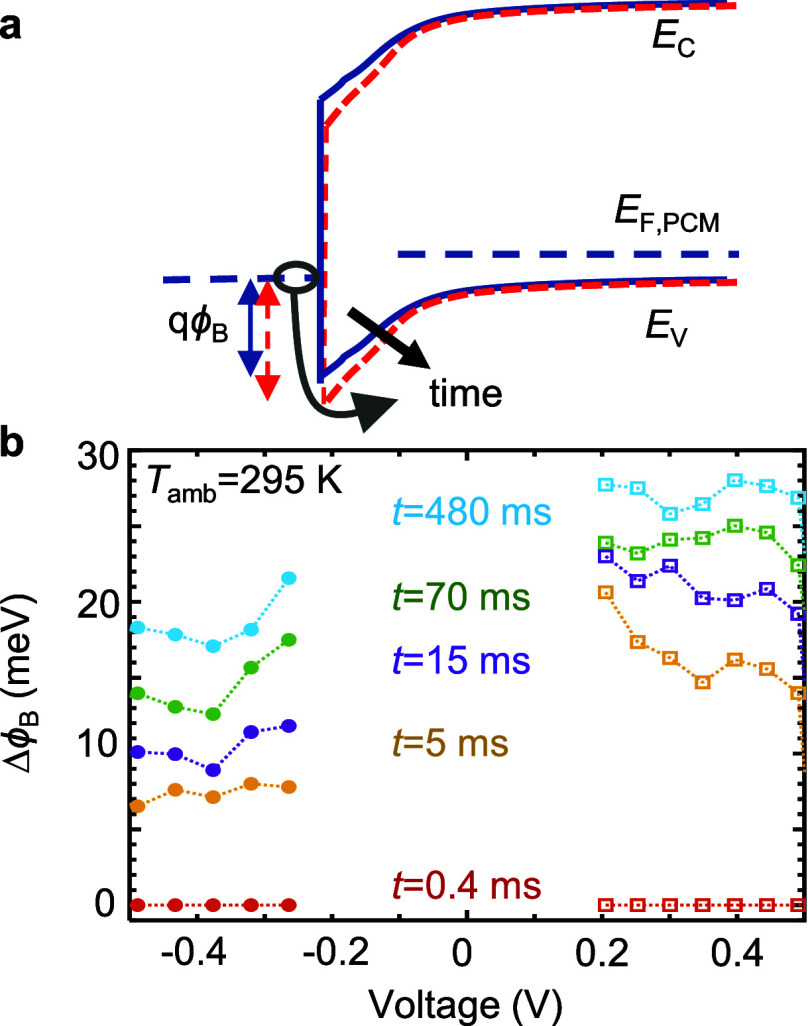
Determining the conduction mechanism as a thermionic emission holds the key to understanding the electrical manifestation of the drift phenomenon in PCM devices. With this understanding we return to the temporal I–V measurements shown in Figure 2, pinpointing the drift to a physical variable, the contact barrier height for hole injection, as illustrated in Figure 7a. Thus, we extract the drift in barrier height (Figure 7b) by performing the following operations on the time dependent I–V measurements:

graphic file with name nn3c11019_m006.jpg 6
graphic file with name nn3c11019_m007.jpg 7

where I0 and t0 are the current and time of the first measurement after reset. More information can be found in Supporting Information Section S6.

Figure 7.

Figure 7

Open in a new tab

Extraction of drift in the Schottky barrier height. (a) Schematic band diagram with barrier height drift. The energy barrier height for hole injection to GST increases with time (drift). GST is a p-type semiconductor. (b) Extraction of the change in barrier height for varying drift times following a reset pulse according to eq 7.

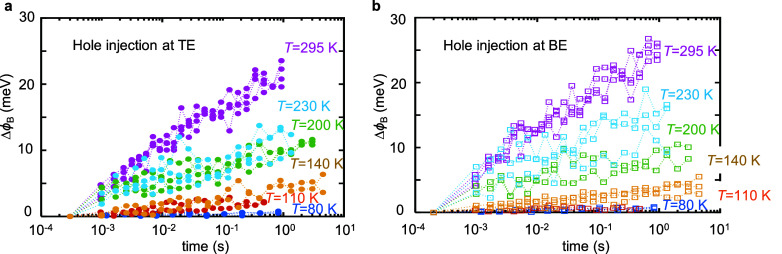
The average drift of the barrier height with time for all measured Tamb values is summarized in Figure 8. The barrier height drifts in the range of ∼1–30 meV for 80–295 K. These results are consistent with the power law behavior of PCM drift, expressed in eq 1. Combining the exponential dependence of the current on an energy barrier (log(R) ∼ qϕB/(kT)), thermionic mechanism) with our observation of a change in barrier height that is proportional to log(t), results in a direct relation between log(R) and log(t). Moreover, the current is exponentially dependent on the barrier height for different temperatures, explaining the strong temperature dependence of the drift coefficient. Our results show that the electrical manifestation of drift in PCM is dominated by the contacts.

Figure 8.

Figure 8

Open in a new tab

Drift in the Schottky barrier height. Extracted change in barrier height (ΔϕB) for hole injection to GST with time (drift) for varying temperatures at (a) TE and (b) BE. ϕB drift becomes more prominent at higher temperatures. However, current or resistance drift is observed even at low temperature due to the exponential dependence of the thermionic emission current on the barrier height. This result shows that the electrical manifestation of drift in the PCM is dominated by the interface (contact).

To clarify, our results do not directly reveal the origin of the drift but rather the electrical manifestation. However, our findings can offer insights into previously unexplained experiments, particularly those related to the behavior of the drift coefficient at low temperatures and its sensitivity to illumination.53 The observation of resistance drift at low temperatures can be explained by the exponential relationship between the current and barrier height. Even when structural relaxation is significantly suppressed at low temperatures, a minor alteration in barrier height can lead to noticeable changes in measured resistance owing to the exponential characteristics of Schottky behavior. In the context of electron energy, previous research has suggested that drift could be attributed to a widening of the band gap over time,13 or changes in midgap states, such as charge traps.18 Both of these factors could potentially impact the barrier height, which, in turn, undergoes drift over time. In summary, our findings align with the structural relaxation explanation, yet they do not rule out a purely electronic origin of the drift.

Conclusion

In conclusion, our work shows that the electrical manifestation of resistance drift in thin amorphous films is dominated by the contacts. We utilized a combination of techniques, including the steady-state transfer length method, contact-end measurements, temperature-dependent current–voltage (I–V ) characteristics, and ultraviolet photoelectron spectroscopy. Our findings reveal that the dominant current transport mechanism in amorphous thin GST-based phase change devices is thermionic emission (Schottky) of holes at the metal–semiconductor interface. Furthermore, our temporal temperature-dependent I–V sweeps indicate that drift in the PCM is reflected by an increase in the Schottky barrier height over time. We observed a strong temperature-dependence of the drift coefficient and a weak voltage-dependence in confined PCM devices with 50 nm thick GST. Our findings underscore the critical role of contacts in the evaluation of thin PCM devices, and enable a better understanding of drift, ultimately mitigating it, making PCM technology viable for neuromorphic applications.

Methods

Device Fabrication

The bright field scanning transmission electron microscope (BF-STEM) cross-section image of a confined PCM cell is shown in Figure 1b, and the devices were fabricated as follows.54 First, tungsten (W) was evaporated, patterned, and etched to form the bottom electrode (BE). Next, SiOx was deposited using plasma enhanced chemical vapor deposition (PECVD) and the confined vias were patterned using electron-beam lithography. The BE was Ar sputter-cleaned to remove oxidation and prevent filament formation, followed by GST and TiN sputter deposition, all without breaking a vacuum. The top electrode (TE) was completed with additional TiN/Pt, and patterned by lift-off. Vias diameter ranges from 125 to 170 nm, and GST thickness is ∼50 nm.

The TLM structure shown in the scanning electron microscope (SEM) images in Figure 4a,b were fabricated as outlined: Planarized TiN contacts were formed by etching trenches in Si3N4, sputter-depositing TiN and planarizing the TiN by chemical mechanical polishing (CMP) such that the TiN surface is flashed with the Si3N4 surface. Argon (Ar) sputtering was used to clean the surface of the TiN contacts, which was followed by GST deposition without breaking the vacuum. This ensures a clean GST/TiN interface. The GST was annealed to form c-GST and was capped with Si3N4 film. Optical lithography followed by reactive ion etching was used to patterned the c-GST into bars, and the device was further encapsulated to prevent oxidation.

Characterization

Electrical characterization of the confined PCM cells was carried out with a Keysight B1500 semiconductor parameter analyzer (SPA) in a JANIS probe station under vacuum conditions (<10–4 Torr) at temperatures ranging from room temperature (near 300 K) to 80 K.

The fast pulses were generated by a Waveform Generator/Fast Measurement Unit (WGFMU) which can generate arbitrary waveforms, such as the one depicted in Figure 1c. The system has an inherent trade-off between the measurement speed and the minimum current measured. Therefore, in order to read the high resistances, ranging from 100 to 350 kΩ, we performed 400 μs I–V sweeps (tsweep). We executed approximately 20–25 consecutive sweeps, and the time between consecutive sweeps was multiplied by ∼1.5–2 (tmultiply). The time between I–V sweeps (twait, marked in red in Figure 1c) can then be calculated using eq 8 for sweep number n:

graphic file with name nn3c11019_m008.jpg 8

During read operations, the highest measured voltage was below the threshold voltage in order to prevent destructive read.

BF-STEM images (Figure 1b) were done on a device from the same die as the device for which the temporal measurements were performed and with a similar via size. This device was reset to high resistance (1.5 MΩ) and then imaged a few weeks later. A top-down SEM image located the cross-section of the confined PCM cell for the focused ion beam (FIB) cut for the BF-STEM. Energy dispersive X-ray spectroscopy (EDX) was used to determine the elemental structure of the cross-section. The lack of diffraction patterns in the inset of Figure 1b suggests the absence of crystallinity, implying that the area between the two electrodes is amorphous. More images and details can be found in Supporting Information Section S7.

The TLM measurements for the crystalline and amorphous GST phases were performed on the same test sites (identical sizes). Initially the GST was in the crystalline phase. After measuring this phase, c-GST was amorphized by ion implantation of Ge.

Previous work has shown that by adjusting the ion dose implanted into c-GST the properties of the amorphized GST (such as the optical properties) can be tuned to match those of melt-quench a-GST.55,56 The electrical measurements on the amorphized GST were performed a few days after amorphization on a time span of less than 1 h, so the drift effects are negligible.

Similarly, the steady state I–V measurements were carried out a week after resetting the device to 500 kΩ to eliminate the influence of drift during data collection.

Acknowledgments

We thank C. M. Neumann and E. Pop, Stanford University, for providing confined GST structures and thank R. Huang, Southampton University, for helpful discussions and insights. Fabrication was performed partially at the Stanford Nanofabrication Facility (SNF), Stanford Nano Shared Facilities (SNSF), and the Technion Micro-Nano Fabrication & Printing Unit (MNF&PU). This work was supported in part by the Israel Science Foundation (ISF) Grant No. 1179/20, as well as ISF No. 3582/21 (joint NSFC-ISF research program), and in part by Russel Berrie Nanotechnology Institute (RBNI), Technion.

Data Availability Statement

The data that support this study are available from the corresponding author upon request. Other correspondence and requests for materials should be addressed to E. Yalon.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.3c11019.

  • Comparison between methods and samples; Transfer length method, additional data; Steady state I–V measurements, additional data; Ultraviolet photoelectron spectroscopy, additional data; Interface dominated multilevel conduction in mushroom-type cells; Schottky barrier height drift, additional data; Transmission electron microscopy images (PDF)

Author Contributions

R.G.N.H and E.Y. conceived the confined-device experiments and wrote the manuscript with input from all authors. G.C. and A.M. fabricated and measured the TLM structures, R.H. performed the UPS measurements, E.B. did the TCAD simulations, L.G. performed BF-STEM imaging, E.O. performed electrical measurements on the mushroom-type cells, and L.S. did ellipsometry measurements.

The authors declare no competing financial interest.

Supplementary Material

nn3c11019_si_001.pdf (930.3KB, pdf)

References

  1. Burr G. W.; Shelby R. M.; Sebastian A.; Kim S.; Kim S.; Sidler S.; Virwani K.; Ishii M.; Narayanan P.; Fumarola A.; Sanches L. L.; Boybat I.; Le Gallo M.; Moon K.; Woo J.; Hwang H.; Leblebici Y. Neuromorphic Computing Using Non-Volatile Memory. Adv. Phys.: X 2017, 2, 89–124. 10.1080/23746149.2016.1259585. [DOI] [Google Scholar]
  2. Fong S. W.; Neumann C. M.; Wong H. S. P. Phase-Change Memory - Towards a Storage-Class Memory. IEEE Trans. Electron Devices 2017, 64 (11), 4374–4385. 10.1109/TED.2017.2746342. [DOI] [Google Scholar]
  3. Stern K.; Wainstein N.; Keller Y.; Neumann C. M.; Pop E.; Kvatinsky S.; Yalon E. Sub-Nanosecond Pulses Enable Partial Reset for Analog Phase Change Memory. IEEE Electron. Device Lett. 2021, 42, 1291. 10.1109/LED.2021.3094765. [DOI] [Google Scholar]
  4. Wong H. S. P.; Raoux S.; Kim S.; Liang J.; Reifenberg J. P.; Rajendran B.; Asheghi M.; Goodson K. E. Phase Change Memory. In Proceedings of the IEEE 2010, 98, 2201–2227. 10.1109/JPROC.2010.2070050. [DOI] [Google Scholar]
  5. Nirschl T.; Philipp J. B.; Happ T. D.; Burrt G. W.; Rajendrant B.; Lee M.-H.; Schrottt A.; Yan M.; Breitwischt M.; Chen C.-F.; Josepht E.; Lamorey M.; Chee R.; Chen S.-H.; Zaidi S.; Raoux S.; Chen Y. C.; Ergmann R. B.; Lunge H.-L.; Lamf C.. Write Strategies for 2 and 4-Bit Multi-Level Phase-Change Memory. In IEEE International Electron Devices Meeting (IEDM); IEEE, 2007. 10.1109/IEDM.2007.4418973. [DOI]
  6. Papandreou N.; Pozidis H.; Pantazi A.; Sebastian A.; Breitwisch M.; Lam C.; Eleftheriou E.. Programming Algorithms for Multilevel Phase-Change Memory. In IEEE International Symposium on Circuits and Systems (ISCAS); IEEE, 2011; pp 329–332. 10.1109/ISCAS.2011.5937569. [DOI]
  7. Ielmini D.; Wong H. S. P. In-Memory Computing with Resistive Switching Devices. Nat. Electron. 2018, 1, 333–343. 10.1038/s41928-018-0092-2. [DOI] [Google Scholar]
  8. Burr G. W.; Shelby R. M.; Sidler S.; Di Nolfo C.; Jang J.; Boybat I.; Shenoy R. S.; Narayanan P.; Virwani K.; Giacometti E. U.; Kurdi B. N.; Hwang H. Experimental Demonstration and Tolerancing of a Large-Scale Neural Network (165 000 Synapses) Using Phase-Change Memory as the Synaptic Weight Element. IEEE Transactions on Electron Devices (TED) 2015, 62 (11), 3498–3507. 10.1109/TED.2015.2439635. [DOI] [Google Scholar]
  9. Kuzum D.; Yu S.; Philip Wong H. S. Synaptic Electronics: Materials, Devices and Applications. Nanotechnology 2013, 24, 382001. 10.1088/0957-4484/24/38/382001. [DOI] [PubMed] [Google Scholar]
  10. Jackson B. L.; Rajendran B.; Corrado G. S.; Breitwisch M.; Burr G. W.; Cheek R.; Gopalakrishnan K.; Raoux S.; Rettner C. T.; Padilla A.; Schrott A. G.; Shenoy R. S.; Kurdi B. N.; Lam C. H.; Modha D. S. Nanoscale Electronic Synapses Using Phase Change Devices. ACM J. Emerg Technol. Comput. Syst 2013, 9 (2), 1. 10.1145/2463585.2463588. [DOI] [Google Scholar]
  11. Kuzum D.; Jeyasingh R. G. D.; Lee B.; Wong H. S. P. Nanoelectronic Programmable Synapses Based on Phase Change Materials for Brain-Inspired Computing. Nano Lett. 2012, 12 (5), 2179–2186. 10.1021/nl201040y. [DOI] [PubMed] [Google Scholar]
  12. Pirovano A.; Lacaita A. L.; Pellizzer F.; Kostylev S. A.; Benvenuti A.; Bez R. Low-Field Amorphous State Resistance and Threshold Voltage Drift in Chalcogenide Materials. IEEE Trans. Electron Devices 2004, 51 (5), 714–719. 10.1109/TED.2004.825805. [DOI] [Google Scholar]
  13. Raty J. Y.; Zhang W.; Luckas J.; Chen C.; Mazzarello R.; Bichara C.; Wuttig M. Aging Mechanisms in Amorphous Phase-Change Materials. Nat. Commun. 2015, 10.1038/ncomms8467. [DOI] [PubMed] [Google Scholar]
  14. Park J. Neuromorphic Computing Using Emerging Synaptic Devices: A Retrospective Summary and an Outlook. Electronics 2020, 9, 1414. 10.3390/electronics9091414. [DOI] [Google Scholar]
  15. Oh S.; Huang Z.; Shi Y.; Kuzum D. The Impact of Resistance Drift of Phase Change Memory (PCM) Synaptic Devices on Artificial Neural Network Performance. IEEE Electron Device Letters (EDL) 2019, 40 (8), 1325–1328. 10.1109/LED.2019.2925832. [DOI] [Google Scholar]
  16. Li J.; Luan B.; Lam C.. Resistance Drift in Phase Change Memory. In IEEE International Reliability Physics Symposium (IRPS); IEEE, 2012.
  17. Boybat I.; Nandakumar S. R.; Le Gallo M.; Rajendran B.; Leblebici Y.; Sebastian A.; Eleftheriou E.. Impact of Conductance Drift on Multi-PCM Synaptic Architectures. In Non-Volatile Memory Technology Symposium (NVMTS); IEEE, 2018.
  18. Ielmini D.; Lavizzari S.; Sharma D.; Lacaitag A. L.. Physical Interpretation, Modeling and Impact on Phase Change Memory (PCM) Reliability of Resistance Drift Due to Chalcogenide Structural Relaxation. In IEEE International Electron Devices Meeting (IEDM); IEEE, 2007.
  19. Zhang W.; Ma E. Unveiling the Structural Origin to Control Resistance Drift in Phase-Change Memory Materials. Materials Today. 2020, 41, 156–176. 10.1016/j.mattod.2020.07.016. [DOI] [Google Scholar]
  20. Boniardi M.; Ielmini D. Physical Origin of the Resistance Drift Exponent in Amorphous Phase Change Materials. Appl. Phys. Lett. 2011, 10.1063/1.3599559. [DOI] [Google Scholar]
  21. Sebastian A.; Krebs D.; Gallo Le M.; Pozidis H.; Eleftheriou E.. A Collective Relaxation Model for Resistance Drift in Phase Change Memory Cells. In IEEE International Reliability Physics Symposium (IRPS); IEEE, 2015.
  22. Noé P.; Sabbione C.; Castellani N.; Veux G.; Navarro G.; Sousa V.; Hippert F.; D’Acapito F. Structural Change with the Resistance Drift Phenomenon in Amorphous GeTe Phase Change Materials’ Thin Films. J. Phys. D Appl. Phys. 2016, 49 (3), 035305. 10.1088/0022-3727/49/3/035305. [DOI] [Google Scholar]
  23. Elliott S. R. Electronic Mechanism for Resistance Drift in Phase-Change Memory Materials: Link to Persistent Photoconductivity. J. Phys. D Appl. Phys. 2020, 53 (21), 214002. 10.1088/1361-6463/ab795e. [DOI] [Google Scholar]
  24. Tashfiq M.; Kashem B.; Sayeed Khan R.; Hasan Talukder A.; Dirisaglik F.; Gokirmak A.. Stopping Resistance Drift in Phase Change Memory Cells and Analysis of Charge Transport in Stable Amorphous Ge2Sb2Te5. arXiv, October 25, 2022. 10.48550/arXiv.2210.14035 (accessed on July 7, 2023). [DOI]
  25. Khan R. S.; Talukder A. H.; Dirisaglik F.; Silva H.; Gokirmak A.. Accelerating and Stopping Resistance Drift in Phase Change Memory Cells via High Electric Field Stress. arXiv, February 28, 2020. 10.48550/arXiv.2002.12487 (accessed on July 7, 2023). [DOI]
  26. Ielmini D.; Zhang Y. Analytical Model for Subthreshold Conduction and Threshold Switching in Chalcogenide-Based Memory Devices. J. Appl. Phys. 2007, 10.1063/1.2773688. [DOI] [Google Scholar]
  27. Le Gallo M.; Krebs D.; Zipoli F.; Salinga M.; Sebastian A. Collective Structural Relaxation in Phase-Change Memory Devices. Adv. Electron Mater. 2018, 10.1002/aelm.201700627. [DOI] [Google Scholar]
  28. Huang R.; Sun K.; Kiang K. S.; Chen R.; Wang Y.; Gholipour B.; Hewak D. W.; De Groot C. H. Contact Resistance Measurement of Ge 2Sb 2Te 5 Phase Change Material to TiN Electrode by Spacer Etched Nanowire. Semicond. Sci. Technol. 2014, 29 (9), 095003. 10.1088/0268-1242/29/9/095003. [DOI] [Google Scholar]
  29. Deshmukh S.; Yalon E.; Lian F.; Schauble K. E.; Xiong F.; Karpov I. V.; Pop E. Temperature-Dependent Contact Resistance to Nonvolatile Memory Materials. IEEE Trans. Electron Devices 2019, 66 (9), 3816–3821. 10.1109/TED.2019.2929736. [DOI] [Google Scholar]
  30. Roy D.; Zandt M. A. A.; Wolters R. A. M. Specific Contact Resistance of Phase Change Materials to Metal Electrodes. IEEE Electron Device Lett. 2010, 31 (11), 1293–1295. 10.1109/LED.2010.2066256. [DOI] [Google Scholar]
  31. Shindo S.; Sutou Y.; Koike J.; Saito Y.; Song Y. H. Contact Resistivity of Amorphous and Crystalline GeCu2Te3 to W Electrode for Phase Change Random Access Memory. Mater. Sci. Semicond Process 2016, 47, 1–6. 10.1016/j.mssp.2016.02.006. [DOI] [Google Scholar]
  32. Ovshinsky S. R. Reversible Electrical Switching Phenomena in Disordered Structures. Phys. Rev. Lett. 1968, 21, 1450. 10.1103/PhysRevLett.21.1450. [DOI] [Google Scholar]
  33. Kim S.; Lee B.; Asheghi M.; Hurkx F.; Reifenberg J. P.; Goodson K. E.; Wong H. S. P. Resistance and Threshold Switching Voltage Drift Behavior in Phase-Change Memory and Their Temperature Dependence at Microsecond Time Scales Studied Using a Micro-Thermal Stage. IEEE Transactions on Electron Devices (TED) 2011, 58 (3), 584–592. 10.1109/TED.2010.2095502. [DOI] [Google Scholar]
  34. Ielmini D.; Lavizzari S.; Sharma D.; Lacaita A. L. Temperature Acceleration of Structural Relaxation in Amorphous Ge 2 Sb2 Te5. Appl. Phys. Lett. 2008, 10.1063/1.2930680. [DOI] [Google Scholar]
  35. Karpov I. V.; Mitra M.; Kau D.; Spadini G.; Kryukov Y. A.; Karpov V. G. Fundamental Drift of Parameters in Chalcogenide Phase Change Memory. J. Appl. Phys. 2007, 10.1063/1.2825650. [DOI] [Google Scholar]
  36. Kang D. H.; Lee J. H.; Kong J. H.; Ha D.; Yu J.; Um C. Y.; Park J. H.; Yeung F.; Kim J. H.; Park W. I.; Jeon Y. J.; Lee M. K.; Park J. H.; Song Y. J.; Oh J. H.; Jeong G. T.; Jeong H. S.. Two-Bit Cell Operation in Diode-Switch Phase Change Memory Cells with 90nm Technology. In IEEE Symposium on VLSI Circuits; IEEE, 2008.
  37. Shindo S.; Shuang Y.; Hatayama S.; Saito Y.; Fons P.; Kolobov A. V.; Kobayashi K.; Sutou Y. The Importance of Contacts in Cu2GeTe3phase Change Memory Devices. J. Appl. Phys. 2020, 10.1063/5.0019269. [DOI] [Google Scholar]
  38. Schroder D. K.Contact Resistance and Schottky Barriers. In Semiconductor Material and Device Characterization; Wiley-Interscience, 2006; pp 127–184. [Google Scholar]
  39. Savransky S. D.; Karpov I. V. Investigation of SET and RESET States Resistance in Ohmic Regime for Phase-Change Memory. Mater. Res. Soc. 2008, 10.1557/PROC-1072-G06-09. [DOI] [Google Scholar]
  40. Adnane L.; Dirisaglik F.; Cywar A.; Cil K.; Zhu Y.; Lam C.; Anwar A. F. M.; Gokirmak A.; Silva H. High Temperature Electrical Resistivity and Seebeck Coefficient of Ge2Sb2Te5 Thin Films. J. Appl. Phys. 2017, 10.1063/1.4996218. [DOI] [Google Scholar]
  41. Simmons J. G. Conduction in Thin Dielectric Films. J. Phys. D: Appl. Phys. 1971, 4 (613), 613. 10.1088/0022-3727/4/5/202. [DOI] [Google Scholar]
  42. Kao K. C.Dielectric Phenomena in Solids with Emphasis on Physical Concepts of Electronic Processes; Elsevier Academic Press, 2004. [Google Scholar]
  43. Sze S. M.; Li Y.; Ng K. K.. Physics of Semiconductor Devices; Wiley-Interscience, 2006. [Google Scholar]
  44. Nardone M.; Simon M.; Karpov I. V.; Karpov V. G. Electrical Conduction in Chalcogenide Glasses of Phase Change Memory. J. Appl. Phys. 2012, 10.1063/1.4738746. [DOI] [Google Scholar]
  45. Roderick E.Metal-Semiconductor Contacts; Clarendon Press, 1978. [Google Scholar]
  46. Fang L. W. W.; Zhang Z.; Zhao R.; Pan J.; Li M.; Shi L.; Chong T. C.; Yeo Y. C. Fermi-Level Pinning and Charge Neutrality Level in Nitrogen-Doped Ge 2 Sb2 Te5: Characterization and Application in Phase Change Memory Devices. J. Appl. Phys. 2010, 10.1063/1.3475721. [DOI] [Google Scholar]
  47. Sze S. M.; Crowell C. R.; Kahng D. Photoelectric Determination of the Image Force Dielectric Constant for Hot Electrons in Schottky Barriers. J. Appl. Phys. 1964, 35 (8), 2534–2536. 10.1063/1.1702894. [DOI] [Google Scholar]
  48. Yeargan J. R.; Taylor H. L. The Poole–Frenkel Effect with Compensation Present. J. Appl. Phys. 1968, 39 (12), 5600–5604. 10.1063/1.1656022. [DOI] [Google Scholar]
  49. Pirovano A.; Lacaita A. L.; Benvenuti A.; Pellizzer F.; Bez R. Electronic Switching in Phase-Change Memories. IEEE Trans. Electron Devices 2004, 51 (3), 452–459. 10.1109/TED.2003.823243. [DOI] [Google Scholar]
  50. Lazarenko P. I.; Sherchenkov A. A.; Kozyukhin S. A.; Babich A. V.; Timoshenkov S. P.; Gromov D. G.; Shuliatyev A. S.; Redichev E. N.. Electrical Properties of the Ge2Sb2Te5 Thin Films for Phase Change Memory Application. In AIP Conference Proceedings; American Institute of Physics Inc., 2016; Vol. 1727. 10.1063/1.4945968. [DOI]
  51. Fugazza D.; Ielmini D.; Lavizzari S.; Lacaita A. L.. Distributed-Poole–Frenkel Modeling of Anomalous Resistance Scaling and Fluctuations in Phase-Change Memory (PCM) Devices. In IEEE International Electron Devices Meeting (IEDM); IEEE, 2009.
  52. Kroezen H. J.; Eising G.; Ten Brink G.; Palasantzas G.; Kooi B. J.; Pauza A. Schottky Barrier Formation at Amorphous-Crystalline Interfaces of GeSb Phase Change Materials. Appl. Phys. Lett. 2012, 10.1063/1.3691179. [DOI] [Google Scholar]
  53. Khan R. S.; Dirisaglik F.; Gokirmak A.; Silva H. Resistance Drift in Ge2Sb2Te5 Phase Change Memory Line Cells at Low Temperatures and Its Response to Photoexcitation. Appl. Phys. Lett. 2020, 10.1063/1.5144606. [DOI] [Google Scholar]
  54. Neumann C. M.The Effect of Interfaces on Phase Change Memory Switching: A Dissertation; Stanford University, 2019. http://purl.stanford.edu/rq703nq8223 (accessed on July 16, 2023). [Google Scholar]
  55. Privitera S. M. S.; Rimini E. Ion Beam Irradiation of Phase Change Materials: A Route to Material Properties Investigation and Engineering. Mater. Sci. Semicond. Process. 2021, 135, 106087. 10.1016/j.mssp.2021.106087. [DOI] [Google Scholar]
  56. Raoux S.; Cohen G.; Shelby R.; Cheng H.-Y.; Jordan-Sweet J. Amorphization of Crystalline Phase Change Material by Ion Implantation. MRS Online Proc. Libr. 2010, 10.1557/PROC-1251-H02-06. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn3c11019_si_001.pdf (930.3KB, pdf)

Data Availability Statement

The data that support this study are available from the corresponding author upon request. Other correspondence and requests for materials should be addressed to E. Yalon.

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES