Inferring cellular and molecular processes in single-cell data with non-negative matrix factorization using Python, R and GenePattern Notebook implementations of CoGAPS

Abstract

Non-negative matrix factorization (NMF) is an unsupervised learning method well suited to high-throughput biology. However, inferring biological processes from an NMF result still requires additional post hoc statistics and annotation for interpretation of learned features. Here, we introduce a suite of computational tools that implement NMF and provide methods for accurate and clear biological interpretation and analysis. A generalized discussion of NMF covering its benefits, limitations and open questions is followed by four procedures for the Bayesian NMF algorithm Coordinated Gene Activity across Pattern Subsets (CoGAPS). Each procedure will demonstrate NMF analysis to quantify cell state transitions in a public domain single-cell RNA-sequencing dataset. The first demonstrates PyCoGAPS, our new Python implementation that enhances runtime for large datasets, and the second allows its deployment in Docker. The third procedure steps through the same single-cell NMF analysis using our R CoGAPS interface. The fourth introduces a beginner-friendly CoGAPS platform using GenePattern Notebook, aimed at users with a working conceptual knowledge of data analysis but without a basic proficiency in the R or Python programming language. We also constructed a user-facing website to serve as a central repository for information and instructional materials about CoGAPS and its application programming interfaces. The expected timing to setup the packages and conduct a test run is around 15 min, and an additional 30 min to conduct analyses on a precomputed result. The expected runtime on the user’s desired dataset can vary from hours to days depending on factors such as dataset size or input parameters.

Introduction

The central challenge of high-throughput biology, as exemplified by single-cell analysis, pertains to the reduction of extremely high-dimensional data into a format from which we can observe patterns, formulate mechanistic hypotheses and design new experiments. High-throughput experiments are now ubiquitous across many areas of biomedical and biological research. As technology advances to perform these experiments, algorithmic strategies and computing capabilities must develop just as swiftly to keep up with the increasing amount of data they yield.

Non-negative matrix factorization (NMF) is a mathematical technique with a long history in the field of genomics for the analysis of bulk RNA-sequencing (RNA-seq) data¹, and it has been widely adopted as a powerful dimensionality reduction tool for single-cell data as well². NMF reduces the expression of thousands of genes across numerous cells from single-cell (sc)RNA-seq data, to a small number of patterns across those cells. The additive nature of solutions from NMF yields interpretable patterns that can be associated directly with biological processes. Thus, NMF solutions, by definition, encode many characteristics of each cell simultaneously, including identity, state transitions, molecular processes and even technical artifacts³. Moreover, as many of these cellular and molecular processes are unknown a priori in single-cell data, this learning method is particularly well suited for unsupervised analyses.

Multiple software packages implement NMF, many of which apply to single-cell data⁴. Still, biological interpretation of NMF solutions requires further functionalization and practical, end-to-end workflows developed specifically for omics data. Technical components, such as algorithm assumptions, convergence and dimensionality all impact the analysis findings⁵. Biologically interpretable solutions of NMF analysis also rely on custom, post hoc visualization and statistics of the patterns learned from the data⁶. These steps are often customized for each analysis and are not previously codified into a cohesive description of the workflow required for interpretable NMF analysis.

Here, we present four procedures for interpretable analysis of scRNA-seq data with our sparse, Bayesian NMF algorithm Coordinated Gene Activity in Pattern Sets (CoGAPS⁷) based on previous findings of its robustness to initial conditions⁸. CoGAPS was originally released in an R/Bioconductor package by the same name⁹. Our four procedures demonstrate step-by-step NMF analysis across distinct software platforms. They are applied to characterize malignant epithelial cell state transitions in pancreatic cancer using public domain scRNA-seq data¹⁰, which we collated and annotated for 25,422 epithelial cells from tumor and control samples previously¹¹. The first procedure demonstrates PyCoGAPS, a new Python interface for CoGAPS that enhances accessibility and runtime of this algorithm, which we demonstrate has faster performance than our previous R/Bioconductor package. In the second procedure, we provide an option for deploying PyCoGAPS with Docker, allowing users to quickly and easily set up the package and its dependencies through a virtual container. The third procedure performs the same analysis using the R/Bioconductor interface for CoGAPS. The fourth procedure demonstrates running CoGAPS with large scRNA-seq datasets using a web-based, cloud-based computing environment built with GenePattern Notebook¹². This range of options makes NMF accessible to users regardless of their programming background or access to computing architecture. To further guarantee accessibility, we constructed a public-facing CoGAPS website, which serves as a central repository for information about CoGAPS and its application programming interfaces (APIs), including tutorials, explanatory information and links to source code: https://fertiglab.github.io/CoGAPSGuide/.

Key components and considerations for NMF analysis

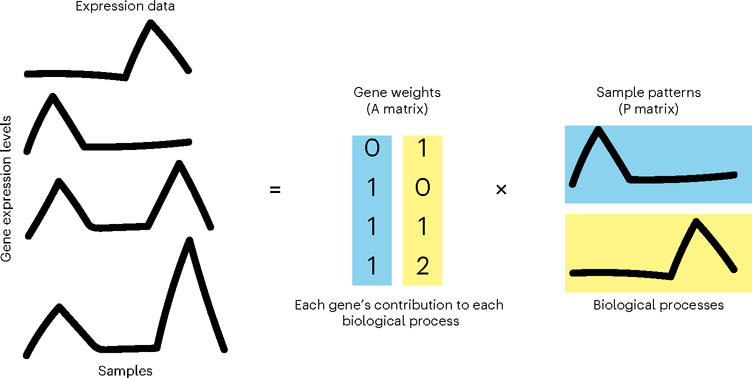
NMF approximates an input data matrix as the product of two lower-dimensional matrices with non-negative entries. If the input matrix of single-cell data contains genes along its rows and cells along its columns, the first result matrix is of dimension genes-by-patterns and the second patterns-by-cells. The number of patterns (or equivalently, features) that define the inner dimension of the two matrices in the factorization is an input variable to the algorithm, which will here be referred to as κ, represented in our code as the parameter nPatterns. When applying NMF to analyses of other high-dimensional data modalities, ‘genes’ and ‘cells’ in this protocol could be replaced by any number of other variables, depending on the experiment and measurement technology. Following the standardized notation for factorization analyses from Stein-O’Brien et al.⁶, we here refer to the genes-by-patterns matrix as the amplitude matrix (A) and the patterns-by-cells matrix as the pattern matrix (P). A variety of alternate nomenclature has been assigned to these matrices in other studies; often the amplitude matrix is referred to as the weights matrix¹³ or meta-genes¹, and the pattern matrix as the heights matrix¹³ or meta-cells. The amplitude matrix describes the association of each gene with each pattern, and the pattern matrix provides information about the relative contribution of each pattern to the phenotype of each cell or sample. The non-negativity assumption in NMF yields non-negative features in these matrices that add together to reconstruct the signal in the input data (Fig. 1). This non-negative constraint contributes to the solution’s biological interpretability, as negative quantities do not exist in nature⁶.

Fig. 1 |. NMF learns signal in input data.

NMF factorizes expression data into lower-dimensional amplitude (A) gene weights matrix and pattern (P) sample weights matrix whose product approximates the input.

There are a wide variety of NMF techniques used for high-throughput molecular analysis, most recently for scRNA-seq analysis³. Algorithms used to solve the NMF problem can be divided into two major classes: gradient-based methods that seek a single solution that optimizes a cost function¹³ and Bayesian methods that estimate the posterior distribution of the amplitude and pattern matrices¹⁴. Both classes can be modified to encode additional constraints on top of non-negativity, further differentiating the various NMF techniques. For example, the Bayesian NMF CoGAPS⁹ and gradient-based LS-NMF¹⁵ both model the uncertainty in the expression data in the factorization. In addition, CoGAPS also leverages the Bayesian architecture through an atomic prior¹⁶ to model sparsity in both the amplitude and pattern matrices.

The NMF packages ccFindR¹⁷ and cNMF¹⁸ are also both well designed for use in single-cell experimentation. Both use prior distributions to create estimates of the amplitude and pattern matrices. ccFindR, however, implements Cemgil’s¹⁹ variational Bayesian inference algorithm, enabling update of both the prior and the hyperparameters, and cNMF implements neighbor clustering for outlier detection. CoGAPS is unique among these examples in that it models the prior distribution using an atomic domain. The algorithm implements update steps creating, removing or changing the values of individual atoms within the domain. This provides the algorithm with a set of fine revision tools, allowing it to make minute adjustments to the estimate after each iteration to yield a more precise approximation. In a benchmarking study comparing latent factor models in single-cell data, CoGAPS was shown to perform equally or better than other single-cell NMF algorithms²⁰.

Ultimately, choice of algorithm should be driven by the question and data at hand, and, if a different algorithm for NMF is used, the downstream analysis and interpretation methods presented here, and general principles described, will still be applicable. While all the procedures we present are readily adaptable for analysis with other NMF algorithms or even other forms of matrix factorization, we demonstrate analysis with CoGAPS.

Overview of NMF analysis

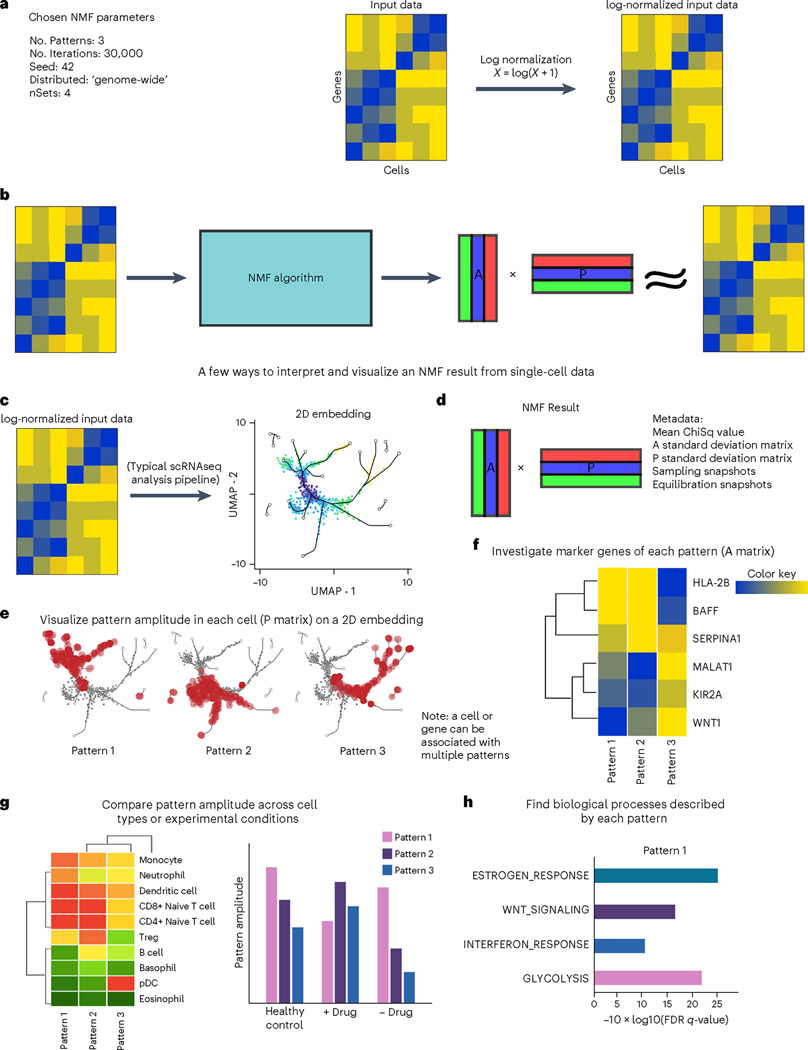
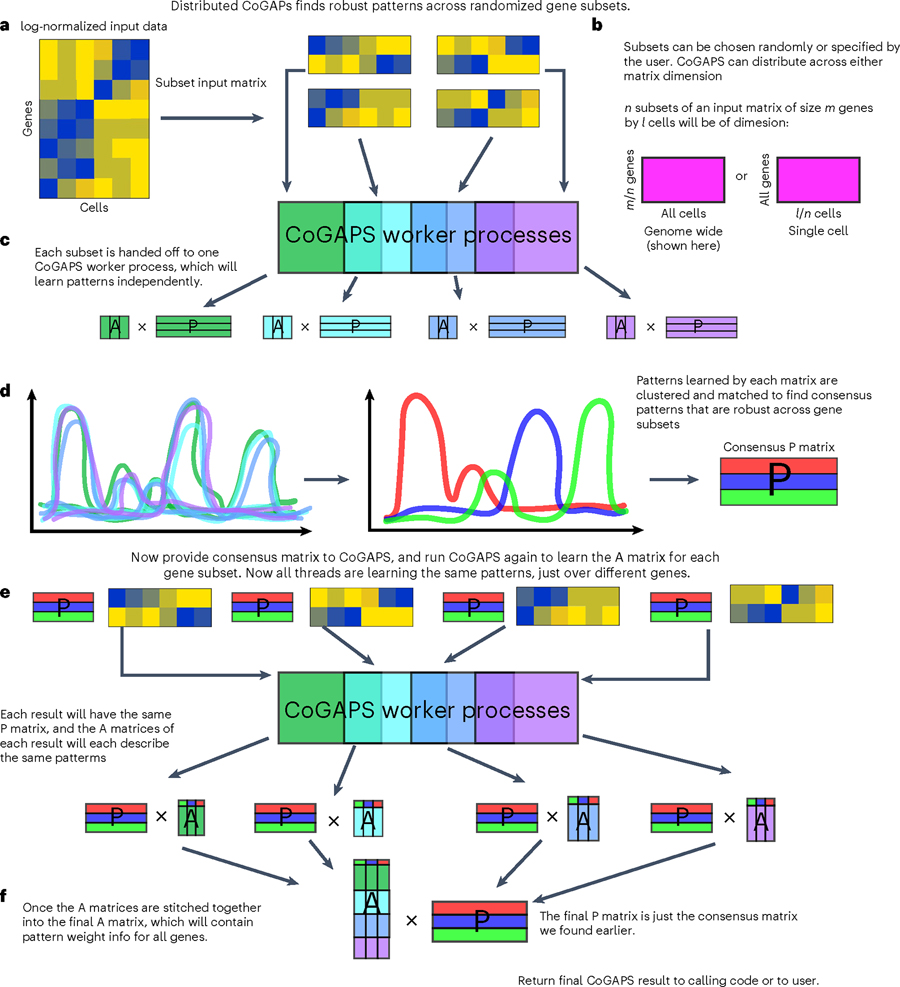
A generalized workflow for NMF analysis of single-cell data is summarized in Fig. 2. Each step in this workflow is described generally to facilitate customization of the template protocols to other factorization methods, non-negative and otherwise. The mechanism by which CoGAPS distributes across multiple sets when run in ‘distributed’ mode, as is recommended for most single-cell data, is illustrated in Fig. 3 (for more details, see the ‘Finding robust patterns using consensus across parallel sets’ section below).

Fig. 2 |. A generalized workflow for performing NMF on single-cell data.

a, NMF algorithms take as input a list of parameters and a data matrix. For scRNA-seq data, the counts matrix should be log-normalized. b, NMF yields an amplitude matrix (A) and a pattern matrix (P), which approximately factorize the input data. c, NMF results can supplement a dimension reduction analysis pipeline and can easily be visualized on a UMAP. 2D, two-dimensional. d, An NMF result typically consists of A and P matrices along with metadata about the run. e, To visualize the pattern weight in each cell, the P matrix can be used to color a UMAP or other dimension-reduction plot. f, The P matrix can also be used to compare pattern weights across cell types or experimental conditions. g,h, The A matrix can be used to find marker genes for each pattern (g), which can then be useful in GSEA (h), identifying biological processes and terms associated with each pattern. FDR, false discovery rate. Note that all specific genes, cell types and biological process terms referenced in this figure are merely examples and do not represent real data.

Fig. 3 |. Distributed CoGAPS finds robust patterns across randomized gene or sample subsets.

a, Subsetting is performed to break the input matrices into smaller components that can each be handed off to a worker process for NMF. b, Subsetting for parallelization can be performed across either matrix dimension. c, Each data subset yields its own NMF result. d, To identify the patterns that manifest themselves consistently across all NMF results, clustering is performed across all patterns returned by every thread, and a consensus matrix is generated from a process of matching cognate patterns. e, NMF is now run again on the same data subsets, this time with the consensus matrix provided as a ground truth from which the other matrix can be learned. This run is significantly faster than the first. f, Now that all threads have been forced to learn the same patterns, the portion of the NMF result that was not fixed can be stitched together to yield the final solution.

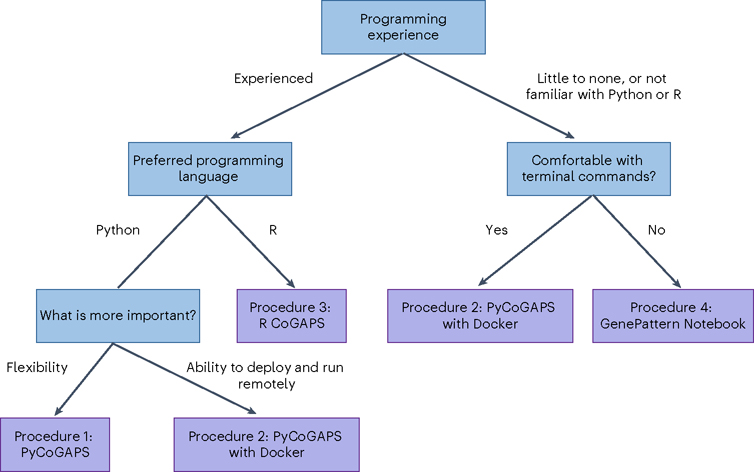
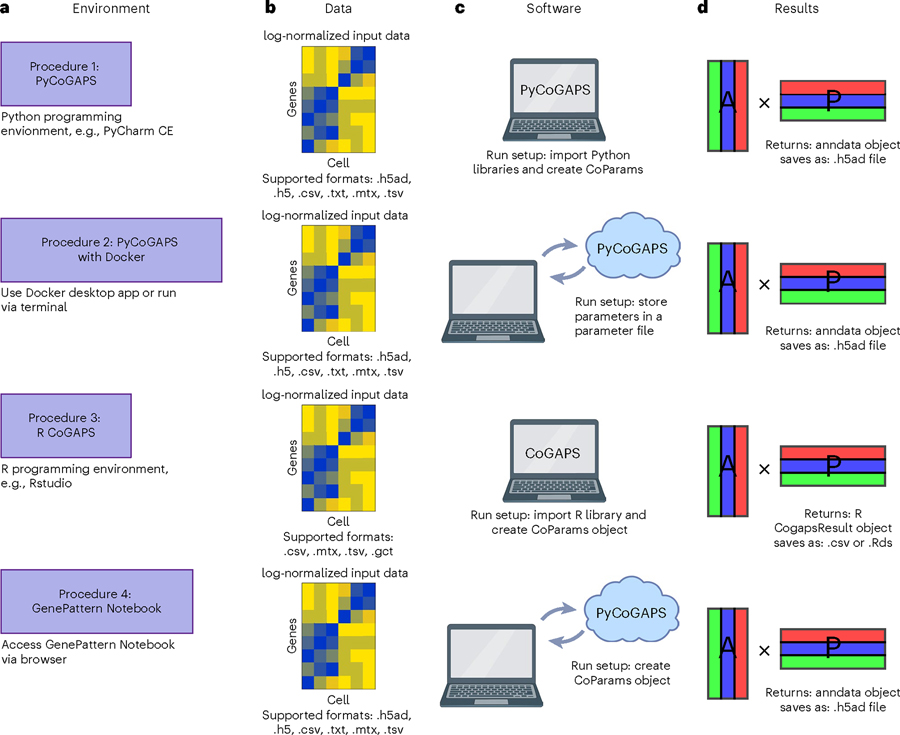
We provide four independent, equivalent procedures (procedures 1–4) for NMF analysis. Figure 4 is a decision tree to assist the user in deciding which protocol is best for them, and Fig. 5 compares the workflows visually. First, we provide two options for running CoGAPS via PyCoGAPS (procedures 1 and 2). Procedure 1 demonstrates using the PyCoGAPS package in a Python script, and Procedure 2 demonstrates automatic deployment of the computing job using a Docker image. Both options are functionally equivalent, so the user’s choice of interface should depend on factors such as familiarity with Python and/or Docker, and desire for flexibility and modification. Procedure 1 provides a full walkthrough of PyCoGAPS package capabilities. To deploy and run PyCoGAPS in fewer steps but with limited flexibility, follow Procedure 2.

Fig. 4 |. Decision tree for selecting the most appropriate PyCoGAPS or CoGAPS procedure to follow.

We provide four independent procedures (Procedures 1–4) for NMF analysis. Procedure 1 demonstrates PyCoGAPS with Python scripts, Procedure 2 demonstrates how to use PyCoGAPS with Docker, Procedure 3 demonstrates R CoGAPS and Procedure 4 demonstrates using PyCoGAPS within GenePattern Notebook.

Fig. 5 |. Graphical comparison of the procedures.

All four procedures in this protocol follow the same general steps, but each has its own technical requirements. a–d, Each procedure contains instructions to set up a CoGAPS workspace (a), a data loading step (b), parameter specification and run setup (c) and suggestions for analyzing and interpreting the CoGAPS result object (d).

Procedure 3 demonstrates the R CoGAPS API, and Procedure 4 demonstrates browser-based GenePattern Notebook. All these procedures follow equivalent steps and share the same CoGAPS backend, so the user’s choice of interface should depend on factors such as computing performance, familiarity with the programming language, and programming expertise. Please refer to Fig. 4 and/or Table 1 to determine which procedure is most appropriate to follow. For a comprehensive index of CoGAPS software, please visit the CoGAPS website, https://fertiglab.github.io/CoGAPSGuide/.

Table 1 |.

Workflow comparison for running Procedure 1: PyCoGAPS, Procedure 2: PyCoGAPS deployed through Docker, Procedure 3: R CoGAPS or Procedure 4: GenePattern Notebook

Procedure Choice	PyCoGAPS		CoGAPS: Procedure 3	GenePattern Notebook: Procedure 4:
	Procedure 1	Procedure 2
Overview	Using the CoGAPS Python package	Plug in parameters and run CoGAPS in a prepared Docker container	Using the CoGAPS R package	Run CoGAPS using prewritten code cells in a web browser environment
Preferred programming language	Python	Python/no preference	R	Python/no preference
Recommended programming experience	Experienced	Little to none	Experienced	Little to none
Install dependencies?	Yes	No	Yes	No
Customization flexibility	High	Limited	High	Limited
Parameter handling	Call functions	Easy plug-in	Call functions	Easy plug-in
Run location	Locally or own server	Locally or own server	Locally or own server	Remotely using Amazon Web Services

Users are recommended to choose the appropriate procedure based on factors including programming experience or preference.

Each procedure first provides details on setting up the relevant software (Procedure 1 Steps 1–3; Procedure 2 Step 1; Procedure 3 Step 1; Procedure 4 Steps 1–3). The user is then instructed to conduct a run on a simulated, small toy dataset called ModSim to quickly ensure proper setup of the package and environment (Procedure 1 Steps 4–7; Procedure 2 Step 2; Procedure 3 Steps 3–5; Procedure 4 Steps 4–7). Then, each procedure demonstrates running and analysis on a larger scRNA-seq pancreatic ductal adenocarcinoma (PDAC) dataset to draw biological conclusions (Procedure 1 Steps 8–13; Procedure 2 Steps 3–5; Procedure 3 Steps 6–8; Procedure 4 Steps 8–9). Figure 5 provides a general procedure workflow overview for running each procedure. Finally, each procedure details approaches to analyzing the output results (Procedure 1 Steps 14–19; Procedure 2 Steps 6–8; Procedure 3 Steps 9–13; Procedure 4 Step 10).

We will now discuss several best practices and open questions for NMF and offer strategies for choosing parameters and assessing the learned solutions.

Data preprocessing and input

The majority of NMF analyses are performed on normalized and log-transformed data²¹, which is recommended as a preprocessing step in our CoGAPS protocols (Procedure 1 Step 10; Procedure 2 Step 4; Procedure 3 Step 6; Procedure 4 Step 8). We note that regardless of how the input data is transformed, it must contain only non-negative values, as this is a central requirement of NMF. We note that some emerging NMF algorithms have error models designed for raw count data²², and therefore do not require this normalization.

Many scRNA-seq technologies are subject to drop-out, resulting in zero values for a large proportion of measurements from technical rather than biological conditions. Several imputation approaches have been developed to estimate the signal in these missing data before analysis²³. Still, it is not necessary to impute the input data for NMF analysis and indeed the reconstruction of the data estimated from the product of the inferred amplitude and pattern matrices can be used as an alternative imputation scheme²⁴. Moreover, the sparsity model in the atomic prior from CoGAPS is tailored to the sparsity of scRNA-seq data, motivating our selection of this algorithm as the foundation for this protocol⁹. If the user desires, imputed data is acceptable for input, but we note that the imputation algorithm employed will impact the inferred solutions.

Technical aspects of scRNA-seq experiments, such as library preparation, processing day, dissociation quality, etc., can introduce further artifacts in the signal from scRNA-seq data, leading to numerous batch correction approaches for scRNA-seq data²⁵. Some batch correction algorithms do not change the raw data and focus instead on aligning the embedding used to visualize scRNA-seq data²⁶, and therefore would not impact the factorization results. Other batch correction algorithms attempt to remove these technical signals from the data²⁷. These batch correction approaches may also affect the solution and should be used with caution. This is especially important as some algorithms, such as CoGAPS, have been demonstrated to concurrently learn technical and biological signals, making preprocessing to eliminate batch effects unnecessary⁸. Likewise, NMF approaches can also provide a unified embedding between datasets²⁸. We acknowledge that these first steps must often vary greatly depending on the biological context and invite the user to validate optimized custom preprocessing workflows for that context. Comprehensive reviews of preprocessing pipelines for scRNA-seq data have been previously published²⁹.

Iterative assessment of optimality of solutions

Biological inference based upon solutions of the amplitude and pattern matrices for a dataset relies on the assumption that the NMF algorithm has returned a stable and biologically relevant factorization. Determining optimality of factorization remains an open question, with various metrics developed to assess performance. These metrics will vary based on the type of NMF analysis used. Bayesian methods for NMF, including CoGAPS, estimate the posterior probability distribution for amplitude and pattern matrices. Bayesian NMF methods for genomics analysis employ a wide variety of Markov chain Monte Carlo (MCMC) and variational algorithms to learn these distributions. Whereas gradient-based and variation methods are subject to local minima, many MCMC methods are designed to overcome local optima, which is crucial in biological applications where there may be many semi-stable states and thus many local optima. However, this gain in the global optimality of solutions occurs at a cost: these algorithms must be run over many iterations, often resulting in long runtimes, which can be addressed with parallelization³⁰ or graphics processing unit computing³¹. Likewise, the local optima of gradient-based techniques can be overcome by leveraging parallel computing to determine the global optima by sampling solutions from multiple initial conditions.

After an MCMC run on a given dataset is complete, it remains to be assessed whether it was run for a sufficient number of iterations to attain accurate sampling from the posterior distributions for both the amplitude and pattern matrices—a property known as convergence— and whether the user-specified number of patterns learned corresponds appropriately to the biological question under investigation. When convergence is reached, increasing the number of iterations will enhance the density of sampling from the posterior distribution to improve analytic estimates of the distribution but will no longer improve the learned solution. The application of Bayesian convergence metrics to determine the stopping criterion for Bayesian NMF algorithms remains an open area of research. Therefore, it is critical to empirically evaluate the stability of the likelihood calculation over the chain to assess the optimal number of iterations for each Bayesian NMF algorithm.

As CoGAPS uses MCMC sampling to find the values of the A and P matrices, the results are stochastic. While results will vary between simulations, we have observed that solutions from multiple runs tend to have qualitatively similar gene signatures and cell weights in permuted pattern order. For reproducibility of CoGAPS results, we recommend setting the seed for each run and saving CoGAPS results after completion of the run as an intermediate object before interpretation.

The convergence metrics for each NMF algorithm depends on the details of the mathematical formulation of the model used for the factorization. In the case of CoGAPS, this algorithm performs factorization of a transcriptional dataset $D_{i,j}$ with genes $(i)$ and cells $(j)$, according to the Bayesian model $D_{i,j}\sim N(A_{i,.}{P}_{.,j},\mathrm{\Sigma });P(A_{i,k})\sim \mathrm{\Gamma }({\alpha }_{i,k}^A,{\lambda }^A);P(P_{k,j})\sim \mathrm{\Gamma }({\alpha }_{k,j}^P,{\lambda }^P)$ where $N(·,·)$ indicates a univariate normal distribution, the shape parameters are modeled according to a Poisson prior with hyperparameter $\mathrm{\alpha }$, and the additional hyperparameters are fixed to model transcriptional data³⁰. Implementing this model through an atomic prior¹⁶ enables Gibbs sampling and yields a sparse NMF solution, with matrix elements able to be exactly zero in cases where ${\alpha }_{i,k}^A$ and ${\alpha }_{k,j}^P$ are identically zero. For our purposes, we consider convergence to be attained when additional iterations no longer reduce the chi-squared value, that is, when it has stabilized (Fig. 6). Previously, we have found robust performance on scRNA-seq for $\mathrm{\alpha }=0.01$ and convergence after approximately 50,000 iterations for both equilibration and sampling³². Therefore, we use this algorithm and these parameters for the examples in this protocol (for parameter setting, please see Table 2 and Procedure 1 Step 11; Procedure 2 Step 4; Procedure 3 Step 7; Procedure 4 Step 5).

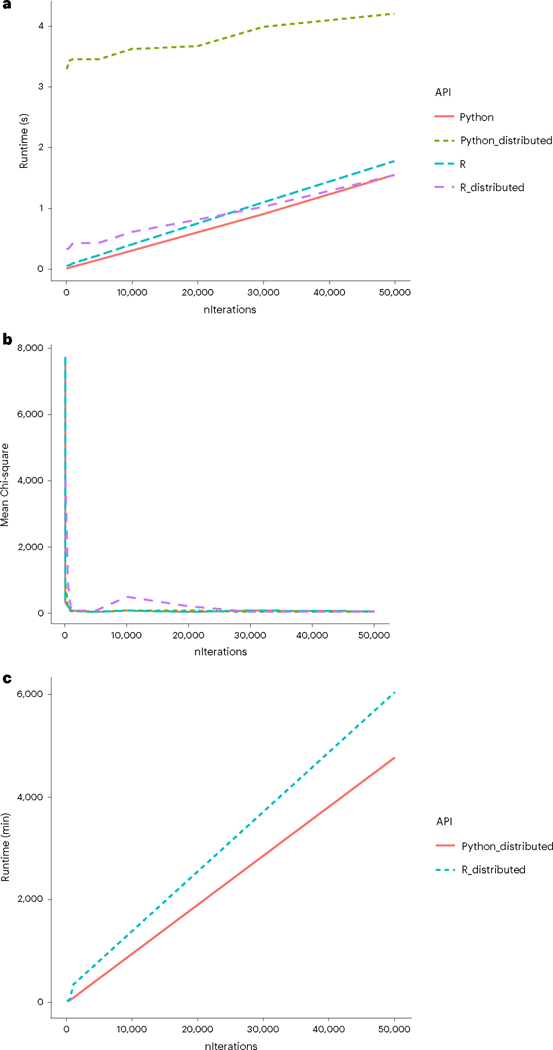
Fig. 6 |. Comparison of runtimes of R CoGAPS versus PyCoGAPS.

a, Benchmarking on a small dataset showed a startup cost associated with multiprocessing in distributed PyCoGAPS. b, In this small dataset, meanChiSq converges after a small number of iterations. meanChiSq values may differ slightly between distributed and single-threaded CoGAPS runs due to differing input matrix dimension. c, Benchmarking on a large single-cell dataset yielded these estimated runtimes, with Python slightly outperforming R.

Table 2 |.

Key parameters for CoGAPS/PyCoGAPS and guidance on setting their values

Parameter	Description	Guide to Setting
path	Path to data	Make sure data is log-normalized if providing a path rather than a data object
result_file	Name of result .h5ad file to output	Give this a descriptive name based on your data and run, such as PDACresult_50kiterations.h5ad
Standard parameters
nPatterns	Number of patterns CoGAPS will learn	The optimal number of patterns to learn will vary based on your data and may require several runs of varying values to observe learned features. We recommend starting off with selecting a value that represents the number of experimental conditions, cell types and/or biological processes expected from your data, as well as technical batches present
nIterations	Number of iterations of each phase of the algorithm	Higher iterations (i.e., 50,000 iterations) is recommended as it will lead to better convergence. However, higher iterations greatly increases runtime, so we invite the user to play around with values to observe the tradeoff and determine the appropriate value
useSparseOptimiz ation	Speeds up performance with sparse data	Set to true if using sparse data, i.e., if roughly >80% of data is zero
Run parameters
nThreads	Maximum number of threads to run on. Allows the underlying algorithm to run on multiple threads and has no effect on the mathematics of the algorithm	The precise number of threads to use depends on many factors such as hardware and data size. The best approach is to play around with different values and see how it affects the estimated time. This is separate from the distributed CoGAPS parallelization mechanism, which sets up multithreaded computing in a different way.
transposeData	Whether to transpose data	Whether to transpose the data matrix before running CoGAPS. Set to true if data is stored as samples × genes format (CoGAPS defaults to genes × samples format)
Distributed parameters
distributed	Whether to run distributed	Recommended in most cases for single-cell analysis. Set to ‘genome-wide’ for parallelization across genes, or ‘single-cell’ for parallelization across cells
nSets	Number of sets to break data into	For distributed with ‘genome-wide’, do not set value to below 2,000 genes per set. For distributed with ‘single-cell’, make sure this value captures sufficient representation of all cell types in the data
minNS	Minimum number of individual set contributions a cluster must contain	Be cautious in setting this value too high as increasing robustness may also cause misses in rare phenomenon or cells
maxNS	Maximum number of individual set contributions a cLuster can contain	Modifying this parameter is only important for highly correlated processes

Dimensionality estimation

The solutions learned by NMF depend critically upon the dimensionality $\kappa$ of the factorization, which is equal to the number of patterns, and therefore also equal to the number of columns in the amplitude matrix and the number of rows in the pattern matrix⁶. How to estimate the optimal dimensionality remains an open question in the field of unsupervised learning. In performing robustness analyses to estimate $\kappa$, we have found that these statistics may also have local minima for pattern robustness at different dimensions. In this case, greater resolution of multiple biological components often occurs at the second, higher value of $\kappa$, for which stability is first lost. Moreover, these two dimensions at which the local optima occur may both reflect distinct, hierarchical information about the underlying biological system with the dataset¹. For example, in a bulk genomics dataset of head and neck tumors, we found that NMF at $\kappa =2$ separated tumor and normal samples whereas NMF at $\kappa =5$ separated known head and neck cancer subtypes³³.

Choosing an optimal $\kappa$ for NMF is currently an unsolved problem in the field of mathematics, with current consensus being that there is probably no one true $\kappa$ for NMF, but rather different biological features are uncovered at different dimensions³⁴. Similar observations have been found in genomics analysis with other unsupervised learning techniques, including recently with autoencoders³⁵.

On the basis of these findings, we recommend and describe dimensionality estimation based on tests that require solving for a range of $\kappa$ values (for parameter setting, please see Table 2 and Procedure 1 Step 11; Procedure 2 Step 4; Procedure 3 Step 7; Procedure 4 Step 5). Linking solutions from multiple dimensionalities based on similarity and gene membership can not only provide information about robustness, but also uncover hierarchical relationships between patterns³⁶. Additionally, the cophenetic correlation coefficient can be used to assess the stability of sample clustering at a given dimensionality as described in Brunet et al.¹. When the clustering within a dimensionality is perfectly stable, the cophenetic correlation coefficient equals 1. Thus, increasing the dimensionality until the magnitude of the cophenetic correlation coefficient is >1 can determine the maximum $\kappa$ at which cluster stability is preserved.

For the workflows and datasets we present here, we chose nPatterns = 8 based on multiple runs at a range of nPatterns from 8 to 12. We settled on 8 patterns as marker gene analysis of the results, as using nPatterns = 10 and nPatterns = 12 showed that, from the perspective of our analysis, patterns learned at the higher dimensionalities also represented the same biological processes in the nPatterns = 8 results based on overrepresentation analysis of pattern marker genes with hallmark gene sets while additional patterns were learned¹¹. Thus, the choice of 8 patterns was made because this is the dimensionality that captured processes of interest that also predominated at higher dimensionality, while not diluting signal across a larger number of patterns.

We note that regardless, $\kappa$ must be far less than either dimension of the input dataset to yield theoretically identifiable solutions from NMF. However, similarly to other machine learning paradigms, the stability of solutions beyond this theoretical upper bound has been observed. Thus, is it likely that NMF may also experience a double-descent phenomenon.

Analysis and visualization of inferred cellular features in the pattern matrix

Single-cell experiments can provide measurements associated with numerous features of biological systems, including cell type, cell state, temporal transitions, cell cycle and metabolic states, and spatial localization³⁷. Yet the data also includes numerous technical artifacts from features, notably batch effects between libraries, dissociation protocols and dropout³⁸. A critical advantage of NMF for scRNA-seq data is its ability to learn separate patterns associated with each of the biological and technical features from a single analysis². Nonetheless, uncovering these features from an NMF analysis of scRNA-seq data depends critically upon relating the weights of the matrix elements for each row of the pattern matrix and amplitude matrix to the biological feature or technical artifact that they represent⁶ (Fig. 2).

The most direct means of assessing the biological meaning of each pattern is to correlate its values with annotations of the experimental conditions or cell type calls in the single-cell data (Procedure 1 Step 17; Procedure 3 Step 11). However, these statistics will not delineate the cellular heterogeneity within these conditions that incentivize the use of single-cell data in these studies. Therefore, visualization is a critical component of this biological interpretation of the pattern matrix (Fig. 2). Dimensionality reduction tools such as t-distributed stochastic neighbor embedding (t-SNE) or Uniform Manifold Approximation and Projection (UMAP) are used for visualizing single-cell analysis, and in the case of CoGAPS, they can be used for interpreting patterns in low-dimensional space (Procedure 1 Step 15; Procedure 3 Step 10; Procedure 4 Step 10). Dynamic transitions are then apparent from high pattern weights in intermediate states between cell types or areas of high RNA velocity³⁹. These dynamics will also often be apparent along pseudotime trajectories. Thus, correlation or linear models associating pattern weights to pseudotime trajectories can be used to quantify these relationships. A critical advantage of NMF is its ability to learn the interrelationships between cell type and experimental conditions that are not readily apparent from the visualizations used in a typical single-cell analysis workflow. Statistical tests such as multivariate analyses of variance (MANOVAs), t-tests or other factor-based tests of the pattern weights for these conditions with the experimental covariates such as treatment, condition, age, sex, etc. can assess the significance of these learned relationships. We provide functions in both Python PyCoGAPS and R CoGAPS to statistically assess the ability of learned patterns to differentiate groups of cells with MANOVA (Procedure 1 Step 16; Procedure 3 Step 14; Procedure 4 Step 10). We additionally provide statistics for assessing significance of genes as they correlate to patterns (Procedure 1 Step 18; Procedure 3 Step 12; Procedure 4 Step 10) (Fig. 2e,g).

Assessing the biological function of gene signatures from the amplitude matrix

Association of genes and pathways with the features learned from NMF analysis facilitates annotation to inform biological interpretation and hypothesis generation (Fig. 2f). For each row of the pattern matrix, there is a corresponding column in the amplitude matrix containing gene weights for the learned feature that can be used for these associations⁶ (Fig. 1). Each feature can be associated with biological processes or pathways by performing gene set enrichment analyses of the gene weights in each column of the amplitude matrix with pre-annotated sets (Fig. 2h) such as those curated in MSigDB⁴⁰ (Procedure 1 Step 19; Procedure 3 Step 13; Procedure 4 Step 10). In the case of Bayesian methods such as CoGAPS, these set statistics have been developed to leverage Z-scores that account for the posterior distribution of the amplitude matrix⁴¹.

An advantage of NMF for pathway discovery is its ability to highly weigh one gene in multiple columns of the amplitude matrix, reflecting the natural multipurpose nature of many genes that are active in multiple biological processes, pathways or cell types. However, this tends to hinder the identification of unique genes associated with each of the learned patterns. These marker genes are essential to define biomarkers of the learned process and prioritize candidates for experimental validation. Statistics that instead quantify the unique association of genes with each column in the amplitude matrix can be used for this analysis⁴².

For example, the patternMarker statistic in CoGAPS and PyCoGAPS (Procedure 1 Step 18; Procedure 3 Step 12; Procedure 4 Step 10) ranks genes according to this unique association by ranking every gene for every pattern by scaling the gene weights in the amplitude matrix to their maximum value, and then iteratively matching genes to the pattern with the lowest distance from the identity vector for that pattern, and returning a list of ‘marker genes’ for each pattern, which can then be used to interpret their biological significance. The patternMarkers function has two modes designated by the threshold parameter (Box 1). When threshold = ‘all’, each gene is designated as a marker for whichever pattern it is most associated with, and the number of markers will equal the number of genes (each gene is a marker of one pattern). When threshold = ‘cut’, marker genes returned will be the subset of genes that are associated with each pattern, such that they are not more greatly associated with another one of the patterns. We provide both options to account for cases where a user would want statistics for every gene present, and cases when the user would want a shorter list of summary genes most uniquely associated with that pattern. The former statistic could be used downstream to perform enrichment analysis, and the latter could have utility for preranked gene set analysis. We demonstrate use of these statistics and provide protocols for their interpretation in the procedures (Procedure 1 Steps 14–19; Procedure 2 Steps 6–8; Procedure 3 Steps 9–13; Procedure 4 Step 10).

Box 1. PatternMarkers ‘threshold’ parameter.

The patternMarkers() CoGAPS function finds genes associated with each pattern and returns a dictionary of information containing lists of marker genes, their ranking, and their ‘score’ for each pattern. This is vital because genes are often associated with multiple patterns.

The three components of the returned dictionary pm are:

• PatternMarkers

  • a list of marker genes for each pattern
  • Can be determined using two threshold metrics, see below, and the ‘Assessing the biological function of gene signatures from the amplitude matrix’ section of the Introduction.
• PatternMarkerRank

  • each gene ranked by association for each pattern
  • Whole natural numbers, assigning each marker gene a place in the rank for each pattern
  • Lower rank indicates higher association and vice versa
• PatternMarkerScores

  • scores describing how strongly a gene is associated with a pattern.
  • A lower score value indicates the gene is more associated with the pattern, and vice versa
  • Scores have nonnegative values mostly falling between 0 and 2

If threshold = ‘all’, each gene is treated as a marker of one pattern (whichever it is most strongly associated with). The number of marker genes will always equal the number of input genes. If threshold = ‘cut’, a gene is considered a marker of a pattern if and only if it is less significant to at least one other pattern. Counterintuitively, this results in much shorter lists of patternMarkers and is a more convenient statistic to use when functionally annotating patterns.

We note that often NMF analyses yield one ‘flat’ pattern that is roughly constant across all cells, accounting generally for highly expressed genes⁴³. This pattern, while useful in other ways, should be excluded from the calculation of the patternMarker statistic to avoid falsely thresholding highly expressed genes. Creating a heat map of the input data with genes ordered by their rank for each pattern can provide a clear visualization of the learned patterns⁴³.

Finding robust patterns using consensus across parallel sets

One limitation to the Bayesian structure of CoGAPS over other NMF approaches is the computational costs of numerous iterations to estimate the distribution of the amplitude and pattern matrices. The computational cost of these iterations increases as a function of the size of the dataset. To overcome this computational cost, CoGAPS supports a ‘distributed’ mode of running (Procedure 1 Step 8; Procedure 2 Step 4; Procedure 3 Step 7; Procedure 4 Step 8) in which the input data is sampled into n subsets of genes across every cell (genome-wide mode) or n subsets of cells across every gene (single-cell mode) in an highly parallel manner³⁰ (Fig. 3 and Box 2). Subsetting can be performed randomly, explicitly or using weighted assignments to ensure an even distribution of cell types among sample subsets. These supervised options are critical for users who wish to discover patterns associated with a rare cell type. For example, a pattern representing semi-stable cell state transitions from normal to cancer was identified in the PDAC data by selecting only epithelial cells for analysis¹¹.

Box 2. Running Distributed CoGAPS.

If you wish to run distributed CoGAPS, which we recommend for most cases, set the ‘distributed’ parameter to ‘genome-wide’ (parallelize across genes), or ‘single-cell’ (parallelize across cells). Please see Fig. 3 for a full explanation of the mechanism.

cut, minNS and maxNS control the process of matching patterns across subsets and in general should not be changed from defaults. More information about these parameters can be found in the original papers.

nSets controls how many subsets are run in parallel when using the distributed version of the algorithm. Setting nSets requires balancing available hardware and runtime against the size of your data. In general, nSets should be less than or equal to the number of nodes/cores that are available. If that is true, then the more subsets you create, the faster CoGAPS will run; however, some robustness can be lost when the subsets get too small. The general rule of thumb is to set nSets so that each subset has between 1,000 and 5,000 genes or cells to give robust results, but ideally, we would want as many cells per set as possible. More information on these parameters can be found in Table 2.

If explicitSets are not provided, the data will be randomly fragmented into the number of sets specified by nSets parameter, with the default being 4. Subsets can also be chosen randomly, but weighted according to a user-provided annotation in parameters samplingAnnotation and samplingWeight.

Next, CoGAPS is run on each input matrix and these results are clustered and transformed into a smaller set of consensus patterns, the rationale being that robust biological patterns will manifest themselves across multiple subsets of genes or cells. For randomly sampled independent subsets, the robustness of the learned patterns can be statistically quantified. The resulting consensus matrix (either A or P depending on the mode) is then given as input to another CoGAPS run across the same subsets. This forces each thread to learn only the nonfixed matrix, so the patterns returned from this run will all be directly comparable across subsets (i.e., pattern 1 in subset 1 is the same as pattern 1 in subsets 2, 3 and 4). This process enables the results to be combined into complete A and P matrices that factor the original input matrix. By using this consensus process, not only is there a significant increase in computational efficiency, but also an increased robustness of the final solution¹⁸.

Multi-omic methods

The protocols presented here are focused on scRNA-seq data. Still, they could be extended to multi-omics analysis for data from different technologies. Coupled NMF methods⁴⁴ that simultaneously decompose multiple datasets can reveal shared features with the visualizations and post hoc statistics on the output matrices as described above. This can be achieved by modifying our workflows to input concatenated datasets between data modalities, combined along rows or columns depending on the analysis task⁴⁵. While applicable for multi-omics analysis⁴⁴, the implicit assumptions of these coupled methods may not accurately model timing differences between datasets or features unique to one.

As an alternative, transfer learning methods that project the gene weights from the amplitude matrix learned in one source dataset onto the other datasets to compare the use of features in this new dataset. This would be accomplished by applying our protocols described below to learn patterns in a single reference dataset, and then subsequently applying our projectR method for transfer learning to the new query dataset⁴⁶. We have found that only biological features, not technical, successfully transfer between related datasets and enable comparison between data platforms, species, tissues and molecular modalities²⁶. This transfer learning approach can be used to annotate features in the original input source dataset based on information from the new target dataset. For example, our NMF analysis of scRNA-seq data from epithelial cell state transitions resulting from fibroblast interactions were preserved in co-culture scRNA-seq data from an in vitro organoid model¹¹. In the context of cancer immunotherapy, this approach also enables the discovery of preserved cell state transitions from therapy that are shared between preclinical models and human tumors⁴⁷. Likewise, this transfer learning approach can enable integration with spatial single-cell data or high-resolution imaging data to enable mapping of non-spatially resolved single-cell data⁴⁸. CoGAPS has complete support for analysis of spatial transcriptomics data in the new package SpaceMarkers⁴⁹ and can also be readily extended to spatial and non-spatial single-cell proteomics data.

Limitations

While we focus on NMF analysis of scRNA-seq data with CoGAPS in this protocol, we note that many of the visualization and interpretation steps are also applicable to results obtained with alternative factorization methods and that there is no universal consensus as to the most robust factorization method for single-cell data. We selected CoGAPS due to the sparse and robust nature of its solution, found previously to enhance biological interpretation over other methods⁵. A limitation of CoGAPS is its long runtime, due to the sequential MCMC approach employed to estimate the posterior distribution according to an adaptive sparse prior distribution⁹. Future work will address this limitation through the development of a graphics processing unit implementation, as has been developed for alternative Bayesian NMF models³¹.

The unsupervised nature of NMF can limit the interpretation of features to prior knowledge or annotations of the biological system measured with the single-cell data. New techniques for independent assessment of biological robustness and interpretation are essential for biological discovery. Although beyond the scope of this protocol, NMF analyses comparing multiple datasets enable assessment of the robustness of learned features and discover new relationships between distinct biological contexts²⁸.

Another limitation inherent in this approach is the strict requirement for a choice of κ, the number of patterns to learn. This is an absolute requirement because the base matrices must be initialized at their final and only size, and dimensions must be such that matrix multiplication will yield a matrix of the same dimension as the input data. (m by κ) × (κ by p) = (m by p), where m = number of gene features (or equivalent), p = number of cells (or equivalent). We note that matrix factorization can be valid for any κ, as long as κ < m, p and for a large number of those cases, but certainly not all, a coherent factorization can and will be reached by CoGAPS. The existence of a theoretical ‘optimal κ for a given dataset, or in this case, a ‘true’ number of patterns present in the input data, is currently an open question in the field of mathematics, with some recent work showing that there can be no single optimal κ³⁴.

Materials

Data

All four procedures are demonstrated with publicly available data which we preprocessed and made available for convenience.

ModSim is a small, simulated dataset that will be used to ensure proper setup and run of PyCoGAPS/CoGAPS in each procedure.

• (Required) ModSim simulated dataset and a reference NMF result live in CoGAPS/pycogaps github repositories in the data/directories.

  • Name: ModSimData.txt (25 ‘genes’ × 20 ‘cells’, simulated data)
  • Reference result: ModSimResult.h5ad (anndata result object)

  The single-cell protocol is demonstrated using preprocessed and harmonized scRNA-seq data of 25,422 pancreatic epithelial cells from two studies of PDAC. In the Python vignette, this is retrieved from inputdata.h5ad, and in R, it can be loaded as a Seurat object from inputdata. Rds. We note that this is the same data in two different formats necessitated by the different languages of the APIs.

• (Optional) scRNA-seq PDAC dataset

  • We encourage the user to download the appropriate annotated and prepared .h5ad (for Python) r .Rds (for R) files available at https://zenodo.org/record/7709664.
    The necessary data files may be automatically included in pycogaps, but they will not be automatically included in a fresh R CoGAPS installation.
  • Reference dataset: inputdata.h5ad (Python) inputdata.Rds (R) (dimension: 15,219 genes × 25,422 cells)
  • Reference result: cogapsresult.h5ad (Python) cogapsresult.Rds (R) (dimension: 15,219 genes × 25,422 cells)

  All code and data needed to reproduce the results of these workflows can be found hosted on Zenodo⁵⁰ at https://zenodo.org/record/7709664.

Software

CRITICAL For a comprehensive overview of all available CoGAPS software, tutorials and links to source code, please visit the CoGAPS website:

Software specifications

• Operating system: MacOS, Linux, Windows or the Ubuntu subsystem for Windows (https://docs.microsoft.com/en-us/windows/wsl/install)

If following Procedure 1, PyCoGAPS with Python scripts

• Python v3.8 or later (https://www.python.org/downloads/release/python-380/)

• C++ compiler (Box 3)

• Python integrated development environment (IDE) software such as VS Code, PyCharm or Jupyter

Box 3. C++ Compiler Information.

Linux: C++ compiler comes standard with most if not all distributions

MacOS: ensure XCode is installed on your machine. If using the M1 chip, we recommend updating your software to at least MacOS Monterey 12.2.1 as it fixes a crucial issue with compiler linkages.

Windows: you may need to install Microsoft Build Tools. If you experience significant issues during compilation, we recommend building CoGAPS on the Ubuntu subsystem, which is available on the Windows application store.

If following Procedure 2, PyCoGAPS with Docker

• Docker (https://docs.docker.com/get-docker/)

• For Windows users only:

  • Ensure hyper V and virtualization is enabled
  • Install linux to get WSL2, with default Ubuntu

If following Procedure 3, R CoGAPS

• R (recommended v4 or later; known to be stable for R 4.2.1)

• RStudio (https://www.rstudio.com/products/rstudio/download/)

If following Procedure 4, GenePattern Notebook:

• No software is needed

Hardware

CoGAPS can be run on most laptops and compute clusters. Due to the nature of the CoGAPS algorithm, memory and random access memory requirements will scale with the size of data being analyzed, number of patterns requested, number of threads and number of iterations.

Procedure 1: running PyCoGAPS: user startup guide for the Python CoGAPS API

Software setup

● TIMING 5–10 min

• 1
  To download PyCoGAPS from GitHub with all data included (~2 GB memory), run the following command:

  git clone https://github.com/FertigLab/pycogaps.git —recursive
  

  The expected output is shown in Supplementary Note 1. Alternatively, to download PyCoGAPS without the large files (inputresult.h5ad and cogapsresult.h5ad), run the following command:

  GIT_LFS_SKIP_SMUDGE=1 git clone https://github.com/FertigLab/pycogaps.git --recursive
  

  Please note that the files (inputresult.h5ad and cogapsresulth5ad) are also available for download from Zenodo: https://zenodo.org/record/7709664.

  ◆ TROUBLESHOOTING

• 2
  Install the required package dependencies. Users may wish to install these dependencies in an Anaconda⁵¹ environment (Box 4):

  cd pycogaps
  pip install -r requirements.txt
  

• 3
  Now run the setup script to install the C++ core CoGAPS library.

  python3 setup.py install
  

  When PyCoGAPS has installed and built correctly, you should see this message, indicating PyCoGAPS is ready to use:

  Finished processing dependencies for pycogaps==0.0.1
  

  ◆ TROUBLESHOOTING

Box 4. Anaconda environment.

Install Anaconda from here: https://docs.anaconda.com/anaconda/install/

Instructions for setting up a conda environment can be found here: https://conda.io/projects/conda/en/latest/user-guide/getting-started.html

Users may wish to create a conda environment and install all requirements and run code from within here. We note that conda is not a required dependency of CoGAPS and its use is down to preference.

Running PyCoGAPS on simulated data

● TIMING 3–5 min

CRITICAL This code be found in the reference file modsimvignette.py.

• 4
  Import libraries. In the python script, import the PyCoGAPS functions with the following lines:

  from PyCoGAPS.parameters import *
  from PyCoGAPS.pycogaps_main import CoGAPS
  import scanpy as sc
  

• 5
  Load sample data from data directory.

  modsimpath = “data/ModSimData.txt”
  modsim = sc.read_text(modsimpath)
  

  The new modsim object in the python console is an anndata object of dimension 25 × 20.

  modsim
  AnnData object with n_obs × n_vars = 25 × 20
  

• 6
  Next, set the run parameters to be used by PyCoGAPS. First, create a CoParams object. printParams() displays all parameters currently set for the parameter object. Since this object was just generated using the constructor, all default parameters are currently set.

  params = CoParams(path=modsimpath)
  params.printParams()
  -- Standard Parameters --
  nPatterns: 3
  nIterations: 1000
  seed: 0 sparseOptimization: False
  -- Sparsity Parameters -- alpha: 0.01
  maxGibbsMass: 100.0
  

  Then, set parameters by calling the setParams function. As we recommend simulating a full-length run on this very small matrix, change nIterations. Many parameters can be changed at once using this dictionary syntax:

  setParams(params, {
  ‘nIterations’: 50000,
  ‘seed’: 42,
  ‘nPatterns’: 3
  })
  

  For now, only modify the ‘nIterations’, ‘seed’ and ‘nPatterns’ parameters. Setting the seed fixes the random number generator so that the stochastic, MCMC algorithm used to solve for the A and P matrices in CoGAPS provides identical solutions between runs.

  Verify nIterations was updated as anticipated:

  params.printParams()
  -- Standard Parameters -- nPatterns: 3
  nIterations: 50000
  seed: 42 sparseOptimization: False
  -- Sparsity Parameters -- alpha: 0.01
  maxGibbsMass: 100.0
  

  More description of the parameters and parameter tuning can be found in Table 2.

• 7
  As parameters and data are now ready, start the PyCoGAPS run. As a best practice, we recommend always timing CoGAPS runs for your own records.

  start = time.time()
  modsimresult = CoGAPS(modsim, params) print(“TIME:”, end - start)
  

  Since modsim is a small, toy dataset, the expected runtime is only ~3 s. Verify that the following output appears as in Supplementary Note 2. Also inspect the result object (Supplementary Note 3), to ensure that there are two resulting base matrices filled with plausible values. If PyCoGAPS has been set up and run correctly, proceed to analyzing experimental single-cell data.

Running PyCoGAPS on single-cell data

● TIMING 5 min to 2 d (depending on whether user runs NMF or uses precomputed result)

CRITICAL This code be found in the reference file pdacvignette.py

• 8
  Import necessary libraries, wrapped in check:

  if __name__ == “__main__”:
  from PyCoGAPS.parameters import *
  from PyCoGAPS.pycogaps_main import CoGAPS
  import scanpy as sc
  

  CRITICAL STEP Whenever distributed (i.e., multithreaded) options are used, all calling code must be wrapped in a check like this so it will only be called by the parent process. Missing this line will send calling code into infinite recursion. All subsequent calling code, not just the imports, must fall under this check such that it will only be executed when the check succeeds. Note that single-threaded CoGAPS, such as the run demonstrated above with ModSim data, does not require this check. It is a perfectly valid and correct way to run CoGAPS. We show distributed-friendly code here because it will be relevant to most single-cell analysis users, who stand to gain both in performance and robustness of solution.

• 9
  A single-cell dataset has been provided for this vignette. If it is not already located in the ‘data’ folder when we cloned the repository, please download it from https://zenodo.org/record/7709664 and place it there. Read in the data as an anndata object.

  path = “data/inputdata.h5ad”
  adata = sc.read_h5ad(path)
  

  While CoGAPS can handle multiple data formats, we strongly recommend converting your data to anndata format using the anndata package⁵² or another utility designed for translating between data structures. The returned object will be in anndata format.

• 10
  The data matrix is stored in sparse compressed row format, and it is strongly recommended to normalize data before running PyCoGAPS. Decompress and normalize the data matrix, using the scanpy package⁵³ to perform log normalization.

  adata.X = adata.X.todense()
  sc.pp.log1p(adata)
  

  CoGAPS expects genes in .obs and cells in .var, which is the opposite of scanpy’s convention. Therefore, after normalizing, transpose the matrix into CoGAPS expected format.

  adata = adata.T
  

  Examine adata:

  adata
  AnnData object with n_obs × n_vars = 15219 × 25442
  obs: ‘gene_ensembl_ID’, ‘gene_short_name’, ‘feature_in_nCells’ var:
  ‘barcode_raw’, ‘celltype’, ‘sample_ID’, ‘sample_ID_celltype’,
  ‘TN’, ‘TN_manuscript’, ‘manuscript’, ‘nCount_RNA’, ‘nFeature_RNA’,
  ‘percent.mt’, ‘Size_Factor’, ‘TN_cluster_resolution_5’, ‘TN_assigned_
  cell_type’, ‘TN_assigned_cell_type_immune’, ‘TN_assigned_cell_
  type_immune_specific’, ‘TN_assigned_cell_type_immune_broad’, ‘cc’,
  ‘ccstage’, ‘Classifier_T_duct’, ‘Classifier_T_Fibroblast_only’,
  ‘Classifier_T_Fibroblast_Stellate’
  uns: ‘log1p’
  varm: ‘X_aligned’, ‘X_pca’, ‘X_umap’
  

  This is an anndata object consisting of scRNA-seq data from 25,422 pancreatic epithelial cells, with reads from 15,219 genes. The .obs and .var matrices contain metadata such as gene names, cell annotations and clustering results.

  CRITICAL STEP Any transformation or scaling you choose to perform on your count matrix must result in all non-negative values due to the core constraint of NMF.

• 11
  Next, create a parameters object that stores run options in a dictionary format. Note that the easiest way to decrease runtime is to run for fewer iterations, and you may want to set nIterations = 1,000 for a test run before starting a complete CoGAPS run on your data.

  params = CoParams(adata=adata) setParams(params, {
  ‘nIterations’: 50000,
  ‘seed’: 42,
  ‘nPatterns’: 8,
  ‘useSparseOptimization’: True,
  ‘distributed’: “genome-wide”
  })
  

  We recommend running distributed for most cases to decrease runtimes. If doing so, you must run this line, where you can specify how many sets will be created and parallelized across, as well as specify cutoffs for how stringently a consensus matrix is determined.

  params.setDistributedParams(nSets=7)
  

  Please refer to Box 2 for further details on running distributed PyCoGAPS. A description and guide for setting key PyCoGAPS parameters can be found in Table 2. To view the parameter values that have been set, we include a printParams function (Box 5). There are many more additional parameters that can be set depending on your goals, which we invite the reader to explore in our GitHub documentation.

• 12
  With all parameters set, a PyCoGAPS run can be started with the following command:

  start = time.time()
  result = CoGAPS(adata, params)
  end = time.time()
  print(“TIME:”, end - start)
  

  While CoGAPS is running, you will see periodic status messages, described in Box 6, and when the run is finished, CoGAPS will print a message like the one shown in Box 7. Please note that this is the most time-consuming step of the procedure. Timing can take several hours and scales nlog(n) based on dataset size (see the ‘Timing’ section below), as well as the parameter values set for ‘nPatterns’ and ‘nIterations’. Time is increased when learning more patterns, when running more iterations and when running a larger dataset, with iterations having the largest variable impact on the runtime of the NMF function. As this step has a long runtime, users who want to load an already-complete NMF run and proceed to the analysis portion of this vignette can skip to Step 14.

  ◆ TROUBLESHOOTING

• 13
  When CoGAPS has finished running, write the NMF result to disk. We strongly recommend saving your result object as soon as it returns. This can be done by directly saving the anndata object (for more details about the CoGAPS output data format, please see Box 8):

  result.write(“data/my_pdac_result.h5ad”)
  To save as a .csv file, use the following line:
  result.write_csvs(dirname=‘./’, skip_data=True, sep=‘,’)
  

  PAUSE POINT Now we have successfully generated and saved a CoGAPS result. The procedure may be paused.

Box 5. Viewing all Parameters in PyCoGAPS.

To see all parameters that have been set, call:

params.printParams()

Expected output:

running genome-wide. if you wish to perform single-cell distributed
cogaps, please run setParams(params, “distributed”, “single-cell”)
setting distributed parameters - call this again if you change nPatterns
-- Standard Parameters --
nPatterns: 8
nIterations: 50000
seed: 42
sparseOptimization: True
-- Sparsity Parameters --
alpha: 0.01
maxGibbsMass: 100.0
-- Distributed Parameters --
cut:8
nSets:7
minNS:4
maxNS:11

Box 6. CoGAPS status messages.

While CoGAPS is running, you will see periodic status messages in the format of the example below reporting how many iterations have been completed, the current ChiSq value and how much time has elapsed out of the estimated total runtime. When running multithreaded, each thread may output progress messages to the console separately. For n threads, you will see each message repeated n times.

20000 of 25000, Atoms: 2932(80), ChiSq: 9728, time: 00:00:29 /00:01:19

This message tells us that CoGAPS is at iteration 20,000 out of 25,000 for this phase and that 29 s out of an estimated 1 min 19 s have passed. It also tells us the size of the atomic domain, which is a core component of the algorithm but can be ignored for now. Finally, the ChiSq value tells us how closely the A and P matrices reconstruct the original data. In general, this value should go down, but it is not a perfect measurement of how well CoGAPS is finding the biological processes contained in the data. CoGAPS also prints a message indicating which phase is currently happening. There are two phases to the algorithm: Equilibration and Sampling.

Box 7. PyCoGAPS anndata result and metadata.

The PyCoGAPS result is returned in anndata format, with observation and variable annotation Matrices containing the returned amplitude and pattern matrices. Additional information about The run can be found the the unstructured annotation component of the anndata object.

AnnData object with n_obs × n_vars = 15219 × 25442
obs: ‘Pattern1’, ‘Pattern2’, ‘Pattern3’, ‘Pattern4’, ‘Pattern5’,
‘Pattern6’, ‘Pattern7’, ‘Pattern8’
var: ‘Pattern1’, ‘Pattern2’, ‘Pattern3’, ‘Pattern4’, ‘Pattern5’,
‘Pattern6’, ‘Pattern7’, ‘Pattern8’
uns: ‘asd’, ‘atomhistoryA’, ‘atomhistoryP’, ‘averageQueueLengthA’,
‘averageQueueLengthP’, ‘chisqHistory’, ‘equilibrationSnapshotsA’,
‘equilibrationSnapshotsP’, ‘meanChiSq’, ‘meanPatternAssignment’, ‘psd’,
‘pumpMatrix’, ‘samplingSnapshotsA’, ‘samplingSnapshotsP’, ‘seed’,
‘totalRunningTime’, ‘totalUpdates’
varm: ‘X_aligned’, ‘X_pca’, ‘X_umap’

Box 8. The PyCoGAPS result object.

The CoGAPS result is returned in anndata format. CoGAPS stores the lower-dimensional representation of the samples (P matrix) in the .var slot and the weight of the features (A matrix) in the .obs slot. If you transpose the matrix before running CoGAPS, the opposite will be true. Running single cell is equivalent in every way to transposing the data matrix and running single cell. The standard deviation across sample points for each matrix as well as additional metrics are stored in the .uns slots. Please refer to https://github.com/FertigLab/pycogaps#readme for complete documentation of output metrics.

Analyzing the PyCoGAPS result

(Reference code can be found in the file analyzepdac.py)

● TIMING 20–30 min

CRITICAL This section demonstrates a basic analysis of both the A and P matrix (gene and sample associated pattern weights), describing how to analyze and visualize the generated saved data result. These helper functions are a starting point for interpreting single-cell NMF patterns, but most users will almost certainly wish to export their NMF result and incorporate it into their existing single-cell pipeline.

• 14
  Load the saved result file, which can be your own NMF result generated from the previous step, or the precomputed one, cogapsresult.h5ad from https://zenodo.org/record/7709664 or supplied in our repository. Enter the following command to use the precomputed result, or to use your own object, simply replace the path with your own:

  import anndata
  import pandas as pd
  import scanpy as sc
  cogapsresult = anndata.read_h5ad(“data/cogapsresult.h5ad”)
  

  Inspect the object:

  » cogapsresult
  AnnData object with n_obs × n_vars = 15176 × 25442
  obs: ‘Pattern_1’, ‘Pattern_2’, ‘Pattern_3’, ‘Pattern_4’, ‘Pattern_5’,
  ‘Pattern_6’, ‘Pattern_7’, ‘Pattern_8’
  var: ‘Pattern_1’, ‘Pattern_2’, ‘Pattern_3’, ‘Pattern_4’, ‘Pattern_5’,
  ‘Pattern_6’, ‘Pattern_7’, ‘Pattern_8’, ‘cell_type’
  

  Built-in PyCoGAPS functions can now be called to analyze and visualize the data. Please see the ‘Anticipated results’ section for more discussion of the result object.

• 15
  We recommended immediately visualizing pattern weights on a UMAP as this will immediately show whether there is a strong signal and whether the patterns make sense. We provide instructions to visualize patterns and compare them with clusters and annotations using UMAP and the scanpy package https://scanpy-tutorials.readthedocs.io/en/latest/pbmc3k.html. First import the analysis functions module (decoupled from NMF module) with the following command (please note, if you are at this step following Procedure 2, you should have already imported analysis_functions, and do not need to include the line above, i.e., you do not need to install the PyCoGAPS dependency):

  from PyCoGAPS.analysis_functions import *
  

  We provide a wrapper function to perform basic clustering workflow in scanpy (all default parameters) and produce a plot of each pattern’s intensity displayed on the data’s UMAP embedding. Call wrapper function:

  plotPatternUMAP(cogapsresult)
  

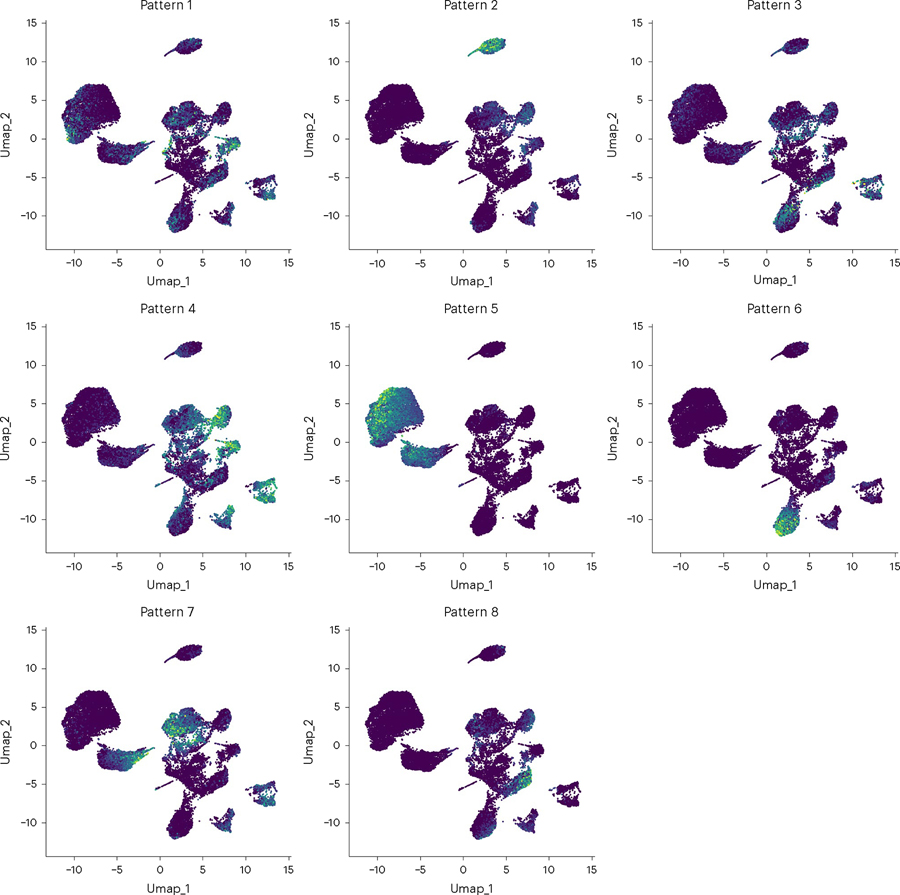
  Expected results are shown in Fig. 7. Expected output to the python console is shown in Supplementary Note 4.

• 16
  To generate statistics on the association between certain sample groups and patterns, we provide a wrapper function around statsmodels’ MANOVA function⁵⁴. This allows users to explore whether the patterns we have discovered lend to statistically significant differences in the sample groups. First, load in the original data if it is no longer in your environment.

  orig = anndata.read_h5ad(“data/inputdata.h5ad”).T
  

  Our original data contains many sample groups; however, to explore the associations of a subset of the groups with biological relevance, in this case ‘celltype’ and ‘TN_assigned_cell_type’:

  interested_vars = [‘celltype’, ‘TN_assigned_cell_type’]
  manova_result = MANOVA(cogapsresult, orig, interested_vars)
  

  The function will print out the MANOVA results for each pattern learned based on the variables of interest.

• 17
  Violin plots can be used to visualize associations between patterns and annotated cell types.

  pattern_names = [col for col in cogapsresult.var.columns if col.
  startswith(‘Pattern’)] # gather pattern names
  sc.pl.stacked_violin(cogapsresult.T, pattern_names, groupby=‘cell_type’)
  

  Expected results are shown in Fig. 8.

• 18
  Next, find the markers of each pattern using PyCoGAPS’ patternMarkers function. Identifying genes that are strongly correlated with each learned pattern allows users to begin to decipher what biological processes or states it may represent. The command below uses the default threshold parameter, but this can be modified as described in Box 1.

  pm = patternMarkers(cogapsresult, threshold=“cut”)
  

  To view marker genes for a pattern, access it as follows:

  pm[“PatternMarkers”][“Pattern_7”]
  [‘SPEF2’, ‘PAH’, ‘FAM117B’, ‘SFTPA2’, ‘PDLIM4’, ‘ZNF503’, ‘CITED2’,
  ‘GTPBP4’, ‘ZSWIM8’, ‘CHD5’, ‘TNFRSF9’, ‘CD3EAP’, ‘AMIGO2’, ‘STX3’,
  ‘CAMK2G’, ‘RACGAP1’, ‘SOWAHB’, ‘ABRACL’, ‘LTBP2’, ‘CDK11B’, ‘MFAP1’,
  ‘UNK’, ‘PLEKHH3’, ‘C1orf115’, ‘SATB1’, ‘BBOX1’, ‘SPN’, ‘UHRF1BP1’,
  ‘PVR’, ‘NLRP4’, ‘CAMK4’, ‘ZNF324’, ‘WWTR1’, ‘DYDC2’, ‘SHANK2’, ‘GBF1’,
  ‘HSPH1’, ‘VDAC2’, ‘FAM229A’, ‘COG3’, ‘RFTN1’, ‘KRT81’, ‘GLP2R’,
  ‘NR3C1’, ‘BNIP1’, ‘SLFN13’, ‘RABL3’, ‘TNKS’, ‘RAB30’, ‘ARHGAP21’,
  ‘ABTB2’, ‘ETNK1’, ‘DUS4L’, ‘PDK4’, ‘SLC35A3’, ‘ABCC5’, ‘NRK’, ‘ZNF439’,
  ‘TYSND1’, ‘SYAP1’, ‘GAR1’, ‘NOS3’, ‘POLR2M’, ‘SERPINI1’]
  

• 19
  Perform gene set enrichment analysis (GSEA) on lists of marker genes for each pattern in order to annotate the molecular processes in the learned patterns. This is accomplish this using a wrapper around the GSEApy library⁵⁵. First, run the following commands:

  gsea_res = patternGSEA(cogapsresult, patternmarkers=None,
  verbose=True, gene_sets = [‘MSigDB_Hallmark_2020’], organism=“human”)
  

  To see all patterns for which GSEA was computed:

  gsea_res.keys()
  dict_keys([‘Pattern1’, ‘Pattern2’, ‘Pattern3’, ‘Pattern4’, ‘Pattern5’,
  ‘Pattern6’, ‘Pattern7’, ‘Pattern8’])
  

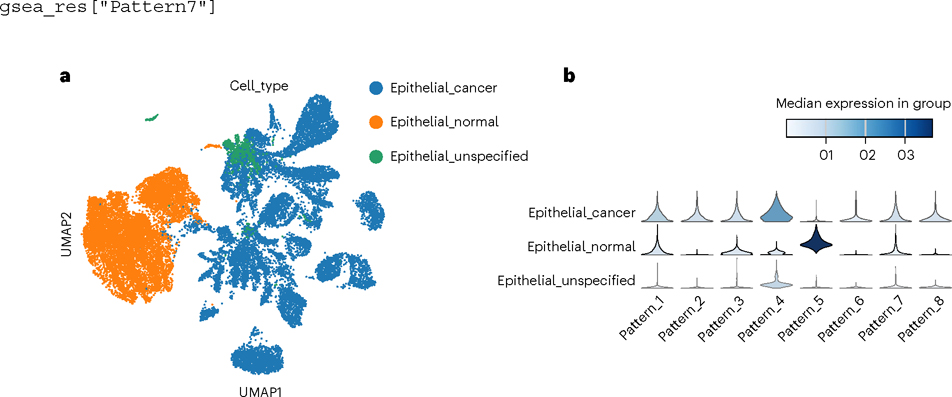
  To demonstrate the utility of this gene set analysis, we focus on Pattern 7. To view a pattern’s GSEA result:

  gsea_res[“Pattern7”]
  

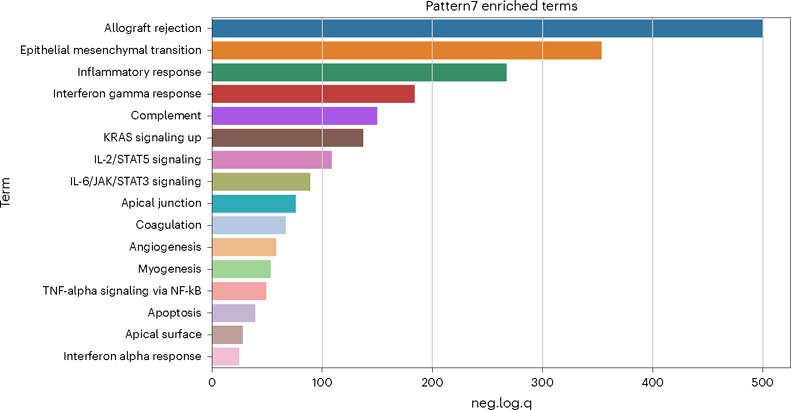
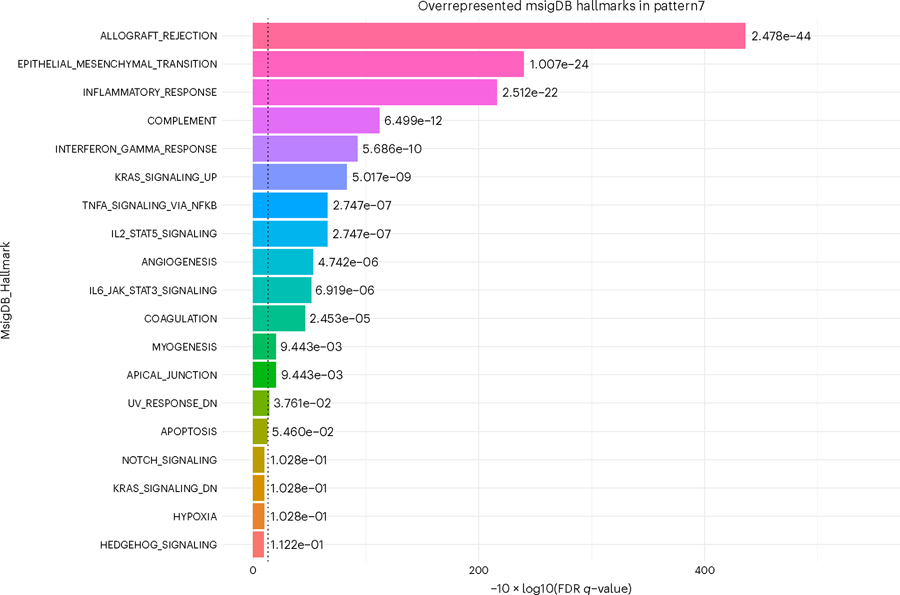
  To generate a simple histogram summarizing the statistically significant enriched terms for a given pattern, use the wrapper provided around scanpy’s box plot function (Fig. 9).

  plotPatternGSEA(gsea_res, whichPattern = 7)
  

  Expected results are shown in Fig. 9. The plotPatternMarkers function will also generate a plot colored by every column in the adata.var matrix. However, for single-cell data analysis, this is probably too large of a matrix to be useful by visual inspection.

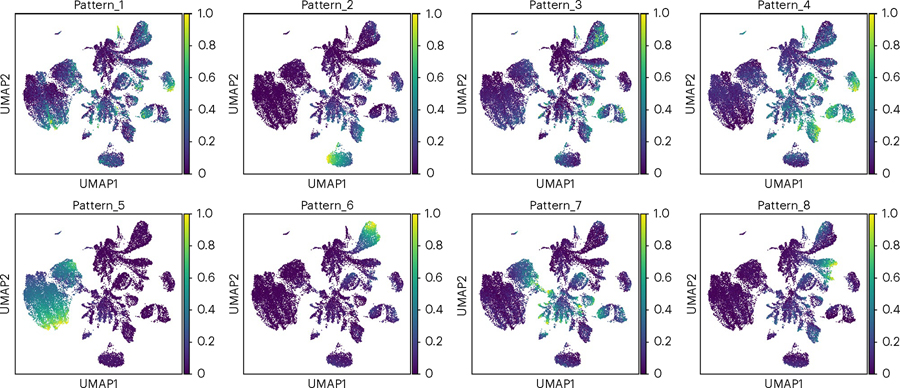
Fig. 7 |. UMAP of patterns learned by PyCoGAPS.

Each dot represents one cell in the input data and is colored according to its expression of each pattern.

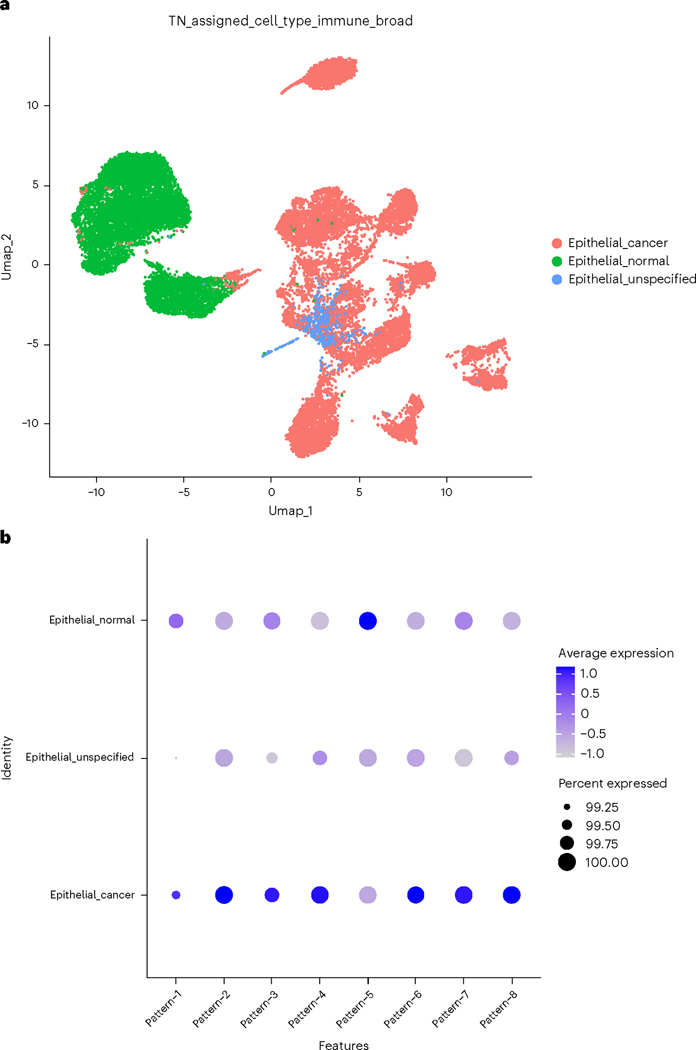
Fig. 8 |. Comparing statistical overlap between a biologist’s single-cell annotations and the learned CoGAPS to associate patterns with biological processes.

a,b, Patterns are visualized on a UMAP (a) and then compared between conditions (b).

Fig. 9 |. Python hallmark GSEA.

This histogram shows negative log quotient (degree of association) of pattern 7 in the PyCoGAPS analysis, with statistically significant MSigDB Hallmark terms (FDR-corrected P-value reported by gseapy <0.05).

Procedure 2: running PyCoGAPS using Docker

Software Setup

● TIMING 5 min

1. Pull the PyCoGAPS Docker container and set up the working directory.

   • For Mac users, copy the commands and paste in terminal:

     docker pull fertiglab/pycogaps
       mkdir PyCoGAPS
     cd PyCoGAPS
     curl -O
     

     https://raw.githubusercontent.com/FertigLab/pycogaps/master/params.yaml

     mkdir data cd data curl -O
     

     https://raw.githubusercontent.com/FertigLab/pycogaps/master/data/ModSimData.txt

     cd.
     

   • For Windows (Ubuntu) users, copy the commands and paste in terminal:

     docker pull fertiglab/pycogaps
     mkdir PyCoGAPS
     cd PyCoGAPS
     curl.exe -o index.html https://raw.githubusercontent.com/FertigLab/pycogaps/master/params.yamlmkdir data
     cd data
     curl.exe -o index.html https://raw.githubusercontent.com/FertigLab/pycogaps/master/data/GIST.csv cd ..
     

     ◆ TROUBLESHOOTING

Running PyCoGAPS on simulated toy data

● TIMING 2 min

• 3
  To ensure PyCoGAPS is running properly on your computer, first perform a setup and run on the ModSim dataset (running PyCoGAPS on the single-cell data will be performed later in Step 3). The dataset has already been downloaded in Step 1. Run the following commands in terminal:

  docker run -v $PWD:$PWD fertiglab/pycogaps $PWD/params.yaml
  

  For users with an M1 processing chip, please add the following flag to the above command:

  --platform linux/amd64
  

  This produces a CoGAPS run on a simple dataset with default parameters. The expected PyCoGAPS Docker Output is shown in Supplementary Note 5. When CoGAPS has successfully completed running, the result file is saved as result.pkl in a created output/ folder. The working directory is the PyCoGAPS folder with the following structure and files:

Running PyCoGAPS on single-cell data

● TIMING 5 min to 2 d (depending on whether user runs NMF or uses precomputed result)

• 4
  Having confirmed that PyCoGAPS has been set up and run correctly, proceed to analyzing experimental single-cell data. Navigate to the ‘data’ folder created earlier, and run the following command:

  cd data curl -O
  

  https://raw.githubusercontent.com/FertigLab/pycogaps/master/data/inputdata.h5ad

  CRITICAL STEP Always make sure to move the data you seek to analyze into the created ‘data’ folder.

• 5Modify the default parameters before running PyCoGAPS. All parameter values can be modified directly in the params.yaml file already downloaded in Step 1.
  To do this, first open params.yaml with any text or code editor. Then, modify the following line to:

  path: ‘data/inputdata.h5ad’
  

  Then, modify any additional desired parameters and save the file (as described in Box 9). A description and guide for setting key PyCoGAPS parameters can be found in Table 2. There are many more additional parameters that can be set depending on your goals, which we invite the reader to explore in our GitHub documentation. Note the ‘distributed’ parameter enables parallelization to decrease runtimes, which we recommended for most cases. Please refer to Box 10 for how to run distributed PyCoGAPS. For distributed PyCoGAPS, once all worker threads have started running their iterations, you will see periodic output as shown in Box 8.

• 6
  Now that all parameters are set, run PyCoGAPS with the following command in terminal:

  docker run -v $PWD:$PWD fertiglab/pycogaps $PWD/params.yaml
  

  The result object will automatically save in the ‘output’ folder, with the name given by the ‘result_file’ parameter. Please note that this is the most time-consuming step of the procedure. Timing can take several hours and scales nlog(n) based on dataset size (see the ‘Timing’ section below), as well as the parameter values set for ‘nPatterns’ and ‘nIterations’. Time is increased when learning more patterns, when running more iterations, and when running a larger dataset, with iterations having the largest variable impact on the runtime of the NMF function.

  PAUSE POINT Now we have successfully generated and saved a CoGAPS result. The procedure may be paused.

Box 9. Example snippet of params.yaml.

The params.yaml file holds all parameters that can be inputted to PyCoGAPS. A snippet of params. yaml is shown below, where we have changed some default parameter values to our own specified example values.

## This file holds all parameters to be passed into PyCoGAPS.
## To modify default parameters, simply replace parameter values below with user-specified values, and save file.
# RELATIVE path to data -- make sure to move your data into the created data/ folder
path: data/ModSimData.txt
# result output file name result_file: ModSimResult.h5ad
standard_params:
# number of patterns CoGAPS will learn nPatterns: 10
# number of iterations for each phase of the algorithm nIterations: 5000
# random number generator seed seed: 0
# speeds up performance with sparse data (roughly >80% of data is zero), note this can only be used with the default uncertainty useSparseOptimization: True
…

A complete list of input options and their descriptions can be found as comments in params.yaml and guide to setting key parameters in Table 2.

Box 10. Distributed PyCoGAPS in Docker.

A snippet of params.yaml is shown below where distributed_params parameters are modified.

## This file holds all parameters to be passed into PyCoGAPS.
…
distributed_params:
# either null or genome-wide distributed: genome-wide
# number of sets to break data into nSets: 4
# number of branches at which to cut dendrogram used in pattern matching
cut: null
# minimum of individual set contributions a cluster must contain minNS: null
# maximum of individual set contributions a cluster can contain maxNS: null

Analyzing the PyCoGAPS result

● TIMING 20–30 min

• 7
  Download the analysis functions and requirements files with the following command:

  curl -O https://raw.githubusercontent.com/FertigLab/pycogaps/master/
  PyCoGAPS/analysis_functions.py
  curl -O https://raw.githubusercontent.com/FertigLab/pycogaps/master/
  PyCoGAPS/requirements_analysis.txt
  

• 8
  Install the analysis functions dependencies with the following command:

  pip install -r analysis_requirements.txt
  

• 9
  Open a new Python file (in any preferred IDE, see the ‘Software’ section above) and include the following line:

  from analysis_functions import *
  

  ◆ TROUBLESHOOTING

• 10Follow the ‘Analyzing the PyCoGAPS result’ in Procedure 1 Step 14 to continue following the analysis and visualization workflow.

Procedure 3: running CoGAPS—user startup guide for the R CoGAPS API

Software Setup

● TIMING 1–5 min

• 1
  Install CoGAPS directly from the FertigLab Github repository using R devtools:

  devtools::install_github(“FertigLab/CoGAPS”)
  

  When CoGAPS has installed correctly, you will see this message:

  ** installing vignettes
  ** testing if installed package can be loaded from temporary location
  ** checking absolute paths in shared objects and dynamic libraries
  ** testing if installed package can be loaded from final location
  ** testing if installed package keeps a record of temporary
  installation path
  * DONE (CoGAPS)
  

R script setup

● TIMING 1 min

• 2
  Import the CoGAPS library with the following command:

  library(CoGAPS)
  

Running CoGAPS on simulated toy data

● TIMING 3–5 min

• 3To ensure CoGAPS is working properly, first load in the simulated toy data for a test run.
  Single-cell data will be loaded later in step 6.

  modsimdata <- read.table(“./data/ModSimData.txt”)
  modsimdata
  head(modsimdata, c(5L, 5L))
  V1V2V3V4V5
  1 0.0777640.94742 4.2487 7.0608 4.8730
  2 0.0814670.99253 4.4507 7.3906 5.0387
  3 0.0851701.03760 4.6527 7.7204 5.2044
  4 0.0888731.08270 4.8547 8.0502 5.3700
  5 0.0925761.12790 5.0567 8.3800 5.5357
  dim(modsimdata)
  [1] 25 20
  

• 4
  Next, set the parameters to be used by CoGAPS. First, create a CogapsParams object, then set parameters with the setParam function.

  # create new parameters object params <- new(“CogapsParams”)
  # view all parameters params
  -- Standard Parameters -- nPatterns 7
  nIterations 50000
  seed 718
  sparseOptimization FALSE
  -- Sparsity Parameters -- alpha 0.01
  maxGibbsMass 100
  # get the value for a specific parameter getParam(params, “nPatterns”)
  [1] 7
  # set the value for a specific parameter params <- setParam(params, “nPatterns”, 3)
  getParam(params, “nPatterns”)
  [1] 3
  

• 5
  Run CoGAPS on the ModSim data. Since this is a small dataset, the expected runtime is only ~5–10 s.

  cogapsresult <- CoGAPS(modsimdata, params, outputFrequency = 10000)
  

  The expected output is shown in Supplementary Note 6. This output means that the underlying C++ library has run correctly, and everything is installed how it should be. Examine the result object (Supplementary Note 7). If both matrices—sampleFactors and featureLoadings—have reasonable values, users can be confident that CoGAPS is working as expected and can proceed with single-cell analysis.

Running CoGAPS on single-cell data

● TIMING 5 min to 2 d (depending on whether user runs NMF or uses precomputed result)

• 6
  Read in the single-cell dataset, which we demonstrate with the provided input file, which is available at https://zenodo.org/record/7709664.

  pdac_data <- readRDS(“inputdata.rds”)
  pdac_data
  An object of class Seurat
  15184 features across 25442 samples within 2 assays
  Active assay: originalexp (15176 features, 2000 variable features)
  1 other assay present: CoGAPS
  5 dimensional reductions calculated: PCA, Aligned, UMAP, pca, umap
  

  Extract and normalize the transcript counts matrix to provide directly to CoGAPS.

  pdac_epi_counts <- as.matrix(pdac_data@assays$originalexp@counts)
  norm_pdac_epi_counts <- log1p(pdac_epi_counts)
  

• 7
  Most of the time some parameters are set before running CoGAPS. Parameters are managed with a CogapsParams object. This object will store all parameters needed to run CoGAPS and provides a simple interface for viewing and setting the parameter values. Set parameters using the following command:

  pdac_params <- CogapsParams(nIterations=100, # run for 100 iterations
  seed=42, # for consistency across stochastic runs
  nPatterns=8, # each thread will learn 8 patterns
  sparseOptimization=TRUE, # optimize for sparse data
  distributed=“genome-wide”) # parallelize across sets
  

  To run distributed CoGAPS, which is recommended to improve the computational efficiency for most large datasets, call the setDistributedParams function. For a complete description of the parallelization strategy used in distributed CoGAPS, please refer to the Introduction section titled ‘Finding robust patterns using consensus across parallel sets’, as well as Fig. 3 and Box 2.

  pdac_params <- setDistributedParams(pdac_params, nSets=7)
  setting distributed parameters - call this again if you change
  nPatterns
  

  Follow Box 11 to view all parameters that have been set and their values.

• 8
  With all parameters set, run CoGAPS with the following command:

  startTime <- Sys.time()
  pdac_epi_result <- CoGAPS(pdac_epi_counts, pdac_params)
  endTime <- Sys.time()
  saveRDS(pdac_epi_result, “./data/pdac_epi_cogaps_result.Rds”)
  

  To also save the result in .csv, format use the following line:

  saveCSV(pdac_epi_result, “path/to/location/pdac_epi_result.csv”)
  

  While CoGAPS is running, it periodically prints status messages (Box 8). Please note that this is the most time-consuming step of the procedure. Timing can take several hours and scales nlog(n) based on dataset size (Fig. 6 and Table 3), as well as the parameter values set for ‘nPatterns’ and ‘nIterations’. Time is increased when learning more patterns, when running more iterations and when running a larger dataset, with iterations having the largest variable impact on the runtime of the NMF function. As this step has a long runtime, users who want to load an already-complete NMF run and proceed to the analysis portion of this vignette can skip to Step 9.

  ◆ TROUBLESHOOTING

Box 11. Viewing all parameters in CoGAPS.

Run the following to view all parameters that have been set, and their values:

pdac_params
-- Standard Parameters --
nPatterns 8
nIterations 100
seed 42
sparseOptimization TRUE
distributed genome-wide
-- Sparsity Parameters --
alpha 0.01
maxGibbsMass 100
-- Distributed CoGAPS Parameters
nSets 7
cut 8
minNS 8
maxNS 23

Table 3 |.

Timing of PyCoGAPS (Python time) versus CoGAPS (R time) on a small dataset with varying input parameters

Dataset	Size	dim 1	dim 2	nPatterns	nIterations	API	Runtime	meanChiSq
modsim	3.6 KB	25	20	3	100	R	0.05178118	7718.748
modsim	3.6 KB	25	20	3	500	R	0.05663395	295.1525
modsim	3.6 KB	25	20	3	1,000	R	0.08855605	36.23537
modsim	3.6 KB	25	20	3	5,000	R	0.223259	36.62024
modsim	3.6 KB	25	20	3	10,000	R	0.40043	35.13767
modsim	3.6 KB	25	20	3	20,000	R	0.7454391	36.69391
modsim	3.6 KB	25	20	3	30,000	R	1.093563	35.25447
modsim	3.6 KB	25	20	3	50,000	R	1.773327	12.74943
modsim	3.6 KB	25	20	3	100	Python	0.005910873413	7718.747559
modsim	3.6 KB	25	20	3	500	Python	0.01748609543	295.1524963
modsim	3.6 KB	25	20	3	1,000	Python	0.033478260 04	36.23537064
modsim	3.6 KB	25	20	3	5,000	Python	0.149089098	36.62024307
modsim	3.6 KB	25	20	3	10,000	Python	0.2985670567	35.13766861
modsim	3.6 KB	25	20	3	20,000	Python	0.5989601612	36.69391251
modsim	3.6 KB	25	20	3	30,000	Python	0.8996288776	35.25447464
modsim	3.6 KB	25	20	3	50,000	Python	1.547122955	12.74942684
modsim	3.6 KB	25	20	3	100	R_distributed	0.3206151	4052.322
modsim	3.6 KB	25	20	3	500	R_distributed	0.3453848	842.0198
modsim	3.6 KB	25	20	3	1,000	R_distributed	0.4187911	28.01583
modsim	3.6 KB	25	20	3	5,000	R_distributed	0.4270132	28.74847
modsim	3.6 KB	25	20	3	10,000	R_distributed	0.6068029	471.4499
modsim	3.6 KB	25	20	3	20,000	R_distributed	0.809824	184.6889
modsim	3.6 KB	25	20	3	30,000	R_distributed	1.019847	18.10658
modsim	3.6 KB	25	20	3	50,000	R_distributed	1.543682	15.68454
modsim	3.6 KB	25	20	3	100	Python_distributed	3.292124032	828.8723755
modsim	3.6 KB	25	20	3	500	Python_distributed	3.428723812	116.0221786
modsim	3.6 KB	25	20	3	1,000	Python_distributed	3.451946974	28.20919037
modsim	3.6 KB	25	20	3	5,000	Python_distributed	3.451797009	11.72956944
modsim	3.6 KB	25	20	3	10,000	Python_distributed	3.622226954	49.45440674
modsim	3.6 KB	25	20	3	20,000	Python_distributed	3.667319775	52.24369431
modsim	3.6 KB	25	20	3	30,000	Python_distributed	3.986222982	9.30820179
modsim	3.6 KB	25	20	3	50,000	Python_distributed	4.204113007	18.50210381

Analyzing the CoGAPS result

● TIMING 20–30 min

• 9Now that the CoGAPS run is complete, learned patterns can be investigated. Due to the stochastic nature of the MCMC sampling in CoGAPS and long runtime, it is generally a good idea to immediately save your CoGAPS result object to a file (as instructed in Step 8), then read it in for downstream analysis. A detailed description of the CoGAPS result object can be found in Box 12. If you wish to use the precomputed result, please download cogapsresult. Rds from https://zenodo.org/record/7709664.
  1. Load and examine a precomputed result object with the following command:

     cogapsresult <- readRDS(“data/cogapsresult.Rds”)
     cogapsresult
     [1] “CogapsResult object with 15176 features and 25442 samples”
     [1] “8 patterns were learned”
     

  2. Load your own result, by simply editing the file path as follows:

     cogapsresult <- readRDS(“./data/pdac_epi_cogaps_result.Rds”)
     

     PAUSE POINT Now we have successfully generated and saved a CoGAPS result. The procedure may be paused.

• 10
  We recommendimmediately visualizing pattern weights on a UMAP as this will immediately show whether there is a strong signal and whether the patterns make sense. Since pattern weights are all continuous and nonnegative, they can be used to color a UMAP in the same way as one would color by gene expression. The sampleFactors matrix is essentially just nPatterns different annotations for each cell, and featureLoadings is likewise just nPatterns annotations for each gene. This makes it very simple to incorporate pattern data into any data structure and workflow. Use the following commands to store CoGAPS patterns as an assay within a Seurat object (recommended):

  # make sure pattern matrix is in same order as the input data
  patterns_in_order <-t(cogapsresult@sampleFactors[colnames(pdac_data),])
  # add CoGAPS patterns as an assay
  pdac_data[[“CoGAPS”]] <- CreateAssayObject(counts = patterns_in_order)
  

  With the help of Seurat’s FeaturePlot function, generate a UMAP embedding of the cells colored by the intensity of each pattern.

  DefaultAssay(inputdata) <- “CoGAPS”
  pattern_names = rownames(inputdata@assays$CoGAPS)
  library(viridis)
  color_palette <- viridis(n=10)
  FeaturePlot(inputdata, pattern_names, cols=color_palette, reduction = “umap”) & NoLegend()
  

  The expected output is shown in Fig. 10.

• 11
  Compare pattern weight between annotated cell groups. Make another UMAP, this time color each cell based on a biologist’s annotations¹¹ stored in the object metadata.

  DimPlot(pdac_data, reduction = “umap”, group.by=“TN_assigned_cell_type_immune_broad”)
  

  Directly visualize correlations between patterns and annotated cell groups with a dot plot.

  DotPlot(pdac_data, features = pattern_names) + RotatedAxis()
  

  Expected output shown in Fig. 11.

• 12
  To assess pattern marker genes, we provide a patternMarkers() CoGAPS function to find genes associated with each pattern and returns a dictionary of information containing lists of marker genes, their ranking, and their ‘score’ for each pattern. Run this function with the follow command:

  pm = patternMarkers(cogapsresult)
  

  This is vital because genes are often associated with multiple patterns. For a complete discussion of the patternMarkers statistic, please refer to Box 1.

• 13
  The PatternHallmarks function provides a wrapper around the fgsea⁵⁶ fora method and associates each pattern with msigDB⁵⁷ hallmark pathway annotations using the list of marker genes attained from the patternMarkers statistic. To perform gene set analysis on pattern markers, create a list of data frames ‘hallmarks’, each containing hallmark overrepresentation statistics corresponding to one pattern:

  hallmarks <- PatternHallmarks(cogapsresult)
  

  To generate a histogram of the most significant hallmarks for any given pattern, run:

  pl_pattern7 <- plotPatternHallmarks(hallmarks, whichpattern = 7)
  pl_pattern7
  

  The expected output is shown in Fig. 12.

• 14
  To generate statistics on the association between certain sample groups and patterns, we provide a wrapper function, called runMANOVA. This allows users to explore whether the patterns discovered lend to statistically significant differences in the sample groups. First load in the original data (if not already done earlier):

  pdac_data <- readRDS(“inputdata.rds”)
  

  Then, create a new matrix called ‘interestedVariables’ consisting of the metadata variables of interest in conducting analysis on.

  interestedVariables <- cbind(pdac_data@meta.data[[“celltype”]], pdac_data@meta.data[[“TN_assigned_cell_type”]])
  

  Last, call the wrapper function, passing in the result object as well.

  manovaResult <- MANOVA(interestedVariables, cogapsresult)
  

  The function will print the MANOVA results for each pattern in the CoGAPS result object based on the chosen variables.

Box 12. The CoGAPS result object.

A and P matrices learned by CoGAPS. In this package, the A matrix of sample weights is called ‘sampleFactors’ and the P matrix of gene weights is called ‘featureLoadings’.

Standard deviation matrices factorStdDev and loadingStdDev corresponding to sampleFactors and featureLoadings.

Metadata, which contains information for the run such as how it was parallelized (subsets), the mean ChiSq value during the run (meanChiSq) and the parameters used in the run (params). Since the run parameters are attached to the result object, it can keep track of the provenance of your CoGAPS results.

Other information may be present in the metadata depending on your run options.

Fig. 10 |. UMAP of patterns learned by CoGAPS.

Each dot represents one cell in the input data and is colored according to its expression of each pattern.

Fig. 11 |. Pattern amplitude by cell group.

a,b, Here, we examine how all patterns vary between cell groups selected by a biologist, first visualizing these groupings on a UMAP (a) and then noting which patterns associate with healthier or diseased cells, and which associate with both or neither (b).

Fig. 12 |. R CoGAPS hallmark GSEA.

This shows negative log quotient (degree of association) of the pattern’s gene set with statistically significant MSigDB Hallmark terms (FDR-corrected P-value reported by fgsea <0.05, threshold indicated by vertical dotted line).

Procedure 4: running GenePattern Notebook—user startup guide for the web-based CoGAPS API

Notebook Setup

● TIMING 5 min

• 1Log in to the GenePattern Notebook workspace, http://notebook.genepattern.org. If you do not have an account, click the ‘Register a new GenePattern Account’ button, provide the registration information and log in. Registration for GenePattern Notebook is free.
• 2Scroll to ‘Public Library’. You will see a list of available public project notebooks.
• 3In the ‘Search Library’ box, search ‘PyCoGAPS’.

Running PyCoGAPS on simulated toy data

● TIMING 8–10 min

• 4Select the ‘Single-Cell Workflow with PyCoGAPS’ project notebook by clicking anywhere in its description and selecting ‘Run Notebook’. A copy of the project notebook will be saved in your account.
• 5Open the file called ‘Single-cell Analysis with PyCoGAPS.ipynb’, which describes each step in this protocol and contains cells that will allow you to input datasets and set parameters. In the first cell, log in to your account (Supplementary Fig. 1).
• 6Follow the instructions in each blue panel, providing information where requested (Supplementary Fig. 2). You will need to input the ‘input_file’ parameter, which in this simulated toy data case, is the ‘ModSimData.txt’ file in the project folder. ‘num patterns’ and ‘num iterations’ are the most important parameters, but all parameter descriptions can be explored in the cell, or in Table 2 for guidance on setting these and other key parameters. Click run once you have set desired parameters (Supplementary Fig. 2). Please note that once a run has been submitted, the status in the cell will change from ‘Pending’ to ‘Running’ to ‘Completed’.

  ◆ TROUBLESHOOTING

• 7As described in the notebook instructions, ensure that the result file is saved locally first, then re-upload it to the project notebook (Supplementary Fig. 4).

Running PyCoGAPS on single-cell data

● TIMING 5 min to 2 d (depending on whether user runs NMF or uses precomputed result)

• 8Click the ‘+’ button of the PyCoGAPS cell to display the parameter inputs again. You may reset the parameters by selecting the settings icon. To run PyCoGAPS, on the provided PDAC dataset, the link to the file can be found here and directly passed into the ‘input_file’ cell (there is no need to download the data and re-upload it to the project folder): https://datasets.genepattern.org/?prefix=data/module_support_files/PyCoGAPS/inputdata.h5ad.

  Once desired parameters have been set, run the cell to submit the job.

Analyzing the PyCoGAPS result

● TIMING 20–30 min

• 9Follow and run the cells to perform analysis of your output PyCoGAPS results. These cells will call the various functions described in other procedures of this manuscript to allow you to visualize and interpret your data. Screenshots are shown in Supplementary Figs. 5–8.

Troubleshooting

Advice for troubleshooting can be found in Table 4.

Table 4 |.

Troubleshooting table

Step	Problem	Possible reason	Solution
Procedure 1, Step 1	Error with cloning repository due to large files (inputdata.h5ad, cogapsresult.h5ad)	Git large file storage (LFS) is not installed	Run the following command: brew install git-lfs or disable git-lfs and instead download files from https://zenodo.org/record/7709664
Procedure 1, Step 3	Upon running setup.py, receive the error message: No module named pybind11	pybind11 was not successfully installed	pip install pybind11. If using conda, run: conda install -c conda-forge pybind11
	Upon running setup.py, a ‘file not found’ error for a CoGAPS header file is displayed	CoGAPS library was not downloaded	Make sure you use --recursive flag when cloning pycogaps
Procedure 1, Step 12	Runtime is prohibitively long, given reasonable scales of data (typical timing is as given in n*log(n))	If runtimes are prohibitive within reasonable scales of data, this may result from algorithm overfitting zeros	We recommend filtering the data only to genes that are reasonably expressed or filtering to a limited subset of genes (e.g., high variance)
Procedure 2, Step 1	Cannot connect to the Docker daemon at unix:///var/run/docker.sock. Is the docker daemon running?	Docker is not started up/running	Open the Docker application or run the following command: docker run -d -p 80:80 docker/getting-started
Procedure 2, Step 8	ModuleNotFoundError: no module named ‘analysis_functions’	analysis_function s.py file is not in the same directory as your new Python file	Make sure analysis_functions.py and your new Python file for calling the functions are in the same directory
Procedure 3, Step 8	Runtime is prohibitively long, given reasonable scales of data (typical timing is as given in n*log(n))	If runtimes are prohibitive within reasonable scales of data, this may result from algorithm overfitting zeros	We recommend filtering the data only to genes that are reasonably expressed or filtering to a limited subset of genes (e.g., high variance)
Procedure 4, Step 6	FileNotFoundError	Data file not uploaded to project folder	Go to the project folder, and click ‘Upload’ to upload your file to the data folder
	Error after running the PyCoGAPS cell	Path parameter not updated	Make sure to replace the default path parameter with the ‘Upload’ button to upload your data

Timing

Procedure 1

Steps 1–3, software setup: 5–10 min

Steps 4–7, running PyCoGAPS on simulated data: 3–5 min

Steps 8–13, running PyCoGAPS on single-cell data: 5 min to 2 d

Steps 14–19, analyzing the PyCoGAPS result: 20–30 min

Procedure 2

Step 1, software setup: 5 min

Step 2, running PyCoGAPS on simulated data: 2 min

Steps 3–5, running PyCoGAPS on single-cell data: 5 min to 2 d

Steps 6–9, analyzing the PyCoGAPS result: 20–30 min

Procedure 3

Step 1, software setup: 1–5 min

Step 2, R script setup: 1 min

Steps 3–5, running CoGAPS on simulated data: 3–5 min

Steps 6–8, running CoGAPS on single-cell data: 5 min to 2 d

Steps 9–14, analyzing the CoGAPS result: 20–30 min

Procedure 4

Steps 1–3, notebook setup: 5–10 min

Steps 4–7, running PyCoGAPS on simulated data: 8–10 min

Steps 8, running PyCoGAPS on single-cell data: 5 min to 2 d

Step 9, analyzing the PyCoGAPS result: 20–30 min

Anticipated results

The output you should obtain from a PyCoGAPS run (procedures 1, 2 or 4) is an anndata object, stored as an .h5ad file. In the anndata object, the lower dimensional representation of the samples (P matrix) is stored in the .var slot and the weight of the features (A matrix) is stored in the .obs slot. For an m by p dimension gene expression input, the P matrix or .var slot should have dimension m by κ, and the A matrix or .obs slot should have dimension κ by p, where k is the number of patterns.

Further metrics are stored in the .uns slot of the result object. This includes standard deviations across the sample points for both the P and A matrix stored in ‘psd’ and ‘asd’, respectively, the mean chi-squared value stored in ‘meanchisq’, the total running time stored in ‘totalRunningTime’ and more. An example output including all metadata can be found in Box 7.

The output you should obtain from an R CoGAPS run (Procedure 3) is an .Rds file. In this object, the lower dimensional representation of the samples (P matrix) is stored in the ‘featureLoadings’ slot and the weight of the features (A matrix) is stored in the ‘sampleFactors’ slot. For an m by p dimension gene expression input, the P matrix should have dimension m by κ, and the A matrix should have dimension κ by p, where κ is the number of patterns. Standard deviation matrices are stored in the slots ‘factorStdDev’ and ‘loadingStdDev’, corresponding to sampleFactors and featureLoadings.

Additionally, metadata contains information for the run such as how it was parallelized stored in ‘subsets’, the mean chi-squared value during the run stored in ‘meanChiSq’, and the parameters used in the run stored in ‘params’. Other information may be present in the metadata depending on your run options shown in Box 13.

Box 13. CoGAPS Metadata.

Run statistics and more information can be found in the metadata portion of the CoGAPS object.

cogapsresult
[1] “CogapsResult object with 15176 features and 25442 samples”
[1] “8 patterns were learned”
names(cogapsresult@metadata)
[1] “meanChiSq” “firstPass” “unmatchedPatterns” “clusteredPatterns”
[5] “CorrToMeanPattern” “subsets” “params” “version”
[9] “logStreamName”

CoGAPS has a theoretical scaling of mlog(m) + plog(p). As illustrated in benchmarking on the ModSim and PDAC epithelial datasets in Fig. 6 and Table 3, runtime scales with the input dimensions and the number of iterations. It is also apparent that Python and R perform similarly on lower-dimension data, while Python has an advantage of speed for higher-dimension data. This may be due to differences in memory handling between the two programming languages, with Python being better suited to tasks requiring large matrices to be accessed and modified at each step.

We will now focus on the results of analyzing the PDAC epithelial datasets to illustrate the sorts of biological inferences that can be made using CoGAPS. In the analysis we observe each pattern is enriched in a different part of the UMAP embedding, and all patterns seem to have a signal (Figs. 7 and 10). This is a sign that the number of patterns we selected is sufficient to distinguish signals present in our dataset.

By visual inspection it is apparent that pattern 5 seems to associate only with those epithelial cells annotated as ‘normal’. Pattern 2, pattern 4, pattern 6 and pattern 8 appear to light up specific, distinct groupings of epithelial cells annotated as ‘cancer’ (Figs. 8 and 11). Patterns 1, 3 and 7, however, show signal in both classes of epithelial cells. We note that the epithelial normal cluster is mixed between cells from true normal samples and normal cells that are tumor adjacent. This leads to hypotheses about which patterns might represent gene programs that distinguish, or co-occur, in malignant epithelial cells or related to signaling associated with field carcinization or unannotated precancer neoplastic cells in the sample.

We note that pattern 7 was found to be associated with cancer cells and matched normal epithelial cells from adjacent tissue, but not in normal epithelial cells from true healthy control samples. Looking at the set of genes that are positively associated with pattern 7, we obtain these statistics and see the Hallmark set for inflammatory response and allograft rejection (Figs. 9 and 12). We hypothesized this inflammatory process resulting from a transition during carcinogenesis resulting from interactions between epithelial cells and other cells in the microenvironment. We observed a high correlation of this pattern with the presence of fibroblasts, and have tested this hypothesis with experimental validation using co-culture organoid experiments¹¹.

Key points.

• This protocol describes procedures for learning cellular and molecular processes from single-cell RNA-sequencing data using the non-negative matrix factorization algorithm Coordinated Gene Activity across Pattern Subsets. This is implemented and demonstrated in Python and R, with additional vignettes covering how to run Coordinated Gene Activity across Pattern Subsets via Docker deployment and GenePattern Notebook.

• This protocol presents an end-to-end, optimized workflow that is usable, flexible, totally optimized for contemporary single-cell data formats, accessible and intuitive for computational biologists.

Related links

Key references using this protocol

Stein-O’Brien, G. L. et al. Cell Syst. 8, 395–411.e8 (2019): https://doi.org/10.1016/j.cels.2019.04.004

Clark, B. S. et al. Neuron 102, 1111–1126.e5 (2019): https://doi.org/10.1016/j.neuron.2019.04.010

Data availability

The data analyzed in these examples is freely available under accession code GSA: CRA001160, and from the Genome Sequence Archive, where it has the ID: PRJCA001063.