From the Automated Calculation of Potential Energy Surfaces to Accurate Infrared Spectra

Abstract

Advances in the development of quantum chemical methods and progress in multicore architectures in computer science made the simulation of infrared spectra of isolated molecules competitive with respect to established experimental methods. Although it is mainly the multidimensional potential energy surface that controls the accuracy of these calculations, the subsequent vibrational structure calculations need to be carefully converged in order to yield accurate results. As both aspects need to be considered in a balanced way, we focus on approaches for molecules of up to 12–15 atoms with respect to both parts, which have been automated to some extent so that they can be employed in routine applications. Alternatives to machine learning will be discussed, which appear to be attractive, as long as local regions of the potential energy surface are sufficient. The automatization of these methods is still in its infancy, and the generalization to molecules with large amplitude motions or molecular clusters is far from trivial, but many systems relevant for astrophysical studies are already in reach.

It is the dream of a theoretical spectroscopist to provide just a reasonable geometry of the target molecule and to let the program do the rest until a high quality spectrum pops out at the end of the calculation. For some sorts of spectroscopy this may come close to reality, but for vibrational spectroscopies this is a long way to go, which requires a high degree of automatization, computationally very efficient and generally applicable methods, and still, even more patience.

In cases when the harmonic approximation is not sufficient and the account of quantum effects becomes important, the arsenal of methods remains limited, and usually such calculations include many demanding steps, which need to be controlled for numerical stability. Of course, these steps differ with respect to the chosen method, which can be time-dependent or time-independent, being based on vibrational perturbation theory or a variational ansatz and so on.¹ And, of course, this depends strongly on the system under investigation; i.e., is it a small molecule in the gas phase² or in an environment,^3,4 is it a bulk liquid,⁵ is it a biomolecule⁶ or a single crystal?⁷ Clearly, the degree of automatization of the underlying approaches is very different for these specific situations. We note here that this perspective is limited to small molecules or molecular clusters in the gas phase, but analogies to related fields of research are on hand.

In the following we will exclusively focus on time-independent variational methods, namely, (ro)vibrational configuration interaction theory (VCI and RVCI),⁸ which inherently account for all sorts of quantum effects and which are formally unlimited in accuracy. Within this setup, the steps to be controlled comprise (1) a geometry optimization for the determination of the equilibrium structure, (2) a harmonic frequency calculation for determining a first initial guess and, once normal coordinates shall not be used, a meaningful set of coordinates, (3) the determination of a multidimensional potential energy surface (PES) and property surfaces in these coordinates, (4) an optimization of the vibrational basis, (5) the determination of state energies and converged (ro)vibrational wave functions, and (6) finally the calculation of infrared or Raman intensities.

While geometry optimizations and the calculation of harmonic frequencies are routine applications, the automated generation of a good set of coordinates is not trivial at all, which is reflected by the plethora of coordinate definitions which have been investigated.⁹⁻¹² While normal coordinates or different sorts of linear combinations of them were found to be suitable for automated routines (see for example the work on localized or optimized coordinates), less has been done with respect to curvilinear internal coordinates and variants of them. In this context, polyspherical coordinates show the advantage that the kinetic energy operator can be formulated analytically in an efficient manner.¹³

Moreover, the calculation of the PES and the determination of (ro)vibrational wave functions constitute computational bottlenecks, which request approximations to be monitored by the user or automated error-correction schemes. Within this Perspective, we will focus primarily on aspects concerning an automated construction of a reliable but local PES and the efficient calculation of accurate vibrational transitions. The automatization of these steps is fairly demanding and requires fast but reliable approximations. For example, once the Hamiltonian (or parts of it) is expanded in some sort of series, its truncation must be monitored with respect to the convergence of the final results. As long as the underlying ab initio calculations are computationally cheap, this is fairly easy as high-order terms can be afforded. However, in the case of demanding calculations, this is no longer true and hampers the approach. Consequently, automatization and the efficiency of the algorithms go together.

Automated Construction of Multidimensional Potential Energy Surfaces

The calculation of a multidimensional PES is computationally very costly and usually requires certain limitations. A full-dimensional (3N – 6) calculation is only feasible for the smallest systems once high-level ab initio methods are employed to solve the electronic Schrödinger equation. One can fight this problem following different routes: one can (1) restrict the number of coordinates, (2) lower the accuracy of the electronic structure calculations (e.g., using density functional theory instead of coupled-cluster approaches) or even use modeling schemes as for example machine learning,^14,15 or (3) use some kind of expansion up to a given order to restrict the mode-coupling range. Of course, all these techniques can be combined to gain even better performance. The utilization of an expansion requires an expansion point (usually some kind of stationary point), which typically restricts its application to a very limited number of local minima on the PES only. Once a system shows several minima, which need to be considered at the same time, usually dynamical, i.e., time-dependent, approaches relying on an on-the-fly calculation of the electronic energy appear to be more appropriate.^16,17 However, as very many energy evaluations are needed in the latter approaches, these methods usually rely on density functional theory, density functional tight binding methods, or machine learning based PESs.

Let us now consider a semirigid molecule, which is sufficiently characterized by a single minimum. In that case the use of an early truncated expansion of the PES is justified.¹⁸ However, the question arises as to which order is safe to truncate? For example, is a (semi)quartic force field (QFF) sufficient? The latter is given by

1

In eq 1, ω_i are the harmonic vibrational frequencies and the ϕ_ijk... are anharmonic force constants, i.e., derivatives of the energy with respect to the (dimensionless) normal coordinates q_i at the equilibrium geometry. A more flexible alternative is the n-mode expansion

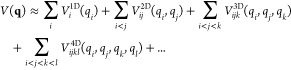2

where V^nD_ijk... are component functions depending only on a subset of the coordinates q. These nD subsurfaces depend on the lower dimensional surfaces; e.g., the 3D term V^3D_ijk can be constructed from the full ab initio energy V⁰_ijk(q_i, q_j, q_k) by

3

Note that in both eqs 1 and 2 the total electronic energy at the reference geometry V₀ has been omitted since it is not important for the description of the dynamics. It is rather obvious from eqs 1–3 that the number of grid points increases rapidly with the order of the expansion term, and hence a parallelized evaluation of them is more important for high-order than for low-order terms. In order to study the dependence of vibrational structure calculations on the specific PES representation, we have used the fully automated PES generator as implemented in the Molpro package.¹⁹

Truncation of PES Expansions

To answer the above question concerning the truncation order of the PES expansion, we have performed benchmark calculations for a set of molecules, and the results are summarized in Table 1 and are graphically depicted in Figure 1. All results are obtained from coupled-cluster methods using multilevel schemes (see below).

Table 1. Mean Absolute Deviation (MAD) and Maximum (MAX) Deviation (in Parentheses) of Fundamental Transition Frequencies (in cm^–1) with Respect to Experimental Reference Data of Some Benchmark Molecules, Dependent on the Method of Computation.

Molecule	VPT2	VCI(QFF)	VCI(2D)	VCI(3D)	VCI(4D)
H2CO	1.5 (3.1)	6.2 (12.3)	13.1 (51.5)	2.4 (7.4)	1.4 (3.2)
CH2F2	1.8 (5.3)	5.4 (16.2)	11.1 (80.8)	2.0 (8.4)	1.5 (3.8)
HCSCN	3.0 (8.0)	9.7 (17.2)	6.4 (17.2)	5.4 (15.3)	2.7 (7.5)
CHFClBr	0.7 (3.8)	3.0 (9.8)	1.5 (4.0)	1.1 (3.5)	1.1 (3.2)
H2NBH2	4.1 (12.6)	29.0 (91.1)	15.7 (58.8)	9.8 (19.8)	4.3 (7.5)
C2H4	2.9 (9.0)	9.9 (26.2)	10.7 (27.4)	10.6 (34.0)	2.7 (5.9)
C2H3F	2.2 (6.4)	16.3 (57.1)	16.9 (88.5)	3.2 (10.2)	3.0 (5.9)
NH2CHO	28.7 (173.5)	192.1 (474.1)	30.2 (125.2)	22.8 (70.1)	3.2 (9.4)
HCCCHO	4.7 (11.9)	38.0 (186.1)	46.8 (165.2)	3.6 (6.4)	2.9 (7.0)
H3COPO	4.2 (12.9)	20.4 (66.2)	24.8 (139.7)	7.3 (32.3)	3.6 (8.2)
H2CCNH	3.7 (14.6)	22.7 (66.8)	7.8 (14.9)	2.6 (6.7)	2.9 (5.6)
C3H4		10.5 (23.7)	24.5 (107.5)	4.7 (10.8)	2.6 (6.3)
C2H4O	11.1 (86.5)	17.7 (81.3)	15.8 (91.9)	20.0 (91.0)	3.8 (11.7)
C2H4S	3.7 (9.7)	8.9 (26.5)	12.1 (26.5)	7.6 (38.1)	2.9 (9.0)
C2H6		13.3 (69.0)	16.9 (40.4)	8.7 (33.8)	1.5 (3.6)
C2H5F	8.2 (38.6)	14.0 (50.6)	23.5 (80.8)	8.0 (44.7)	3.2 (6.6)
B2H6	3.8 (14.2)	7.8 (23.6)	20.1 (88.5)	10.2 (29.8)	2.6 (8.6)
H3NBH3		12.9 (36.0)	19.9 (34.2)	6.8 (33.8)	4.0 (6.6)
Average	5.6 (27.3)	24.3 (74.1)	17.2 (64.9)	7.6 (27.3)	2.7 (6.6)

Figure 1.

Comparison of mean absolute deviation (MAD) and maximum (MAX) deviations of fundamental transition frequencies (in cm^–1) with respect to experimental reference data of some benchmark molecules. Note that MAX for formamide (NH₂CHO) exceeds the shown energy range (474.1 cm^–1; cf. Table 1).

These calculations show that the most accurate and consistent results are obtained from VCI calculations based on a 4-mode coupling potential, which, of course, has to be expected. Second-order vibrational perturbation theory (VPT2) calculations²⁰⁻²³ based on a QFF yield remarkably accurate results for most of these molecules, while those with strongly anharmonic potentials, internal rotational degrees of freedom, or strong resonances, which are prevalent in larger molecules, may lead to maximal errors, which are too large for certain applications or detailed analyses. For example, the exceptional maximal deviation for oxirane (C₂H₄O) arises from a type II Fermi resonance, and the perturbed VPT2 solution is in much better agreement than after the resonance correction, one of the major obstacles in VPT2 theory.

The main question now is, why does VPT2 yield such nice results for rigid systems? Certainly, one argument is that the leading correction term in VPT2 theory is of the same form as the analytic correction term in the solution for a Morse oscillator. Consequently, if a Morse oscillator is a good representation of the 1D potential curve and coupling between different vibrational modes is weak, then VPT2 should work fine. And, clearly, the calculation of a QFF for VPT2 is less demanding than calculating a 4-mode coupling potential for a highly accurate VCI calculation. It is not only the reduced number of grid points to be computed but also the small elongations from the equilibrium structure in order to determine the needed derivatives that stabilize the calculation by avoiding convergence problems in the electronic structure calculations.

On the contrary, VCI calculations based on QFFs yield results of much lower accuracy being comparable with the quality obtained from VCI calculations based on 2-mode coupling terms. A straightforward task would be to replace the QFF by a sextic force field (SFF) as has been done by several groups in the past.²⁴ However, this approach is not without problems. For some of the molecules listed in Table 1 one yields very much improved VCI results when employing SFFs (e.g., formaldehyde (H₂CO), MAD = 2.5 cm^–1, MAX = 4.4 cm^–1; ethylene (C₂H₄), MAD = 3.5 cm^–1, MAX = 9.0 cm^–1), which are often comparable with the VPT2 results. For other molecules of this test set, the underlying vibrational self-consistent field (VSCF) equations do not converge at all when using SFFs or, in case a simple harmonic oscillator basis has been used, result in very bad VCI solutions, e.g., C₃H₄, C₂H₆, HCCCHO, or C₂H₅F.

This problem arises from regions far away from the expansion point of the Taylor series and is sketched in Figure 2 for the CH₂ wagging mode of allene. While the n-mode expansion requests strong displacements from the reference structure and relies solely on interpolation, the Taylor expansion essentially extrapolates. Within the QFF calculations the number of terms is too small to allow for a strong flexibility of the curve, but in the case of SFF calculations the volatility due to the high-order terms increases, which leads to improved results close to the minimum but to severe problems in the outer regions. The integration until infinity and the inclusion of high-lying correlation functions in the VCI approach cause the calculations to fail. Consequently, VCI calculations based on high-order Taylor expansions are by nature less stable than those relying on interpolation as is the case in n-mode representations. Note, these problems have already been discussed by Czakó et al. about 20 years ago for some triatomic molecules.²⁵ Besides this, in our benchmark calculations, SFFs requested the calculation of many more grid points than n-mode expansions being truncated after the fourth order.

Figure 2.

Potential energy curve of the degenerate CH₂ wagging mode of allene depending on its representation. Anharmonic wave functions corresponding to the lowest 12 levels as obtained from variational calculations with harmonic basis functions are depicted. The data shown (black markers) correspond to the ab initio points that define the potential energy curve.

The mean absolute deviations (MAD) and maximal deviations (MAX) of the test molecules in Table 1 decrease nicely with increasing order of the n-mode expansion of the PES and the user may choose the accuracy that serves the requirements of the project. The remaining error bar in the VCI(4D) calculations with respect to gas phase measurements is in the same range as that observed by comparing matrix isolation experiments with gas phase results. While Ne matrix shifts have been reported between 1 and 3 cm^–1, those in the Ar matrix are slightly larger, i.e., 4–5 cm^–1.²⁶ Those observed from para-H₂ matrixes are usually in between these values.²⁷ Usually, matrix shifts are largest for strongly resonating states. With that, VCI(4D) calculations can compete directly with these experiments.

In order to reduce the error bar even further, it is not only sufficient to increase the order of the PES expansion but rather requires the inclusion of core correlation effects, relativistic contributions, higher-order coupled-cluster terms, diagonal Born–Oppenheimer corrections, etc. within the electronic structure calculations, which can only be afforded for the smallest molecules.²⁸⁻³⁰ Therefore, there is a high need for approximate but cheap techniques to estimate the impact of high-order correlation effects, e.g., the continued fraction approach,^31,32 and to accelerate the calculation of 4-mode coupling potentials.

Multilevel Approaches

As outlined above, it is safe to truncate an n-mode expansion of the PES for semirigid molecules after the fourth-order terms once an accuracy of several wavenumbers is sufficient; i.e., PESs obtained from explicitly correlated coupled-cluster calculations yield MADs of 2–3 cm^–1 and maximum deviations usually below 10 cm^–1 with respect to experimental gas-phase data for the fundamental modes of organic molecules. However, the determination of an n-mode representation of the PES up to fourth order by coupled-cluster calculations is very demanding and, as will be shown below, often unnecessary.³³⁻³⁶

This shall be demonstrated by exemplary calculations on difluoromethane (cf. Table 2). Three different calculations were performed for this molecule. The first one relies on a PES, which has been determined exclusively by MP2/cc-pVTZ calculations. However, the results are disappointing, as the MAD with respect to experimental data is huge. The same calculation, but relying on a PES obtained from explicitly correlated coupled-cluster results, yields nice results with a mean deviation as low as 1.6 cm^–1, but the calculation runs for more than 3 days. Note, due to the reduced basis set sensitivity of explicitly correlated electronic structure calculations, significantly smaller basis sets can be used in comparison to conventional calculations, which in turn leads to large CPU time savings. Consequently, these 3 days of CPU time are not too bad. However, a multilevel scheme,^33,34,36 in which the different orders of the n-mode expansion have been evaluated at different levels of electronic structure theory, combine the positive aspects of both, i.e., high accuracy and a reasonably fast evaluation. A graphical representation of such schemes is given in Figure 3. Multilevel approaches have also been employed in the context of force fields and VPT2 calculations for a long time.²⁰ In more recent work^22,37−41 these are termed hybrid force fields, i.e., high-level coupled-cluster harmonic frequencies are combined with low-level anharmonic cubic and quartic force constants. The speedup can be understood easily, as the vast amount of grid points to be calculated can be determined by calculations of lower accuracy. Note that, in the given example, the calculation of the 4-mode coupling terms is less demanding (1.4 h) than the calculation of the 3-mode terms (2.6 h) and thus: Once 3-mode couplings can be afforded, 4-mode couplings do not constitute a bottleneck and can be afforded as well. In principle, we could have used completely different multilevel schemes, which, for example, employ density functional theory (DFT), which is a frequent choice, for example in condensed phase or solid state calculations. DFT is appealing as a low-level method for the high-order terms of the PES, because of an improved convergence of the SCF iterations for strongly distorted structures on the PES. On the contrary, very tight integration grids are required to ensure smooth potential functions, which renders these calculations rather costly and therefore not very attractive for the purposes in this context.

Table 2. Mean Absolute Deviation (MAD) and Maximum (MAX) Deviation of VCI Fundamental Frequencies (in cm^–1) with Respect to Experimental Gas Phase Results for the Fundamental Transitions of CH₂F₂ Depending on the Accuracy of the PES^a.

		Level	MAD	MAX	CPU
1)	1D - 4D:	MP2/VTZ	23.9	53.1	1.98
2)	1D - 4D:	CCSD(T)-F12a/VTZ-F12	1.6	4.0	79.32
3)	1D:	CCSD(T)-F12a/VTZ-F12
	2D:	DCSD-F12a/VTZ-F12
	3D:	DCSD-F12a/VDZ-F12
	4D:	MP2/VTZ	1.5	3.8	6.27

^aCPU times (in h) needed for the determination of the PES are given in the last column.

Figure 3.

Schematic representation of a multilevel scheme for the efficient determination of a molecular PES within the n-mode expansion. Depicted is a “common” structuring of the reduction where the computational cost decreases from method A to B and from B to C. The schematic error corresponds to the error in the resultant vibrational transition depending on the maximum V^nD employed. Due to the structure of the n-mode expansion, cf. eqs 2 and 3, lower dimensionality surfaces need to be evaluated for Methods B and C.

The presented example of CH₂F₂ of course is a rigid molecule, and the employed normal modes are a meaningful set of coordinates. Consequently, the 1-mode terms being determined at the CCSD(T)-F12a/cc-pVTZ-F12 level contribute significantly to the potential, which is relevant for the vibrational wave functions. In case of a more floppy molecule with large amplitude motions, for which the rectilinear normal coordinates are less appropriate, the contributions of the high-order terms of the PES expansion become more important and thus the quality of the final results of a multilevel calculation most likely will decrease. However, this consideration shows that it is not so much the multilevel scheme in itself, which may cause problems, rather than the choice of the coordinate system.

The question arises, if it is meaningful to use multilevel schemes in the training of machine learning potentials or in dynamical on-the-fly calculations, which has not yet been studied by means of benchmark calculations. Currently, machine learning potentials (MLPs) for representing PESs are almost exclusively trained on data sets being obtained from a single level of electronic structure theory, which renders the calculation of the reference points a very demanding task. The use of multilevel techniques in the context of MLPs could circumvent this bottleneck. A few studies aiming in that direction have appeared in the last couple of years based on Δ-learning^42,43 or transfer learning.⁴⁴ However, the question which paradigm is more efficient is still subject of current research.^45,46

An Alternative to Machine Learning

The multilevel approach presented in the last section is a powerful approximation to reduce the computational cost for molecules with more than three atoms. In principle, the high-order terms of the n-mode expansion of such calculations need not be determined by ab initio calculations but allow for any modeling schemes. For example, one could train a MLP on the basis of the high-level grid points of the 1D and 2D terms in order to predict the 3D and 4D terms. However, this requires a fast training procedure combined with an automated error control as this step is just an integral part of the PES construction and is meant to be performed without any external control by the user. Furthermore, MLPs typically require a rather extensive data set for training, which the 1D and 2D terms might not provide.⁴⁷ As a MLP essentially implies the optimization of parameters for a given set of functions, this entails all the associated problems of local minima, extrapolation, etc. A closely related approach is based on optimization of the parameters within a more physically motivated set of functions.

Semiempirical molecular orbital (MO) theory,⁴⁸ which has successfully been used over decades, usually contains a set of about a dozen parameters per atom, which can also be optimized with respect to the high-level low-order grid points.^49,50 As such, machine learning approaches and the reparametrization of semiempirical MO theory share a common philosophy and are strongly related to each other. In fact, combinations have been investigated in the last couple of years, in which ML is used to learn the parameters within semiempirical MO theory.^51,52 Furthermore, reparametrization of the PM6 semiempirical method has recently also been incorporated in the construction of QFFs for large molecular systems such as polycyclic aromatic hydrocarbons.^53,54

Table 3 shows exemplary calculations, in which the 1D and 2D terms of an n-mode expansion PES have been obtained at the levels presented in Table 2 for the multilevel scheme, but different approximations were used for the large number of grid points required in constructing the 3D and 4D terms. In the first step, the 3D and 4D terms of the PES expansion were neglected altogether. As a result, the MAD and the maximum deviation grow significantly (in comparison to the values in Table 2), simply indicating the importance of the neglected 3D and 4D mode couplings. Approximating these terms by simple semiempirical AM1 calculations leads to a tremendous reduction of the errors, but they remain well above the reference values of Table 2. However, an automated reparametrization of the semiempirical parameters with respect to the available 1D and 2D terms of the PES leads to deviations, which are only slightly larger than those provided in Table 2 using sophisticated electronic structure methods.

Table 3. Mean Absolute Deviation (MAD) and Maximum (MAX) Deviation of VCI Fundamental Frequencies (in cm^–1) with Respect to Experimental Gas Phase Results for the Fundamental Transitions of CH₂F₂ Depending on the Treatment of the 3-Mode and 4-Mode Coupling Terms.

Level	MAD	MAX
3D/4D: neglect	11.1	80.8
3D/4D: AM1	3.7	7.2
3D/4D: AM1 reparametrized	1.7	5.3

As significantly more advanced semiempirical MO theories have been developed since the introduction of AM1,⁵⁵ it is very likely that even better results can be obtained with these modern variants.⁴⁸ With respect to CPU time, the effect is enormous: The calculation of the 3D and 4D terms required less than 3 min instead of 4 h as needed within the multilevel calculation presented in Table 2. However, this does not include the time for the least-squares reparametrization procedure, which for small molecules is much more expensive than the calculation of the high-order mode coupling terms. But this holds likewise true for the training in ML based methods. For the example of CH₂F₂ the reparametrization requested about 48 min, leading to an overall calculation time for the PES of 2.3 h, which is considerably faster than for the multilevel scheme presented above (cf. Table 2).

Clearly, for larger molecules, the benefits will be even larger. Consequently, the combination of highly accurate ab initio methods with molecule-specific modeling schemes allows for an automated and fairly accurate determination of potential energy surfaces. While the reparametrization process has already been fully automated and can simply be controlled by some very few keywords in the input stream, the training of MLPs usually requires strong user control and is often done in separate calculations (see, e.g., ref (47) and references therein). Work in the direction of an automated and efficient training of MLPs for vibrational structure calculations is highly desirable.⁵⁶⁻⁵⁸

Vibration Correlation Calculations

Vibrational configuration interaction (VCI) calculations have the reputation of being expensive and thus being unfeasible for larger systems. In comparison to VPT2²⁰⁻²² this is certainly true, but very much effort has been put in improving the efficiency of VCI methods,⁵⁹⁻⁶¹ which renders them nowadays much more attractive than a decade ago.⁸ It is the use of contraction schemes, the introduction of configuration classes, the screening of the correlation space in configuration-selective approaches, and other techniques that lead to tremendous CPU-time savings. Of course, alternative correlation methods,⁶² which are often based on perturbation theory, e.g., VMP2,⁶³ can be employed as well, but usually these approaches show limitations due to frequently occurring resonances in the vibrational spectra. Vibrational linear response approaches being based on vibrational coupled-cluster calculations for vibrational ground states, are favored by Christiansen et al.⁶⁴ and are an interesting alternative to VCI, but of course, linear response methods and VCI are both linear in the ansatz and are thus somewhat related.

In the following, we will exclusively concentrate on configuration-selective VCI (cs-VCI) approaches, which are among the most frequently used methods in this context. Within these state-specific calculations, an individual VCI matrix is set up for each vibrational state to be computed. Without configuration selection, this is a meaningless task as all state energies can be retrieved from a single matrix. However, configuration selection allows us to tailor the configuration space to those configurations only, which show meaningful contributions to the targeted state. This usually overcompensates for the disadvantage of retrieving just a single state from the VCI matrix and allows for a very simple parallelization over all states to be computed. For example, within the VCI calculation for thiirane, C₂H₄S (cf. Table 1), a VCI calculation including sextuple excitations results in about 7.5 × 10⁶ initial Hartree products per irrep. This not only leads to severe memory problems but also prohibits a diagonalization of this matrix. Contrarily, configuration-selective cs-VCI reduces this to dimensions ranging from 4 × 10³ to 12 × 10³ for the individual states. Exploiting sparsity leads to further memory savings and iterative state-specific eigenvalue-solvers⁶⁵ allow for an efficient evaluation of the vibrational state energies. Of course, truncated VCI expansions suffer from the size-extensivity problem, but as long as high excitation levels are employed, which are requested once high-order PES expansions are used, this issue is of minor importance as results close to the full VCI limit (FVCI) can be achieved for systems of up to 12 atoms or even more.

Figure 4 shows the accuracy and performance of cs-VCI calculations depending on the excitation level, i.e., singles, doubles, triples, etc., and the expansion order of the PES for some of the molecules of Table 1. Considering cs-VCI calculations relying on 4-mode couplings potentials, it can be seen from panel a of Figure 4 (solid lines) that almost converged results can be obtained once the order of the excitation level is at least higher by one than the expansion order of the PES. This conclusion somehow appears not to hold once the PES has been truncated after the 3-mode coupling terms. An analysis revealed that an incomplete PES, i.e., a PES being truncated after low orders, may lead to artificial resonances in the subsequent VCI calculations. This, for example, has been discussed in the context of VCI calculations for diborane.⁶⁶ Due to the deficiencies in the PES, i.e., the incompleteness of the Hamiltonian, the MADs shown in Figure 4a do not converge but scatter in a certain region. Therefore, the inclusion of high-order excitations in calculations based on low-order PES expansions is meaningless and leads to unbalanced calculations. It is the appearance of these artificial resonances (small leading VCI coefficients) that leads to large deviations for some of the fundamentals (see the MAX values in Table 1) and thus to worse MADs. As resonances are fairly sensitive, this leads to an enhanced sensitivity of the VCI calculations with respect to any parameters of these calculations. Consequently, it should be guaranteed that the Hamiltonian is as complete as possible, but of course a reliable metric for that is missing. Likewise effects may arise from incomplete correlation spaces.

Figure 4.

Mean absolute deviations (MAD) of VCI results with respect to experimental data depending on the excitation level and the expansion order of the PES (panel a), wall clock times for calculating VCI infrared spectra based on the fundamental transitions (panel b), and average CPU times for a single VCI state calculation (panel c).

Figure 4 panels a and b show the performance of the cs-VCI calculations. While panel b shows the wall clock time for the calculation of all fundamental transitions including the corresponding infrared intensities, panel 4c shows the average CPU-time for calculating a single transition (without the intensity calculation). All calculations were performed on a customary workstation with 24 cores. As must be expected, the calculation times increase rapidly with the excitation level, but once the rule of thumb, that the excitation level should be higher by one order than the expansion order of the PES, is obeyed, the calculation times remain modest, although being much longer than for corresponding VPT2 calculations. As can be seen from panel b, the overall calculation time of the VCI calculations including sextuple excitations for diborane is longer once a PES being truncated after the 3-mode coupling terms has been used in comparison to calculations including 4-mode couplings, although the latter calculation requires the calculation of many more integrals. This is again a result of the artificial resonances, which in the iterative configuration-selective VCI approach may lead to many more selected Hartree products than in the case of the 4D calculations. This result also indicates that the configuration-selective calculation of high lying overtones and combination bands, which are often plagued by strong resonances, is usually more demanding than for the fundamentals in the fingerprint region.

These examples demonstrate that VCI calculations have reached a level of maturity and efficiency, which allows for almost black-box calculations in routine applications, which is what has been done in generating Table 1. In other words: when the generation of a PES including 4-mode couplings can be afforded, the corresponding cs-VCI calculation including up to sextuple excitations can be afforded as well. Further developments in the field of cs-VCI theory focus on specialized approaches for multicore architectures and smaller VCI matrices.^67,68

Rovibrational Approaches, RVCI

Rotational and rovibrational infrared spectra are the workhorse in astrophysical studies focusing on the identification of new molecular species in space. The simulation of such spectra is usually based on the calculation of spectroscopic constants, which can be obtained from vibrational perturbation theory. The constants, which refer to Watson’s A or S-reduced Hamiltonians,⁶⁹⁻⁷² can subsequently been fed into these model Hamiltonians to retrieve the desired line lists.⁷³ As such, these calculations rely on Taylor expansions and thus have to deal with the limitations in accuracy, as outlined above. Alternatively, one can calculate these line lists from rovibrational VCI theory (RVCI) directly,⁷⁴ but little has been done in that direction for obvious reasons: (a) PESs of very high accuracy are required to allow for a direct comparison with experimental data. This prompted several groups to adjust their PESs to experimental data,⁷⁵ which of course prohibits the theoretical prediction of unknown species. However, the explicit inclusion of high-order coupled cluster terms usually cannot be afforded for systems with more than 4 atoms, and thus this remains an open field of research currently (vide supra). (b) RVCI calculations can be fairly demanding when the total angular momentum quantum number grows large, which usually is the case for systems with more than 6 or 7 atoms. This arises from the fact that all eigenpairs of the RVCI matrices are needed, which cannot straightforwardly be reduced, as in the case of cs-VCI calculations. Besides this, very many vibrational states need to be considered for the simulation of a rovibrational spectrum, which leads to polyad schemes or screening approaches. However, in the recent past some progress has been made in the direction of calculating rovibrational spectra of molecules with more than 4 or 5 atoms, which at least allows for a qualitative comparison.^76,77

This shall be exemplified by RVCI calculations for formamide,⁷⁸ a molecule that can hardly be described by VPT2 calculations (cf. Table 1). Within RVCI theory, the eigenvectors obtained from the cs-VCI theory can be used as basis functions for the subsequent rovibrational calculations. Table 4 shows a comparison of the computed fundamental transitions with experimental gas phase data. Of course, the states associated with the fundamental transitions do not constitute a sufficiently large basis in RVCI calculations, and hence, the calculation of RVCI spectra requests at least overtones and combination bands with three excited quanta. Figure 5 shows the rovibrational spectra of the problematic and strongly quartic NH₂ wagging mode of formamide, as obtained from measurements and RVCI calculations. Panel a depicts the experimental spectrum of McNaughton et al.⁸⁰ In line with the near-prolate nature of formamide (κ = −0.952), the band resembles a perpendicular band of a prolate symmetric top with a strong central Q-branch and the typical P- and R-branches. The simulated spectrum including line broadening effects (panels b–d) mirror the main features, however, depending on the employed broadening parameter (full width at half-maximum, FWHM) to a varying degree. For example, while the shoulder of the central Q-branch is only clearly visible in panel d, the overall intensity in the P-branch seems to be reproduced better with 0.5 cm^–1 FWHM (panel c). In contrast, the intricate structure of the P-branch observed in panel a is not reproduced in any of the broadened spectra, but the positions of the peaks of the R-branch are nicely resolved. The most dramatic effect concerns the difference between the bar plot (panel e), which simply presents the rovibrational line list, and the spectra including line broadening effects. Note, that in all calculations the same line list has been used to obtain the spectra. It is clear that rovibrational spectra show an extremely strong dependence on environmental effects which are the main source for line broadening, and thus there is a high need for experimental high-resolution spectra, which minimize these effects. At the same time, a fully theoretical description and routine prediction of the broadening beyond simple parametrized Gaussian profiles with a globally fixed FWHM would be highly desirable.⁸¹ Note that there is a large body of experimental data on measured line shapes which should be ideal for benchmarking future developments.^82,83

Table 4. Fundamental Transitions (in cm^–1) and Infrared Intensities (in kilometers/mol) of Formamide.

#	Sym	Expa	Expb	VCI	IR
ν1	a′	3563.5	3563.7	3569.0	14.7
ν2		3439.3	3439.5	3442.6	11.3
ν3		2853.6	2853.6	2853.5	59.9
ν4		1754.1	1754.1	1757.5	341.9
ν5		1576.9	1578.9	1578.1	43.5
ν6		1390.2	1390.7	1391.1	3.7
ν7		1258.2	1258.2	1257.7	92.3
ν8		1045.6	1045.7	1041.0	7.7
ν9		581	565.8	562.0	11.5
ν10	a″	1021.2	1033.3	1023.6	2.5
ν11		602.8	602.4	596.9	16.8
ν12		288.7	289.0	286.8	174.9

^aTaken from ref (79).

^bTaken from ref (80).

Figure 5.

Rovibrational spectrum of the NH₂ wagging mode of formamide. (a) Experimental spectrum reproduced with permission from ref (80). Copyright 1999, with permission from Elsevier. (b–d) Simulated spectra including line broadening effects with a FWHM of 1.0, 0.5, and 0.2 cm^–1. (e) Stick spectrum as obtained from the RVCI line list.

Summary, Conclusions, and Outlook

Calculations for infrared spectra with maximum deviations below 10 cm^–1 and a mean absolute deviation of just a few wavenumbers with respect to experimental reference data are feasible nowadays. However, within variational approaches these request the inclusion of at least 4-mode coupling terms within an n-mode expansion of the PES. Alternatives to machine learning have been discussed, which can be easily automated, bear a significant potential, and lead to considerable CPU time savings. With that, the computational bottleneck within the construction of a multidimensional PES is not given by the high-order terms of the n-mode expansion but the high-level electronic structure methods needed for the accurate evaluation of the low-order terms of the PES. Current implementations of highly efficient (explicitly correlated) coupled-cluster methods relying on pair natural orbitals appear not to be numerically stable enough to allow for an efficient calculation of smooth potential curves. Besides that, low-cost methods for approximating high-order coupled-cluster terms are highly desirable, to further increase the accuracy of such calculations as needed for rovibrational studies in astrophysics.

Although the accuracy of MLPs has been increased tremendously within the last years,⁸⁴⁻⁸⁶ the generation of such potentials is currently still fairly costly and far from being automated. In particular, this holds true for the generation of the reference data and the training process. Additionally, the final accuracy is often not yet competitive with the conventional fitting of PESs once high accuracy is needed. While the automated construction of PESs based on normal coordinates has reached some degree of sophistication,^24,87−90 the likewise construction based on internal coordinates as needed for molecules with large amplitude motions is technically less mature.⁹¹ Progress in that direction accompanied by the automated identification of a meaningful or best coordinate system is highly desirable.

Very much progress has been made in the development of vibrational structure methods, exemplified here for configuration-selective vibrational configuration interaction calculations.⁸ These methods enable the high accuracy of the high-dimensional PES representations, and calculations with sextuple excitations are feasible for systems with more than 12 atoms in reasonable time frames. Of course, this picture alters once high-lying states need to be computed. Although the computational bottleneck created by huge correlation spaces is smaller than that for the construction of the PES, further accelerations and stabilizations are needed for energy regions showing a high state density or strongly quartic potentials. While a bunch of methods have been developed for nonrotating molecules, approaches for rovibrational calculations currently remain limited to configuration interaction approaches. This is at least partly because often millions of eigenpairs are needed for the simulations of these spectra, which renders these calculations rather expensive. Automatization in that field of research is still in its infancy, but highly desirable as the progress in astrophysical observations requires rovibrational reference calculations for systems with more than 4 or 5 atoms, e.g., complex organic molecules.

Biographies

Benjamin Schröder received his PhD in chemistry in 2019 from the University of Göttingen. He joined the group of Guntram Rauhut at the University of Stuttgart as a postdoctoral fellow to work on novel implementations of vibrational structure theory. In 2022 he returned to Göttingen where he is now a postdoctoral researcher within the BENCh research training group. His research interests are in composite methods for subwavenumber accuracy in rovibrational spectroscopy, machine learning methods for molecular potential energy surfaces and the theoretical (ro)vibrational spectroscopy of molecules relevant for astrochemistry.

Guntram Rauhut graduated from the University of Erlangen-Nürnberg, Germany, with a PhD in chemistry in 1993. He was a postdoctoral associate with Peter Pulay (USA) and is now professor for theoretical chemistry at the University of Stuttgart, Germany. He is a coauthor of the Molpro package of ab initio programs and leads a research group in the field of theoretical spectroscopy. His main interests are the development of accurate vibrational structure methods, the automated calculation of potential energy surfaces, and the application of these methods to astrophysically relevant molecules.

The authors declare no competing financial interest.