Measuring CHAOS? Evaluating the short-form Confusion, Hubbub And Order Scale

Abstract

The Confusion, Hubbub and Order Scale (CHAOS) – short form – is a survey tool intended to capture information about home environments. It is widely used in studies of child and adolescent development and psychopathology, particularly twin studies. The original long form of the scale comprised 15 items and was validated in a sample of infants in the 1980s. The short form of the scale was developed in the late 1990s and contains six items, including four from the original scale, and two new items. This short form has not been validated and is the focus of this study. We use five samples drawn from twin studies in Australia, the UK, and the USA, and examine measurement invariance of the CHAOS short-form. We first compare alternate confirmatory factor models for each group; we next test between-group configural, metric and scalar invariance; finally, we examine predictive validity of the scale under different conditions. We find evidence that a two-factor configuration of the six items is more appropriate than the commonly used one-factor model. Second, we find measurement non-invariance across groups at the metric invariance step, with items performing differently depending on the sample. We also find inconsistent results in tests of predictive validity using family-level socioeconomic status and academic achievement as criterion variables. The results caution the continued use of the short-form CHAOS in its current form and recommend future revisions and development of the scale for use in developmental research.

The effects of home environments on childhood functioning and development has been a topic of research interest for decades (Bradley, 2015; Evans, 2006). Bronfenbrenner’s widely-known bioecological model of human development defines the home environment as a key context for proximal processes that influence childhood development (Bronfenbrenner, 1986; Bronfenbrenner & Ceci, 1994; Bronfenbrenner & Morris, 2006). In particular, Bronfenbrenner argued that stability in home environments was particularly important for development (Bronfenbrenner & Evans, 2000), and disruptions to routine family life were centrally important in poor childhood psychological functioning (Bronfenbrenner & Ceci, 1994).

Identifying the features of stable and consistent family home environments, and examining the effects of variability in home contexts, has therefore been important for testing the propositions of the bioecological theory of development. To achieve this aim, however, home environmental features must be recorded or measured in some way. The purpose of the current study, therefore, was to examine the measurement properties of a widely-used short-form scale, which was developed with the intention of capturing variability in home environments, the Confusion, Hubbub And Order Scale (CHAOS; Matheny et al., 1995). We begin with some background on the measurement of home environments before providing a brief history of the CHAOS measure.

Capturing the variability in home environments

In the mid-20^th century researchers recorded information about differences between home environments via in-person observations (e.g. Wilson & Matheny, 1983). Research assistants spent many thousands of hours attempting to unobtrusively observe aspects of home environments, including interactions between parents and children, the number of visitors coming and going, ambient noise levels (both internal and external to the home), observable routines established by parents, among other features (Evans, 2006). These efforts to measure the quality of home environments were expensive, and limited in that a finite number of households in a geographically constrained area could be visited by research assistants within a given timeframe. In the 1980s, therefore, measurement of household environments began to shift from a reliance on observations, recorded as both qualitative information and observer ratings on quantitative scales, to self-report scales, where parents were asked to rate aspects of their homes according to questionnaire items.

The CHAOS scale was one of several self-report instruments established during the latter decades of the 20^th century (the HOME scale is another widely used instrument; c.f. Bradley, 2015 for a review). Two versions of the CHAOS scale have been used in research since its inception: the original 15-item version proposed by Matheny et al. (1995), and a short-form 6-item version. The scale has been used extensively in research: there are over 500 citations to date of the paper reporting the psychometric properties of the original scale (Matheny et al.), and a library database search identified 305 articles and 62 dissertations referencing the name of the scale (June, 2022). It is difficult to identify how many of these research articles use the long form and how many use the short form of the scale given that both have the same title. The latter, short-form is the focus of this study, however some background on the original long-form is relevant here.

The 15-item CHAOS measure was developed in a sample of over 400 families of twins participating in the Louisville Twin Study during the 1980s. The original scale (reproduced in Figure 1.) comprised true/false scored items, half reverse scored, which were summed to produce an overall measure of the (in)stability of the household environment. Conceptually the scale captured aspects of household confusion and disorder, including high levels of noise, clutter, disorganization and “frenetic activities” (p.432). Matheny et al. (1995) validated the 15-item scale using a subsample of 123 mothers of infants ranging in age from 6 to 30 months reporting a reliability coefficient of α = .79. A further subsample of 42 mothers completed the questionnaire at a 12-month interval with a test-retest correlation of r=.74. Matheny et al. noted that the 15-item CHAOS scale accounted for a unique proportion of systematic within-home differences that could not be attributed to parent education or SES measures. Nonetheless, direct observations of the home environment were not interchangeable with the CHAOS scale: there was a significant, but not high, degree of overlap between the two measures in the study (R² = .39). The 15-item scale was further validated in two different samples of preschool (n = 106) and school-aged children (n = 676; Dumas et al., 2005), demonstrating overlap with, but distinction from, measures of socioeconomic status, and good internal consistency reliability (α = .83 / .81).

Figure 1. Original 15-item Confusion, Hubbub and Order Scale (CHAOS) from Matheny et al. (1995).

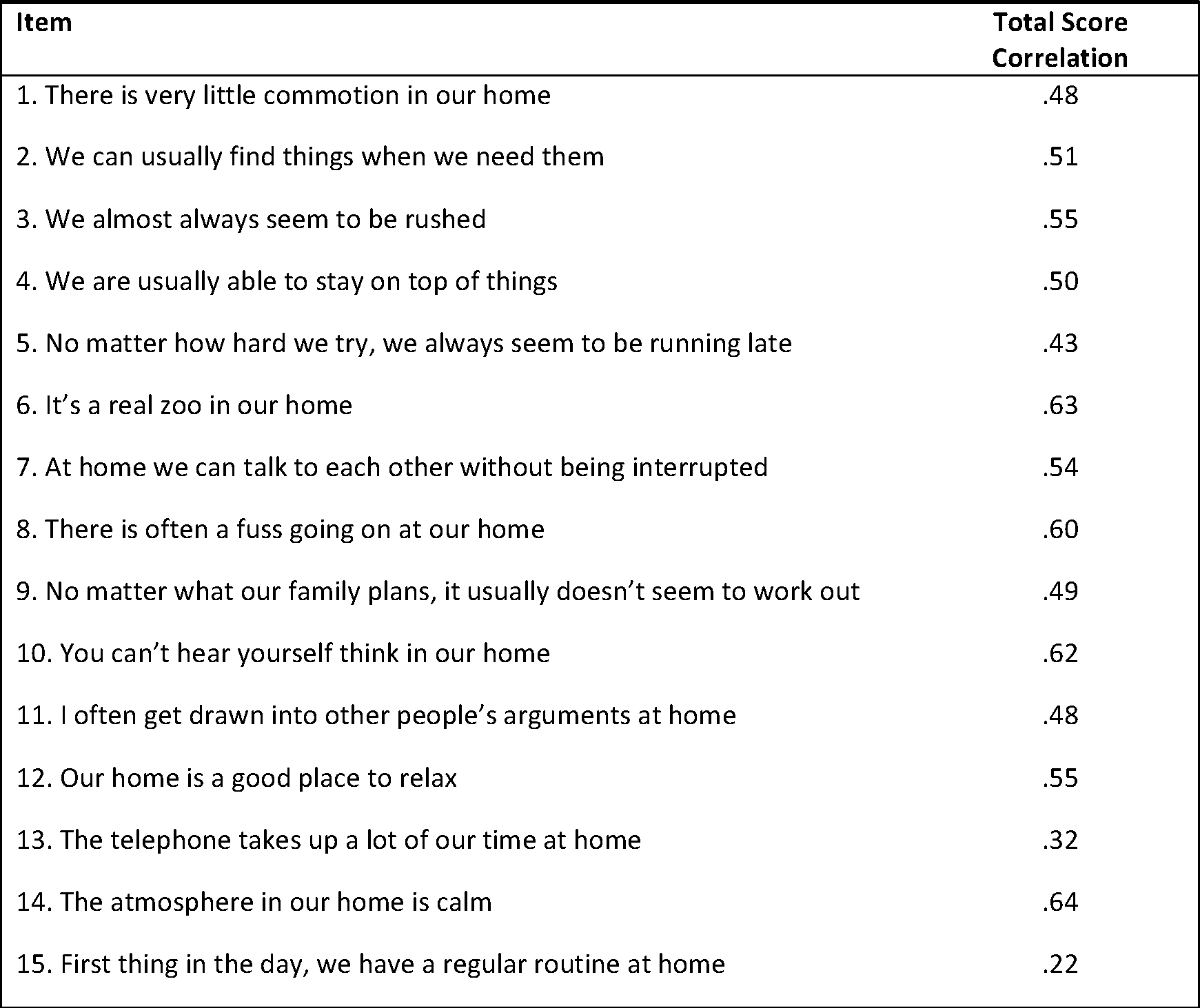
Note. Parents responded true / false to each item. Scores were summed to create a composite with higher scores representing greater ‘chaos’

The short 6-item form of the CHAOS measure was first used in the late 1990s by studies including the Twins Early Development Study (TEDS; e.g. Asbury et al., 2003) and the Western Reserve Reading and Math Project (WRRMP; e.g. Hart et al., 2006). The short-form of the scale is reproduced in Figure 2. This form consists of 4 items from the original Matheny et al. (1995) 15-item scale, plus the addition of two items not appearing in the original scale: Item 1 The children have a regular bedtime routine and item 5 There is usually a television turned on somewhere in our home. There is no published information on why these 6 items were chosen for inclusion in the short-form CHAOS and no evaluations of whether the short form captures the full range of the original intended construct (e.g. Smith et al., 2000). In published articles using the short-form, construct validity evidence is universally attributed to the article which reports the validity of the long-form, 15-item scale (Matheny et al., 1995), and reliability information is usually reported as Cronbach’s coefficient alpha, with estimates ranging from α = 0.52 – 0.68.

Figure 2. Six items in the short-form version of the CHAOS scale with variations for different studies.

Note. * indicates item that did not appear in the original 15-item scale. ⁱ indicates variables reverse-coded for analysis so that higher scores = greater ‘chaos’.

Notwithstanding the lack of published evidence that the short-form CHAOS scale reliably measures the same construct as that proposed by the long-form, many studies have used the 6-item scale to examine links between the home environment and childhood functioning. Table S1 in the supplementary material shows details of 21 papers that we could identify published between 2003 and 2019 that used the short-form CHAOS. Studies have examined associations between CHAOS and cognitive development (Petrill et al., 2004; Pike et al., 2006), reading skills (Johnson et al., 2008), language development (Asbury et al., 2005), and behavioural problems (Coldwell et al., 2006; Deater-Deckard et al., 2009; Laurent et al., 2014; Peviani et al., 2019), consistently finding that higher ratings of household CHAOS are associated with worse functioning or development. The short scale has also been used in studies examining social determinants of health and wellbeing (Ganasegeran et al., 2017; Suku et al., 2019). Many of the studies that have collected data on the CHAOS short-form have been twin studies which examine home environments within the behaviour genetics theoretical framework: home environments are considered an aspect of shared environments, i.e. environmental features which serve to make twins more similar to one another (Plomin et al., 2013), although it is acknowledged that twins can perceive the same objective environment differently (Hanscombe et al., 2010). Several studies have examined the extent to which home environments mediate or moderate genetic influences on childhood outcomes (Asbury et al., 2003; Gould et al., 2018; Harlaar et al., 2005; Hart et al., 2007; Petrill et al., 2004), and one study attempted unsuccessfully to identify genetic influences on reports of CHAOS using a genome-wide association design (Butcher & Plomin, 2008).

The short-form scale has also undergone several additional transformations, including translations into languages other than English (e.g. Deater-Deckard et al., 2019; Ganasegeran et al., 2017), and versions where children or adolescents themselves rate their home environments on a three-point likert response scale. Using this adolescent self-report data, studies have examined links between CHAOS and academic achievement, behavioural functioning (Hanscombe et al., 2010, 2011; Kim-Spoon et al., 2017), and brain activity in functional MRI studies (Lauharatanahirun et al., 2018). An even shorter version of the short-form, comprising only five items, is also evident in the literature. This five-item version is used in the Parenting across Cultures Study, which recruited 511 urban families in six low-to-middle income countries (China, Kenya, the Philippines, Thailand, Colombia and Jordan; Deater-Deckard et al., 2019). In this version, item 5 There is usually a television turned on somewhere in our home, was omitted because of the possibility that families in low income countries do not own televisions. There is, as yet, no published scale evaluation information indicating this item performs badly. Despite this additional variation, the studies emerging from the Parenting Across Cultures project report the original Matheny et al. (1995) article as evidence of the reliability of the scale for capturing “a harsh and unpredictable environment” (Chang et al., 2019a, p.4; Chang et al., 2019b; Deater-Deckard et al., 2019).

Given the widespread use of the short-form CHAOS, and its attractiveness in terms of minimal time commitment of respondents in multivariate surveys, the lack of reliability and construct validity information for the scale is of concern. The present study thus aims to examine the measurement properties of the short-form CHAOS scale. We use several approaches and five datasets to adjudicate whether the scale is valid and reliable for measuring the quality of home environments. In defining validity, we take the position of Borsboom et al. (2004) who argued simply that “a test is valid if it measures what it purports to measure” (p.1061). Furthermore, we define reliability as “an index of measurement precision” (p. 1070) that can be evaluated within a scale (i.e. how well do items measure the same construct) and across measurement occasions (i.e. between samples or within samples over time). In this study we therefore: 1) examine the factor structure of the six items, 2) evaluate whether the measure is invariant across groups, and 3) examine the predictive validity of the scale using a measure of socioeconomic status and childhood academic achievement as criterion variables. In this way we collate evidence of the validity and reliability of the scale as an adequate measure of the quality of home environments in different populations.

Measurement invariance

Combining multiple survey items into a single composite score is very common practice in social science research. Creating a sum or average from several items, however, assumes that the scale in question captures one underlying factor (McNeish & Wolf, 2020). In cases where the construct of interest has been shown to capture a single factor, using composites is a defensible strategy (Widaman & Revelle, 2022), however, there is minimal documentation regarding the most appropriate factor structure of the short-form CHAOS (except in Johnson et al., 2008). Furthermore, use of a scale in different populations also assumes that the measure captures the same latent construct regardless of context (Millsap & Olivera-Aguilar, 2012). Any differences in the means or variances of the observed items is assumed to be related to differences in the latent construct itself, rather than differences between populations that are not related to household order and routine. In this study we test the assumptions that a) a single factor underlies the six items in the short-form CHAOS, b) the factor structure is the same across samples, and c) differences on the observed variables are caused by differences on the latent construct, and are not due to unobserved, external differences between the populations of interest.

We can begin to test these assumptions using confirmatory factor analyses and a measurement invariance procedure. We follow the typical procedure for testing measurement invariance recommended by methodologists (e.g. Millsap & Olivera-Aguilar, 2012; van de Schoot et al., 2012): namely, the same confirmatory factor model is first estimated in each group, then increasingly restrictive equality conditions are introduced for different sets of parameters. If measurement invariance holds across samples, we can be confident that comparing the results of studies using the CHAOS scale in different contexts is valid and informative. On the other hand, if the analyses indicate that the measure is non-invariant, response patterns on the observed items could be systematically influenced by unobserved differences between populations, for example interpretive differences for specific items, rather than by differences in the latent domain of interest (i.e. household order and routine).

This study

Our hypotheses for the study are informed by, 1) the consistently low reliability reported in studies using the short-form CHAOS (α = .52 - .68), 2) evidence from one study that the six items are better represented by two factors rather than one (Johnson et al., 2008), and 3) preliminary evidence generated by an exploratory factor analysis indicating a two-factor solution (see below). Given this information, we hypothesised that a two-factor dimensional structure will better fit the data on the CHAOS items in all samples. Preliminary analyses also inform our hypothesis that the measure will be non-invariant across the five samples: that is, we do not expect the six items to behave similarly in all samples, nor do we expect the factor structure to be repeatable across samples. Finally based on the research findings described above we predict that higher CHAOS will be negatively associated with both family socioeconomic status and academic achievement, however in the case where a two-factor model is most appropriate, it is not clear whether one or both factors will be significantly associated with each criterion variable. Johnson et al. (2008) demonstrated that only one of two factors (household order but not noise) was associated with several measures of childhood literacy, however whether the factor structure identified in this previous analysis holds across all samples will only become evident after the initial invariance testing across all five samples. Preliminary hypotheses and an overview of the study were preregistered at the Open Science Framework (https://osf.io/akmf4). Subsequent to preregistration we gained access to an additional dataset not noted in the preregistration (the Project KIDS data). Ethical approval for this study was obtained from the first author’s institution (Human Research Ethics Committee Approval# HE22–093).

Methods

Secondary data for the project was sourced from: three studies located in the US, the Western Reserve Reading and Math Project (WRRMP; Hart et al., 2007; Petrill et al., 2006), the Florida Twin Project on Reading, Behavior and Environment (FTP-RBE; Taylor et al., 2019), and Project KIDS (Kids and Individual Differences in Schools; van Dijk et al., 2022); one study located in the UK, the Twins Early Development Study (TEDS; Oliver & Plomin, 2007; Rimfield et al., 2019); and one study located in Australia, the Academic Development Study of Australian Twins (ADSAT; Larsen et al., 2020). These studies were selected because all collected parent reports on the English language short-form CHAOS using a five-point likert response scale (see Figure 2.), and the children of interest were aged between 3 (earliest wave of TEDS) to 12 years (upper age of FTP-R, ADSAT and Project KIDS wave 1 samples). Descriptive statistics of participants in all samples and data collection waves are in Table 1.

Table 1.

Descriptive statistics of the five samples included in the analysis

Study Sample (Acronym)	Country	Wave	N i	Female ii (%)	Age iii		α iv	ωh v
					M	SD
Academic Development Study of Australian Twins (ADSAT)	Australia	1	1294	50%	8.79	0.45	0.67	0.54
Florida Twin Project on Reading, Behavior and Environment (FTP-RBE)	USA	1	568	46%	11.16	2.52	0.55	0.37
		2	437		13.30	2.44	0.63	0.53
		3	313		15.24	2.51	0.50	0.48
Project KIDS	USA	1	442	49%	11.07	3.07	0.59	0.50
Western Reserve Reading and Math Project (WRRMP)	USA	1	580	57%	6.09	0.69	0.68	0.56
		2	512		7.16	0.67	0.65	0.29
		3	494		8.21	0.82	0.70	0.63
		4	352		9.81	0.98	0.62	0.58
		5	362		10.90	1.01	0.67	0.37
		6	368		12.21	1.20	0.64	0.45
		7	246		15.05	1.45	0.59	0.48
Twins Early Development Study (TEDS)	UK	1	6009	50%	3.01	0.14	0.63	0.44
		2	8014		4.03	0.15	0.66	0.59

ⁱN=families; for twin studies the number of twins is twice the number of families.

ⁱⁱProportion as at study commencement.

ⁱⁱⁱAge calculated in years: decimal places indicate proportion of a year.

^ivCronbach’s Alpha calculated for all six items.

^vMcDonald’s omega (hierarchical).

Samples and Measures

The Academic Development Study of Australian Twins (ADSAT) recruited a national sample of 2762 families of Australian school aged twins between 2012 and 2017 (Larsen et al., 2020). The design of study recruitment was partly prospective and partly retrospective. For the current investigation we selected only families who were recruited to the study and had completed the CHAOS measure when their twins were in Grades 3, 4 or 5 (n=1294; age 8 to 11 years). This age group was selected in an attempt to align the ages of participating children as closely as possible across samples. For an initial exploratory factor analyses we used an additional sub-sample of 596 families participating in the ADSAT who also completed the CHAOS form on enrolment into the study. Parents completed the CHAOS measure only once.

Academic achievement was measured by standardized scores on reading comprehension and mathematics tests undertaken by children as part of the National Assessment Program: Literacy and Numeracy (NAPLAN; ACARA, 2017). For this study we used scores on the Grade 3 assessments to align with when the CHAOS items were collected. Socioeconomic status in this dataset is a factor score comprising the highest educational attainment of both parents, the occupational prestige ranking of both parents and an indicator of neighbourhood socioeconomic advantage (see Larsen et al., 2020 for details).

The Florida Twin Project on Reading, Behavior and Environment (FTP-RBE) is a subsample of the 2753 twin pairs recorded in the Florida State Twin Registry (FSTR; Taylor et al., 2019). Beginning in 2012, a subsample of families with twins enrolled in the FSTR were invited to enrol in the FTP-RBE, which involved completing a questionnaire, containing in part the CHAOS items, every other year over six years (i.e., three waves of questionnaire assessment). The mean age of twins for the first wave of the questionnaire data collection was 11.16 years. In total, 568 families (72% of the invited participants) provided data on the CHAOS at wave 1, reducing to 447 at wave 2 and 313 at wave 3. Academic achievement was measured by scores on the Florida Comprehensive Assessment Tests (FCAT) reading subtest, undertaken by students in the 2011–12 and 2012–13 school years. The FCAT test is a standardized assessment of reading, completed by students at the end of grades 3 to 11. FCAT data were provided by Florida’s Progress Monitoring and Reporting Network (PMRN). Socioeconomic status is a factor score generated using five observed variables: estimated family income, both parents’ highest educational attainment, and both parents’ occupational prestige.

Project KIDS is a repository of data collected in nine randomized control trials of reading interventions undertaken in the US between 2005 and 2011 (see van Dijk et al., 2022). Data on the CHAOS short form was collected in 2013 from a sub-sample of 442 families of singleton children who had participated in at least one trial. Data on school achievement was collected in the same parent survey. For both English Language Arts and Math, parents reported their children’s achievement on a 5-point rating scale, ranging from A/Excellent (1) to F/Fail (5). Achievement variables were reverse coded before analysis so that higher ratings indicated better achievement, similar to other achievement tests used in this study. Socioeconomic status observed variables and factor score estimation was identical to that in the FTP-RBE study described above.

Western Reserve Reading and Math Project (WRRMP) is a longitudinal cohort-sequential study which recruited families of twins, primarily in the state of Ohio, USA, beginning in 2002. Twins were in kindergarten or first grade on recruitment (mean age = 6.09 years) and were followed up on measures of literacy and CHAOS approximately annually over seven waves of data collection. Across all waves, 794 families provided at least some data to the project. The short-form CHAOS was collected at each wave of the study, with 580 families answering the items in wave 1, reducing gradually to 246 families responding by wave 7.

We selected five assessments of academic skills in both reading and math domains collected across all waves of the WRRMP. These included, a) two assessments of reading comprehension, the PIAT-R/NU (Dunn & Markwardt, 1998) and the WRMT-R passage comprehension assessments (Woodcock, 1987), and b) three assessments of math subdomain skills, the Woodcock-Johnson calculation, applied problems, and quantitative concepts tests (Woodcock, 1987). All children who were able to be followed up at each wave provided data on these assessments. For the WRRMP study we used a proxy of socioeconomic status using variables that were available in the dataset: an average of both parents’ highest educational attainment.

The Twins Early Development Study (TEDS) recruited a nationally representative sample of 13,732 families of infant twin pairs in the United Kingdom from 1994–1996 (Oliver & Plomin, 2007). For this study we use wave 3 and 4 of data collection, when twins were aged 3 and 4 years, respectively. Parents responded to the short-form CHAOS in both waves, with 6009 parents providing data in wave 3, and 8014 in wave 4. Later collections on the CHAOS measure used a 3-point likert response scale and/or asked twins themselves to respond, rather than parents. We omit these waves and focus on the CHAOS measure obtained in the same manner as that for the other data collections in this study. Academic achievement was assessed when twins were aged approximately 7 years. All students in the UK undertake National Curriculum assessments in core subjects. Standardized assessment results for English and Mathematics were sourced from government data collections. We use the socioeconomic status variable available in the TEDS dataset, a composite variable generated from five variables: occupational prestige of both parents, highest educational levels of both parents, and mother’s age at the birth of the first child.

We note that four of the five studies included in this project were studies of child and adolescent twins. For each dataset, the CHAOS items and SES variables were collected at the family level (i.e. one set of responses by family for each wave in each study), therefore we did not need to account for the nested nature of data collected on twin pairs. Academic achievement variables were collected for each twin separately, however, so in instances where we use achievement as criterion variables, we selected one twin at random from each pair. We do not report results for the second randomly-selected twin, but findings were no different.

Analysis plan

In this study we aimed to test the factor structure, measurement invariance and predictive validity of the short-form CHAOS using five samples collected in different contexts. We first wanted to test whether the usual approach to using the six items – i.e. combining them into a single mean or sum score – is the optimal approach to the use of the scale. Only one study to date has reported an exploratory factor analysis of the items (Johnson et al., 2008). Using the WRRMP Wave 1 data this study demonstrated a two-factor solution in an exploratory factor analysis (EFA) with one factor comprising items 1, 4 and 5 (termed “household order and routine”), the second factor comprising items 2, 3 and 6 (“quietness of the household”; Johnson et al., p. 5). The two factors correlated at r = .33. The proportion of variance explained by the two-factor solution and the factor loadings of the items were not reported. Items were subsequently summed within each factor for further analyses. Given this study is the only one to date to examine the factor structure of the short-form CHAOS, the first step in the analysis for the current study was an EFA using a subsample of participants in the ADSAT (n=596). Specifically, a principal components analysis using full information maximum likelihood estimation was undertaken. Due to the results in Johnson et al. we expected that a two-factor solution would fit the data better than a one-factor model. Therefore, we examined eigenvalues, compared the proportion of variance explained by one- and two-factor solutions, and examined item-factor loadings.

To further examine whether a one- or two-factor structure of the six items was best supported by all datasets, we next ran confirmatory factor analyses (CFA) separately for each sample. For CFAs comprising two factors we allowed factors to correlate, but did not allow any cross-loadings of items, nor any residual covariances. We examined model fit statistics, and compared nested models to identify the best solution in each sample. We predicted that two-factor models would be a better fit to the data than one-factor models for all samples, however we made no specific predictions about whether the configuration of items reported by Johnson et al. (2008) would be the best fit in each sample.

Next, measurement invariance was examined via multiple-group confirmatory factor models. In this step we consider each dataset a different group since each study was conducted in a different context, and three countries are represented by the five datasets, Australia, the UK and the USA. We followed the procedure suggested in several sources and tested i) configural, ii) metric, and iii) scalar invariance (e.g. Byrne, 2012; Meredith & Teresi, 2006; Millsap & Olivera-Aguilera, 2012; Putnick & Bornstein, 2016). We did not expect strict invariance (i.e. invariance of residuals) to hold across groups so planned to test this step only where scalar invariance was confirmed. Specifically, configural invariance models force the same factor structure across groups but allow item loadings, item intercepts and residuals to vary. Because we planned to first test confirmatory factor models for each group, and select the best-fitting model, we expected configural invariance to hold. Metric invariance forces equivalence of factor loadings across groups and assesses whether this restriction leads to a significant reduction in model fit. Scalar invariance tests for equivalence of item intercepts across groups retaining the equivalence of factor loadings tested in the previous step. Strict invariance retains the equivalence constraints introduced by metric and scalar invariance, and constrains item residuals to equality. If at any step model fit statistics suggested significantly poorer fit, we examined the parameters constrained by that step to identify potential sources of model misfit.

Model fit was assessed using several statistics. Given that χ² goodness of fit is affected by large samples or variable sample sizes in multiple group models (Byrne, 2012), we report this statistic along with several others. In particular, we examine the root mean square error of approximation (RMSEA), which ideally should fall ≤ 0.08 (Byrne, 2012). We also examine the comparative fit index (CFI), which provides an estimate of incremental fit of the model compared with a baseline model. Current advice suggests CFI values of ≥ 0.95 indicate adequate model fit (West et al., 2012).

For assessing the model fit of the nested models, such as those in each step of the measurement invariance tests, we examine the change in χ² relative to change in degrees of freedom (df). Ideally the change in χ² for each df should have p >.001, indicating that the more restricted model is not a worse fit to the data than the less restricted model. When equating parameters across groups in measurement invariance analyses, particularly when large numbers of groups are compared, ΔRMSEA and ΔCFI can also be examined (Rutkowski & Svetina, 2014). A change of 0.010 (RMSEA) and −0.010 (CFI) are indicative of non-invariance between groups when parameters are constrained to equality for metric or scalar invariance tests (Cheung & Rensvold, 2002; OECD, 2010). Finally, Akaikes Information Criterion (AIC) can provide additional information about fit for non-nested models with smaller values indicating better model fit. We report and interpret ΔAIC where appropriate (West et al., 2012).

It is important to note that interpreting change in model fit statistics to assess measurement invariance across more than two groups, as we do in this study, can generate information without clear or simple interpretations. For example, should model fit decrease significantly at any step of measurement invariance testing, with five groups in the model, it may not be clear whether one sample is driving model misfit, while others are sufficiently comparable. Notwithstanding this interpretational problem, the main aim of the study is to evaluate whether the CHAOS measure behaves similarly across contexts, therefore non-invariance of even one sample is problematic for the applicability, use, and interpretation of the scale in different contexts.

Finally, we planned to examine the predictive validity of the CHAOS measure using two criterion variables. We examined zero-order correlations between CHAOS and a socioeconomic status variable (or proxy), and academic achievement variables available in each dataset. We compared results using a) a one-factor model of CHAOS, b) a two-factor model, and c) analyses where the CHAOS items are composed as factor scores, with results when items are composed as mean scores, as is more common in the published literature.

All analyses were run in the statistical program R (R Core Team, 2020) using the psych package (Revelle, 2022) for descriptive statistics, reliability statistics, creating factor scores and exploratory factor analyses, the lavaan package (Rosseel, 2012) for confirmatory factor models and invariance testing, and ggplot2 (Wickham, 2016) for figures. Code for confirmatory factor analyses, and invariance testing is at the OSF (https://osf.io/akmf4). Data from FTP-RBE, Project KIDS and the WRRMP is available at LDBase repository (Hart et al., 2020). Data from the ADSAT is available on request to the first author, and data from TEDS is available on request from data managers (Kings College London, 2022, https://www.teds.ac.uk/researchers/teds-data-access-policy).

Results

For each sample means, standard deviations, skew, and kurtosis of each item, and zero-order correlations between items were generated. These are reported in Tables S2–S11 in the supplementary material. We report three waves of data for multi-wave studies, except TEDS, which contains only two waves of parent-report on the CHAOS scale. Correlations between items were all positive, with some variation in the strength of correlations across the samples. Perhaps most notable were the differences in correlations between item 5. There is usually a television on somewhere in our home, and the remaining items. In the Project KIDS and FTP-RBE samples, correlations between this item and the remaining five were generally smaller (r ≤.17) than those in the ADSAT, WRRMP and TEDS samples (r ≤ .34). On the other hand, the strongest correlation in all samples was between items 2. You can’t hear yourself think in our home (reversed) and 3. It’s a real zoo in our home (r=.56 - .77).

Variation is also evident in item means and distributions across studies. Figures S1–S5 (supplementary materials) show item distributions for each dataset when selecting one wave from each multi-wave study. Response patterns were similar over waves within studies (i.e. for TEDS, WRRMP and FTP-RBE). The mean of item 2. You can’t hear yourself think in our home (reversed) varied from 1.95 (Project KIDS) to 3.29 / 3.27 (TEDS sample, wave 1 / wave 2). Similarly, item 5, There is usually a television on somewhere in our home, also shows variable response patterns across studies, as does item 3, It’s a real zoo in our home. Finally of note is the strong agreement with item 1, The children have a regular bedtime routine across all studies (i.e. most respondents selected Somewhat true or Definitely true for this question).

Given the six items in the scale are most often used as a sum or average score, we also computed coefficients alpha (α) and omega (hierarchical, ω_h). These are reported in Table 1 and range from α = 0.55–0.70, and ω_h = 0.29–0.63, indicating that internal consistency for the six-item scale is poor across samples. In particular, given that ω_h is arguably a more appropriate indicator of reliability because it allows for different factor loadings of items (McNeish, 2018), the coefficients of <0.65, with three <0.50, suggested that a one-factor model for the six items would not be supported in confirmatory factor analyses.

Exploratory factor analysis.

To support decisions about whether a one-factor or a two-factor solution would be most appropriate across all samples, we next undertook an exploratory factor analysis (EFA) on a subsample of participants in the ADSAT (n=596). We selected the ADSAT data for the EFA because the first author had access to these data before obtaining permission to access the remaining four datasets. Table S12 (in the supplementary materials) shows eigenvalues and proportion of variance explained for each principal component in the EFA, estimated using the maximum likelihood method. The first two components collectively explained 57% of the variance, and both had eigenvalues > 1. Remaining components had eigenvalues < 1, and the parallel analysis plot (Figure S6 in supplementary materials) also supported a two-factor solution.

Factor loadings and communalities for a two-factor solution are reported in Table S12 (supplementary material). Interestingly the EFA in this sample suggested a different pattern of items loading on each of two factors to that indicated by the published example using the WRRMP data (Johnson et al., 2008). In the WRRMP data, items 1, 4, and 5 comprised one factor, termed ‘order and routine’, and items 2, 3 and 6 comprised the second factor, labelled ‘quietness of the household’. In the ADSAT data, by contrast, items 2, 3 and 5 loaded on one factor and appeared to represent household noise, while item 6 cross-loaded on both factors. This cross-loading suggests the wording of item 6, The atmosphere in our house is calm, could be interpreted in the light of either household noise, or routine. Given this inconsistent result, we opted to test two different configurations of the six items in confirmatory factor models. The configuration identified by Johnson et al. grouped items 1, 4 and 5 (routine), and 2, 3 and 6 (quietness). The second configuration informed by the EFA described here grouped items 1, 4 and 6 (disorder), and items 2, 3, and 5 (noise).

Confirmatory Factor Analysis by sample.

To evaluate whether the one-factor, or either of the proposed two-factor structures of the six items was consistently reproduced over the five samples, we first tested the three models separately in all samples and waves. First, and in alignment with the common usage of the scale as a sum or average of the six items, we tested a one-factor model, forcing all items to load on one latent variable with no residual correlations (Table 2, Model A. in all samples and waves). We compared this one-factor model with the two different configurations of a two-factor model, each allowing three items to load on each factor (see justification above). Because the two-factor models are not nested (the same number of parameters is estimated in both) we compare each (i.e. Models B. and C. in each panel of Table 2.) with the one-factor model. While this comparative process is imperfect given that Models B. and C. cannot be directly compared using most fit statistics, evaluating the fit of each model against the one-factor option does provide some information on which solution may be more appropriate. In addition, an examination of the AIC provides additional information about which two-factor model might be retained.

Table 2.

Model fit statistics testing one- and two-factor models in all samples and all waves

Sample		Model	χ2 (df)	RMSEA [90%CI]	CFI	AIC	Model Comparisons Δχ2 (Δdf)	p for Δχ2
ADSAT	Wave 1	A. One-factor	126.53 (9)	0.101 [0.086, 0.117]	0.92	19821
		B. Two-factor i	102.51 (8)	0.096 [0.080, 0.113]	0.94	19799	A vs B = 24.02 (1)	<.001
		C. Two-factor ii	50.14 (8)	0.064 [0.048, 0.081]	0.97	19747	A vs C = 76.39 (1)	<.001
FTP-RBE	Wave 1	A. One-factor	123.12 (9)	0.150 [0.127, 0.174]	0.77	9632
		B. Two-factor	82.04 (8)	0.128 [0.104, 0.154]	0.85	9592	A vs B = 41.08 (1)	<.001
		C. Two-factor	62.59 (8)	0.110 [0.085, 0.136]	0.89	9573	A vs C = 60.53 (1)	<.001
	Wave 2	A. One-factor	42.54 (9)	0.093 [0.066, 0.122]	0.92	7451
		B. Two-factor	29.49 (8)	0.079 [0.050, 0.110]	0.95	7440	A vs B = 13.05 (1)	<.001
		C. Two-factor	24.71 (8)	0.069 [0.039, 0.101]	0.96	7435	A vs C = 17.83 (1)	<.001
	Wave 3	A. One-factor	34.05 (9)	0.095 [0.062, 0.130]	0.89	5327
		B. Two-factor	29.56 (8)	0.093 [0.059, 0.131]	0.90	5325	A vs B = 4.49 (1)	.034
		C. Two-factor iii	14.92 (8)	0.053 [0.000, 0.094]	0.97	5310	A vs C = 19.13 (1)	<.001
Project KIDS	Wave 1	A. One-factor	74.74 (9)	0.129 [0.103, 0.157]	0.84	7615
		B. Two-factor	56.31 (8)	0.117 [0.090, 0.147]	0.89	7598	A vs B = 18.43 (1)	<.001
		C. Two-factor	35.35 (8)	0.088 [0.060, 0.119]	0.94	7577	A vs C = 39.39 (1)	<.001
TEDS	Wave 1	A. One-factor	743.79 (9)	0.117 [0.110, 0.124]	0.87	101084
		B. Two-factor	724.80(8)	0.122 [0.115, 0.130]	0.88	100657	A vs B = 18.99 (1)	<.001
		C. Two-factor	313.88	0.080 [0.072, 0.087]	0.95	100656	A vs C = 429.92 (1)	<.001
	Wave 2	A. One-factor	946.69 (9)	0.114 [0.108, 0.120]	0.89	133164
		B. Two-factor	919.65 (8)	0.119 [0.113, 0.126]	0.90	133139	A vs B = 27.04 (1)	<.001
		C. Two-factor	374.34 (8)	0.076 [0.069, 0.082]	0.96	132594	A vs C = 572.35 (1)	<.001
WRRMP	Wave 1	A. One-factor	72.57 (9)	0.110 [0.088, 0.135]	0.91	9161
		B. Two-factor	39.12 (8)	0.082 [0.057, 0.108]	0.96	9129	A vs B = 33.44 (1)	<.001
		C. Two-factor	49.47 (8)	0.095 [0.070, 0.121]	0.94	9139	A vs C = 23.09 (1)	<.001
	Wave 2	A. One-factor	51.03 (9)	0.096 [0.071, 0.122]	0.94	7953
		B. Two-factor	40.74 (8)	0.089 [0.063, 0.118]	0.95	7944	A vs B = 10.29 (1)	<.001
		C. Two-factor	29.54 (8)	0.073 [0.046, 0.101]	0.97	7933	A vs C = 21.49 (1)	<.001
	Wave 3	A. One-factor	113.30 (9)	0.153 [0.129, 0.179]	0.86	7718
		B. Two-factor	103.94 (8)	0.156 [0.130, 0.183]	0.87	7711	A vs B = 9.36 (1)	.002
		C. Two-factor	75.45 (8)	0.131 [0.105, 0.158]	0.91	7683	A vs C = 37.85 (1)	<.001
	Wave 4	A. One-factor	39.69 (9)	0.098 [0.068, 0.131]	0.92	5630
		B. Two-factor	21.72 (8)	0.070 [0.035, 0.106]	0.96	5614	A vs B = 17.97 (1)	<.001
		C. Two-factor	31.63 (8)	0.092 [0.060, 0.126]	0.94	5624	A vs C = 8.06 (1)	.004
	Wave 5	A. One-factor	52.62 (9)	0.115 [0.086, 0.146]	0.91	5754
		B. Two-factor	21.43 (8)	0.068 [0.034, 0.103]	0.97	5725	A vs B = 31.19 (1)	<.001
		C. Two-factor	50.64 (8)	0.121 [0.090, 0.153]	0.91	5754	A vs C = 1.98 (1)	.159
	Wave 6	A. One-factor	53.66 (9)	0.116 [0.087, 0.147]	0.92	5664
		B. Two-factor	14.56 (8)	0.047 [0.000, 0.085]	0.99	5627	A vs B = 39.10 (1)	<.001
		C. Two-factor	48.79 (8)	0.118 [0.087, 0.150]	0.93	5661	A vs C = 4.87 (1)	.027
	Wave 7	A. One-factor	16.68 (9)	0.059 [0.000, 0.102]	0.97	4036
		B. Two-factor	7.51 (8)	0.000 [0.000, 0.072]	1.00	4028	A vs B = 9.17 (1)	.002
		C. Two-factor	16.43 (8)	0.065 [0.016, 0.111]	0.96	4037	A vs C = 0.26 (1)	.614

ⁱModel B. Two-factor tests the model proposed by Johnson et al. (2008).

ⁱⁱModel C. Two-factor tests the model suggested by the exploratory factor analysis of the ADSAT data.

ⁱⁱⁱThis model returned negative variances (i.e. Heywood cases) for the HomeZoo and HomeCalm items.

In all samples, a one factor model (A.) was a poor fit to the data according to all criteria (Table 2., first row of each panel). In all cases the RMSEA statistic did not fall within the acceptable range, and the CFI and TLI statistics were <.95. Model B tested the two-factor solution reported in Johnson et al. (2008), with factors termed ‘quietness’ and ‘routine’. Change in χ² (df), RMSEA, CFI and AIC for the two-factor model compared with the one-factor model showed an improvement in fit in all samples. Nonetheless, in most cases fit statistics were poor or borderline. The exception was the WRRMP dataset (that used by Johnson et al.), which showed borderline-good model fit for this configuration of items in five of seven waves.

Model C tested the alternative configuration of the six items suggested by the EFA in the ADSAT data. This model fit the data better than the one-factor model according to all fit statistics (Table 2, model C.). AIC statistics indicated that this alternative two-factor configuration was a better fit to the data than that tested in model B for all samples and waves except for the WRRMP data. In the ADSAT, Project KIDS, wave 2 of the WRRMP, and both waves of TEDS data, fit statistics were acceptable or borderline for model C.

Nonetheless, despite the improvement relative to model A, the fit of model C in the FTP-R data and wave 3 of the WRRMP remained poor when evaluating the RMSEA, CFI and TLI against suggested cut-off criteria. Notwithstanding this problem, we retained the first wave of the FTP-R data for multiple group invariance testing because this wave had the least missingness. We also retained wave 2 of the TEDS sample (older age group and less missingness), and wave 2 of the WRRMP data (best fit for model C.), the ADSAT and Project KIDS samples.

Measurement Invariance.

Table 3. shows fit statistics for each step of invariance testing incorporating all five samples. The configural invariance model forces the same configuration of items loading on factors across all groups with no cross-loadings or residual covariances for observed items. Factor loadings, intercepts, variances and covariances are allowed to vary by group. Notwithstanding the poor fit of the models for some individual samples noted above, the configural invariance model (Table 3, Model 1) showed borderline acceptable fit to the data when evaluated by the RMSEA (0.077, 90% CI [0.071, 0.083]) and CFI (0.957) statistics. Next, model 2A. (Table 3) tested for metric invariance by constraining factor loadings of all items to equivalence across groups. According to the AIC and the χ² difference relative to degrees of freedom (Δχ² (Δdf) = 99.10 (16), p <.001), the fit of model 2A was significantly worse than model 1. However, the ΔRMSEA (0.007), and ΔCFI (0.007) indicated the fit of this model was not worse relative to model 1 (using cutoff values of 0.010 for each; Rutkowski & Svetina, 2014). Given this mixed information, we examined the factor loadings across the five samples in the configural invariance model. The loadings for item 5 There is usually a television turned on somewhere in our home (reversed) were notably different across samples, ranging from 0.07 (FTP-R) and 0.09 (Project KIDS) to 0.47 (TEDS), 0.37 (WRRMP) and 0.35 (ADSAT). Consequently, we released the constraint on the loading for this item, and tested a partial metric invariance model with the remaining five item-loadings constrained to equivalence.

Table 3.

Model fit statistics for measurement invariance tests including one wave from each of five samples

Model	χ2(df)	RMSEA [90% CI]	CFI	AIC	Model Comparisons Δχ2 (Δdf)	p for Δχ2
1. Configural Invariance	551.96 (40)	0.077 [0.071, 0.083]	0.957	177424
2A. Metric Invariance	651.06 (56)	0.070 [0.065, 0.075]	0.950	177492	1 vs 2A = 99.10 (16)	<.001
2B. Partial Metric Invariance	582.70 (52)	0.069 [0.064, 0.074]	0.955	177431	1 vs 2B = 30.74 (12)	.002
3. Scalar Invariance i	1343.26 (68)	0.093 [0.089, 0.097]	0.892	178160	2B vs 3 = 760.57 (16)	<.001

ⁱThe scalar invariance model allowed for partial metric invariance – i.e. factor loadings of the TV item were allowed to vary across groups. Retained models are in bold.

The partial metric invariance model (2B. in Table 3) fit the data significantly better than the full metric invariance model (2B vs 2A: Δχ² (Δdf) = 68.36 (4)), and was not a worse fit to the data than the configural invariance model (2B vs 1: Δχ² (Δdf) = 30.74 (12), p=.002; ΔRMESA = 0.002; ΔCFI = 0.002). We thus retained the partial metric invariance model and next tested scalar invariance by constraining all item intercepts to equivalence across the five samples. Fit statistics for scalar invariance (model 3, Table 3) show that this model was a worse fit to the data on all criteria compared with the partial metric invariance model (Δχ² (Δdf) = 3320.65 (16), p<.001; ΔRMESA = 0.092; ΔCFI = 0.278). We therefore retained the partial metric invariance model and examined the item intercepts by group for possible reasons why scalar invariance was not supported.

Table 4. shows factor loadings and intercepts for each dataset for the retained partial metric invariance model for five samples. There is considerable variation in intercepts for some items across the five groups, after holding loadings constant for all but one item.

Table 4.

Factor loadings, intercepts and R-square values for each item and group for the retained partial metric invariance model

	ADSAT			Florida Twin Study			Project Kids			WRRMP			TEDS
Item	Loading	Intercept	R2	Loading	Intercept	R2	Loading	Intercept	R2	Loading	Intercept	R2	Loading	Intercept	R2
Factor 1
2. HomeNoise	0.86	2.63	.62	0.86	2.25	.46	0.86	1.95	.51	0.86	2.51	.70	0.86	3.27	.68
3. HomeZoo	0.92	2.13	.70	0.92	1.83	.67	0.92	1.74	.76	0.92	2.32	.73	0.92	2.66	.65
5. HomeTV1	0.35	2.72	.07	0.07	3.63	.002	0.09	3.71	.006	0.37	3.09	.09	0.47	3.26	.14
Factor 2
1. BedRoutine	0.15	1.43	.04	0.15	1.61	.05	0.15	1.84	.03	0.15	1.46	.05	0.15	1.38	.05
4. HomeControl	0.32	1.81	.22	0.32	1.81	.19	0.32	1.94	.16	0.32	1.92	.24	0.32	1.89	.18
6. HomeCalm	0.72	2.55	.60	0.72	2.25	.76	0.72	2.11	.77	0.72	2.65	.65	0.72	2.85	.60

Note. Standardized latent factors (M=0; SD=1).

¹Loadings are allowed to vary for this item, all other items loadings are constrained to equality.

For example, the intercepts for item 2, You can’t hear yourself think in our home (reverse coded), range from 1.95 in the Project KIDS sample to 3.27 in the TEDS sample; similarly, for item 3. It’s a real zoo in our home, intercepts range from 1.74 in the Project KIDS sample to 2.66 in the TEDS sample (N.B. because these item intercepts are allowed to vary by group, the model essentially reproduces item means reported in Tables S1–S10). The loadings for most other items have a smaller range, for example, 1.81–1.94 for item 4. We are usually able to stay on top of things. These differences in factor loadings indicate that response patterns vary across samples, potentially for reasons which are unrelated to differences in the latent construct under consideration (i.e. the confusion, hubbub and order of the home environment).

The r-square values reported in Table 4 provide additional information about the extent to which the variance in each item is captured by the final model. Of note is the low R² for two items. First, for item 5. There is usually a television turned on somewhere in our home, variance explained ranged from 0.2% (FTP-RBE), to 7% (ADSAT), to 14% (TEDS). Similarly, for item 1. The children have a regular bedtime routine, R² values were persistently low, with 3–5% of the variance explained by the factor model in all datasets. It is worth noting that both these items were first introduced when the short-form CHAOS was created, and did not appear in the original 15-item scale. For remaining items R² ranged from 16 to 77%.

Predictive validity.

To examine the predictive validity of the short-form CHAOS, we estimated correlations between two different configurations of the six items and available academic achievement variables for each dataset. We selected the same wave of data as that selected for between group measurement invariance tests described above. First, we generated a single-variable factor score using all six items, following the most common use of the scale. Secondly, we generated factor scores for two variables based on the two-factor solution with the best-fitting model. Specifically, these factors comprised three variables each and were termed disorder (items 1, 4 and 6), and noise (items 2, 3, and 5). Using the psych package in R (Revelle, 2022), factor scores were generated separately for each configuration of items, producing variables with M=0 and SD=1. Table 5 shows correlations between factor scores and criterion variables for one- and two-factor configurations of items. For comparative purposes, we also generated composite variables for both combinations of the six items, i.e. single variable averaging across the six CHAOS items, and two variables using averages of the same three items as used in the factor score models. Table 6 shows correlations between average CHAOS scores and criterion variables.

Table 5.

Correlations between one-factor and two-factor CHAOS, socioeconomic status (SES) and academic achievement criterion variables.

Study	Correlated variable	One-factor	Two-factor
		Chaos	Noise	Disorder	Factor correlation
ADSAT	SES	−.12***	−.11***	−.09***	.45***
	Grade 3 Reading	−.11***	−.12***	−.04
	Grade 3 Math	−.07*	−.07*	−.03
FTP-RBE Wave 1	SES	−.10*	−.15***	−.09*	.21***
	FCAT Reading 2011–12	−.16*	−.26**	−.06
	FCAT Reading 2012–13	−.21***	−.27***	−.08
Project KIDS	SES	−.09	−.23***	−.07	.29***
	English Language Arts Grade	− .18***	−.20***	−.20***
	Math Grade	− .06	−.07	− .17***
WRRMP Wave 4i	SES ii	−.04	−.03	.01	.20***
	PIAT passage comprehension	.01	.00	.01
	WRMT passage comprehension	−.04	−.05	−.00
	WJ Calculation	−.06	−.06	−.03
	WJ applied problems	−.01	−.02	−.04
	WJ quantitative concepts	−.03	−.04	.00
TEDS Wave 4	SES	−.23***	−.24***	−.05***	.33***
	English National Curriculum Assessment iii	−.16***	−.16***	−.07*
	Math National Curriculum Assessment iii	−.11***	−.12***	−.04*

Note. Correlations are between factors and criterion variables.

^*p <.05;

^**p <.01;

^***p <.001.

ⁱFor the WRRMP Wave 4 data we use the same configuration of items as the remaining datasets for the two factor models, notwithstanding the better fit of the alternative model. Interestingly correlations remained non-significant with the alternative item configuration reported in Johnson et al. (2008).

ⁱⁱSES proxy variable comprising an average of both parents’ educational attainment.

ⁱⁱⁱEnglish and math assessments at age 7.

Table 6.

Correlations between CHAOS average composites, socioeconomic status (SES) and academic achievement criterion variables

Study	Correlated variable	One variable	Two variables
		Chaos	Noise	Disorder	Composite score correlation
ADSAT	SES	−.21***	−.23***	−.10***	.41***
	Grade 3 Reading	−.16***	−.20***	−.04
	Grade 3 Math	−.12***	−.15***	−.04
FTP-RBE Wave 1	SES	−.21***	−.23***	−.10*	.27***
	FCAT Reading 2011–12	−.24***	−.30***	−.06
	FCAT Reading 2012–13	−.25***	−.29***	−.10
Project KIDS	SES	−.21***	−.25***	−.07	.31***
	English Language Arts Grade	−.26***	−.22***	−.20***
	Math Grade	−.15***	−.07	−.18***
WRRMP Wave 4i	SESii	−.15*	−.19***	−.03	.39***
	PIAT passage comprehension	−.09	−.12*	−.01
	WRMT passage comprehension	−.16***	−.20***	−.04
	WJ Calculation	−.10	−.13*	−.03
	WJ applied problems	−.10	.14*	.00
	WJ quantitative concepts	−.07	−.12	.02
TEDS Wave 4	SES	−.32***	−.38***	−.09***	.36***
	English National Curriculum assessment iii	−.21***	−.23***	−.09***
	Math National Curriculum Assessment iii	−.15***	−.17***	−.06***

Note. Composite variables created by averaging six items for one-factor CHAOS; three items each for Noise and Disorder.

ⁱⁱSES proxy variable in this dataset is an average of the educational attainment of both parents.

ⁱⁱⁱEnglish and math assessments at age 7.

Correlations with achievement were either negative (as expected), or negligible, varying by sample and whether a one-factor or two-factor combination of items was used. For four of the five datasets – the ADSAT, FTP-RBE, Project KIDS and TEDS – the correlations reported in Table 5 supported our prediction that higher levels of parent-reported confusion, hubbub and disorder in homes would be negatively associated with measures of academic achievement. In these four datasets, correlations between a one-factor CHAOS measure and achievement ranged between −.07 to −.21. Interestingly, when the six variables were separated into two factors, only the Noise factor consistently correlated with achievement, while the Disorder factor did not. The most notable exception was the Project KIDS data where the Disorder factor correlated negatively with both English and Math grades (r = −.20 / −.17 respectively), even though the correlation between Math grades and the one-factor CHAOS was small and not significantly different from zero (r = −.06). By contrast, the correlations between one-factor CHAOS variable and the two factors (Noise and Disorder) were small and non-significant for the WRRMP across several high-quality measures of both reading comprehension and mathematics sub-domain skills (calculation, applied problems, and quantitative concepts).

Results were similar to those reported for the factor scores when composite variables were created by averaging across items (see Table 6). One exception was noted in the WRRMP data, where the WRMT passage comprehension measure correlated negatively with the composite score of six items (r = −.16) and with the Noise composite (r = −.20), and three of four other reading and math measures correlated negatively with the Noise composite.

Correlations between SES and CHAOS also differed by sample, whether one or two scores were used, and method of creating variables (factors or averages). When average scores were used (Table 6), SES correlated negatively with the one-variable CHAOS across all datasets (r= −.15 to −.32). Similar to the academic achievement variables, when CHAOS was separated into the two composites, SES correlated more consistently with the Noise composite and not the Order composite. When factor scores were used to generate the CHAOS variables (Table 5), patterns of correlations with SES were similar, but notably smaller in all datasets, and not significantly different from zero in the WRRMP sample. In the Project KIDS sample the Noise factor alone correlated with CHAOS (r= −.23, p<.001) even though the composite using all six CHAOS items did not (r = −.09, p = .06).

Discussion

The central aim of this study was to examine the measurement properties of the short form of the Confusion, Hubbub and Order Scale (CHAOS) with a goal to provide some recommendations on the use of the scale – both in pre-existing datasets and new research. On the whole, our results indicate that the six items in the short-form CHAOS are not reliable and valid enough to capture variability in the quality of home environments across different contexts, age ranges of child study participants, and time. Ideally, reduction of a long-form to a short-form scale should be accompanied by evidence that the short form itself is a) reliable, b) valid, and c) captures the breadth of the construct indicated by a long-form (Clarke & Watson, 1995, 2019; Smith et al., 2000). Because these steps were not documented for the short-form CHAOS, this study thus provides some of the information necessary to guide the use of the scale in future applied research. The motivation for this study was additionally underpinned by the growing calls for more rigorous approaches to the development and evaluation of survey measures, and iterative reconsiderations of conceptual clarity as necessary precursors for advancing educational and psychological sciences (Bringmann et al., 2022; Flake, 2021; Smaldino, 2019; van Dijk et al., 2020).

To date internal consistency reliability estimates (i.e. coefficient alpha) have been the only consistently documented evidence of scale reliability for the short-form CHAOS. Estimates of alpha are universally low (i.e. <.70 in all cases) in the samples included in this study, and in other samples reported in the published literature, suggesting that the internal consistency of the items may not be sufficient for combining them in a single composite (McNeish & Wolf, 2020). In all but one of the published studies using the short-form CHAOS, the six items are either summed or averaged to compute a single composite. Creating a single composite from several items, however, assumes that a scale captures a single latent domain (McNeish & Wolf, 2020). However, previous published evidence for the short-form CHAOS (Johnson et al., 2008) and our own exploratory factor analysis suggested that the six items better represent two latent domains. An interpretational difficulty arose however, with the identification of two different patterns of item-to-factor loadings in the exploratory factor models for each of these samples. These different item-to-factor patterns, along with poor model fit in confirmatory factor models in several samples (see Table 3), support our conclusion that the short-form CHAOS may not satisfactorily capture the quality of home environments suggested by theoretical descriptions (Bradley, 2015; Bronfenbrenner & Evans, 2000; Bronfenbrenner & Ceci, 1994; Matheny et al., 1995).

Furthermore, results of measurement invariance analyses indicated that the short-form CHAOS was non-invariant across the five included samples. Specifically, while the configural invariance model incorporating five samples was an adequate fit to the data (see Table 3, model 1.), neither the full metric invariance, nor the full scalar invariance models were acceptable according to multiple model fit criteria (Rutkowski & Svetina, 2014; West et al., 2012). The retained model was a partial metric invariance model, which constrained the factor loadings of five items to equality, and allowed the loading of one item to vary (item 5. There is usually a television turned on somewhere in our home). While this model was acceptable, scalar invariance was not supported, indicating that the intercepts of the items differed too greatly across samples for them to be constrained to equality. Because we included five samples in the analyses, it is neither easy nor straightforward to identify which samples and/or items were driving the scalar non-invariance – it could be a combination of any number of items across some or all samples.

The worst performing items across all samples were the two which appeared in the short-form that did not appear in the long-form version of the CHAOS: item 5. There is usually a television turned on somewhere in our home and item 1. The children have a regular bedtime routine. In terms of face validity, item 5 has become particularly dated in western cultures in the 25 years since the short-form CHAOS was proposed. For example, the data in the TEDS project was collected in the late 1990s, whereas the most recent data collection, Project KIDS, was in 2017. Compared with the 1990s, 21^st century middle-class families (and children) now have access to an abundance of portable electronic devices, including smartphones, tablets, and laptops. Children and adults have access to headphones, volume control, voice-activated commands and individualized options. If the television item intended to capture ambient noise within a household, it may be outdated. If the item intended to capture parents’ lack of control over children’s media consumption, again, the item will likely no longer capture the range of digital media currently available to children and adolescents (Graafland, 2018).

Secondly, while the face validity of the bedtime routine item might be acceptable for samples of very young children, this routine might not be applicable to older children and adolescents. The question may capture something about personality, or developmental changes in sleep patterns (CITE), rather than an aspect of household management under the control of a parent. Unpacking the assumptions embedded in the question as it relates to variability in household order and routine raises additional questions: Is it problematic or damaging if older children lack a strictly adhered-to bedtime routine every evening? Is the amount and nature of sleep itself a better predictor of positive childhood development than regularity in bedtimes (e.g. Dewald et al., 2010)? If the CHAOS scale is to be applied in research spanning early childhood to mid-adolescence, as is currently the case, these questions, and the face validity of all the items, should be examined in the light of advancements to developmental theory, and changes to family life that have occurred since the mid-1980s when the scale was first developed in a sample of infants and toddlers.

Thirdly, the contrasting results of the two exploratory factor analyses (i.e our own and that reported by Johnson et al., 2008) suggest that item 6 the atmosphere in our house is calm potentially lacks conceptual clarity (Borsboom et al., 2004; Bringmann et al., 2022). In the WRRMP data, this item loaded with others representing ‘quietness of the household’ (Johnson et al., 2008), whereas in the ADSAT data this item cross-loaded highly onto both factors, suggesting that respondents may have varying interpretations of a calm atmosphere in the home. Furthermore, whether or not a calm atmosphere is representative of poor household environments is arguable, and potentially tied to cultural norms, thus perhaps leading to the inconsistent properties of this item across datasets.

Finally, our investigation of the predictive validity of the short-form CHAOS scale was limited by the finding of measurement non-invariance. However, using two different approaches to collating variables (i.e. factor scores or averaged composites) and comparing correlations with socioeconomic status and academic achievement variables is nonetheless instructive. Using either approach to combining items, higher ratings of CHAOS correlated with poorer academic achievement in four of five samples. Factor-score correlations were generally smaller than those observed when items were averaged to create composite variables. In the WRRMP sample, CHAOS did not consistently correlate with any of the five reading or math assessments. Similarly, while SES and CHAOS were negatively correlated in general across the five samples, of note are the differences in the strength of correlations (and their statistical significance) when the average score was used rather than the factor score. In all samples, correlations using an average CHAOS composite were larger than those using the factor score. For the WRRMP and Project KIDS samples, correlations with the factor score were not significantly different from zero, whereas the correlations with the average composite were significantly different from zero. It is worth reiterating that measurement error of observed items is retained in composite variables, and can subsequently inflate or reduce covariations in unpredictable ways (Cole & Preacher, 2014; McNeish & Wolf, 2020) – as we have observed in these comparisons. While this problem can be somewhat rectified by the use of factor scores which allow differential weighting of items comprising each factor, if the observed items do not reliably capture the underlying theoretical construct, a factor score approach does not completely resolve the measurement problems (Hancock, 2003; Rhemtulla et al., 2020). The only resolution in this and many other cases is careful and considered development and renewal of items in the light of theoretical construct of interest.

Recommendations.

Since there are multiple studies that have collected data on the short form CHAOS over the past 20 years, and several of these data sources are now accessible to researchers for secondary analyses, we provide some tentative recommendations on the use of the six CHAOS items. Given the finding that a two-factor solution is more defensible than the commonly used one-factor model we recommend that future researchers should use the two-factor configuration of the six observed items with factors termed Noise and Disorder. Results using the two-factor approach can also be compared with the one-factor approach commonly reported in the literature. We would also suggest that using factor scores, allowing items in the subscales to be differentially weighted, is more appropriate than using sum or average scores – particularly given the variation in correlation coefficients using each approach. These recommendations, however, should not be taken as rules, and should not preclude researchers from carefully examining the properties of the items in samples not included in this study.

Limitations

A major limitation of the analyses presented here is the non-definitive nature of the information obtained from measurement invariance tests when more than two samples are included. While we suggest that the item relating to television may be driving metric non-invariance, other items could also be contributing to this result. A second limitation is the differing ages of the children included in each sample. While we made efforts to select samples with similarly aged children, this was not always possible due to the secondary data accessed for the study. Mean age ranged from 4 years in the TEDS sample, to 11 years in both the FTP-RBE and Project KIDS samples. Differing ages of children when parents respond to the items could drive differential response patterns across samples. Nonetheless, if this is the case, it is further evidence that the short-form CHAOS is not as broadly applicable across childhood and adolescence as it is intended to be.

Finally, because the analyses are largely data-driven, the analytic choices, and the order in which different steps were undertaken in this study were affected by researcher degrees of freedom (Gelman & Loken, 2013). It would be possible to attempt different analyses and obtain different results, for example, is a one-factor solution acceptable if the television item is omitted? Or both the television and bedtime items? These different choices, however, would not get us closer to the main object of interest, which is to identify whether the six items in the short-form CHAOS are valid and reliable measure of the quality of home environments. Future work may consider these and other options within a broader program of scale development and renewal.

Conclusion

Studies of the links between the nature of home environments and childhood development are decades old (e.g. Elardo et al., 1977; Bronfenbrenner, 1981). The original 15-item CHAOS measure clearly identified the aspects of home environments it was intended to capture. These included household disorder, high ambient noise, and lack of routine (Matheny et al., 1995) and items were developed from a wealth of earlier theorizing about how variation in home environments might relate to different aspects of early childhood development. However, the results we report here do not provide strong evidence that the short-form CHAOS adequately captures this broad and theoretically consistent construct. The rationale for selecting the six items is arguably clear: in terms of face validity and relevance, the items do cover the scope of the original construct, albeit in a more limited way. However, our findings indicate that the short form items should now be reconsidered and the scale revised in the light of more contemporary theory and contexts (e.g. Clark & Watson, 1995, 2019). In our view, a re-evaluation and update of the 15 items in the original version of the Confusion, Hubbub and Order Scale (Matheny et al., 1995) may be a useful starting point.

Data Accessibility Statement

ADSAT data is accessible by application to the first and third authors

Available at the LDBase repository https://ldbase.org/ are:

• - FTB-RBE (doi:10.33009/ldbase.1624451991.3667)

• - Project KIDS (doi: 10.33009/ldbase.1619716971.79ee) and

• - WRRMP (doi: 10.33009/ldbase.1643647076.d4b2)

TEDS data available by agreement with the Kings’ College London https://www.teds.ac.uk/researchers/teds-data-access-policy