Bias-adjusted spectral clustering in multi-layer stochastic block models

Abstract

We consider the problem of estimating common community structures in multi-layer stochastic block models, where each single layer may not have sufficient signal strength to recover the full community structure. In order to efficiently aggregate signal across different layers, we argue that the sum-of-squared adjacency matrices contain sufficient signal even when individual layers are very sparse. Our method uses a bias-removal step that is necessary when the squared noise matrices may overwhelm the signal in the very sparse regime. The analysis of our method relies on several novel tail probability bounds for matrix linear combinations with matrix-valued coefficients and matrix-valued quadratic forms, which may be of independent interest. The performance of our method and the necessity of bias removal is demonstrated in synthetic data and in microarray analysis about gene co-expression networks.

1. Introduction

A network records the interactions among a collection of individuals, such as gene co-expression, functional connectivity among brain regions, and friends on social media platforms. In the simplest form, a network can be represented by a binary symmetric matrix A ∈{0,1}^n×n where each row/column represents an individual and the (i, j)-entry of A represents the presence/absence of interaction between the two individuals. In the more general case, A_ij may take values in ${ℝ}^1$ to represent different magnitudes or counts of the interaction. We refer to Kolaczyk (2009), Newman (2009), and Goldenberg et al. (2010) for general introduction of statistical analysis of network data.

In many applications, the interaction between individuals are recorded multiple times, resulting in multi-layer network data. For example, in this paper, we study the temporal gene co-expression networks in the medial prefrontal cortex of rhesus monkeys at ten different developmental stages (Bakken et al., 2016). The medial prefrontal cortex is believed to be related to developmental brain disorders, and many of the genes we study are suspected to be associated with autism spectrum disorder at different stages of development. Other examples of multi-layer network data are brain imaging, where we may infer one set of interactions among different brain regions from electroencephalography (EEG), and another set of interactions using resting-state functional magnetic resonance imaging (fMRI) measures. Similarly, one may expect the brain regions to form groups in terms of connectivity. The wide applicability and rich structures of multi-layer networks make it an active research area in the statistics, machine learning, and signal processing community. See Tang et al. (2009), Dong et al. (2012), Kivelä et al. (2014), Xu and Hero (2014), Han et al. (2015), Zhang and Cao (2017), Matias and Miele (2017) and references within.

In this paper, we study multi-layer network data through the lens of multi-layer stochastic block models, where we observe many simple networks on a common set of nodes. The stochastic block model (SBM) and its variants (Holland et al., 1983; Bickel and Chen, 2009; Karrer and Newman, 2011; Airoldi et al., 2008) are an important prototypical class of network models that allow us to mathematically describe the community structure and understand the performance of popular algorithms such as spectral clustering (McSherry, 2001; Rohe et al., 2011; Jin, 2015; Lei and Rinaldo, 2015) and other methods (Latouche et al., 2012; Peixoto, 2013; Abbe and Sandon, 2015). Roughly speaking, in an SBM, the nodes in a network are partitioned into disjoint communities (i.e., clusters), and nodes in the same community have similar connectivity patterns with other nodes. A key inference problem in the study of SBM is estimating the community memberships given an observed network.

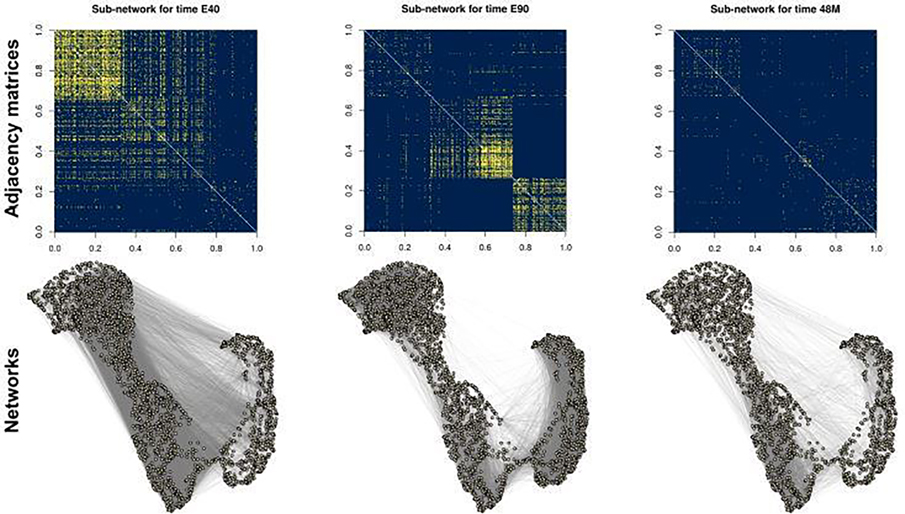
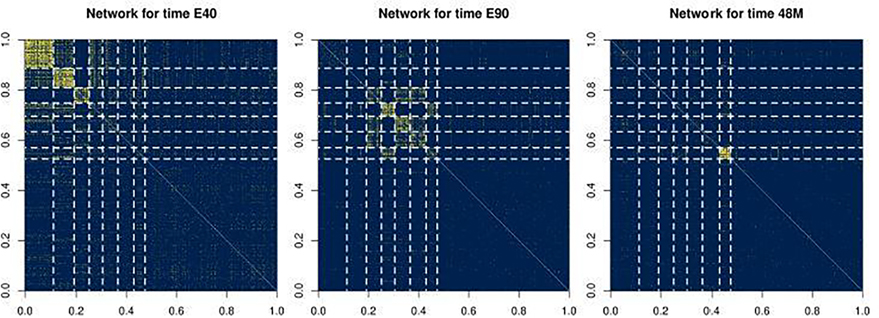
Compared to an individual layer, a multi-layer network contains more data and hopefully enables us to extract salient structures, such as communities, more easily. On the other hand, new methods must be developed in order to efficiently combine the signal from individual layers. To demonstrate the necessity for these methods, we plot the observed gene co-expression networks collected from Bakken et al. (2016) in Figure 1. The three networks correspond to gene co-expression patterns within the medial prefrontal cortex tissue of rhesus monkeys collected at different stages of development. We plot only the sub-network formed by a small collection genes for simplicity. A quick visual inspection across the three networks suggests that the genes can be approximately divided into four common communities (i.e., clusters that persist throughout all three networks), where genes in the same community exhibit similar connectivity patterns. However, different gene communities are more visually apparent in different layers. For example, in the layer labeled as “E40” (for tissue collected 40 days of development in the embryo), the last three communities are indistinguishable. In contrast, in the layer labeled as “E90,” the first community is less distinguishable, and in the layer labeled “48M” (for the tissue collected 48 months after birth), nearly all of the communities are indistinguishable. These qualitative observations are of scientific interest since these time-dependent densely-connected communities are evidence of “gene coordination,” a biological concept that describes when a community of genes is synchronized in ramping up or down in gene expression at certain stages of development (Paul et al., 2012; Werling et al., 2020). Hence, we can infer two potential advantages of analyzing such multi-layer network data in an aggregated manner. First, an aggregated analysis is able to reveal global structures that are not exhibited by any individual layer. Second, the common structure across different layers can help us to better filter out the noise, which allows us to obtain more accurate inference results. We describe the analysis in more detail and return to analyze the full dataset in Section 6.

Fig. 1.

The adjacency matrix (top row, yellow denoting the presence of an edge and blue denoting the lack of) and the corresponding network (bottom row) for three different developmental times of the rhesus monkey’s gene co-expression in the medial prefrontal cortex based on selected set of genes to visually demonstrate the varying network structures. Likewise, the ordering of the genes in the adjacency matrices is chosen to visually demonstrate the clustering structure, and persist throughout all three adjacency matrices. The three developmental times are E40, E90 (for 40 or 90 days in the embryo) and 48M (for 48 months after birth), corresponding to the pair of plots on the left to the pair of plots on the right. The full dataset is analyzed in Section 6.

The theoretical understanding of estimating common communities in multi-layer SBMs is relatively limited compared to those in single-layer SBMs. Bhattacharyya and Chatterjee (2018) and Paul and Chen (2020) studied variants of spectral clustering for multi-layer SBMs, but the strong theoretical guarantee requires a so-called layer-wise positivity assumption, meaning each matrix encoding the probability of an edge among the communities must have only positive eigenvalues bounded away from zero. In contrast, Pensky and Zhang (2019) studied a different variant of spectral clustering, but established estimation consistency under conditions similar to those for single-layer SBMs. These results only partially describe the benefits of multi-layer network aggregation. Alternatively, Lei et al. (2019) considered a least-squares estimator, and proved consistency of the global optima for general block structures without imposing the positivity assumption for individual layers, but that method is computationally intractable in the worst case.

The first main contribution of this paper is a simple, novel, and computationally-efficient aggregated spectral clustering method for multi-layer SBMs, described in Section 2. The estimator applies spectral clustering to the sum of squared adjacency matrices after removing the bias by setting the diagonal entries to 0. In addition to its simplicity, this estimator has two appealing features. First, summing over the squared adjacency matrices enables us to prove its consistency without requiring a layer-wise positivity assumption. Second, compared with single-layer SBMs, the consistency result reflects a boost of signal strength by a factor of L^1/2, where L is the number of layers. Such a L^1/2 signal boost is comparable to that obtained in Lei et al. (2019), but is now achieved by a simple and computationally tractable algorithm. The removal of the diagonal bias in the squared matrices is shown to be crucial in both theory (Section 3) and simulations (Section 5), especially in the most interesting regime where the network density is too low for any single layer to carry sufficient signal for community estimation. Interestingly, similar diagonal-removal techniques have also been discovered and studied in other contexts, such as Gaussian mixture model clustering (Ndaoud, 2018), principal components analysis (Zhang et al., 2022), and centered distance matrices (Székely and Rizzo, 2014).

Another contribution of this paper is a collection of concentration inequalities for matrix-valued linear combinations and quadratic forms. These are described in Section 4, which are an important ingredient for the aforementioned theoretical results. Specifically, an important step in analyzing our matrix-valued data is to understand the behavior of the matrix-valued measurement errors. Towards this end, many powerful concentration inequalities have been obtained for matrix operator norms under various settings, such as random matrix theory (Bai and Silverstein, 2010), eigenvalue perturbation and concentration theory (Feige and Ofek, 2005; O’Rourke et al., 2018; Lei and Rinaldo, 2015; Le et al., 2017; Cape et al., 2017), and matrix deviation inequalities (Bandeira and Van Handel, 2016; Vershynin, 2011). The matrix Bernstein inequality and related results (Tropp, 2012) are also applicable to linear combinations of noise matrices with scalar coefficients. In order to provide technical tools for our multi-layer network analysis, we extend these matrix-valued concentration inequalities in two directions. First, we provide upper bounds for linear combinations of noise matrices with matrix-valued coefficients. This can be viewed as an extension of the matrix Bernstein inequality to allow for matrix-valued coefficients. Second, we provide concentration inequalities for sums of matrix-valued quadratic forms, extending the scalar case known as the Hanson–Wright inequality (Hanson and Wright, 1971; Rudelson and Vershynin, 2013) in several directions. A key intermediate step in relating linear cases to quadratic cases is deriving a deviation bound for matrix-valued U-statistics of order two.

2. Community Estimation in Multi-Layer SBM

Throughout this section, we describe the model, theoretical motivation, and our estimator for clustering nodes in a multi-layer SBM. Motivated by such multi-layer network data with a common community structure as demonstrated in Figure 1, we consider the L-layer SBM containing n nodes assigned to K different communities,

$$A_{\ell ,ij}~\mathrm{Bernoulli}(\rho B_{\ell ,{\theta }_i{\theta }_j})\text{for}1\le i<j\le n,1\le \ell \le L,$$ (1)

where ℓ is the layer index, θ_i ∈{1,...,K} is the membership index of node i for i ∈ {1,...,n}, ρ ∈(0,1] is an overall edge density parameter, and B_ℓ ∈[0,1]^K×K is a symmetric matrix of community-wise edge probabilities in layer ℓ. We assume A_ℓ is symmetric and A_ℓ,ii = 0 for all ℓ ∈{1,...,L} and i ∈{1,...,n}.

Our statistical problem is to estimate the membership vector θ = (θ₁,...,θ_n)∈{1,...,K}ⁿ given the observed adjacency matrices A₁,...,A_L. Let $\widehat{\theta }\in {\{1,\dots ,K\}}^n$ be an estimated membership vector, and the estimation error is the number of mis-clustered nodes based on the Hamming distance,

$$d(\widehat{\theta },\theta )=\underset{\pi }{\min }\sum _{i=1}^{n}1({\theta }_i\ne \pi ({\widehat{\theta }}_i)),$$ (2)

for the indicator function 1(·), where the minimum is taken over all label permutations π:{1,...,K} ↦ {1,...,K}. An estimator $\widehat{\theta }$ is consistent if $n^{-1}d(\widehat{\theta },\theta )=o_P(1)$.

The assumption of a fixed common membership vector θ can be relaxed to each layer having its own membership vector but close to a common one. The theoretical consequence of this relaxation is discussed in Remark 1, after the main theorem in Section 3. We assume that K is known. The problem of selecting K from the data is an important problem and will not be pursued in this paper. Further discussion will be given in Section 7.

When L = 1, the community estimation problem for single-layer SBM is well-understood (Bickel and Chen, 2009; Lei and Rinaldo, 2015; Abbe, 2017). If K is fixed as a constant while n → ∞, ρ → 0 with balanced community sizes lower bounded by a constant fraction of n, and B is a constant matrix with distinct rows, then the community memberships can be estimated with vanishing error when nρ → ∞. Practical estimators include variants of spectral clustering, message passing, and likelihood-based estimators.

As mentioned in Section 1, in the multi-layer case, consistent community estimation has been studied in some recent works. The theoretical focus is to understand how the number of layers L affects the estimation problem. Paul and Chen (2020) and Bhattacharyya and Chatterjee (2018) show that consistency can be achieved if Lnρ diverges, but under the aforementioned positivity assumption, meaning that each B_ℓ is positive definite with a minimum eigenvalue bounded away from zero. Such assumptions are plausible in networks with strong associativity patterns where nodes in the same communities are much more likely to connect to one another than nodes in different communities. But there are networks observed in practice that do not satisfy this assumption, such as those in Newman (2002) and Litvak and Van Der Hofstad (2013). See Lei (2018) and the references within for additional discussion on such positivity assumptions in a more general context. To remove the positivity assumption, Lei et al. (2019) considered a least-squares estimator, and proved consistency when L^1/2nρ diverges (up to a small poly-logarithmic factor) and the smallest eigenvalue of $\sum _{\ell }{B}_{\ell }^2$ grows linearly in L. A caveat is that the least-squares estimator is computationally challenging, and in practice, one may only be able to find a local minimum using greedy algorithms.

In the following subsections, we will motivate a spectral clustering method from the least-squares perspective, investigate its bias, and derive our estimator with a data-driven bias adjustment.

2.1. From least squares to spectral clustering

In this subsection, we motivate how least-squares estimators is well-approximated by spectral clustering, which lays down the intuition of our estimator in Section 2.3. Let ψ ∈{1,...,K}ⁿ be a membership vector and Ψ = [Ψ₁,...,Ψ_K] be the corresponding n × K membership matrix where each Ψ_k = (Ψ_1,k,...,Ψ_n,k) is an n×1 vector with Ψ_i,k = 1(ψ_i = k). Let I_k (ψ) = {i ∈{1,...,n} : ψ_i = k} and n_k (ψ) = |Ik (ψ)|, the size of the set Ik (ψ).

The least-squares estimator of Lei et al. (2019) seeks to minimize the residual sum of squares,

$$\widehat{\theta }=\underset{\psi \in {\{1,\dots ,K\}}^n}{\mathrm{argmin}}\sum _{\ell =1}^L\sum _{1\le i<j\le n}{(A_{\ell ,ij}-{\widehat{B}}_{\ell ,{\psi }_i{\psi }_j}(\psi ))}^2$$ (3)

where

$${\widehat{B}}_{\ell ,kl}(\psi )=\{\begin{array}{l}\frac{\sum _{i,j\in I_k(\psi )}{A}_{\ell ,ij}}{n_k(\psi )(n_k(\psi )-1)}\text{when}k=l,\\ \frac{\sum _{i\in I_k(\psi ),j\in I_l(\psi )}{A}_{\ell ,ij}}{n_k(\psi )n_l(\psi )}\text{when}k\ne l,\end{array}$$

is the sample mean estimate of B_ℓ under a given membership vector ψ. Recall that the total-variance decomposition implies the equivalence between minimizing within-block sum of squares and maximizing between-block sum of squares. Hence, if we accept the approximation $n_k(\psi )(n_k(\psi )-1)\approx n_k^2(\mathrm{\psi })$, then after multiplying the least-squares objective function (3) by 2 and using the total-variance decomposition, the objective function becomes

$$\underset{\psi \in {\{1,\dots ,K\}}^n}{\max }\sum _{\ell =1}^L\sum _{1\le k,l\le K}\frac{{({\mathrm{\Psi }}_k^T{A}_{\ell }{\mathrm{\Psi }}_l)}^2}{n_k(\psi )n_l(\psi )},$$

which is equivalent to

$$\underset{\psi \in {\{1,\dots ,K\}}^n}{\max }\sum _{\ell =1}^L\sum _{1\le k,l\le K}{({\tilde{\mathrm{\Psi }}}_k^T{A}_{\ell }{\tilde{\mathrm{\Psi }}}_l)}^2=\underset{\psi }{\max }\sum _{\ell =1}^L{\Vert {\tilde{\mathrm{\Psi }}}^T{A}_{\ell }\tilde{\mathrm{\Psi }}\Vert }_F^2,$$

where ‖·‖_F denotes the matrix Frobenius norm, and $\tilde{\mathrm{\Psi }}=\left[{\tilde{\mathrm{\Psi }}}_1,\dots ,{\tilde{\mathrm{\Psi }}}_K\right]$ with ${\tilde{\mathrm{\Psi }}}_k={\mathrm{\Psi }}_k/\sqrt{n_k(\psi )}$ is the column-normalized version of Ψ where each column of $\tilde{\mathrm{\Psi }}$ has norm 1. This means $\tilde{\mathrm{\Psi }}$ is orthonormal, i.e., ${\tilde{\mathrm{\Psi }}}^T\tilde{\mathrm{\Psi }}=I_K$. The benefit of considering orthonormal matrices is that for any orthonormal matrix $U\in {ℝ}^{n\times K}$ and symmetric matrix $A\in {ℝ}^{n\times n}$,

$${\Vert U^{T}AU\Vert }_F^2=\mathrm{tr}(U^{T}AU{U}^{T}AU)\le \mathrm{tr}(U^T{A}^{2}U).$$

The right-hand side of the above inequality is maximized by the leading K eigenvectors of A, where the eigenvalues ordered by absolute value. For this U, the inequality becomes equality. Additionally, under the multi-layer SBM, the expected values of adjacency matrices {P₁,...,P_L} (where $P_{\ell }=\mathbb{E}{A}_{\ell }$ for ℓ ∈{1,...,L}) share roughly the same leading principal subspace as determined by the common community structure. Putting all these facts together, we intuitively expect $U=\tilde{\mathrm{\Theta }}$ to correspond to an approximate solution of the original least-squares problem, where $\tilde{\mathrm{\Theta }}$ is the column-normalized version of the true membership matrix Θ.

Therefore, a relaxation of the approximate version of the original problem (3) is

$$\underset{U\in {ℝ}^{n\times K}:U^{T}U=I_K}{\max }\mathrm{tr}\left[U^T\left(\sum _{\ell =1}^L{A}_{\ell }^2\right)U\right],$$ (4)

which is a standard spectral problem. For this reason, we often call U the “spectral embedding.” The community estimation is then obtained by applying a clustering algorithm to the rows of $\widehat{U}$, a solution to (4).

2.2. The necessity of bias adjustment

Let $P_{\ell }=\mathbb{E}{A}_{\ell }$ denote the expected adjacency matrix, meaning that P_ℓ is the matrix obtained by zeroing out the diagonal entries of ${\tilde{P}}_{\ell }=\rho \mathrm{\Theta }{B}_{\ell }{\mathrm{\Theta }}^T$. We now show that $\sum _{\ell }{A}_{\ell }^2$ is a biased estimate of $\sum _{\ell }{P}_{\ell }^2$, and that we can correct for this bias by simply removing its diagonal entries. Let X_ℓ = A_ℓ − P_ℓ be the noise matrix. Then

$$\sum _{\ell =1}^L{A}_{\ell }^2=(\sum _{\ell =1}^L{P}_{\ell }^2)+(\sum _{\ell =1}^L(X_{\ell }{P}_{\ell }+P_{\ell }{X}_{\ell }))+S,$$ (5)

where $S=\sum _{\ell }{X}_{\ell }^2$. The first term is the signal term, with each summand close to ${\tilde{P}}_{\ell }^2={\rho }^2\mathrm{\Theta }{B}_{\ell }^2{\mathrm{\Theta }}^T$, and will add up over the layers, because each matrix $B_{\ell }^2$ is positive semi-definite. The second term is a mean-0 noise matrix, which can be controlled using matrix concentration inequalities developed in Section 4 below.

The third term $S=\sum _{\ell }{X}_{\ell }^2$ is a squared error matrix and will also add up over the layers, which may introduce bias if the overall edge density parameter ρ is too small.

We use a simple simulation study to illustrate the necessity of bias adjustment in spectral clustering applied to the sum of squared adjacency matrices. We set K = 2 and consider two edge-probability matrices,

$$B^{(1)}=\left[\begin{array}{cc}3/4& \sqrt{3}/8\\ \sqrt{3}/8& 1/2\end{array}\right],\text{and}{B}^{(2)}=\left[\begin{array}{cc}7/8& 3\sqrt{3}/8\\ 3\sqrt{3}/8& 1/8\end{array}\right].$$

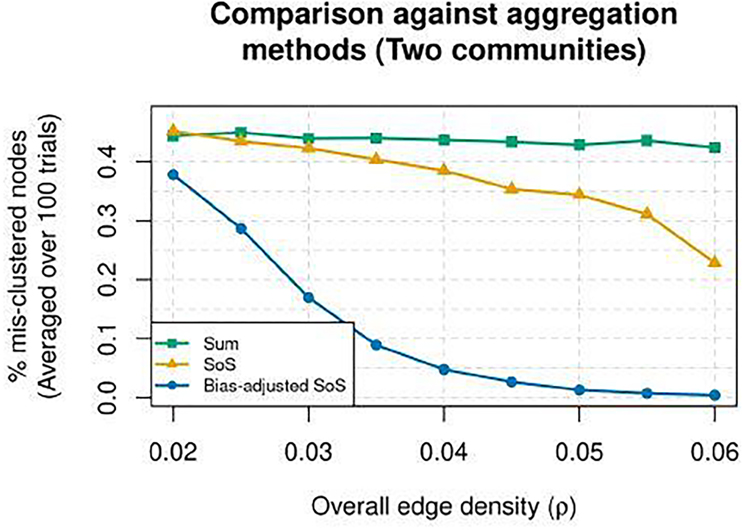
These two matrices are chosen such that spectral clustering applied to the sum of the adjacency matrices and the sum of squared adjacency matrices would be either sub-optimal or inconsistent in the very sparse regime. We set n = 200 nodes with 100 nodes in each community, the number of layers to be L = 30, and for each layer ℓ, B_ℓ is randomly and independently chosen from B⁽¹⁾ and B⁽²⁾ with equal probability. We use five different values of the overall edge density parameter ρ between 0.02 and 0.06. For each value of ρ, we generate a multi-layer SBM according to (1) and apply spectral clustering to three matrices: (1) the sum of adjacency matrices without squaring (i.e., “Sum”), (2) the sum of squared adjacency matrices (i.e., “SoS”), and (3) a bias-adjusted sum of squared adjacency matrices (i.e., “Bias-adjusted SoS”), which will be introduced in the next subsection. The results across 100 trials are reported in Figure 2. By construction, the “Sum” method performs poorly since the sum of adjacency matrices has only one significant eigen-component, meaning the result is sensitive to noise when K = 2 eigenvectors are used for spectral clustering. In fact, as described in Example 1 below, it is also easy to generate cases in which the sum of adjacency matrices carries no signal at all. The “SoS” method also performs poorly. This is because although the sum of squared adjacency matrices contains signal for clustering, the aforementioned bias is large when ρ is small. In contrast, our method “Bias-adjusted SoS” performs the best. A more detailed simulation study is presented in Section 5.

Fig. 2.

The average proportion of mis-clustered nodes for three methods (measured via Hamming distance $n^{-1}d(\widehat{\theta },\theta )$ shown in (2), averaged over 100 trials), with n = 200 and two equal-sized communities among overall edge densites ranging from ρ ∈[0.02, 0.06] and L = 30 layers. Three methods’ performance are shown: Sum (green squares), SoS (orange triangles), and Bias-adjusted SoS (blue circles).

2.3. Bias-adjusted sum-of-squared spectral clustering

We are now ready to quantify the amount of bias, and to describe our aforementioned bias-adjusted sum-of-squared method to cluster nodes in a multi-layer SBM. From (5), we see that the diagonal entries of the squared error term $\mathcal{S}$ have positive expected value and hence may cause systematic bias in the principal subspace of $\sum _{\ell }{A}_{\ell }^2$. Now consider a further decomposition S = S₁ + S₂ where ${\mathcal{S}}_1$ and ${\mathcal{S}}_2$ correspond to the off-diagonal and diagonal parts of $\mathcal{S}$, respectively. Observe that only the diagonal entries of $\mathcal{S}$ have positive expected value, so our effort will focus on removing the bias caused by ${\mathcal{S}}_2$. Towards this end, observe that by construction, we have

$$\begin{gathered} {(S_2)}_{ii}=S_{ii}=\sum _{\ell =1}^L\sum _{j=1}^n{X}_{\ell ,ij}^2 \\ =\sum _{\ell =1}^L\sum _{j=1}^n{P}_{\ell ,ij}^{2}1(A_{\ell ,ij}=0)+{(1-P_{\ell ,ij})}^{2}1(A_{\ell ,ij}=1) \\ \le Ln\underset{\ell ,ij}{\max }{P}_{\ell ,ij}^2+\sum _{\ell =1}^L{d}_{\ell ,i} \end{gathered}$$ (6)

where $d_{\ell ,i}=\sum _j{A}_{\ell ,ij}$ is the degree of node i in layer ℓ. The expected value of $\sum _{\ell }{d}_{\ell ,i}$ is $\sum _{\ell ,j}{P}_{\ell ,ij}\asymp Ln{\max }_{\ell ,ij}{P}_{\ell ,ij}$. In the very sparse regime, max_ℓ,ij P_ℓ,ij is very small so $\sum _{\ell }{d}_{\ell ,i}$ is the leading term in (S₂)_ii.

Combining this calculation with a key observation that $\sum _{\ell }{d}_{\ell ,i}$ can be computed from the data, we arrive at the following bias-adjusted sum-of-squared spectral clustering algorithm. Let D_ℓ be the diagonal matrix consisting of the degrees of A_ℓ where (D_ℓ)_ii = d_ℓ,i. The bias-adjusted sum of squared adjacency matrices is

$$S_0=\sum _{\ell =1}^L(A_{\ell }^2-D_{\ell }).$$ (7)

The community membership is estimated by applying a clustering algorithm to the rows of the matrix whose columns are the leading K eigenvectors of ${\mathcal{S}}_0$ given in (7).

3. Consistency of bias-adjusted sum-of-squared spectral clustering

We now describe our theoretical result characterizing how multi-layer networks benefit community estimation. The hardness of community estimation is determined by many aspects of the problem, including number of communities, community sizes, number of nodes, separation of communities, and overall edge density. Here, we need to consider all of these aspects jointly across the L layers. To simplify the discussion, we primarily focus on the following setting but discuss additional settings in later remarks.

Assumption 1.

1. The number of communities K is fixed and community sizes are balanced. That is, there exists a constant c such that each community size is in [c⁻¹n / K, cn / K].

2. The relative community separation is constant. That is, B_ℓ = ρB_ℓ,0 where B_ℓ,0 is a K × K symmetric matrix with constant entries in [0,1].

   Furthermore, the minimum eigenvalue of $\sum _{\ell }{B}_{\ell ,0}^2$ is at least cL for some constant c > 0.

Part (a) simplifies the effect of the community sizes and the number of communities. This setting has been well-studied in the SBM literature for L = 1 (Lei and Rinaldo, 2015). Part (b) puts the focus on the effect of the overall edge density parameter ρ, and requires a linear growth of the aggregated squared edge-probability matrices in terms of the minimum eigenvalue. This is much less restrictive than the layer-wise positivity assumption used in other work mentioned in Section 2 which require each B_ℓ,0 to be positive definite. We give two examples in which Assumption 1(b) is satisfied but the layer-wise positivity is not.

Example 1 (Identicially distributed random layers). Consider a theoretical scenario in which the B_ℓ,0 ‘s have i.i.d. Uniform(0,1) entries subject to symmetry. It is easy to verify that the expected sum matrix $\mathbb{E}\sum _{\ell }{B}_{\ell }$ is a constant matrix with each entry being L_ρ / 2. Therefore it is impossible to reconstruct the block structure from the sum of adjacency matrices $\sum _{\ell }{A}_{\ell }$ when ρ is small.

Example 2 (Community merge and split). Consider a more realistic scenario in which for {B_ℓ :1 ≤ ℓ ≤ L}, some layers ℓ and community indices k, k′ have B_ℓ,kj = B_ℓ,k′j for all j. This can be interpreted as the merge of communities k and k′ at layer ℓ. In such cases, each layer may not contain full community information, and we must aggregate the layers to recover the full community structure. In our real data example, we actually observe that in most layers, all but one or two communities merge with a large, null community, and each non-null community is active in one or two layers.

Based on these assumptions, in the asymptotic regime n → ∞ and ρ → 0, it is well-known that consistent community estimation is possible for L = 1 when nρ → ∞. Hence, in the multi-layer setting when L → ∞, one should expect a lower requirement on overall density as we aggregate information across layers. This is shown in our following result.

Theorem 1. Under Assumption 1, if L^1/2nρ ≥ C₁ log^1/2(L + n) and nρ ≤ C₂ for a large enough positive constant C₁ and a positive constant C₂, then spectral clustering with a constant factor approximate K-means clustering algorithm applied to $S_0$, the bias-adjusted sum of squared adjacency matrices in (7), correctly estimates the membership of all but a

$$C\left(\frac{1}{n^2}+\frac{\log (L+n)}{L{n}^2{\rho }^2}\right)$$

proportion of nodes for some constant C with probability at least 1−O((L + n)⁻¹).

An immediate consequence of Theorem 1 is the Hamming distance consistency of the bias-adjusted sum-of-squared spectral clustering, provided that L^1/2nρ / log^1/2(L + n) → ∞. This demonstrates the boost of signal strength by a factor of L^1/2 made possibly due to aggregating layers (up to a poly-logarithmic factor) that we alluded to in Section 1.

The proof of Theorem 1 is given in Appendix D, where the main effort is to establish sharp operator norm bounds for the linear noise term $\sum _{\ell }{X}_{\ell }{P}_{\ell }$ and the quadratic noise term $\sum _{\ell }(X_{\ell }^2-D_{\ell })$. A refined operator norm bound for the off-diagonal part of $\sum _{\ell }(X_{\ell }^2-D_{\ell })$ plays an important role (Theorem 5). Once the operator norm bound is established, the clustering consistency follows from a standard analysis of the K-means algorithm (Lemma D.1). These concentration inequalities indeed hold for more general classes of matrices, and we provide a systematic development in the next section.

Theorem 1 is stated in a simple form for brevity. It can be generalized in several directions to better suit practical scenarios with more careful bookkeeping in the proof. We describe some important extensions in the remarks below, where ‖·‖ denotes the operator norm (i.e., largest singular value).

Remark 1 (Varying membership across layers). Theorem 1 can be extended to accommodate varying membership across the layers. In particular, assume that the ℓ th layer has membership matrix Ψ_ℓ ∈{0,1}^n×K, such that each Ψ_ℓ is close to a common membership matrix Ψ ∈{0,1}^n×K,

$$\Vert {\mathrm{\Psi }}_{\ell }-\mathrm{\Psi }\Vert \le {ϵ}_{\ell }\sqrt{n},$$ (8)

for some positive constant ϵ_ℓ. Then we have the following generalization of Theorem 1.

Corollary 2 (Consistency under varying membership). Assume the multilayer adjacency matrices A₁,...,A_L are generated from individual membership matrices Ψ₁,...,Ψ_L satisfying (8) for some sequence ϵ₁,...,ϵ_L and common membership matrix Ψ. Under the same condition as in Theorem 1, if in addition $\overline{ϵ}:=L^{-1}\sum _{\ell }{ϵ}_{\ell }\le C_3$ for some positive constant C₃, then the error bound of the bias-adjusted sum of squared spectral clustering is no more than

$$C\left(\frac{1}{n^2}+{\overline{ϵ}}^2+\frac{\log (L+n)}{L{n}^2{\rho }^2}\right)$$

with high probability.

Remark 2 (Other regimes of network density). The condition L^1/2nρ ≥ C₁ log^1/2(L + n) is required in order for the error bound in Theorem 1 to imply consistency, and is suitable for the linear squared signal accumulation assumed in Part (b) of Assumption 1. If we assume a different growth speed of the minimum eigenvalue of $\sum _{\ell }{B}_{\ell ,0}^2$, this requirement needs to be changed accordingly. Second, the condition nρ ≲ 1 is used for notational simplicity. The regime nρ ≫ 1 would allow for consistent community recovery even when L = 1. For multilayer models, if nρ ≥ C₂ for some constant C₂, the error bound in Theorem 1 becomes

$$C\left(\frac{1}{n^2}+\frac{\log (L+n)}{Ln\rho }\right).$$

for some constant C with high probability. Detailed explanations of this claim are given in Appendix D.

Remark 3 (More general conditions on community sizes). Let $n_{\min }={\min }_{1\le k\le K}{\Vert {\mathrm{\Psi }}_{\cdot k}\Vert }_1$ be the size of the smallest community, and denote α = n_min / n. Our analysis can also allow the number of communities, K, and α to change with other model parameters (n, L, ρ). In particular, the lower bound of the signal term in (5) will be multiplied by α since the operator norm of is Ψ proportional to α. All the matrix concentration results, such as Theorem 5 and Lemma C.1 still hold as they do not rely on any block structures. Therefore under the same setting as Theorem 1, if we allow K and α to vary with (n, L, ρ), but have αL^1/2nρ ≥ C₁ log^1/2(L + n) for some constant C₁, then with high probability, Theorem 1 holds with error bound

$$CK{\alpha }^{-2}\left(\frac{1}{n^2}+\frac{\log (L+n)}{L{n}^2{\rho }^2}\right).$$

4. Matrix Concentration Inequalities

We generically consider a sequence of independent matrices $X_1,\dots ,X_L\in {ℝ}^{n\times r}$ with independent mean-0 entries. The goal is to provide upper bounds for operator norms of linear combinations of the form $\sum _{\ell }{X}_{\ell }{H}_{\ell }$ with $H_{\ell }\in {ℝ}^{r\times m}$ for ℓ ∈{1,...,L}, and quadratic forms $\sum _{\ell }{X}_{\ell }{G}_{\ell }{X}_{\ell }^T$ with $G_{\ell }\in {ℝ}^{r\times r}$ for ℓ ∈{1,...,L}. Here, H_ℓ and G_ℓ are non-random. To connect with the notations in previous sections, let H_ℓ = P_ℓ, then an operator norm bound of $\sum _{\ell }{X}_{\ell }{P}_{\ell }$ will help control the second term in (5). Let G_ℓ = Ir be the r × r identity matrix, then $\sum _{\ell }{X}_{\ell }{G}_{\ell }{X}_{\ell }^T$ corresponds to the third term in (5). Our general results cover both the symmetric and asymmetric cases, as well as more general entries of X_ℓ beyond the Bernoulli case.

Concentration inequalities usually require tail conditions on the entries of X_ℓ. A standard tail condition for scalar random variables is the Bernstein tail condition.

Definition 1. We say a random variable Y satisfies a (v, R)-Bernstein tail condition (or is (v, R)-Bernstein), if $\mathbb{E}\left[|Y{|}^k\right]\le \frac{v}{2}k!R^{k-2}$ for all integers k ≥ 2.

The Bernstein tail condition leads to concentration inequalities for sums of independent random variables (van der Vaart and Wellner, 1996, Chapter 2). Since we are interested not only in linear combinations of X_ℓ ‘s, but also the quadratic forms involving $X_{\ell }{G}_{\ell }{X}_{\ell }^T$, we need the Bernstein condition to hold for the squared entries of X₁,...,X_L. Specifically we consider the following three assumptions.

Assumption 2. Each entry X_ℓ,ij is (v₁, R₁)-Bernstein, for all ℓ ∈ {1,...,L} and i, j ∈{1,...,n}.

Assumption 3. Each squared entry $X_{\ell ,ij}^2$ is (v₂, R₂)-Bernstein, for all ℓ ∈{1,...,L} and i, j ∈{1,...,n}.

Assumption 3’. The product $X_{\ell ,ij}{\tilde{X}}_{\ell ,ij}$ is (v₂′, R₂′)-Bernstein, for all ℓ ∈{1,...,L} and i, j ∈{1,...,n}, where ${\tilde{X}}_{\ell }$ is an independent copy of X_ℓ.

There are two typical scenarios in which such a squared Bernstein condition in Assumption 3 holds. The first is the sub-Gaussian case: If a random variable Y satisfies the sub-Gaussian condition $\mathbb{E}{e}^{Y^2/{\sigma }^2}\le 2$ for some σ > 0, then we have $\mathbb{E}{Y}^{2k}\le 2{\sigma }^4{({\sigma }^2)}^{k-2}k!$, and hence Y² is (4σ⁴, σ²)-Bernstein. The second scenario is centered Bernoulli: If a random variable Y satisfies $\mathbb{P}(Y=1-p)=1-\mathbb{P}(Y=-p)=p$ for some p ∈[0,1 / 2], then we have $\mathbb{E}{Y}^{2k}=p{(1-p)}^{2k}+(1-p)p^{2k}\le p$, and hence Y² is (2p,1)-Bernstein. Our proof will also use the fact that if Y² is (v₂, R₂)-Bernstein, then the centered version $Y^2-{\mathbb{E}}_s(Y^2)$ is also (v₂, R₂)-Bernstein (Wang et al., 2016, Lemma 3).

We require Assumption 3’ in order to use a decoupling technique in establishing concentration of quadratic forms. One can show that if Assumption 3 holds then Assumption 3’ holds with (v₂′, R₂′) = (v₂, R₂). However, when X_ℓ,ij ‘s are centered Bernoulli random variables with parameters bounded by p ≤ 1 / 2, then Assumption 3’ holds with v₂′ = 2p² and R₂′ = 1, while Assumption 3 holds with v₂ = 2p and R₂ = 1, so that v₂′ can potentially be much smaller than v₂. We will explicitly keep track of the Bernstein parameters in our results for the sake of generality.

4.1. Linear combinations with matrix coefficients

Theorem 3. Let X₁,...,X_L be a sequence of independent n × r matrices with mean-0 independent entries satisfying Assumption 2, and H_ℓ be any sequence of r × m non-random matrices. Then for all t > 0,

$$\begin{array}{l}\mathbb{P}\left[\Vert \sum _{\ell =1}^L{X}_{\ell }{H}_{\ell }\Vert \ge t\right]\\ \le 2(m+n)\exp \left(-\frac{t^2/2}{v_1(n\Vert \sum _{\ell }{H}_{\ell }^T{H}_{\ell }\Vert \vee \sum _{\ell }{\Vert H_{\ell }\Vert }_F^2)+R_1{\max }_{\ell }{\Vert H_{\ell }\Vert }_{2,\infty }t}\right).\end{array}$$ (9)

A similar result holds, with t² / 2 replaced by t² / 8 and 2(m + n) replaced by 4(m + n) in (9), for symmetric X_ℓ ‘s of size n × n with independent (v₁, R₁)-Bernstein diagonal and upper-diagonal entries and H_ℓ of size n × m.

The proof of Theorem 3, given in Appendix B, combines the matrix Bernstein inequality (Tropp, 2012) for symmetric matrices and a rank-one symmetric dilation trick (Lemma B.1) to take care of the asymmetry in X_ℓH_ℓ.

Remark 4. If n = m = r = 1, then Theorem 3 recovers the well-known Bernstein’s inequality as a special case with a different pre-factor.

If n ≥ min{m, Lr}, then $n\Vert \sum _{\ell }{H}_{\ell }^T{H}_{\ell }\Vert \ge \sum _{\ell }{\Vert H_{\ell }\Vert }_F^2$ and the probability upper bound in Theorem 3 reduces to

$$\mathbb{P}\left[\Vert \sum _{\ell =1}^L{X}_{\ell }{H}_{\ell }\Vert \ge t\right]\le 2(m+n)\exp \left(-\frac{t^2/2}{v_{1}n\Vert \sum _{\ell }{H}_{\ell }^T{H}_{\ell }\Vert +R_1{\max }_{\ell }{\Vert H_{\ell }\Vert }_{2,\infty }t}\right).$$ (10)

If n = 1 then $n\Vert \sum _{\ell }{H}_{\ell }^T{H}_{\ell }\Vert \le \sum _{\ell }{\Vert H_{\ell }\Vert }_F^2$ and the probability bound reduces to

$$\mathbb{P}\left[\Vert \sum _{\ell =1}^L{X}_{\ell }{H}_{\ell }\Vert \ge t\right]\le 2(m+n)\exp \left(-\frac{t^2/2}{v_1\sum _{\ell }{\Vert H_{\ell }\Vert }_F^2+R_1{\max }_{\ell }{\Vert H_{\ell }\Vert }_{2,\infty }t}\right).$$ (11)

Remark 5. When L = 1, the setting is similar to that considered in Vershynin (2011). In the constant variance case (e.g., sub-Gaussian), $v_1^{1/2}\asymp R_1\asymp 1$, Theorem 3 implies a high probability upper bound of $C\sqrt{\log (m+n)}(\sqrt{n}\Vert H\Vert +\Vert H{\Vert }_F)$, which agrees with Theorem 1.1 of Vershynin (2011). The extra $\sqrt{\log (n+m)}$ factor in our bound is because our result is a tail probability bound while Vershynin (2011) provides upper bounds on the expected value. However, in the sparse Bernoulli setting, where v₁ ≪ R₁ = 1, the upper bound in Theorem 3 is better because it correctly captures the $\sqrt{v_1}$ factor multiplied by $\sqrt{n}\Vert H\Vert +\Vert H{\Vert }_F$, whereas the result in Vershynin (2011) leads to $v_1^{1/4}(\sqrt{n}\Vert H\Vert +\Vert H{\Vert }_F)$.

4.2. Matrix U-statistics and quadratic forms

Let

$$S=\sum _{\ell =1}^L{X}_{\ell }{G}_{\ell }{X}_{\ell }^T=\sum _{\ell =1}^L\sum _{(i,j),(i^{\prime },j^{\prime })}{X}_{\ell ,ij}{X}_{\ell ,i^{\prime }{j}^{\prime }}{e}_i{e}_{i^{\prime }}^T{G}_{\ell ,j{j}^{\prime }}$$ (12)

where the summation is taken over all pairs (i, j), (i′, j′) ∈{1,...,n}² and e_i is the canonical basis vector in ${ℝ}^n$ with a 1 in the ith coordinate. In this subsection, we will focus on the symmetric case because the bookkeeping is harder compared to the asymmetric case. The treatment for the asymmetric case is similar and the corresponding results are stated separately in Appendix B for completeness.

Because X_ℓ has centered and independent diagonal and upper diagonal entries, a term in (12) has non-zero expected value only if (i, j) = (i′, j′) or (i, j) = (j′, i′) since this would imply $X_{\ell ,ij}{X}_{\ell ,i^{\prime }{j}^{\prime }}=X_{\ell ,ij}^2$. This motivates the following decomposition of $S$ into a quadratic component with non-zero entry-wise mean value

$$\begin{array}{l}{S}_2=[\sum _{\ell =1}^L\sum _{1\le i<j\le n}{X}_{\ell ,ij}^2(e_i{e}_i^T{G}_{\ell ,jj}+e_j{e}_j^T{G}_{\ell ,ii}+e_i{e}_j^T{G}_{\ell ,ji}+e_j{e}_i^T{G}_{\ell ,ij})]\\ +[\sum _{\ell =1}^L\sum _{1\le i\le n}{X}_{\ell ,ii}^2{e}_i{e}_i^T{G}_{\ell ,ii}],\end{array}$$ (13)

and a cross-term component with entry-wise mean-0 value

$$S_1=S-S_2.$$ (14)

It is easy to check that $\mathbb{E}{S}_2=\mathbb{E}S$ and $\mathbb{E}{S}_1=0$. Intuitively, the spectral norm of ${\mathcal{S}}_1$ should be small since it is the sum of many random terms with zero mean and small correlation, which can be viewed as a U-statistic with a centered kernel function of order two. This U-statistic perspective is a key component of the analysis and will be made clearer in the proof. For a similar reason, $S_2-\mathbb{E}{S}_2$ should also be small. Hence, the main contributing term in $\mathcal{S}$ should be the deterministic term $\mathbb{E}{S}_2$. To formalize this, define the following quantities,

$$\begin{array}{l}{\sigma }_1^2=\sum _{\ell =1}^L{\Vert G_{\ell }\Vert }^2,\\ {\sigma }_2=\underset{\ell }{\max }\text{max}\left\{{\Vert G_{\ell }\Vert }_{2,\infty },{\Vert G_{\ell }^T\Vert }_{2,\infty }\right\}\\ {({\sigma }_2^{\prime })}^2=\sum _{\ell =1}^L\sum _{j=1}^n{G}_{\ell ,jj}^2,\\ {\sigma }_3=\underset{\ell }{\max }{\Vert G_{\ell }\Vert }_{\infty },\end{array}$$

where ‖·‖_2,∞ is the maximum L₂-norm of each row, and ‖·‖_∞ is the maximum entry-wise absolute value. The following theorem quantifies the random fluctuations of $S_1$, $S_2$ and $S$ around their expectations.

Theorem 4. If X₁,...,X_L are independent n × n symmetric matrices with independent diagonal and upper diagonal entries satisfying Assumption 2 and Assumption 3’. Let G₁,...,G_L be n × n matrices. Define $S=\sum _{\ell }{X}_{\ell }{G}_{\ell }{X}_{\ell }^T$ and $S_1$, $S_2$ as in (13) and (14). Then there exists a universal constant C such that with probability at least 1−O((n + L)⁻¹),

$$\begin{array}{l}\Vert S_1\Vert \le C[v_{1}n\log (L+n){\sigma }_1+\sqrt{v_1}{R}_1\sqrt{Ln}{\log }^{3/2}(L+n){\sigma }_2\\ +\sqrt{{v_2}^{\prime }}\log (L+n)(\sqrt{L}{\sigma }_2+{\sigma }_2^{\prime })+(R_1^2+R_2^{\prime }){\log }^2(L+n){\sigma }_3].\end{array}$$ (15)

If in addition Assumption 3 holds, then with probability at least 1−O((n + L)⁻¹),

$$\Vert S_2-\mathbb{E}{S}_2\Vert \le C\left[\sqrt{v_2}\log (L+n)(\sqrt{L}{\sigma }_2+{\sigma }_2^{\prime })+R_2\log (L+n){\sigma }_3\right].$$ (16)

and consequently,

$$\begin{array}{l}\Vert S-\mathbb{E}S\Vert \le C[v_{1}n\log (L+n){\sigma }_1+\sqrt{v_1}{R}_1\sqrt{Ln}{\log }^{3/2}(L+n){\sigma }_2\\ +\sqrt{{v_2}^{\prime }+v_2}\log (L+n)(\sqrt{L}{\sigma }_2+{{\sigma }_2}^{\prime })+(R_1^2+R_2+{R_2}^{\prime }){\log }^2(L+n){\sigma }_3].\end{array}$$ (17)

The proof of Theorem 4 is given in Appendix B, where the main effort is to control ‖S₁‖. Unlike the linear combination case, the complicated dependence caused by the quadratic form needs to be handled by viewing $S_1$ as a matrix-valued U-statistic indexed by the pairs (i, j), and using a decoupling technique due to de la Peña and Montgomery-Smith (1995). This reduces the problem of bounding ‖S₁‖ to that of bounding $\Vert \sum _{\ell }{X}_{\ell }{G}_{\ell }{\tilde{X}}_{\ell }^T\Vert$, where ${\tilde{X}}_1,\dots ,{\tilde{X}}_L$ are i.i.d. copies of X₁,...,X_L. The upper bounds in Theorem 4 look complicated. This is because we do not make any assumption about the Bernstein parameters or the matrices G_ℓ. The bound can be much simplified or even improved in certain important special cases. In the sub-Gaussian case, where $R_1\asymp v_1^{1/2}\asymp R_2^{1/2}\asymp v_2^{1/4}$, the first term v₁n log(L + n)σ₁ in (15) dominates. This reflects the L^1/2 effect for sums of independent random variables. For example, in the case G_ℓ = G₀ for all ℓ and X_ℓ are i.i.d., we have $\Vert \mathbb{E}S\Vert \approx L\Vert X_1{G}_0{X}_1^T\Vert \asymp v_{1}nL\Vert G_0\Vert$, but when we consider the fluctuations contributed by $S_1$, we have $\Vert S_1\Vert \lesssim v_{1}n{L}^{1/2}\Vert G_0\Vert$ ignoring logarithmic factors. In other words, the signal is contained in $\mathbb{E}{S}_2$ whose operator norm may grow linearly as L, while the fluctuation in the operator norm of $S_1$ only grows at a rate of L^1/2.

Additionally, in the Bernoulli case, the situation becomes more complicated when the variance v₁ is vanishing, meaning that $v_1\asymp v_2\asymp {(v^{\prime })}_2^{1/2}\ll R_1\asymp R_2$. In the simple case of G_ℓ = I_n, we have σ₁ = L^1/2, σ₂ = σ₃ = 1. Thus the second term (v₁Ln)^1/2σ₂ in (15) may dominate the first term when nv₁ ≪ 1. In this case, we also have σ₂′ = (Ln)^1/2. Therefore, it is also possible that the term $v_2^{1/2}{\sigma }_2$ in (16) may be large. It turns out that in such very sparse Bernoulli cases, the bound on the fluctuation term ‖S₁‖ can be improved by a more refined and direct upper bound for $\Vert \sum _{\ell }{X}_{\ell }{X}_{\ell }^T\Vert =\Vert S\Vert$. The details are presented in the next subsection.

4.3. Sparse Bernoulli matrices

In this section, we focus on the case where G_ℓ = I_n for all ℓ, and the X_ℓ ‘s are symmetric with centered Bernoulli entries whose probability parameters are bounded by ρ. Here, ρ can be very small. In this case, Assumptions 2, 3 and 3’ hold with v₁ = v₂ = 2ρ, R₁ = R₂ = R₂′ = 1, v₂′ = 2ρ², and the matrices G_ℓ satisfy σ₁ = L^1/2, σ₂ = σ₃ =1, σ₂′ = (Ln)^1/2.

Ignoring logarithmic factors, the first part of Theorem 4 becomes

$$\Vert S_1\Vert \lesssim C\left[L^{1/2}n\rho +{(Ln\rho )}^{1/2}+1\right],$$

where the second term (Lnρ)^1/2 can be dominating when nρ is small and Lnρ is large. This is suboptimal since intuitively we expect that the main variance term L^1/2nρ is the leading term as long as its value is large enough, which only requires nρ ≫ L^1/2. To investigate the cause of this suboptimal bound, observe that (Lnρ)^1/2 originates from the second term R₁(v₁Ln)^1/2σ₂ in (15). Investigating the proof of Theorem 4, this term is derived by bounding $\sum _{\ell }\Vert H_{\ell }^T{H}_{\ell }\Vert$ by ${\sum _{\ell }\Vert H_{\ell }\Vert }^2$, which is suboptimal in this sparse Bernoulli case when applying the decoupling technique. The following result shows a sharper bound in this setting using a more refined argument.

Theorem 5. Assume G_ℓ = I_n for all ℓ ∈{1,...,L} and X₁,...,X_L are symmetric with centered Bernoulli entries whose parameters are bounded by ρ. If L^1/2nρ ≥ C₁ log^1/2(L + n) and nρ ≤ C₂ for some constants C₁, C₂, then with probability at least 1−O((n + L)⁻¹),

$$\Vert S_1\Vert \le C{L}^{1/2}\rho n{\log }^{1/2}(L+n)$$ (18)

for some constant C.

The proof of Theorem 5 is given in Appendix C where we modify our usage of the decoupling technique. At a high level, the decoupling technique reduces the problem to controlling the operator norm of $\tilde{S}=\sum _{\ell }{X}_{\ell }{\tilde{X}}_{\ell }^T$ where ${\tilde{X}}_{\ell }$ is an i.i.d. copy of X_ℓ. Instead of directly applying Theorem 3 with $H_{\ell }={\tilde{X}}_{\ell }$, we instead shift ${\tilde{X}}_{\ell }$ back to the original Bernoulli matrix by considering $\tilde{S}=\sum _{\ell }{X}_{\ell }{\tilde{A}}_{\ell }-\sum _{\ell }{X}_{\ell }{P}_{\ell }$, where ${\tilde{A}}_{\ell }$ is the original uncentered binary matrix and $P_{\ell }=\mathbb{E}{\tilde{A}}_{\ell }$. Then Theorem 3 is applied to $\sum _{\ell }{X}_{\ell }{P}_{\ell }$ and $\sum _{\ell }{X}_{\ell }{\tilde{A}}_{\ell }$ separately, where the entry-wise non-negativity of ${\tilde{A}}_{\ell }$ allows us to use the Perron–Frobenius theorem to obtain a sharper bound for $\Vert \sum _{\ell }{\tilde{A}}_{\ell }^2\Vert$.

5. Further simulation study

In the following simulation study, we show that bias-adjusting sum of squared adjacency matrices constructed in (7) has a measurable impact on the downstream spectral clustering accuracy, and that our method performs favorably against other competing methods. This builds upon the simulation initially shown in Section 2.2.

Data-generating process.

We design the following simulation setting to highlight the importance of bias adjustment for $\sum _{\ell }{A}_{\ell }^2$. We consider n = 500 nodes per network across K = 3 communities, with imbalanced sizes n₁ = 200, n₂ = 50, n₃ = 250. We construct two edge-probability matrices that share the same eigenvectors,

$$W=\left[\begin{array}{ccc}1/2& 1/2& -\sqrt{2}/2\\ 1/2& 1/2& \sqrt{2}/2\\ \sqrt{2}/2& -\sqrt{2}/2& 0\end{array}\right].$$ (19)

The two edge-probability matrices are

$$\begin{array}{l}{B}^{(1)}=W\left[\begin{array}{ccc}1.5& 0& 0\\ 0& 0.2& 0\\ 0& 0& 0.4\end{array}\right]W^{\top }\approx \left[\begin{array}{ccc}0.62& 0.22& 0.46\\ 0.22& 0.62& 0.46\\ 0.46& 0.46& 0.85\end{array}\right],B^{(2)}\\ =W\left[\begin{array}{ccc}1.5& 0& 0\\ 0& 0.2& 0\\ 0& 0& -0.4\end{array}\right]W^{\top }\approx \left[\begin{array}{lll}0.22\hfill & 0.62\hfill & 0.46\hfill \\ 0.62\hfill & 0.22\hfill & 0.46\hfill \\ 0.46\hfill & 0.46\hfill & 0.85\hfill \end{array}\right].\end{array}$$

We then generate L = 100 layers of adjacency matrices, where each layer is drawn by setting the edge-probability matrices B_ℓ = ρB⁽¹⁾ for ℓ ∈{1,...,L / 2} and B_ℓ = ρB⁽²⁾ for ℓ ∈{L / 2 + 1,..., L}. Using this, we generate the adjacency matrices via (1), with ρ varying from 0.025 to 0.2.

We choose this particular simulation setting for two reasons. First, the first two eigenvectors in W are not sufficient to distinguish between the first two communities. Hence, methods based on $\sum _{\ell }{A}_{\ell }$ are not expected to perform well since the third eigen-component cancels out in the summation. Second, the average degrees among the three communities are drastically different, which are 251ρ, 191ρ and 327ρ respectively. This means the variability of degree matrix D_ℓ ‘s diagonal entries will be high, helping demonstrating the effect of our method’s bias adjustment.

Methods we consider.

We consider the following four ways to aggregate information across all L layers, three of which were used earlier in Figure 2: 1) the sum of adjacency matrices without squaring (i.e., considering $M=\sum _{\ell }{A}_{\ell }$, “Sum”), 2) the sum of squared adjacency matrices (i.e., considering $M=\sum _{\ell }{A}_{\ell }^2$, “SoS”), 3) our proposed bias-adjusted sum of squared adjacency matrices (i.e., considering (7), or equivalently $M=\sum _{\ell }{A}_{\ell }^2$ and then zeroing out the diagonal entries, “SoS-Debias”), and 4) column-wise concatenating the adjacency matrices together, specifically, considering

$$M=\left[\begin{array}{llll}{A}_1\hfill & A_2\hfill & \dots \hfill & A_L\hfill \end{array}\right]\in {ℝ}^{n\times (Ln)}.$$

(i.e., “Tensor matricization”). This method is commonly-used in the tensor literature (see Zhang and Xia (2018) for example), where the L adjacency matrices can be viewed as a n × n × L tensor, and the column-wise concatenation converts the tensor into a matrix. Then, using one of the four construction of the aggregated matrix M, we then apply spectral clustering onto M, meaning we first compute the matrix containing the leading K left singular vectors of M and perform K-means on its rows.

Additionally, we consider two methods that developed in Paul and Chen (2020) called Linked Matrix Factorization (i.e., “LMF”) and Co-regularized Spectral Clustering (i.e., “Co-reg”). These two methods fall outside the framework of the four methods discussed above. Instead, they use optimization procedures designed with different so-called fusion techniques to solve for an appropriate low-dimensional embedding shared among all L layers, and then perform K-means clustering on its rows.

Results.

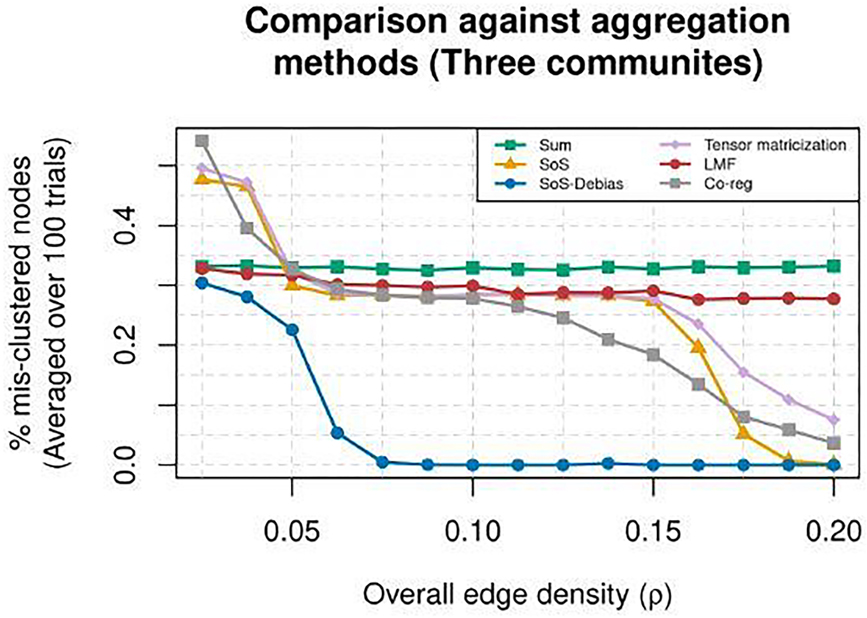
The results shown in Figure 3 demonstrate that bias-adjusting the diagonal entries of $\sum _{\ell }{A}_{\ell }^2$ has a noticeable impact on the clustering accuracy. Using the aforementioned simulation setting and methods, we vary ρ from 0.025 to 0.2 in 15 equally-spaced values, and compare the methods for each setting of ρ across 100 trials by measuring the average Hamming distance (i.e., $n^{-1}d(\widehat{\theta },\theta )$ defined in (2)) between the true memberships in θ and the estimated membership $\widehat{\theta }$. We observe phenomenons in Figure 3 which all agree with our intuition and theoretical results. Specifically, summing the adjacency matrices hinders our ability to cluster the nodes due to the cancellation of positive and negative eigenvalues (green squares), and the diagonal bias induced by squaring the adjacency matrices has a profound effect in the range of ρ ∈[0.08, 0.17], which our bias-adjusted sum-of-squared method removes (purple diamonds verses blue circles). We also see that our bias-adjusted sum-of-squared method out-performs Linked Matrix Factorization (red circles) and Co-regularized Spectral Clustering (gray squares). While the LMF method and Co-reg method show some improvements over the Sum and SoS methods, respectively, they still behave qualitatively similar. This observation suggests that these two methods may have similar difficulty in aggregating layers without positivity or removing the diagonal bias.

Fig. 3.

The average proportion of mis-clustered nodes for eight methods (measured via Hamming distance $n^{-1}d(\widehat{\theta },\theta )$ shown in (2), averaged over 100 trials), with n = 500 with three unequally-sized communities among overall edge densities ranging from ρ ∈[0.025, 0.2] and L = 100 layers. Six methods’ performance are shown: “Sum” (green squares), “SoS” (orange triangles), “Bias-adjusted SoS” (blue circles), “Tensor matricization” (purple diamonds), “LMF” (red circles), and “Co-reg” (gray squares).

Intuition behind results.

We provide additional intuition behind the results shown in Figure 3 by visualizing the impact of the diagonal terms on the overall spectrum and quantifying the loss of population signal due to the bias.

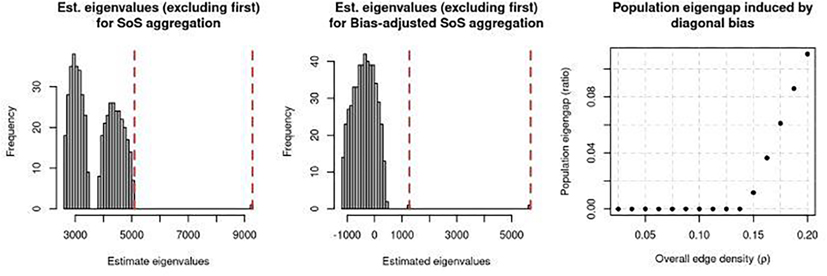
First, we demonstrate in Figure 4 that the third leading eigenvalue of $\sum _{\ell }{A}_{\ell }^2$ when ρ = 0.15 is indistinguishable from the remaining bulk “noise” eigenvalues if the diagonal bias is not removed (left), but becomes well-separated if so (middle). Recall by construction (19), all three eigenvectors are needed for recovering the communities. Hence, if the third eigenvalue of $\sum _{\ell }{A}_{\ell }^2$ is indistinguishable from fourth through last eigenvalues (i.e., the “noise”), then we should expect many nodes to be mis-clustered. This is exactly what Figure 4 (left) shows, where the third eigenvalue (denoted by the left-most red vertical line) is not separated from the remaining eigenvalues. However, when we appropriately bias-adjust $\sum _{\ell }{A}_{\ell }^2$ via (7), then Figure 4 (middle) shows that the third eigenvalue is now well-separated from the remaining eigenvalues. This demonstrates the importance of bias-adjustment for community estimation in this regime of ρ.

Fig. 4.

(Left): For one realization of A₁,...,A_L given the setup described in the simulation with ρ = 0.15, a histogram of all 500 eigenvalues of $\sum _{\ell }{A}_{\ell }^2$, where the red vertical dashed lines denote the second and third eigenvalues. (The first eigenvalue is too large to be shown.) (Middle): Similar to the left plot, but showing the 500 eigenvalues of the bias-adjusted variant of $\sum _{\ell }{A}_{\ell }^2$ (i.e., setting the diagonal to be all 0’s). (Right): The population eigengap (λ₃ – λ₄) / λ₃ computed from $\sum _{\ell }{P}_{\ell }^2+{\tilde{D}}_{\ell }$ for varying values of ρ.

Next, in Figure 4 (right), we show that this lack-of-separation between the third eigenvalue and the noise can be observed on the population level. Specifically, we show that the population counterpart of $\sum _{\ell }{A}_{\ell }^2$ has considerable diagonal bias that makes the accurate estimation of the third eigenvector nearly impossible when ρ is too small. To show this, for a particular value of ρ, recall from our theory that the population counterpart of $\sum _{\ell }{A}_{\ell }^2$ is

$$\sum _{\ell =1}^L(P_{\ell }^2+{\tilde{D}}_{\ell })\text{,}\text{for}\text{a}\text{diagonal}\text{matrix}{\tilde{D}}_{\ell }\text{where}{\tilde{D}}_{\ell ,ii}=\sum _{j=1}^n{P}_{\ell ,ij}\text{for}1\le i\le n,$$

and $P_{\ell }=\mathbb{E}{A}_{\ell }$. Let λ_1,...,λ_n denote the n eigenvalues of the above matrix, dependent on ρ. We then plot (λ₃ – λ₄) / λ₄ against ρ in Figure 4 (right). This plot demonstrates that when ρ is too small, the diagonal entries (represented by ${\tilde{D}}_{\ell }$ ‘s) add a disproportionally large amount of bias that makes it impossible to accurately distinguish between the third and fourth eigenvectors. Additionally, the raise in the eigengap in Figure 4 (right) at ρ = 0.15 corresponds to when “SoS” starts to improve in Figure 3 (orange triangles). This means starting at ρ = 0.15, the effect of the diagonal bias starts to diminish, and at larger values of ρ, the sum of squared adjacency matrices contains accurate information for community estimation (both with and without bias adjustment). We report additional results in Appendix E, where we report the time needed for each method, visualize the lack of concentration in the nodes’ degrees in sparse graphs and its effect on the spectral embedding, and also report that the qualitative trends in Figure 3 remain the same when we either consider the varying-membership setting (described in Corollary 2) or an additional variant of spectral clustering where the eigenvectors are reweighted by its corresponding eigenvalues.

6. Data application: Gene co-expression patterns in developing monkey brain

We analyze the microarray dataset of developing rhesus monkeys’ tissue from the medial prefrontal cortex introduced in Section 1 that was originally collected in Bakken et al. (2016) to demonstrate the utility of our bias-adjusted sum-of-squared spectral clustering method. As described in other work that analyze this data (Liu et al. (2018) and Lei et al. (2019)), this is a suitable dataset to analyze as other work have well-documented that the gene co-expression patterns in monkeys’ tissue from this brain region change dramatically over development. Specifically, the data from Bakken et al. (2016) consists of the gene co-expression network of ten different developmental times (starting from 40 days in the embryo to 48 months after birth) derived from microarray data, where each of the developmental time points corresponds to post-mortem tissue samples of multiple unique rhesus monkeys. With this data, we aim to show that our bias-adjusted sum-of-squared spectral clustering method produces insightful gene communities.

Preprocessing procedure.

The microarray dataset from Bakken et al. (2016) contains n = 9173 genes measured among many samples across the L = 10 layers, which we preprocess into ten adjacency matrices in the following way in line with other work like Langfelder and Horvath (2008). We use these specific set of n genes, following the analysis in Liu et al. (2018), since they map to the human genome. First, for each layer ℓ ∈{1,...,L}, we construct the Pearson correlation matrix. Then, we convert each correlation matrix into adjacency matrix by hard-thresholding at 0.72 in absolute value, resulting in ten adjacency matrices A₁,...,A_L. We choose this particular threshold since it yields sparse and scale-free networks that have many disjoint connected components individually but have one connected component after aggregation, as reported in Appendix F. Lastly, we remove all the genes corresponding to nodes whose total degree across all ten layers is less than 90. This value is chosen since the median total degree among all nodes that do not have any neighbors in five or more of the layers (i.e., a degree of zero in more than half the layers) is 89. In the end, we have ten adjacency matrices A1,...,AL ∈{0,1}^7836×7836, each representing a network corresponding to 7836 genes. We note that the above procedure of transforming correlation matrices into adjacency matrices is unlikely to procedure networks that severely violate the layer-wise positivity assumption commonly required by other methods – this hypothetically could happen if many pairs of genes display high negative correlations, but this is not typical in genomic data. Nonetheless, we are interested in what insights the bias-adjusted sum-of-squared spectral clustering method can reveal for this dataset.

Results and interpretation.

The following results show that bias-adjusted sum-of-squared spectral clustering finds meaningful gene communities. Prior to using our method, we select the dimensionality and number of communities to be K = 8 based on a scree plot of the singular values of the bias-adjusted variant of $\sum _{\ell }{A}_{\ell }^2$. We perform our bias-adjusted spectral clustering on this matrix with K = 8, and visualize three out of the ten adjacency matrices using the estimated communities in Figure 5 (which are the full adjacency matrices corresponding to the three adjacency matrices shown in Figure 1). We see that as development occurs from 40 days in the embryo to 48 months after birth, there are different gene communities that are most-connected. This visually demonstrates different biological processes in brain tissue that are most active at different stages of development. Labeling the communities 1 through 8 from top left to bottom right, our results show that starting at 40 days in the embryo, Community 1 is highly coordinated (i.e., densely connected), and ending at 48 months after birth, Community 7 is highly coordinated. All the genes in Community 8 are sparsely connected throughout all ten adjacency matrices, suggesting that these genes are not strongly correlated with many other genes throughout development.

Fig. 5.

Three of ten adjacency matrices where the genes are ordered according to the estimated K = 8 communities. Blue pixels correspond to the absence of an edge between the corresponding genes in A_ℓ ‘s, while yellow pixels correspond to an edge. The dashed white lines denote the separation among the K = 8 gene communities. The adjacency matrices shown in Figure 1 correspond to the same three developmental times (from left to right), and are formed by selecting only the genes in Communities 1, 4, 5, and 7.

To interpret these K = 8 communities, we perform a gene ontology analysis, using the cluster- Profiler::enrichGO function on the gene annotation in the Bioconductor package org.Mmu.eg.db to analyze the scientific interpretation of each of the K communities of genes within rhesus monkeys. Table 1 shows the results. We see the first seven communities are highly enriched for cell processes closely related to brain development – we can interpret Figure 5 and Table 1 together as which biological systems are most active in a coordinated fashion at different developmental stage. Since genes in the eighth community are sparsely-connected across all developmental time and is not enriched for any cell processes, we infer that these genes are unlikely to be coordinated to drive any process related to brain development. Together, these results demonstrate that the bias-adjusted sum-of-squared spectral clustering is able to find meaningful gene communities. Visualizations of all ten adjacency matrices, beyond those shown in Figure 5 and explicit reporting of the edge densities, as well as stability analyses that demonstrate how the results vary when different tuning parameters are used, are included in Appendix F.

Table 1.

Gene ontology of the estimated K = 8 communities of genes. Here, “GO” denotes the gene ontology ID, and “p-value” denotes the Fisher’s exact test to denote an enrichment (i.e., significance or over-representation) of a particular GO for the genes in said community compared to all other genes.

Community	Description	GO ID	p-value
1	RNA splicing	GO:0008380	1.07 × 10−11
2	Nuclear transport	GO:0051169	3.15 × 10−5
3	Neuron development	GO:0048666	2.08 × 10−8
4	Chromosome segregation	GO:0007059	1.31 × 10−8
5	Neuron projection development	GO:0031175	1.51 × 10−5
6	Regulation of transporter activity	GO:0032409	5.68 × 10−6
7	Anchoring junction	GO:0070161	8.86 × 10−5
8	None

7. Discussion

While we establish community estimation consistency in this paper, there are two major additional theoretical directions we hope our results will help shed light into for future work. First, an important theoretical question in the study of stochastic block models is the critical threshold for community estimation. This involves finding a critical rate of the overall edge density and/or the separation between rows of B_ℓ,0, and proving achievability of certain community estimation accuracy when the density and/or separation are above this threshold, as well as impossibility for non-trivial community recovery below this threshold. For single-layer SBMs, this problem has been studied by many authors, such as Massoulié (2014), Abbe and Sandon (2015), Zhang and Zhou (2016), and Mossel et al. (2018). The case of multi-layer SBMs is much less clear, especially for generally structured layers. The upper bounds proved in Paul and Chen (2020) and Bhattacharyya and Chatterjee (2018) imply achievability of vanishing error proportion when Lnρ → ∞ under a layer-wise positivity assumption. Our results requires a stronger L^1/2nρ / log^1/2 (L + n) → ∞ condition, but does not require a layer-wise positivity assumption. Ignoring logarithmic factors, is a rate of L^1/2 the right price to pay for not having the layer-wise positivity assumption? The error analysis in the proof of Theorem 1 seems to suggest a positive answer, but a rigorous claim will require a formal lower bound analysis. We note that the simplified constructions such as that in Zhang and Zhou (2016) designed for single-layer SBMs are unlikely to work, since they do not reflect the additional hardness brought to the estimation problem by unknown layer-wise structures.

Second, the consistency result for multi-layer SBMs also makes it possible to extend other inference tools developed for single-layer data to multi-layer data. One such example is model selection and cross-validation (Chen and Lei, 2018, Li et al., 2020). The probability tools developed in this paper, such as Theorem 3 and Theorem 4 and Theorem B.2, may be useful for other statistical inference problems involving matrix-valued measurements and noise. For example, our theoretical analyses could refine the theoretical analyses for multilayer graphs that go beyond SBMs, such as degree-corrected SBMs or random dot-product graphs in general (Nielsen and Witten, 2018; Arroyo et al., 2021). Alternatively, in dynamic networks where the network parameters change smoothly over time, one may use nonparametric kernel smoothing techniques in Pensky and Zhang (2019) and the matrix concentration inequalities developed in this paper to control the aggregated noise and perhaps obtain more refined analysis in those settings.