Abstract
Cardiac arrhythmias such as atrial fibrillation (AF) are recognised to be associated with re-entry or rotors. A rotor is a wave of excitation in the cardiac tissue that wraps around its refractory tail, causing faster-than-normal periodic excitation. The detection of rotor centres is of crucial importance in guiding ablation strategies for the treatment of arrhythmia. The most popular technique for detecting rotor centres is Phase Mapping (PM), which detects phase singularities derived from the phase of a signal. This method has been proven to be prone to errors, especially in regimes of fibrotic tissue and temporal noise. Recently, a novel technique called Directed Graph Mapping (DGM) was developed to detect rotational activity such as rotors by creating a network of excitation. This research aims to compare the performance of advanced PM techniques versus DGM for the detection of rotors using 64 simulated 2D meandering rotors in the presence of various levels of fibrotic tissue and temporal noise. Four strategies were employed to compare the performances of PM and DGM. These included a visual analysis, a comparison of -scores and distance distributions, and calculating p-values using the mid-p McNemar test. Results indicate that in the case of low meandering, fibrosis and noise, PM and DGM yield excellent results and are comparable. However, in the case of high meandering, fibrosis and noise, PM is undeniably prone to errors, mainly in the form of an excess of false positives, resulting in low precision. In contrast, DGM is more robust against these factors as -scores remain high, yielding as opposed to the best PM across all 64 simulations.
Keywords: Directed Graph Mapping, Phase Mapping, Performance comparison, Simulated rotors, Meandering, Fibrosis, Noise
Highlights
-
•
DGM obtains F2-scores 0.931 for 64 rotor simulations of various complexities.
-
•
DGM detects more rotors that are closer to the ground truth than PM.
-
•
PM suffers from false positives especially in high meandering, fibrosis and noise regimes.
-
•
DGM in essence generalises PM by detecting all possible loop shapes and sizes.
1. Introduction
Rotors are of significant importance in the theory of cardiac arrhythmia. Specifically, they refer to a functional type of re-entry characterised by the absence of a predetermined anatomical obstacle. These functional re-entries or rotors are increasingly being recognised as crucial to at least some subset of atrial fibrillation (AF) [1], [2]. Computer simulations have suggested that both stationary and meandering rotors could be potential sources of AF [3], [4]. Moreover, these rotors are typically present in fibrotic tissue [5], [6], [7], [8], [9], [10], [11], [12]. Thus, it is essential to track the core of rotors to guide ablation strategies for the treatment of patients during AF.
Rotors have been investigated for decades in simulation studies, and numerous methods have been developed to track the core of rotors. One such method involves computing the intersection of the isocontours of two state variables [13]. However, this method requires complete knowledge of the values of two state variables, which is not readily accessible in clinical or experimental datasets. Alternatively, Phase Mapping (PM) is widely used to find the core of rotors. PM assigns a phase to any signal per time frame and tracks phase singularities, which is usually a ring of electrodes for which the phase differences add up to approximately [14]. However, most PM methods require a regular grid and can be prone to errors [15]. Although more systematic research is needed, meandering [16], [17], fibrosis [18], and noise [19], [20], [21], [22], [23] have been shown to negatively affect the detection of rotors of PM.
Recently, a novel method called Directed Graph mapping (DGM) has been developed [21], which creates a directed network of excitation of measured electrical activity. Analysing the cycles in this network enables the detection of any type of rotational activity, including rotors. DGM has been successfully applied to simulated data of stable rotors and clinical data of regular ATs [21], [24] and VTs [25], but it remained uncertain how DGM would perform for the detection of meandering rotors in the presence of fibrotic tissue and noise.
Therefore, this paper aims to compare PM and DGM for various types of 2D simulated rotors encompassing various levels of meandering, fibrosis and noise.
2. Methods
The following sections outline the methods used for this research. First, the explanation of the rotor simulation process is included, which details the incorporation of meandering, fibrosis, and noise, as well as the method for extracting the electrogram (EGM) from the simulation. Second, the phase mapping procedure is thoroughly elucidated which consists of three main components: phase map construction, rotor detection and clustering. Third, the DGM workflow is summarised. Finally, the methodology for comparing PM and DGM is provided, comprising four strategies: visual analysis, comparison of -scores and distance distributions, and calculation of mid-p values obtained from the McNemar test.
2.1. Rotor simulation recipe and extracting the electrogram
To construct a testing data set, 64 different rotors on a regular square 2D mesh (Fig. 2) were simulated, encompassing 4 four levels of meandering, fibrosis and noise. In the next sections, further elucidation will be provided on how these factors were simulated. All simulations were done with the openCARP software [26], [27], from which the single-cell Luo-Rudy model published in 1991 designed for ventricular tissue was adopted [28]. The ion current conductances , and equal to the time-dependent potassium current, slow inward calcium current and fast sodium current were modified. The values of these parameters regulate the level of meandering of rotors and are illustrated in Table 4. The dimensions of the 2D square mesh were and the tissue was isotropic with a conductivity of , resulting in a conduction velocity of the electrical waves of . The default openCARP values were maintained for all remaining parameters in the Luo-Rudy model.
Fig. 2.
Illustration of 64 2D rotor simulations with various levels of fibrosis, meandering and noise (video).
To initiate all rotors, two pulses were generated. The first pulse P1 originated from one side of the tissue, after which a planar wave arises and propagates along the tissue. After the planar wave was stable, a second stimulus P2 with a duration of and amplitude of was applied to one-quarter of the mesh. The interaction between the resulting waves caused a rotor to form. The total simulation duration was and data was extracted for (between and ). It must be acknowledged that the standard rotor simulation already contained slight meandering.
The measured signal in simulated data is the transmembrane voltage , which indicates the potential differences between the membranes of cells. In practice, however, these currents are never measurable. The EGM signal provides an approximation to these potential differences by aggregating the transmembrane voltage fields of different neighbouring cells, which depends on the distance of the measuring tool to these cells. One method that calculates EGM signals from transmembrane voltages is called the recovery method, which calculates the transmembrane currents and utilises the following equation to determine the EGM [29]:
| (1) |
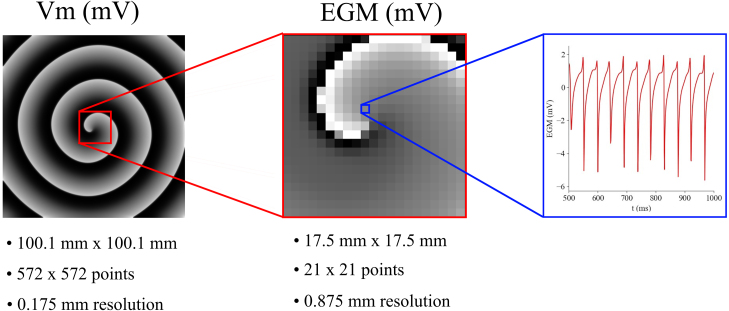
where and are the field and source positions and is the conductivity. In this paper, a 21 × 21 electrode grid of with an inter-electrode distance of was used for the 2D simulations (Fig. 1). EGMs with peak values lower than were discarded.
Fig. 1.
Illustration of how the electrogram (EGM) mesh is extracted from the original simulated transmembrane voltage () mesh.
2.1.1. Adding meandering
To increase the meandering of the rotor tip, modifications to the ion current conductances were employed, listed in Supplementary Table 4 in the Appendix. The concentration of ion currents lies at the foundation of the shape of the action potential. High values result in elevated excitability of the cardiac tissue, yielding a decreased radius of rotation and increased meandering (Kodama et al. [30]). Another procedure to stimulate meandering is by raising currents, leading to higher action potential duration and meandering (Panfilov et al. [30]). The potassium current conductance maintained a constant value of for all four meandering rotors, which is different from the default value of in the LuoRudy91 model. However, these linear relations between meandering, measured as root mean squared displacement (RMSD), and the currents were not always observed. This is illustrated in Table 4, as the RMSD occasionally decreases with increasing , in contrast to the reasoning explained before. As such, the rotors were sorted by increasing RMSD value to yield a steady increase in meandering. The meandering patterns and the RMSD values of the manually labelled rotor tip are displayed in Figure 11 in the Appendix.
2.1.2. Adding fibrosis
Fibrotic tissue consists of unexcitable cells called fibroblasts or scar tissue, which can affect wave propagation in the heart. In this paper, homogeneous fibrosis was mimicked by randomly sampling a percentage of the total amount of points and labelling these points as scar tissue in the simulation [31]. These percentages were chosen to be 0%, 10%, 20% and 30%, as in clinical cases of heart failure, values up to 43% have been recorded in the end stage of heart failure [32].
2.1.3. Adding noise
Once EGM signals were obtained from the simulated transmembrane voltages, Gaussian white noise was implemented. The standard deviation was assumed to be proportional to the maximum standard deviation of all the EGM signals. The rationale behind selecting the maximum value was to ensure that the noise in the EGM signals remains independent of the measurement location. The logarithmic signal-to-noise ratio was then defined as follows:
| (2) |
| (3) |
where and are the noise and maximal signal power. A amounts to equal power of signal and noise, and a to zero noise. With this in mind, four values for were chosen namely and . The noise was applied to the original EGM signals as follows:
| (4) |
2.2. Phase mapping
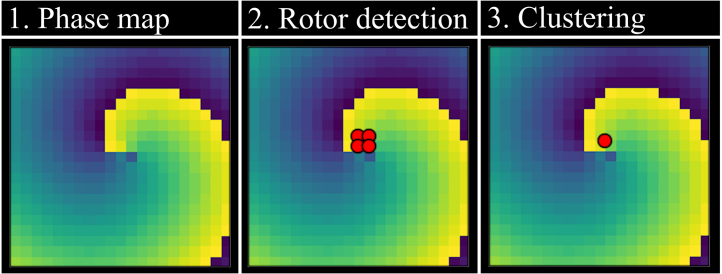
A phase map is a combination of phases of periodic signals on a grid. The PM workflow (Fig. 3) consists of the calculation of a phase map (Sawtooth or Hilbert), detection of rotor centres (2D convolution, 2D double loop method) and finishes with optional clustering (DBSCAN). In the following sections, the building blocks of 3 PM methods will be discussed. The combinations employed in this paper are shown in the following list (see Table 1):
Fig. 3.
Illustration of the PM workflow explained in Sections 2.2.1, 2.2.2, 2.2.3.
Table 1.
| Label | Phase map | Rotor detection | Clustering |
|---|---|---|---|
| PM1 | Sawtooth | 2D convolution | DBSCAN |
| PM2 | Hilbert transform | 2D convolution | DBSCAN |
| PM3 | Hilbert transform | Double loop | No clustering |
2.2.1. Phase maps: Sawtooth and Hilbert transform methods
The Sawtooth method
The Sawtooth method [21], [33] of calculating phases of signals takes only the local activation time (LAT) value of the signal into account. For EGM signals, LAT values are defined as the times when the temporal derivative of the unipolar EGM signal is minimal [34]. In the case of bipolar EGM signals, it is determined as the minimal bipolar EGM [34]. There are several methods to determine the LAT values of a unipolar EGM signal. One method uses a sliding window with a constant width to detect the minima of the bipolar EGM. A disadvantage of this method is that a certain regular time interval between peaks is assumed, which is not general, as rotors can vary in rotation frequency. Another approach selects a threshold value and determines the times when the signal crosses this value. This approach can be applied to rotors of different rotation frequencies but has the disadvantage that it is susceptible to noise. The impact of adding noise to the dataset (see Section 2.1.3 for more details) was analysed through visual analysis, comparing -scores, distance distributions and p-values for levels varying from 90 dB to 5 dB. Thus, the latter approach using peak detection with a sliding window of was implemented in this paper to yield the best results possible for the Sawtooth method.
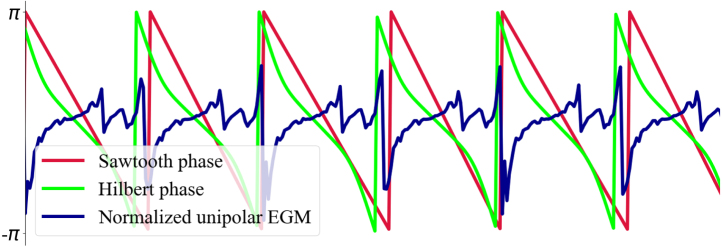
The phase of the signal between two consecutive LAT values is determined as a linear gradient from to , giving rise to the Sawtooth shape (red curve, Fig. 4). The calculation of for t values between consecutive LATs is described in the following equation:
| (5) |
The Sawtooth phase map parameter values are listed in Supplementary Table 5 in the Appendix.
Fig. 4.
Illustration of the Sawtooth and Hilbert transform phases obtained from a normalised unipolar EGM.
The Hilbert transform method
The Hilbert transform [35] is applied to real periodic signals , which can be written as a sum of positive and negative frequency components: . The Hilbert transform shifts the phase of the signal’s positive and negative frequency components by respectively and . It is mathematically defined as the principal value of the convolution of a time-dependent periodic signal with the Cauchy kernel :
| (6) |
The principal value is taken, as the Cauchy kernel is not integrable for . Any periodic signal can then be represented in its analytical form where only positive frequencies remain using the Hilbert transform as follows:
| (7) |
To obtain the phase (green curve, Fig. 4) from the analytical signal , the angle between the complex vector and the real axis is determined as follows:
| (8) |
where k is either 0 or 1 depending on which quadrant the complex vector resides in. In this paper, the following form with additional minus signs was adopted where the Hilbert transform is applied to the EGM signal:
| (9) |
This adjustment was made to ensure that the Sawtooth and Hilbert transform phases have similar shapes (Fig. 4).
Signal processing necessary to apply the Hilbert transform
To utilise the Hilbert transform, the EGM signals must undergo processing. The Hilbert transform yields valid results for clean, periodic signals, unlike the noisy EGM signals that comprise various frequencies. A slightly modified version of the signal processing method developed by Roney et al. [36] was adopted in this paper. This method was developed to detect rotor centres during AF and can detect rotors with diverse frequencies. Part of this method is based on Botteron’s approach [37].
The adjustments were implemented based on empirical observations. The first adjustment was made to the low pass filter which was set to 30 Hz instead of 10 Hz as rotor frequencies reached values up to 24 Hz, which would be filtered out when employing the default low pass value. Subsequently, the Cubic Hermite Spline modification was implemented. This modification was chosen because the resulting splines retain the tangent of the signal at its minima and maxima, taking into account the signal’s derivative. Moreover, the Cubic Hermite Spline modification demonstrated a slight performance improvement for PM2 and PM3, as evidenced by higher -scores compared to the Cubic Splines approach. All the Hilbert transform method parameter values are listed in Supplementary Table 5 in the Appendix.
2.2.2. Rotor detection: 2D convolution and double loop methods
PM rotor detection methods are based on the theoretical calculation of the integral of the phase gradient along an infinitesimal closed loop [38]. The points where the value of this contour integral is equal to , where the sign denotes the rotation direction, are defined as phase singularities [38]. The mathematical formulation of this problem is described as follows, where the topological charge denotes the normalised contour integral of the phase gradient:
| (10) |
In practice, the exact phase gradient is never calculable due to limited resolution; hence, a discrete approximation can be attempted. This approximation consists of adapting the contour integral to a summation along a set of points forming a closed loop and transforming continuous derivatives to discrete difference schemes. An important prerequisite is that all phase differences are restricted to the [] interval by transforming phase differences to their equal counterparts when required.
In this approximation, two parameters are relevant in determining the sensitivity and range of phase singularity detection. The first parameter that determines sensitivity is the threshold phase, which must be exceeded when summing all the phase differences along the closed loop. The second parameter is the loop size, which determines the detection range. Smaller loop sizes yield more accurate positional information but might fail to detect rotor centres due to resolution/noise effects. In the following sections two approaches to approximating Eq. (10) will be discussed.
The 2D convolution method
Following Bray et al. [38] Eq. (10) can be approximated in the case of regular 2D grids (where ) in the following way:
| (11) |
with the nabla 3 × 3 convolution kernels and a forward difference scheme for and analogously for . As a remark, the row index i corresponds to the coordinate and the column index j to the × coordinate. Eq. (11) is zero at points where is differentiable as the rotor of the gradient of any continuously twice-differentiable scalar field is zero. Phase singularities correspond to points where the phase is undefined, as multiple phases are in the infinitesimal neighbourhood of these points. At phase singularities will not be differentiable hence Eq. (11) will not equal zero. As a final remark, the matrix convolution combines the differentiation operation of the curl operator and the summation operation of the integral (Bray et al. [38]).
The exact value of might not be achieved in practice due to discretisation errors, hence a lower threshold value of for rotor detection is adopted in this paper. This threshold value determines the sensitivity of the detections. The 2D convolution method parameter values are listed in Table 5 in the Appendix.
The 2D double loop method
The 2D double loop method detects phase singularities by stating that phase singularities are accompanied by two loops that contain an odd number of positive or negative phase jumps. Phase jumps are defined as neighbouring pairs of nodes on a loop where the difference of phases of these pairs (in the clockwise direction) exceeds a threshold value. This threshold value (analogous to the topological charge threshold) determines the sensitivity of the detection algorithm, as lower threshold values give rise to more detections.
The 2D double loop method developed by Kuklik et al. [23] employs the concept of an odd number of phase jumps in addition to considering not one, but two loops. These loops are illustrated in Fig. 5. The advantage of this algorithm is that false phase singularities decline as both loops require the detection of an odd number of positive or negative phase jumps. This algorithm is thus resistant to noise to a certain extent, which will be illustrated in the results of this paper. Other loop shapes are discussed in Kuklik et al. [23] where the loop employed in this paper gave the most optimal result in a comparison study. The 2D double loop method parameters are listed in Supplementary Table 5 in the Appendix.
Fig. 5.
Illustration of the geometry of the rings used in the double loop method (Kuklik et al. [23]).
2.2.3. Clustering
If the detection range of the used algorithm is high or the mesh resolution is low, multiple phase singularities (PSs) can be detected. In this case, it proves useful to cluster multiple PSs together and classify PSs that are not part of a cluster as noise points to be discarded. This procedure can be done using the DBSCAN algorithm, where points are classified as either core points, border points or noise points (Li et al. [39]). The two essential parameters of DBSCAN are the neighbourhood radius and the minimal number of samples min_samples that must be in the neighbourhood of a point for it to be classified as a core point. The DBSCAN parameters are listed in Supplementary Table 6 in the Appendix.
2.3. Directed graph mapping
DGM is a novel mapping technique developed by Vandersickel et al. [21] that utilises network theory to construct a directed graph of cardiac activation patterns from measured LAT values in any geometrical setting. Nodes with similar LAT values are connected in the direction of the conduction velocity. This network can then be searched using cycle-finding algorithms in network theory to determine where anatomical re-entry and rotors are present. The algorithm is outlined briefly in the following steps:
-
1.
The LAT values and spatial coordinates of each node serve as input for DGM. In this paper, LAT values derived from both clean and noisy EGM signals were acquired using an approach akin to the Sawtooth method (Section 2.2.1).
-
2.Four graph-building steps are done:
-
(a)Neighbouring nodes are connected (undirected edge) based on a maximal distance threshold value .
-
(b)Connections between nodes where absolute LAT differences exceed are discarded.
-
(c)For each point and its neighbour, the spatial distance between these points is divided by the difference in LAT values , yielding a conduction velocity . A lower bound and upper bound are selected depending on the problem at hand. If the calculated CV falls in the interval , the connection is retained and a directed arrow (directed edge) is drawn between the node and its neighbour, from lower to higher LAT. All connections with CVs outside of this interval are discarded. This process is repeated to create a full network for each time step of the input data.
-
(d)Graphs that are a time distance apart are merged to yield a more connected graph; all graphs in the interval are merged pairwise to form a new graph at time .
-
(a)
-
3.
Directed cycles are identified by Dijkstra’s shortest path algorithm, which explores neighbouring nodes from a starting node in the network. This process is then repeated for each neighbouring node until all nodes are searched. Directed cycles through node are found by taking the shortest path between node and its nearest neighbour B for which a directed arrow from to is present.
-
4.
Directed cycles are reduced to their cycle centres by calculating the mean of the starting positions of all arrows.
-
5.
Cycle centres are clustered using the DBSCAN algorithm.
The DGM parameter values are listed in Supplementary Table 6 in the Appendix. The optimal parameter set was obtained using parameter sensitivity to -scores shown in Figure 12 in the Appendix.
2.4. Performance comparison between PM and DGM
The following sections contain four strategies for comparing the quality of the detected rotors of the three PM methods and DGM compared to the true rotor tip. The true rotor tip was manually labelled for 16 of the 64 simulations (as the four noise levels do not influence the rotor tip position). This was performed for yielding labelled rotor tips for each of the 64 simulations. Times ranging from to were neglected to avoid the last incomplete rotation, as for all rotors the maximal duration of a full rotation did not exceed .
2.4.1. Visual analysis
The EGM signal of the simulations is presented along with the detected and true rotor tips of all four methods (PM1, PM2, PM3 and DGM). A single time frame is illustrated and a video is provided showing the full simulation duration. This illustration and video serve as a qualitative performance measure, as an excess or absence of detections indicates unsatisfactory performance. Effective methods should only detect one rotor tip for each time frame in the simulation at the correct location, as only one rotor is present. More quantitative measures of performance are discussed further.
2.4.2. Performance metrics
The values of true and false positives, and true and false negatives (TP, FP, TN, FN) of the confusion matrix were calculated for the duration of the simulation. First, a neighbourhood radius was selected to be considering that catheter ablation usually creates a lesion size from to (Li et al. [39]). The classification of points on the mesh and detected rotors is illustrated in Table 2:
Table 2.
Table showing the rules for determining confusion matrix values resulting from the classification of mesh points and detected rotors.
| TP | For every true rotor with a detected rotor in its neighbourhood |
| FP | For every extra detected rotor in the neighbourhood of a true rotor |
| for every detected rotor without a true rotor in its neighbourhood | |
| FN | For every true rotor without a detected rotor in its neighbourhood |
| TN | For every mesh point outside every true rotor neighbourhood that is not a detected rotor |
Using these confusion matrix values, the precision, recall and -score were determined. The precision equals the fraction of detected rotors that are true rotors and is related to the location of the true rotor. Recall determines the fraction of true rotors that are detected and is related to whether a rotor exists or not. Recall is the more important quantity in a medical context; the knowledge of the existence of a disease is more important than its exact location. The -score determines a weighted sum of precision and recall, where recall has times more weight than precision. In this way, a was chosen to give twice as much importance to recall than precision [39]. These quantities were calculated as follows:
| (12) |
| (13) |
| (14) |
2.4.3. Distance from true tip
The Euclidean distance between the true rotor and calculated rotor was calculated to serve as a performance metric. In case rotors are detected, all distances are calculated:
| (15) |
These distances were plotted in violin plots for both PM and DGM for all 64 rotor simulations. The third quantile of this distribution signifies the distance value above which 25% of the distribution resides. This value serves as an indication of performance, as high values of indicate poor performance. High values exceeding a threshold value imply that 25% or more of the rotor detections are further away from the true rotor tip than the threshold value.
2.4.4. mid-p McNemar test
The mid-p McNemar test [40] was incorporated to assess significant differences in performance between PM and DGM. This test is based on a contingency table generated from instances where either one or both methods are correct or false (Table 3). A method is deemed correct for each time frame if it produces 1 TP, 0 FN, and 0 FP, given the consistent presence of exclusively one rotor in all simulations. TN values were excluded due to their dependence on the simulation and the rotor’s proximity to the mesh edge. The mid-p-value was computed from discordant pairs and utilising the binomial probability density function and cumulative distribution for :
| (16) |
Traditional statistical tests such as t-tests or ANOVA were not conducted due to their assumptions of Gaussian distributions. The results, consisting of -scores ranging between 0 and 1, do not adhere to a normal distribution. Moreover, the distance distributions exhibit non-normal characteristics, evident from their long-tailed behaviour.
Table 3.
Table showing the contingency table comparing DGM and PM. The values a, b, c and d count the number of time frames in the simulation where either one or both methods are correct or false.
| DGM incorrect | DGM correct | |
|---|---|---|
| PM incorrect | ||
| PM correct |
3. Results
The performance of PM1, PM2 and PM3 is compared with DGM for the 64 different simulations encompassing rotors with various levels of meandering fibrosis and noise. The following sections contain the results including (3.1) the visualisations of the rotor detections (Fig. 7), (3.2) the -scores (Fig. 8, Table 9), (3.3) the violin plots (Fig. 9) showing the distribution of distances between detected and true rotor tips and (3.4) the mid-p McNemar test (Fig. 10). The results for precision (Figure 13, Table 7) and recall (Figure 14, Table 8) are illustrated and discussed in the Appendix. As a reminder, the PM methods can be found in Table 1.
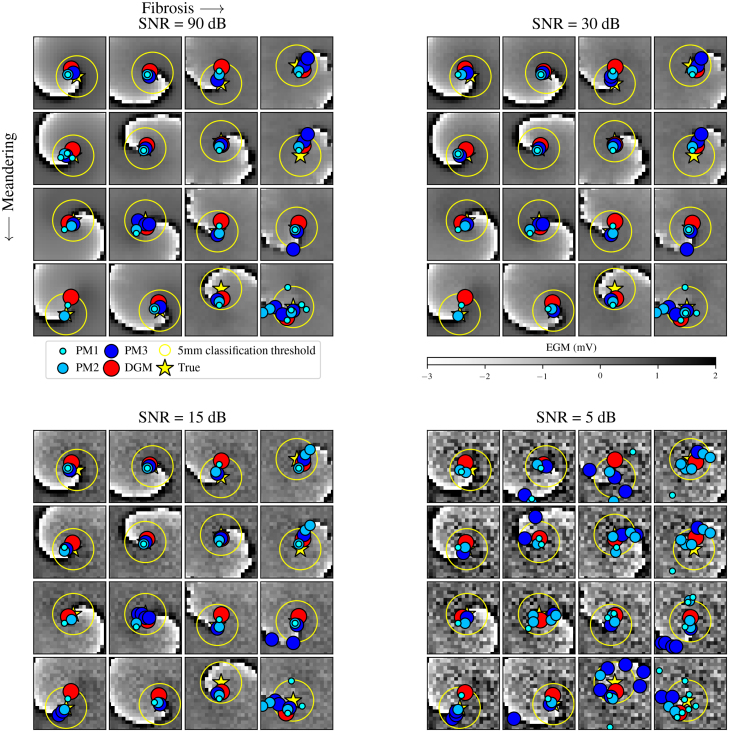
Fig. 7.
Illustration of a single time frame of the 64 simulations depicting the EGM values in greyscale, the detected rotors for the four rotor detection methods (blue and red) in addition to the manually labelled true rotor tip (yellow) along with the classification threshold (video).
Fig. 8.
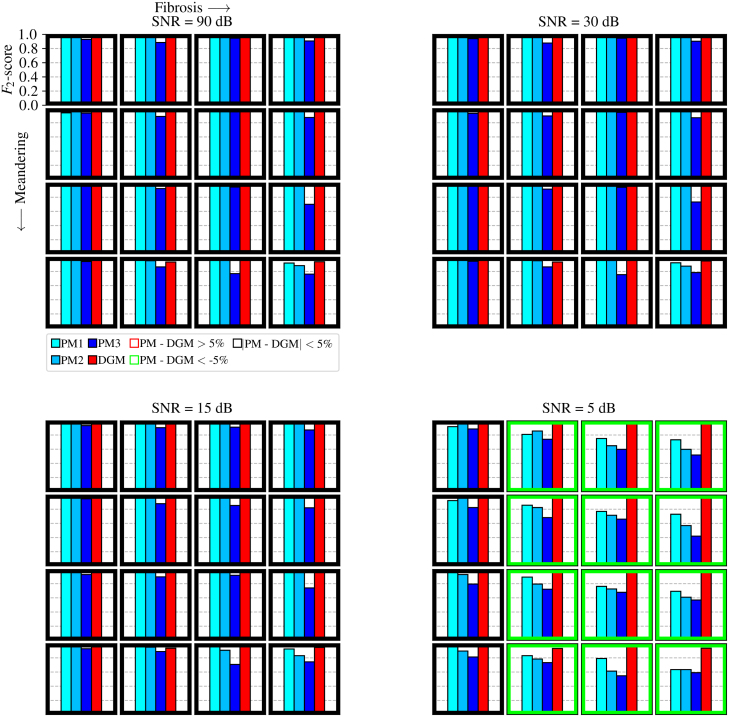
Illustration of the -score values for the full duration of all 64 simulations for the four rotor detection methods. The coloured squares around each plot signify if the best PM method is better than, equal to or worse than DGM (red, black, green respectively) where a threshold of 5% is employed.
Fig. 9.
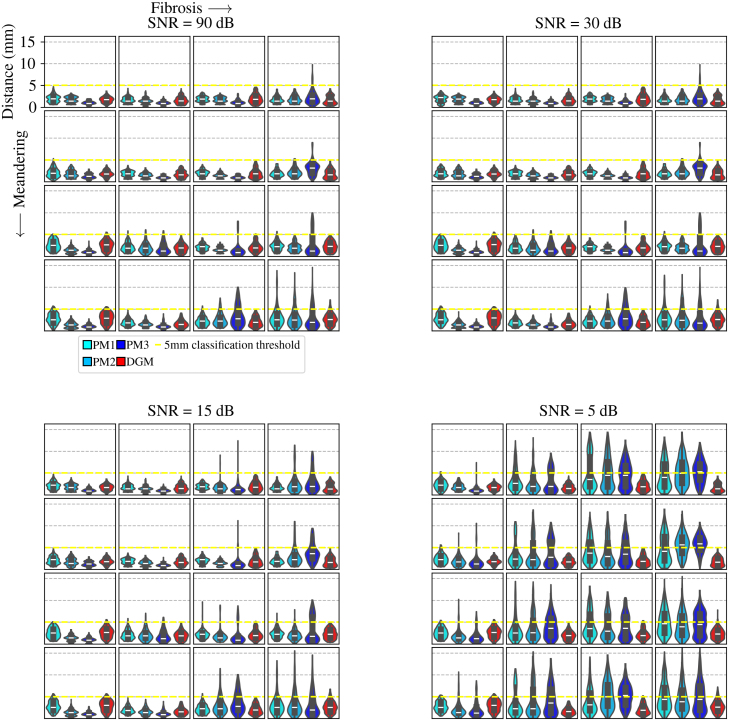
Illustration of the violin plots showing the distribution of distances between detected rotors and true rotors for the full simulation duration. Additionally, the classification threshold is shown as a dashed yellow line.
Fig. 10.
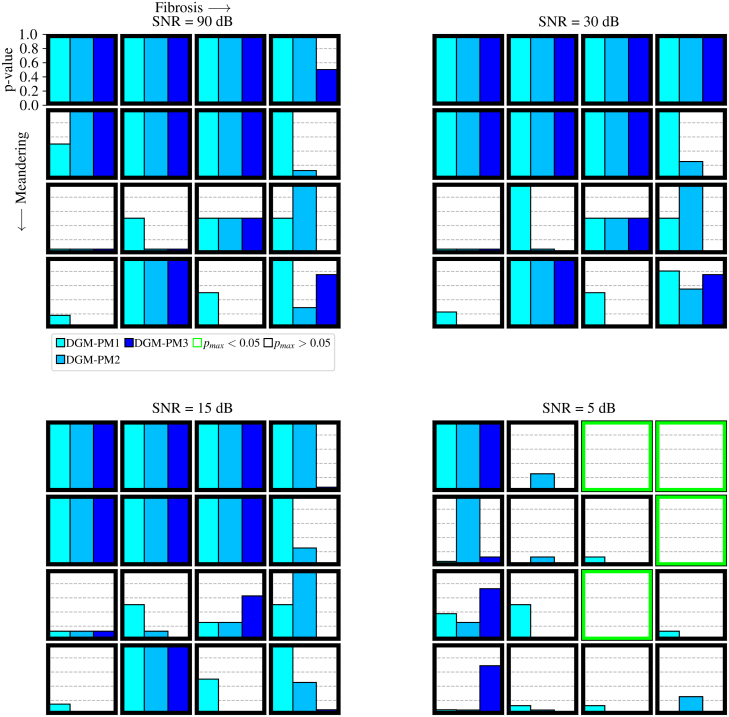
Illustration of the mid-p McNemar test comparing DGM and PM1, PM2, PM3. If the -value is smaller than 0.05 (green square), the null hypothesis (DGM and are comparable) should be rejected.
3.1. Rotor detection visualisations
Fig. 7 demonstrates a snapshot at of all simulations where the detections of each method in addition to the EGM signals of the rotors are visible. The panels separate the various levels of noise. Each panel contains 16 simulations of rotors where meandering increases from the top to the bottom row and fibrosis increases from the left to the right column. This figure contains detections of every method tested (PM1, PM2, PM3 and DGM) as coloured circles with various sizes on top of the true tip marked with a yellow star. Additionally, the classification threshold radius of around the true tip is included. Immediately noticeable is the amount of false positives (FPs) present in the bottom right panel, representing the noisiest rotors. This is reflected in low precision resulting in low -scores and suggests that PM is highly sensitive to noise. In particular, PM3 seems to suffer the most from FPs. This indicates that the double loop method is more sensitive to noise than the convolution method for rotor detection. Other problems with the PM methods are reflected in False Negatives (FNs). On the top left panel illustrating rotors, the bottom row and the first column, an absence of PM3 detections is observed. These FNs will be reflected in lower recall scores and thus lower scores in later results. Furthermore, the robustness of DGM is prevalent across all 64 simulations. DGM detections appear unaffected when comparing the influence of noise across all four panels. The video shows that these observations are not restricted to the single snapshot depicted in Fig. 7 but are present across the full duration of the simulation. The video illustrates that one of the rotors (row 4, column 2) meanders outside the extracted EGM grid. This complication was averted by restricting data extraction to time frames before this event.
3.2. -score
Fig. 8 illustrates four bars per simulation where the bar height signifies the value of the -score for all four methods (PM1, PM2, PM3 and DGM). The figure again consists of four panels signifying the different noise levels, with meandering and fibrosis increasing for different rows and columns respectively. Furthermore, the figure highlights the simulations where the best PM method is either better than, equal to or worse than DGM, depicting a red, black and green square border respectively. In this classification, a threshold of 5% was employed (e.g. if for a particular simulation, the -score of the best PM method was 0.05 higher than DGM, this simulation would have a red border). A remarkable observation is that there are no red borders across all 64 simulations, meaning PM does not exceed the performance of DGM by more than 5%. Furthermore, the -score value of DGM appears unaffected across all 64 simulations and does not drop below the value of 0.931 (see Supplementary Table 9). This is in contrast to the PM methods, which all seem to be sensitive to the noise gradient as is observed in panel four containing the rotors. The best-performing PM method (PM1) obtains an -score value above 0.635 for all 64 simulations. Additionally, a performance drop is visible for PM3 for increasing fibrosis and to a lesser extent for PM1 and PM2. This indicates that the convolution method is more robust against these factors than the double loop method for rotor detection. The exact values of the -score are listed in Supplementary Table 9.
3.3. Distribution of distance between detected and true rotor tip
Fig. 9 presents violin plots, which are combinations of box plots and kernel density estimate (KDE) plots. These violin plots repeat the same structure as the previous figures and depict the distribution of the Euclidean distances between the detected and true rotor spatial positions for all four methods (PM1, PM2, PM3 and DGM). Additionally, the classification threshold represented by a dashed yellow line is included. The figure illustrates the effects of meandering, fibrosis and noise on the distance distribution. In the top left panel containing rotors, the effect of increasing meandering and fibrosis has a clear effect on the shape of the violin plot for all four methods, but most significantly for PM methods. This effect is most prevalent in the rotor located at row 4, column 4. The tails of the PM distributions elongate as fibrosis and meandering increase, signifying that more detections are located at further distances from the true tip, indicative of low precision. These effects are more pronounced as noise is increased, which is observed most clearly in the bottom right panel containing rotors with . In this panel, the PM distribution tails are significantly longer than the DGM distribution tail. In addition to this, for PM1, PM2 and PM3, the third quantile (25% of the distribution lies above ) exceeds the classification threshold in 9, 11 and 18 out of 64 simulations respectively. This is in contrast to DGM violin plots, where exceeds the classification threshold for 0 out of 64 simulations.
3.4. mid-p McNemar test
The results in Fig. 10 indicate significant differences between DGM and PM, especially in high noise scenarios, with some variations noticeable even at lower noise levels. Notably, comparisons between DGM and specific PM variants (e.g., PM2 and PM3) reveal performance distinctions that may be attributed to the use of different phase maps. PM1 employs the sawtooth phase map, assuming a predefined static rotation frequency, while PM2 and PM3 utilise the Hilbert phase map, automatically detecting the rotation frequency, potentially rendering them more error-prone. The influence of meandering and fibrosis on p-values remains somewhat unclear. While there is a general trend of decreasing p-values with increasing fibrosis and meandering, suggesting stronger performance differences between DGM and PM, this trend does not consistently hold. The effect of fibrosis and meandering on performance differences appears to be smaller than that of noise. An inverse correlation between p-values and -score differences is observed in general: smaller p-values tend to accompany larger -score differences. However, it is essential to interpret p-values cautiously as they are highly dependent on sample sizes. The statistical significance test aligns with the comparison of -scores and distance distributions. These observations highlight the substantial impact of meandering, fibrosis, and noise on PM performance, whereas DGM remains comparatively unaffected.
4. Discussion
In this study, the differences between three versions of PM and DGM have been highlighted by systematically exploring the impact of noise, meandering and fibrosis in 64 different combinations. Especially the effect of fibrosis on PM has received limited attention in previous research. Furthermore, three distinct methods of PM have been examined. In addition to PM1 (using the Sawtooth method with 2D convolution and clustering), more sophisticated techniques such as PM2 (utilising the Hilbert transform with 2D convolution and clustering) and PM3 (employing the Hilbert transform with double-loop rotor detection) were explored. While PM remains a standard in analysing simulations, the findings of this paper reveal inherent limitations.
The following sections discuss the relation of this research to the previous studies done. Furthermore, the main findings are discussed, and an explanation for the differences observed between DGM and PM is provided. Finally, the limitations of this paper are acknowledged.
4.1. Relation to previous studies
In previous work by Vandersickel et al. [21] a comparative analysis of DGM and PM1 (Sawtooth phase map) performance was conducted on a stable rotor with 256 electrodes. This investigation included the presence of Gaussian white noise with a progressively increasing standard deviation on the LATs (ranging from 0 to 30 ms). The findings indicated that DGM exhibited lower sensitivity to noise. Subsequently, in Martinez et al. [17], basket catheter ECG measurements of a meandering rotor in the left atrium revealed numerous false positive detections by PM. This PM version will be referred to as PM4. In Van Nieuwenhuyse et al. [41], it was demonstrated that DGM outperformed PM4 in this dataset for the distinction of true positives from false positives, resulting in higher precision. However, in the current study, more sophisticated versions than PM4 were implemented, namely PM1, PM2 and PM3, for a fairer comparison with DGM.
The following paragraph elucidates the difference between PM4 from Van Nieuwenhuyse et al. [41] and the PM methods adopted in this paper. Firstly, the phase map of PM4 is calculated merely using a bandpass of 7–10 Hz on the extracted EGMs after which the phase is calculated using the Hilbert Transform. This differs from PM2 and PM3, which employ a more sophisticated algorithm to determine the phase of a signal. Secondly, PM4 merely takes into account the vertices of each triangle in the mesh for calculating phase singularities. The sum of the phase differences is then calculated for each triangle, which is used to calculate phase singularities. This is in contrast to the PM methods of this paper, as both the matrix convolution approach developed by Bray et al. (PM1, PM2) and the double loop method developed by Kuklik et al. (PM3) [23] are explored. These methods have larger loops, allowing for a broader detection range. Additionally, false positive detections are reduced due to multiple loops present in the PM3 algorithm (Kuklik et al.). Lastly, PM4 has no clustering, which allows additional false positive detections to affect the performance of PM4. This is in contrast to PM1 and PM2 from this study, which employ DBSCAN to cluster rotors detected from PM.
Furthermore, this paper exhibits significant differences from Li et al. [39]. In the study by Li et al. four different PM methods were compared on data from patients undergoing persistent ablation. The methods included a 2D image processing-based and neighbour-indexing algorithm, a 3D neighbour-indexing algorithm, a 2D kernel convolutional algorithm estimating topological charge (similar to PM2), and a topological charge estimation on a 3D mesh. The data collection involved a non-contact MEA catheter with 64 electrodes, and the EnSite system was utilised to estimate potentials on the endocardium. Notably, in Li et al. the ground truth was absent, as data was collected from patients experiencing atrial fibrillation, and rotors were manually annotated through visual inspection. In contrast, this paper explores simulated data with known ground truth. Additionally, Li et al. did not thoroughly investigate the impact of meandering, fibrosis, and noise on rotors, nor did they categorise rotors based on these factors.
4.2. Main findings
The following paragraph discusses the results in Section 3 and the Appendix. The results indicate that PM methods generate many FPs compared to DGM at elevated meandering, fibrosis and noise levels as can be observed in Fig. 7. This performance difference is reflected in the precision and -score illustrated in Figures 13, 8 and Supplementary Tables 7,9. The distance distributions are largely in favour of DGM for heightened levels of meandering, fibrosis and noise, as the tails of PM methods extend further than DGM, which can be inferred from Fig. 9. This suggests that the percentage of detections within the neighbourhood () of the true rotors in these regimes is considerably larger for DGM than PM in strong meandering, fibrosis and noise conditions. Additionally, significant performance differences for noisy rotors are reflected in low p-values obtained from the McNemar test shown in Fig. 10 in the Appendix. Nevertheless, this performance discrepancy is imperceptible at low levels of meandering, fibrosis, and noise, as indicated by the aforementioned figures and tables. Of all the PM methods, PM1 appears most robust against fibrosis, noise and meandering as the score reaches a minimal value of 0.635 across all 64 simulations as compared to PM2 and PM3 that reach minimal values of 0.568 and 0.420 respectively. This can be clarified by the constant peak detection window of the Sawtooth phase map algorithm of PM1 whereas PM2 and PM3 use automatic peak detection windows, rendering them more error-prone in high fibrosis, noise and meandering conditions. This suggests that adopting a simple Sawtooth phase map might be more beneficial in cases where rotor frequencies are available. However, in cases where rotors vary significantly in frequency, the PM2 and PM3 methods are expected to outperform PM1. Although PM1 begins with the same input as DGM (LAT values), DGM outperforms it significantly. This is especially noticeable for the simulation with , 30% fibrosis and level 4 meandering on Fig. 8 and Table 9 (row 8, column 8). A possible underlying reason is that DGM utilises LAT values globally, in contrast to the local character of PM1. This suggests that DGM could serve as a valuable complement to various PM methods for phase singularity detection as both local and global sensitivity can be of importance.
4.3. Understanding the difference between PM and DGM
DGM is more robust against data that is predominantly polluted by noise, as it attempts to retrieve all possible cycles in its network generated from the mesh. In contrast, PM has a limited detection range and thus neglects certain rotational activity in cases of highly noisy data. To elaborate on this further, the detection range and sensitivity of both methods can be considered. DGM automatically detects all possible loops of any shape or length in a network using Dijkstra’s shortest path algorithm, allowing for both short and long-range detection depending on which loop size is desired. This is in contrast to PM, where a single predefined loop size is chosen (kernel in PM1, PM2 and loop size or shape in PM3) and convoluted or slid across the mesh. The sensitivity of detections of DGM is reflected in the neighbourhood radius, the limitation of the conduction velocities to a specific range , in addition to the parameter, all of which influence the connectivity of the network. In contrast, PM utilises the topological charge threshold (PM1, PM2) or phase jump threshold (PM3) as a sensitivity parameter. In this sense, DGM can be interpreted as a more robust version of PM as all possible loop shapes and sizes are attempted in its detection algorithm. Furthermore, it was observed that the clusters of detections of DGM appeared more concentrated than those of PM methods. DGM clusters easily exceeded 200 detections for elementary rotors (Fig. 6) while PM clusters contained a significantly smaller amount of detections as low as three or four for PM1 and PM2 and one for PM3, which is why no clustering was performed for PM3. This resulted in larger optimal min_samples values for DGM than PM (Tables 6 and 7). Herein lies the great strength of DGM as it detects a single big coherent cluster whereas PM detects a plethora of incoherent tiny clusters. This results in an excess of FPs produced by PM as compared to DGM. In contrast, PM seems to be more precise for low values of meandering, fibrosis and noise as can be inferred from Fig. 7, Fig. 9. This can be attributed to the more local (more precise) detection range of PM compared to the high (less precise) detection range of DGM. However, as most DGM detections reside under the threshold, these performance differences are believed to be of negligible value.
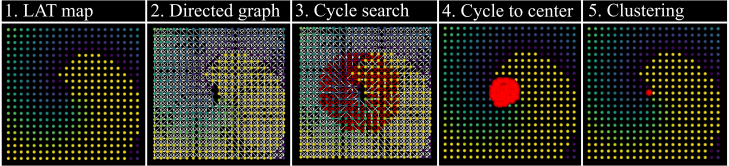
Fig. 6.
Illustration of the DGM workflow for rotor centre detection.
Given the small EGM grid size in the 64 simulations, methods like DGM, which appear to consistently detect a single rotor at the mesh center (Fig. 7), could arguably yield reliable results, as the classification threshold encompasses a significant portion (25%) of the mesh. It might be the case that the detection is not truly tracking the rotor tip, even though the detection is inside the classification circle of the true tip. However, this can be disproven by observing the results for high-meandering rotors. These rotors require precise detections to attain large values. In this sense, it is certain that DGM precisely detects highly meandering rotor tips, which can is clearly illustrated in the video and is reflected in high precision (Figure 13, Table 7) and -scores (Fig. 8, Table 9) for DGM.
4.4. Beyond computational studies
In this paper, all methods were exclusively applied to simulated rotors. Conducting a similar study for clinically or experimentally observed rotors poses a challenge due to the absence of ground truth data, shifting the interest of most studies investigating PM to simulations. However, the potential for such investigations exists if rotors could be recorded with high-resolution optical mapping methods and subsequently analysed by the approach proposed in this paper. Such studies are envisioned to be conducted in the future, particularly focusing on optical mapping data related to ventricular fibrillation. Notably, DGM has already been employed in clinical scenarios to analyse atrial tachycardia. Previous works [21], [24] showcase DGM’s proficiency in identifying anatomical and localised re-entry in complex atrial tachycardia cases. Similarly, positive outcomes were observed in ventricular tachycardia analysis [25]. In contrast, PM has limited application in the analysis of atrial and ventricular tachycardia, as its utility is primarily geared towards rotors (functional re-entry), as opposed to anatomical re-entry.
4.5. Limitations
-
•
All parameters of PM were manually optimised using trial and error starting from an optimal parameter set obtained from Li et al. [39] for overlapping PM algorithms adopted in both this and their research. A more detailed comparison study could have been conducted using cross-validation for parameter tuning, as was done in Li et al. [39]. However, this would have proven very computationally expensive, as PM methods contain five, ten, and ten parameters for PM1, PM2, and PM3, respectively (Table 5). Despite this complication, a rudimentary parameter optimisation strategy for DGM was performed as discussed in the Appendix and shown in Figure 12.
-
•
The effect of spatial resolution of the EGM electrodes was not investigated. The resolution was kept at a constant value of for the × EGM grid.
-
•
Since there are limited clinical cases containing clear rotors from which the ground truth is known, the data set is restricted to simulations and no real-world clinical cases are tested. Clear clinical cases, such as atrial tachycardia, contain anatomical and/or localised re-entry.
-
•
No 3D simulations were performed. However, the detection of simple rotors on a 3D curved mesh is locally equivalent to detecting rotors on a 2D mesh.
-
•
No analysis of computational time was conducted, although it is a crucial factor to consider when comparing models. It was observed that DGM computations were longer than those of PM methods.
-
•
For this paper, cycles were reduced to their centres to calculate the performance metrics of PM and DGM similarly. Utilising cycle centres was crucial for calculating the distance to the true tip, a key component in deriving -scores. However, it is important to acknowledge the potential limitations of this approach. Specifically, two cycle centres originating from completely different cycles might coincidentally be clustered together. Considering this, clustering cycles instead of cycle centres during rotor detections could offer a more informative perspective. It is worth mentioning that the authors of this paper are actively developing tools for cycle clustering. These tools, once completed, could prove valuable in addressing these challenges and further enhancing the robustness of the DGM methodology in future applications.
5. Conclusion
In conclusion, at low values of meandering, fibrosis and noise, PM and DGM are both comparable and show excellent performance for the detection of simulated 2D rotors. This is observed visually and reflected in high values, distance distributions that are below a threshold of and low p-values. However, PM methods undeniably suffer from false positives for increasing meandering, fibrosis and noise for simple 2D rotor simulations resulting in low precision and -scores dropping as low as 0.635 for the highest scoring PM method (PM1). This is in contrast to DGM, which delivers consistently high for all 64 2D rotor simulations with various amounts of meandering, fibrosis and noise. This suggests that DGM could serve as a valuable complement to PM for phase singularity detection. Furthermore, combining these methods can enhance the overall confidence in analysing phase singularities across diverse datasets. Therefore, using the combination of PM and DGM is advised to gain a more insightful perspective.
CRediT authorship contribution statement
Sebastiaan Lootens: Writing – review & editing, Writing – original draft, Visualization, Validation, Software, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Iris Janssens: Data curation. Robin Van Den Abeele: Writing – review & editing, Supervision. Eike M. Wülfers: Supervision. Arthur Santos Bezerra: Supervision. Bjorn Verstraeten: Validation. Sander Hendrickx: Software. Arstanbek Okenov: Software. Timur Nezlobinsky: Software. Alexander V. Panfilov: Writing – review & editing, Validation, Supervision, Resources, Methodology, Funding acquisition. Nele Vandersickel: Writing – review & editing, Validation, Supervision, Software, Resources, Project administration, Methodology, Funding acquisition.
Declaration of Generative AI and AI-assisted technologies in the writing process
During the preparation of this work, the authors used ChatGPT in order to enhance the readability of this work. After using this tool, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.
Declaration of competing interest
None Declared.
Acknowledgments
Funding
This research was supported by a ‘Starting Grant’ from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant No. 900008), awarded to Nele Vandersickel.
A.V. Panfilov’s research at Sechenov University was financed by the Ministry of Science and Higher Education of the Russian Federation within the framework of state support for the creation and development of World-Class Research Centers “Digital Biodesign and personalised healthcare” (Grant No 075-15-2022-304).
Footnotes
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.compbiomed.2024.108138.
Appendix A. Supplementary data
The following is the Supplementary material related to this article.
The Appendix details simulation and method parameters, while performance metrics results are visually presented, discussed, and listed in tables.
References
- 1.Lin Y.-J., Lo M.-T., Chang S.-L., Lo L.-W., Hu Y.-F., Chao T.-F., Chung F.-P., Liao J.-N., Lin C.-Y., Kuo H.-Y., et al. Benefits of atrial substrate modification guided by electrogram similarity and phase mapping techniques to eliminate rotors and focal sources versus conventional defragmentation in persistent atrial fibrillation. JACC: Clin. Electrophysiol. 2016;2(6):667–678. doi: 10.1016/j.jacep.2016.08.005. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 2.Calvo D., Rubín J., Pérez D., Morís C. Ablation of rotor domains effectively modulates dynamics of human: long-standing persistent atrial fibrillation. Circ.: Arrhythm. Electrophysiol. 2017;10(12) doi: 10.1161/circep.117.005740. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 3.Morgan R., Colman M.A., Chubb H., Seemann G., Aslanidi O.V. Slow conduction in the border zones of patchy fibrosis stabilizes the drivers for atrial fibrillation: insights from multi-scale human atrial modeling. Front. Physiol. 2016;7:474. doi: 10.3389/fphys.2016.00474. [Online]. Available: [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Vigmond E., Pashaei A., Amraoui S., Cochet H., Hassaguerre M. Percolation as a mechanism to explain atrial fractionated electrograms and reentry in a fibrosis model based on imaging data. Heart Rhythm. 2016 doi: 10.1016/j.hrthm.2016.03.019. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 5.Zahid S., Cochet H., Boyle P.M., Schwarz E.L., Whyte K.N., Vigmond E.J., Dubois R., Hocini M., Haïssaguerre M., Jaïs P., Trayanova N.A. Patient-derived models link reentrant driver localization in atrial fibrillation to fibrosis spatial pattern. Cardiovasc. Res. 2016 doi: 10.1093/cvr/cvw073. [Online]. Available: [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sánchez J., Nothstein M., Unger L., Saiz J., Trénor B., Dössel O., Loewe A. Influence of fibrotic tissue arrangement on intracardiac electrograms during persistent atrial fibrillation. 2019 Computing in Cardiology; CinC; IEEE; 2019. pp. 1–4. [Online]. Available: [DOI] [Google Scholar]
- 7.Sim I., Razeghi O., Karim R., Chubb H., Whitaker J., O’Neill L., Mukherjee R.K., Roney C.H., Razavi R., Wright M., et al. Reproducibility of atrial fibrosis assessment using CMR imaging and an open source platform. JACC: Cardiovasc. Imaging. 2019;12(10):2076–2077. doi: 10.1016/j.jcmg.2019.03.027. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 8.Kircher S., Arya A., Altmann D., Rolf S., Bollmann A., Sommer P., Dagres N., Richter S., Breithardt O.-A., Dinov B., et al. Individually tailored vs. standardized substrate modification during radiofrequency catheter ablation for atrial fibrillation: a randomized study. Ep Eur. 2018;20(11):1766–1775. doi: 10.1093/europace/eux310. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 9.Chen J., Arentz T., Cochet H., Müller-Edenborn B., Kim S., Moreno-Weidmann Z., Minners J., Kohl P., Lehrmann H., Allgeier J., et al. Extent and spatial distribution of left atrial arrhythmogenic sites, late gadolinium enhancement at magnetic resonance imaging, and low-voltage areas in patients with persistent atrial fibrillation: comparison of imaging vs. electrical parameters of fibrosis and arrhythmogenesis. EP Eur. 2019;21(10):1484–1493. doi: 10.1093/europace/euz159. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 10.Zhao Y., Dagher L., Huang C., Miller P., Marrouche N.F. Cardiac MRI to manage atrial fibrillation. Arrhythm. Electrophysiol. Rev. 2020;9(4):189. doi: 10.15420/aer.2020.21. [Online]. Available: [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sánchez J., Luongo G., Nothstein M., Unger L.A., Saiz J., Trenor B., Luik A., Dössel O., Loewe A. Using machine learning to characterize atrial fibrotic substrate from intracardiac signals with a hybrid in silico and in vivo dataset. Front. Physiol. 2021;12 doi: 10.3389/fphys.2021.699291. [Online]. Available: [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Haissaguerre M., Shah A.J., Cochet H., Hocini M., Dubois R., Efimov I., Vigmond E., Bernus O., Trayanova N. Intermittent drivers anchoring to structural heterogeneities as a major pathophysiological mechanism of human persistent atrial fibrillation. J. Physiol. 2016;594(9):2387–2398. doi: 10.1113/jp270617. [Online]. Available: [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Winfree A.T. Varieties of spiral wave behavior: An experimentalist’s approach to the theory of excitable media. Chaos. 1991;1(3):303–334. doi: 10.1063/1.165844. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 14.Gray R.A., Pertsov A.M., Jalife J. Spatial and temporal organization during cardiac fibrillation. Nature. 1998;392(6671):75. doi: 10.1038/32164. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 15.Vijayakumar R., Vasireddi S.K., Cuculich P.S., Faddis M.N., Rudy Y. Methodology considerations in phase mapping of human cardiac arrhythmias. Circ.: Arrhythm. Electrophysiol. 2016;9(11) doi: 10.1161/circep.116.004409. [Online]. Available: [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Roney C.H., Cantwell C.D., Bayer J.D., Qureshi N.A., Lim P.B., Tweedy J.H., Kanagaratnam P., Peters N.S., Vigmond E.J., Ng F.S. Spatial resolution requirements for accurate identification of drivers of atrial fibrillation. Circ.: Arrhythm. Electrophysiol. 2017;10(5) doi: 10.1161/CIRCEP.116.004899. [Online]. Available: [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Martinez-Mateu L., Romero L., Ferrer-Albero A., Sebastian R., Matas J.F.R., Jalife J., Berenfeld O., Saiz J. Factors affecting basket catheter detection of real and phantom rotors in the atria: A computational study. PLoS Comput. Biol. 2018;14(3) doi: 10.1371/journal.pcbi.1006017. [Online]. Available: [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Almeida T.P., Nothstein M., Li X., Masè M., Ravelli F., Soriano D.C., Bezerra A.S., Schlindwein F.S., Yoneyama T., Dössel O., et al. 2020 Computing in Cardiology. IEEE; 2020. Phase singularities in a cardiac patch model with a non-conductive fibrotic area during atrial fibrillation; pp. 1–4. [Online]. Available: [DOI] [Google Scholar]
- 19.Jacquemet V. A statistical model of false negative and false positive detection of phase singularities. Chaos. 2017;27(10) doi: 10.1063/1.4999939. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 20.Jacquemet V. Phase singularity detection through phase map interpolation: Theory, advantages and limitations. Comput. Biol. Med. 2018;102:381–389. doi: 10.1016/j.compbiomed.2018.07.014. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 21.Vandersickel N., Nieuwenhuyse E.V., Cleemput N.V., Goedgebeur J., Haddad M.E., Neve J.D., Demolder A., Strisciuglio T., Duytschaever M., Panfilov A.V. Directed networks as a novel way to describe and analyze cardiac excitation: Directed graph mapping. Front. Physiol. 2019 doi: 10.3389/fphys.2019.01138. [Online]. Available: [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.He Y.-J., Li Q.-H., Zhou K., Jiang R., Jiang C., Pan J.-T., Zheng D., Zheng B., Zhang H. Topological charge-density method of identifying phase singularities in cardiac fibrillation. Phys. Rev. E. 2021;104 doi: 10.1103/physreve.104.014213. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 23.Kuklik P., Zeemering S., van Hunnik A., Maesen B., Pison L., Lau D.H., Maessen J., Podziemski P., Meyer C., Schaffer B., Crijns H., Willems S., Schotten U. Identification of rotors during human atrial fibrillation using contact mapping and phase singularity detection: Technical considerations. IEEE Trans. Bio-Med. Eng. 2017;64:310–318. doi: 10.1109/TBME.2016.2554660. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 24.Van Nieuwenhuyse E., Teresa S., Guiseppe L., Milad E.H., Goedgebeur Jan V.C.N., Duytschaever Mattias K.S., Nele V. Evaluation of directed graph mapping on complex Atrial Tachycardias. JACC EP. 2020 doi: 10.1016/j.jacep.2020.12.013. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 25.Hawson J., Van Nieuwenhuyse E., Van Den Abeele R., Al-Kaisey A., Anderson R.D., Chieng D., Segan L., Watts T., Campbell T., Hendrickx S., et al. Directed graph mapping for ventricular tachycardia: A comparison to established mapping techniques. Clin. Electrophysiol. 2023;9(7_Part_1):907–922. doi: 10.1016/j.jacep.2022.08.013. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 26.openCARP consortium J., Augustin C., Boyle P.M., Colin R., Gsell M., Houillon M., Huang Y.-L.C., Hustad K.G., Karabelas E., Loewe A., Neic A., Nothstein M., Plank G., Prassl A., Sánchez J., Seemann G., Stary T., Thangamani A., Tippmann N., Trevisan Jost T., Vigmond E., Wülfers E.M. 2022. openCARP. [Online]. Available: https://git.opencarp.org/openCARP/openCARP. [Google Scholar]
- 27.Plank G., Loewe A., Neic A., Augustin C., Huang Y.-L.C., Gsell M., Karabelas E., Nothstein M., Sánchez J., Prassl A., Seemann G., Vigmond E. The openCARP simulation environment for cardiac electrophysiology. Comput. Methods Programs Biomed. 2021;208 doi: 10.1016/j.cmpb.2021.106223. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 28.Luo C., Rudy Y. A model of the ventricular cardiac action potential. Depolarization, repolarization, and their interaction. Circulation Research. 1991;68(6):1501–1526. doi: 10.1161/01.res.68.6.1501. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 29.Bishop M., Plank G. Bidomain ECG simulations using an augmented monodomain model for the cardiac source. IEEE Trans. Biomed. Eng. 2011;58(8):2297–2307. doi: 10.1109/TBME.2011.2148718. [Online]. Available: [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Panfilov A., Dierckx H. In: Cardiac Electrophysiology : From Cell to Bedside. Zipes D., Jalife J., Stevenson W., editors. Elsevier; 2018. Theory of rotors and arrhythmias; pp. 325–334. [Online]. Available: [DOI] [Google Scholar]
- 31.Ten Tusscher K.H., Panfilov A.V. Influence of diffuse fibrosis on wave propagation in human ventricular tissue. Europace. 2007;9(suppl_6):vi38–vi45. doi: 10.1093/europace/eum206. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 32.de Jong S., van Veen T.A.B., van Rijen H.V.M., de Bakker J.M.T. Fibrosis and cardiac arrhythmias. J. Cardiovasc. Pharmacol. 2011;57(6):630–638. doi: 10.1097/fjc.0b013e318207a35f. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 33.Kuklik P., Zeemering S., Maesen B., Maessen J., Crijns H.J., Verheule S., Ganesan A.N., Schotten U. Reconstruction of instantaneous phase of unipolar atrial contact electrogram using a concept of sinusoidal recomposition and Hilbert transform. IEEE Trans. Biomed. Eng. 2014;62(1):296–302. doi: 10.1109/tbme.2014.2350029. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 34.Paul T., Moak J.P., Morris C., Garson A., Jr. Epicardial mapping: How to measure local activation? Pacing Clin. Electrophysiol. 1990;13(3):285–292. doi: 10.1111/j.1540-8159.1990.tb02042.x. [Online]. Available: https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1540-8159.1990.tb02042.x. [DOI] [PubMed] [Google Scholar]
- 35.Clayton R.H., Nash M.P. Analysis of cardiac fibrillation using phase mapping. Card. Electrophysiol. Clin. 2015;7 1:49–58. doi: 10.1016/j.ccep.2014.11.011. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 36.Roney C.H., Cantwell C.D., Qureshi N.A., Chowdhury R.A., Dupont E., Lim P.B., Vigmond E.J., Tweedy J.H., Ng F.S., Peters N.S. Rotor tracking using phase of electrograms recorded during atrial fibrillation. Ann. Biomed. Eng. 2016;45(4):910–923. doi: 10.1007/s10439-016-1766-4. [Online]. Available: [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Castells F., Cervigón R., Millet J. On the preprocessing of atrial electrograms in atrial fibrillation: Understanding botteron’s approach. Pacing Clin. Electrophysiol. 2014;37(2):133–143. doi: 10.1111/pace.12288. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 38.Bray M.-A., Lin S.-F., Aliev R.R., Roth B.J., Wikswo J.P. Experimental and theoretical analysis of phase singularity dynamics in cardiac tissue. J. Cardiovasc. Electrophysiol. 2001;12(6):716–722. doi: 10.1046/j.1540-8167.2001.00716.x. [Online]. Available: [DOI] [PubMed] [Google Scholar]
- 39.Li X., Almeida T.P., Dastagir N., Guillem M.S., Salinet J., Chu G.S., Stafford P.J., Schlindwein F.S., Ng G.A. Standardizing single-frame phase singularity identification algorithms and parameters in phase mapping during human atrial fibrillation. Front. Physiol. 2020;11 doi: 10.3389/fphys.2020.00869. [Online]. Available: [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Fagerland M.W., Lydersen S., Laake P. The McNemar test for binary matched-pairs data: mid-p and asymptotic are better than exact conditional. BMC Med. Res. Methodol. 2013;13(1) doi: 10.1186/1471-2288-13-91. [Online]. Available: [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nieuwenhuyse E.V., Martinez-Mateu L., Saiz J., Panfilov A.V., Vandersickel N. Directed graph mapping exceeds phase mapping in discriminating true and false rotors detected with a basket catheter in a complex in-silico excitation pattern. Comput. Biol. Med. 2021;133 doi: 10.1016/j.compbiomed.2021.104381. [Online]. Available: [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The Appendix details simulation and method parameters, while performance metrics results are visually presented, discussed, and listed in tables.