Atom-by-atom imaging of moiré transformations in 2D transition metal dichalcogenides

Abstract

Understanding the atomic-scale mechanisms that govern the structure of interfaces is critical across materials systems but particularly so for two-dimensional (2D) moiré materials. Here, we image, atom-by-atom, the thermally induced structural evolution of twisted bilayer transition metal dichalcogenides using in situ transmission electron microscopy. We observe low-temperature, local conversion of moiré superlattice into nanoscale aligned domains. Unexpectedly, this process occurs by nucleating a new grain within one monolayer, whose crystal orientation is templated by the other. The aligned domains grow through collective rotation of moiré supercells and hopping of 5|7 defect pairs at moiré boundaries. This provides mechanistic insight into the atomic-scale interactions controlling moiré structures and illustrates the potential to pattern interfacial structure and properties of 2D materials at the nanoscale.

Electron microscopy reveals unexpected atomic-scale mechanism of interfacial rearrangement in 2D moiré superlattice.

INTRODUCTION

A rich array of emergent properties has been found in twisted two-dimensional (2D) moiré systems, including superconductivity (1), strongly correlated states (2–6), moiré excitons (7–10), magnetism (11, 12), and interfacial ferroelectricity (13, 14). The interfacial alignment, such as the relative rotation, translation, and lattice mismatch between adjacent layers, is a critical knob to modulate the properties of moiré materials. While the average, global alignment of 2D moirés can be tuned through various fabrication and processing techniques (15–18), understanding and controlling the local moiré structures remains a challenge. The structure and properties of 2D multilayers are often highly heterogeneous (19), varying widely both between and within individual samples in response to defects (20, 21), strain (22–24), and pinning sites (25). Moreover, rather than being static, 2D moirés are known to reconfigure readily under external stimuli, such as heating (26–29), bending (30), and shear (31). As a result, understanding the atomic-scale mechanisms that govern the structural evolution of 2D moirés is key to designing the properties of 2D multilayers.

Here, we use in situ transmission electron microscopy (TEM) and scanning TEM (STEM) to directly image the thermally driven structural rearrangements of twisted bilayer transition metal dichalcogenide (TB-TMD) homo- and heterostructures down to the atomic scale. We prepare single-crystal monolayers of WSe₂ and MoSe₂ using chemical vapor deposition (CVD) and then fabricate graphene-encapsulated TB-TMDs using the pick-up technique (32, 33). We then transfer the samples onto microelectromechanical system (MEMS)–based E-chips (Fig. 1A) for in situ heating experiments (33). The MEMS-based heating chips heat and cool rapidly (up to 1000°C/ms) (34), making it possible to access and image metastable states. The graphene encapsulation produces a solid-state reaction chamber that mitigates electron-beam damage and prevents sample sublimation at high temperatures, preserving the atomic-resolution capability of STEM (35). This approach enables acquisitions of multiple (S)TEM images to comprehensively survey the structural transformation during heating.

Fig. 1. In situ heating of twisted bilayer WSe₂/WSe₂ and MoSe₂/WSe₂ under pulsed heating.

(A) Schematic of graphene encapsulated twisted bilayer transition metal dichalcogenides (TMDs) on a MEMS-based heating chip. (B) Heating profile and crystallographic alignment of MoSe₂/WSe₂ sample before and after heating. The sample undergoes a series of 0.5-s heat pulses between 100° and 1000°C. The cartoons and pie charts depict the specimen geometry and relative crystal orientation, before (left) and after (right) heating. Before heating, the sample consists of two bilayer domains with 7.6° and 18.2° relative twist; after heating, a portion of the sample converts to aligned bilayer. DFTEM images associated with the cartoons are provided in the Supplementary Materials. (C and D) Fourier-filtered ADF-STEM images of 7.6°-twisted MoSe₂/WSe₂ hetero-bilayer before and after in situ heating. (E) Post-heating Fourier-filtered ADF-STEM image of an antiparallel (AA′) domain in 3.3°-twisted WSe₂/WSe₂ homo-bilayer. Dashed yellow lines outline position of the AA′ domain. Additional stacking orders including moiré, AB′, and shear-misaligned are labeled. Scale bars, 5 nm [(C) to (E)].

RESULTS

Figure 1 (A and B) shows our experimental design. We characterize the samples using optical microscopy and STEM imaging before heating to verify the sample quality and stacking angle (fig. S1). We study a total of four samples, two WSe₂/WSe₂ homo-bilayers and two MoSe₂/WSe₂ hetero-bilayers with twist angles between 3.3° and 45.0° [see (33) and fig. S2]. Here, 0° and 60° are defined as parallel (AB′ or 3R) and antiparallel (AA′ or 2H) stacking (36), respectively. We apply a sequence of short, 0.5-s heat pulses from 100° to 1000°C to the TB-TMDs (see heating profile in Fig. 1B) and acquire (S)TEM images between pulses to reduce thermal drift.

Nucleation of nanoscale aligned domains

Figure 1B shows the interlayer alignment of a MoSe₂/WSe₂ sample before and after heating. The sample consists of two bilayer regions, one with a 7.6° interlayer twist angle (Fig. 1C) and the other with an 18.2° twist as measured from selected-area electron diffraction (see fig. S3 for TEM images and diffraction patterns). These two different twist regions occur because of a partial tear in the MoSe₂ layer during transfer. After the sequence of heat pulses, we observe the formation of nanoscale aligned areas via atomic-resolution annular dark-field (ADF)–STEM (Fig. 1D and fig. S2, C and D) and dark-field TEM (DFTEM) (fig. S3). Notably, only 0.04 μm² of the 16.76 μm² WSe₂ lattice becomes aligned after the heating (fig. S3), indicating local reconstruction instead of the global, whole-flake rotations that have been previously observed in other 2D systems (3, 26–28). The fractional conversion is likely due to the short overall heating time (<10 s in total, see Fig. 1B). Longer thermal annealing at high temperature (e.g., 800°C for 1 hour) does lead to full conversion of twisted to aligned structure (37). We do not observe any tears between the moiré domains and the newly formed aligned domains. Instead, the aligned domains are produced through the nucleation of a new crystal grain within one layer that is rotationally aligned to the other. For example, in the 7.6° twisted region, the WSe₂ produces a new grain aligned with the MoSe₂ layer, while the reverse is true in the 18.2° twisted region [see (33) and fig. S4].

After the sequence of heat pulses, the bilayer structures are highly heterogeneous. Figure 1E shows an atomic-resolution ADF-STEM image of a WSe₂/WSe₂ homo-bilayer post-heating, with a global twist angle of 3.3°. In this ~300 nm² field of view, a range of inhomogeneous stacking arrangements is visible, including twist moirés (3.3°), an AB′-stacked region (0°), and stacking faults. Unexpectedly, we also observe an ~5-nm AA′ stacked (60°) area (yellow triangle in Fig. 1D), although the initial twist angle is closer to 0° rather than 60°.

By comparing the structural transformation of all four samples studied, we can extract general trends about the formation of aligned regions [see (33) and fig. S5 for statistics of aligned regions in all samples]. In each sample, several distinct regions, from several nanometers to micrometers across, convert into aligned bilayers after heating [see (33) and figs. S3 and S5]. We observe a larger aligned domain in the 18.2°-twisted region than the 7.6°. Higher twist angles correspond to larger interfacial stacking energy and correspondingly a larger energy difference between twisted and aligned states (38). Therefore, we would expect larger aligned domains to form in the bilayer with large twist angle, although other effects such as pinning, strain, and sample edges may also play substantial roles. Typically, the final stacking arrangement of the aligned structure depends on the initial twist angle such that a minimum angular change occurs (i.e., <30° converts to 0° and >30° converts to 60°; see fig. S5). Although in our experiments most of the twist angle changes result in aligned domains, we also occasionally observe conversion from one misaligned twist to another; for example, a 56.4°-twisted domain formed next to a 45°-twist domain (fig. S6).

In situ growth of aligned domains

To visualize the nucleation and growth of the aligned domains, we analyze DFTEM images on a MoSe₂/WSe₂ twisted bilayer sample. Both layers are initially single crystals, as verified by electron diffraction (Fig. 2A). After each heat pulse, a pair of complimentary DFTEM images is acquired using the Bragg spots of each monolayer (see movies S1 and S2). Formation of an aligned domain appears as a bright region in one of the DFTEM images (Fig. 2, B to E, and movie S1) along with a corresponding dark region at the same position in the complimentary DFTEM image (movie S2). An aligned bilayer domain is visible in the DFTEM images starting at 200°C (see movie S1). Notably, this temperature is in the 90° to 350°C range commonly used to anneal 2D heterostructures (1, 39), indicating that nanoscale aligned regions may be introduced during typical 2D device processing.

Fig. 2. In situ growth and boundary structure of aligned domain in a MoSe₂/WSe₂ hetero-bilayer.

(A) Selected-area electron diffraction pattern of 7.6°-twisted MoSe₂-WSe₂ hetero-bilayer. Colored circles mark the positions of objective aperture used to generate DFTEM images of MoSe₂ (red) in (B) to (E) and WSe₂ (yellow) layers in the Supplementary Materials. Scale bar, 5 nm⁻¹. Inset cartoon illustrates geometry of the hetero-bilayer. (B to E) DFTEM image series under heating, obtained with objective aperture position 2. Bright region represents the formation of a new grain in the WSe₂ layer, aligned with the MoSe₂ lattice. Images are smoothed using Gaussian blurring with a radius of 2 pixels. (F) Line traces of aligned domain boundaries measured from DFTEM images. The color indicates the temperature of the heat pulse after which the image is acquired. The brown arrow illustrates the growth direction of the aligned domain. Scale bars, 100 nm (B to F). (G) Fourier-filtered ADF-STEM image of interface between the aligned domain and the moiré lattice. A 7.6° rotational grain boundary is located in the WSe₂ layer. Scale bar, 2 nm. (H and I) Structural cartoons of MoSe₂ and WSe₂ layers of the region shown in (G). W atoms in three 5|7 defect pairs are labeled in blue. (J) ADF-STEM image overlaid with grain boundary structure.

Figure 2F shows how the positions of the domain boundaries of the aligned region evolve during heating, extracted via edge detection on DFTEM images (33). After the full heating sequence, the aligned domain is ~0.03 μm², with an irregular and anisotropic shape. The aligned domain growth approximately follows an Arrhenius relation with respect to temperature from 200° to 1000°C [see (33) and fig. S7], consistent with the temperature dependence of grain boundary mobility in bicrystals (40). From the Arrhenius plot, we extract an activation energy of this reconstruction to be 3.54 ± 0.03 eV/nm². This is equivalent to four bonds broken per moiré supercell, considering the 4.3-eV bond dissociation energy in WSe₂ (41).

Figure 2G shows a post-heating, atomic-resolution ADF-STEM image of the domain boundary in a MoSe₂/WSe₂ heterostructure. We solve the structure by separating the two monolayers in the image using Fourier filtering (Fig. 2, H to J; see Materials and Methods). As illustrated in Fig. 2 (H to J), the domain boundary is formed by a grain boundary in the WSe₂ layer consisting of 5|7 defect pairs. We observe a similar domain boundary structure in the WSe₂/WSe₂ bilayer (fig. S9). The grain boundary structures are consistent with previous observations of the atomic structure of grain boundaries in 2D TMDs (42, 43).

The formation and growth of an aligned domain is a competition between the interfacial stacking energy (which decreases with the area of the aligned domain) and the grain boundary energy (which increases with the length and twist angle of the grain boundary). According to first-principles studies (38), WSe₂ twisted bilayers are 0.2 to 0.3 eV/nm² higher energy than aligned bilayers, with similar values expected for other TMD bilayers (44). Meanwhile, the energetic cost associated with a grain boundary is 1.4 to 3 eV/nm (45), for the grain boundary angles in our study. By balancing these two energetic terms, we can estimate a critical size above which growth of the aligned domains is favored. For twisted bilayer WSe₂, we find that the critical domain radius, which is a function of the twist angle, ranges between 1 and 20 nm [see (33) and fig. S8].

Next, we study the atomic-scale growth mechanism for the aligned domains using in situ aberration-corrected STEM. Figure 3 (A to D) shows an atomic-resolution ADF-STEM image series detailing the grain boundary migration (see movie S3 for complete image series) in a 45.0°-twisted WSe₂/WSe₂ homo-bilayer. After six 0.5-s heat pulses between 400° and 900°C, the grain boundary, indicated by colored lines in Fig. 3, displaces up to 5 nm. We also observe the formation of vacancies, multi-atom voids (Fig. 3A), and small nearly aligned (57.2°-twisted) domains (fig. S10) during heating; such defects as well as strain may alter the activation energies and equilibrium structures formed.

Fig. 3. Atomic-resolution imaging of in situ growth of aligned domain in a 45°-twisted WSe₂/WSe₂ homo-bilayer.

(A) ADF-STEM image of 45.0° moiré-AA′ interface at 900°C. Colored lines mark the positions of the interface from 400° to 900°C. Nanometer-scale voids and trilayer patches are also visible as darker and brighter regions. Scale bar, 5 nm. (B to D) Magnified ADF-STEM images of the interface from the region marked with the white box in (A) after heat pulses at 500°, 600°, and 700°C. Dashed colored lines mark the positions of the interface. Colored pentagons and heptagons mark the positions of the 5|7 defect pairs at the interface. Colored blocks mark moiré supercells. Gray pentagons and heptagons in (C) mark positions of 5|7 defect pairs after 500°C heat pulse. Gray diamond in (C) marks a single moiré cell transformed to aligned region after 600°C heat pulse. Scale bar, 2 nm. All images are aligned by cross-correlating the ADF-STEM images in the large (~100 nm) field of view.

As shown in Fig. 3 (B to D), the 5|7 dislocation cores are preferentially located at the edges of the moiré supercells in each frame; these positions are represented as the unshaded regions, where the interlayer lattice misalignment is greatest. For example, Fig. 3 (B and C) shows that, between the 500° and 600°C frames, two 5|7 pairs hop to approximately equivalent sites at the adjacent moiré supercell, thus converting an area of the size of one moiré unit cell into aligned bilayer (gray diamond in Fig. 3C). Correspondingly, the displacement of the domain boundary progresses in discrete units, approximately equal to the radius of a moiré supercell (1.1 nm at θ = 45.0°; see fig. S11 for additional regions). This mechanism is notably different from grain boundary migration in monolayer TMDs, which proceeds by continuous gliding of defect pairs (32, 46, 47).

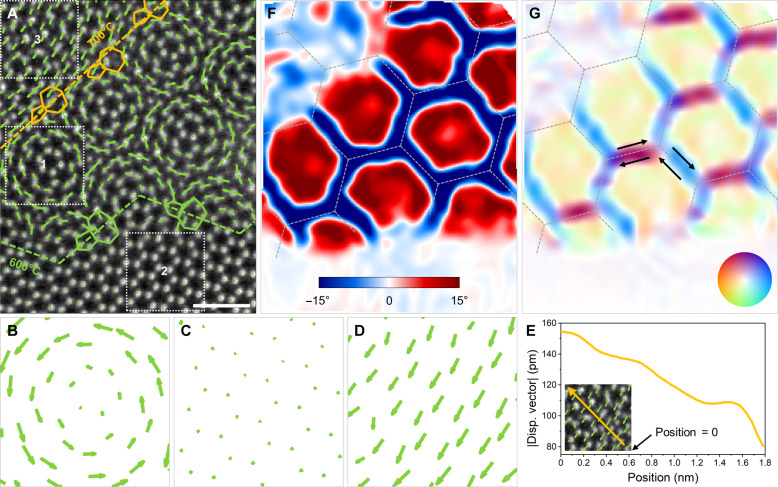
Figure 4 analyzes the atom-by-atom transformation during the aligned domain growth. Focusing on a small subregion from Fig. 3A, we obtain atomic coordinates from each STEM image in the temperature series and track the atoms between consecutive image frames using a global best-fit algorithm (33, 48). Figure 4A shows the atomic displacements of the reconstructing WSe₂ monolayer after the 700°C heat pulse, overlaid on a STEM image acquired just before the heat pulse. We observe three main types of atomic motions, depicted in Fig. 4 (B to D), which correspond to the three main regions in the sample. The most notable rearrangements occur in region 1 (Fig. 4A), which converts from twisted to aligned bilayer after the pulse. Here, we observe that the atoms in one WSe₂ monolayer rearrange, producing rotational displacements with the periodicity of the moiré lattice (Fig. 4B). In contrast, in region 2 (Fig. 4A), which contains aligned bilayer both before and after the heat pulse, the atoms remain stationary (Fig. 4C) to within our measurement error. In region 3, which represents twisted bilayer in both time steps, we observe large, 80- to 154-pm translations (Fig. 4D), corresponding to sliding of the WSe₂ layer. The magnitude of such translation is largest (~150 pm) at the 700°C grain boundary and decreases linearly away from the grain boundary (Fig. 4E), indicating that it accommodates changes in stress resulting from the dislocation motion.

Fig. 4. Atomic displacements in a moiré-to-antiparallel reconstruction.

(A) Atomic displacement field showing the lattice transformation before and after 700°C pulse. A Fourier-filtered ADF-STEM image, acquired before the 700°C pulse, is overlaid with the vectors (green arrows) showing atomic displacements after the 700°C pulse. Vectors are 1:1 scale. Colored dashed lines label positions of the grain boundary at 600° and 700°C. Pentagons and heptagons mark 5|7 defect pairs. Scale bar, 1 nm. (B to D) Magnified regions of interest (ROIs) displaying rotational, close to stationary, and translational atomic displacements, respectively. (E) Line profile of average magnitude of the displacement vectors in ROI 3 as a function of position. Zero position is defined at the 700°C grain boundary. Inset is cropped from ROI 3 in (A). Yellow arrow marks the position and direction of line profile. (F and G) Strain tensor components derived from the displacement field in (A) showing rotation (ω) and shear [ε_xy + $\frac{1}{2}$(ε_xx − ε_yy)]. In (F), positive rotations are defined as counterclockwise. Color wheel in the phase map in (G) represents the shear direction (color) and magnitude (intensity). The strain and rotation fields are relative to the previous frame rather than equilibrium atomic structures.

We calculate the local change in rotation and shear between frames using the spatial derivatives of the displacement fields (Fig. 4, E and F) (33, 48). The rotation maps in Fig. 4F show a uniform counterclockwise rotation of +15° within each moiré supercell, consistent with the angle difference between the initial 45° twist angle and final AA′ aligned stacking (60°). Figure 4G shows that shear concentrates at the supercell edges, where displacement vectors across the boundary point in opposite directions. Note that values in Fig. 4 (F and G) are defined as changes in strain between frames, not an absolute strain relative to the equilibrium atomic structure.

Together, the data in Figs. 3 and 4 indicate that, to allow each moiré supercell to rotate while maintaining a continuous 2D layer, bonds break and reform at the edges of the moiré supercells, while atoms stay bonded within the supercells. This mechanism minimizes the number of covalent bonds broken per unit area during the growth of the aligned bilayer and is consistent with the small activation energy we measured using DFTEM image series. Because the interlayer alignment progresses via local rotation of nanometer-scale regions, this mechanism should be favored over whole-flake rotation when the activation energy for the creation and migration of dislocations is smaller than the sliding energy barrier integrated over the system size. We expect this mechanism to be applicable to twist angles within the rigid moiré and part of the small-angle reconstruction regimes (including 7.6°, rigid moiré and the 3°, partially reconstructed samples measured here). In the case of extremely small twist angles (0° to 2°), a large fraction of the moiré superlattice is already aligned. In the small twist angle limit, where the system can be described as an aligned lattice containing a dilute soliton network, thermally activated soliton motion has previously been shown to dominate lattice reconstructions (20).

DISCUSSION

In summary, using in situ (S)TEM in a solid-state graphene reaction chamber, we report a mechanism for the nucleation and growth of nanometer-scale aligned domains in TB-TMDs. Here, bilayers align through the formation and migration of grain boundary dislocations in one of the 2D layers, combined with the collective motion of atoms within a moiré supercell. This process enables the nucleation of aligned domains in both homo- and hetero-bilayers with a wide range of twist angles at temperatures as low as 200°C, within the range of typical processing temperatures for 2D heterostructures. Our results can explain some of the inconsistent and heterogeneous properties measured in moiré-based devices and may lead to new, bottom-up routes to fabricate and design structures to control and pattern the twist angle on the nanoscale.

MATERIALS AND METHODS

CVD growth of MoSe₂ and WSe₂ monolayers

To synthesize monolayers of WSe₂ and MoSe₂ by CVD, we used SiO₂ (285 nm)/Si substrates in 2-inch quartz tube under ambient pressure. For monolayer WSe₂, we used a quartz boat with WO_2.9 powder (99.99%, Alfa Aesar) and KI powder (99.99%, Alfa Aesar) placed at the center of the furnace and the SiO₂/Si substrate suspended face-down on top of the boat. Another quartz boat with selenium powder (99.99%, Sigma-Aldrich) was located upstream of the quartz tube at a distance of 19.5 cm from the center of the furnace. The furnace temperature was raised to 800°C at a rate of 50°C/min, maintained for 15 min, and cooled to room temperature. We flew 300 standard cubic centimeters per minute (sccm) of Ar during the whole growth process and 10 sccm of H₂ during the cooling process. For monolayer MoSe₂, we used MoO₃ powder (99.97%, Sigma-Aldrich). The furnace temperature was raised to 750°C at a rate of 50°C/min, maintained for 20 min, and cooled to room temperature. All other parameters are the same as used for WSe₂.

Fabrication of graphene encapsulated twisted bilayer TMD homo/heterostructures

We exfoliated flakes of hexagonal boron nitride (hBN) and graphene from bulk crystals onto SiO₂ (285 nm)/Si substrates. Monolayer WSe₂ and MoSe₂ were either mechanically exfoliated from bulk crystals (from HQ Graphene) or synthesized from CVD. We identified the thickness of monolayers with optical contrast, photoluminescence measurements, and atomic force microscopy. Next, we assembled the hBN/Gr/WSe₂/MoSe₂/Gr heterostructures with polycarbonate (PC)/polydimethylsiloxane (PDMS) stamp using dry-transfer method (49). The pick-up temperature for hBN, TMDs, and graphene was around 115°, 75°, and 75°C. After stacking, we transferred the heterostructures onto a clean SiO₂ (285 nm)/Si substrate by releasing the PC film from the PDMS lens at 180°C. Transferred samples were placed in chloroform for 3 hours to remove PC. We used few-layer graphene to prevent degradation of heterostructures during annealing and hBN as top layer to detach graphene from the substrate (50). We then used XeF₂ gas to selectively etch hBN (51) to obtain graphene encapsulated TB-TMD samples.

Sample preparation for in situ (S)TEM experiments

We prepared TEM samples using a poly(methyl methacrylate) (PMMA)–based wet transfer method. We transferred graphene encapsulated TB-TMD/PMMA on MEMS-based heating chips (Protochips, E-FHDN-VO-10) and removed PMMA by acetone bath for 24 hours.

Electron microscopy imaging

The samples were imaged in a Thermo Fisher Scientific Themis Z aberration–corrected (S)TEM. The microscope was operated at 80 kV to minimize knock-on damage of the 2D materials. The aberration-corrected ADF-STEM images and DFTEM images were obtained using the STEM and TEM capabilities of the instrument, respectively. We used a convergence angle of 25.2 mrad.

In situ heating

We used a heating holder (Fusion Select, Protochips) to apply heat pulses of 0.5 s from 100° to 1000°C. DFTEM and/or ADF-STEM images were acquired after each 0.5-s heat pulse was applied, and the samples were quenched to room temperature. The temperatures for DFTEM image series are 100° to 400°C at 100°C temperature steps and 400° to 1000°C at 50°C temperature steps. The temperatures for ADF-STEM imaging are 400° to 900°C at 100°C temperature steps.

Supplementary Materials

This PDF file includes:

Materials and Methods

Figs. S1 to S12

Tables S1 and S2

Legends for movies S1 to S3

References

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S3