Derived energy storage systems from Brayton cycle

Summary

Various energy storage systems (ESS) can be derived from the Brayton cycle, with the most representative being compressed air energy storage and pumped thermal electricity storage systems. Although some important studies on above ESS are reported, the topological structure behind those systems (i.e., derivations of the Brayton cycle) has not been studied, and the underlying thermodynamic ideas still need to be further explored. This paper first introduces the topological structure and the symmetry of ESS and their based Brayton cycles. The formation method of ESS based on paths and separation points is specified. It is found that round-trip path can form ESS directly. Then various ESS formed are compared. Finally, the synergistic effect and gain principle of thermal cycle and ESS are revealed. This work helps to reveal the intrinsic relationship between thermal cycles and ESS, understand the general laws behind ESS, and guide the combination of thermal cycles and ESS.

Graphical abstract

Highlights

• •A method of using the Brayton cycle to derive energy storage systems is proposed
• •Energy storage systems with different lengths and characteristics are evaluated
• •The gain principle of integrating A-CAES system and the Brayton cycle is revealed

Physics; Thermal property

Introduction

Brayton cycle is an important thermodynamic cycle that is easy to implement in engineering and can achieve large-scale continuous output of work. The ideal Brayton cycle includes adiabatic compression and expansion processes, and two constant-pressure heat transfer processes, and each of the processes can be currently performed in mature and efficient equipment. The Brayton cycle is most widely used in the applications of gas turbine power generation or aviation engines,^1,2 which mainly uses air and gas as working fluids.

Research on the Brayton cycle continues with recent focuses on developing derivative cycles based on Brayton’s, finding new working fluids, integrating with renewable energy, creating new configurations, etc. For example, the Brayton and its derivative cycles using CO₂ as working fluid shows advantages of high efficiency, compact components, and applicability for various kinds of heat sources. Wang et al.³ made a detailed review on the dynamic performance and control strategy of supercritical CO₂ Brayton cycle. Chen et al.⁴ proposed a micro thermoelectric conversion system (∼3 m³) based on a closed-air Brayton cycle. Modeling results indicate that the maximum system power density is 402.34 kW/m³ with the cycle efficiency of 24.86%. Le Roux et al.⁵ highlighted perspectives, conflicts, and recommendations about the derivation of an objective function considering various geometries of different components of a solar thermal Brayton cycle. Furthermore, some scholars also derived the electrochemical Brayton power generation cycle based on the Brayton cycle.⁶ Chen et al.⁶ firstly proposed the electrochemical Brayton cycle (EBC) for power generation, which is realized by flow batteries and heat exchangers. The results indicate that the ideal EBC without over potential has a maximum power density of 690 W/m² and a relative efficiency to the Carnot efficiency of 52.3%. Rajan et al.⁷ conceptualized an electrochemical refrigeration cycle and demonstrated a proof-of-concept prototype in continuous operation based on the Brayton cycle.

In recent years, large-scale energy storage receives increasing attention because of the rapid development of renewable energy. Among them, compressed air energy storage (CAES)^8,9 and pumped thermal energy storage (PTES)^10,11,12 are two representative energy storage systems (ESS) derived from the Brayton cycle. For CAES system, the compression and expansion of the Brayton cycle serve as the energy storage and release processes, respectively. In the energy storage process, electricity is converted to mechanical exergy of the stored air through a compressor; in energy release, the mechanical exergy of air is released and converted into work in expander. PTES system can be composed of a reverse Brayton cycle and a Brayton cycle. During energy storage process, electricity is converted to thermal and cold energy through the reverse Brayton cycle. During energy release, the thermal and cold energy are then converted into work through the Brayton cycle. In addition to CAES and PTES systems, some other ESS can also be derived from the Brayton cycle.¹³

Therefore, the thermodynamic analysis of CAES systems can mimic the methods for analyzing the Brayton cycles and their components. For example, the key parameters of the CAES systems also include compressor pressure ratio/efficiency, expander expansion ratio, heat exchanger efficiency, heat exchanger pressure loss, etc. The analysis methods also use energy balance analysis and exergy balance methods.¹⁴ However, due to the fact that the evaluation index of CAES (i.e., round-trip efficiency) is different from that of Brayton cycle (i.e., thermal efficiency), the variation trends of system efficiency with key parameters are different between these two systems. Our previous work¹⁴ has provided various considerations for the thermodynamic design of CAES systems. Specifically, in contrast with that for the Brayton cycle machines, the design parameters of the CAES also include the number of stages, the pressure range of the air storage chamber, the thermal storage temperature, and the storage/release time. Moreover, CAES efficiency is basically linearly related to the compressor/expander efficiency and the temperature difference and pressure loss of heat exchanger,¹⁵ while the variation trend of system efficiency with stage and pressure ratio depends on the relative magnitude of compressor efficiency and heat storage efficiency.¹⁶ In practice, various thermodynamic variables are interdependent, such as compressor/expander efficiency and pressure ratio, heat exchanger efficiency and pressure loss. In addition, the efficiency of CAES systems also depends on the system configurations such as isothermal CAES, underwater CAES, and liquid air storage (LAES), and variable operating conditions.^14,17 Liang et al.¹⁸ studied the thermodynamic characteristics of LAES system, including the influence of key parameters on the system thermal performance, and the influence of the cold and thermal storage efficiency and the dynamic operation of packed bed on the system efficiency. They found that the system efficiency stabilizes after multiple cycles. Liu et al.¹⁹ investigated an under-water CAES (UW-CAES) system that is integrated with electrically heated solid thermal energy storage (STES). The system behavior of the UW-CAES strongly depends on the water depth at 0–100 m (storage pressure<10bar), and the thermal behavior is much better than the system without STES when combined with renewable energy. White et al.²⁰ quantified the influence of varied storage pressure (for a constant-volume chamber) on the exergy loss of each part of the system. They found that the cavern temperature variations and the associated losses depend mainly on the minimum and maximum pressure in the cavern and on a dimensionless heat-transfer parameter.

Compared to CAES systems, PTES systems have more components and are more complex. Early conceptualization of the PTES systems was based on ideal Carnot cycles. Recently, significant progress has been made in more practical PTES systems based on Rankine or Brayton cycles,^21,22 while the Brayton PTES yields higher energy density because of the absorption heat at higher temperature.²¹ Figure 1 presents the schematic of a PTES system based on Brayton cycle. In charge process, the system runs anticlockwise, forming a reversed Brayton cycle. The heat and cold energy generated by the compressor and expander is stored in the hot tank and cold tank, respectively. As a result, electricity is converted to heat and cold energy for storage since the compressor consumption is greater than the expander output. In discharge process, a Brayton cycle is formed by the clockwise operation of the system, and the compressor and expander are exchanged. System can output electricity due to the higher inlet temperature of expander than the outlet temperature of compressor. As a result, heat and cold energy is converted back to electricity. Some scholars have reported the performance of the Brayton PTES system. For instance, White et al.²³ showed that for given compression and expansion efficiencies, the cycle performance is primarily governed by the ratio between the highest and lowest temperature in each reservoir rather than by the cycle pressure ratio. Olympios et al.²⁴ studied the influence of temperature ratio of Brayton cycle, power ratio of expander to compressor, heat to power ratio, and working fluid on cycle performance and system design. Moreover, McTigue et al.¹⁰ reported the influence of turbomachinery efficiency and heat exchanger effectiveness on a PTES system based on a regenerative Brayton cycle. In addition, there are also some studies on the influence of the inherit instability (i.e., temperature fluctuations) of thermal storage devices on system performance. For example, Wang et al.²⁵ presented arrayed TES reservoirs to cope with the temperature fluctuation issue. With the proposed system and the “temperature complementation” operating mode, the variation delivery power decreased by 13.2% with a round-trip efficiency of 64.2%. Albert et al.²⁶ proposed an additional latent heat storage to maximize the duration of the high power region, and the round-trip efficiency was predicted up to 80% using isentropic reciprocating compressor/expander, which is close to the theoretically predicted limit.

Figure 1.

PTES configuration based on Brayton cycle

In charge process, the system runs anticlockwise, converting electrical energy into thermal and cold energy for storage. In discharge process, a Brayton cycle is formed by the clockwise operation of the system. The compressor and expander used for energy storage are replaced by the expander and compressor, respectively, and the stored heat and cold energy is converted back to electricity.

Furthermore, there are also many studies on optimizing the Brayton cycle–based PTES system or even proposing different systems. For example, McTigue et al.²⁷ optimized a Brayton PTES system that uses a packed bed for heat and cold storage. It is shown that a high storage density can be attained with a slightly reduced system efficiency. Farres-Antunez et al.¹¹ integrated CAES, PTES, and liquefaction systems for a higher energy density. Their simulation results indicated that the overall energy density of the integrated system can be two times that of the separate cycles. Sun et al.²⁸ proposed a supercritical CO₂ PTES system based on the reversible Brayton cycle. Their modeling results indicate that the configuration using recompression shows the highest round-trip efficiency of 69.38%.

Although there has been a lot of research on CAES systems and PTES systems based on the Brayton cycle, the topological structure behind them has not been studied, and the underlying thermodynamic ideas still need to be explored. From the perspective of topology, both CAES and PTES systems are derived from the Brayton cycle, so there must be some inherent relationships between them regardless of their different operating principles. As an example, we present the relationship between CAES system (topologically simplified) and the Brayton cycle in Figure 2. Figure 2A is the schematic of a common multi-stage adiabatic CAES system, which can be topologically simplified into a single-stage CAES system as shown in Figure 2B. In general, each compressor/expander shares equal compression/expansion ratio for improved system efficiency in Figure 2A.²⁹ The two systems are expected to show a similar efficiency if they share the same single-stage compression/expansion ratio (see the third part of results for more details). Furthermore, the single-stage CAES system can be decomposed into two symmetric processes, i.e., compression (Figure 2D) and expansion (Figure 2E), since the compression and the expansion can be treated as a part of reversed Brayton cycle and Brayton cycle, respectively, as shown in Figure 2C. As a result, by solely analyzing single-stage compression efficiency η_c, one can obtain the approximate system efficiency of the multi-stage CAES system by η_sys≈η²_c given the similar efficiencies of compressor and expander. Therefore, using the topological structure can significantly simplify the process to analyze ESS and gain a deep understanding. The objective of this study is to reveal the inherent relationships among the Brayton cycle based ESS, and the relationship between general thermal-power cycles and ESS. The results can also provide a pathway to explore the combination of thermal-power cycles with ESS.

Figure 2.

Topological structure of CAES system

(A) Configuration of multi-stage CAES system, in which CS and TS represent cold and thermal storage, respectively. In general, each compressor/expander shares equal compression/expansion ratio for improved system efficiency.²⁹

(B) Configuration of single-stage CAES system, in which C and E represents compressor and expander, respectively.

(C) Configuration of simple Brayton cycle and reversed Brayton cycle.

(D) Compression process: a compressor followed by a heat exchanger, which comes from the decomposing of single-stage CAES system or reversed Brayton cycle.

(E) Expansion process: an expander with an inlet heater, which also comes from the decomposing of single-stage CAES system or Brayton cycle.

Accordingly, this paper is structured as follows. Firstly, it analyzes the basic topological structure of the Brayton cycle. Then, the basic relationship between energy storage and thermal cycle is introduced. Tirdly, it compares different ESS formed under different storage points and paths. Lastly, the integrated system of energy storage and thermal cycle is studied, and the principle of improving the coupling performance of the two is provided.

Results

Topology of Brayton cycle

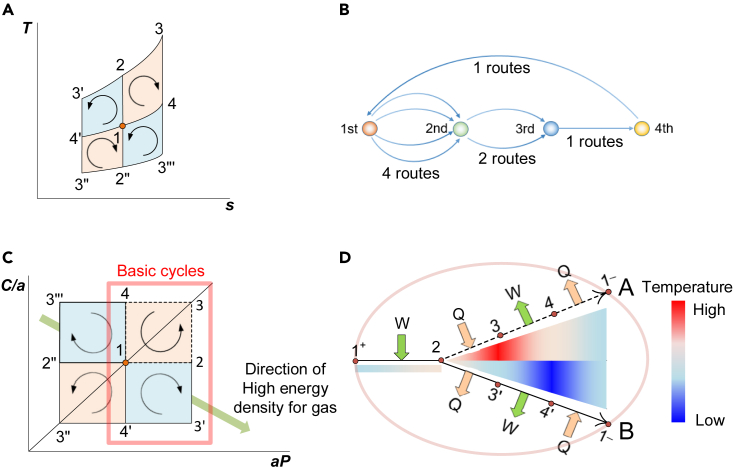
Assuming there is a point 1 in the T-s diagram (see Figure 3A), there are 8 topological choices to draw a Brayton cycle using point 1 as a vertex, resulting in 8 cycles: starting from point 1, there are 4 choices for the second point, i.e., 2, 2″, 4, and 4’; then each of them has 2 choices for the third point; for the forth point, only 1 choice is left for each third point. Multiplying all the choices gives 4∗2∗1 = 8 paths, as shown in Figure 3B. This can also be understood by the 4 cycles drawn in Figure 3A while each cycle can be reversed, resulting in 8 cycles in total.

Figure 3.

Brayton cycle topology

(A) T-s diagram of 4 key Brayton cycle topologies, in which the first step is compression or expansion.

(B) the paths with point 1 as the vertex of the Brayton cycle.

(C) C-P diagram of 4 key Brayton cycle topologies. The “a” is a constant to position the point 1 on the angular bisector of the two axes.

(D) Topologies of basic cycles in C. The orange elliptical line represents that the three points above it are in the same state. A and B represent different paths. W represents work flux, and Q represents heat flux.

When the first step of the cycle is either compression or expansion, there are only four cycles left, as shown in Figure 3A (or Figure 3C). It should be noted that when the first step is endothermic or exothermic, another four cycles, which are the reversed cycles of those in Figure 3A (or Figure 3C), can also be formed, but they are not plotted in this paper for simplicity. Figure 3A is the traditional T-s diagram of topological structures of these four cycles, while Figure 3C is the corresponding diagram on our previously proposed C-P diagram³⁰ (C is thermal-mechanical coefficient, and C = T/(p^(r−1)b/r), P=p^(r−1)b/r, in which T is temperature, p is pressure, r is specific-heat ratio, 1.4 for diatom ideal gas. b is the function of the polytropic efficiency of the compressor or expander), based on which the symmetry of these cycles can be easily observed. In Figure 3C, the left and right cycles (e.g., 1-2-3′-4′-1 and 1–2″-3″-4′-1) exhibit a reflection symmetry due to the reflection symmetry relationship between the first step of compression and expansion. Similarly, the up and down cycles (e.g., 1-2-3′-4′-1 and 1-2-3-4-1) also have a reflection symmetry relationship since the path starting from the second step points (2) has a reflection symmetry relationship. This reflective symmetry cycle has a common process rather than a complementary process, so a cycle cannot form a large loop with its reflective symmetry cycle, and the effects of the two symmetric cycles, when combined, have a mutual cancellation effect. This is consistent with the conclusion we have drawn, “reflective symmetry is not conducive to increasing system output.”³⁰ Obviously, when adjacent cycles are asymmetric, they can be stacked, and the stacking effect is gain. At this point, we weaken the reflection symmetry and increase the system’s work/heat output.

As introduced earlier, various ESS can be derived from the Brayton cycle. Specifically, both the Brayton cycle and the related ESS share the same thermodynamic process (i.e., compression, expansion and heat exchange), which has corresponding electricity (or heat) consumption and output. Thus, various ESS can be formed by disassembling and simply reconstructing the Brayton cycle. For electricity ESS, the first step is usually compression to convert electricity (those starts with thermal storage are excluded for their low exergy efficiency). Therefore, we can focus on the ESS derived from the basic cycles in Figure 3C, which are also drawn in Figure 3D. The topological structure starts from 1, and the process from 1 to 2 is absorption of work. After point 2, it is divided into two paths, one of which operates along 2-3-4-1 (path A) while the other follows 2–3′-4′-1 (path B). It can be seen that the temperature ranges of the two cycles are different as path A has a higher temperature. Figure 3C also draws the high-density direction (the green arrow) for gas media during storage, that is, the direction with higher pressure and lower temperature. Therefore, if gas is to be stored, the energy density increases along this direction.

Formation of energy storage and thermal cycles

As shown in Figure 3C, thermodynamic cycles (e.g., 1-2-3-4-1 and 1-2-3′-4′-1) can be formed without overlapping path. Besides, energy storage cycles such as 1-2-3′-2-1 and 1-2-3′-4′-1-4′-3′-2-1 can also be formed, which are featured with a starting point and separation point, overlapping paths, and reciprocation. Meanwhile, the energy storage cycle also has the characteristic of "time splitting", with the energy storage point being the splitting point of time. In the rest of the paper, the point close to the ambient temperature and pressure (i.e., the inlet condition of compressor in charge process) is set as point 1 for convenience.

Figure 4 presents several typical ESS topology based on the topological structure in Figure 3D. Each of them is the most simplified unit of this type of system, referred to as the “energy storage unit” in the following of this paper. As indicated by the red line, the cycle shown in Figure 4A is 1-2-3' (storage point, separation point)-2-1, representing an A-CAES (adiabatic CAES) system. In Figure 4B, the cycle is 1-2-3′(storage point, separation point)-2-3-4-1, which is a traditional CAES system. In Figure 4C, the cycle is 1–2(storage point)-3′-4′(storage point)-1(separation point)-4′-3′-2-1, which is a PTES system. The cycle shown in Figure 4D is 1-2-3′-L(storage point, separation point)-3′-2-1, which is a liquid air ESS. It can be seen that when circulating working media with work capacity is stored, the storage point is also the separation point, as in A-CAES, traditional CAES, and LAES. When the energy instead of the working media is stored, the storage point and separation point are not the same, as in a heat pump ESS. It is worth noting that the ESS unit shown in Figure 4B not only has energy storage characteristics (reciprocating), but also has cyclicity. Actually, it is a coupled system of ESS and thermal cycle, which will be analyzed in the last part of the Results in detail.

Figure 4.

Several general energy storage system units

(A) A-CAES system unit. SP represents separation point. TP represents starting point.

(B) traditional CAES system unit.

(C) PTES system unit.

(D) LAES system unit, in which 3′ reaches liquid point L through liquefaction process.

Based on different storage points and paths, other ESS can also be formed. In addition, different units can be integrated with each other to form a new ESS/unit as well. The composition and performance of different ESS are shown in the following part.

Energy storage system: Selection of different separation points and paths

As mentioned earlier, different separation points and paths can generate different ESS. This part is only focused on the system using compression as the first step and without external heat input. We use the branch below in Figure 3D (the topology structure in Figure 4C) as an example unit (as it can achieve high energy density) to elaborate the influence of paths and separation points on system performance. Figure 5 shows the organizational forms of the interested system, in which Figure 5A shows the overall superposition of the topological structure (one energy storage unit) shown in Figure 4C, with S representing the number of units stacked. Figure 5B shows the superposition of compression and heat transfer processes in the topological structure shown in Figure 4C. To ensure a consistent thermal storage temperature at all compression stages, the symmetric translation of compression and heat transfer processes among all stages is adopted.

Figure 5.

Organizational forms of energy storage systems with different paths and separation points

(A) stack of entire Brayton cycle unit. S represents the stack number.

(B) stack of the compression with heat exchanging (part of Brayton cycle unit), and these sub-unit has translational symmetry. N represents the stack number.

(C) Organizational principle of energy storage systems here, in which, the energy release path is the reverse route of the energy storage path.

In Figure 5A, energy storage cycle starts from point 1 to the separation point, and then follows the original path back to release energy (see Figure 5C), achieving energy storage and release. As the separation point gradually moves away from point 1, the “path” of the energy storage process becomes longer. During this path, when there is excess heat and cold in energy storage, it is necessary to store them using thermal and cold storage working fluids. When the energy storage process does not constitute a cycle, the working fluid needs to be stored when the working fluid at the separation point is at high pressure or far from room temperature. Since we take air as an example, storage of working fluid at atmospheric pressure and temperature is not considered. When the energy storage working fluid forms a cycle during energy storage, there is no need to store the working fluid because there is no mass accumulation phenomenon.

In Figure 5A, the energy storage path can be included in one unit (S = 1) or multiple units in series (S = m, m > 1). In the latter case, the energy storage process can be understood as m-1 PTES plus the remaining part of one unit.

It is worth noting that following the original path back as the energy release process derives from the "reflection symmetry".³¹ Based on our previous work,³¹ if non-similar processes (such as compression and heat transfer) occur at the symmetrical positions of energy storage and release processes, they exhibit an overall effect of thermal-to-power conversion in the system cycle, which is not beneficial to energy storage.

In Figure 5B, we demonstrate another structure of energy storage, which involves local (such as one-stage compression followed by heat exchange) symmetric translation within a unit, which is currently a common way to obtain high-pressure working fluids.

In Figure 5A, different separation points can generate different ESS. Figure 6 shows the influence of separation points on system efficiency and energy density. The highest pressure of the system is selected as 10 bar, and the thermal and cold storage working fluids are thermal oil and pebbles, respectively. We analytically modeled the ESS, see details in STAR Methods section. It can be seen that when the ESS is generated within a unit, the system efficiency decreases with increasing the path distance, and the efficiency from 3′ to 4′ decreases more significantly. The reason lies in that the loss in turbomachinery has doubled from 3′ to 4′ since the number of machines has doubled while the increase in the number of heat exchanger has a relatively small impact on system efficiency. Meanwhile, when the separation points are 4′ and 1, the amount of stored energy becomes the difference between compressor consumption and expander output, which is significantly less than the stored energy when the separation points are 2 and 3’ (the stored energy is compressor consumption). Therefore, the ratio of the increased turbomachinery loss to the stored energy significantly increases from 3′ to 4′, resulting in a lower system efficiency. The exergy destruction results of A-CAES and PTES systems are shown in Figure S1.

Figure 6.

Performance comparison of energy storage systems with different separation points

In the figure, N = 2 is for stating 100bar.

At the same time, the ESS with 4′ as the separation point (i.e., PTES system) exhibits a much higher energy density than other systems, because it does not require gas storage and thus avoids larger-volume gas storage chambers (see the comparison between heat storage volume and gas storage volume in the STAR Methods section). However, it should be pointed out that the storage pressure of the ESS with gas storage as the main energy storage unit is generally much greater than 10 bar Figure 6 shows that when the gas storage pressure increases to 100 bar (with two-stage compression), the energy density of the system can be increased by 34 times, where the A-CAES energy density is about 1/3 of PTES. However, when the PTES cold storage part adopts dual tank cold storage, the difference between the two can be further narrowed.

The modeling results of this paper are compared with the A-CAES and PTES data in reference. For the A-CAES, its system efficiency, varying in a range of 63%–75%,^9,32 is closely related to the configuration and parameters. Our efficiency for A-CAES with simple single-stage compression/expansion and heat storage is calculated to be 76.5%, which is close the upper limit of 75% in reference. The difference of 1.5% is attributed to that our model is single stage with less exergy loss, to better understand the basic characteristics of various ESS, compared to the model in reference. For PTES, our result is verified with the analytical model (see Equation 1) by A White.²³ The efficiency by Equation 1 is calculated to be 39.9% by substituting an average efficiency of 0.87 for compressor and expander and the corresponding ideal temperature increment ratio of 1.93. The 39.9% is close to our result of 40.4%, indicating the reliability of our model.

$${\eta }_{\text{ptes}}=\frac{\theta {\eta }_{\text{cp}}^2-1}{\theta -{\eta }_{\text{cp}}^2}$$ (Equation 1)

where η_ptes is PTES system efficiency; θ=T₂/T_3’, the ratio of temperature increments in ideal compression of Figure 5A; η_cp is the isentropic efficiency of compressor and expander.²³

In Figure 6, when S>=2, the system efficiency and energy density exhibit periodic fluctuations with S. The reason is that for a system with the separation point in the S-th unit, it is equivalent to embed S-1 PTES systems. Thus, as S increases, the highest point of system efficiency gradually decreases, and the change in system efficiency within each unit is consistent with the change of system efficiency within the first unit. Due to the nested PTES systems, as S increases, the overall energy density of the system decreases from S = 2, but remains below the energy density at 1' (S = 1). This is because the point of 1′ was not considered in S = m (m > 1, as this is a simple repetition of PTES system), and the subsequent systems all have air storage units.

The above results do not take the pressure loss in heat exchanger into account. When considering the pressure loss in heat exchanger, the decrease in system efficiency can be more significant as the separation point moves backward (in a single unit or at the same position of different units). Thus, long-path energy storage shows a significant disadvantage in efficiency. Even though the decrease of system efficiency can negatively affect the energy density, this negative effect is much less than effect of energy storage media. The energy storage media may differ for ESS of various length. Specifically, when the electricity is stored by the pressure energy of gas, the ESS requires a large storage volume, and the energy density is low (e.g., short-path A-CAES system). When the electricity is mainly stored in the format of heat and cold energy, only a small volume is needed and the energy density is high (e.g., long-path PTES system). Therefore, a balance between system efficiency and energy density is needed in practice.

For the case shown in Figure 5B without considering pressure loss, when N = n, the n units of compression/expansion and heat exchange have a translational symmetry. The system efficiency stays unchanged when equal compression and expansion ratios are distributed. In fact, the influence of pressure loss on system efficiency is not significant, so multi-stage compression/expansion with heat exchange cannot significantly reduce system efficiency. Different from the result in Figure 6, this increment of path length by translational symmetry cannot significantly reduce system efficiency. However, after multi-stage compression, the energy density can be significantly increased because the storage pressure is evidently increased. Therefore, increasing the number of stages is an effective way to improve energy density, ensuring that system efficiency does not decrease significantly. At the same time, multi-stage compression can also reduce the heat storage temperature at higher pressure, making it easier in engineering and reducing costs. In addition, pressure grading can improve the efficiency of compressor/expander by reducing the single stage pressure ratio, which to some extent offsets the negative impact of system-level efficiency.¹⁴

Analysis of energy storage combined with thermal cycle

Since mechanical ESS evolves from thermodynamic cycles, are there any general rule for the coupling between ESS and thermodynamic cycles? There have been works on the synergy between CAES and gas turbine operation.³³ Through synergy, when the flow ratio of the gas turbine and A-CAES was 1:1.33, the increases in net power and generated energy are 31.5% and 12.6%, respectively, and the roundtrip efficiency is increased by 3.4%. This paper will explore the synergy between A-CAES and Brayton cycles from the perspective of system topology and thermodynamics.

Figure 7A shows an integrated system of A-CAES and simple gas turbine (simple Brayton cycle). In this system, the high-pressure air in the A-CAES cavern can be extracted and fed into the combustion chamber of the gas turbine, decreasing the energy consumption of the gas turbine. When the mass flow rates of E1 and C1 in Figure 7A are close, the system can be simplified as shown in Figure 7B. Then the topological structure of the simplified system is shown in Figure 7C and its C-P diagram is shown in Figure 7D. In essence, this integration forms a traditional CAES with thermal storage, which can be regarded as a thermodynamic cycle with function of energy storage. For this coupled thermal cycle 1-2-3′-2-3-4-1, due to the nested ESS that requires high correspondence,³¹ the ESS requires a longer 1–2 path (with an increase in aP span), which enhances the reflection symmetry of the thermal cycle. Therefore, the system efficiency of the thermal cycle increases when nesting an ESS with high reflection symmetry.

Figure 7.

Integration of energy storage and thermal cycle

(A) integration of A-CAES and gas turbine. In the integrated system, the high-pressure air in the cavern can be extracted and fed into the combustion chamber of the gas turbine, decreasing the energy consumption of the gas turbine.

(B) the system can be simplified as shown when the mass flow rate of extraction equals to that of the compressor of gas turbine.

(C) the topological structure of a Brayton cycle integrated with a single-stage A-CAES (1-2-3′-2-1) cycle.

(D) C-P diagram of the integrated cycle.

The thermal cycle with energy storage capability, as shown in Figure 7B, should be evaluated differently. In the following, the impact of implicit ESS on the thermal cycle is discussed. First, we consider the case when the heat absorption of the thermal cycle increases, which can be analyzed using Figure 8. Here we focus on cycles 1-2-3-4. We do not consider the off-design effects induced by the constant-volume gas storage, so we assume that the gas storage chamber is a constant-pressure type. The compressor and expander shown in Figure 8A are both reversible, while Figure 8B shows irreversible compressor and expander. Equations 2 and 3 represent the system efficiency corresponding to the ideal case (Figure 8A) and the irreversible case (Figure 8B), respectively. Here, we consider an ESS nested within the thermal cycle. Obviously, in the ideal case, due to the absence of losses in the compressor and expander, the energy storage process 1–2 is first transformed into 2-1 during the energy release process, and then coupled with a thermal cycle 1-2-3-4-1. For the actual process, due to the losses of the compressor and expander, the energy storage process 1–2 is first transformed into 2′-1′, and then coupled with a cycle 1′-2′-3-4-1′. Therefore, for the ideal cycle, the efficiency of the nested ESS is η_storage = 1. For the actual cycle, the efficiency of the nested actual ESS is η_storage = A_{1’-2’-7’-6’-1’}/A_{1-2-7″-6″-1’}<1 (A is area). The proof of this relationship uses the method in our previous work.³⁴

$${\eta }_{1-2-3-4-1}^{ideal}=\frac{W_{3-4}-W_{1-2}^{cha}}{Q_{2-3}}=\frac{W_{3-4}-W_{1-2}^{dis}/{\eta }_{storage}}{Q_{2-3}}$$ (Equation 2)

where η is efficiency; W is the ratio of input to output work during the specific process; Q is the ratio of input to output heat. The superscript “ideal” represents ideal condition; “cha” and “dis” represent energy charging and discharging periods, respectively.

$${\eta }_{1-2-3-4-1}^{real}=\frac{W_{3-4}-W_{1-2}^{cha}}{Q_{2^{\prime }-3}}=\frac{W_{3-4}-W_{1\text{'}-2\text{'}}^{dis}/{\eta }_{storage}}{Q_{2^{\prime }-3}}$$ (Equation 3)

where the superscript “real” represents actual condition.

Figure 8.

Thermal efficiency of Brayton cycle with energy storage function under reversible and irreversible conditions

(A) C-P diagram of ideal condition, and the regenerative is not applicable.

(B) C-P diagram of real condition of compressor and expander, and the regenerative is not applicable.

(C) actual thermal cycle can be decomposed in energy storage system and semi-real cycle. In the figure, as seen in Equation 5, $Y=\left(L_{1\text{'}-2\text{'}}{C}_{2^{\prime }}/a\right)/\left(L_{2^{\prime }-3}{P}_{2^{\prime }}\right)$.

It can be seen that our traditional thermal cycle efficiency includes an actual energy storage efficiency. If we exclude the energy storage cycle, the actual thermal cycle 1-2-3-4-1 implies another ideal cycle: 1′-2′-3-4-1. For convenience, this article refers to it as the semi-real cycle, which has a system efficiency of

$${\eta }_{1’-2^{\prime }-3-4-1}^{semi-real}=\frac{W_{3-4}-W_{1\text{'}-2\text{'}}^{dis}}{Q_{2^{\prime }-3}}=\frac{P_3-P_4}{P_{2^{\prime }}}$$ (Equation 4)

where P is the function of pressure as mentioned above. Specifically, P=p^(r−1)b/r, where p is pressure and r is specific-heat ratio (1.4 for air). The superscript “semi-real” denotes semi-real cycle.

The actual cycle includes both an energy storage cycle and a semi-real cycle, and the relationship between the three is shown in Figure 8C. The semi-real cycle efficiency is greater than the actual cycle efficiency (Equation 5). Therefore, when evaluating a Brayton cycle with energy storage capability, if we consider the implicit energy storage efficiency of 1-2-2′-1′-1 as an independent consideration, the cycle efficiency should be considered as the semi actual cycle efficiency (its value is greater than the actual cycle efficiency, and when evaluating only use the actual cycle efficiency, the cycle efficiency is underestimated when considering the actual energy storage efficiency), and the combined effect of the above two independent efficiencies is the actual cycle efficiency.

From another perspective, if we only want to evaluate the system using actual thermal cycles, then the implied virtual ESS efficiency is 1! The reason is that for the actual cycle, we can imagine that the power consumption of the compressor is completely released during the actual expander output. Therefore, after an efficient Brayton cycle operates as an ESS with time sharing, not only is the overall thermal efficiency higher, but the energy storage efficiency is also apparent to be 1!

When the compression/expansion ratio and compressor/expander polytropic efficiency are constant, the energy storage efficiency and efficiency of semi-real cycle are constant. As the heat absorption increases, due to the different proportions of the above two cycle, as shown in Equation 5, the actual cycle efficiency gradually increases (the denominator of the second item increases).

$${\eta }_{1-2-3-4-1}^{real}=\frac{L_{3-4}{C}_3/a-\left(L_{1\text{'}-2\text{'}}{C}_{2^{\prime }}/a\right)/{\eta }_{storage}}{L_{2^{\prime }-3}{P}_{2^{\prime }}}={\eta }_{1’-2^{\prime }-3-4-1}^{semi-real}-\frac{\left(1-1/{\eta }_{storage}\right)L_{1\text{'}-2\text{'}}{C}_{2^{\prime }}/a}{L_{2^{\prime }-3}{P}_{2^{\prime }}}$$ (Equation 5)

where L represents the process length in C-P diagram. C is thermal-mechanical coefficient.

For the ideal cycle (Figure 8A), due to the implicit energy storage efficiency of 1, the thermal efficiency of the thermal cycle remains unchanged as the heat absorption increases. As described in Equation 6, this efficiency is only related to the pressure ratios.

$${\eta }_{1-2-3-4-1}^{ideal}=\frac{L_{2-3}\left(P_3-P_4\right)}{L_{2-3}{P}_2}=\frac{P_3-P_4}{P_2}$$ (Equation 6)

Figure 9 provides the influences of pressure ratio and maximum temperature on different efficiencies based on Equation 5. For the thermodynamic cycle with energy storage capability, the energy storage efficiency is greater than 0.8 when only the loss in the compressor and expander is considered, and it increases with pressure ratio. Meanwhile, the thermal efficiency of the semi-real cycle (without energy storage cycle) is approximately 5–30% greater than that of the original cycle. This increment of efficiency becomes even greater when increasing pressure ratio and decreasing maximum temperature. When heat regeneration (the inlet temperature of expander is greater than that of compressor) is considered, the efficiency of the semi-real cycle is still 10–15% greater than that of the original cycle even though both efficiencies are improved with high heat regeneration.

Figure 9.

Changes of various efficiencies of the integrated system

Influences of (A) pressure ratio and (B) maximum temperature on various efficiencies of the integrated system (parameters for sensitivity analysis: maximum pressure ratio of 10, compressor efficiency of 0.84, expander efficiency of 0.9, and maximum temperature of 800°C).

Conclusions

The topological structure of Brayton cycle and its derived ESS are studied in depth. We reveal the derivation mechanism of ESS based on thermal cycle, and compares the derived ESS in general conditions. Finally, the synergistic effect and gain principle of thermal cycle and ESS are revealed. Specific conclusions are drawn as follows.

• (1)We presented the topology of the Brayton cycle on the C-P diagram and specified the formation of the ESS and thermal-power cycles. Taking a certain point as the vertex of the Brayton cycle can form 8 cycles. Different from thermal-power cycles, the path in the C-P diagram that can form ESS has overlapping path, resulting in reciprocation of process. We demonstrated the simple topology of A-CAES, traditional CAES, PTES, and LAES, which are referred to as “energy storage units”.
• (2)Selecting different separation points can form a series of ESS with different path lengths. When S>=2 (S is the number of linked “basic Brayton cycle”), the storage efficiency and energy density exhibit periodic fluctuations with S, and the changes in system efficiency within each unit are consistent with each other. As the separation point moves backward, the efficiency at the same position system with different S decreases significantly, namely, long-path energy storage has obvious disadvantage in efficiency. It is also shown that the link of local symmetric part in one unit has potential to improve system performance.
• (3)The combination of thermal-power cycle (e.g., Brayton cycle) and ESS (e.g., A-CAES) exhibits the following benefits. For the thermal cycle, the reflection symmetry of the cycle is enhanced and the efficiency is improved due to the nesting of high-correspondence ESS. For the ESS, when an efficient Brayton cycle is running as an ESS with time splitting, the overall thermal efficiency is improved and an apparent energy storage efficiency of 1 is achieved. Moreover, we can dispose a thermal cycle to an energy storage cycle and a semi-real cycle for evaluating thermal cycle efficiency more suitably.

Accordingly, the reflection symmetry should be enhanced to improve the efficiency of ESS, so the “symmetric return” path proposed in this paper can be one important method in creating high-efficiency ESS. In practice, there is balance between system efficiency and energy density. Under a certain energy storage pressure, multi-stage compression and expansion sometimes improve system efficiency because the lower pressure/expansion ratio makes the compressor and expander more efficient. Furthermore, when energy storage is integrated with a high-efficiency thermodynamic cycle, the apparent efficiency of the nest energy storage can be improved.

It is worth noting that the methodology reported here can be adopted in analyzing the topological structure of other thermodynamic cycles (e.g., the Rankine cycle and those with chemical processes) and developing new ESS. Our research in combining thermal-power cycles and ESS may also guide future study on complex energy systems (involving multiple energy storage units) by building topological structures and discovering cycle units.

Limitations of the study

This paper only studies the ESS organized with two symmetric topological structures as shown in Figure 5, while there are many more ESS structures that can be derived from the Brayton cycle. For example, the translational part may not be the entire cycle unit or the compression/expansion process with heat exchange; translation of other specific parts can also form ESS. These expanded topological structures deserve further study.

The system efficiency and energy density of various ESS derived by the Brayton cycle should also be evaluated for working pressure greater than 10 bar. Ideal gas model is used here for the low pressure adopted, but for high pressure, real gas model may be needed.

The integrated system of thermal cycle and ESS is relatively simple in this paper, i.e., the integration of one simple A-CAES and one Brayton cycle, and the influence of operating strategies on system performance is not considered. Both aspects need more study.

This paper only studies the ESS derived from the Brayton cycle, but the methodology here can also be applied to study the ESS derived from other cycles such as the Rankine cycle. Those ESS also show symmetry and can be integrated with thermal cycles.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Distribution of exergy destruction of A-CAES and PTES systems	This paper	The solution is provided in the Figure S1

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Yujie Xu (xuyujie@iet.cn).

Materials availability

This study did not generate any unique materials.

Data and code availability

• •All the data involved in this article is in the main text and supplemental information.
• •This paper does not report original code.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request

Method details

Modeling of energy storage systems

When modeling ESS with different separation points, we selected air as the working fluid, dual tank indirect heat storage as the heat storage form, and the heat storage medium was thermal oil. The cold storage form was a packed bed, and the cold storage medium was pebbles due to its wide temperature range and stability. Since this article is a conceptual design, in order to facilitate calculation and capture relevant laws, the following assumptions are made: 1) air is an ideal gas²⁴;2) the specific heat capacity of the air is a constant value; 3) the heat exchanger losses are not considered separately, which is only included in heat/cold storage losses.

The outlet temperature of the i-th compressor is:

$$T_{i,\text{cout}}=T_{i,\text{cin}}{\epsilon }_{\mathrm{c}}^{\frac{r-1}{r{\eta }_{i,\mathrm{n},\mathrm{c}}}}$$ (Equation 7)

where T is temperature. η_i,_n,c is the polytropic efficiency of the i-th compressor. ε is pressure ratio. r is specific heat ratio, which is 1.4 for ideal air. Subscript i represents i-th component. Subscript cout, cin represents outlet and inlet of compressor, respectively. Subscript c represent compressor. The Nomenclature is shown in Table S1.

The work consumption for each compressor for unit mass of air is

$$w_{i,\mathrm{c}}=c_{\mathrm{p}}\left(T_{i,\text{cout}}-T_{i,\text{cin}}\right)$$ (Equation 8)

Where c_p is the specific heat capacity.

The outlet temperature of the i-th expander is

$$T_{i,\text{tout}}=T_{i,\text{tin}}/{\pi }_{i,\mathrm{t}}^{\frac{{\eta }_{n,\mathrm{t}}\left(r-1\right)}{r}}$$ (Equation 9)

where π is expansion ratio. η_n,t is the polytropic efficiency of expander. Subscript tout, tin represents outlet and inlet of expander, respectively. Subscript t represents expander.

The output work of each expander for unit mass of air is

$$w_{i,\mathrm{t}}=c_{\mathrm{p}}\left(T_{i,\text{tin}}-T_{i,\text{tout}}\right)$$ (Equation 10)

In the process of energy storage, due to not considering heat exchange losses, in order to simplify the problem, we assume that the heat exchange capacity of the heat exchanger adjacent to the compressor is the same as the power consumption of the compressor at the front end. During the energy release process, the energy exchanged capacity of adjacent heat exchanger and expander is different, which is calculated based on the efficiency of each component.

When the system stores air at high pressure, there is a loss of air storage pressure, which is described using a K value,³⁴ and the relationship between energy release pressure and energy storage pressure is as follows.

$$\ln p_{\text{dis}}=K\ln p_{\text{cha}}$$ (Equation 11)

Where p is pressure. K is used to characterize the relationship between energy release pressure and energy storage pressure, K=lnp_dis/lnp_cha, which adopts 0.92 in this paper. Subscript cha, dis represents charging and discharging parameter, respectively.

When atmospheric and low-temperature air storage is used in a system, due to the low pressure, the pressure loss is very small, and then constant-pressure storage can be used. In this situation, the pressure loss of atmospheric and low-temperature air storage is not considered.

Heat storage efficiency is used to characterize of heat storage loss:

$$Q_{\text{dis}}={\eta }_{\text{heat}}{Q}_{\text{cha}}$$ (Equation 12)

Where Q is exchanged heat. η_heat is the efficiency of heat storage and transfer.

Finally, the expression for the system efficiency is:

$${\eta }_{\text{sys}}=\frac{{\dot{m}}_{\text{dis}}{t}_{\text{dis}}(\sum w_{i,\mathrm{t},\text{dis}}-\sum w_{i,\mathrm{c},\text{dis}})}{{\dot{m}}_{\text{cha}}{t}_{\text{cha}}(\sum w_{i,\mathrm{c},\text{cha}}-\sum w_{i,\mathrm{t},\text{cha}})}$$ (Equation 13)

where $\dot{m}$ is the air mass flow rate; t is time.

The calculation method for gas storage volume is as follows. When air is stored at low- temperature and atmospheric pressure (air can be completely released):

$$V_{\text{air},\text{consp}}=\frac{{\dot{m}}_{\mathrm{c}}{t}_{\text{cha}}R{T}_{\text{storage}}}{p_0}$$ (Equation 14)

where V is volume. p₀ is the ambient pressure. T_storage is the mean temperature in the air storage chamber. R is gas constant, 287 J/(kg·K) here. Subscript consp represent constant-pressure condition.

When air is stored at high pressure. According to ref. 35, the volume of the air storage chamber is

$$V_{\text{air}}=\frac{{\dot{m}}_{\mathrm{c}}{t}_{\text{cha}}Rr{T}_0}{p_{\max }-p_{\min }}$$ (Equation 15)

where p_max and p_min represent the maximum and minimum pressure is the air storage chamber during the whole cycle.

The high-temperature heat storage volume using heat-transfer oil is:

$$V_{\text{oil}}=\frac{2{\dot{m}}_{\mathrm{c}}{c}_{\mathrm{p},\text{air}}{t}_{\text{cha}}}{c_{\mathrm{p},\text{oil}}{\rho }_{\text{oil}}}$$ (Equation 16)

Where ρ is density. Subscript oil represents oil.

The volume of using a packed bed for cold storage is

$$V_{\mathrm{r}}=\frac{3{\dot{m}}_{\mathrm{c}}{c}_{\mathrm{p},\text{air}}{t}_{\text{cha}}}{c_{\mathrm{p},\mathrm{r}}{\rho }_{\mathrm{r}}}$$ (Equation 17)

where the constant 3 considers the porosity and boundary effects of the packed bed. Subscript r represents pebbles. The specific heat capacity of the stone is:

$$\{\begin{array}{l}{c}_{\mathrm{r}}=7\times {10}^{-6}{T_{\mathrm{r}}}^2-0.003T_{\mathrm{r}}+1.05T_{\mathrm{r}}\ge 273.15\\ c_{\mathrm{r}}=0.0019T_{\mathrm{r}}+0.2502T_{\mathrm{r}}<273.15\end{array}$$ (Equation 18)

Hence the energy density of the studied energy storage system is

$$D_{\text{sys}}=\frac{{\dot{m}}_{\text{dis}}{t}_{\text{dis}}(\sum w_{i,\mathrm{t},\text{dis}}-\sum w_{i,\mathrm{c},\text{dis}})}{V_{\text{air}}+V_{\text{oil}}+V_{\mathrm{r}}}$$ (Equation 19)

By comparing Equations 14, 15, 16, and 17, it can be seen that the volume of heat and cold storage is significantly smaller than the volume of air storage, which is the reason for the high energy density of PTES.

The basic parameters for simulation of ESS are shown in Table S2.

Published: March 8, 2024