Abstract

An understanding of the nature of molecular interactions among the ion pairs of 1-ethyl-3-methylimidazolium bis(fluorosulfonyl)imide [EMI[FSI]] can offer a starting point and significant insight into the more dynamic and multiple interactions within the bulk liquid state. In this context, close inspection of ion pair conformers can offer insight into the effects in bulk [EMI][FSI] liquid. The current work, therefore, gives a detailed analysis of the [EMI][FSI] ion pair conformers through analysis of the interaction energies, stabilization energies, and natural orbital of the ion pair conformers. The structures of the cations, anions, and cation–anion ion pairs of the conformers are optimized systematically by the ωB97X-D method with the DGDZVP basis sets, considering both the empirical dispersion corrections and the presence of a polar solvent, and the most stable geometries are obtained. The [FSI]− anions, unlike [TFSI]− anions, exist at the top position with respect to imidazolium rings. The presence of out-of-plane interactions between the [EMI]+ and [FSI]− ions is in good agreement with the stronger interactions of the [FSI]− anions with alkyl group hydrogens. The presence of out-of-plane conformers could also be related to the interaction of the anion with the π clouds of the [EMI]+ ring. In the [EMI]+ cation, the aromatic ring is π-acidic due to the presence of a positive charge in the N1–C1–N2 ring, which leads to the presence of [FSI]− anion donor [EMI]+ π-acceptor type interactions. The [EMI]+ cation and [FSI]− anions tend to form multiple σ* and π* interactions but reduce the strength of the individual contributions from a potential (linear) maximum. For the ion pair [EMI][FSI], the absolute value of the interaction energies is lower than the normal hydrogen bond energy (50 kJ/mol), which indicates that there is a very weak electrostatic interaction between the [EMI]+ cations and [FSI]− anions. The weaker attraction between the [EMI]+ and [FSI]− ions is suggested to contribute to the larger diffusion coefficients of the ions.
1. Introduction
The limited safety of present-day organic carbonate-based electrolytes for lithium ion battery (LIB) technology represents a major drawback of commercially available LIBs.1,2 For these reasons, ionic liquids (ILs) are considered to be good substitutes for organic solvents for electrolytic applications in LIBs.3,4 Among all possible IL-based potential candidates for electrolytic solvents in LIBs, 1-ethyl-3-methylimidazolium bis(fluorosulfonyl)imide [EMI[FSI]] is the most noteworthy, mainly due to its relatively low viscosity. [EMI][FSI] has better intrinsic ionic conductivity than its structural analogue, 1-ethyl-3-methylimidazolium bis(trifuorosulfonyl)imide [EMI][TFSI], which makes it a solvent of choice for the formulation of safer electrolytes in LIB.5 ILs involving [TFSI]− anions are, generally, more viscous than ILs involving [FSI]− anions.6 Furthermore, [FSI]−, unlike the [TFSI]− anion, has fewer problems of aluminum corrosion.7,8 By comparison, ionic liquids based on the [FSI]− anion show reversible Li+ intercalation/extraction at graphite electrodes, whereas [TFSI]− containing ionic liquids do not form a stable solid electrolyte interface (SEI) layer and, thus, do not allow reversible Li+ intercalation/extraction on the graphite electrode. Thus, interesting electrochemical performance can be obtained by combining the [EMI]+ cation with the [FSI]− anion instead of the [TFSI]− anion.9 Clearly, it is important to balance the prospects of developing LIB electrolytes with enhanced electrochemical properties against any concerns about the stability of these compounds. It is important to understand, at a molecular level, the underlying molecular and electronic interactions that influence the viscosity and transport properties of such ILs.10 The interaction between the [FSI]− and [EMI]+ ions can be one of the main causes of the lower viscosity of the [EMI] [FSI] IL. An understanding of the nature of this interaction among the ion pairs of an IL can offer a starting point and significant insight into more dynamic and multiple interactions within the bulk liquid state. In this context, close inspection of ion pair conformers can offer insight into the effects of the bulk EMIM-FSI liquid. Although numerous structural studies on [EMI][FSI] ion pair conformers have been reported so far, there are relatively few detailed structural analyses of [EMI][FSI] ion pair conformers that have multiple interaction sites for the anion. The current work, therefore, gives a detailed analysis of the [EMI][FSI] ion pair conformers by analyzing the interaction energies, stabilization energies, and natural orbitals of the ion pair conformers. There have been previously reported studies on the geometries of the [EMI][FSI] complex at the MP2/cc-pVTZ//MP2/6-311G** level calculations by Tsuzuki et al.11,12 However, no indications were made on the conformational preference of the [EMI]+ cation (as either nonplanar staggered [EMI]+ and/or planar cis-[EMI]+ cation), and thus, there were missing details on the optimized geometry of minimum energy structures.11,12 In our study, all possible combinations of planar cis-[EMI]+–cis-[FSI]−, planar cis-[EMI]+–trans-[FSI]−, nonplanar staggered-[EMI]+–cis-[FSI]−, and nonplanar staggered-[EMI]+–trans-[FSI]− interactions were analyzed. With this in mind, therefore, the purpose of the current study is to present detailed structural and electronic insights into [EMI][FSI]-based ILs, which are potential candidates for next-generation LIB electrolytes. We report on the molecular-level study of individual ions and ion pair conformers and explore the nature of molecular interactions.
Quantum chemical methods are an indispensable tool in developing and understanding, at the molecular level, the molecular interactions between cations and anions, and the interplay between the short-range and long-range interactions, which govern the details of physicochemical properties of ILs. The Kohn–Sham (KS) density functional theory (DFT) is most often used for electronic structure calculations in quantum chemistry.13 However, in general, the drawback of all of the common functionals is their inability to describe long-range electron correlations responsible for noncovalent interactions.13 It has been shown that DFT methods without HF exchange or dispersion are clearly inferior to hybrid-DFT methods that include some HF exchange, and methods that include HF exchange and dispersion corrections have been reported to reach a qualitative accuracy of 5–10 kJ/mol.14 Thus, for ILs, the dispersion-corrected functional that needs to be employed must be at a minimum good level.14 The effects of dispersion are particularly pronounced for ILs, which involve H-bonding, π-stacking, and anion–π types of interactions.14 The effect of dispersion, for example, may result in variations in the relative geometries and orientations of the constituent ions in ILs. Thus, to get accurate geometries of imidazolium-based ILs, the use of dispersion-corrected methods makes it the minimum requirement.15 DFT-D methods have been shown to provide energetic accuracies comparable to the CCSD(T)/CBS and SAPT levels for intermolecular interactions.15,16 Good reviews are available by Hunt et al.,14 which include a discussion of QC methods and their limitations, providing some assessment of the quality of different approaches. The ωB97X-D functional is shown to have the best performance in calculating the intermolecular interactions energies for large benchmark sets of noncovalent molecules with very satisfactory results.17
The ωB97X-D functionals are range-separated functionals where the self-interaction error is corrected by including more exact HF exchange at a long range; ω is the range parameter controlling the switchover point.18 Furthermore, although basis set superposition error (BSSE) corrections may be applied for an accurate assessment of H-bond type interactions, there are scientific reports showing that the use of BSSE corrections is less significant.19 For IL ion pairs, BSSE and ZPE may lead to appreciable absolute corrections, particularly when employing the MP2 method with a double-ζ basis set. When comparing different IL conformers, however, the differences in BSSE and ZPE between the conformers are much less significant.15 In this paper, we use the ωB97X-D functional in combination with the DGDZVP basis set for the calculation of interaction and stabilization energies of ion pair conformers. The DGDZVP basis set in combination with the ωB97X-D functional performs as good as triple-ζ basis sets, and at least better than other double-ζ basis sets, which makes it well-suited for calculating halogen bond strengths on large complexes.17,20
The review is structured as follows. First, we give a summary of the computational methods employed in the current work. This is followed by a discussion of the structures of [FSI]− and [EMI][FSI] ion pairs. The fully geometry-optimized structures of the [EMI][FSI] ion pairs are used to calculate the interaction energies, stabilization energies, and natural orbital analysis of the ion pair conformers. After this, the details of cation–anion interactions are discussed by analyzing the interaction energies, stabilization energies, and natural bond orbitals (NBOs). We end this article with conclusions.
2. Computational Methods
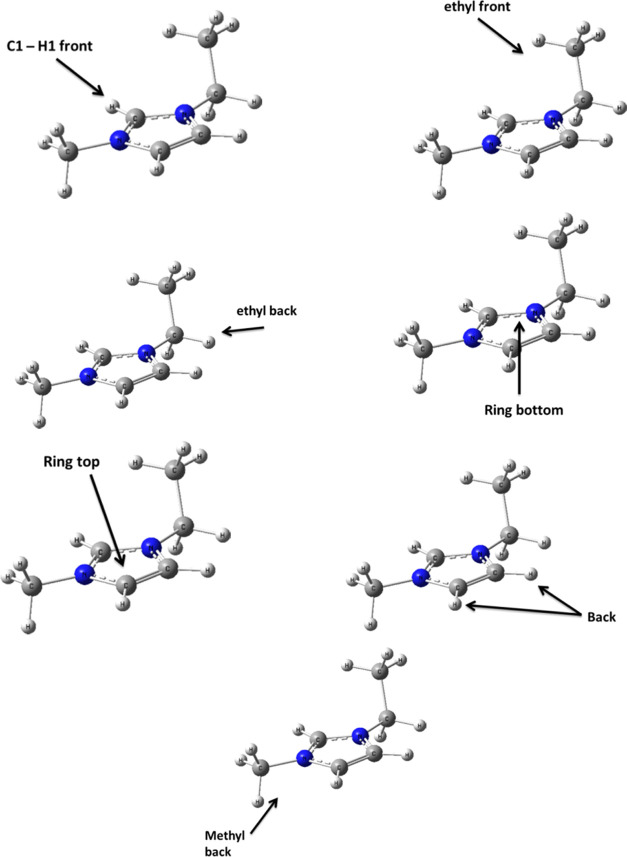
Our DFT calculations were carried out with the Gaussian 09 suite of programs21 using density functional theory with Grimme’s B97D functional, including dispersion.22 All possible initial (input) structures for orientations/configurations were considered during the optimization of [EMI][FSI] ion pairs. The initial configurations of the ion pairs were selected based on the different orientations of the cationic and anionic portions, as shown in Figure 1. They are ethyl-front (anion located infront of the ethyl chain), ethyl-back (anion located at the back of the ethyl chain), and back (anion located at the back of the cation), as shown in Figure 1. Experimental observations such as X-ray or NMR results,11,23, as well as some of references, including Dong et al.25 and Tsuzuki et al.,11 have been used as reference guides to design possible initial configurations. All ion pair calculations were carried out using the ωB97X-D method, with DGDZVP basis sets. Electrostatic interactions of the ion pair with surrounding ions were accounted for by introducing an apparent dielectric constant ε (acetonitrile) to the ionic liquid environment. The choice of polarizable continuum model (PCM) was based on prior reported MD simulation results26,27 that imidazolium-based ILs show somewhat larger solvatochromic shifts, and based on previous results that show that this approach, originally introduced for quadrupolar solvents, such as benzene and supercritical carbon dioxide, was able to describe solvation effects in nondipolar solvents.28−30 Natural bond orbital (NBO) analysis, which helps us to identify specific orbital interactions, NBO charges, and descriptions of orbital hybridization for all of the ILs was made using the ωB97X-D method with the DGDZVP basis set using the polarizable continuum model (PCM). The vibrational frequencies of all of the optimized structures were also calculated to ensure that the optimized structure represented the true minimum. The basis set superposition error (BSSE) correction was not employed, as its contribution to the interaction energy for an ionic salt were reported to be insignificant.31,32
Figure 1.
[EMI]+ cations showing possible initial (input) structures for orientations/configurations that were considered during the optimization of [EMI][FSI] ion pairs.
3. Results and Discussion
3.1. Geometric Analysis
3.1.1. Structures of Isolated Cations and Anions
One of the distinctive features of ionic liquids containing the imidazolium [EMI]+ cation, bis(trifluorosulfonyl) imide [TFSI]− and bis(fluorosulfonyl) imide [FSI]− anions that the charge delocalization and/or the asymmetry of these ions generally determines the unusual properties of these ionic liquids. The fact that these large ions are nonrigid and can adopt different conformations is another key feature of these ionic liquids. It is, therefore, worth analyzing and revising the conformational behavior of the constituent ions corresponding to these ionic liquids. To better understand the interaction between the [EMI]+ cation and [FSI]− anion, the structures of the most stable geometry of the isolated [FSI]− anion were first analyzed and revised. The structures of the fully optimized [EMI]+ cation have already been discussed in our previous reports.33 The vibrational frequencies of all of the optimized structures have also been calculated to ensure that the optimized structure represents the true minimum. The atomic numbering scheme employed in this work is shown in Figure 2. The structures of the fully optimized [FSI]− anion and [EMI]+ cation are shown in Figure 3. The selected structural parameters for the [FSI]− anion are compiled in Table 1.
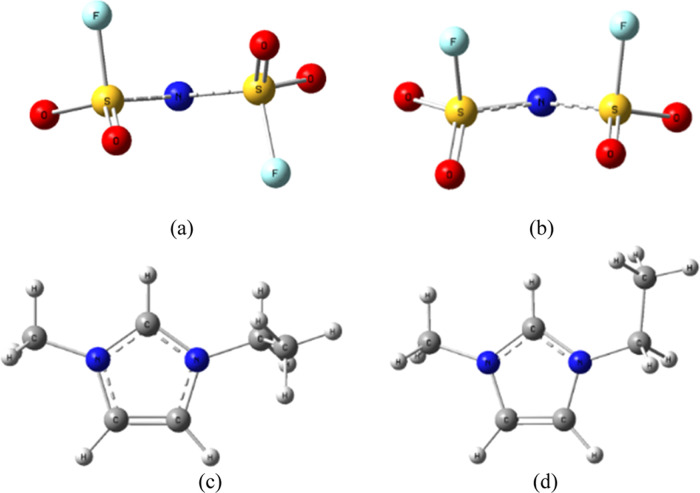
Figure 2.
Atomic numbering scheme employed in the present work: (a) [EMI]+ and (b) [FSI]−.
Figure 3.
Structures of the fully optimized [FSI]− anion and [EMI]+ cation: (a) trans-[FSI]−, (b) cis-[FSI]−, (c) staggered [EMI]+, and (d) planar [EMI]+.
Table 1. Structural Parameters of the cis-[FSI]− and trans-[FSI]− Conformers in the Gas and in the Dielectric Continuum using the ωB97X-D Functionala.
|
trans-[FSI] |
cis-[FSI] |
|||
|---|---|---|---|---|
| ωB97X-D/DGDZVP | ωB97X-D/DGDZVP | ωB97X-D/DGDZVP | ωB97X-D/DGDZVP | |
| bond length (Å) | gas | solvent | gas | solvent |
| S–N | 1.594 | 1.594 | 1.593 | 1.593 |
| S–O | 1.443 | 1.446 | 1.444 | 1.444 |
| S–F | 1.641 | 1.634 | 1.645 | 1.637 |
| bond angle (deg) | ||||
| F–S–O | 103.49 | 103.85 | 103.55 | 104.36 |
| F–S–N | 102.61 | 102.57 | 102.86 | 102.64 |
| O–S–N | 116.19 | 115.80 | 116.44 | 116.51 |
| dihedral angle (deg) | ||||
| F–S–N–S | 76.1 | 76.5 | 64.0 | 66.4 |
| O–S–N–S | –36.2 | –35.6 | –48.5 | –45.9 |
| relative E (kJ/mol) | 195.869 | 0.000 | 200.373 | 4.300 |
Conformer energies are reported relative to the lowest energy conformer.
The [FSI]− anion has two minimum energy structures: one with trans-symmetry, where the F atoms are on opposite sides of the O–S–N–S dihedral angle, and the other with cis-symmetry, where the F atoms are on the same side of the O–S–N–S dihedral angle (see Figure 3). On the basis of the ωB97X-D method and in the presence of a polarizable dielectric continuum medium, we found that the conformers with the O–S–N–S dihedral angles −35.6° (trans-[FSI]−) and −45.9° (cis-[FSI]−) give the global and local minima, respectively, with an SCF energy difference of 4.3 kJ mol–1. Similarly, previous studies conducted on the same [FSI]− anion showed that the [FSI]− anion could exist as the cis-[FSI]− or trans-[FSI]− conformers, which are located either at the cis or trans position with respect to the F–S–N–S–F skeleton.34 Experimentally, the cis-[FSI]− anion conformer was observed in the crystals of [M]+[FSI]− (M+ = Li+, K+, C6H6, Ag+).35 The trans-[FSI]− anion conformer was observed in the crystals of [M]+[FSI]− (M+ = Cs+, CHCl3, Ph3C+, Ph3PH+, and (CH3)3Pb+).36,37 Two stable conformers of anti-[FSI]− and cis-[FSI]- have also been identified by Hartree–Fock (HF) calculations,38 MP2-level calculations,39 MD simulations,40 DFT calculations, and Raman spectroscopy.41 Our calculated results for the S–N–S–F dihedral angles are 66.3° for the cis conformer and 76.5° for the trans conformer. The ωB97X-D functional approach, in which dispersion interactions are generally regarded as the most excellent alternative to deal with ionic liquids containing imidazolium-based systems, the effect of dispersion interactions leads to ring stacking interactions and intermolecular interactions like H-bonding.42
3.1.2. Structures of Isolated Ion Pair Conformers
The transport properties of ionic liquids, such as viscosity and diffusion coefficients, are controlled by the intermolecular interactions among the ions, and the nature of this intermolecular interaction, in turn, is governed by the type of specific molecular conformation adopted by each ion. Both experimental and theoretical studies have shown that the anions and cations that constitute ionic liquids could exhibit the same conformational landscape in the liquid phase as the ones calculated by using ab initio (DFT) methods for the isolated ions.43 In the liquid state, the ions do have enough freedom to adopt the conformations dictated by their internal structures and may also have enough freedom to interconvert among different conformations. A close inspection of the [FSI]− anion and [EMI]+ cation, which can adopt different conformational states, could shed some light on a better understanding of the nature of intermolecular interactions in the 1-ethyl-3-methylimidazolium bis(fluoromethylsulfonyl)imide ([EMI][FSI]) ionic liquid. To find the most stable geometry and the molecular interactions of [EMI][FSI] ion pairs, geometry optimization of each ion pair conformer was done on isolated ion pairs with the ωB97X-D/DGDZVP level of theory and basis set. Electrostatic interactions of the ion pair with surrounding ions were effectively accounted for by introducing an apparent dielectric constant (acetonitrile) in the ionic liquid environment. The results of the selected parameters for the interionic bond lengths, angles, and dihedral angles in different ion pair conformations are listed in Table 2. For convenience, the atomic numbering scheme employed in the present work is displayed in Figure 1. A total of six optimized minimum energies were obtained for the [EMI][FSI] ion pair that could be connected via the most acidic proton (H1) of the cation or via the other protons of the methyl and ethyl groups of the cation (see Figure 4). THe vibrational frequencies of all of the optimized structures were also calculated to ensure that the optimized structure represented the true minimum.
Table 2. Bond Distance, Bond Angle, and Dihedral Angles between the [EMI]+ Cation and [FSI]− Anion in Dielectric Continuum Using the ωB97X-D/DGDZVP Level of Theory and Basis Set.
| acceptor–donor | C1 | C2 | C3 | C4 | C5 | C6 |
|---|---|---|---|---|---|---|
| bond length (Å) | ||||||
| C1–H1 | 1.077 | 1.078 | 1.079 | 1.077 | 1.080 | 1.078 |
| C1–H1···O1 | 2.736 | 2.902 | 2.834 | 2.777 | 2.255 | 2.917 |
| C5–H8···O1 | 2.857 | 2.832 | 2.966 | 2.871 | 2.419 | 2.817 |
| C5–H8–O2 | 2.610 | |||||
| C2–H2–O2 | 2.506 | 2.511 | 2.511 | 2.496 | 2.764 | 2.563 |
| C6–H9–O2 | 2.616 | |||||
| C5–H8···F1 | 2.887 | |||||
| C5–H8···F3 | 2.738 | |||||
| C1–H1···N1 | 3.310 | 3.442 | 2.469 | 3.298 | 3.806 | 3.363 |
| C6–H9···N1 | 2.775 | 2.737 | 2.816 | |||
| bond angle (deg) | ||||||
| <C1–H1···O1 | 98.84 | 92.59 | 92.56 | 98.75 | 142.35 | 94.31 |
| <C5–H8···O1 | 104.16 | 102.37 | 94.04 | 105.77 | 149.48 | 105.01 |
| <C5–H8–O2 | 149.48 | |||||
| <C2–H2···O2 | 135.29 | 138.01 | 143.46 | 137.34 | 134.68 | |
| <C6–H9–O2 | 124.26 | |||||
| <C1–H1···N1 | 65.90 | 62.83 | 115.36 | 65.04 | 124.97 | 63.14 |
| <C6–H9···N1 | 130.16 | 124.47 | 128.30 | |||
| dihedral angle (deg) | ||||||
| <N2–C1–H1–O1 | –64.5 | –63.5 | 65.1 | –65.0 | 21.6 | –63.1 |
| <N1–C1–H1–O1 | 113.5 | 115.2 | –113.3 | 112.9 | –157.3 | 115.5 |
| dipole moment (μ) | 16.1 | 16.4 | 19.3 | 16.6 | 19.3 | 17.1 |
| relative E (kJ/mol) | 4.637 | 4.434 | 4.586 | 0.163 | 5.849 | 0.000 |
Figure 4.
Optimized geometrical structures of cation–anion pairs in order of their energy relative to the lowest energy conformer (kJ/mol). C1 (planar cis[EMI]···cis[FSI]), C2 (staggered nonplanar[EMI]···cis[FSI] anti), C3 (staggered nonplanar[EMI]···cis[FSI] syn), C4 (planar cis[EMI]···trans[FSI]), C5 (staggered nonplanar[EMI]···trans[FSI]), and C6 (staggered nonplanar[EMI](anti)···trans[FSI]).
The geometries of the [EMI][FSI] complex at the MP2/cc-pVTZ//MP2/6-311G** level have been reported by Tsuzuki et al.12 In that study, the geometries of the [EMI][FSI] complex were optimized from 54 initial geometries, of which 29 geometries of the [EMI][FSI] complex were obtained. Both the trans and cis forms of the [FSI]− anion conformers were used for the geometry optimization of the [EMI][FSI] complex; however, no indications were made on the conformational preference of the [EMI]+ cation (as either nonplanar staggered [EMI]+ and/or planar cis-[EMI]+ cation) and, thus, there were missing details on the optimized geometry of the minimum energy structures.11 Moreover, the results were sensitive to the computational method and basis set. For example, the optimized geometries of the [EMI][FSI] ion pair at the MP2/cc-pVTZ//MP2/6-311G** level, as shown in Figure 8 (1Y) of ref (12) involve [FSI]− anions in between the cisoid and transoid configurations (guach configuration), which when reoptimized at the ωB97X-D functional resulted in the [EMI][FSI] ion pair with the [FSI]− anion in the cis-configuration. Moreover, the optimized structures, which are reported in Figures 8 and 2S of ref (12) did not take into account the presence of planar cis-[EMI]+···cis-[FSI]− and planar cis-[EMI]+···trans-[FSI]− combinations. These studies failed to report C1 (planar cis[EMI]···cis[FSI]), C2 (staggered nonplanar[EMI]···cis[FSI] anti), C4 (planar cis[EMI]···trans[FSI]), and C6 (staggered nonplanar[EMI](anti)···trans[FSI]) ion pair conformers, which are extensively discussed in our work. Thus, to obtain accurate optimized geometeries, higher-level methods with very good and extended basis sets need to be employed. In our study, all possible combinations of planar cis-[EMI]+···cis-[FSI]−, planar cis-[EMI]+···trans-[FSI]−, nonplanar staggered-[EMI]+···cis-[FSI]−, and nonplanar staggered-[EMI]+···trans-[FSI]− interactions were analyzed. As presented in Figure 4, a total of six different minimum energy stable ion pair conformers (C1–C6) were obtained. The energy difference relative to the lowest energy ion pair conformer ranged from 0.163 to 5.849 kJ/mol (Table 2). According to our results, the C6 (Figure 4) ion pair conformer was found to be the lowest energy conformer. From our closer inspection of the C6 ion pair conformer, we found that the C6 ion pair conformer constitutes a nonplanar staggered [EMI]+–cis[FSI]− ion pair configuration with the [FSI]− anion at the top position. The second, third, fourth, fifth, and sixth lowest energy conformations predicted were, respectively, nonplanar staggered-[EMI]+ (anti)–cis-[FSI]− (C2), nonplanar staggered-[EMI]+ (syn)–cis-[FSI]− (C3), planar cis-[EMI]+–cis-[FSI]− (C1), and nonplanar staggered-[EMI]+ (syn)–trans-[FSI]− (C5). The [FSI]− anion, in all of the C1–C6 states, was found to be in the top position with respect to the imidazolium rings. For the [EMI][TFSI] ion pair conformers, however, both in-plane and out-of-plane configurations were possible.32 The [FSI]− anion adopts a cis conformation for C1 C2, and C3 for the C–S–S–C dihedral angle, whereas a trans conformation for the [FSI]− anion was predicted for C4, C5, and C6 ion pair conformers. The [FSI]− anion in the two most stable ion pair conformers adopted a trans configuration. The values of the dihedral angles N1–C1–H1–O1 for all of the C1–C6 ion pair conformers are in the range of 112.9–115.5°, indicating that the [FSI]− anion is in the top position with respect to the imidazolium rings.
For imidazolium-based ILs, weak H-bonds are usually formed with the C1–H1 group of the cation as the primary H-bond donor unit,44 and the presence of a hydrogen bond between the C1–H1 unit of the imidazolium ring and the oxygen atom of the [TFSI]− anion has been reported.23,45,46 Intermolecular forces such as H-bonds and π-type interactions that simultaneously occur in [EMI][FSI]-based ionic liquids are worth mentioning. Despite the absence of a conclusive and universally accepted definition of the H-bond, H-bonding is still a key area of debate regarding the properties of ionic liquids. The strength of the H-bond can be related to the donor–acceptor distance and angle as a first estimate.47−49 This, of course, also depends on the nature of the atoms involved and the angle between them. Figure 5 shows the possible H-bond interaction sites between the [EMI]+ cation and the [TFSI]− anion. Generally, an H-bond distance of less than 250 pm is considered to be a very strong H-bond, an H-bond distance between 250 and 265 pm is considered as a strong or moderately strong H-bond, and a, H-bond distance greater than 280 pm is considered very weak. On the basis of distance criteria, the [EMI][FSI] complex shows distances of rather weak hydrogen bonds (see Table 2). The values of the distances of Cl–H1···O1 for the ion pair conformers C1, C2, C4, C5, and C6, respectively, are 2.78, 2.90, 2.83, 2.78, 2.26, and 2.92 Å, indicating that only the C5 ion pair conformer is within the accepted criteria of the C1–H1···Ol primary H-bonds. The C5 ion pair conformer exhibits bifurcated C–H···O1 inter-ion interactions through the primary C1–H1 (2.26 Å) and terminal methyl group C5–H8 cation H-bonds (2.42 Å) (see Figure 4). The terminal methylene H-bond interactions through C2–H2–O2 were observed for the C1 (2.50 Å), C2 (2.51 Å), C3 (2.51 Å), and C6 (2.56 Å) ion pair conformers. From Table 2, it can be seen that the structures of the [EMI]+ cation rings show very little changes for the distance of C1–H1, except for C5 ion pair conformer (1.08 Å), which indicates that only the C5 conformer has C1–H1···Ol primary H-bond interactions. On the basis of geometric criteria given in Table 2, there are no C–H···F interactions observed for the [EMI][FSI] single ion pair conformers. The presence of the out-of-plane interactions between the [EMI]+ and [FSI]− ions is in good agreement with the stronger interaction of the [FSI]− anions with the alkyl group hydrogens. The presence of out-of-plane conformers could also be related to the interactions of the anion with the π clouds of the [EMI]+ ring, which is further discussed in Section 3.3 from the natural orbital analysis of the conformers. In the [EMI]+ cation, the aromatic ring is π-acidic due to the presence of a positive charge in the N1–C1–N2 ring, which leads to the presence of [FSI]− anion donor [EMI]+ π-acceptor type interactions.
Figure 5.

[EMI]+ cation showing the possible H-bond interaction sites for the [FSI]− anion.
3.2. Interaction Energies of Isolated Ion Pair Conformers
The intermolecular interactions between the anions and cations of ionic liquids are the most important factors that dictate the transport properties of such liquids. Despite extensive studies on the magnitude of the interaction energy between ions and their influence on the structure and physical properties of ionic liquids, however, little is known about their magnitude and dependence on the ions. Ever since the first report on the presence of hydrogen bonding in the structure of 1-alkyl-3-methylimidazolium salts by Seddon et al., further studies for the presence of hydrogen-bonded ion–ion interactions were conducted by Dymek et al., Avent et al., and Elaiwi et al. in the early 1990s.11,25,34,50,51 Studies have been carried out since then, and different explanations have been proposed to explain the nature of the intermolecular interactions. While some authors provided both theoretical and experimental evidence in support of the role of hydrogen bonding, others strongly challenged the presence of hydrogen bonds in ILs, arguing that hydrogen bonding is not essential for understanding the properties of ILs.11,25,34,50,51 Ab initio molecular orbital calculation methods are the method of choice for the investigation of intermolecular interaction energies. As long as a large basis set is used, and electron correlation is properly implemented, ab initio calculations could provide accurate values of interaction energies.49,,53 Aiming at investigating the molecular interactions and the occurrence of H-bonding in [EMI][FSI] ion pairs, the interaction energies of the different ion pair conformations were calculated, and the results are shown in Figure 6. The interaction energy between the cation and anion of the ILs was calculated according to the following expression (eq 1):
| 1 |
where E(IP) is the energy of the ion pair and E (cation) and E (anion) are the energies of the cation and anion, respectively.
Figure 6.

Correlation between the interaction and relative conformer energies of different ion pair conformers of the [EMI][FSI] ion pairs.
The correlations between the interactions and relative conformer energies of different [EMI][FSI] conformers are shown in Figure 6. The C4 ion pair conformer has the maximum, and the C5 conformer has the minimum absolute interaction energy. A comparison between the interaction and relative conformer energies reveals that there are very important differences between the ordering of the calculated relative and interaction energy values. According to Figure 6, the values of the relative optimized energies of the six conformers change in the following order: C6 > C4 > C2 > C3 > C1 > C5, whereas the absolute interaction energies change in the following order: C4 > C1 > C6 > C2 > C3 > C5. The absolute values of the interaction energies of conformers C1, C4, and C6 are 44.011, −44.186, and −40.466 kJ/mol, respectively, which are higher than those of C2 (40.332 kJ/mol), C3(40.180 kJ/mol), and C5 (−34.616 kJ/mol). The relative energy of the C6 ion pair conformer is lower than that of the ion pair conformers of C4 by 0.163 kJ/mol (see Table 2). On the other hand, the absolute interaction energy of the C4 conformer (44.186 kJ/mol) is greater than the absolute interaction energy of the C6 conformer(40.466 kJ/mol). The question of why the C6 ion pair (global minimum) conformer has less absolute interaction energy than C4 (local minimum) is likely to arise. Ludwig and co-workers have shown that agreement with experimental data can only be obtained by choosing conformers that hold higher absolute interaction energies than the global minimum. Thus, the sole importance of the global minimum structure for the condensed phase is highly questionable.50 Apparently from the results in Figure 6, for the ion pair [EMI][FSI], the absolute value of the interaction energies is lower than the normal hydrogen bond energies (50 kJ/mol), which indicates that there exists a very weak electrostatic interaction between the [EMI]+ cations and [FSI]− anions. The weaker attraction between the [EMI]+ and [FSI]− ions is suggested to contribute to the larger diffusion coefficients of the ions. The lower viscosity of the [EMI][FSI] compared to that of [EMI][TFSI]-based ionic liquids originates from its relatively smaller interaction energy. Similar conclusions were drawn by Tsuzuki et al.12 for the [FSI]− complex with [EMI]+ by ab initio molecular orbital methods.
Further to our analysis of the ion pair conformers, we also stress the importance of H-bonding between the C1–H1 of the [EMI]+ ring and the [FSI]− anion. The values of the interaction energies are not well reflected in the geometry of the H-bond (donor–acceptor distance and angle), indicating that the H-bond is not the only interaction. For example, the absolute value of the interaction energies is the lowest for the C5 ion pair conformed, which has the strongest and most linear C1–H1···O1 interactions (see Table 2). On the other hand, the value of this interaction energy is the highest for the C4 conformer, while this conformer has the weakest and nonlinear C1–H1···O1 primary H-bond interactions, indicating that the [FSI]− anion interaction with the C1–H1 proton of the [EMI]+ ring has little influence on the interaction of the conformers. Tsuzuki et al.51 have drawn similar conclusions because they obtained a smaller angle (lacking directionality) in energetically stable conformers than those in linear arrangements.
From our geometry optimizations, we found ion pairs with a wide range of H-bond lengths and angles. The C5 ion pair conformer has shorter and stronger primary H-bond interactions with the C1–H1 hydrogen of the [EMI]+ cation, while it has the lowest absolute interaction energy. On the other hand, C1, C4, and C6 ion pair conformers have weaker primary H-bond interactions with C1–H1 of the [EMI]+ cation but yet stronger and more linear secondary H-bond interactions with the methylene hydrogen (C2–H2) of the [EMI]+ cation, and have higher values of absolute interaction energy. Prior reported studies have argued that the interaction between the C1–H1 hydrogen atom of the [EMI]+ cation was not an H-bond-like interaction, and the distance from the nearest hydrogen atom was not the main factor determining the size of the attraction.11 In those reports, it has been shown that the nature of the interaction between the C1–H1 hydrogen atom of the [EMI]+ cation and a range of anions was considerably different from that of conventional hydrogen bonds and this interaction did not show any dependence on orientation for these authors have found that small angles (lacking directionality) in energetically more stable conformers than those with linear arrangement.11 When imidazolium cations are associated with large anionic groups, like the [FSI]− anion, there exist varying levels of H-bond strengths and interactions, and additionally, the [FSI]− anion takes preferential on-top distributions above and below the imidazolium rings, leading to π-type interactions. The interplay of H-bond and π-type interactions in [EMI][FSI] ionic species depends on the particular [EMI][FSI] ion pair conformer, and in general, weak interaction energies have been observed.54 However, an individual [EMI][FSI] ion pair may undergo multiple interactions within the liquid environment, increasing the overall energy contribution from the H-bonds.
3.3. Stabilization Energies of Isolated Ion Pair Conformers
The mode of intermolecular interactions between the [EMI]+ cations and larger anions such as [TFSI]− and [FSI]− has been the subject of continuing scientific debate and discussions. Some authors believe that the ions in ionic liquids are held together by H-bonding, while others believe that the role of the H-bond is minor compared to the role of electrostatic interactions.11,14,25 The natural bond orbital (NBO) carried out on DFT-optimized [EMI][FSI] ion pair structures gives a unique feature for analyzing the electron density, which thereby allows the analysis of intermolecular donor–acceptor orbital interactions. Therefore, we carried out an NBO analysis of the different [EMI][FSI] ion pair conformers. This analysis, which has been proven to provide reliable (in a chemical sense) information regarding the change in charge densities of donor and acceptor ions, is also less method-dependent.55 The H-bond strength of the nY → σ*X–H donor–acceptor follows the same trend with NBO stabilization energies (E2n→σ*), as expressed in eq 2(56) For each donor NBO(i) and acceptor NBO(j) orbitals, the stabilization energy E(2) associated with the delocalization of the electron pair from the donor orbital (i) to the acceptor orbital (j) is defined as
| 2 |
where qi is the donor orbital occupancy, εi and εj are the diagonal elements (orbital energies), and F(i,j) is the interaction element between the donor and acceptor orbitals and is known as the diagonal NBO Fock matrix element. The value of the stabilization energy (E(2) (kcal/mol)) is obtained from second-order perturbation theory.55 When electrons are shared via the lone pairs of oxygen and nitrogen atoms to the σ-type and π-type antibonding orbital of the C–H, C=C, and N–C bonds (Ylp → σ*C–H, Ylp → π*C=C, Ylp → π*C–N), where Y = N, O; this is equivalent to transferring electron density from the lone pair of N and/or O atoms into the σ*C–H, π*C=C, and/or π*C–N orbitals. The magnitude of the cation–anion interactions can be related to the charge transfer component of E(2)n → σ*, E(2)n → π*C=C, and/or E(2)n → π*C–N, which is proportional to the amount of electron density (qi) donated from the filled donor lone-pair orbital into the empty σ* and/or π* antibonding orbital, moderated by the energy difference between these two fragment orbitals (Δε), and thus the NBO analysis on the DFT-optimized structure allows the analysis of intermolecular donor–acceptor orbitals interactions.56
Early studies on NBO analysis on ionic liquids have been limited to various alkyl-imidazolium derivatives with simple poly/monatomic anions.25,56 However, there have not been any prior reported studies on the detailed NBO analysis of alkyl-imidazolium derivatives with bis(fluoromethylsulfonyl)imide [FSI] ion pair conformers that have multiple interaction sites for the anion. In this article, we report how stabilization energy obtained from NBO analysis of different ion pair conformers of [EMI][FSI] helps to get the details of orbital interactions between the empty σ*C–H, π*C=C and π*C–N fragment orbitals (FO) of the [EMI][FSI] ion pair complex at the ωB97X-D level using the DGDZVP basis set and the presence of a dielectric continuum medium, and the results are compiled in Tables S1–S6. Previous reports11,54−56 have shown that imidazolium-based ion pairs with weak H-bond acceptor anions such as [BF4]− and [PF6]− have E(2)n → σ* = 50–60 kJ/mol, while those with strong H-bond acceptor anions such as Cl– and [NO3]− have E(2)n → σ* = 110–180 kJ/mol. H-bond interaction is not a binary on–off phenomenon but occurs on a graduated scale, which makes quantifying and demarking H-bonding difficult. Generally, weak H-bonds have E(2)n → σ* < 30 kJ/mol and strong hydrogen bonds have E(2)n → σ* > 150 kJ/mol44 and those lying between these extremes are moderate hydrogen bonds. A more robust level of knowledge is required to relate the E(2)n → σ* parameter with respect to hydrogen bonds in ionic liquids containing the [EMI]+ cation and large, more diffuse anions such as [FSI]−. It requires a close inspection and analysis of a large range of ionic liquid ion pair conformers, geometric influences, and the impact of multiple concomitant hydrogen bonds that need to be better understood.
From Tables S1–S6, we observed, in general, that, for [EMI][FSI] ion pair conformers, charge transfer occurs mainly from the lone pairs of oxygen and nitrogen atoms to the σ-type antibonding orbital of C–H, and to the π-type antibonding orbitals of N–C and C=C bonds. This is evident from the values of the stabilization energy (E(2)) associated with the delocalization of each electron from the donor to acceptor orbitals. The [FSI]− anion transfers charge to the [EMI]+ cation, and this extra electron density is distributed over the N1, N3, and C4/5-H centers. There is a rough correlation between the amount of charge transferred and the relative value of the stabilization energy: the greater the value of the stabilization energy, the more stable the ion pair, and the more charge is transferred. Apparently, from the above results, it is noticeable that for the [EMI][FSI] ion pair conformers, the values of the stabilization energy E(2) are generally small (E(2)n → σ* < 2 kcal/mol) for the individual E(2)n → σ*, E(2)n → π*C=C, and/or E(2)n → π*N–C interactions. The [EMI]+ cation and [FSI]− anions tend to form multiple σ* and π* interactions but reduce the strength of the individual contributions from a potential (linear) maximum. The relative contribution from each of these is not easily resolved via the association energy, which includes the ionic and combined H-bond contributions.
The shorter the C1–H1···O H-bond distance, the larger the charge transfer, and the larger the corresponding stabilization energy E(2) associated with electron delocalization from the donor to acceptor antibonding orbital. The ion pair conformer C5, for example, has the shortest C1–H1···O1 bond (2.26 Å) and a more linear angle (142.35°), and thus relatively with a greater value of second-order perturbation energy for O1 → σ*C1–H1 (E(2) = 1.37 kcal/mol) among all ion pair conformers investigated. NBO analysis of the [EMI][FSI] ion pair conformers also revealed that the lone pairs of oxygen and nitrogen atoms donate electrons to the σ-type (σ*C1–H1) and π-type antibonding orbital for π*N1–C1 and π*C4=C5 bonds. The occurrence of NBO interactions of n → π*N1–C1 and n → π*C4=C5 implies the existence of anion donor–π* interactions in these systems. The LP(1)F, LP(2)F, and LP(1)F (donor NBO)→ BD*(2)C1–N1 (acceptor NBO) interactions show the presence of weak N1–C1···F anion donor–π* interactions for the C5 ion pair conformer. Furthermore, for the C5 conformer, the LP(1)O1 and LP(3)O1 (donor NBO)→ BD*(2)C1–N1 (acceptor NBO) interactions show the presence of weak N1–C1···O anion donor–π* interactions. Similar types of weak N1–C1···O anion donor−π* interactions have been observed for all other types of C1–C5 conformers. A second type of weak C=C···O anion donor−π* interactions has also been observed for C2 and C6 ion pair conformers.
Further to our analyses of the ion pair conformers, the NBO method has also been employed to characterize the natural orbital coefficients and orbital hybridization of the different conformers of the [EMI][FSI] ion pair. The main listing of NBOs, displaying occupancy, natural atomic hybrids, polarization coefficient, and spλ composition of the different conformers of the [EMI][FSI] ion pair for a selected set of NBOs are shown in Tables S7–S11. For the ion pair conformer C5, which has relatively higher value of E(2) values for C1–H1···O interactions, the σ*C1–H1 NBO is formed from an sp0.34 hybrid (62.03% p-character) on carbon interacting with hydrogen (100.00%) s-character corresponding to a linear combination of atomic orbitals 0.6097*C(p1.64)–0.7926*H (s) comprising a larger polarization coefficient of H. The orbital interaction between lone pair orbitals LP(1)O1 and σ*(1)C1–H1 (E(2) = 1.37 kcal/mol) has sp1.63 hybrid orbital with s(75.44%) character and p(24.55%) character; and the orbital interaction between lone pair orbitals of LP(2)O1 and σ*(1)C1–H1 (E(2) = 1.15 kcal/mol) with s(0.01%) character and p(99.70%) character for LP(2)O1 orbital. Similarly, for the C2 ion pair conformer, the π*C4=C5 NBO is formed from an sp0.34 hybrid of carbon (C4) with p (99.87%) character and carbon (C5) with p (99.88%) character, corresponding to the linear combination of the orbitals 0.7061*C(sp0.34)–0.7081*C(sp0.34) with nearly equivalent polarization carbon atoms. The natural bond orbital (NBO) interactions of the different conformers C2–C6 of the [EMI][FSI] ion pairs are shown in Figure 7.
Figure 7.
Selected natural bond orbital (NBO) interactions between the different conformers of [EMI][FSI] ion pairs in a dielectric continuum medium using the ωB97X-D method and DGDZVP basis set. C1 (planar cis[EMI]···cis[FSI]), C2 (staggered nonplanar[EMI]···cis[FSI] anti), C3 (staggered nonplanar[EMI]···cis[FSI] syn), and C5 (staggered nonplanar[EMI]···trans[FSI]).
Selected partial charges for the different ion pair conformers of [EMI][FSI] are also reported in Tables S7–S11. The hydrogen atoms that interact with the [FSI]− anion are more positive, and the associated carbon atoms are slightly more negative. NBO analyses of the [EMI][FSI] ion pair conformers were performed to obtain the NBO charge distribution. For the C5 ion pair conformer, the NBO charge of H1 (0.25252) is more positive than that of other hydrogen atoms, while the NBO charges of O1(−0.97161) is more negative than that of other oxygen/fluorine atoms, which is ascribed to the C1 - H1···O1 H-bond interactions. Similarly, the anion donor π-type antibonding interactions between the most electronegative N1 and O1 atoms of the [FSI]− anion with the π*N1–C1 antibonding orbital of the [EMI]+ cation leads to more positive charges on the C1 atoms of the C1(0.34293), C2(0.35193), and C5(0.35038) ion pair conformers. The greater the magnitude of the anion donor π*N1–C1 antibonding interaction, the higher the positive charges on the C1 atoms of the [EMI]+ cation.
4. Conclusions
The nature of the optimized geometries of a series of ion pair conformers of the 1-ethyl-3-methylimidazolium bis(fluoromethylsulfonyl)imide ionic liquid has been thoroughly discussed by analyzing the interaction energies, stabilization energies, and natural orbital of the ion pair conformers. The [FSI]− anions, unlike the [TFSI]− anions, exist at the top position with respect to the imidazolium rings. The presence of the out-of-plane interactions between the [EMI]+ and [FSI]− ions is in good agreement with the higher interactions of the [FSI]− anions with the alkyl group hydrogens. The presence of out-of-plane conformers could also be related to the interactions of the anion with the π clouds of the [EMI]+ ring. In the [EMI]+ cation, the aromatic ring is π-acidic due to the presence of a positive charge in the N1–C1–N2 ring, which leads to the presence of [FSI]− anion donor [EMI]+ π-acceptor type interactions. For the ion pair [EMI][FSI], the absolute value of the interaction energies is lower than the normal hydrogen bond energy (50 kJ/mol), which indicates that there exist very weak electrostatic interactions between the [EMI]+ cations and [FSI]− anions. The weaker attraction between the [EMI]+ and [FSI]− ions is suggested to contribute to the larger diffusion coefficients of the ions. The lower viscosity of the [EMI][FSI] compared to [EMI][TFSI]-based ionic liquids originates from its relatively smaller interaction energy. Charge transfer occurs via the lone pairs of oxygen and nitrogen atoms to the σ-type antibonding orbital of the C–H bonds (Ylp → σ*C–H), π-type antibonding orbitals of the C=C bonds (Ylp → π*C=C), and π-type antibonding orbitals of the N - C bonds (Ylp → π*C–N), where Y = N, O, or F. The values of the stabilization energy E(2) for the [EMI][FSI] ion pair conformers are generally small (E(2)n → σ* < 2 kcal/mol) for individual E(2)n → σ*, E(2)n → π*C=C, and/or E(2)n → π*N–C interactions. The [EMI]+ cation and [FSI]− anions tend to form multiple σ* and π* interactions, but reduce the strength of the individual contributions from a potential (linear) maximum.
Acknowledgments
Hawassa University is acknowledged for providing financial support for graduate study. Addis Ababa Science and Technology University is also acknowledged for providing a research bursary. ICTP-Rwanda is acknowledged for providing remote HPC access for supercomputing.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.4c00104.
The results of the calculated NBO parameters of the cation–anion ion pairs, stabilization energies, and natural orbital analysis of the ion pair conformers. (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Grey C. P.; Hall D. S. Prospects for lithium-ion batteries and beyond-a 2030 vision. Nat. Commun. 2020, 11, 6279 10.1038/s41467-020-19991-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Q.; Ping P.; Zhao X.; Chu G.; Sun J.; Chen C. Thermal runaway caused fire and explosion of lithium ion battery. J. Power Sources 2012, 208, 210–224. 10.1016/j.jpowsour.2012.02.038. [DOI] [Google Scholar]
- Rogers J. R. D.; Seddon K. R.. Ionic Liquids: Industrial Application to Green Chemistry, ACS Symposium Series; ACS Publications: Washington, 2002; Vol. 818. [Google Scholar]
- Ohno H.Electrochemical Aspects of Ionic Liquids; John Wiley & Sons Inc.: Hoboken, NJ, 2005. [Google Scholar]
- Sayah S.; Ghamouss F.; Santos-Peña J.; Tran-Van F.; Lemordant D. The Intriguing Properties of 1-Ethyl-3-methylimidazolium bis(fuorosulfonyl)imide Ionic Liquid. J. Solution Chem. 2019, 48, 992–1008. 10.1007/s10953-018-0814-0. [DOI] [Google Scholar]
- Appetecchi G. B.; Montanino M.; Passerini S. Ionic liquid-based electrolytes for high energy, safer lithium batteries. ACS Symp. Ser. 2012, 1117, 67–128. 10.1021/bk-2012-1117.ch004. [DOI] [Google Scholar]
- Michot C.; Armand M.; Sanchez J. Y.; Choquette Y.; Gauthier M.. Ionic Conducting Material Having Good Anticorrosive Properties. U.S. Patent US5,916,475, 1999.
- Han H. B.; Zhou S. S.; Zhang D. J.; Feng S. W.; Li L. F.; Liu K.; Feng W. F.; Nie J.; Li H.; Huang X. J. Lithium bis(fluorosulfonyl)imide (LiFSI) as conducting salt for nonaqueous liquid electrolytes for lithium-ion batteries: Physicochemical and electrochemical properties. J. Power Sources 2011, 196, 3623–3632. 10.1016/j.jpowsour.2010.12.040. [DOI] [Google Scholar]
- Best A. S.; Bhatt A. I.; Hollenkamp A. F. Ionic liquids with the bis(fuorosulfonyl)imide anion: electrochemical properties and applications in battery technology. J. Electrochem. Soc. 2010, 157, A903. 10.1149/1.3429886. [DOI] [Google Scholar]
- Dong K.; Liu W.; Dong A. H.; Zhang X.; Zhang S. Multiscale Studies on Ionic Liquids. Chem. Rev. 2017, 117, 6636–6695. 10.1021/acs.chemrev.6b00776. [DOI] [PubMed] [Google Scholar]
- Tsuzuki S.; Tokuda H.; Hayamizu K.; Watanabe M. Magnitude and directionality of interaction in ion pairs of ionic liquids: Relationship with ionic conductivity. J. Phys. Chem. B 2005, 109, 16474–16481. 10.1021/jp0533628. [DOI] [PubMed] [Google Scholar]
- Tsuzuki S.; Hayamizu K.; Seki S. Origin of the Low-Viscosity of [emim][(FSO2)2N] Ionic Liquid and Its Lithium Salt Mixture: Experimental and Theoretical Study of Self-Diffusion Coefficients, Conductivities, and Intermolecular Interactions. J. Phys. Chem. B 2010, 114, 16329–16336. 10.1021/jp106870v. [DOI] [PubMed] [Google Scholar]
- Valdes H.; Kristýna P.; Michal P.; Jan Ř.; Pavel H. Benchmark database on isolated small peptides containing an aromatic side chain: comparison between wave function and density functional theory methods and empirical force field. Phys. Chem. Chem. Phys. 2008, 10, 2747–2757. 10.1039/b719294k. [DOI] [PubMed] [Google Scholar]
- Hunt P. A. Quantum Chemical Modeling of Hydrogen Bonding in Ionic Liquids. Top Curr. Chem. 2017, 375, 59. 10.1007/s41061-017-0142-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews R. P.; Welton T.; Hunt P. A. Competitive pi interactions and hydrogen bonding within imidazolium ionic liquids. Phys. Chem. Chem. Phys. 2014, 16 (7), 3238. 10.1039/c3cp54672a. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements. J. Chem. Phys. 2010, 132 (15), 154104 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Lu Y. X.; Zou J. W.; Fan J. C.; Zhao W. N.; Jiang Y. J.; Yu Q. S. Ab initio calculations on halogen-bonded complexes and comparison with density functional methods. J. Comput. Chem. 2009, 30, 725–732. 10.1002/jcc.21094. [DOI] [PubMed] [Google Scholar]
- Chai J.-D.; Head-Gordon M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. 10.1039/b810189b. [DOI] [PubMed] [Google Scholar]
- Mentel Ł. M.; Baerends E. J. Can the Counterpoise Correction for Basis Set Superposition Effect Be Justified?. J. Chem. Theory Comput. 2014, 10 (1), 252–267. 10.1021/ct400990u. [DOI] [PubMed] [Google Scholar]
- Aragó J.; Sancho-García J. C.; Enrique O.; Beljonne D. Ab Initio Modeling of Donor Acceptor Interactions and Charge-Transfer Excitations in Molecular Complexes: The Case of Terthiophene-Tetracyanoquinodimethane. J. Chem. Theory Comput. 2011, 7, 2068–2077. 10.1021/ct200203k. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X. H. P.; Hratchian A. F.; Izmaylov J.; Bloino G.; Zheng J. L.; Sonnenberg M.; Hada M.; Ehara K.; Toyota R.; Fukuda J.; Hasegawa M.; Ishida T.; Nakajima Y.; Honda O.; Kitao H.; Nakai T.; Vreven J. A.; Montgomery J. E. Jr.; Peralta F.; Ogliaro M.; Bearpark J. J.; Heyd E.; Brothers K. N.; Kudin V. N.; Staroverov R.; Kobayashi J.; Normand K.; Raghavachari A.; Rendell J. C.; Burant S. S.; Iyengar J.; Tomasi M.; Cossi N.; Rega J.; M Millam M.; Klene J. E.; Knox J. B.; Cross V.; Bakken C.; Adamo J.; Jaramillo R.; Gomperts R. E.; Stratmann O.; Yazyev A. J.; Austin R.; Cammi C.; Pomelli J. W.; Ochterski R. L.; Martin K.; Morokuma V. G.; Zakrzewski G. A.; Voth P.; Salvador J. J.; Dannenberg S.; Dapprich A. D.; Daniels O.; Farkas J. B.; Foresman J. V.; Ortiz J.; Cioslowski D.; Fox J.. Gaussian 09, revision D.01; Gaussian Inc.: Wallingford, CT, 2009.
- Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
- Holbrey J. D.; Reichert W. M.; Rogers R. D. Crystal structures of imidazolium bis (trifluoromethanesulfonyl) imide ‘ionic liquid’salts: the first organic salt with a cis-TFSI anion conformation. Dalton Trans. 2004, 2267–2271. 10.1039/B405901H. [DOI] [PubMed] [Google Scholar]
- Fujii K.; Soejima Y.; Kyoshoin Y.; Fukuda S.; Kanzaki R.; Umebayashi Y.; Yamaguchi T.; Ishiguro S.-I.; Takamuku T. Liquid structure of room-temperature ionic liquid, 1-ethyl-3-methylimidazolium bis- (trifluoromethanesulfonyl) imide. J. Phys. Chem. B 2008, 112, 4329–4336. 10.1021/jp7105499. [DOI] [PubMed] [Google Scholar]
- Dong K.; Song Y.; Liu X.; Cheng W.; Yao X.; Zhang S. Understanding structures and hydrogen bonds of ionic liquids at the electronic level. J. Phys. Chem. B 2012, 116, 1007–1017. 10.1021/jp205435u. [DOI] [PubMed] [Google Scholar]
- Shim Y.; Jeong D.; Manjari S.; Choi M. Y.; Kim H. J. Solvation, Solute Rotation and Vibration Relaxation, and ElectronTransfer Reactions in Room-Temperature Ionic Liquids. Acc. Chem. Res. 2007, 40, 1130–1137. 10.1021/ar700061r. [DOI] [PubMed] [Google Scholar]
- Shim Y.; Kim H. J. Dielectric Relaxation and Solvation Dynamics in a Room-Temperature Ionic Liquid: Temperature Dependence. J. Phys. Chem. B 2013, 117, 11743–11752. 10.1021/jp406353j. [DOI] [PubMed] [Google Scholar]
- Jeon J.; Kim H. J. Free Energies of Electron Transfer Reactions in Polarizable, Nondipolar, Quadrupolar Solvents. J. Phys. Chem. A 2000, 104, 9812–9815. 10.1021/jp002146q. [DOI] [Google Scholar]
- Jeon J.; Kim H. J. A Continuum Reaction Field Theory of Polarizable, Nondipolar, Quadrupolar Solvents: Ab Initio Study of Equilibrium Solvation in Benzene. J. Solution Chem. 2001, 30, 849–860. 10.1023/A:1012715929287. [DOI] [Google Scholar]
- Jeon J.; Kim H. J. A continuum theory of solvation in quadrupolar solvents. II. Solvation free energetics, dynamics, and solvatochromism. J. Chem. Phys. 2003, 119, 8626–8635. 10.1063/1.1605377. [DOI] [Google Scholar]
- Rappe A. K.; Bernstein E. R. Ab initio calculation of nonbonded interaction: are we there yet?. J. Phys. Chem. A 2000, 104, 6117–6128. 10.1021/jp0008997. [DOI] [Google Scholar]
- Meng Z.; Dolle A.; Carper W. R. Gas phase model of an ionic liquid: semiemperical and ab initio bonding and molecular structure. J. Mol. Struct.: THEOCHEM 2002, 585, 119–128. 10.1016/S0166-1280(02)00056-8. [DOI] [Google Scholar]
- Wagaye A. M.; Yohannes T.; Workneh G. A. Structure and molecular interactions in 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ion pair conformers: abinitio DFT based study. Discovery Appl. Sci. 2024, 6, 60. 10.1007/s42452-024-05627-5. [DOI] [Google Scholar]
- Fujii K.; Seki S.; Fukuda S.; Kanzaki R.; Takamuku T.; Umebayashi Y.; Ishiguro S. Anion conformation of low-viscosity room-temperature ionic liquid 1-ethyl-3-methylimidazolium bis(fluorosulfonyl) imide. J. Phys. Chem. B 2007, 111, 12829–12833. 10.1021/jp074325e. [DOI] [PubMed] [Google Scholar]
- Žák Z.; Růžička A.; Michot C. Structures of bis(fluorosulfonyl)imide HN(SO2F)2, bis(trifluoromethylsulfonyl)imide HN(SO2CF3)2, and their potassium salts at 150 K. Z. Kristallogr. – Cryst. Mater. 1998, 213, 217–222. 10.1524/zkri.1998.213.4.217. [DOI] [Google Scholar]
- Sawyer J. F.; Schrobilgen G. J.; Sutherland S. X-Ray crystal and multinuclear NMR study of FXeN(SO2F)2; the first example of a xenon–nitrogen bond. Inorg. Chem. 1982, 21, 4064. 10.1021/ic00141a037. [DOI] [Google Scholar]
- Faggiani R.; Kennepohl K.; Lock C. J. L.; Schrobilgen G. The XeN(SO2F)2+ and F[XeN(SO2F)2+ cations: synthesis and x-ray structure of XeN(SO2F)2Sb3F16– and Raman and multinuclear magnetic resonance studies of the AsF6– and Sb3F16– compounds. Inorg. Chem. 1986, 25, 563–571. 10.1021/ic00224a035. [DOI] [Google Scholar]
- Johansson P.; Gejji S. P.; Tegenfeldt J.; Lindgren J. The imide ion: potential energy surface and geometries. Electrochim. Acta 1998, 43, 1375–1379. 10.1016/S0013-4686(97)10047-0. [DOI] [Google Scholar]
- Lopes J. N. C.; Pa′dua A. A. H. Modeling Ionic Liquids Using a Systematic All-Atom Force Field. J. Phys. Chem. B 2004, 108, 2038–2047. 10.1021/jp0362133. [DOI] [Google Scholar]
- Deetlefs M.; Hardacre C.; Nieuwenhuyzen M.; Pa′dua A. A. H.; Sheppard O. Structure of ionic liquid-benzene mixtures. J. Phys. Chem. B 2006, 110, 1593–1598. 10.1021/jp047742p. [DOI] [PubMed] [Google Scholar]
- Fujii K.; Fujimori T.; Takamuku T.; Kanzaki R.; Umebayashi Y.; Ishiguro S. Conformational Equilibrium of Bis- (trifluoromethanesulfonyl) Imide Anion of a Room-Temperature Ionic Liquid: Raman Spectroscopic Study and DFT Calculations. J. Phys. Chem. B 2006, 110, 8179. 10.1021/jp0612477. [DOI] [PubMed] [Google Scholar]
- Katayanagi H.; Hayashi S.; Hamaguchi H.; Nishikawa K. Structure of an ionic liquid, 1-n-butyl-3-methylimidazolium iodide, studied by wide-angle X-ray scattering and Raman spectroscopy. Chem. Phys. Lett. 2004, 392, 460. 10.1016/j.cplett.2004.04.125. [DOI] [Google Scholar]
- Lopes J. N. C.; Shimizu K.; Pa′dua A. H.; Umebayashi Y.; Fukuda S.; Fujii K.; Ishiguro S. A Tale of Two Ions: The Conformational Landscapes of Bis(trifluoromethanesulfonyl)amide and N,N-Dialkylpyrrolidinium. J. Phys. Chem. B 2008, 112, 1465–1472. 10.1021/jp076997a. [DOI] [PubMed] [Google Scholar]
- Hunt P. A.; Ashworth C. R.; Matthews R. P. Hydrogen bonding in ionic liquids. Chem. Soc. Rev. 2015, 44, 1257–1288. 10.1039/C4CS00278D. [DOI] [PubMed] [Google Scholar]
- Wulf A.; Fumino K.; Ludwig R. Comment on “new interpretation of the CH stretching vibrations in imidazolium-based ionic liquids. J. Phys. Chem. A 2010, 114, 685–686. 10.1021/jp9080146. [DOI] [PubMed] [Google Scholar]
- Aakeröy C. B.; Seddon K. R. The hydrogen bond and crystal engineering. Chem. Soc. Rev. 1993, 22, 397–407. 10.1039/CS9932200397. [DOI] [Google Scholar]
- Gilli P.; Pretto L. Predicting hydrogen-bond strengths by structural and thermodynamic databases. Acta Crystallogr. 2007, 63, s73. 10.1107/S0108767307098418. [DOI] [Google Scholar]
- Gilli P.; Bertolasi V.; Ferretti V.; Gilli G. Evidence for resonance-assisted hydrogen bonding. Covalent nature of the strong homonuclear hydrogen bond. Study of the O-H--O system by crystal structure correlation methods. J. Am. Chem. Soc. 1994, 116, 909–915. 10.1021/ja00082a011. [DOI] [Google Scholar]
- Gilli P.; Bertolasi V.; Pretto L.; Ferretti V.; Gilli G. Covalent versus Electrostatic Nature of the Strong Hydrogen Bond: Discrimination among Single, Double, and Asymmetric Single-Well Hydrogen Bonds by Variable-Temperature X-Ray Crystallographic Methods in -Diketone Enol RAHB Systems. J. Am. Chem. Soc. 2004, 126, 3845–3855. 10.1021/ja030213z. [DOI] [PubMed] [Google Scholar]
- Ludwig R. Thermodynamic properties of ionic liquids—a cluster approach. Phys. Chem. Chem. Phys. 2008, 10, 4333–4339. 10.1039/b803572e. [DOI] [PubMed] [Google Scholar]
- Tsuzuki S.; Tokudab H.; Mikamia M. Theoretical analysis of the hydrogen bond of imidazolium C2–H with anions. Phys. Chem. Chem. Phys. 2007, 9, 4780–4784. 10.1039/b707419k. [DOI] [PubMed] [Google Scholar]
- Buckingham A. D.; Fowler P. W.; Hutson J. M. Theoretical studies of van der Weds molecules and intermolecularforces. Chem. Rev. 1988, 88, 963–988. 10.1021/cr00088a008. [DOI] [Google Scholar]
- Stone A. J.The Theory of Intermolecular Forces; Clarendon Press: Oxford, U.K., 1996. [Google Scholar]
- Jeffrey G. A.An Introduction to Hydrogen Bonding; Oxford University Press: Oxford, 1997. [Google Scholar]
- Reed A. E.; Curtiss L. A.; Weinhold F. Intermolecular interactions from a natural bond orbital, donor–acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. 10.1021/cr00088a005. [DOI] [Google Scholar]
- Fumino K.; Wulf A.; Ludwig R. The potential role of hydrogen bonding in aprotic and protic ionic liquids. Phys. Chem. Chem. Phys. 2009, 11, 8790–8794. 10.1039/b905634c. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.