Skip to main content
NCBI home page
JACS Au logoLink to JACS Au
. 2024 Mar 6;4(3):1134–1141. doi: 10.1021/jacsau.3c00838

Unveiling Hidden Shake-Up Features in the Uranyl M4-Edge Spectrum

Jordan N Ehrman †, Kirill Shumilov †, Andrew J Jenkins †, Joseph M Kasper ‡, Tonya Vitova §, Enrique R Batista ‡, Ping Yang ‡,*, Xiaosong Li †,*
PMCID: PMC10976573  PMID: 38559711

Abstract

graphic file with name au3c00838_0006.jpg

The M4,5-edge high energy resolution X-ray absorption near-edge structure (HR-XANES) spectra of actinyls offer valuable insights into the electronic structure and bonding properties of heavy-element complexes. To conduct a comprehensive spectral analysis, it is essential to employ computational methods that accurately account for relativistic effects and electron correlation. In this work, we utilize variational relativistic multireference configurational interaction methods to compute and analyze the X-ray M4-edge absorption spectrum of uranyl. By employing these advanced computational techniques, we achieve excellent agreement between the calculated spectral features and experimental observations. Moreover, the calculations unveil significant shake-up features, which arise from the intricate interplay between strongly correlated 3d core-electron and ligand excitations. This research provides important theoretical insights into the spectral characteristics of heavy-element complexes. Furthermore, it establishes the foundation for utilizing M4,5-edge spectroscopy as a means to investigate the chemical activities of such complexes. By leveraging this technique, we can gain a deeper understanding of the bonding behavior and reactivity of heavy-element compounds.

Keywords: heavy element, M-edge spectroscopy, core electron excitation, X-ray absorption, shake-up peaks

The chemistry of actinide complexes is foundational to a variety of applications, including not only nuclear waste separations1,2 but also catalysis3,4 and nanomaterials.5−7 However, the electronic structure and bonding of heavy elements remain less well-understood than metal–ligand bonding with light elements, with the covalency of the 5f electrons playing a central role.8,9 X-ray spectroscopy has become an experimental tool of choice as the characteristics of the X-ray spectrum are not only element-specific but also sensitive to the chemical environment. Analyses of the spectral shifts and intensities at the M-edge (excitations from the n = 3 orbital level) have been shown to provide important information about the covalency of 5f electrons in the bonding interactions of heavy elements.10−17 M-edge absorption spectra calculations, similar to that of L-edge spectra,18,19 necessitate the use of a relativistic treatment, including scalar relativistic and spin–orbit coupling terms. The complexity of the electronic structures of heavy elements poses a challenging frontier in the theoretical prediction of their M-edge spectra due to the need to treat relativistic effects (scalar relativities and spin–orbit couplings) as well as static and dynamic correlations on an equal footing.

Recent advances in variational relativistic many-body theory20−24 have opened a new avenue to provide accurate calculations that can complement and interpret new multifaceted experimental probes of heavy-element complexes. In the framework of a variational relativistic multireference configuration interaction (MRCI) approach,22,25 relativistic corrections are included in the orbital optimization, and the static correlation is described by the complete active space self-consistent-field (CASSCF), followed by an additional configuration interaction (CI) treatment to add dynamic correlation. In this work, we investigate the spectroscopic features of the uranyl ion (UO2+2) M-edge spectrum using the variational relativistic exact-two-component (X2C) MRCI approach (see the Methods section), aiming to provide a very accurate probe into the spectral characteristics of early actinide complexes. Fundamental knowledge gleaned from this study will aid in our understanding of the electronic structures of uranium complexes. These complexes can exhibit unique reactivities and photophysical properties, underpinning their vital role in various areas of chemical science.26

Figure 1 illustrates the molecular orbital (MO) diagram for uranyl, providing a foundation for analyzing its electronic structure.8,27,28 In M4,5-edge XAS (X-ray absorption spectroscopy), the excitations from the uranium 3d orbitals to unoccupied frontier orbitals, including the 5f manifold, are probed following the ΔJ = 0, ±1 and Δl = ±1 selection rules. 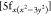The lower-lying unoccupied orbitals consist of the nonbonding δu and ϕu type formed from the UInline graphic, U[5fxyz], UInline graphic, and UInline graphic manifold. Through the mixing of U[5f] with the O[2p] orbitals, hybridized or covalent bonding is formed, leading to the occupied two πu orbitals (hybridization of U[5fyz2] and U[5fxz2] with O[2p]) and a σu orbital (hybridization of U[5fz3] with O[2p]), all with the ungerade (u) symmetry. The hybridization of the U[6d] orbitals with O[2p] yield the bonding orbitals of gerade (g) symmetry, two πg hybridizing uranium 6dxz and 6dyz and one σg hybridizing uranium 6dz2. The antibonding counterparts reside in the unoccupied space, two π*u, two π*g, one σ*u, and one σ*g.

Figure 1.

Figure 1

Open in a new tab

Uranyl qualitative molecular orbital diagram.

Previous works have shown that modeling X-ray spectra using time-dependent density functional theory (TDDFT) with relativistic corrections is capable of capturing some of the spectral features in uranyl core-excitations and yields qualitatively correct spectra.29−31 However, the correlation captured by TDDFT is incomplete, shown by the importance of double excitations in the accurate modeling of M-edge spectra in multireference methods with perturbative spin–orbit coupling.11,12,32 On the other hand, the manifestation of double excitation and its physical characteristics in the uranyl M-edge spectrum remain largely unexplored.

To investigate the intricate interplay between the 5f and 6d manifolds and to assess the impact of electron correlations observed in the uranyl M4-edge HR-XANES, a comprehensive approach is employed. In this method, fully optimized core-hole orbitals including spin–orbit coupling are assigned to X2C-MRCI spaces, considering the RAS (restricted active space) partitioning scheme depicted in Figure 2 (for detailed computational information, please refer to the Methods section). Four distinct correlated X2C-MRCI schemes were carefully selected and designed to analyze the correlation effects arising from the bonding and antibonding 5f and 6d manifolds. These schemes systematically increase the size of the active space, allowing for a thorough investigation of the correlation effects in the system.

  • Scheme A is considered the minimal X2C-MRCI scheme where RAS1 includes the four U[3d3/2] core electrons and spinor orbitals (4 electrons and 4 orbitals) corresponding to the M4-edge, and RAS3 includes four π*u and two σ*u antibonding U[5f]–O[2p] spinor orbitals (0 electron and 6 orbitals).

  • Scheme B adds to Scheme A four πu and two σu correlating electrons and spinor orbitals in RAS1 (10 electrons and 10 orbitals). RAS3 is the same as in Scheme A.

  • Scheme C adds to Scheme B the four πg and two σg correlating electrons and spinor orbitals, arising from U[6d]–O[2p] interactions, in RAS1 (16 electrons and 16 orbitals). RAS3 is the same as in Scheme A.

  • Scheme D expands upon Scheme C by adding the four δ*g, four π*g, and two σ*g spinor orbitals in RAS3 (0 electron and 16 orbitals).

Figure 2.

Figure 2

Open in a new tab

Uranyl X2C-MRCI partitioning schemes. Schemes A, B, C, and D progressively include a greater number of correlating orbitals and electrons, as detailed in the text regarding partitioning.

All schemes include the eight δ/ϕ orbitals in RAS2. These four X2C-MRCI schemes provide a valuable framework for assessing the significance of bonding orbitals in the 5f and 6d manifolds as well as the electron correlation contributions from antibonding orbitals, with respect to the spectral characteristics. It is worth noting that all schemes include the 3d core electrons of uranium, ensuring that excitations from the RAS1 space are responsible for the observed M4-edge spectral features.

In these schemes, the RAS1 space allows for the inclusion of two core holes, while the RAS3 space permits the inclusion of two electrons. This restriction facilitates both single and double excitations from the RAS1 space. Consequently, this X2C-MRCI approach not only enables the calculation of single excitations but also facilitates the exploration of shake-up/shake-down or satellite states, offering a comprehensive understanding of the system’s electronic structure.

Figure 3 illustrates the computed uranyl M4-edge spectra obtained using four distinct X2C-MRCI schemes, each characterized by an increasing size of the correlation space, as previously described. Within the experimental spectral region, all calculations exhibit three prominent peaks denoted as α, β, and γ.

Figure 3.

Figure 3

Open in a new tab

Uranyl M4-edge calculated with X2C-MRCI using the four different active space schemes and an X2C-RASSCF core-hole reference, compared to experiment. Normalized intensities and excitation energies are shifted to be equal at the major peak. Lorentzian broadening parameter is set to an fwhm of 1.0 eV based on the observed experimental broadening profile. The calculated spectra under Schemes A, B, C, and D are shifted by 161.46, 158.32, 158.08, and 156.72 eV, respectively, to best align with the experimental α feature.

If no correlation of the inner valence bonding electrons is included—X2C-MRCI employing Scheme A—a qualitative agreement with the experiment is obtained, with spectral shifts of 3.1 and 9.7 eV for the β and γ peaks, respectively. However, a substantial improvement is achieved by incorporating correlating occupied πu and σu orbitals through Scheme B, resulting in shifts of 2.4 and 7.7 eV for the β and γ peaks, respectively. The enhancement in predictive accuracy can be attributed to the consideration of electron correlations from covalent pairs of orbitals, πu/σu and π*u/σ*u. This observation aligns with the expectation that these orbitals, involved in covalent bonding, play a crucial role in accurately describing the spectral behavior.

The accuracy of the spectral prediction improved with the inclusion of the 6d orbitals in the active space. In X2C-MRCI Scheme C, correlation with the 6d bonding orbitals (πg and σg) is introduced, while Scheme D incorporates additional correlation involving the antibonding π*g and σ*g orbitals, as well as nonbonding δg orbitals. By expanding the correlation spaces with these additional orbitals, the convergence of the β peak in the uranyl M4-edge spectrum toward the experimental result is achieved. Moreover, the inclusion of these orbitals through Scheme D results in a substantial improvement in the prediction of the γ peak, bringing it very close to the experimental observation.

Overall, we found that Scheme B successfully reached a converged result for the β peak and significantly improved the position of the γ peak, confirming previous theoretical investigations.11,16,32 This observation suggests that including the correlating 5f bonding orbitals is crucial for the accurate prediction of the M-edge spectra of UO2+2.

The excellent agreement observed between the computed spectrum using X2C-MRCI and the experimental data instills a high level of confidence in the theoretical analysis of the spectral characteristics. To further deepen our understanding of the M4-edge spectra, Figure 4 presents a partial intensity analysis that elucidates the contributions from specific MOs. This insightful analysis facilitates an enhanced comprehension of the underlying nature and distinctive features exhibited by the M-edge spectra.

Figure 4.

Figure 4

Open in a new tab

Partial intensity analysis of the uranyl M4-edge spectrum. The normalized intensity of each excitation is projected onto the molecular orbital space (see the Methods section).

In order of increasing energy, the three peaks were initially assigned to 3d → δu/ϕu, 3d → π*u, and 3d → σ*u transitions.33 Such an assignment suggests that these transitions are nonoverlapping one-electron excitations. Given that the 3d → δu/ϕu transition is pinned in the spectrum, the splitting observed between the M4-edge spectral peaks provides valuable insights into the level of covalency present, reflecting a similar concept to that of MO interaction.10

The spectral analysis conducted using Scheme A in Figure 4 confirms the initial experimental assignment, indicating simple single-electron excitations from 3d3/2 to δu/ϕu, π*u, and σ*u orbitals, respectively. While this agreement with the experimental peak positions and transition assignments seems reasonable, it is important to note that Scheme A lacks correlations arising from the 5f and 6d bonding orbitals. Without considering the correlations stemming from the 5f and 6d manifolds, the computed spectra may fail to capture the intricate electronic interactions and multielectron effects that can significantly influence the observed spectral features. Therefore, although Scheme A yields satisfactory agreement in terms of peak positions and transition assignments, it is crucial to recognize the potential limitations and the possibility of misinterpretation due to the absence of relevant correlations.

Indeed, the analysis of the partial intensity using the larger correlation spaces shows a very different picture and would suggest an alternative assignment of the transitions. The α peak predominantly involves transitions from the 3d3/2 manifold to the δu/ϕu nonbonding orbitals, aligning with our expectations. However, intriguingly, the presence of significant contributions from the nonbonding δu/ϕu orbitals is also detected in the β peak in addition to features originating from 3d3/2 to π*u transitions. This observation raises questions as the spectral characteristics would typically produce a single peak if the δu/ϕu orbitals were truly nonbonding and exhibited degenerate 5f character.

There are two possible mechanisms that can give rise to δu/ϕu orbital splitting in the M4-edge HR-XANES spectrum. If δu/ϕu are mixed with σu and πu, it will lead to a frontier orbital and spectral splitting. However, the orbital analysis does not show any mixing between these orbitals. The second possible mechanism will be that these peaks arise from the shake-up transitions, which involved two electron processes in the absorption spectrum.

To gain deeper insights into the nature of the observed transitions, we conducted an analysis of electron transitions between orbital pairs and corresponding intensities (see the Methods section), as shown in Figure 5. These figures provide a population analysis for each M4-edge excitation, offering valuable information about the contributing orbitals. Detailed analyses of the CI vectors for M4-edge states were carried out using Scheme D. The results, including percentages of single and double electron excitations in each state and their leading contributions, are presented in the Supporting Information.

Figure 5.

Figure 5

Open in a new tab

Transition population analysis for each M4-edge excitation based on the calculation using Scheme D. Electron excitations from/to 6d orbitals are negligible and thus are not shown. The negative/positive values indicate the molecular orbitals from/to which the electrons are excited, respectively. (a–c) The electron populations in each calculated transition are for peaks α, β, and γ, respectively. (d–f) The partial normalized intensity for each calculated transition is shown in peaks α, β, and γ, respectively. Different colors represent various orbitals involved in the transitions, as illustrated in panel (f).

For the α peak shown in Figure 5a, the excitations involve one-electron transitions from the 3d3/2 orbital to the nonbonding δu/ϕu orbitals, aligning with our initial expectations. Notably, a substantial proportion of excitations also stems from two electron excitations involving coupled transitions from the σu and 3d3/2 orbitals, manifesting clear shake-up characteristics. However, shake-up transitions in this specific region exhibit a small transition dipole moment. As a result, a total of 91% of the intensity in the region of the α peak can be attributed to the one-electron 3d3/2 → δu/ϕu transition, as shown in Figure 5d. This means that, despite a considerable presence of shake-up phenomena originating from the valence transitions between δu/ϕu orbitals, these remain spectroscopically dark within the α peak spectral range.

In contrast, the β peak displayed in Figure 5b exhibits more complex behavior with contributions from multiple two-electron excitations. This peak involves many simultaneous transitions from both the 3d3/2 and σu orbitals to the δu/ϕu nonbonding orbitals, as well as the π*u antibonding orbitals. Such observations again indicate the presence of shake-up transitions, representing concerted processes involving core-electron and valence-electron excitations. However, as shown in Figure 5e, the majority of the transitions have a small contribution to the dipole oscillator strength, which is limited by symmetry considerations. Approximately 60% of the intensity in the region of the β peak can be ascribed to transitions between the 3d3/2 and δu/ϕu orbitals. The remaining roughly 40% of the intensity comes from contributions from the σu to π*u transitions, signifying a pronounced shake-up feature.

Analyzing the γ peak depicted in Figure 5c reveals an even more pronounced shake-up feature. This peak involves excitations not only from the 3d3/2 core orbital but also from the πu bonding orbitals to the δu/ϕu nonbonding orbitals and the π*u antibonding orbitals. Additionally, a transition into the experimentally assigned σ*u antibonding orbital is observed, although this spectral feature may be obscured by the presence of the shake-up peaks. Figure 5f shows that, similar to the β peak, only a small fraction of the shake-up transitions contributes to the dipole oscillator strength. In the region of the γ peak, 62% of the total intensity can be attributed to the 3d3/2 and δu/ϕu orbitals, with an additional 32% arising from πu and π*u. The remaining 6% of the intensity involves the σu and σ*u orbitals.

Conclusions

In summary, we utilized variational relativistic MRCI methods to compute and analyze the X-ray M-edge absorption spectrum of uranyl. The obtained results demonstrate an excellent agreement between the computed and experimentally observed peak positions and intensities, emphasizing the significance of incorporating correlations from 5f and 6d bonding and antibonding orbitals. Including 5f and 6d orbital correlations reduces the percent errors in peak separations by an average of ∼40%. This highlights the critical role these orbitals play in accurately describing the spectral characteristics.

Upon closer examination, it is clear that the experimentally determined spectral characteristics do not adequately account for key shake-up features. An estimated 33% of all electrons excited in the M4-edge spectrum come from the valence 5f bonding orbitals, making a significant contribution to these shake-up phenomena. The presence of strong shake-up peaks within the uranyl M4-edge spectral range has the potential to obscure the analysis of covalency in actinide complexes. These shake-up peaks represent concerted excitations involving core and valence electrons, contributing to a more comprehensive understanding of the electronic interactions and bonding nature.

Methods

In this work, we use the relativistic Hamiltonian in the form of the X2C method,23,25,34−50 which is similar to the normalized elimination of the small component (NESC) technique,51−58 both allowing for variational treatment of relativistic corrections in electronic structure theory. The X2C and NESC approaches transform four-component Dirac–Hartree–Fock into an electron-only two-component method, where scalar relativistic and spin–orbit effects can be variationally included at the orbital level. We use an X2C state-averaged restricted active space self-consistent field (X2C-SA-RASSCF) method in the Kramers’ unrestricted framework to generate the reference orbitals,20,22,23,25 followed by an X2C-MRCI treatment of the dynamical correlation. The X2C-MRCI step is mapped onto the restricted active space (RAS) partitioning scheme,22,59,60 which allows a natural extension to study X-ray spectra.19,61−69 For details on the X2C-MRCI theory and implementation, we refer readers to ref (22).

The relativistic X2C-MRCI framework for the uranyl M4-edge calculation starts with the 3d core-hole orbital optimization using X2C-RASSCF. A state-averaged X2C-RASSCF calculation is run with the four 3d3/2 orbitals in RAS1, the eight δ/ϕ orbitals in RAS2, and an empty RAS3. One electron is allowed to excite out of RAS1 and into RAS2, producing 32 core-electron excited states. All orbitals are optimized with respect to all 32 core-electron excited states to account for the core-hole relaxation. These orbitals are better suited for modeling the core-hole excited states necessary for subsequent spectrum generation.

In the following correlated X2C-MRCI treatment, three RASs are structured:

  • RAS1: Correlated core space consists of spinor orbitals that are occupied in all reference determinants but can be excited in MRCI.

  • RAS2/CASSCF: Complete active space consists of active spinor orbitals in the X2C-CASSCF reference.

  • RAS3: Correlated virtual space consists of orbitals that are unoccupied in all reference determinants but can be occupied in MRCI.

After assigning orbitals in the three spaces, the X2C-MRCI excitation list can be generated given the correlation level of choice (e.g., single, double, or triple excitation). In this work, single-and double-electron excitations out of the RAS1 space are allowed. Introducing the RAS framework into the X2C-MRCI partitioning scheme gives rise to flexibility in both the choice of correlation space and excitation level and allows for an efficient generation and tracking of unique excited configurations, such as those in M-edge XAS. Since inner valence bonding orbitals are included in RAS1, the X2C-MRCI calculations will produce additional low-lying excited states. The energy-specific Davidson algorithm70−72 is used to solve for only spectral features in the M-edge range.

For excitation from state I to state J, we evaluate δρp = γJpp – γIpp. Here, γpp is the diagonal element of the one-particle reduced density matrix, corresponding to the p-th orbital occupation. δρp represents the change in orbital occupation upon the excitation. The negative and positive values of δρp indicate the MOs from and to which the electrons are excited, respectively. The partial oscillator strength can be computed as fIJp = δρpfIJ, where fIJ is the total oscillator strength for the excitation.

The molecular geometry for uranyl is linear with the U–O bond length set to be 1.760 Å taken from literature values.73 The ANO-RCC-VTZP basis set74−76 was applied to the uranium atom, and the aug-cc-pVTZ basis set77 was utilized for the oxygen atoms. All calculations were performed in a development version of the Gaussian quantum chemistry package.78 Neither point group symmetry nor Kramers symmetry was enforced in any of the calculations.

The experimental spectrum was measured for UO2+2 in aqueous 1 M perchloric acid (HClO4). Different chemical environments can result in a small variation of ±0.2 eV in the measured spectrum, manifested as a shift in the overall spectrum while leaving the peak splittings unchanged.10 Since perchloride anion is a noncoordinating ligand and the environment-induced difference in spectral shift is not significant for the peak splittings, the computed results represent a generalized average of M4 X-ray spectrum of UO2+2.

Acknowledgments

The study of heavy-element complex is supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, in the Heavy-Element Chemistry program (grant no. DE-SC0021100 to X.L. and contract DE-AC52-06NA25396 at Los Alamos National Laboratory). Computations were facilitated through the use of advanced computational, storage, and networking infrastructure provided by the Hyak supercomputer system at the University of Washington, funded by the Student Technology Fee. J.M.K. acknowledges funding from a Director’s Postdoctoral Fellowship from Los Alamos National Laboratory (LANL). Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. DOE (contract 89233218CNA000001). J.N.E. acknowledges the Summer Graduate Research Associate Fellowship sponsored by the G. T. Seaborg Institute at LANL. T.V. acknowledges the funding from the European Research Council (ERC) Consolidator grant 2020 under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 101003292, “The Actinide Bond”).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.3c00838.

  • Detailed analyses, including excitation energies, percentages of single- and double-electron excitations in each state, and their leading contributions (PDF)

Author Contributions

∥ J.N.E., K.S., and A.J.J. contributed equally.

The authors declare no competing financial interest.

Supplementary Material

au3c00838_si_001.pdf (137.4KB, pdf)

References

  1. Kaltsoyannis N. Does Covalency Increase or Decrease Across the Actinide Series? Implications for Minor Actinide Partitioning. Inorg. Chem. 2013, 52, 3407–3413. 10.1021/ic3006025. [DOI] [PubMed] [Google Scholar]
  2. Dam H. H.; Reinhoudt D. N.; Verboom W. Multicoordinate Ligands for Actinide/Lanthanide Separations. Chem. Soc. Rev. 2007, 36, 367–377. 10.1039/B603847F. [DOI] [PubMed] [Google Scholar]
  3. Arnold P. L.; McMullon M. W.; Rieb J.; Kühn F. E. C–H Bond Activation by f-Block Complexes. Angew. Chem., Int. Ed. 2015, 54, 82–100. 10.1002/anie.201404613. [DOI] [PubMed] [Google Scholar]
  4. Batrice R. J.; Eisen M. S. Catalytic Insertion of E–H bonds (E= C, N, P, S) into Heterocumulenes by Amido–Actinide Complexes. Chem. Sci. 2016, 7, 939–944. 10.1039/C5SC02746B. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Vallejo K. D.; Kabir F.; Poudel N.; Marianetti C. A.; Hurley D. H.; Simmonds P. J.; Dennett C. A.; Gofryk K. Advances in Actinide Thin Films: Synthesis, Properties, and Future Directions. Rep. Prog. Phys. 2022, 85, 123101. 10.1088/1361-6633/ac968e. [DOI] [PubMed] [Google Scholar]
  6. Pallares R. M.; Abergel R. J. Transforming Lanthanide and Actinide Chemistry with Nanoparticles. Nanoscale 2020, 12, 1339–1348. 10.1039/C9NR09175K. [DOI] [PubMed] [Google Scholar]
  7. Bonato L.; Virot M.; Dumas T.; Mesbah A.; Dalodière E.; Dieste Blanco O.; Wiss T.; Le Goff X.; Odorico M.; Prieur D.; et al. Probing the local structure of nanoscale actinide oxides: a comparison between PuO2 and ThO2 nanoparticles rules out PuO2+x hypothesis. Nanoscale Adv. 2020, 2, 214–224. 10.1039/c9na00662a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Pepper M.; Bursten B. E. The electronic structure of actinide-containing molecules: a challenge to applied quantum chemistry. Chem. Rev. 1991, 91, 719–741. 10.1021/cr00005a005. [DOI] [Google Scholar]
  9. Neidig M. L.; Clark D. L.; Martin R. L. Covalency in f-Element Complexes. Coord. Chem. Rev. 2013, 257, 394–406. 10.1016/j.ccr.2012.04.029. [DOI] [Google Scholar]
  10. Vitova T.; Pidchenko I.; Fellhauer D.; Bagus P. S.; Joly Y.; Pruessmann T.; Bahl S.; Gonzalez-Robles E.; Rothe J.; Altmaier M.; Denecke M. A.; Geckeis H. The Role of the 5f Valence Orbitals of Early Actinides in Chemical Bonding. Nat. Commun. 2017, 8, 16053. 10.1038/ncomms16053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Sergentu D.-C.; Duignan T. J.; Autschbach J. Ab Initio Study of Covalency in the Ground versus Core-Excited States and X-ray Absorption Spectra of Actinide Complexes. J. Phys. Chem. Lett. 2018, 9, 5583–5591. 10.1021/acs.jpclett.8b02412. [DOI] [PubMed] [Google Scholar]
  12. Bagus P. S.; Schacherl B.; Vitova T. Computational and Spectroscopic Tools for the Detection of Bond Covalency in Pu(IV) Materials. Inorg. Chem. 2021, 60, 16090–16102. 10.1021/acs.inorgchem.1c01331. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Cross J. N.; Su J.; Batista E. R.; Cary S. K.; Evans W. J.; Kozimor S. A.; Mocko V.; Scott B. L.; Stein B. W.; Windorff C. J.; Yang P. Covalency in Americium(III) Hexachloride. J. Am. Chem. Soc. 2017, 139, 8667–8677. 10.1021/jacs.7b03755. [DOI] [PubMed] [Google Scholar]
  14. Löble M. W.; Keith J. M.; Altman A. B.; Stieber S. C. E.; Batista E. R.; Boland K. S.; Conradson S. D.; Clark D. L.; Lezama Pacheco J.; Kozimor S. A.; Martin R. L.; Minasian S. G.; Olson A. C.; Scott B. L.; Shuh D. K.; Tyliszczak T.; Wilkerson M. P.; Zehnder R. A. Covalency in Lanthanides. An X-ray Absorption Spectroscopy and Density Functional Theory Study of LnCl 6x-(x = 3, 2). J. Am. Chem. Soc. 2015, 137, 2506–2523. 10.1021/ja510067v. [DOI] [PubMed] [Google Scholar]
  15. Minasian S. G.; Keith J. M.; Batista E. R.; Boland K. S.; Bradley J. A.; Daly S. R.; Kozimor S. A.; Lukens W. W.; Martin R. L.; Nordlund D.; Seidler G. T.; Shuh D. K.; Sokaras D.; Tyliszczak T.; Wagner G. L.; Weng T.-C.; Yang P. Covalency in Metal – Oxygen Multiple Bonds Evaluated Using Oxygen K-edge Spectroscopy and Electronic Structure Theory. J. Am. Chem. Soc. 2013, 135, 1864–1871. 10.1021/ja310223b. [DOI] [PubMed] [Google Scholar]
  16. Polly R.; Schacherl B.; Rothe J.; Vitova T. Relativistic Multiconfigurational Ab Initio Calculation of Uranyl 3d4f Resonant Inelastic X-ray Scattering. Inorg. Chem. 2021, 60, 18764–18776. 10.1021/acs.inorgchem.1c02364. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Su J.; Batista E. R.; Boland K. S.; Bone S. E.; Bradley J. A.; Cary S. K.; Clark D. L.; Conradson S. D.; Ditter A. S.; Kaltsoyannis N.; Keith J. M.; Kerridge A.; Kozimor S. A.; Löble M. W.; Martin R. L.; Minasian S. G.; Mocko V.; La Pierre H. S.; Seidler G. T.; Shuh D. K.; Wilkerson M. P.; Wolfsberg L. E.; Yang P. Energy-Degeneracy-Driven Covalency in Actinide Bonding. J. Am. Chem. Soc. 2018, 140, 17977–17984. 10.1021/jacs.8b09436. [DOI] [PubMed] [Google Scholar]
  18. Kasper J. M.; Stetina T. F.; Jenkins A. J.; Li X. Ab Initio Methods for L-edge X-ray Absorption Spectroscopy. Chem. Phys. Rev. 2020, 1, 011304. 10.1063/5.0029725. [DOI] [Google Scholar]
  19. Jenkins A. J.; Hu H.; Lu L.; Frisch M. J.; Li X. Two-Component Multireference Restricted Active Space Configuration Interaction for the Computation of L-Edge X-ray Absorption Spectra. J. Chem. Theory Comput. 2022, 18, 141–150. 10.1021/acs.jctc.1c00564. [DOI] [PubMed] [Google Scholar]
  20. Jenkins A. J.; Liu H.; Kasper J. M.; Frisch M. J.; Li X. Variational Relativistic Two-Component Complete-Active-Space Self-Consistent Field Method. J. Chem. Theory Comput. 2019, 15, 2974–2982. 10.1021/acs.jctc.9b00011. [DOI] [PubMed] [Google Scholar]
  21. Knecht S.; Jensen H.; Saue T. Relativistic quantum chemical calculations show that the uranium molecule U2 has a quadruple bond. Nat. Chem. 2019, 11, 40–44. 10.1038/s41557-018-0158-9. [DOI] [PubMed] [Google Scholar]
  22. Hu H.; Jenkins A. J.; Liu H.; Kasper J. M.; Frisch M. J.; Li X. Relativistic Two-Component Multireference Configuration Interaction Method with Tunable Correlation Space. J. Chem. Theory Comput. 2020, 16, 2975–2984. 10.1021/acs.jctc.9b01290. [DOI] [PubMed] [Google Scholar]
  23. Lu L.; Hu H.; Jenkins A. J.; Li X. Exact-Two-Component Relativistic Multireference Second-Order Perturbation Theory. J. Chem. Theory Comput. 2022, 18, 2983–2992. 10.1021/acs.jctc.2c00171. [DOI] [PubMed] [Google Scholar]
  24. Hoyer C. E.; Lu L.; Hu H.; Shumilov K. D.; Sun S.; Knecht S.; Li X. Correlated Dirac–Coulomb–Breit Multiconfigurational Self-Consistent-Field Methods. J. Chem. Phys. 2023, 158, 044101. 10.1063/5.0133741. [DOI] [PubMed] [Google Scholar]
  25. Hoyer C. E.; Hu H.; Lu L.; Knecht S.; Li X. Relativistic Kramers-Unrestricted Exact-Two-Component Density Matrix Renormalization Group. J. Phys. Chem. A 2022, 126, 5011–5020. 10.1021/acs.jpca.2c02150. [DOI] [PubMed] [Google Scholar]
  26. Costa Peluzo B. M. T.; Kraka E. Uranium: The Nuclear Fuel Cycle and Beyond. Int. J. Mol. Sci. 2022, 23, 4655. 10.3390/ijms23094655. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Wadt W. R. Why UO 22+Is Linear and Isoelectronic ThO2 Is Bent. J. Am. Chem. Soc. 1981, 103, 6053–6057. 10.1021/ja00410a011. [DOI] [Google Scholar]
  28. Kaltsoyannis N. Computational Study of Analogues of the Uranyl Ion Containing the -N = U=N- Unit: Density Functional Theory Calculations on UO 22+, UON+, UN2, UO(NPH3)3+, U(NPH3)24+, [UCl4{NPR3}2](R = H, Me), and [UOCl4{NP(C6H5)3}]−. Inorg. Chem. 2000, 39, 6009–6017. 10.1021/ic000891b. [DOI] [PubMed] [Google Scholar]
  29. Denning R. G.; Green J. C.; Hutchings T. E.; Dallera C.; Tagliaferri A.; Giarda K.; Brookes N. B.; Braicovich L. Covalency in the Uranyl Ion: A Polarized x-Ray Spectroscopic Study. J. Chem. Phys. 2002, 117, 8008–8020. 10.1063/1.1510445. [DOI] [Google Scholar]
  30. Wiebke J.; Weigand A.; Weissmann D.; Glorius M.; Moll H.; Bernhard G.; Dolg M. Combined Computational and Experimental Study of Uranyl(VI) 1:2 Complexation by Aromatic Acids. Inorg. Chem. 2010, 49, 6428–6435. 10.1021/ic902496u. [DOI] [PubMed] [Google Scholar]
  31. Misael W. A.; Severo Pereira Gomes A. Core Excitations of Uranyl in Cs2UO2Cl4 from Relativistic Embedded Damped Response Time-Dependent Density Functional Theory Calculations. Inorg. Chem. 2023, 62, 11589–11601. 10.1021/acs.inorgchem.3c01302. [DOI] [PubMed] [Google Scholar]
  32. Stanistreet-Welsh K.; Kerridge A. Bounding [AnO2 ]2+ (An = U, Np) Covalency by Simulated O K-edge and An M-edge X-ray Absorption near-Edge Spectroscopy. Phys. Chem. Chem. Phys. 2023, 25, 23753–23760. 10.1039/d3cp03149g. [DOI] [PubMed] [Google Scholar]
  33. Vitova T.; Green J. C.; Denning R. G.; Löble M.; Kvashnina K.; Kas J. J.; Jorissen K.; Rehr J. J.; Malcherek T.; Denecke M. A. Polarization Dependent High Energy Resolution X-ray Absorption Study of Dicesium Uranyl Tetrachloride. Inorg. Chem. 2015, 54, 174–182. 10.1021/ic5020016. [DOI] [PubMed] [Google Scholar]
  34. Dyall K. G. Interfacing Relativistic and Nonrelativistic Methods. I. Normalized Elimination of the Small Component in the Modified Dirac Equation. J. Chem. Phys. 1997, 106, 9618–9626. 10.1063/1.473860. [DOI] [Google Scholar]
  35. Dyall K. G. Interfacing Relativistic and Nonrelativistic Methods. II. Investigation of a Low-Order Approximation. J. Chem. Phys. 1998, 109, 4201–4208. 10.1063/1.477026. [DOI] [Google Scholar]
  36. Kutzelnigg W.; Liu W. Quasirelativistic Theory Equivalent to Fully Relativistic Theory. J. Chem. Phys. 2005, 123, 241102. 10.1063/1.2137315. [DOI] [PubMed] [Google Scholar]
  37. Liu W.; Peng D. Infinite-Order Quasirelativistic Density Functional Method Based on the Exact Matrix Quasirelativistic Theory. J. Chem. Phys. 2006, 125, 044102. 10.1063/1.2222365. [DOI] [PubMed] [Google Scholar]
  38. Peng D.; Liu W.; Xiao Y.; Cheng L. Making Four- and Two-Component Relativistic Density Functional Methods Fully Equivalent Based on the Idea of from Atoms to Molecule. J. Chem. Phys. 2007, 127, 104106. 10.1063/1.2772856. [DOI] [PubMed] [Google Scholar]
  39. Iliaš M.; Saue T. An infinite-order two-component relativistic Hamiltonian by a simple one-step transformation. J. Chem. Phys. 2007, 126, 064102. 10.1063/1.2436882. [DOI] [PubMed] [Google Scholar]
  40. Liu W.; Peng D. Exact Two-component Hamiltonians Revisited. J. Chem. Phys. 2009, 131, 031104. 10.1063/1.3159445. [DOI] [PubMed] [Google Scholar]
  41. Liu W. Ideas of Relativistic Quantum Chemistry. Mol. Phys. 2010, 108, 1679–1706. 10.1080/00268971003781571. [DOI] [Google Scholar]
  42. Saue T. Relativistic Hamiltonians for Chemistry: A Primer. ChemPhysChem 2011, 12, 3077–3094. 10.1002/cphc.201100682. [DOI] [PubMed] [Google Scholar]
  43. Li Z.; Xiao Y.; Liu W. On the Spin Separation of Algebraic Two-Component Relativistic Hamiltonians. J. Chem. Phys. 2012, 137, 154114. 10.1063/1.4758987. [DOI] [PubMed] [Google Scholar]
  44. Peng D.; Middendorf N.; Weigend F.; Reiher M. An Efficient Implementation of Two-Component Relativistic Exact-Decoupling Methods for Large Molecules. J. Chem. Phys. 2013, 138, 184105. 10.1063/1.4803693. [DOI] [PubMed] [Google Scholar]
  45. Egidi F.; Goings J. J.; Frisch M. J.; Li X. Direct Atomic-Orbital-Based Relativistic Two-Component Linear Response Method for Calculating Excited-State Fine Structures. J. Chem. Theory Comput. 2016, 12, 3711–3718. 10.1021/acs.jctc.6b00474. [DOI] [PubMed] [Google Scholar]
  46. Goings J. J.; Kasper J. M.; Egidi F.; Sun S.; Li X. Real Time Propagation of the Exact Two Component Time-Dependent Density Functional Theory. J. Chem. Phys. 2016, 145, 104107. 10.1063/1.4962422. [DOI] [PubMed] [Google Scholar]
  47. Konecny L.; Kadek M.; Komorovsky S.; Malkina O. L.; Ruud K.; Repisky M. Acceleration of Relativistic Electron Dynamics by Means of X2C Transformation: Application to the Calculation of Nonlinear Optical Properties. J. Chem. Theory Comput. 2016, 12, 5823–5833. 10.1021/acs.jctc.6b00740. [DOI] [PubMed] [Google Scholar]
  48. Egidi F.; Sun S.; Goings J. J.; Scalmani G.; Frisch M. J.; Li X. Two-Component Non-Collinear Time-Dependent Spin Density Functional Theory for Excited State Calculations. J. Chem. Theory Comput. 2017, 13, 2591–2603. 10.1021/acs.jctc.7b00104. [DOI] [PubMed] [Google Scholar]
  49. Liu J.; Cheng L. Relativistic Coupled-Cluster and Equation-of-Motion Coupled-Cluster Methods. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2021, 11, 1536. 10.1002/wcms.1536. [DOI] [Google Scholar]
  50. Sharma P.; Jenkins A. J.; Scalmani G.; Frisch M. J.; Truhlar D. G.; Gagliardi L.; Li X. Exact-Two-Component Multiconfiguration Pair-Density Functional Theory. J. Chem. Theory Comput. 2022, 18, 2947–2954. 10.1021/acs.jctc.2c00062. [DOI] [PubMed] [Google Scholar]
  51. Filatov M.; Cremer D. A New Quasi-Relativistic Approach for Density Functional Theory Based on the Normalized Elimination of the Small Component. Chem. Phys. Lett. 2002, 351, 259–266. 10.1016/S0009-2614(01)01357-4. [DOI] [Google Scholar]
  52. Zou W.; Filatov M.; Cremer D. Development and Application of the Analytical Energy Gradient for the Normalized Elimination of the Small Component Method. J. Chem. Phys. 2011, 134, 244117. 10.1063/1.3603454. [DOI] [PubMed] [Google Scholar]
  53. Zou W.; Filatov M.; Cremer D. Development, Implementation, and Application of an Analytic Second Derivative Formalism for the Normalized Elimination of the Small Component Method. J. Chem. Theory Comput. 2012, 8, 2617–2629. 10.1021/ct300127e. [DOI] [PubMed] [Google Scholar]
  54. Filatov M.; Zou W.; Cremer D. Relativistically Corrected Electric Field Gradients Calculated with the Normalized Elimination of the Small Component Formalism. J. Chem. Phys. 2012, 137, 054113. 10.1063/1.4742175. [DOI] [PubMed] [Google Scholar]
  55. Zou W.; Filatov M.; Cremer D. Analytical Energy Gradient for the Two-component Normalized Elimination of the Small Component Method. J. Chem. Phys. 2015, 142, 214106. 10.1063/1.4921915. [DOI] [PubMed] [Google Scholar]
  56. Zou W.; Guo G.; Suo B.; Liu W. Analytic Energy Gradients and Hessians of Exact Two-Component Relativistic Methods: Efficient Implementation and Extensive Applications. J. Chem. Theory Comput. 2020, 16, 1541–1554. 10.1021/acs.jctc.9b01120. [DOI] [PubMed] [Google Scholar]
  57. Makoś M. Z.; Zou W.; Freindorf M.; Kraka E. Metal–ring Interactions in Actinide Sandwich Compounds: A Combined Normalized Elimination of the Small Component and Local Vibrational Mode Study. Mol. Phys. 2020, 118, e1768314 10.1080/00268976.2020.1768314. [DOI] [Google Scholar]
  58. Peluzo B. M. T. C.; Makoś M. Z.; Moura R. T. J.; Freindorf M.; Kraka E. Linear versus Bent Uranium(II) Metallocenes: A Local Vibrational Mode Study. Inorg. Chem. 2023, 62, 12510–12524. 10.1021/acs.inorgchem.3c01761. [DOI] [PubMed] [Google Scholar]
  59. Olsen J.; Roos B. O.; Jo/rgensen P.; Jensen H. J. A. Determinant Based Configuration Interaction Algorithms for Complete and Restricted Configuration Interaction Spaces. J. Chem. Phys. 1988, 89, 2185–2192. 10.1063/1.455063. [DOI] [Google Scholar]
  60. Malmqvist P. Å.; Rendell A.; Roos B. O. The Restricted Active Space Self-consistent-field Method, Implemented with a Split Graph Unitary Group Approach. J. Phys. Chem. 1990, 94, 5477–5482. 10.1021/j100377a011. [DOI] [Google Scholar]
  61. Engel N.; Bokarev S. I.; Suljoti E.; Garcia-Diez R.; Lange K. M.; Atak K.; Golnak R.; Kothe A.; Dantz M.; Kühn O.; Aziz E. F. Chemical Bonding in Aqueous Ferrocyanide: Experimental and Theoretical X-ray Spectroscopic Study. J. Phys. Chem. B 2014, 118, 1555–1563. 10.1021/jp411782y. [DOI] [PubMed] [Google Scholar]
  62. Guo M.; Sørensen L. K.; Delcey M. G.; Pinjari R. V.; Lundberg M. Simulations of Iron K Pre-edge X-ray Absorption Spectra Using the Restricted Active Space Method. Phys. Chem. Chem. Phys. 2016, 18, 3250–3259. 10.1039/C5CP07487H. [DOI] [PubMed] [Google Scholar]
  63. Pinjari R. V.; Delcey M. G.; Guo M.; Odelius M.; Lundberg M. Restricted Active Space Calculations of L-edge X-ray Absorption Spectra: From Molecular Orbitals to Multiplet States. J. Chem. Phys. 2014, 141, 124116. 10.1063/1.4896373. [DOI] [PubMed] [Google Scholar]
  64. Pinjari R. V.; Delcey M. G.; Guo M.; Odelius M.; Lundberg M. Cost and Sensitivity of Restricted Active-space Calculations of Metal L-edge X-ray Absorption Spectra. J. Comput. Chem. 2016, 37, 477–486. 10.1002/jcc.24237. [DOI] [PubMed] [Google Scholar]
  65. Delcey M. G.; Sørensen L. K.; Vacher M.; Couto R. C.; Lundberg M. Efficient Calculations of a Large Number of Highly Excited States for Multiconfigurational Wavefunctions. J. Comput. Chem. 2019, 40, 1789–1799. 10.1002/jcc.25832. [DOI] [PubMed] [Google Scholar]
  66. Bokarev S. I.; Dantz M.; Suljoti E.; Kühn O.; Aziz E. F. State-dependent electron delocalization dynamics at the solute-solvent interface: Soft-x-ray absorption spectroscopy and Ab initio calculations. Phys. Rev. Lett. 2013, 111, 083002. 10.1103/PhysRevLett.111.083002. [DOI] [PubMed] [Google Scholar]
  67. Lundberg M.; Delcey M. G. In Transition Metals in Coordination Environments: Computational Chemistry and Catalysis Viewpoints; Broclawik E., Borowski T., Radoń M., Eds.; Springer International Publishing: Cham, 2019; pp 185–217. [Google Scholar]
  68. Josefsson I.; Kunnus K.; Schreck S.; Föhlisch A.; de Groot F.; Wernet P.; Odelius M. Ab Initio Calculations of X-ray Spectra: Atomic Multiplet and Molecular Orbital Effects in a Multiconfigurational SCF Approach to the L-Edge Spectra of Transition Metal Complexes. J. Phys. Chem. Lett. 2012, 3, 3565–3570. 10.1021/jz301479j. [DOI] [PubMed] [Google Scholar]
  69. Carreras A.; Jiang H.; Pokhilko P.; Krylov A. I.; Zimmerman P. M.; Casanova D. Calculation of Spin–orbit Couplings Using RASCI Spinless One-particle Density Matrices: Theory and Applications. J. Chem. Phys. 2020, 153, 214107. 10.1063/5.0029146. [DOI] [PubMed] [Google Scholar]
  70. Liang W.; Fischer S. A.; Frisch M. J.; Li X. Energy-Specific Linear Response TDHF/TDDFT for Calculating High-Energy Excited States. J. Chem. Theory Comput. 2011, 7, 3540–3547. 10.1021/ct200485x. [DOI] [PubMed] [Google Scholar]
  71. Peng B.; Lestrange P. J.; Goings J. J.; Caricato M.; Li X. Energy-Specific Equation-of-Motion Coupled-Cluster Methods for High-Energy Excited States: Application to K-Edge X-Ray Absorption Spectroscopy. J. Chem. Theory Comput. 2015, 11, 4146–4153. 10.1021/acs.jctc.5b00459. [DOI] [PubMed] [Google Scholar]
  72. Lestrange P. J.; Nguyen P. D.; Li X. Calibration of Energy-Specific TDDFT for Modeling K-Edge XAS Spectra of Light Elements. J. Chem. Theory Comput. 2015, 11, 2994–2999. 10.1021/acs.jctc.5b00169. [DOI] [PubMed] [Google Scholar]
  73. Allen P.; Bucher J.; Shuh D.; Edelstein N.; Reich T. Investigation of Aquo and Chloro Complexes of UO 22+, NpO2+, Np4+, and Pu3+ by X-ray Absorption Fine Structure Spectroscopy. Inorg. Chem. 1997, 36, 4676–4683. 10.1021/ic970502m. [DOI] [PubMed] [Google Scholar]
  74. Roos B. O.; Lindh R.; Malmqvist P.-Å.; Veryazov V.; Widmark P.-O. Main Group Atoms and Dimers Studied with a New Relativistic ANO Basis Set. J. Phys. Chem. A 2004, 108, 2851–2858. 10.1021/jp031064+. [DOI] [Google Scholar]
  75. Roos B. O.; Lindh R.; Malmqvist P.-Å.; Veryazov V.; Widmark P.-O. New Relativistic ANO Basis Sets for Transition Metal Atoms. J. Phys. Chem. A 2005, 109, 6575–6579. 10.1021/jp0581126. [DOI] [PubMed] [Google Scholar]
  76. Roos B. O.; Lindh R.; Malmqvist P.-Å.; Veryazov V.; Widmark P.-O.; Borin A. C. New Relativistic Atomic Natural Orbital Basis Sets for Lanthanide Atoms with Applications to the Ce Diatom and LuF3. J. Phys. Chem. A 2008, 112, 11431–11435. 10.1021/jp803213j. [DOI] [PubMed] [Google Scholar]
  77. Dunning T. H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. the Atoms Boron Through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
  78. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A. V.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams-Young D.; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A.; Peralta J. E.; Ogliaro F.; Bearpark M. J.; Heyd J. J.; Brothers E. N.; Kudin K. N.; Staroverov V. N.; Keith T. A.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A. P.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.. Gaussian Development Version Revision J.14+; Gaussian Inc.: Wallingford CT, 2023.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

au3c00838_si_001.pdf (137.4KB, pdf)

Articles from JACS Au are provided here courtesy of American Chemical Society

RESOURCES