Chemically Specific Systematic Coarse-Grained Polymer Model with Both Consistently Structural and Dynamical Properties

Abstract

The coarse-grained (CG) model serves as a powerful tool for the simulation of polymer systems; its reliability depends on the accurate representation of both structural and dynamical properties. However, strong correlations between structural and dynamical properties on different scales and also a strong memory effect, enforced by chain connectivity between monomers in polymer systems, render developing a chemically specific systematic CG model a formidable task. In this study, we report a systematic CG approach that combines the iterative Boltzmann inversion (IBI) method and the generalized Langevin equation (GLE) dynamics. Structural properties are ensured by using conservative CG potentials derived from the IBI method. To retrieve the correct dynamical properties in the system, we demonstrate that using a combination of a Rouse-type delta function and a time-dependent short-time kernel in the GLE simulation is practically efficient. The former can be used to adjust the long-time diffusion dynamics, and the latter can be reconstructed from an iterative procedure according to the velocity autocorrelation function (ACF) from all-atomistic (AA) simulations. Taking the polystyrene as an example, we show that not only structural properties of radial distribution function, intramolecular bond, and angle distributions can be reproduced but also dynamical properties of mean-square displacement, velocity ACF, and force ACF resulted from our CG model have quantitative agreement with the reference AA model. In addition, reasonable agreements are observed in other collective properties between our GLE-CG model and the AA simulations as well.

1. Introduction

Molecular dynamics simulation has emerged as a powerful tool for predicting and explaining experimental results in the study of polymers. Although ab initio and all-atomistic (AA) simulations can provide significantly more accurate results, simulating polymer systems ranging from atomistic to continuum scales is practically a prohibitive task. For instance, the dynamics of entangled polymers scale with O(N^3.4),¹ where N is the chain length, while the microscopic phase size of block copolymers is on the order of ∼10–100 nm,² which rapidly exceeds the current computational power. The coarse-grained (CG) model is a crucial technique for simulating system properties at the mesoscopic scale, bridging the gap between the microscopic and macroscopic scales.^3,4 By grouping several atoms into larger CG units, the elimination of unnecessary degrees of freedom on small length scales allows for simulations of larger systems over longer time scales with reduced computational cost. However, intramolecular connectivity between monomers in the polymer chain enforces strong interdependences between features on different spatial and temporal scales. Such scale interdependences have actually been widely discussed in some of the representative review articles⁴⁻⁶ and also in the polymer physics textbook.⁷

For a brief description, we illustrate such scale-interdependences in Scheme 1, where both the representative structural and dynamical properties of the polymer system are plotted at different spatial and temporal scales. For instance, (i) along the length scale axis (spatial dimension), polymers with different chemistry will first have a different monomer size and thereafter, at the intramolecular level, different chain rigidity, statistical Kuhn length, tube diameter (d_T), and a different radius of gyration (R_g)/end-to-end distance(R_ee) at the entire chain dimension size, etc. Similarly, at the intermolecular level, they will also have different radial distribution functions (RDFs) (packing in space) between monomers and even assembly/phase separated structures (if any) in multicomponent systems;⁸ (ii) along the time scale axis (temporal dimension), there are chemical bond vibrations occur on the scale of femtoseconds, monomer relaxes at nanoseconds, and thereafter, Rouse or disentanglement dynamics happen at microseconds or even larger. After that, there will be assembly dynamics, stress relaxation modulus, G(t), etc. at the macroscopic scale.⁶

Scheme 1. Illustration of the Interdependence between Structural and Dynamical Properties in Poylmer Systems at Different Length and Time Scales, From a Microscopic Bottom-Up Perspective. Each Item in This Scheme Represent One of the Representative System Property on Corresponding Scale.

Note that we are not trying to include all system properties in this scheme.

Due to the chain connectivity between monomers along the chain backbone and the many-body characteristic nature of interactions between monomers, especially in the melt state, the above system properties (both structural and dynamical) have strong scale-interdependences. For instance, at the intramolecular level, monomer chemistry is the deterministic factor influencing the chain rigidity and, therefore, the Kuhn length and R_g or R_ee of the chain. Similarly, along the temporal dimension, detailed chemical bond vibrations occurring on the scale of femtoseconds will influence the relaxations not only on the monomer scale but also on the scale of Rouse time, even disentanglement dynamics happen at microseconds or even larger. Moreover, there is interdependence between structural and dynamical properties at all scales along both the lines of the length and time scales. For instance, monomer chemistry (free volume) will not only influence the chemical bond vibrations but also the entangled dynamics or even the stress relaxation modulus at the macroscopic scale.⁵ On the other hand, bond vibrations or monomer dynamics positioned at the beginning of the time axis can also influence the RDF or assembly structures at relatively the end of the length scale dimension.⁹ For instance, according to the tube model of Doi and Edwards,⁷ reptation time for an entangled polymer chain in a melt state can be expressed as 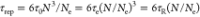, where τ₀ is the relaxation time of monomer, N_e is the Kuhn length, and 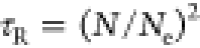is the Rouse time. Apparently, the dynamical (τ_e, τ_R, and τ_rep) and structural (N and N_e) properties are interdependent.

Over the past few decades, many chemically specific systematic CG models have been developed to tackle the above scale-interdependences.¹⁰ The ultimate goal is to achieve the simulation accuracy as the AA model but gain computational efficiency by coarse-graining. Unfortunately, it is not possible to simplify a complex many-body potential by just rewriting it in terms of fewer CG variables. Enhancing the representability and transferability of the CG model over system properties is a fundamental challenge in the field of CG simulations.^11,12 Thus, the coarse-graining process is often treated as an optimization problem that requires compromise among the structural, dynamical, and thermodynamic properties. Among the available CG methods, well-known approaches include iterative Boltzmann inversion (IBI),^13,14 force matching (FM),^15,16 trajectory matching (TM),¹⁷ energy renormalization (ER),^18,19 hybrid particle-field MD-SCFT,²⁰ etc.

Researchers often begin addressing the coarse-graining problem by attempting to reproduce the many-body potential of mean force (PMF) of CG variables.²¹ The first step is extracting the probability density of CG variables P_CG from an equilibrium atomistic reference, and then the PMF can be derived from a simple Boltzmann inversion U_CG = −k_BT ln P_CG. However, the P_CG is in principle a high-dimensional function that cannot be analytical for a complex system, especially for macromolecules other than simple toy models. One practical method is to approximate the PMF to the linear combination of a set of independent potentials with low-dimensional CG variables, for instance, intermolecular and intramolecular potentials. The IBI method is a popular approach to developing these potentials, where one can iteratively improve the fidelity of the CG potentials by updating the CG interactions according to the RDF or other intramolecular distribution functions. It is simple, effective, and has been extensively applied to many macromolecular systems.^14,22−27 Beyond the IBI methods, many other approaches based on variational principles,²⁸⁻³⁰ static correlation,^31,32 and energetics^33,34 have been used to develop CG models. All of the forces generated by the CG potential discussed above are classified as a conservative forces. However, no matter how close the CG potential is to the PMF, the direct application of the CG potential can lead to an artificial acceleration of dynamics. This can be understood from the fact that CG free energy landscapes are typically smoother than AA ones, which further reduces the direct friction between CG particles. Hence, without the correct friction of the original dynamics, CG dynamics can be misleading and difficult to link to its underlying AA dynamics.^8,35

A natural idea to handle the above accelerated CG dynamics is to understand the entropy change in the system since many degrees of freedom are eliminated during coarse-graining.^36,37 The excess entropy scaling method³⁸ is usually utilized to develop the dynamical relationship between CG and fine-grained (FG) systems. Rondina et al.³⁹ have shown the scaling relationship between excess entropy and dynamic variables of polymer melt in the coarse-graining process. More recently, Jin et al.⁴⁰⁻⁴² have developed a systematic framework for accurately measuring the excess entropy for both FG and CG systems. They have demonstrated that there exist universal scaling exponents for the FG models and their corresponding CG models.⁴⁰ Another common approach is time mapping, which determines the speedup factor by comparing the diffusion coefficient between the CG and AA models.⁴³⁻⁴⁵ The speedup factor can also be derived using a first-principle approach.⁴⁶⁻⁴⁹ By doing so, Guenza et al.⁵⁰ were able to derive analytical expressions for the dynamic speedup factor of the diffusion coefficient in a chemically realistic polybutadiene melt. Meinel and Müller-Plathe^51,52 pointed out that there is a linear relationship between the change in molecular roughness and the speedup factor in the coarse-graining process. However, these are postprocessing methods that do not generate realistic dynamics in simulations, and scaling factors are often only associated with long-time dynamical properties (such as diffusion coefficients and viscosity). It becomes more complex when the entanglement effect should be considered, and the slip-spring model⁵³⁻⁵⁶ is usually employed to effectively capture the reptation dynamics of polymer chains. Another direction is to incorporate additional friction into the equations of motion (EOM), which can be considered an effective consideration of the contributions from the lost degrees of freedom. The EOM is typically formulated using dissipative particle dynamics (DPD)⁵⁷ and Langevin dynamics (LE),⁵⁸⁻⁶¹ which allows the assignment of the friction parameters for every pair of interacting CG beads or the separate friction constants for every single CG particle or even beyond particle entities.⁶² These methods primarily focus on reproducing the low-frequency dynamics, such as long-time diffusion properties like zero-shear viscosity and diffusion coefficient of the center of mass of the chain, while ignoring the performance in high-frequency ballistic and subdiffusive regimes.^57,59 Polymer systems typically exhibit long subdiffusive dynamics, which can significantly impact material properties, such as the stress relaxation modulus at different frequencies. Therefore, it is important to develop a CG model capable of accurately reproducing the AA dynamical properties over all frequencies.

The above approaches are more or less in a top-down fashion, a more bottom-up approach is the Mori–Zwanzig (MZ) formalism.^63,64 Using this method, Akkermans and Briels⁶⁵ CG bead–spring chains into a super CG model with each chain mapped onto a dimer of CG blobs, under the DPD framework by determining DPD friction parameters using MZ formalism from FG simulations. Later on, the “MZ-DPD” method is further developed by Hijón and co-workers.⁶⁶ Recently, this method has been applied to derive CG DPD models for different oligomers or polymers.⁶⁷⁻⁶⁹ Han et al.⁷⁰ also further developed the many-body DPD model in the bottom-up approach by including density-dependent many-body DPD terms and the resultant CG EOM, which has demonstrated important to reproduce the correct properties of classical liquid. Among these models, the Markovian assumption is usually taken, in which the time scale is completely separated between slow and fast variables, and therefore, a single friction parameter is extracted from reference FG models. However, in most dense systems, such a time scale separation of characteristic processes at different scales is incomplete, and there is a severe non-Markovian effect,⁷¹⁻⁷³ for instance, in the linear polymer due to the chain connectivity in the system. Therefore, incorporating memory kernel terms is necessary to develop dynamically consistent non-Markovian CG models.⁷⁴ Such an approach has been successful in developing dynamically consistent CG models for simple molecule liquids,⁷⁵⁻⁷⁷ star polymers,⁷⁸⁻⁸⁴ and colloids,⁸⁵⁻⁸⁷ capturing the dynamical properties from AA model at all frequencies. In these models, each molecule, star polymer, and colloidal nanoparticle is typically CG into one CG bead. In comparison, situations are much more complex in the case of linear polymers due to intramolecular chain connectivity between monomers/CG beads. More importantly, there are many challenges to reproducing the non-Markovian dynamics due to the rich time scales and strong memory effect in such complex systems, as demonstrated in a recent work that derived the analytical form of the memory kernel from the end-to-end vector relaxation dynamics for Rouse chains.⁸⁸ Therefore, it is still a challenge to develop CG models for linear polymers, which can successfully capture the correct dynamics at all frequencies so that not only the monomer dynamics but also the dynamical properties at large scale, for instance, stress relaxation modulus, can be reconstructed from the reference AA models.

In this work, we take unentangled linear polystyrene (PS) as an example. We start with the previously developed CG model²³ derived from the IBI method, which has a good ability to reproduce structural properties from reference AA simulations. In order to capture the correct dynamical properties, an effective memory kernel is determined based on the generalized Langevin equation (GLE). We demonstrate that decomposition of the kernel into a Rouse-type delta function and a time-dependent short-time kernel is practically efficient. The monomer resolution is adopted, caused by more faithful revelation of local structure and dynamics, compared to other Kuhn-scale CG models.⁸⁹ This work is organized as follows. The simulation methods and models we adopted are presented in Section 2, where we provide the details of the AA simulations and a brief introduction to the theoretical background of the GLE. In addition, how do we derive the conservative CG potential, as well as the decomposition and an iterative reconstruction procedure of the memory kernel, are also introduced in this section. In Section 3, the main results and model performance are shown. Finally, we draw our conclusions in Section 4.

2. Simulation Methods and Models

2.1. Reference All-Atomistic Polymer System

In this work, we take PS as an example. As a prototypical polymer, it has been extensively studied in both experiments and simulations.^22,90 In our AA simulation model, we placed 200 10-mer atactic PS chains in the simulation box. The simulations were performed using the GROMACS^91,92 package. The initial configuration was generated using the Packmol⁹³ at an initial density of ∼340 g/cm³. We first performed energy minimization of the initial configuration to eliminate the unphysical overlaps. Subsequent equilibrium simulations were then carried out under a constant NPT ensemble at 1 atm by using the Berendsen thermostat (coupling time 0.5 ps) and barostat (coupling time 5.0 ps). The nonbonded interaction cutoff was set at 1.0 nm, and the PME approach was used to calculate long-range Coulomb interactions. The configuration was subsequently simulated at 1000 K for 1 ns, then gradually cooled to 500 K within 150 ns, and finally equilibrated at 500 K for another 50 ns. The above cooling and equilibration process was performed under constant NPT condition. Afterward, a production constant NPT simulation of 200 ns was carried out to sample configurations for parametrization of the conservative forces. For the sampling of various dynamical properties for the construction of a memory kernel, another NVT run of 200 ns was performed. Nosé-Hoover thermostat^94,95 (coupling time 0.5 ps) and Parrinello–Rahman barostat^96,97 (coupling time 5.0 ps) were used for controlling temperature and pressure (p = 1 atm), respectively. All AA simulations were performed with the OPLS-AA force field.⁹⁸

2.2. Derivation of the Conservative Coarse-Grained Potential

In systematic bottom-up approaches, one usually eliminates unnecessary degrees of freedom by defining a linear mapping operator M: r → R = M(r) that determines a CG configuration R for the corresponding AA configuration r.¹² Thus, the equilibrium distribution p_R(R) of the CG variable can be given by inserting the mapping operator M into integral of the configuration space of the AA equilibrium distribution p_r(r) to ensure the consistency of the CG model in configurational space²⁸

1

The CG interaction potential that satisfies eq 1 in equilibrium (hence follows the Boltzmann distribution) is the many-body PMF W(R) in a canonical ensemble⁹⁹

2

in this case, β = 1/k_BT represents the inverse temperature, V is for volume, n and N are the number of particles in the AA and CG models, respectively, and u is the potential function of the AA model. It becomes evident that PMF represents an excess Helmholtz free energy generated by the mapping process. Unfortunately, W(R) is intrinsically a complex many-body function, particularly for complex molecular systems beyond the simple toy model, making it impractical to precisely determine an analytical form.

In practice, bottom-up CG potential often is expressed as a linear combination of independent low-dimension terms, for instance, nonbonded and bonded potentials akin to the molecular mechanics force fields^98,100−102

3

where U^CG_nonbonded(R) usually adopts the standard pairwise approximation. We refer to these interactions as conservative interactions. In this study, a previously developed CG PS model²³ derived from the IBI method is adopted. More details about IBI method can be found elsewhere.^13,23,25 In brief, a 1:1 CG mapping scheme as illustrated in Scheme 2 is used, i.e., one CG bead represents one styrene monomer. The CG bead is located at the center of mass of the monomer. Note that the intermolecular potentials are further optimized with a larger cutoff distance of r_c = 1.75 nm, which can safely cover all characteristic peaks of the RDF.

Scheme 2. Illustration of the 1:1 CG Mapping Scheme for PS, Where Each Monomer Is Represented by a CG bead.

VMD package^103,104 is used for visualization.

2.3. GLE

The MZ formalism is a projection technique that projects the fast variables on the slow variables in phase space evolution. The projection operator is inserted into the EOM of the atomistic system and projects out the microscopic Hamiltonian dynamics of the atomistic system to the CG variables, allowing one to rigorously trace out the effective EOM of the reduced CG systems. A systematic derivation of the MZ formalism can refer to refs (105–107).

Once the specific (time-independent) projection operator is determined, the well-known GLE can be derived. Many project operators have been proposed in the particle-based MZ formalism, different operators will lead to different GLEs.^{63,64,66,106,108−110} For instance, Vroylandt and Monmarché¹⁰⁹ demonstrated the following GLE form by incorporating a position-dependent memory kernel

4

We consider slow variables A = (R, P), where R and P are the coordinate and momentum of the CG bead, respectively. These variables in the CG representation are typically obtained through linear combinations of their AA counterparts. W(R) represents the many-body PMF of the CG coordinates. K(t, R) is the position-dependent memory kernel, denoted as an n × n matrix, and F^R(t) is the random force acting on the CG bead.

However, it is difficult to practically apply eq 4 to complex systems due to the challenges associated with extracting the many-body PMF and the position-dependent memory kernel. Simplifications can be made to enhance its practicability

5

where F^C(t) denotes the conservative force that can be determined from the state-of-art CG methods, i.e., IBI, FM, TM, etc. V(t) is the velocity of the CG particles. In such a case, we ignore all cross-memory terms between different particles and replace the matrix K(t, R) with a homogeneous memory kernel K(t). The second fluctuation–dissipation theorems are obeyed such that ⟨F^R(t)F^R(0)⟩ = 3k_BTK(t)I, where I is the identity tensor. Such an approach has been extensively used to simulate systems of polymer solution^82,111 and star polymer melts.^80,84 Note that eq 4 is motivated by the MZ formalism and a convolutional representation of the CG model to describe the non-Markovian effect. If the time scale of the random force fluctuation is sufficiently fast compared to that of the CG bead motion, the memory kernel can be further approximated as a delta function, i.e., known as the Markovian approximation. As a result, eq 5 can be reduced to the Langevin equation

6

where 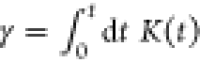. In the overdamped limit, eqs 5 and 6 are expected to be equal, as the memory kernel has completely decayed. A recent work by Lyu and Lei¹¹² has highlighted the crucial role of a heterogeneous state-dependent memory kernel in accurately capturing FG dynamics. In their work, a machine-learning-based CG model is constructed based on the rigorous MZ formalism and naturally includes the contribution from the heterogeneous state-dependent memory term. In our current study of the homogeneous amorphous polymer melt, we simply selected eq 5 as the EOM due to its simplicity and convenience of parametrization. Indeed, while the DPD form can introduce a more realistic position-dependence, the slow temporal relaxation and strong spatial (intramolecular versus intermolecular) correlation of linear polymers pose challenges in obtaining a well-defined radial memory kernel. Therefore, using the simple form in eq 5 is a reasonable starting point. Later in Section 3.2, we will validate this approximation by demonstrating that at least short-time dynamics is well reproduced, thereby proving that a simple mean-field-type memory kernel still provides a reasonable and useful approximation in polymer systems. However, we acknowledge that more complicated position-dependence will be important and will be investigated in our future study.

2.4. Direct Extraction of the Memory Kernel

There have been numerous attempts to construct the memory kernel in various physical systems, which have recently been extensively reviewed in refs (8, 35, and 74). A straightforward approach is to multiply eq 5 with V(0) and take the ensemble average in both sides, results in a one-dimensional form

7

where the fluctuation force is defined as δF(t) = F(t) – F^C(t), note the orthogonality condition ⟨F^R(t)V(0)⟩ = 0. The eq 7 takes the form of a Volterra equation of the first kind and is first introduced to infer the memory kernel for the Brownian particles.¹¹³ Numerically solving the Volterra equation of first kind is an ill-posed question and often needs appropriate normalization, detailed discussions can be found in ref (113). However, attempts to solve the above Volterra equation have failed to parametrize our model in which we observe a large oscillation and numerical instability of the resulting memory kernel. Some trial results can be found in the Supporting Information. Compared with the previous works on model star polymers, where one star is mapped onto a single CG bead, the connectivity between CG beads in our linear polymer system is a major difference and poses a major challenge. For the former, the memory kernel can be safely inferred since the molecular motion is rather homogeneous and therefore the mean-field approximation adopted in eq 7 is valid. However, it is questionable to simply use such a mean-field kernel to describe the overall dynamics for polymer systems in which the monomer motions are highly dictated by directional connectivity between monomers along the chain backbone.

2.5. Decomposition and Iterative Reconstruction of the Memory Kernel for Polymer System

In this study, we start from a more “polymeric” perspective to address the CG dynamics of a polymer melt. Our approach is inspired by the works by Guenza,^46−48,50 where the GLE for cooperative dynamics (CD-GLE) is effectively employed to describe the behavior of unentangled polymers. Considering a system composed of M chain molecules and each of them is N-monomers long, by employing a rigorous MZ projection, the ath monomer position r_a⁽ⁱ⁾(t) of the ith molecule r⁽ⁱ⁾(t) = {r₁⁽ⁱ⁾(t),r₂⁽ⁱ⁾(t),···,r_a⁽ⁱ⁾(t),···,r_M⁽ⁱ⁾(t)} has the following EOM when subjected to an overdamped limit

8

where n represents the number of monomers within the interaction range by the many-body PMF. Ψ[r^(j)(t)] and g[r^(j)(t),r^(k)(t)] are the intramolecular and intermolecular distributions of monomers, respectively. F_a^Q(i)(t) is the random force acting on the ath monomer of the ith molecule. The effective friction coefficient for each monomer, ζ_eff, can be expressed as a linear combination of different terms: the bare Rouse friction, ζ₀ = β⟨F_a⁽ⁱ⁾·F_a^Q(i)⟩/3, the intramolecular memory function (i = j), and the intermolecular memory function (i ≠ j), which accounts for the time–space correlation of random forces

9

In practice, it is difficult to do a straightforward inference of the three individual terms on the right side of eq 9 from AA simulations. If we do not distinguish intermolecular and intramolecular contributions and account for them using an effective kernel, k(t), the above equation can be simplified as

10

where the second term is an integral of the non-Markovian kernel k(t). It is, in principle, to be integrated over a time period until the kernel completely decays. For instance, for a linear polymer chain melt, the chain relaxation time might be a good choice. However, CG GLE simulation using such a long kernel is impractical. Therefore, we expect a short-time kernel, which can effectively capture the essential dynamical properties of the system with an affordable computational efficiency. For this purpose, we can simply apply a truncation in the time integral of the kernel

11

where 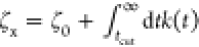is a Rouse-type friction coefficient that also effectively includes the contribution from the truncated long-time memory kernel after a truncation in time, t_cut. Accordingly, the kernel can be written as

12

where k_x(t) is a delta function located at t = 0, corresponding to ζ_x. Here, we approximate that k_x(t) has a fast decay; therefore, we can ignore its memory effect. We know that the non-Markovian nature of the kernel originates from the many-body correlations in the system, and it is typically strong in the nearest neighborhood of the CG monomer, which corresponds to a short-time kernel k(t). Results of the velocity autocorrelation function (ACF) (as shown in Section 3.2) also show that rich information resides in the short-time range. Therefore, we truncate the contribution after t_cut in the second term in eq 11 after which the velocity ACF curve starts to converge. The t_cut can be selected as the caging time corresponding to the Debye–Waller factor ⟨u²⟩. This characteristic time has been successfully used in the ER method to measure the ER factor and accurately reproduce the dynamic properties across a broad temperature range for various polymer systems.^18,19

One has to be aware that after the above treatment, it is still impossible to obtain both the Rouse term and the non-Markovian term on the right side of eq 11 analytically. Alternatively, one can turn to iterative construction processes.^{77,85−87,114,115} According to ref (86), we set velocity ACF from AA simulation as the target during the iterative optimization of the kernel as follows

13

with

14

where α is a relaxation parameter, and it is proven that an introduction of this parameter ensures a fair performance of iteration.¹¹⁶ The complete form of α can be expressed as α = γM²/k_BT.⁸⁶ The M and T are the mass of the CG bead and simulated temperature, respectively. The γ value is system- and time step-dependent and can be determined by a series of tests. The best convergence is achieved when it is set as 10 in our system with a time step of 0.005 ps. The window size parameter t_cor is set as 0.05 ps in our optimization process.

Note that during the iteration process, we need to fix the total friction at a certain value, ζ^*_eff, such that the diffusion coefficient resulted from CG simulation matches with that of AA simulation, i.e., D_CG = D_AA. There are some similarities between our method with refs (87 and 77), where they use the integral of memory kernel 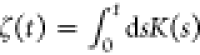as the optimization target. In addition, the kernel is treated numerically during the iteration process. Therefore, the boundary condition can be written as

15

where Δt is the time step size. Where ζ^*_eff is the total friction, and it is kept as a constant and is initially parametrized by fitting the long-time diffusion coefficient of the CG model to the AA model. The second term at the right-hand side of the equation corresponds to the memory kernel, while the first term k_x(0) is the Rouse-type friction. Indeed, initially, we do not know the respective contributions from these two terms. Therefore, we first used the iterative process to optimize the short-time memory kernel k(t) by setting the velocity ACF as the target. Afterward, k_x(0) is determined using eq 15. Note that the ζ^*_eff = 1780 amu·ps^–1 is determined for our current system using the parametrization approach used in refs (57 and 58).

For the above iterative optimization, 25 ps GLE simulations were performed for each iteration using the PYGAMD package.¹¹⁷ The Brünger-–Brooks–Karplus¹¹⁸ integrator is used. The integration time step is set to be Δt = 5 fs. The colored noise was generated to develop random force using the Fourier transform.^85,119 The total iterative process was conducted, as shown in Scheme 3. The caging time can be determined by analyzing the transition region of the velocity ACF, during which the dynamics of the monomers undergo a transition from local collisions to hydrodynamic interactions. In our present system, we measure the caging time to be between 2 and 4 ps, which is in line with previous studies.^18,19,58 To improve computational efficiency, we choose t_cut = 2 ps for the memory kernel in subsequent GLE simulations. In addition, benchmark calculations show that there is no obvious difference if we use a longer time of t_cut = 4 ps, details are shown in the section “Memory kernel developed by different t_cut” in the Supporting Information.

Scheme 3. Iterative Optimization Procedure of the Memory Kernel.

3. Simulation Results

3.1. Iterative Reconstruction of the Kernel

First, we reconstruct the kernel using the algorithm proposed by Jung et al.,⁸⁶ as demonstrated in eqs 13 and 14. The evolution of both the kernel and corresponding velocity ACF is shown in Figure 1a,b, respectively. Although we have overall a satisfactory alignment between GLE and AA simulations before ∼0.4 ps, there is a significant damping effect emerges in the tail of the velocity ACF, leading to an eventual divergence of the CG curve from the AA counterpart. This finding aligns with the results in ref (116), which also find a “lack of convergence for very small and large absolute frequencies” using an exponential kernel. We find that such a damping effect can be eliminated by the introduction of a 0th-order iterative correction term into the kernel

16

Figure 1.

Intermediate (a) memory kernels and (b) velocity ACFs during iteration using eq 13. After 90 iterations, we switch to use eq 16 for another 40 iterations. Changes of memory kernel are shown in (c), and the resulted velocity ACFs are compared in (d).

Here, α_s can be expressed as α_s = γ_sM²/k_BT, and it is different from α in eq 13, it has a unit of ps^–1. The best convergence is achieved when γ_s is set as 4 ps^–1 in our system with a time step of 0.005 ps. The further optimization of the kernel using the 0th-order term mentioned above significantly enhances the numerical stability, particularly at relatively low frequencies. As such, a combination of eqs 13 and 16 can be utilized to augment the overall convergence of the iterative process; a full convergence of the velocity ACF is shown in Figure 1d. In principle, the superior performance of eq 16 can be elucidated by using Laplace analysis. However, numerical discretization and the complexity of the kernel form pose significant challenges to mathematical analysis. Intuitively, the modification via the above 0th-order derivative term yields a smoother correction to the kernel, as shown in the tail part in Figure 1c, thereby eliminating the substantial damping contribution of the first-order correction term. Note that the velocity ACF used for the above iteration is smoothed to filter out very high frequencies that could potentially compromise the stability of the simulation. After 90 iterations using eq 13 and followed by 40 iterations with eq 16, the velocity of ACF resulting from the GLE simulation converges to that of the AA simulation, as depicted in Figure 1d. The iteration is judged to be converged until the error function 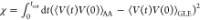is less than 0.0005.

3.2. Performance of the Model on Dynamical Properties

After the successful reconstruction of the kernel, as shown above, we calculated the mean square displacement (MSD) curves, velocity ACFs, and force ACFs and compared the corresponding results from AA simulations, LE simulation with ζ* (denoted as LE in the following), and CG simulation without any kernel (denoted as CG), respectively. The results are shown in Figure 2a–c, respectively. Not surprisingly, we find good agreement between the GLE simulation and the AA simulation. Although a good reproduction of both the velocity ACF and force ACF can be expected since the former is set as the target for the iteration and the latter is a derivative of the former, we have to note that both the results from the CG and LE simulations have a large deviation from the AA results. One of the primary contributions of our method is its ability to accurately reconstruct local dynamics while maintaining structural consistency, which distinguishes it from previous approaches. When compared with other CG PS models, our model has certain advantages. For instance, the time mapping approach⁴⁴ only uses a constant to fit the long-time diffusion dynamics, but it fails in adequately describing local dynamics. Similarly, the Markovian model can only treat with long-time diffusion dynamics by incorporating external frictions between CG beads.^57,58 Instead, the ER method can though effectively capture local dynamics, but it often leads to deviations in structures due to the use of the simple Lennard-Jones form.¹⁸

Figure 2.

(a) MSD curves, (b) velocity ACFs, and (c) force ACFs calculated from AA simulation, GLE simulation with the final optimized kernel, LE simulation with ζ^*_eff and CG simulation without any friction, respectively.

In addition, we note that the MSD curve resulting from a conventional CG simulation without any memory kernel is orders of magnitude faster than the AA counterparts, as shown in Figure 2a. On the other hand, although the LE simulation using a single friction constant of ζ* have overall a good agreement with the AA simulation, there is a noticeable underestimation in the transition region from ballistic to subdiffusive region, which corresponds to the dynamic behavior in the first neighboring shell. In contrast, the MSD curve resulted from the GLE simulation with a determined memory kernel has obviously a better match with that from the AA simulation. We observe a slight deviation in the MSD between GLE and AA simulations at the intermediate scale (10–200 ps). This discrepancy can be attributed to the inadequate consideration of hydrodynamic interactions for unentangled polymer melt.¹²⁰ A more comprehensive discussion on this topic can be found in Supporting Information. The self-diffusion coefficients calculated by different models are listed in Table 1. As expected, the diffusion coefficients resulted from GLE and LE simulations are both in good agreement with the AA model. We also note that although the GLE model has the same total friction ζ^*_eff as the LE model, the GLE model exhibits slower diffusion. Similar results have been found in other studies.^84,121,122 This discrepancy can be attributed to the influence of dynamical modes coupled with the memory kernel on subsequent modes, even though the temporal scale of the memory kernel is 3 orders of magnitude lower than that of the diffusion. This interdependence between temporal scales deserves further investigation.

Table 1. Comparison of Self-Diffusion Coefficients Calculated from Different Models.

	AA	GLE	LE	CG
D/×10–5 cm2·s–1	0.0686	0.0654	0.0704	3.14

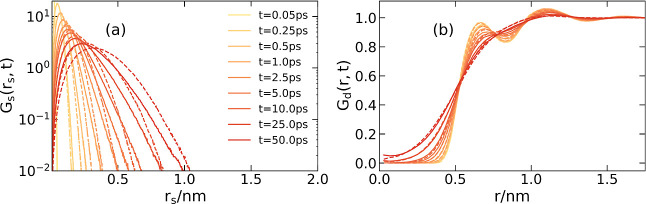
Other collective dynamical properties were calculated to validate our model, including the self- and distinct van Hove functions (VHFs), and the incoherent intermediate scatter function (ISF). The one-dimensional self VHF is the probability density of finding a particle i at a Euclidean distance of motion r_s at time t, given that the particle was initially at the origin t = 0

17

Similarly, the distinct VHF is defined as

18

where ρ represents the number density and N is the number of particles in the simulation box.

The incoherent ISF is actually the spatial Fourier transform of the self VHF. Instead of using the Fourier transform, the one-dimensional incoherent ISF is directly computed from the trajectories in our analysis

19

In Figure 3, we compare the self- and distinct VHF of the GLE model with the AA reference. Other results about the LE and CG models can be found in the Supporting Information for the sake of clarity. The GLE simulation effectively controls the self-displacement distribution, as shown Figure 3a. However, noticeable shifts in the distribution are observed for GLE simulations compared to AA references when the time exceeds 10 ps. This observation aligns with the findings from the MSD curves, where the MSD resulted from GLE simulation is slightly faster than that in AA simulation at the time scale of 10–100 ps, as marked by an arrow in Figure 2a. On the other hand, the distinct VHF exhibits a higher consistence between AA and GLE simulations, suggesting a good reproduction of pair correlation in both structural and dynamical evolution.

Figure 3.

(a) Self-VHF and (b) distinct VHF for AA reference (solid line) and the GLE model (dashed line).

The incoherent ISF curves were calculated at different q values, capturing structural relaxations occurring at various spatial scales, and the results are shown in Figure 4, where q ≈ 12 nm^–1 in Figure 4b corresponds to the monomer size (∼0.5 nm). We note a good agreement between GLE and AA simulations in the short-time regime where the memory kernel is present. After which, the ISFs resulting from GLE simulations quickly converged to those of the LE simulations, indicating a faster relaxation compared to the ISFs of the AA simulations. Nevertheless, our findings indicate that a simple mean-field memory kernel can adequately describe the local dynamics at a short time scale, though it falls short in capturing the intricate dynamics on longer times. It would be intriguing to investigate whether an extended memory kernel could match the AA curves at longer times, yielding improved reproduction of the relaxation modes.

Figure 4.

Incoherent ISF F_s(q, t) calculated from different simulations, as a function of time. Different q values are used to represent multiple spatial scales: (a) q = 18q₀, (b) q = 14q₀, (c) q = 9q₀, and (d) q = 5q₀, with q₀ = 2π/L and L = 7.22 nm.

To further evaluate other collective ability of our CG model, we compute the stress relaxation modulus G(t) with

20

where we use all the off-diagonal components of the stress tensor to improve the calculation.^59,123 According to Mondello and Grest,¹²⁴ a fair comparison of G(t) can be made with the AA trajectory mapped to the monomer scale, corresponding to the CG mapping scheme. Since we only use conservative forces in the calculation of σ in GLE simulation, we define G_mapped(t) as a convolution of G_AA(t) and 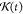as the AA reference

21

Here, G_AA(t) is calculated from the fully AA trajectory and the 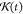is a sliding function used to eliminate the dissipation and random contributions from fast degrees of freedom. The 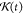is naturally related to the memory kernel K(t) and has the form of 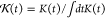. The results of G(t) from the GLE simulation are compared with G_mapped(t), as shown in Figure 5. They have a good agreement within 100 ps. It can be attributed to a successful description of other collective properties, such as the results of G_d(t) in Figure 3b, since G_d(t) describes the time evolution of interparticle distances and therefore interparticle forces. Finally, we also note that with the optimized kernel included, the good performance of the IBI potentials on static structures remain untouched since the conservative interactions remain invariant, as shown in Figure 6.

Figure 5.

Comparison of the stress relaxation modulus G(t) calculated from GLE and AA simulations.

Figure 6.

(a) RDF, (b) bond length distribution, and (c) angle distributions between CG beads calculated from AA simulation, GLE simulation with the final optimized kernel, and CG simulation without any friction, respectively.

4. Discussion and Conclusions

In this study, we present a bottom-up approach to effectively developing a chemically specific, systematic CG polymer model with both consistent structural and dynamical properties. In particular, conservative forces are inferred by using the IBI method, allowing for an accurate representation of the structural properties observed from the reference AA simulations. These properties include the RDF, bond length distribution, angle distribution, and density. To retrieve the correct inherent dynamical properties of the system, the GLE simulation is performed with a time-dependent memory kernel. Importantly, a straightforward extraction of the memory kernel from Volterra equation (eq 7) suffers from numerical instability for the polymer system. Practically, we decomposed the memory kernel into two parts: one represents a Rouse-type delta function, which determines long-time diffusion dynamics; and the other using a time-dependent short-time kernel to control the high-frequency motions. Specifically, the latter is reconstructed from an iterative procedure. In our iterative procedure, the integral of the memory kernel is constrained for reproducing the diffusion coefficient of the monomers from the AA simulation. The velocity ACF extracted from the AA simulations is set as a target for the iterative optimization of the kernel. The proposed procedure was applied to a PS melt system, as an example. We adopted a mapping scheme in which each CG bead represents one styrene monomer. The results show that a proper reconstruction of the memory kernel enables the reproduction of important dynamical properties of the system, such as velocity ACF, force ACF, and the MSD curve of monomers.

To further investigate the performance of our model, we calculated other collective properties, including VHFs, ISF, and stress relaxation modulus. By comparing self-VHFs and ISF, we observe good agreements between AA and GLE simulations in the structural evolution at short time, albeit the deviations arise at long time due to the vanish of the memory kernel. The stress relaxation function G(t) exhibits consistence on longer temporal scales up to 100 ps. This can be attributed to the better performance of the GLE model on the distinct VHF, which represents the evolution of pairwise structures, corresponding to the evolution of conservative forces.

Other than the structural and dynamical properties, as we discussed here in this work, another important direction is to treat the representability and transferability issues of the CG model under different thermodynamic conditions. So far, many efforts have been devoted in this direction, mainly on the representability and transferability issues of conservative CG models. Readers can refer to refs (21, 36, 125, and 126). We have to note that the above method presented is, at the moment, applicable only to one-component homogeneous polymer melt systems without significant dynamical heterogeneity. For multicomponent systems, especially for systems where inhomogeneous self-assembly or phase separated structures come into play, one also has to treat the competitions between different interaction pairs. A preliminary work can be found in our previous study for binary diblock copolymer and blend systems of PS and poly(methyl methacrylate).²⁵ Moreover, for the dynamics properties in such multicomponent systems, the things are much more complicated. For that, data-driven approaches^112,127 may be useful for developing more inhomogeneous memory kernels for such systems. Nevertheless, we still anticipate that the approaches presented in this work can be readily applied to homogeneous polymer systems and make a meaningful contribution to the field of polymer simulation.

Data Availability Statement

The GLE models and related MD packages are available at https://github.com/greenbridge918/pygamd-GLE.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.3c00756.

• Direct inferring of the memory kernel by solving the Volterra equation; memory kernel developed by t_cut; discussion about hydrodynamic interactions; van Hove functions of LE and CG models; and dynamical properties of polymer chain (PDF)

Author Contributions

^† The authors contributed equally to this work.

The authors declare no competing financial interest.