Abstract

FeN4 motifs, found, for instance, in bioinorganic chemistry as heme-type cofactors, play a crucial role in man-made FeNC catalysts for the oxygen reduction reaction. Such single-atom catalysts are a potential alternative to platinum-based catalysts in fuel cells. Since FeNC catalysts are prepared via pyrolysis, the resulting materials are amorphous and contain side phases and impurities. Therefore, the geometric and electronic nature of the catalytically active FeN4 site remains to be clarified. To further understand the behavior of FeN4 centers in electrochemistry and their expected spectroscopic behavior upon reduction, we investigate two FeN4 environments (pyrrolic and pyridinic). These are represented by the model complexes [Fe(TPP)Cl] and [Fe(phen2N2)Cl], where TPP = tetraphenylporphyrin and phen = 1,10-phenanthroline. We predict their Mössbauer, UV–vis, and NRV spectral data using density functional theory as windows into their electronic structure differences. By varying the axial ligand, we further show how well small chemical changes in both complexes can be discerned. We find that the differences in ligand field strength in pyrrolic and pyridinic coordination result in different spin ground states, which in turn leads to distinct Mössbauer spectroscopic properties. As a result, pyrrolic nitrogen donors with a weaker ligand field are predicted to show more pronounced spectroscopic differences under in situ and operando conditions, while pyridinic nitrogen donors are expected to show less pronounced spectroscopic changes upon reduction and/or ligand loss. We therefore suggest that a weaker ligand field leads to better detectability of catalytic intermediates in in situ and operando experiments.
Keywords: iron; single-atom catalysts; FeNC, oxygen reduction reaction; redox chemistry; spectroscopy
Introduction
The oxygen reduction reaction (ORR) is important for several technological applications such as metal air batteries, chlorine electrolyzers with oxygen depolarized cathodes, and (reversible) fuel cells.1−3 Besides platinum-based catalysts, single-atom catalysts can catalyze the ORR. A prominent example is the group of FeNC catalysts in which single iron ions are thought to be bound by four nitrogen donor atoms that are embedded in a graphene-like matrix.4 While almost as active as platinum, their long-term stability remains to be improved.56 Since FeNC catalysts are obtained by pyrolysis, they are highly amorphous and have a heterogeneous composition in terms of side phases and impurities.2,6−8 Therefore, classical methods for structure elucidation, such as X-ray diffraction, fall short. This complicates the identification of the composition and structure of the catalytically active site(s) and, thus, precludes a complete understanding of the catalytic cycle. Even the exact number and nature of the nitrogen ligands remains under debate, see Figure 1.9−16
Figure 1.

Sketch of some of the open questions around the active site(s) in single-atom catalysts for the oxygen reduction reaction, left, and the FeN4 model complexes [Fe(TPP)Cl] (top) and [Fe(phen2N2)Cl] (bottom) with ligand spheres P1 and P2, respectively, studied here in terms of their electronic and spectroscopic properties.
Iron ions and their environments can be studied with Mössbauer spectroscopy, which is sensitive to their oxidation and spin states that are in turn influenced by their ligand field.17,18 In an operando Mössbauer study,11 we have recently shown that the catalytically active iron ions are coordinated by nitrogen atoms in five-membered rings, i.e., a pyrrolic environment, or “FeN4C12” in the nomenclature of the field where the subscript on carbon indicates the shortest circumference of carbon atoms around the iron ion. The alternative discussed in the literature comprises nitrogen donor atoms in six-membered rings, i.e., a pyridinic environment or “FeN4C10”. This alternative type of site was previously implicated by us in the transformation of peroxide in the ORR in an in situ Mössbauer study.10
Jaouen and co-workers assigned their in situ data to the presence of a high-spin Fe(III) site (D1) and a low or intermediate spin Fe(II) site (D2).14 They observed structural changes for one of their presumably catalytically active sites, D1, while they attributed the main activity to the second site, D2, that remained unchanged upon applied potential.14 They interpreted this with the presence of a durable and a nondurable active site in their FeNC catalyst. In contrast, Li et al. did not observe any significant changes under in situ conditions for their FeNC catalysts in acidic media while some changes occurred in alkaline media.15 It thus appears that both types of sites might be present in FeNC catalysts, but they may have different catalytic roles. Notably, different preparations yield FeNC catalyst materials with different impurities, side phases, and activities.14,19−22 The preparation conditions might thus play a role in determining which active site motif is dominant, in terms of quantity and catalytic capability.
A deeper understanding of the electronic structures of the two kinds of FeN4 sites is hence imperative for a more detailed analysis of spectroscopic data on FeNC catalysts. We note that other factors than the type of nitrogen donor will influence the spectroscopic properties, e.g., the extent of the graphene sheet and possible dopants within it, or the presence and nature of an axial ligand besides the substrate or catalytic intermediate, see Figure 1.23
The interpretation of Mössbauer data benefits greatly from density functional theory (DFT) calculations if the methodology is calibrated carefully, and both the isomer shift and the quadrupole splitting are used for assignments.24 Similarly, other structurally or electronically sensitive spectroscopic properties can be predicted well with DFT.25,26 While many questions on FeNC catalysts can be answered by Mössbauer spectroscopy, having access to complementary information from other methods that probe the valence electronic structure (UV–vis, K pre-edge X-ray absorption spectroscopy, and valence to core X-ray emission spectroscopy)12,27−32 or the interactions in the first coordination sphere [infrared (IR) spectroscopy, nuclear resonance vibrational spectroscopy (NRVS), and extended X-ray absorption fine structure] would be highly beneficial.33−35 While not all of these methods are applicable to FeNC catalysts –notably UV–vis and IR spectroscopy due to the black, amorphous nature of FeNC catalyst materials– having a principal understanding of expected changes will be fundamentally important for studies with FeNC catalysts. Additionally, these windows into the electronic structure will be relevant for studies with model complexes, whether in a homogeneous catalytic setting or after immobilization on an electrode.
To address the question of how sensitive spectroscopic methods are to changes in the coordination environment, we had previously studied23 the discernibility of spin state, axial ligand, and bridging atom for Marshall-Roth’s complex, [Fe(phen2N2)Cl].9 Our results suggested that axial ligands may be differentiated by the UV–vis and Fe K pre-edge spectra and the Mössbauer quadrupole splitting, and doping atoms will influence the IR, UV–vis, and iron K pre-edge spectra.23 In a separate study, we discussed the influence of porphin substituents on the redox potentials in organic and aqueous solvents.35
Herein, we build on these studies to compare pyrrolic and pyridinic environments, i.e., [Fe(TPP)Cl] and [Fe(phen2N2)Cl], see Figure 1, and the influence that single reduction or ligand loss have on the ligand field and accessible spin states. We discuss the implications for the discernibility of these species by Mössbauer, UV–vis, and NRV spectroscopies. As axial ligands, we chose Cl– and OH– since they are commonly found in model complexes and are expected to be present in FeNC catalysts. We find that the differences in ligand field strength in pyrrolic and pyridinic coordination result in different spin ground states which in turn leads to distinct spectroscopic properties. Most importantly, the Mössbauer signals of iron ions in pyridinic environments fall in a narrow region, whereas ligand loss and reduction are readily detectable for pyrrolic nitrogen donors with a weaker ligand field. This finding implies that spectroscopic changes under in situ and operando conditions of real FeNC catalysts may reveal the catalytic activity at the pyrrolic sites but not at the pyridinic sites. We suggest that differences in ligand field strengths lead to better detectability of pyrrolic sites in in situ and operando experiments but not necessarily to superior catalytic properties. Nonetheless, a direct correlation of quantitative spectroscopic changes of a species under operando conditions with catalytic activity is a strong indicator of its catalytic relevance.
Results
Parent Complexes
We study two series of complexes, [Fe(TPP)Cl] and [Fe(phen2N2)Cl], which in the following are described as [FeIIIP1Cl] and [FeIIIP2Cl], see Figure 2 for the ligand variations. In both complexes, the FeIII ion is pentacoordinate with a planar macrocyclic N-donor ligand and chloride as an axial ligand. The spin ground state of [FeIIIP1Cl] is S =5/2 according to magnetic susceptibility and EPR measurements,36 whereas for [FeIIIP2Cl], a spin ground state of S =3/2 was assigned from its Mössbauer parameters.9 These spin states are correctly identified as the lowest energy spin states in single-point calculations [OLYP/CP(PPP):def2-TZVP] on fully relaxed structures (TPSS/def2-TZVP:def2-SVP), see the Computational Details section.
Figure 2.

Structural formulas of the complexes studied here: (a) pyrrolic [FeIIP1] and its congeners (P1a to P1e) and (b) pyridinic [FeIIP2] and variants (P2a, P2b). Optimized geometries of (c) [FeIIIP1Cl] and (d) [FeIIIP2Cl]. Iron atoms are depicted in orange, nitrogen in blue, chlorine in green, carbon in gray, and hydrogen in white.
In [FeIIIP1Cl], there are five occupied spin up (α) d orbitals with empty spin down (β) counterparts, i.e., conforming to the expected S = 5/2 occupation pattern (xy)1(xz)1(yz)1(z2)1(x2 – y2)1, see Figure 3a. Besides the nonbonding iron d(xy) orbital, the occupied MOs with Fe 3d character are bonding or antibonding interactions with the chloride p(x) and p(y) and π orbitals of the porphin ligand, see Figures S1 and S2 and Tables S1–S2. The α and β HOMOs are dominated by porphin π character with some d(z2) admixture. The β LUMO is a nonbonding 3d(xy) orbital.
Figure 3.

Schematic representations of the MOs dominated by Fe 3d atomic orbitals for (a) P1 and (b) P2 ligand environment before and after reduction. The energy spacings are not drawn to scale; detailed MO schemes are shown in Supporting Information. In a square-planar ligand field, orbitals with z-components would be stabilized, so that the d(z2) orbital may become the most stabilized orbital.37 For multideterminant cases, one representative electronic configuration is shown.
In [FeIIIP2Cl], the d orbital occupation pattern is (xy)2(xz)1(yz)1(z2)1(x2 – y2)0, see Figure 3b. Accordingly, the α HOMO has iron d(z2) character with significant contributions of the in-plane and axial ligand orbitals, see Figure S2. The β HOMO is of pure d(xy) character. We note that the C2v symmetry leads to nondegenerate π* MOs with iron d(xz) or d(yz) and chloride p character.
As expected for iron complexes, the other spin states are energetically close. For [FeIIIP1Cl], the intermediate-spin state S = 3/2 is found only 2.4 kcal mol–1 above the S = 5/2 ground state. The gap is larger in [FeIIIP2Cl], where the high-spin state S = 5/2 is predicted at 7.0 kcal mol–1 above the S = 3/2 ground state.
The structural parameters obtained computationally by geometry relaxation of [FeIIIP1Cl] are in good agreement with the crystal structure, see Table 1.37 For [FeIIIP2Cl], no crystal structure is available. The Fe–N bond lengths are shorter than those for [FeIIIP1Cl], whereas the Fe–Cl distance is longer. This can be attributed largely to the different spin ground states: in the computationally predicted high-spin geometry of [FeIIIP2Cl], the Fe–N and Fe–Cl distances are found to be closer to those of the TPP complex. Notably, the trans,trans–N–Fe–N angles show that the iron ion is more strongly displaced from the ligand plane in [FeIIIP2Cl] than that in [FeIIIP1Cl], especially in the high-spin case where the angle between the two phenanthroline subunits is significantly diminished, see Table 1.
Table 1. Structural Properties of Optimized Structures of [FeIIIP1Cl] and [FeIIIP2Cl] in Different Spin Statesa.
| S | Fe–N1 | Fe–N2 | Fe–N3 | Fe–N4 | Fe–Cl | |
|---|---|---|---|---|---|---|
| [FeIIIP1Cl] | 5/2 | 2.091 | 2.092 | 2.091 | 2.092 | 2.242 |
| [FeIIIP2Cl] | 3/2 | 2.043 | 2.044 | 2.045 | 2.044 | 2.298 |
| [FeIIIP2Cl] | 5/2 | 2.068 | 2.068 | 2.068 | 2.068 | 2.234 |
| S | N1FeN2 | N2FeN3 | N3FeN4 | N4FeN1 | N1FeN3 | N2FeN4 | |
|---|---|---|---|---|---|---|---|
| [FeIIIP1Cl] | 5/2 | 87.0 | 87.0 | 87.0 | 87.0 | 153.2 | 153.7 |
| [FeIIIP2Cl] | 3/2 | 83.5 | 88.2 | 83.5 | 88.1 | 148.7 | 148.7 |
| [FeIIIP2Cl] | 5/2 | 81.0 | 82.7 | 81.0 | 82.7 | 135.8 | 135.8 |
Redox Chemistry
Experimentally, the FeIII/FeII redox event of [FeIIIP1Cl] is observed at −0.05 V vs RHE in the organic solvent, dichloromethane.35 For [FeIIIP2Cl], no data in organic solvents are available.9 The redox potential is highly sensitive to the solvation environment and immobilization. This is exemplified for carbon-supported [FeIIIP1Cl] and [FeIIIP2Cl] immobilized on an electrode, where the FeIII/FeII redox event in the acidic electrolyte is observed at 0.19 V vs RHE11 and 0.59 V vs RHE,9 respectively. The reduction of [FeIIIP1Cl] is associated with loss of the chloride ligand.35 Marshall-Roth et al. stated that the redox event in the P2 case is better described as FeIII–OH/FeII–H2O,9 suggesting rapid ligand exchange with the electrolyte and a concerted proton-transfer step. Therefore, hydroxide is studied here as an alternative axial ligand. Since the individual steps of one electron reduction and axial ligand loss are easily separable in computational studies, we discuss below the plausible intermediates; see Figure 4a.
Figure 4.

(a) Square scheme for the reduction and ligand abstraction steps. Gibbs energy diagrams calculated at the TPSS/def2-TZVP:def2-SVP level of theory for (b) [FeP1] and (c) [FeP2]. The red and orange lines in part b refer to the axial ligand being Cl– and OH–, respectively. The dark blue and light blue lines in (c) refer to the axial ligand being Cl– and OH–, respectively.
Electronic Structures
Two different spin states, S = 1 and S = 2, can form, in principle, upon reduction. For [FeIIP1Cl]−, the S = 2 and S = 1 states are predicted at almost equal energies. Considering only the electronic energies, S = 1 is preferred by 2.0 kcal mol–1 over S = 2; including thermodynamic corrections leads to degenerate S = 1 and S = 2 states [ΔE(HS,IS) = 0.2 kcal mol–1]. These subtle differences exemplify the notorious difficulties in predicting the correct spin states and point out the difficulties single-determinant methods like DFT face when studying iron complexes.38−41 We note that electronic structures with a noninnocent macrocyclic ligand can in principle arise, but none are relevant here. With hydroxide as the axial ligand, both the oxidized parent complexes and the reduced species show the same spin state behavior, albeit with a more pronounced Gibbs energy preference for S = 2, see Supporting Information.
In contrast, the S = 1 spin state is preferred in [FeIIP2Cl]− over the alternative S = 2 spin state by 9.3 kcal mol–1 considering the electronic energies; thermodynamic corrections lower this splitting to 6.8 kcal mol–1. Only with a change in the second coordination sphere, specifically if the bridging atom between the two phenanthroline units is oxygen, there are S = 2 states isoenergetic (ΔE(HS,IS) < 2 kcal mol–1) regardless of the identity of the axial ligand. The fact that the pentacoordinate complexes with a porphyrin ligand can access S = 5/2 and S = 2 spin states demonstrates that the porphin core exerts a weaker ligand field than the phenanthroline-based environment.
Evaluating the reduction event in the absence of an axial ligand, i.e., for the square-planar complexes, we observe less pronounced differences in the electronic structures. Both complexes have the same spin ground states: the FeIII complexes are predicted as S = 3/2 and the FeII complexes as S = 1 species. Alternative spin ground states are found at least 12 kcal mol–1 higher in energy with both types of macrocyclic ligand, see Tables S1 and S2.
Reaction Free Energies
Turning now to the reaction free energies for the redox events, we consider these in an electrochemical setting and report the energies in eV (1 eV = 23.06 kcal mol–1). An overview of the reduction and ligand loss steps in terms of a square scheme is given in Figure 4a. The loss of an anionic ligand is always endergonic; see Figure 4b,c. This may be partly attributed to the separation of charges that are only implicitly solvated. In the FeIII cases, the loss of hydroxide and chloride is more endergonic in the phenanthroline-like environment. For instance, ΔG for chloride loss amounts to 1.31 eV, whereas in the porphyrin environment, chloride loss is associated with a ΔG of 1.08 eV. In the FeII cases, ligand loss is less endergonic than that in the FeIII cases. Releasing the chloride ligand from [FeIIP1Cl]− and [FeIIP2Cl]− comes at a cost of 0.37 and 0.40 eV, respectively. Hydroxide release from [FeIIP2OH]− is uphill by only 0.06 eV, while for [FeIIP1OH]−, it is associated with 0.44 eV. As shown in Figures S8–S10 and Table S6, exergonic ligand loss reactions can be achieved with different substituents on the P1 ligand or different bridging atoms in the P2 ligand.
The reduction events without a loss of the axial ligand are calculated from energy differences between the oxidized and reduced species considering electronic and thermodynamic contributions. These Gibbs energy differences always appear as exergonic reactions since the oxidation half reaction is not explicitly formulated. They recently were correlated to their redox potentials vs RHE in the aqueous electrolyte for the [FeIIIPiL] series of complexes, see also Figure S11.35 Reduction in the square-planar complexes has a ΔG that is more than 1 eV larger than reduction in the square-pyramidal environments. However, since ligand loss from the parent species is uphill already, the reaction path from [FeIIIPiL] to [FeIIPi] presumably occurs via [FeIIPiL]− or as a concerted reaction. Comparing the P1 and P2 ligands, the differences in ΔG for the reduction events amount to, at most, 0.3 eV.
Modulating redox potentials via substitution in the second ligand sphere can help in designing an optimal catalytic reaction landscape. Including electron donating or withdrawing groups on the phenyl substituents in [FeIIIP1L], see Figure 1, alters the FeII/FeIII redox potential as expected with more positive potentials for the more strongly electron-withdrawing groups35 independent of the axial ligand. Similarly, the Gibbs free enthalpy for ligand loss increases with more strongly electron-withdrawing character of the phenyl substituents in both the FeIII 35 and FeII complexes with either choice of axial ligand. While these are the broad trends, some outliers exist within the series; all data are given in Table S6. In the [FeIIIP2L] series, the second ligand sphere effects are much more pronounced since the structural modification alters the electronic structure, specifically as a direct influence of the π system of the equatorial ligand. While for the carbon-bridged system P2a the Gibbs free enthalpy differences for all four steps are generally lower than that for P2, those of the oxygen-bridged system P2b are higher, see Figure S10 and Table S6.
Spectroscopic Discernibility
The electronic structure differences discussed above suggest that electronic spectroscopy may be used to detect these changes. We discuss below UV–vis, Mössbauer, and NRV spectroscopies. This question is of particular importance with a view toward identifying in situ and operando changes in FeNC catalysts where a multitude of iron environments coexist and undergo changes upon applying a potential or exposing the material to dioxygen.10,11,14,15,42 The spectroscopic predictions below may also be relevant for studying molecular model catalysts anchored to or incorporated into an electrode or as homogeneous catalysts.
UV–Vis Spectra
The UV–vis spectra as predicted with TD-DFT calculations show pronounced differences in energy and intensity among the four species of the ligand loss and reduction sequence and between the two ligand environments; see Figure 5. The [FeP1] spectra increase in intensity upon reduction, as would be expected with an additional electron in the valence region. Ligand loss leads to a decrease in intensity, as can also be easily rationalized due to missing dipole-allowed transitions between orbitals that contain both Fe 3d and ligand 2p character. Changes due to modifications of the axial ligand and in the second coordination sphere are subtle, as shown in Figures S15–S19. The changes in the [FeP2] spectra are much less pronounced than those in [FeP1]. Importantly, however, the oscillator strength of the transitions in the [FeP2] series is much lower than that for the [FeP1] series. This implies that in a catalyst material where both types of environment are putatively present, [FeP2] species may be at risk of being overlooked with UV–vis spectroscopy. Whether this holds for other spectroscopies that probe the unoccupied valence space would have to be studied explicitly.
Figure 5.
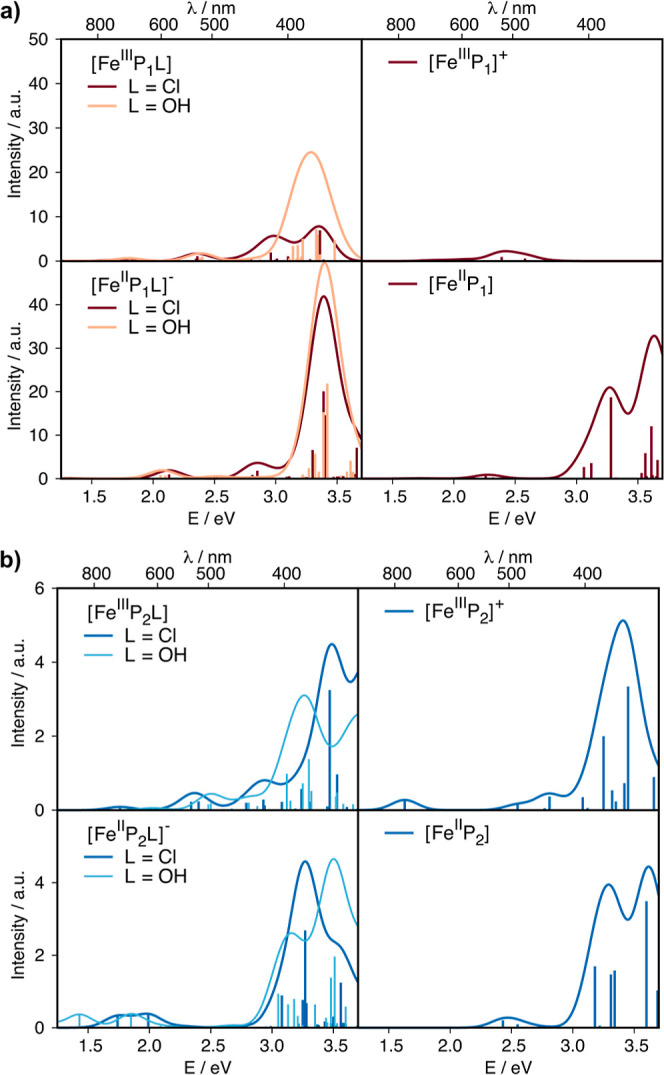
UV–vis spectra predicted with TDDFT at the B3LYP/def2-TZVP(-f) level of theory for all species in the square scheme in their lowest energy spin states; (a) [FeP1] and (b) [FeP2]. The spectrum of the S = 1 [FeIIP1L]− case is shown in Figure S14. The y-axis reflects the calculated oscillator strength of the vertical transitions scaled by applying an artificial broadening of 0.25 eV to obtain the line spectrum and is hence labeled as intensity with arbitrary units (a.u.).
Mössbauer Spectra
Mössbauer spectroscopy allows a more differentiated look at iron spin and oxidation states. For electrodes of carbon-supported [FeP1]Cl, the appearance of an FeII high-spin species was observed under reductive conditions (−0.05 V vs RHE) in the absence of dioxygen with Mössbauer parameters that are characteristic for high-spin FeII.43 Under similar conditions, FeII high-spin species were also found for differently prepared FeNC catalyst materials at reductive potentials.A111042 For the as-prepared material, it is not clear a priori whether the reduction of these sites will be associated with ligand loss. Therefore, studies on well-defined molecular complexes are often used to formulate expectations for changes that can be observed under in situ or operando conditions.
The two ligand environments of the parent complexes lead to different Mössbauer signals, so that they are discernible by their isomer shifts and quadrupole splittings; see Figure 6. The predicted values are in good agreement with the experimental data; the predicted isomer shift values fall within the trust region established by our calibration study {[FeP1]Cl exp. (4.2 K): 0.41 mm s–1,44,45 calc.: 0.51 mm s–1; [FeP2]Cl exp. (80 K):9 0.39 mm s–1, calc.: 0.32 mm s–1}, whereas the difference between theory and experiment is more pronounced for the quadrupole splitting values ([FeP1]Cl exp. (4.2 K): 0.46 mm s–1,44,45 calc.: 0.40 mm s–1; [FeP2]Cl exp(80 K): 3.06 mm s–1,9 calc.: 2.12 mm s–1). The significantly higher quadrupole splitting in the P2 environment than that in the P1 environment can be attributed to the less symmetric electron distribution and thus higher electric field gradient in the S = 3/2 than that in the S = 5/2 ground state. The calculated Mössbauer parameters for the different axial ligands suggest that this change is too small to be detectable.
Figure 6.

Mössbauer data predicted for all species in the square scheme; (a) [FeP1] and (b) [FeP2]. The error bars for isomer shift and quadrupole splitting from a calibration study are shown in the bottom right corner (trust regions for δiso: ±0.065 mm s–1, ΔEQ: ±0.18 mm s–1).24
The reduced form of [FeIIIP1L], [FeIIP1L]−, has close-lying high-spin and intermediate-spin states (vide supra). The Mössbauer parameters of the high-spin form are close to values measured experimentally (calc: δiso = 1.00 mm s–1 and ΔEQ = 4.58 mm s–1, exp:43 δiso = 1.08 mm s–1 and ΔEQ = 3.72 mm s–1). The two axial ligands can be differentiated by the quadrupole splitting values that differ by more than 0.88 mm s–1, whereas [FeIIP1OH]− gives a better match to the experiment mentioned above (calc: δiso = 1.00 mm s–1 and ΔEQ = 3.70 mm s–1). The energetically close-lying intermediate spin species [FeIIP1L]− are found at lower values: δiso = 0.72/0.68 mm s–1 and ΔEQ = 2.22/1.40 mm s–1 for L = Cl/OH, respectively. We note that in this case, identification of the axial ligand in an experiment would be more difficult since square-planar FeII species are expected to have Mössbauer parameters in this region.23 The variation of the Mössbauer parameters with different second sphere substituents follows the expected trends of electron-donating and withdrawing groups35 but is much smaller than variations due to oxidation and spin state changes, see Figure S12 and Table S7.
In the [FeP2L] complexes, the axial ligands alter the quadrupole splitting to a similar extent as in the [FeP1L] complexes. Most importantly, however, all values fall in a very similar range of isomer shift values. This can be easily rationalized by the stronger ligand field exerted by the phenanthroline-like ligand environment as discussed above, which stabilizes S = 1 and S = 3/2 spin states. As a corollary, we suspect that the [FeIIP2L]− species formed in an in situ experiment could not be distinguished from the doublet of the parent compound. With modification of the second ligand sphere in terms of the bridging atoms, similar Mössbauer parameters are found for the carbon-bridged phenanthroline ligand [FeP2aL]. In contrast, since a high-spin state can be stabilized in the oxygen-bridged [FeIIP2bL]− case, well-isolated doublets at δiso = 0.98/0.97 mm s–1 and ΔEQ = 3.55/2.71 mm s–1 for L = Cl/OH are predicted, see Figure S13 and Table S7.
NRV Spectra
A second iron-specific spectroscopy that is highly beneficial for the characterization of iron environments in FeNC materials is NRVS (also known as nuclear inelastic scattering). It detects all vibrations in which iron participates and thus is sensitive to the coordination environment of iron. Analogous to IR spectroscopy, specific regions are characteristic for certain types of vibration, e.g., out-of-plane vibrations including the so-called doming mode are situated below 200 cm–1, in-plane vibrations dominate the region between 200 and 400 cm–1, and axial ligand vibrational modes are typically found in the range between 400 and 600 cm–1, see Figure 7.46
Figure 7.

NRV spectra predicted at the TPSS/def2-TZVP:def2-SVP level of theory for all species in the square scheme in their lowest energy spin states; (a) [FeP1] and (b) [FeP2]. A line broadening of 15 cm–1 was applied.
In the present cases, the axial ligands are discernible via different frequencies for [FeIIIP1L], see Figure 7a. The Fe–Cl stretch is predicted at 330 cm–1 (exp: 358 cm–135), whereas for the hydroxide ligand, the Fe–O ligand stretch and Fe–O–H bending modes are predicted at higher frequencies, 539 and 608 cm–1. When reduced to [FeIIP1L]−, the frequency of the Fe–Cl stretch decreases to 252 cm–1, which overlaps with the vibrations of the in-plane ligand. A coupled Fe–OH stretching and bending vibration is also red-shifted to a value of 457 cm–1, with an Fe–OH wagging motion seen at 677 cm–1. Reduction leads to occupation of the nonbonding 3d(xy) orbital, so that the bond strength of iron with the axial ligand is not directly affected in terms of occupying a metal–ligand antibonding orbital. The observed decrease of the axial ligand stretches is more pronounced than may have been expected based on simplistic MO considerations, but in agreement with the less pyramidal iron and longer iron-ligand bond length in the reduced case.
Upon ligand abstraction, the in-plane modes between 400 and 500 cm–1 gain intensity, and an overall shift to higher frequencies is seen. This is a reporter of an increased iron–nitrogen bond strength, which is in line with the square-planar environment. No significant difference between the FeIII and FeII cases is predicted as may be expected from the very similar iron–nitrogen bond lengths, i.e., 1.959 Å for FeIII and 1.985 Å for FeII. Changes in the second coordination sphere of [FeP1a-eL] reveal only minor differences in intensity and position; the same trends upon reduction and ligand loss are predicted (Figures S22–S26). Overall, the calculations demonstrate that it will be difficult to discern all species: the most significant changes are found in a spectral region above 400 cm–1 that can have low intensities depending on the axial ligand.46
The phenanthroline-like environment P2 (Figure 7b) has an overall different shape of the spectrum with the dominant intensity features found between 200 and 500 cm–1 (cf. 150–350 cm–1 for P1). Consequently, the identity of the axial ligand is not as clearly resolvable. The higher frequencies mostly related to Fe–N vibrations are indicative of stronger Fe–N bonds, i.e., shorter bond lengths. This is congruent with the stronger ligand field of the P2 environment that was already deduced from the molecular orbital diagrams and energetically preferred spin states. The abstraction of an axial ligand from [FeP2L] is barely detectable, and upon reduction, a small shift toward higher frequencies is observed. From the MO considerations, the newly occupied orbital is of metal–ligand π* character, which would be expected to lead to a weaker Fe–L bond vibration. The Fe–L bond stretch is not shifted significantly upon reduction (e.g., 251 cm–1 to 247/333 cm–1 for Cl and 288/374/423/604 cm–1 to 260/369/428/682 cm–1 for OH). Meanwhile, slightly stronger Fe–N bonds with iron situated in-plane lead to a general shift of the spectrum to higher frequencies. Looking at the second coordination sphere of P2, the CH-bridged system P2a is predicted to behave similarly and is not discernible from P2. The O-bridged P2b, which is associated with a possible spin state change, shows a slight overall shift to lower frequencies upon reduction, which again is in line with longer bond lengths (i.e., FeIII–N 1.96 Å to FeII–N 2.08 Å), weaker Fe–N bonds, and a stronger pyramidal character of the observed ferrous high-spin state. We note that these changes are similar to those observed in the porphyrin complexes above. The axial ligands are more discernible in the NRV spectrum of P2b, e.g., the FeIII–Cl stretch is observed at 342/361 cm–1 while the FeIII–O stretch is observed at 515 cm–1. Upon reduction, the σ*-antibonding d(x2 – y2) orbital is occupied, and besides the expected increase of the Fe–L bond distances, the Fe–N bond lengths vary by < 0.05 Å. The frequencies for Fe-L increase subtly for FeII–Cl, and more clearly for FeII–O, they increase to 559 cm–1. The tetracoordinate complexes for the O-bridged P2b are similar to P2 and P2a, and due to this pronounced change in the overall spectral shape an abstraction of OH > 500 cm–1 can most likely be detected in the spectra.
As general trends, we observe that pyramidal character and bond distances define the spectral shape: in intermediate-spin states, the geometries have a more planar iron coordination environment, leading to stronger bonds with the equatorial ligands and thus generally a shift to higher frequencies. For weaker ligand fields, where spin state changes are associated with a more pyramidal character, weaker bonds with the macrocyclic donors and hence a shift to lower frequencies is seen. In these cases, the ligands can be more easily discerned. This also leads to a better detectability of reduction events in square-pyramidal cases than that in square-planar cases. In analogy to the conclusions drawn above for the Mössbauer spectra, less pronounced spectroscopic changes are expected for stronger ligand fields—here the pyridinic model complex—potentially hampering their identification in experiments. We note that especially in real catalyst materials where several types of iron site coexist, it thus appears highly challenging to resolve these sites by NRVS.
Discussion
The redox and spectroscopic properties of two types of FeII and FeIII complexes with different macrocycles (pyrrolic: P1 and pyridinic: P2) were presented above. In the following, we discuss the implications of these observations for FeNC catalyst materials and the challenges experiment and theory face in identifying the catalytically active species.
As a first observation, pyrrolic and pyridinic environments have different preferred spin states due to their different ligand field strengths and hence different spectroscopic properties. In the pyrrolic environment, different oxidation states and coordination numbers can be distinguished easily. In contrast, the pyridinic environment has similar Mössbauer signals in different oxidation states and coordination numbers. This leads to a cluster of Mössbauer signals that moreover overlap with other frequently observed doublets. Therefore, we cannot expect a characteristic “smoking gun” feature that would point out catalytically active sites with pyridinic coordination environments of FeII and FeIII. However, modifications in the second coordination sphere can have a significant influence, implying that dopants that weaken the ligand field may assist in detecting pyridinic sites in real FeNC catalysts. Thinking toward the design of molecular, carbon-supported model catalysts, carefully designing the ligand sphere may improve the spectroscopic detectability of catalytic intermediates and hence aid in a detailed understanding of the catalytic cycle.
We can thus conclude that a weak ligand field leads to better detectability upon reduction. Given the differences in detectability, both pyrrolic and pyridinic intermediates were present during catalysis. Detecting spectroscopic changes under in situ or operando conditions by Mössbauer spectroscopy may thus represent only a fraction of the chemically altered sites. To identify catalytically relevant sites in operando experiments, changes in spectral intensity must be quantitatively correlated to the electrochemical turnover and the number of active sites. Especially if different active sites take on different catalytic roles, e.g., 2-electron vs 4-electron reduction in the ORR, this level of detail is indispensable for a complete understanding of the catalyst.
Tetracoordinate FeIII species are unlikely to be present according to the predicted endergonic formation enthalpies. If they were present, they would be expected to be detectable by Mössbauer spectroscopy. Signals in the predicted range (δiso < 0.4 mm s–1; ΔEQ > 4.5 mm s–1) are not reported in in situ and operando studies on FeNC catalysts.10,11,14,15 While Fe(IV) species are relevant to the ORR catalytic cycle, e.g., as Fe(IV)=O intermediates, they are not discussed here explicitly because they have not been observed experimentally for FeNC materials. Upon reduction of the pentacoordinate [FeIIIPiL] starting compounds, it can be expected that the axial ligand is retained in [FeIIPiL]− with both types of macrocycle since ligand loss is predicted to be slightly endergonic.
Conclusions
To summarize, we have discussed the specific influences of ligand field strengths in macrocyclic ligands with pyridinic and pyrrolic N-donors on the spin states and spectroscopic properties of iron ions in the formal oxidation states +II and +III with and without an axial ligand. The series includes variations of substituents on the porphin core and the bridging atom between the two phenanthroline units. We found that Mössbauer, UV–vis, and NRV spectroscopies can help identify the electronic structure and coordination environment of molecular complexes in terms of oxidation and spin states or axial ligands, which is relevant for homogeneous catalysis or heterogenized molecular complexes. Importantly, we infer from these findings that the spectroscopic discernibility of active site candidates in FeNC catalyst materials is highly dependent on the ligand field strength of the catalytically active site. In addition to the types of spectroscopy discussed here, complementary X-ray-based electronic spectroscopies will likely be helpful in identifying active sites.
Our data suggest that signals detected in in situ and operando experiments on FeNC catalysts are not unique identifiers of catalytically active species. It is thus imperative to obtain rigorous and quantitative correlations between changes in spectral intensity, the electrochemical turnover, and the number of active sites when analyzing operando experiments. This finding most likely extends to other single-atom catalysts for various reactions. Therefore, a joint effort of different spectroscopies, model complexes with extended π systems, quantum chemistry, and catalytic studies will be needed to refine our understanding of catalytically active sites in single-atom catalysts for small molecule activation.
Methods
All calculations were performed using the ORCA 4.2.1 suite of programs,47 as reported in previous studies.11,23,24 Based on in-house reference and calibration studies with molecular complexes with guidance from the literature, we use different density functionals and basis sets for specific properties, as explained in the following. In our experience, the choice of density functional for the optimization of structures appears less critical than that for the prediction of correct spin ground states. Before applying the protocols described below to other complexes, we recommend careful validation of the resulting electronic structures and robustness of the computational approach. The structures were optimized using the TPSS48 density functional with “tight” convergence criteria for the self-consistent field algorithm and geometry optimization in ORCA nomenclature. The Ahlrichs-type def2-TZVP basis set was used for iron and all other elements except carbon and hydrogen, which were described using the def2-SVP basis set of the same family;.49 this combination is noted as “def2-TZVP:def2-SVP” in the text. The split-RI-J resolution integral was used50 with the auxiliary basis set def2/J.51 The size of the integration and angular grid was set to 6.0 in the ORCA nomenclature. To account for environmental effects, the SMD model with water as the modeled solvent was chosen.52 Grimme’s dispersion correction with Becke– Johnson damping D3BJ was employed.53,54 Redox potentials were estimated using the difference in Gibbs free energies of the oxidized and reduced species by using the respective relaxed geometries. Electronic energies (final single-point energies, FSPEs) were corrected using the electronic energies of single-point calculations with the OLYP55,56 density functional. In OLYP single-point calculations, the CP(PPP) basis set57 was used for iron, while all other elements were described using Ahlrichs’ def2-TZVP basis set;49 this combination is noted as “CP(PPP):def2-TZVP” in the text. Integration grid was increased to 7.0 in the ORCA nomenclature. The chain-of-spheres approximation, RIJCOSX,58 was used with the def2/J51 auxiliary basis set. Dispersion correction was omitted in order to better reproduce spin ground states.11 Single-point calculations with the OLYP density functional were used to determine the spin ground states. Gibbs free energies of all reactants and products were corrected as follows
| 1 |
Gibbs free energies of reactions were calculated as isodesmic reactions and are listed in Table S6. Mössbauer parameters were computed with the “eprnmr”-module of ORCA using the same settings as for OLYP single-point calculations, but with the B3LYP55,59 density functional and the same dispersion correction as for the geometry optimization (D3BJ).53,54 For vibrational spectroscopies such as NRVS, the setting for standard frequency calculations were used. No scaling factor was applied. To extract the spectra, the orca_vib and orca_mapspc modules in the ORCA were used. The computation of electronic transitions for UV–vis spectra was performed using time-dependent DFT with the Tamm–Dancoff-approximation,60 as implemented in ORCA. The B3LYP density functional and the zeroth-order regular approximation for relativistic effects (ZORA)61−63 were used. As basis sets, the scalar-relativistically reconstructed basis set def2-TZVP(-f) and the SARC/J auxiliary basis set were chosen.64,65
For the computation of UV–vis spectra, 60 roots were considered; the spectra shown in this work include a Gaussian line broadening of 0.25 eV.
Acknowledgments
All computations for this work were conducted on the Lichtenberg II high performance computer at TU Darmstadt.
Glossary
Abbreviations
- ORR
oxygen reduction reaction
- DFT
density functional theory
- NRVS
nuclear resonance vibrational spectroscopy
- TPP
tetraphenylporphyrin,
- phen
phenantroline
- HS
high spin
- IS
intermediate spin
- LS
low spin
- MO
molecular orbital
Data Availability Statement
The quadrupole splitting of the square-planar FeII complex is overestimated by ca. 1.5 mm s–1 due to multireference effects66.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.3c00714.
Molecular orbital diagrams and data, UV–vis and NRV spectra, Mössbauer parameters, Gibbs free enthalpies and additional thermodynamic data, electronic structure information, and structural data (PDF)
Author Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript. CRediT: Charlotte Gallenkamp conceptualization, data curation, formal analysis, investigation, methodology, validation, visualization, writing-original draft, writing-review & editing; Ulrike I. Kramm funding acquisition, validation, writing-review & editing; Vera Krewald conceptualization, formal analysis, funding acquisition, investigation, methodology, validation, project administration, supervision, writing-original draft, writing-review & editing.
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—CRC 1487, “Iron, upgraded!”—project number 443703006.
The authors declare no competing financial interest.
Supplementary Material
References
- Haller S.; Gridin V.; Hofmann K.; Stark R. W.; Albert B.; Kramm U. I. Application of Non-Precious Bifunctional Catalysts for Metal-Air Batteries. Energy Tech 2021, 9 (7), 2001106. 10.1002/ente.202001106. [DOI] [Google Scholar]
- Dodelet J.-P.Oxygen Reduction in PEM Fuel Cell Conditions: Heat-Treated Non-Precious Metal-N4Macrocycles and Beyond. In N4-Macrocyclic Metal Complexes; Zagal J. H., Bedioui F., Dodelet J.-P., Eds.; Springer New York: New York, NY, 2006, pp 83–147. 10.1007/978-0-387-28430-9_3. [DOI] [Google Scholar]
- Zhang H.; Chung H. T.; Cullen D. A.; Wagner S.; Kramm U. I.; More K. L.; Zelenay P.; Wu G. High-Performance Fuel Cell Cathodes Exclusively Containing Atomically Dispersed Iron Active Sites. Energy Environ. Sci. 2019, 12 (8), 2548–2558. 10.1039/C9EE00877B. [DOI] [Google Scholar]
- Chung H. T.; Cullen D. A.; Higgins D.; Sneed B. T.; Holby E. F.; More K. L.; Zelenay P. Direct Atomic-Level Insight into the Active Sites of a High-Performance PGM-Free ORR Catalyst. Science 2017, 357 (6350), 479–484. 10.1126/science.aan2255. [DOI] [PubMed] [Google Scholar]
- Kumar K.; Dubau L.; Jaouen F.; Maillard F. Review on the Degradation Mechanisms of Metal-N-C Catalysts for the Oxygen Reduction Reaction in Acid Electrolyte: Current Understanding and Mitigation Approaches. Chem. Rev. 2023, 123 (15), 9265–9326. 10.1021/acs.chemrev.2c00685. [DOI] [PubMed] [Google Scholar]
- Ünsal S.; Girod R.; Appel C.; Karpov D.; Mermoux M.; Maillard F.; Saveleva V. A.; Tileli V.; Schmidt T. J.; Herranz J. Decoupling the Contributions of Different Instability Mechanisms to the PEMFC Performance Decay of Non-Noble Metal O 2 -Reduction Catalysts. J. Am. Chem. Soc. 2023, 145 (14), 7845–7858. 10.1021/jacs.2c12751. [DOI] [PubMed] [Google Scholar]
- Leonard N. D.; Wagner S.; Luo F.; Steinberg J.; Ju W.; Weidler N.; Wang H.; Kramm U. I.; Strasser P. Deconvolution of Utilization, Site Density, and Turnover Frequency of Fe-Nitrogen-Carbon Oxygen Reduction Reaction Catalysts Prepared with Secondary N-Precursors. ACS Catal. 2018, 8 (3), 1640–1647. 10.1021/acscatal.7b02897. [DOI] [Google Scholar]
- Scharf J.; Kübler M.; Gridin V.; Wallace W. D. Z.; Ni L.; Paul S. D.; Kramm U. I. Relation between Half-cell and Fuel Cell Activity and Stability of FeNC Catalysts for the Oxygen Reduction Reaction. SusMat 2022, 2 (5), 630–645. 10.1002/sus2.84. [DOI] [Google Scholar]
- Marshall-Roth T.; Libretto N. J.; Wrobel A. T.; Anderton K. J.; Pegis M. L.; Ricke N. D.; Voorhis T. V.; Miller J. T.; Surendranath Y. A Pyridinic Fe-N4 Macrocycle Models the Active Sites in Fe/N-Doped Carbon Electrocatalysts. Nat. Commun. 2020, 11 (1), 5283. 10.1038/s41467-020-18969-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ni L.; Gallenkamp C.; Paul S.; Kübler M.; Theis P.; Chabbra S.; Hofmann K.; Bill E.; Schnegg A.; Albert B.; Krewald V.; Kramm U. I. Active Site Identification in FeNC Catalysts and Their Assignment to the Oxygen Reduction Reaction Pathway by In Situ57 Fe Mössbauer Spectroscopy. Adv. Energy Sustainability Res. 2021, 2 (2), 2000064. 10.1002/aesr.202000064. [DOI] [Google Scholar]
- Ni L.; Gallenkamp C.; Wagner S.; Bill E.; Krewald V.; Kramm U. I. Identification of the Catalytically Dominant Iron Environment in Iron- and Nitrogen-Doped Carbon Catalysts for the Oxygen Reduction Reaction. J. Am. Chem. Soc. 2022, 144 (37), 16827–16840. 10.1021/jacs.2c04865. [DOI] [PubMed] [Google Scholar]
- Saveleva V. A.; Ebner K.; Ni L.; Smolentsev G.; Klose D.; Zitolo A.; Marelli E.; Li J.; Medarde M.; Safonova O. V.; Nachtegaal M.; Jaouen F.; Kramm U. I.; Schmidt T. J.; Herranz J. Potential-Induced Spin Changes in Fe/N/C Electrocatalysts Assessed by In Situ X-ray Emission Spectroscopy. Angew. Chem. Int. Ed 2021, 60 (21), 11707–11712. 10.1002/anie.202016951. [DOI] [PubMed] [Google Scholar]
- Choi C. H.; Lim H.-K.; Chung M. W.; Chon G.; Ranjbar Sahraie N.; Altin A.; Sougrati M.-T.; Stievano L.; Oh H. S.; Park E. S.; Luo F.; Strasser P.; Dražić G.; Mayrhofer K. J. J.; Kim H.; Jaouen F. The Achilles’ Heel of Iron-Based Catalysts during Oxygen Reduction in an Acidic Medium. Energy Environ. Sci. 2018, 11 (11), 3176–3182. 10.1039/C8EE01855C. [DOI] [Google Scholar]
- Li J.; Sougrati M. T.; Zitolo A.; Ablett J. M.; Oğuz I. C.; Mineva T.; Matanovic I.; Atanassov P.; Huang Y.; Zenyuk I.; Di Cicco A.; Kumar K.; Dubau L.; Maillard F.; Dražić G.; Jaouen F. Identification of Durable and Non-Durable FeNx Sites in Fe-N-C Materials for Proton Exchange Membrane Fuel Cells. Nat. Catal. 2020, 4 (1), 10–19. 10.1038/s41929-020-00545-2. [DOI] [Google Scholar]
- Li X.; Cao C.-S.; Hung S.-F.; Lu Y.-R.; Cai W.; Rykov A. I.; Miao S.; Xi S.; Yang H.; Hu Z.; Wang J.; Zhao J.; Alp E. E.; Xu W.; Chan T.-S.; Chen H.; Xiong Q.; Xiao H.; Huang Y.; Li J.; Zhang T.; Liu B. Identification of the Electronic and Structural Dynamics of Catalytic Centers in Single-Fe-Atom Material. Chem 2020, 6 (12), 3440–3454. 10.1016/j.chempr.2020.10.027. [DOI] [Google Scholar]
- Hu X.; Chen S.; Chen L.; Tian Y.; Yao S.; Lu Z.; Zhang X.; Zhou Z. What Is the Real Origin of the Activity of Fe-N-C Electrocatalysts in the O2 Reduction Reaction? Critical Roles of Coordinating Pyrrolic N and Axially Adsorbing Species. J. Am. Chem. Soc. 2022, 144 (39), 18144–18152. 10.1021/jacs.2c08743. [DOI] [PubMed] [Google Scholar]
- Kramm U. I.; Ni L.; Wagner S. 57Fe Mössbauer Spectroscopy Characterization of Electrocatalysts. Adv. Mater. 2019, 31 (31), 1805623. 10.1002/adma.201805623. [DOI] [PubMed] [Google Scholar]
- Gütlich P.; Bill E.; Trautwein A. X.. Mössbauer Spectroscopy and Transition Metal Chemistry; Springer, 2011. 10.1007/978-3-540-88428-6 [DOI] [Google Scholar]
- Kramm U. I.; Herrmann-Geppert I.; Fiechter S.; Zehl G.; Zizak I.; Dorbandt I.; Schmeißer D.; Bogdanoff P. Effect of Iron-Carbide Formation on the Number of Active Sites in Fe-N-C Catalysts for the Oxygen Reduction Reaction in Acidic Media. J. Mater. Chem. A 2014, 2 (8), 2663–2670. 10.1039/C3TA13821F. [DOI] [Google Scholar]
- Kramm U. I.; Lefevre M.; Bogdanoff P.; Schmeißer D.; Dodelet J. P. Analyzing Structural Changes of Fe-N-C Cathode Catalysts in PEM Fuel Cell by Mossbauer Spectroscopy of Complete Membrane Electrode Assemblies. J. Phys. Chem. Lett. 2014, 5 (21), 3750–3756. 10.1021/jz501955g. [DOI] [PubMed] [Google Scholar]
- Menga D.; Low J. L.; Li Y.-S.; Arčon I.; Koyutürk B.; Wagner F.; Ruiz-Zepeda F.; Gaberšček M.; Paulus B.; Fellinger T.-P. Resolving the Dilemma of Fe-N-C Catalysts by the Selective Synthesis of Tetrapyrrolic Active Sites via an Imprinting Strategy. J. Am. Chem. Soc. 2021, 143 (43), 18010–18019. 10.1021/jacs.1c04884. [DOI] [PubMed] [Google Scholar]
- Yang Z.; Chen Y.; Zhang S.; Zhang J. Identification and Understanding of Active Sites of Non-Noble Iron-Nitrogen-Carbon Catalysts for Oxygen Reduction Electrocatalysis. Adv. Funct Materials 2023, 33 (26), 2215185. 10.1002/adfm.202215185. [DOI] [Google Scholar]
- Gallenkamp C.; Kramm U. I.; Krewald V. Spectroscopic Discernibility of Dopants and Axial Ligands in Pyridinic FeN 4 Environments Relevant to Single-Atom Catalysts. Chem. Commun. 2021, 57 (7), 859–862. 10.1039/D0CC06237E. [DOI] [PubMed] [Google Scholar]
- Gallenkamp C.; Kramm U. I.; Proppe J.; Krewald V. Calibration of Computational Mössbauer Spectroscopy to Unravel Active Sites in FeNC Catalysts for the Oxygen Reduction Reaction. Int. J. Quantum Chem. 2021, 121 (3), e26394 10.1002/qua.26394. [DOI] [Google Scholar]
- Neese F. Prediction of Molecular Properties and Molecular Spectroscopy with Density Functional Theory: From Fundamental Theory to Exchange-Coupling. Coord. Chem. Rev. 2009, 253 (5–6), 526–563. 10.1016/j.ccr.2008.05.014. [DOI] [Google Scholar]
- Cramer C. J.; Truhlar D. G. Density Functional Theory for Transition Metals and Transition Metal Chemistry. Phys. Chem. Chem. Phys. 2009, 11 (46), 10757–10816. 10.1039/b907148b. [DOI] [PubMed] [Google Scholar]
- Ebner K.; Herranz J.; Saveleva V. A.; Kim B.-J.; Henning S.; Demicheli M.; Krumeich F.; Nachtegaal M.; Schmidt T. J. Fe-Based O2 -Reduction Catalysts Synthesized Using Na2CO3 as a Pore-Inducing Agent. ACS Appl. Energy Mater. 2019, 2 (2), 1469–1479. 10.1021/acsaem.8b02036. [DOI] [Google Scholar]
- Zitolo A.; Goellner V.; Armel V.; Sougrati M. T.; Mineva T.; Stievano L.; Fonda E.; Jaouen F. Identification of Catalytic Sites for Oxygen Reduction in Iron- and Nitrogen-Doped Graphene Materials. Nat. Mater. 2015, 14 (9), 937–942. 10.1038/nmat4367. [DOI] [PubMed] [Google Scholar]
- Zitolo A.; Ranjbar-Sahraie N.; Mineva T.; Li J.; Jia Q.; Stamatin S.; Harrington G. F.; Lyth S. M.; Krtil P.; Mukerjee S.; Fonda E.; Jaouen F. Identification of Catalytic Sites in Cobalt-Nitrogen-Carbon Materials for the Oxygen Reduction Reaction. Nat. Commun. 2017, 8 (1), 957. 10.1038/s41467-017-01100-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia Q.; Ramaswamy N.; Hafiz H.; Tylus U.; Strickland K.; Wu G.; Barbiellini B.; Bansil A.; Holby E. F.; Zelenay P.; Mukerjee S. Experimental Observation of Redox-Induced Fe-N Switching Behavior as a Determinant Role for Oxygen Reduction Activity. ACS Nano 2015, 9 (12), 12496–12505. 10.1021/acsnano.5b05984. [DOI] [PubMed] [Google Scholar]
- Jia Q.; Ramaswamy N.; Tylus U.; Strickland K.; Li J.; Serov A.; Artyushkova K.; Atanassov P.; Anibal J.; Gumeci C.; Barton S. C.; Sougrati M.-T.; Jaouen F.; Halevi B.; Mukerjee S. Spectroscopic Insights into the Nature of Active Sites in Iron-Nitrogen-Carbon Electrocatalysts for Oxygen Reduction in Acid. Nano Energy 2016, 29, 65–82. 10.1016/j.nanoen.2016.03.025. [DOI] [Google Scholar]
- Jia Q.; Liu E.; Jiao L.; Pann S.; Mukerjee S. X-Ray Absorption Spectroscopy Characterizations on PGM-Free Electrocatalysts: Justification, Advantages, and Limitations. Adv. Mater. 2019, 31 (31), 1805157. 10.1002/adma.201805157. [DOI] [PubMed] [Google Scholar]
- Kneebone J. L.; Daifuku S. L.; Kehl J. A.; Wu G.; Chung H. T.; Hu M. Y.; Alp E. E.; More K. L.; Zelenay P.; Holby E. F.; Neidig M. L. A Combined Probe-Molecule, Mössbauer, Nuclear Resonance Vibrational Spectroscopy, and Density Functional Theory Approach for Evaluation of Potential Iron Active Sites in an Oxygen Reduction Reaction Catalyst. J. Phys. Chem. C 2017, 121 (30), 16283–16290. 10.1021/acs.jpcc.7b03779. [DOI] [Google Scholar]
- Wagner S.; Auerbach H.; Tait C. E.; Martinaiou I.; Kumar S. C. N.; Kubel C.; Sergeev I.; Wille H. C.; Behrends J.; Wolny J. A.; Schunemann V.; Kramm U. I. Elucidating the Structural Composition of an Fe-N-C Catalyst by Nuclear- and Electron-Resonance Techniques. Angew. Chem., Int. Ed. 2019, 58 (31), 10486–10492. 10.1002/anie.201903753. [DOI] [PubMed] [Google Scholar]
- Heppe N.; Gallenkamp C.; Paul S.; Segura-Salas N.; Von Rhein N.; Kaiser B.; Jaegermann W.; Jafari A.; Sergueev I.; Krewald V.; Kramm U. I. Substituent Effects in Iron Porphyrin Catalysts for the Hydrogen Evolution Reaction. Chem.—Eur. J. 2023, 29 (10), e202202465 10.1002/chem.202202465. [DOI] [PubMed] [Google Scholar]
- Maricondi C.; Swift W.; Straub D. K. Thermomagnetic Analysis of Hemin and Related Compounds. J. Am. Chem. Soc. 1969, 91 (19), 5205–5210. 10.1021/ja01047a003. [DOI] [PubMed] [Google Scholar]
- Hoard J. L.; Cohen G. H.; Glick M. D. The Stereochemistry of the Coordination Group in an Iron(III) Derivative of Tetraphenylporphine. J. Am. Chem. Soc. 1967, 89 (9), 1992–1996. 10.1021/ja00985a004. [DOI] [Google Scholar]
- Swart M. Spin States of (Bio)Inorganic Systems: Successes and Pitfalls. Int. J. Quantum Chem. 2013, 113 (1), 2–7. 10.1002/qua.24255. [DOI] [Google Scholar]
- Daul C.; Zlatar M.; Gruden-Pavlović M.; Swart M.. Application of Density Functional and Density Functional Based Ligand Field Theory to Spin States. In Spin States in Biochemistry and Inorganic Chemistry, 2015; pp 7–34, 10.1002/9781118898277.ch2. [DOI] [Google Scholar]
- Radon M. Benchmarking Quantum Chemistry Methods for Spin-State Energetics of Iron Complexes against Quantitative Experimental Data. Phys. Chem. Chem. Phys. 2019, 21 (9), 4854–4870. 10.1039/C9CP00105K. [DOI] [PubMed] [Google Scholar]
- Phung Q. M.; Nam H. N.; Saitow M. Unraveling the Spin-State Energetics of FeN4 Complexes with Ab Initio Methods. J. Phys. Chem. A 2023, 127 (36), 7544–7556. 10.1021/acs.jpca.3c04254. [DOI] [PubMed] [Google Scholar]
- Ni L.; Theis P.; Paul S.; Stark R. W.; Kramm U. I. In Situ57Fe Mössbauer Study of a Porphyrin Based FeNC Catalyst for ORR. Electrochim. Acta 2021, 395, 139200. 10.1016/j.electacta.2021.139200. [DOI] [Google Scholar]
- Bouwkamp-Wijnoltz A. L.; Visscher W.; Van Veen J. A. R.; Boellaard E.; Van Der Kraan A. M.; Tang S. C. On Active-Site Heterogeneity in Pyrolyzed Carbon-Supported Iron Porphyrin Catalysts for the Electrochemical Reduction of Oxygen: An In Situ Mössbauer Study. J. Phys. Chem. B 2002, 106 (50), 12993–13001. 10.1021/jp0266087. [DOI] [Google Scholar]
- Maricondi C.; Straub D. K.; Epstein L. M. Moessbauer Studies on Hemin Derivatives of.Alpha., Beta., Gamma., Delta.-Tetraphenylporphine. J. Am. Chem. Soc. 1972, 94 (12), 4157–4159. 10.1021/ja00767a017. [DOI] [PubMed] [Google Scholar]
- Dolphin D.The Porphyrins; Academic Press: New York, 1978. [Google Scholar]
- Scheidt W. R.; Li J.; Sage J. T. What Can Be Learned from Nuclear Resonance Vibrational Spectroscopy: Vibrational Dynamics and Hemes. Chem. Rev. 2017, 117 (19), 12532–12563. 10.1021/acs.chemrev.7b00295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neese F. The ORCA Program System. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2 (1), 73–78. 10.1002/wcms.81. [DOI] [Google Scholar]
- Tao J.; Perdew J. P.; Staroverov V. N.; Scuseria G. E. Climbing the Density Functional Ladder: Nonempirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91 (14), 146401. 10.1103/PhysRevLett.91.146401. [DOI] [PubMed] [Google Scholar]
- Weigend F.; Ahlrichs R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7 (18), 3297–3305. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- Neese F. An Improvement of the Resolution of the Identity Approximation for the Formation of the Coulomb Matrix. J. Comput. Chem. 2003, 24 (14), 1740–1747. 10.1002/jcc.10318. [DOI] [PubMed] [Google Scholar]
- Weigend F. Accurate Coulomb-Fitting Basis Sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8 (9), 1057–1065. 10.1039/b515623h. [DOI] [PubMed] [Google Scholar]
- Marenich A. V.; Cramer C. J.; Truhlar D. G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113 (18), 6378–6396. 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Antony J.; Ehrlich S.; Krieg H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132 (15), 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Ehrlich S.; Goerigk L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32 (7), 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron-Density. Phys. Rev. B 1988, 37 (2), 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- Handy N. C.; Cohen A. J. Left-Right Correlation Energy. Mol. Phys. 2001, 99 (5), 403–412. 10.1080/00268970010018431. [DOI] [Google Scholar]
- Neese F. Prediction and Interpretation of Isomer Shifts in 57Fe Mössbauer Spectra by Density Functional Theory. Inorg. Chim. Acta 2002, 337C, 181–192. 10.1016/S0020-1693(02)01031-9. [DOI] [Google Scholar]
- Neese F.; Wennmohs F.; Hansen A.; Becker U. Efficient, Approximate and Parallel Hartree-Fock and Hybrid DFT Calculations. A ‘Chain-of-Spheres’ Algorithm for the Hartree-Fock Exchange. Chem. Phys. 2009, 356 (1–3), 98–109. 10.1016/j.chemphys.2008.10.036. [DOI] [Google Scholar]
- Becke A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98 (7), 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
- Hirata S.; Head-Gordon M. Time-Dependent Density Functional Theory within the Tamm–Dancoff Approximation. Chem. Phys. Lett. 1999, 314 (3–4), 291–299. 10.1016/S0009-2614(99)01149-5. [DOI] [Google Scholar]
- van Lenthe E.; Baerends E. J.; Snijders J. G. Relativistic Total-Energy Using Regular Approximations. J. Chem. Phys. 1994, 101 (11), 9783–9792. 10.1063/1.467943. [DOI] [Google Scholar]
- van Lenthe E.; Snijders J. G.; Baerends E. J. The Zero-Order Regular Approximation for Relativistic Effects: The Effect of Spin-Orbit Coupling in Closed Shell Molecules. J. Chem. Phys. 1996, 105 (15), 6505–6516. 10.1063/1.472460. [DOI] [Google Scholar]
- van Wüllen C. Molecular Density Functional Calculations in the Regular Relativistic Approximation: Method, Application to Coinage Metal Diatomics, Hydrides, Fluorides and Chlorides, and Comparison with First-Order Relativistic Calculations. J. Chem. Phys. 1998, 109, 392–399. 10.1063/1.476576. [DOI] [Google Scholar]
- Pantazis D. A.; Chen X. Y.; Landis C. R.; Neese F. All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms. J. Chem. Theory Comput. 2008, 4 (6), 908–919. 10.1021/ct800047t. [DOI] [PubMed] [Google Scholar]
- Pantazis D. A.; Neese F. All-Electron Basis Sets for Heavy Elements. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2014, 4 (4), 363–374. 10.1002/wcms.1177. [DOI] [Google Scholar]
- Pápai M.; Vankó G. On Predicting Mössbauer Parameters of Iron-Containing Molecules with Density-Functional Theory. J. Chem. Theory Comput. 2013, 9 (11), 5004–5020. 10.1021/ct4007585. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The quadrupole splitting of the square-planar FeII complex is overestimated by ca. 1.5 mm s–1 due to multireference effects66.


