Abstract
Pretreatment patient-specific quality assurance (prePSQA) is conducted to confirm the accuracy of the radiotherapy dose delivered. However, the process of prePSQA measurement is time consuming and exacerbates the workload for medical physicists. The purpose of this work is to propose a novel deep learning (DL) network to improve the accuracy and efficiency of prePSQA. A modified invertible and variable augmented network was developed to predict the three-dimensional (3D) measurement-guided dose (MDose) distribution of 300 cancer patients who underwent volumetric modulated arc therapy (VMAT) between 2018 and 2021, in which 240 cases were randomly selected for training, and 60 for testing. For simplicity, the present approach was termed as “IVPSQA.” The input data include CT images, radiotherapy dose exported from the treatment planning system, and MDose distribution extracted from the verification system. Adam algorithm was used for first-order gradient-based optimization of stochastic objective functions. The IVPSQA model obtained high-quality 3D prePSQA dose distribution maps in head and neck, chest, and abdomen cases, and outperformed the existing U-Net-based prediction approaches in terms of dose difference maps and horizontal profiles comparison. Moreover, quantitative evaluation metrics including SSIM, MSE, and MAE demonstrated that the proposed approach achieved a good agreement with ground truth and yield promising gains over other advanced methods. This study presented the first work on predicting 3D prePSQA dose distribution by using the IVPSQA model. The proposed method could be taken as a clinical guidance tool and help medical physicists to reduce the measurement work of prePSQA.
Keywords: Radiotherapy, Deep learning, Invertible and variable augmented network, Pretreatment patient-specific quality assurance, Volumetric modulated arc therapy
Introduction
Radiotherapy is one of the most important treatment modalities for cancer patients that has been commonly used as a curative, adjuvant, or palliative treatment method [1]. More than 50% of cancer patients require radiation therapy during treatment [2]. Compared with traditional radiotherapy techniques, intensity-modulated radiation therapy (IMRT) and volumetric modulated arc therapy (VMAT) are able to control the irradiation areas more conformal and reduce unnecessary radiation to surrounding normal tissues [3–8]. However, these advanced radiotherapy techniques are more complicated with a greater probability of errors in radiotherapy [9–14]. Therefore, the pretreatment patient-specific quality assurance (prePSQA) has been routinely performed to verify dose calculation and delivery, which is particularly important and essential for modern radiation modalities [15–18]. Nevertheless, the radiotherapy process is so complicated that prePSQA consumes more time to ensure accuracy and effectiveness. To solve this problem, many researchers have done a lot of investigations in prePSQA prediction.
In recent years, the application of machine learning (ML) in prePSQA has grown rapidly through traditional approaches including Poisson regression, support vector machine, multilayer perceptron, decision trees, k-nearest-neighbor, and random forest [19–27]. However, the traditional ML algorithms rely on manual extraction and learning of complex handcrafted features, and the prediction accuracy is not high enough. In contrast to the conventional ML algorithms, deep convolutional neural networks (DCNNs) can automatically extract its own low/mid/high-level features from datasets and integrate them into an end-to-end multilayer network for prediction [28–36]. Liu et al. developed a DCNN model to predict proton dose distributions from prompt gamma images [37]. Similarly, Zhang et al. applied a U-Net model to predict EPID transmission images based on the dose distribution of solid water [38]. Gong et al. successfully developed a DVH-based pretreatment prePSQA for VMAT with combined deep learning (DL) and ML models [39]. They first used a modified Res-UNet model to predict the three-dimensional (3D) measurement-guided dose (MDose) distribution and then used XGBoost algorithm to classify pass or not. With the MDose distribution, it is possible to fully reconstruct the dose-volume histograms (DVHs) of all structures and show the detailed 3D dose differences, enabling better detection of clinically relevant dose errors better than the widely used gamma indexes (GIs). However, the CNN-based prePSQA prediction model involves multiple pooling layers within the networks, which potentially reduces the image resolution and loses important spatial information [40–43]. Moreover, the radiotherapy for head and neck (H&N) involves numerous micro-targets and organs at risk (OARs), and the loss of local spatial information in the prediction networks may lead to dose errors.
In this work, inspired by the recent study of Gong et al.’s innovative work in 3D prePSQA dose prediction [39], we proposed a novel invertible and variable augmented network-based approach for prePSQA (IVPSQA) by exploring its feasibility in the field of MDose prediction. Compared to traditional convolutional neural networks (CNN), IVPSQA has a special network structure that can be summarized mainly as follows: (1) The traditional CNN-based prePSQA networks generally consisted of multiple layers of neurons and weighted connections between layers [37–39]. The activation functions of hidden layer neurons in these networks enable them to capture the nonlinear relationship between input and output data, which focus on forward prediction processes and have no reverse reasoning capability. However, the DL-based IVPSQA is built on invertible neural networks, which can perform inverse inference well for dose prediction. (2) Based on the multi-component loss function incorporated in the network architecture, the IVPSQA has better robustness and can achieve more accurate prediction tasks. (3) By introducing the variable augmentation ideology into the invertible network, the IVPSQA has a stronger training and learning capability. As a result, the IVPSQA network has better performance and can achieve more accurate prediction results in terms of 3D prePSQA dose prediction.
Methods
Invertible Neural Networks
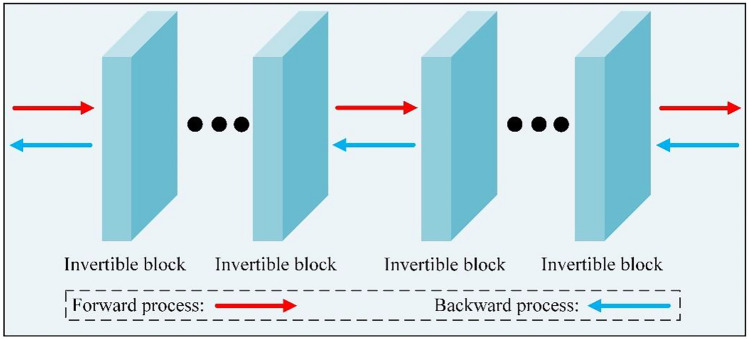
The invertible network is structured with several invertible blocks, where each invertible block consists of invertible convolution and affine coupling layers. Because of the unique structural properties, it can achieve the invertibility of one single network and then avoid the problem of inaccurate bijective mapping. The general architecture of the invertible network is shown in Fig. 1. The invertible network learns the mapping as , which is fully invertible as . Thus, the information is fully preserved during both the forward and reverse transformations. Due to the properties such as reversibility, memory savings, and simple design, the invertible networks are selected as the footstone of the proposed PSQA prediction method for radiotherapy in this work. During the training stage, we compute the deviation of the model output from the network prediction with a loss denoted as , where is the loss associated with the label and the invertible model. In this case, the network aims to map a treatment planning system (TPS) dose (RTDose) image into its corresponding measured dose image via the mapping function. In the predicted stage, information is extracted from the RTDose image and fed into the invertible network, which maps RTDose patches to the predicted MDose (PDose) image. The information lossless of the invertible network can preserve the detailed information of the input data, and the constant mapping can solve the problem of network degradation and ensure the stability of its data generation. Hence, the invertible network has powerful advantages in predicted measured dose image generation.
Fig. 1.
Structure of invertible network consisting of invertible blocks
The proposed IVPSQA
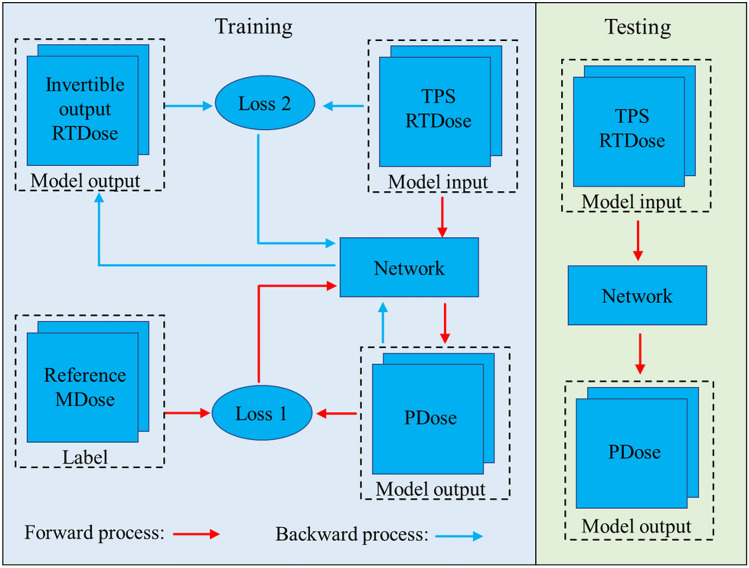
An invertible network-based model is implemented to predict PDose from RTDose and MDose. The proposed IVPSQA comprises two independent stages for training retrospective data and reconstructing new data. As shown in Fig. 2, the training data of the IVPSQA includes RTDose and reference MDose. The reference MDose is used as a learning target during the generation of the PDose. Subsequently, the IVPSQA iteratively estimated PDose and compared them to the reference MDose.
Fig. 2.
The training and testing pipeline of IVPSQA
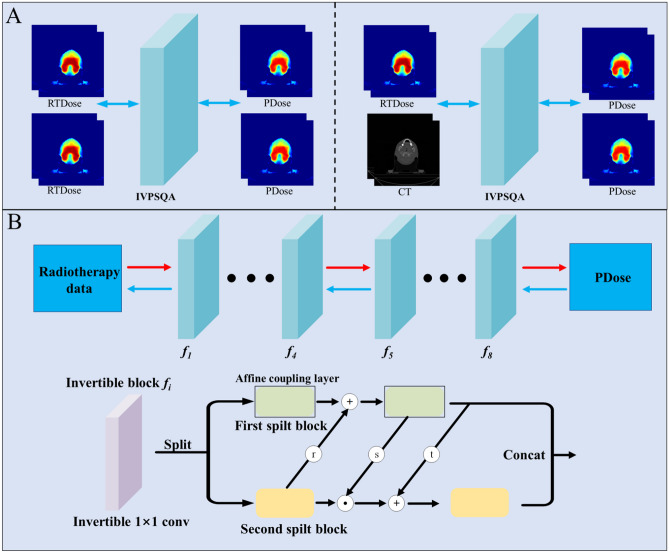
We add dummy variables and duplicated them in the network based on the thought of variable augmentation, so that the network input and output have the same channel dimensions [44]. More specifically, the input data of the network is and the output data of the network is . In addition, to explore the spatial structure information of CT images, we try another mixed input mode: PDose and CT images are simultaneously input into the network as dual channels for training (Fig. 3A).
Fig. 3.
A: Illustration of two different input modes of IVPSQA; B: The detailed architecture of IVPSQA
To achieve map the data point from input data space X to output data space Y, we need to find a bijective function. The classical neural networks need two independent networks to approximate and , which leads to inaccurate bijective mapping and may accumulate the error of one mapping into the other. The invertibility of one single network is achieved by using the affine coupling layers in the study [45, 46]. Subsequently, we construct the IVPSQA by composing a stack of invertible and tractable bijective functions , i.e., . For a given observed data sample x, we can derive the transformation to the target data sample y through the following formula:
| 1 |
| 2 |
The bijective model fi is achieved through the affine coupling layers. In each affine coupling layer, given a D dimensional input m and d < D, the output n is calculated as
| 3 |
| 4 |
where s and t represent scale and translation functions from , and is the Hadamard product. Note that the scale and translation functions are not necessarily invertible; hence, we achieve them by the neural networks. The coupling layer leaves some input channels unchanged, which greatly restricts the representation learning power of this architecture [45]. To alleviate this problem, we enhance the coupling layer [47] by
| 5 |
where r can be arbitrary function from . The inverse step is easily obtained by
| 6 |
| 7 |
Next, the invertible 1 × 1 convolution is used as the learnable permutation function to reverse the order of channels for the next affine coupling layer.
Figure 3B illustrates the detailed architecture of IVPSQA. The input data is split into two halves along the channel dimension. s, t, and r are transformations equal to a dense block that consists of five 2D convolution layers with filter size 3 × 3. Each layer learns a new set of feature maps from the previous layer. The size of the receptive field for the first four convolutional layers is 3 × 3, and the stride is 2, followed by a rectified linear unit. The last layer is a 3 × 3 convolution without ReLU. The purpose of the Leaky ReLU layers is to avoid overfitting to the training set and further increase nonlinearity [48], which can improve the learning ability of the invertible network to generate high-quality PDose. In the forward process, the input data is transformed to output data by a stack of bijective functions .
Multi-component Loss Function
As described above, the network relies on continuous improvement of a sequence of invertible blocks including affine coupling layers and activation normalization layers. The accuracy of these two invertible blocks depends directly on designing of the corresponding loss function. Herein, we use the multi-component loss functions to optimize the network to guarantee the quality of the generated images [49, 50]. The invertible network doubles the process of training by enforcing an inverse mapping constraint on the model, improving the accuracy of PDose. Therefore, based on the unique invertible nature, we use the multi-component loss function to guide the invertible network to simultaneously capture both forward and reverse information of input data. In addition, the multi-component loss function based on L1-norm or L2-norm is simple and easy to train. L1-norm and L2-norm can be mathematically expressed as follows:
| 8 |
| 9 |
where y is the ground-truth (MDose) and is the output data PDose from the source image x by the IVPSQA network f. represents the L1-norm and represents the L2-norm. stands for the loss function between the PDose and ground-truth. stands for the loss function between the invertible output data and the input data. λ is hyper-parameter that is used to balance the two losses.
In summary, the implementation of the present IVPSQA algorithm for prePSQA dose reconstruction can be described as follows:
Experiments and Results
Data Collection
A total of 300 patients who underwent VMAT between 2018 and 2021 were enrolled, in which 240 cases were selected for training and 60 for testing. Table 1 lists the characteristics of the cancer patients included in this study. CT images were acquired using Somatom Confidence (Siemens Health-care, Forchheim, Germany). Magnetic resonance imaging and positron emission tomography images were used to help contour the target volumes by senior radiation oncologists. VMAT plans were generated by Monaco TPS (clinical version 5.11) utilizing the Monte Carlo algorithm with a 6-MV photon beam and delivered on an Elekta Infinity equipped with agility MLC. All plans were optimized to reach clinically acceptable target volume coverage and OAR sparing. Online treatment monitoring system named Dolphin-Compass system (version 3.0, IBA Dosimetry, Schwarzenbruck, Germany) was applied for prePSQA measurement. Strict commissioning of Dolphin-Compass including the validation of accuracy for array measurement, beam modeling, and dose reconstruction was performed in advance according to the manufacturer’s standards.
Table 1.
Clinical characteristics of cancer patients enrolled in this study
| Characteristics | Sample number | Percentage |
|---|---|---|
| Gender | ||
| Male | 191 | 63.7% |
| Female | 109 | 36.3% |
| Age (years) | ||
| < 20 years | 25 | 8.3% |
| 20–60 years | 96 | 32.0% |
| > 60 years | 179 | 59.7% |
| Cancer site | ||
| H&N | 115 | 38.3% |
| Chest | 87 | 29.0% |
| Abdomen | 98 | 32.7% |
Experiment Setup
To validate and evaluate the performance of the present IVPSQA approach, two different DL approaches were carried out for comparison including the U-Net, Res-UNet [39], and cycleGAN [51]. These methods can be summarized as follows: (1) U-Net. This is a classical coding and decoding network which has recently been used for dose prediction [29–36]. (2) Res-UNet. This network has recently been used for the prediction of MDose distribution for prePSQA, whose input data includes CT, structure, and RTDose derived from TPS, as well as dose distributions measured by the Dolphin Compass system and ArcCHECK-3DVH system [39]. (3) cycleGAN. This method uses a cycle consistency loss to enable training without the need for paired data. In the experiments, we use the paired data to train the network [51]. In this work, we evaluated the proposed model using two input modes, i.e., A: prediction from RTDose to PDose (RTDose → PDose); B: prediction from RTDose and CT to PDose (RTDose + CT → PDose). The PSQA dose prediction model was evaluated with metrics of root mean square error (RMSE), mean absolute error (MAE), and structural similarity (SSIM) by comparing the predicted PSQA dose and the actual measured dose. In addition, the statistical significance of the differences between the results obtained by several methods was tested by SPSS v27.0 (IBM Corp.) analyses. Values of P < 0.05 were considered statistically significant results.
During the experiment, the selection of the parameters could affect the accuracy of prediction results. Therefore, we conducted a series of experiments on parameter selection. Multiple channels are known to enhance the correlation between data. To further investigate the effect of channel number on IVPSQA, we compared the results of 2 channels, 4 channels, and 6 channels in IVPSQA. Furthermore, different loss functions have different effects on network performance and thus produce different prediction results. Specifically, L2-norm penalizes larger errors, but it is more tolerant of smaller errors regardless of the underlying structure in the image. Compared with the L2-norm, the L1-norm does not excessively penalize large errors. Consequently, they may have different convergence properties during the network training procedure. Inspired by this observation, we compared the predicted effect of the loss function equipped with the L1-norm and L2-norm, respectively.
All networks were trained using the Adam solver. We conducted 20 epochs to train the proposed model. The initial learning rate was set to 0.0001. Every 5 epochs the learning rate was halved. During training, the trade-off parameter λ was set to 1. The training and testing experiments were performed with a customized version of Pytorch on an Intel i7-9700KF CPU and a 2080ti GPU.
Results
Table 2 shows the quantitative results of all test cases. It can be observed that the present IVPSQA outperforms other methods on all metrics, and cycleGAN produced better than U-Net and Res-Unet in mode A. The SSIM values of IVPSQA (A: 0.9982 and B: 0.9976) are slightly better than that of other methods. For input mode A, the RMSE and MAE values of the IVPSQA are 68% and 67.6% lower than those of Res-UNet, respectively. For input mode B, the RMSE and MAE values of the IVPSQA are 68.4% and 64.6% lower than those of Res-Unet, respectively. The RMSE and MAE values of the IVPSQA are 36.3% and 39.8% lower than those of cycleGAN. In addition, the differences between the predictions obtained by several methods were statistically significant (P < 0.05), except for the SSIM of cycleGAN and IVPSQA (P > 0.05).
Table 2.
Prediction comparison with three advanced methods in SSIM, RMSE, and MAE (MEAN + STD)
| Tasks | A: RTDose → PDose | B: RTDose + CT → PDose | ||||
|---|---|---|---|---|---|---|
| Metrics | SSIM | RMSE (%) | MAE (%) | SSIM | RMSE (%) | MAE (%) |
| cycleGAN | 0.9981 ± 0.0006 | 0.5457 ± 0.2945 | 0.2122 ± 0.1609 | - | - | - |
| U-Net | 0.9730 ± 0.0077 | 1.6183 ± 0.5399 | 0.5786 ± 0.2495 | 0.9789 ± 0.0076 | 1.5655 ± 0.5712 | 0.5626 ± 0.2553 |
| Res-UNet | 0.9845 ± 0.0055 | 1.0885 ± 0.3918 | 0.3943 ± 0.1620 | 0.9872 ± 0.0056 | 1.1306 ± 0.3967 | 0.4102 ± 0.1754 |
| IVPSQA | 0.9982 ± 0.0007 | 0.3475 ± 0.1459 | 0.1276 ± 0.0718 | 0.9976 ± 0.0009 | 0.3568 ± 0.1464 | 0.1450 ± 0.0719 |
Figure 4 shows the qualitative results from four different cancer cases, i.e., nasopharynx cancer (NPC), lung cancer, bone metastasis, and cervical cancer. The first, third, fifth, and seventh rows represent the transverse dose distribution. The second, fourth, sixth, and last rows illustrate the differences between the ground truth and the predictions. In the visual inspection, the dose difference maps of IVPSQA are much better than those of Res-UNet and U-Net, and the dose difference maps of IVPSQA are also better than those of cycleGAN. In addition, the results with CT input are similar to those without CT input. To further observe the advantage of the IVPSQA approach, Fig. 5 depicts the horizontal profile comparison of the four patients in Fig. 4. It can be clearly observed that the curves of IVPSQA are in better agreement with the MDose. In other words, the present approach yields more promising gains than the other approaches.
Fig. 4.
Visualization results of several comparison methods. The first, third, fifth, and seventh rows represent the PDose distributions in four different patients, i.e., NPC case, lung case, bone case, and cervical case. The second, fourth, sixth, and eighth rows depict the differences between the ground truth and the predictions
Fig. 5.
The horizontal dose difference profiles at different patients for comparison among ground truth and predicted dose
Table 3 shows the performance of IVPSQA with different channels and loss functions. The quantitative results of 4 channels as input slightly improves the network performance, and the prediction results of 6 channels are similar to those of 2 channels. Meanwhile, we observed that increasing the number of channels in the network makes the network take longer, with the training time increasing by about 3 h for each additional 2 channels. After comprehensive consideration, we chosen 2 channels as the input of the network in the experiment. Table 3 also presents the quantitative results of different loss functions. It can be observed that the higher SSIM and lower RMSE and MAE are achieved by the L1-norm constrained loss function. Therefore, we trained the network using L1-norm in this work.
Table 3.
The impact of different channel numbers and different loss functions on IVPSQA (MEAN + STD)
| A: RTDose → PDose | B: RTDose + CT → PDose | |||||
|---|---|---|---|---|---|---|
| Metrics | SSIM | RMSE (%) | MAE (%) | SSIM | RMSE (%) | MAE (%) |
| 2 channels | 0.9982 ± 0.0007 | 0.3475 ± 0.1459 | 0.1276 ± 0.0718 | 0.9976 ± 0.0009 | 0.3568 ± 0.1464 | 0.1450 ± 0.0719 |
| 4 channels | 0.9983 ± 0.0007 | 0.3409 ± 0.1420 | 0.1237 ± 0.0723 | 0.9980 ± 0.0007 | 0.3450 ± 0.1421 | 0.1379 ± 0.0733 |
| 6 channels | 0.9983 ± 0.0007 | 0.3511 ± 0.1544 | 0.1282 ± 0.0790 | 0.9980 ± 0.0008 | 0.3516 ± 0.1528 | 0.1394 ± 0.0816 |
| L1-norm | 0.9982 ± 0.0007 | 0.3475 ± 0.1459 | 0.1276 ± 0.0718 | 0.9976 ± 0.0009 | 0.3568 ± 0.1464 | 0.1450 ± 0.0719 |
| L2-norm | 0.9982 ± 0.0008 | 0.3510 ± 0.1491 | 0.1301 ± 0.0789 | 0.9965 ± 0.0008 | 0.3610 ± 0.1422 | 0.1630 ± 0.0745 |
In addition, Fig. 6 shows the SSIM, RMSE, and MAE values of the three methods for H&N cases, chest cases, and abdominal cases. It can be found that the prediction accuracy for the abdominal cases is lower than that of other parts, the IVPSQA owns the best prediction results for the H&N cases and followed closely by chest cases. The quantitative results further demonstrate that the proposed IVPSQA is superior to other methods in predicting the MDose distribution, especially for H&N case.
Fig. 6.
The SSIM, RMSE, and MAE values from three methods for H&N cases, chest cases, and abdominal cases
Discussion
Research on measurement-guided dose prediction of AI models in radiotherapy is crucial, yet rare. In this study, an invertible network-based prediction methodology is developed for prePSQA which provides an accurate MDose prediction by embedding a variable augmentation strategy. In the case of using only RTDose images as input to achieve satisfactory predictions, making the data processing of the network relatively simple and reducing the computational workload. Further, this is the first attempt to construct a comprehensive measurement dataset from multiple cancer patients underwent VMAT, which makes the dose prediction of prePSQA more robust.
prePSQA is an important verification step in the IMRT/VMAT program, but the work of prePSQA is very complex and time consuming. Recently, many researchers proposed various methods to reduce the prePSQA workload [22–25, 37–39]. The invertible and variable augmentation network proposed in this study can well predict prePSQA dose distribution for multiple cancers based on TPS information. Gong et al. proposed a DVH-based pretreatment prePSQA for VMAT with combined deep learning (DL) and ML models [39]. Similarly, they predicted the prePSQA dose distribution of cancers based on TPS information. Inspired by Gong et al., we improved the input data to achieve prediction from RTDose to MDose [39]. Jia et al. proposed a radioluminescence imaging-based fGAN to validate radiotherapy dose [52]. They used radioluminescence imaging to train the network and introduced the concept of depth cn to achieve 3D dose prediction. To the best of our knowledge, this is the first study to apply invertible networks to prePSQA prediction. To evaluate the performance of our proposed method qualitatively and quantitatively, we compare the IVPSQA with U-Net and Res-UNet and cycleGAN. It is clear from Fig. 4 that the predictions of the U-Net and Res-UNet in the high-dose region are significantly different from those of MDose. The predicted results of cycleGAN were close to MDose, but the prediction results of cycleGAN for cervical cancer had a larger error, while the prediction results of the IVPSQA are very accurate. Secondly, it can be observed from Fig. 5 that the prediction results of U-Net and Res-UNet are jagged and have some errors with those of MDose, which suggests that U-Net and Res-UNet may have lost some detailed information during the training process, while the prediction result of cycleGAN for cervical cancer has a large error with MDose. Because the IVPSQA network is a method of learning information lossless mapping. It stores the details of the input data in advance, solving the problem of network degradation and ensuring the stability of data generation. As a result, the prediction results of the IVPSQA are smoother than the other two methods. But dose prediction based on U-Net and GAN network architectures can also give a good prediction result. Gong et al. and Jia et al. used Res-UNet and fGAN, respectively, for dose prediction and demonstrated clinically acceptable results [39, 52]. Due to the inherent limitations of patient data or DL networks, some inconsistencies between predicted results and measured results are inevitable and will be ameliorated in the future by increasing the number of datasets or optimizing DL networks.
Few studies have reported direct prediction of prePSQA dose based on MDose. However, dose reconstruction with DL has been intensively investigated for automatic planning purpose. Gong et al. used CT images, RT structures, and RTDose as input data to train the 3D Res-UNet and obtained good results [39]. Building on the work of Gong et al., we used only RTDose from TPS as input to train the IVPSQA network. The quantitative results in Table 2 also demonstrate that more accurate predictions are obtained using only RTDose as input data. In addition, the effects of CT channel on the network were also explored. As shown in Tables 2 and 3, we found that the CT channel did not improve the results and even reduced the accuracy, which may be due to the inefficient use of the information contained in the CT images.
Our IVPSQA method still has some limitations. One limitation is that although we have adopted some strategies to optimize the calculation, the network still required approximately 60 h to complete the training. Improving the computation speed can be achieved by using multi-core central processing unit and graphic processing unit. Accelerating the computation of the present IVPSQA approach may be a less concerning issue as fast computers and dedicated hardware are available in the future. Another limitation is that we only use VMAT data for training. IMRT is another widely used radiotherapy technique; the study of multimodal datasets will be our future research topic. Nevertheless, the 3D MDose prediction for prePSQA, combined with the invertible and variable augmented network, is capable of driving improvements in prePSQA and becomes better than current or past clinical practice. In addition, with further improvement of our approach, it is a great help for adaptive radiotherapy and have a considerable role in clinical work.
Conclusion
In this study, we developed a novel DL approach for 3D dose prediction for prePSQA. The experimental results showed that the predicted MDose distributions were in excellent agreement with the ground truth. The study proved that IVPSQA is a useful tool to assist dose verification and can improve the efficiency of prePSQA.
Author Contribution
Zhongsheng Zou: data curation, methodology, project administration, and writing—original draft. Changfei Gong: conceptualization, methodology, formal analysis, writing, review, and editing. Lingpeng Zeng: formal analysis and investigation. Yu Guan: investigation and project administration. Bin Huang: data curation and formal analysis. Xiuwen Yu: data curation and investigation. Qiegen Liu: conceptualization, formal analysis, and editing. Minghui Zhang: methodology, formal analysis, and writing—review and editing.
Funding
The Science and Technology Project of Jiangxi Provincial Health Commission of China (No. 202310023).
Availability of Data and Materials
The datasets during the current study are not publicly available due to some research that has not been completed, but is available from the corresponding author on reasonable request.
Declarations
Ethics Approval and Consent to Participate
The study has been approved by the Institution Review Board and Ethics Committee of Jiangxi Cancer Hospital, and the approval number is 2022ky012.
Competing Interests
The authors declare no competing interests.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Zhongsheng Zou and Changfei Gong contributed equally.
Contributor Information
Qiegen Liu, Email: liuqiegen@ncu.edu.cn.
Minghui Zhang, Email: zhangminghui@ncu.edu.cn.
References
- 1.Liu Z, Fan J, Li M, Yan H, Hu Z, Huang P, Tian Y, Miao J, Dai J. A deep learning method for prediction of three-dimensional dose distribution of helical tomotherapy. Med Phys. 2019;46(5):1972–1983. doi: 10.1002/mp.13490. [DOI] [PubMed] [Google Scholar]
- 2.Delaney G, Jacob S, Featherstone C, Barton M. The role of radiotherapy in cancer treatment: estimating optimal utilization from a review of evidence-based clinical guidelines. Cancer. 2005;104(6):1129–1137. doi: 10.1002/cncr.21324. [DOI] [PubMed] [Google Scholar]
- 3.Das IJ, Cao M, Cheng CW, Misic V, Scheuring K, Schüle E, Johnstone PA. A quality assurance phantom for electronic portal imaging devices. J Appl Clin Med Phys. 2011;12(2):391–403. doi: 10.1120/jacmp.v12i2.3350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Davidson MT, Blake SJ, Batchelar DL, Cheung P, Mah K. Assessing the role of volumetric modulated arc therapy (VMAT) relative to IMRT and helical tomotherapy in the management of localized, locally advanced, and post-operative prostate cancer. Int J Radiat Oncol Biol Phys. 2011;80(5):1550–1558. doi: 10.1016/j.ijrobp.2010.10.024. [DOI] [PubMed] [Google Scholar]
- 5.Deng Z, Shen L, Zheng X, Zhou Y, Yi J, Han C, Xie C, Jin X. Dosimetric advantage of volumetric modulated arc therapy in the treatment of intraocular cancer. Radiat Oncol. 2017;12(1):1–7. doi: 10.1186/s13014-017-0819-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Nguyen K, Cummings D, Lanza VC, Morris K, Wang C, Sutton J, Garcia J. A dosimetric comparative study: volumetric modulated arc therapy vs intensity-modulated radiation therapy in the treatment of nasal cavity carcinomas. Med Dosim. 2013;38(3):225–232. doi: 10.1016/j.meddos.2013.01.006. [DOI] [PubMed] [Google Scholar]
- 7.Quan EM, Li X, Li Y, Wang X, Kudchadker RJ, Johnson JL, Kuban DA, Lee AK, Zhang X. A comprehensive comparison of IMRT and VMAT plan quality for prostate cancer treatment. Int J Radiat Oncol Biol Phys. 2012;83(4):1169–1178. doi: 10.1016/j.ijrobp.2011.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tamborra P, Martinucci E, Massafra R, Bettiol M, Capomolla C, Zagari A, Didonna V. The 3D isodose structure-based method for clinical dose distributions comparison in pretreatment patient-QA. Med Phys. 2019;46(2):426–436. doi: 10.1002/mp.13297. [DOI] [PubMed] [Google Scholar]
- 9.Nguyen D, Long T, Jia X, Lu W, Gu X, Iqbal Z, Jiang S. A feasibility study for predicting optimal radiation therapy dose distributions of prostate cancer patients from patient anatomy using deep learning. Sci Rep. 2019;9(1):1076. doi: 10.1038/s41598-018-37741-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Interian Y, Rideout V, Kearney VP, Gennatas E, Morin O, Cheung J, Solberg T, Valdes G. Deep nets vs expert designed features in medical physics: An IMRT QA case study. Med Phys. 2018;45(6):2672–2680. doi: 10.1002/mp.12890. [DOI] [PubMed] [Google Scholar]
- 11.Kearney V, Chan JW, Haaf S, Descovich M, Solberg TD. DoseNet: a volumetric dose prediction algorithm using 3D fully-convolutional neural networks. Phys Med Biol. 2018;63(23):235022. doi: 10.1088/1361-6560/aaef74. [DOI] [PubMed] [Google Scholar]
- 12.Nguyen M, Chan GH. Quantified VMAT plan complexity in relation to measurement-based quality assurance results. J Appl Clin Med Phys. 2020;21(11):132–140. doi: 10.1002/acm2.13048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tiplica T, Dufreneix S, Legrand C. A Bayesian control chart based on the beta distribution for monitoring the two-dimensional gamma index pass rate in the context of patient-specific quality assurance. Med Phys. 2020;47(11):5408–5418. doi: 10.1002/mp.14472. [DOI] [PubMed] [Google Scholar]
- 14.Fan J, Wang J, Chen Z, Hu C, Zhang Z, Hu W. Automatic treatment planning based on three-dimensional dose distribution predicted from deep learning technique. Med Phys. 2019;46(1):370–381. doi: 10.1002/mp.13271. [DOI] [PubMed] [Google Scholar]
- 15.Kim J, Han MC, Lee E, Park K, Chang KH, Kim DW, Kim JS, Hong CS. Detailed evaluation of Mobius3D dose calculation accuracy for volumetric-modulated arc therapy. Phys Med. 2020;74:125–132. doi: 10.1016/j.ejmp.2020.05.015. [DOI] [PubMed] [Google Scholar]
- 16.Ezzell GA, Galvin JM, Low D, Palta JR, Rosen I, Sharpe MB, Xia P, Xiao Y, Xing L, Yu CX. IMRT subcommitte; AAPM Radiation Therapy committee: Guidance document on delivery, treatment planning, and clinical implementation of IMRT: report of the IMRT Subcommittee of the AAPM Radiation Therapy Committee. Med Phys. 2003;30(8):2089–2115. doi: 10.1118/1.1591194. [DOI] [PubMed] [Google Scholar]
- 17.Ezzell GA, Burmeister JW, Dogan N, LoSasso TJ, Mechalakos JG, Mihailidis D, Molineu A, Palta JR, Ramsey CR, Salter BJ, Shi J, Xia P, Yue NJ, Xiao Y. IMRT commissioning: multiple institution planning and dosimetry comparisons, a report from AAPM Task Group 119. Med Phys. 2009;36(11):5359–5373. doi: 10.1118/1.3238104. [DOI] [PubMed] [Google Scholar]
- 18.Kimura Y, Kadoya N, Tomori S, Oku Y, Jingu K. Error detection using a convolutional neural network with dose difference maps in patient-specific quality assurance for volumetric modulated arc therapy. Phys Med. 2020;73:57–64. doi: 10.1016/j.ejmp.2020.03.022. [DOI] [PubMed] [Google Scholar]
- 19.Kang J, Schwartz R, Flickinger J, Beriwal S. Machine Learning Approaches for Predicting Radiation Therapy Outcomes: A Clinician's Perspective. Int J Radiat Oncol Biol Phys. 2015;93(5):1127–1135. doi: 10.1016/j.ijrobp.2015.07.2286. [DOI] [PubMed] [Google Scholar]
- 20.Oermann EK, Rubinsteyn A, Ding D, Mascitelli J, Starke RM, Bederson JB, Kano H, Lunsford LD, Sheehan JP, Hammerbacher J, Kondziolka D. Using a Machine Learning Approach to Predict Outcomes after Radiosurgery for Cerebral Arteriovenous Malformations. Sci Rep. 2016;6:21161. doi: 10.1038/srep21161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Valdes G, Solberg TD, Heskel M, Ungar L, Simone CB., 2nd Using machine learning to predict radiation pneumonitis in patients with stage I non-small cell lung cancer treated with stereotactic body radiation therapy. Phys Med Biol. 2016;61(16):6105–6120. doi: 10.1088/0031-9155/61/16/6105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Valdes G, Scheuermann R, Hung CY, Olszanski A, Bellerive M, Solberg TD. A mathematical framework for virtual IMRT QA using machine learning. Med Phys. 2016;43(7):4323–4334. doi: 10.1118/1.4953835. [DOI] [PubMed] [Google Scholar]
- 23.Li J, Wang L, Zhang X, Liu L, Li J, Chan MF, Sui J, Yang R. Machine Learning for Patient-Specific Quality Assurance of VMAT: Prediction and Classification Accuracy. Int J Radiat Oncol Biol Phys. 2019;105(4):893–902. doi: 10.1016/j.ijrobp.2019.07.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ma C, Wang R, Zhou S, Wang M, Yue H, Zhang Y, Wu H. The structural similarity index for IMRT quality assurance: radiomics-based error classification. Med Phys. 2021;48(1):80–93. doi: 10.1002/mp.14559. [DOI] [PubMed] [Google Scholar]
- 25.Wall PDH, Hirata E, Morin O, Valdes G, Witztum A. Prospective Clinical Validation of Virtual Patient-Specific Quality Assurance of Volumetric Modulated Arc Therapy Radiation Therapy Plans. Int J Radiat Oncol Biol Phys. 2022;113(5):1091–1102. doi: 10.1016/j.ijrobp.2022.04.040. [DOI] [PubMed] [Google Scholar]
- 26.Schreibmann E, Fox T. Prior-knowledge treatment planning for volumetric arc therapy using feature-based database mining. J Appl Clin Med Phys. 2014;15(2):19–27. doi: 10.1120/jacmp.v15i2.4596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Carlson JN, Park JM, Park SY, Park JI, Choi Y, Ye SJ. A machine learning approach to the accurate prediction of multi-leaf collimator positional errors. Phys Med Biol. 2016;61(6):2514–2531. doi: 10.1088/0031-9155/61/6/2514. [DOI] [PubMed] [Google Scholar]
- 28.LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521(7553):436–444. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- 29.Guerreiro F, Seravalli E, Janssens GO, Maduro JH, Knopf AC, Langendijk JA, Raaymakers BW, Kontaxis C. Deep learning prediction of proton and photon dose distributions for paediatric abdominal tumours. Radiother Oncol. 2021;156:36–42. doi: 10.1016/j.radonc.2020.11.026. [DOI] [PubMed] [Google Scholar]
- 30.Kajikawa T, Kadoya N, Ito K, Takayama Y, Chiba T, Tomori S, Nemoto H, Dobashi S, Takeda K, Jingu K. A convolutional neural network approach for IMRT dose distribution prediction in prostate cancer patients. J Radiat Res. 2019;60(5):685–693. doi: 10.1093/jrr/rrz051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Barragán-Montero AM, Nguyen D, Lu W, Lin MH, Norouzi-Kandalan R, Geets X, Sterpin E, Jiang S. Three-dimensional dose prediction for lung IMRT patients with deep neural networks: robust learning from heterogeneous beam configurations. Med Phys. 2019;46(8):3679–3691. doi: 10.1002/mp.13597. [DOI] [PubMed] [Google Scholar]
- 32.Nguyen D, Jia X, Sher D, Lin MH, Iqbal Z, Liu H, Jiang S. 3D radiotherapy dose prediction on head and neck cancer patients with a hierarchically densely connected U-net deep learning architecture. Phys Med Biol. 2019;64(6):065020. doi: 10.1088/1361-6560/ab039b. [DOI] [PubMed] [Google Scholar]
- 33.Ma M, Kovalchuk N, Buyyounouski MK, Xing L, Yang Y. Incorporating dosimetric features into the prediction of 3D VMAT dose distributions using deep convolutional neural network. Phys Med Biol. 2019;64(12):125017. doi: 10.1088/1361-6560/ab2146. [DOI] [PubMed] [Google Scholar]
- 34.Zhou J, Peng Z, Song Y, Chang Y, Pei X, Sheng L, Xu XG. A method of using deep learning to predict three-dimensional dose distributions for intensity-modulated radiotherapy of rectal cancer. J Appl Clin Med Phys. 2020;21(5):26–37. doi: 10.1002/acm2.12849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kontaxis C, Bol GH, Lagendijk JJW, Raaymakers BW. DeepDose: Towards a fast dose calculation engine for radiation therapy using deep learning. Phys Med Biol. 2020;65(7):075013. doi: 10.1088/1361-6560/ab7630. [DOI] [PubMed] [Google Scholar]
- 36.Hu J, Song Y, Wang Q, Bai S, Yi Z. Incorporating historical sub-optimal deep neural networks for dose prediction in radiotherapy. Med Image Anal. 2021;67:101886. doi: 10.1016/j.media.2020.101886. [DOI] [PubMed] [Google Scholar]
- 37.Liu CC, Huang HM. A deep learning approach for converting prompt gamma images to proton dose distributions: A Monte Carlo simulation study. Phys Med. 2020;69:110–119. doi: 10.1016/j.ejmp.2019.12.006. [DOI] [PubMed] [Google Scholar]
- 38.Zhang J, Cheng Z, Fan Z, Zhang Q, Zhang X, Yang R, Wen J. A feasibility study for in vivo treatment verification of IMRT using Monte Carlo dose calculation and deep learning-based modelling of EPID detector response. Radiat Oncol. 2022;17(1):31. doi: 10.1186/s13014-022-01999-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gong C, Zhu K, Lin C, Han C, Lu Z, Chen Y, Yu C, Hou L, Zhou Y, Yi J, Ai Y, Xiang X, Xie C, Jin X. Efficient dose-volume histogram-based pretreatment patient-specific quality assurance methodology with combined deep learning and machine learning models for volumetric modulated arc radiotherapy. Med Phys. 2022;49(12):7779–7790. doi: 10.1002/mp.16010. [DOI] [PubMed] [Google Scholar]
- 40.Chen L C, Papandreou G, Schroff F, Adam H: Rethinking atrous convolution for semantic image segmentation[J]. arXiv preprint http://arxiv.org/abs/1706.05587, 2017.
- 41.Huang G, Liu Z, Van Der Maaten L, Weinberger K Q: Densely connected convolutional networks[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2017:4700–4708.
- 42.Lin B, Zhang S, Yu X: Gait recognition via effective global-local feature representation and local temporal aggregation[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. 2021:14648–14656.
- 43.Szegedy C, Liu W, Jia Y, Sermanet P, Reed S, Anguelov D, Erhan D, Vanhoucke V, Rabinovich A: Going deeper with convolutions[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2015:1–9.
- 44.Liu Q, Leung H. Variable augmented neural network for decolorization and multi-exposure fusion. Information Fusion. 2019;46:114–127. doi: 10.1016/j.inffus.2018.05.007. [DOI] [Google Scholar]
- 45.Xing Y, Qian Z, Chen Q: Invertible image signal processing. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 6287–6296, 2021.
- 46.Yu H, Torun H M, Rehman M U, Swaminathan M: Design of SIW filters in D-band using invertible neural nets. IEEE, 72–75, 2020.
- 47.Xiao M, Zheng S, Liu C, Wang Y, He D, Ke G, Bian J, Lin Z, Liu T: Invertible image rescaling. Computer Vision–ECCV, 2020.
- 48.Eilertsen G, Kronander J, Denes G, Mantiuk RK, Unger J. HDR image reconstruction from a single exposure using deep CNNs. ACM transactions on graphics (TOG) 2017;36(6):1–15. doi: 10.1145/3130800.3130816. [DOI] [Google Scholar]
- 49.Fan J, Xing L, Ma M, Hu W, Yang Y. Verification of the machine delivery parameters of a treatment plan via deep learning. Phys Med Biol. 2020;65(19):195007. doi: 10.1088/1361-6560/aba165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Jia M, Wu Y, Yang Y, Wang L, Chuang C, Han B, Xing L. Deep learning-enabled EPID-based 3D dosimetry for dose verification of step-and-shoot radiotherapy. Med Phys. 2021;48(11):6810–6819. doi: 10.1002/mp.15218. [DOI] [PubMed] [Google Scholar]
- 51.Zhu J Y, Park T, Isola P, Efros AA. Unpaired image-to-image translation using cycle-consistent adversarial networks[C]//Proceedings of the IEEE international conference on computer vision. 2017:2223–2232.
- 52.Jia M, Yang Y, Wu Y, Li X, Xing L, Wang L. Deep learning-augmented radioluminescence imaging for radiotherapy dose verification. Med Phys. 2021;48(11):6820–6831. doi: 10.1002/mp.15229. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets during the current study are not publicly available due to some research that has not been completed, but is available from the corresponding author on reasonable request.