Benchmarking feature selection and feature extraction methods to improve the performances of machine-learning algorithms for patient classification using metabolomics biomedical data

Abstract

Objective

Classification tasks are an open challenge in the field of biomedicine. While several machine-learning techniques exist to accomplish this objective, several peculiarities associated with biomedical data, especially when it comes to omics measurements, prevent their use or good performance achievements. Omics approaches aim to understand a complex biological system through systematic analysis of its content at the molecular level. On the other hand, omics data are heterogeneous, sparse and affected by the classical “curse of dimensionality” problem, i.e. having much fewer observation, samples (n) than omics features (p). Furthermore, a major problem with multi-omics data is the imbalance either at the class or feature level. The objective of this work is to study whether feature extraction and/or feature selection techniques can improve the performances of classification machine-learning algorithms on omics measurements.

Methods:

Among all omics, metabolomics has emerged as a powerful tool in cancer research, facilitating a deeper understanding of the complex metabolic landscape associated with tumorigenesis and tumor progression. Thus, we selected three publicly available metabolomics datasets, and we applied several feature extraction techniques both linear and non-linear, coupled or not with feature selection methods, and evaluated the performances regarding patient classification in the different configurations for the three datasets.

Results:

We provide general workflow and guidelines on when to use those techniques depending on the characteristics of the data available. To further test the extension of our approach to other omics data, we have included a transcriptomics and a proteomics data. Overall, for all datasets, we showed that applying supervised feature selection improves the performances of feature extraction methods for classification purposes. Scripts used to perform all analyses are available at: https://github.com/Plant-Net/Metabolomic_project/.

Graphical Abstract

1. Introduction

Personalized medicine concerns the development of approaches able to stratify patients based on their disease subtype, risk, prognosis, or treatment response using specialized diagnostic tests [1]. The key idea is to identify medical decision elements based on individual patient characteristics, including molecular biomarkers, rather than on population averages [2]. Lately, the development of precision medicine has seen unprecedented growth, thanks to the development of omics technologies and machine learning approaches [3].

Omics technologies provide a global view of the molecules that compose a cell, a tissue or an organism. They are mainly aimed at the universal detection of genes (genomics), mRNAs (transcriptomics), proteins (proteomics) and metabolites (metabolomics) in a specific biological sample [4]. The fundamental aspect of these approaches is that a complex system can be understood more thoroughly if it is considered as a whole. Each omics represents a layer of information of this complex system and the objective is to study the biological mechanisms in their entirety and the complexity of their interactions.

Modern metabolomics produces high-dimensional datasets comprising hundreds or even thousands of measured metabolites in large-scale human studies involving thousands of participants [5]. One of the key goals of metabolomics, mainly when applied in cancer research, is the discovery of robust and reliable biomarkers for early detection, diagnosis, prognosis, and treatment response prediction. Traditionally, cancer biomarker discovery has focused on genomics and proteomics approaches; however, metabolomics offers several advantages in this regard [6]. Metabolites represent the downstream products of cellular processes, capturing the integrated effects of genetic and environmental factors, as well as dynamic changes in the tumor microenvironment [7]. Moreover, metabolites are accessible through minimally invasive techniques, such as blood or urine sampling, enabling their potential translation into clinical practice [8].

The drawback that prevents wider use of metabolomics, as well as for other omics, is that data collection is financially costly, and the number of clinical research participants is usually limited. This yields uneven datasets in which the number of metabolites measured (features) far exceeds the number of patients (observations) [9]. This issue is known as the curse of dimensionality. Also, with many features, learning models tend to overfit, which may cause performance degradation on unseen data. Furthermore, most of the features are highly correlated and some features are not always directly connected with disease explanation, thus resulting in a high-dimensional space composed of many redundant and non-informative features that can mislead the algorithm training. Therefore, extracting systemic effects from high-dimensional datasets requires dimensionality reduction approaches to untangle the high number of metabolites into the processes in which they participate.

Dimensionality reduction is one of the most powerful tools to address the previously described issues. It can be mainly categorized into two main components: feature selection and feature extraction. Feature selection finds a subset of the original features that maximise the accuracy of a predictive model [10]. It can be based on prior knowledge such as evidence from known literature or based on existing databases [11], [12]. Feature extraction methods project the original high-dimensional features to a new feature space with low dimensionality. The newly constructed feature space is usually a linear or nonlinear combination of the original features. Among the different techniques of feature extraction, we focused here on latent representation learning, which is a machine learning technique that attempts to infer latent variables from empirical measurements [13]. Latent components also called latent space, in contrast to observed variables, are information that is not measurable therefore have to be inferred from the empirical measurements. Several techniques have been developed to infer the latent space with successful applications on omics data however, how to choose the model that fits the best with the available data is very challenging. These difficulties arise because models are often tested on very specific omics datasets with peculiar characteristics (i.e. number of sample/features, biological question) or combinations of multi-omics and thus hardly generalizable to other omics modalities [14], [15], [16], [17].

While during recent years there has been a lot of enthusiasm about the potential of ‘big data’ and machine learning-based solutions, there exist only a few examples that impact current clinical practice [18]. This can be due to technical limitations that can lead to insufficient performance of predictive models and difficulties to interpret complex model predictions [19], [20]. To improve the performances of predictive models, it would be necessary to dispose of a comprehensive list of validated biomarkers to design proper training, testing and validation strategies to evaluate models’ performances. The objective of our work is to explore the performances in patient classification based on their metabolomics profile of several linear and non-linear techniques of feature extraction, feature selection and to provide general guidelines on when to use those techniques depending on the data available. To study the generalization of the proposed techniques, we expanded our testing on transcriptomics and proteomics datasets obtaining similar results.

2. Materials and methods

2.1. Datasets

We used three metabolomics datasets, one transcriptomics and one proteomics dataset whose characteristics are summarized in Table 1. The metabolomics datasets are from three different types of cancer: brain, breast, and lung cancers, and the transcriptomics and proteomics datasets are from breast cancer.

Table 1.

Description of the characteristics of the metabolomics, transcriptomics and proteomics datasets used in this study.

Dataset	Omics	Experimental strategy	# Features	# Samples	Type of sample	Classes	References
BRAIN	Metabolomics	LC-MS/MS	7017	88	Glial tumor tissue	IDH wild-type tumor/ IDH-mutant tumor	Chardin et al. BMC Bioinformatics (2022)
LUNG	Metabolomics	GC–TOFMS	2944	1005	Urine	Cancer patient/ Healthy patient	Mathé E, et al. Cancer Res. (2014)
BREAST	Metabolomics	LC-MS	162	271	Tumor tissue	ER+ tumor/ER- tumor	Budczies J et al. J Proteom. (2013)
BREAST	Transcriptomics	Reverse Phase Protein Array	48405	1224	Tumor and normal tissues	Cancer patient/ Healthy patient	Weinstein et al. Nat Genet (2013)
BREAST	Proteomics	RNA-Sequencing	464	914	Tumor and normal tissues	Cancer patient/ Healthy patient	Weinstein et al. Nat Genet (2013)

A comprehensive table summarizing key features, such as the omics studied, the experimental strategy to obtain data, the number of features and samples, the different sample types and classes in three cancer datasets.

The abbreviations for experimental strategies are LC-MS/MS: Liquid Chromatography coupled to tandem Mass Spectrometry; GC–TOFMS: gas chromatography followed by time-of-flight mass spectrometry; LC-MS: liquid chromatography/mass spectrometry. The abbreviations for classes are: IDH: Isocitrate DeHydrogenase; ER: Estrogen Receptors.

2.1.1. Metabolomics datasets

2.1.1.1. BRAIN dataset

The BRAIN dataset consists of 7017 metabolites from 88 samples of glial tumors: 38 isocitrate dehydrogenase (IDH) wild-type tumors and 50 IDH-mutant tumors. Tumor samples were analyzed in an unbiased metabolomics using Liquid Chromatography coupled to tandem Mass Spectrometry (LC-MS/MS) [21].

2.1.1.2. BREAST dataset

The BREAST dataset includes 162 metabolites from 271 breast cancer tissues: 204 samples which have receptors for estrogen (ER+) and 67 samples which do not have receptors for estrogen (ER−) [22]. The metabolomic analysis was performed by gas chromatography followed by time-of-flight mass spectrometry (GC–TOFMS) as described here [23] and is very peculiar with respect to the other two metabolomics datasets used in this study.

2.1.1.3. LUNG dataset

The LUNG dataset is composed of 2944 metabolites concerning urine samples from 469 Non-Small Cell Lung Cancer (NSCLC) patients prior to treatment and 536 controls [24]. The dataset was obtained after an unbiased liquid chromatography/mass spectrometry approach. It is available at MetaboLights (study identifier MTBLS28).

It is important to notice the very different characteristics of the three metabolomic datasets, both in terms of the number of features and number of patients, furthermore the BREAST dataset was obtained with a different experimental technique as explained before (Table 1). The BRAIN dataset contains a limited number of patients (88) with several features (7017). The BREAST dataset contains a moderate number of patients (271) with a small number of features (162). The LUNG dataset contains a very large number of patients (1005) with a large number of features (2944).

2.1.2. Transcriptomics and proteomics datasets

The transcriptomics and proteomics dataset comes from the TCGA database [25]. Gene expression profiles and/or proteomics profiles were downloaded from the BRCA project. For both omics, we kept only samples from primary tumors and healthy individuals. The transcriptomics dataset is composed of a large number of features, i.e. 48,405, and 1224 patients of which 1111 cancer patients and 113 healthy individuals. The proteomics dataset includes 464 features and 914 patients, of whom 33 are healthy and 881 have a tumor.

2.2. Feature selection methods

Feature selection is a strategy widely adopted in machine learning to effectively reduce dimensionality. The primary objective is to select a subset of relevant features from the original set, based on specific relevance evaluation criteria. This selection often results in improved learning performance, marked by greater classification accuracy, reduced computational expense and improved model interpretability [26], [27], [28], [29]. Here, we define feature selection as a data preprocessing strategy aimed at finding a subset of the original features that maximize the accuracy of a predictive model. The aim is to prepare understandable and clean data to build a simpler and more comprehensible model.

Feature selection methods can be classified into three groups: supervised [30], [31], unsupervised [32], [33] and semi-supervised [34], [35] approaches, depending on the nature of the training set. Each method addresses the challenges posed by labeled and unlabeled datasets, offering tailored solutions for optimizing feature subsets on the basis of available information. There are three main categories in supervised feature selection approaches: filter models, wrapper models and embedded models. Filter-based approaches evaluate the value of each feature regardless of the performance of a specific machine learning algorithm, yielding the bias of a learning algorithm not interacting with the bias of a feature selection algorithm [36], [37], [38]. The wrapper model evaluates the quality of selected features, based on the predictive accuracy of a predefined learning algorithm [39]. However, the use of these methods becomes impractical when dealing with datasets containing a large number of features, due to their high computational costs. Embedded models incorporate feature selection within the learning algorithm itself [10], [37], [40], [41].

We have used two supervised feature selection methods, namely the Kolmogorov–Smirnov (KS) test which is a filter model and Boruta feature selection which is a wrapper model, as well as three unsupervised methods which are filters on the variance of the features. The KS test is a statistical test used to determine whether two distributions differ significantly from each other. It compares the cumulative distribution functions of the two samples and assesses the probability that they come from the same underlying distribution. We used this test to identify the features with the most significant difference between the two classes of samples (e.g., diseased vs healthy). Boruta is a feature selection method based on Random Forest classification [42], [43]. It aims to identify and retain only the most relevant variables while iteratively eliminating less pertinent features through statistical analysis.

The three unsupervised feature selection methods included in this study are based on variance filters. We first calculated the variance of each feature, then filtered the features according to different thresholds. The first filter, named VarQ1, removes all features whose variance is less than the value of quartile 1, i.e. the value separating the first quarter from the rest of the distribution. The second filter, named Median, removes all features whose variance is less than the value of the median. And the last filter, named VarQ3 retains all features whose variance is greater than the value of the third quartile, i.e. the value separating the last quarter from the rest of the distribution. The idea was to progressively remove features with low variance, as this could reflect a small difference in features values between the two populations being compared.

We applied these five feature selection methods on all the datasets, the number of selected features for each method and dataset are reported in supplementary table 1.

2.3. Feature extraction methods

We tested linear and non-linear techniques. Linear techniques suppose that there is a linear relationship between the observed variables and the latent space. Under this assumption, the latent space can then be inferred from observed variables. We test six linear methods: Principal Component Analysis (PCA), Mixture of Probabilistic PCA (MPPCA), High dimensional discriminant analysis (HDDA), Factor Analysis (FA), Linear Discriminant Analysis (LDA) and Partial Least Squares Discriminant Analysis (PLS-DA) and two non-linear: Kernel PCA (KPCA) and Gaussian Process Latent Variable Modeling (GPLVM). We have also run these latent space inference methods on pre-selected features to analyze the impact of this preprocessing on the performance metrics. HDDA, MPPCA and GPLVM methods were implemented in R. All other methods were implemented in Python.

2.3.1. Linear techniques

2.3.1.1. Principal Component Analysis (PCA)

PCA [44] is a dimensionality reduction technique that transforms high-dimensional data into a new coordinate system, in which the first few principal components capture the maximum variance of the original data. These components are linear combinations of the original features. PCA uncovers the most informative aspects of the data, enabling them to be represented in a reduced-dimensional space while preserving as much variance as possible. In PCA, it is possible to identify key variables that contribute to PCA score profiles. For instance, Wu et al. used PCA to identify potential biomarkers to distinguish patients with laryngeal cancer from healthy individuals [45].

2.3.2. Mixture of probabilistic PCA (MPPCA)

MPPCA is a probabilistic model that combines multiple probabilistic PCA (PPCA) models into a mixture model [46]. MPPCA extends the concept of PPCA to capture more complex data distributions and capture data points that may belong to different clusters or components. PPCA is a linear dimensionality reduction technique that assumes a linear relationship between the observed variables and a lower-dimensional latent space. PPCA assumes that the observed data points are generated by adding Gaussian noise to a low-dimensional subspace, which is represented by a linear mapping from the latent space to the observed space. In MPPCA, a mixture model framework is employed to account for multiple components in the data. MPPCA assumes that each observed data point is associated with a latent variable, which indicates the component to which it belongs. The model further assumes that the latent variables follow a certain probability distribution, such as a Gaussian distribution. The mixing coefficients represent the probability of a data point belonging to each component. Nyamundanda et al. successfully used PPCA to identify metabolites which were responsive to pentylenetetrazole (the treatment used in the study) [47]. They also used MPPCA to simultaneously cluster and reduce the dimension of metabolites data. They have demonstrated that the application of those techniques helps in the identification of disease phenotypes or treatment-responsive phenotypes.

2.3.3. Linear Discriminant Analysis (LDA)

LDA is a statistical technique used to find the linear combinations of features that best differentiate several classes in a dataset [48]. LDA aims to maximize the ratio of the variance between classes to the variance within classes, resulting in a set of discriminant functions. These functions serve as decision boundaries, allowing for effective classification of data points into predefined classes. LDA assumes that the features are normally distributed and that the covariance matrices of different classes are equal. By transforming the data into a lower-dimensional space, LDA reduces dimensionality while preserving class-related information, making it a powerful method for feature extraction and classification tasks. LDA has been used in several studies to find linear combinations of metabolic variables and usually achieve very good performances in patients classification [49], [50].

2.3.4. High dimensional discriminant analysis (HDDA)

HDDA extends traditional Linear Discriminant Analysis (LDA) to handle situations where the number of variables or features is large compared to the number of samples [51]. HDDA addresses the challenges of high-dimensional data by incorporating regularization and shrinkage techniques. Regularization methods are employed to stabilize the estimation of the covariance matrix. HDDA performs dimensionality reduction by projecting the high-dimensional data onto a lower-dimensional subspace. This subspace is determined by a set of linear discriminant directions that maximize the separation between classes. The number of discriminant directions is typically smaller than the original dimensionality, allowing for a reduced representation of the data. After dimensionality reduction, HDDA can be used for classification tasks. New samples can be projected onto the reduced subspace, and their class labels can be predicted based on their proximity to the class-specific centroids or by using other classification algorithms.

2.3.5. Partial least squares discriminant analysis (PLS-DA)

PLS-DA is a multivariate statistical method that combines aspects of partial least squares regression and discriminant analysis to model the relationship between predictor variables (features) and categorical response variables (class labels) [52], [53]. It involves finding latent variables that capture the maximum covariance between predictor and response variables. These latent variables are used to create a discriminant model, enabling efficient discrimination of different classes within the data. PLS-DA has been popular in the field of chemometrics, which is why it can handle high-dimensional datasets and be applied to omics data, particularly metabolomics data [54].

2.3.6. Factor analysis (FA)

FA is a statistical method that analyzes the relationships among observed variables to uncover the latent factors that explain their covariation [55]. Hamzehzarghani et al. [56] used factor analysis to profile the metabolic of spikelets of wheat cultivars, Roblin and Sumai3, susceptible and resistant to fusarium head blight, respectively.

In general, FA assumes that the observed variables are influenced by a smaller number of unobserved factors, also known as common factors. First, the correlation matrix from the observed variables is calculated. This matrix represents the pairwise relationships and covariation among the variables. Then, the factor extraction step identifies the underlying factors that explain the observed covariation. However, the application of FA requires certain conditions: the observed variables must be highly correlated, and the number of samples must be at least four times greater than the number of features. The number of factors to be retained is a crucial decision, which is why it is determined by various methods, such as the Kaiser criterion, scree plot examination or the use of more sophisticated statistical criteria such as the Bayesian Information Criterion (BIC) or the Minimum Partial Mean (MPM) test. By combining factors and factors loading they were able to identify metabolites involved in pathogen-stress and their metabolic pathways of synthesis. Choosing the appropriate number of factors requires a balance between capturing sufficient variance in the data and avoiding overfitting.

To check that if the variables in our datasets are highly correlated, we run the Kaiser-Mayer-Olkin (KMO) test. If the KMO value is higher than 0.7, then FA can be performed, otherwise, it is not possible. To determine the optimal number of factors to select, we ran an exploratory factor analysis (EFA) [55] and we selected the most frequently used number of factors.

2.3.7. Non-linear techniques

Non-linear techniques assume that the relationship between the latent space and observed variables is not linear. However, some non-linear techniques can, under some constraints, help to infer linear relationship while linear techniques can only infer linear relationships. We tested 2 non-linear methods: Kernel PCA (KPCA) and Gaussian Process Latent Variable Modeling (GPLVM).

2.3.8. Kernel PCA (KPCA)

KPCA is a non-linear extension of PCA, designed to deal with non-linear relationships within data [57]. This technique has already been applied to nuclear magnetic resonance-based metabolic profiling analysis [58]. It uses a kernel function to map input data into a higher-dimensional space, where linear structures are more apparent. In this expanded space, standard PCA is applied to extract principal components. The main advantage lies in its ability to capture complex, non-linear patterns that traditional PCA might overlook. By utilizing kernel functions such as radial basis function, polynomial, or sigmoid, kernel PCA allows for a more flexible representation of data, making it a powerful tool for dimensionality reduction and non-linear feature extraction. But unlike PCA, it is impossible to determine the importance of features.

2.3.9. Gaussian process latent variable modeling (GPLVM)

GPLVM is a probabilistic dimensionality reduction technique that combines Gaussian processes with latent variable models [59]. GPLVM aims to learn a low-dimensional representation of high-dimensional data by modeling the underlying structure and uncertainty in the data.

GPLVM assumes that the observed high-dimensional data points are generated from a lower-dimensional latent space. Each data point is associated with a set of latent variables that lie in the lower-dimensional space. Gaussian processes are non-parametric models that can represent complex functions. In GPLVM, a Gaussian process is used to model the mapping from the latent space to the observed space. This mapping represents how the latent variables influence the observed data. Then, GPLVM employs Bayesian inference to estimate the latent variables and the parameters of the Gaussian process. It aims to find the most likely values of the latent variables given the observed data. Once the latent variables are estimated, GPLVM provides a reduced-dimensional representation of the data. This lower-dimensional representation retains the most important information and captures the underlying structure in the data.

2.4. Cross-validation

To ensure the development of a predictive model capable of discerning patterns in unbalanced data, a five repeated four4-fold cross-validation approach was employed with default parameters of XGBoost. This technique involves partitioning the dataset into four subsets, utilizing three of them for training and the remaining one for validation in each iteration. This process is repeated four times, with each fold serving as the validation set in a distinct iteration. To ensure a more robust evaluation of the model’s performances, we repeated this process five times, it provides multiple independent estimates of how well the model generalizes to unseen data. Finally, the model undergoes training and evaluation several times, enabling a more thorough assessment of its predictive capabilities in various data subsets. By applying this strategy, we aimed to mitigate the impact of unbalanced class distribution, ensuring that the classifier model learns from patterns effectively and generalizes well to novel and unseen instances, thus contributing to the reliability and efficiency of the predictive modeling process.

2.5. Classification

For feature extraction techniques that do not perform classification already in their model, namely PCA, FA and KPCA, we used the XGBoost classifier model [60]. XGBoost is an implementation of gradient-boosting decision trees sequentially combine decision trees to create an ensemble model, particularly used for classification and regression. It was selected for its speed, scalability, and superior performance, making it a popular choice in various analyses.

2.6. Calculation of metrics for performances evaluation

We have chosen to report seven metrics to evaluate performances of the models.

The accuracy is the number of correct predictions whether positive or negative, defined as:

$$\mathit{Accuracy}=\frac{\mathit{TP}+\mathit{TN}}{\mathit{TP}+\mathit{FP}+\mathit{TN}+\mathit{FN}}$$

Where True Positive (TP) is the number of correct positive predictions, False Positive (FP) is the number of incorrect positive predictions, True Negative (TN) is the number of correct negative predictions and False Negative (FN) is the number of incorrect negative predictions.

The precision quantifies the number of correct positive predictions out of the positive predictions made by the model:

$$\mathit{Precision}=\frac{\mathit{TP}}{\mathit{TP}+\mathit{FP}}$$

The recall, also called the sensitivity, is the number of TP among the real positive samples (TP and FN) that the model obtains, calculated with the following formula:

$$\mathit{Recall}=\frac{\mathit{TP}}{\mathit{TP}+\mathit{FN}}$$

The specificity is the number of correct negative predictions the model can detect.

$$\mathit{Specificity}=\frac{\mathit{TN}}{\mathit{TN}+\mathit{FP}}$$

The F1 score keeps the balance between precision and recall.

$$F1\mathit{score}=2\times \frac{\mathit{precision}\times \mathit{recall}}{\mathit{precision}+\mathit{recall}}$$

The AUC measures the performance of a binary classification model by quantifying the Area Under the Receiver Operating Characteristic (ROC) curve.

For the two unbalanced datasets we calculated the balanced accuracy. It’s the arithmetic mean of sensitivity and specificity.

$$\mathit{Balanced}\_\mathit{accurracy}=\frac{\mathit{sensitivity}+\mathit{specificity}}{2}$$

For all these metrics, we have computed a 95% confidence interval on results of the four-folds repeated five times of the cross validation.

2.7. Feature importance

In the context of cancer, the identification of biomarkers is crucial. Features with a high importance score may be potential biomarkers, indicating their relevance in disease characterization. Understanding the importance of features is essential to accurately identify diagnostic or prognostic biomarkers, to facilitate early detection, risk assessment and personalized treatment strategies for cancer patients.

HDDA, MPPCA, KPCA and GPLVM do not allow to determine the significance of the features. Thus, we performed feature importance only for NFE model, PCA, FA, PLS-DA and LDA.

To compute feature importance for the NFE model, we used SHAP (Shapley Additive exPlanations) values [61]. SHAP values allow us to attribute a specific contribution to each feature for a given prediction and to understand the unique role each feature plays in influencing the model’s decisions. By leveraging SHAP values, we gain a comprehensive and interpretable view of feature importance, contributing to a more informed and transparent analysis of the XGBoost model’s predictive capabilities.

For PCA and FA, feature importance can be calculated with SHAP to extract the principal components or factors contributing the most to classification performances.

In PLS-DA, Variable Importance in Projection (VIP) scores are commonly used to quantify the importance of each feature in the model. The VIP score of a variable is calculated as a weighted sum of the squared correlations between the PLS-DA components and the original variable. The weights correspond to the percentage variation explained by the PLS-DA component in the model. Features with a high VIP score are those that contribute significantly to class separation.

In LDA, the importance of each feature is assessed by its contribution to the discriminative criterion. Features with higher coefficients in the linear discriminant function are considered more important in separating classes.

2.8. Computational workflow

We set up a workflow consisting of three main pipelines (Fig. 1). The two main steps are the execution of a feature extraction model followed by the classification of patients using the newly calculated features. We also included feature selection before the feature extraction model and then classification, or directly the classification.

Fig. 1.

Workflow used in this study to evaluate the classification performances of several feature extraction techniques coupled or not with feature selection. The input of the workflow consists in one omics dataset at the time. The workflow consists of four steps. The first step is the feature selection based on two supervised or three unsupervised methods. Abbreviations for feature extraction method are: HDDA: High dimensional discriminant analysis; MPPCA: Mixture of Probalistic PCA; PCA: Principal Component Analysis (PCA); PLS-DA: Partial least squares discriminant analysis; LDA: Linear discriminant analysis; KPCA: Kernel PCA; GPLVM: Gaussian Process Latent Variable Modeling. The second step is the feature extraction. We included six linear and two non-linear methods. The third step is the sample classification by cross-validation, using their own classification method (indicated with an *) or XGBoost model. Next, from classification results, we calculate metrics to evaluate performances of models. Finally, we perform feature importance when it is possible to find potential biomarkers with Shapley Additive exPlanations (SHAP) values, Variable Importance in Projection (VIP) scores and weights coefficients.

Then the performances on the classification task are evaluated using the aforementioned metrics. When possible (only for NFE, PCA, FA, LDA and PLS-DA), we also calculated the features importance to extract potential biomarkers in each dataset.

Overall, we trained 208 models by feeding with either one of the three metabolomics (124 models) or transcriptomics (38 models) or proteomics (42 models) datasets as features or after performing feature selection. Scripts used to perform all analysis are available at: https://github.com/Plant-Net/Metabolomic_project/.

2.9. Permutation test

To assess the robustness and performance significance of the best-performing models, we permutated the data labels before performing feature extraction model for each dataset. The aim is to differentiate between models with true predictive power and those that randomly predict labels.

To do this, we randomly permuted class labels 100 times while keeping the original feature values to create a scenario in which the relationships between features and class labels are disrupted. Next, we ran the feature extraction model that performed the best among all the models tested and compared the performance of the permuted models with the performance of the best model without permutation. By comparing the performances, we can determine whether the observed classification accuracy has occurred by chance. If the model performs well even on shuffled data, this suggests that the classification accuracy could be due to chance rather than capturing a true pattern in the data. Conversely, if model performance drops significantly on shuffled data, this reinforces confidence that the observed classification success is based on meaningful relationships between features and cancer classes.

3. Results

We applied the experimentation workflow to the three metabolomics datasets as described in the methods section and Fig. 1. Briefly, we implemented five feature selection techniques: two supervised methods (KS test and Boruta) and three unsupervised by applying two filters on the variance distribution and the median (see methods for details). The number of features selected by each method for each dataset is indicated in supplementary table 1. Regarding feature extraction we tested eight methodologies both linear and non-linear, namely HDDA, MPPCA, PCA, FA, PLS-DA, LDA, KPCA, GPLVM; applied upon each feature selection technique or without feature selection first. For each dataset we also directly used the classifier without feature extraction or selection (NFE). In total we implemented 208 models in our workflow. The main characteristics of the datasets are reported in Table 1. Briefly, the BRAIN dataset contains a limited number of patients (88) with a high number of metabolites (features) (7017). The BREAST dataset contains a moderate number of patients (271) with a small number of features (162). This dataset is very different from the other not only for the different number of variables and samples, also extremely unbalanced and contains metabolites extracted with a different mass spectrometry technique. The LUNG dataset contains a very large number of patients (1005) with a large number of features (2944).

3.1. Cross-validation helps to handle unbalanced and small datasets

To evaluate the model’s performance the most commonly used techniques are dataset split into train and test sets, leave one out cross-validation, cross-validation and bootstrap. When it comes to overcoming the challenges posed by small and unbalanced datasets, data set split is not applicable and cross-validation-like methods emerge as a crucial and indispensable strategy in machine learning [62], [63], [64], [65]. Cross-validation and bootstrap are very similar, with the main difference depending on sampling samples with or without replacement. Due to the drawing with replacement, a bootstrapped data set may contain multiple instances of the same original cases, and may completely omit other original cases [66]. In scenarios with unbalanced class distributions or limited data, traditional model evaluation can lead to biased and unreliable results [67]. The type of cross-validation that selects a test set with one single example is called LOOCV (leave one out cross-validation). Sub setting a dataset using LOOCV is computationally expensive, not necessarily leading to better results [67]. Cross-validation, with its ability to iteratively partition the dataset into training and test subsets, offers a more robust solution [66]. By ensuring that each data point participates several times in the evaluation process, cross-validation provides a more complete understanding of a model's performance. This approach is particularly valuable when dealing with unbalanced datasets, where instances of minority classes may be overlooked. Furthermore, in the context of small datasets, cross-validation maximizes the usefulness of limited samples by systematically evaluating model performance in different partitions. Therefore, in our study, we used cross-validation for evaluating all models’ performances.

3.2. Feature selection improves classification performances on all datasets

To evaluate the performances of the 208 different models illustrated in Fig. 1, we used the balanced accuracy, the precision, the recall, the specificity and the F1 score because together they give an overview of model’s performances (supplementary table 2, 3 and 4). A high precision can mask poor performances in capturing positive instances corresponding to low recall, thus a focus on F1 score helps us to find a balance between precision and recall, while specificity gives us an idea of the rate of true negatives. For all datasets, the feature selection performed by the Boruta algorithm provided the best results either with or without feature extraction.

In supplementary table 2, we summarize all the results for the BRAIN dataset. We could not perform FA because the KMO value was equal to 0.56, thus smaller than the required threshold for applicability. For this dataset, when the Boruta algorithm is used, all the scores have comparable ranges for all models, and we do not observe dramatic changes in terms of performances depending on the extraction technique (Fig. 2A). This is probably due to the similar number of samples in the two classes. The best performances were obtained with the Boruta feature selection combined with PLS-DA feature extraction achieving an average balanced accuracy of 89.5 ( ± 6.5%), an average recall of 92.0 ( ± 7.5%), an average specificity of 89.0 ( ± 10.7%) and an average F1 score of 96.9 ( ± 2.8%). Overall, we observe that supervised feature selection with Boruta or KS-test improves the performances of all feature extraction methods, also for methods like PCA and KPCA which obtained very poor scores, almost comparable to a random classifier without supervised feature selection.

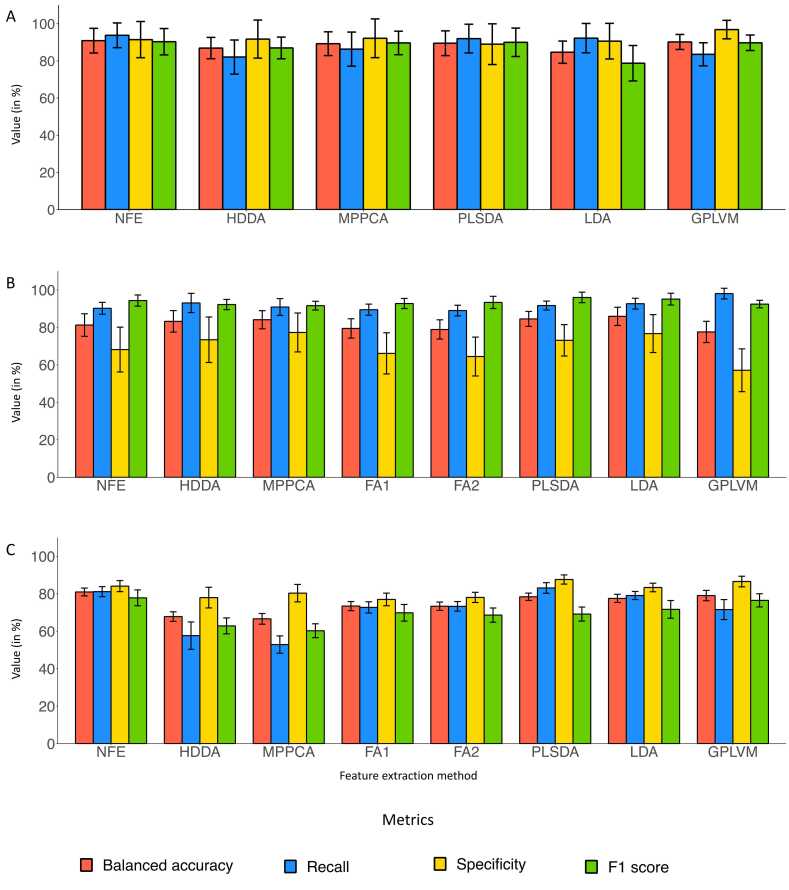
Fig. 2.

Metrics to evaluate the performances of the model used in this study for metabolomics data. Performances after Boruta feature selection application for each feature extraction method in terms of balanced accuracy (salmon), recall (blue), specificity (yellow) and F1 score (green) for BRAIN dataset (A), BREAST dataset (B) and LUNG dataset (C). The abbreviations for feature extraction methods are: NFE: No Feature Extraction; HDDA: High dimensional discriminant analysis; MPPCA: Mixture of Probabilistic PCA; PCA: Principal Component Analysis (PCA); FA: Factor Analysis; PLS-DA: Partial least squares discriminant analysis; LDA: Linear discriminant analysis; KPCA: Kernel PCA; GPLVM: Gaussian Process Latent Variable Modeling. For BRAIN and BREAST dataset, two FA were performed with different numbers of features. For BREAST dataset, five feature were used for FA1 and 12 for FA2. For LUNG dataset, 16 features were used for FA1 and 34 for FA2. For BRAIN, we were unable to perform FA.

Regarding the BREAST dataset, the best performances are achieved by combining Boruta feature selection and the LDA with an average balanced accuracy of 85.9% ( ± 4.7%), an average recall of 92.7% ( ± 2.8%), an average specificity of 76.7% ( ± 9.9%) and an average F1 score of 93.7% ( ± 3.4%) (supplementary table 3). We can also observe that similar scores were obtained with PLS-DA after Boruta feature selection. Independently by the feature extraction technique used, for the best-performing feature selection method, we observe overall good recall but low specificity (Fig. 2B). Contrarily to the previous dataset, the BREAST dataset is highly unbalanced with one class heavily more represented than the other. Although F1 score is a more stable metric especially for unbalanced datasets, it is always preferable to evaluate all the metrics because they have different meanings. Depending on the biomedical question one may prefer to have better specificity or better recall to the detriment of the other. In general, for this dataset, all feature selection techniques but VarQ3 strongly improved the performances of feature extraction methods.

Finally, for the LUNG dataset, feature extraction techniques do not improve the performances obtained by feature selection methods mainly of the supervised techniques. Indeed, the method that achieved the best performances is the combination of Boruta feature selection and XGBoost model, with an average accuracy of 80.9% ( ± 2.0%), an average recall of 81.1% ( ± 2.6%), an average specificity of 84.1% ( ± 2.9%) and an average F1 score of 77.8% ( ± 4.1%) (refer to supplementary table 4 for results for the LUNG dataset). For this dataset, achieving a high recall rather than high precision is crucial as we seek to distinguish healthy from cancer individuals, hence patients erroneously predicted as healthy (FNs) can have dramatic consequences. Overall, we observe that when the Boruta algorithm is applied, for all models we achieve specificity higher than the other metrics, and mainly when PLS-DA is applied on Boruta selection (Fig. 2C). In summary, for two datasets out of three, the combination of feature selection and feature extraction method achieves the best performances. While for BRAIN and BREAST datasets Boruta feature selection combined with PLS-DA and LDA respectively achieved the best performances, for LUNG dataset, the only application of Boruta feature selection without extraction method yielded the best achievement. Overall, we can observe that supervised feature selection before feature extraction always improves classification metrics.

3.3. ROC curves as a useful tool to compare model performances among multiple datasets

The ROC curve and its associated AUC serve as critical tools for evaluating and comparing the performance of different classification methods. The AUC ROC curve evaluates the ratio between a model's true-positive and false-positive rates for different threshold values, providing an overview of its discriminatory power. A higher AUC value indicates better model performance, as it means a greater ability to distinguish positive from negative instances.

We calculated ROC curves for all feature extraction methods and NFE model before and after feature selection. For the BRAIN dataset, performances vary widely from one method to another (Fig. 3A). The two methods that best perform are NFE and PLS-DA when supervised feature selection is used first (KS test and Boruta). The worst-performing method is KPCA, whose performances are close to a random classifier if no feature selection or non-supervised feature selection is employed. Regarding the BREAST dataset, unlike the BRAIN dataset, all the methods, except for KPCA without feature selection or FA1 after VarQ3 feature selection, achieved comparable results (Fig. 3B). For the LUNG dataset, all methods achieved comparable performance if supervised feature selection is used before feature extraction (Fig. 3C). Performances of all feature extraction techniques diminish if a non-supervised feature extraction technique is used for this dataset.

Fig. 3.

ROC curves to compare multiple model performances on multiple datasets for metabolomics data. ROC curves obtained before and after performing feature selection and feature extraction are shown for BRAIN dataset (A), BREAST dataset (B) and LUNG dataset (C). The blue curve represents the ROC curve for no feature extraction (NFE) method, the orange one is for High dimensional discriminant analysis (HDDA), the green one for Mixture of Probabilistic PCA (MPPCA), the beige one for Principal Component Analysis (PCA), the purple one and brown one for Factor Analysis (FA), the yellow one for Partial Least Squares Discriminant Analysis (PLS-DA), the red one for Linear Discriminant Analysis (LDA), the cyan one for Kernel PCA (KPCA) and the pink one for Gaussian Process Latent Variable Modeling (GPLVM). The dashed grey line corresponds to a random classifier. Abbreviations for feature selection methods are: KS: Kolmogorov–Smirnov; VarQ1: variance filter by removing the first quartile; Median: variance filter retaining all features whose variance is greater than the median; VarQ3: variance filter by keeping the third quartile.

To further test the validity of the models, for the best-performing model for each dataset, we also performed a permutation test after feature selection and before feature extraction to test whether model performances are impacted. As shown in supplementary figure 1, model performances are strongly affected suggesting that the best models without permutation have captured a true pattern in the data, they have a true predictive power and that performances are not due to chance (supplementary tables 5, 6 and 7).

In summary, the KPCA method is the worst performer, suggesting that is not suitable for extracting relevant features in the context of metabolomics cancer data. There is no clear difference in performances between linear and non-linear methods. The most stable method, independent of the dataset, appears to be NFE, namely the use of XGBoost model coupled with feature selection to classify samples. Supervised feature selection techniques, especially Boruta, strongly improve the performances of all feature extraction methods.

3.4. Features importance allows identification of potential biomarkers

As last step of our analysis, we inspected features' importance of the best-performing models for each dataset using SHAP explainer [61] when possible to implement, or the feature importance score associated with the model. To note that some models such as HDDA, MPPCA, KPCA, or GPLVM, do not allow the application of an explainer algorithm and do not provide an internal solution to calculate feature importance. We consider these models as black-box and of less employability in the biomedical context. By calculating the features' contribution to the classification, we can identify the metabolites with the most discriminative pattern of expression that might be proposed as putative biomarkers.

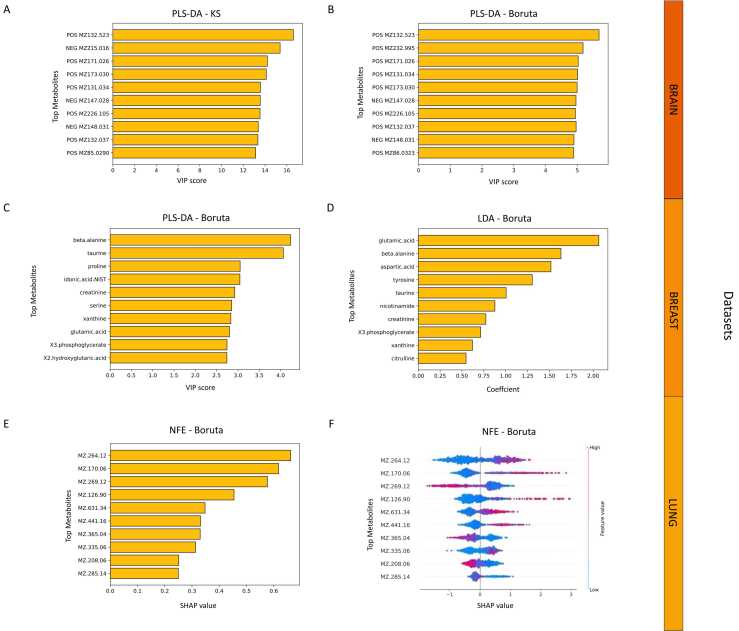
The best model for BRAIN dataset is PLS-DA of features selected by either KS-test or Boruta. PLS-DA provides the VIP scores for each feature (metabolites for our dataset) to estimate the contribution to the model performance. By extracting the top ten for each method (Fig. 4A and B), we observe that only two metabolites are not in agreement between the two. All the metabolites in the top 10, with the exception of the 7th and 10th correspond to different isotopes and adducts of 2-hydroxyglutarate, a specific product of mutated glial cells, as already found in the previous study (Fig. 4A) [21]. Mutations of isocitrate dehydrogenase (IDH) enzyme can produce high levels of 2-hydroxyglutarate to inhibit glioma stem cell differentiation, increase tumor microenvironment formation and produce high levels of hypoxia-inducible factor-1α to promote glioma invasion. Mutations in the IDH enzyme worsen the prognosis of gliomas. It is therefore important to distinguish between the two types of glial tumor in order to tailor treatments and improve prognosis [68].

Fig. 4.

Feature importance barplots. Barplots are reported for the top contributing features according to Variable Importance on Projection (VIP) scores for Partial Least Squares Discriminant Analysis (PLS-DA) model, weight coefficients for Linear Discriminant Analysis (LDA) model and Shapley Additive exPlanations (SHAP) values for no feature extraction (NFE) model for BRAIN dataset (A and B), BREAST dataset (C and D) and LUNG dataset (E, F). On x axis, VIP scores, weight coefficients or SHAP values are represented, depending on the model used. On y-axis, there are the top metabolites/features that contribute to the model. KS: Kolmogorov–Smirnov feature selection.

For the BREAST dataset, the aim is to distinguish the cancer status depending on the hormone receptor (ER) that is crucial for determining which treatment to administer to patients. Indeed, hormone therapy drugs can be used for ER+ breast cancer samples but will be ineffective for ER- breast tumors. The two best-performing methods for discriminating ER+ and ER- tumors are PLS-DA and LDA combined with Boruta feature selection, LDA also provide its own score for feature importance. For both methods we found among the top ten metabolites the beta-alanine and the xhantine (Fig. 4C and D). Both metabolites have already been shown to have significantly different concentrations in ER+ and ER- breast tumors and they have already been suggested to be used as biomarkers to distinguish the two types of breast tumors. We also notice the glutamic acid that indicates higher glutaminolysis, a key feature of metabolic changes in cancer cells [22].

Then we inspected the contribution of the metabolites to the best classification model for the LUNG dataset, which is the simple application of Boruta feature selection without feature extraction. Identifying potential biomarkers for this cancer is fundamental since early detection is pivotal for treating this aggressive cancer. For this model, we applied the SHAP algorithm to calculate feature importance. The advantage of SHAP is that, not only calculates the feature contribution (Fig. 4E), but also indicates whether the contribution is positive or negative to the overall model performances (Fig. 4F). The metabolite that ranked at the first position in feature importance corresponds to the creatine riboside (Fig. 4E and F). This metabolite was described as the most important metabolite to discriminate between lung cancer patients and healthy individuals [24].

Overall, the feature importance on the best-performing models allowed the identification of the most contributing metabolites to discriminate the samples depending on the phenotype and is a valid tool to identify potential biomarkers.

3.5. Application to transcriptomics and proteomics data

To test the generality of our workflow, we applied all models to two other omics datasets (i.e. transcriptomics and proteomics) related to BREAST cancer from the TCGA database [25]. By applying the same workflow, we obtain comparable results as discussed for metabolomics data (Fig. 5, supplementary tables 8 and 9). Overall, feature selection combined with feature extraction improves the performances. While for transcriptomics, supervised feature selection yields the best AUC scores, for proteomics we observe that non-supervised feature extraction techniques obtain the best performances. We then calculated the feature importance for the best-performing model (supplementary figure 2). By inspecting the VIP scores of the top ten genes for the PLS-DA after Boruta feature selection model, we can see that almost all genes are known to be involved in breast cancer (supplementary figure 2 A). VEGF-D has been demonstrated to be involved in promoting tumor angiogenesis and lymphangiogenesis [69] and to be up-regulated in breast cancer [70]. Like VEGF-D, OXTR is up-regulated in breast cancer, creating a microenvironment that promotes mammary tumor growth and metastasis [71].

Fig. 5.

ROC curves to compare multiple model performances on multiple datasets on transcriptomics and proteomics data. ROC curves obtained before and after performing feature selection and feature extraction are shown for transcriptomics dataset and proteomics dataset. The blue curve represents ROC curve for no feature extraction (NFE) method, the orange one is for High dimensional discriminant analysis (HDDA), the green one for Mixture of Probabilistic PCA (MPPCA), the beige one for Principal Component Analysis (PCA), the purple one and brown one for Factor Analysis (FA), the yellow one for Partial Least Squares Discriminant Analysis (PLS-DA), the red one for Linear Discriminant Analysis (LDA), the cyan one for Kernel PCA (KPCA) and the pink one for Gaussian Process Latent Variable Modeling (GPLVM). The dashed grey line corresponds to a random classifier. Abbreviations for feature selection methods are: KS: Kolmogorov–Smirnov; VarQ1: variance filter by removing the first quartile; Median: variance filter retaining all features whose variance is greater than the median; VarQ3: variance filter by keeping the third quartile.

PAMR1, CAVIN2, ADAMTS5, PDE2A and CAV1 were all found to be down-regulated in breast cancer samples compared with normal breast tissue [72], [73], [74], [75]. PAMR1 is known as a putative breast cancer tumor suppressor [72], while PDE2A significantly regulates the growth and invasion of human breast cancer [75]. CAVIN2 plays an important role in inhibiting breast cancer development, so significant down-regulation of CAVIN2 is associated with patient prognosis and correlated with advanced tumor stage [73]. For proteomics, two models achieved comparable performances: LDA combined either with non-supervised VarQ1 feature selection or with Median (supplementary figure 2B and C). Despite the very comparable performances, the top ten proteins in common between the two methods are very few. The gene that ranked at the first position for both models is RAB11A/RAB11B which encodes for RAB11 protein. RAB11A has previously been shown to be up-regulated in the majority of breast cancer tumors [76], suggesting that RAB11A plays an important role in the development and proliferation of human breast cancer. The permutation test applied to the best-performing methods led to similar conclusions as for metabolomics data (supplementary figure 3, supplementary tables 10 and 11).

Overall, these results show that the workflow presented in this study can be applied to omics data beyond metabolomics.

4. Discussion and conclusions

In this paper, we have proposed a workflow to classify two groups of samples using feature selection and feature extraction methods. We discussed the importance of using cross-validation for achieving good classification performances with unbalanced and small datasets, that are very common in the biomedical field. The drawback of implementing cross-validation consists of a considerable extension of training time and a substantial computational cost, requiring significant processing power.

We showed that, independently of the feature extraction technique applied, feature selection is a necessary step method to improve the performances and mainly when supervised methods are used. On the other hand, feature selection can eliminate important features, therefore the feature selection method must be chosen very carefully and adapted to the data and biomedical model under investigation. Importantly, although usually we are seeking for the best performing model, it might be useful to consider that some models do not allow the calculation of feature importance, thus preventing the identification of the molecules that distinguish cancer patients from non-cancer patients or distinguish two different tumor types. In this scenario, the model is not transferable in a prognostic, diagnostic or treatment context.

Unexpectedly, we have found that performances of linear and non-linear methods are similar. Our hypothesis is that the metabolites measurements used in this study are not entangled among each other as for other complex diseases, thus both types of techniques are able to capture the essential characteristics to classify the patients depending on their phenotype. Indeed, urine sample is influenced by many factors such as race, age, lifestyle (diet, smoke, physical activity) and microbiota. Although we have proven the applicability of our workflow to other omics (transcriptomics and proteomics) achieving similar results as for metabolomics, we might expect that in other cases, performances can be different.

Importantly, metabolomics has the potentiality to be a clinical tool for detecting cancer as early as possible to improve survival rates, and for distinguishing between two types of tumors to tailor treatment and improve efficacy. Therefore, the possibility of using metabolomics to find cancer biomarkers, which is an inexpensive and non-invasive method, might be preferred if the performances are good, as shown in our study.

The integration of metabolomics with other omics approaches, such as transcriptomics and proteomics would offer a global perspective not only in cancer biology but in any complex disease, revealing metabolic dysregulations and their interaction with other molecular pathways. In this scenario the datasets will be even more unbalanced than using a single omics because the number of features will increase dramatically, reaching several thousand depending on the omics, and would be hardly comparable to the number of patients. In such perspective the use of features selection and feature extraction methods will become indispensable, and we believe that the guidelines set on this study would help to benchmark these techniques on more complex datasets paving the way toward a more effective precision medicine using multi-omics data.

Funding

This work was supported by the French government, through the UCA JEDI Investments in the Future project managed by the National Research Agency (ANR) under reference number ANR-15-IDEX-01.

CRediT authorship contribution statement

JL: Data curation; Formal analysis; Methodology; Software; Visualization; Roles/Writing - original draft; ENF: Data curation; Formal analysis; Methodology; Software; Writing - review & editing; SB: Conceptualization; Supervision; Roles/Writing - original draft.

Declaration of Competing Interest

None.

Appendix A. Supplementary material

Supplementary material

.