Direct HCN synthesis via plasma-assisted conversion of methane and nitrogen

Abstract

Hydrogen cyanide (HCN) is synthesized from ammonia (NH₃) and methane (CH₄) at ~1200°C over a Pt catalyst. Ammonia synthesis entails several complex, highly emitting processes. Plasma-assisted HCN synthesis directly from CH₄ and nitrogen (N₂) could be pivotal for on-demand HCN production. Here, we evaluate the potential of dielectric barrier discharge (DBD) N₂/CH₄ plasma for decentralized catalyst-free selective HCN production. We demonstrate a single-step conversion of methane and nitrogen to HCN with a 72% yield at <300°C. HCN is favored at low CH₄ concentrations with ethane (C₂H₆) as the secondary product. We propose a first-principles microkinetic model with few electron impact reactions. The model accurately predicts primary product yields and elucidates that methyl radical (·CH₃) is a common intermediate in HCN and C₂H₆ synthesis. Compared to current industrial processes, N₂/CH₄ DBD plasma can achieve minimal CO₂ emissions.

Plasma-assisted conversion of nitrogen and methane at near ambient temperature synthesizes noncatalytic fully electrified HCN.

INTRODUCTION

Hydrogen cyanide (HCN) is a platform chemical primarily used in producing methyl methacrylate and adiponitrile, precursors to poly(methyl methacrylate) and nylon, respectively (1). HCN is commercially produced via the Andrussow (2CH₄ + 2NH₃ + 3O₂ → 2HCN + 6H₂O) or BMA (CH₄ + NH₃ → HCN + 3H₂) processes in conventionally heated reactors (1) or the more recent Invista induction-heated reactor (2). The reaction occurs over a Pt catalyst at high operating temperatures (>1000°C) to achieve high HCN selectivity (>60%) (1, 3) and requires the use of an ammonia feedstock.

Ammonia (NH₃) is central to our current economy. It is primarily used for fertilizers supporting population growth and producing chemicals, such as HCN (1, 4). About 1.1 million metric tons of HCN are produced annually (5) accounting for about 0.3% of ammonia’s market size (6). Ammonia’s production from hydrogen (H₂) and nitrogen (N₂) via the Haber-Bosch process requires multiple upstream energy-intensive steps (methane steam reforming, water gas shift, H₂ purification, and cryogenic air separation) (7). Ammonia synthesis contributes to emissions due to the H₂ compression and its equilibrium limitations leading to low conversions and separation for recycling the reactants (7).

The chemical industry’s defossilation requires the electrification of highly endothermic reactions (8). Nonthermal plasma, dielectric and Joule heating, and plasmonic photocatalysis are such emerging technologies (8, 9). Nonthermal plasma is a gas where excited species, radicals, ions, and neutral molecules at near ambient temperatures (T_g ≤ 10³ K) coexist with high-energy electrons at temperatures (T_e ≥ 10⁴ K) (10). These non-equilibrium thermal conditions enable molecule activation at low temperatures overcoming thermodynamic equilibrium limitations (10–12). There has been limited investigation into HCN synthesis by alternative electrification processes; noncatalytic thermal plasma conversion of N₂ and CH₄ (13), plasma catalytic CH₄ and NH₃ conversion at elevated temperatures (~400°C) over a Cu-supported catalyst, and noncatalytic plasma conversion of CH₄, N₂, and H₂ at reduced pressure (2.5 to 8 kPa) are exemplaries (14–16). The infrastructure for large-scale ammonia synthesis is multistep, complex, energy, and carbon intensive and is incompatible with remote smaller-scale processing. The direct electrified nonthermal conversion of methane and nitrogen to HCN, which avoids using NH₃, could be pivotal but has not been demonstrated yet.

In this work, we propose that electrification may enable alternative direct synthesis pathways compared to conventional industrial processes, bypassing consecutive oxidation and reduction cycles of nitrogen. We introduce an electrified, direct, catalyst-free, and selective HCN synthesis via dielectric barrier discharge (DBD) plasma-assisted conversion of CH₄ and N₂ at low temperatures (<300°C). We develop a reaction network with key active plasma species and the associated microkinetic model (MKM) to replicate the experimental trends. We uncover the prominent chemical pathways and establish that ·CH₃, ·CH₂, ·H₂CN, ·N, and ·NH are crucial intermediates for HCN synthesis, while ·CH₃ is a common precursor to C₂H₆, a competitive product. Last, we compare the HCN energy consumption, E_HCN, and CO₂ equivalent emissions to current industrial processes and showcase the potential for minimal CO₂ equivalent emissions.

RESULTS

Selective plasma-assisted HCN synthesis

We use a coaxial DBD reactor consisting of a brass hollow tube high-voltage (HV) electrode secured on the outer surface of the quartz tubular reactor and a stainless-steel rod ground electrode inside the quartz tube. We monitor the voltage (V) and current (I) waveforms of the AC power supply and the temperature at the reactor outlet. CH₄ flows in the reactor in excess N₂ without an inert gas, such as He or Ar, commonly used in plasmas (see the “Reactor setup and analysis” and the “Thermometry” sections and Supplementary Discussions 1 and 2).

The conversion of an N₂/CH₄ gas mixture requires the dissociation of C─H and N≡N bonds. In plasmas, bond dissociation occurs through collisions of neutral molecules and electrons of kinetic energies higher than a threshold. The energies of C─H and N≡N dissociation by direct electron impact (e-impact) are (17, 18)

$${\text{CH}}_4+\mathrm{e}\stackrel{868 \text{kJ}/\text{mol} }{\to }{\text{·CH}}_3+\text{·H}+\mathrm{e}$$ (1)

$${\mathrm{N}}_2+\mathrm{e}\stackrel{940 \text{kJ}/\text{mol} }{\to }2\text{N·}+ \mathrm{e}$$ (2)

For a feed CH₄ fraction, C_CH4,0, in the range of 0.1 to 10% and a maximum total flow rate of 200 sccm, the required instantaneous power for full methane conversion ranges from 0.2 to 18.6 W (eq. S1). A dissipating power of ~30 W (estimated average of our system based on V-I waveforms (fig. S2B and eq. S2) should be adequate to achieve full conversion.

Fig. 1 (A and B) shows the CH₄ conversion (eq. S3), product selectivity (eqs. S4, S6, and S10), and HCN energy consumption, E_HCN (eq. S8) versus the CH₄ feed fraction. Excitingly, the most prominent carbon-based products are HCN and ethane (C₂H₆), with HCN dominating for low methane concentrations. C₂H₆ selectivity increases with methane feed fraction due to CH₄ radical (·CH_x) oligomerization. Aromatics and coke formation is observed for all experimental conditions, with an average selectivity of 10%. H₂ is another major product with similar selectivity trends to HCN, i.e., highest selectivity at low methane feed fractions. NH₃ formation was not observed (figs. S4 and S5). The highest HCN yield (eq. S7), Y_HCN, is 72% with 80% selectivity and the lowest E_HCN is 44 kJ/mmol HCN produced. The temperature was 282°C (fig. S6A), lower than commercial processes by 700°C. This suggests that a N₂/CH₄ DBD plasma can be a green alternative for selective, direct HCN synthesis from methane and nitrogen, especially of dilute methane streams, bypassing the need for ammonia.

Fig. 1. Performance of CH₄/N₂ plasma.

(A) Effect of CH₄ feed fraction on the carbon-based selectivity of HCN (dark teal), C₂H₆ (teal), other C-products [C₂H₂, C₂H₄, C₃H₆, C₃H₈, acetonitrile (CH₃CN), C₄ hydrocarbons, propionitrile (CH₃CH₂CN), and acrylonitrile (CH₂CHCN)] (light teal) and aromatics/coke (lighter teal) (eq. S4), CH₄ conversion (gray curve) and energy consumption, E_HCN (black curve). Triplicates were conducted for 0.1, 0.5, 2, and 7% C_CH4,0; the displayed selectivity and conversion values are the average. The SD for the remaining conditions was set equal to the highest value. Experimental conditions: 0.47-s residence time, 28.1-W average discharge power, 22-kHz AC voltage frequency. (B) Effect of CH₄ feed fraction on the hydrogen-based selectivity of HCN (dark red), C₂H₆ (red), other C-products [C₂H₂, C₂H₄, C₃H₆, C₃H₈, acetonitrile (CH₃CN), C₄ hydrocarbons, propionitrile (CH₃CH₂CN), and acrylonitrile (CH₂CHCN)] (combined in light red) and hydrogen (light pink) (eq. S10). (C) Comparison of thermodynamic yields of HCN (dark purple) and C₂H₆ (light purple) at 282°C and 1 atm with increasing CH₄ feed fraction as predicted by an equilibrium model, with experimental yields of HCN (dark teal) and C₂H₆ (teal) produced by the N₂/CH₄ DBD plasma at the same conditions. (D) Effect of plasma residence time on carbon-based product distribution, CH₄ conversion, and E_HCN. Triplicates were conducted for all conditions; the displayed selectivity and conversion values are the average. Experimental conditions: 1% feed CH₄ fraction, 28.1-W average discharge power, 22-kHz AC voltage frequency.

Thermodynamic equilibrium limitations are typically the largest barrier to obtaining high yields and conversions in gas phase reactions. Figure 1C displays HCN and ethane yields versus CH₄ feed fraction at our operating conditions, 282°C and 1 atm, as predicted by a thermodynamic equilibrium model (see the “Python multiscale thermochemistry toolbox” section). Experimental yields by the N₂/CH₄ DBD plasma are also included for comparison. In conventionally heated systems at these conditions, ethane is the primary product with minimal HCN yields. Nonthermal plasma activation of nitrogen and methane leads to up to 60% HCN yield. Because of the effective activation of N₂ by high-energy electrons, HCN is selectively produced over C₂H₆ for methane fractions up to 7%, while thermodynamics dictate that in a conventional reactor of the same gas temperature, the maximum CH₄ feed fraction for selective HCN production is 1%.

The CH₄ concentration in the gas feed affects the plasma properties and reacting species. In our operating range, methane and, thus, ·CH_x are the limiting reagents. The primary characteristic of the plasma discharge is the electron energy distribution function (EEDF), which controls the rate of e-impact reactions responsible for the ensuing chemical interactions. EEDF depends on the gas composition, reduced electric field (E/N), discharge power (P), AC field frequency, and gas temperature (T_g). P and T_g are relatively constant at 28.1 W and 282°C, respectively (Supplementary Discussion 3 and fig. S6, A and B). Similarly, E/N remains constant across experimental conditions (Supplementary Discussion 4 and fig. S6C). With the AC field frequency also fixed, the only variable notably affecting EEDF is methane concentration. Hence, the impact of methane concentration on HCN selectivity is the combined effect of the kinetic rates of e-impact, radical-radical, molecule-radical, and molecular reactions.

The effect of plasma residence time on HCN selectivity, S_HCN, and energy consumption is demonstrated in Fig. 1D. Conversion, selectivity, and E_HCN are proportional to residence time. Given P, T_g, and E/N were constant with varying residence time (figs. S6B and S7, A and B), HCN selectivity is primarily controlled by kinetics. The dependence of HCN selectivity on residence time suggests that HCN decomposition reactions are much slower than formation reactions. Examining the individual effect of discharge power, we found that P is linearly correlated with methane conversion and HCN selectivity and has no substantial effect on product distribution (Supplementary Discussion 5 and fig. S8).

The stability of this process was determined through 10-hour continuous operation experiments for the investigated concentrations. Figure S7C depicts HCN yield with time on stream for 0.3% feed CH₄ concentration and 0.47-s residence time. HCN yield is not adversely affected by time on stream, establishing that plasma-assisted conversion of CH₄ and N₂ is a stable process that can be operated continuously. One possibility for the slight increase in HCN yield over time could be the partial rehydrogenation of coke depositions on the reactor walls and inner electrodes and reaction with excited N₂ species.

Chemistry insights

Plasma-assisted CH₄ conversion chemistry has received considerable attention, with emphasis on excited species (17, 19–21). Zero-dimensional (0D) plasma kinetic models typically consider many vibrationally and rotationally excited and metastable species, radicals, and charged and neutral molecules (22–25). For our DBD plasma, e-impact dissociation is the primary excitation channel (23). Thus, we consider 35 neutral radicals (critical intermediates) in state-of-the-art CH₄/N₂ pyrolysis mechanisms (26, 27). We assume steady-state E/N, n_e, and T_g conditions to evaluate the average rates of 62 e-impact reactions and integrate those into the user-friendly compiled software CHEMKIN III (28) to model the kinetics of 251 chemical reactions (see the “MKM setup” section). By doing this, we reduce e-impact reactions by up to 80% compared to typical DBD plasma modeling.

Our first goal was to assess the model’s capability to replicate experimental trends and ascertain suitable E/N, T_g, and electron density (n_e) ranges. Parametric studies by varying E/N, T_g, and n_e (detailed results in Supplementary Discussion 6 and figs. S9 to S11) showed that E/N = 300 Td, T_g = 550 K, and n_e = 10¹¹ cm⁻³ best capture our experimental data. The reduced electric field, ~300 Td, was in the range of the average experimental estimates of 189 and 435 Td (figs. S6C and S12A). The other values correspond to experimental conditions estimated by thermometry, relative irradiance, and other methods (Supplementary Discussion 4).

Figure 2 (A and B) displays the experimental and predicted product yield and CH₄ conversion versus the CH₄ feed fraction. The model captures the experimental yields of HCN and C₂H₆ reasonably, within 30 and 50% average deviation, respectively. A parity plot of HCN yield is shown in fig. S13. The model consistently slightly overpredicts HCN yield over the investigated concentration range, inferring that the validity range of the kinetic model is in the range 0.1 to 100% methane feed fraction. Literature reports similar average deviations of 25 to 37% in product selectivities for a CH₄ DBD reactor (25). This demonstrates that the model successfully predicts experimental major products in DBD plasmas. The conversion and other small carbon product yield trends are not fully captured by the model, which is reasonable considering the complex reaction network.

Fig. 2. Comparison of experimental and MKM results.

(A and B) Effect of CH₄ feed fraction on HCN (dark teal), C₂H₆ (teal), and other product yields (light teal) and CH₄ conversion (gray curve) as observed experimentally (left) and as predicted by the MKM (right). Other products in the MKM model include ethylene, acetylene, acetonitrile, propane, and propylene. Experimental conditions: 0.47-s residence time, 28.1-W average discharge power, 22-kHz AC voltage frequency. MKM conditions: 300 Td E/N, 10¹¹ cm⁻³ n_e, 550 K gas temperature, 1.26-ms residence time. (C to E) Evolution of CH₄ conversion (left), HCN yield (middle), and C₂H₆ yield (right) with residence time for different CH₄ feed fractions as predicted by the MKM. The circular data points at 3 ms correspond to the experimental measurements. The darkest to lightest shades represent the lowest to highest CH₄ feed fraction, respectively. MKM conditions: 300 Td E/N, 10¹¹ cm⁻³ n_e, 550 K gas temperature.

The yields in Fig. 2B correspond to a computed residence time of ~1.3 ms. We estimate a residence time of 0.47 s (eq. S21) based on the reactor volume and gas flow rate. This comparison of experimental and computational residence times indicates that the actual plasma exposure is 100× shorter than our simple estimate. This suggests that the dispersed plasma streamers occupy only a small fraction of the reactor volume. The ratio of the plasma streamers to the empty reactor is ~0.3%. The corresponding number of microdischarges per discharge cycle is 67 (Supplementary Discussion 9).

Having predicted the effect of CH₄ concentration on HCN yield, we examined the effect of residence time. The evolution of CH₄ conversion, HCN, and C₂H₆ yield with residence time up to 3 ms is shown in Fig. 2 (C to E). The trends change dynamically with methane feed fraction in the first 3 ms. Ethane yield is maximized in the first milliseconds and then rapidly declines, indicating prevalent contributions of consumption reactions. The highest HCN yield for longer residence times is achieved by the lowest feed CH₄ fraction. Like experiments (Fig. 1D), the MKM predicts an increase of HCN yield with increasing residence time before seemingly settling around a lower value (fig. S12B). This steady state of HCN yield is also featured over the entire methane feed fraction range investigated (fig. S12C), suggesting an upper limit for each C_CH4,0 condition. Notably, for C_CH4,0 ≥ 2%, the upper limit for HCN yield conglomerates around 48% under these conditions. The increasing conversion with increasing residence time observed experimentally is also corroborated by the model at intermediate conversions (Fig. 2C).

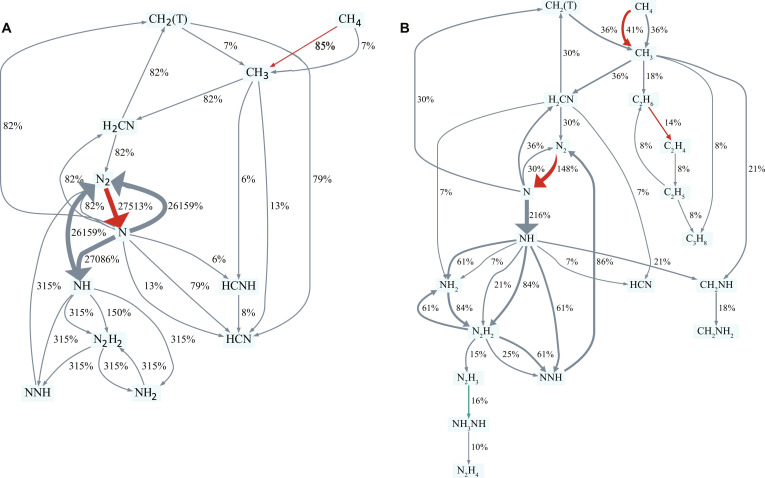
Upon establishing the model’s reasonableness, we elucidate the reaction pathways. Reaction path analysis (RPA) is shown in Fig. 3 (A and B) (more conditions are included in fig. S14). For lower methane concentrations, the most important e-impact dissociation reactions are those of N₂ to ·N and of CH₄ to methyl radical (·CH₃). The remaining notable reactions correspond to thermal reactions, while HCN is the prominent C-derived product (Fig. 3A and fig. S14, A to C). For higher methane concentrations, the thermal contribution to methane decomposition via the disproportionation reaction CH₄ + CH₂ → 2CH₃ increases (Fig. 3B and fig. S14, D and E), and ethane is another major product. The methyl radical is a common intermediate to HCN and C₂H₆, with C₂H₆ production increasing with increasing $C_{{\text{CH}}_4,0}$ due to the bimolecular nature of this reaction (Fig. 3 and fig. S15).

Fig. 3. RPA for plasma assisted HCN synthesis from CH₄/N₂.

H₂ fluxes are implicitly included. CH₂(T) is the triplet CH₂ radical. Red arrows correspond to e-impact reactions, gray arrows to non-equilibrated thermal reactions, and teal arrows to equilibrated thermal reactions. The percentage fluxes are normalized based on CH₄ inflow to the CSTR node (e.g., 27,000% flux of N₂ to ·N indicates that this conversion occurs 27,000 faster than the inflow of methane) and are represented by the thickness of the arrows. Reaction conditions: 300 Td E/N, 10¹¹ cm⁻³ n_e, 550 K gas temperature, 1.26-ms residence time. RPA for 0.1% (A) and 7% (B) CH₄ feed fraction (rates above 10⁻⁷ and $2.3\times {10}^{-5}\frac{\text{mol}}{\mathrm{s}}$ , respectively, are displayed for clarity; the CH₄ inflow rates at 1.26 ms are 2 × 10⁻⁶ and $3.4\times {10}^{-4}\frac{\text{mol}}{\mathrm{s}}$ , respectively).

Reaction pathways contributing to HCN generation for various methane feed fractions are displayed in Fig. 4. For low methane feed fractions (0.1% in Fig. 4), HCN production begins with the e-impact formations of ·CH₃ from CH₄ and ·N from N₂. The methyl radical subsequently reacts with ·N toward methylene amidogen radical (·H₂CN), which then recombines with ·N to form methylene radical (·CH₂) and N₂. ·CH₂ further reacts with ·N to produce HCN, constituting the primary pathway for HCN synthesis. Reactions of ·CH₃ with ·N and imino methyl radical (HCNH·) decomposition also contribute to HCN formation. For higher methane feed fractions (2 and 7% in Fig. 4), ·CH₃ forms both via e-impact dissociation and thermal decomposition of CH₄ (via collisions with ·CH₂). ·H₂CN mainly contributes to HCN production via its reaction with ·NH, which is formed from ·N and ·H. The reaction of ·CH₃ with ·N becomes a primary pathway toward HCN generation, while the reaction of ·CH₂ with ·N is reduced to a lesser flux.

Fig. 4. Crucial intermediates in CH₄/N₂ plasma–assisted HCN synthesis.

Effect of CH₄ feed fraction (0.1, 2, and 7%) on reaction paths. The percentages on the arrows correspond to the normalized contribution of each reaction based on CH₄ inflow to the production of HCN. Conditions: 300 Td E/N, 10¹¹ cm⁻³ n_e, 550 K gas temperature, 1.26-ms residence time.

Ethane production at low methane concentrations is limited by the recombination of two ·C₂H₅ (2C₂H₅ → C₂H₆ + C₂H₄) (fig. S15). For higher concentrations, the rate of formation of C₂H₆ substantially increases through the third-body recombination reaction of methyl radical (2CH₃ + M → C₂H₆ + M). Ethane’s primary consumption pathways include decomposition reactions to C₂H_x (x = 2 to 5) (fig. S15 and Fig. 3B). Figure 4 also demonstrates how increasing ·CH₃ dimerization reduces the total flux to HCN.

To increase HCN throughput, i.e., increase HCN selectivity at higher methane feed concentrations, we investigate the effect of operating conditions on product distribution. HCN yield can be improved by altering plasma operating conditions (increasing reduced electric field and electron density), increasing reactor temperature (fig. S11), or decreasing operating pressure (fig. S16). Figure S16B demonstrates that for 50% methane feed concentration, HCN yield can be increased three times by operating at 0.001 atm instead of 1 atm.

Comparison with existing processes

Direct comparison with established industrial (BMA, Invista) processes and plasma processes with 10 to 40× richer CH₄ feedstock is expectedly not favorable. The energy demand per millimole of HCN is 10 to 40× higher than other reported values (Fig. 5, Supplementary Discussion 10, and eq. S28), because of the low plasma efficiency (11) and dilute CH₄ stream. Optimization of plasma reactors and power generators is still in its early stages, due to the recent emergence of nonthermal plasmas for chemical transformations. Separation and purification energy costs are not considered in Fig. 5 for any process. A comparison between HCN recovery in conventional processes and our N₂/CH₄ plasma is included in Supplementary Discussion 11, demonstrating reduced separation costs by at least 97% for the N₂/CH₄ plasma.

Fig. 5. Performance comparison of this work and other plasma and industrial processes.

Energy consumption, E_HCN (kJ/mmol HCN) and CO₂ equivalent emissions (kg CO₂/kg HCN) of this work, reported industrial (1, 2) and plasma processes (14). The solid bar graph portion represents E_HCN and CO₂ equivalent emissions based on energy efficiency, while the dashed portion is based on input power. The horizontal blue line corresponds to the CO₂ equivalent emissions incurred by an NH₃ feedstock as evaluated by eq. S30.

The energy efficiency of plasma and industrial processes is an integral part of this comparison. Reported plasma processes demonstrate efficiencies below 10% (11, 14, 29), while the BMA process has been rigorously optimized over 50 years to reduce its energy consumption by 70% (30). The Invista process, a more recent induction heated process, also has a high efficiency of 89% (2). The energy efficiency of this work, associated with the chemical reaction, gas heating, and plasma dissociation (eq. S29), is estimated at ~4%. Heat losses in microchemical systems are considerable, and thus, energy efficiency improves markedly with scale up and optimization, something outside the scope of this work. Energy losses related to targeted species excitation and conservation in the plasma region are also substantial and can be improved by optimizing the reactor geometry. Considering the power efficiently dissipated in each reactor, the two plasma processes exhibit the lowest thermodynamic energy requirements. Hence, a more efficient generator and reactor design could bridge the energy gap with industrial processes (11).

Other works in similar DBD systems demonstrate that energy efficiency of plasma processes increases by increasing reactor throughput (16) and using multiple reactors in parallel (31, 32). Industrial ozone production also uses multiple parallel DBD reactors powered by the same generator (11). Scaling up and scaling out the current N₂/CH₄ plasma system to accommodate industrial slip gas volumes will further improve energy efficiency.

With the decarbonization of the chemical industry, CO₂ equivalent emissions are a very important metric for new processes. Electrified reactors can be powered by renewable electricity due to their fast initiation/termination times and reaction rates (33), while conventional reactors are limited to continuous energy sources. Assuming a wind onshore energy source for the Invista and plasma processes and the US electricity grid for the BMA, CO₂ equivalent emissions of this work based on input power are among those of commercial processes (Eq. 3 and Fig. 5).

However, all reported processes use NH₃, which contributes to their CO₂ equivalent emissions by ~1.5 kg CO₂/kg HCN (eq. S30), blue line in Fig. 5). Irrespective of reactor efficiencies, these processes are going to be limited by CO₂ equivalent emissions from NH₃. Our N₂/CH₄ plasma process, limited only by reactor and generator inefficiencies, could reach 0.2 kg CO₂/kg HCN, a much lower threshold than 1.5. Considering that the only impediment to reaching that limit is optimization, N₂/CH₄ plasma paves the way to fully electrified HCN synthesis with minimal CO₂ equivalent emissions.

$$\begin{array}{c}{\text{CO}}_2 \text{eq}.\text{emissions} \left(\frac{\text{kg} {\text{CO}}_2}{\text{kg} \text{HCN}}\right)=\frac{E_{\text{HCN},\text{process}}}{M_{\text{HCN}}}\times 1000\\ \times F_{{\text{CO}}_2,\mathrm{s}}+{\text{CO}}_{2,{\text{NH}}_3}\end{array}$$ (3)

Here, E_HCN,process is the energy consumption of the process (2, 14, 30), $M_{\text{HCN}}=27.03\frac{\mathrm{g}}{\text{mol}}$ is the molecular weight of HCN (34), F_CO2,s is the CO₂ equivalent emission factor of the energy source equal to $0.86\frac{\text{lbs} {\text{CO}}_2}{\text{kWh}}=1.1\times {10}^{-4}\frac{\text{kg} {\text{CO}}_2}{\text{kJ}}$ for the US electricity grid (35) (BMA process) and to $11\frac{\mathrm{g} {\text{CO}}_2}{\text{kWh}}=3.1\times {10}^{-6}\frac{\text{kg} {\text{CO}}_2}{\text{kJ}}$ for a wind onshore source (36) (plasma and Invista processes), and CO_2,NH3 is the contribution of NH₃ feedstock to CO₂ equivalent emissions. Compared to the NH₃/CH₄ prior plasma work (30% CH₄ conversion and ~24% HCN yield, using 5.2 kJ/mmol HCN produced), the direct N₂/CH₄ plasma of this work reaches more than double HCN yield.

DISCUSSION

HCN storage and handling are challenging due to its high volatility, toxicity, and instability in the presence of impurities (1, 37). Developing distributed and small-scale HCN synthesis processing could facilitate on-demand production while minimizing extensive storage requirements. Current HCN production processes are limited by the use of ammonia which requires multiple carbon intensive synthesis steps and is incompatible with small-scale processing (1, 7). Nonthermal plasma has been proposed for decentralized chemical processing powered by renewable electricity due to its intermittent process capability (38).

Here, we have developed an electrified, catalyst-free, N₂/CH₄ plasma process capable of selective HCN synthesis at much lower temperatures than current industrial processes. We achieve a maximum HCN yield of 72% with ethane as a secondary product, notably outperforming conventionally heated systems at the same conditions. We demonstrate that a simplified automated plasma model, i.e., assuming constant plasma conductivity and neutral radicals as the primary reactive species, successfully replicates the yield trends of the prominent products. Methyl radical is a crucial intermediate from CH₄ related to HCN generation and, at higher methane concentrations, to C₂H₆ synthesis. Thermal contributions to methane decomposition increase at higher methane concentrations. Comparing this process to current industrial ones, we show that plasma systems have the lowest thermodynamic energy requirements. We demonstrated that our process has a 10-fold reduction in CO₂ equivalent emissions compared to using NH₃.

In summary, this work establishes N₂/CH₄ plasma as a promising route toward selective HCN synthesis with minimal CO₂ equivalent emissions. The process is best suited to convert methane from leaks and slip from combustion processes that contain a small fraction of CH₄ and a large fraction of N₂ from the oxidant (air).

MATERIALS AND METHODS

Reactor setup and analysis

An overview of the experimental setup and a plasma reactor closeup are displayed in figs. S1 and S2A (top left and bottom right) correspondingly. The DBD reactor used in this study consisted of a brass hollow tube HV electrode [12.7 mm outer diameter (OD), 9.4 mm inner diameter (ID), McMaster-Carr] secured on the outer surface of the quartz tubular reactor (9 mm OD, 7 mm ID, 41-cm length, QSI Quartz Scientific) and a stainless-steel rod as the grounding electrode inside the quartz tube (3 mm in diameter, 69-cm length, McMaster-Carr) (Fig. 1A). The reactor length, i.e., the HV electrode length, was 5 cm. The plasma was generated by an AC power supply (PVM500) at a frequency of 22 kHz connected to the HV and grounding electrodes. A voltage probe (Tektronix P6015A) was connected to the power supply, the HV electrode, and the ground. A current probe (Pearson 2100) was connected to the ground electrode. Both probes were also connected to an oscilloscope (Tektronix MDO34). High purity N₂ (99.999%, Keen Compressed Gas) and a mixture of CH₄/N₂ (14% CH₄, Matheson gas) were premixed and flowed into the reactor at ambient temperature and pressure. Feed gas total flow rates ranged from 50 to 200 sccm and were regulated with mass flow controllers (Brooks GF40). The residence time was controlled by adjusting the gas total flow rate while the reactor volume remained constant at ~1.57 cm³ according to eq. S21. For the inert gas studies, pure argon (Ar) gas (99.999%, Keen Compressed Gas) or helium (He) gas (99.999%, Keen Compressed Gas) was premixed with CH₄ and N₂. Gas products were analyzed with inline gas chromatography (fig. S4). The volume expansion is negligible for our experimental conditions (eqs. S11 and S20 and table S1). Select experiments of each set were performed in triplicate, with the average value shown in the figures. Selectivity and yields were evaluated on a CH₄ basis. Optical emission spectroscopy measurements were acquired during experiments by an optical fiber (400-μm slit width, Avantes) adjusted to a collimating lens and connected to an AvaSpec-ULS4096CL-EVO-UA-10 spectrometer (Supplementary Discussion 12 and fig. S18).

Discharge characteristics

Figure S2B shows the electrical characteristics of the CH₄/N₂ plasma discharge. The current waveform reveals successive nanosecond current pulses occurring at each voltage half cycle, which indicates a streamer (filamentary) discharge mode. The short lifetime of the plasma streamers induces highly non-equilibrium conditions at atmospheric pressure, while the change in polarity disperses the filamentary discharges over the inter electrode volume (17, 39).

Thermometry

The gas temperature was measured by an optical fiber (FOT-L-BA-C1-F1-M2-R1-ST, FISO) suspended between the quartz tube and the inner electrode and 1 cm above the reactor (fig. S1B). The location of the fiber optic was the closest possible to the reactor without affecting the plasma field. The time required for the gas to reach the optical fiber from the reactor outlet was 0.09 to 0.38 s, depending on the flow rate. Hence, the average reaction temperature can be approximated by the gas temperature read by the fiber optic and the signal conditioner (UMI, FISO). The program used to record the temperature signal was FISOCommander 2, and the recording frequency was 1.67 s⁻¹. Figure S3A depicts a typical gas temperature profile with continuous plasma operation time. The gas temperature plateaus for t ≥ 10 min at an average of 282°C, corroborating the assumption of steady-state operation of the reactor. The random distribution of the residual gas temperature values around the average of 282°C further validates the steady-state hypothesis (fig. S3B).

Python multiscale thermochemistry toolbox

The equilibrium concentration of methane, HCN, and ethane at 282°C and 1 atm was evaluated by the equilibrium model of Python multiscale thermochemistry toolbox (pMuTT) developed by Lym et al. (40) (code available at https://github.com/VlachosGroup/pMuTT/blob/master/pmutt/equilibrium/_equilibrium.py). The network of species considered included N₂, CH₄, HCN, C₂H₆, C₂H₄, C₂H₂, C₃H₈, C, H₂, NH₃, cyanogen (CN), diazene (N₂H₂), hydrazine (N₂H₄), acetonitrile (CH₃CN), and methylamine (CH₃NH₂). Thermodynamic data for these species were acquired from the RMG thermodynamic libraries (https://rmg.mit.edu/database/thermo/libraries/primaryNS, https://rmg.mit.edu/database/thermo/libraries/DFT_QCI_thermo, https://rmg.mit.edu/database/thermo/libraries/primaryThermoLibrary, https://rmg.mit.edu/database/thermo/libraries/thermo_DFT_CCSDTF12_BAC).

MKM setup

To elucidate the most prominent chemical reaction pathways in the CH₄/N₂ DBD plasma, we developed a 0D chemical kinetics model. Until now, established 0D plasma kinetic models used a Fortran module (22), such as ZDPlasKin (25, 41), which calls a Boltzmann equation solver (BOLSIG+) (42) at each time integration step to evaluate the electron density, E/N, gas temperature, and reaction rates. While this approach allows transient E/N and n_e calculations, it is computationally intensive.

Here, we used a user-friendly compiled chemical kinetic software CHEMKIN III. We assumed steady-state E/N, n_e, and T_g conditions and used BOLSIG+ to evaluate the average rates of e-impact reactions and input them into CHEMKIN, eliminating the integrated BOLSIG+ loop from previous modules (Supplementary Discussion 13). A graphical representation of this approach is shown in fig. S19.

Since E/N, n_e, and T_g were estimated experimentally but not with high accuracy (Supplementary Discussion 4), they were treated as variables examined over a range of values with the experimental measurements as focal points. E/N, n_e, and T_g were varied over a range of 150 to 500 Td, 10⁹ to 10¹³ cm⁻³, and 450 to 700 K, respectively, to ascertain the conditions most representative of the experimental results. Since the plasma/gas reactor conditions were considered homogeneous, the reaction rates of e-impact reactions were regarded as constant.

In DBDs with E/N ≤ 500 Td, e-impact dissociation reactions are more prominent than ionization reactions; hence, ionization reactions were not included in the MKM (12, 43). For further simplicity, only ground electronic and vibrational states of neutral radicals were considered, essentially assuming that excited CH₄ does not contribute to CH₄ dissociation (17) and that, in a high-energy N₂-rich environment, direct N₂ dissociation produces N atoms sufficiently fast to propagate chemical interactions. However, to accurately estimate the rates of dissociation of e-impact reactions with BOLSIG+ version 12/2019 (42, 44), excitation, momentum transfer, attachment, and ionization reactions were accounted for. The cross-sectional data for CH₄ attachment, elastic momentum transfer, and vibrational excitation were obtained from the Morgan database (45, 46), and those for dissociative excitation and ionization of C_xH_y (x = 1 to 3) species were evaluated on the basis of the data and analytic forms reported by Janev et al. (47, 48) The cross-sectional data for N₂ momentum transfer, attachment, vibrational, rotational and electronic excitation, and ionization were acquired from the Phelps database (49) and those for N₂ and H₂ dissociation from the Itikawa database (18, 46, 50). The cross-sectional data for H₂ momentum transfer, vibrational, rotational, and electronic excitation and ionization were acquired from the Phelps database (46, 49).

The e-impact reactions included in the MKM encompassed all neutral dissociation reactions of CH_x radicals (x = 1 to 4) and the most prominent ones of C₂H_y (y = 0 to 6) and C₃H_z (z = 5 to 8), based on their branching ratios (48), amounting to a total of 62 reactions. Interactions of neutrals and radicals with other excited species, such as electronically excited CH₄ and N₂, as well e-impact dissociation reactions of HCN and other nitriles, could be considered in future work for a more accurate representation of the complete DBD plasma reaction network. A state-of-the-art pyrolysis reaction mechanism was primarily compiled from the “primaryNitrogenlibrary” RMG kinetic library (https://rmg.mit.edu/database/kinetics/libraries/primaryNitrogenLibrary) (26, 51) and the nitrogen combustion network as delineated by Glarborg et al. (27). Select reactions from the “Nitrogen_Dean_and_Bozelli” RMG kinetic library (https://rmg.mit.edu/database/kinetics/libraries/Nitrogen_Dean_and_Bozzelli) (26, 51) and the GRI-Mech version 3.0 released on 30 July 1999 (http://combustion.berkeley.edu/gri-mech/overview.html) were also included. Since the gas temperature was measured ~550 K, only reactions active below 1000 K at near atmospheric pressure were considered, constituting a network of 189 neutral reactions. The total number of species involved was 67. Thermodynamic data for species considered in the reaction mechanism were acquired from the GRI-Mech version 3.0 thermodynamics released on 30 July 1999 and RMG thermodynamic libraries (https://rmg.mit.edu/database/thermo/libraries/primaryNS, https://rmg.mit.edu/database/thermo/libraries/DFT_QCI_thermo, https://rmg.mit.edu/database/thermo/libraries/primaryThermoLibrary, https://rmg.mit.edu/database/thermo/libraries/thermo_DFT_CCSDTF12_BAC). The thermodynamic and gas reaction input scripts used in the MKM for this work can be found in the Reactions and Thermdat files, respectively.

The software used for the MKM was CHEMKIN-III (28, 52). E-impact reactions were imported into CHEMKIN as monomolecular reactions after multiplying the reaction rate constant as evaluated with BOLSIG+ with the electron density (25, 43). In calculating reaction rate constants using the Boltzmann equation solver BOLSIG+, we assumed a steady state, uniform electric field, a negligible effect of superelastic collisions, temporal growth of electron production, and equal energy sharing after ionization (42). For E/N, n_e, and feed CH₄ concentration parametric studies, the reaction rate constants of e-impact reactions were modified accordingly. The reactor was modeled as an isothermal plug flow reactor (PFR) [series of 100 Continuous stirred-tank reactors (CSTRs)], and the reaction conditions were 1-atm pressure and 200-sccm gas flow rate.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S19

Table S1

Data S1 and S2

References