Numerical simulation and study on heat and mass transfer in a hybrid ultrasound/convective dryer

Abstract

Susceptibility of airborne ultrasonic power to augment heat and mass transfer during hot air dehydration of peppermint leaves was investigated in the present study. To predict the moisture removal curves, a unique non-equilibrium mathematical model was developed. For the samples dried at temperatures of 40‒70 °C and the power intensities of 0‒104 kW m⁻³, the diffusion of moisture inside the leaves and coefficients for of mass and heat transfer varied from 0.601 × 10^–4 to 5.937 × 10^–4 s⁻¹, 4.693 × 10^–4 to 7.975 × 10^–4 m s⁻¹ and 49.2 to 78.1 W m⁻² K⁻¹, respectively. In general, at the process temperatures up to 60 °C, all the studied transfer parameters were augmented in the presence of ultrasonic power.

Introduction

Amongst different drying systems utilized industrially, fixed deep-bed dryers (FDBD) are known as the most important dryers widely practiced in agricultural and other industries. In these systems, the working fluid (air) enters into the drying bed and moves from bottom to its top, and heat and mass transfer phenomena occur simultaneously between the drying air and subjected product throughout the bed (Naghavi et al. 2010). Because of high amounts of vaporization heat, relatively weak thermal conduction and wasting a main portion of the supplied thermal energy, like as other convective drying systems, FDBDs pose serious shortcomings mainly including low moisture removal rates and energy efficiencies and dried product with deteriorated quality. In addition, the dryers face with moisture gradient along the bed, as a unique problem. Based on the findings reported in the literature, it is efficient to use higher drying temperatures to reduce the process time and energy requirement at the same time. However, due to quality loss, increasing the temperature is restricted (Gamboa-Santos et al. 2014).

Recently, combination of technologies with non-thermal quiddity with traditional hot air dryers has become increasingly of interest to overcome their disadvantages. In case of assisted ultrasound utilization, practicing combined air-born ultrasonic power drying systems has been studied and reported as an effective approach to reduce the process duration as well as achieve better quality for some products such as potato (Xi et al. 2020) and pear (Liu et al. 2019).

As the most cost-effective as well as time-saving technique, mathematical modeling is widely used to simulate different processes of bioproducts mainly those related to thermodynamic and fluid dynamic (Jayapragasam et al. 2021). In a convective batch dryer, due to temperature and moisture gradients, heat and mass transfer take place simultaneously between the drying air and material over the process time and along the bed. In case of drying, appropriately constructed mathematical models and accurate simulation could be effectively used to predict moisture removal kinetics, develop new dryers and improve the exited systems (Naghavi et al. 2010).

To date and best knowledge of the authors, the influence of ultrasonic power on the heat and mass transfer parameters of the products in FDBD has not been addressed. So, in the present study, deep-beds of peppermint leaves were dried in a combined ultrasonic power/hot air dryer and simulated using a non-equilibrium mathematical model. Also, the transfer parameters were determined and analyzed.

Development of mathematical model for fixed bed

In this work, drying of fresh peppermint leaves were conducted in a combined ultrasonic power/hot air drying system. To better understand the moisture elimination from the leaves, the bed was separated into thin layers consisting two phases: (1) solid phase including cold and wet leaves and (2) the gas phase including hot and dry air. As the drying process begins, air enters the first layer of the leaves bed where heat transfer takes place from the air to the drying object due to temperature gradient. Air enthalpy is partially transferred and heats the leaves and consequently evaporates moisture from the leaves. On the other hand, moisture content of the airflow is increased. The air flow, with less temperature and more humidity than the entering air, exits the other side of the bed layer and enters the next layer. This mechanism is repeated layer by layer to the end of the bed.

The main purpose of mathematical modeling is to predict instantaneous moisture variation of the leaves. Therefore, the equation describing the variations along the drying bed and over the time will be the key equation of the model. On the other hand, coefficients for heat and mass transfer in the air as well as the moisture diffusivity inside the leaves are governed by temperature and humidity of the air and the product temperature. So, distribution of temperature and moisture along the bed are required. The enthalpy and mass balances are used to obtain the temperature and the moisture distributions, respectively. Two separate control volumes are required to write the equilibrium mass and enthalpy equations. One of the volumes is related to the wet leaves (thin-layer containing a moist leaf horizontally placed) and the other includes the air in the layer.

Writing the equilibrium equations for mass and enthalpy balances in the leaf and the air control volumes‒placed at an arbitrary location in the drying bed‒, a set of equations containing four partial differential equations (PDE) is obtained. Therefore, the mathematical model for a FDBD includes the following equations:

• Changes in residual moisture of leaf,

• Variations in the air humidity,

• Changes in leaf temperature and

• Air temperature variations.

Distributions of leaf moisture and temperature are obtained by writing the mass and enthalpy balances on a part of a single leaf, respectively. These distributions are considered to be symmetric in each and therefore, the solution domain of the obtained equations will be half thickness of the leaf. The distributions of air humidity and temperature are obtained by writing the mass and enthalpy balances on the layer of the drying bed.

Since the model variables change over the process time, the mathematical model is unsteady. The model was developed considering the following simplifying assumptions:

• The drying bed is primarily homogeneous and isotropic,

• Each leaf behaves similar to an infinite slab,

• Shrinkage of leaves are negligible during the dehydration process,

• Effective moisture diffusion and conductive heat transfer coefficient in the leaves depend on temperature and

• Due to the uniform distribution of air in the bed, heat and mass transfers occur just in one dimension.

Consequently, considering the general equilibrium equation (Eq. 1), the mass and enthalpy balances were drawn as follows:

$$Accumulation=Input+Generagtion-Output-demand$$ 1

Mass balance for leaves

The entering moisture is:

$$m_{w}A$$ 2

where, mass flow of the moisture (m_w) is determined based on the second law of Fick:

$$m_w=-D\frac{\partial \left({\rho }_{\mathit{ds}}\tau \right)}{\partial x}$$ 3

The outlet moisture from the control volume is:

$$m_{w}A+\frac{\partial \left(m_{w}A\right)}{\partial x}dx$$ 4

The accumulated moisture in the volume is:

$$\frac{\partial }{\partial t}\left({\rho }_{\mathit{ds}}\tau Adx\right)=Adx{\rho }_{\mathit{ds}}\frac{\partial \tau }{\partial t}$$ 5

Therefore, by replacing and on simplifying:

$$\frac{\partial }{\partial x}\left(D{\rho }_{\mathit{ds}}\frac{\partial \tau }{\partial x}\right)={\rho }_{\mathit{ds}}\frac{\partial \tau }{\partial t}$$ 6

Considering a dimensionless distance (Eq. 7), mass balance for the control volume could be written as Eq. (8).

$$z=\frac{x}{L}\to dx=Ldz$$ 7

$$\frac{\partial \tau }{\partial t}=\frac{D}{L^2}\frac{{\partial }^2\tau }{\partial z^2}$$ 8

Energy balance for leaves

During the process, the leaf moisture diffused from internal region to reach the surface and then evaporated by drying air. This moisture flow contains enthalpy (h_w) and therefore, as the moisture transfers, the enthalpy moves along the leaf. In addition, the enthalpy is transferred by the conductive heat transfer (q). Mathematical expression for inlet, outlet and accumulated enthalpy in the leaf is represented by Eqs. (9‒11), respectively:

$$m_{w}A{h}_w+qA$$ 9

$$m_{w}A{h}_w+\frac{\partial \left(m_{w}A{h}_w\right)}{\partial x}+qA+\frac{\partial \left(\mathit{qA}\right)}{\partial x}$$ 10

$$\begin{array}{c}\frac{\partial }{\partial x}\left[Adx{\rho }_{\mathit{ds}}\left(C_{P,ds}(T)+\tau C_{P,w}(T)\right).T_s\right]=Adx{\rho }_{\mathit{ds}}\frac{\partial }{\partial t}\left[\left(C_{P,ds}(T)+\tau C_{P,w}(T)\right).T_s\right]=\\ Adx{\rho }_{\mathit{ds}}\left[\left(C_{P,ds}(T)+\tau C_{P,w}(T)\right)\frac{\partial T_s}{\partial t}+C_{P,w}(T).T_s\frac{\partial \tau }{\partial t}\right]\\ \end{array}$$ 11

Water enthalpy and conductive heat transfer are represented as follows:

$$h_w=C_{P,w}(T).T_s$$ 12

$$q=k(\tau )\frac{\partial T}{\partial x}$$ 13

Therefore, by replacing and upon simplifying, Eq. (14) is obtained for represented changes in leaf temperature during the drying process:

$$\frac{\partial T_s}{\partial t}=\frac{1}{{\rho }_{\mathit{ds}}\left(C_{P,ds}(T)+\tau C_{P,w}(T)\right)}\left[\frac{D}{L^2}{\rho }_{\mathit{ds}}\frac{\partial \tau }{\partial z}{C}_{P,w}(T)\frac{\partial T_s}{\partial z}-\frac{\partial }{\partial z}\left(\frac{k(\tau )}{L^2}\frac{\partial T_s}{\partial z}\right)\right]$$ 14

Mass balance air humidity

The carried water vapor into the control volume by the air stream is:

$$m_a{X}_e$$ 15

The entering water vapor into the control volume through moisture evaporation from the leaf is:

$$-M_{\mathit{ds}}\frac{d\overline{\tau }}{\mathit{dt}}$$ 16

The water carried out from the control volume by the air stream is:

$$m_a{X}_a$$ 17

The rate of accumulated humidity in the control volume of air is:

$${\rho }_{\mathit{da}}\epsilon V\frac{d{X}_a}{\mathit{dt}}$$ 18

Finally, by replacing the equations, the mass balance for the humidity of the air control volume results in Eq. (19):

$$\frac{d{X}_a}{\mathit{dt}}=\frac{1}{{\rho }_{\mathit{da}}\epsilon V}\left[m_a\left(X_e-X_a\right)-M_{\mathit{ds}}\frac{d\overline{\tau }}{\mathit{dt}}\right]$$ 19

Energy balance for air

A layer of the drying bed was considered as the control volume of air where each of the mass flows entering and exiting the layer has its own enthalpy content. In addition, heat transfer from the air to the leaves causes an energy outflow from the layer. Therefore, each component of Eq. (1) for enthalpy balance of the air will be as follows:

The contribution of entering enthalpy by the air stream into the control volume is:

$${\int }_{T_0}^{a,in}{m}_a\left(C_{P,da}+X_e{C}_{P,v}\right)d{T}_a$$ 20

The enthalpy carried out of the control volume by the air is:

$${\int }_{T_0}^{a,ex}{m}_a\left(C_{P,da}+X_e{C}_{P,v}\right)d{T}_a$$ 21

The entering enthalpy into the control volume through moisture evaporation of the samples is equal to:

$$\left[\left(X_e-X_a\right)m_a-\epsilon V{\rho }_{\mathit{da}}\frac{d{X}_a}{\mathit{dt}}\right]{\int }_{Ts(1,t)}^{a,ex}{C}_{P,v}d{T}_a$$ 22

The discharged enthalpy from the control volume through the convective heat transfer is:

$$\left(1-\epsilon \right)V\frac{h}{L}\left(T_a-T_{s(1,t)}\right)$$ 23

The accumulated enthalpy in the control volume is:

$$\epsilon V{\rho }_{\mathit{da}}\left[C_{P,da}+X_a{C}_{P,v}\right]\frac{d{T}_a}{\mathit{dt}}$$ 24

Finally, upon simplification, the enthalpy balance for the air control volume results in:

$$\begin{array}{c}\frac{d{T}_a}{\mathit{dt}}=\frac{1}{\epsilon V{\rho }_{\mathit{da}}\left(C_{P,da}+X_a{C}_{P,v}\right)}\\ \left[m_a{\int }_{T_{a,ex}}^{a,in}\left(C_{P,da}+X_a{C}_{P,v}\right)d{T}_a+\left[\left(X_e-X_a\right)m_a-\epsilon V{\rho }_{\mathit{da}}\frac{d{X}_a}{\mathit{dt}}\right]{\int }_{T(1,t)}^{a,ex}{C}_{P,v}d{T}_a+(1-\epsilon )V\frac{h}{L}\left(T_{s(1,t)}-T_a\right)\right]\\ \end{array}$$ 25

Governing initial and boundary conditions

For completing the mathematical model and solving the set of PDEs, four initial as well as four boundary conditions are needed. The governing initial conditions would be as follows

$$\tau \left(z,0\right)={\tau }_{\mathit{initial}}$$ 26

$$X\left(z,0\right)=X_{\mathit{initial}}$$ 27

$$T_s\left(z,0\right)=T_{sinitial}$$ 28

$$T_a\left(z,0\right)=T_{ainitial}$$ 29

The boundary conditions are defined as follows:

Distribution of temperature and moisture in leaves is symmetric and therefore:

$${\left(\frac{\partial \tau }{\partial z}\right|}_{z=0}=0$$ 30

$${\left(\frac{\partial T_s}{\partial z}\right|}_{z=0}=0$$ 31

The convective transferred heat from air to surface of the leaf increases temperature and evaporates the superficial moisture of the leaf:

$$-\frac{h}{L}\left[T_s(1,t)-T_a\right]=\frac{k(\tau )}{L^2}\frac{\partial T_s}{\partial z}(1,t)-\frac{D}{L^2}{\rho }_{\mathit{ds}}\frac{\partial \tau }{\partial z}(1,t)Q_s\left(T_s(1,t)\right)$$ 32

Moisture diffused from inside into the leaf surface is evaporated at the same rate by the air flow:

$$-\frac{D}{L^2}{\rho }_{\mathit{ds}}\frac{\partial \tau }{\partial z}(1,t)=\frac{h_{\mathit{mv}}}{L}\left[{\rho }_{\mathit{dai}}{X}_{\mathit{eq}}-{\rho }_{\mathit{da}}{X}_a\right]$$ 33

Because of assumed symmetric distribution of the moisture in the leaves, the average moisture value in the samples could be determined as follows:

$$\overline{\tau }={\int }_0^1\tau (z,t)dz$$ 34

Furthermore, effective diffusivity is represented as a function of the air temperature by using an Arrhenius type equation.

Coefficients for heat and mass transfer

Adequate estimation of the transfer coefficients is the main problem in case of applying non-constant boundary conditions. Sitompul et al. (2001) modeled and simulated deep-bed grain dryers by developing the coupled equations for heat and mass transfer within intraparticles based on the Luikov’s model. The researchers correlated the average transfer coefficients between the gas stream and surface of grain using dimensionless groups characterize the flow condition. The coefficients could be effectively calculated using empirical equations containing dimensionless numbers in the following forms:

$$h_{\mathit{mv}}=\frac{Sh.D_{\mathit{AB}}}{L_c}$$ 35

$$h=\frac{Nu.k_a}{L_c}$$ 36

The Nusselt and Sherwood numbers were determined using Eqs. (37) and (38), respectively (Sitompul et al. 2001):

$$Nu=\frac{a}{\epsilon }{\text{Re}}^b{Pr}^{\frac{1}{3}}$$ 37

$$Sh=\frac{a}{\epsilon }{\text{Re}}^{b}S{c}^{\frac{1}{3}}$$ 38

$$\text{Re}=\frac{{\rho }_{\mathit{da}}{V}_s{D}_p}{{\mu }_a}$$ 39

$$Pr=\frac{C_{P,da}{\mu }_a}{k_a}$$ 40

$$Sc=\frac{{\mu }_a}{{\rho }_{\mathit{da}}{D}_{\mathit{AB}}}$$ 41

Physical characteristics of air and the product

Some physical characteristics of the mixture of air–vapor as well as the leaves are required to solve the developed model. The desired properties could be calculated by suitable equations relating them to recognized parameters summarized in Table 1. Furthermore, physical properties of the leaves including bulk density and the bed prosity were experimentally determined to be approximately 66.35 kg m³ and 0.9, respectively. Particle density of the leaves was determined using standard toluene method and for fresh and dried samples was obtained to be 664.89 and 715.53 kg m⁻³, respectively. Furthermore, average thickness and moisture content of the fresh leaves were measured as 0.15 mm and 0.77 (in wet basis), respectively.

Table 1.

Descriptions for physical properties used in simulation the drying process of peppermint leaves

Property	Description	References
RH	$RH=101.3H{(0.62189P_{\mathit{vs}}+H{P}_{\mathit{vs}})}^{-1}$	Naghavi et al. (2010)
Pvs	$P_{\mathit{vs}}=0.1exp\left(27.0214-\frac{6887}{T_{\mathit{abs}}}-5.31ln\left(\frac{T_{\mathit{abs}}}{273.16}\right)\right)$	Tohidi et al. (2017)
hv	$\begin{array}{cc}{h}_v=2.503\times {10}^6-2.386\times {10}^3\left(T_{\mathit{abs}}-273.16\right)& 273.16\le T_{\mathit{abs}}\le 533.16\end{array}$	Naghavi et al. (2010)
μa	${\mu }_a=1.691\times {10}^5+4.984\times {10}^{-8}{T}_a-3.187\times {10}^{-11}{T}_a^2+1.319\times {10}^{-14}{T}_a^3$	Tohidi et al. (2017)
CP,v	$C_{P,v}=10384.59-50.37T_a+7.4\times {10}^{-2}{T}_a^2$	Tohidi et al. (2017)
CP,w	$C_{P,w}=276370-2090.1T_s+8.125T_s^2-0.014116T_s^3+9.3701\times {10}^{-6}{T}_s^4$	Naghavi et al. (2010)
He	$He=0.622\frac{P_{\mathit{vs}}}{\left(101.33-P_{\mathit{vs}}\right)}$	Naghavi et al. (2010)
eRH	$eRH=\frac{101.3He}{\left(\begin{array}{cc}0.62189& P_{\mathit{vs}}\end{array}\right)+\left(He\times P_{\mathit{vs}}\right)}$	Naghavi et al. (2010)
Me	$M_e=\frac{\left[\left(55.4994-0.1272T_a\right){\left(\frac{\mathit{eRH}}{\left(1-eRH\right)}\right)}^{0.2275}\right]}{100}$	Botheju et al. (2011)
ka	$k_a=\frac{0.00031417T_a^{0.7786}}{\left(1-\frac{0.7116}{T_a}+\frac{2121.7}{T_a^2}\right)}$	Naghavi et al. (2010)
CP,da	$C_{P,da}=2.9275\times {10}^{-7}{T}_a^3+4.7047\times {10}^{-4}{T}_a^2+1.782\times {10}^{-2}{T}_a+1005.3$	Tohidi et al. (2017)
DAB	$D_{\mathit{AB}}=1.4738\times {10}^{-4}exp\left(\frac{-523.78}{T_a}\right)$	Rodríguez et al. (2014)
Qs	$Q_s=\gamma -\frac{R}{M_w}\frac{\partial \left(ln(a_w)\right)}{\partial \left(\frac{1}{T}\right)}$	Rodríguez et al. (2014)
aw	$a_w=exp\left[-exp\left(3.24827-0.00000279325T_a^{3.13475}\right){\tau }_{\mathit{eq}}^{-1.47820}\right]$	Rodríguez et al. (2014)
k	$k=1.418\times {10}^{-1}+\frac{4.{9310}^{-1}\tau }{\left(1+\tau \right)}$	Rodríguez et al. (2014)

Solution of the model

The non-equilibrium mathematical model for stationary deep bed of the leaves consist of a set of equations including (Eqs. 8, 14, 19, and 25 coupled and must be solved simultaneously employing numerical solution techniques. Today, finite difference method (FDM) is the main approach being practiced for numerical solutions of PDEs due to its individual characteristics and advantages (Naghavi et al. 2010). So, in this study, the same procedure was selected and used to solve the developed model.

Computational domain

To solve the numerical equations of moisture and temperature of the leaves, one leaf is meshed from the center of each leaf to its surface. For the air, one layer of the bed is meshed from the point of air entry into the bed towards the exit. Figure 1 shows meshing of the computational domain includs the coordinates $x_i=i\mathrm{\Delta }x,i=1.2.\cdots .m$ and $t_j=j\mathrm{\Delta }t.j=1.2.\cdots .n$ for the grid points.

Fig. 1.

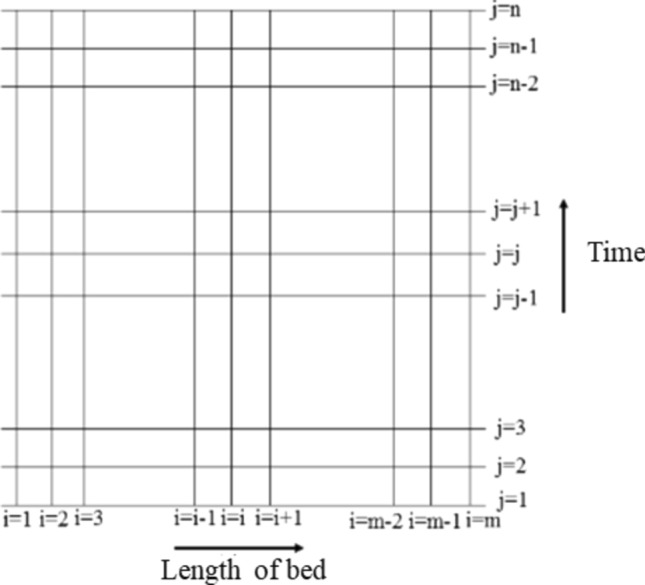
Computational domain with mesh and grid points for numerical solution using FDM

Approximation of the partial derivatives and solution of the equations set

Different approaches to approximate differences in partial differential equations have been studied. These approximations are formulated in explicit and implicit forms. In the explicit method, for each finite difference equation, only one unknown is expressed whereas the implicit method consists of more than one unknown. Stability of finite difference equations is the most important benefit of the implicit methods. In this study, as one of the implicit formulations, the Oiler (BTC) method was used. To approximate the PDE at an inner point $P(x_i.t_j)$, the first partial derivative according to t was replaced by the backward difference quotient. Also, the partial derivatives according to x are replaced by the central difference quotients.

Then, discretizing of the partial derivatives for Eqs. (8), (14), (19), and (25) and rearranging the equations results as:

Mass balance for leaves (Eq. 8):

$$-\left(\frac{\mathrm{\Delta }t}{{(\mathrm{\Delta }z)}^2}\frac{D}{L^2}\right){\tau }_{i-1}^j+\left(1+2\frac{\mathrm{\Delta }t}{{(\mathrm{\Delta }z)}^2}\frac{D}{L^2}\right){\tau }_i^j-\left(\frac{\mathrm{\Delta }t}{{(\mathrm{\Delta }z)}^2}\frac{D}{L^2}\right){\tau }_{i+1}^j={\tau }_i^{j-1}$$ 42

Enthalpy balance for leaves (Eq. 14):

$$\begin{array}{c}{T}_{s_i}^j-T_{s_i}^{j-1}=\\ \frac{\mathrm{\Delta }t}{{\rho }_{\mathit{ds}}\left(C_{P,ds}(T)+{\tau }_i^j{C}_{P,w}(T)\right)}\left[\frac{D}{L^2}\frac{{\rho }_{\mathit{ds}}{C}_{P,w}(T)}{2\mathrm{\Delta }z}\left(\frac{{\tau }_{i+1}^j-{\tau }_i^j}{\mathrm{\Delta }z}\right)\left({\tau }_{s_{i+1}}^j-{\tau }_{s_{i-1}}^j\right)-\frac{k({\tau }_i^j)}{L^2{(\mathrm{\Delta }z)}^2}\left(T_{s_{i+1}}^j-2T_{s_i}^j+T_{s_{i-1}}^j\right)\right]\\ \end{array}$$ 43

Mass balance for air (Eq. 19):

$$\left(1+\frac{m_a\mathrm{\Delta }t}{{\rho }_{\mathit{da}}\epsilon V}\right)X_a^j=X_a^{j-1}+\frac{m_a\mathrm{\Delta }t}{{\rho }_{\mathit{da}}\epsilon V}{X}_e^j-\frac{M_{\mathit{ds}}\mathrm{\Delta }t}{{\rho }_{\mathit{da}}\epsilon V}\left(\frac{{\overline{\tau }}_i^j-{\overline{\tau }}_i^{j-1}}{\mathrm{\Delta }t}\right)$$ 44

Enthalpy balance for air (Eq. 25):

$$\begin{array}{c}\frac{T_a^j-T_a^{j-1}}{\mathrm{\Delta }t}=\\ \frac{1}{\epsilon V{\rho }_{\mathit{da}}\left(C_{P,da}+X_a{C}_{P,v}\right)}\times \\ \left[m_a{\int }_{T_{a,ex}}^{a,in}\left(C_{P,da}+X_e{C}_{P,v}\right)d{T}_a+\left[m_a(X_e^j-X_a^j)-\epsilon V{\rho }_{\mathit{da}}\left(\frac{X_a^j-X_a^{j-1}}{\mathrm{\Delta }t}\right)\right]{\int }_{T_{s(1,t)}}^{Ta,ex}{C}_{P,v}d{T}_a+\left[(1-\epsilon )V\frac{h}{L}\left(T_{s(1,t)}-T_a\right)\right]\right]\\ \end{array}$$ 45

Coefficients of k₁‒k₇ were defined as below:

$$k_1=\left(\frac{\mathrm{\Delta }t}{{(\mathrm{\Delta }z)}^2}\frac{D}{L^2}\right)$$ 46

$$k_2=\frac{\mathrm{\Delta }t}{{\rho }_{\mathit{ds}}\left(C_{P,ds}(T)+{\tau }_i^j{C}_{P,w}(T)\right)}$$ 47

$$k_3=\frac{D}{L^2}\frac{{\rho }_{\mathit{ds}}{C}_{P,w}(T)}{2\mathrm{\Delta }z}\left(\frac{{\tau }_{i+1}^j-{\tau }_i^j}{\mathrm{\Delta }z}\right)$$ 48

$$k_4=\frac{k({\tau }_i^j)}{L^2{(\mathrm{\Delta }z)}^2}$$ 49

$$k_5=\frac{\mathrm{\Delta }t}{{\rho }_{\mathit{da}}\epsilon V}$$ 50

$$k_6=\frac{1}{\epsilon V{\rho }_{\mathit{da}}\left(C_{P,da}+X_a{C}_{P,v}\right)}$$ 51

$$k_7=m_a(X_e^j-X_a^j)-\epsilon V{\rho }_{\mathit{da}}\left(\frac{X_a^j-X_a^{j-1}}{\mathrm{\Delta }t}\right)$$ 52

Finally, Eqs. (42‒45) were rewritten as Eqs. (53‒56), respectively:

$$\left\{\begin{array}{c}-k_1{\tau }_{i-1}^j+\left(1+2k_1\right){\tau }_i^j-k_1{\tau }_{i+1}^j={\tau }_i^{j-1}\\ i=2,3,...,m-1\\ j=1,2,...,n\\ \end{array}\right)$$ 53

$$\left\{\begin{array}{c}{T}_{s_i}^{j-1}=\left(k_2{k}_4-k_2{k}_3\right)T_{s_{i+1}}^j+\left(1-2k_2{k}_4\right)T_{s_i}^j+\left(k_2{k}_3+k_2{k}_4\right)T_{s_{i-1}}^j\\ i=2,3,...,m-1\\ j=1,2,...,n\\ \end{array}\right)$$ 54

$$\left\{\begin{array}{c}{X}_a^j=\frac{1}{\left(1+m_a{k}_5\right)}\left(X_a^{j-1}+m_a{k}_5{X}_e^j-M_{\mathit{ds}}{k}_5\left(\frac{{\overline{\tau }}_i^j-{\overline{\tau }}_i^{j-1}}{\mathrm{\Delta }t}\right)\right)\\ \\ i=2,3,...,m\\ j=1,2,...,n\\ \end{array}\right)$$ 55

$$\left\{\begin{array}{c}{T}_{a,ex}^j=\frac{\mathrm{\Delta }t{k}_6{m}_a\left(C_{P,da}+X_e^j{C}_{P,v}\right)T_{a,in}^j+\left(\mathrm{\Delta }t(1-\epsilon )V\frac{h}{L}-\mathrm{\Delta }t{k}_7{C}_{P,v}\right)T_{s(1,t)}^j}{1+\mathrm{\Delta }t{k}_6{m}_a\left(C_{P,da}+X_e^j{C}_{P,v}\right)-\mathrm{\Delta }t{k}_7{C}_{P,v}+\mathrm{\Delta }t(1-\epsilon )V\frac{h}{L}}\\ \\ i=2,3,...,m\\ j=1,2,...,n\\ \end{array}\right)$$ 56

Solving the derived equations should lead to calculate the unknown variables at all points of the bed during the drying process. Solution of the equations set was done based on the procedure defined by Naghavi et al. (2010) by developing and implementing a computer program in MATLAB (R2012b.v8) environment.

Experimental data

A convective dryer assisted an ultrasonic system was used to perform the drying experiments. Different air temperatures (40‒70 °C) and the power intensities (0‒104 kW m⁻³) were applied to dry the peppermint leaves. During the experiments, the air velocity was controlled and adjusted to be 1 m s⁻¹; and the bed height of leaves in the drying chamber was selected as 120 mm. AS laser thermometer was used to measure initial temperature of the leaves. Furthermore, changes in temperature and humidity of the drying air were monitored using appropriate digital sensors. For details of drying system, experiments and measuring instruments see Ghanbarian et al. (2020).

Results and discussion

Prediction of moisture removal curves

To verify the developed mathematical model and the solution procedure, the model accuracy in predicting of moisture removal curves of the peppermint leaves was evaluated through the following criteria:

$$RE=\frac{\left|V_{\mathit{exp}},-,V_{\mathit{pre}}\right|}{V_{\mathit{pre}}}\times 100$$ 57

$$MRE=\frac{1}{n}\sum _{i=1}^n\frac{\left|V_{exp.i},-,V_{pre.i}\right|}{V_{exp.i}}\times 100$$ 58

In the case of dryer simulation, maximum relative error (RE_max) up to about 15% and a mean relative error of less than 10% are usually considered to be satisfactory for the modeling accuracy. Table 2 represents the obtained MRE and RE_max for predicting drying curves by the model. From the table, the model could accurately describe the dehydration curves.

Table 2.

Mean relative error (MRE) and maximum relative error (RE_max) for predicting drying curves by the model

Temperature (°C)	USP (kW m−3)	REmax (%)	MRE (%)
40	0	5.60	2.31
	26	8.74	3.75
	52	5.31	2.63
	78	6.87	3.38
	104	5.29	2.15
50	0	11.62	7.11
	26	6.79	3.30
	52	8.41	5.98
	78	7.96	5.65
	104	7.06	3.15
60	0	8.26	6.37
	26	6.29	3.79
	52	7.93	4.81
	78	6.76	4.68
	104	5.91	3.42
70	0	9.21	7.46
	26	11.05	7.51
	52	12.19	8.53
	78	8.41	5.94
	104	13.82	8.86

Heat and mass transfer parameters

Average values estimated for the moisture diffusion and convective mass transfer coefficient of the peppermint leaves ranged from 0.601 × 10^–4 to 5.937 × 10^–4 s⁻¹ and from 4.693 × 10^–4 to 7.975 × 10^–4 m s⁻¹, respectively. In spite of numerous works focused on moisture diffusivity of different biological products, surface mass transfer coefficient has been rarely studied and reported in the open literature. The values obtained for mass transfer parameters in the present work are comparable with the findings for various leaves dried using different drying systems and conditions. Rodríguez et al. (2014) evaluated the influence of drying air temperature and ultrasonic power on the transport-related parameters of thyme leaves. They carried out the experiments using a bed thickness of about 3 cm. The average diffusivity and the convective coefficient were reported to range from 0.62 × 10^–4 to 8.48 × 10^–4 s⁻¹ and from 1.37 × 10^–4 to 2.93 × 10^–4 kW m⁻² K⁻¹, respectively.

Ndukwu et al. (2017) dried three varieties of cocoyam slices practicing different drying methods and conditions and reported the parameters to be changed from 1.72 to 11.34 × 10^–10 m²/s and from 1.01 to 3.45 × 10^–6 m/s, respectively. For dill leaves, the diffusivity was calculated to be in the range of 4.02 × 10^–9‒9.65 × 10^–9 m² s⁻¹ while the transfer coefficient changed from 2.38 × 10^–7 to 6.33 × 10^–7 m s⁻¹ (Darvishi et al. 2017). Altay et al. (2019) practiced different methods including sun, freeze, convective and microwave to dry purple basil leaves and reported the moisture diffusivity range of 1.62 × 10^–9‒7.09 × 10^–8 m² s⁻¹. Beigi (2019) determined moisture diffusivity for mint leaves dried in a hot air system changed from 5.09 × 10^–9 to 1.73 × 10^–8 m² s⁻¹. In addition to intrinsic properties of different leaves, dryer and practicing conditions, determined values for mass transfer parameters are significantly influenced by the procedure used for calculation. In most of the conducted studies, the effective diffusivity has been calculated through conventional solution of Fick’s equation where the bed of drying leaves considered as an infinite rigid slab and thickness of an individual leaf ignored.

Influence of temperature and USP on heat and mass transfer parameters

Moisture diffusivity

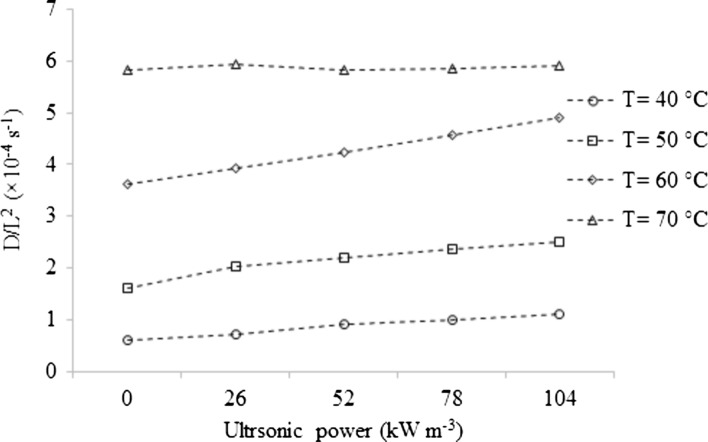
During drying of a material, two factors resist moisture removal including (1) the material itself and (2) the boundary layer. Inside a media with porous structure, moisture transport is usually described by the moisture diffusivity where the content and gradient of the moisture primarily influence the liquid water transport inside the object. Moreover, under specific conditions, several other parameters e.g., temperature, dissolved matter concentration, pressure difference and the external overpressure can be important (Wang et al. 2023). As shown (Fig. 2), the average moisture diffusivity was enhanced at the higher temperatures. The finding is mainly due to the reduced viscosity and facilitated water movement inside the product. The same observation can be seen in the studies conducted by different researchers such as Beigi (2018), Cuevas et al. (2019) and Chen et al. (2020).

Fig. 2.

Influence of temperature and ultrasonic power on the average moisture diffusivity of the peppermint leaves

The influence of ultrasonic power on effective moisture diffusivity of the leaves can also be discussed from Fig. 2. Form the results, combination of ultrasonic power increased the diffusivity value of the leaves mainly at drying temperatures up to 60 °C. The finding may be related to decrease of the internal resistance. In the presence of acoustic energy, high frequency mechanical stresses (sponge effect) are caused in a solid result in microscopic channels developing inside the product and facilitated water diffusion (Chen et al. 2016). The finding is strongly confirmed by the observations reported for diffusivity of strawberry (Gamboa-Santos et al. 2014) and garlic (Tao et al. 2018).

Heat and mass transfer coefficients

Moisture removal from a product at atmospheric pressure, moisture evaporation form a solid surface is characterized by interaction of heat and mass transfer occurring simultaneously between the drying medium and the material. During the convective process, air velocity as well as the thermal and concentration boundary conditions across the material surface strongly affect the phenomena. Velocity boundary layer resists heat transfer between surface of the material and free air stream as well as water evaporation. The layer is initially laminar and then becomes turbulent. Molecular diffusion is the governing mechanism controlling the transport of moisture, temperature and momentum across the laminar layer, while the transports are importantly improved by fluctuations of local transverse velocity in turbulent flow (Tohidi et al. 2017).

Based on the classical theory of heat transfer, the thermal boundary layer develops where a temperature gradient is between the solid surface and the stream. The concentration boundary layer initiates due to concentration difference between the stream and surface. The concentration boundary is almost same as the temperature boundary layer. Therefore, the mass transfer coefficient could be practically analogically from heat transfer. Convective heat transfer between a material and fluid medium flows over it is mainly quantitated by the heat transfer coefficient. From basic thermodynamic, heat will be transfer between two objects with different temperatures. So, greater temperature differences result in higher heat transfer rates. Increased heat transfer coefficients at higher drying temperatures have been reported by Rodríguez et al. (2014) for thyme leaves and Ekka and Palanisamy (2020) for red chilli.

In addition to increased heat transfer between the air stream and the subjected product, the influence of temperature can be discussed according to the interfacial concentration that depends on wet bulb temperature of the air. Therefore, increasing air temperature enhances the concentration of the product interfacial moisture resulting in higher moisture evaporation rate from the surface and increased mass transfer (Tohidi et al. 2017). The observation in term of the temperature effect on convective mass transfer coefficient agrees well with the observations of Ndukwu et al. (2017) and Arif Khan et al. (2021).

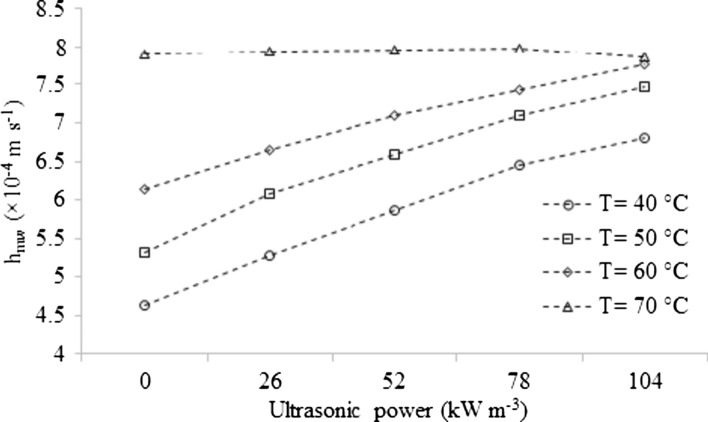
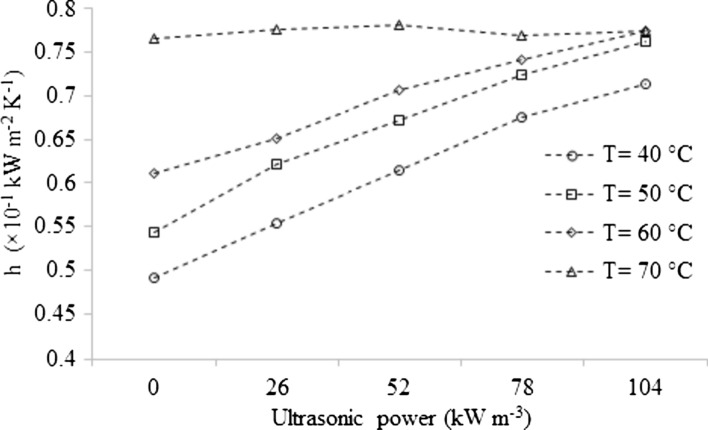
Along with the thermal properties of the medium (the hydrodynamic of flow), heat and mass transfer coefficients depend on the hydrodynamic and thermal boundary conditions. From the results (shown in Figs. 3 and 4), at the air temperatures up to 60 °C, applying ultrasonic power resulted accelerated transfer of the both heat and mass. In addition, hiher power level in the practiced range resulted in an increment in the heat and mass transfer coefficients. Besides the increased energy level within the boundary layer by applying ultrasonic power also enhances, the enhanced heat and mass transfer coefficients may be due to the fact that cavitation in the air stream generated by the ultrasonic power disturbs the boundary layer as well as bubbles caused in it. The phenomenon result in a thinner boundary layer enhances the heat and mass transfer rates. The same findings in term of ultrasonic power applying has been reported for thyme leaves (Rodríguez et al. 2014) and blackberry (Tao et al. 2021).

Fig. 3.

Influence of temperature and ultrasonic power on the average mass transfer coefficient of the peppermint leaves

Fig. 4.

Influence of temperature and ultrasonic power on the average heat transfer coefficient of the peppermint leaves

Conclusion

Heat and mass transfer parameters of peppermint leaves in a hybrid convective/ultrasonic power drying system were investigated through conducting an experimental and numerical modeling research work. Based on the obtained findings, moisture diffusivity as well as heat and surface moisture transfer coefficients of the samples were meaningfully increased by any increment in drying temperature in the practiced range. The performance of ultrasonic power was affected by the temperature where applying the power combined with the air flow at the temperatures up to 60 °C augmented all the heat and mass transfer parameters. However, at temperature of 70 °C, no positive effect of the power was observed.

Abbreviations

A

Leaf area (m²)

a

Equation parameter

a_w

Water activity

b

Equation parameter

C_p,da

Specific heat of dry air (J kg⁻¹ K⁻¹)

C_p,ds

Specific heat of dry solid (J kg⁻¹ K⁻¹)

C_p,v

Specific heat of water vapor (J kg⁻¹ K⁻¹)

C_p,w

Specific heat of water (J kg⁻¹ K⁻¹)

D

Effective moisture diffusion in leaf (m² s⁻¹)

D_AB

Water diffusivity in air (m² s⁻¹)

D_p

Bed diameter (m)

h

Heat transfer coefficient (J m⁻² K s⁻¹)

h_mv

Mass transfer coefficient (m s⁻¹)

k

Thermal conductivity of leaf (W m⁻¹ K⁻¹)

k_a

Thermal conductivity of air (W m⁻¹ K⁻¹)

L

Half thickness of leaf (m)

L_c

Thickness of bed (m)

m_a

Mass flow rate of dry air (kg s⁻¹)

m_ds

Mass of dry leaf (kg)

m_w

Mass flow rate of moisture (kg m⁻³)

q

Conduction heat flux (kJ s⁻¹ m⁻²)

Q_s

Sorption heat (kJ kmol⁻¹)

t

Time (s)

T_a

Air temperature (K)

T_a,ex

Air temperature at bed outlet (K)

T_a,in

Air temperature at bed inlet (K)

T_s

Leaf temperature (K)

V

Bed volume (m⁻³)

V_a

Air velocity (m s⁻¹)

x

Coordinate (m)

X_a

Moisture content of outlet air (d.b.)

X_e

Moisture content of inlet hot air (d.b.)

Z

Dimensionless coordinate

Greeks

ɛ

Bed porosity (−)

μ_a

Air viscosity (kg m⁻¹ s⁻¹)

ρ_da

Dry air density (kg m⁻³)

ρ_ds

Dry solid density (kg m⁻³)

τ

Moisture content of leaf (d.b.)

$\overline{\tau }$

Average moisture content of leaf (d.b.)

Author contributions

KC: Writing—Review & Editing (Revision), MT: Conceptualization, Methodology, Data curation, Mathematical modeling, Validation, Writing original draft; DG: Conceptualization, Supervision, Review & Editing; MB: Data curation, Formal analysis, Mathematical modeling, Writing original draft; TKA: Formal analysis, Review & Editing.

Funding

Not applicable.

Data availability

Data will be available in request.

Code availability

Not applicable.

Declarations

Conflict of interest

Not applicable.

Ethical approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.