Graph-pMHC: graph neural network approach to MHC class II peptide presentation and antibody immunogenicity

Abstract

Antigen presentation on MHC class II (pMHCII presentation) plays an essential role in the adaptive immune response to extracellular pathogens and cancerous cells. But it can also reduce the efficacy of large-molecule drugs by triggering an anti-drug response. Significant progress has been made in pMHCII presentation modeling due to the collection of large-scale pMHC mass spectrometry datasets (ligandomes) and advances in machine learning. Here, we develop graph-pMHC, a graph neural network approach to predict pMHCII presentation. We derive adjacency matrices for pMHCII using Alphafold2-multimer and address the peptide–MHC binding groove alignment problem with a simple graph enumeration strategy. We demonstrate that graph-pMHC dramatically outperforms methods with suboptimal inductive biases, such as the multilayer-perceptron-based NetMHCIIpan-4.0 (+20.17% absolute average precision). Finally, we create an antibody drug immunogenicity dataset from clinical trial data and develop a method for measuring anti-antibody immunogenicity risk using pMHCII presentation models. Our model increases receiver operating characteristic curve (ROC)-area under the ROC curve (AUC) by 2.57% compared to just filtering peptides by hits in OASis alone for predicting antibody drug immunogenicity.

INTRODUCTION

Major histocompatibility complex class II (MHCII) molecules play an essential role in the immune system’s defense against pathogens. Peptides presented on MHCII (pMHCII) are primarily derived from extracellular proteins, and pMHCII can then be recognized by CD4+ helper T lymphocytes (CD4 T cells) to stimulate cellular and humoral immunity [1]. Due to the complexity of determining which peptides are likely to be presented by MHCII, deep learning-based computational tools have been developed and used extensively for various applications [2–5].

Three main strategies have emerged for modeling: (1) multilayer perceptrons (MLPs), exemplified by NetMHCIIpan-4.0 [6], (2) sequence-based models, such as the transformer-based MHCAttnNet [7], and (3) convolutional neural networks (CNNs), such as PUFFIN [8]. Each of these approaches: MLP, transformers/recurrent neural networks (RNNs) and CNN, bring their own inductive bias [9]—assumptions made in the design of the model—to the pMHCII prediction task. Although pMHCII models have made dramatic improvements over the years, they still lag behind MHC class I predictors in performance [6, 10], and are often combined with structural modeling approaches to address this limitation [11, 12]. Graph neural networks (GNNs) better capture real protein systems by leveraging prior knowledge of edges that connect and show interactions between nodes (residues). In contrast, methods like MLP, RNN and CNN treat the peptide and MHC only as a sequence, neglecting important information about these structural interactions. Recently, a GNN model was proposed for MHC class I modeling, but used a fully connected graph between peptide and MHC residues, and therefore did not incorporate structural information (with this approach, peptide–MHC residue interactions which are too distant to interact in a meaningful way are not eliminated from a fully connected graph, and a fully connected graph is generated in an a priori manner) [13]; however, modest improvement over NetMHCPan-4.1 was reported. For pMHCII, a logistic regression model using AlphaFold2’s residue–residue accuracy estimate on pMHCII complexes was recently reported (implicitly using structural information), but failed to achieve better performance than NetMHCIIpan-4.0 [14]. These studies suggest that a hybrid approach, that combines structural information with GNN training on large pMHCII ligandomes, may be more powerful than one based strictly on structure models.

We are particularly interested in the application of these models to biotherapeutic (particularly antibody drugs) deimmunization. Anti-drug antibodies (ADAs), which the immune system uses to clear biotherapeutics, impact the safety of 60% of biotherapeutics, and similarly 40% of biotherapeutics report a reduction in efficacy [15]. Traditionally, humanization strategies like complementarity-determining region grafting are applied to reduce ADAs [16] but require additional human expert knowledge for support. Deep learning-based humanization has recently been shown to be predictive of antibody ADA responses, but these findings have been primarily limited for mouse-derived antibody drugs [17]. pMHCII prediction models have also been employed to deimmunize proteins [18–20], but a high-quality dataset of similar biotherapeutics is lacking to assess these disparate deimmunization methods.

In this work, we introduce graph-pMHC, a pMHCII peptide presentation model that can provide state-of-the-art performance. We leverage Alphafold2-multimer (AF2) [21] to generate canonical pMHC adjacency matrices for the MHCII binding grooves, and an alignment-based approach to learn the correct binding core location within a peptide by enumerating possible graphs. This approach overcomes the limitations of previous GNN approaches for pMHCII by using an adjacency matrix defined by a structural model, while still employing a deep learning-based strategy for updating node embeddings, enabling the expressive learning from the large datasets available. Despite some limitations for protein and protein–peptide complex prediction, AF2 is remarkably accurate [22, 23] and has been used productively to learn about protein complexes [24–26]. We demonstrate that this strategy dramatically outperforms current literature methods [with a significant (absolute) margin of 20.00% average precision (AP)], and has a near optimal inductive bias. To assist this analysis, we develop a new test-train split strategy that ensures even distributions of ontologies and k-mers of the proteins. Finally, we introduce a new biotherapeutic immunogenicity dataset with 109 antibodies and their ADA rates, and a novel immunogenicity risk scoring method, which outperforms a similar strategy based only on OASis [17] by 2.57%. This work represents both a large step forward in the performance of pMHCII presentation models, as well as introducing new, high-quality datasets for them to be compared in the future.

RESULTS

Alphafold2-predicted pMHC residue interactions are concordant with crystal structures

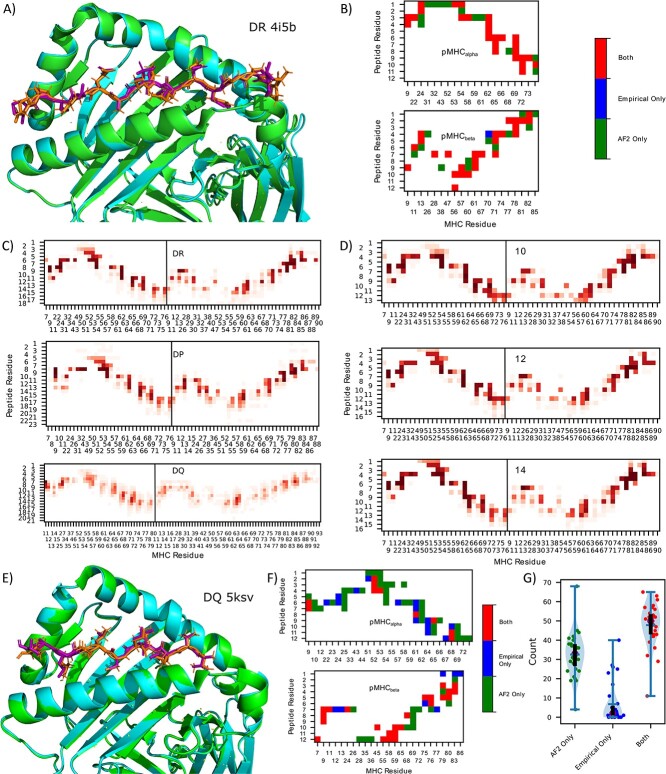
HLA-DR, -DP and -DQ, the different genes encoding MHCII, differ in their loci and polymorphisms (although not their role in presenting antigens to T cells), leading to variations in antigen presentation [1], and thus may differ in their pMHCII structures. We first identify the adjacency matrices for pMHCII using alphafold2-multimer [21] (AF2) to predict the graph structure of pMHCII residue interactions. This step is necessary due to the limited peptide and allele diversity (36 unique peptides and 32 unique alleles) in the available empirical crystal structures [found in the Protein Data Bank (PDB)], which is dramatically less than the thousands of allotypes registered on the Immunogenetics Information System (IMGT) [27], and the tens of thousands of unique peptides measured in pMHCII ligandomes. Indeed, no crystal structures exist for HLA-DP gene with a non-covalently linked peptide. As AF2 is too computationally expensive to obtain predictions for all pMHCII in our dataset, we sought to obtain a single canonical adjacency matrix for each gene, HLA-DR, HLA-DP and HLA-DQ. Thus, we must determine if adjacencies are conserved across alleles, peptide sequences and peptide lengths. Figure 1B depicts the derived adjacency matrices corresponding to the empirical crystal structure and the AF2-solved structure of HLA-DRA^*01:01/HLA-DRB1^* VVKQNCLKLATK (Figure 1A) shows the corresponding 3D structure. A notable alignment can be seen between the AF2 structure and the empirical structure, with AF2 predicting a slightly higher number of adjacencies, albeit missing adjacency. Below we discuss aggregate results on available PDB structures.

Figure 1.

AF2-derived adjacency matrix. (A) 3D structure of empirical crystal structure (PDB ID: 4i5b) of pMHCII and AF2 predictions for 4i5b, HLA-DRA^*01:01/HLA-DRB1^* VVKQNCLKLATK. (B) Contact map (<4 Å) between pMHCII for the empirical crystal structure and the AF2 predictions corresponding to the pMHC in (A). (C) DR (upper) (166 adjacencies), DP (57 adjacencies) (center) and DQ (89 adjacencies) (lower) contact map aggregates over various lengths and alleles (alpha and beta chains are concatenated in the plot). (D) Contact map for 10mer (upper) (18 adjacencies), 12mer (center) (17 adjacencies) and 14mer (lower) (22 adjacencies) peptides predicted by AF2 for various DR alleles (one peptide per allele). (E) 3D structure of empirical crystal structure of pMHCII (cyan, purple) and AF2 predictions (green, orange) for 5ksv, HLA-DQA1^*05/DQB1^*02 MATPLLMQALPMGAL. (F) Contact map (<4 Å) between pMHCII for empirical crystal structure and AF2 predictions corresponding to the pMHCII in (E). (G) Violin plot of the adjacencies found only by AF2, only in the empirical source, and both, respectively for each PDB structure. The blue horizontal bar represents the median value, the purple dot represents the mean value, the black line runs from the first to third quartile.

Using this approach, we obtained AF2 pMHCII structure predictions for three different peptides (see methods for peptide selection criteria) for each of the 115 allotypes in our presentation dataset (discussed below) and plot the adjacencies in Figure 1C. As only a subset of peptide residues (the binding core, usually assumed to be nine residues) dock into the binding groove of MHC [28], we align the peptides relative to MHC (changing the absolute peptide index to achieve consistent binding core locations, see Methods). For DR and DP genes (DQ discussed below), we observe many highly conserved (yet distinct for DR/DP) adjacencies, and thus use them for the canonical adjacency matrices.

For the single adjacency per gene approach to be valid, the adjacency of peptides with different lengths as well as different alleles must be conserved across different structures. This aspect becomes particularly noteworthy for peptides with fewer residues than those typically in contact with the MHC molecule. In Figure 1D) we show aggregate adjacencies across the 33 DR alleles (one peptide per allele) for lengths 10, 12 and 14. We find that even in this case, the conserved adjacencies found before are again conserved for these short peptides.

From Figure 1C, we observe significantly more variation in the adjacencies (as well as adjacency differences) for DQ alleles than DR and DP. Yet, comparison of an AF2 structure with the empirical crystal structure shown in Figure 1E shows good agreement. The contact map displayed in Figure 1F once again demonstrates an overprediction of AF2 contacts, but now with somewhat more contacts missed by AF2 prediction. DQ is an interesting case in pMHCII presentation, with models generally performing worse than DR and DP, the substantial variations in contact observed may play a role in driving this phenomenon.

Analyzing 43 pMHCII structures obtained from the PDB, we observe general agreement between AF2 and PDB, with the median number of contacts found exclusively in the empirical sources to be 2. Figure 1G depicts violin plots of the (dis)agreement between empirical sources and AF2. Surprisingly, AF2 routinely places peptides binding in the opposite orientation (eg, C-N instead of N-C), with 11 of the 43 structures being placed in this reversed orientation. Although some studies suggest that these are possible orientations [29–31], none were in agreement with pdb structures, and so all the opposite-orientation peptides are filtered out prior to our creation of a canonical adjacency matrix (and are not plotted in Figure 1G). We also find AF2 placing 1 of the 43 structures in a non-flat orientation, we similarly filter out all non-flat peptides when determining the canonical adjacency matrix. Finally, AF2 predicts one peptide’s binding core starting position in disagreement with PDB, yielding bad predictions for adjacency, as observed as an outlier in Figure 1G. These results show that, although not perfect, AF2 captures the vast majority of pMHCII adjacencies, and show that there is sufficient uniformity of adjacency within genes for our canonical gene adjacency approach. We note, however, that these complexes are likely in AF2’s training data, which makes these performance estimates overly optimistic.

The graph-MHC model

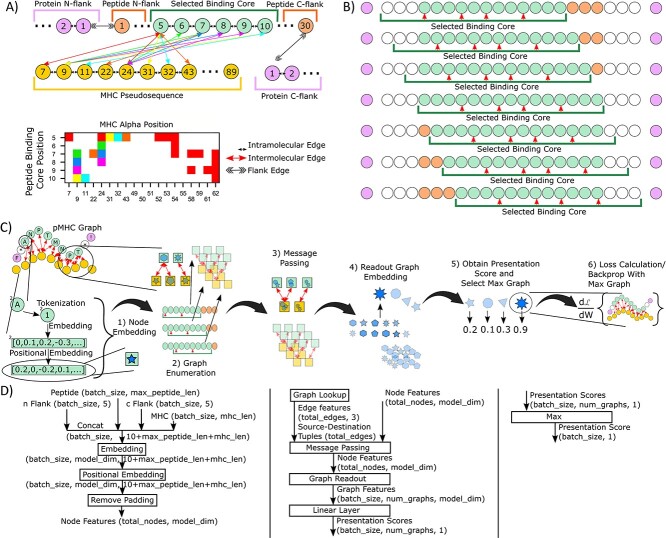
Figure 2A depicts a schematic of the graph structure of the pMHCII model used in this work. Here, we define the peptide binding core using the anchor residues, resulting in a 9mer binding core. Both the peptide binding core, as well as the peptide flanking residues (which are not in contact with MHCII) are included into the graph. Similar to other work [6, 28], we use a pseudosequence to represent the MHC, where only MHC residues adjacent to the peptide are included. Importantly, we take advantage of graph edge features to inform the model of the type of interactions between residues, namely intermolecular interactions (those between peptide and MHC), intramolecular interactions (those within a peptide, MHC or flank sequence) and division of protein flanks (between peptide and flank sequences). By connecting these sequences with its own unique edge token, we are able to create an end-to-end model of the entire presentation pathway.

Figure 2.

graph-pMHC scheme. (A) Schematic of the graph generation approach used in this work. Intermolecular edges in the graph (upper) are color-matched with the adjacency matrix (lower) for clarity. Different edge types are used for intermolecular, intramolecular and flank edges. Circles represent graph nodes, which are amino acid residues from the peptide, MHC and flank sequences. The various sequences listed are defined as follows, protein flanks: residues adjacent to the peptide from the protein that the peptide was derived from, peptide flanks: residues in the peptide that are adjacent to the binding core, selected binding core: residues that are adjacent to the MHC sequence, MHC psuedosequence: residues from the MHC sequence which are in contact with the binding core. (B) Schematic of the ‘graph enumeration’ procedure used in this work. A green bar below the peptide represents the 9mer binding core, while red arrows denote the anchor residues. Green circles represent the selected binding core, orange circles represent the residues in the peptide flanking the binding core and purple circles represent flanking residues obtained from the protein from which the peptide was derived. (C) Pictorial schematic of graph-pMHC, the GNN model framework used. Circles represent amino acid residues, squares and various shapes represent vector node embeddings. (D) Flow chart schematic of graph-pMHC. Rectangles represent transformations that are applied, text represents the inputs, intermediary outputs and output of the model, with the shape of the object. Block numbering corresponds to Algorithm 1 shown in the Supplementary Methods.

In general, a peptide may be larger than the size of the binding core, thus requiring an alignment procedure to select the residue where the binding core starts. Here we enumerate all binding core starting positions with a sliding window, which we refer to as ‘graph enumeration’, as illustrated in Figure 2B. Most pMHCII presentation data come from mutli-allotypic (MA) samples, and so we perform an additional enumeration process across all possible peptide-allotype pairs.

Our general model framework, graph-pMHC, is depicted in Figure 2C and D). First, residues are tokenized and embedded with a learned lookup table. Then, we apply a positional encoding using a learned lookup table for each position. The use of positional encodings for GNNs is uniquely applicable to our domain, adding extra information about the absolute position of the binding core. Next, graph enumeration is performed, generating all possible peptide-allotype and binding core starting position graphs. Typical GNN message passing is then performed separately for each graph to update the residue embeddings. Subsequently, a graph readout strategy is used to get a single vector embedding for the graph. In the ablation study below, we show how the choice of message passing and graph readout strategies impact performance. Finally, fully-connected layers map these graph embeddings to a presentation likelihood, such that the allotype-peptide-binding core with the best likelihood is taken as the canonical graph for the sample and is used to calculate loss and perform backpropagation.

Train/test split strategy to minimize gene ontology biases

To train our model, we have assembled large pMHCII ligandomes that have recently been published across nine studies (Figure 3A ). In total, we aggregate 527 302 peptide:genotype pairs, with 250 643 unique peptides and 75 unique alpha and beta MHCII chains. The data are heavily skewed towards MA, with 408 111 MA peptide:genotype pairs and 119 191 single allotypic peptide:genotype pairs.

Figure 3.

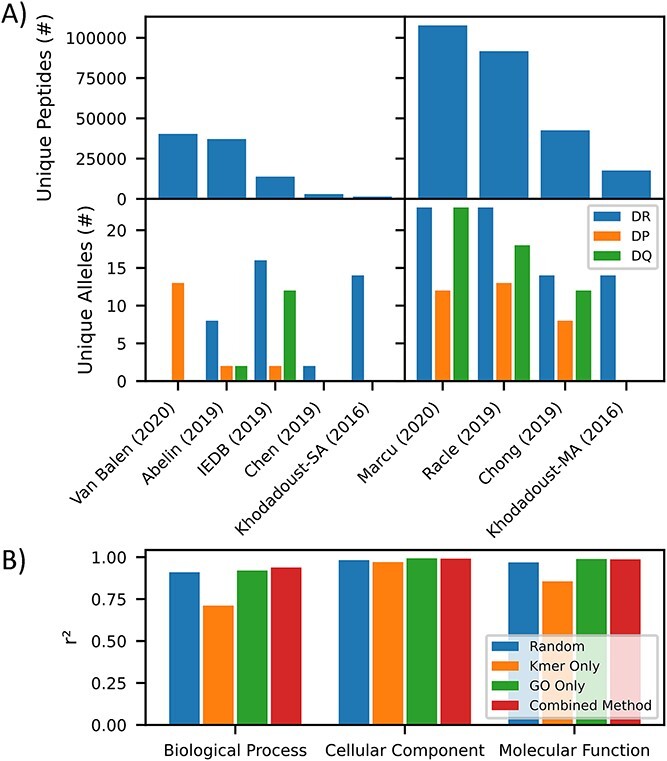
pMHCII dataset. (A) Barchart depicting the number of unique peptides (upper) and unique alleles (lower) for monoallelic (left) and multiallelic sources (right) [32, 48–54]. (B) Barchart depicting goodness of split of genes with various biological processes, cellular components and molecular function between our train and test datasets, as measured by r² for various test–train splitting methods (random, kmer, GO and our combined method).

We desire a test/train split method that best reflects the model’s true performance. Others have already noted the importance of ensuring that 9mer overlap between test and train will skew test performance higher [28]. Yet, little focus has been placed on ensuring good splitting of various gene ontologies into test and train, which could lead to misleading performance metrics for underrepresented ontologies in the test data. To this end, we developed a method combining 9mer overlap and gene ontology (GO) awareness to reduce 9mer overlap between train and test while eliminating gene overlap between test and train, and maintaining a relatively even distribution of genes with various cellular localizations (cc), molecular functions (mf) and biological processes (bp) across train and test (see Methods). Figure 3B depicts the quality of split (measured by r²) for the various splitting methods. One may observe that the traditional kmer overlap strategies for producing test–train splits leads to different ccs, mfs and bps being over represented in either test or train compared to a random selection. A GO-based split solves the issue, but leaves identical 9mers in both train and test. Our combined strategy achieves much of the GO splitting while only allowing minimal 9mer overlap, with 0.35% overlap compared to 0.0029% overlap for the kmer-only strategy and 2.09% overlap compared to a random split by peptide.

Investigating the optimal model architecture and adjacency matrix

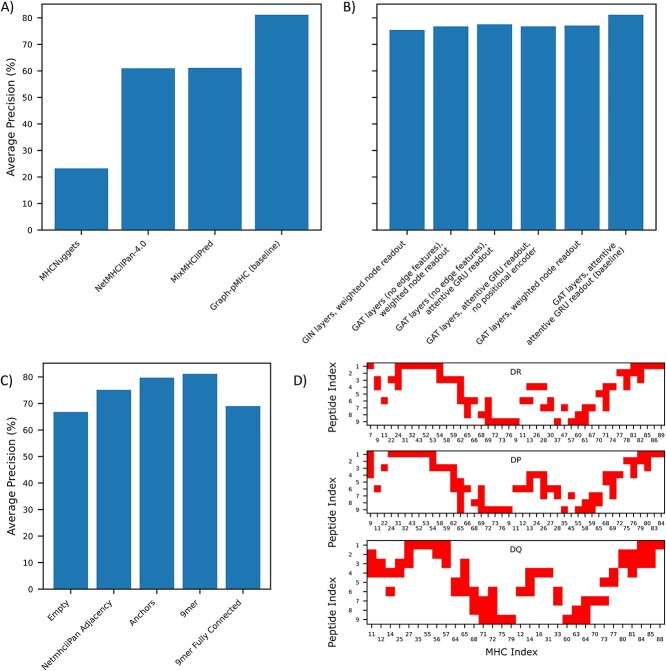
Figure 4A depicts the performance (measured using AP) of baseline graph-pMHC on our pMHCII presentation dataset and compares it to other models in the literature. For graph-pMHC, we produce two additional protein splits with non-intersecting test sets to obtain a cross-validation AP of 81.7% +/− 0.4%. Comparison to other models is difficult, as different models are trained using different datasets, and have different restrictions for which samples can be processed. NetMHCIIpan-4.0 [6], although not available for re-training, is a pan-allelic, pan-allotypic model trained with a relatively up to date dataset, our baseline graph-pMHC significantly outperforms NetMHCIIpan-4.0 by 81.14% to 60.97% on our presentation test set. MixMHCIIPred-1.2 [32], also not available for re-training and trained on a recent dataset, is limited to the monoallelic alleles that it is trained on and performs similarly (61.24%, after supersampling negatives to ensure 10% negatives to match the other datasets). MHCNuggets [33], which utilizes a long short-term memory network is unfortunately trained on the older NetMHCIIpan-3.0 [28] dataset which is limited in its data, and MHCNuggets’ performance reflects the data limitations. Notably, our test data could potentially feature data points present in the training data of some of these methods but not in that of graph-pMHC’s training set. Despite this potential overlap, the improvement in performance we observed is noteworthy.

Figure 4.

pMHCII presentation performance on our test set (​​# positives: 57,519). (A) Comparison of Graph-pMHC test set performance with other models found in the literature. All models are only evaluated on subsets of our test dataset for which inference can be performed. P-values are 9.9 × 10⁻¹³⁰, 3.9 × 10⁻¹⁷⁸, 2.3 × 10⁻¹⁸⁹, for MixMHCIIPred-1.2, NetMHCIIPan-4.0 and MHCNuggets, respectively, calculated over 100 bootstraps. (B) Impact of alternative model choices on test set performance. (C) Barchart of test set performance with the various contact maps used to observe the impact of inductive bias on test set performance. (D) Diagram of the various contact maps used.

To identify the most critical features of graph-pMHC, we conduct an ablation study, depicted in Figure 4B). We find that choice of message passing layers is the most important factor in model performance, with graph attention layers (GAT) [34] performing the best. Edge features make a prominent impact, its exclusion results in an AP drop of 3.59%. The positional encoder is the second most important ablation, excluding it results in an AP drop of 4.37%. The choice of graph readout is similarly important, contributing a 4.06% boost over weighted node readout. This combination of positional encoding and attentive gated recurrent unit (GRU) readout is notable, resulting in a model with many similar features with sequence-based models often used in this field. The attentive GRU readout and GAT message passing also result in a model similar to the AttentiveFP [35] model developed for small molecule drug discovery.

Given the prominent sequence modeling features in our model, we seek to test the importance of the adjacency matrix that was derived above, shown in Figure 4C. We find that an empty adjacency matrix achieves an AP of 66.77%, a significant reduction. Similarly, a fully connected peptide–MHC adjacency achieves a 69.00% AP, demonstrating that the inductive bias provided by narrowing the adjacency to just the physically plausible is extremely impactful. We find that anchor residue adjacencies are not quite enough to capture the useful information, with an AP of 79.22%. Finally, the adjacency matrix derived for NetMHCIIpan [36] results in a 6.00% drop, showing the importance of having different adjacency matrices for different genes, and the utility of AF2 in capturing adjacency.

We also validate our results on pMHCII presentation by evaluating a dataset of immunogenic responses to CD4+ neoantigens, shown in Supplementary Figure 1 [37]. As the exact epitope is not known for the long neoantigens in this dataset, the epitopes are tiled across all possible 12–20mer peptides, and the possible peptide with the largest score from each model is used as the overall score on the neoantigen. As the epitopes in the dataset are generated synthetically and do not reflect the rules of natural antigen presentation [37], we trained a version of graph-pMHC without flanks and used it for predictions. After bootstrapping 500 times, we observed an improvement on this immunogenicity dataset from 22.5% AP for NetMHCIIpan-4.0, 23.1% AP of MixMHCIIPred-1.2, to 23.8% AP of graph-pMHC (with P-values of 3.67 × 10⁻³ compared to MixMHCIIPred-1.2 and 3.31 × 10⁻⁸ compared to NetMHCIIpan-4.0).

Graph-pMHC can also be used to understand the underlying biology in the pMHCII presentation pathway. To this end, we investigate peptide processing signals uncovered by the model using the allotype DRA^*01:01/DRB1^*12:01. Figure 5A–C depicts motifs derived from the most likely 0.1% presenters from 1 million random 15mer peptides. One may observe the conservation of the binding core motif regardless of binding core starting position. Interestingly though, one can observe a consistent lysine and proline enrichments in peptide positions 15 and 14, respectively. The conservation of this enrichment, regardless of binding core starting position, was measured experimentally in Barra et al. [38] and suggests that these are signals to processing enzymes to cut the peptide at these positions. The model also predicts a strong enrichment of peptides whose peptide flanking regions hang off the MHC binding pocket preferentially in the N direction, as depicted in Figure 5D. One can observe a preference in later binding core starting positions, until positions 6 and 7, where incompatible enrichment of anchors and processing signals leads to a precipitous drop.

Figure 5.

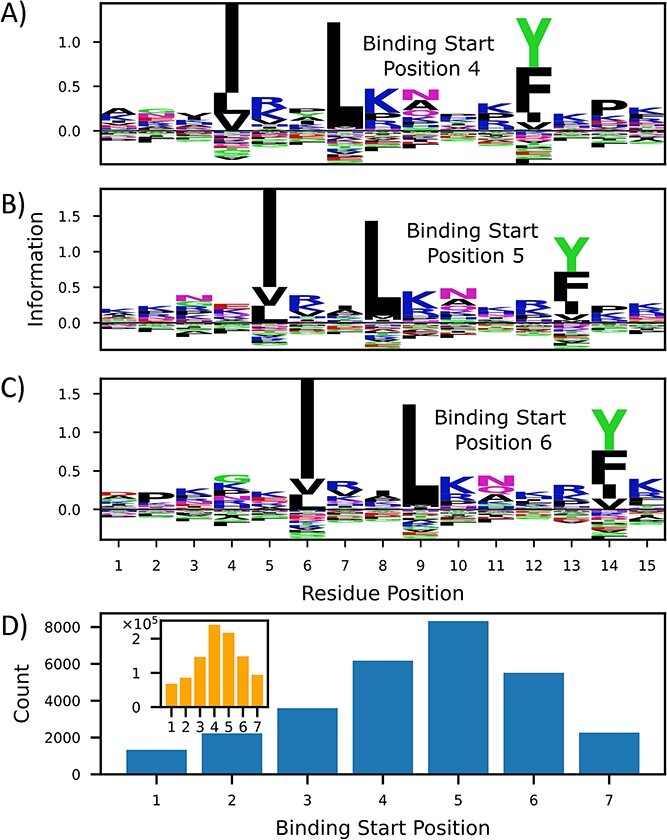
The importance of processing signals on graph-pMHC predictions. (A–C) Peptide motifs of very likely presenters determined by graph-pMHC for DRA^*01:01/DRB1^*12:01. KL divergence of residue type with respect to observed residue frequency in humans for various binding core starting positions is depicted. (B) Enrichment of likely binders for different starting positions versus (inset) the overall number of binding core starting positions.

Application to antibody immunogenicity

Deimmunizing antibody drugs is a key application of pMHCII models, and so we have curated a dataset of 109 ABs with the observed antidrug-antibody (ADA) response observed in published clinical trials. To evaluate the ADA risk of antibodies, we must first develop a method of summarizing the ADA risk of an AB from the peptide constituents. An additional difficulty in the evaluation is that t-cells capable of recognizing self-cells will be negatively selected to prevent an autoimmune response, so even if a peptide is presented, it may not lead to an immune response [1]. Thus, we must also remove self-peptides from the evaluation. Figure 6A depicts our approach for creating an AB ADA risk. First, presentation scores and binding cores are obtained for all length 12–19 peptides which can be derived. Next, we remove any peptide whose binding core (as determined by graph-pMHC) is found via the OASis [17] pipeline to exist in more than 22 subjects from OAS [39]. Next, peptides with a presentation logit score under 0 are removed (or likely binders for NetMHCIIpan-4.0), and the total number of peptides is obtained. This is repeated for eight common DR alleles, which were chosen to span most of the DR supertype families [40], and the total number of unique binding cores is used to represent the AB ADA risk.

Figure 6.

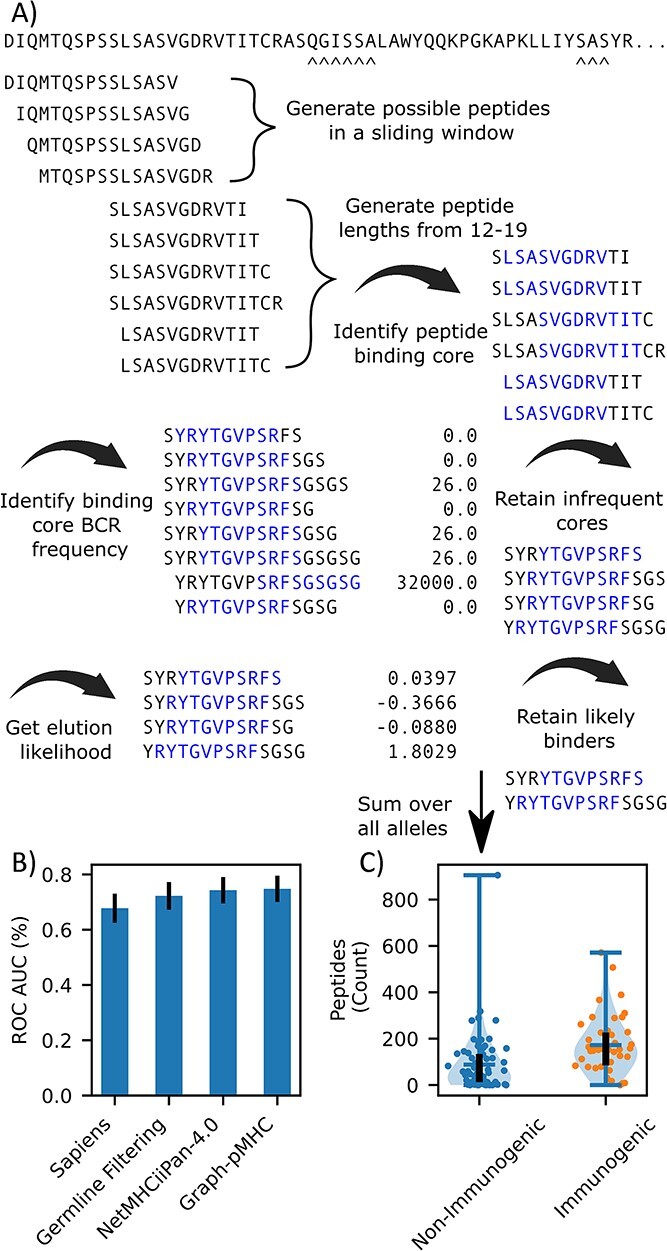
Application of pMHCII to AB ADA risk assessment. (A) Schematic depicting how ADA risk of an AB is calculated. All derivable peptides are obtained, and then various filters are applied to eliminate human-like peptides, and then the number of presentable peptides is counted. (B) Barchart of the bootstrapped (500) ROC-AUC for germline filtering alone, germline filtering and NetMHCIIpan-4.0 and Graph-pMHC. (C) Violin plot of AB ADA risk for the ABs in the dataset predicted by Graph-pMHC. The bar on the left represents the median value, the black line runs from the first to third quartile, both of the dots represent the number of peptides identified for non-immunogenic, and immunogenic AB, respectively.

Figure 6C depicts the ROC-AUC achieved by graph-pMHC and NetMHCIIpan-4.0. In this task, little measurable difference (0.5%, P = 0.16) is observed using graph-pMHC over NetMHCIIpan-4.0. We attribute this to the fact that the task is merely to identify presented peptides, and not rank peptides, as in presentation ranking considered above. Clinically useful separation between the immunogenic and non-immunogenic ABs is observed for both models, as observed for graph-pMHC in Figure 6B, and a 2.57% ROC-AUC improvement over just filtering with OASis is achieved (P = 3.2 ×10⁻¹⁵). We compared the strategy we developed here using pMHCII presentation prediction models to Sapiens, a transformer-based deep learning model trained to access the similarity of ABs with human-derived BCRs; however, we found that for a large subset of non-immunogenic ABs, Sapiens gives low human-ness scores.

DISCUSSION

At its core, the task of predicting which peptides will be presented by MHC class II is a biophysical problem, which is determined by the interactions of amino acid residues between the peptide and MHC allotype. GNNs are uniquely capable of capturing the interaction behavior by modeling adjacent residues in the peptide–MHCII complex (pMHCII) using graph edges, thus only mixing node information of adjacent residues. Due to this, we believe that GNNs should have a superior inductive bias for the pMHCII presentation than the popular sequence-based and MLP-based methods that currently dominate the field.

We believe that our new GO-based test–train splitting procedure introduces a much needed consideration to peptide–MHC presentation prediction. As models, such as Graph-pMHC presented here, get more sophisticated, they are able to increasingly leverage more abstract features of the dataset to improve performance. Without a protein level split in train and test, a model may be able to improve performance by inferring the likelihood of a particular peptide being derived from a particular protein. This could be leveraged to give higher scores to peptides that are derived from highly expressed proteins (such as mitochondrial proteins), improving performance when this is relevant, but reducing performance when it is not (such as for antibody drug immunogenicity prediction). This approach does introduce some limitations. Designing a simple k-folds cross validation where all data eventually are found in a test set is much more challenging, and evaluating peptides derived from training set proteins will be different from those derived from test set proteins.

Our analysis of pMHCII structures suggests a few constraints for a GNN approach which are born out in the ablation study conducted in Figure 4B. First, a model must be able to perform an alignment of the peptide binding core relative to MHCII, and to address this challenge we introduce our graph enumeration strategy. Second, although adjacencies are strongly conserved for different pMHCII, substantial variations are evident, which leads us to consider employing a GAT-based approach, which has demonstrated superior performance in our tests, allowing the model to suppress unphysical interactions. Third, the limited diversity in pMHC graphs yields an interaction system somewhere between what traditional sequence-based machine learning and graph-based machine learning can achieve. Due to this, positional encoding is applicable and significantly boosts performance, partly by helping inform the model about shifting binding cores. Finally, as binding is driven primarily by anchor residues, a GNN approach must have a sophisticated way of altering the representation of one anchor based on another, despite the fact that the anchors have no connecting edges. Indeed, we find that an attentive GRU graph readout adds significant value compared to simple weighted node readouts.

The primary motivation of a GNN approach is the inductive bias that they bring. Unlike other methods, GNNs enable us to directly inform the model about which residues should exchange information with one another. In Figure 4A, we benchmark the performance of popular models in the literature with a broad array of inductive biases. Yet, these approaches significantly underperform graph-pMHC, demonstrating the utility of the GNNs structure-informed inductive bias for the task.

Finally, we provide a new dataset for evaluating antibody immunogenicity, which is mediated by CD4 T cells. Previous datasets were almost completely composed of mouse-derived antibodies, limiting their usefulness in modern antibody engineering. By obtaining more human-derived antibodies, we enable the evaluation of methods for obtaining antibody immunogenicity. Indeed, the previous antibody immunogenicity dataset used by Sapiens [17] led to no statistically significant separation of immunogenic and non-immunogenic human antibodies by their model, where good performance of their model is observed on our dataset [17]. Furthermore, we develop a strategy for using pMHCII presentation models to create an AB immunogenicity.

Our approach is not without its limitations however. In machine learning, there is a characteristic trade-off between model interpretability and performance. As a deep learning model with several components (embedding, message passing, graph readout, and an output linear layer), we have heavily sacrificed model interpretability for performance. Yet, we believe that the natural binding core assignment provided by our graph enumeration strategy does lend to some interesting interpretation of our data. Indeed, our analysis of peptide processing signals in Figure 5A–C) reveals a lysine/proline enrichment outside the binding core, which (to the best of our knowledge) has not been reported previously enriched in a model. Although this approach is revealing and appears to lead to better performance than NetMHCIIPan-4.0’s-related nnAlignMA strategy, it does have some limitations for binding core selection. As a MLP, NetMHCIIPan-4.0 will only give high predictions to binding cores whose anchor residues appear at the expected positions (this is because different neural network weights process different positions). In the baseline Graph-pMHC model, we have a RNN performing graph readout, this machinery is not as sensitive to positional shifts in the input sequence, and thus (in principle) can still make good predictions even if the binding core is shifted. From Figure 5A–C, this concern appears not to be meaningful, as good binding cores with high information are identified, yet for this reason, Graph-pMHC may not produce binding core predictions that are not as good as NetMHCIIPan-4.0, although large ground truth datasets to evaluate this are not available so it is currently unknown.

Another important limitation is the application of models trained on presentation data to immunogenicity prediction. After peptide presentation, there are significant and important steps in the immunogenicity pathway, of particular importance is the recognition of the antigen by CD4+ T cells with their T-cell receptors [1]. This step, and others, greatly reduce the predictive power of pMHCII models on immunogenicity datasets, and one can observe a significant degradation in AP for all models from our pMHCII test set to the CD4+ neoantigens dataset shown in Supplementary Figure 1. For our analysis of population level immunogenicity in our antibody immunogenicity dataset, there are even more factors that complicate analysis by pMHCII models. Primarily, the allele (or alleles) driving patients’ immune response are not known (unlike in the CD4+ epitope dataset), and so our analysis is hampered by significant noise created by including alleles in our evaluation which do not participate in the immune response. This effect likely drives the only small improvement observed for pMHCII models compared to OASis-based tolerization filtering alone. Regardless, meaningful improvements are observed, and the guidance of pMHCII models gives actionable insights into how to deimmunize antibody drugs.

In future works, we plan to create a pipeline for assessing antibody immunogenicity on pre-clinical data. pMHCII presentation models could be particularly useful as an oracle for an antibody generation model to ensure that minimal predicted presented peptides can be derived from an antibody, a regime where few clinical antibodies show signs of ADA. This work could also be aided by larger pre-clinical antibody drug databases which also include additional modes of information [41], such as biomarker studies [42] and antibody platforms beyond mABs [43].

METHODS

Contact map generation with Alphafold2-mutlimer (AF2)

The three most likely presented peptides for each allele (as chosen by a graph-pMHC model with NetMHCIIpan adjacency), along with the top peptide for each peptide length shown in Figure 1D are used to derive adjacency matrices. These sequences, along with the MHC sequences (taken from the IMGT), are used to obtain structure-based interactive predictions from AF2 on the default settings. Peptides which are predicted not to lay flat in the binding groove, or run N-C (opposite typical peptides) in the binding groove are filtered out. An adjacency matrix is constructed by identifying contacts within 4 Å between any atom on any peptide residue with any atom on any MHC residue. Peptides are aligned by the residue which is in contact with the eighth MHC residue (or 10th MHC residue if no contact is observed with the 8th residue). The canonical gene adjacency matrix is then defined using contacts which occur in at least one in three contact maps for a particular gene (DR,DP,DQ).

Graph generation

The AF2 contact map is used to define bidirectional intermolecular edges between peptide and MHC, adjacent residues in each sequence are given bidirectional intramolecular edges (MHC residues not in contact with peptide are not included in the graph to save computation, and nearest neighbors in the pseudosequence are given intramolecular edges). Bidirectional flank edges are made between the n-most residue in the protein c-flank and the c-most residue in the peptide c-flank. The c-most residue of the protein n-flank and the n-most residue in the peptide n-flank are also linked in this way. Intermolecular, intramolecular and flank edges are defined as one-hot encoded vectors, resulting in an edge dimension of 3. To amortize the graph generation process, all possible graphs are generated once, and a lookup table is used to assign flank-peptide-flank-MHC sequences to the appropriate graphs, which is fully defined by the lengths of the peptide, flanks, MHC gene and binding core starting position.

Once the lookup table of all possible graphs is established, the set of graphs that are possible for a particular row of the dataset can be selected from it. Graphs in the lookup table differ by the lengths of the peptide, n-flank, c-flank and allele, and so graphs from the lookup table which have different lengths from the row of interest are not used. Graphs also differ by the gene (e.g. HLA-DR, DP or DQ) as the canonical adjacency matrix is derived for each gene, thus graphs with different genes than the row of interest are not used. Graphs also differ by the binding core starting position, which offsets the peptide–MHC adjacency (see Figure 2A and B). As the binding core starting position is not known and is learned during training, all of these are included in the possible graphs for the row of interest. Similarly, for multiallelic data, it is not known which allele presented the peptide, so the considerations above are repeated for all alleles, then this set of graphs are the possible graphs for the row of interest. This operation is vectorized so that the lookup can be performed across an entire batch of data at once for speed. Algorithms 2 and 3 in the supplementary methods give psuedocode for the graph generation and graph selection processes.

pMHCII presentation model implementation

Graph-pMHC is depicted diagrammatically in Figure 2C and algorithmically below. Input into the model is a batch of the various sequences, including n-flank, peptide, c-flank and up to 12 allotypes. (The n- and c-flanking sequences are included into the model as they may contain residues that promote the processing of the source protein by various enzymes into the peptide [44]. As peptides must be processed to be presented, these features can improve the performance of presentation models [45].) First, n-flank, peptide, c-flank, allele pairs are generated for each allele. Node features are generated for each residue (empty flanks are given a special token) in these pairs via nn.embedding (dim 64), and positional embedding is applied by adding a unique token per position which is embedded via nn.embedder (dim 64). Graphs and edge features are looked up for each pair for every possible binding core starting position, and these are used in GAT layers [34] (dim 128, n_layers 2, dropout 0.1) to update the node features. These node features are sent through an attentive GRU [46], described in AttentiveFP [35] (dim 128, time_steps 2, dropout 0.2), to generate graph features. [GAT layers are a popular message passing layer where the importance of neighboring nodes is dynamically weighted by an attention mechanism. An attentive GRU for graph readout involves treating all of the node features as a sequence and sending them through a GRU (a type of RNN) with a learned context vector that weights the elements of the sequence.] The graph features are sent through a linear layer to one output node which captures the presentation likelihood. Each possible graph is sent through the model, and so the binding core starting position and allele with the highest logit score for each input peptide is found, and loss is calculated using that combination. As this is performed in the forward loop of the model, the binding score calculation is improved by backpropagation after each iteration, resulting in more accurate choices of the graph as training progresses. For clarity, the adjacency matrix is not learned during training, just the appropriate choice of possible adjacency matrices from the complete list derived in the graph generation. Graph-pMHC is implemented in pytorch and deep graph library and uses the fast.ai library for constructing its training loop (which includes features such as the default fit one cycle learning rate scheduling). Binary cross entropy loss and the Adam optimizer are used in their default settings. As with previous work, we use negative set switching between epochs [47]. Algorithm 1 in the supplementary methods give detailed pseudocode for the forward loop of Graph-pMHC.

We performed a rough, manual, hyperparameter sweep over learning rate (lr), model dimension, head dropout and transformer dropout. The presentation test set performance was used to select the hyperparameters. Batch size was fixed at 64 to maximize the utilization of a V100 GPU, lr was tested between 0.0001 and 0.01 with 2 rates for each power of 10 (0.0005 was selected). Node and graph dimensions were varied between {64,128,256} (64 and 128 were selected, respectively). Message passing, graph readout and classifier dropout were varied between {0,0.1,0.2,0.4,0.5} (0.1, 0.2 and 0.4 were chosen respectively). All models are trained for 30 epochs (412 331 steps) to keep training time under 24 h for 1 V100. Supplementary Figure 2 depicts a loss curve on the train and test set, little overfitting behavior is observed, and we do not attempt to train to convergence.

Train/Test split development

Our full dataset consists of 527 302 rows of data obtained from nine studies worth of mass spectrometry measurements of peptides which are putatively presented by MHC class II molecules. Each row consists of a peptide (with lengths ranging from 9 to 30 residues), n and c flanking residues (up to 5), and the genotype of the sample that the row was obtained from. In total, our dataset contains 99 genotypes and 75 unique alpha and beta chains.

To minimize 9mer overlap, we began with a set of all protein sequences within the proteome (Ensembl v90). For each Ensembl gene, we generated a set of unique 9mers from all of their associated Ensembl proteins. From these sets of unique 9mers, we generated a table of the most common 9mers across Ensembl genes. We sought to place the most common kmers from the proteome within the training set, while retaining more unique kmers for the test set. To quantify overlap, we measured the number of overlapping 9mers between train and test relative to the number of unique 9mers.

To minimize skew of protein function, process and localization between train and test, we leveraged GO information. GO domains (molecular function, biological process and cellular compartment) and terms were mapped to Ensemble genes and limited to GO terms containing at least 10 member genes (given our desired 9:1 split, smaller terms would be impossible to divide evenly). To measure evenness of GO term distribution, we measured the R² of the proportion of each GO term within the train and test sets.

To integrate and balance these two objectives (minimized kmer overlap and relatively even GO term distribution), we implemented an iterative process to separate genes into train and test. At a high level, we iterated through each GO term, separating genes associated with that term into train and test based on whether they contained globally frequent proteome kmers. This process continued across GO terms until all genes had been placed. More specifically, beginning with the smallest GO term in the molecular function domain, we took all genes associated with that term. Then beginning with the most abundant kmer in the global kmer table, added all gene’s containing that kmer to the list of training genes. We continued this process down the global kmer list until ≥90% of genes associated with the GO term were found in the list of training genes. We repeated this process for each GO term in the molecular function domain, accounting for genes that had been assigned in previous iterations as well. We then repeated this process for GO terms in the biological process and cellular component domains and finally for the genes that had no GO term annotation.

Model evaluation

When evaluating models for presentation datasets, we use the AP metric. AP is calculated with the python package sci-kit learn and is the AP over all threshold values that change the number of predicted positives. This is equivalent to the area under the curve of a precision-recall curve (for this reason its maximal value is 1 and so we report AP as a percentage). We choose to use this metric over ROC-AUC (area under the receiver operator curve), which tends to give very high performance values when the proportion of test peptides is highly skewed towards negatives, and is more appropriate in the case of a balanced test set or when the number of test data points is small.

When evaluating models for antibody immunogenicity risk, we use the ROC-AUC metric. ROC-AUC is calculated with the python package sci-kit learn and is the area under the true positive rate, false positive rate curve. This is equivalent to the area under the curve of a precision-recall curve (for this reason its maximal value is 1 and so we report AP as a percentage). We choose this metric of AP for this case because our immunogenicity dataset is skewed towards negative immunogenicity cases, but it is likely that random antibodies are more often immunogenic than not. ROC-AUC normalizes for positive:negative ratio and so is more reflective of reality than AP in this case.

Antibody immunogenicity risk assessment

Our strategy for antibody (AB) immunogenicity risk assessment is depicted diagrammatically in Figure 6A). All peptides with length 12–19 are generated in a sliding window across each AB (with flanks), these peptides are paired with DRB1^*01:01, DRB1^*03:01, DRB1^*04:01, DRB1^*07:01, DRB1^*08:01, DRB1^*11:01, DRB1^*13:01, DRB1^*15:01. Graph-pMHC is used to obtain elution likelihood scores and binding core starting predictions for each peptide-allele pair, and pairs with score less than 0 are filtered out (for NetMHCII-pan, peptides rated less than weak binders are filtered out). The binding core frequency dataset is created from OASis [17]. Graph-pMHC identified binding cores from the AB dataset are filtered out if they appear in 23 subjects. The number of unique binding cores per allele is summed up, and this is used as the immunogenicity risk. Antibodies are considered immunogenic if they exceed 10% population ADA response (the exact threshold chosen is unimportant, see Supplementary Figure 3).

This clinical antibody immunogenicity dataset contains 109 monoclonal antibodies with data reported by clinical trials from phase 1 to phase 3. The ADA response was obtained from the FDA website, and when multiple trials were conducted, we used the largest ADA value observed. The raw ADA rate was expressed as a percentage and used without further processing.

Key Points

• We propose Graph-pMHC, a GNN approach to antigen presentation on MHC class II (pMHC) that utilizes Alphafold2-multimer-derived graph adjacency matrices.

• Graph-pMHC outperforms existing models such as NetMHCIIpan-4.0 and MixMHCIIPred-1.2 on pMHC our curated presentation test dataset.

• We developed a method to derive an antibody immunogenicity risk assessment which produces meaningful separation between antibodies with low and high clinical ADA response.

Author Biographies

William John Thrift is a principal scientist in the department of computational sciences, Genentech, His research interests include machine learning and immunology.

Jason Perera is a bioinformatics Contractor at Genentech, his research interests include cancer immunogenomics and HLA presentation.

Sivan Cohen, PhD, is a trained immunologist and senior principal scientist in the Department of Bioanalytical Sciences at Genentech. Her research interests include investigating the mechanisms of T cell and B cell immunity, antigen prediction, and developing computational and experimental methods for assessing immune responses and antibody generation to biotherapeutics.

Nicolas W. Lounsbury is a Computational Scientist 3 at Genentech. His research interests include AI, computational biology and cancer immunology.

Hem R. Gurung is a PhD at the Department of Microchemistry Proteomics & Lipidomics. His research interests include immunopeptidomics and quantitative proteomics.

Christopher M. Rose is the Senior Director of Discovery Proteomics and a Distinguished Scientist in the Department of Microchemistry, Proteomics, Lilpidomics and Next Generation Sequencing. His research interests include quantitative proteomics, immunopeptidomics, and single cell proteomics.

Jieming Chen is an employee of Genentech (gCS). His research interests include computational biology, cancer immunology and immunotherapies.

Suchit Jhunjhunwala is a director in Oncology Bioinformatics, Computational Sciences, Genentech Research and Early Development. His interests include computational biology and machine learning in oncology and cancer immunology research.

Kai Liu is currently the Vice President of Deep Learning at SES AI corp. When this paper was conducted, Kai was the director of Artificial Intelligence at the Early Clinical Development informatics department of Genentech. His interests include machine learning, deep learning, large language models, AI agents and AI for Science.

CODE AVAILABILITY STATEMENT

Code for performing inference using our baseline Graph-pMHC model is available at: https://github.com/Genentech/gpmhc.

DATA AVAILABILITY

Our full MHCII train and test dataset is available at: https://zenodo.org/record/8429039. Baseline Graph-pMHC predictions are provided on the entire dataset, NetMHCIIpan-4.0 predictions are provided on the test portion of the dataset, MixMHCIIPred-1.2 and MHCNuggets predictions are provided on the portion of the test dataset that they can provide inference on. The 109 antibody dataset with immunogenicity rates and predicted number of peptides through our pipeline is available at: https://zenodo.org/record/8429039. The dataset of all 12–19mer peptides derived from the 109 antibodies and Graph-pMHC and NetMHCIIPan-4.0 predictions is also provided.