Abstract
Task errors are used to learn and refine motor skills. We investigated how task assistance influences learned neural representations using Brain-Computer Interfaces (BCIs), which map neural activity into movement via a decoder. We analyzed motor cortex activity as monkeys practiced BCI with a decoder that adapted to improve or maintain performance over days. The dimensionality of the population of neurons controlling the BCI remained constant or increased with learning, counter to expected trends from motor learning. Yet, over time, task information was contained in a smaller subset of neurons or population modes. Moreover, task information was ultimately stored in neural modes that occupied a small fraction of the population variance. An artificial neural network model suggests the adaptive decoders contribute to forming these compact neural representations. Our findings show that assistive decoders manipulate error information used for long-term learning computations, like credit assignment, which informs our understanding of motor learning and has implications for designing real-world BCIs.
Introduction
We learn new motor skills by incrementally minimizing movement errors and refining movement patterns [1]. This process may require forming entirely new motor control policies [2], and involves computations distributed across cortical and subcortical circuits [3]. While motor computations are distributed, behavioral improvements that emerge over extended practice as we master a skill have been linked to targeted neurophysiological changes [4, 5, 6]. Such coordinated circuit changes are thought to be mediated by a “credit assignment” process where movement errors lead to adjustment in select neural structures [7]. However, the precise mechanisms underlying the coordination of single neurons and populations are unknown, and may be difficult to detect with standard population analysis methods [8].
Intracortical brain-computer interfaces (BCIs) provide a powerful framework to study the neurophysiological signatures of motor learning and how task errors shape neural changes [9, 10]. BCIs define a direct mapping—often referred to as a decoder (Fig. 1A)—between neural activity and the movement of an external device such as a computer cursor [11, 12, 13]. The explicit relationship between neural activity and movement defined by a BCI decoder improves the ability to interpret neural activity changes and makes it possible to causally interrogate learning. BCIs have been used to apply perturbations to well-learned sensory-motor mappings, analogous to perturbations applied to natural movement [14, 15], to probe the neural mechanisms of adaptation within a single practice session [16, 17]. These adaptation studies use decoder changes to introduce task errors that are countered through changes in neural activity. Alternately, BCIs can define novel sensory-motor mappings to study de novo learning over multiple practice sessions to identify neural mechanisms potentially related to skill formation [18, 19, 20, 21]. BCI skill learning uses a decoder that provides limited task performance, again requiring the brain to reduce task errors through changes in neural activity. In stark contrast, application-motivated BCIs often manipulate decoders to improve or simply maintain task performance over practice sessions (Fig. 1A,B) [13, 22, 23, 24, 25, 26, 27, 28, 29, 30]. These assistive perturbations change the relationship between neural activity and behavior, which alters error feedback. The extent to which altered feedback from adaptive algorithms interacts with the brain’s long-term skill learning computations is not well understood.
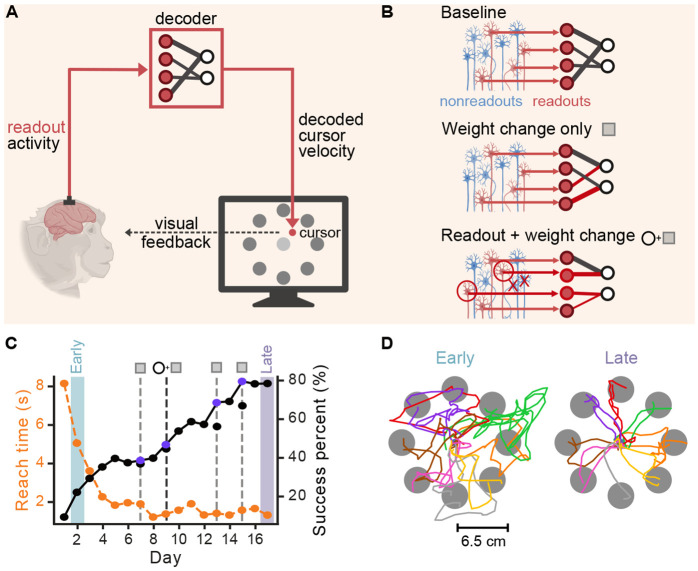
Figure 1. Experimental setup and example behavior.
(A) Schematic of BCI setup: Monkeys controlled a cursor in a 2D point-to-point reaching task using their neural activity, which was translated into cursor movements by a decoder, with visual feedback. (B) Schematic of BCI decoder mapping and adaptation. We recorded multiple units within the motor cortex: readouts (red) and nonreadouts (blue). The initial decoder mapped the activity of readout units into cursor velocities (baseline). During learning, the decoder was adapted in two ways: changing the weights relating readout units to velocity while keeping the identify of readout units constant (Weight change only), and altering both the contributing readout units and their corresponding decoder weights (Readout + weight change). (C) Success percentage (solid black line) and mean reach time (dashed orange line) across days for an example learning series for monkey J (jeev070412_072012). Early (blue) and late (purple) training phases are indicated. Vertical dashed lines indicate days where decoder was adapted - gray dashed lines (weight change only) and black dashed lines (readout + weight change). (D) Cursor trajectories during early (left) and late (right) training phases for the selected series in panel C. Monkey and neuron icons for schematics A and B are created with BioRender.com
BCI studies show that long-term learning over extended practice leads to changes in both neuronal populations and single neurons. Practice with the same decoder over several days leads to performance refinements and the formation of stable neural representations measured at the single neuron level [18]. At the population level, this learning leads to more coordinated activity across neurons and progressive decreases in the dimensionality of these coordinated patterns [31, 32], consistent with reduced neuronal variability seen in natural motor learning [33]. Yet, the BCI paradigm has revealed that some learning-related changes appear to be targeted to select neurons. BCIs define a subset of neurons the decoder uses as the direct "readout" of behavior, in contrast to “nonreadout” neurons that may take part in circuit computations but do not directly influence movement (Fig. 1B). Extended BCI practice leads to preferential task modulation of readout neurons compared to nonreadouts, consistent with the possibility that credit assignment computations contribute to skill learning [32, 34, 35, 36, 37, 38]. Population-level changes, such as increased coordination among neurons, also appear to be primarily subserved by changes in readout neurons [32].
Interestingly, neural activity also changes over extended practice with adaptive BCI decoders. Decoder adaptation updates the neural-activity–to-movement mapping to reduce movement errors. Decoder adaptation can also be used to compensate for unstable neural measurements by modifying which units are part of the readout ensemble [30] (Fig. 1B). Decoder adaptation therefore creates a dynamic mapping between neural activity and motor outcomes and yet, adaptive decoders can produce consistent, skillfull BCI control over many practice sessions [13, 23, 30, 38]. Adaptive decoders appear to interact synergistically with brain learning: if the decoder adapts very little, neural representations will shift more to improve task performance. This corresponds to reduced neural activity changes, such as shifts in neuronal tuning, when decoders adapt to provide high task performance [30]. While adaptive decoding can shift some of the need to adapt onto the decoder, as opposed to the brain, evidence suggests that decoder adaptation does not eliminate long-term skill learning processes in the brain. BCI studies using adaptive decoders to assist performance consistently observe performance improvements beyond what would be expected from decoder parameter changes, which co-occur alongside neuronal changes over consecutive days of training [13, 23, 30, 38, 39, 40]. How these learning processes are impacted by decoder changes, which alter error information, is unclear. We hypothesized that adaptive BCIs may influence properties of learned neural representations, potentially via altering the targeted and population-level neural changes that occur during BCI skill learning. Insights into whether assistive decoder manipulations influence learning computations in the brain will inform BCI applications that widely use these kinds of manipulations and provide further insights into the computations guiding long-term sensorimotor learning.
Here, we investigated how decoder manipulations that improve or maintain task performance influence the formation of neural activity patterns during skill acquisition over many days of BCI practice. We used a combination of experimental data from our previous co-adaptive BCI learning study [30] and a recurrent neural network (RNN) model to explore the influence of adaptive decoders. The experimental data provided insights into real-world neural adaptation, while the RNN model allowed for direct comparisons that are challenging to perform experimentally. Motivated by the learning dynamics observed in previous multi-day BCI studies, we used a combination of population- and neuron-level analysis methods. We found that adaptive decoding altered trends in neural population activity, leading to little change or increases in the variance and dimensionality of solutions with learning. Yet, we also found that the learned neural representations were highly targeted to a subset of neurons, or neural modes, within the readout population. To further elucidate this finding, we then used RNN models to compare learning dynamics and neural representations with and without decoder adaptation in a controlled and idealized setting. Doing so, we showed that decoder manipulations actively contribute to establishing the compact representations observed in our experimental data. Our combination of analyses and simulations revealed seemingly contradictory learning dynamics at the level of individual neurons and the population. Reconciling these perspectives revealed that the learning we observed in adaptive BCIs occurs largely in low-variance components of the neural population, which are often less studied and missed by standard population analysis methods [8]. Together, our findings provide evidence that adaptive decoders influence the encoding learned by the brain. This sheds new light on how manipulating error feedback shapes neural activity during learning.
Results
Two rhesus macaques (monkeys J and S) learned to perform point-to-point movements with a computer cursor controlled with neural activity (Fig. 1A), as previously described [30]. We measured multi-unit action potentials from chronically-implanted microelectrode arrays in the arm area of the primary- and pre-motor cortices. The binned firing rate (100 ms) of a subset of recorded units, termed readout units, were fed to a Kalman filter decoder that used neural activity to control cursor velocity and position (Fig. 1A-B). The subjects were rewarded for successfully moving from a central position to one of eight targets within an allotted time and briefly holding the final position (Fig. 1C, D).
Each monkey learned to control the cursor over several consecutive days, which we call a learning series. We focused on learning series lasting four days or longer (N = 7 for monkey J; N = 3 for monkey S). Learning series used different methods to train the initial decoder, varied in length, and included different numbers of adaptive decoder changes (Closed-Loop Decoder Adaptation (CLDA) events, see Methods). The amount of initial CLDA varied across series, but aimed to provide sufficient control to move the cursor throughout the workspace, ensuring all targets could be reached. Midseries CLDA events solely aimed to maintain performance when neural measurements varied. As previously shown [30], performance improved over multiple days, resulting in increased task success rates and decreased reach times (Fig. 1C, a selected series for monkey J; all subsequent single-series example analyses use this series for consistency. See Fig. S1A for an example series for monkey S, and Fig. S1C for an additional example series from Monkey J). The decoder was adapted during learning to adjust the parameters ("weight change only", Fig. 1B) or to replace non-stationary units and update parameters ("readout + weight change", Fig. 1B). Readout unit selection for both initial decoder training and in the event of readout ensemble changes were based on unit recording properties (e.g., stability of measurements) only; functional properties such as information about the task or arm movements were not considered. To quantify learning within each series, we defined an ‘early’ and ‘late’ training day, which correspond to the first and last day of a learning series with at least 25 successful reaches per target direction, respectively (day 2 and 17 in Fig. 1C, D). To increase the number of trials to analyze on early days, we included any trial wherein the target was reached whether or not they held successfully once reaching the target. Improvements in task success rate and reach time were accompanied by more direct and accurate reaches (Fig. 1D , Fig. S1B and [30]). The dataset included series where the amount of CLDA performed on day 1 varied, resulting in varying initial performance [30]. The selected series (shown in Fig. 1C, D) is an example where minimal CLDA was performed on day 1. Performance improvements were observed across all series, including series where CLDA led to high performance on day 1 [30].
Adaptive decoders alter the evolution of neural population dimensionality during learning
Decreased trial-to-trial variability, leading to lower-dimensional neural activity patterns, is a hallmark of motor learning in natural [33, 41, 42] and BCI systems [31]. We therefore examined trends in neural dimensionality to explore population-level learning phenomena in the presence of an adaptive decoder. We quantified the overall population dimensionality using the participation ratio (PR), a linear measure derived from the covariance matrix [43, 44]. When PR = n, neural activity occupies all dimensions of neural space equally; when PR = 1, activity occupies a single dimension. To ease comparison across series, animals, neural populations and experiments, we normalized PR using the number of units to yield , which varies between 0, when PR = 1, and 1, when PR = n (see Methods).
Counter to expectations from other motor learning studies, we did not observe decreases in dimensionality of neural activity patterns in BCIs with adaptive decoders (Fig. 2). We found that dimensionality either increased or did not change between early and late days across series and animals (Fig. 2A,B). This trend was also preserved when considering non-normalized PR (Fig. S2L). (Also see Fig. S2M for late dimensionality in relation to number of readouts.) To control for the possibility that analysis differences could explain our findings, we applied the same participation ratio measures of dimensionality to data from closely-related BCI experiments with a fixed decoder [18, 31, 32] . We confirmed that showed the expected decreasing trend across multiple animals in absence of CLDA (Fig. 2B (control) and Fig. S2A). We note that the time axes used to analyze the fixed and adaptive datasets are different. Due to poor performance in early days for the fixed decoder, we adopted the approach of grouping data into epochs, defined as segments with a consistent number of trials [31, 32]. The adaptive decoder led to a sufficient number of trials in the early learning stages to track dimensionality trends across days. These differences in the time axes may reduce our resolution of ’early’ days, but still allow us to compare changes across many days, which is our primary focus. Moreover, the trend of non-decreasing dimensionality for adaptive decoders were robust to changes in analysis, including: square-root-transforming spike counts (to “gaussianize” them [45]; Fig. S2B), using other non-linear dimensionality metrics (Two NN [46, 47]; Fig. S2B), changing the day used as "early" (Fig. S2C), considering only the readout units that were consistently used throughout the entire BCI series (stable readouts only) (Fig. S2D), or using an alternative normalization of the participation ratio (Fig. S2E). Additionally, the non-decreasing dimensionality trends were specific to BCI training and did not appear in arm control task data collected on the same days as BCI training, ruling out recording instabilities as a possible explanation for the observed trends (Fig. S2K). We did not observe a consistent trend in the dimensionality of nonreadout units during learning, suggesting that learning-related changes were primarily targeted to the readout population (Fig. S2F).
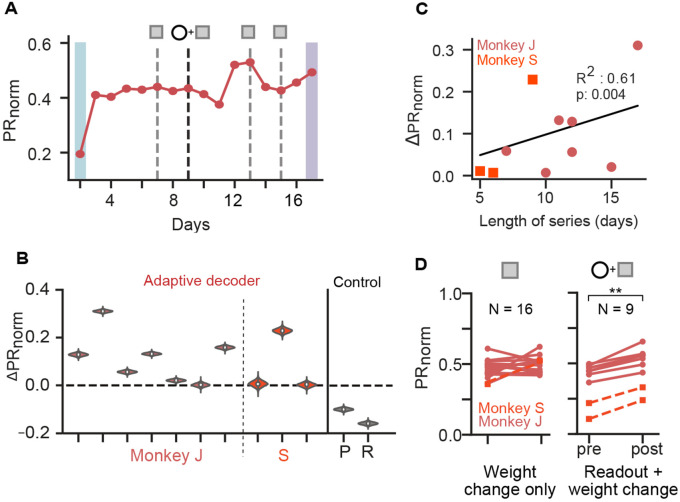
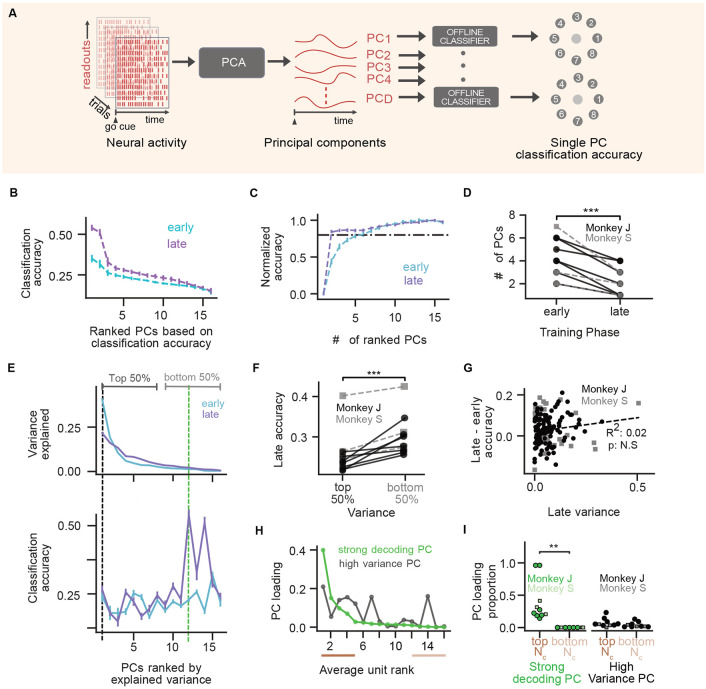
Figure 2. Assistive decoders influence neural population dimensionality.
(A) Normalized participation ratio () for an example adaptive decoder learning series (same as in Fig. 1D). Error bars are 95% confidence intervals estimated via bootstrapping (see Methods). Note that most error bars are hidden by data point markers. (B) distributions for learning series with adaptive decoders (N = 7 for monkey J and N = 3 for monkey S). Control data is from 2 monkeys (P and R) using fixed decoders (data from [18]). (C) as a function of training duration in days. (D) before and after decoder adaptation, grouped by the type of change (with (right) and without (left) readout unit changes) across all series and monkeys (Weight change only: p = 0.16 (ns), N = 16; readout + weight change: p = 0.0039 (**), N = 9, for pre < post, one-sided Wilcoxon signed-rank test).
We then aimed to understand potential drivers of dimensionality changes (or lack thereof) in the presence of decoder adaptation within each series. We found that the change in dimensionality was moderately correlated with the duration of training with an adaptive decoder (Fig. 2C). This result suggests that prolonged interactions with the changing decoder contributed to dimensionality changes. To better understand whether decoder adaptation events drove changes in dimensionality, we compared before and after each adaptation event. Importantly, the experiments include two types of decoder changes: those where the units remain the same (weight change only), and those where the readout units were changed along with the decoder weights (Fig. 1B). We found that decoder adaptation events led to significant increases in dimensionality, but only when readout units were changed (Fig. 2D, right). This effect, however, was not observed when considering only the stable readout ensemble, which controls for changes in the readout ensemble membership (Fig. S2G,H). Together, these results reveal that decoder adaptation influences the evolution of neural population dimensionality during learning and highlight the importance of readout unit identity (and changes thereof) in learning dynamics.
Brain learning leads to credit assignment to readout units
Adaptive decoders were associated with changes in the long-term trends for the population variance compared to fixed decoders, suggesting that decoder adaptation influences neural responses.. Variance alone, however, may not capture the extent of the relationships between task variables and neural activity. Further probing neural representations during skill acquisition, however, is challenging because the behavior also changes (e.g., kinematics of trajectories change dramatically, Fig. 1C,D). We therefore used an offline classification analysis to quantify how information about the fixed target identity is distributed within neural activity during learning. As further outlined below, we wished to derive a quantity that would act as a proxy for the predictive contribution of neural activity to the task, i.e. its assigned credit, that is not necessarily captured by population variance the decoder used for the task. To this end, we used multiclass logistic regression to predict target identity on each trial using trial-aligned neural activity (Fig. 3A; Methods). The classifier was trained anew each day and all classification accuracies were computed using cross-validation (Methods). We note that, while powerful, the offline classification analyses did not extend as readily to fixed decoder datasets, due in part to limited numbers of trials, and we therefore focus on adaptive decoder datasets hereafter. We will revisit comparisons of different decoder paradigms using closely-related analyses within our RNN model, which allows exhaustive and more systematic comparisons that lead to important validations and insights.
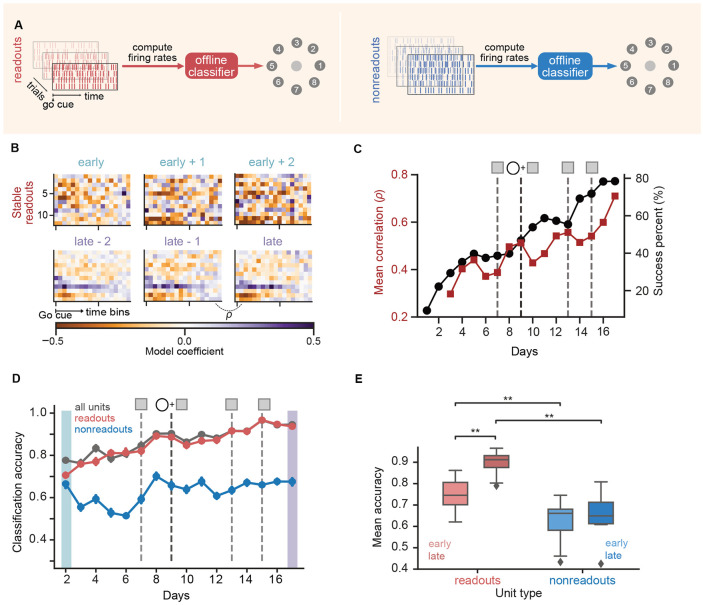
Figure 3. Credit assignment to readout units.
(A) Schematic of offline classification model. (B-D) Classifier analyses results for the selected series (Fig. 1D). (B) Heatmap representation of the classifier weights to predict a single target (2) for the stable readout population on multiple days. (C) Success percentage (black; reproduced from Fig. 1D) and mean correlation coefficient (dark red) between classifier weights on consecutive days plotted across days. (D) Classification accuracy for all units (gray), readout units (red) and nonreadout units (blue) across training days. Error bars represent 95% confidence intervals on test accuracy (see Methods). (E) Early vs late classification accuracy for readout (shades of red) and nonreadout populations (shades of blue) across all series for both monkeys (readout-early vs readout-late : p = 0.0058 (**); readout-early vs nonreadout-early: p = 0.0019 (**); readout-late vs nonreadout-late: p = 0.0019 (**); nonreadout-early vs nonreadout-late: p = 0.13 (ns). For all comparisons in this panel, N = 10, Two-sided Wilcoxon Signed Rank test)
The logistic regression model weighted the contribution of each unit’s firing rate towards classifying target identity. These weights thus represent an encoding of task information, and are related to parametric analyses of neuron activity such as direction tuning (Fig. S3C). We found that optimized classifier weights varied day to day, but became more similar as learning progressed (Fig. 3B). The correlation coefficient of the weights of stable readouts on consecutive days increased during learning (Fig. 3C), consistent with a progressive stabilization of task encoding representations that mirrors performance improvements (Fig. 1D). These findings are consistent with previous observations that co-adaptive BCIs lead to stable directional tuning in readout neurons [30].
We then used offline classification to assess credit assignment by examining how task information was distributed between readout and nonreadout neural ensembles. The classification accuracy of target identity increased during BCI training when using all neurons, mirroring the improvement in BCI performance (Fig. 3D). However, this improvement in classification accuracy was mostly driven by the readout units (Figs. 3D, E). Across series, classification accuracy was higher for the readout units compared to the nonreadout units, both early and late in training. More importantly, only the readouts’ accuracy significantly increased from early to late (Figs. 3E; Fig. S3F for individual animal results), showing that learning-related changes in classification accuracy are driven predominantly by changes within the readout population. The distinct difference in classification performance between the two neural populations is particularly striking when considering that the experiments used notably fewer readout neurons than nonreadouts (Monkey J: 15-16 readouts, 29-41 nonreadouts; Monkey S: 11-12 readouts, 66-121 nonreadouts). Similar results were obtained with other classification models, such as Support Vector Machines, Naive Bayes, or logistic regression with different penalties (Fig. S3A). To rule out the possibility that these differences in classification accuracy simply reflected other factors such as neural recording quality, we performed the same analysis on data recorded when Monkey J performed the same task via arm movements, which showed no significant difference between the readout and nonreadout populations for size-matched neural populations (Fig. S3D, E). Further, to tease out the possibility that changes in performance (e.g., task kinematics) with learning might confound task information measures, we analyzed neural activity immediately after the go cue (0-200 ms) before feedback likely impinges on neural dynamics. We found that target identity was encoded from movement onset, with readouts showing significant increases in classification accuracy but no significant change in nonreadout populations (Fig. S3G). To examine whether decoder interventions specifically contributed to these credit assignment computations, we compared classification accuracies pre- and post-decoder change events. We did not observe any significant changes (Fig. S3H), suggesting that credit assignment processes emerged over longer timescales. Thus, despite altered population variance, assistive decoder perturbations lead to the formation of a stable neural encoding that is primarily instantiated by readout units, similar to BCIs with fixed decoders [18, 34]. This further shows a coarse-grained signature of credit assignment computations relevant to behavior acquisition.
Brain learning leads to compaction of neural representations
Our classifier analysis revealed a striking pattern: within a given readout ensemble, a small number of readouts carried the majority of weight for target prediction (Fig. 3B, bottom row). This suggested credit assignment processes may also occur within the readout population. To quantify whether specific readouts contained more task information than others, we conducted a rank-ordered neuron adding curve analysis [48]. This technique quantifies the impact of each unit’s inclusion to the overall classification performance to identify the most influential neurons. On each day (early, late), we first quantified the classification accuracy of a unit in isolation, and then constructed a rank-ordered neuron adding curve by adding units to our decoding ensemble from most to least predictive (Fig. 4A).
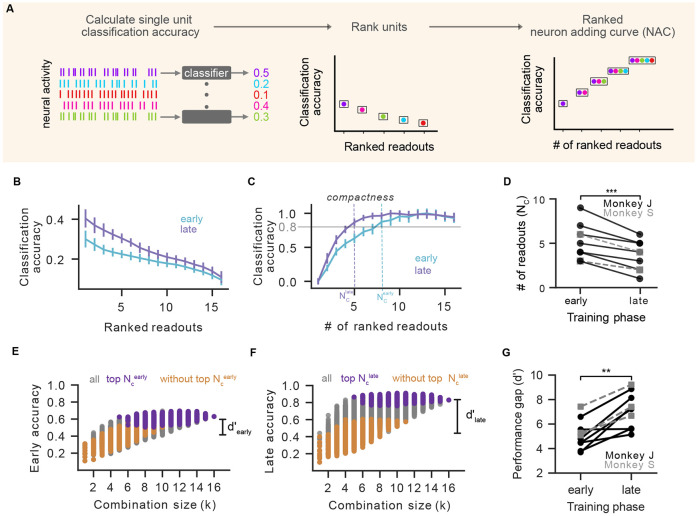
Figure 4. Learning leads to compaction of neural representations:
(A) Schematic of the ranked Neuron Adding Curve (NAC) analysis. We first estimated classification accuracies of individual units (left), ranked units based on their classification power (middle) and then constructed a neuron adding curve by starting with the best unit, adding the second best unit and so on (right) (see Methods). (B) Ranked classification accuracy of individual units on early (cyan) and late (purple) day for the selected series. (C) Ranked NAC on early (cyan) vs late (purple) day for the selected series. Each day’s classification accuracy was normalized to the day’s peak performance. Vertical dashed lines indicate number of units required to reach 80% of peak accuracy (). (D) Comparison of and across series (, p = 9.8 × 10−4(* * *), N = 10, one sided Wilcoxon signed-rank test). Monkey J data shown in black circles; monkey S shown in grey squares. (E) Classification accuracy as a function of readout population size (combinatorial NAC) for early day. Combinations with top units (deep purple) and without top units (orange). Distance between distributions defined as the discriminability index . (F) Same as (E) for late day. (G) Comparison of distance between distributions between early and late learning ( vs ) across series (, p = 1.9 × 10−3(**), N = 10, one sided Wilcoxon signed-rank test). Formatting as in panel D.
As expected given overall improvements in classification, individual unit classification accuracy improved between early and late learning (Fig. 4B). Beyond these global shifts, the relationship between classification accuracy and the number of ranked readout units used for prediction changed with learning. To visualize this, we normalized each day’s neuron-adding curves, which revealed that the classification accuracy reaches plateau more rapidly late in learning compared to early (Fig. 3C, see Fig. S4A for non-normalized curves). We quantified this effect by computing the number of neurons needed to reach 80% of the normalized classification accuracy () at each learning stage (Fig 4C, D). We found that fewer readout neurons were needed to accurately predict task behavior across all learning series (Fig 4D). This phenomenon was even larger when performing the same analysis on all recorded units (readouts and nonreadouts, Fig. S4B). Shifts in the number of neurons needed to accurately predict target identity were not observed in arm movement tasks, suggesting changes were specific to BCI learning and not related to recording quality or drift (Fig. S4C). Interestingly, beyond this within-series (early vs. late) trend, we noticed a general decrease in across chronologically-ordered series for each animal (Fig. S4D). We explored whether there was a correlation between the amount of compaction and the number of readout units added or removed by decoder perturbations, but our data did not reveal a clear trend (Fig. S4F). Moreover, late in learning a smaller proportion of readouts was necessary to accurately reconstruct cursor velocities offline, suggesting changes in the neurons contributing to skilled movement (Fig. S4G-I and Supplementary Methods). We term this reduction in the number of neurons needed to accurately decode behavior over time ’compaction’, to indicate the brain forming an encoding of task information with a smaller number of neurons.
We then asked whether the compaction of neural representations reflected a situation where task information was encoded within a specific subset of readout neurons, or a more general increase in encoding efficiency. We performed a combinatorial variant of the neuron-adding curve analysis, in which we computed classification accuracy for all combinations of units as we vary the number of units used to decode (within readout units only). On each day, we identified the top readout units and labeled combinations that contained all top units (purple), did not contain any of the top units (orange), combination that contained some of the top units (gray) (Fig 4E,F). Early and late in learning, combinations with top units held the most classification power (Fig 4E, F). Comparing the distributions between early and late, however, reveals that the overall increase in classification power was driven solely by the increase in classification power from top units. We quantified the performance gap between combinations with or without the top units using a discriminability index (), which quantifies the impact of the most influential units on overall accuracy. This performance gap increased with learning across series (Fig 4G), showing that learning-related changes in target encoding are targeted to a specific subset of readout neurons.
The compaction of neural representations may seem at odds with the non-decreasing population dimensionality (Fig. 2). An explanation of this apparent contradiction can be found in Fig. 6 below, where it will be revealed that task information actually comes to reside in low-variance modes on late day, allowing dimensionality to remain equal to or higher than that on early day. Before untangling these threads, we first investigated more directly the role of decoder adaptation in generating more compact neural representations by using a model of the BCI task.
Figure 6. Task information emerges in low-variance modes.
(A) Schematic of decoding analysis with PC modes. (B) Individual PC classification accuracy (similar to Fig. 4B) for early (cyan) and late (purple) learning phases from selected series. PCs ranked by classification accuracy. (C) Ranked dimension adding curve (similar to ranked NAC in Fig. 4C) for early and late days for the example series. (D) Comparison of number of PCs needed for 80% classification accuracy on early and late days across series( late < early, , (p = 9.7 × 10−4, N = 10), one sided Wilcoxon signed-rank test ). Monkey J data shown in black circles; monkey S data shown in grey squares. (E) Top: Variance explained by each PC (ranked by variance explained). Bottom: Classification accuracy per PC, ordered by variance explained, Error bars denote 95% confidence intervals from 104 random draws of trials. The strongly decoding PC (green) has the highest accuracy. (F) Comparison of mean classification accuracy from top 50% vs bottom 50% PCs during late learning day across series (Top 50% is lower than bottom 50%: p = 0.001, N = 10, one sided Wilcoxon signed-rank test). Data formatting as in D. (G) Change in classification accuracy (late - early) plotted versus late variance per PC. No significant trend (R2 = 0.01, p = 0.26, N = 10). Data formatting as in D. (H) Square of PC loadings from each readout unit for the strong decoding PC (green) and high variance PC (black). Units on the x-axis are ranked by their average classification performance. (I) Comparison of sum of squares of PC loadings from top 4 ranked readouts and bottom 4 ranked readouts from strong decoding PC and high variance PC across all series. (strong decoding PC: p = 0.0019(**), N = 10; high variance PC: p = 0.3750(n.s), N = 10, two sided Wilcoxon signed-rank test ).
Assistive decoder adaptation contributes to learning compact representations: modeling analysis
Our analysis of neural data revealed that BCI training with assistive decoder perturbations led to compact neural representations over multiple days. However, it is unclear whether these representations reflect a general property of sensorimotor learning, or if the adaptive decoder played a causal role in shaping learned representations. Furthermore, current BCI experimental data may miss potentially confounding population-level mechanisms due to practical limitations like sparsely sampled neural activity and an inability to measure in vivo synaptic strengths. To explore these possibilities and causally test the influence of assistive decoders, we simulated BCI task acquisition using an artificial neural network (Fig. 5A). With this model, we could directly compare the BCI learning strategies for identically initialized neural networks when training with a fixed or an adaptive decoders. The precise question was whether compact representations still emerge without decoder adaptation.
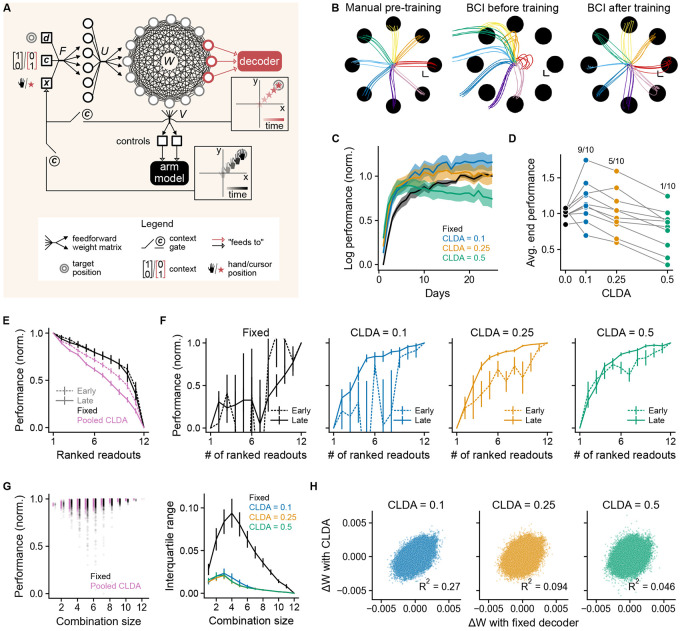
Figure 5. Decoder adaptation contributes to learning compact representations: modeling analysis.
(A) Model schematic. Input (target position , context information and visual feedback about the cursor/arm state) was encoded using a random linear projection via matrix . Outputs of the recurrent neural network (with input, recurrent and output weight matrices , and , respectively) were controls that drove a two-link planar arm model. Sensory information came from either the BCI cursor or the model arm, depending on the state of the context gates. (B) Learning stages. The network (here with CLDA intensity = 0.25) was first trained on the arm movement task (left), then decoder parameters were fitted using arm trajectories (middle) and, finally, the context was set to ‘BCI’ and the network was trained on the BCI task (right). Scale bars are 1 cm. (C) Normalized log performance (Methods, Eq. 7) for different CLDA intensities. (D) Normalized log performance averaged over last 5 days. Ratios at the top are the fraction of seeds for which the performance with the adaptive decoder was greater than with the fixed decoder. (E) Ranked individual-unit normalized performance (Methods, Eq. 8). Results for adaptive decoders were pooled together (pink lines). (F) Unit-adding curves analogous to NAC but evaluates online performance in model as units are added (Methods, Eq. 9). (G) Combinatorial unit-adding curve for a given random initialization of the network parameters (left) and interquartile ranges of the distributions across realizations (right). (H) Change in recurrent weights () with CLDA as a function of the corresponding change with a fixed decoder. In panels C, E, F and G (right), we plotted mean ± SEM, for n = 10 seeds, i.e. random initializations of the network.
The model was composed of a recurrent neural network (RNN) representing a motor cortical circuit and receiving sensory and task information (Fig. 5A). Our goal was to study the simplest model consistent with biology and that reproduces basic learning dynamics of BCI experiments. We first trained the network on an arm movement center-out task (Fig. 5B, left) to establish a plausible inductive bias for the subsequent BCI training and to mirror the experimental approach which consisted in training the subject on arm-based tasks prior to BCI training [30]. Context information about the nature of the task (arm vs BCI) was provided to the network together with information about the position of the effector and of the target. After the initial arm movement training, the context was switched to ‘BCI’, a random subset of 12 units (out of 100 in the network) was selected to be readouts, and a velocity Kalman filter (see Methods) was trained on manual reach trajectories (Fig. 5B, middle). Finally, the network was trained on the BCI task (Fig. 5B, right). In all contexts the REINFORCE algorithm [49] was used to update the parameters of the recurrent neural network and of the input layer (matrix in Fig. 5A); all other parameters (encoding matrix and output matrix ) were randomly initialized and remained fixed. REINFORCE does not rely on the backpropagation of task errors through the BCI decoder or the arm model, thus making it more biologically plausible.
Assistive decoding in the model followed CLDA algorithms used in experiments [30]. We virtually rotated actual cursor velocities towards the target position (under the assumption that this corresponds to the user’s intention), refit the decoder, and then updated decoder parameters (see Methods). We did not change the readout ensemble during BCI training (Fig. 1B, middle) to focus on the impact of decoder weight changes on learned representations. CLDA was performed on each “day”, with a day corresponding to seeing each target 100 times. Irrespective of the CLDA intensity (a factor representing how much the decoder was changed; see Methods, Eq. 2), an adaptive decoder sped up performance improvements in the first days compared to a fixed decoder (Fig. 5C). However, CLDA did not necessarily improve the final BCI performance (Fig. 5D). A possible explanation is that CLDA’s objective, “reach towards the target”, was conflicting with the task objective, “reach the target with vanishing velocity in a specified time” (Methods, Eqs. 4-5). Towards the end of training, the task objective was nearly completed and therefore large decoder alterations negatively impacted performance. We reasoned that stopping CLDA when a given performance threshold has been attained could help recover good end-of-training performances. Using such protocol, we obtained equal or better end-of-training performances for all CLDA intensities (Fig. S5A). Overall, decoder-weight adaptation in the model facilitated acquisition of the BCI task, as in experiments, and underscored potential shortcomings of its undiscerned long-term application.
Next, we explored whether representations became more compact with learning in the model. While this property of neural representations had to be assessed offline in the data (Fig. 3), the model allowed for an online computation using the loss (Methods, Eqs. 4-5) as the performance metric. Each individual readout unit was used to move the cursor in turn and reach performance was evaluated both ‘early’ (at the end of the first day) and ‘late’ (at the end of the last day) during training. Readout units were then ranked according to their reach performances. Differences between the early and late individual unit performances (Methods, Eq. 8) appeared only for adaptive decoders (Fig. 5E and Fig. S5C,E), with the ranked contribution of each unit decreasing faster late in training compared to early (Fig. 5E, pink lines). Thus, at the individual unit level, the dominant units became relatively more dominant on average under co-adaptation of the network and decoder parameters. We then used these individual unit rankings to compute a ranked NAC (Methods, Eq. 9). Consistent with our findings based on experimental data, adaptive decoders contributed to evoking more compact representations of task performance (Fig. 5F and Fig. S5D). With a fixed decoder, the ranked NAC for the early and late stages had a large degree of variability across seeds, and there were no signs of increased compactness late in training as 11 ranked readout units were required to reach 80% of the maximal performance (Fig. 5F, left). We also note that stopping CLDA early in training not only helped recover good performances (as mentioned above), but it also tended to prevent the emergence of compact representations (Fig. S5B). Our model thus suggests decoder-weight changes single-out certain units for BCI control and progressively shape more compact task representations.
Using the online loss metric, we next obtained combinatorial unit-adding curves (Fig. 5G, left) and computed the corresponding interquartile ranges (IQR; Fig. 5G, right). These IQRs measured the dispersion of performances (Methods, Eq. 10) for each combination size. The IQRs were significantly greater for a fixed decoder, which was caused by few units with very low contributions to the overall performance (Fig. 5E and Fig. S5C). Therefore, while decoder adaptation contributed to compact representations characterized by only a few dominant units (with potential impacts on the long-term robustness of BCIs; see Discussion), it also seemed to protect against these unreliable units.
Both in the model and in the data, BCI learning with an adaptive decoder evoked compact representations of task information. Moreover, the model suggests that neural plasticity alone (i.e., learning the network parameters with a fixed decoder) does not produce compact representations on average. This suggests that decoder adaptation must interact with brain plasticity to shape this feature of neural representations. To show this, we calculated the total changes in recurrent weights across learning, , with and without decoder adaptation, and computed their coefficients of determination (Fig. 5H). All connections—among and across readout and nonreadout units—were included, because all connections participate in the network dynamics (Methods, Eq. 3). Since our simulations were precisely matched in terms of random number generation across CLDA intensities, comparing these weight changes one-to-one was meaningful. The coefficients of determination decreased when the CLDA intensity increased, meaning that the total weight changes with the adaptive decoder became increasingly uncorrelated from the total weight changes with a fixed decoder. Overall, these results suggest that brain-decoder co-adaptation elicits specific plastic changes in neural connections which underlie the emergence of more compact representations.
Reconciling population and unit-level perspectives: task information emerges in low-variance modes
Our model results showed that plasticity was altered by the presence of assistive decoders, leading to the formation of neural representations that become compact at the unit-level observed in our experimental data. However, our experimental data also revealed that the assistive decoder influenced learning phenomena at the level of neural populations, eliminating (or even reversing) reductions in neural population dimensionality that are often observed in sensorimotor learning (Fig. 2). How is it possible for task representations to become contained within a small number of neurons without decreasing the population dimensionality? To reconcile these two seemingly-conflicting descriptions of learning trends, we developed and performed a series of analyses to link population-level descriptions of neural activity to task information and neurons.
We first asked whether the phenomenon of compacting representations was specific to unit-level representations, or would also be observed within population-level descriptions of neural activity. We performed a variation of our neuron-adding curve analysis where we used population-level "modes" as the relevant neural features for classification instead of individual units. We estimated population-level modes for each day (early, late) using principal components analysis (PCs) (see Methods) and then used neural activity projected onto these modes for classification (Fig. 6A). We ranked PCs based on their classification accuracy (Fig. 6B) and performed a rank ordered PC adding curve (Fig. 6C). Similar to the compaction observed at unit level, We found that the number of PCs required for 80% classification accuracy decreased with learning (Fig. 6C,D). These results show that learning leads to the formation of task representations that are compact in terms of individual units and population modes, an observation that is not trivially true in general (see Supplementary Discussion).
We then aimed to understand how representations can more compactly represent task information without necessarily decreasing in dimensionality. We did this by linking variance captured by population-level modes with task information across learning. As learning progressed, variance was more distributed across modes (Fig. 6E, top), as expected from dimensionality analyses. Yet, if we examine classification accuracy, we see that modes which capture the largest variance of population activity were not necessarily strongly predictive (Fig. 6E, bottom). To quantify the relationship between variance-explained and task information for population modes, we divided PCs into two groups for each learning series: the top 50%, which explained approximately 80-84% of population variance, and the bottom 50%, which explained 16-22% of population variance. Across all learning series, the average classification accuracy on late days was larger in the bottom 50% group compared to the top 50% group (Fig. 6F), showing that task information was more often found in low-variance modes after learning. Moreover, changes in task encoding during learning were not correlated with the variance explained by that mode (Fig. 6G). Thus, adaptive decoders lead to the formation of compacted representations that do not decrease in overall population dimensionality because task-relevant information becomes embedded in the low-variance modes.
Lastly, we examined whether, after learning, task-predictive units contributed preferentially to task-predictive population modes. We ranked readouts based on their single unit predictive power and then quantified their influence on PC modes using the squared PC loadings (the loadings are the components of the eigenvectors of the activity covariance matrix; see Methods for more detail). Comparing PC loadings for an example high-variance PC with those of a strong decoding PC revealed starkly different patterns of unit contributions (Fig. 6H). As expected, strongly decoding PCs receive large contributions from strongly decoding units. In contrast, high variance PCs have contributions from a seemingly random mix of units, both task decoding and not. To quantify this effect across all learning series, we calculated the sum of squared PC loadings from the top task predictive units vs. bottom task predictive units for the strongest decoding PC and highest variance PC in each series (Fig. 6I). Strongly decoding PCs consistently drew more from the top-performing units, with negligible input from the least predictive units, a pattern not observed in high variance PCs (Fig. 6I). This suggests task information is encoded in low variance population modes, and that population activity dimension might not be indicative of coding mechanisms, especially in the presence of significant credit assignment learning phenomena like those found with with assistive decoders.
Discussion
Our study reveals that learning with assistive sensory-motor mappings in brain-computer interfaces (BCIs) influences the neural representations learned by the brain. Specifically, we found that assistive decoder perturbations led to neural representations that compact task information into a small number of neurons (or neural modes) which capture a relatively small amount of the overall neural population variance. Our analyses reveal new insights into the neurophysiological changes underlying skill learning with adapting sensory-motor maps, and highlight the complex mixture of targeted neuron-level and distributed population-level phenomena involved. These findings shed light on the neural computations driving skill acquisition and their relationship to adaptive error manipulation. Moreover, our results expose a critical entangling of how neural populations "encode" task information and the algorithms we use to "decode" that information, which has important implications for designing BCI therapies.
Neural variability and the encoding of task information within low-variance neural modes
A hallmark of motor learning is gradual reduction in behavioral variability that correlates with a reduction in neural variability [33]. BCI learning with fixed decoders seems consistent with this characterization [31]. Factor analysis indicates that the amount of neural variance that is “shared” among neurons increases with learning while private, unit-specific, variance decreases [31, 32]. Moreover, both the shared dimensionality—which is based on shared covariance only [31, 32]—and the overall neural dimensionality (Fig. 2C, left) tend to decrease. We found that BCI learning with adaptive decoders leads to departures from these trends in dimensionality (Fig. 2C, right). Preliminary results also suggest that private variance, but not shared variance, might behave differently for fixed- and adaptive-decoder BCI learning [50]. Therefore, it appears that assistive decoders may engage additional learning processes at the level of individual neurons that support the non-decreasing dimensionality.
Why does the variability of individual neurons become important in BCI skill acquisition with an adaptive decoder? The participation ratio (our dimensionality metric) and other variance-based analyses provide limited insight because they do not take task information explicitly into account. In contrast, the offline classification of target identity with neural data (Fig. 4) and the online assessment of neuronal contributions to control in the model (Fig. 5) integrate such information. These analyses, paired with our RNN model, revealed that adaptive decoders strongly influence which neurons participate in the task, leading to a more exaggerated credit assignment to fewer neurons. Moreover, offline classification using population activity modes suggested why dimensionality does not decrease: late in learning, task-relevant information was preferentially contained within modes that capture relatively low variance in the neural population (Fig. 6). While variance-based analyses have uncovered important aspects of neural computation, they may overlook key mechanisms that operate locally and in low-variance modes [8].
We cannot yet identify the mechanisms leading the brain to learn this type of representation, but recent studies offer possible hypotheses. Adapting to altered dynamic environments in arm movements produces “indexing” of stored motor memories within motor cortex activity in non-task-coding dimensions [51]. Do adaptive BCIs drive the brain to store motor memories in spaces that are distinct from other tasks? This possibility is consistent with our finding that dimensionality tends to increase with longer series, where more decoder perturbations occur (Fig. 2D). Previous studies also propose that sparse, high-dimensional neural representations enhance computational flexibility [52, 53, 54]. Our paired observations of increasingly compact representations that do not decrease in dimensionality suggests that adaptive BCIs may increase pressure on the brain to learn efficient and flexible solutions. A testable prediction of this hypothesis could be that the neural activity of natural motor control interferes less with learned BCI representations emerging from adaptive mappings compared to fixed mappings.
Signatures of learning at multiple levels
We investigated how task information is represented at the level of neural ensembles, population modes and multi-unit activity, and we examined relationships between these representations. As in prior work [32, 34, 35, 36, 37], we observed learning processes specifically targeted the readout ensemble, which we interpret as a form of credit assignment (Fig. 3D,E). Within the readout ensemble, credit was assigned more strongly to specific units (Figs. 4, 5). Representations also became more compact with learning when we considered a population-level description of readout activity involving principal components rather than units (Fig. 6B-D). Importantly, population-mode compactness does not trivially follow from unit-level compactness in general (see Supplementary Discussion), despite the dominant units contributing to the strongly-decoding low-variance modes (Fig. 6H-I). These results suggest that the learning and credit-assignment computations we observe during extended BCI practice operate at multiple levels, from ensembles to units and to population modes. How these different mechanisms interact remains an open question.
BCI perturbations that disrupt performance have also revealed neural changes at multiple levels. In some experiments, the preferred decoding directions of a subset of the readout units were artificially rotated, effectively implementing a visuomotor rotation [16, 37]. Adaptation to the perturbation was first dominated by global changes to neural activity which affect both the rotated and non-rotated units [16], while more local changes appeared over time on top of these global changes [37]. In other experiments, the BCI was designed to control the cursor via shared population factors and the perturbation could be either aligned or not with this mapping [17]. Aligned perturbations are learned on short time scales (within a day) because neural correlations can be repurposed rapidly [55]; unaligned perturbations can be learned only over many days because some degree of neural exploration outside the correlation structure is required [56]. These experiments suggest a strong link between the training duration after a perturbation and the neural representation level at which learning occurs.
The analyses used in our study cannot precisely resolve timescales of learning computations, in part because of the inherent difficulty to quantify changes in neural activity during skill acquisition. Indeed, existing analysis methods are often designed to leverage assumptions about common structure in neural dynamics invariant over time [57]. In experiments involving disruptive perturbations of well-practiced skills, the consequences of the perturbation can be directly compared to representations acquired before the perturbation. Such shared structures stem in part from consistency in behavior [41, 42], which is not necessarily true when a new ability is being acquired (e.g., Fig. 1C,D) and the differences we seek to measure are themselves changes over time. To circumvent some of these difficulties, we have focused on the encoding of target identity, which does not vary from day to day (in contrast to cursor trajectories) and thus facilitates a fine-grained comparison of early and late representations (Figs. 4 and 6). However, we did not test whether this method could yield significant results at finer temporal scales. Ultimately, a better understanding of the neural computations underlying skill acquisition, with or without assistive devices, will likely require developing new analytical approaches.
Adaptive decoders shape learned representations via error manipulation
Our findings add to our understanding of how the decoders we use in a BCI shape the encoding learned by the brain. Past work highlights how decoders can influence the learning demands placed on the brain. For example, the brain may only reorganize neural activity patterns when the decoder is changed in such a way that violates existing neural population correlations [17, 56]. Similar to this, adapting a BCI decoder to improve initial task performance also reduces the degree to which neural representations, such as direction tuning, change [30]. Our findings reveal new observations that assistive decoder perturbations notably alter the structure of learned neural activity patterns over time. These findings highlight the complexity of "error" signals in BCI learning. Most studies perturb decoders to introduce task errors [16, 17, 37, 55, 56]. In contrast, our experiments incorporate decoder perturbations that either maintain or improve task performance in closed loop [30]. Our results highlight that BCI decoder changes, even if they do not introduce task errors, represent external error manipulations that interact with the brain’s innate error-driven learning computations. This makes a prediction that the brain uses internally-generated error signals, generated through mechanisms like an "internal model" [58], to shape long-term changes to neural representations such as credit assignment.
Our model revealed that adaptive decoder error manipulations influence synaptic-level changes within the network (Fig. 5H). While we cannot yet experimentally validate this prediction, motor learning studies provide evidence consistent with this perspective. Acquiring motor and BCI skills is generally thought to involve multiple learning processes, one that is “fast” (within a training session) and one that is “slow” (occurring over many days of training) [1, 3, 37, 59]. Evidence also suggest that these processes have different error sensitivities [60]. The neural mechanisms associated with fast and slow learning process are not fully understood, but recent work suggests that fast adaptation may not require significant modification to synaptic connections [55, 61]. One possibility is that initial performance enhancements from adaptive decoders effectively supplement or even supplant the brain’s rapid learning mechanisms, while slow mechanisms that shape synaptic changes remain and are impacted by the algorithm. BCI learning targeted to specific neural populations are most often observed after multiple training sessions [34, 35, 37], potentially as part of "slow" learning mediated via synaptic plasticity [20]. We observe that adaptive decoders clearly alter these slower credit-assignment processes. BCI experiments with systematic decoder perturbations will provide new avenues to fully dissect the neural computations involved in learning, their error sensitivities, and the potential sources of these error signals.
Encoder-decoder interactions and implications for BCI technology
Our findings further highlight that the brain adapts over extended BCI practice, even when decoders aim to assist performance. This is consistent with studies of longitudinal BCI use, which show performance improvements and changes in neural encoding over time [13, 23, 30, 38, 39]. Some form of adaptive decoding will likely be required due to measurement instabilities over the lifetime of any BCI. This therefore implies that real-world BCIs will likely involve some form of optimal co-adaptation between the brain and decoder. Our work reveals complexities in this co-adaptation process due to interactions between neural representations and decoders. Specifically, we found that assistive BCI decoders can lead the brain to learn compact neural representations, whether measured at the level of single neurons or population-level modes (Figs. 4, 5, 6). This suggests that the brain and BCI decoder together rely on a smaller set of neural features to communicate task information. These representation features may be driven by computational demands, but reveal potential challenges for maintaining BCI performance over time. The brain’s encoding of information presents a fundamental bottleneck on the long term performance of any BCI — we cannot decode information that is not present in neural activity. Compact representations could therefore lead to significant drops in BCI performance if, for instance, measurement shifts leads to the loss of the small number of highly informative neural features. On the other hand, assistive decoders and the compact representations they produce may lead to BCI task encoding that is more easily separated from other behaviors, which could reduce interference from other task requirements. Understanding the mechanisms by which assistive perturbations shape task encoding and its functional implications will improve our ability to design BCIs that provide high performance for someone’s lifetime. This may also have implications for non-BCI clinical interventions that leverage learning, such as assistive movement-based rehabilitation methods after stroke and other brain trauma (see e.g. [62, 63]).
Our model, validated by experimental observations, provides a valuable testbed to study how compact representations form. For example, simulations revealed that stopping adaptive decoding early (before reaching maximum task performance) can provide faster performance improvements while avoiding overly compact representations, a form of "overfitting". CLDA aims to fit decoder parameters to match the brain’s representation at a point in time. If the brain has a biased representation, with some features more strongly contributing to the task, CLDA will increase the contribution of these features to the decoded predictions. Assuming feedback about how a feature contributes to movement influences learning and credit assignment computations (e.g., [20, 64]), this would further enhance biased encoding in the brain. Adaptive decoding procedures like those in our experiment repeat this process over time, which could lead to accelerated “winner-take-all” dynamics. Similar phenomena have been observed in deep networks where the dominance of a few strong but informative features can prevent more subtle information from influencing learning (“gradient starvation”), which can be mitigated with network training methods that better regularize weights [65]. Deeper insights into the neural mechanisms of learning in BCI, paired with simulation testbeds to explore a wide range of algorithms, will allow us to design machine learning algorithms that robustly interact with a learning brain.
Our dataset includes nearly daily BCI training spanning over a year and a half, which reveals that the brain adapts over extended timescales potentially independent of task errors. For instance, beyond the compactness changes within a 1-2 week learning series (Fig. 4), we also noticed that representations became more compact across learning series (Fig. S4D). This is consistent with the possibility that assistive decoder perturbations strongly influence slow learning phenomena like credit assignment, as discussed above. This raises the possibility that adaptive BCIs may influence other phenomena thought to contribute to long-term learning, like representational drift [66]. Most efforts to maintain BCI performance over time focus on technical challenges like non-stationary neural measurements and do not explicitly consider learning-related changes to neural representations. Indeed, many recent approaches for long-term BCI decoder training aim to leverage similarity in neural population structure over time [42, 67, 68, 69, 70], which can be sensitive to large shifts in neural activity [71]. Emerging alternatives instead use similarity in task structure for decoder re-training [71, 72], which may be more compatible with long-term learning. Understanding how shifts in neural representations over time influence BCI control will likely be important for real-world BCI applications. Critically, our findings highlight that representations of task information will be influenced by the decoder algorithms used for BCI. This opens the possibility to develop new generations of adaptive decoders that not only aim to improve task performance, but also contain explicit objectives to shape and guide underlying neural representations for robust long-term performance.
Methods
Experiment
Neural data and behavioral task
We analyzed neural activity as two male rhesus macaques (Macaca Mulatta, monkeys S and J) learned to control a 2D BCI cursor with CLDA intermittently performed across days. Monkeys performed a point-to-point reaching task with a radial target configuration (Fig.1D). The task required animals to initiate a trial by moving the cursor to the central target. After reaching the center, one of eight peripheral targets would appear. After a brief hold at the center, a target color change would cue the animal to initiate a movement to the peripheral target. Successfully completing a trial required the monkey to enter the peripheral target within a specified reach time (3-10 seconds) and hold the cursor inside the target briefly (250-400ms). Successfully completing a reach resulted in receiving a liquid reward. We restrict our analyses to successfully-initiated trials (where the animal moved to the center and completed the center hold), which likely reflect active attempts to complete trials.
Both monkeys were implanted with 128 microwire electrode arrays in motor and premotor cortices to record spiking activity. Spike-sorted multi-unit activity (monkey S) or unsorted threshold crossings defining channel-level multi-unit activity (monkey J) were used for BCI control. We refer to neural activity for both animals as "units". A subset of recorded units was used for the real-time BCI cursor control, which defines the readout neural population. Readout neurons were chosen based primarily on their stability across days, assessed qualitatively by experimenters by observing recordings over time. Functional properties, such as tuning for arm movements or offline task predictive power, were not used to inform readout unit selection. Units that were recorded on the same array, but not used as inputs to the BCI decoder for cursor control, define the nonreadout neural population. Stable readout units were defined as units consistently used throughout an entire BCI series.
BCI control with adaptive decoders
Readout neural activity controlled the 2D cursor using a position-velocity Kalman filter (KF) [22, 25, 30, 73]. The KF is a state-based decoder that includes a linear state transition model, which determines cursor dynamics (e.g., position is the integral of velocity, velocities are related in time), and a linear observation model, which determines the relationship between neural activity and cursor states (position, velocity). KF parameters were trained and intermittently updated using previously-developed algorithms that estimate parameters during closed-loop BCI control (closed-loop decoder adaptation, CLDA) [22]. CLDA re-estimates the parameters of the KF using the subject’s neural activity and estimated motor intent during BCI control and updates the decoder used for BCI control in real-time. Updates to the KF BCI used the SmoothBatch algorithm [22] (monkey J) to update only the KF observation model, or the ReFIT algorithm [25] (monkey S) that updates all KF parameters (state and observation models; see below for details).
Monkeys practiced with a given decoder mapping (and subsequently updated versions of that mapping) for multiple days, defining a learning series. CLDA served two main purposes: (1) to enhance closed-loop performance from the initial decoder, and (2) to sustain performance despite shifts in neural activity, such as the loss of a unit within the BCI ensemble. The initial CLDA session (Day 1) of a decoder series lasted approximately 5–15 minutes, providing the subject with sufficient performance to reach all targets successfully. Intermittent updates included (1) alterations to decoder parameters without changing the readout unit identities (weight change only) if there was a noticeable performance drop, assessed as a success rate decrease of approximately 10%–20%, and (2) interventions where readout unit identities were altered to address loss of a unit previously in the readout ensemble along with decoder weight changes (readout + weight change) (Fig. 1B). In these cases, CLDA was briefly run for 3–5 minutes, corresponding to 1-2 updates of the Kalman Filter weights. Readout unit swaps and weight adjustments were made only if previously used readout units could no longer be isolated or identified. When a performance drop from the previous day was observed but all readout units remained present, only weight changes were made without altering readout units. CLDA therefore had 2 primary effects: initial CLDA led to large decoder changes that boosted performance to facilitate reaches to all targets, akin to initial "calibration"; mid-series CLDA made notably smaller adjustments to decoder parameters, which primarily maintained or modestly improved performance [30]
Monkey J and monkey S learned 13 and 6 adaptive decoder mappings in total, respectively [30]. This analysis focused on extended learning series (longer than four days) that included intermittent CLDA on the KF decoder (monkey J: 7, monkey S: 3). Each learning series varied in length and continued until performance plateaued. Information about the number of readouts and CLDA events in each learning series is shown in Supplementary table 1. Monkey S had a reduced frequency of mid-series CLDA, which does not necessarily imply better task performance than Monkey J, but may potentially reflect more stable neural recordings. We also note that several of Monkey S’s series were shorter than Monkey J’s, which may have contributed to the reduced number of CLDA events. The original study intentionally manipulated the degree of initial CLDA to vary BCI performance on Day 1, with each learning series having different initial performances based on the extent of decoder adaptation (Fig. 1C, Fig. S1C). Some series began with lower or poor initial performance due to minimal or no CLDA applied at the outset. To quantify changes during a series, we compared "early" and "late" training days. We defined an early training day as the first day with at least 25 trials per target direction. A late training day was the last day in the learning series with at least 25 trials per target direction. Full details on adaptive decoder methods and the dataset are provided in Orsborn et al. [30].
Behavioral performance
We assessed behavioral improvements using standard performance metrics such as mean success percentage and reach times (Fig 1C). Success percentage was computed as the fraction of rewarded trials to the total number of trials initiated. Reach time was the time between cursor leaving center target and entering peripheral target.
Data analysis
Neural data preprocessing
Neural activity was binned at 100 ms and trial-aligned to the go cue. We included neural activity from the onset of the go cue to 1800 ms after as inputs to an offline decoding model (see below). Altering the time included (from go cue to a range of 500 to 1800 ms post go-cue) was not found to qualitatively change reported findings (not shown). For a given day, we considered all trials where the cursor enters the peripheral target, both rewarded and unrewarded. Unrewarded trials in this case were solely unsuccessful due to a failure to hold at the peripheral target. Because reach times vary over the course of learning, trials with a post-go-cue duration shorter than 1800 ms were zero-padded; this was most common in late phases of learning.
Participation ratio
We computed the neural dimensionality for readouts and nonreadouts using the participation ratio (PR) [43, 44, 74]. PR summarizes the number of collective modes, or degrees of freedom, that the population’s activity explores. It provides information about the spread of data and can be directly computed from the pairwise covariances among units in a population. It is defined by
We estimated population dimensionality for readouts and nonreadouts separately each day. , but since we had different number of nonreadout units that were recorded each day and different number of readout units across series, we normalized PR using
Therefore, with when and when . Note that a small difference in yields a big change in actual dimension (PR of 9.5 normalizes to whereas PR of 11.2 normalizes to for ).
We estimated the dimensionality each day (Fig. 2B) using trials with completed reaches by creating a single time-series of concatenated spike counts from all reach segments (from go cue to the cursor entering the peripheral target, . The readout population dimensionality was estimated using only the readout units used in the decoder that day. The readout populations before/after readout unit changes (Fig. 2E) did not include any units that were swapped to match the populations being compared. The change in dimensionality between early and late learning (Fig 2C) was estimated by . We computed the 95% confidence intervals for PR calculations (Fig. 2B,C) by re-sampling the original trials with replacement, matching target identity distributions (N = 104). As noted below, the number of trials to each target varies over days. We found that matching the number of trials for each day (as done for decoding analyses described below) did not qualitatively change results, and including all trials allowed us to better estimate properties of the neural populations.
Dimensionality analysis for BCI learning with a fixed decoder (Fig. 2A,C) was performed on the dataset from [18]. It used the same method as above except that training epochs were used instead of days [31, 32]. Each consecutive training epoch contains a constant number of trials, which may combine data across training days. Note that our analyses differ from past studies [31, 32], which computed a measure of dimensionality based on the shared covariance extracted using factor analysis, instead of the total covariance as used by the PR metric.
Logistic regression model
We analyzed changes in neural representations with multiclass logistic regression (LR) models that used neural activity (Figs. 3, 4) or transformations thereof (Fig. 6; see below), to predict target identity. The classifier model received the activity across all units and time bins for each trial as input, and generated an output corresponding to the predicted target. To control for variability in the number of trials completed to each target across days, we generated a training set where trials were randomly selected (without replacement) to match the number of trials to each target across days. We selected 25 trials per reach direction (200 trials per day), matching our criteria for defining "early" training phases. The remainder of trials on a day were used as a test set. Unit firing rates were z-scored across trials for each set separately. We performed 100 training-test splits on each day, randomly selecting 200 trials for training (25 trials per reach direction) and designating the remaining trials for the test set in each draw. This approach allowed us to calculate error bars as the 95% confidence interval on classification accuracy. We used the mean accuracy across the training-test splits to compare classification accuracy across series and animals (Fig. 3E). We implemented our LR models using the Python library Scikit-learn [75] with the L-BGFS solver and L2 regularization (hyperparameters: C = 1, max_iters = 1000). We did not observe any considerable changes in classification accuracy between LR models with or without regularization on late days (Fig. S3A). The hyperparameter C represents the inverse of regularization strength, with smaller values indicating stronger regularization, which helps prevent overfitting by penalizing large coefficients. We conducted a grid search for C ranging from C = 1e-5 to 1, across different neural populations—namely, all, readouts, and non-readouts. The purpose of this analysis was to confirm that our results are not merely due to the model performing unevenly across these groups. We found that classification accuracy was not more or less sensitive to the choice of C for any particular neural population (Fig. S3B). We note that this is not an analysis aiming to optimize the model’s classification performance for each population.
Parameter values (model weights) for a single training-test split and for a single target (target 2) were used to illustrate the LR model (Fig. 3B). We quantified the similarity of decoder weights across days by calculating the similarity between the model weight matrices on consecutive days, namely , (Fig. 3C), similar to previous analyses [18, 30]. This evaluation was performed by calculating the correlation coefficient between the flattened matrices of model weights (where weights for each target are concatenated) from each day.
Rank-ordered neuron adding curve
We estimated the contribution of each individual unit to target identity prediction by running a LR model for each unit separately (Fig. 4A, left). We then ranked units based on their classification accuracy (Fig. 4A, middle and Fig. 4B). A ranked-ordered Neuron Adding Curve (NAC) was produced by calculating the classification accuracy with the highest ranking unit, then with the first highest and second highest ranking units, and so on (Fig.4A, right and Fig.4C) [48]. These analyses used the same training-test split protocol described above. To account for the lower maximum classification accuracy on early days compared to later days, we normalized the NAC classification scores to each day’s maximum performance using a linear scaling. We then computed the number of ranked units () required to achieve 80% normalized prediction accuracy for early and late days. We performed a Wilcoxon signed-rank test using the ’s across series and monkey with alternative hypothesis (Fig. 4D). The “combinatorial” NAC, as described in the main text, tested all possible combinations of units for each ensemble size. We evaluated the separability between the classification accuracy distributions with and without the top units (Fig. 4E-G) using a discriminability index, , where and are the mean and standard deviation of distribution , respectively. A higher indicates that two distributions are more separable.
Classification using neural modes
We performed principal component analysis (PCA) on the readout activity for the early and late day separately (Fig. 6A). All trials for each day were used for PCA, and readout firing rates were z-scored for each day. We constructed PC adding curves and analyzed compaction in the PCs in the same way as in the above rank-ordered NAC, but using PCs instead single-unit activity (Fig. 6B-D). Importantly, we kept all PCs (no dimensionality reduction) and thus the number of PCs was equal to the number of readouts. We compared classification accuracy in low and high-variance PCs by spliting PCs into two groups (top 50% and bottom 50%) (Fig. 6F). These groups were defined by ranking PCs according to variance explained and assigning the first (last) PCs into the top (bottom) group.
PC loadings
The loadings are the components of the vectors produced by PCA, which generate the PCs by projecting a random vector variable onto them [76]. After normalizing the loading vector, we took the square of a readout’s loading to represent its relative contribution to the PC. For each learning series, on late days, we identified the PC with the highest variance and the PC with the strongest classification accuracy (Fig. 6E), and the corresponding loading vector. For these PCs, we plotted the squared PC loading for each unit against its average rank based on its classification accuracy (Fig. 6H). We calculated the average rank for a unit from the distribution of their ranks across the training/test splits. Finally, we computed the sum of squared loadings (that we called the PC loading proportion) for the leading and trailing units, according to their average rank (Fig. 6I).
Statistics
To evaluate statistical differences between early and late phases of learning, we applied the Wilcoxon signed-rank test for pairwise comparison. Significance levels are indicated as follows: ****: p ≤ 10−4, ***: 10−4 < p ≤ 10−3, **: 10−3 < p ≤ 10−2 ,*: 10−2 < p ≤ 0.05, ns: p > 0.05. The absence of a statistics comparison line in figures between two groups indicates that no statistically significant difference was found. Unless specified otherwise, the sample size for all such early vs late comparisons was N = 10 learning series for the BCI task, consisting of 3 series from monkey S and 7 series from monkey J. Inclusion of all learning series as opposed to only extended (> 4 days) series, did not qualitatively change the trends observed (not shown). In analyses examining the impact of decoder weight adjustments and combined changes in decoder weight and readout membership on dimensionality (Fig. 2E), N represented the total instances of “weight change only" and “readout + weight change" across all series. In the supplementary material, control data from N = 6 learning series obtained from monkey J related to the arm movement task were used (Suppl. Figs. S3D,E and S4C).
Model
Simulations were implemented in C++ using the Eigen library [77]. Analyses were performed in Python, using the Numpy and Scipy packages. Values for parameters are included in Table 1. Code will be made publicly available upon publication.
Table 1.
Parameters of the model. For the arm model, we combined data from Ref. [80] and from the morphology of the subjects in Ref. [30].
| Parameters of the arm model | |||
|---|---|---|---|
| symbol | value | unit | description |
| 0.25 | kg | mass of upper arm link | |
| 0.20 | kg | mass of lower arm link | |
| 0.12 | m | length of upper arm link | |
| 0.16 | m | length of lower arm link | |
| 0.075 | m | distance from center upper arm to center of mass | |
| 0.075 | m | distance from center lower arm to center of mass | |
| 0.0018 | kg·m2 | moment of inertia of upper arm | |
| 0.0012 | kg·m2 | moment of inertia of lower arm | |
| 40 | ms | time constant connecting torques and controls | |
| Parameters of the network dynamics | |||
| 100 | — | number of units | |
| 0.2 | — | reciprocal of time constant | |
| 0.02 | — | noise intensity | |
| Parameters of the objective | |||
| 0.01 | m | scaling factor for position | |
| 0.02 | m/s | scaling factor for velocity | |
| 0.08 | m/s2 | scaling factor for acceleration | |
| (arm) | 0.25 | — | velocity cost hyperparameter for arm control |
| (BCI) | 0.1 | — | velocity cost hyperparameter for BCI control |
| 0.05 | — | acceleration cost hyperparameter for arm control | |
| 0.005 | N−2·m−2 | effort penalty hyperparameter | |
| Parameters of the learning algorithm | |||
| 0.3 | — | relative weight factor for reward traces | |
| — | 2 × 10−5 | — | learning rate |
Arm model
Our Recurrent Neural Network (RNN) models were initially trained to control an arm. We used a planar torque-based arm model [78] consisting of a shoulder and an elbow joint; the arm only moved in the horizontal plane. The dynamical variables were the angle of each joint (), their velocity () and the applied torque (). These were linked through the dynamics
| (1) |
where
is a 2 × 2 inertia matrix,
represents the centripetal and Coriolis force vector and
is the joint friction matrix. Parameters , and are functions of the moments of inertia (), masses (), lengths () and distances from joint center to center of mass () of the two links (see Table 1), with , and . The torques corresponded roughly to muscle activations and were related to the control signals generated by the network dynamics by [79]. In simulations, these equations were time-discretized using the standard Euler scheme. The RNN defined below generated controls and the arm’s dynamics produced a sequence of states starting from an initial condition . The position, velocity and acceleration of the end effector (hand) are denoted by , and , respectively. The initial condition was that the end effector be motionless () with its initial position drawn from a uniform distribution centered on the center of the workspace, with radius 0.5 cm. The end effector position was obtained by a transformation of the joint coordinates, with the length of each link, and , as parameters: . The corresponding end effector velocity was , where is the Jacobian of the transformation from to . An expression for the end effector acceleration, needed in the learning objective described below, was obtained by differentiating with respect to time.
Decoder
The RNN models were then trained to perform BCI control. As in Ref. [30], the BCI decoder was a velocity Kalman filter, using arm trajectories and neural activities to encode the Kalman model parameters, and then inverting the state and observation equations (defined below) to decode newly recorded neural activity. In discrete time, the state and observation equations read
where and are independent Gaussian random vectors, is the firing activity and is the average rate. The dimension of vectors , and was the same as the number of readouts in the model, . Note that only the end effector velocity appears here, corresponding to a scenario where uncertainty on velocity does not propagate to position [25]. The position was determined by integrating the velocity.
Matrices , , and were determined from simulation data during arm control following the algorithm described in Ref. [22]. To decode the cursor velocity while measuring neural activity online, we used the update equations
where is the Kalman gain with . For simplicity, we set the initial estimate with perfect precision, so that the error covariance matrix was .
Closed-loop decoder adaptation (CLDA) was implemented following SmoothBatch [22, 30] using data recorded under brain control. Recorded velocities were rotated towards the current target, representing intended velocities [25]. This data with the rotated velocities produced new estimates for matrices and and vector , denoted , and , and the values from the last step were replaced according to
| (2) |
where and is the CLDA intensity; corresponds to a fixed decoder.
Network model
The RNN contained units fully connected by a recurrent weight matrix (see Table 1). The units’ output were their firing rates , which were obtained from their “membrane potential” by applying an activation function elementwise: , i.e., for each unit . The transfer function was the rectified linear unit (ReLU), producing non-negative firing rates. The membrane potentials obeyed
| (3) |
where . These dynamics integrate with time constant a recurrent input from other units in the network , an external input representing information about the task ()—e.g., the position of the target to reach; see below—, a bias () and a zero-mean Gaussian white noise (). The initial condition for the membrane potential was drawn from a uniform distribution .
The input was given by , where is the input weight matrix and is the activity of the input layer. This input layer activity encoded premotor information. The encoding was a simple random projection of delayed information about target position , end effector position and context —either for arm control or for BCI control—followed by the ReLU operation. Symbolically, , where is a non-learnable random matrix and is the delay. The output of the network—the controls applied to the arm models—was a linear mapping of the network activity [81]: , where is the output matrix.
Training objective
Let , , represent the position of the peripheral targets at a distance cm from the center target, with . The training objective was to minimize
| (4) |
where
| (5) |
Therefore, the objective was to reach the target at the end of the trial (first term) with vanishing velocity (second term) and acceleration (third term), and with an effort penalty (fourth term). Parameters , and were used to rescale the position, velocity and acceleration terms. Hyperparameters , and controlled the relative weight of the velocity, acceleration and effort costs with respect to the position loss. Hyperparameters and were nonzero only under arm control (see Table 1).
Learning
The recurrent weights , input weights and biases were plastic while the output matrix and the encoding matrix were fixed. Learning was performed via node perturbation using the REINFORCE algorithm [49, 82]. The noise independently applied to all units in Eq. 3 evoked small end effector jitters. In reinforcement learning, jitters that increase reward should be reproduced, and network parameters should be updated accordingly. Here, the reward was taken to be minus the learning objective, . The gradient with respect to was estimated using
where and are the noise and activity when target is presented. The reward trace provided an estimate of the expected reward for target [83] and was computed as a moving average
| (6) |
where is a factor that weights the relative contribution of the present reward () and the expected reward in memory () in computing the new reward estimate. For , one simply replace by ; for , the summation is over only. Parameter updates were computed after seeing all targets (an epoch) using Adam updates with standard hyperparameters [84].
Analysis of the model
To allow clear comparison across seeds (i.e. across random initializations of the network’s parameters), we normalized the BCI training loss relative to the loss with a fixed decoder, denoted . For each seed, we computed the of and for the last epoch of each day and we defined a new performance metric (“normalized log performance”, Fig. 5C) as
| (7) |
where and are the losses with a fixed decoder on the first and last day, respectively. This linear transformation seeks to transform the loss for the fixed decoder to the interval [0,1].
Single-unit normalized performances (Fig. 5E) were computed by first evaluating the reach performance for each individual unit and ranking them from the most important to the least important. The performance of each unit was measured by restricting the Kalman filter parameters , and to that unit and recomputing the Kalman gain accordingly. This ensured that only that unit was controlling the cursor. Now, let be the loss of the most dominant unit () to the least dominant unit () for a given seed and for a given value of CLDA intensity. The single-unit normalized reach performance was defined by
| (8) |
We thus have and .
A similar transformation was performed to obtain the normalized performance in Fig. 5F. If is the loss after the th most dominant unit has been added to the pool of readout units, then the normalized performance was
| (9) |
Here, we have and .
Combinatorial unit-adding curves (Fig. 5G) were computed by sampling all combinations of size , for , and evaluating the loss when each such combination was moving the cursor. To allow comparison across CLDA intensities, we normalized each loss using the minimum and maximum losses (across all subset sizes) when a fixed decoder was used:
| (10) |
where is the loss incurred for a specific combination.
The coefficients of determination in Fig. 5H were computed using the function linregress from the Python package scipy.stats. Each point in the scatter plots represents the change in a recurrent weight during learning with an adaptive decoder versus the weight change of the same connection with a fixed decoder, for a given network realization (random seed). Each plot contains 1002 weights for each of the 10 realizations.
Supplementary Material
Acknowledgements
The authors thank Jose M. Carmena, who shared data collected in his laboratory for this study. The authors’ research was supported in part by an IVADO postdoctoral fellowship, Canada First Research Excellence Fund/Apogée (AP), an NSF Accelnet INBIC fellowship (PR), a Simons Collaboration for the Global Brain Pilot award (898220, GL and ALO), a Google Faculty Award (ALO and GL), an NSERC Discovery Grant (RGPIN-2018-04821, GL), the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NIH K12HD073945, ALO), and NIH grant R01 NS134634 (ALO). GL further acknowledges support from the Canada CIFAR AI Chair Program and the Canada Research Chair in Neural Computations and Interfacing (CIHR, tier 2). The content of the present paper is solely the responsibility of the authors and does not necessarily represent the official views of the funding agencies.
Footnotes
Declaration of Interests
A.L.O. is a scientific advisor for Meta Reality Labs. G.L. is a scientific advisor for BIOS Health and Neural Drive.
References
- [1].Krakauer John W. et al. “Motor Learning”. en. In: Comprehensive Physiology. John Wiley & Sons, Ltd, 2019, pp. 613–663. isbn: 978-0-470-65071-4. [DOI] [PubMed] [Google Scholar]
- [2].Telgen Sebastian, Parvin Darius, and Diedrichsen Jörn. “Mirror Reversal and Visual Rotation Are Learned and Consolidated via Separate Mechanisms: Recalibrating or Learning De Novo?” en. In: Journal of Neuroscience 34.41 (Oct. 2014). Publisher: Society for Neuroscience; Section: Articles, pp. 13768–13779. issn: 0270-6474, 1529-2401. doi: 10.1523/JNEUROSCI.5306-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Dayan Eran and Cohen Leonardo G.. “Neuroplasticity Subserving Motor Skill Learning”. en. In: Neuron 72.3 (Nov. 2011), pp. 443–454. issn: 0896-6273. doi: 10.1016/j.neuron.2011.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Wang Ling et al. “Structural plasticity within highly specific neuronal populations identifies a unique parcellation of motor learning in the adult brain”. In: Proceedings of the National Academy of Sciences 108.6 (Feb. 2011). Publisher: Proceedings of the National Academy of Sciences, pp. 2545–2550. doi: 10.1073/pnas.1014335108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Xu Tonghui et al. “Rapid formation and selective stabilization of synapses for enduring motor memories”. en. In: Nature 462.7275 (Dec. 2009). Number: 7275 Publisher: Nature Publishing Group, pp. 915–919. ISSN: 1476-4687. doi: 10.1038/nature08389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Fu Min et al. “Repetitive motor learning induces coordinated formation of clustered dendritic spines in vivo”. en. In: Nature 483.7387 (Mar. 2012). Number: 7387 Publisher: Nature Publishing Group, pp. 92–95. ISSN: 1476-4687. doi: 10.1038/nature10844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Richards Blake A and Lillicrap Timothy P. “Dendritic solutions to the credit assignment problem”. en. In: Current Opinion in Neurobiology. Neurobiology of Learning and Plasticity; 54 (Feb. 2019), pp. 28–36. ISSN: 0959-4388. doi: 10.1016/j.conb.2018.08.003. [DOI] [PubMed] [Google Scholar]
- [8].Dyer Eva L. and Kording Konrad. “Why the simplest explanation isn’t always the best”. In: Proceedings of the National Academy of Sciences 120.52 (Dec. 2023). Publisher: Proceedings of the National Academy of Sciences, e2319169120. doi: 10.1073/pnas.2319169120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Golub Matthew D et al. “Brain–computer interfaces for dissecting cognitive processes underlying sensorimotor control”. In: Current Opinion in Neurobiology. Neurobiology of cognitive behavior; 37 (Apr. 2016), pp. 53–58. issn: 0959-4388. doi: 10.1016/j.conb.2015.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Orsborn Amy L. and Pesaran Bijan. “Parsing learning in networks using brain-machine interfaces”. eng. In: Current Opinion in Neurobiology 46 (Oct. 2017), pp. 76–83. issn: 1873-6882. doi: 10.1016/j.conb.2017.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Chapin John K. et al. “Real-time control of a robot arm using simultaneously recorded neurons in the motor cortex”. en. In: Nature Neuroscience 2.7 (July 1999). Number: 7 Publisher: Nature Publishing Group, pp. 664–670. issn: 1546-1726. doi: 10.1038/10223. [DOI] [PubMed] [Google Scholar]
- [12].Carmena Jose M. et al. “Learning to Control a Brain–Machine Interface for Reaching and Grasping by Primates”. en. In: PLOS Biology 1.2 (Oct. 2003). Publisher: Public Library of Science, e42. issn: 1545-7885. doi: 10.1371/journal.pbio.0000042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Taylor Dawn M., Helms Stephen I. Tillery, and Schwartz Andrew B.. “Direct Cortical Control of 3D Neuroprosthetic Devices”. In: Science 296.5574 (June 2002). Publisher: American Association for the Advancement of Science, pp. 1829–1832. doi: 10.1126/science.1070291. [DOI] [PubMed] [Google Scholar]
- [14].Shadmehr R. and Mussa-Ivaldi F. A.. “Adaptive representation of dynamics during learning of a motor task”. In: The Journal of Neuroscience: The Official Journal of the Society for Neuroscience 14.5 (May 1994), pp. 3208–3224. issn: 0270-6474. doi: 10.1523/JNEUROSCI.14-05-03208.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Krakauer John W. et al. “Learning of Visuomotor Transformations for Vectorial Planning of Reaching Trajectories”. In: Journal of Neuroscience 20.23 (Dec. 1, 2000). Publisher: Society for Neuroscience Section: ARTICLE, pp. 8916–8924. issn: 0270-6474, 1529-2401. doi: 10.1523/JNEUROSCI.20-23-08916.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Jarosiewicz Beata et al. “Functional network reorganization during learning in a brain-computer interface paradigm”. In: Proceedings of the National Academy of Sciences of the United States of America 105.49 (Dec. 2008), pp. 19486–19491. issn: 0027-8424. doi: 10.1073/pnas.0808113105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Sadtler Patrick T. et al. “Neural constraints on learning”. en. In: Nature 512.7515 (Aug. 2014). Number: 7515 Publisher: Nature Publishing Group, pp. 423–426. issn: 1476-4687. doi: 10.1038/nature13665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Ganguly Karunesh and Carmena Jose M.. “Emergence of a Stable Cortical Map for Neuroprosthetic Control”. en. In: PLOS Biology 7.7 (July 2009). Publisher: Public Library of Science, e1000153. issn: 1545-7885. doi: 10.1371/journal.pbio.1000153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Koralek Aaron C. et al. “Corticostriatal plasticity is necessary for learning intentional neuroprosthetic skills”. en. In: Nature 483.7389 (Mar. 2012). Number: 7389 Publisher: Nature Publishing Group, pp. 331–335. issn: 1476-4687. doi: 10.1038/nature10845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Athalye Vivek R, Carmena Jose M, and Costa Rui M. “Neural reinforcement: re-entering and refining neural dynamics leading to desirable outcomes”. en. In: Current Opinion in Neurobiology. Neurobiology of Behavior; 60 (Feb. 2020), pp. 145–154. issn: 0959-4388. doi: 10.1016/j.conb.2019.11.023. [DOI] [PubMed] [Google Scholar]
- [21].Orsborn Amy and Carmena Jose. “Creating new functional circuits for action via brain-machine interfaces”. In: Frontiers in Computational Neuroscience 7 (2013). issn: 1662-5188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Orsborn Amy L. et al. “Closed-loop decoder adaptation on intermediate time-scales facilitates rapid BMI performance improvements independent of decoder initialization conditions”. eng. In: IEEE transactions on neural systems and rehabilitation engineering: a publication of the IEEE Engineering in Medicine and Biology Society 20.4 (July 2012), pp. 468–477. issn: 1558-0210. doi: 10.1109/TNSRE.2012.2185066. [DOI] [PubMed] [Google Scholar]
- [23].Benabid Alim Louis et al. “An exoskeleton controlled by an epidural wireless brain-machine interface in a tetraplegic patient: a proof-of-concept demonstration”. In: The Lancet. Neurology 18.12 (2019), pp. 1112–1122. issn: 1474-4465. doi: 10.1016/S1474-4422(19)30321-7. [DOI] [PubMed] [Google Scholar]
- [24].Li Zheng et al. “Adaptive Decoding for Brain-Machine Interfaces Through Bayesian Parameter Updates”. In: Neural Computation 23.12 (Dec. 2011), pp. 3162–3204. issn: 0899-7667. doi: 10.1162/NECO_a_00207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Gilja Vikash et al. “A high-performance neural prosthesis enabled by control algorithm design”. en. In: Nature Neuroscience 15.12 (Dec. 2012), pp. 1752–1757. issn: 1546-1726. doi: 10.1038/nn.3265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Gilja Vikash et al. “Clinical translation of a high-performance neural prosthesis”. In: Nature Medicine 21.10 (Sept. 28, 2015), pp. 1142–1145. issn: 1078-8956, 1546-170X. doi: 10.1038/nm.3953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Shenoy Krishna V. and Carmena Jose M.. “Combining Decoder Design and Neural Adaptation in Brain-Machine Interfaces”. en. In: Neuron 84.4 (Nov. 2014), pp. 665–680. issn: 0896-6273. doi: 10.1016/j.neuron.2014.08.038. [DOI] [PubMed] [Google Scholar]
- [28].Jarosiewicz Beata et al. “Virtual typing by people with tetraplegia using a self-calibrating intracortical brain-computer interface”. In: Science Translational Medicine 7.313 (Nov. 2015). Publisher: American Association for the Advancement of Science, 313ra179–313ra179. doi: 10.1126/scitranslmed.aac7328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Pandarinath Chethan et al. “High performance communication by people with paralysis using an intracortical brain-computer interface”. In: eLife 6 (Feb. 2017). Ed. by Kastner Sabine. Publisher: eLife Sciences Publications, Ltd, e18554. issn: 2050-084X. doi: 10.7554/eLife.18554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Orsborn Amy L. et al. “Closed-Loop Decoder Adaptation Shapes Neural Plasticity for Skillful Neuroprosthetic Control”. en. In: Neuron 82.6 (June 2014), pp. 1380–1393. issn: 0896-6273. doi: 10.1016/j.neuron.2014.04.048. [DOI] [PubMed] [Google Scholar]
- [31].Athalye Vivek R. et al. “Emergence of Coordinated Neural Dynamics Underlies Neuroprosthetic Learning and Skillful Control”. eng. In: Neuron 93.4 (Feb. 2017), 955–970.e5. issn: 1097-4199. doi: 10.1016/j.neuron.2017.01.016. [DOI] [PubMed] [Google Scholar]
- [32].Zippi Ellen L. et al. Selective modulation of population dynamics during neuroprosthetic skill learning. en. Pages: 2021.01.08.425917 Section: New Results. Jan. 2021. doi: 10.1101/2021.01.08.425917. [DOI] [Google Scholar]
- [33].Dhawale Ashesh K., Smith Maurice A., and Ölveczky Bence P.. “The Role of Variability in Motor Learning”. In: Annual Review of Neuroscience 40.1 (2017). _eprint: https://doi.org/10.1146/annurev-neuro-072116-031548, pp. 479–498. doi: 10.1146/annurev-neuro-072116-031548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Ganguly Karunesh et al. “Reversible large-scale modification of cortical networks during neuroprosthetic control”. en. In: Nature Neuroscience 14.5 (May 2011). Number: 5 Publisher: Nature Publishing Group, pp. 662–667. issn: 1546-1726. doi: 10.1038/nn.2797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Gulati Tanuj et al. “Neural reactivations during sleep determine network credit assignment”. en. In: Nature Neuroscience 20.9 (Sept. 2017). Number: 9 Publisher: Nature Publishing Group, pp. 1277–1284. issn: 1546-1726. doi: 10.1038/nn.4601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Arduin Pierre-Jean et al. ““Master” Neurons Induced by Operant Conditioning in Rat Motor Cortex during a Brain-Machine Interface Task”. en. In: Journal of Neuroscience 33.19 (May 2013). Publisher: Society for Neuroscience Section: Articles, pp. 8308–8320. issn: 0270-6474, 1529-2401. doi: 10.1523/JNEUROSCI.2744-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Zhou Xiao et al. “Distinct types of neural reorganization during long-term learning”. In: Journal of Neurophysiology 121.4 (Apr. 2019). Publisher: American Physiological Society, pp. 1329–1341. issn: 0022-3077. doi: 10.1152/jn.00466.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Silversmith Daniel B. et al. “Plug-and-play control of a brain–computer interface through neural map stabilization”. en. In: Nature Biotechnology 39.3 (Mar. 2021). Number: 3 Publisher: Nature Publishing Group, pp. 326–335. issn: 1546-1696. doi: 10.1038/s41587-020-0662-5. [DOI] [PubMed] [Google Scholar]
- [39].Collinger Jennifer L et al. “High-performance neuroprosthetic control by an individual with tetraplegia”. In: The Lancet 381.9866 (Feb. 2013), pp. 557–564. issn: 01406736. doi: 10.1016/S0140-6736(12)61816-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Wodlinger B. et al. “Ten-dimensional anthropomorphic arm control in a human brain-machine interface: difficulties, solutions, and limitations”. eng. In: Journal of Neural Engineering 12.1 (Feb. 2015), p. 016011. issn: 1741-2552. doi: 10.1088/1741-2560/12/1/016011. [DOI] [PubMed] [Google Scholar]
- [41].Gallego Juan A. et al. “Cortical population activity within a preserved neural manifold underlies multiple motor behaviors”. en. In: Nature Communications 9.1 (Oct. 2018). Number: 1 Publisher: Nature Publishing Group, p. 4233. issn: 2041-1723. doi: 10.1038/s41467-018-06560-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Gallego Juan A. et al. “Long-term stability of cortical population dynamics underlying consistent behavior”. en. In: Nature Neuroscience 23.2 (Feb. 2020). Number: 2 Publisher: Nature Publishing Group, pp. 260–270. issn: 1546-1726. doi: 10.1038/s41593-019-0555-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Mazzucato Luca, Fontanini Alfredo, and La Camera Giancarlo. “Stimuli reduce the dimensionality of cortical activity”. In: Frontiers in systems neuroscience 10 (2016). Publisher: Frontiers Media SA, p. 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Recanatesi Stefano et al. “Dimensionality in recurrent spiking networks: Global trends in activity and local origins in connectivity”. In: PLoS Computational Biology 15.7 (July 2019), e1006446. issn: 1553-734X. doi: 10.1371/journal.pcbi.1006446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Kihlberg J. K., Herson J. H., and Schotz W. E.. “Square Root Transformation Revisited”. In: Journal of the Royal Statistical Society. Series C (Applied Statistics) 21.1 (1972). Publisher: [Wiley, Royal Statistical Society; ], pp. 76–81. issn: 0035-9254. doi: 10.2307/2346609. [DOI] [Google Scholar]
- [46].Facco Elena et al. “Estimating the intrinsic dimension of datasets by a minimal neighborhood information”. en. In: Scientific Reports 7.1 (Sept. 2017). Number: 1 Publisher: Nature Publishing Group, p. 12140. issn: 2045-2322. doi: 10.1038/s41598-017-11873-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Altan Ege et al. “Estimating the dimensionality of the manifold underlying multi-electrode neural recordings”. en. In: PLOS Computational Biology 17.11 (Nov. 2021). Publisher: Public Library of Science, e1008591. issn: 1553-7358. doi: 10.1371/journal.pcbi.1008591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Lebedev Mikhail A.. “How to read neuron-dropping curves?” In: Frontiers in Systems Neuroscience 8 (May 2014). issn: 1662-5137. doi: 10.3389/fnsys.2014.00102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Williams Ronald J.. “Simple statistical gradient-following algorithms for connectionist reinforcement learning”. en. In: Machine Learning 8.3 (May 1992), pp. 229–256. issn: 1573-0565. doi: 10.1007/BF00992696. [DOI] [Google Scholar]
- [50].You Albert K. et al. Flexible Modulation of Neural Variance Facilitates Neuroprosthetic Skill Learning. en. Pages: 817346 Section: New Results. Mar. 2020. doi: 10.1101/817346. [DOI] [Google Scholar]
- [51].Sun Xulu et al. “Cortical preparatory activity indexes learned motor memories”. en. In: Nature 602.7896 (Feb. 2022). Number: 7896 Publisher: Nature Publishing Group, pp. 274–279. issn: 1476-4687. doi: 10.1038/s41586-021-04329-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Cayco-Gajic N. Alex, Clopath Claudia, and Silver R. Angus. “Sparse synaptic connectivity is required for decorrelation and pattern separation in feedforward networks”. In: Nature Communications 8 (Oct. 2017), p. 1116. issn: 2041-1723. doi: 10.1038/s41467-017-01109-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Spanne Anton and Jörntell Henrik. “Questioning the role of sparse coding in the brain”. English. In: Trends in Neurosciences 38.7 (July 2015). Publisher: Elsevier, pp. 417–427. issn: 0166-2236, 1878-108X. doi: 10.1016/j.tins.2015.05.005. [DOI] [PubMed] [Google Scholar]
- [54].Stringer Carsen et al. “High-dimensional geometry of population responses in visual cortex”. en. In: Nature 571.7765 (July 2019). Number: 7765 Publisher: Nature Publishing Group, pp. 361–365. issn: 1476-4687. doi: 10.1038/s41586-019-1346-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Golub Matthew D. et al. “Learning by neural reassociation”. en. In: Nature Neuroscience 21.4 (Apr. 2018), pp. 607–616. issn: 1097-6256, 1546-1726. doi: 10.1038/s41593-018-0095-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Oby Emily R. et al. “New neural activity patterns emerge with long-term learning”. en. In: Proceedings of the National Academy of Sciences 116.30 (July 2019), pp. 15210–15215. issn: 0027-8424, 1091-6490. doi: 10.1073/pnas.1820296116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Cunningham John P and Yu Byron M. “Dimensionality reduction for large-scale neural recordings”. en. In: Nature Neuroscience 17.11 (Nov. 2014), pp. 1500–1509. issn: 1097-6256, 1546-1726. doi: 10.1038/nn.3776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Wolpert Daniel M. and Flanagan J. Randall. “Motor prediction”. English. In: Current Biology 11.18 (Sept. 2001). Publisher: Elsevier, R729–R732. issn: 0960-9822. doi: 10.1016/S0960-9822(01)00432-8. [DOI] [PubMed] [Google Scholar]
- [59].Karni Avi et al. “The acquisition of skilled motor performance: Fast and slow experience-driven changes in primary motor cortex”. In: Proceedings of the National Academy of Sciences 95.3 (Feb. 1998). Publisher: Proceedings of the National Academy of Sciences, pp. 861–868. doi: 10.1073/pnas.95.3.861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Smith Maurice A., Ghazizadeh Ali, and Shadmehr Reza. “Interacting Adaptive Processes with Different Timescales Underlie Short-Term Motor Learning”. en. In: PLOS Biology 4.6 (May 2006). Publisher: Public Library of Science, e179. issn: 1545-7885. doi: 10.1371/journal.pbio.0040179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Perich Matthew G., Gallego Juan A., and Miller Lee E.. “A Neural Population Mechanism for Rapid Learning”. en. In: Neuron 100.4 (Nov. 2018), 964–976.e7. issn: 0896-6273. doi: 10.1016/j.neuron.2018.09.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Kim YH Chang WH. “Robot-assisted Therapy in Stroke Rehabilitation”. In: J Stroke (Sept. 2013). doi: doi: 10.5853/jos.2013.15.3.174.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Shankar Ravi Reddy Y et al. “Impact of Constraint-Induced Movement Therapy (CIMT) on Functional Ambulation in Stroke Patients—A Systematic Review and Meta-Analysis”. In: International Journal of Environmental Research and Public Health 19 (Oct. 2022), p. 12809. doi: 10.3390/ijerph191912809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Feulner Barbara and Clopath Claudia. “Neural manifold under plasticity in a goal driven learning behaviour”. en. In: PLOS Computational Biology 17.2 (Feb. 2021). Publisher: Public Library of Science, e1008621. issn: 1553-7358. doi: 10.1371/journal.pcbi.1008621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Pezeshki Mohammad et al. “Gradient Starvation: A Learning Proclivity in Neural Networks”. In: Advances in Neural Information Processing Systems. Vol. 34. Curran Associates, Inc., 2021, pp. 1256–1272. [Google Scholar]
- [66].Driscoll Laura N., Duncker Lea, and Harvey Christopher D.. “Representational drift: Emerging theories for continual learning and experimental future directions”. In: Current Opinion in Neurobiology 76 (Oct. 2022), p. 102609. issn: 0959-4388. doi: 10.1016/j.conb.2022.102609. [DOI] [PubMed] [Google Scholar]
- [67].Degenhart Alan D. et al. “Stabilization of a brain-computer interface via the alignment of low-dimensional spaces of neural activity”. In: Nature biomedical engineering 4.7 (July 2020), pp. 672–685. issn: 2157-846X. doi: 10.1038/s41551-020-0542-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Sussillo David et al. “Making brain–machine interfaces robust to future neural variability”. en. In: Nature Communications 7.1 (Dec. 2016). Number: 1 Publisher: Nature Publishing Group, p. 13749. issn: 2041-1723. doi: 10.1038/ncomms13749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Karpowicz Brianna M. et al. Stabilizing brain-computer interfaces through alignment of latent dynamics. en. Pages: 2022.04.06.487388 Section: New Results. Nov. 2022. doi: 10.1101/2022.04.06.487388. [DOI] [Google Scholar]
- [70].Ma Xuan et al. “Using adversarial networks to extend brain computer interface decoding accuracy over time”. eng. In: eLife 12 (Aug. 2023), e84296. issn: 2050-084X. doi: 10.7554/eLife.84296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Wilson Guy H. et al. Long-term unsupervised recalibration of cursor BCIs. en. Pages: 2023.02.03.527022 Section: New Results. Feb. 2023. doi: 10.1101/2023.02.03.527022. [DOI] [Google Scholar]
- [72].Fan Chaofei et al. Plug-and-Play Stability for Intracortical Brain-Computer Interfaces: A One-Year Demonstration of Seamless Brain-to-Text Communication. arXiv:2311.03611 [cs, q-bio]. Nov. 2023. doi: 10.48550/arXiv.2311.03611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Kalman R. E.. “A New Approach to Linear Filtering and Prediction Problems”. In: Journal of Basic Engineering 82.1 (Mar. 1960), pp. 35–45. issn: 0021-9223. doi: 10.1115/1.3662552. [DOI] [Google Scholar]
- [74].Gao Peiran et al. A theory of multineuronal dimensionality, dynamics and measurement. en. Tech. rep. Company: Cold Spring Harbor Laboratory Distributor: Cold Spring Harbor Laboratory Label: Cold Spring Harbor Laboratory Section: New Results Type: article. Nov. 2017, p. 214262. doi: 10.1101/214262. [DOI] [Google Scholar]
- [75].sklearn.linear_model.LogisticRegression — scikit-learn 0.24.1 documentation.
- [76].Jolliffe I.T.. Principal Component Analysis. Second edition. Springer Series in Statistics. New York, NY: Springer, 2002. ISBN: 978-0-387-95442-4. [Google Scholar]
- [77].Guennebaud Gaël, Jacob Benoît, et al. Eigen v3. http://eigen.tuxfamily.org. 2010. [Google Scholar]
- [78].Li Weiwei and Todorov Emanuel. “Iterative linear quadratic regulator design for nonlinear biological movements systems”. en. In: Proceedings of the First International Conference on Informatics in Control, Automation and Robotics. 2004, pp. 222–229. ISBN: 978-972-8865-12-2. doi: 10.5220/0001143902220229. [DOI] [Google Scholar]
- [79].Todorov Emanuel. “Optimal Control Theory”. In: Bayesian Brain: Probabilistic Approaches to Neural Coding. _eprint: https://direct.mit.edu/book/chapter-pdf/2321908/9780262294188_cal.pdf. The MIT Press, Dec. 2006. ISBN: 978-0-262-29418-8. doi: 10.7551/mitpress/1535.003.0018. [DOI] [Google Scholar]
- [80].Cheng Ernest J. and Scott Stephen H.. “Morphometry of Macaca mulatta forelimb. I. Shoulder and elbow muscles and segment inertial parameters”. en. In: Journal of Morphology 245.3 (2000), pp. 206–224. issn: 1097-4687. doi: . [DOI] [PubMed] [Google Scholar]
- [81].Todorov Emanuel. “Direct cortical control of muscle activation in voluntary arm movements: a model”. en. In: Nature Neuroscience 3.4 (Apr. 2000), pp. 391–398. issn: 1546-1726. doi: 10.1038/73964. [DOI] [PubMed] [Google Scholar]
- [82].Chen Jiahao and Qiao Hong. “Motor-Cortex-Like Recurrent Neural Network and Multi-Tasks Learning for the Control of Musculoskeletal Systems”. In: IEEE Transactions on Cognitive and Developmental Systems (2020), pp. 1–1. issn: 2379-8939. doi: 10.1109/TCDS.2020.3045574. [DOI] [Google Scholar]
- [83].Frémaux Nicolas, Sprekeler Henning, and Gerstner Wulfram. “Functional Requirements for Reward-Modulated Spike-Timing-Dependent Plasticity”. en. In: Journal of Neuroscience 30.40 (Oct. 2010), pp. 13326–13337. issn: 0270-6474, 1529-2401. doi: 10.1523/JNEUROSCI.6249-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [84].Kingma Diederik P. and Ba Jimmy. “Adam: A Method for Stochastic Optimization”. In: arXiv:1412.6980 [cs] (Jan. 2017). arXiv: 1412.6980. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.