Results of an interlaboratory study on the working curve in vat photopolymerization

Abstract

The working curve informs resin properties and print parameters for stereolithography, digital light processing, and other photopolymer additive manufacturing (PAM) technologies. First demonstrated in 1992, the working curve measurement of cure depth vs radiant exposure of light is now a foundational measurement in the field of PAM. Despite its widespread use in industry and academia, there is no formal method or procedure for performing the working curve measurement, raising questions about the utility of reported working curve parameters. Here, an interlaboratory study (ILS) is described in which 24 individual laboratories performed a working curve measurement on an aliquot from a single batch of PAM resin. The ILS reveals that there is enormous scatter in the working curve data and the key fit parameters derived from it. The measured depth of light penetration D_p varied by as much as 7x between participants, while the critical radiant exposure for gelation E_c varied by as much as 70x. This significant scatter is attributed to a lack of common procedure, variation in light engines, epistemic uncertainties from the Jacobs equation, and the use of measurement tools with insufficient precision. The ILS findings highlight an urgent need for procedural standardization and better hardware characterization in this rapidly growing field.

1. Introduction

Since the pioneering article by Paul Jacobs over three decades ago, the measurement of a resin’s working curve has been seen as a fundamental measurement in the field of photopolymer additive manufacturing (PAM) [1]. Ideally a working curve will allow a user to determine optimal processing parameters for a particular photopolymer resin. Based on Beer-Lambert absorption of light through a resin and assuming some critical exposure of light must be absorbed prior to solid forming, the Jacobs equation then follows

$$C_{\text{d}}=D_{\text{p}}\text{ln}\left(\frac{E_0}{E_{\text{c}}}\right)$$ (1)

Where C_d is a measured cure depth and E₀ is an incident radiant exposure. A semi-log fit of these data yields two parameters. The first is the light penetration depth D_p (the depth traveled before the incident light intensity has attenuated by 1/e ≈ 37%) that is related to the absorptive/spectral properties of the resin-light source pairing. The second fit parameter is the critical exposure E_c, which is the radiant exposure of light required to form a solid (i.e., the gel point). Both D_p and E_c are expected to be a function of irradiation wavelength due to varying molar absorptivity at different wavelengths. It should be noted that the PAM field historically has referred to E₀ as a “dose”. A dose is measured in a mass-normalized basis in the Système International unit convention, while an area-normalized parameter like E₀ is more correctly referred to as a “radiant exposure”. Here the term radiant exposure, or sometimes simply exposure, will be used to refer to the area-normalized optical energy input into the system, with units of mJ cm⁻² [2]. Recently, D_p and E_c values have been reported in the specification sheets of some commercially available photopolymer resins. Furthermore, these two fit parameters are now ubiquitous in the PAM literature. The topics of these literature studies include: sources of uncertainty in cure depth measurements [3], development of new methods of measuring the working curve [4–7], or revisiting the fundamental assumptions and functional form of the Jacobs equation [8–12]. Even in light of this ongoing research and a lack of standards, it is not uncommon for publications to include or reference working curve data as part of characterizing a novel photocurable resin [13–19].

Despite the recognized importance and ubiquitous use of this measurement, there remains no standardized method to perform a working curve measurement. Compounding this issue is the lack of a reference material available to benchmark a given working curve protocol. As the field continues to grow, it is imperative that PAM has rigorous standards to improve the reproducibility of commercial printed products and published works. Here we present an interlaboratory study on the working curve. Volunteer participants were given an aliquot from the same production lot of the open-source resin PR48, which has a known composition and has been widely studied previously [3,6,20–22]. A total of 35 datasets were collected from 24 participants. It was found that reported D_p values varied by as much as 7x while reported E_c values varied by up to 70x. The results suggest that the large variability stems from numerous aspects of the measurement including light engine characteristics, exposure range, thickness measurement, and epistemic (i.e., model) uncertainty. These differences highlight the need for refinement and standardization in this field.

2. Methods and results

All participants were provided an aliquot of the same batch of the open-source resin, prototyping resin 48 (PR48), purchased from CPS (Boulder, CO). It is important to note that the current formulation of PR48 deviates from the version that has been studied in past publications [3,20,22]. The oligomer Ebecryl 8210 (ca. 40% by mass of the original PR48 formulation) has now been replaced by a similar oligomer, Sartomer PRO13514, in commercially available PR48. Participants were asked to provide a summary of their working curve measurement procedure. Key aspects from these reported procedures are summarized in Table 1. The instructions for reporting both data and procedural details were intentionally open-ended to avoid biasing how participants collected data for the interlaboratory study. Very few respondents gave specific details on the instrument used for measuring cure depths although thickness measurement method is known to strongly affect results [3]. The predominant nominal wavelength used was 405 nm. Despite many attempts in the literature to develop separate dedicated light sources for measuring working curves [3,6,8,12], the vast majority of respondents used a printer as their light engine. Only a few respondents provided a spectrum of their light engine, and only one explicitly noted that their peak wavelength, λ_max, did not match their light source’s nominal wavelength.

Table 1.

Working curve fit parameters and experimental conditions for participant-provided datasets.

	λa (nm)	Irradiance (mW cm−2)	Dp (μm)	Ec (mJ cm−2)	Cd,minb (μm)	Cd,maxc (μm)	Dp,reportedd (μm)	Ec,reportedd (mJ cm−2)	Light Source	Thickness Measurement	Thickness Precision (μm)
Dataset 1	405	10.0	70 ± 2	20 ± 3	5	102	70 ± 2	20 ± 3	DLP printer	Low force micrometer	± 0.1
Dataset 2	405	5.36	69 ± 4	10 ± 3	60	160	69	9.951	Top-down light exposure	Digital thickness gauge	± 25
Dataset 3	405	1.987	167 ± 5	50 ± 9	68	329	168	50.486	DLP printer	Micrometer	± 1
Dataset 4	405	Unknown	108 ± 3	26 ± 5	40	320	116.3	30.0	SLA printer	Calipers	Unknown
Dataset 5	405	12	134 ± 7	50 ± 20	32	184	127 ± 10	45 ± 6	Laser	Not reported
Dataset 6	405	6.96	119 ± 8	40 ± 20	17.50	286.14	121 ± 4	40 ± 2	Filtered broadband UV lamp	Rheometer	Unknown
Dataset 7	405	21	71 ± 2	20 ± 2	46.94	109.51	70.825	20.284	DLP printer	LSCMh	± < 0.05
Dataset 8	405	9.231	169 ± 5	40 ± 7	24.13	560.07	132	33.476	DLP printer	Micrometer	Unknown
Dataset 9	405	10.0	93 ± 3	19 ± 3	18	309	95.3	20.2	DLP printer	Dial micrometer	± 1
Dataset 10	405	3.031	112 ± 4	27 ± 5	64	250	113.85	26.811	LCD printer	Micrometer	Unknown
Dataset 11	405	10.33	109 ± 9	16 ± 6	57.5	162.5	109 ± 9	16 ± 2	DLP printer	Digital caliper	Unknown
Dataset 12	405	8.22	119 ± 8	18 ± 6	50.0	145.0	119 ± 8	18 ± 1	DLP printer	Digital caliper	Unknown
Dataset 13	405	6.15	90 ± 10	14 ± 7	57.5	110.0	92 ± 10	14 ± 2	DLP printer	Digital caliper	Unknown
Dataset 14	405	402–1660	190 ± 20	700 ± 500	50	575	173.7 201.5	625.9 698.9	Top-down LED spot curing system	Calipers	Unknown
Dataset 15	405	2.7	89 ± 6	18 ± 6	0	244	89	18.376	LCD printer	Dial micrometer	± 1
Dataset 16	405	63.9	156 ± 7	9 ± 2	346.8	736.7	155.77	8.54	Top-down Independent LED	Stylus profilometer	± < 0.05
Dataset 17	405	32.34	136 ± 6	17 ± 5	81.3	436.5	136.34	17.45	Top-down Independent LED	Stylus profilometer	± < 0.05
Average 405 e			120 ± 40	60 ± 160	58	295
Aggregate 405 f			89 ± 4	18 ± 4	–	–
Dataset 18	385	10.0	46.3 ± 0.6	12.4 ± 0.7	7	88	46.3 ± 0.6	12.4 ± 0.7	DLP printer	Low force micrometer	± 0.1
Dataset 19	385	5.0	310 ± 20	12 ± 2	70	290	–	–	DLP printer	Calipers	Unknown
Dataset 20	385	5.0	37 ± 2	4.6 ± 0.9	68	95	37	4.632	DLP printer	Digital thickness gauge	Uknown
Dataset 21	385	4.74	42 ± 5	10 ± 5	34	86	43	10.3	DLP printer	Calipers	Unknown
Dataset 22	385	5.0	51.2 ± 0.4	10.1 ± 0.4	14	179	51.2	10.1	DLP printer	Dial micrometer	± 1
Dataset 23	385	5.03	56 ± 2	22 ± 5	15	174	56	21.5	DLP printer	Calipers	Unknown
Dataset 24	385	100	48.2 ± 0.4	7.4 ± 0.3	11.908	209.613	47.93 48.52	7.40 7.41	DLP printer	LSCMh	± < 0.05
Dataset 25	388.5g	0.9 – 3.2	62 ± 1	21 ± 2	60.7	143.5	63 ± 2	21 ± 1	DLP printer	Micrometer	Unknown
Dataset 26	385	5.0	47 ± 2	13 ± 3	33	148	47	12.598	DLP printer	Dial micrometer	± 1
Dataset 27	385	0.85 – 27.1	100 ± 10	20 ± 10	47	439	–	–	Projector
Dataset 28	385	10.37	60 ± 2	15 ± 3	35	285	60 ± 5	0.86 ± 0.02	DLP printer	Micrometer	Unknown
Average 385 e			80 ± 80	13 ± 6	33	192
Aggregate 385 f			55 ± 2	12 ± 2	–	–
Dataset 29	365	6.48	110 ± 20	13 ± 9	39	535	203	13.931	Independent LED	Optical profilometer	± 1
Dataset 30	365	3.131	37 ± 1	13 ± 2	66	94	36.93	12.789	DLP printer	Micrometer	Unknown
Dataset 31	365	4.688	32 ± 1	8 ± 1	70	94	32.12	8.089	DLP printer	Micrometer	Unknown
Dataset 32	365	9.96	34.1 ± 0.4	3.5 ± 0.2	81	129	34.14	3.550	DLP printer	Micrometer	Unknown
Dataset 33	365	13.34	60 ± 3	6 ± 1	58.838	206.97	5.89	59.367	Top-down Independent LED	Stylus profilometer	± < 0.05
Dataset 34	365	6.95	32 ± 2	2.1 ± 0.4	42.148	150.83	2.11	32.122	Top-down Independent LED	Stylus profilometer	± < 0.05
Average 365 e			50 ± 30	8 ± 5	60	202
Aggregate 365 f			50 ± 8	9 ± 7	–	–
Dataset 35	Broad Spectrum	Unknown	97 ± 1	11.0 ± 0.7	160	299	97	11.0	Mercury lamp	Digital micrometer	± 3

^a)Nominal unless otherwise reported.

^b)Minimum measured cure depth.

^c)Maximum measured cure depth.

^d)Participant-reported fit parameters and uncertainty, if provided.

^e)Unweighted arithmetic mean of reported fit parameters from participants. Uncertainty is standard deviation of fit parameters.

^f)Data reported from pooling and fitting all datasets within a wavelength.

^g)Wavelength measured and reported by participant.

^h)Laser scanning confocal microscopy.

In general, there was little consistency to the substrate type or the lateral dimensions of cured areas that participants used for cure depth measurements. Some participants followed protocols resembling online guides for measuring a working curve [23,24], while others cured into resin droplets on top of glass slides placed atop the print window. While most measurements used a bottom-up configuration (i.e., the light source was below the resin), some participants cured a droplet of resin top-down, collecting a floating film of cured photopolymer for cure depth measurements. Participants did not typically report the washing or postprocessing conditions used. However, washing and postprocessing are known to affect part surface finish and properties, which may affect thickness at the scale of working curve measurements [25–27]. Additionally, there was little reporting and no attempt by participants to exert control over laboratory environmental factors. Parameters such as partial pressure of oxygen (which would vary by elevation), relative humidity, and dissolved oxygen content (which can vary on the basis of lab temperature or elevation) may have an effect on the polymerization kinetics and thus E_c [28]. Consensus on substrate, pattern size, and postprocessing is a relatively straightforward means of reducing variability, although their specific impact was not explored systematically here.

Anonymized plots of C_d vs E₀ for the three predominant nominal wavelengths of interest (405 nm, 385 nm, and 365 nm) are shown in Fig. 1 (an additional dataset for a broad-spectrum mercury light source is shown in the supporting info, Fig. S1). The scatter in these data is clear upon visual inspection, highlighting the interlaboratory inconsistency in the chosen working curve methods. Several parameters from these plots are summarized in Table 1, including the fit parameters D_p and E_c along with the thinnest and thickest cure depths measured by each participant. Participant-provided information about instruments used for measuring cure depth are also shown in Table 1.

Fig. 1.

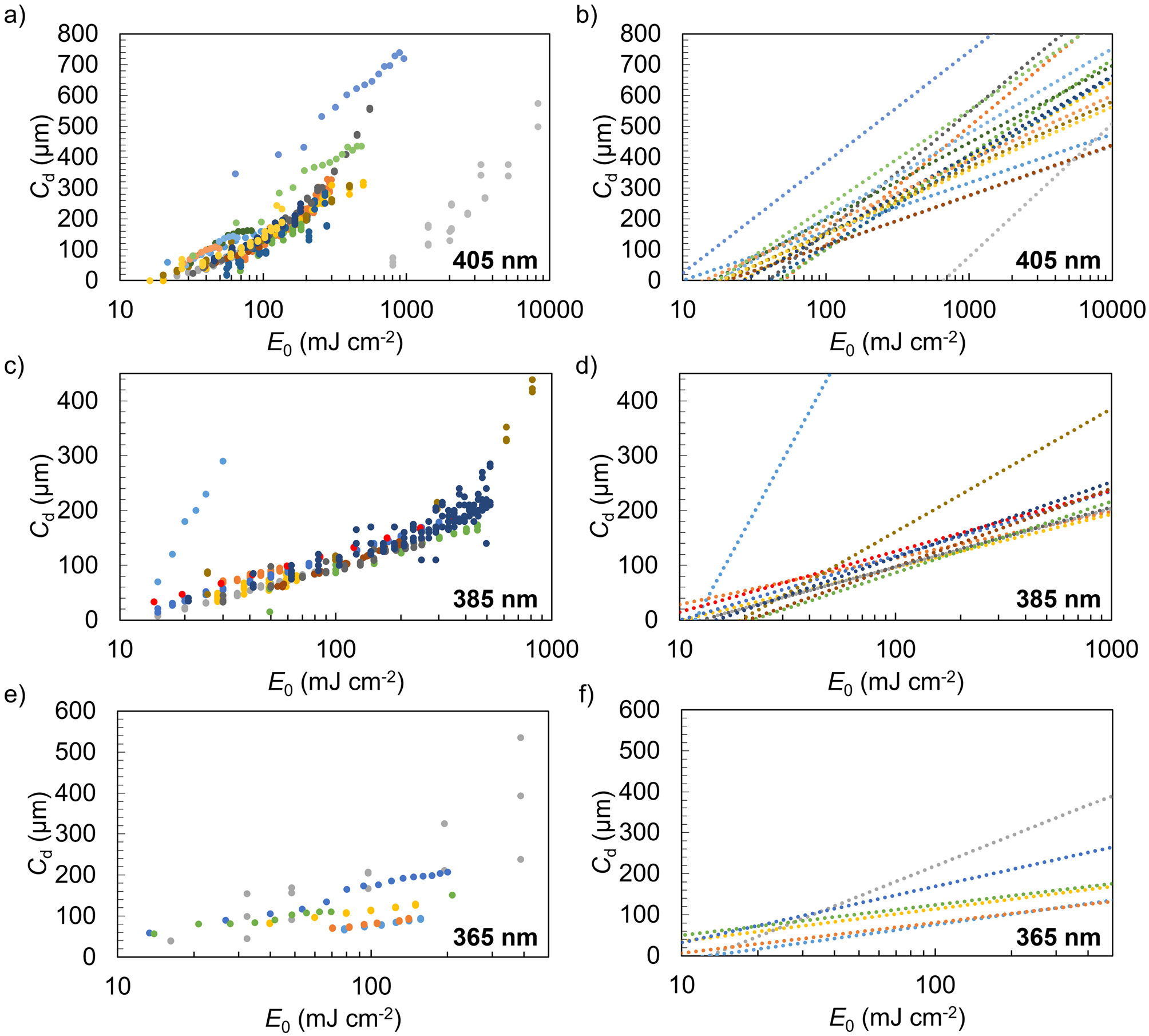
Cure depth C_d vs exposure E₀ data reported by study participants at nominal wavelengths (a) 405 nm, (c) 385 nm, and (e) 365 nm. Fits to the Jacobs equation are shown in panels (b), (d), and (f) to highlight the origin of the scatter in D_p and E_c.

Fit parameters provided in Table 1 for every dataset were extracted from the LINEST function in Excel using the raw C_d vs ln(E₀) data provided by participants [29]. The associated error in E_c was obtained from propagating the LINEST uncertainty in the x-intercept through the Jacobs equation. The Jacobs equation fits are shown in the righthand panels of Fig. 1 to highlight the origin of the scatter in D_p and E_c. A consistent linear regression methodology was used across all individual participant datasets to ensure that extracted fit parameters and uncertainties were consistently calculated. Table 1 also shows participant-reported D_p and E_c, which were generally consistent with fit parameters obtained with the uniform methodology.

For the 405 nm datasets, the extracted D_p values (mean = 120 μm, σ = 40 μm) vary from as low as 60 μm to as high as 190 μm, which is a >3-fold difference. Showing even larger variation, the E_c values (mean = 60 mJ cm⁻², σ = 160 mJ cm⁻²) span nearly 2 orders of magnitude from 10 mJ cm⁻² to as much as 700 mJ cm⁻². One dataset reported an extreme outlier (Grubbs test p< 0.01)[30] in both E_c (700 mJ cm⁻²) and in irradiance (between 402 mW cm⁻² and 1660 mW cm ⁻²). Neither value was excluded from arithmetic mean calculation in Table 1. It is unclear if this very large E_c value is related to inaccurate optical power measurement or if this is an anomalous chemical phenomenon caused by extreme irradiances [31]. Within single participant datasets, data exist wherein more than 10% cure depth variation is observed at the same nominal radiant exposure (denoted by arrows in the zoomed in graph shown in Fig. S2) indicating either poor print reproducibility or insufficient precision of the cure depth measurement. Print irreproducibility may originate from inhomogeneity of intensity and/or wavelength across the print window [21].

For the nominally 385 nm datasets, most of the data are clustered with similar slope (and thus D_p). D_p values (mean = 80 μm, σ = 80 μm) range from 37 μm to 310 μm. The E_c values (mean = 13 mJ cm⁻², σ = 6 mJ cm⁻²) varied between 4.6 mJ cm⁻² and 22 mJ cm⁻² (roughly a 5-fold difference). Rejecting the two largest D_p data sets, the remainder have a mean of 49 μm and a standard deviation of 8 μm. For this reduced data set, E_c has a mean of 13 mJ cm⁻² and a standard deviation of 6 mJ cm ⁻², nearly identical to the full 385 nm data set. The relatively more consistent D_p values with a wider variance in E_c values for the reduced data set suggests that inaccurate radiometry may have contributed to these differences. Visually, inspection of Fig. 1c gives the appearance of several nearly parallel lines with varying x-intercepts. Four of the six collected datasets at 365 nm (Fig. 1e,f) also exhibit nearly-parallel line behavior. So long as precise (i.e., consistent) relative irradiance values are obtained, inaccuracy in absolute irradiance measurement will reflect only in E_c and not in D_p (which is most strongly dependent on accurate measurement of thickness), which would explain the variance obtained in many of the 385 nm datasets.

The spread in the reported D_p and E_c values are shown in Fig. 2a and Fig. 2b, respectively. The tighter cluster of D_p values for the 385 nm datasets are apparent in this plot, as are the relatively larger variation in the 405 nm and 365 nm datasets. E_c values are reported on a logarithmic scale to capture the extreme outlying irradiance of Dataset 14 in the 405 nm dataset. The relatively smaller number of 365 nm datasets is responsible for the larger apparent variation in those data.

Fig. 2.

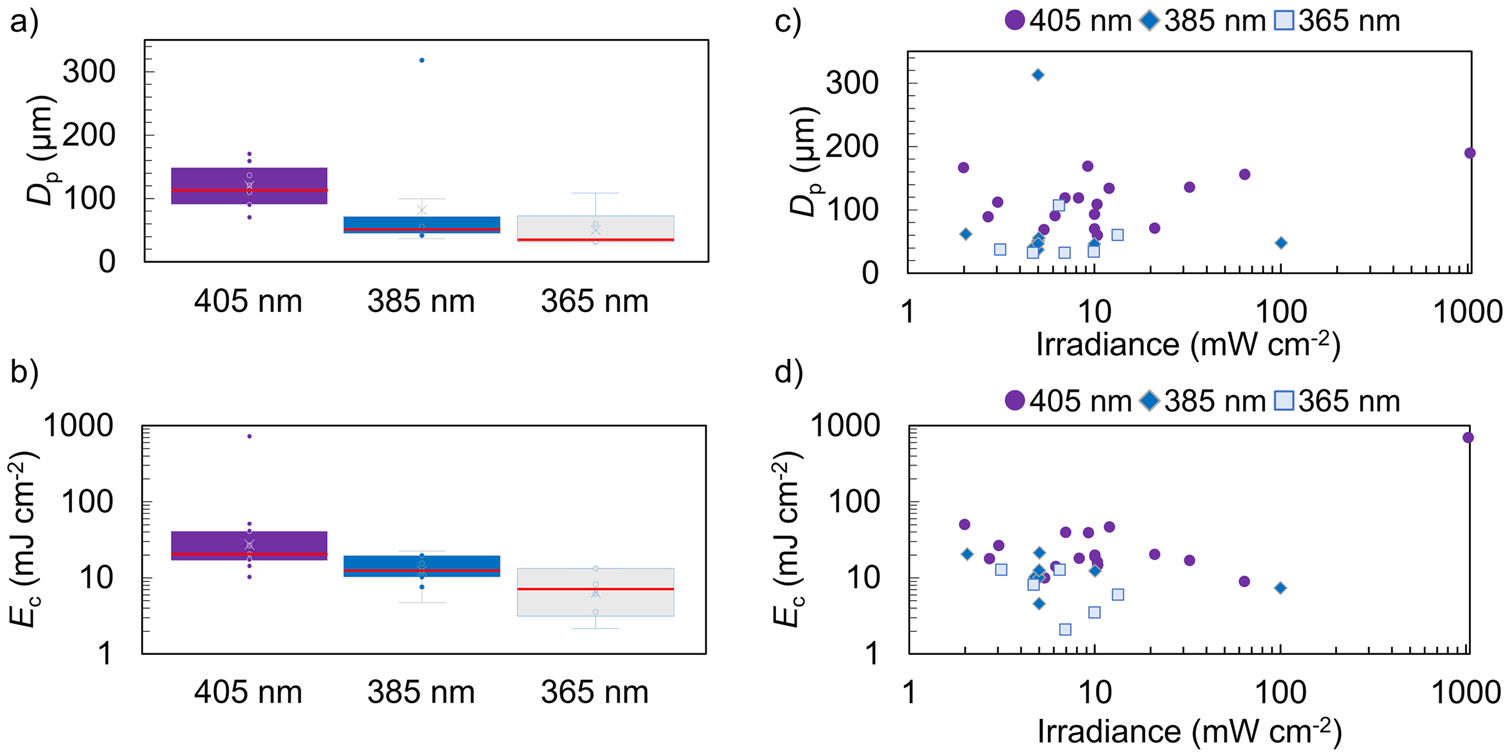
Box plots of (a) D_p and (b) E_c displaying the spread in the fit parameters at the three wavelengths of note for this study. Data reductions are shown displaying (c) D_p vs irradiance and (d) E_c vs irradiance.

A naive data reduction was performed to investigate any potential irradiance effects on the reported D_p and E_c values. These reductions are shown in Fig. 2c,d. To evaluate the presence of a correlation between D_p or E_c and irradiance, t-tests of linear fits of D_p or E_c vs irradiance were performed for each wavelength considered in this interlaboratory study. The outputs of the t-test analysis can be found in Table S1. The 405 nm data were evaluated either including or excluding Dataset 14. The values from Dataset 14 are of significantly higher leverage on fit coefficients because of their order-of-magnitude higher irradiance value than the other submitted 405 nm datasets [32]. This influence can be seen from the extremely high Cook’s Distance value of Dataset 14 (Figure S3), which suggest inadequate data in the vicinity of those points to draw conclusions about correlations [33]. The lack, generally, of a strong correlation between D_p or E_c and irradiance suggests that the differences among participant-supplied data is a result of systematic differences in how data are collected (printing, post-processing, and characterization) from one participant to another. The data shown in Fig. 2 also highlight the scatter in fit parameters, even at nominally identical wavelengths. The data also show that irradiances used span several orders of magnitude. Considering the non-reciprocal nature of photopolymerizations to intensity and radiant exposure [31,34], a standardized irradiance would be of interest to the field, in addition to further studies to understand the interplay between exposure, intensity, and cure depth.

3. Discussion

The variation in working curve results was generally larger than participants would like to tolerate, although not out of line with expectations given the lack of standardization. To improve reproducibility, numerous parts of the measurement should be considered and refined.

Some participants (particularly those who used a nominally 405 nm light source) commented on the tendency of the working curve to “bend” upwards (i.e., exhibit nonlinear behavior on the semilog plot towards higher cure depths) as radiant exposure increased. Indeed this has been noted many times in the literature and is a well-known phenomenon [3, 6,12]. Despite this curvature, it is common in the literature to see a linear Jacobs equation fit applied to these nonlinear measured working curves. In Fig. 3 we demonstrate the inaccuracy of using this approach. An arbitrarily chosen subset of participant data at 405 nm were pooled and fit according to Jacobs equation. The subset was generally selected from the participants who used cure depth measurement techniques with 1 μm precision or better, and whose working curves were all polymerized bottom-up onto a substrate. The curvature to this collection of data is readily apparent on the semilog axes. Three different fits to the Jacobs equation are shown: One is fit on the lower quartile of measured cure depths, and another on the upper quartile. Finally, an “aggregate” fit for all data is included as well. The extracted Jacobs model fit parameters are displayed in Fig. 3a. From a single data set, the cure depth range used for fitting can alter D_p and E_c by a factor of ≈3 fold between the upper and lower quartile fits. It is apparent from the fit lines that the aggregate and upper-quartile fit lines intersect the x-axis above the range indicated by the experimental data. In contrast, the lower quartile fit intercepts the x-axis in the vicinity of the lowest cured depth experimental data. The sensitivity of D_p and E_c to the fitted cure depth highlights epistemic uncertainty with the current state of working curve methodologies. The Jacobs model was derived implying a number of assumptions including: (1) a nominally monochromatic, gaussian light source such as a laser (2) reciprocity such that the working curve is independent of irradiance (3) the system does not photobleach [1]. These assumptions are violated in many current printers and resins; thus, caution must be exercised when applying the Jacobs model to data where semi-log linearity is clearly not obeyed.

Fig. 3.

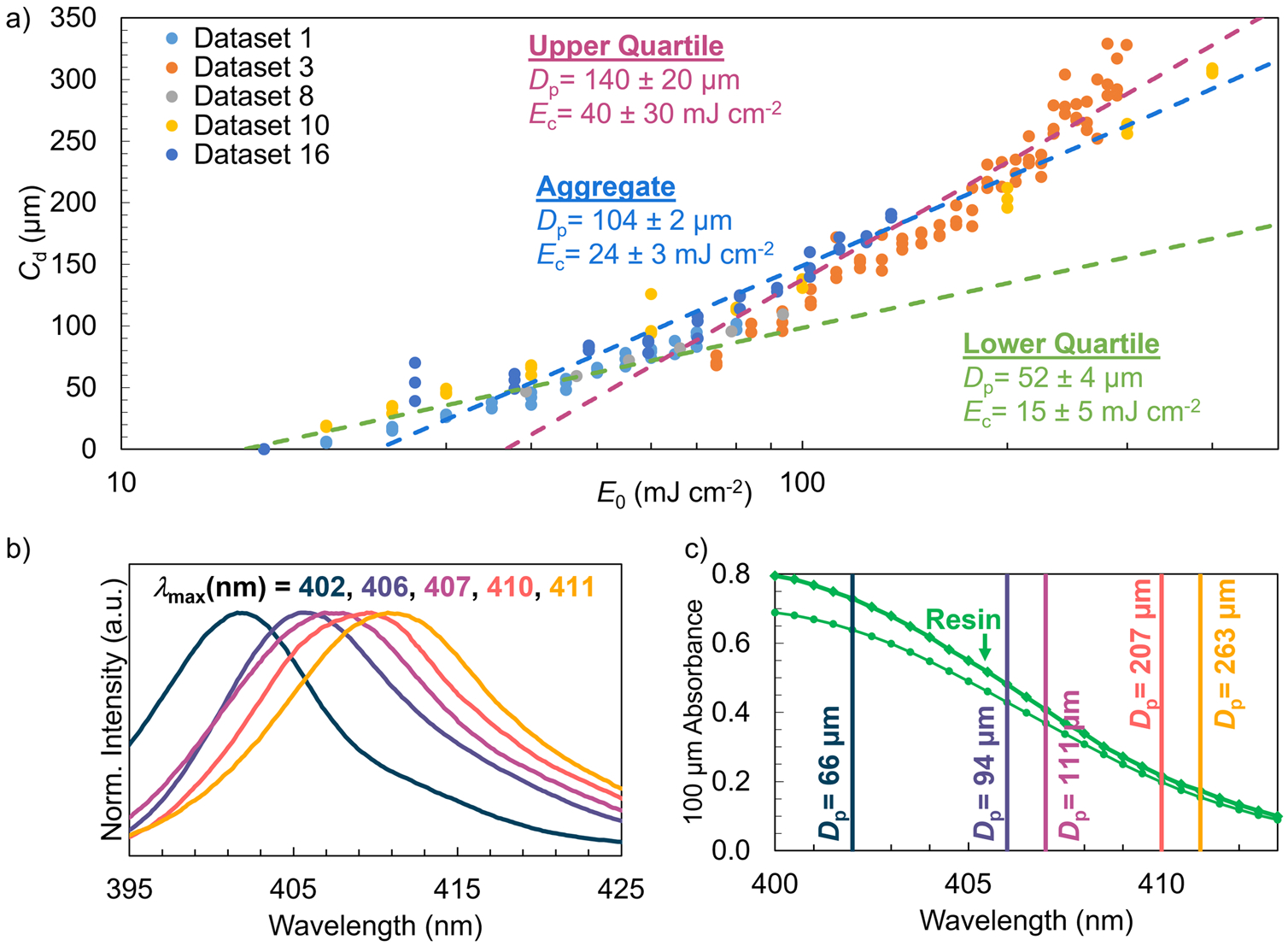
(a) Down-selected 405 nm dataset collected from ILS participants. The separate fits to the Jacobs model are shown for the lower quartile, upper quartile, and entire range (aggregate) of the data. The fit parameters and uncertainties are displayed in the plot area. The D_p values span a range of 52 μm to 140 μm, while the E_c values span a range of 15 mJ cm⁻² to 40 mJ cm⁻² for the different ranges of the same data. This variation in fit values highlights epistemic uncertainty in the working curve measurement. (b) Spectra from five nominally 405 nm printers showing nearly 10 nm variation in peak wavelength λ_max. (c) Green traces are UV/Visible spectra of the studied resin collected on a variable pathlength spectrometer (circles) and in a conventional spectrometer with a 100 μm cuvette (diamonds). The “optical” D_p that is extracted from the absorbance data are shown for each of the peak wavelengths in the LEDs shown in (b).

Additional possible sources of working curve variation were investigated by considering representative spectral variation observed in DLP printers and LED light engines. LED-driven DLP printers were the most common class of light engine amongst ILS participants. As discussed earlier, few participants reported spectral details of their printer. The spectra measured by NIST from five different, nominally 405 nm DLP printers are shown in Fig. 3b and show a range of λ_max values from 402 nm to 411 nm. This range overlaps with a significant shoulder in the absorption spectrum of common photoinitiators. We have reported previously on the significant change in initiation efficiency that would be expected from seemingly-small spectral shifts in the light engine [21]. An optical D_p can be extracted from the UV/Visible absorption spectrum of the resin at a particular wavelength (a sample calculation for this is shown in the supporting information). Fig. 3c shows optical D_p values for the five reported printer λ_max values, based on UV/Visible spectra from two different spectrometers. In the range of 402 nm to 411 nm the optical D_p exhibits a nearly 4-fold increase. Working curve D_p values track optical D_p values in well-behaved systems, thus the inherent variability of the emission from different participant’s printers could have strongly affected their working curve results [9]. While this possible difference is significant, it is much smaller than the range of D_p values reported by participants, suggesting that multiple sources of error are contributing to the reported variations.

Overall, these insights suggest that the Jacobs model could be refined or extended to fit a broader range of resin and light source characteristics, while working curve methodologies must strive for the utmost consistency between practitioners. Light engines must be carefully controlled to have nearly identical spectral emission and well-calibrated power output. Finally, accurate and precise thickness measurements are essential to accurate, reproducible working curves. Contact based measurements may prove adequate for measurements on stiff (giga-pascal modulus) plastics, but working curve methods for elastomers and gels likely require further consideration. The PAM field should strive for development of a standard practice for working curve measurements as soon as possible to facilitate continued growth and interoperability of data. Adoption of a standardized protocol for measuring working curves will also allow for quantitative understanding of the influence of environmental factors on the working curve measurement and facilitate standardization of those environmental factors if necessary.

4. Conclusion

An interlaboratory study on the working curve measurement was performed where participants all measured a working curve on aliquots of the same production lot of a resin. The fit parameters extracted from the 35 provided datasets indicates a scatter (notably, up to a 7-fold difference in D_p values and up to a 70-fold difference in E_c values) that prohibits the measurement in its current form from being useful across different laboratories or for technical data sheets. These differences are explained in part by a demonstrated sensitivity of D_p and E_c to the cure depth range studied, indicating epistemic uncertainty in the working curve measurement. An additional source of error is significant spectral variability among nominally similar commercial printers that can lead to a 4-fold change in D_p even in the absence of other uncertainties. Community consensus on a standardized working curve method with precise light engine and thickness measurement specification, along with consistency on other aspects of the protocol are expected to dramatically reduce variation. It is imperative that a standardized method be developed and adopted in short order for continued growth of the photopolymer AM field.

Data Availability

All data used for this study are available from NIST free of charge at: https://doi.org/10.18434/mds2-3137