Vortex sorting of rare particles/cells in microcavities: A review

Abstract

Microfluidics or lab-on-a-chip technology has shown great potential for the separation of target particles/cells from heterogeneous solutions. Among current separation methods, vortex sorting of particles/cells in microcavities is a highly effective method for trapping and isolating rare target cells, such as circulating tumor cells, from flowing samples. By utilizing fluid forces and inertial particle effects, this passive method offers advantages such as label-free operation, high throughput, and high concentration. This paper reviews the fundamental research on the mechanisms of focusing, trapping, and holding of particles in this method, designs of novel microcavities, as well as its applications. We also summarize the challenges and prospects of this technique with the hope to promote its applications in medical and biological research.

I. INTRODUCTION

The isolation of rare cells from heterogeneous solutions is a prerequisite for cell analysis in stem cell research,^1,2 disease diagnosis,^3,4 and drug screening.⁵ For example, cancer liquid biopsies using circulating tumor cells (CTCs) with small blood sample volumes have become an effective test for tumor detection.^6–9 However, as the number of CTCs in peripheral blood is extremely low (1–100 per ml),⁹ it is a necessary to accurately and efficiently isolate and enrich the CTCs from billions of blood cells.¹⁰

Microfluidics or lab-on-a-chip (LOC) technology is a multidisciplinary research field that has achieved outstanding development in the last two decades, becoming a new platform for cell analysis.¹¹ Utilizing fluid flow in microchannels to manipulate the motion of microsamples (cells, particles, droplets, or drugs), microfluidics has excellent application prospects in biological, chemical, and medical research fields.^12–15 The goal of microfluidics is to integrate the sample preparation, reaction, separation, detection, analysis, and other operations into a small microfluidic chip of several centimeters in size.¹⁶ Because of their unique structures, microfluidic chips have advantages such as high throughput, high precision, and integration,¹⁷ providing a new way to manipulate the motions of target cells and particles.¹⁸

Many microfluidic technologies for the separation of rare cells have been proposed in the literature, which can be generally divided into biochemical type and physical type. The physical type can be further divided into active and passive methods (Fig. 1). Active methods can achieve particle separation with high resolution and accurate.²⁸ However, they require additional external force fields such as sound,^19,29,30 light,^20,31,32 electric fields,^33–35 and magnetic fields,^21–23 leading to integration difficulties.³⁶ In contrast, passive methods such as inertial flow, pinched flow, lateral displacement, and microfiltration take advantage of differences in cell physical properties (such as size, shape, density, and deformability) and fluid flow characteristics to achieve efficient separation of particles/cells without requiring additional force fields or complex operations.^{24–26,37,38} The passive methods rely on the design of special microchannel structures and offer advantages such as being label-free, low cost, easy operation, and high throughput.^39–44

FIG. 1.

Physical sorting methods of microfluidics: active methods and passive methods.^19–27 Reproduced with permission from Adams et al., Appl. Phys. Lett. 97, 064103 (2010). Copyright 2010 AIP Publishing LLC; Reproduced with permission from MacDonald et al., Nature 426, 421–424 (2003). Copyright 2003 Springer Nature; Reproduced with permission from Hosic et al., Anal. Chem. 88, 354–380 (2016). Copyright 2016 ACS Publications; Reproduced with permission from Yamada et al., Anal. Chem. 76, 5465–5471 (2004). Copyright 2004 ACS Publications; Reproduced with permission from Zheng et al., Biomed. Microdevices. 13, 203–213 (2011). Copyright 2011 Springer Nature; Reproduced with permission from Wang et al., Microfluid. Nanofluid. 22, 1–12 (2018). Copyright 2018 Springer Nature; Reproduced with permission from Al-Faqheri et al., Microfluid. Nanofluid. 21, 1–23 (2017). Copyright 2017 Springer Nature; Reproduced with permission from Zhou et al., Sci. Rep. 8, 9411 (2018). Copyright 2018 Authors, licensed under a CC BY 4.0 License; and Reproduced with permission from Sollier et al., Lab Chip 14, 63–77 (2014). Copyright 2014 Royal Society of Chemistry.

Compared with other passive methods, inertial microfluidics has simple structures and can enable particle manipulations such as focusing, sorting, and isolation primarily through precise control of their inertial effects. Inertial microfluidics can be divided into two categories based on the channel structure and flow behaviors: (i) secondary Dean flow in curved, spiral, or serpentine channels and (ii) vortex flow in microcavities. The first category has received significant research attention^40,45–50 and has been reviewed in many papers.^22,24 The second category combines the inertial migration of particles in a straight microchannel with vortex trapping and isolation of target particles/cells within sidewall microcavities.²⁷ By optimizing the inlet flow conditions and cavity geometries, this vortex sorting method not only sorts rare particles based on their size from flowing samples but also simultaneously enriches target particle concentration without requiring further enrichment operations for cell analysis.⁵¹ Compared with other methods,⁵² this method provides high throughput, high purity, high integration, and parallelized separation of particles/cells.^53,54 Due to the unique advantages,⁵⁴ this method is particularly suitable for sorting rare CTCs from blood samples with enrichment in concentration.

Many experiments and numerical simulations have been conducted to investigate the effects of geometrical factors, particle sizes, and inlet flow conditions on the performance of the vortex sorting method, which includes two aspects: vortex trapping efficiency and cavity capacity for holding target particles/cells.⁵⁵ Manty efforts have been devoted to technically improving the vortex trapping efficiency by optimizing the length-to-width ratio of rectangular cavities.^55,56 However, recent studies have shown that the cavity holding ability, identified as the maximum number of particles accommodated in each microcavity, plays a vital role in sorting performance.^55–57 It is expected that each cavity could contain as many particles as possible to improve the sorting efficiency. The cavity holding ability is closely related to the dynamics of particle orbiting motion in the vortex, giving rise to many new fluid mechanics problems such as vortex characteristics, particle orbiting motion behaviors, and fluid–particle interactions.^56,58 Although several laboratory applications of this method have been reported,⁵⁶ its underlying physics and mechanisms are complex and still unclear.

Many papers have reviewed the notable work of various microfluidic technologies in particles/cells separation,^21–23 including the inertial microfluidics. In 2019, Volpe et al.³⁶ specially reviewed the history and development of the vortex sorting method, providing a comprehensive understanding of this technology. However, there is still a need to further review the latest findings and underlying physics of this method, such as the vortex characteristics in microcavities and particle motion behaviors (migrating, trapping, and orbiting), which play an essential role in improving particle sorting performance. This review focuses on the physics of this method from a fluid mechanics perspective with the aim to provide a deep understanding of the underlying mechanisms involved.

This review is organized as follows: Sec. II presents the physics and mechanisms governing particle motions; Sec. III summarizes various cavity structures and discusses the influencing factors; Sec. IV explains fundamental studies on the vortex dynamics and particle motion behaviors; Sec. V briefly introduces applications of this method; and Sec. VI concludes the paper with suggestions on how to design new cavity structures for improving the sorting performance of this method in more wide practical applications.

II. PARTICLE MOTIONS AND MECHANISMS

For a neutrally buoyant spherical particle, the sorting process in a microcavity includes three steps:^56,59,60 particle inertial focusing in a straight microchannel, particle sorting and trapping in the microcavity entrance, and particle orbital motion along a peculiar trajectory within the vortex, as shown in Fig. 2. Particle inertial migration is the basis of controlling the separation of particles with different sizes.⁶¹ The particle motions of focusing, sorting, trapping, and isolation are determined by many factors, including the particle characteristics, vortex characteristics, confinements of the cavity walls, and so on.^62,63 The hydrodynamic mechanisms of particle motions are always the research focuses, which involve many new basic scientific problems of fluid mechanics and play an essential role in improving the sorting performance of this method.^56,57 At present, particles are mainly used to replace cells to carry out relevant mechanism research.^55–58

FIG. 2.

Particle sorting process: (I) inertial focusing, (II) sorting and trapping, and (III) orbiting motion.

A. Particle inertial focusing

Generally, flow in a microchannel can be characterized by the inlet Reynolds number,⁵⁸ $\mathrm{Re}=\rho U_m{D}_h/\mu$, where $\rho ,U_m$, and $\mu$ are the fluid density, mean flow velocity, and fluid dynamic viscosity, respectively. $D_h$ is the hydraulic diameter of the microchannel, defined as $D_h=2WH/(W+H)$, where W is the channel width and H is the channel height.

Before entering the cavity, particles flowing in a straight microchannel with a rectangular section show two migration stages.⁶¹ In the first stage, the parabolic nature of the laminar velocity profile in Poiseuille flow induces a shear-gradient lift force, $F_{LS}=f_L\rho U_m^2{a}^3/W$,⁶⁴ where a is the particle diameter and $f_L$ is the dimensionless lift coefficient determined by the parabolic flow profile. The $F_{LS}$ acts on the flowing particles, pushing them to migrate from the channel centerline toward the channel walls [Fig. 3(a)]. When the particles migrate closer to the channel walls, they experience a wall effect-induced lift force, $F_{LW}=f_L\rho U_m^2{a}^6/W$.⁶⁴ Consequently, the particles migrate across flow streamlines toward their equilibrium positions near the channel walls, where the total net force is zero.^66,67 The number of equilibrium positions also depends on the channel's cross-sectional shape.

FIG. 3.

(a) Particle inertial focusing in a straight microchannel.⁶⁵ The shear-gradient lift force $F_{LS}$ drives particles to migrate away from the channel center, while the wall effect-induced lift force $F_{LW}$ pushes particles away from the channel walls. Finally, particles migrate across flow streamlines toward their equilibrium positions near the channel walls. Reproduced with permission from Guo et al., Sensors 18, 1762 (2018). Copyright 2018 MDPI Publishing. (b) Two-stage inertial focusing in a rectangular microchannel with a high height/width aspect ratio. $F_{\mathrm{\Omega }}$ represents the rotation-induced lift force driving particles to the center of the long channel wall.⁶³ Reproduced with permission from Wang et al., Lab Chip 15, 1350–1359 (2015). Copyright 2015 Royal Society of Chemistry.

The second stage occurs once the initial equilibrium is reached, and a rotation-induced lift force $F_{\mathrm{\Omega }}$ dominates the particles' motion near the channel walls, reducing the number of equilibrium positions to two in a rectangular microchannel with a high height/width aspect ratio [Fig. 3(b)]. Therefore, the particles finally equilibrate at the center of each sidewall, completing the two-stage inertial migration.⁶³

The minimum downstream length L necessary for focusing particles can be given by $L=3\pi \mu D_h^2/4\rho U_m{a}^3(H/C_L^{-}+W/C_L^{+}),H<W$, where $C_L^{-}$ is the negative lift coefficient related to the first migration stage and $C_L^{+}$ is the positive lift coefficient related to the second migration stage.⁶⁸ This equation provides a theoretical support for designing microfluidic device dimensions. Values for $C_L^{-}$ and $C_L^{+}$ can be obtained from earlier work.⁶⁹ Meanwhile, the lateral equilibrium position of the focused particles moves toward the channel walls with increasing Re, possibly improving the particle capture efficiency. More details of the underlying physics of particle inertial focusing can be found in the related reviews.^21–23

B. Particle sorting and trapping

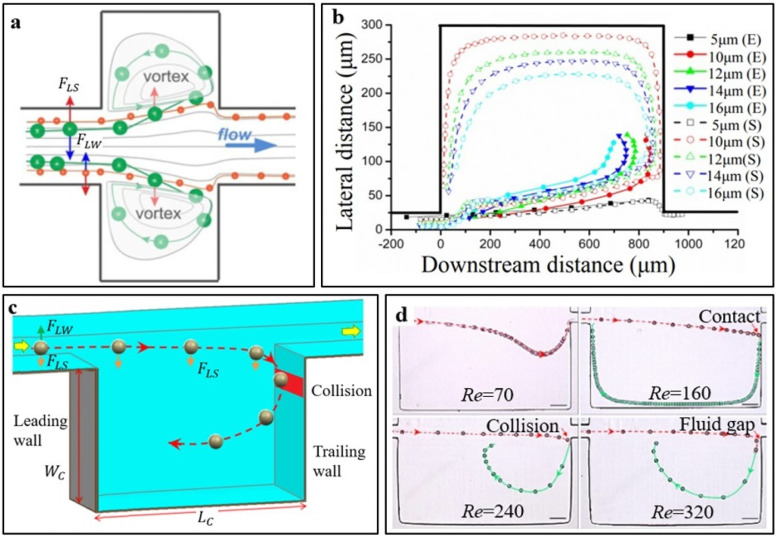
When the focused particles flow into the cavity entrance region where the $F_{LW}$ is significantly reduced because of the vanishing of the channel sidewall, they migrate across the boundary streamline (separatrix) into the vortex driven by the $F_{LS}\sim a^3$.^64,66,67 Therefore, big particles experience a more significant lateral lift force than small particles. Moreover, this lift force can be assumed to be balanced by the Stokes drag force, $F_D=3\pi \mu a{U}_L$, and the lateral migration velocity of particles scales with the particle size as $U_L\propto U_m^2{a}^2$.³⁶ Therefore, big particles with diameters above 10 μm can migrate faster across the separatrix with a longer migration distance than small particles with diameters below 8 μm.⁶⁷ As a result, the big particles enter the cavity, where they are captured by the vortex and isolated from the microchannel flow, while small particles remain in the microchannel because of insufficient lateral migration distance and flow passing the cavity without trapping by the vortex [Fig. 4(a)]. This explanation can be referred to as traditional particle trapping mechanism, which is based on different particle sizes and lateral migration distances.⁵⁵

FIG. 4.

(a) Schematic illustration of the traditional mechanism of particle sorting and trapping in the cavity entrance, where the wall effect-induced lift force, $F_{LW}$, is significantly reduced. The shear-gradient lift force, $F_{LS}$, drives big particles that migrate across the streamlines faster to be captured by the vortex in the cavity, while small particles can pass over the cavity without trapping.⁵⁵ Reproduced with permission from Zhou et al., Microfluid. Nanofluid. 15, 611–623 (2013). Copyright 2013 Springer Nature. (b) Numerical simulation (S) and experimental observation (E) of particle lateral migration trajectories during the sorting process in the cavity entrance region.⁷⁰ Reproduced with permission from Zhang et al., in IEEE/ASME International Conference on Advanced Intelligent Mechatronics (IEEE, 2013), pp. 1266–1271. Copyright 2013 IEEE Publishing. (c) Schematic illustration of cavity trailing wall collision-induced particle trapping mechanism.⁷¹ (d) Experimental observations different particle trapping modes at Re of 70–320 using a high-speed imaging microscopy at 6000 fps: no trapping (Re = 70), contact trapping (Re = 160), wall-collision trapping (Re = 240), and rapid trapping (Re = 320).⁷¹ Reproduced with permission from Shen et al., Phys. Fluids 31, 042002 (2019). Copyright 2019 AIP Publishing LLC.

Significant efforts have been devoted to testing the traditional particle trapping mechanism.^{54,55,67,70,72,73} For example, Zhang et al.⁷⁰ investigated the effect of particle size (a = 5–16 μm) on their motion trajectories during the sorting process in the cavity entrance region. They utilized a software of COMSOL Multiphysics (COMSOL, Burlington, MA) to calculate the flow field and carried out flow visualization experiments using an inverted microscope (CKX41, Olympus, Japan) to record the particle trapping trajectories in the microcavity entrance. Their numerical simulations were well consistent with experimental results, indicating that big particles can migrate laterally a longer distance and enter the vortex region earlier than small particles [Fig. 4(b)]. The morphology of the particle trajectory is a composite result of particle–vortex interactions and interparticle interactions.⁷² Moreover, to demonstrate the flexibility of the vortex sorting method, Volpe et al.⁷³ numerically explored the hydraulic resistance of channel, $R_h=(f\mathrm{Re})\mu L/2D_h^{2}A$, where f, L, and A are the channel friction factor, length, and cross-sectional area of the channel, which is a quantity that measures its opposition to the fluid motion. The critical separation diameter, $a_c$, can be precisely tuned by modulating the resistance ratio of the side channel to the main channel $(r/R)$. Wang et al.⁶³ experimentally found that increasing the $r/R$ from 5.4 to 10 at Re = 110 leads to a parabolic increase in the $a_c$ from 14 to 19 μm. Furthermore, considering the time it takes particles to pass through the cavity entrance $(\mathrm{\Delta }t=L_C/U_m)$ at Re > 150, Shen et al.⁷⁴ estimated the particle lateral migration distance as $X_{md}={\int }_0^{\mathrm{\Delta }t}{v}_{t}dt$, where $v_t$ is the lateral migration velocity, which value should be higher than the offset distance of the curved separatrix.

The traditional mechanism has been accepted by many researchers, which predicts that a higher inlet Re in the microchannel results in a larger U_L, leading to more particles trapped in the cavity. However, Haddadi and Di Carlo⁵⁶ experimentally observed that the number of particles trapped in the cavity decreases with the Re increasing, which is inconsistent with the traditional mechanism. Recent studies show that when the Re is relatively high, the particle trapping behavior becomes complex, which is also affected by other factors, such as the acceleration of particle motion, separatrix morphology and location, and cavity dimensions (width, $W_C$, and length, $L_C$).^56,58,74

In addition to previous factors, the cavity trailing wall also has significant effects on the particle trapping behaviors. Haddadi and Di Carlo⁵⁶ predicted that particles will collide with the trailing wall at high Res. However, the phenomenon of particle–wall collision has not been observed in their study as the collision process is extremely short. Using a high-speed imaging microscopy (6000 fps), Shen et al.⁷¹ carried out flow visualization experiments and first observed the particle–wall collision phenomenon that a single particle collides with the cavity trailing wall and enters the vortex, directly verifying the collision-induced trapping mechanism [Fig. 4(c)]. To thoroughly explore the effects of the cavity trailing wall on the particle capture behaviors, they further recorded the particle trajectories at Re of 70–320 and observed two other new trapping phenomena, namely, contact trapping (Re = 160) and rapid trapping (Re = 320) [Fig. 4(d)].⁷¹ These interesting phenomena indicate that the trailing wall can affect the particle trapping behaviors in a complex way, and further theoretical, experimental, and simulation studies are required to explore the underlying physics.

C. Trajectory of particle orbiting motion

After becoming trapped in a cavity, the target particles will recirculate periodically along a particular limit cycle trajectory within the vortex. In early studies, researchers mainly focused on the trapping mechanism, and relatively little attention was paid on revealing the dynamics of particle orbiting motion. However, with deeper research into this method, it is found that the particle orbiting motion significantly affects the cavity holding capacity of target particles.

Using high-speed microscope photography, Dhar et al.⁵⁴ carried out visualization experiments and quantitatively measured the position deviation of a single particle (a = 20 μm) in multiple orbital motions in cavities and found that the deviation is below 0.6%, proving that the captured particle can recirculate along a stable trajectory in the vortex. Zhou et al.⁵⁵ observed that trapped fluorescent particles form a pair of particle rings in two 400 × 400 μm² cavities [Fig. 5(a)]. Using high-speed microscope photography, Match et al.⁷² observed the orbiting motion of two polydimethylsiloxane (PDMS) particles in a 300 × 1000 μm² cavity, finding that the particle trajectory takes on a shuttle shape and the big 30-μm particle's trajectory is contained inside the small 20-μm particle's trajectory [Fig. 5(b)]. Moreover, Haddadi et al.⁵⁶ measured the velocity distribution of a finite-size particle orbiting along a limit cycle trajectory [Fig. 5(c)]. Using theoretical analysis and numerical simulation of lattice Boltzmann method (LBM), they also explored the continuous fluid exchange with the cavity and the formation of a stable orbit for the particle [Fig. 5(d)].⁵⁸ The results show that the stable orbit results from the balance between the inward and outward migrations, and the same stable orbit eventually will be formed whether the particles are released at the inlet or within the cavity.

FIG. 5.

(a) Fluorescent image of traces of trapped particles in a pair of 400 × 400 μm² cavities.⁵⁵ Reproduced with permission from Zhou et al., Microfluid. Nanofluid. 15, 611–623 (2013). Copyright 2013 Springer Nature. (b) Time-lapse high-speed image of two PDMS particles traveling in two separate orbits inside a vortex. The big particle occupies the orbit closer to the vortex center, while the small particle recirculates along the outer orbit.⁷² The scale bar is 100 μm. Reproduced with permission from Mach et al., Lab Chip 11, 2827–2834 (2011). Copyright 2011 Royal Society of Chemistry. (c) Particle velocity distribution along an orbit in a 930 × 310 μm² cavity at Re = 123. The color bar specifies the particle velocity scaled by the average flow velocity inside the channel.⁵⁶ Reproduced with permission from Haddadi et al., J. Fluid Mech. 811, 436–467 (2017). Copyright 2017 Cambridge University Press. (d) Schematic illustration of continuous fluid exchange with the cavity and the formation of a stable limit cycle trajectory for a finite-size particle. The sample streamline depicts the entry and exit of fluid from the vortex. Unlike the fluid, a finite-size particle forms a stable limit cycle trajectory and remains inside the cavity. The particle's outward migration toward the vortex boundary is opposed by an inward migration induced by the shear-gradient lift force. The fluid velocity profile at an arbitrary location is shown in the figure.⁵⁸ Reproduced with permission from Haddadi et al., Biomicrofluidics 12, 014112 (2018). Copyright 2018 AIP Publishing LLC.

The morphology and dynamic stability of the particle trajectory in the cavity are the result of many influencing factors, including the vortical flow field structure, particle characteristics (shape, size, density, elasticity, and surface properties of cells), and the confinement effects of cavities with different shapes and dimensions. Although some progress has been made in particle trajectory kinematics, an understanding of their mechanisms is still incomplete, and further flow visualization experiments, numerical simulations, and theoretical analyses are needed to characterize the complex interactions between particles, vortices, and cavity walls. This area of research is relatively new in fluid mechanics, and many fundamental issues are still unclear, such as vortex characteristics within microcavities, dynamic behavior of particle orbiting motion in vortices, and the exerting forces on moving particles.^56,74

III. EVOLUTION OF CAVITY STRUCTURES

A. Regular rectangular cavity

Using inertial microfluidics, Hur et al.⁶⁷ and Mach et al.⁷² first presented the vortex sorting method in 2011. Subsequently, many effects have been devoted to revealing the factors that affect the trapping efficiency of particles.^55,67,72 Hur et al.⁶⁷ designed an innovative microchannel with rectangular microcavities [Fig. 6(a)]. This approach can trap and isolate rare target cells (yellow) into rectangular cavities (400 × 400 μm²) from a heterogeneous sample solution, while small cells (red) remain in the microchannel. The separation of particles is realized only based on their different sizes because of the exerting shear-gradient lift force, which is related to the particle size. Their vortex sorting chip consists of eight parallel microchannels, each of which contains ten rectangular microcavities (or expansion–contraction structures) on the sidewall. A total of 80 laminar vortices can be created to separate particles simultaneously [Fig. 6(b)]. They investigated the influences of inlet flow rate, particle size, and cell concentration on the capturing efficiency. By loading fluorescently stained live HeLa cells spiked in dilute blood into the parallel microchannel, they found that the capture efficiency increased to more than 40% as the number of Hela cells increased from 200 to 900 for each experiment. They successfully separated HeLa cells (a = 12.4 μm) and MCF7 (a = 20 μm) from small blood cells with the capture efficiencies of 10% and 23%, respectively. Furthermore, in their visualization experiments, the maximum number of cells captured by each cavity was about 11–25, depending on the cell size.

FIG. 6.

(a) Design and working principle of a microchannel with rectangular microcavities. Big cells (yellow) are captured in 400 × 400 μm² microcavities, while small cells (red) remain in the microchannel.⁶⁷ (b) The design of a vortex sorting chip with 80 microcavities (400 × 400 μm²). The microchannel width and height are 50 and 70 μm, respectively. The channel length for particle focusing is 1.5 cm.⁶⁷ Reproduced with permission from Hur et al., Biomicrofluidics 5, 022206 (2011). Copyright 2011 AIP Publishing LLC.

Using 300 × 1000 μm² rectangular cavities, Mach et al.⁷² studied the vortex structure and capture efficiency of particles/cells. When the vortex occupies the entire cavity, a maximum number of ∼40 MCF cells (a = 20 μm) can be maintained. They found that the capture efficiency increased from 10% to 20% as the blood concentration decreased from 20% to 5%. The reason is that higher blood concentration leads to higher fluid viscosities which modify the vortex size and position. In addition, they demonstrated that this method could achieve a 20-flod volumetric concentration of target cells from heterogeneous solutions within 3 min, which is conducive to further detections. Furthermore, the authors found that the cells captured in the cavity maintained high levels of viability (90.1%) and could be available for standard molecular assays.

In the above studies,^67,72 microcavity structures were mainly designed based on the authors' experience and experimental observations of particle solutions. To enhance the particle capture efficiency in various rectangular cavities, Zhou et al.⁵⁵ carried out visualization experiments and modeled the cavity flow using a commercial computational fluid dynamics (CFD) software CFD-ACE + (ESI Group Inc.). Factors such as inlet flow rate, cavity size, and target particle concentration were explored to elucidate their influences on the particle trapping behaviors. Their results show that an approximate 300% increase in cavity capacity of holding particles was achieved by increase of the cavity width from 300 to 400 μm, while that is about 200% when the cavity length increases from 300 to 400 μm. The reason is that larger cavities provide more space in the development of vortices, helping to reduce particle–particle interactions. Their optimized 300 × 400 μm² microcavity could enhance the sorting performance for applications of separation of rare CTCs.

B. Special layout of rectangular cavity

The particles isolated in a vortex may interact with each other, impairing the stability of the orbiting motion. To limit the particle–particle interactions and increase the cavity trapping efficiency, Paiè et al.⁷⁵ presented a new microcavity layout by introducing a rectangular obstacle into a standard rectangular microcavity. Their numerical simulations and experimental results demonstrate that the obstacle can split the fluid streamlines into two flow circulations, driving some particles to flow in the lateral fluidic circuit [Fig. 7(a)]. The authors also optimized the obstacle configuration and validated that due to the larger reservoir area and increased orbital stability, the maximum number of captured particles was increased by 19% [Fig. 7(b)].

FIG. 7.

(a) A new layout of the microcavity geometry with a rectangular obstacle.⁷⁵ The fluid streamlines (black) are split into two flow circulations by the obstacle. (b) Simulation results of flow characteristics in microcavities with different obstacle dimensions, showing the influence of the obstacle dimensions on the trapped particle path.⁷⁵ Reproduced with permission from Paiè et al., Microfluid. Nanofluid. 21, 1–11 (2017). Copyright 2017 Springer Nature. (c) Visualization of the streamline structures in two close cavities using fluorescent imaging at Re = 63, 154, and 216.⁵⁸ (d) The number of cells entrapped in each cavity for the device in (c).⁵⁸ Reproduced with permission from Haddadi et al., Biomicrofluidics 12, 014112 (2018). Copyright 2018 AIP Publishing LLC.

To address the effect of the distance between adjacent cavities on cells entrapment, Haddadi et al.⁵⁸ proposed a microfluidic chip with serial placement of multiple cavities in proximity along a microchannel. Figure 7(c) shows one possible cavity placement arrangement and the visualized flow streamlines at $Re$ of 63, 154, and 216. It can be found that the vortex morphologies in the first and second cavities are different. Moreover, their experimental results show that the first cavity can capture more cells while the second cavity remains depleted [Fig. 7(d)]. The result can be attributed to the asymmetry of the vortices and an insufficient restoration length between two adjacent cavities.

Inspired by previous study,⁷⁵ Mohamadsharifi et al.⁷⁶ recently redesigned a new rectangular microcavity by elevating the cavity height to capture more particles and consequently reduce particle–particle collision. They employed this height-variable chip to isolate 20 μm particles representing CTCs from 8 μm particles. Using the software of COMSOL Multiphysics 6.0 and Lagrangian particle tracing module, they simulated the fluid flow and particle motion behaviors to investigate the third axis contribution to the separation mechanism. Taking advantage of 3D vortex in the cavity, the proposed chip demonstrated more than three times higher capacity in retaining orbiting particles up to 1300 for 96 cavities in peak performance without sacrificing efficiency compared to earlier single-layer designs.

C. Adding side channels

When the number of particles captured in the cavities reaches a certain level, the interaction between them may lead to particle loss from the vortex and re-entry into the microchannel. Therefore, to expel the captured target particles in time, Wang et al.⁶³ proposed an innovative microcavity scheme by adding two side channels [Fig. 8(a)]. This cavity geometry separates the flow into main channel and sheath flows, which exit through the main and side outlets. The captured particles can be continuously expelled from the cavity using the sheath flows beside the vortex. The red dashed line in Fig. 8(a) indicates the boundary streamline (separatrix) separating the main and sheath flow regions. Big particles (blue) migrate far enough across the separatrix because of a larger $F_{LS}$ and are extracted from the side outlets, while small particles (red) remain in the main flow because of insufficient lateral migration. Using a software of CFD-ACE+, the streamline distribution in the symmetric microcavities was modeled. The numerical and experimental results show that the position of the separatrix could be precisely changed by adjusting the input velocity $U_m$ and changing the side and main outlet channel lengths or widths to achieve different channel fluid resistance ratios $r/R$, where r is the resistance of the side outlet channel and R is the resistance of the main outlet. As $r/R$ increases, the separatrix moves toward the channel wall, leading to sorting of particles with different sizes [Fig. 8(b)].

FIG. 8.

(a) Microcavity scheme with one main outlet and two side outlets designed by Wang et al.⁶³ In this cavity structure, flow is separated into a main flow (red), sheath flows (blue), and vortices (gray). (b) The influence of the channel resistance ratio $r/R$ on the separatrix position on the cavity trailing wall. The red dashed line indicates the separatrix morphology in the cavity entrance.⁶³ (c) A microfluidic resistance network for multimodal separation using two sets of microcavities with side channels.⁶³ Reproduced with permission from Wang et al., Lab Chip 15, 1350–1359 (2015). Copyright 2015 Royal Society of Chemistry. (d) The fluidic resistance network of an integrated device consisting of two vortex sorting units for double sorting and purification. Butter is introduced at inlet 2 to create a high flow condition for the sorting in the second unit.⁷⁷ Reproduced with permission from Wang et al., Technology 4, 88–97 (2016). Copyright 2016 World Scientific Publishing. (e) Schematic illustration of a two-branch device with four microcavities. The lateral outlets are above a microwell, which is used to collect target particles.⁷⁸ Reproduced with permission from Volpe et al., Microfluid. Nanofluid. 23, 1–10 (2019). Copyright 2019 Springer Nature.

In practice, real samples often include mixtures of multiple microparticle components. However, most inertial microfluidic devices can only achieve bimodal separation with a single cutoff diameter,^42,43,79,80 inhibiting efficient separation of real samples. Therefore, Wang et al.⁶³ designed a separation device to achieve continuous multimodal microparticle sorting by adjusting the inlet flow rate and the fluidic resistance of the side outlet channel [Fig. 8(c)]. The microfluidic resistance network was investigated by using an analogous electrical circuit model. Wang et al^.77 further improved their device by injecting butter from inlet 2 to create a high flow condition for the sorting in the second cavity [Fig. 8(d)]. With a properly designed fluidic resistance network and optimized flow conditions, large target cells physics can be trapped in the first cavity and then pass into the second cavity to be double-sorted, leading to a higher target cell purity. The device demonstrates a high efficiency (>90%) and enhanced purity (>1500×) for continuous sorting of spiked human cancer stem-like cells from human blood. The authors stated that this technique could be a feasible tool for sorting and purifying large target cells from small background cells for applications of cell biology research and clinical diagnostics. To enhance the throughput and facilitation, Volpe et al.⁷⁸ designed a two-branch device with four microcavities [Fig. 8(e)] partly inspired by the work of Wang et al.⁶³ In this layout, target particles leaving from the side outlets can be directly collected into a microwell below for further analysis. This device can achieve a maximum particle capture efficiency of >80% at a higher flow rate (0.3 ml/min). In the above studies,^63,77,78 however, due to the side channels, the number of microcavities is limited, which reduces the sorting efficiency.

D. Round cavity

Significant effort has been devoted to increasing the number of particles captured in microcavities.^55,56 However, the particle trajectory can occupy only a part of the rectangular cavity, and there are no target particles in the two bottom corners of the cavity. Therefore, a new round cavity-based vortex sorting method was first proposed by Shen et al.⁵⁷ to increase the ratio of particle orbital area (A_p) to cavity area (A_c) [Fig. 9(a)]. Comparative experimental studies were conducted to record the particle motion behaviors. The results show that round cavities can improve the holding capacity by 2.2–7.8 times higher than that of rectangular cavities. The influences of the inlet Re (267–476), cavity entrance length (200, 400, 800, and 1200 μm), and particle diameter (10, 15, and 20 μm) have been investigated, finding that the round cavity with a 400-μm entrance length has the best holding performance. A commercial software of Ansys-Fluent 17.0 was employed to simulate the vortex streamlines. By comparing particle recirculating orbits and simulated vortex structures in round and rectangular cavities, the results show that the morphologies of the particle orbit and vortex structure match the shape of the round cavity better than that in rectangular cavity [Fig. 9(b)]. To quantitatively characterize the cavity holding capacity, the authors also proposed an area ratio, $S=A_p/A_c$, and a particle concentration, $C_p=N_p/A_c$, where N_p is the maximum number of captured particles [Fig. 9(c)]. In the 400-μm round cavity, the maximum value of S and $C_p$ are 95% and 376/mm², compared to that of 56% and 281/mm² in the 400 × 400 μm² rectangular cavity.

FIG. 9.

(a) Schematic illustration of the particle entrapping and holding mechanisms in round and rectangular cavities.⁵⁷ (b) Experimental results of stacked particle images of long-term particle orbiting behavior within vortices in two cavities.⁵⁷ (c) Schematic illustration of the particle recirculation area, revealing why the round cavity has a higher holding capacity for particles than the rectangular cavity.⁵⁷ Reproduced with permission from Shen et al., Phys. Fluids 33, 082002 (2021). Copyright 2021 AIP Publishing LLC.

IV. FUNDAMENTAL STUDIES ON VORTEX AND PARTICLE DYNAMICS

A. Vortex flow field characteristics

The microcavity vortex flow field characteristics have important effects on particle sorting behaviors. Many researchers conducted experimental and simulation studies on the flow fields in various cavities.^56,81 Yu et al.⁸² experimentally found that vortex generation mechanism in a 50 × 50 μm² cavity differs from at macro-scales. Osterman et al.⁸¹ numerically found that the vortex number increases from 1 to 3 as the cavity length increases [Fig. 10(a)]. Heaton et al.⁸³ simulated the influences of the Re and cavity size on the vortex number and structures [Fig. 10(b)]. Using a software of CFD-ACE+, Zhou et al.⁵⁵ conducted a numerical simulation and found that the vortex has a three-dimensional structure due to the confinement effects of the upper and lower cavity walls [Fig. 10(c)]. Haddadi et al.⁵⁶ observed the effects of the Re and cavity size on the flow patterns of tracer particles in microcavities with different aspect ratios, α = L_c/W_c [Fig. 10(e)].

FIG. 10.

(a) Numerical modeling of vortex structures in a long microcavity.⁸¹ Reproduced with permission from Osterman et al., Microfluid. Nanofluid. 20, 1–10 (2016). Copyright 2016 Springer Nature. (b) Streamlines in cavities with length/width aspect ratios of 0.9, 1.5, and 3.0.⁸³ Reproduced with permission from Heaton et al., Phys. Fluids 20, 103102 (2008). Copyright 2008 AIP Publishing LLC. (c) Perspective view and side view of the 3D vortex structure. The particle orbits (blue) are located at 1/4H and 3/4H, vertically centered at each of the two vortices (red).⁵⁵ Reproduced with permission from Zhou et al., Microfluid. Nanofluid. 15, 611–623 (2013). Copyright 2013 Springer Nature. (d) Fluid streamlines in cavities with length/width aspect ratios, α = 3 and α = 5 at various Res. The arrows specify the direction of the channel flow.⁵⁶ Reproduced with permission from Haddadi et al., J. Fluid Mech. 811, 436–467 (2017). Copyright 2017 Cambridge University Press. (e) Micro-PIV results of the attached, transitional, and separated flow patterns in a 300 × 200 μm² microcavity at Re of 3, 46.3, and 92.6.⁸⁴ Reproduced with permission from Shen et al., Microfluid. Nanofluid. 19, 403–417 (2015). Copyright 2015 Springer Nature. (f) Water flow patterns (downward) at the cavity region of a microchannel. Fluid circulations are formed only near the leading cavity wall at Re = 72.1 (highlighted by the dashed line arrows on the top-right image). The right half of the bottom-left image shows the simulated fluid streamlines at the corresponding experimental condition (Re = 96.2). The scale bar is 100 μm.⁸⁵ Reproduced with permission from Raihan et al., Micromachines 12, 836 (2021). Copyright 2021 MDPI Publishing.

Using a particle image velocimetry (micro-PIV), Fishler et al.⁸⁶ measured the velocity distributions in round cavities, finding that the average velocity of the vortex is much lower than that in the microchannel (<10⁻²). Shen et al.⁸⁴ also conducted micro-PIV measurements to systematically investigate the influences of the Re and α on the vortex structures in rectangular cavities. According to the vortex structure, they defined three flow forms: attached, transitional, and separated flows in a 300 × 200 μm² cavity [Fig. 10(f)]. They also found that vortex characteristics are different in square cavities with different sizes.⁸⁷ Raihan et al.⁸⁵ visualized the vortices evolution of in a 506 × 223 μm² cavity at Re of 24.1–192.4 [Fig. 10(d)]. A pair of small-lip vortices form near the cavity leading walls at Re = 33.7. These symmetric corner vortices grow in their size at Re = 72.1 and touch the trailing wall at Re = 120.3 as their cores move downstream. Further increasing the inlet flow rate shifts the vortex cores further toward the trailing walls because of the enhanced fluid inertia.

Different flow patterns in the microcavity can be used to manipulate the motion of particles in different ways. For example, the attachment flow can be used to expel target particles. The traditional particle trapping mechanism mentioned above can only apply to the transition flow, while the influence of the cavity trailing wall on the particle trapping behaviors must be considered in the separated flow.^71,74 Although both transitional and separated flows can be employed to trap target particles, the separated flow can contain more particles. However, the larger the microcavity size, the higher the critical Re required for forming the separated flow. Too high flow rate may induce high flow shear force, leading to damage of the cells. To better understand the effects of vortices on particle motions, it is necessary to obtain the vortex characteristics.

B. Single-particle orbiting trajectory

Because of the complexity of particle–particle interactions in the microvortex, it is a feasible approach to study single-particle orbiting motion first. Hur et al.⁶⁷ observed that trapped 10 μm particles could form stable recirculating trajectories in a 400 × 400 μm² cavity, while 5 μm particles could not. Mach et al.⁷² recorded that big polymer particles (a > 15 μm) can recirculate in a stable limit cycle around the vortex center in a 300 × 1000 μm² cavity [Fig. 11(a)]. Interestingly, Khojah et al.⁸⁸ experimentally found that the particle orbiting trajectory evolves in a complex way. When the Re < 100, big-sized particles occupy the inner trajectory, while small-sized particles occupy the outer trajectory. With the Re increasing (100–300), the trajectory of big particles gradually expands outward, while that of small particles gradually shrinks inward. Eventually, the big and small particles exchange their relative positions [Fig. 11(b)]. The background physics for the trajectory change phenomena has not been addressed by the authors and further research is needed.

FIG. 11.

(a) Time-lapse high-speed image of a PDMS particle during trapping and orbiting around the vortex center in a stable limit cycle.⁷² The scale bar is 100 μm. Reproduced with permission from Mach et al., Lab Chip 11, 2827–2834 (2011). Copyright 2011 Royal Society of Chemistry. (b) High-speed time-lapse of bright field images of single polystyrene bead motions in a square microcavity, showing the transition of size-based equilibrium orbits in three capture phases. The relative radial position of the trajectories of big (red) and small (blue) beads change, and $\lambda$ is the ratio of the bead diameter, a, to the cavity depth (H = 70 μm).⁸⁸ The scale bar is 120 μm. Reproduced with permission from Khojah et al., Lab Chip 17, 2542–2549 (2017). Copyright 2017 Royal Society of Chemistry. (c) Evolution of a single-particle (a = 30 μm) orbiting trajectory in a 600 × 600 μm² microcavity. In particular, the particle double-cycle trajectory appears at Re = 176.⁸⁹ Reproduced with permission from Shen et al., J. Phys. D: Appl. Phys. 54, 025401 (2020). Copyright 2020 IOP Publishing. (d) Sketched particle orbiting and rotating motions in a 400 × 400 μm² microcavity.⁷⁴ Reproduced with permission from Shen et al., Appl. Phys. Express 10, 097301 (2017). Copyright 2017 IOP Publishing.

Using high-speed photographic experiments, Shen et al.⁸⁹ investigated the evolution of a single-particle (a = 30 μm) orbiting trajectory in a 600 × 600 μm² cavity, finding that the particle trajectory gradually expends with $Re$ increasing from 58 to 313 [Fig. 11(c)]. In particular, they first observed an interesting phenomenon that the particle trajectory develops from a single orbit into a double-cycle trajectory at Re = 176. The particle can recirculate along the inner and outer cycle alternately and periodically. With increasing Re, the inner cycle gradually shrinks to the vortex center, while the outer cycle gradually expands to the cavity walls. The authors attribute the main reason for this phenomenon to the trailing wall effects on the inertial particle.

While orbiting in a vortex, the particle also has a spin motion due to the non-uniformity of the vortex flow field.⁷² Using high-speed microscope photography at 6000 fps, Shen et al.⁷⁴ observed the orbiting motion of a spotted particle in a 400 × 400 μm² microcavity and found that the particle also rotates around itself in a counterclockwise direction with a rotational frequency of one per periodic orbital motion [Fig. 11(d)]. Using the LBM method, Jiang et al.⁹⁰ simulated the orbiting and rotating motions of particles in a microcavity, which results consistent with that of Shen et al.⁷⁴ Current studies have enriched the understanding of particle orbiting behaviors and are helpful in revealing the complex exerting forces.

C. Preliminary studies of exerting forces

In recent years, precise control of particle motions has become one of the hot research topics in the microfluidics research area.^21–23,36 The forces exerting on the particles are always crucial in studying the particle–fluid two-phase flow.^22,24 Compared with the Dean flow methods,^45–50 the reviewed vortex sorting method was proposed relatively late. There are relatively few studies on the forces exerting on the particles orbiting in vortices. Shelby et al.⁹¹ reported a vortex-based method to control the high-speed rotation of particles in a diamond-shaped microcavity and proposed a simplified force balance model, which is based on the centrifugal force, displacement force, and lift force. The authors stated that although there also exists a Stokes drag forces, its magnitude is negligible in comparison with these three forces. To form a stable recirculating orbit of particles, these three forces must be balanced at the radial location of the orbit. According to this model, the diameter of the orbit of recirculating particles increases with the applied inertial force.

Mach et al.⁷² approximated the particle trajectory as a circle and proposed a force balance model using the centrifugal force and inertial lift. Haddadi et al.⁵⁸ used the following Basset–Boussinesq–Oseen (BBO) equation to analyze the forces exerting on particles:

$$\begin{array}{rl}{m}_P{\displaystyle \frac{dV}{dt}=}& {m_f{\displaystyle \frac{Du}{Dt}}|}_{Y(t)}-{\displaystyle \frac{1}{2}{m}_f{\displaystyle \frac{d}{dt}\left(V(t)-u[Y(t),t]-{\displaystyle \frac{1}{10}{a^2{\mathrm{\nabla }}^{2}u|}_{Y(t)}}\right)}}\\ & +f-6\pi a\eta \left(V(t)-u[Y(t),t]-{\displaystyle \frac{1}{6}{a^2{\mathrm{\nabla }}^{2}u|}_{Y(t)}}\right),\end{array}$$

where V represents the center-of-mass velocity of a particle located at $Y(t)$ at time t and u, $m_f$, $m_p$, and $\eta$ denote the undisturbed fluid velocity, suspending fluid mass, particle mass, and fluid viscosity, respectively. In the BBO equation, particle motion is affected by the force of the undisturbed flow and additional hydrodynamic contributions from the disturbance flow generated by the particle's finite size and rigidity. The first term on the right-hand side of the BBO equation represents the force of the undisturbed flow, while other terms represent forces arising from the disturbance flow. This BBO equation is just a baseline description of the particle orbiting motion in a vortex.⁵⁶ There are presently no exact formulas to describe these various forces, for example, the inertial action, additional mass force, $F_{LW}$, $F_{LS}$, differential pressure force, Stokes force, Saffman force, Magnus force, and Basset force.^56,58

In microfluidic systems, small tracer particles tend to flow with the surrounding fluid, following the fluid well. However, finite-size particles that are the same size as the microchannel deviate from the streamlines under the action of inertial effects. Therefore, the target particle trajectory is inconsistent with the surrounding streamlines, especially in flow fields with fluid velocity acceleration and deceleration or curved streamlines.

By comparing micro-PIV results with those from microscopic high-speed imaging system, Shen et al.⁹² first identified the deviations between particle trajectories and surrounding streamlines [Fig. 12(a)]. Their results indicate that a finite-sized particle moving along its trajectory (red line) constantly crosses the vortical streamline (black line), leading to a morphological deviation and a velocity mismatch between the particle and fluid. The deviation between them substantially affects particle motion and is also the key to revealing particles' dynamics and force analysis at microscales. Furthermore, according to the deviation, they divided the particle trajectory into three stages: accelerating, swerving, and following stages. In the accelerating stage [Fig. 12(b)], the particle is accelerated mainly by the fluid drag force, $F_{\mathrm{drag}}=3\pi \mu d{v}_t(1+0.15R{e}_p^{0.687})$, where $v_t$ is the difference between the fluid and the particle velocities. Then, when the particle moves to the rear cavity wall, it deviates horizontally inward toward the vortex center under the action of the fluid shear-gradient lift force, F_LS. The particle is also affected by a centrifugal force, $F_{ctf}=\pi d^3({\rho }_p-\rho )v_p^2/6r$, where r is the local radius of the particle's orbital curvature, and the direction is away from the vortex center. $F_{ctf}$ increases near the rear wall. In the swerving stage [Fig. 12(c)], the wall-induced lift force, F_LW, increases noticeably with the decreasing distance between the particle and the rear wall, and the particle begins a second lateral migration under the action of the wall-induced lift force. In the following stage [Fig. 12(d)], the particle exhibits a good fluid following performance because the local fluid velocity in this stage is relatively low, and the drag force on the particle becomes relatively small.

FIG. 12.

Deviations between the particle trajectory and vortex streamlines.⁹² (a) Deviation in morphological characteristics. (b) Velocity deviation between the particle and fluid in the accelerating stage. The particle accelerates in the x-direction and migrates laterally in the y-direction. (c) Particle swerving near the cavity trailing wall with decreasing velocity in the swerving stage. (d) Particle following of the streamlines in the following stage at relatively low speeds. Reproduced with permission from Shen et al., Appl. Phys. Lett. 120, 024101 (2022). Copyright 2022 AIP Publishing LLC.

In practice, the particle dynamic motion and exerting forces during orbiting in a vortex involve many complicated issues (strange orbits, changing speeds, and complex forces), which are relatively new research topics in fluid mechanics. Three factors lead to the complexity of particle forces: (i) non-uniformity of the vortex field; (ii) variable particle motion speeds; and (iii) constant change of the trajectory curvature.^56,58 Therefore, the magnitudes and directions of the various forces mentioned above constantly change with positions along the trajectory, and their accurate formulas are still absent. The results of single-particle orbiting motion, which are the basis for studying multi-particle motions in vortices, enrich the research scope of the particle–fluid two-phase flow^93,94 and provide guidance for particle manipulations in microfluidics.⁹⁵

D. Flow patterns of particle suspension

To further understand the particle flow pattern in a microvortex, Zhou et al.⁵⁵ injected a suspension of 20 μm particles into a microchannel and observed the particle trajectory evolution in two pairs of microcavities [Fig. 13(a)]. They found that the particle trajectories are approximately semicircular, which areas increase when Re increases from 69 to 289. The enlargement of the particle trajectory could result from a higher vortical flow velocity that strengthens the centrifugal force pushing particles outward. In addition, the higher flow velocity may also distort the particle trajectory at Re = 289 in the 400 × 400 μm² cavity. The author attributed the reason to the particle escape. Meanwhile, they observed that two particle trajectories appear in each cavity at Re = 154, which is an interesting phenomenon and similar to observations by Hur et al.⁶⁷ The authors attributed the double trajectory phenomenon to the three-dimensional structure of the confined vortex. Note that the double trajectory phenomena in Fig. 13(a) are different with that in Fig. 11(c). In Fig. 13(a), due to the high particle concentration, particle–particle interactions are inevitable.

FIG. 13.

(a) Observations of particle flow patterns at Re of 69–289. In the upper images, the cavity size is 300 × 300 μm², where the trajectory evolves from a single small semicircular shape at Re = 69 to double trajectories at Re = 154, then to a large trajectory at Re = 180. In the lower images, the cavity size is 400 × 400 μm², where double trajectories form at Re = 154. At Re = 205, particles fill the gap between the double trajectories, while at Re = 289, the trajectory distorts, and particles escape.⁵⁵ Reproduced with permission from Zhou et al., Microfluid. Nanofluid. 15, 611–623 (2013). Copyright 2013 Springer Nature. (b) High-speed time-lapse images of polystyrene particle suspensions illustrating the transition between three phases (upper row pictures). All scale bars represent 120 μm. Scatterplots of polydisperse polystyrene beads illustrate the orbital transition toward the vortex core between phase I and phase III (lower row pictures). The color scale represents the scaled bead diameter $(\lambda =a/H)$.⁸⁸ Reproduced with permission from Khojah et al., Lab Chip 17, 2542–2549 (2017). Copyright 2017 Royal Society of Chemistry.

Khojah et al.⁸⁸ experimentally observed the dynamics of polystyrene bead suspensions (a = 10, 15, 20, and 30 μm) in a 600 × 600 μm² cavity [Fig. 13(b)]. According to the morphologies of the trajectories, they found three trapping phases, in which big particles gradually expand outward, while small particles gradually shrink inward with Re increasing. The scatterplots of the particle distribution and the average orbital radii basically agree with the results of a single particle. The flow pattern results from many complicated factors, among which the particle–particle interactions must be considered. Understanding of the flow pattern evolution is vital for improving the cavity holding capacity. However, due to its intrinsic complexity, further quantitative experimental studies are needed to explore the influences of various factors.

E. Cavity holding mechanism

Because of the limited space in a microcavity, the number of captured particles will reach a maximum (N_p) sometime after separation. Increasing N_p can improve the separation efficiency and enhance the particle concentration.^55–57 At present, how to improve the cavity holing capacity, characterized by N_p, has become the focus of research of the vortex sorting method. The influence factors include the vortex structure, cavity size and shape, particle density and size, and so on.^55,56 Zhou et al.⁵⁵ experimentally investigated the effects of inlet $Re$, microchannel height, cavity size, and particle concentration on the holding capacity of rectangular cavities [Fig. 14(a)]. They found that the number of particles held in a cavity became saturated in about 1 min. Moreover, the N_p in one cavity first increases and then decreases with Re increasing, with a maximum of 25–30 at Re = 239 in each. The authors speculated that the reason is that the interaction between particles becomes stronger at high flow rates, leading to unstable orbits and particles escape.

FIG. 14.

(a) Time-lapse images illustrating progressive trapping and enrichment of 20 μm particles in a 500 × 400 μm² cavity.⁵⁵ Reproduced with permission from Zhou et al., Microfluid. Nanofluid. 15, 611–623 (2013). Copyright 2013 Springer Nature. The effects of cavity length (b) and width (c) on the maximum number of entrapped particles (N_p) in a pair of cavities under Re of 50–300.⁵⁶ The cavity width in (b) was fixed at Wc = 310 μm, and the cavity length in (c) was fixed at in Lc = 930 μm. Reproduced with permission from Haddadi et al., J. Fluid Mech. 811, 436–467 (2017). Copyright 2017 Cambridge University Press. (d) Snapshots of captured particles in round and rectangular cavities at the Re of 316, 366, and 433. $N_1$ and $N_2$ represent the maximum numbers of particles held in the round and rectangular cavities, respectively.⁵⁷ The scale bar is 100 μm. (e) Comparison of the N_p in round and rectangular cavities.⁵⁷ Reproduced with permission from Shen et al., Phys. Fluids 33, 082002 (2021). Copyright 2021 AIP Publishing LLC.

To improve the cavity holding capacity, Haddadi et al.⁵⁶ systematically investigated the effects of Re and cavity aspect ratios (α = L_C/W_C) on the $N_P$. It can be found that both the peak value of $N_P$ and optimal Re increase with increasing the cavity length [Fig. 14(b)]. As the cavity width increases, the peak value of N_p increases without an obvious change in the optimal Re [Fig. 14(c)]. After optimization, the maximum value of N_p in a pair of cavities is about 40–150. Moreover, the authors also observed that N_p decreases at Re > 200 in Fig. 14(c) and attributed this phenomenon to the interactions between particles.

Notably, most of the prior researchers used rectangular cavities. Recently, Shen et al.⁵⁷ proposed a round cavity for particle sorting. The calculated N_p in round and rectangular cavities increase from N₁ = 59 and N₂ = 35 at Re = 316 to N₁ = 86 and N₂ = 42 at Re = 366 and then decreases to N₁ = 50 and N₂ = 32 at Re = 433 [Fig. 14(d)]. The curves of the N_p–Re in the two cavities in Fig 14(e) first rise as $Re$ increases from 267 to 366 and then decrease as Re increases to 467. The results show that the holding capacity in the round is much higher than that of the rectangular cavity. Moreover, the particle concentration, $C_p=N_p/A_c$, in the round cavity is also higher than that in the rectangular cavity under the same working conditions, indicating that the round cavity has a better sorting performance than the rectangular cavity. The authors attributed the significantly increased number of particles contained in the round cavity to the similarity of the arc-shaped cavity wall to the particle trajectory morphologies. However, because the particle–particle, particle–fluid, and particle–wall interactions are very complex, further studies are needed to explore the round cavity holding mechanism. Although some efforts have been devoted to improving the cavity holding capacity, until now the background mechanism has not been investigated as a separate problem, which is a relatively new problem in fluid mechanics.

F. Non-Newtonian fluid sorting

Using xanthan gum (XG) solutions, Raihan et al.⁹⁶ achieved vortex sorting of particles at Re < 15. Due to the shear-thinning effect in XG solutions, the formation and evolution of vortices in microcavities are distinct from those in Newtonian fluid flows.^84,85,87 When particles enter the cavity entrance [Fig. 15(a)], they begin experiencing a wall-directed rheological lift, $F_{rL\to W}$, and shear-gradient inertial lift, $F_{iL\mathrm{\_}S}$, both of which direct toward the cavity bottom, driving big particles to trace streamlines and advance toward the vortices in the rear corners of the cavity, while small particles remain in the main channel flow.⁹⁷ Figure 15(b) demonstrates the separation of 5 and 15 μm particles in a 600 × 266 μm² cavity using a 1000 ppm XG solution at a 4 ml/h flow rate. The authors state that as a result of the relatively low Re, the shear force exerted on the cells by the microchannel flow is also low, which prevents the cells from being damaged by the shearing force and is conducive to the subsequent study of captured cells. However, only a few particles can be held by each vortex, and the cavity holding capacity could be improved by optimizing the cavity geometry and flow conditions.

FIG. 15.

(a) Schematic illustration of the size-selective focusing, trapping, and separation of particles in a shear-thinning XG solution flowing through a pair of rectangular microcavities.⁹⁶ (b) Vortex trapping and separation of 15 μm (dark) particles from 5 μm (bright) particles in a 1000 ppm XG solution flow at a 4 ml/h flow rate.⁹⁶ Reproduced with permission from Raihan et al., Appl. Phys. Lett. 116, 183701 (2020). Copyright 2020 AIP Publishing LLC.

V. APPLICATIONS

Compared with macroscopic vortices, microcavity vortices have the ability to manipulate particles and cells due to the micro-scale effects. Vortices in various microcavities have demonstrated many biological- and chemical-related applications, such as micro-hemangioma, microcavity cleaning, micro-gap oil flooding, biomimetic study of flow in alveolar, and cells trapping and culture.^98–100 This paper briefly reviews the research of vortex-based sorting of particles, specifically for CTCs, which are extremely rare malignant cells originating from primary tumors or metastatic sites and can travel through the bloodstream to other organs.¹⁰¹ Because CTCs can provide genetic and phenotypic information about the tumor evolution, liquid biopsy for CTCs has become an effective test for cancer detection.^9,102,103 However, the concentration of CTCs in the blood of tumor patients is very low and there are only 1–100 CTCs per milliliter in whole blood sample. Therefore, accurate and efficient separation of CTCs from other non-target cells in human blood is essential to this test,¹⁰⁴ especially because high purity and enrichment is crucial for cell analysis such as gene expression analysis and sequencing.⁸ The vortex sorting method is an important microfluidics for separation and enrichment of rare CTCs from the real blood samples of tumor patients,^18,105,106 having advantages of simple structure, low vortical velocity, high target particle content, high efficiency, and parallelization.^55,72

According to the particle/cell characteristics, the applications of the vortex sorting method can be classified into three stages: separation of target particles from particle solutions, separation of cultured CTCs, and separation of rare CTCs from patients' blood samples. Most reported applications are in the former two stages,^55,62,77 while reported third stage applications are relatively few.^57,72 Until now, most reported applications have been carried out in the laboratory, and clinical applications are still lacking. Due to space limitations, only a few applications are listed in this paper (Table I).

TABLE I.

Table of applications of the vortex sorting method in various microcavities.

References	Main channel (W × H)	Microcavity details (LC × WC)	Re	Target particles/cells	Efficiency	Particles number per cavity
Hur et al.67	50 × 70 μm2	400 × 400 μm2	215 270	Blood and Hela cells (12.4 μm) Blood and MCF-7 cells (20 μm)	10% 23%	11–25 …
Mach et al.72	…	1000 × 300 μm2	4.4 ml/min	MCF-7 cells (20 μm)	∼20%	∼40
Wang et al.62	50 × 100 μm2	500 × 500 μm2 With side channels	110 110	18.5 + 21 μm particles RBCs + 21 μm particles	∼90% ∼86%	… …
Zhou et al.55 (2013)	45 × 80 μm2	500 × 400 μm2	69 239	15 μm particles 20 μm particles	/ ∼20%	/ ∼55
Sollier et al.27	40 × 80 μm2	720 × 480 μm2	… 7 ml/min 4 ml/min	CTCs (7.5 ml blood) 19 μm particles PBS + MCF-7 cells	… 36.8% ∼20%	4–8 … …
Wang et al.63	50 × 100 μm2	500 × 500 μm2 With side channels	110	10–27 μm particles	…	…
Wang et al.77	30 × 50 μm2	500 × 500 μm2 With side channels	80 80 84.2	7 and 18.5 μm microbeads RBCs + 18.5 and 23 μm beads RBCs + HuSLCs	… 94% >90%	… … …
Paiè et al.75	50 × 70 μm2	720 × 245 μm2 With obstacles	5 ml/min	20 μm particles	67%	∼19
Haddadi et al.56	40 × 70 μm2	930 × 310 μm2 930 × 660 μm2 1550 × 310 μm2	123–216 123 216	20 μm particles	… … …	∼70 ∼146 ∼116
Renier et al.107	40 × 70 μm2	720 × 480 μm2	…	Prostate cancer cells from blood	59%	…
Haddadi et al.58	40 × 70 μm2	930 × 310 μm2	100–250	PC3 cells	…	∼30
Dhar et al.108	40 × 70 μm2	720 × 230 μm2	0.03–0.3 ml/min	Spiked prostate cancer cells	>40%	…
Volpe et al.78	50 × 60 μm2	480 × 270 μm2 With side channels	100	6 and 15 μm beads	>80%	…
Rastogi et al.109	…	720 × 480 μm2 With orthogonal side channel	57–62	15 and 20 μm beads 20 μm beads and RBCs	…	…
Shen et al.57	80 × 110 μm2	R = 283 μm L = 400 μm Round cavity	308–467 267–476 317	15 μm particles 20 μm particles Big cells from blood	… … …	∼126 ∼86 ∼117
Amini et al.110	40 × 70 μm2	900 × 300 μm2 Enhanced H of 110 μm	150	MCF-7 cells 20 μm beads	45% 75%	∼50 ∼65

Hur et al.⁶⁷ utilized the laminar vortex to selectively sort particles (10 μm), Hela cells (12.4 μm), and MCF7 cells (20 μm) from blood solutions, finding that particles/cells with sizes above their critical cutoff values can be trapped and isolated by the vortex in 400 × 400 μm² cavities. Wang et al.⁶² injected a mixture of 21 and 18.5 μm particles into 500 × 500 μm² rectangular cavities with side channels to demonstrate separation selectivity. The purity of 21 μm particles from the side outlet was 93%, while the purity of 18.5 μm particles from the main outlet was 91%. In addition, they added 21 μm particles into diluted human blood sample to mimic spheroid cells and injected the sample into the cavity for separation. Their results show that the 21 μm particles are concentrated by a factor of 5× in the side outlet, while nearly all red blood cells (RBCs, ∼99%) exit from the main outlet, indicating that the vortex sorting technology is very promising in efficiently sorting big cells from mixtures. Using vortices formed in round microcavities, Shen et al.⁵⁷ tested the cavity holding capacity of big cells from untreated whole blood samples of eight patients, finding that the captured cell numbers are consistent with the initial, moderate, and terminal stages of patients. The results prove that cancer detection and treatment effect may be evaluated using this approach.

Sollier et al.²⁷ used the vortex sorting method to extract and enumerate high-purity CTCs from the blood of patients with breast cancer (N_p = 4 from 25 to 51 CTCs/7.5 ml) and lung cancer (N_p = 8 from 23 to 317 CTCs/7.5 ml) [Fig. 16(a)]. When using spiked cell samples, they could routinely achieve purity of 80%–100%.

FIG. 16.

(a) Big cells (violet dashed lines) experiencing a larger $F_{LS}$ are pushed away from the channel center through the separatrix and into the vortices, where they are stably isolated. Small cells (red dashed line) remain in the main flow.²⁷ Reproduced with permission from Sollier et al., Lab Chip 14, 63–77 (2014). Copyright 2014 Royal Society of Chemistry. (b) Each vortex microfluidic chip contains two parts. Each part consists of 16 parallel channels with 9 serial cavity pairs. Big target cells, such as CTs, are trapped in the microcavities by vortices, while unwanted red blood cells (RBCs) and white blood cells (WBCs) flow off the chip.¹¹¹ Reproduced with permission from Vander Plaetsen et al., Prenat. Diagn. 41, 1171–1178 (2021). Copyright 2021 John Wiley and Sons. (c) Laminar vortices trap big cancer cells in rectangular cavities, while small blood cells (RBCs and WBCs) either pass through or are not stably trapped during the wash step (red dotted box). Sample processing involves (i) priming the cavities with a wash solution to remove air bubbles; (ii) infusing the sample and capturing target cells; (iii) switching to a wash solution at the same flow rate; and (iv) releasing captured cells by lowering the flow rate to dissipate the vortices.¹⁰⁷ Reproduced with permission from Renier et al., NPJ. Precis. Oncol. 1, 1–11 (2017). Copyright 2017 Springer Nature. (d) An integrated microfluidic system that integrates isolation, reagent exchange, and encapsulation functions for single-cell secretion analysis of rare cells.¹⁰⁸ Reproduced with permission from Dhar et al., Proc. Natl. Acad. Sci. U.S.A. 115, 9986–9991 (2018). Copyright 2018 Proceedings of the National Academy of Sciences of the United States of America.

Similarly, using laminar vortices, Vander Plaetsen et al.¹¹¹ carried out a proof-of-concept study to enrich circulating trophoblasts (CTs) from maternal blood based on their larger cell size [Fig. 16(b)]. Blood of 8 ml was collected from 15 pregnant women and processed with an automated VTX-1 liquid Biopsy System (Vortex Biosciences, Pleasanton, USA), which is based on the vortex technology and can enrich target cells within 1.5 ml. After an estimation, the number of CTs recovered from 8 ml of blood was between 2 and 6. Moreover, their spiking experiments with trophoblast cells from a JEG-3 cell line resulted in a recovery of 35%±5.49% (n = 6) of CTs with 1524 ± 569 retained maternal blood cells, which simplifies subsequent cell analyses.

Renier et al.¹⁰⁷ used a microfluidic vortex chip to isolate CTCs from 22 patients with advanced prostate cancer and, from an enumeration study on 18 of these patients, captured CTCs with high purity (from 1.74 to 37.59%) and efficiency (from 1.88 to 93.75, CTCs/7.5 ml) in less than 1 h [Fig. 16(c)]. Interestingly, 1.25–2.50 atypical large circulating cells in 7.5 ml blood in five 46–77 years old healthy donors were identified, while that was zero in five 21–27 years old healthy donors. Using a threshold (3.37 CTCs/ml), they identified CTCs in 80% of the prostate cancer patients. The authors stated that the use of this label-free Vortex technology would give access to more clinical information for targeted therapy selection through a workflow for genomic analysis.

Dhar et al.¹⁰⁸ proposed an integrated microfluidic system that combined the vortex sorting method with droplets encapsulation technology to sort CTCs from blood first and then encapsulate them into nanoliter-scale droplets, which could preserve the physiologic state of target analyzed cells [Fig. 16(d)]. This system can concentrate rare cancer cells over 100 000-fold from 1 ml of whole blood into ∼50 000 2-nl drops composed of assay reagents within 15 min. They found that CTCs from prostate cancer patients possess above baseline levels of metalloprotease activity (1.7- to 200-fold) and CTCs may secrete higher levels of enzymes than normal circulating cells in situ.

Meanwhile, many studies have been conducted to design innovative cavity structures for various applications. The design of cavities with side channels has been applied to selective and continuous separation of particles/cells from main flow (Table I). The capture efficiency of cavities with side channels has been significantly improved (∼90%), and the $Re$ required for particle sorting becomes relatively low (<110).^62,77 Moreover, Rastogi et al.¹⁰⁹ presented an orthogonal vortex chip to carry out size-differentiated trapping at significantly 38% lower velocities, avoiding cell damage and protecting their viability for subsequent assays. In addition, by increasing the cavity height (H = 110 μm), Amini et al.¹¹⁰ designed a new chip structure and achieved 40% and 20% increases in the sorting efficiency for 20-μm polystyrene beads and MCF-7 cells, respectively. They also demonstrated that 80% efficiency and 80% purity after three repeated cycles of separation cancer cells. The maximum $Re$ for sorting was about 200 in the conventional device, while the new proposed structure presented in their work was 150. Lowering the optimal flow rate will reduce the speed of particles in the cavity area and reduce their collisions, resulting in an increase in the saturation number of particles for each cavity in the new chip.

Shen et al.⁵⁷ tested the sorting performance of round cavities in clinical application by using untreated whole blood samples (3 ml) taken from eight patients with colon cancer. The samples were diluted by a factor of 10 using PBS without any further treatments (e.g., lysis of red blood cells or centrifuge treatment) and continuously injected into the microchannel for 3 min. At Re = 272, the isolated larger cells occupied most of the flow region of the round cavity and their number increased to 16, while there were only four target cells in the rectangular cavity. The calculated concentration of larger cells in the blood samples were 120–380 cells/ml. The results demonstrate that the round cavity could achieve approximately four times better sorting performance than the rectangular cavity. Moreover, the numbers of isolated larger cells were related to the patient’s stage. Specifically, the isolated larger cell number decreased from 18 to 5 before and after surgery for No. 8 patient at terminal stage. The authors stated that the round cavity-based vortex sorting method would be useful in many clinical applications, e.g., assistance in cancer diagnosis, quick cancer screening, point-of-care testing, cancer precision medicine, and single cancer cell analysis.

VI. CONCLUSIONS AND OUTLOOK

This paper reviews the fundamentals and research progress of the vortex sorting method, which combines particle inertial migration with vortex trapping and holding in microcavities. Compared with other methods, it is a passive method with many unique advantages, such as being label-free, having a simple structure, high efficiency, high purity, parallelizing of multiple cavities, and particularly enrichment of rare CTCs. This makes it a promising method for practical applications.^39–41

The method consists of three steps: first particle inertial focusing in a straight microchannel; then particle sorting and trapping in the cavity entrance region; and finally, orbiting motion of trapped particles in the vortex. The traditional mechanism of particle sorting and trapping, based on particle sizes and lateral migration distances, has been accepted by most researchers.^63,70,74 However, the effects of the cavity trailing wall on particle trapping behaviors should be considered at high Reynolds numbers when the particles reach the region near the trailing wall. With an increase in the Reynolds number, the cavity trailing wall significantly affects both the flow field structure and the motion mode of particles entering the cavity. Three new trapping phenomena—contact trapping, collision trapping, and rapid trapping—indicate that particle–wall interactions are complex and require further exploration in future studies.⁷¹ Moreover, the trajectory motion of trapped particles in a laminar vortex plays an essential role in improving cavity holding capacity of particles. However, so far, only a few studies have focused on physics related to particle orbiting motion within the vortex, which is a relatively new research area of fluid mechanics.

To enhance the sorting performance of this method, many experimental and numerical studies have been conducted on the effects of cavity geometrical factors, particle size, and Re on the trapping efficiency and holding capacity in various microcavities. While most studies have focused on optimizing the length-to-width ratio of rectangular microcavities, some new cavity layouts have also been designed.^58,75,76 Specifically, by adding side channels to each cavity, captured target particles can be expelled out of the cavity in time.⁶² Moreover, it has been demonstrated that round cavities exhibit better holding capacity for captured particles compared to rectangular cavities with a 2.2–7.8 times higher rate.⁵⁷ For practical applications, further studies are required to guide the design of new layout microcavities that can achieve high efficiency, purity, concentration, parallelization, and easy collection of target particles. Examples include geometries based on multiple round cavities with side channels.

Many fundamental questions are involved in this method including vortex characteristics within microcavities, dynamic behavior of single-particle orbiting motion in vortices, and the exerting forces.^56,84,92 Although progress has been made regarding particle trajectory morphologies, understanding about cavity holding mechanisms remains incomplete. Further flow visualization experiments along with numerical simulations and theoretical analyses are required to explore the underlying physics, such as fluid–particle interactions, particle–particle interactions, and confinements of cavity walls. The exerting forces on the orbiting particle are complex and more quantitative measurements combined with theoretical and numerical studies are needed.

In conclusion, the vortex sorting method represents a distinctive microfluidic particle separation technique with extensive potential for various applications. Currently, most reported applications of this method have been conducted in laboratory settings using particles or cultured CTCs, and there is great anticipation for its practical clinical application in sorting rare CTCs from patients' blood samples.^{57,107,108,111} The orbiting motion of particles within vortices poses a novel challenge in the field of fluid mechanics. To enhance the capacity of holding particles in cavities and ensure timely release of captured cells, further fundamental investigations are required to elucidate the cavity holding mechanism, while also considering future design possibilities for new cavity structures. Additionally, to facilitate the clinical implementation of this method, interdisciplinary collaborations among researchers are necessary to address practical issues related to improving stability, efficiency, and automation of this method. Furthermore, from an application standpoint, future studies could expand on characterizing CTCs morphology and viability as well as analyzing CTCs and CTCs clusters; these additional aspects may provide supplementary prognostic information beyond mere enumeration.^107,112

AUTHOR DECLARATIONS

Conflict of Interest

The authors have no conflicts to disclose.

Author Contributions

Feng Shen: Funding acquisition (equal); Investigation (equal); Supervision (equal); Writing – original draft (equal); Writing – review & editing (equal). Jie Gao: Investigation (equal); Writing – original draft (equal); Writing – review & editing (equal). Jie Zhang: Investigation (equal); Resources (equal); Writing – review & editing (equal). Mingzhu Ai: Investigation (equal); Resources (equal); Writing – review & editing (equal). Hongkai Gao: Resources (equal); Writing – review & editing (equal). Zhaomiao Liu: Funding acquisition (equal); Supervision (equal); Writing – review & editing (equal).

DATA AVAILABILITY

Data sharing is not applicable to this article as no new data were created or analyzed in this study.