Absence of 3a₀ charge density wave order in the infinite-layer nickelate NdNiO₂

Abstract

A hallmark of many unconventional superconductors is the presence of many-body interactions that give rise to broken-symmetry states intertwined with superconductivity. Recent resonant soft X-ray scattering experiments report commensurate 3a₀ charge density wave order in infinite-layer nickelates, which has important implications regarding the universal interplay between charge order and superconductivity in both cuprates and nickelates. Here we present X-ray scattering and spectroscopy measurements on a series of NdNiO_2+x samples, which reveal that the signatures of charge density wave order are absent in fully reduced, single-phase NdNiO₂. The 3a₀ superlattice peak instead originates from a partially reduced impurity phase where excess apical oxygens form ordered rows with three-unit-cell periodicity. The absence of any observable charge density wave order in NdNiO₂ highlights a crucial difference between the phase diagrams of cuprate and nickelate superconductors.

Samples of NdNiO_2+x are prepared with meticulous control of the oxygen content. Their X-ray scattering and spectroscopy measurements then reveal that the previously reported charge density wave in undoped infinite-layer nickelates is, in fact, a spurious effect.

Main

The discovery of superconductivity in infinite-layer nickelates¹, and its analogy to its cuprate antecedents, offers a unique opportunity to better understand the key ingredients for high-temperature superconductivity. Although nickelates and cuprates share many commonalities, including a broadly similar crystal and electronic structure¹, strong correlations, antiferromagnetic excitations^2,3 and a superconducting dome^4–6, there are also many distinctions between the two families. These include the very different transition temperatures^1,4,5, the relative oxygen and 3d character of the doped holes^7,8, and the hybridization between the 3d and rare-earth states⁹. One important apparent similarity between the two families is the report of charge density wave order in a variety of infinite-layer nickelates by resonant soft X-ray scattering (RSXS)^10–13. This discovery, if correct, would suggest a ubiquitous interplay between charge order and superconductivity in the phase diagram of both cuprates and nickelates, with important implications for a universal theory of high-temperature superconductivity.

Nevertheless, there are clear distinctions between the charge order reported in cuprates and nickelates. In cuprates, the wavevector is typically incommensurate and strongly doping dependent^14–16, whereas in NdNiO₂ and PrNiO₂, it is locked to q = (1/3, 0) (refs. ^11–13). Additionally, charge ordering in cuprates is strongly temperature dependent^15–20, whereas reports in nickelates exhibit a weak temperature dependence with no clear transition or onset^10,12,13. To better understand the nature of putative charge ordering in the infinite-layer nickelates, we have investigated the q = (1/3, 0) superlattice peak in a series of samples with varying levels of reduction. We discover that the superlattice peak is entirely absent in fully reduced, single-phase NdNiO₂ samples, and instead arises from partially reduced impurity phases, namely, NdNiO_2.33 (Nd₃Ni₃O₇) or NdNiO_2.67 (Nd₃Ni₃O₈), produced during the reduction process, where excess apical oxygen atoms form ordered rows with three-unit-cell periodicity. This reveals that charge ordering with 3a₀ periodicity is not intrinsic to the infinite-layer nickelates—a discovery with important implications for our understanding of the phase diagram of nickelates and its relationship to cuprates.

To produce a sequence of NdNiO₂ samples with nominally identical Nd:Ni stoichiometry²¹ and variable oxygen content, we have employed a combination of reactive-oxide molecular-beam epitaxy to synthesize the precursor perovskite and atomic hydrogen reduction to access the oxygen-deficient phases. A consistent series of perovskite films of NdNiO₃ (20 pseudocubic unit cells thick) with excellent crystallinity and sharp metal–insulator transitions were synthesized on SrTiO₃. Following synthesis, all the films were capped by 2–3 unit cells of SrTiO₃ and exposed to a beam of >50% atomic hydrogen produced by a thermal cracker²². Although the reduction of perovskite nickelates has typically been achieved using CaH₂ and NaH powder^1,5,23, atomic hydrogen offers the benefit of independent control over the sample temperature and reducing environment, as well as fast reaction times (<20 min).

Using this approach, we have synthesized a series of samples ranging from the pristine parent perovskite NdNiO₃ (sample A) to oxygen-deficient intermediate phases NdNiO_2+x (samples B and C) and infinite-layer NdNiO₂ (samples D–I), all of which were characterized by conventional X-ray diffraction (XRD) and transport measurements. All the NdNiO₂ samples appear highly crystalline and single phase by XRD, with low-temperature resistivities of 350–700 μΩ cm, comparable with or lower than undoped films on SrTiO₃ (refs. ^4,5,24) and LSAT²⁵ (Fig. 1a,b; Supplementary Information shows the data for samples G–I). Further information about the growth and reduction procedures are available in Methods.

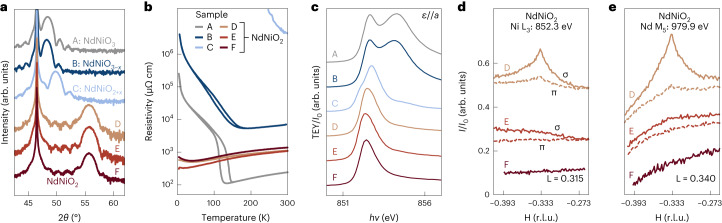
Fig. 1. Characterization of perovskite NdNiO₃, oxygen-deficient NdNiO_2+x and infinite-layer NdNiO₂.

a, Cu Kα θ–2θ XRD measurements of a sequence of thin films ranging from NdNiO₃ (sample A) to partially reduced NdNiO_2+x (samples B and C) and NdNiO₂ (samples D–F). b, Electrical transport measurements of the same series of samples. c, Total-electron-yield (TEY) XAS measurements of this sample series taken at the Ni L₃ edge with the electric field ε parallel to the sample a axis. d,e, RSXS measurements of NdNiO₂ samples D–F; rocking curves through the nominal charge order position of q = (–1/3, 0) at the Ni L₃ (d) and Nd M₅ (e) edges at σ and π polarizations, respectively. The plotted intensity is the measured scattered intensity I divided by the incident-beam intensity I₀, without any background subtraction. Traces in a and c–e have been vertically offset for clarity.

Source data

X-ray absorption spectroscopy (XAS) measurements on all the samples are shown in Fig. 1c, and RSXS measurements on three representative infinite-layer NdNiO₂ samples (samples D–F) are presented in Fig. 1d,e. The XAS spectra of all three NdNiO₂ samples appear similar and closely match with the published measurements^9,26, with a single peak at the Ni L₃ edge (852.4 eV) with no visible prepeak at the O K edge. Despite the apparent similarity between these samples, only sample D exhibits a superlattice peak at the putative charge order wavevector of q = (1/3, 0). As shown in previous reports, this peak is observed on the Ni L edge (Fig. 1d) as well as the Nd (rare-earth) M edge (Fig. 1e), and exhibits a strong polarization dependence, namely, I_σ/I_π ≈ 4 at hν = 852.3 eV, consistent with prior measurements^11,13. The estimated in-plane correlation length of ξ = 12–20 nm is also qualitatively similar to earlier reports^10–13. Finally, a weak dependence on the out-of-plane momentum transfer L is observed with a maximum at roughly L = 0.31(2) reciprocal lattice units (r.l.u.), again consistent with earlier measurements (all the momenta in this text are quoted in r.l.u. with reference to the NdNiO₂ lattice; a = 3.905 Å, c = 3.286 Å). In contrast, the superlattice peak was not observed in samples E and F, which is notable since sample E exhibited the lowest resistivity of all the samples. Additional measurements on samples G and H were measured at a separate beamline and exhibited an extremely weak q = (1/3, 0) feature at the sample centre, whereas sample I showed no superlattice features whatsoever. Supplementary Information provides further details of the measurements on samples E–I.

This discrepancy across nominally similar NdNiO₂ samples suggests that some unknown variable, potentially associated with sample disorder or oxygen non-stoichiometry, influences the presence of the 3a₀ superlattice peak. One possibility is that the charge density wave order is intrinsic to infinite-layer nickelates, but triggered by the presence of atomic-scale disorder within the lattice. Alternatively, the peak could originate from an impurity phase produced during the reduction process, which would imply that the charge order observed to date does not play a role in the phase diagram of infinite-layer nickelates.

To distinguish between these scenarios, we have investigated partially reduced, oxygen-deficient perovskite phases NdNiO_2+x (samples B and C). Sample B was only lightly reduced, with its XRD data nearly indistinguishable from the perovskite (sample A), but with a substantially broadened metal–insulator transition and increased sample resistance (Fig. 1a,b). Sample C was reduced further and shows an intermediate out-of-plane lattice constant of c = 3.66 Å and highly insulating electrical transport as expected for a predominantly oxygen-deficient perovskite phase²⁷. The XAS spectra of sample B exhibit the typical two-peak structure observed in perovskite nickelates on the Ni L₃ edge²⁸, as well as a strong prepeak at the O K edge; sample C is markedly different, with a sharp peak at 852.7 eV, shoulder at 852.0 eV and weak secondary peak at 854.3 eV, indicative of an oxygen-deficient perovskite phase^29,30.

In Fig. 2a, we show the RSXS measurements of sample C, which exhibit a peak at q = (1/3, 0) virtually identical to the superlattice peak in sample D and the literature^10–13 in nearly all respects: wavevector, energy dependence, polarization dependence, temperature dependence and correlation length, with the exception that it is extremely intense (100–400 times stronger than that observed in sample D). This peak also displays a strong L dependence, with a maximum at 0.30 r.l.u (d/3 = 3.65 Å). The strong similarity between the superlattice features in samples C and D suggests a common origin: ordered oxygen-deficient phases arising from an incomplete reduction process. In reduced nickelates, excess apical oxygens can form ordered phases, such as the brownmillerite structure of La₂Ni₂O₅ (refs. ^31–33), where the apical oxygen atoms form alternating rows. Other related structures also exist with different periodicities, such as Nd₃Ni₃O₇ (refs. ^34–36), Pr₃Ni₃O₇ (refs. ^34,35), La₃Ni₃O₈ (ref. ³⁷) and (Pr,Ca)₄Ni₄O₁₁ (ref. ³⁸). Recent in situ XRD studies indicate that the reduction pathway from bulk NdNiO₃ to NdNiO₂ occurs first via the formation of an intermediate-phase Nd₃Ni₃O₇ (ref. ³⁶), where one-third of the apical oxygen sites are occupied and are ordered into chains with 3a₀ periodicity (Fig. 2c). This 3 × 1 × 3 superstructure of the original pseudocubic unit cell would naturally give rise to a superlattice peak at q = (1/3, 0, 1/3). This suggests that sample C is probably predominantly Nd₃Ni₃O₇, and that an incomplete reduction of any NdNiO₂ samples would also leave traces of the Nd₃Ni₃O₇ phase behind (sample D).

Fig. 2. X-ray scattering measurements of oxygen-deficient perovskite, NdNiO_2+x, samples B and C.

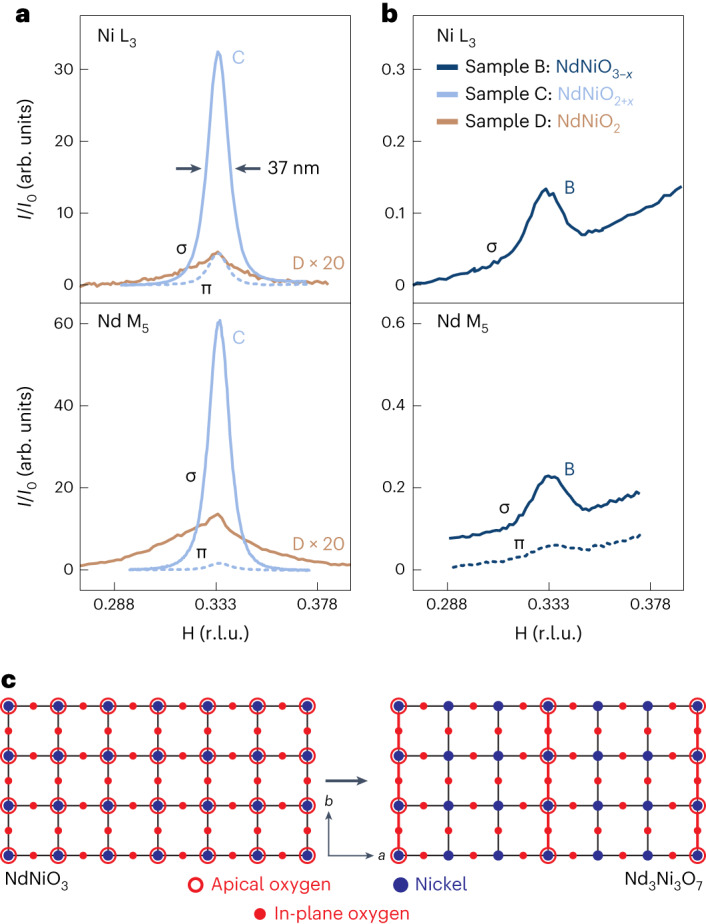
a, H scans, at constant L, at the Ni L₃ and Nd M₅ edges for sample C are presented without background subtraction. Data for sample D, after removal of a cubic fluorescent background and rescaling for visibility, are included for reference. b, Rocking curves through q = (1/3, 0) on lightly reduced sample B, presented without background subtraction but vertically offset for clarity. c, Illustration of a potential intermediate-phase structure for Nd₃Ni₃O₇ from a top-down view of the a–b plane of NiO₂ where two-thirds of the rows of apical oxygen atoms are removed, forming a 3a₀ supercell along the a axis.

Source data

To further investigate this hypothesis, we have also performed RSXS measurements on sample B, which should only be in the initial stages of the conversion from NdNiO₃ into a brownmillerite-like Nd₃Ni₃O₇ phase. The XRD and XAS measurements of this sample (Fig. 1a,c) are indistinguishable from the data for pristine NdNiO₃ (sample A). Nevertheless, RSXS measurements (Fig. 2b) also show the q = (1/3, 0) peak with identical characteristics (L, energy and polarization dependence) and comparable intensity with sample D. The fact that sample B exhibits no obvious trace of the infinite-layer phase and still exhibits a clear q = (1/3, 0) superlattice peak demonstrates that this feature does not originate from intrinsic charge ordering within the infinite-layer phase itself. In fact, the q = (1/3, 0) peaks appear to be more reminiscent of Bragg peaks observed in resonant scattering from cuprates with oxygen ordering (for example, ortho-YBa₂Cu₃O_6+δ), as opposed to intrinsic charge density wave order^39,40. There, the strong resonant enhancement on the Cu L edge arises from the local oxygen environment strongly modifying the electronic structure of the Cu atoms, and a similar resonant enhancement at the Ni L edge should likewise occur for oxygen ordering in nickelates.

In Fig. 3a, we show the energy dependence of the q = (1/3, 0, 1/3) peak intensity in samples C and D (shaded), together with the background fluorescence measured off the superlattice peak (white). Because the superlattice peak intensity is far stronger in sample C, the relative strength of the background fluorescence in sample D is much larger than in sample C. Nevertheless, a two-peak resonance profile is apparent in both samples at the Ni L₃ edge with only a weak response at the L₂ edge, similar to prior measurements on NdNiO₂ (ref. ¹¹). Assuming a structural origin arising from oxygen ordering, the superlattice peak should also be observable in the off-resonance case. In Fig. 3b,c, we show a series of scans across q = (1/3, 0) for samples C and D, spanning a 235 eV range about the Ni and Nd resonances. Although the intensity is weaker than the on-resonance case, the persistence of the peak strongly supports a structural origin. The temperature dependence of the scattering peak is shown for samples B–D (Fig. 3d). Similar to prior reports^10,12,13, the peak shows a smooth decrease in intensity by 15–20% between 20 and 370 K, with no obvious change in the correlation length. This weak dependence—without a transition—is fairly similar to the temperature dependence of superlattice peaks resulting from the oxygen ordering in YBa₂Cu₃O_6+δ (refs. ^40,41), as opposed to the more dramatic temperature dependence of the CDW order^18,40.

Fig. 3. Energy and temperature dependence of the q = (1/3, 0) scattering peak.

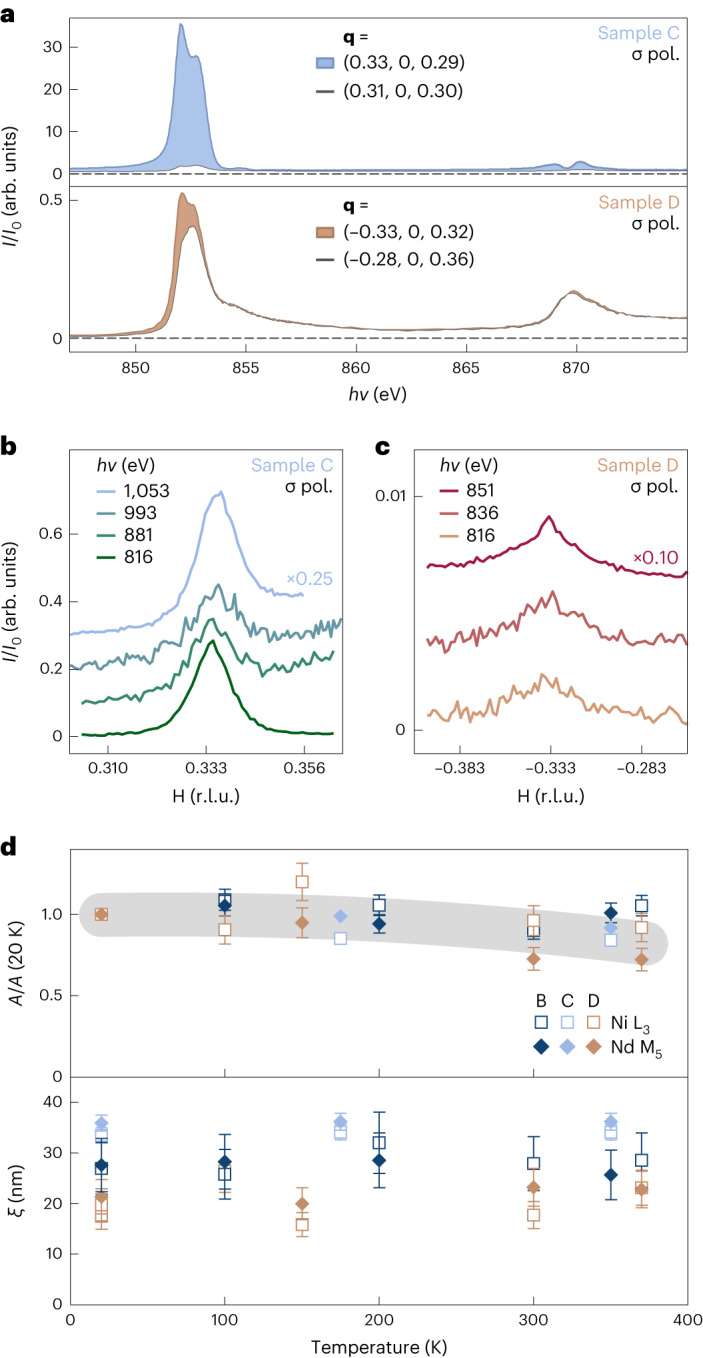
a, Fixed-wavevector resonant energy profiles both on and off the scattering peak for samples C and D. The shaded region indicates intensity attributable to the resonant scattering above the fluorescent background (white). b,c, Rocking curves through q = (1/3, 0) for a wide range of photon energies around the Ni L and Nd M resonances for sample C (b) and sample D (c); traces have been vertically offset for clarity, but no background subtraction has been applied. d, Temperature dependence of peak amplitude A and correlation length ξ = 2π/Δq, at both edges for samples B–D. The error bars represent the fitting uncertainty in the extracted quantities (A and ξ); they define the range of values obtained by fitting the RSXS data with different models of the fluorescence background (that is, different polynomial degrees and fits over different ranges). The grey line is a guide to the eye.

Source data

We also observe a strong dependence of the q = (1/3, 0) peak intensity in sample G for the measurement location on the 10 × 10 mm² sample (Supplementary Information). Due to the spread of the atomic hydrogen beam and thermal gradients, the edges of the sample are not as well reduced as the centre—correspondingly, we observe a clear superlattice peak near the edge of the sample, which decreases in intensity approaching the sample centre. Spatially resolved synchrotron hard XRD measurements at the same locations confirm the prevalence of intermediate reduction products at the edge of sample G, versus fully reduced NdNiO₂ near the centre, thereby correlating the presence of the resonant feature with that of intermediate phases on the same sample.

Prior powder XRD studies of bulk Nd₃Ni₃O₇ reveal that the excess apical oxygens form octahedrally coordinated chains that run perpendicular to the NiO₂ planes and which are separated by 3a₀ (ref. ³⁴). Another potential arrangement is to have the apical oxygens form pyramidal chains that lie within the NiO₂ plane and are oriented along the a axis (Fig. 4a). In addition, Nd₃Ni₃O₈ (NdNiO_2.67), where two rows of apical oxygens are occupied followed by a row of vacancies, would likewise generate the same superlattice peak at q = (1/3, 0, 1/3), although this phase has not been previously reported. Scanning transmission electron microscopy (STEM) measurements on a separate, partially reduced sample (sample J) are detailed in Fig. 4b,c,d. The Fourier transform of a high-angle annular dark-field image reveals 1/3-order diffraction peaks corresponding to 3a₀ ordering along both a and c, consistent with other recent transmission electron microscopy measurements on uncapped NdNiO₂ films⁴². Additionally, annular bright-field data show regions with two filled apical oxygen chains alternating with a single vacant chain, consistent with the Nd₃Ni₃O₈ structure shown in Fig. 4a, where the apical oxygen chains are directed into the page. Sample J was prepared using the same conditions as samples D–I, but with a four-unit-cell SrTiO₃ cap. Although RSXS measurements were not performed on sample J, XRD and transport measurements (Supplementary Information) indicate that this sample is less reduced than sample D as both NdNiO₂ and intermediate-phase peaks are visible in lab-based XRD. Since the difference in formation energies of the various ordered oxygen structures is small, it is possible that multiple compositions or structures of Nd₃Ni₃O_7,8 could exist within our series of samples, depending on factors such as the reduction conditions or epitaxial strain⁴³. A more detailed investigation of the precise structures of Nd₃Ni₃O₇ or Nd₃Ni₃O₈ in our thin films is currently the subject of further investigation. Nevertheless, the key point is that all the configurations of Nd₃Ni₃O₇ or Nd₃Ni₃O₈ will form a 3 × 1 × 3 supercell that will generate the q = (1/3, 0) superlattice peak at the observed wavevector. Finally, a macroscopic sample would be expected to possess equal domains of chains along both in-plane directions, in which case the superlattice peaks would then be observable along both H and K directions.

Fig. 4. Outline of the multistage reduction process of nickelate films and high-resolution STEM images of a partially reduced film showing 3a₀ ordering.

a, Schematic of the reduction pathway from the perovskite NdNiO₃ to the intermediate oxygen-deficient phases of Nd₃Ni₃O₇ or Nd₃Ni₃O₈ and the infinite-layer NdNiO₂; the corresponding samples measured in this study that lie on this pathway are also shown. b–d, STEM images of a mixed-phase sample (sample J) containing Nd₃Ni₃O_7,8 intermediate phases. Fourier transform image (b) and corresponding high-angle annular dark-field image (c) of a defective region are shown. The positions of the third-order peaks in the Fourier transform are circled in green. An annular bright-field image showing two filled rows of apical oxygens (d), followed by one row of missing apical oxygen positions, corresponding to the schematic for Nd₃Ni₃O₈ in a. In this image, the apical oxygen chains run into the page.

Source data

Our results suggest the scenario illustrated in Fig. 4a. The reduction of NdNiO₃ into NdNiO₂ occurs via the production of an intermediate, partially reduced Nd₃Ni₃O₇ and/or Nd₃Ni₃O₈ phase, where excess apical oxygen atoms (or vacancies) are ordered into rows with 3a₀ periodicity forming a 3 × 1 × 3 supercell with a superlattice peak at the putative charge order wavevector of q = (1/3, 0, 1/3) (sample C). Because of its extremely strong intensity in the on-resonance case, this peak is detectable even if very small amounts of the partially reduced phase are present at levels nearly undetectable by conventional techniques (XRD, transport and XAS; that is, samples B, D and H). This picture is supported by a multitude of our observations: (1) the superlattice peak is absent in the plurality of low-resistivity, fully reduced NdNiO₂ samples (samples E, F and I); (2) the superlattice peak from Nd₃Ni₃O_7,8 (sample C) exhibits nearly identical energy, polarization and temperature dependence to NdNiO₂ (sample D) as well as prior measurements on RENiO₂ (refs. ^10–13); (3) the peak is commensurate to the lattice and observable well off-resonance, indicating a strong structural component; (4) even a lightly reduced NdNiO₃ sample devoid of any detectable NdNiO₂ exhibits the superlattice peak (sample B); (5) position-dependent measurements correlate the q = (1/3, 0) peak, observed by RSXS, with the presence of partially reduced phases, observed by hard XRD at the same locations on the same sample (sample G); and (6) the direct observation of excess apical oxygen ordering with 3a₀ periodicity in a partially reduced sample by STEM (sample J).

The presence of an ordered oxygen impurity phase also explains numerous discrepancies and unusual features in the literature. The strong intensity on the rare-earth edge is surprising for a charge ordering scenario, since the coupling of the rare-earth 4f electrons to the Ni3d electrons should be relatively weak and indirect, but should naturally occur for a structural Bragg peak where the Nd ions are displaced due to oxygen ordering. In addition, prior reports claim the presence/absence of a superlattice peak in uncapped versus capped samples of NdNiO₂. Our measurements indicate that although the capping layer alone does not dictate the presence of the superlattice peak (all the samples were capped), even small variations in reduction conditions can result in residual amounts of Nd₃Ni₃O_7,8. The doping dependence of the intensity of the superlattice peak, which is the strongest for the undoped parent compound and vanishing near x = 0.20, may also be naturally explained by the presence of an excess oxygen impurity phase. Bulk studies indicate that Sr doping, which increases the average targeted Ni valence of RE_1−xSr_xNiO₂, makes the material easier to reduce³⁶. Thus, the addition of Sr may naturally diminish the amount of residual RE₃Ni₃O_7,8 in a sample and suppress the intensity of the q = (1/3, 0) Bragg peak. Finally, although our study is limited to NdNiO_2+x, these findings should broadly apply to all infinite-layer nickelates, since Pr₃Ni₃O₇ and La₃Ni₃O₈ also form 3 × 1 × 3 superstructures and are known to be the reduction products of PrNiO₃ and LaNiO₃, respectively^34,35,37. Although the superlattice peak in LaNiO₂ shares many overall similarities with those in (Nd,Pr)NiO₂, including its energy and temperature dependence, it does exhibit some subtle apparent differences, particularly a very slight displacement from the commensurate q = (1/3, 0) wavevector (Δq ≈ 0.01 r.l.u) (ref. ¹⁰) at x = 0. Future experiments will be important for conclusively determining the origins of the superlattice peak in the other members of infinite-layer nickelates. Although we focus here specifically on ordered excess oxygen phases, this highlights the role that excess oxygen may play in reduced films more broadly. The ordered excess oxygen phases appear to be highly insulating, and therefore, small inclusions may not substantially contribute to the electrical properties as a whole when averaging over an entire macroscopic sample. Nevertheless, if low concentrations of excess apical oxygen ions are randomly distributed, it is conceivable that they could potentially act as hole dopants, which could be consistent with traces of superconductivity observed in nominally undoped LaNiO₂ (ref. ⁶).

Through a multimodal investigation of a large sequence of samples with varying levels of reduction, we conclude that charge ordering with 3a₀ periodicity is not intrinsic to the infinite-layer nickelates. The superlattice peak previously identified as charge ordering at q = (1/3, 0) originates from the three-unit-cell ordering of excess apical oxygen ions in small amounts of brownmillerite-like inclusions of Nd₃Ni₃O₇ or Nd₃Ni₃O₈ produced during the reduction process. Topotactically reduced complex oxides present an exciting new frontier in quantum materials^1,44, but this work also highlights some of the materials challenges inherent in these systems. We demonstrate RSXS as a highly sensitive and powerful probe for investigating these reduced compounds, which can detect even trace amounts of impurity phases. Although the phase diagrams of nickelates and cuprates show many similarities, including a superconducting dome and strong antiferromagnetic fluctuations on the underdoped side, this work establishes a clear distinction between the two families, namely, the fact that charge ordering does not appear to be directly relevant to the phase diagram of nickelates. This finding should have important implications for understanding universal models of high-temperature superconductivity, and may help to explain some of the key differences between the two families of materials.

Methods

Sample synthesis and characterization

Thin films of NdNiO₃ were grown on SrTiO₃(100) substrates using reactive-oxide molecular-beam epitaxy in a Veeco GEN10 system using elemental beams of Nd (Alfa Aesar, 99.900%) and Ni (Alfa Aesar, 99.995%). Substrates were etched to prepare a TiO₂-terminated surface⁴⁵ and annealed before growth at 650 °C until a clear reflection high-energy electron diffraction pattern was observed. Growths were performed at substrate temperatures between 480 and 500 °C in background pressures between 2 and 6 × 10⁻⁶ torr of ~80% distilled ozone. Initial flux calibration was performed by monitoring the reflection high-energy electron diffraction oscillations during the growths of binary oxides Nd₂O₃ on (ZrO₂)_0.905(Y₂O₃)_0.095(111) and NiO on MgO(100) using the parameters outlined elsewhere⁴⁶. Further stoichiometric optimization was performed by minimizing the NdNiO₃(002)_pc plane spacing²¹. Following the growth of the nickelate layer, a SrTiO₃ capping layer was grown at 500 °C in a background pressure of 2 × 10⁻⁶ torr, following the calibration of the Sr and Ti sources by monitoring the reflection high-energy electron diffraction oscillations.

Samples were reduced using a beam of atomic hydrogen produced by a thermal source^22,47, where molecular H₂ is passed through a heated tungsten capillary (>1,900 °C) where it disassociates into individual atoms before interacting with the sample. Reductions were performed in an ultrahigh-vacuum chamber (P_base < 1 × 10⁻¹⁰ torr) located on the same vacuum manifold as the molecular-beam epitaxy growth system at temperatures between 250 and 310 °C and hydrogen fluxes ranging between 1.8 and 2.7 × 10¹⁵ atoms cm^–2 s^–1. Typical reductions involved between 12 and 15 min of exposure to the atomic hydrogen beam to produce samples appearing fully reduced by lab-based XRD (samples D–I).

The structural quality of both perovskite and reduced samples were determined using Cu Kα₁ XRD measurements performed on a PANalytical Empyrean X-ray diffractometer. Electrical transport measurements were performed using both a custom-built liquid-helium-cooled four-point probe measurement station (base temperature, 4 K) and a Quantum Design physical property measurement system (base temperature, 2 K). Finite-size factors were accounted for using the methods discussed elsewhere⁴⁸. Contacts were prepared by either application of a dot of indium metal underneath a gold contact pin or by ultrasonic aluminium wire bonding.

RSXS measurements

The RSXS measurements were performed at the REIXS beamline of the Canadian Light Source on a four-circle diffractometer in an ultrahigh-vacuum chamber (P < 5 × 10⁻¹⁰ torr). The nominal photon flux and energy resolution were I₀ = 5 × 10¹¹ photons s^–1 and ΔE/E ≈ 2 × 10⁻⁴, respectively. The incoming X-ray polarization was selected to be in either the σ (ε_⊥ scattering plane) or π (ε_∥ scattering plane) configuration with the polarization of scattered X-rays unmeasured. The measurements were conducted at photon energies between 815 and 1,050 eV with either a microchannel plate or a silicon drift detector with an angular acceptance of 0.9°. The silicon drift detector is an energy-resolved detector, with a resolution larger than 50 eV, which allows for the removal of the substantial oxygen fluorescence background produced by the SrTiO₃ substrate. A precise alignment to the film crystallographic axes was achieved by detecting the (001), (101) and $\left(\overline{1}01\right)$ Bragg peaks of the SrTiO₃ substrate with an energy of 2.5 keV.

Additional RSXS measurements (Supplementary Information) were performed at beamline 8.0.1 of the Advanced Light Source. For these measurements, a fixed π-polarization geometry was used and the nominal photon flux and energy resolution were ~10¹³ photons s^–1 and ΔE/E ≈ 7 × 10⁻⁴, respectively. The fluorescence yield and scattering signal were recorded using a GaAsP photodiode (with an aluminium window to block visible light and photoelectrons) mounted at 100 mm from the sample with an acceptance angle of 3°. To consistently calibrate the photon energies between different beamlines, a perovskite–nickelate sample (sample A) was measured at both endstations as an energy reference. The energy scale was then defined with respect to the NdNiO₃ Ni L₃ peaks at 852.6 and 854.3 eV and O K prepeak at 527.9 eV to align with prior literature measurements^9,10,28,49. All the momenta are quoted in r.l.u. relative to the NdNiO₂ lattice, where a = 3.905 Å and c = 3.286 Å.

All the RSXS traces in the manuscript, with the exception of the data shown in Fig. 2a, are presented as unsubtracted raw data, namely, I/I₀, where I is the intensity measured on the detector and I₀ is the incident-beam intensity determined from the current on a mesh located upstream on the beamline. In Fig. 2a, a cubic background was subtracted only from sample D, to better compare it with sample C. In Fig. 3d, the temperature dependence of the peak areas and correlation lengths were obtained after subtracting a fixed, temperature-independent second- or third-order polynomial background, which was unchanged (apart from a scaling factor) for each sample. Supplementary Fig. 4 shows the raw data for these temperature series.

Spatially resolved hard XRD measurements

Scanning X-ray microdiffraction measurements were conducted at beamline 26-ID of the Advanced Photon Source at Argonne National Laboratory. A liquid-nitrogen-cooled Si(111) double-crystal monochromator was used to achieve an energy resolution of ΔE/E = 10⁻⁴ at a photon energy of 10.0 keV, and the scattered X-ray signal was recorded with an area detector, each pixel extending 0.00075 Å⁻¹ along the Ewald sphere. The collimated X-ray beam was reduced to a spot size of 100 μm (full-width at half-maximum) using slits, yielding a flux of ~10¹⁰ photons s^–1. The beam was vertically rastered along the sample, perpendicular to the scattering plane, to minimize the beam footprint and ensure that the spatial resolution of the linescan matched the beamwidth. A three-dimensional reciprocal-space map was obtained every 100 μm along a 4 mm line by rocking the sample by 4° per step in 41 steps and measuring a spatial linescan at each angle; Supplementary Fig. 11b shows projections of the map onto the L axis of the substrate/film.

STEM measurements

STEM characterization was performed on a cross-sectional lamella prepared with the standard focused-ion-beam lift-out procedure using a Thermo Fisher Helios G4 UX focused ion beam. High-angle annular dark-field imaging and annular bright-field–STEM imaging were performed on a Cs-corrected Thermo Fisher Scientific Spectra instrument at 300 kV and 30 mrad probe convergence semiangle. For high-precision structural measurements, a series of 40 rapid-frame images were acquired and subsequently realigned and averaged by a method of rigid registration optimized to prevent lattice hops⁵⁰, resulting in a high-signal-to-noise-ratio, high-fidelity image of the atomic lattice.

Online content

Any methods, additional references, Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at 10.1038/s41563-024-01797-0.

Author contributions

C.T.P. and K.M.S. conceived the research and designed the experiment. C.T.P., Y.W. and V.A. synthesized, reduced and characterized the thin-film samples, with input from D.G.S. and K.M.S. C.T.P., N.K.G., Y.W., V.A., M.B., R.G., R.S., Y.-D.C., D.G.H. and F.H. performed the RSXS measurements. L.B. and L.F.K. performed the STEM experiments. B.Z.G., A.L., T.Z. and A.S. performed the synchrotron hard XRD experiments. The results were analysed and interpreted by C.T.P., N.K.G., Y.W., V.A., G.H., D.G.H. and K.M.S. C.T.P. and K.M.S. wrote the manuscript, with input from all authors.

Peer review

Peer review information

Nature Materials thanks Giacomo Ghiringhelli, Xingye Lu and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Data availability

All data needed to evaluate the conclusions of this study are available in this Article and its Supplementary Information. Datasets generated and analysed during the course of this study are available at 10.34863/r44d-xt74. Source data are provided with this paper.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41563-024-01797-0.