Abstract
Studies typically use publication-based authorship data to study the relationships between collaboration networks and knowledge diffusion. However, collaboration in research often starts long before publication with data production efforts. In this project we ask how collaboration in data production networks affects and contributes to knowledge diffusion, as represented by patents, another form of knowledge diffusion. We drew our data from the metadata associated with genetic sequence records stored in the National Institutes of Health’s GenBank database. After constructing networks for each year and aggregating summary statistics, regressions were used to test several hypotheses. Key among our findings is that data production team size is positively related to the number of patents each year. Also, when actors on average have more links, we tend to see more patents. Our study contributes in the area of science of science by highlighting the important role of data production in the diffusion of knowledge as measured by patents.
Keywords: collaboration networks, data authors, knowledge diffusion, metadata analytics, scientometric measures
1 |. INTRODUCTION
Studies of collaboration networks and knowledge diffusion have traditionally used publication-based authorship data as the primary data source to measure the extent, types, and networks of co-authorships, or research collaboration, such as the large scale study of scientific collaboration networks by Newman (2001a, 2001b, 2001c), and the types and levels of interdisciplinary research collaboration by Qin, Lancaster, and Allen (1997). These studies offer insight into the dynamics and structures of publication-based collaboration networks and provide evidence for the formation of science policy making.
Collaboration in research starts much earlier than the publication phase of a research lifecycle. Whether a collaboration can succeed in accomplishing the goal of a research project is largely dependent on the success of data production, by which we mean all the work related to collecting/generating, cleaning, managing, aggregating/transforming research data. The data production phase of a research lifecycle is especially important and complex in data-intensive science and often requires specialized knowledge. While collaboration in the form of co-authorships tells the story at the end of a research life-cycle, the story of data production in the data-to-knowledge process has long been understudied since it falls under the shadow of publication glory.
The proliferation of data repositories and their importance in the science research enterprise prompted us to ask: how does collaboration in data production affect and contribute to knowledge diffusion (as represented by publications and patents)? In this paper we address this overarching research problem by looking at the following specific questions: How is the data production network related to knowledge diffusion? What variables in the data submission network help predict knowledge diffusion as measured by patents? How is the publication network related to knowledge diffusion, as measured by patents? What variables in the publication network help predict knowledge diffusion, as measured by patents?
Note that publication-based authorship data are insufficient to answer these questions because information about data production is left not included. Addressing the above questions requires new data sources that include the “footprints” from the data production phase in a research lifecycle as well as new perspectives that can help us gain insights into the missing links in data-to-knowledge networks. Thus, this work helps us gain a fuller understanding of the research life cycle.
To begin to address this research problem, we will first review relevant literature to provide some background and theoretical support for the rationale of this study as well as for data source selections. The computational framework will then be presented and argued in the methodology section. The longitudinal metadata from a data repository—GenBank1—will be analyzed using network science and multiple regression methods.
In this work we find a significant relationship between social network measures of the data production network for a given year and the number of patents for that year. Patents are a proxy measure for knowledge diffusion (for that year). This work also suggests that larger teams are getting a disproportionately larger number of patents; most data production teams are very small.
Our study makes a contribution in the area of science of science by highlighting the important role of data production in the diffusion of knowledge as measured by patents and suggests new avenues for future research.
2 |. LITERATURE REVIEW
Collaboration in research has become the norm in modern science enterprise. The efficacy of collaborative research has an impact on the rate and scale of knowledge diffusion at all levels and is one of the main concerns of science policy makers and funding agencies (Cummings, 2018). Addressing such concerns requires a sound theoretical framework and a set of measures that can explain phenomena emerging from research “footprints” or traces. From Derek de Solla Price’s Little Science, Big Science (1963) to the Fourth Paradigm (Hey, 2009), collaborations in research have changed not only in scale and capacity, but also in complexity and structures. This literature review focuses on two areas among the vast research publications on scientific collaboration: (a) metrics for research collaboration networks and (b) theory of knowledge transfer and diffusion.
2.1 |. Metrics for research collaboration networks
Collaboration in research is typically measured by coauthorship on publications. If two scientists wrote a paper together, they are considered collaborators. Coauthorship can occur at the international, inter-institutional (i.e., same country), interdepartmental (i.e., same institution), or departmental level (Qin, 1994). Researchers in a collaboration network are called nodes or vertices. The relationships (i.e., co-authorship) between nodes are called links or edges. Collaboration networks within a field can have very large numbers of nodes, reflecting the number of publishing researchers in a field. The distribution of the number of edges that nodes have tends to be highly skewed such that some researchers have many links, while most have a more modest number of edges. Repeated collaborations mean that some edges have greater weight than others. The skewed distribution of edges affects local network structures and such networks consist of clusters or communities of researchers, which are self-organized, may be interconnected in numerous ways, and evolve over time.
Over the last 50 years, since de Solla Price’s work Little Science, Big Science (1963), scientific collaboration networks have been studied extensively, from a wide range of disciplines (Bozeman & Corley, 2004; Girvan & Newman, 2002; Newman, 2001c; Powell, White, Roput, & Owen-Smith, 2005). Barabási et al. (2002) give an excellent summary of the research on collaboration networks, which include: (a) most networks have the “small world” property, (b) real networks have an inherent tendency to cluster, more so than comparable random networks, and (c) the distribution of the number of edges for nodes (degree distribution) “contains important information about the nature of the network, for many large networks following a scale-free power-law distribution” (p. 591).
Statistical measures for collaboration networks have gained increasing significance in the last two decades. Questions of interest for complex network researchers include the typologies and properties of complex networks, interaction between these two components in a network, and the tools and measurements for capturing “in quantitative terms” the underlying organizing principles of real networks (Albert & Barabási, 2002). Well-known theories include those of random graph, percolation, small-world networks, scale-free networks, networks with community structure, and evolving networks, for which Albert and Barabási (2002) and Costa, Rodrigues, Travieso, and Boas (2007) provided exhaustive surveys.
In the discussion of each of these theories and models, Albert and Barabási (2002) used the average path length, clustering coefficient, and degree distribution, among others, to explain the statistical mechanics of the theories and models, which are considered as three robust measures of a network’s topology (Albert & Barabási, 2002). A number of properties of scientific collaboration networks have been identified in these studies: small worlds are common in scientific communities; the networks are highly clustered; and biomedical research appears to have a much lower degree of clustering compared to other disciplines such as physics (Newman, 2001c). The evolution of scientific collaboration networks shows that the degree distribution follows a power law and key network properties (diameter, clustering coefficient, and average degree of the nodes) are time dependent, that is, the average separation decreases over time and the clustering coefficient decays with time (Barabási et al., 2002).
The theories and models shed light on studying complex collaboration using large-scale data. Studies on scientific collaboration are abundant in scientometric and information science scholarly journals. Most of them are often limited in that the data used are filtered by discipline and time period from a single database and are almost exclusively publication-based authorship data, as seen in the studies cited earlier. The limitations of single source, variant time scales, and ambiguous coverage boundaries make it very difficult, if not impossible, for understanding the complexity of scientific collaboration networks spanning from data production to publications to patents.
2.2 |. Knowledge diffusion
Discussions of knowledge diffusion involves several “epistemological assumptions about human beings and the world to be known, and their interaction” (Spender, 2008). Simply put, the term refers to the diffusion of data and of meaning. Data diffusion is relatively straightforward as it helps “receivers distinguish, within an agreed field of possibilities, the noted from unnoted”, while diffusion of meaning must “rely on receivers to add something of their own construction…diffusion means creating a new practice, guided rather than determined by prior practice” (Spender, 2008, p. 282). From a social network point of view, knowledge diffusion is also “a social phenomenon in which people as potential adopters are engaged” (Klarl, 2014, p. 738). As such, the process of knowledge diffusion is driven by social ties between and within the group of adopters as well as by individual’s attributes.
This connotation of knowledge diffusion helps explain the phenomenon of scientific collaboration and, in particular, cyberinfrastructure (CI)-enabled scientific collaboration. The CI-enabled collaboration can be characterized as networks of collaborating researchers connected not only by social and disciplinary ties but also supported by a plethora of CI services such as data submission, sharing, and reuse in additional information discovery services (Costa, Qin, & Bratt, 2016). The large number of different types of data repositories and search tools at the National Center for Biotechnology Information (NCBI) is an example of cyberinfrastructure on which collaborative research is conducted and knowledge is diffused through interactions between scientists, between scientists and data/information, and between data and information. Much of these activities and interactions falls into the domain of scientific dissemination, which is considered as “an activity of knowledge diffusion” (Tarango and Machin-Mastromatteo, Tarango & Machin-Mastromatteo, 2017).
How is knowledge diffused in a collaboration network situation? Most of research on this topic has been focused on building mathematical models, for example, Kim and Park’s model for examining the relationships between network structures and knowledge diffusion (Kim & Park, 2009). Another model focused on the concentration of knowledge flows inside firm boundaries to measure how collaboration networks informed or drove the knowledge diffusion patterns (Singh, 2005). From a theoretical standpoint, a tighter network decreases the time distance between early and late adoptions by moving late adoption decisions from the future to the present as heterophilicity2 in subgroups of the network is decreasing which accelerates knowledge diffusion (Klarl, 2014).
Previous research on collaboration networks and knowledge diffusion have developed metrics and theories for measuring and interpreting the phenomenon of research collaboration while raising new questions, particularly as data production becomes increasingly integrated as part of the knowledge diffusion process. This paper addresses four major questions brought about by the data-intensive science:
How is the data production network related to knowledge diffusion?
What variables in the data submission network help predict knowledge diffusion as measured by patents?
How is the publication network related to knowledge diffusion, as measured by patents?
What variables in the publication network help predict knowledge diffusion, as measured by patents?
3 |. METHODOLOGY
3.1 |. Data
The data source used for this paper is a subset of data from an ongoing project (Bratt, Hemsley, Qin, & Costa, 2017; Costa et al., 2016; Qin et al., 2014, 2015) analyzing GenBank metadata. In the GenBank repository, an annotation record consists of a metadata section and the molecular sequence data section. The metadata section documents the nature, authorship, associated references, and release date of a sequence as well as data submission information. These annotation records are available from the GenBank FTP server as compressed semi-structured text files. We downloaded all the annotation records from 1982 to 2018 and extracted the metadata section from all annotation records in January 2019, which were then parsed into a relational database (we excluded the genetic sequence data, which comprised 80% of the data volume). This process resulted in 227,905,057 annotation records, in which 44,480,172 publications were referenced. This data collection also includes 42,511,832 patent references.
Similar to other scientometric research that uses metadata as the data source, we performed author name disambiguation for all years, accomplishing 89% accuracy by using the Kaggle solution from Chin et al. (2014) and by cross-checking the results with author metadata from Web of Science, SCOPUS, and Microsoft Academic graph. After the disambiguation process, the collection has 877,134 unique authors names (nodes), of which 519,719 are in the publication network, 523,013 in the submission network, and 214,197 unique scientists in the patent network.
We then selected subsets of the data to generate scientific collaboration networks. The subsets consisted of three different types of research activities: co-production of data submissions, co-authorship of publications, and co-ownership of patents. The longitudinal analysis range selected was from 1992–2018. This range was chosen because a substantive level of data submissions started only in 1992 with a more stabilized user base and policies around submission, as compared to that in GenBank’s early years (1982 – 1991).
3.2 |. Hypotheses
We used regression analysis to answer our research questions. Our unit of analysis is the overall activity and network for a year for a type of research activity. That is, the variables for the regression were drawn from descriptive statistics and network measures from the subsets of data for each year, for each of the three research activities. Descriptive statistics included measures like overall number of data submissions to GenBank, publications or patents for the year. The network measures are described in more detail below.
The networks were constructed from co-authorships for each of the research activity types, for each year. For example, the data submission network consists of authors as the nodes who were listed in the data submission metadata. If two authors showed up in the same submission record, they were linked in the network. This is a typical approach for a co-author network (Costa et al., 2016). Variables like team size were calculated by parsing individual authors from the author list and counting individuals on a single data submission or publication. All network measures were calculated using the iGraph package (https://igraph.org/r/) in R.
We used a standard ordinary least squares (OLS) multivariate regression (Faraway, 2014) to answer our questions. For each regression (models and variables described below), we validated the model assumptions by examining diagnostic plots and running variance inflation factor to check for multicollinearity (Faraway, 2014). We found that while the models basically adhered to the requirement for normality, the models did suffer from some mild heteroscedasticity. As such we also ran a robust regression for each model. Since the robust models’ results were quite similar to the OLS regressions, we have opted to report the OLS regression results.
Based on the three questions (see the end of literature review section), we constructed the following hypotheses:
H1: The number of data submissions in a given year is positively related to the increase in number of patent applications.
This hypothesis addresses the first research question about the relations between data production and knowledge diffusion. In the era of data-intensive science, sequencing technologies has increased the capability and scale of data production while the publication output remained relatively flat, which increased the ratio of data submissions per publication.
Certainly, knowledge diffusion is a broad topic with many factors that can be related to it. Here we are focused patents as one proxy measure for knowledge diffusion and elements of data production, including its network, as independent variables.
H2: The team size in data submission networks are positively related to the number of patent applications for a given year.
H3: How well-connected actors are in the data submission network is positively related to the number of patent applications for a given year.
These two hypotheses address the second research question about which network measures predict the impact on knowledge diffusion. Equation [1] was developed as a general regression model to test H1 – H3.
| (1) |
where x1 = submission count, x2 = submission mean team size, and x3 = submission mean degree.
Variable x1 is the number of data submissions per author to GenBank in a given year. It is used to test H1. The variable assumes that a higher number of data submissions over time would generate more patent applications during that time. Realizing the lagging between publication date and date of patent application, we looked at last year’s number of data submissions as it related to this year’s patents, but such models tended not to perform as well. This may indicate that data are typically entered into GenBank upon the completion of a project.
Variable x2 is the mean number of data submitters on the annotation record. That is, the distinct count of the disambiguated individual names associated with the dataset. We opted to use mean over median because between the two centrality measures, mean is sensitive to extremes. Thus, mean will be pulled up higher in years where very large teams are present. This variable tests H2.
Variable x3 tests H3 and measures how many links, or co-authors, each author has for a given year in the data submission network. Mean is used for a similar reason as it is for team size: capturing the presence of highly well-connected authors in the network.
H4: The number of publications is positively related to the number of patent applications for a given year.
This hypothesis test addresses the third research question about the relationship between the number of publications in a given year and knowledge diffusion, as measured by patents.
H5: Publication team size is positively related to the number of patent applications for a given year.
The last research question, number 4, is addressed with H5, which tests if team size is predictive of knowledge diffusion. The model for H4 and H5 is similar to equation [1], but the variables are drawn from the publication network dataset. Thus, model 2 is shown in equation [2]. The independent variables are drawn from the publication research activity network and thus our model looks at the relationships between knowledge creation and knowledge diffusion.
| (2) |
where x1 = publication count and x2 = publication team size mean.
The Variable x1 in equation [2] is simply the. Publication count3 for a given year in the database and used to test H4. The authors of these publications make up the publication network. Here we are testing for an overall relationship between number of publications for a given year and number of patents.
The Publication team size mean variable (x2 in equation [2]) tests if larger (smaller) teams of authors on publications is related to a higher (lower) number of patents each year. Like model 1, we find the mean number of authors on publications, and the mean is used for its sensitivity to very large teams.
4 |. RESULTS
4.1 |. Key statistical properties
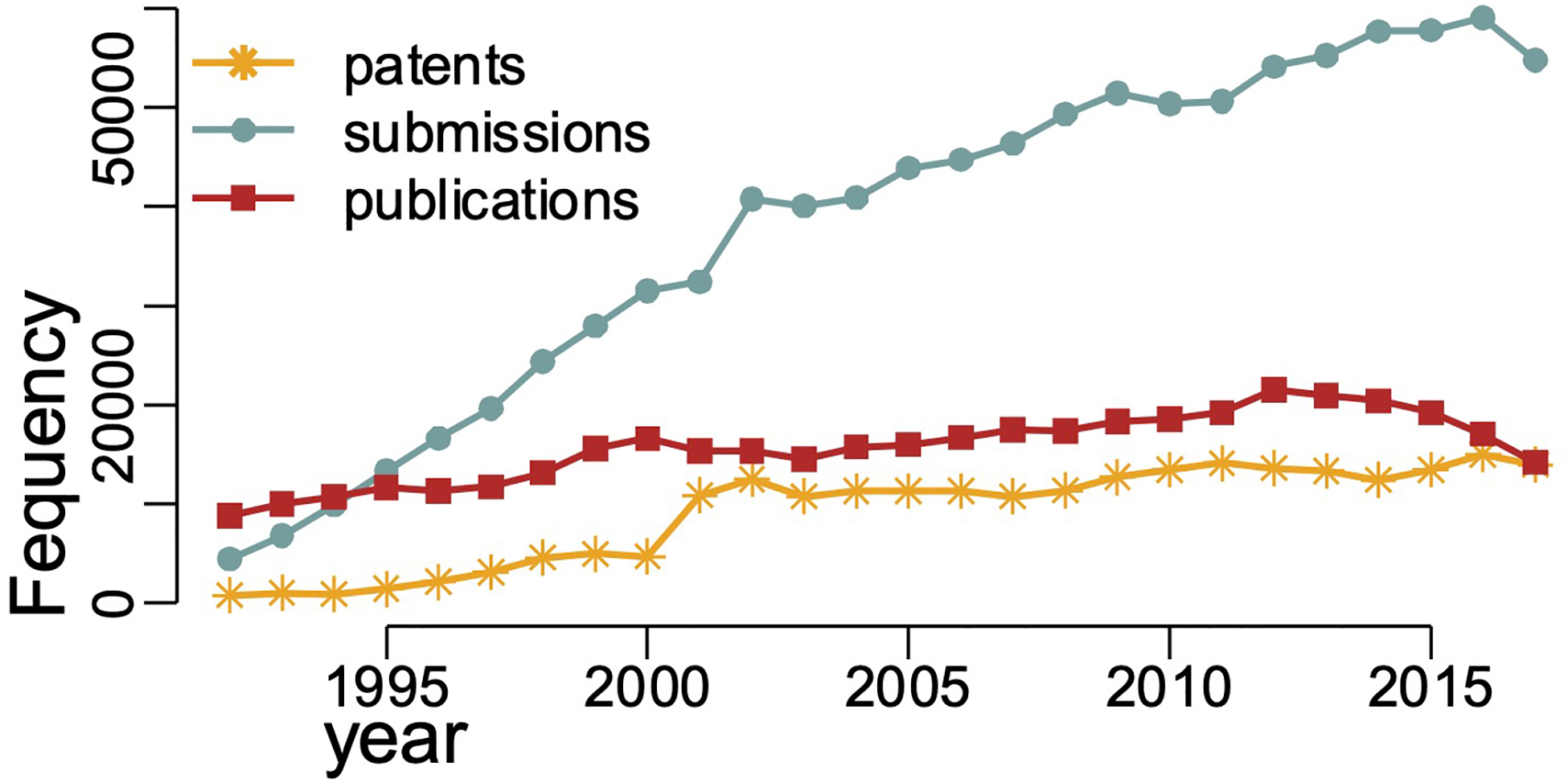
To give an overall sense of how the trends in the numbers of patents, data submissions, and publications have changed over time, we first include a plot (Figure 1) showing the growth in each over time. Of particular interest is the rapid and sustained growth of data submissions, compared to the others.
FIGURE 1.
Number of data submissions, publications, and patents for 1992–2018
Based a diagnostic analysis of the data, we selected three measures—mean team size, mean degree, and clustering coefficient—to provide an overview of the key features of these networks.
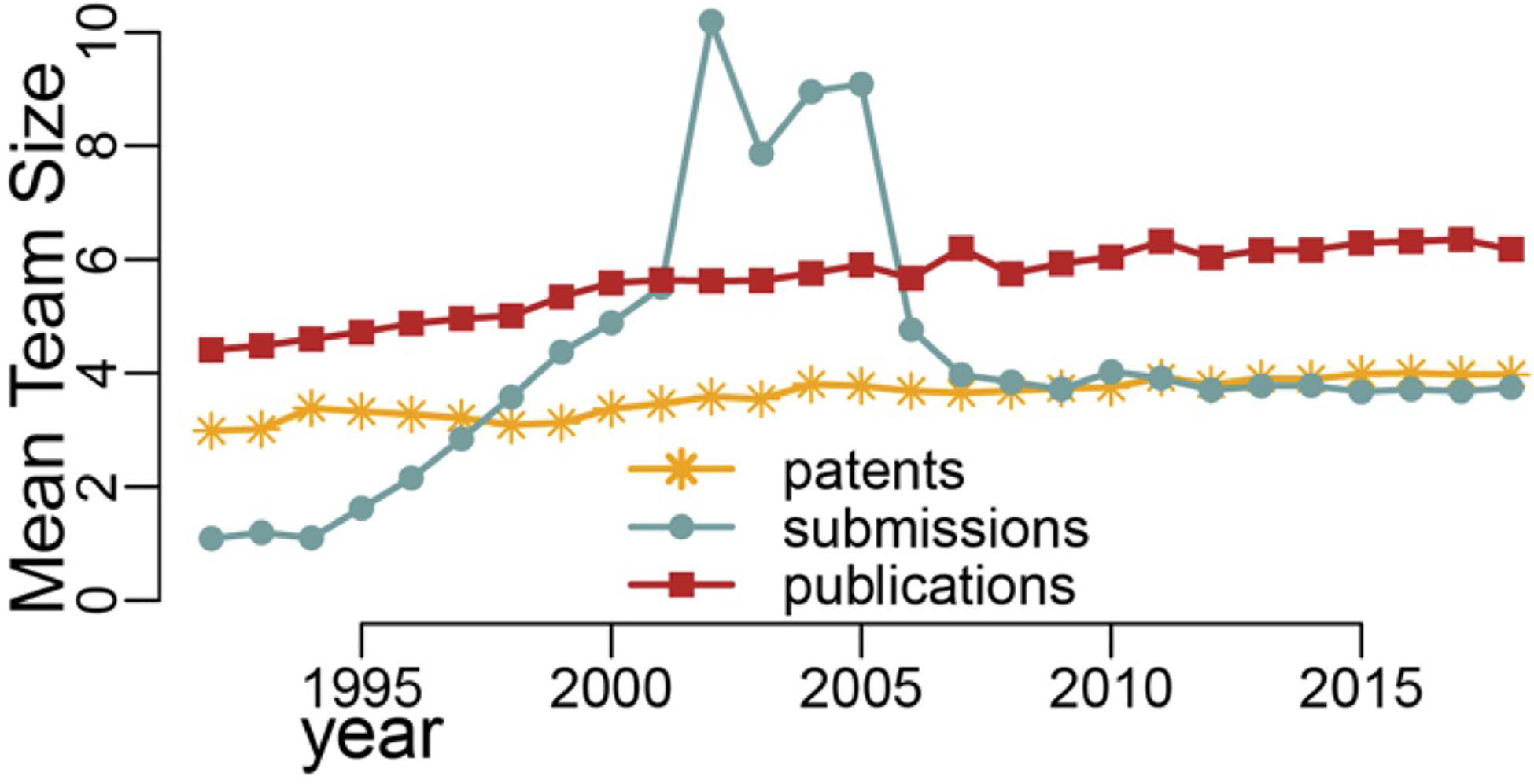
Figure 2 shows that the mean team sizes for the submission network doubled at the turn of the millennium, then spiked almost in parallel during the first 5 years after 2000 before settling on a stable development state. Note that while the publication team size has grown slowly over time, the patent team size has remained almost unchanged over the 27 years.
FIGURE 2.
Mean team sizes for the data submission, publication, and patent networks: 1992–2018
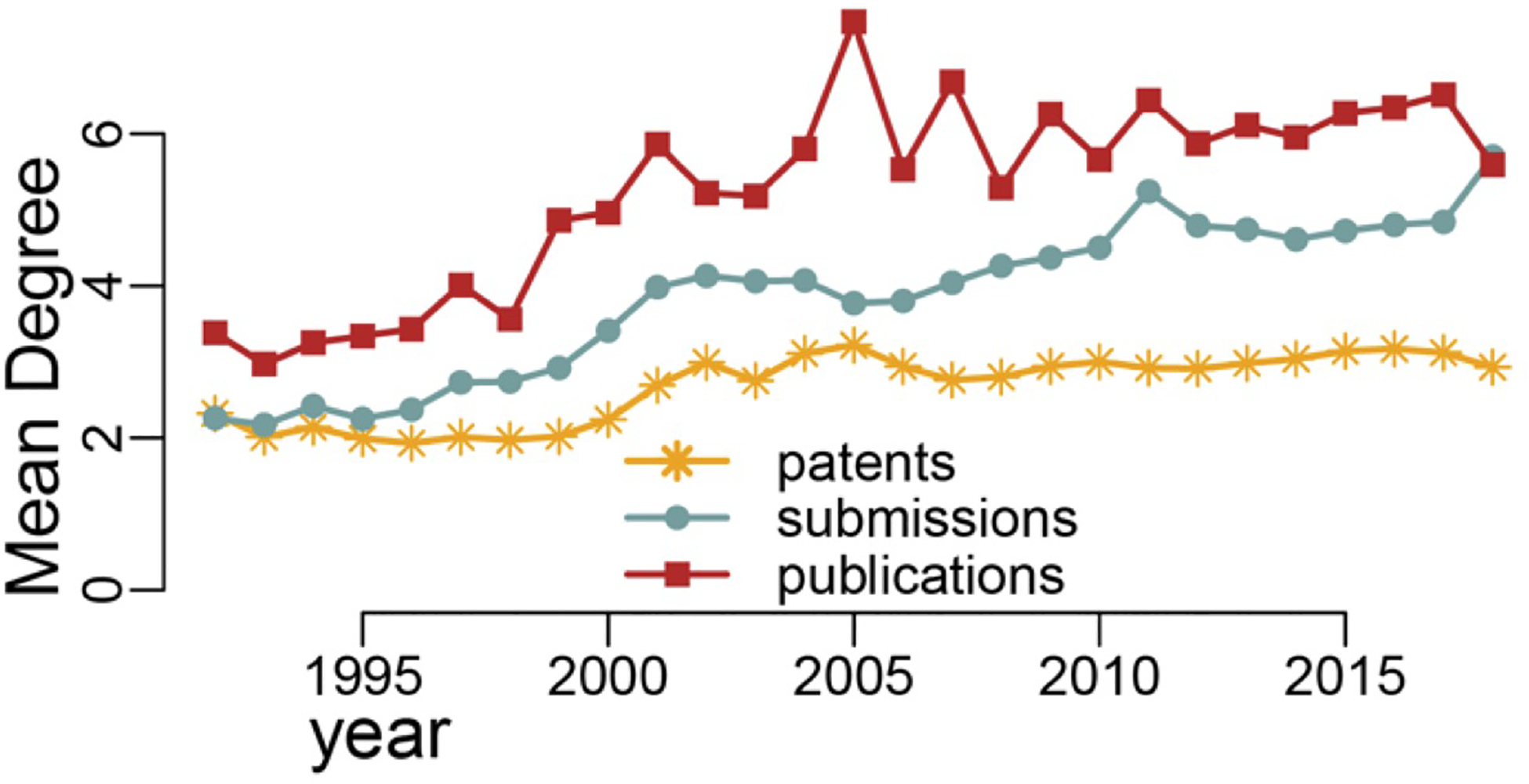
The mean value of degrees was calculated for each node, and then averaged for each year. This measure reflects how connected researchers were to other researchers over the years. In Figure 3, the mean degree for the publication network was consistently higher than those of the other two networks throughout the entire period measured here. The mean degree of the data submission network reflects a similar pattern as that of the publications network, though with a much lower magnitude, while that of the patent network was consistently the lowest and more stable among the three. We observed similar distribution patterns in the three networks such that the team sizes and mean degree for the publication network remained the highest among the three networks in both Figures 2 and 3. These two measures for the patent network showed smaller changes and were consistently lower, compared to the submission and publication network.
FIGURE 3.
Mean degrees for the data submission, publication, and patent networks: 1992–2018
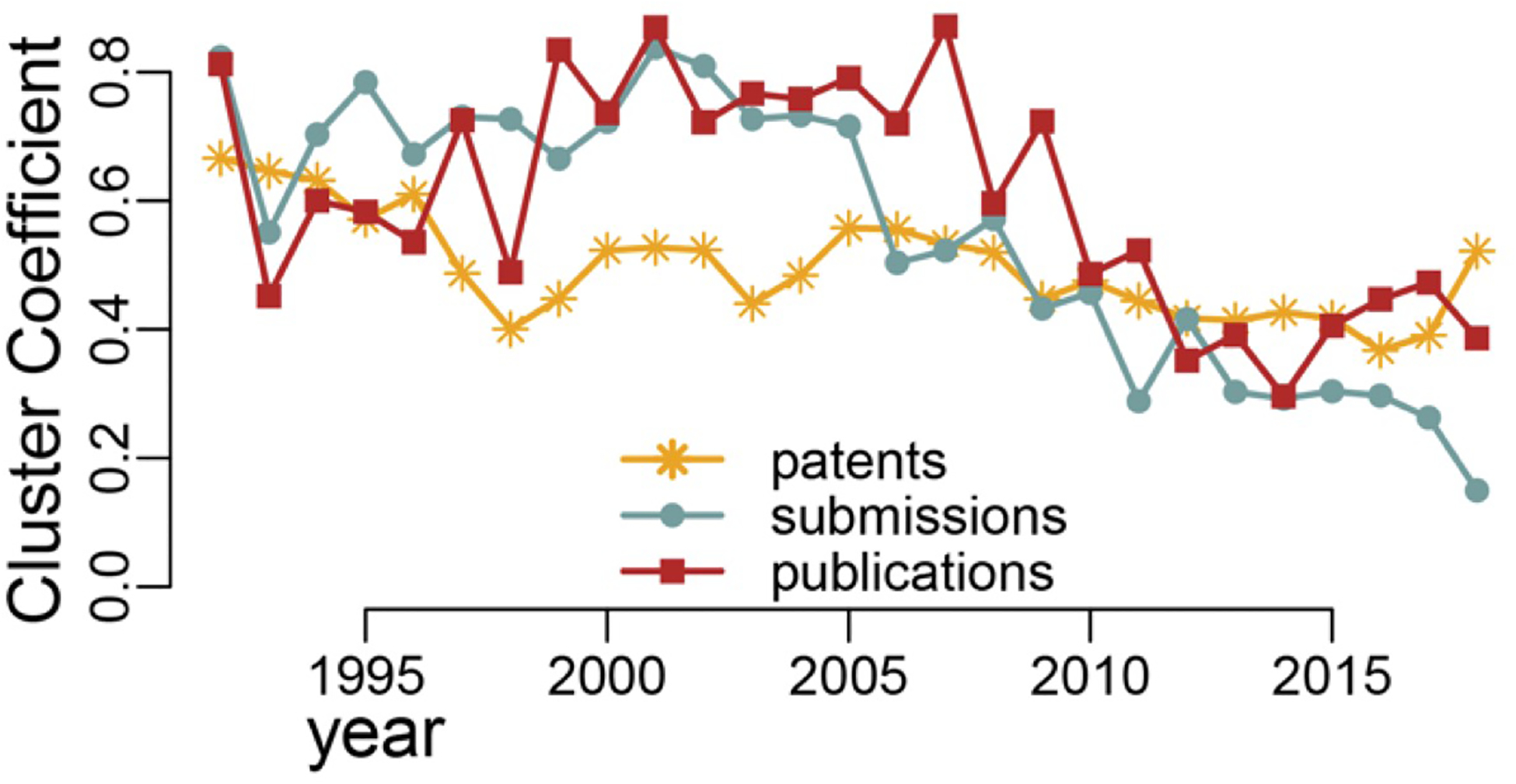
Clustering coefficient measures the degree to which nodes in a network tend to cluster together. In other words, the greater the value of clustering coefficient, the tighter the nodes are clustered in a network. This means that not only does a node itself have many connections to other nodes but also these other nodes are connected among themselves. The distribution of clustering coefficient for three networks in Figure 4 show a decreasing trend as time went on and the values for publication and data submission networks decreased at a faster rate than in the patent network. Of note in Figure 4 is that overall it remained quite steady with only small fluctuations, while the value for patent network was much lower compared to the other two networks.
FIGURE 4.
Clustering coefficient for the data submission, publication, and patent networks: 1992–2018
In the last decade (from approximately 2009–2018) the clustering coefficient for patent network was at about the same level as the other two and started growing higher in the last 2 years (Figure 4). The decrease in clustering coefficient presents evidence that the networks became flatter, that is, nodes were becoming less clustered around a small number of highly connected “hubs” and more smaller clusters emerged that are likely local and not necessarily have direct links to the hub nodes.
4.2 |. Hypothesis tests
Table 1 shows the results from model 1. All of the theoretical variables included in the model are positive and significant. The submission count of 0.185 indicates that for each data submissions in GenBank, patents increase by 0.185. This significant and positive relationship means that for H1, we reject the null hypothesis. This suggests a positive relationship between data submission efforts and patent output, or between collaboration in data production and knowledge diffusion. But it also shows that it takes many submissions, on average and holding all else constant, for patents to emerge.
Table 1:
Model 1: predicting patent outputs with the submission network variables
| Coefficients | Estimate | Std. Err. | t-value | p-value |
|---|---|---|---|---|
| (intercept) | −4802.623 | 874.884 | −5.489 | 0.000014 *** |
| Sub count | 0.185 | 0.022 | 8.478 | 0.000000 *** |
| Sub team size mean | 286.044 | 93.593 | 3.056 | 0.005598 ** |
| Sub mean degree | 1476.184 | 360.298 | 4.097 | 0.000442 *** |
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1020 on 23 degrees of freedom
Multiple R-squared: 0.9619, Adjusted R-squared: 0.9569
F-statistic: 193.6 on 3 and 23 DF, p-value: < 0.00000000000000022
In addressing H2 we find that team size is significant and positive. The interpretation is that, while holding other factors constant, for each new team member, patents would increase by 286. This sounds like a pretty big effect, but again, it is while holding the other variables constant. Also, if we look at the mean data submission team size for most years it is around 4. And in fact, the data is skewed such that there is a very large number of very small teams and just a few large ones. Given this, it is reasonable to interpret this such that larger teams are going to be getting more, probably most, of the patents. In any case, this suggests support for H2.
Finally, mean degree is also significant and positive, and so H3 is supported. Again, this looks like a very big effect. That is, for each additional link, we see many more patents. But again, this distribution is highly skewed such that there are a very large number of actors with just a few links. So being well connected confers a great advantage in terms of getting patents and thus having knowledge diffuse.
Model 2, shown in table 2, uses the publication network to predict patent output. The model results suggest that the number of publications is not significantly related to patent output at the 0.05% level. Thus, we cannot reject the null hypothesis for H4 (p = .0517).
Table 2:
Model 2 examines the relationship between the publication research process and knowledge diffusion as measured by the number of patents in a given year
| Coefficients | Estimate | Std. Err. | t-value | p-value |
|---|---|---|---|---|
| (intercept) | −29705.4297 | 3504.1025 | −8.477 | 0.0000000111 *** |
| Pub count | 0.3133 | 0.1524 | 2.056 | 0.0508. |
| Pub team size mean | 6020.0500 | 882.0403 | 6.825 | 0.0000004650 *** |
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1740 on 23 degrees of freedom
Multiple R-squared: 0.8891, Adjusted R-squared: 0.8746
F-statistic: 61.47 on 3 and 23 DF, p-value: 0.00000000003889
However, we also note that the p-value is significant at the 0.10 level. Given that we do find a correlation between number of patents and number of publications (PPMCC: 0.81, p-value: .0508), we suspect with more years of data we would have more degrees of freedom and our model would find a significant relationship. That said, in model 1 the number of data submissions does have a significant relationship to the number of patents. We will revisit this point in the discussion.
Finally, for H5 the results show a positive significant relationship between patent output and mean team size on publications (p-value .0137). This suggests support for H5. We can interpret the team size for publications in a similar way to how we interpreted team size for submissions. That is, it’s probable that larger teams tend to get most of the patents.
Note that we also examined how clustering coefficient performed in the models, but that variable was not significant and was dropped. In an effort to examine and control for other network factors, we experimented with other network measures (e.g., closeness, density, betweenness), but none were significant. However, we know that for each variable we add to the models, the regression loses degrees of freedom and so becomes less powerful. Given the age of GenBank, we are limited to 27 years for our analysis. Future work in 5 or 10 years may be able to rely on more powerful models and add more variables.
We also note that in the GenBank data we do not have direct links between submissions and patents or publications and patents. As such, we cannot trace the flow of knowledge creation and diffusion at the individual reference level. Rather, in this work, by aggregating by year and using regression modeling we examine factors that contribute to macro-level trends over time. We hope this work can inform future work that can dig deeper.
5 |. DISCUSSION
The overarching research problem this paper tries to address is how collaboration in data production affects and contributes to knowledge diffusion as represented by publications and patents. Authorship data in GenBank data submissions was used as a novel data source together with traditional publication and patent authorship data to expand the collaboration networks from data production to publications to patent applications. In the knowledge diffusion processes, research data are facts, evidence that are unfiltered, uncondensed and generated from the early stage of a research lifecycle. The diffusion journey from data to knowledge as is embodied in publications and patents entails close interactions between scientists and between scientists and information. These interactions in many ways are embedded in research collaborations at various levels and scales. The novel data source – GenBank genetic sequence submissions – enabled us to examine the knowledge diffusion journey from an unprecedented scale and gain insights into the relationship between data production and knowledge diffusion that were little known to science of science researchers.
Since data submission to open repositories became a mandatory policy in the mid-1990’s, data submissions to GenBank has been doubling roughly every 18 months since 1982 (NCBI, 2020). But how is the increase in data production related to knowledge diffusion? The key statistical properties of data submission, publication, and patent networks offer some explanation from a scientific collaboration perspective. The spikes in the average team size for GenBank data submissions coincided with large projects such as the Human Genome Project (1990–2003), while advances in sequencing technologies that afforded much faster and lower cost in sequencing production (Mardis, 2008) may have contributed to the flat mean team size for data submissions after the spikes in early 2000s.
The mean degree distribution for three networks in Figure 3 offers some insights into the knowledge diffusion phases in terms of data, publications, and patents. If data are a more atomic-level representation of information, then publications can be considered as the products from the action of diffusing data – analysis, generalization, synthesis, and summarization – into knowledge. Patents are one phase further in that they provide detailed description of the invention, which usually are built on publications. Data production can often require specialized scientific-technical (S&T) human capital. An implication of specialization is that the process of diffusing data to create formal knowledge – that is publications – is not done only for the purpose of scientific knowledge creation but also as a crediting action. Although not all data authors will be included in publication authors, the opposite is also true because a paper author may not be involved in data production at all. Under these assumptions, well-connected nodes, that is higher mean degrees, are more likely to reside in multiple networks at the same time and be high performers for a relatively longer period of time.
The decrease in clustering coefficient in all three networks raises an interesting question: what factors have contributed to the flattening – less hierarchical – networks? In relation to the other two key statistical properties of GenBank collaboration networks, we may reason from a broader perspective. On the one hand, the cyberinfrastructure and services, as well as advances in sequencing technology, made it easier for small teams to collaborate and perform at a more productive level than before. On the other hand, advantages in small team operations allow for more disruptive discoveries (Wu, Wang, & Evans, 2019).
The regression models described in this paper examine the relationships between the number of patents in a given year with the number of data submissions and network measures from the submission networks in the first model and the number of patents and publications and publication networks for the second model. Specifically, we find that the number of patents is positively related to the number of data submissions, how big data teams are, and how well-connected the researchers are in the data submission networks. We also find that the number of patents is positively related to the number of publications and to publication team size. This work also suggests that larger teams are getting a disproportionately larger number of patents.
The significant and positive relationship between data submission network measures and patent counts indicates the value for including data production in studying knowledge diffusion in research collaboration, a promising area that needs further investigation. Although the null hypothesis for H4 cannot be rejected, we expect it to become significant if more years of data become available as GenBank matures.
6 |. CONCLUSION
This paper presented the analysis of metadata from GenBank data submissions in the effort to identify the role of collaboration networks in data production, publications, and patent applications. By aggregating data by year, the novel data source of GenBank data submission metadata shows macro level trends in the study of data-to-knowledge and has proved to be valuable for examining the role and impact of collaboration networks in knowledge diffusion. The analysis results presented in this paper show some promising leads to further research in uncovering high performers’ career trajectories, and collaboration capacity vs. its enablers in policy, cyberinfrastructure, and S&T human capital.
We see this work as a start and suggest that future work can focus on a range of different areas around data production in research, not just the relationship between data production and knowledge diffusion. For example, in this work we did not study the relationship between data production and publications, and we did not trace authors throughout the research cycle, that is, the stages of production from data to publication and patent. Work in those areas could yield rich insights into the science of science.
ACKNOWLEDGMENTS
The authors thank the support of National Science Foundation (award #1561348) and National Institute of General Medical Sciences (award #1R01GM137409-01), and Amit Dadaso Jadhav for technical assistance.
Footnotes
83rd Annual Meeting of the Association for Information Science & Technology October 25–29, 2020.
GenBank is a data repository that curates molecular sequence data (https://www.ncbi.nlm.nih.gov/genbank/)
Connection between actors of different categories or classes.
There are also white papers, conference proceedings, and pre-prints though they comprise a minority at about 10%. These publications are selected by the dataset submitter as “relevant,” that is, papers in GenBank are those containing an explanation of the dataset, its processing, and other details to provide context for the next user.
REFERENCES
- Albert R, & Barabási AL (2002). Statistical mechanics of complex networks. Review of Modern Physics, 74(1), 47–97. [Google Scholar]
- Barabási AL, Jeong H, Néda Z, Ravasz E, Schubert A, & Vicsek T (2002). Evolution of the social network of scientific collaboration. Physica A, 311, 590–614. [Google Scholar]
- Bozeman B, & Corley E (2004). Scientists’ collaboration strategies: Implications for scientific and technical human capital. Research Policy, 33(4), 599–616. 10.1016/j.respol.2004.01.008 [DOI] [Google Scholar]
- Bratt S, Hemsley J, Qin J, & Costa M (2017). Big data, big metadata and quantitative study of science: A workflow model for big scientometrics. Proceedings of the Association for Information Science and Technology, 54(1), 36–45. [Google Scholar]
- Chin WS, Juan YC, Zhuang Y, Wu F, Tung HY, Yu T, … & Huang KH (2013, August). Effective string processing and matching for author disambiguation. In Proceedings of the 2013 KDD Cup 2013 workshop (pp. 1–9). [Google Scholar]
- Costa L. d. F., Rodrigues FA, Travieso G, & Boas PRV (2007). Characterization of complex networks: A survey of measurements. Advances in Physics, 56(1), 167–242. [Google Scholar]
- Costa MR, Qin J, & Bratt S (2016). Emergence of collaboration networks around large scale data repositories: A study of the genomics community using GenBank. Scientometrics, 108(1), 21–40. 10.1007/s11192-016-1954-x [DOI] [Google Scholar]
- Cummings JN (2018). Science Policy Research Report: Funding Team Science. Retrieved from https://netvis.fuqua.duke.edu/papers/Funding_Team_Science_Report_Final.pdf
- Faraway JJ (2014). Linear models with R. Boca Raton, FL: CRC Press. [Google Scholar]
- Girvan M, & Newman MEJ (2002). Community structure in social and biological networks. Proceedings of National Academy of Science, 99(12), 7821–7826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hey AJG (Ed.). (2009). The fourth paradigm: Data-intensive scientific discovery. Redmond, WA: Microsoft Research. [Google Scholar]
- Kim H, & Park Y (2009). Structural effects of R&D collaboration network on knowledge diffusion performance. Expert Systems with Applications, 36(5), 8986–8992. 10.1016/j.eswa.2008.11.039 [DOI] [Google Scholar]
- Klarl T (2014). Knowledge diffusion and knowledge transfer revisited: Two sides of the medal. Journal of Evolutionary Economics, 24(4), 737–760. 10.1007/s00191-013-0319-3 [DOI] [Google Scholar]
- Mardis ER (2008). The impact of next-generation sequencing technology on genetics. Trends in Genetics, 24(3), 130–141. 10.1016/j.tig.2007.12.007 [DOI] [PubMed] [Google Scholar]
- NCBI. (2020). Growth of GenBank and WGS. Retrieved from http://www.ncbi.nlm.nih.gov/genbank/statistics
- Newman MEJ (2001a). Scientific collaboration networks. I. Network construction and fundamental results. Physics Review E, 64(1), 23–25. Retrieved from http://pre.aps.org/pdf/PRE/v64/i1/e016131 [DOI] [PubMed] [Google Scholar]
- Newman MEJ (2001b). Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality. Physics Review E, 64(1), 43–44. Retrieved from http://pre.aps.org/pdf/PRE/v64/i1/e016132 [DOI] [PubMed] [Google Scholar]
- Newman MEJ (2001c). The structure of scientific collaboration networks. Proceedings of National Academy of Science, 98(2), 404–409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powell WW, White DR, Roput KW, & Owen-Smith J (2005). Network dynamics and field evolution: The growth of interorganizational collaboration in the life sciences. American Journal of Sociology, 110(4), 1132–1205. [Google Scholar]
- Qin J, Hemsley J, & Bratt S (2001). Collaboration capacity: measuring the impact of cyberinfrastructure-enabled collaboration networks. International Journal of Technology Management, 22, 636–655. [Google Scholar]
- Qin J, Lancaster FW, & Allen B (1997). Levels and types of collaboration in interdisciplinary research. Journal of the American Society for Information Science, 48(10), 893–916. [Google Scholar]
- Qin J (1994). An investigation of research collaboration in the sciences through the Philosophical Transactions of the Royal Society, 1901–1991. Scientometrics, 29(2), 219–238. [Google Scholar]
- Singh J (2005). Collaborative networks as determinants of knowledge diffusion patterns. Management Science, 51(5), 756–770. 10.1287/mnsc.1040.0349 [DOI] [Google Scholar]
- Spender JC (2008, 2008). Knowledge, diffusion of international encyclopedia of the social sciences. In Darity WA Jr. (Ed.), (Vol. 4, 2nd ed., pp. 281–282). Macmillan Reference USA. Retrieved from https://www.encyclopedia.com/social-sciences/applied-and-social-sciences-magazines/knowledge-diffusion [Google Scholar]
- Tarango J, & Machin-Mastromatteo JD (2017). Conceptualization of scientific productivity, production, dissemination, and communication. In Tarango J & Machin-Mastromatteo JD (Eds.), The role of information professionals in the knowledge economy: Skills, profile and a model for supporting scientific production and communication (pp. 27–70). Cambridge, MA: Chandos Publishing. [Google Scholar]
- Wu L, Wang D, & Evans JA (2019). Large teams develop and small teams disrupt science and technology. Nature, 566(7744), 378–382. 10.1038/s41586-019-0941-9 [DOI] [PubMed] [Google Scholar]


