Abstract
Survey scores are often the basis for understanding how individuals grow psychologically and socio-emotionally. A known problem with many surveys is that the items are all “easy”—that is, individuals tend to use only the top one or two response categories on the Likert scale. Such an issue could be especially problematic, and lead to ceiling effects, when the same survey is administered repeatedly over time. In this study, we conduct simulation and empirical studies to (a) quantify the impact of these ceiling effects on growth estimates when using typical scoring approaches like sum scores and unidimensional item response theory (IRT) models and (b) examine whether approaches to survey design and scoring, including employing various longitudinal multidimensional IRT (MIRT) models, can mitigate any bias in growth estimates. We show that bias is substantial when using typical scoring approaches and that, while lengthening the survey helps somewhat, using a longitudinal MIRT model with plausible values scoring all but alleviates the issue. Results have implications for scoring surveys in growth studies going forward, as well as understanding how Likert item ceiling effects may be contributing to replication failures.
Keywords: ceiling effects, survey design, item response theory, multidimensional IRT models, growth modeling
Much of what we know about how people develop psychologically and socio-emotionally is based on survey item responses. In particular, researchers often tend to give the same survey instrument to cohorts of people over time, and analyze how those scores change. For example, in education, studies examine issues like whether students show positive or negative growth in academic self-efficacy as children move into and through middle school (Caprara et al., 2008). In psychology, researchers have studied the longitudinal associations between negative affect and alcohol use, with the former being based in part on survey item responses (e.g., Chassin et al., 2013). Scores from repeated survey measures are then used in a variety of longitudinal models, such as cross-lag panel models and, perhaps most frequently, latent growth curve models (LGCMs; McArdle & Epstein, 1987).
One known problem with many survey instruments, especially those concerned with socio-emotional outcomes, is that writing “difficult” survey items is not straightforward. In both achievement testing and item response theory (IRT) contexts, “difficulty” has a distinct meaning; here, in a survey context, a difficult item is one that most respondents do not endorse. 1 For instance, if one administers “yes/no” items, an easy item might be one where almost everyone selects “yes,” and a difficult one where most respondents select “no.” Without difficult items, a survey likely does not lead to reliable measurement of individuals who are high on the latent construct, with respondents often using only the top response categories (e.g., DeWalt et al., 2013; Soland et al., 2022; Soland & Kuhfeld, 2021). These item ceiling effects are distinct from response style biases, which occur when respondents use the response scales in ways not related to the true construct, as in the case of socially desirable responding (Bolt & Newton, 2011). This issue is also distinct from the problem of measuring a construct with “performance limits” (Feng et al., 2019), which occurs when the construct itself actually has a true, natural ceiling. In short, there are many reasons that respondents might use only the top response categories, but the problem of having no difficult survey items is an issue with the measure itself that creates ceiling effects, not an issue with the respondents’ own behaviors (e.g., response style bias) or the nature of the construct (performance limits).
One could imagine that this common problem of lacking difficult items (DeWalt et al., 2013; Soland & Kuhfeld, 2021) being particularly problematic when surveys are used to examine growth and change over time. If, hypothetically, one is trying to estimate growth over four timepoints, and most respondents are already at the top of the item response scale at Time 1 because there are not enough difficult items, then ceiling effects could lead to understated estimates of growth. This potential concern is not far-fetched. As an example, the CORE school districts in California, which serve over 1.5 million students, administer surveys of socio-emotional constructs to students each year as they move through school (Gehlbach & Hough, 2018). Responses on those CORE surveys tend to be clustered towards the upper end of the Likert scale, and there is evidence that the surveys have few difficult items even after accounting for response style biases (Soland & Kuhfeld, 2021). These CORE surveys are also often used to examine growth and change over time (e.g., Fricke et al., 2021; West et al., 2020). Despite the plausibility of item ceiling effects biasing growth estimates when using CORE surveys and myriad other instruments, few studies thoroughly investigate such a scenario and its impact on LGCM growth parameter estimates (Bauer & Curran, 2016; Kuhfeld & Soland, 2022).
Given potential concerns about item ceiling effects in longitudinal contexts, researchers have various strategies they can use to mitigate potential biases. First, approaches could be taken in the survey design phase to address item ceiling effects. Those options include writing more difficult items (Masino & Lam, 2014) and simply developing longer surveys such that reliability improves and there is more variability in item responses, even in the presence of ceiling effects. Second, one could address this issue when modeling growth, such as by using a Tobit growth model or Tobit mixed effects model (e.g., Wang, Zhang, McArdle, & Salthouse, 2008). A third and understudied approach to mitigating item ceiling effects is how one models the item responses. For instance, longitudinal multidimensional IRT (MIRT) models (e.g., Bauer & Curran, 2016) allow respondents to have distinct scores across timepoints even if a given person uses the same response pattern at more than one timepoint.
In this study, we use simulation and empirical analyses to help researchers using longitudinal survey data better understand consequences of, and solutions for, item ceiling effects. We begin by showing how item ceiling effects can impact growth estimates when surveys are scored using “typical” approaches, including sum scores and unidimensional IRT models. Next, we investigate two possible solutions to any bias introduced by item ceiling effects. For one, we consider whether lengthening the survey without changing the item difficulties can mitigate ceiling effects. For another, we investigate whether using a range of longitudinal MIRT models designed to account for differences over time (coupled with various IRT-based scoring approaches) can mitigate the impact of item ceiling effects. All told, these analyses allow us to answer two research questions:
1. Does administering only “easy” Likert items lead to biased growth estimates when using typical scoring approaches like sum scores?
2. Does using a longer survey reduce bias more or less compared to using a measurement model designed for longitudinal data?
Background
Measurement Models Available for Item Responses in Longitudinal Contexts
Sum Scores
Many researchers in the psychological literature prefer to measure relevant constructs using observed scores (either sum scores or means of items) from survey instruments (Bauer & Curran, 2016; Flake et al., 2017). While sum scores do not technically involve a measurement model, they are roughly equivalent to fitting a highly constrained measurement model (McNeish & Wolf, 2020) and are a sufficient statistic for Rasch-style IRT scores. Specifically, McNeish and Wolf (2020) pointed out that sum scoring is essentially equivalent to fitting a factor model in which all item slopes and residual variances are constrained equal. Thus, even at a single point in time, sum scores make a range of strong assumptions, including that all students have received and answered the same item set, all items should be weighted equally, and items display measurement invariance. Sum scores used in longitudinal models require several additional assumptions, including that items demonstrate longitudinal invariance. Though largely unstudied, sum scores may be impacted by ceiling effects on the item responses. For example, which response corresponds to which item does not matter for sum scoring, likely making it harder to differentiate among respondents only using the extremes of the response scale.
Calibration Using a Unidimensional IRT Model
An alternative to using sum scores is to calibrate item parameters using a single timepoint per person with a unidimensional IRT model. 2 Once the item parameters are obtained using a unidimensional IRT model, the parameters are treated as fixed for the other waves and used to score the item responses in the remaining timepoints. For Likert-type items, item calibration and scoring can be accomplished using the graded response model or GRM (Samejima, 1969). Let there be items and individuals. Let the response from individual i to item j at timepoint t be where has K response categories. It can be assumed that takes integer values from ( ). Let the cumulative category response probabilities be
| (1) |
The category response probability is the difference between two adjacent cumulative probabilities
| (2) |
where is equal to 1 and is zero. The item parameter is the slope parameter describing the relationship between item j and the latent factor, and are a set of (strictly ordered) parameters. The thresholds denote the point on the latent variable separating category from category .
In the unidimensional case, the logit in equation (1) can be re-expressed in a more convenient slope-threshold form as , where is the threshold (also referred to as severity or difficulty) parameter for category . The th threshold denotes the point on the latent variable separating category from category . However, the slope-threshold form does not generalize well to multidimensional models, so we adopt the slope–intercept parameterization here and for all remaining IRT models presented.
There are multiple possible limitations in using just a single timepoint to calibrate scores for longitudinal research. In particular, the calibration approach often includes only one observation per person and does not model whether the construct of interest varies within persons across time, nor how those scores are correlated over time. Kuhfeld and Soland (2022) found that unidimensional IRT parameter calibration often led to severe understatement of latent growth slopes and variances, in some cases introducing more bias than when using sum scores. These models may also have limitations in the context of item ceiling effects. For instance, a unidimensional model assumes a single population mean and variance. As a result, the same score patterns will result in the same scores by timepoint.
Calibration Using a Longitudinal MIRT Model
Another approach uses longitudinal MIRT to model item responses across time. Syntax for this model in flexMIRT and R can be found in the supplemental online materials (SOM). Item response data from each timepoint are combined and calibrated simultaneously across the T timepoints for a given cohort such that each timepoint has its own latent variable with unique mean and variance. Item response data from each timepoint are combined and calibrated simultaneously across the T timepoints. We use a multidimensional extension of the GRM. Let the cumulative category response probabilities be
| (3) |
As with the unidimensional model, the category response probability is the difference between two adjacent cumulative probabilities. The difference between the unidimensional and multidimensional GRM is that is now a T×1 vector of latent traits and a vector of slopes. Given the same items are repeated across timepoints, one typically includes a set of equality constraints for the item parameters of the repeated items (measurement invariance). Further, the first latent dimension is often (but not always) constrained for identification purposes to follow a standard normal distribution , and the mean, variance, and covariance of the other latent factors are freely estimated relative to the first timepoint.
Unlike when using sum scores or unidimensional IRT models, the MIRT approach explicitly accounts for over-time correlations in the model, as well as unique latent variable variances by timepoint. Bauer and Curran (2016) hypothesized that such a model would lead to better recovery of latent growth parameters, and Kuhfeld and Soland (2022), as well as Gorter et al. (2020), demonstrated as much via Monte Carlo simulation. Though unstudied, this calibration approach could have benefits in the context of item ceiling effects and growth. For example, unlike in the unidimensional model, someone with identical item response patterns at Time 1 and Time 4 would not necessarily get identical scores.
IRT-based Scoring Approaches and Their Implications for Ceiling Effects
Maximum Likelihood Estimation
Once item parameters have been calibrated, the question becomes how to produce scores for use in LGCMs. One option is maximum likelihood estimation (MLE). MLE produces an estimate of the uncertainty in the score specific to each student (the “standard error of measurement”), is efficient, and can be used with an IRT model that allows item weights to differ (unlike sum scores). However, MLE also has limitations, especially when short survey scales are being scored. In particular, MLE cannot produce a score if a survey respondent gets the maximum possible sum score on a survey. Thus, the researcher would have to decide whether to treat that score as missing, or simply replace it with some arbitrary maximum value (e.g., assume that anyone who uses only the top response category would have an IRT-based score of 4 standard deviations [SDs] above the mean). This issue could have implications in the context of ceiling effects. For instance, if many respondents use only the top response categories, their score would be undefined and either omitted or placed with an arbitrary maximum.
Bayesian Scoring Approaches
Expected a Posteriori Scoring
Meanwhile, Bayesian methods such as expected a posteriori (EAP) scoring do not share such limitations. Bayesian methods incorporate information about the population through the specification of a prior distribution of scores, either using something generic like the standard normal distribution or factoring in previous information (Bock & Mislevy, 1982). EAP scoring approaches address uncertainty by shrinking noisy scores toward the population mean, and the degree of shrinkage depends on the test length and reliability (Thissen & Orlando, 2001). In the context of ceiling effects, while being able to produce scores for individuals using only the top or bottom response category could help avoid biased growth estimates, EAP does nothing to differentiate such scores when using a unidimensional model. That is, EAP with a unidimensional model would shrink all scores to a single mean regardless of timepoint, and thus, scores from individuals using only the top or bottom categories would be the same across timepoints. By contrast, when using a longitudinal MIRT model, scores would be shrunken differentially by timepoint, which would mean there could be variability in scores across timepoints even for those using the top response categories.
Plausible Values
Yet another approach to producing scores is to use plausible values (PV) scoring. PVs represent multiply imputed scores obtained from a latent regression or population model. PVs are used to obtain more precise estimates of group-level scores than would be obtained through an aggregation of point estimates (Mislevy, 1991; Mislevy & Sheehan, 1987; Thomas, 2002; von Davier et al., 2006, 2009). The goal is to reduce uncertainty and measurement error for quantities used in analyses, including large-scale surveys designed to make valid group-level comparisons rather than optimal point estimates for individual respondents. That is, PVs are designed to provide group-level scores to describe populations.
In the context of the longitudinal MIRT model, the population latent variable at the first timepoint has a mean of zero and SD of one, but the population level means and variances of the latent variables for subsequent timepoints are freely estimated during calibration. These means and variances are then used as priors in the scoring. Thus, each set of PVs represents a random draw from a posterior specific to each timepoint. For example, with four timepoints, one could make draws from posterior distributions for the four latent variables. Then, those draws could be modeled in a missing data context, such as when using multiple imputation models. While this imputation strategy has been shown to help recovery of true LGCM parameters (Gorter et al., 2020), no research has been conducted on recovery of those parameters in the presence of item ceiling effects.
Simulation Study
Simulating Data
Data were simulated in two steps. First, a population model with known growth parameters was used to generate true scores at four timepoints. Then, true item parameters were used along with the true scores from the prior step to produce observed item responses in flexMIRT (Cai, 2017; v. 3.51). As we describe below, IRT difficulty parameters were shifted to induce varying severity of item ceiling effects. For all simulations, we used a sample size of 1000 simulees, a number chosen such that IRT item parameters could be properly estimated (Sahin & Anil, 2017), but that was not so large as to no longer resemble a prototypical longitudinal study in psychology or education (Yeager & Walton, 2011). As a sensitivity check to ensure that poor item parameter recovery was not driving results, we also conducted a subset of simulations using a sample size of 5000. Given computational time for some of the MIRT models, all conditions were replicated 100 times.
Population Model
We assumed that individual i’s vector of true latent scores followed a linear latent growth model. Specifically, we assumed that
| (4) |
where is a fixed factor loading matrix, is a vector representing a student’s latent intercept and growth term, and is a 4 × 1 vector of time-specific random disturbance terms assumed to be normally distributed with means of zero and variance . Each of the individual’s can be decomposed into two parts
| (5) |
where is the population average, and represents an individual deviation from that average. The model-implied mean vector and variance-covariance matrix for the latent growth model are
| (6) |
| (7) |
where is variance-covariance matrix for the latent factors, and is the residual variance-covariance matrix. The generating parameters for the current simulation study are
| (8) |
where can take the value of 0, 0.2, or 0.5 depending on the condition. That is, simulees either have true growth per timepoint equal to 0 standard deviations (SDs), .2 SDs, or .5 SDs. We selected these generating values based on a prior analysis of socio-emotional growth across four years (Authors, In Press). We also varied the cells in such that the variance of the slopes, as well as the covariance of the intercept and slope, differed (details in the SOM).
Baseline Item Parameters
After generating the true values in flexMIRT using the model-implied mean vector and variance-covariance matrix, the item responses were simulated using a longitudinal multidimensional GRM with five response categories. The generating item parameters—including slopes and baseline intercepts in the “easy” difficulty condition described below—were adapted from an existing measure of children’s interpersonal competencies (DeWalt et al., 2013). Three sets of generating item parameters are used (shown in SOM Table A1). These conditions correspond to “mixed” difficulty items, “easy” items, and “very easy” items. The mean proportion falling in the top response category is ∼ .28 for the mixed condition, ∼.50 for the easy condition, and ∼.75 for the very easy condition. 3
To examine the effects of lengthening the survey on ceiling effects (per Research Question 2), we simulated three survey instrument lengths: 5, 10, and 15 items. As McNeish (2022) pointed out, Flake et al. (2017) found that the average scale length across hundreds of survey instruments reviewed was just under 5 items, with an SD of 6.4. The median number of scale items was similar in reviews by Jackson et al. (2009) and D’Urso et al. (2022). Thus, the 5-item condition roughly represents the average scale length, the 10-item condition is about 1 SD above average, and the 15-item is roughly 2 SDs about average. Finally, for a smaller set of replications, we used a 50-item scale to see if using an extremely long instrument had a bigger effect on parameter recovery in the presence of ceiling effects.
Analyzing Simulated Data
IRT calibration/scoring was conducted in two broad ways. To answer Research Question 1, sum scores, as well as unidimensional IRT models employing both MLE and EAP scoring approaches in flexMIRT were used. For MLE scoring, undefined scores were replaced with an arbitrary maximum/minimum of +/− 4 SDs. 4 The unidimensional models were estimated using maximum likelihood via the Bock-Aitken EM algorithm. Item parameters calibrated based on the first timepoint only were used to estimate scores for later timepoints. To answer Research Question 2, longitudinal MIRT models were used to calibrate the item parameters. Then, those item parameters were used to produce EAP scores and PV draws from the posterior (MLE scoring is not recommended in conjunction with MIRT models when using flexMIRT). 5 After scoring simulated item responses, LGCMs were estimated in Stata version 15 using the SEM package. One used the true underlying scores, another used standardized sum scores, and the third one used the various estimated scores 6 from the unidimensional and MIRT models. While analyses mainly examined parameter recovery, we also considered latent slope mean Type I and II errors.
Results
Item Parameter Recovery
Before turning to growth model results, we should point out that item parameter recovery for all IRT and MIRT models was sufficient. Therefore, results do not tend to be driven by miscalibrated item parameters. Figure 1 shows kernel density plots of bias in the estimated intercept parameters by item difficulty condition. The figure includes results for sample sizes of 1000 and 5000 (the “mixed” difficulty condition does not include the N = 5000 results because replications with this combination of conditions were not included in the sensitivity analyses). The subtitle of each plot in Figure 1 shows the bias mean and SD for the N = 1000 condition. In general, intercepts were recovered with a mean bias of zero, with the exception of slight downwards bias in the intercepts for the very easy condition. Variability in the bias differed little except for the very easy item condition, where variability was higher. The SD of the intercept parameters for all four intercepts was above one, and the SD of the bias was between 0.13 and 0.20. These results indicate that, while one cannot rule out poor item parameter recovery contributing somewhat to bias in growth estimate results for the very easy item condition, poor item parameter recovery is not likely the driving force in slope estimate bias, an issue discussed in more detail shortly.
Figure 1.
Density plots of bias in the IRT-based intercepts by difficulty condition. Note. Each plot includes the mean and standard deviation of the bias by intercept for N = 1000. So, for example, c1 m = .02 indicates that the mean bias for the first intercept when all conditions are included (N = 1000) is .02 units, where bias is the estimated item parameter minus the generating item parameter.
Q1. How Do Ceiling Effects Impact Growth Estimates Using Typical Scoring Approaches?
Figure 2 shows boxplots of LGCM slope parameter estimates by item difficulty condition and scoring approach (sum score, unidimensional EAP, and unidimensional MLE). 7 The graphs include vertical lines corresponding to the different slope parameters (0.0 SDs, 0.2 SDs, and 0.5 SDs). The vertical axis shows the number of items and the true growth parameter for a given estimate. As Figure 2 illustrates, bias in the slope estimates can be extreme in the presence of ceiling effects. For example, when growth is 0.5 SDs and items are very easy, EAP often understates growth by more than 50%. Sum scores also perform extremely poorly, especially in the presence of item ceiling effects. Even when the survey items are only easy (not very easy), there can still be substantial bias in the slope estimates. Thus, these results raise the real possibility that many current empirical studies that use surveys and sum scores to understand psychological or socio-emotional development are severely misrepresenting true growth.
Figure 2.
Growth estimates by scoring approach and true slope, Question 1.
Q2. How Much Does Lengthening the Survey Instrument versus Using a Longitudinal MIRT Model Improve Recovery of Latent Slope Estimates?
Returning to Figure 2, tripling the length of the survey from 5 to 15 items does little to improve recovery of LGCM slope estimates when using typical scoring approaches. That is, any improvement in how well LGCM parameters are recovered when using sum or unidimensional IRT scores with a 15-item survey compared to 5 is marginal. Even a 50-item survey is not sufficient to overcome ceiling effects. Figure 3 shows plots of slope estimates for the three different slope conditions with estimates using true scores on the horizontal axis, and estimates using sum scores on the vertical. The figure only uses the easy item condition. Results are presented for 5-item and 50-item surveys. As the results show, while 50 items lead to better slope recovery, the improvement is marginal.
Figure 3.
Growth estimates for true versus sum scores when using 5 items compared to 50 items.
By contrast, Figure 4 shows the same plot as in Figure 2, but when using a longitudinal MIRT model, including directly parameterizing the latent slope. Several takeaways from this figure are discernible. First, bias is substantially reduced for virtually all of these measurement modeling approaches. Thus, using a measurement model that parallels the multi-timepoint nature of the data appears to pay dividends. Second, not all models and approaches perform equally well. For example, the MIRT plus PV scoring approach produced far and away the best results. Even with true growth of 0.5 SDs and very easy survey items, bias in the latent slopes was fairly minimal when using PV scoring. Third, there was also often an interaction between the length of the survey instrument and the bias, with bias often the worst when using a short (5-item) survey. Finally, as shown in SOM Section B, these results hold even when using a sample size of 5,000, which suggests that poor item parameter recovery is not the primary explanation for slope bias.
Figure 4.
Growth estimates by scoring approach and survey length, Question 2.
Type I and II Errors
All scoring approaches tended to produce fairly comparable Type I error rates. However, sum scores often produced more Type I errors. For example, with 5 items and sum scoring, even the mixed item difficulty condition resulted in Type I errors that exceeded 20% of the replications. Further, in the easy item condition, Type I errors tended to occur well over 50% of the time when using sum scores. Given that the easy item condition is based on empirical data (as compared to the very easy condition, which is meant to serve as an extreme but plausible point of comparison), this finding raises the possibility that many significant growth estimates from empirical studies may represent Type I errors given how often sum scores are used (Kuhfeld & Soland, 2022; McNeish & Wolf, 2020). As for longitudinal MIRT scores, they tended to produce only slightly more Type I errors than when using true scores except for the very easy item condition. Turning to Type II errors, very few were produced except when using the unidimensional MLE scores. By contrast, none of the other calibration/scoring approaches generated high Type II errors (with the exception of sum scores in the very easy item condition).
Empirical Example
In this empirical analysis, we used data from a socio-emotional learning survey consisting of four constructs that was administered to students in California longitudinally between 2015 and 2018. We used those data to identify constructs/items with varying degrees of skew, score them in different ways, then estimate and compare growth parameters. While such analyses do not allow us to disentangle whether growth estimates differ due to the (a) construct, (b) calibration/scoring approach, or (c) level of skew in the item responses, they nonetheless allow us to see if patterns in (c) are associated with growth in a manner comparable to what we observed in the simulation studies. That is, the intent of the empirical analyses is to examine whether the patterns of skew in the item responses correspond to similar skew in the IRT-based scores, as well as to impacts on growth estimates akin to those from the Monte Carlo results.
Measures and Sample
The survey used by the districts in our sample included 18 items (4 items for growth mindset [α = .70], 4 for self-efficacy [α = .86], 7 for self-management [α = .85], 6 for social awareness [α = .81]). Students rated each item on a 5-point Likert scale. Examples included, for growth mindset, “I can change my intelligence with hard work” and for social awareness, “How well do you get along with students who are different from you?” Students in the sample were in grades 4–12 and took the survey each year from 2015 to 2018. Thus, we had four years of longitudinal data. To examine the issue of how ceiling effects on surveys might impact growth, we identified the constructs and cohorts (e.g., students who were in fourth grade during 2015 vs. eighth grade) that had the most and least skew in their item responses at Time 1. Those constructs ended up being growth mindset and social awareness for students beginning in fifth grade. We used an intact four-year cohort of students beginning in fifth grade (N = 2774 students).
Analytic Strategy
As in the simulation studies, we produced three sets of scores: sum scores, unidimensional IRT with MLE scoring (calibrated at Time 1), and longitudinal MIRT with EAP and PV scoring. We examined these scores to see how skewed they were relative to each other, as well as to the scores from our various simulation conditions. Finally, we fit growth models and compared parameter estimates, in particular latent slope means and variances.
Results
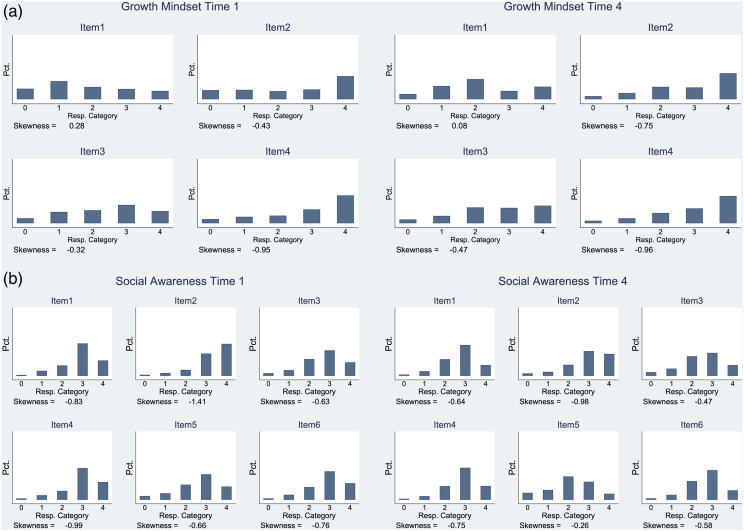
Figure 5 shows distributions of item responses in growth mindset and social awareness by timepoint, and Figure 6 shows the different scores for the two constructs. 8 Though not universally true, growth mindset items tended to show less skew at Time 1 and more at Time 4. By contrast, social awareness often showed more skew at Time 1, but less at Time 4. Per Figure 6, differences in means of the score distributions by timepoint did not differ noticeably within-construct by scoring approach, with the exception of a noticeable difference in the means by timepoint for growth mindset sum scores compared to MLE scores. Notably, the skew in the scores was generally much less pronounced in the empirical analyses than in the most extreme simulation conditions, and in some cases even compared to the easy item simulation condition. This finding does not necessarily mean that the Monte Carlo conditions are too extreme; rather, that the particular sample and survey scales we have did not produce results as extreme as they could have been (DeWalt et al., 2013).
Figure 5.
Item response distributions from the empirical data for (a) growth mindset and (b) social awareness.
Figure 6.
Score distributions for Times 1 and 4 from the empirical data.
Finally, Table 1 presents growth model parameter estimates by calibration/scoring approach and construct. While less so than in the simulations, slope estimates were somewhat sensitive to scoring approach. For example, growth mindset items showed more cases of using the top two response categories at Time 4 than Time 1. Thus, perhaps unsurprisingly, the MLE scores show an estimated latent growth mean of .15 (possibly resulting due to more Time 4 scores being replaced with an arbitrary maximum than Time 1), while sum scores showed a mean slope estimate of .11 (potentially because ceiling effects at later timepoints muted growth). As in the simulation studies, the MIRT models using Bayesian scoring approaches produced slope estimates in between those using sum scores and unidimensional IRT with MLE. In short, though more muted, these patterns are similar to Monte Carlo results. Specifically, MLE scores most likely inflated slopes because extreme scores are replaced with arbitrarily large values, and sum scores likely understated slope estimates due to the ceiling effects.
Table 1.
Parameter Estimates From Empirical Analyses for Growth Mindset and Social Awareness Across Scoring Approaches.
| Construct | Parameter | Sum scores | Unidim. MLE scores | MIRT EAP scores | MIRT PV scores | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Est | S.E. | p-value | Est | S.E. | p-value | Est | S.E. | p-value | Est | S.E. | p-value | ||
| Growth | Covariance | −0.01 | 0.01 | 0.33 | 0.02 | 0.02 | 0.53 | 0.00 | 0.01 | 0.43 | 0.00 | 0.02 | 0.92 |
| Mindset | Intercept mean | −0.01 | 0.02 | 0.75 | 0.11 | 0.03 | 0.00 | −0.01 | 0.02 | 0.75 | −0.02 | 0.03 | 0.53 |
| Slope mean | 0.11 | 0.01 | 0.00 | 0.15 | 0.01 | 0.00 | 0.13 | 0.01 | 0.00 | 0.12 | 0.01 | 0.00 | |
| Intercept variance | 0.37 | 0.03 | 0.00 | 0.85 | 0.06 | 0.00 | 0.57 | 0.02 | 0.00 | 0.55 | 0.08 | 0.00 | |
| Slope variance | 0.02 | 0.01 | 0.00 | 0.07 | 0.01 | 0.00 | 0.04 | 0.00 | 0.00 | 0.05 | 0.01 | 0.00 | |
| Social | Covariance | −0.07 | 0.01 | 0.00 | −0.13 | 0.02 | 0.00 | −0.09 | 0.01 | 0.00 | −0.10 | 0.01 | 0.00 |
| Awareness | Intercept mean | 0.03 | 0.02 | 0.12 | 0.09 | 0.02 | 0.00 | 0.03 | 0.02 | 0.11 | 0.03 | 0.02 | 0.15 |
| Slope mean | −0.13 | 0.01 | 0.00 | −0.15 | 0.01 | 0.00 | −0.14 | 0.01 | 0.00 | −0.14 | 0.01 | 0.00 | |
| Intercept variance | 0.49 | 0.03 | 0.00 | 0.79 | 0.04 | 0.00 | 0.63 | 0.02 | 0.00 | 0.63 | 0.08 | 0.00 | |
| Slope variance | 0.05 | 0.01 | 0.00 | 0.07 | 0.01 | 0.00 | 0.05 | 0.00 | 0.00 | 0.06 | 0.01 | 0.00 | |
Discussion
Scores from survey scales are often used as the basis for understanding how individuals develop psychologically and socio-emotionally. Yet, the impact of item ceiling effects on growth estimates is understudied. Our results provide several useful takeaways for researchers who use survey data in longitudinal contexts. First, we show that, when using traditional approaches to scoring surveys like sum scores and unidimensional IRT models, item ceiling effects can bias growth estimates, in some cases hugely. For example, sum scores and unidimensional IRT scores using EAP scoring led to downwardly biased estimates of growth. Thus, given how many studies use sum scores or unidimensional IRT models (Bauer & Curran, 2016; Flake et al., 2017; Kuhfeld & Soland, 2022), there is a real chance that some studies in psychology and education drastically misrepresent the degree of growth occurring. Second and related, we show that lengthening the survey without adding more difficult items does relatively little to ameliorate the impact of item ceiling effects. Lengthening the survey had marginal benefits when using sum scores, even when increasing the survey length to 50 items (10 times the typical survey length). For example, when using sum scores, bias in growth estimates was still large.
Third, while using a longitudinal MIRT model with PV scoring does not totally alleviate bias introduced into growth estimates due to ceiling effects, it comes close. For example, the slope parameter estimates showed little bias even in extreme cases, such as when all items were very easy and respondents grew at a rate of .5 SDs per year. Thus, while the MIRT PV scores were not immune to item ceiling effects, they were much less affected comparatively.
Limitations
Like any study, ours has several limitations. For one, we could not include an exhaustive set of simulation conditions. As an example, we only used a single sample size that was large enough to estimate item parameters effectively, but small enough to be relatively representative of a “typical” study in psychology or education. We addressed this issue in part by conducting replications with a subset of conditions and a sample size of 5000. Nonetheless, future studies could examine the sample size issue in greater detail. Further, we do not directly address the case of quadratic growth, nor of results using items that are not akin to a Likert format. To partially remedy these issues, we include sensitivity analyses that use a generating latent growth curve model with a quadratic term (SOM Section C), and one that uses binary item responses (SOM Section D). Despite these supplemental analyses, our results may not hold when different item formats are used, or when differently parameterized growth models are employed.
Additionally, while we saw some evidence of ceiling effects in the item responses provided in our own empirical analyses, they were not as extreme as documented in other empirical studies (DeWalt et al., 2013). Thus, while our empirical example does provide some evidence that item ceiling effects can impact results using real data and in ways that parallel Monte Carlo Results, it does not help illustrate just how impactful those ceiling effects might be. Future research could replicate our findings with empirical data with evidence of even more skew in the item responses patterns.
Conclusion
A frequently overlooked problem with many surveys is that the items are all “easy”—meaning that individuals tend to use only the top one or two response categories. In this study, we show that such item ceiling effects can bias estimates of growth. The issue is especially pronounced when using unidimensional IRT models and sum scores. Fortunately, bias introduced into growth estimates by item ceiling effects can be reduced substantially by using a longitudinal IRT model with PV scoring, especially in conjunction with a longer survey.
Supplemental Material
Supplemental Material for How Scoring Approaches Impact Estimates of Growth in the Presence of Survey Item Ceiling Effects by Kelly D. Edwards, and James Soland in Applied Psychological Measurement
Acknowledgments
We would like to thank Megan Kuhfeld for her feedback on this draft.
Notes
Note that difficulty in IRT is relative to an individual person. Thus, a difficult item for a given person is an item that the individual in question is not likely to endorse.
Alternatively, one could use all timepoints at once and simply ignore the longitudinal nature of the data.
While the easy condition was based on DeWalt et al. (2013), the mixed and very easy conditions were created by manipulating the original thresholds to produce the proportions described above.
As noted below, MLE was only used for unidimensional models. Therefore, the mean/SD are based on the calibration sample.
MLE is not recommended for use with multidimensional models because it does not use information from the population distribution, which can cause convergence issues in score estimation, and undefined standard errors (Houts & Cai, 2020).
In the case of PV scoring, it is not strictly accurate to refer to PVs as estimated scores. They are draws from the posterior distribution.
Results differed little dependent on the random effects variance-covariance matrix conditions for the population growth model. Therefore, results aggregated across those conditions are reported. Also, parameter recovery was near perfect when using true scores.
MIRT PV scores are not shown because results are very similar to the EAP scores.
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) received no financial support for the research, authorship, and/or publication of this article.
Supplemental Material: Supplemental material for this article is available online
ORCID iD
James Soland https://orcid.org/0000-0001-8895-2871
References
- Bauer D. J., Curran P. J. (2016). The discrepancy between measurement and modeling in longitudinal data analysis. In Harring J. R., Stapleton L. M., Beretvas S. N. (Eds.), Advances in multilevel modeling for educational research (pp. 3–38). Information Age Publishing. [Google Scholar]
- Bock R. D., Mislevy R. J. (1982). Adaptive EAP estimation of ability in a microcomputer environment. Applied Psychological Measurement, 6(4), 431–444. 10.1177/014662168200600405 [DOI] [Google Scholar]
- Bolt D. M., Newton J. R. (2011). Multiscale measurement of extreme response style. Educational and Psychological Measurement, 71(5), 814–833. 10.1177/0013164410388411 [DOI] [Google Scholar]
- Cai L. (2017). FlexMIRT R version 3.51: Flexible multilevel multidimensional item analysis and test scoring [Computer software]. Vector Psychometric Group. [Google Scholar]
- Caprara G. V., Fida R., Vecchione M., Del Bove G., Vecchio G. M., Barbaranelli C., Bandura A. (2008). Longitudinal analysis of the role of perceived self-efficacy for self-regulated learning in academic continuance and achievement. Journal of Educational Psychology, 100(3), 525–534. 10.1037/0022-0663.100.3.525 [DOI] [Google Scholar]
- Chassin L., Sher K. J., Hussong A., Curran P. (2013). The developmental psychopathology of alcohol use and alcohol disorders: Research achievements and future directions. Development and Psychopathology, 25(4 Pt 2), 1567–1584. 10.1017/S0954579413000771 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeWalt D. A., Thissen D., Stucky B. D., Langer M. M., Morgan DeWitt E., Irwin D. E., Lai J. S., Yeatts K. B., Gross H. E., Taylor O., Varni J. W., Varni J. W. (2013). PROMIS pediatric peer relationships scale: Development of a peer relationships item bank as part of social health measurement. Health Psychology: Official Journal of the Division of Health Psychology, American Psychological Association, 32(10), 1093–1103. 10.1037/a0032670 [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Urso E. D., De Roover K., Vermunt J. K., Tijmstra J. (2022). Scale length does matter: Recommendations for measurement invariance testing with categorical factor analysis and item response theory approaches. Behavior Research Methods, 54(5), 2114–2145. 10.3758/s13428-021-01690-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng Y., Hancock G. R., Harring J. R. (2019). Latent growth models with floors, ceilings, and random knots. Multivariate Behavioral Research, 54(5), 751–770. 10.1080/00273171.2019.1580556 [DOI] [PubMed] [Google Scholar]
- Flake J. K., Pek J., Hehman E. (2017). Construct validation in social and personality research: Current practice and recommendations. Social Psychological and Personality Science, 8(4), 370–378. 10.1177/1948550617693063 [DOI] [Google Scholar]
- Fricke H., Loeb S., Meyer R. H., Rice A. B., Pier L., Hough H. (2021). Stability of school contributions to student social-emotional learning gains. American Journal of Education, 128(1), 95–145. 10.1086/716550 [DOI] [Google Scholar]
- Gehlbach H., Hough H. J. (2018). Measuring social emotional learning through student surveys in the CORE districts: A pragmatic approach to validity and reliability: Policy Analysis for California Education. [Google Scholar]
- Gorter R., Fox J. P., Riet G. T., Heymans M. W., Twisk J. W. R. (2020). Latent growth modeling of IRT versus CTT measured longitudinal latent variables. Statistical Methods in Medical Research, 29(4), 962–986. 10.1177/0962280219856375 [DOI] [PubMed] [Google Scholar]
- Houts C. R., Cai L. (2020). FlexMIRT user’s manual version 3.6: Flexible multilevel multidimensional item analysis and test scoring. Vector Psychometric Group. [Google Scholar]
- Jackson D. L., Gillaspy J. A., Jr., Purc-Stephenson R. (2009). Reporting practices in confirmatory factor analysis: An overview and some recommendations. Psychological Methods, 14(1), 6–23. 10.1037/a0014694 [DOI] [PubMed] [Google Scholar]
- Kuhfeld M., Soland J. (2022). Avoiding bias from sum scores in growth estimates: An examination of IRT-based approaches to scoring longitudinal survey responses. Psychological Methods, 27(2), 234–260. 10.1037/met0000367 [DOI] [PubMed] [Google Scholar]
- Masino C., Lam T. C. (2014). Choice of rating scale labels: Implication for minimizing patient satisfaction response ceiling effect in telemedicine surveys. Telemedicine Journal and e-Health: The Official Journal of the American Telemedicine Association, 20(12), 1150–1155. 10.1089/tmj.2013.0350 [DOI] [PubMed] [Google Scholar]
- McArdle J. J., Epstein D. (1987). Latent growth curves within developmental structural equation models. Child Development, 58(1), 110–133. 10.2307/1130295 [DOI] [PubMed] [Google Scholar]
- McNeish D. (2022). Limitations of the sum-and-alpha approach to measurement in behavioral research. Policy Insights from the Behavioral and Brain Sciences, 9(2), 196–203. 10.1177/23727322221117144 [DOI] [Google Scholar]
- McNeish D., Wolf M. G. (2020). Thinking twice about sum scores. Behavior Research Methods, 52(6), 2287–2305. 10.3758/s13428-020-01398-0 [DOI] [PubMed] [Google Scholar]
- Mislevy R. J. (1991). Randomization-based inference about latent variables from complex samples. Psychometrika, 56(2), 177–196. 10.1007/bf02294457 [DOI] [Google Scholar]
- Mislevy R. J., Sheehan K. M. (1987). Marginal estimation procedures. In Beaton A. E. (Ed.), The NAEP 1983/84 technical report (NAEP Report 15-TR-20 (pp. 293–360): Educational Testing Service. [Google Scholar]
- Sahin A., Anil D. (2017). The effects of test length and sample size on item parameters in item response theory. Educational Sciences: Theory and Practice, 17(1), 321–335. [Google Scholar]
- Samejima F. (1969). Estimation of latent ability using a response pattern of graded scores. Psychometrika, 34(S1), 100–114. 10.1007/bf03372160 [DOI] [Google Scholar]
- Soland J., Kuhfeld M. (2021). Do response styles affect estimates of growth on social-emotional constructs? Evidence from four years of longitudinal survey scores. Multivariate Behavioral Research, 56(6), 853–873. 10.1080/00273171.2020.1778440 [DOI] [PubMed] [Google Scholar]
- Soland J., Kuhfeld M., Edwards K. (2022). How survey scoring decisions can influence your study’s results: A trip through the IRT looking glass. In Psychological methods. Online first publication. 10.1037/met0000506 [DOI] [PubMed] [Google Scholar]
- Thissen D., Orlando M. (2001). Item response theory for items scored in two categories. In Thissen D., Wainer H. (Eds.), Test scoring (pp. 85–152). Routledge. [Google Scholar]
- Thomas N. (2002). The role of secondary covariates when estimating latent trait population distributions. Psychometrika, 67(1), 33–48. 10.1007/bf02294708 [DOI] [Google Scholar]
- Von Davier M., Gonzalez E., Mislevy R. (2009). What are plausible values and why are they useful? In IERI monograph series. Issues and methodologies in large scale assessments; Vol. 2. [Google Scholar]
- Von Davier M., Sinharay S., Oranje A., Beaton A. (2006). Statistical procedures used in the national assessment of educational progress (NAEP): Recent developments and future directions. In Rao C. R., Sinharay S. (Eds.), Handbook of statistics psychometrics (Vol. 26, pp. 1039–1056). Elsevier. [Google Scholar]
- Wang L., Zhang Z., McArdle J. J., Salthouse T. A. (2008). Investigating ceiling effects in longitudinal data analysis. Multivariate Behavioral Research, 43(3), 476–496. 10.1080/00273170802285941 [DOI] [PMC free article] [PubMed] [Google Scholar]
- West M. R., Pier L., Fricke H., Hough H., Loeb S., Meyer R. H., Rice A. B. (2020). Trends in student social-emotional learning: Evidence from the first large-scale panel student survey. Educational Evaluation and Policy Analysis, 42(2), 279–303. 10.3102/0162373720912236 [DOI] [Google Scholar]
- Yeager D. S., Walton G. M. (2011). Social-psychological interventions in education: They’re not magic. Review of Educational Research, 81(2), 267–301. 10.3102/0034654311405999 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental Material for How Scoring Approaches Impact Estimates of Growth in the Presence of Survey Item Ceiling Effects by Kelly D. Edwards, and James Soland in Applied Psychological Measurement