Keywords: decoding accuracy, ethyl butyrate, firing rate model, retronasal olfaction, synaptic inhibition
Abstract
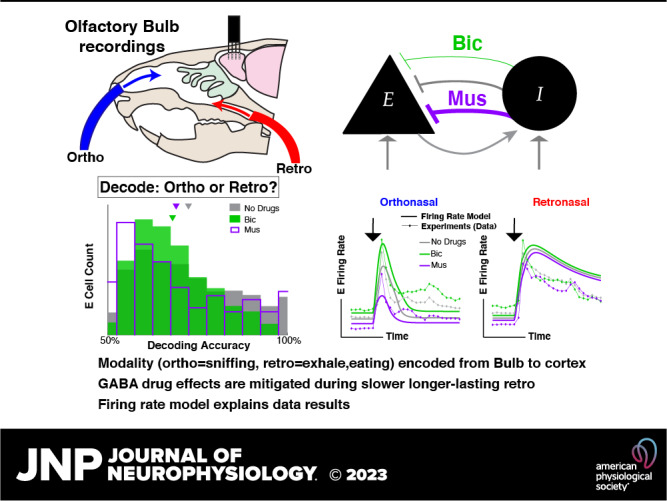
Odor perception is the impetus for important animal behaviors with two predominate modes of processing: odors pass through the front of the nose (orthonasal) while inhaling and sniffing, or through the rear (retronasal) during exhalation and while eating. Despite the importance of olfaction for an animal’s well-being and that ortho and retro naturally occur, it is unknown how the modality (ortho vs. retro) is even transmitted to cortical brain regions, which could significantly affect how odors are processed and perceived. Using multielectrode array recordings in tracheotomized anesthetized rats, which decouples ortho-retro modality from breathing, we show that mitral cells in rat olfactory bulb can reliably and directly transmit orthonasal versus retronasal modality with ethyl butyrate, a common food odor. Drug manipulations affecting synaptic inhibition via GABAA lead to worse decoding of ortho versus retro, independent of whether overall inhibition increases or decreases, suggesting that the olfactory bulb circuit may naturally favor encoding this important aspect of odors. Detailed data analysis paired with a firing rate model that captures population trends in spiking statistics shows how this circuit can encode odor modality. We have not only demonstrated that ortho/retro information is encoded to downstream brain regions but also used modeling to demonstrate a plausible mechanism for this encoding; due to synaptic adaptation, it is the slower time course of the retronasal stimulation that causes retronasal responses to be stronger and less sensitive to inhibitory drug manipulations than orthonasal responses.
NEW & NOTEWORTHY Whether ortho (sniffing odors) versus retro (exhalation and eating) is encoded from the olfactory bulb to other brain areas is not completely known. Using multielectrode array recordings in anesthetized rats, we show that the olfactory bulb transmits this information downstream via spikes. Altering inhibition degrades ortho/retro information on average. We use theory and computation to explain our results, which should have implications on cortical processing considering that only food odors occur retronasally.
INTRODUCTION
Olfaction is driven by odor molecules entering the nasal cavity, inducing a cascade of action potentials in the nervous system that transmit and process odor information. There are two routes by which odor molecules can enter the nasal cavity: through the nostrils during inhalation and sniffing (ortho) or from the throat during exhalation and while eating (retro). Orthonasal stimulation is by far the most commonly studied modality, despite the fact that retronasal delivery naturally occurs during eating. Prior imaging studies have shown differences in the activation of the regions of the nasal epithelium with ortho and retro stimulation (1–3). Moreover, humans are able to discriminate whether food odors are delivered orthonasally or retronasally without being told which modality and without active sniffing (4). Imaging studies have shown that at least with food odors, ortho/retro are two distinct modalities, rather than two different routes to the same modality, independent of odor intensity (5). Importantly, there is evidence that cortical processing depends on whether odors are delivered ortho- versus retronasally (6, 7), and humans report perceiving the same smells differently depending on ortho or retro modality (8, 9). Together these studies convincingly show that ortho versus retro information is transmitted to cortical brain regions, but the details of how this occurs and the core network mechanisms that facilitate this encoding are largely unknown.
There are several ways that ortho/retro information could be made available to higher brain regions. As ortho and retro stimuli are naturally dictated by inhalation and exhalation, the motor signals that control breathing could provide efferent copies of this information to various brain regions. Moreover, even without such motor signals, the mechanical stimulation of neurons in the nasal cavity by breath-driven airflow generates strong breath-related signals throughout the olfactory system (10, 11). However, previous experiments have delivered stimuli independently of the breath cycle and still found significant differences in ortho versus retro response in cortex (9, 12) and olfactory receptor neuron (ORN) input to olfactory bulb (OB) (2). Thus, there are important breath-independent aspects of ortho/retro coding. Although these different mechanisms for odor modality encoding are all plausible, here we designed our experiments to study “bottom up” breath-independent mechanisms. We specifically performed a double tracheotomy, which redirected the rats’ breath to bypass the nasal cavity entirely and allowed us to deliver ortho and retro stimuli at times that were independent of inhale and exhale times. So, the mechanisms of ortho and retro coding that we study here are independent of any motor or mechanosensory signals caused by breathing.
Before odor information reaches the brain, it is processed in the olfactory bulb (OB) and relayed to higher brain regions via excitatory mitral cells (MCs) (and tufted cells). Thus, the OB is critical for determining whether ortho versus retronasal odors are encoded before being conveyed to the brain for processing and perception. More broadly, OB activity is tied to odor perception (13). Although the role of inhibitory cells in influencing OB processing of ortho versus retro odors is unknown, inhibition is known to play a key role in many other aspects of OB processing. OB inhibition is known to alter activity patterns that represent odors (14), granule cells that provide inhibition reflect changes in odor concentration (15), and OB inhibition levels alter odor discrimination dynamics (16). These facts motivated us to both decrease and increase the levels of GABAA synaptic inhibition via drug manipulations in our experiments, which consist of in vivo recordings of MCs in the OB of double tracheotomized rats.
We show that the mode of olfaction (ortho vs. retro) is indeed transmitted to cortical brain regions with a common food odor, ethyl butyrate (EB). We find that encoding is generally good and well above chance level for the intact circuit and even with altered levels of inhibition. Thus, downstream brain regions may readily have access to ortho versus retronasal odor modality encoded via firing rate from the OB. Importantly, the altered circuits with both increases [via muscimol (Mus) application, a GABAA agonist] and decreases in inhibition [via bicuculline (Bic), a GABAA antagonist] result in worse individual encoding on average. This suggests that the intact OB circuit may be advantageous for encoding ortho versus retro modality.
Our data enable investigation of the OB circuit mechanisms that promote this encoding with a computational model. We show how a simple excitatory-inhibitory (E-I) reciprocally coupled model captures the modality-dependent differences in the population firing rate. Our data show that the GABAA (ant-)agonists do not significantly alter the odor-evoked population firing rate with slower longer-lasting retronasal stimulation, in contrast to ortho stimulation. Our model captures these aspects of our data, exploiting the temporal differences, i.e., the slow retro stimulation leads to short-term synaptic depression of the excitatory synapse to diminish the effects of the inhibition. Furthermore, we model trial-to-trial spike rate variability to be largely consistent with our data, so that the model can encode ortho/retro-like stimuli. We find that average encoding is degraded when inhibition is either increased or decreased, as observed in our data. Given the commonality of reciprocally coupled excitatory-inhibitory circuits, these results may apply outside of the OB, specifically to where stimuli have temporal differences.
MATERIALS AND METHODS
Ethics Statement
All procedures were carried out in accordance with the recommendations in the Guide for the Care and Use of Laboratory Animals of the National Institutes of Health and approved by University of Arkansas Institutional Animal Care and Use Committee (Protocol No. 14049). Isoflurane and urethane anesthesia were used and urethane overdose was used for euthanasia.
Electrophysiological Recordings
Data were collected from eight adult male rats (240–427 g; Rattus norvegicus, Sprague-Dawley outbred, Harlan Laboratories, TX) housed in an environment of controlled humidity (60%) and temperature (23°C) with 12-h light-dark cycles. The experiments were performed in the light phase.
Surgical preparations.
Anesthesia was induced with isoflurane inhalation and maintained with urethane [1.5 g/kg body wt (bw) dissolved in saline, intraperitoneal injection (ip)]. Dexamethasone (2 mg/kg bw, ip) and atropine sulfate (0.4 mg/kg bw, ip) were administered before performing surgical procedures. Throughout surgery and electrophysiological recordings, core body temperature was maintained at 37°C with a thermostatically controlled heating pad. To isolate the effects of olfactory stimulation from breath-related effects, we performed a double tracheotomy surgery as described previously (2). A Teflon tube (OD 2.1 mm, upper tracheotomy tube) was inserted 10 mm into the nasopharynx through the rostral end of the tracheal cut. Another Teflon tube (OD 2.3 mm, lower tracheotomy tube) was inserted into the caudal end of the tracheal cut to allow breathing, with the breath bypassing the nasal cavity. Both tubes were fixed and sealed to the tissues using surgical thread. Local anesthetic (2% Lidocaine) was applied at all pressure points and incisions. Subsequently, a craniotomy was performed on the dorsal surface of the skull over the right olfactory bulb (2 mm × 2 mm, centered 8.5 mm rostral to bregma and 1.5 mm lateral from midline).
Olfactory stimulation.
A Teflon tube was inserted into the right nostril to deliver orthonasal stimuli, and the left nostril was sealed by suturing. The upper tracheotomy tube inserted into the nasopharynx was used to deliver odor stimuli retronasally. Odorized air was delivered for 1 s in duration at 1-min intervals, with a flow rate of 250 mL/min and 1% of saturated vapor. Two odors were used: ethyl butyrate (EB, a food odor) and 1-Hexanol (Hex, a nonfood odor). Here, we limited our analysis to EB trials because food odors are perceived ortho- and retronasally (9); nonfood odors do not naturally occur retronasally.
Electrophysiology.
A 32-channel microelectrode array (MEA, A4x2tet, NeuroNexus, MI) was inserted 400-μm deep from dorsal surface of OB targeting tufted and mitral cell populations. The MEA probe consisted of four shanks (diameter: 15 μm, intershank spacing: 200 μm), each with eight iridium recording sites arranged in two tetrode groups near the shank tip (intertetrode spacing: 150 μm, within tetrode spacing 25 μm). Voltage was measured with respect to an AgCl ground pellet placed in the saline-soaked gel foams covering the exposed brain surface around the inserted MEAs. Voltages were digitized with 30 kHz sample rate (Cereplex + Cerebus, Blackrock Microsystems, UT). Recordings were band-pass filtered between 300 and 3,000 Hz and semiautomatic spike sorting was performed using Klustakwik software, which is well suited to the type of electrode arrays used here (17).
Pharmacology.
We topically applied GABA antagonists (bicuculline 20 μM) or agonists (muscimol 20 μM) dissolved in artificial cerebrospinal fluid (ACSF). Gel foam pieces soaked in the ACSF + drug solutions were placed on the surface of OB surrounding the recording electrodes. Note that the concentration of (ant-)agonists can vary over orders of magnitude; some laboratories use 10 μM (18, 19) and others use up to 10–104 higher concentration levels (20, 21). The gel foams were placed 10 min before beginning a recording.
Data Analysis
Data were collected in vivo from the mitral cell (MC) layer in the olfactory bulb (OB) of multiple anesthetized rats using a multielectrode array recording. The data consisted of spike recordings of multiple MC spike responses to EB and Hex presented by the two routes of stimulation, orthonasally and retronasally, for a total of 20 trials, 10 for each ortho and retro, with the order alternating (10 ortho before 10 retro, then 10 retro before 10 ortho trials). The spike counts were calculated using 100 ms overlapping time windows. Three separate drug preparations were used to analyze inhibitory effects on MC spiking responses: no drug (control), Bicuculline (GABAA antagonist, i.e., decreasing inhibition), and Muscimol (GABAA agonist, i.e., increasing inhibition). Data were obtained from eight viable rats in total. After spike sorting, we identified and eliminated units (cells) that had firing rates below 0.008 Hz or more than 49 Hz, calculated over the entire recording duration. We took this conservative approach to eliminate potential artifacts yielding units that had unrealistically high or low firing; see Table 2 for the reported number of total rats and individual cells for each drug preparation. Note that some cells around the odor onset (t = 0) will have much larger (> 49 Hz) or smaller firing rates than our criteria to eliminate units, but the entire recording duration is much longer with approximately a minute between trials.
Defining single-cell decoding.
We used a form of linear discriminant analysis (LDA) for decoding accuracy. Decoding accuracy is defined as the fraction of trials correctly classified by a threshold that maximizes decoding accuracy. Letting sk(t) be the spike train of the kth trial (k = 1, 2, …, N) that at each time t is either = 0 (no spike) or = δ(t − tj,k), where tj,k denotes the jth spike on the kth trial. The entries of the spiking rate are:
| (1) |
where t = 0 is the time the odor is presented. There are N = 20 trials total (10 ortho, 10 retro) for each individual cell. We consider N different threshold values θk:
and use both classification schemes (decode stimulus as ortho if xk < θ and retro if xk > θ, or as ortho if xk > θ). From this comprehensive list, we select an optimal threshold θ* and classification scheme that results in the best decoding accuracy. Here ε ≈ 10−16 is machine precision and is there to ensure that each trial is categorized as ortho or retro. Since decoding accuracy is the percent of correctly classified trials (ortho or retro) and N = 20, it varies between 0.5 (chance) and up to 1 in increments of 0.05 for each cell.
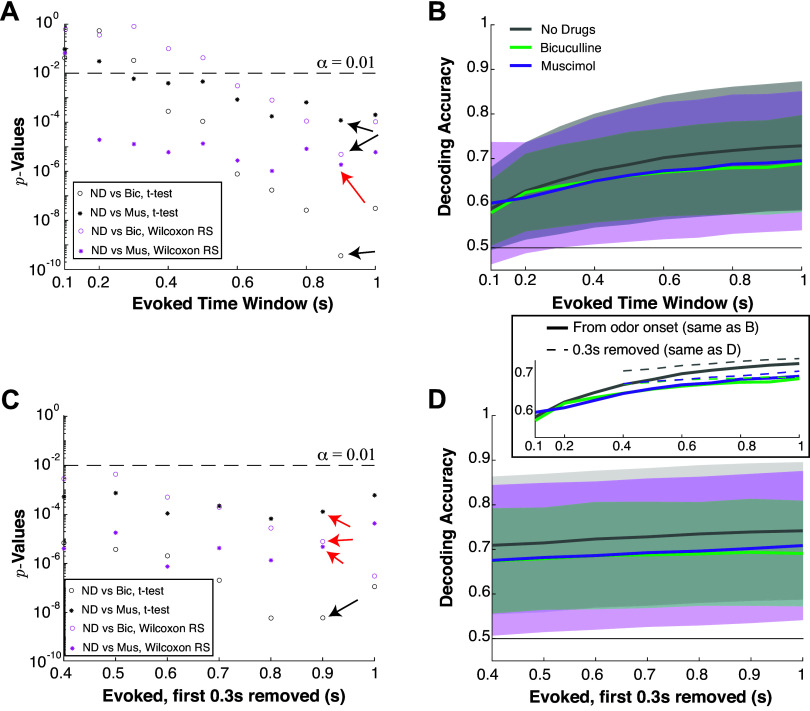
To systematically compare differences in decoding accuracy, we select a fixed time window for all drug preparations and modalities based on two statistical tests (two-sample t test assuming unequal variances and Wilcoxon rank-sum test) and their P values. We evaluated decoding accuracy from Tev = 100 ms to Tev = 1 s in 100 ms increments in the evoked state for each drug preparation. We analyzed differences in mean between no drug preparation and Bicuculline, as well as no drug preparation and Muscimol. This resulted in four different P values for each time window; we found that Tev = 900 ms had the most significant P values for both combinations of no drug/Bicuculline and no drug/Muscimol, see Fig. A2, A and C. Figure A2, B and D, shows the population decoding accuracies (mean across the population and one standard deviation in shaded region).
Statistical significance.
We use three tests to assess whether a given effect is statistical significant: 1) two-sample t test with unequal variance, 2) Wilcoxon rank-sum test, and 3) one-way ANOVA. Each of these tests is used to rule out the null hypothesis that the population means are the same in two different categories (22). Each test is different and has various underlying assumptions: 1) normal samples, 2) nonparametric test assuming independent groups and equal variance, and 3) including sample variance to assess differences in means assuming equal variance and normally distributed residuals. We consider three tests to provide a more complete picture of the results and to demonstrate robustness, or lack thereof, for a given effect.
In addition to the P values that indicate the probability of the null hypothesis holding (no effect, same population means), we also report the effect sizes. We use the conventions outlined in Cohen (22) and Tomczak and Tomczak (23) that provide formulas for effect sizes, and a qualitative “rule of thumb” for when effect sizes are small, medium, or large. For two groups of length n1 and n2, respectively, the effect sizes we use:
| (2) |
| (3) |
| (4) |
| (5) |
The variables μj and denote the sample mean and variances of the jth group. Effect sizes for t test and Wilcoxon rank-sum test with values: (0,0.2] are considered small, (0.2,0.5] are medium, (0.5,0.8] and above are large (22, 23). Effect sizes for one-way ANOVA with values (0,0.01] are considered small, (0.01,0.06] are medium, (0.06,0.14], and above are large (22).
Population decoding.
The two methods are applied to each population of simultaneously recorded MCs.
PCA + LDA: For each recording, principal component analysis (PCA) was applied to the concatenated matrix X of size 20 × M, where M is the number of MCs (Fig. 6A), rows 1–10 correspond to the spiking rate with ortho and rows 11–20 correspond to retro. We only use the first two principal components and apply linear discriminate analysis (LDA) to find a line in the two-dimensional plane that maximizes classification accuracy (24). We used built-in MATLAB routines pca, fitcdiscr, predict (see GitHub for code).
Figure 6.
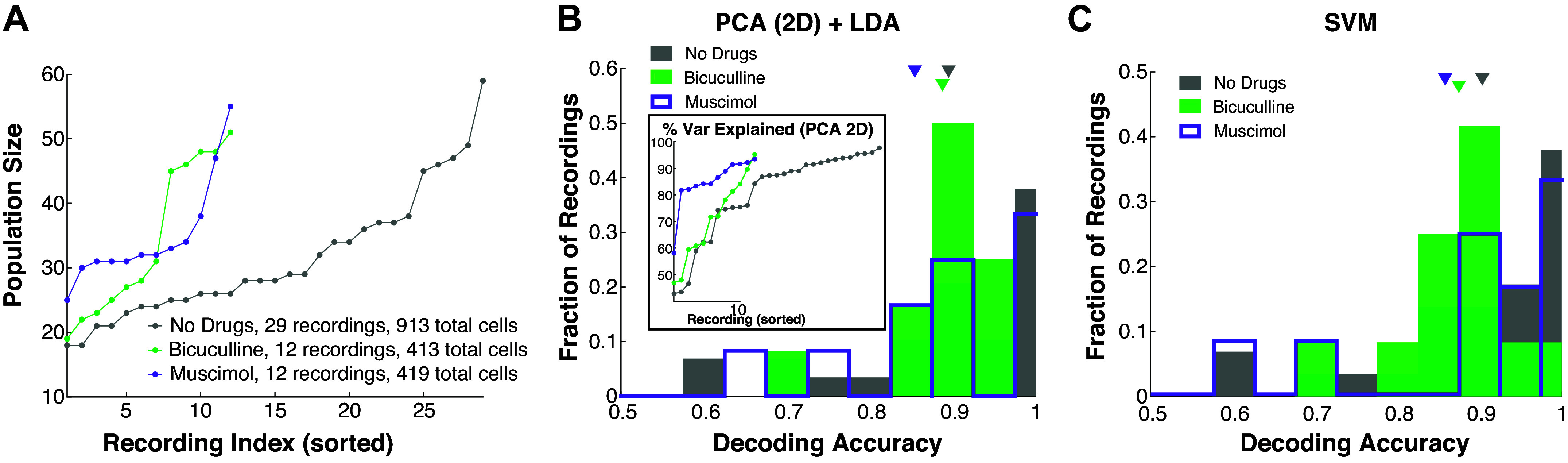
Population decoding of ortho versus retro is reliable and robust to altered inhibition. A: each drug preparation has a different number of recordings and each recording has a different number of simultaneously recorded MCs. Showing recording index and MC population size, sorted by population size. B: decoding accuracies (one for each simultaneous recording) for all drug preparations using a 2-D PCA dimension reduction following by LDA. Inset shows percent variance explained by PCA versus recording index (sorted by percent variance explained). C: decoding accuracies using full dimensional support vector machine (SVM) classification. Average decoding accuracies by both methods (B and C) are statistically indistinguishable (minimum P value for all relationships and all three statistical tests is P ≥ 0.32 for PCA+LDA, P ≥ 0.13 for SVM). MC, mitral cell; LDA, linear discriminant analysis.
SVM: We use support vector machine with supervised “learning” to classify data into ortho or retro. We use a nonlinear classification method with Gaussian kernels, and Bayesian optimization to find the best kernel scale and box constraints for the SVM (we ensured that for all recordings and drug preparations, the objective was minimized within the allowable function evaluations). After the SVM is fit to the data, the decoding accuracy is the correct classification rate obtained from the MATLAB function kfoldLoss using 10-fold cross-validation. We used built-in MATLAB routines (see GitHub link for code).
Firing Rate Model
We use a space-clamped Wilson-Cowan rate model of coupled E-I cells: E (MC, excitatory) and I (inhibitory from PGC, GC, etc.). The models of the respective cell firing rate, Aj(t) j ∈ (M, P), are represented by the following ordinary differential equations:
| (6) |
| (7) |
where the synaptic term, Sj j ∈ {E, I}, is defined by synapses with rise and decay time scales (same τrise, τdecay for E/I) as follows:
| (8) |
| (9) |
In Eqs. 6 and 7, Ij(t) is the sum of external currents (e.g., stimulus input and other currents) that varies over time to account for stimulus input, worn,j are the coupling strengths of olfactory receptor neuron (ORN) input to j, wjk are the coupling strengths from cell k to j, and the transfer function F is a threshold linear function:
| (10) |
Without synaptic depression, we fix wIE = 1. With synaptic depression, wIE(t) is governed by:
| (11) |
| (12) |
with initial value wIE(0) set to its steady-state value at t = −0.5 s in Eqs. 6–12.
The trial-to-trial variability of spiking rate is modeled as a negative binomial random variable:
| (13) |
Given output from the Wilson-Cowan model AE(t), we set:
| (14) |
by manually determining the ρ parameter in the negative binomial distribution (see Table 1) for each drug preparation, and setting the parameter r = μNBρ/(1 − ρ).
Table 1.
| Parameter | Value |
|---|---|
| τE | 10 ms |
| τI | 5.5 ms |
| τdecay | 10 ms |
| τrise | 2 ms |
| τw | 100 ms |
| worn , E | 1 |
| worn , I | 1.1875 (ortho), 0.3 (retro) |
| Drug Preparation |
|||
|---|---|---|---|
| No Drug | Bic | Mus | |
| wEI | 0.2 | 0.15 | 0.25 |
| ρ for ortho | 0.32 | 0.32 | 0.32 |
| ρ for retro | 0.32 | 0.53 | 0.052 |
Last 2 rows describe the parameter ρ in simulated trial variability using negative binomial distribution. Bic, bicuculline; Mus, muscimol.
RESULTS
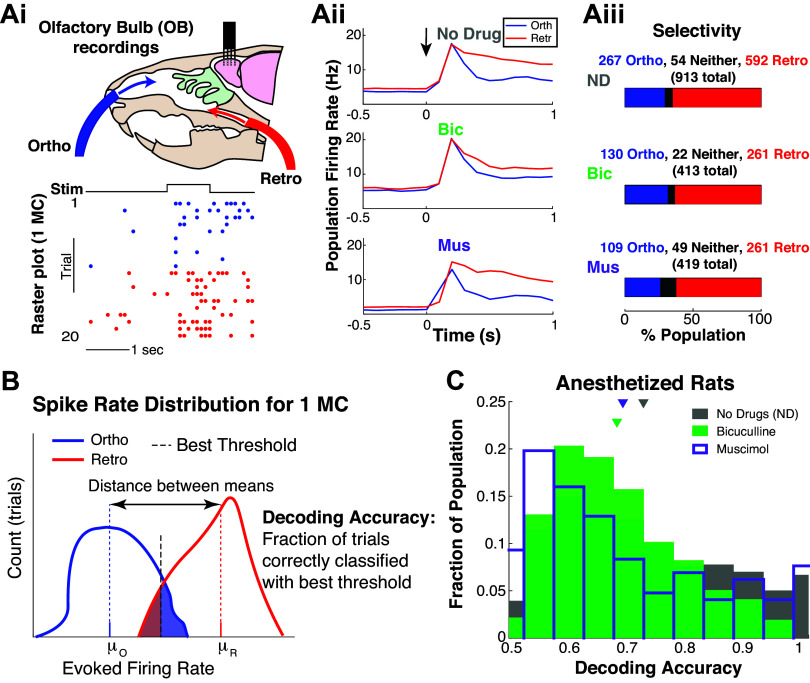
We collected spike data with multielectrode array recordings of urethane anesthetized rats from the OB mitral cell layer, where each cell (MC) was subject to the same odor delivered with ortho and retro stimulation (Fig. 1Ai), repeated for 10 trials for each modality. In addition, two drugs were applied to alter the circuit: a GABAA antagonist (Bicuculline) and a GABAA agonist (Muscimol), see Table 2. For reference, Fig. 1Aii shows the population-averaged firing rate (trial-averaged and population-averaged firing rate) by modality for a given drug preparation, with t = 0 denoting time of odor presentation, held for 1 s. This is commonly referred to as the peristimulus time histogram (PSTH).
Figure 1.
Individual mitral cells encode modality. Ai: experiment setup to test whether OB MCs encode ortho versus retro stimulation, with example raster plot for 1 MC. Aii: population-averaged firing rate (trial- and population-averaged), i.e., PSTH for each modality and drug preparation; t = 0 denotes when ethyl butyrate (EB, a food odor) is presented. Aiii: the proportion of population that fire more for ortho (or retro), i.e., ortho selective ⇔ higher trial-averaged firing rate for ortho than retro in 0.9 s after odor onset. B: schematic of how decoding accuracies are calculated for each MC based on trial firing rates: μR/0 are the trial-averaged firing rates. Shaded regions correspond to incorrect decoding, unshaded regions to correct decoding. C: distribution of decoding accuracies of MC with three different preparations: intact no drug (gray), less inhibition via Bic (green), and more inhibition via Mus (purple). Mean decoding accuracy for no drug is 0.724; with Bic and Mus the means are: 0.680, 0.690 (resp.). Differences are all statistically significant (α = 0.01 with two-sample t test assuming unequal var, Wilcoxon rank-sum test, and one-way ANOVA) with mostly “medium” effect size, see Table 3. Time window Tev = 0.9 s was determined systematically, see Fig. A2, A and C, and materials and methods. Bic, bicuculline; MC, mitral cell; Mus, muscimol; PSTH, peristimulus time histogram.
Table 2.
Number of rats and respective individual cells for each drug preparation subject to the food odor ethyl butyrate
| No Drug | Bicuculline | Muscimol | |
|---|---|---|---|
| Rats | 8 | 4 | 3 |
| Cells | 913 | 413 | 419 |
Individual MCs Encode Ortho versus Retro
To remain agnostic to how higher brain regions decode population activity, we predominately consider individual MCs odor modality encoding, a logical first step (25). We use odor-evoked firing rate in a given trial as the source of encoding. Specifically, the firing rate in the kth trial, xk, is the sum of the evoked spike counts normalized by time window Tev = 0.9 s:
| (15) |
for k = 1, 2, …, 20, same as Eq. 1 in materials and methods. The time window Tev is systematically chosen from a range of possible values, see Fig. A2, A and C, in appendix and materials and methods for details. To assess whether MCs might prefer one modality over the other, we compare the trial-averaged firing rate for ortho and retro as a measure of selectivity (Fig. 1Aiii). Most MCs “prefer” or spike more with retro than ortho (≈63%), and the proportions do not vary much across drug preparations (but see appendix and Table A1 for analysis of Off-Response cells).
We define decoding accuracy as the fraction of trials correctly classified by a threshold that maximizes decoding accuracy; this is a measure of information accessible by an ideal observer from each MC individually (Fig. 1B). We only consider EB, a common food odor, because typically only food odors are perceived retronasally (9). It has been shown that nonfood odors artificially delivered retronasally can be perceived as well as food odors (9). However, numerous studies have shown that human perception of nonfood odors delivered retronasally is degraded compared with food odors (4, 5, 8).
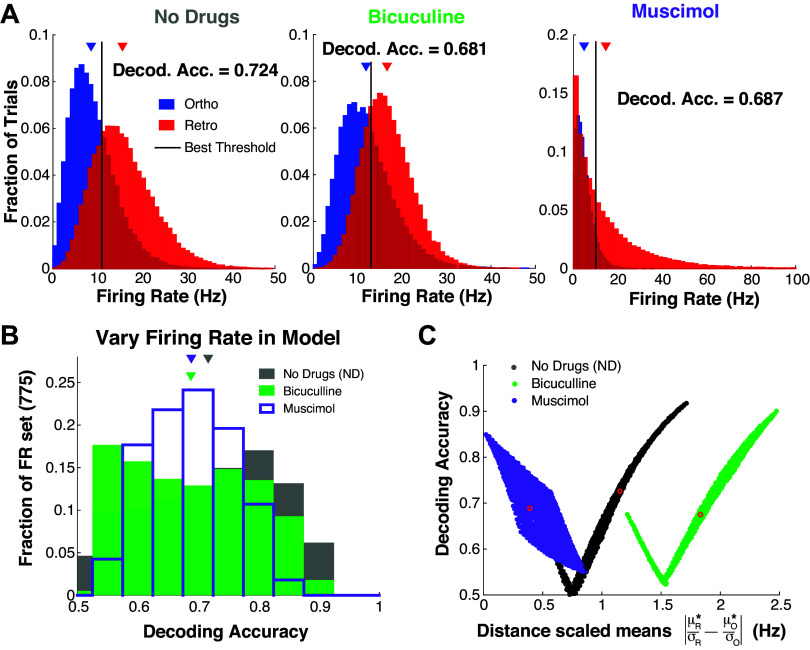
The OB circuit encodes ortho versus retro very well. Figure 1C shows the spiking activity of individual MCs encode (measured by decoding accuracy) ortho versus retro for the vast majority of cells. MCs have a wide range of decoding accuracies varying between 0.5 (chance) and 1 (perfect decoding). With no drugs, the mean decoding accuracy (0.724) is better than both Bic and Mus, which have lower average decoding accuracies of 0.680 and 0.690, respectively. These averages are numerically small in difference, but note that the range of decoding accuracies is only 0.5. Furthermore, the differences in the mean decoding accuracy are all statistically significant (α = 0.01) using three tests: two-sample t test, Wilcoxon rank-sum test, and one-way ANOVA. Table 3 demonstrates that the P values are all small and that the effect size is generally “medium,” with some “small” (see Statistical Significance in materials and methods).
Table 3.
Population decoding accuracy: significance measured by P values of average decoding accuracies over MC, shown in Fig. 1C
| Relationship/P Value | t Test | Rank Sum | ANOVA |
|---|---|---|---|
| Bic < ND | 3.6 × 10−10 | 4.9 × 10−6 | 1.8 × 10−8 |
| Mus < ND | 1.2 × 10−4 | 1.8 × 10−6 | 7.1 × 10−5 |
| Relationship/Effect Size | t Test | Rank Sum | ANOVA |
|---|---|---|---|
| Bic < ND | 0.336 (medium) | 0.126 (small) | 0.0237 (medium) |
| Mus < ND | 0.235 (medium) | 0.131 (small) | 0.0118 (medium) |
Using three tests: two-sample t test assuming unequal variance, Wilcoxon rank-sum test, and one-way ANOVA. Bottom section of table shows effect size (see materials and methods). Bic, bicuculline; MC, mitral cell; Mus, muscimol; ND, no drug.
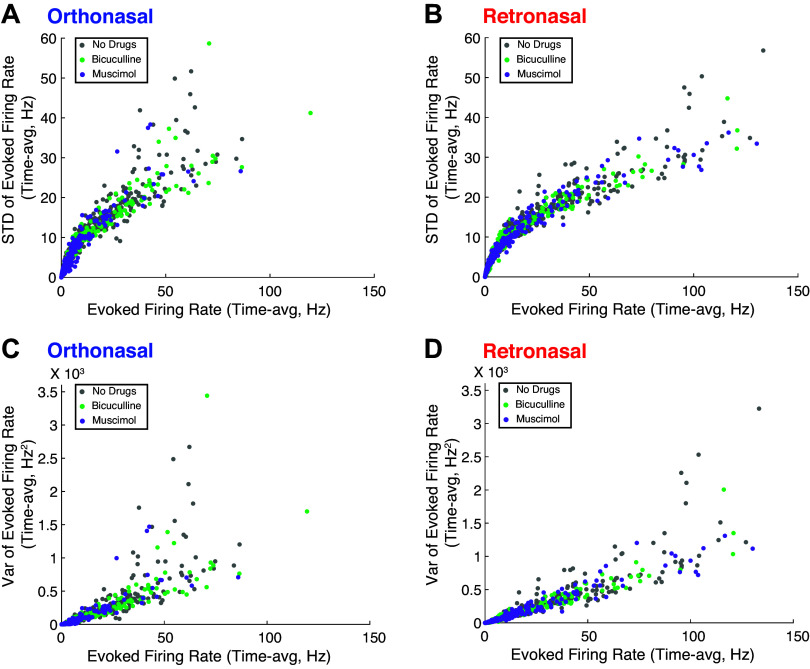
Figure 2 shows a more complete picture of the entire (pooled) population’s spike rate statistics across drug preparations and modality, beyond the PSTH in Fig. 1Aii. There are very strong positive correlations between the mean firing rates and standard deviations (across trials) in all drug preparations and both modalities (see Fig. A3 and Table A2). For further discussion on the modulation of evoked spiking variability in the OB, see Ref. 26.
Figure 2.
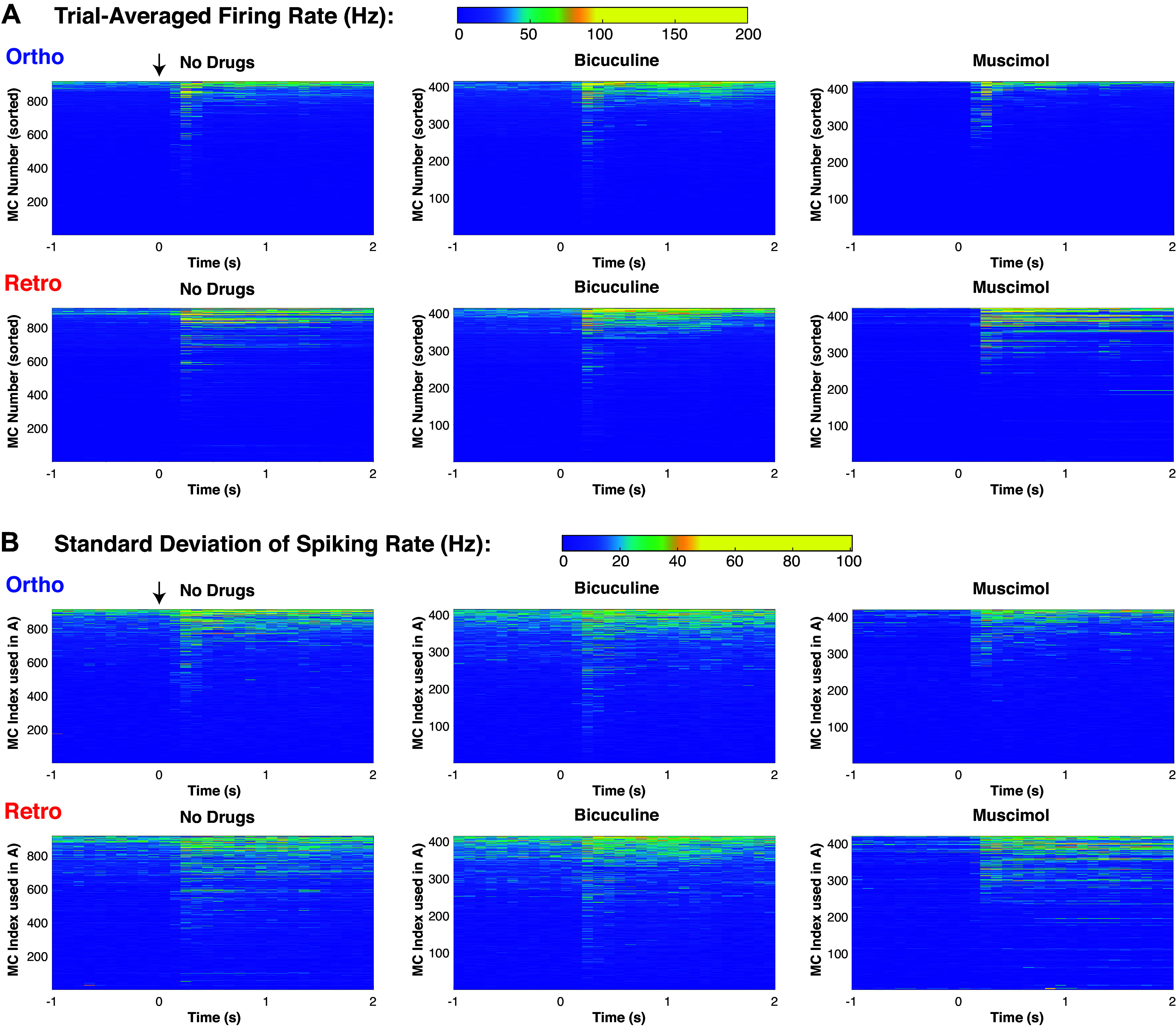
Detailed spiking rate statistics of (pooled) MC populations. A: colormap showing trial-averaged spiking rate of individual MC (individual PSTH), each of the three columns is sorted in three different ways, by time-averaged firing rate of ortho firing rate (4 s total, 2 s in spontaneous and evoked, but only showing 1 s of spontaneous). B: colormap showing trial variability of spiking rate (measured by standard deviation across trials) of individual MC, using the same corresponding index in top row (ortho firing rate). To see relative differences across MC, the color scales were effectively thresholded so that the larger values did not obscure the entire population. See Fig. A3 for more on relationship between firing rate and trial-to-trial variability. MC, mitral cell; PSTH, peristimulus time histogram.
Drug Effects on Average Population Spiking
To better understand the dynamics of MC decoding accuracy, we consider how GABAA (ant-)agonists affect population activity. Although population activity is a coarse measure that neglects individual cell heterogeneity, it can still be insightful for determining average trends. A characteristic of an individual MC that might be indicative of encoding fidelity is the distance between the scaled trial-averaged firing rate of ortho and retro stimulation (Fig. 1B). We expect larger distances to coincide with better decoding accuracy than smaller distances, if all other factors are equal. Figure 3A shows moderate to strong correlations (Pearson’s and Spearman’s rank) between and decoding accuracies for all drug preparations. The spread in the horizontal direction is large for a given decoding accuracy value and the correlations are not 100%. Nevertheless, this motivates considering the population-averaged spiking activity as a means to better understand the dynamics of decoding accuracy.
Figure 3.
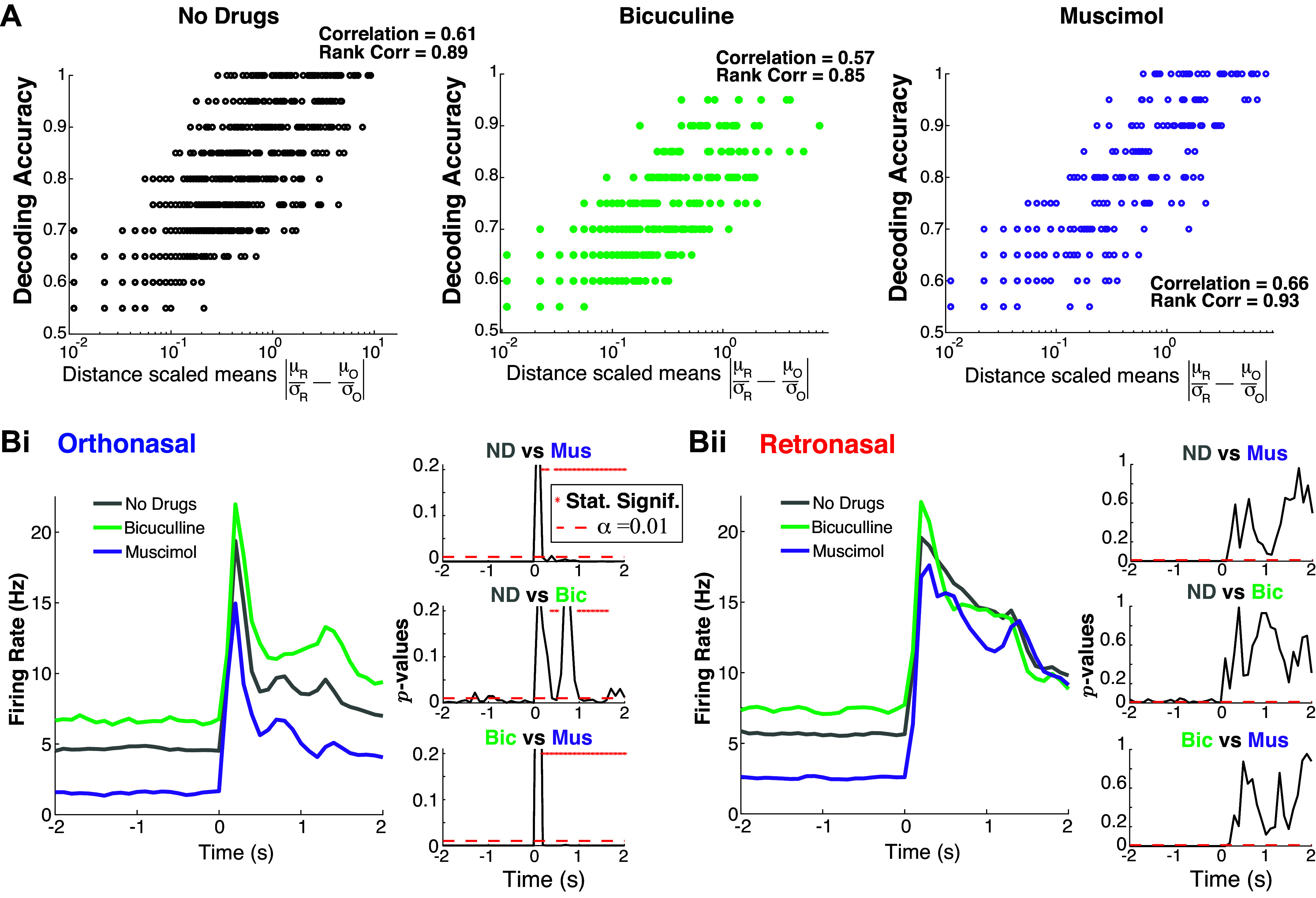
Population activity: retronasal response is less affected by changes in OB inhibition. A: distance between scaled trial-averaged mean is correlated with decoding accuracy. The “Correlation” is Pearson’s correlation coefficient, and “Rank Correlation” is Spearman’s. B: drug effects on evoked population PSTH are different with statistically significant effects only with ortho stimulation (Bi) but not retro (Bii). The right panels with three subplots show the time series of P values from two-sample t test assuming unequal variances, comparing pairs of drug preparations. Bic, bicuculline; Mus, muscimol; ND, no drug; OB, olfactory bulb; PSTH, peristimulus time histogram.
The effects of the GABAA (ant-)agonists on population firing rate depend on the odor modality; only ortho-evoked firing rates show statistically significant differences in the mean (over MC population) firing rate (Fig. 3B). As expected, Mus (increased inhibition) results in lower firing rates and Bic (less inhibition) results in higher firing rates compared with no drug, especially in the spontaneous state. However, the evoked firing rates are only significantly different (α = 0.01) across drug preparations with ortho stimulation and not significantly different with retro stimulation. This holds for nearly all time points (see * in P value plots of two-sample t test with unequal variance). This effect is clear in the right panels of Fig. 3, Bi and Bii. For completeness, the appendix shows the PSTH in Figs 1Aii and 3B for a longer timeframe (Fig. A1, A and B).
If we assume these population trends (Fig. 3B) hold individually for MCs (i.e., drugs only affect spiking rate in ortho but not retro), then we might expect decoding accuracies to change in specific ways: if ortho firing rate is less than retro with no drug, then Bic should increase firing rate (shift firing rate histograms to the right) causing more overlap and lower decoding accuracy. For exposition purposes, these results are detailed in appendix and Fig. A4 where predictions on decoding changes based on individual MC’s relationship of ortho versus retro firing rate are partially verified.
Drug Effects on Trial-to-Trial Variability
The trial-to-trial variability plays a key role in decoding accuracy differences. We analyze trial variance for each MC to test whether the population average is different across drug preparations. We find with Mus application, the average trial variability is smallest, followed by Bic, then no drug (i.e., Mus < Bic < ND), for both ortho and retro. The significance measured by P values and effect size are shown in Tables 4 and 5 for ortho and retro trials, respectively, using the same three statistical tests. For ortho stimulation, Mus < ND is significant for two of the three tests (α = 0.01), whereas Bic < ND and Mus < Bic are only significant with Wilcoxon rank-sum test. For retro stimulation, again only the Wilcoxon rank-sum test shows this relationship is significant (all with α = 0.01 except for Bic < ND for retro where P = 0.038). Overall, the Bic < ND relationship is not as strong as the others, and the trend Mus < Bic < ND is stronger with ortho stimulation. Note that the effect size is considered “small” in all cases, see Tables 4 and 5.
Table 4.
Ortho stimulation only: significance (P values) of average (over MC) trial variance differences between drugs with various statistical tests
| Relationship/P Value | t Test | Rank Sum | ANOVA |
|---|---|---|---|
| Mus < ND | 1.8 × 10−3 | 7.7 × 10−8 | 0.021 |
| Mus < Bic | 0.055 | 2.4 × 10−13 | 0.053 |
| Bic < ND | 0.82 | 5.0 × 10−4 | 0.82 |
| Relationship/Effect Size | t Test | Rank Sum | ANOVA |
|---|---|---|---|
| Mus < ND | 0.137 (small) | 0.147 (small) | 0.00402 (small) |
| Mus < Bic | 0.134 (small) | 0.254 (medium) | 0.00450 (small) |
| Bic < ND | 0.0137 (small) | 0.0955 (small) | 4.06 × 10−5 (small) |
Using same three tests as before; ND = “no drug”; bottom table shows effect size. Bic, bicuculline; MC, mitral cell; Mus, muscimol; ND, no drug.
Table 5.
Retro stimulation only: significance (P values) of average (over MC) trial variance differences between drugs with various statistical tests
| Relationship/P Value | t Test | Rank Sum | ANOVA |
|---|---|---|---|
| Mus < ND | 0.039 | 1.9 × 10−4 | 0.11 |
| Mus < Bic | 0.57 | 7.6 × 10−7 | 0.57 |
| Bic < ND | 0.26 | 0.038 | 0.30 |
| Relationship/Effect Size | t Test | Rank Sum | ANOVA |
|---|---|---|---|
| Mus < ND | 0.0953 (small) | 0.102 (small) | 0.00193 (small) |
| Mus < Bic | 0.0399 (small) | 0.171 (small) | 3.98 × 10−4 (small) |
| Bic < ND | 0.0610 (small) | 0.0569 (small) | 7.97 × 10−4 (small) |
Using same three tests as before; ND = “no drug”; bottom table shows effect size. Bic, bicuculline; MC, mitral cell; Mus, muscimol; ND, no drug.
Within all three drug preparations, the average trial variances for ortho compared with retro are statistically indistinguishable, consistent with study by Craft et al. (27) who did similar analyses but on only one rat instead of eight rats.
Model Connects Network Dynamics and Decoding Accuracy
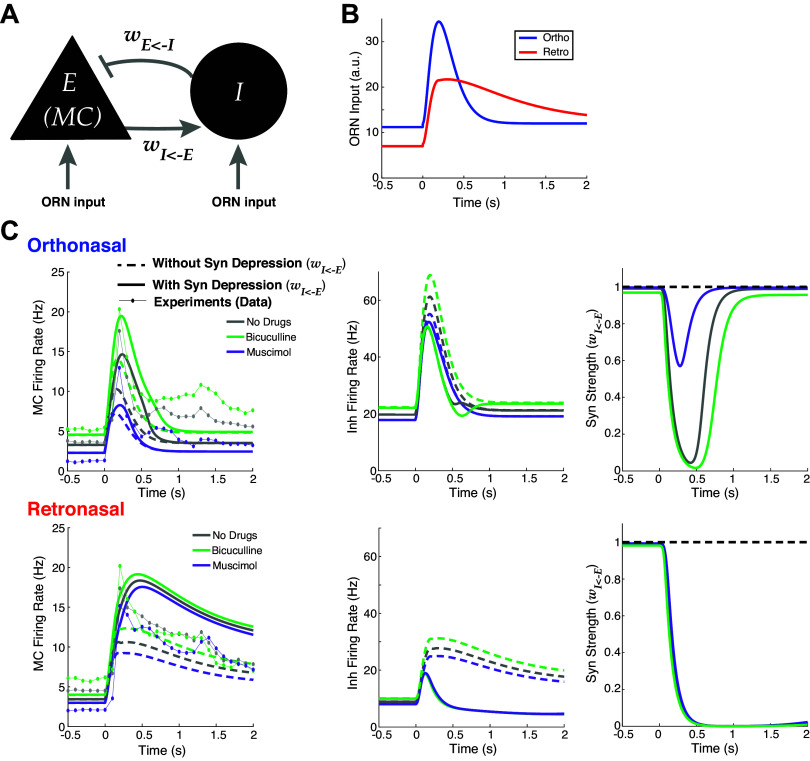
To reveal the neural network dynamics that explain our experimental data results, we use a simple firing rate model. Our rich dataset with three total drug preparations enables a model framework that is highly constrained by data (26, 28, 29). In addition, we incorporate known differences in temporal dynamics of ORN inputs to MCs with ortho versus retro stimulation (1–3, 30, 31). Ortho stimulation results in a fast increase and fast decrease of ORN inputs to MCs while retro input results in a slower increase and slower decrease of ORN inputs than ortho (Fig. 4B). Figure 2C of Furudono et al. (1) suggests that the amplitude of ORN inputs with ortho are larger than retro (Fig. 4B). We develop a principled model that is structurally the same with both odor modalities but effectively have different dynamics stemming from different ORN inputs (27); note that paper had a different purpose with data only from intact circuit with no drug manipulations. We decided not to use the biophysical model by Craft et al. (27) because 1) individual MC spiking statistics are modulated by net inhibitory inputs, distinguishing interneurons is a complication more relevant for joint statistics of MC populations; 2) resolving trial-average spike statistics is more computationally expensive, making parameter tuning to capture both firing rate differences and average decoding accuracies across three drug preparations impractical; and 3) calculating many decoding accuracies where each parameter set has an optimal threshold that has to be determined exhaustively (see Fig. 5, B and C, below) is a necessary additional component here [not in Craft et al. (27)] that is also computationally expensive.
Figure 4.
Firing rate model captures effects of drugs, with better alignment with data when including synaptic depression. A: schematic of reciprocally coupled E-I pair. B: fixed ORN input profiles for ortho and retro based on experiments (1–3, 30, 31) (see main text). C: Wilson-Cowan firing rate model (Eqs. 6–12) output for ortho (top) and retro (bottom) stimulation, compared when synaptic depression is included (solid lines) or not (dashed lines). Left column: E cell (MC) output; center column: I cell output; right column: synaptic strengths (WIE). Data from experiments also shown for comparison (dot-lines) in left column. E-I, excitatory-inhibitory; MC mitral cell; ORN, olfactory receptor neuron.
Figure 5.
Model decoding accuracies with simulated trial variability. A: histograms of simulated firing rate assuming negative binomial trial-to-trial variability with the mean set to: [see Eqs. 6–12, and solid curves in left column of Fig. 4 for AE(t)]. B and C: systematically varying the mean to show that the specified ρ parameter (Table 1) in negative binomial distribution generally results in no drug having best decoding accuracy (see main text for details). C: same model results in B but showing relationship with distance between (scaled) means; red circles correspond to regimes in A.
We first set out to implement an OB model that accounts for the large changes in population PSTH with GABAA (ant-)agonists with ortho stimulation only and small (or no significant) changes in population PSTH with retro (Fig. 3B). We use a reciprocally coupled two-cell E-I network (Fig. 4A), consistent with OB networks that have many such E-I pairs [granule and periglomerular cells are reciprocally connected to MCs with fast dendrodendritic synapses (32)]. We model the drug effects of Bic (Mus) by decreasing (increasing) the coupling strength from I to E cell by 25% of the baseline value (wEI = 0.2 with no drugs, arbitrary units, see Eqs. 6 and 7 and Table 1).
The data show that effects of drugs altering inhibition are largely absent with slower longer-lasting retro stimulation (Fig. 3B), thus finding a neural network principle that effectively removes the inhibitory cell input is imperative and might be indicative of the core mechanisms. We hypothesize that short-term plasticity on the excitatory synapse (E → I) could be a factor in explaining the differences of population firing between ortho versus retro with GABAA (ant-)agonists because of known temporal differences in ORN inputs. There is indeed evidence of plasticity in the OB circuit (33), specifically for short-term synaptic depression in the main OB (34) and from MC to granule cells (35). As the relative differences in firing rate with ortho are already large without plasticity (1st column in Table 6), honing in on decreasing the firing rate differences in retro (3rd column in Table 6) would make the model more consistent with the data (Fig. 3B). We use short-term synaptic depression as a means to nonlinearly change the retro firing rates to diminish the differences because retro has longer lasting stimuli. Although Dietz and Murthy (35) showed that E → I synapses in OB have both facilitation and depression with facilitation appearing more prominent, we found that short-term facilitation alone made our model less consistent with our data.
Table 6.
Relative differences of firing rate model between no drug and inhibitory drugs in both modalities
| Ortho |
Retro |
|||
|---|---|---|---|---|
| Relative Differences (%) | Without Depression | With Depression | Without Depression | With Depression |
| No Drug/Bicuculline | 37.87 | 38.16 | 16.08 | 6.04 |
| No Drug/Muscimol | 30.31 | 45.09 | 12.90 | 6.25 |
| Ortho |
Retro |
|||
|---|---|---|---|---|
| Without Depression | With Depression | Without Depression | With Depression | |
| No Drug | 6.11 | 8.58 | 9.64 | 15.65 |
| Bicuculline | 8.43 | 11.86 | 11.19 | 16.59 |
| Muscimol | 4.26 | 4.71 | 8.40 | 14.67 |
All percent differences (top table) are relative to no drug: . Bottom section of table shows average firing rate (Hz), i.e., the components of the relative differences.
Figure 4C shows comparisons of various model outputs (Eqs. 6–12). The model indeed follows the firing rate modulation with GABAA (ant-)agonists with both odor modalities, whether or not synaptic depression is included. Specifically, ortho MC firing rates (Fig. 4, top left) with different drug preparations are well-separated, whereas the retro MC firing rates are pretty close together (Fig. 4, bottom left). The effects of synaptic depression significantly narrow the differences in retro population PSTH among all three drug applications, while with ortho, the differences across drug preps remain large (see Table 6 for relative differences). Taken together, synaptic depression is crucial for capturing the data (Fig. 3B) with this model. With retro stimulation in all three drug preparations, the E → I synaptic connections are depressed for longer so that the I-cell fires less, giving a boost to E-cell firing. In both modalities, there is overall higher E (MC) firing with short-term synaptic depression because of less inhibition (for all three drug preparations). Synaptic depression effectively diminishes the reciprocal loop so that the inhibitory drug effects are weakened. In principle, Mus should have the opposite effect as Bic, but the coupling strength wEI has moderate variation: 0.15 (Bic), 0. 2 (ND), and 0.25 (Mus). Also, we modeled short-term depression so that inhibition is almost completely turned off with retro, resulting in MC being effectively decoupled from the I cell. Our model does not have realistic levels of synaptic depression, Cang and Isaacson (33) report moderate levels of synaptic depression. If synaptic depression was limited in our model so that the minimum wIE was 0.5, the ortho firing would be similar but the retro firing would strongly modulate with drug effects, which is inconsistent with our data. And anesthetized rats have less active granule cells (33) than awake, so perhaps other interneurons would have to be active for our model to be consistent with our data. The exact type of inhibitory neurons in the OB that would have to be involved and their corresponding dynamics with excitation are unknown to us.
With the neural dynamics captured in our model, we turn to connecting the model to decoding accuracy. The firing rate model does not explicitly have trial-to-trial variability, an important piece for decoding accuracy. A natural choice would be to assume Poisson statistics for the spike counts, but this single parameter distribution results in trial variance ordered by the firing rate: Mus < ND < Bic, which is inconsistent with our data and has perfect (100%) decoding accuracy with these firing rate models. Capturing the trial variability trends in our data seems to require tunable parameters that are not directly tied to the (mean) firing rate. We use a simple two-parameter model that makes simulation easy and transparent: the negative binomial distribution. Note that there may be other models of trial variability that are more realistic in relation to MCs, but that is unlikely to be as pragmatic for capturing firing rate and decoding accuracy trends. Specifically, for each drug (ND/Bic/Mus) and each input (ortho/retro), we fit a negative binomial distribution to the average decoding accuracy. The two distribution parameters were chosen so that 1) the mean of distribution coincided with the model spiking rate (solid curves in Fig. 4C, left column) and 2) the decoding accuracy matches the averages in the experimental data.
The negative binomial distribution has distribution: with parameters: ρ ∈ (0, 1) and r > 0 that are not directly related to the physiology. We manually (by trial and error) determine the parameter ρ for each modality and drug preparation, which are all the same ρ except for retro with Bic and Mus (see Table 1), after which the r parameter is determined by:
| (16) |
since the mean of the negative binomial is . We choose ρ for each regime so that the resulting decoding accuracy is close to the averages from the experiments: 0.724 (no drug), 0.680 (Bic), and 0.690 (Mus).
The results are summarized in Fig. 5A. We simulated 50,000 trials and found the optimal threshold to get decoding accuracies that match the data.
We check whether our model results are consistent with the trial-to-trial variability of our data by calculating the variances of firing rate over trials, which is simply for the negative binomial distribution. The values listed in Table 7 show that trial variance is consistent with the data: Mus < ND < Bic, except for retro Mus firing that has the largest variance. Recall in our data that the trends for variance of firing rate was weakest with retro stimulation with larger P values (Table 5).
Table 7.
Simulated trial variance of the model:
| Muscimol | No Drug | Bicuculline | |
|---|---|---|---|
| Ortho | 14.73 | 26.83 | 37.06 |
| Retro | 282.12 | 48.90 | 31.31 |
A test of our model is to determine whether the specified parameter values for ρ results in ND generally having better decoding accuracy than Bic and Mus. We start with the base model of spiking rate: (solid curves in Fig. 4C, left column) and perturb these values to get different means: , where M0 ∈ {−2, …, 4} Hz on 25 equally spaced points and M0 ∈ {−6, …, 9} Hz on 31 equally spaced points. Once a mean is specified, we use the same ρ (Table 1) and set r* to correspond to the mean μ*:
| (17) |
we simulate 50,000 trials to get a decoding accuracy value for each set of parameters. We get 775 decoding accuracy values corresponding to the different ( combinations for each drug preparation (Fig. 5B). Importantly, our model does not soundly capture many details of realistic MC heterogeneities in our data (Figs. 1C and 5B have different shapes), but Fig. 5B at least matches the result that ND on balance has better decoding accuracy than Bic and Mus. Finally, Fig. 5C shows how decoding accuracy varies with scaled distance . The decoding accuracies can vary for a given drug preparation, but the ND and Bic have strong positive correlations (like the data, see Fig. 3A), but Mus has strong negative correlations that are inconsistent with the data.
Population Decoding Results
Thus far, we have focused on decoding odor modality using the firing rate of individual MCs. Although this approach avoids making assumptions about how higher-level cortical regions might use the population as a whole (25), population coding is known to be important for complicated tasks (36). We apply standard population coding metrics to assess how well odor modality can be decoded from populations of MCs. We show that modality is well-encoded, but that the differences with GABAA manipulations are minor.
We applied two approaches to population decoding. First, we used principal component analysis (PCA) to project the population response onto a two-dimensional subspace that captures the most variance (first 2 PCs) and then applied linear discriminant analysis (LDA) to find an optimal decoder in that subspace (PCA + LDA). Second, we used a support vector machine (SVM), a common supervised learning algorithm to (nonlinearly) classify data. We use the first two PCs in PCA + LDA because it is a natural extension of 1-D decoding with LDA that was the primary focus of prior sections. The SVM is at another extreme using all dimensions possible; together, these two provide a glimpse into the various accuracies of population decoding.
With both methods, we find odor modality is still encoded well above chance even when inhibition is altered (Fig. 6, B and C). Not only is the average decoding accuracy (across separate recordings) higher than before (Fig. 1C) but there are no longer decoding accuracies near the chance level (0.5). This is perhaps expected because these metrics (PCA + LDA, SVM) exploit the higher dimensional population activity to perform optimally in a binary classification problem when in reality the MCs encode other aspects of stimuli. Note that nearly 35% of recordings with no drug and Mus have perfect decoding accuracy (Fig. 6, B and C).
In contrast to the case of a single MC’s encoding (Fig. 1C), we do not find any statistically significant differences between the mean decoding accuracy across drug preparations. In fact, the minimum P value for all relationships and all three statistical tests is P ≥ 0.32 for PCA + LDA, P ≥ 0.13 for SVM. We expect population coding to perform better than individual cell coding, especially given the large dimensionality of population activity and that these metrics (PCA + LDA, SVM) were optimized for a binary classification task.
DISCUSSION
We have shown that MCs in the OB encode odor modality with our experimental data and use an OB model inspired by many prior studies and constrained by our rich data to analyze plausible network components that support these dynamics. Our study uncovers further details for how ortho versus retro information is encoded to early cortical regions via the OB, which is consistent with reports that humans are able to discriminate whether food odors are delivered ortho or retronasally without being told which modality (4). Imaging studies of the human mouth have shown that with food odors, ortho stimuli delivery versus retro are two distinct modalities, rather than two different stimulus routes to the same modality, independent of odor intensity (5). Based on in vivo rat data, we found significant differences in decoding accuracies (our proxy for encoding assuming an ideal observer) for classifying ortho and retronasal odors across different drug preparations. The intact (no drug) circuit had the best (average) decoding accuracy, suggesting that the OB might be structured to encode this important aspect of odor input.
Our model framework used prior results, data constraints (26, 28, 29), and simplicity to account for the results of our data analysis. Many prior studies (1–3, 30, 31) showed that there are differences in the temporal dynamics of ORN response to ortho versus retro stimulation. We used this to investigate the OB circuit components that promote efficient coding of individual mitral cells with drug manipulations of inhibitory synapses. Further data analysis revealed that inhibitory drugs have a stronger effect on the population firing with ortho stimulation than retro. Using these insights, we constructed a standard firing rate model that captures the various drug effects for ortho versus retro stimulus, using only a pair of E – I cells. Including synaptic depression was crucial for capturing the different drug effects of firing rate. We did not explore varying the many parameters of the model to find a “best fit” to data, rather we wanted a simple yet informative model that demonstrates a plausible mechanism. The model PSTH fits to the data are imperfect and qualitative (Fig. 4C); the spontaneous firing of ortho and retro in the model are different because of differences in the ORN input strengths, the ortho model firing decays faster than the data. In fact, for retro, it looks like the model fits the data better without synaptic depression (although the differences with GABAA manipulations are large and inconsistent with the data). In theory the model could be better fit to the data PSTH, for example, if the ORN inputs (Fig. 4B) are held fixed and an optimization routine is performed on a set of parameters, but then the decoding accuracy would have to be accounted for (Fig. 5A), perhaps in the objective. We thus opted to manually determine the model parameters. Lastly, we simulated trial-to-trial variability by assuming a negative binomial distribution with mean defined by the firing rate model output. The resulting model captured both decoding accuracy trends (ND is better) and some aspects of firing rate trial variability.
There have been prior studies that implemented an OB circuit model with varying levels of realism, but none that we are aware of that use an OB model to account for coding of odor modality and firing rate dynamics. We previously developed a realistic biophysical OB network model (27) and used it to account for different neural network dynamics (trial-averaged) with ortho/retro inputs, but did not focus on decoding accuracy for a given trial (which is more computationally taxing). In our prior work (27), the PSTH for ortho versus retro is different from here (Figs. 1Aii and 3B) because we previously used only one rat versus eight rats here. There are biophysical models of particular OB cells (37, 38) and of the OB network (39, 40), and other have used models (firing rate or Bayesian) to investigate coding of mixed odors (41) and learning new odors (and their concentration levels) (42), but we are unaware of an OB model that captures coding of odor modality. Note that muscimol increases tonic E-cell inhibition independent of I-cell firing; our simple model does not disentangle these two components.
A limitation of this study is the use of one odor (EB, a food odor) with one concentration. We collected data from a nonfood odor (1-Hexanol), but since typically only food odors are experienced retronasally (9), we did not include 1-Hexanol in our study. It is well-known that nonfood odors delivered retronasally are not perceived as well as retro food odors by humans (4, 5, 8). Other food odors have different physicochemical properties that impact differences in ortho versus retro responses (31), so the generalization of our results merits further investigation. Firing rates vary with odor concentration (15) and is thus a confounding factor in distinguishing ortho versus retro from firing rates alone. Whether higher brain regions rely on other signals to account for concentration or different patterns of activation in OB to reliably estimate ortho/retro is important but beyond the scope of this study. Our data were collected from anesthetized rats with forced air to model ortho/retro (2, 7, 43), which has clear advantages: control and a fair decoding “task” so that ortho and retro are mechanically similar with the same stimulus duration. In addition to the intact circuit, our data also had both increased and decreased GABAA synaptic inhibition with direct manipulations in the OB. Via pooling data from many rats, we had a large number of MCs. Although data from awake rats during eating would shed light on coding odor modality in a more natural state, we are unaware of such data of recorded MC spiking activity for the purposes of comparing ortho versus retro during feeding. There are freely available MC spike data with awake rodents [mice in Bolding and Franks (44, 45)] but not during feeding and not with direct manipulation of OB inhibitory synapses.
As the temporal dynamics of odors can be crucial in OB processing, we systematically varied the evoked time window and even considered removing the first 300 ms of the evoked state (see Fig. A2). We found that the population-average (and standard deviation) decoding accuracy varied slightly (Fig. A2, B and D), and indeed, with the first part of the evoked state removed, the average decoding accuracy increased. In the context of our study, the temporal patterning differences between ortho and retro have minor effects on decoding. In awake, intact animals, the timing of the breath cycle determines the timing of ortho and retro stimulation (11). In principle, brain areas downstream from OB could use a breath-timing-based decoding scheme to entirely distinguish ortho from retro. However, our experiments show that timing is not the only mechanism that impacts ortho versus retro coding. In our experiments, the breath of the anesthetized rats did not pass through the nose at all; it was redirected through a tracheotomy tube. Thus, the timing of ortho and retro signals in our experiments was decoupled from breath timing and we kept the stimulation parameters (concentration and flow rate) the same, changing only the direction of airflow. Yet, we found differences in ortho and retro response in OB. Also, when instructed not to breathe and actively sniff, humans can correctly report ortho versus retro odor modality with food odor without being told the modality (4). Thus, we conclude that the OB encodes ortho and retro stimuli not only with the timing of the breath but also with other mechanisms. Nonetheless, it is likely that intact, awake animals would use both timing (inhale vs. exhale) and the mechanisms we identify here. Disentangling the relative importance of these different possible contributions to ortho versus retro coding will require further experiments.
Our results predominately center on population averages of individual MC decoding accuracy because it is a logical first step (25). Given the importance of population coding for many complicated tasks (36), we also considered two standard population decoding accuracy measures: PCA + LDA and SVM and found in both cases that the intact circuit was not statistically significant better (on average). However, decoding accuracy was again much higher than chance levels and better compared with average individual MC decoding accuracy. Developing a heterogeneous OB model that accounts for the population coding results and dynamics is a potential next step but beyond the scope of this current study.
DATA AVAILABILITY
See https://github.com/michellecraft64/Modality for MATLAB code implementing the data analysis and firing rate model.
See https://doi.org/10.6084/m9.figshare.14877780.v1 for raw data collected from the Shew Lab.
GRANTS
This work was supported by National Science Foundation Grants IIS-1912352 (to W. L. Shew), IIS-1912338 (to C. Ly), IIS-1912338 (to M. F. Craft), IIS-1912320 (to A. K. Barreiro), and IIS-1912352 (to S. H. Gautam).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
M.F.C., W.L.S., and C.L. conceived and designed research; S.H.G. and W.L.S. performed experiments; M.F.C., A.K.B., S.H.G., W.L.S., and C.L. analyzed data; S.H.G. and W.L.S. interpreted results of experiments; M.F.C. and C.L. prepared figures; M.F.C. and C.L. drafted manuscript; A.K.B., W.L.S., and C.L. edited and revised manuscript; M.F.C., A.K.B., S.H.G., W.L.S., and C.L. approved final version of manuscript.
APPENDIX
The main text focuses on the 1-s duration of the odor, which is longer than most breath cycles. However, there are dynamics beyond the duration of the odor that may be insightful and of interest, so the population PSTHs extended to 5 s after odor onset are shown in Fig. A1, A and B. By visual inspection, there appears to be an increase in the firing rate after the odor is off, e.g., ortho with Bic and retro with Mus. Whether this change is statistical significant and the underlying mechanisms to explain this are fascinating but beyond the scope of this current study. For the interested readers, we report the fraction of “Off-Response” cells that have higher firing rates when the odor is removed than with odor, a well-known phenomenon dating back many decades (46). We report the fraction of the MC population that has a higher firing rate (time- and trial-averaged) in 1 ≤ t ≤ 2 s than in 0 ≤ t ≤ 1 s in Table A1.
Figure A1.
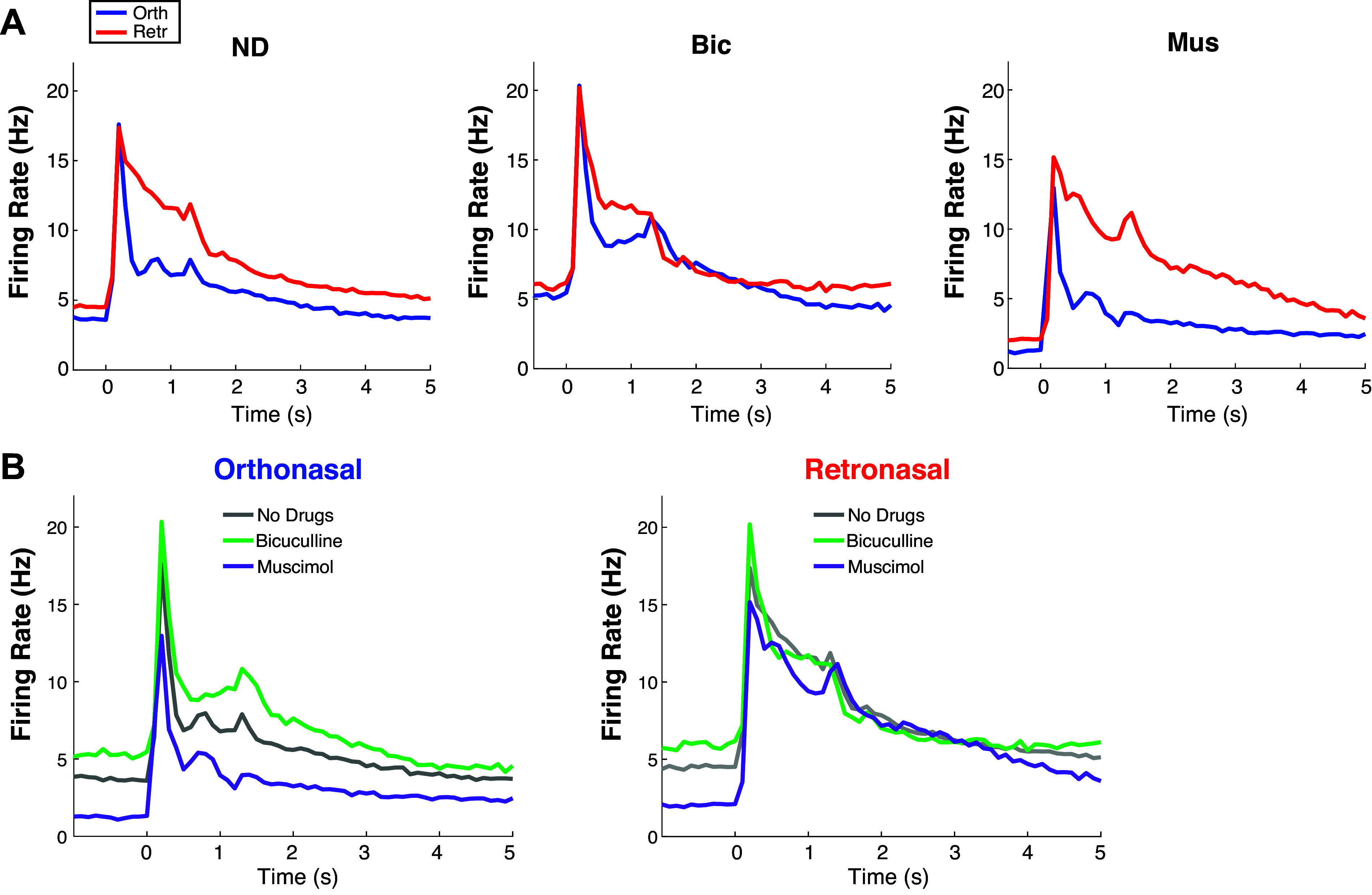
Supplemental data analysis: extended time of PSTHs in main text. Extended timeframe for Fig. 1Aii (A) and Fig. 3B (B). Bic, bicuculline; Mus, muscimol; ND, no drug; PSTH, peristimulus time histogram.
Table A1.
Fraction of “Off-Response” cells: cells that have a higher firing rate (time- and trial-averaged) in the immediate time (1 s) after odor is removed than during the 1 s odor stimulation
| Fraction of Off-Response MCs | ND | Bic | Mus |
|---|---|---|---|
| Ortho | 30.12% | 36.08% | 27.45% |
| Retro | 27.05% | 18.64% | 42.00% |
Bic, bicuculline; MC, mitral cell; Mus, muscimol; ND, no drug.
Figure A2, A–B, details how the time window in the evoked state was chosen and how the optimal decoding accuracies vary with time window.
Figure A2.
How we choose the time window; decoding accuracy as time window varies. Varying time windows on evoked firing rate to select for data analysis (A and C) and decoding accuracy. A: vertical axes show P values (log-scale) from comparisons of average decoding accuracies with different drug preparations using two different statistical tests: two-sample t test assuming unequal variance (black) and Wilcoxon rank-sum test (magenta). Open circles compare no drug to Bic, stars compare no drug to Mus (see legend). B: showing the population average decoding accuracy and ± 1 SD in shaded region. Longer time windows generally lead to larger average decoding accuracy. C and D are similar to A and B except the first 300 ms of the evoked state are removed to test whether decoding accuracies increase are significant; this was based on the population PSTH being similar for ortho and retro immediately after stimulus onset (Fig. 1Aii). Decoding accuracies are significantly different (α = 0.01, denoted by dashed black line) for a large range of time windows, but we chose 0.9 s for evoked because this value resulted in the smallest P values generally, the exception being denoted by the red arrows where other time bins have slightly smaller P values. We decided to keep the entire time, not excluding the first 300 ms, for simplicity and because the P values are similar. All data analysis is with EB odor input. Bic, bicuculline; EB, ethyl butyrate; Mus, muscimol; ND, no drug; PSTH, peristimulus time histogram.
Figure A3 shows how the trial-averaged firing rate is related to trial-to-trial variance (and standard deviation) of firing rate by odor modality and drug preparation. Related to this is Table A2, which shows the correlations between trial-averaged firing rate and trial-to-trial variability by odor modality and drug preparation.
Figure A3.
Trial-averaged firing rate is positively correlated with trial-to-trial variability. For each MC in a given modality and drug preparation, showing the trial-averaged firing rate versus the standard deviation (A and B) or variance (C and D) of firing rate (across trials). With orthonosal stimulation (A); with retronasal stimulation (B). C and D are similar except showing the variance of evoked firing rate. We plot the time average to resolve the many instances with no spiking so that each MC has a single number for the firing rate and a single number for the variance. MC, mitral cell.
Table A2.
Correlation between trial-mean and trial-standard deviation (top) and variance (bottom) of spiking rate
| Ortho |
Retro |
|||
|---|---|---|---|---|
| Pearson’s | Spearman’s Rank | Pearson’s | Spearman’s Rank | |
| Trial Standard Deviation | ||||
| No Drug | 0.932 | 0.986 | 0.935 | 0.995 |
| Bicuculline | 0.930 | 0.989 | 0.937 | 0.988 |
| Muscimol | 0.907 | 0.989 | 0.920 | 0.996 |
| Trial-Variance | ||||
| No Drug | 0.841 | 0.986 | 0.908 | 0.995 |
| Bicuculline | 0.835 | 0.989 | 0.963 | 0.988 |
| Muscimol | 0.852 | 0.989 | 0.968 | 0.996 |
DECODING ACCURACY DYNAMICS FROM DRUG EFFECTS ON POPULATION-AVERAGED FIRING RATES
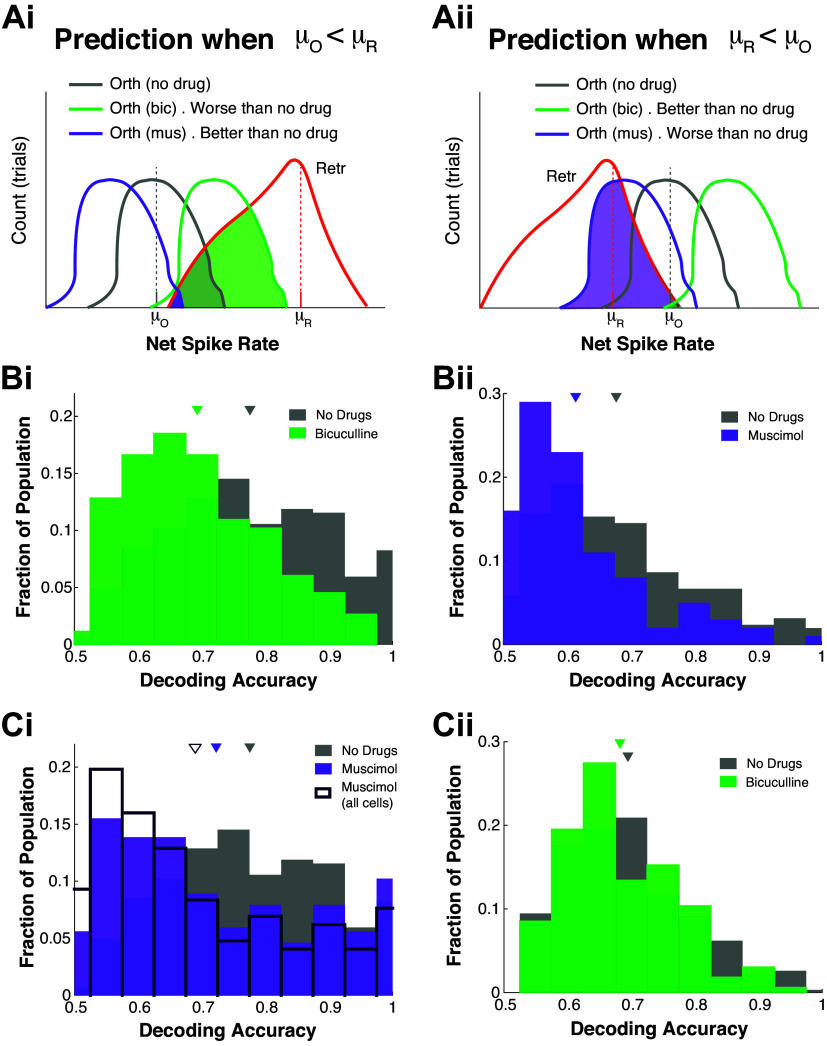
If we assume the population trends in Fig. 3B hold individually for MCs (drugs only affect spiking rate with ortho but not retro), then we might expect decoding accuracies to change in specific ways, as illustrated in Fig. A4, Ai and Aii. If ortho spiking is less than retro with no drug (μ0 < μR, see Fig. A4Ai), Bic should increase spiking (shift gray curve to the right, green curve) causing more overlap and lower decoding accuracy, whereas Mus should decrease spiking (shift gray curve left, purple curve) leading to less overlap and higher decoding accuracy. Similar arguments can be made for when retro spiking is less than ortho spiking μ0 < μR, Fig. A4Aii). Thus, the predictions from observations of the population firing rates (Fig. 2B) are:
-
1)
When μ0 < μR:
(a) Bicuculline = less accuracy*
(b) Muscimol = more accuracy
-
2)
When μR < μ0:
(a) Muscimol = less accuracy*
(b) Bicuculline = more accuracy
Figure A4.
Decoding accuracy dynamics from drug effects on population-averaged firing rates. Left: cells where μ0 < μR. Right: cells where μR < μ0. Ai and Aii: predicted decoding accuracy for different drug preparations. Histogram of decoding accuracies for no drug and Bic when μ0 < μR (Bi), and no drug with muscimol when μR < μ0 (Bii); triangle is mean decoding accuracy over all such MCs. Differences in middle row (Bi and Bii) are statistically significant. Ci: histogram of decoding accuracies for no drug and muscimol when μ0 < μR, also showing the histogram for muscimol decoding accuracy for all cells (i.e., not only those where μ0 < μR) in dark purple outline. Although no drug is better than muscimol, muscimol with cells μ0 < μR have better decoding than all cells with muscimol. Cii: no drug and Bic when μR < μ0 do not have statistically significant differences in mean. See text for P values. Bic, bicuculline; MC, mitral cell.
The results of these predictions are shown in Fig. A4, B and C. Predictions 1a and 2a (Fig. A4B) denoted by asterisk are statistically significant in difference [t test (PND,Bic = 5.3 × 10−16, PND,Mus = 1.8 × 10−6), Wilcoxon rank-sum test (PND,Bic = 3.1 × 10−14, PND,Mus = 6.9 × 10−7), and one-way ANOVA (PND,Bic = 1.1 × 10−15, PND,Mus = 5.6 × 10−6)]. The other two predictions (1b and 2b, Fig. A4C) do not precisely hold; interestingly, it is because no drug preparation retains a higher average decoding accuracy than with the two drug applications. Two caveats: in Fig. A4Ci, with Mus, the average decoding accuracy is better when μ0 < μR (purple filled) compared with all cells μ0 < μR and μ0 ≥ μR (dark purple outline) [t test (PMus − all,Mus = 1.2 × 10−8), Wilcoxon rank-sum test (PMus − all,Mus = 9.4 × 10−6), and one-way ANOVA (PMus − all,Mus = 3.0 × 10−6)]; in Fig. A4Cii, the difference between Bic and no drug are no longer statistically significant [t test (PND,Bic = 0.22), Wilcoxon rank-sum test (PND,Bic = 0.58), and one-way ANOVA (PND,Bic = 0.26)], so that with μR < μ0, cells with Bic and no drug have indistinguishable averages. This all shows that the observation that ortho stim is more affected by GABAA manipulation than retro has consequences for decoding accuracy modulation, even if the predictions are imperfect.
REFERENCES
- 1. Furudono Y, Cruz G, Lowe G. Glomerular input patterns in the mouse olfactory bulb evoked by retronasal odor stimuli. BMC Neurosci 14: 45, 2013. doi: 10.1186/1471-2202-14-45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Gautam SH, Verhagen JV. Retronasal odor representations in the dorsal olfactory bulb of rats. J Neurosci 32: 7949–7959, 2012. doi: 10.1523/JNEUROSCI.1413-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Sanganahalli BG, Baker KL, Thompson GJ, Herman P, Shepherd GM, Verhagen JV, Hyder F. Orthonasal versus retronasal glomerular activity in rat olfactory bulb by fMRI. Neuroimage 212: 116664, 2020. doi: 10.1016/j.neuroimage.2020.116664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Frasnelli J, Ungermann M, Hummel T. Ortho-and retronasal presentation of olfactory stimuli modulates odor percepts. Chem Percept 1: 9–15, 2008. doi: 10.1007/s12078-007-9000-2. [DOI] [Google Scholar]
- 5. Bender G, Hummel T, Negoias S, Small DM. Separate signals for orthonasal vs. retronasal perception of food but not nonfood odors. Behav Neurosci 123: 481–489, 2009. doi: 10.1037/a0015065. [DOI] [PubMed] [Google Scholar]
- 6. Blankenship ML, Grigorova M, Katz DB, Maier JX. Retronasal odor perception requires taste cortex, but orthonasal does not. Curr Biol 29: 62–69.e3, 2019. doi: 10.1016/j.cub.2018.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Gautam SH, Verhagen JV. Direct behavioral evidence for retronasal olfaction in rats. PLoS One 7: e44781, 2012. doi: 10.1371/journal.pone.0044781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Hannum ME, Fryer JA, Simons CT. Non-food odors and the duality of smell: impact of odorant delivery pathway and labeling convention on olfactory perception. Physiol Behav 238: 113480, 2021. doi: 10.1016/j.physbeh.2021.113480. [DOI] [PubMed] [Google Scholar]
- 9. Small DM, Gerber JC, Mak YE, Hummel T. Differential neural responses evoked by orthonasal versus retronasal odorant perception in humans. Neuron 47: 593–605, 2005. doi: 10.1016/j.neuron.2005.07.022. [DOI] [PubMed] [Google Scholar]
- 10. Iwata R, Kiyonari H, Imai T. Mechanosensory-based phase coding of odor identity in the olfactory bulb. Neuron 96: 1139–1152.e7, 2017. doi: 10.1016/j.neuron.2017.11.008. [DOI] [PubMed] [Google Scholar]
- 11. Shusterman R, Smear MC, Koulakov AA, Rinberg D. Precise olfactory responses tile the sniff cycle. Nat Neurosci 14: 1039–1044, 2011. doi: 10.1038/nn.2877. [DOI] [PubMed] [Google Scholar]
- 12. Heilmann S, Hummel T. A new method for comparing orthonasal and retronasal olfaction. Behav Neurosci 118: 412–419, 2004. doi: 10.1037/0735-7044.118.2.412. [DOI] [PubMed] [Google Scholar]
- 13. Mandairon N, Linster C. Odor perception and olfactory bulb plasticity in adult mammals. J Neurophysiol 101: 2204–2209, 2009. doi: 10.1152/jn.00076.2009. [DOI] [PubMed] [Google Scholar]
- 14. Wilson RI, Laurent G. Role of GABAergic inhibition in shaping odor-evoked spatiotemporal patterns in the Drosophila antennal lobe. J Neurosci 25: 9069–9079, 2005. doi: 10.1523/JNEUROSCI.2070-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Tan J, Savigner A, Ma M, Luo M. Odor information processing by the olfactory bulb analyzed in gene-targeted mice. Neuron 65: 912–926, 2010. doi: 10.1016/j.neuron.2010.02.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Abraham NM, Egger V, Shimshek DR, Renden R, Fukunaga I, Sprengel R, Seeburg PH, Klugmann M, Margrie TW, Schaefer AT, Kuner T. Synaptic inhibition in the olfactory bulb accelerates odor discrimination in mice. Neuron 65: 399–411, 2010. doi: 10.1016/j.neuron.2010.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Rossant C, Kadir S, Goodman D, Schulman J, Hunter M, Saleem A, Grosmark A, Belluscio M, Denfield G, Ecker A, Tolias A, Solomon S, Buzsáki G, Carandini M, Harris K. Spike sorting for large, dense electrode arrays. Nat Neurosci 19: 634–641, 2016. doi: 10.1038/nn.4268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Li W, Li S, Shen L, Wang J, Wu X, Li J, Tu C, Ye X, Ling S. Impairment of dendrodendritic inhibition in the olfactory bulb of APP/PS1 mice. Front Aging Neurosci 11: 2, 2019. doi: 10.3389/fnagi.2019.00002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Sharp AA, Finger TE. GABAergic modulation of primary gustatory afferent synaptic efficacy. J Neurobiol 52: 133–143, 2002. doi: 10.1002/neu.10073. [DOI] [PubMed] [Google Scholar]
- 20. Kollo M, Schmaltz A, Abdelhamid M, Fukunaga I, Schaefer AT. ‘Silent’ mitral cells dominate odor responses in the olfactory bulb of awake mice. Nat Neurosci 17: 1313–1315, 2014. doi: 10.1038/nn.3768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Wachowiak M, Cohen LB. Presynaptic inhibition of primary olfactory afferents mediated by different mechanisms in lobster and turtle. J Neurosci 19: 8808–8817, 1999. doi: 10.1523/JNEUROSCI.19-20-08808.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Cohen J. Statistical Power Analysis for the Behavioral Sciences. London: Taylor & Francis, 2013. [Google Scholar]
- 23. Tomczak M, Tomczak E. The need to report effect size estimates revisited. An overview of some recommended measures of effect size. Trends Sport Sci 1: 19–25, 2014. [Google Scholar]
- 24. Cunningham JP, Yu BM. Dimensionality reduction for large-scale neural recordings. Nat Neurosci 17: 1500–1509, 2014. doi: 10.1038/nn.3776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Rolls ET, Treves A. The neuronal encoding of information in the brain. Prog Neurobiol 95: 448–490, 2011. doi: 10.1016/j.pneurobio.2011.08.002. [DOI] [PubMed] [Google Scholar]
- 26. Ly C, Barreiro AK, Gautam SH, Shew WL. Odor-evoked increases in olfactory bulb mitral cell spiking variability. iScience 24: 102946, 2021. doi: 10.1016/j.isci.2021.102946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Craft M, Barreiro A, Gautam S, Shew W, Ly C. Differences in olfactory bulb mitral cell spiking with ortho- and retronasal stimulation revealed by data-driven models. PLoS Comput Biol 17: e1009169, 2021. doi: 10.1371/journal.pcbi.1009169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Barreiro A, Gautam S, Shew W, Ly C. A theoretical framework for analyzing coupled neuronal networks: application to the olfactory system. PLoS Comput Biol 13: e1005780, 2017. doi: 10.1371/journal.pcbi.1005780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Xiao Z-C, Lin KK, Young L-S. A data-informed mean-field approach to mapping of cortical parameter landscapes. PLoS Comput Biol 17: e1009718, 2021. doi: 10.1371/journal.pcbi.1009718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Carey RM, Verhagen JV, Wesson DW, Pírez N, Wachowiak M. Temporal structure of receptor neuron input to the olfactory bulb imaged in behaving rats. J Neurophysiol 101: 1073–1088, 2009. doi: 10.1152/jn.90902.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Scott JW, Acevedo HP, Sherrill L, Phan M. Responses of the rat olfactory epithelium to retronasal air flow. J Neurophysiol 97: 1941–1950, 2007. doi: 10.1152/jn.01305.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Rall W, Shepherd GM, Reese TS, Brightman MW. Dendrodendritic synaptic pathway for inhibition in the olfactory bulb. Exp Neurol 14: 44–56, 1966. doi: 10.1016/0014-4886(66)90023-9. [DOI] [PubMed] [Google Scholar]
- 33. Cang J, Isaacson JS. In vivo whole-cell recording of odor-evoked synaptic transmission in the rat olfactory bulb. J Neurosci 23: 4108–4116, 2003. doi: 10.1523/JNEUROSCI.23-10-04108.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Wang Z-J, Sun L, Heinbockel T. Cannabinoid receptor-mediated regulation of neuronal activity and signaling in glomeruli of the main olfactory bulb. J Neurosci 32: 8475–8479, 2012. doi: 10.1523/JNEUROSCI.5333-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Dietz SB, Murthy VN. Contrasting short-term plasticity at two sides of the mitral–granule reciprocal synapse in the mammalian olfactory bulb. J Physiol 569: 475–488, 2005. doi: 10.1113/jphysiol.2005.095844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Saxena S, Cunningham JP. Towards the neural population doctrine. Curr Opin Neurobiol 55: 103–111, 2019. doi: 10.1016/j.conb.2019.02.002. [DOI] [PubMed] [Google Scholar]
- 37. Li G, Cleland TA. A two-layer biophysical model of cholinergic neuromodulation in olfactory bulb. J Neurosci 33: 3037–3058, 2013. doi: 10.1523/JNEUROSCI.2831-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Viertel R, Borisyuk A. A computational model of the mammalian external tufted cell. J Theor Biol 462: 109–121, 2019. doi: 10.1016/j.jtbi.2018.10.003. [DOI] [PubMed] [Google Scholar]
- 39. Bathellier B, Lagier S, Faure P, Lledo P-M. Circuit properties generating gamma oscillations in a network model of the olfactory bulb. J Neurophysiol 95: 2678–2691, 2006. [Erratum in J Neurophysiol 95: 3961–3962, 2006]. doi: 10.1152/jn.01141.2005. [DOI] [PubMed] [Google Scholar]
- 40. Li G, Cleland TA. A coupled-oscillator model of olfactory bulb gamma oscillations. PLoS Comput Biol 13: e1005760, 2017. doi: 10.1371/journal.pcbi.1005760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Grabska-Barwińska A, Barthelmé S, Beck J, Mainen ZF, Pouget A, Latham PE. A probabilistic approach to demixing odors. Nat Neurosci 20: 98–106, 2017. doi: 10.1038/nn.4444. [DOI] [PubMed] [Google Scholar]
- 42. Hiratani N, Latham PE. Rapid Bayesian learning in the mammalian olfactory system. Nat Commun 11: 3845, 2020. doi: 10.1038/s41467-020-17490-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Gautam SH, Short SM, Verhagen JV. Retronasal odor concentration coding in glomeruli of the rat olfactory bulb. Front Integr Neurosci 8: 81, 2014. doi: 10.3389/fnint.2014.00081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Bolding K, Franks K. Simultaneous extracellular recordings from mice olfactory bulb (ob) and piriform cortex (pcx) and respiration data in response to odor stimuli and optogenetic stimulation of ob.https://crcns.org/data-sets/pcx/pcx-1. [Google Scholar]
- 45. Bolding KA, Franks KM. Recurrent cortical circuits implement concentration-invariant odor coding. Science 361: eaat6904, 2018. doi: 10.1126/science.aat6904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Meredith M. Neural circuit computation: complex patterns in the olfactory bulb. Brain Res Bull 29: 111–117, 1992. doi: 10.1016/0361-9230(92)90014-o. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
See https://github.com/michellecraft64/Modality for MATLAB code implementing the data analysis and firing rate model.
See https://doi.org/10.6084/m9.figshare.14877780.v1 for raw data collected from the Shew Lab.