Coiled-coil domains are sufficient to drive liquid-liquid phase separation in protein models

Abstract

Liquid-liquid phase separation (LLPS) is thought to be a main driving force in the formation of membraneless organelles. Examples of such organelles include the centrosome, central spindle, and stress granules. Recently, it has been shown that coiled-coil (CC) proteins, such as the centrosomal proteins pericentrin, spd-5, and centrosomin, might be capable of LLPS. CC domains have physical features that could make them the drivers of LLPS, but it is unknown if they play a direct role in the process. We developed a coarse-grained simulation framework for investigating the LLPS propensity of CC proteins, in which interactions that support LLPS arise solely from CC domains. We show, using this framework, that the physical features of CC domains are sufficient to drive LLPS of proteins. The framework is specifically designed to investigate how the number of CC domains, as well as the multimerization state of CC domains, can affect LLPS. We show that small model proteins with as few as two CC domains can phase separate. Increasing the number of CC domains up to four per protein can somewhat increase LLPS propensity. We demonstrate that trimer-forming and tetramer-forming CC domains have a dramatically higher LLPS propensity than dimer-forming coils, which shows that multimerization state has a greater effect on LLPS than the number of CC domains per protein. These data support the hypothesis of CC domains as drivers of protein LLPS, and have implications in future studies to identify the LLPS-driving regions of centrosomal and central spindle proteins.

Significance

The liquid-liquid phase separation of coiled-coil proteins has been implicated in the formation of membraneless organelles such as the centrosome and central spindle. Little is known about the features of these proteins that might drive their phase separation. We developed a modeling framework to investigate the potential role of coiled-coil domains in phase separation, and show that these domains are sufficient to drive the phenomenon in simulation. We additionally show the importance of multimerization state on the ability for such proteins to phase separate. This work suggests that coiled-coil domains should be considered for their contribution to protein phase separation.

Introduction

Liquid-liquid phase separation (LLPS) is important for the formation of biomolecular condensates. LLPS occurs in cells when macromolecules interact favorably with each other, demix from bulk cytosol, and form a concentrated coexisting phase. This phase can be liquid-like or become more gel-like, losing its liquid character (1,2). Here, we use LLPS broadly to describe condensates of varying viscoelastic characteristics. LLPS provides a mechanism for cells to localize protein and chemical function (3) without the need for membrane enclosure into aptly named membraneless organelles (3,4,5,6). Examples of membraneless organelles that are thought to form via LLPS include P-bodies, nucleoli, stress granules (6,7), centrosomes (8,9,10), and the central spindle (11). The formation of condensates in vitro is well supported but the role of biologically relevant LLPS, specifically in the biogenesis of membraneless organelles, is actively debated.

There is recent evidence that coiled-coil (CC) proteins have the propensity for LLPS. The formation of the centrosome and central spindle in particular seems to rely on the LLPS of CC proteins. Examples of phase-separating centrosomal proteins include spd-5 (12), centrosomin (13), and pericentrin (14,15). MAP65 and its mammalian homolog PRC1, both of which help form the central spindle, can undergo LLPS as well (11). In these examples, LLPS propensity is assessed qualitatively by the formation of putative LLPS condensates either in cells or in vitro. Recent studies with spd-5 provide evidence that interactions between its CC domains drive its supramolecular assembly (16,17); experiments with pericentrin and centrosomin also suggest an important role of their CC domains in LLPS (13,15). There are other CC proteins that LLPS, such as the Golgi structural protein GM130 (18), the measles phosphoprotein (19), transcription factors FLL2 (20) and TAZ (21), the endocytic trafficking protein Ede1 (22), a protein encoded by retrotransposable element LINE-1 ORF1 (23), the RNA-binding protein Whi3 (24), and a carboxysome-positioning protein McdB (25). There have also been recent advances in the engineering of membraneless organelles using CC domains. Hilditch et al. (26) showed that enzymes fused to engineered CC domains can phase separate into functional condensates in bacteria. Ramšak et al. (27) demonstrated that proteins made from a suite of orthogonally designed CC domains can form coexisting condensates in mammalian cell systems and can also be functionalized. These studies support a narrative that CC domains are involved in LLPS, but it is unknown how they might be contributing and if they themselves are sufficient to drive the process in naturally occurring proteins. We are motivated by these examples of phase-separating CC proteins and in this paper we attempt to answer the question: Do the physical features of CC domains enable them to drive the LLPS of proteins?

LLPS is typically driven by multivalency (28,29,30), which is the ability of molecules to form many attractive interactions with other, similar molecules. A useful conceptual framework for LLPS that is driven by multivalent interactions is the stickers-and-spacers model of associative polymers (28,31). In this framework, stickers are specific macromolecular components (e.g., residues, domains, or globular patches on proteins) that interact associatively, whereas spacers are the remainder of the macromolecule that tether the stickers together. This framework applies equally well to intrinsically disordered proteins (IDPs) with stickers being individual residues, as it does for proteins where folded domains are stickers and the spacers are flexible linkers tethering the domains together. Multivalency thus increases as the number of stickers in a protein increases. It has also been shown that increasing the multivalency of a protein not only increases its network connectivity (32) in condensates (33), but can also affect material properties such as increasing apparent condensate viscosity (34). There are a few examples that show the effect of folded-domain-stickers on protein LLPS, such as the synthetic SH3-PRM system introduced by Li et al. (35) and ubiquitin shuttle proteins p62 and UBQLN2 (36,37). Herein, we use the term polymeric multivalency to refer to the number of stickers in a single protein chain.

Multimerization of individual stickers is a plausible, but not well explored, multivalency mechanism in proteins. Most discussion of multivalency in proteins has focused on dimers, rather than interactions of larger valency. This is likely because sticker interactions are often assumed to be 1:1, meaning the entirety of one sticker interacts only with the entirety of one other sticker. This is an assumption that comes from the simplifications used in polymer theory models, e.g., theory of associative polymers (28,31). Higher orders of multimers likely occur naturally between residue-level stickers, however. Charged (38) and polar amino acids can engage in multiple interactions simultaneously, for example, in the coordination of metal ions (39,40). Multivalent interactions for residue-level stickers can be an important factor in protein LLPS (41,42). Multimerization between protein domains can also occur naturally to increase LLPS propensity (37), and this requires treating entire protein domains as individual stickers. There are few recent studies that have explored multimerization and its effects on LLPS. Carter et al. (43) showed that mutants of TDP-43 containing a tetramerization domain have higher LLPS propensity than wild-type TDP-43 with its dimerization domain. A cornucopia of examples of LLPS affected by multimerization have been reported (summarized by Mohanty and Kapoor (37)), but beyond these few the role that multimerization plays in affecting multivalency has not been well explored. In this paper we use the term multimeric multivalency to refer to the number of partners that an individual sticker is capable of interacting with at once. We use the familiar terms dimer, trimer, tetramer, etc., to describe specific varieties of multimers.

CC proteins could potentially utilize both polymeric and multimeric multivalency mechanisms to drive LLPS through their CC domains. If we apply the stickers-and-spacers framework to CC proteins and treat the CC domains as the stickers, we see that these proteins harness both polymeric and multimeric multivalency. CC proteins can show varying degrees of polymeric multivalency dependent on the number of CC domains in the protein. CC domains also have intrinsic multimeric multivalency because of their ability to form dimers (44), trimers, tetramers, and larger multimers (45). Proteins containing many CC domains could realize LLPS through a combination of polymeric and multimeric multivalence mechanisms; the extent to which this may happen is not understood.

We hypothesize that CC domains are sufficient to drive the LLPS of proteins and that this phenomenon can be tuned by both their polymeric and multimeric multivalency. We generated a novel modeling framework to test our hypothesis by coarse-grained (CG) molecular simulation (Fig. 1). We use this framework to build CC proteins where CC domains are tethered to other CC domains with disordered linker regions (Fig. 1 A). This framework allows us to specify the polymeric multivalency of CC proteins by changing the number of CC domains in a given protein chain (Fig. 1 C) as well as the multimeric multivalency of each CC domain (Fig. 1 D). For the purposes of this paper, we restrict our attention to dimer-, trimer-, and tetramer-type multimers. In our study, we define LLPS propensity generally as the ability to form an LLPS droplet at any of the tested temperatures. This allows us to compare proteins’ LLPS propensity by apparent melting temperature, or the lowest temperature where no droplet exists in simulation. The phase-separated state generally has lower entropy, and thus becomes stable at lower temperatures. Simulated proteins, which form droplets at high temperatures, have higher LLPS propensity than proteins whose droplets exist at a lower temperature. Assessing LLPS propensity of proteins by ranking melting temperature is a common method used in the LLPS field (7,46,47). We designed our modeling framework to focus on general physical properties of phase separation of CC proteins when treated as associative polymers.

Figure 1.

The CC LLPS framework can be used to make CC proteins with varying polymeric and multimeric multivalency. (A) Coil segments and linker segments can be combined in any number to make a coil protein, e.g., a 2-coil-1-linker protein. Haloed spheres represent the CG beads, and are removed in later visualizations for clarity. Helices are the coil segments. Light gray tubes are the linker segments. (B) Schematic representation of the maximally specific interaction scheme used in this study, where only interchain interactions between the same type of coil segment are permitted, indicated by a solid black line. Dotted lines with red “x” labels are prohibited interactions within our framework. (C) The polymeric multivalency of a CC protein can be modified by changing the number of coil segments in the protein. Only two to five coil segments are shown, but there could be an arbitrarily large number of coil segments per protein (represented by ellipses). (D) The multimeric multivalency of a protein can be modified by changing the type of multimer that a coil segment is favored to form. Both top-down and side views of multimers are presented for clarity. Individual coils are colored separately purely for visual clarity, and do not have additional meaning. All molecular visualizations were produced using open-source PyMOL v.2.5.0. To see this figure in color, go online.

Methods

Software

All molecular dynamics (MD) simulations were performed using unmodified GROMACS (48) v.2022.1. GROMACS was compiled with GCC v.11.2.0 and Open MPI v.4.1.1 for parallel processing on the Alpine high-performance computing resource at the University of Colorado Boulder, and with GCC v.10.2.0 and Open MPI v.4.0.5 for Bridges-2. Non-MPI enabled versions of GROMACS v.2022.1 were used for small-scale simulations and some data analysis and processing. These versions were compiled on a Ubuntu machine (22.04.2 LTS) with GCC 11.2.0 and MacOS 12.6 with AppleClang 14.0.0. Additional analysis code was written in Python 3.9.

Code availability

Files from this study, including MD parameter files, relevant topologies, analysis scripts, etc., are available on the GitHub repository associated with this manuscript: https://github.com/dora1300/cc_llps_framework.

Creating the CG framework for CC-driven LLPS

We developed a bespoke, CG MD framework to study CC LLPS, inspired by other types of CG models of CC proteins (49,50). Computational methods have been critical in the understanding of protein LLPS (29), but before this study there were no tools specifically designed for studying CC-driven LLPS. We designed our framework to be easy to use and readily modifiable, with defined specificity between coil segments (Fig. 1 B), and the ability to represent a variety of different CC proteins of arbitrary size (Fig. 1 C) with coils of any desired multimerization state (Fig. 1 D).

We define CC proteins as linear combinations of coil segments (stickers) and linker segments (spacers) (Fig. 1 A), which is inspired by the organization of centrosomal proteins (17,51). Coil segments are regions of the protein that represent CC domains, and linker segments are the tethers between coil segments. We specifically choose this language to avoid confusion with terms like “domains,” which can have multiple meanings. This organization allows us to treat CC proteins as associative polymers, where each coil segment acts as a single sticker and each linker segment as a spacer. We implemented the framework with the following design goals and simplifying assumptions in mind: 1) coil segments are always helical, and linkers are always disordered, 2) attractive protein–protein interactions only occur through coil segments, 3) coil segments retain a heptad-repeat-like CG bead organization so that coils interact in a similar geometry to real CC domains, and 4) all other protein-protein interactions, other than coil-coil interactions, have effective attraction energies equal to that of protein-solvent interactions. We therefore treat the solvation effects implicitly and omit any solvent particles themselves, modeling linker segments with only the repulsive component of the Lennard-Jones potential (see supporting material, section II; Eq. 1). Given the box sizes involved, treating solvation in this manner greatly increases accessible timescales.

Our framework uses C-α coarse-graining, which represents every amino acid as a single CG bead. These beads are centered at the same coordinates as the C-α carbons of amino acids in a corresponding atomistic representation of a protein. The C-α CG procedure maps traditional φ,ψ angles into CG space (52). The corresponding CG pseudobond angles and pseudotorsions allow us to reproduce correct secondary structure geometries in the CG structures. A CG representation thus has significantly fewer beads than an atomistic representation (on average, 19 atoms are replaced by 1 bead), which greatly increases computational efficiency in molecular simulation, as well as increasing the time step allowed by increasing the effective masses of the aggregated particle. Additional information about the framework’s structural features and interaction parameters (along with details about each bead type used, Fig. 2) are provided below and in supporting material, sections I and II, respectively. Importantly, we restrict interactions between coil segments such that only interchain interactions between coils of the same type can occur. We term this the maximally specific interaction regime. This interaction scheme is biologically motivated—CC domains are known to interact specifically in a sequence-dependent manner (53,54), both in naturally occurring and engineered proteins (27,55,56). We would not expect multiple CC domains of different sequences, within a single CC protein, to interact equally with all other CC domains in the same protein and thus the maximally specific interaction regime is a reasonable scheme to study in the context of CC proteins.

Figure 2.

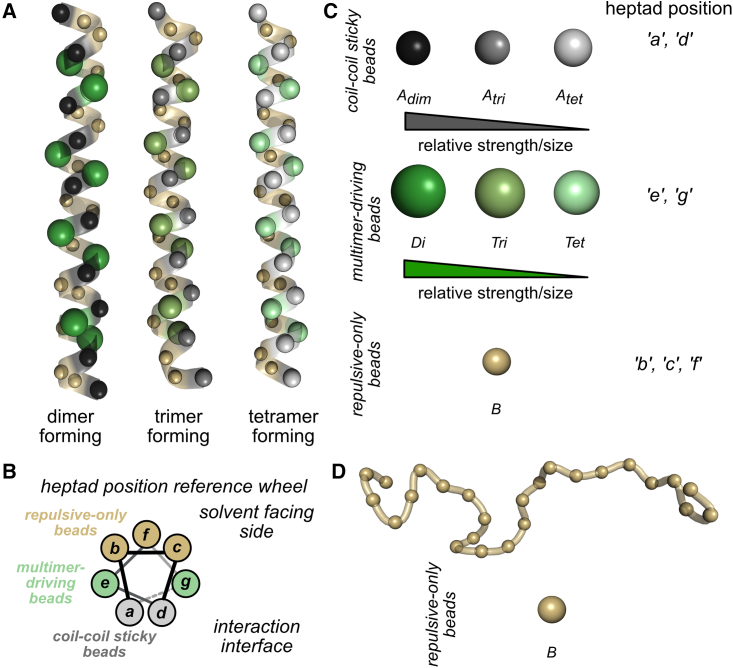
Schematic of bead types used in the CC-LLPS framework following the nomenclature used in Table S3. In all panels, gray-scale spheres refer to coil-coil sticky beads, green-scale spheres refer to multimer-driving beads, and gold spheres refer to repulsive-only beads. Bead sizes in (A, C, and D) are scaled relative to the size of the Di multimer-driving bead based on each bead’s σ parameter listed in Table S3. Visualizations produced using open-source PyMOL v.2.5.0. (A) Representative coil segments containing 32 CG beads similar to coils used in this study. Dimer-, trimer-, and tetramer-forming coils are shown with their respective bead types. Backbone is shown in transparent ribbon-style. Coils are positioned with the coil-coil sticky beads facing the viewer. (B) CC helical wheel demonstrating the canonical heptad repeat. CC wheel is constructed top-down as viewed through the central axis of a CC segment. Bonds between beads are represented as a gray scale beam, with beams close to the viewer shown as solid black lines, and beams farther from the viewer shown as light gray. The dotted beam indicates where the heptad repeat restarts. (C) Diagram of each coil segment bead separated by bead type and organized by relative strength and size, along with their heptad position location. (D) Representative linker segment containing 25 CG beads similar to linkers used in this study. The backbone is shown in transparent ribbon-style. To see this figure in color, go online.

MD parameters

We used a consistent set of MD run parameters throughout the study, and any deviations from these parameters are noted in the respective methods. Energy minimization was performed using steepest descent to a force tolerance of $<$50 kJ/mol/nm and a step size of 2 pm. Equilibration and production simulations were done with Langevin dynamics using the sd integrator with a friction coefficient of 0.2 ps⁻¹. The center of mass translational velocity was removed every 10 steps. Lennard-Jones potentials were shifted and cutoff at 1.1 nm, consistent with other CG force fields (57). The verlet-buffer-tolerance, a GROMACS-specific setting for Verlet list updates, was set to $1\times {10}^{-7}$. Setting this parameter correctly is important for reproducibility because using default larger numbers for verlet-buffer-tolerance results in simulation instability, due apparently to density inhomogeneity in phase-separated simulation boxes. Random seeds for each simulation were generated pseudorandomly by GROMACS. Periodic boundary conditions were applied in all three dimensions. We used a single box size for slab simulations to maintain consistent configurational entropy between experiments. The final box size for slab simulations is 25 × 25 × 150 nm, which is similar to previous studies (7).

Validating structural distribution of a CG CC dimer

We verified that simulated CG CC dimers reproduce similar structural distributions and equilibrium folding propensity to atomistic simulations of a CC dimer. Thomas et al. (58) performed 100 ns atomistic temperature replica-exchange (REMD) of two, 32-amino-acid-long CCs starting in a dimer configuration and published the backbone root mean-squared displacement (RMSD) of each replica. We reconstructed a mean RMSD distribution of their replicas to serve as our reference for a stable, CC dimer (Fig. S2 A). We performed simulations of a CG CC dimer in our framework and compared our backbone RMSD distribution with the reference. Specific details are provided in supporting material, section V. Fig. S2, B and C shows the backbone RMSD distributions across different coil-coil sticky interaction strengths at 293 K (Fig. S2 B) and 310 K (Fig. S2 C). We generated Gaussian kernel density estimates for all of the RMSD distributions and determined the similarity between our CG RMSD data to the atomistic reference distribution by calculating the Kullback-Leibler divergence (Table S4). The lowest Kullback-Leibler divergence at both temperatures was from the 5.5 kJ/mol simulations (298 K, 0.90 nats; 310 K, 1.01 nats). Thus, 5.5 kJ/mol was chosen as the optimal coil-coil sticky interaction strength (for dimer-forming coils) for our framework.

Parameterizing disordered linker segments

We fine-tuned the linker segment parameters by systematically weakening the magnitude of the linker structural parameter force constants starting from the coil segment values, and determined the optimal force constants by comparing simulated R_g values of 23 IDPs against experimentally determined R_g values (details in supporting material, section VI). The interaction parameters of the linker beads was left unaltered in all cases. Fig. S3 shows a parity plot comparing simulated with experimental R_g values for the 23 tested proteins, with structural parameter force constants 100$\times$ weaker than coil segment (i.e., helix-forming) parameters. This level of weakening produced the best correlation between simulated and experimental data. The Pearson correlation coefficient between simulated and experimental data is 0.753. The slope of the simulated versus experimental data is 0.814 and is qualitatively close to the parity line. We judge that this qualitative agreement to real IDPs is sufficient for this study, even in the absence of amino-acid-specific chemical information and attractive interactions between the repulsive-only linker beads.

Assessing multimerization capacity of coil segments

We confirmed that we have moderate control over the multimerization of coil segments in the CC LLPS framework. We verified this by simulating several copies of a 3-coil-2-linker protein with each of the multimer-driving bead types and quantified the multimer species present in the simulations (details provided in supporting material, section VII). We organized the interacting CG beads within the coil segments to mimic the heptad-repeat seen in real CCs (Fig. 2, A and B). The parameter design of the interacting beads was based on the distances between CC domains from experimentally determined crystal structures of dimers, trimers, and tetramers so that we could better capture the biophysics of multimer formation within our CG framework (additional details in supporting material, section III).

Simulations with the dimer multimer-driving beads (Fig. S4 A) show that dimers are the dominant multimer present at about 60% composition over simulation time. Simulations with the trimer multimer-driving beads (Fig. S4 B) produce a mixture of multimers with the dominant multimer species being the trimer at 46% of composition averaged over time. Tetramer multimer-driving beads result in a structure that still favors trimers but can form tetramers (Fig. S4 C), with the trimer and tetramer multimer species comprising 38 and 26% of composition over time, respectively, at a coil-coil sticky interaction strength of 4 kJ/mol. Despite this structure having more trimer than tetramer species, we will refer to it as the tetramer-forming model as it is the only one that forms an appreciable amount of tetramers. Attempts to shift the multimer population toward the tetramer species by changing the coil-coil sticky interaction strength either ablated multimer formation (3 kJ/mol) or resulted in pentamers appearing in the simulation (5 kJ/mol), suggesting that 4 kJ/mol is near optimal strength for tetramer-forming beads (Fig. S4 C) in our model framework.

The coil-coil sticky interaction parameter (i.e., the effective pair interaction strength parameter) for both the trimer- and tetramer-forming models is weaker than the dimer-forming model to prevent the formation of aberrantly large multimers. It is necessary to make the trimer- and tetramer-specific coil-coil sticky strengths weak because trimers and tetramers involve more coil segment interactions than dimers and each participating coil would contribute too much interaction energy if their parameters were identical to the dimer-specific parameters. The strength of multimer-driving beads (the bead type that helps provide specificity in the type of multimer formed, see Fig. 2, A and C) is also decreased in the trimer- and tetramer-specific models compared with the dimer parameters for the same reason. Fig. 2 C shows a schematic of the relative bead size and strengths in each of the multimer-forming models. Increasing the interaction strength for all types of multimer-driving beads resulted in multimers with more than four coils. The lack of full specificity in the trimer- and tetramer-forming coils might be a fundamental limitation of using a C-α coarse-graining approach, but the specificity achieved is sufficient to demonstrate the trends in this paper.

Determining the relative energies of multimer interactions

The interaction strength between coil segments (i.e., stickers) might affect the phase separation behavior of interacting proteins, apart from any polymeric or multimeric multivalency. We determined that trimer- and tetramer-forming coils have moderately weaker interaction energy on a per-binder basis upon multimer formation compared with dimer-forming coils. We performed temperature replica exchange MD simulations of dimer-, trimer-, and tetramer-forming coils using parameters listed in Table S3. For each type of multimer-forming coil, we simulated 2, 3, and 4 copies of individual coil segments in a box to assess multimerization energy. Specific simulation details are provided in supporting material, section VIII. Fig. S5 shows, for each system, multimer-dissociation curves that are the average Lennard-Jones energy at each of the temperature replicas. Table S2 shows the Lennard-Jones energy of each system at 10 K, along with the average per-binder energy, which is used to compare the relative interaction strength between the different multimer-forming coils. Per-binder interaction energies demonstrate that dimer-forming coils are stronger than trimer- or tetramer-forming coils for 2 and 3 coils in a box (Table S2). For 4 coils in a box, dimer- and tetramer-forming coils have comparable interaction strength while trimer-forming coils are weaker (Table S2). These results indicate that any observed LLPS propensities in subsequent phase coexistence simulations are primarily a result of multivalency and not from large differences in interaction energy between the different multimer-forming coils.

Determining phase coexistence using the slab simulation protocol

We used the slab simulation (7,59,60) protocol to directly simulate phase coexistence of CC protein models. This procedure involves the following steps: generating configurations of each protein of interest, placing copies of those configurations in a simulation box, compressing the box in one dimension in the NPT ensemble to generate the slab, expanding the box in the same compressed dimension, equilibrating the slab to the desired temperature in the NVT ensemble, and, finally, production simulation in the NVT ensemble. We note that during the packing of the simulation box, copies of proteins are placed randomly throughout, but we fix the total number of protein copies so that all simulations have the same total number of coil segments. This allows us to make comparisons between simulations of different proteins.

Generating starting configurations of CC proteins

We generated proteins of interest using the PeptideBuilder strategy (supporting material, section IX) and then used MD to equilibrate the structure of each protein and prepare it for slab simulation. A single copy of each protein is placed into a simulation box large enough to accommodate the initial structure. Single molecules were energy minimized and then equilibrated in the NVT ensemble for 500 ps with a time step of 25 fs. NVT equilibrations were used so that the linker segments could relax out of the initial helical configuration and closer to the defined equilibrium angles. At this point, for each protein structure we generated a unique single-molecule simulation for every temperature that would be used in the forthcoming slab simulations, i.e., 253, 273, 293, and 313 K. Production MD simulations in the NVT ensemble were performed on all equilibrated structures for 5 μs with a time step of 25 fs at their corresponding temperatures. Only one replicate simulation was used for each single-molecule simulation at each temperature.

We begin the slab protocol by randomly packing copies of our proteins of interest in a simulation box. The single-molecule simulations served as the pool of configurations from which we pack the starting box. We standardized the total number of coil segments in a simulation box to 450 coils for all protein models. Simulations with four coils per protein had a total of 448 coils in each box. The following protein copy numbers were used to achieve the desired number of coil segments: 225 copies of 2-coil proteins; 150 copies of 3-coil proteins; and 112 copies of 4-coil proteins. We mitigated configurational bias by randomly choosing 5 configurations from the equilibrated portion of the single-molecule simulations (equilibrated state began by 100 ns), using random numbers generated from Random.org. Each of the 5 configurations from each protein was copied so that the total coil density in the simulation would reach the desired number (450). We prepared three replicate simulations at every desired temperature, with different random numbers for each replicate, using only the corresponding single-molecule trajectories to provide the structures. packmol v.20.11.1 (61) was used to pack all the initial slab boxes, with a tolerance of 1.0 nm between every protein copy, into a box size of 25 × 25 × 100 nm to ensure all copies would fit inside. We generated initial slab simulation boxes for every protein of interest, at every desired temperature, in triplicate.

Slab simulation approach

Packed boxes were energy minimized and then equilibrated in the NPT ensemble for 200 ns with a time step of 20 fs at 150 K. The goal of this step is to create the actual protein slab to assess phase coexistence. Semi-isotropic pressure coupling was applied only in the z-dimension of the box. The Parrinello-Rahman barostat was used with a reference pressure of 1 bar, compressibility of 3 $\times$ 10^-4 bar^-1, and a time constant of 5 ps for the coupling. Simulation boxes are compressed to approximately 10–20% of the starting z axis length at the end of NPT equilibration. Proteins were “unwrapped” before expanding the box to prevent aberrant expansion of individual proteins. The simulation box was edited such that the z-dimension became the final length of 150 nm, and the protein slab was kept centered in the simulation box during expansion. Slabs in expanded boxes were then equilibrated in the NVT ensemble for 200 ns with a time step of 20 fs, at the desired temperatures. We then performed production MD simulations in the NVT ensemble for each temperature-equilibrated slab for a total of 20 μs with a time step of 25 fs, with the GROMACS parameter rdd set to 1.6 nm (important for domain decomposition). We found that long simulation times for our proteins are necessary when compared with other studies with the slab method (7,60,62) to ensure that our systems reach our definition of density equilibrium.

Determining equilibrium in slab simulations

Equilibrium was assessed by monitoring the number density stability in several locations in the simulation box during the time course of each simulation. Equilibrium assessments were only calculated after any observed droplet was centered in the simulation box, for each analyzed frame (see additional details below, section “Density profile and binodal analysis”). We calculated the average number density in the center of the box (coordinates 55–95 nm in the z-dimension) to measure the stability of the putative dense region. We additionally calculated the average number density across the periodically connected ends of the box (coordinates 0–24 nm, and 126–150 nm in the z-dimension) to measure the stability of the dilute region. Number density is calculated per frame using gmx_density. Fig. S6 A shows a schematic of the regions analyzed for equilibration in reference to a simulation box for visual interpretation.

We considered the simulation/slab to be equilibrated when the density of both these regions was stable. Fig. S6 shows two representative equilibration series for a 2-coil-1-linker dimer-forming protein (Fig. S6 B) and a 3-coil-2-linker tetramer-forming protein (Fig. S6 C) at each simulated temperature. Only the equilibrated portions of trajectories were used for downstream analysis. Almost half of all simulations equilibrated within 2.5–5 μs, but some simulations, particularly the 4-coil containing proteins and proteins with tetramer-forming coils, took up to 10 μs to equilibrate.

Assessing multimer formation in slab simulations

We quantified the populations of multimers in each of the slab experiments to determine if the same multimerization patterns that exist in initial parameterization are maintained in the slaps. We used a similar analysis approach used to parameterize the different multimer-forming beads (Fig. S4; supporting material, section VII). Slab simulations of dimer-forming coils (Fig. S7) show that different polymeric multivalencies all result in dimer species that are approximately 60% of composition averaged over time at 293 K. This is similar to the behavior observed during model parameterization at 298.15 K (Fig. S4 A). Slab simulations of trimer-forming coils (Fig. S8) result in a slightly higher percentage composition of trimer species at 293 K, ranging from 50 to 62%, than the model parameterization data (Fig. S4 B). Slab simulations of tetramer-forming coils (Fig. S9) result in a range of tetramer species compositions of 21–32% averaged over time, which is around the value of 26% tetramer composition observed during parameterization (Fig. S4 C). Aberrantly large multimers were not observed in slab simulations, with the exception of low percent composition of trimers in dimer-forming coil proteins at 253 K. These data show slight deviations of multimerization behavior between model parameterization and slab simulations, but support that multimer formation behaves largely as expected for all phases.

We also observed that increasing polymeric multivalency from 2- to 4-coils for dimer-forming coil proteins (Fig. S7) results in less dimer species and more monomer species in terms of average percent composition of simulation time at all simulated temperatures. A similar polymeric-multivalency-dependent decrease in the target multimer species for trimer- (Fig. S8) and tetramer-forming (Fig. S9) coils is also seen. This suggests that, for our specifically interacting CC proteins (see supporting material, section IV for explanation of specifically interacting), there is a slight penalty in multimer species formation as polymeric multivalency is increased.

Density profile and binodal analysis

We performed density analysis of each density equilibrated trajectory using the gmx_density module in GROMACS. Trajectories for density analysis are first modified so that the largest cluster in each frame is centered in the simulation box, which is necessary for generating density profiles. Trajectory centering was performed on a frame-by-frame basis, using a two-step approach. Protein molecules in each trajectory were corrected for movement across periodic boundaries using two sequential calls to gmx_trjconv, first using “-pbc nojump” and then using “-pbc whole”. Coarse density profiles, on the periodic boundary-corrected trajectories, were calculated using gmx_density by dividing the simulation box into 20 equal-sized slices along the z-dimension. The entire system was then translated so that the slice containing the highest density is placed in the center. Then, we identified the largest cluster in the same frame using gmx_clustsize and translated the entire system again so that the center of mass of the largest cluster was placed in the center of the box. This two-step method is needed to avoid the rare instances that arise when a slab exists across the periodic boundary in the z-dimension, which causes the second step of the method to fail. Density (reported as number density/nm³) was calculated using the slab-centered trajectories in 2 nm slices along the z axis of the simulation box, and the average density in each 2 nm slice for the entire density equilibrated trajectory was output. Density was calculated every 10 ns of simulation. Density profiles along the z axis were averaged across three replicate simulations and plotted as mean (solid line) ± SD (shaded region). These data are used in determining LLPS in combination with molecular cluster analysis (described below). We also used the density output to calculate binodals. For a single trajectory, number densities in the center of a slab corresponding to 70–80 nm in the z-dimension were averaged to describe the dense region. Number densities at the edges of the box not corresponding to a slab, ranging from 1 to 35 and 115–150 nm in the z-dimension, were averaged to represent the dilute region. The coordinates corresponding to the dense and dilute regions here are different to those used to determine equilibration. Dense and dilute regions across triplicate simulations were averaged and plotted along with standard deviation in binodals.

Molecular cluster analysis

Molecular cluster size distributions were determined from every 10 ns of equilibrated trajectories using the gmx_clustsize module in GROMACS. Cluster sizes for whole molecules were calculated using a distance cutoff of 0.9 nm between interacting pairs. The output cluster size populations were normalized to probabilities and averaged for each temperature replicate for each protein of interest, and are reported as mean ± SD over three replicate simulations. Molecular cluster analysis is used to help determine LLPS in slab simulations in combination with density profile analysis. Both a molecular cluster containing nearly all of the proteins in a simulation and the simultaneous presence of a density transition in the z-direction are markers of LLPS.

Analyzing mean-squared displacement and effective diffusion

The average mean-squared displacement (MSD) for each type of protein was calculated using the gmx_msd module in GROMACS. The MSD of individual protein molecules was calculated from each molecule’s center of mass. Analysis occurred every 10 ns from the final 10 μs of each trajectory. Molecules were made whole, and periodic boundary conditions were accounted for in all three dimensions. The configuration at time 10 μs was used as the reference. Individual protein MSD data were then averaged for each replicate. Effective diffusion coefficients at all temperatures for proteins that form LLPS droplets were estimated from the MSD data from 1 to 5 (μs) lag-time via bootstrapping. A total of 450 data points were sampled with replacement randomly from any of the three replicate MSD data sets for any given protein. A line was fit to each set of 450 randomly sampled points, and the diffusion coefficient was calculated by dividing the estimated slope by 6. The averaged effective diffusion coefficient and standard deviation was calculated from 5000 bootstrap cycles. Due to long-timescale kinetic trapping in simulations with LLPS, we do not expect MSD to be linear through all lag-times. Thus the effective diffusion coefficients are likely high compared with the true diffusion coefficients for each system. Effective diffusion coefficients were not corrected for box size, as only the qualitative relative differences in diffusion constants are of interest.

Results

Dimer-forming coil segments can drive LLPS of CC proteins

We hypothesized that CC proteins would readily form LLPS droplets in simulation due to physical features of CC domains that could enable both polymeric and multimeric multivalency mechanisms. We developed a custom simulation framework to study the phase separation of CC proteins, and observed LLPS over a range of polymer multivalency, multimer multivalency, and temperatures.

We first investigated the minimum number of dimer-forming coil segments that are needed in a protein to see LLPS. We designed three CG test CC proteins—2-coil-1-linker, 3-coil-2-linker, and 4-coil-3-linker (Fig. 1 B, first three proteins shown), all with dimer-forming coils—for LLPS propensity using the slab method. We also designed two control proteins—1-coil-0-linker and 1-coil-1-linker with dimer-forming coils—which we expected would not LLPS. An LLPS droplet is determined quantitatively from density profile and molecular cluster analyses and exists when there is both a sharp density transition and the presence of a molecular cluster whose size is close to the number of proteins in the simulation. Averaged density profiles and molecular cluster size distributions for all test proteins are reported in Fig. S12. In addition, density profiles are presented on a semilog y axis in Fig. S13 to show the densities of the dilute phases.

CC proteins with two or more coil segments formed LLPS at 253 K, the lowest of the temperatures that we simulated (reflected in representative snapshots in Fig. 3 and in phase diagrams in Fig. S18 A). This demonstrates that proteins with as few as two coil segments can LLPS at low temperatures. In contrast, LLPS did not occur with either the 1-coil-0-linker (Fig. S10 A) or 1-coil-1-linker (Fig. S11 A) protein at 253 K, as measured by density profiles and molecular cluster analysis. We did observe filamentous-like fibrils in the 1-coil-0-linker protein simulations (Fig. S10 B). The supramolecular fibrils form due to staggered coil segment interactions, which allow multiple coils to stack. Staggered interactions likely arise from the sliding of CC registers long their interaction face (50) and from our choice of dimer-specific interaction bead sizes. One-coil-1-linker dimer-forming coil proteins do not form such fibrils (Fig. S11 B), suggesting a role that flexible linkers might have in limiting coil segment interactions.

Figure 3.

CC proteins with varying number of coil segments all phase separate. Images from slab simulations of 2-coil-1-linker (left), 3-coil-2-linker (middle), and 4-coil-3-linker (right) proteins show that LLPS is supported at varying polymeric multivalency for dimer-forming coils. Snapshots are from simulations at 253 K and 20 μs. Proteins are made whole for visualization, but would wrap through the box boundaries during actual simulation. Visualizations produced using open-source PyMOL v.2.5.0. To see this figure in color, go online.

At temperatures T $\ge$ 293 K, LLPS is not observed and proteins are dilute throughout the system. The 3-coil and 4-coil proteins also formed LLPS droplets at 273 K, unlike the 2-coil protein. Increases in polymeric multivalency is known to increase LLPS propensity (4,35,63,64), and our observations with dimer-forming coils are in line with these reports. Fig. 4 shows a binodal plot for the 3-coil dimer-forming protein (Fig. 4 A) along with a series of snapshots at each temperature corresponding to the points on the binodal (Fig. 4 B). Snapshots of 2-coil (Fig. S14 A) and 4-coil (Fig. S14 B) dimer-forming proteins at each temperature are also presented. These combined data (Figs. 4 and S14) highlight that high temperatures destabilize LLPS droplets and result in dispersed proteins in simulation. These data demonstrate that dimer-forming coil segments are sufficient to drive LLPS of proteins, and that increasing polymeric multivalency slightly increases LLPS propensity.

Figure 4.

LLPS behavior varies with temperature for dimer-forming coil proteins. (A) Binodal plot for a 3-coil-2-linker protein, which also appears in Fig. 6B. Data points on the left-hand side are for dilute regions, and those on the right-hand side are for dense (droplet) regions. No points are shown at 293 K and above as no phase separation occurs at those temperatures. Data points are presented as mean (circles) ± SD (red bars) from three replicate simulations at each temperature. (B) Snapshots (at 20 μs) from slab simulations from one replicate set for a 3-coil-2-linker protein with dimer-forming coils. Gray dotted lines illustrate the correspondence between data in (A) and the approximate associated regions within a simulation box. The snapshot at 253 K is the same as in Fig. 3. Proteins are made whole for visualization, but would wrap through the box boundaries during actual simulation. Density profiles for each temperature shown here can also be seen graphically in Fig. S12A, left column, middle row. Visualizations produced using open-source PyMOL v.2.5.0. To see this figure in color, go online.

It is notable that a 2-coil-1-linker dimer-forming protein can form an apparent LLPS droplet. It might be expected that assemblies of this protein would form one or more long continuous chains and not a network necessary for LLPS. We analyzed the populations of different multimers in the slabs and found that there is a small percent composition of trimers in simulations of dimer-forming 2-coil proteins at 253 K (Fig. S7 A). The ratio of average dimer:trimer percent composition for 2-coil proteins at 253 K is 73:2.2%, or 33.2. Interestingly, this small percent composition of trimers in simulations of the 2-coil dimer-forming protein appears sufficient to allow an LLPS-compatible network can form.

Multimerization greatly affects LLPS propensity, whereas polymer multivalency only weakly affects LLPS propensity

We varied the multimeric state of the three test proteins (2-coil, 3-coil, and 4-coil proteins) and the two control proteins (1-coil-0-linker and 1-coil-1-linker) to make trimer-forming and tetramer-forming versions. We ran slab simulations on these proteins and analyzed the trajectories for evidence of LLPS. The control proteins do not LLPS at 253 K (Figs. S10 A and S11 A) with either trimer- or tetramer-forming coils, and none form fibril-like structures (Figs. S10 B and S11 B).

Density profiles and molecular cluster distributions show an increasing propensity for LLPS as the multimer state increases (Fig. S12). We inspected the trajectories and observed a multimer-state-dependent slab compaction, as demonstrated in Fig. 5 for 2-coil proteins, whereby increasing the multimer state results in a more dense and compact LLPS droplet. This behavior is demonstrated graphically in Fig. 5 A, which additionally highlights a sharp density transition indicative of LLPS. The observed compaction is also evident when examining the dilute phase densities in Fig. S15, where the slab compaction becomes even more apparent. This compaction behavior was observed for 3-coil and 4-coil proteins as well when inspecting representative snapshots (Fig. S16) and density profiles (Fig. S12 A; log-scale y axis density plots in Fig. S13).

Figure 5.

Multimeric multivalency is associated with LLPS droplet compaction. (A) Density profiles for dimer-, trimer-, and tetramer-forming 2-coil-1-linker proteins at 253 K. Solid lines represent mean, and shaded regions are SD, from three replicate simulations. (B) Snapshots (at 20 μs) from simulations shown in (A). Snapshot of dimer-forming protein is same as Fig. 3A, but with different coloring of proteins. Proteins wrap through the box boundaries during simulation, but atoms are shifted into neighboring cells to keep proteins visually intact. Colors are coordinated between (A) and (B). Visualizations produced using open-source PyMOL v.2.5.0. To see this figure in color, go online.

We next quantified the impact that polymeric and multimeric multivalency has on the LLPS propensity of our proteins. Our simulations show two results: 1) polymeric multivalency only slightly impacts LLPS of CC proteins and 2) for a protein with fixed polymeric multivalence, increasing the multimer multivalency dramatically increases LLPS propensity. These results are shown by phase diagrams that compare the phase behavior for all tested proteins (Fig. S18). Increasing polymeric multivalency slightly increased LLPS for dimer-forming coils (Fig. S18 A), but we did not see a similar trend for trimer-forming (Fig. S18 B) or tetramer-forming (Fig. S18 C) coils. We found that, as the multimeric multivalency of the system increased, for a fixed polymer multivalence, the LLPS propensity was more robust, i.e., the apparent melting temperature for all proteins increased as the coil-multimer state increased (Fig. S18). The behavior of the 3-coil and 4-coil tetramer-forming proteins might differ above 313 K, but additional simulations closer to their melting points are needed.

We constructed binodals from all of the simulations for a qualitative picture of LLPS for each of the proteins. Fig. 6 shows the binodals for the (A) 2-coil-1-linker, (B) 3-coil-2-linker, and (C) 4-coil-3-linker proteins, as coil-multimeric state is varied. Data points on the left side of each plot correspond to average densities from the dilute region of the simulation box, and data points on the right side of each plot correspond to average densities from the dense region. We omitted points at temperatures where the dense and dilute regions have overlapping number density, as this represents a one-phase regime and is not shown in binodals. Select data are also shown in Fig. S17 on a log-x scale to highlight the magnitude of densities in the dilute region. These data clearly show that increasing multimeric multivalency strongly increases LLPS propensity and melting temperature of protein droplets. The combination of Fig. S18 and Fig. 6 demonstrate that polymeric multivalence has a relatively small impact on the LLPS propensity of our CC proteins, whereas multimeric multivalence has a much greater influence.

Figure 6.

Multimeric multivalency greatly impacts LLPS propensity. Binodal plots for (A) 2-coil-1-linker proteins, (B) 3-coil-2-linker proteins, and (C) 4-coil-3-linker proteins compare the effect that multimerization has on LLPS propensity. Dimer-, trimer-, and tetramer-forming proteins are represented as black, gold, and silver, respectively. Data points on the left-hand branch of plots are for dilute regions, and those on the right-hand branch are for dense regions. Data points are presented as mean (circles) ± SD (bars) from three replicate simulations. To see this figure in color, go online.

The presence of zero-protein concentrations in the dilute phase, particularly for the tetramer-forming coil models (Fig. S12 A), may suggest that we might not have run the slab simulations for long enough time to observe the rare event of a protein diffusing away from the slab in the limit of a large equilibrium constant between high- and low-density phases. One possible consequence is that our slab simulations might not be equilibrated, despite satisfying our density equilibration metric, which would impact our ability to assess the LLPS propensity of our coil models. To investigate the effect of improved sampling, all trimer- and tetramer-forming slab simulations were extended for an additional 20 μs of simulation time to 40 μs total.

Fig. S19 shows a comparison of density profiles (Fig. S19 A) and cluster profiles (Fig. S19 B) between the 20 and 40 μs slab simulations. There is no significant change in LLPS behavior following the additional 20 μs of simulation time, other than that some density profiles become smoother in the location of the slab (Fig. S19 A). Semilog plots of density profiles from the 40 μs simulations (Fig. S20), which highlight the dilute phase regime, also show no significant change compared with the 20 μs simulations (Fig. S20). Binodal (Fig. S21 A) and semilog binodal (Fig. S21 B) plots are also qualitatively similar to data from the 20 μs simulations. Zero-protein concentrations are not uncommon in profile density plots and binodals for strongly phase-separating systems (e.g., Silmore et al. (60) and Wang et al; (65)), and so our data suggest that, within the timescales accessible to us, our slab simulations are or are close to equilibrated.

We additionally assessed the LLPS propensity of trimer- and tetramer-forming proteins by performing simulations of these models starting from a dispersed state. Both the slab and dispersed state simulations should show evidence of large cluster formation for proteins capable of LLPS (7). Fig. S22 shows the fraction of protein molecules in small clusters and large clusters (see supporting material, section X) over time for trimer- and tetramer-forming proteins at low temperatures. These data show that, at 253 K for almost all proteins, the formation of large clusters from a dispersed state happens fast, within 100 ns, and the resulting large clusters are stable for the duration of the simulation. Simulations at higher temperatures (273 and 293 K) also show that formation of large clusters is fast, but we occasionally see evidence of large clusters breaking and reforming, such as for 2-coil-1-linker tetramer-forming proteins (Fig. S22 B) at 293 K. The breaking and reforming of large clusters happens when large clusters separate into moderately smaller cluster sizes, then rejoin. This is not inconsistent with LLPS, however, as observing the formation of a system-large stable cluster takes more time than assessing phase coexistence using the slab method (7). Our collective data (Figs. 6, S12, S19, and S22) support our interpretation of LLPS propensity in our coil models despite the potential limitation of not having long enough slab simulations. Data analyzed from slab simulations in the remainder of the paper come from the 20 μs, not the 40 μs, simulations.

Protein dynamics within LLPS droplets are affected differently by polymer and multimer multivalencies

Following the multimer-dependent slab compaction observation (Figs. 5 and S16), we characterized the dynamics of proteins within slabs and hypothesized that increasing multimer states reduces the dynamics of individual proteins. We calculated the MSD of individual proteins for all simulations where LLPS occurs (Fig. S18) to estimate the effective diffusion coefficient of proteins within a droplet. We caveat that proteins in a droplet are almost certainly kinetically trapped and thus only partially diffusive on these timescales, hence describing them as effective diffusion coefficients. These effective diffusion coefficients, estimated by bootstrap on MSD analyses, are plotted in Fig. 7 and listed in Table S5. Linear fits from bootstrap analysis used to estimate the diffusion coefficients are shown on MSD plots in Figs. S23 and S24. Generally, both polymeric and multimeric multivalency reduces protein diffusion, but increasing multimer state does so more drastically than polymeric state (Fig. 7). The effect of multimer and polymer state on diffusion is most clear at 253 K (Fig. 7 A), the condition at which all proteins form LLPS. At this temperature, both trimer- and tetramer-forming proteins have dramatically slower effective diffusion coefficients than dimer-forming proteins. The largest difference is between 2-coil proteins of varying multimer states, where dimer-forming coils diffuse $\sim 25-$ and $\sim 2100$-fold faster than trimer- and tetramer-forming coils, respectively. Increasing polymer state also decreases protein diffusion for all proteins at 253 K, but the effect is less evident for trimer- and tetramer-forming proteins due to the strong effect of multimerization on reducing protein dynamics in droplets. Multimer and polymer multivalency-dependent slowing of diffusion is seen at the other temperatures (Fig. 7, B–D), but fewer comparisons between proteins can be made due to reduced LLPS propensity at higher temperatures.

Figure 7.

Multimeric multivalency significantly impacts the dynamics of proteins within droplets. Plots of effective diffusion coefficients at (A) 253 K, (B) 273 K, (C) 293 K, and (D) 313 K. Data on the y axis are shown in log-scale, and only proteins that form LLPS droplets are plotted. Average effective diffusion coefficient (circles) and SD (red error bars) are estimated via bootstrapping on MSD analyses from three replicate simulations for each protein. To see this figure in color, go online.

That the changes in effective diffusion as polymeric and multimeric multivalency is increased suggests there might be multivalency-dependent material differences between the LLPS droplets. The stark difference in effective diffusion between dimer and tetramer systems (for example, >2000-fold decrease in diffusion for 2-coil-1-linker proteins as multimeric multivalency increases from dimer to tetramer) and the apparent density inhomogeneities in the density profiles for tetramer systems (Fig. S12) suggests that tetrameric LLPS droplets might be kinetically arrested. The similar interaction energy associated with multimer formation (Fig. S5; Table S2) of the different coil models suggests that interaction strength between coils does not explain the difference in dynamics. Instead, it suggests that network connectivity arising from multimeric multivalency contributes to the observed differences in droplet dynamics. It is beyond the scope of this study, however, to characterize those dynamical differences and how they might translate to time-dependent material properties such as viscosity.

Secondary structure is necessary for CC-driven LLPS

In this model, secondary structure—specifically, helical structure in the coil segments—is necessary for CC-driven LLPS. We tested the importance of helical secondary structure on CC-driven LLPS by performing slab simulations on unstructured versions of the 2-coil-1-linker and 4-coil-3-linker proteins, with dimer-, trimer-, and tetramer-forming coils. We generated unstructured versions of these proteins by replacing every bead’s structural parameters with the linker segment type parameters (see supporting material, section I), while retaining all the interaction parameters as in the structured version of the protein. This means that the interaction strength for each individual coil-coil sticky bead and multimer-driving bead is the same between the unstructured and structured protein versions.

Unstructured coil proteins do not LLPS at 253 K in either the 2-coil-1-linker protein (Fig. 8 A) or 4-coil-3-linker (Fig. 8 B) protein for dimer-, trimer-, and tetramer-forming coil segments. Fig. S25 shows the density profile and molecular cluster size analyses for each of the simulated unstructured proteins. There is no indication of LLPS for any of the unstructured proteins. We did not test any lower temperatures as 253 K was the lowest examined for the structured proteins, but we acknowledge that there may be some low temperature where LLPS of the unstructured proteins can occur. The data in Fig. S25, taken together with the evidence of LLPS for structured versions of our proteins (Figs. 6 and S12) show that the structural and geometric arrangements of beads in space within a helical coil segment is important for the multivalent interactions in CC-driven LLPS.

Figure 8.

Protein models without helical structure do not LLPS. Representative single-molecule structure of (A) a 2-coil-1-linker unstructured protein, with dimer-forming coil segments, and (B) a 4-coil-3-linker unstructured proteins, with dimer-forming coil segments. Snapshots (at 20 μs) from slab simulations for each type of unstructured protein are also shown. Golden cartoon regions indicate the unstructured coil segment portion of each protein, and the black tubes correspond to the linker segments. Proteins wrap through the box boundaries during simulation, but atoms are shifted into neighboring cells to keep proteins visually intact. Visualizations produced using open-source PyMOL v.2.5.0. To see this figure in color, go online.

Discussion

We report in this paper 1) a novel CG framework for studying the phase separation of CC proteins (CC LLPS framework), 2) evidence that CC domains can be sole drivers of LLPS in physically motivated CG protein models, 3) evidence that multimerization of stickers has a strong influence on LLPS propensity and protein diffusion in droplets, and 4) that helical structure is necessary for coil segment-driven LLPS.

Our findings that CC protein models can LLPS over a range of temperatures (Fig. 6) show that structured CC domains can be plausible LLPS-driving features of proteins. This suggests that, for proteins like spd-5 (C. elegans) or pericentrin (H. sapiens), one or more of their CC domains could be contributing to their LLPS. Indeed, experimental studies with some phase-separating CC proteins also suggests that CC domains can drive LLPS. For example, truncation studies of TAZ (H. sapiens) and Ede1 (S. cerevisiae) that lack their CC domains show that these mutants lose the ability to LLPS compared with wild-type (21,22). A paper studying McdB (cyanobacteria S. elongatus PCC 7942) performed similar truncation studies and found that a large central CC domain is necessary for its LLPS (25). Thus, there is indication of LLPS driven by CC domains in a wide range of organisms from cyanobacteria to mammals. Rios et al. (17) identified CC domains important for the LLPS of spd-5 through cross-linking mass spectrometry, and they show that a large fraction of spd-5-spd-5 interactions occur through CC domains. They also identified a key interaction between a PReM-containing and CM2-like domain in phosphorylated spd-5 (17), both of which are CCs. This interaction is similar to an interaction found in centrosomin (13), an essential centrosomal protein in fruit flies. Our findings also show that helical structure is a necessary feature for CC domains to drive LLPS. The alignment of sticky beads (both coil-coil sticky and multimer-driving) into a heptad-repeat arrangement is seemingly important for LLPS, even though this places a geometric limitation on how coils interact. The results that unstructured versions of our CC protein models do not LLPS suggests that CC-driven LLPS arises from cooperativity in interactions between individual coil segments. Our findings that CC domains can be sufficient for LLPS and that helical structure is necessary, combined with experimental evidence of CC-specific interactions in centrosomal proteins, further supports CC domains as potentially sole or primary drivers of LLPS in some proteins.

Our simulations demonstrate the importance of multimeric multivalency on protein LLPS. The flexibility to alter polymeric and multimeric multivalency is a feature we designed in our simulation framework to allow us to easily study the contribution of each type of multivalence to CC-driven LLPS. By directly changing the number of coil segments in a protein and how those segments multimerize, we show that multimerization of coil segments has a stronger effect on LLPS propensity (Figs. 5 and 6) than polymeric multivalency. Analogous experiments with real or designed proteins would be challenging to accomplish, and simulations provide the advantage of testing hypotheses for how proteins interact to drive LLPS before experimental investigations. Other simulation studies have shown how polymeric multivalency affects LLPS (7,63,66,67,68), but our results are some of the first to investigate multimeric multivalency. Recent experimental work with spd-5 (16,17) and McdB (25) demonstrates the importance of multimerization on CC-driven LLPS. In addition, in a related study, Rana et al. (69) investigated the effect of multimerization on the formation of multiphase condensates composed from mixtures of synthetic IDPs. They showed that increasing the multimerization state of each of the component IDPs causes the multiphasic condensates to demix into separate droplets of just one type of IDP. This indicates that multimerization not only enhances LLPS, but can affect the balance between homo- versus heterotypic interactions that might have an effect on condensate composition. These findings also suggest there might exist an upper limit to the degree of multimerization of proteins in a multicomponent membraneless organelle such as the centrosome. If this upper limit is infringed, perhaps through mutations that affect multimerization capabilities of LLPS-driving domains such as splicing mutants or point mutations, then the ability for the membraneless organelle to assemble and function physiologically might be impaired. Our results, which show that multimerization strongly affects LLPS propensity, in combination with experimental findings, support a model for multimerization as a valid mechanism in modulating protein LLPS. Further understanding of how CC proteins LLPS will require consideration for how CC domains multimerize, not just how many CC domains might be in a protein.

It is notable that coil multimerization state has such a dramatic effect on LLPS propensity and effective diffusion considering the framework’s only moderate control over specific multimer formation, e.g., simulations designed to contain tetramers also contain dimers and trimers at equilibrium (Fig. S4). The polymeric multivalence-dependent decrease in diffusion is in line with other studies that show that increasing the number of stickers in a protein increases the viscosity of the resulting condensate (34,70), with the caveat that we measured effective protein diffusion instead of droplet viscosity. A lack of precise multimer formation somewhat limits our efforts to establish a quantitative relationship between phase behavior and multimerization state. The trends we observe, however—that higher multimerization states result in greater LLPS propensity and reduced protein dynamics—are still valid. At a fixed multimerization state, polymeric multivalency has less impact on LLPS propensity as determined by apparent melting temperature. For any multimer-forming coil it is unknown how many additional coil segments are needed, above a two-coil protein, to start seeing a significant increase in melting temperature. Additional studies may more clearly show the difference that polymeric versus multimeric multivalency has on these CG CC systems.

In our systems, we restricted all CC interactions to interchain interactions, where only coil segments of a specific type can interact (Fig. 1 B). Intrachain interactions, however, will also likely modulate LLPS propensity of CC proteins similar to what has been seen for IDPs. Dignon et al. (71) demonstrated that single-molecule properties of IDPs, such as the theta temperature, correlate well with phase behavior. Similarly, random phase approximation theoretical analysis of charged IDPs show that radii of gyration correlate strongly with phase behavior (72). These findings suggest that, for IDPs, intrachain contacts can become the interchain contacts necessary to support droplet formation. The interplay between intra- and interchain interactions is also known to affect LLPS behavior. Rana et al. (73) showed by simulation that, for proteins with arbitrary numbers of stickers that can undergo both inter- and intrachain interactions, it is the pattern of the stickers that predicts their LLPS propensity. We expect that sticker patterning will also be important for CC-driven LLPS, once intrachain interactions are introduced.

There are ways our framework could be modified to more accurately reflect biologically relevant CC proteins, which might be worth future investigation. These improvements could include: adding parallel versus antiparallel coil orientations like those seen in real CC domains (44,45); adding amino-acid-specific interaction terms into our framework, similar to CG force fields developed to study IDPs and LLPS (7,62,74); having coil monomers exist as partially unfolded and requiring them to pay a free energy cost of folding during multimerization, which is how real CC domains are thought to behave (75,76,77,78,79); and changing the size and effective solvation of linkers, which is known to affect protein LLPS propensity (37,68,80). The model in its current implementation, however, is well-suited to test the hypothesis of CC-driven LLPS and can be easily adapted to explore models of CC-driven LLPS.

CC domains as drivers of LLPS represents a new way to think about mechanisms of protein phase separation. The most frequent way to view stickers is as individual residues in intrinsically disordered regions of proteins, despite the flexibility of the stickers-and-spacers framework to be applied to various levels of protein organization (28). This is likely because a majority of proteins identified in biomolecular condensates are intrinsically disordered (81), making IDP components good candidates to study as drivers of LLPS. Our results provide additional evidence that CC domains could be valid stickers and should be studied in their own right in driving protein phase separation. Our study, in conjunction with recent knowledge about how spd-5 is thought to interact (16,17), also justifies studying CC domains as drivers in the phase separation of centrosomal proteins such as pericentrin. Existing data are insufficient to say if CC proteins are the primary domains responsible for LLPS of centrosomal and similar proteins, but these results suggest that future studies to identify driving domains should examine intrinsically disordered and CC domains alike.

Author contributions

Methodology, D.A.R.; software, D.A.R.; investigation, D.A.R.; visualization, D.A.R.; writing, D.A.R., L.E.H., and M.R.S.; conceptualization, L.E.H. and M.R.S.; supervision, L.E.H. and M.R.S.; project administration, M.R.S.

Editor: Jeetain Mittal.

Supporting citations

References (82,83,84,85,86) appear in the supporting material.