Assessment of Time Lag Between Blood Flow, Retinal Nerve Fiber Layer Thickness and Visual Field Sensitivity Changes in Glaucoma

Abstract

Purpose

This study investigates the temporal relationship between blood flow changes and alterations in retinal nerve fiber layer thickness (RNFLT) and mean deviation (MD) in individuals with glaucoma.

Methods

Blood flow, measured by mean blur rate in optic nerve head vessels (MBRv) and tissues (MBRt) using laser speckle flowgraphy (LSFG)-NAVI, was analyzed using structural equation models (SEMs). SEMs assessed whether the previous rate of one parameter predicted the current rate of the other parameter, adjusted for its own rate in the previous time interval. Data from 345 eyes of 174 participants were gathered from visits every six months.

Results

Rates of change of both MBRv and MBRt were significantly predicted by their own rate in the previous time interval and by the rate of change of MD in the previous time interval (P < 0.001 and P = 0.043, respectively), but not by the rate of MD in the concurrent interval (P = 0.947 and P = 0.549), implying that changes in MD precede changes in blood flow. Rates of change of RNFLT were predicted by their own previous rate and the rate of change of MBRv and MBRt in either the previous interval (P = 0.002 and P = 0.008) or the concurrent interval (P = 0.001 and P = 0.018), suggesting that MBR may change before RNFLT.

Conclusions

The evidence supports a temporal sequence where MD changes precede blood flow changes, which, in turn, may precede alterations in RNFLT.

Glaucoma remains one of the leading causes of irreversible blindness worldwide and poses a substantial public health challenge. As this complex and progressive optic neuropathy unfolds, it is marked by the gradual loss of retinal ganglion cells, which in turn gives rise to corresponding visual field defects.¹ These structural changes are mirrored by alterations in the optic nerve head (ONH) and retinal nerve fiber layer thickness (RNFLT). We have recently determined a time lag between true functional change, which predicts and precedes changes to RNFLT (even though structural changes may be detectable sooner because of lower test-retest variability).²

Although it has been well established that ocular blood flow is compromised in individuals with glaucoma,^3–6 the exact nature of these alterations continues to be a subject of ongoing investigation. Retinal blood flow may initially increase at the earliest stages of glaucoma but then decreases.^7,8 Autoregulation mechanisms responsible for maintaining consistent blood flow are frequently disrupted in glaucomatous eyes, resulting in fluctuations that may also exacerbate the damage to the ONH.⁹ It is not yet known whether these changes contribute to axon loss, are secondary to reduced demand due to axon loss, occur as a consequence of ONH damage, or represent a complex interplay of factors.

The interplay between glaucoma and ocular hemodynamics has prompted exploration of blood flow metrics as potential biomarkers and therapeutic targets. Laser speckle flowgraphy (LSFG) has emerged as a valuable tool, offering noninvasive and real-time assessment of ocular blood flow in vivo. LSFG uses the laser speckle phenomenon, whereby the laser light reflects off the moving erythrocytes in the vessels and tissues, creating a speckle pattern. LSFG technology enables the quantification of various dynamic blood flow parameters, including the mean blur rate (MBR) in the ONH. MBR is calculated by analyzing the contrast and fluctuations in the speckle pattern produced and is proportional to the blood flow.¹⁰ A higher MBR indicates faster blood flow, whereas a lower MBR suggests reduced blood flow in the examined region.¹¹ MBR can provide critical insights into the microvascular dynamics of the retina and ONH and has been found to correlate with both RNFLT thinning and changes in mean deviation (MD) in people with glaucoma.^12,13 However, it remains unclear in what temporal sequence these changes take place. Little is known about the temporal dynamics of ocular blood flow and whether axon loss causes blood flow reduction or whether that reduction contributes to axon loss.

These findings prompt us to investigate the potential presence of a time lag between changes in MD, a marker of visual field loss, and MBR, as well as between RNFLT and MBR. By exploring these temporal relationships in the ONH vessels and tissue, we aim to uncover essential insights into the changes in ocular blood flow that may underlie the progression of glaucoma. Our aim is to use structured equation modeling (SEM) to determine whether there is any clinically relevant time lag between them (i.e., greater than six months, which would be long enough to be relevant for clinical diagnostics purposes).

Methods

Participants

Participant data featured in this assessment was sourced from the ongoing Portland Progression Project (P3). This longitudinal research is conducted at the Devers Eye Institute in Portland, Oregon and is funded by National Institutes of Health. The P3 study features a battery of vision assessments, including standard automated perimetry (SAP), optical coherence tomography (OCT), and LSFG, approximately every six months. All testing protocols were approved by the Legacy Health Institutional Review Board. The study adheres to the tenets of the Declaration of Helsinki and complies with the Health Insurance Portability and Accountability Act of 1996. After the risks and benefits of participation was explained to participants, written informed consent was provided. To ensure representation of a typical clinical population, study inclusion criteria incorporated individuals diagnosed with open-angle glaucoma or those deemed likely to develop glaucoma, as determined by their clinician. Individuals with a history of angle closure, the presence of other ocular pathologies that could potentially impact visual field assessments (e.g., macular degeneration), those who are unable to reliably undergo visual field testing, or individuals likely unable to provide high-quality OCT images, were excluded from the study.

Retinal Blood Flow–LSFG Assessment

Laser speckle flowgraphy–NAVI (LSFG-NAVI; Sofcare Co., Fukutsu, Japan) was used to measure average MBR within a four-second acquisition period and quantified using LSFG Analyzer software (V3.8.0.4). The LSFG technique used to measure blood flow has been previously described in detail.^7,10 In brief, the LSFG-NAVI system features a fundus camera equipped with an 830-nm diode laser and a charge-coupled device camera, focused on 750 × 360 pixel area (approximately 6 × 3.8 mm). All measurements were conducted with participants in a seated position, and phenylephrine drops were used to dilate pupils. The MBR average value for a specific pixel is determined by considering the intensity at that pixel within the current frame, as well as at each of the eight adjacent pixels in that frame, and at the same nine pixels in the previous and subsequent frames.⁷ To assess the ONH, an elliptical “rubber band” was positioned around the ONH by a trained examiner (G.C.). The software then categorizes pixels within this area as either “vessel” or “tissue,” using a definitive threshold established by a histogram method. The Pigmagic function was used to account for the influence of pigment in the eye on the LSFG outcome parameters. Two parameters of interest for the current study are output: the average value of MBR among pixels within the major vessels inside the ONH MBRv, and the average among the remaining pixels within the ONH tissue MBRt.

Disease Severity–Imaging and Functional Assessment

Using the Spectralis OCT2 (Heidelberg Engineering GmbH, Heidelberg, Germany), we conducted spectral domain OCT testing with a circumpapillary circle scan encompassing a 6° radius centered on the ONH. Peripapillary RNFLT was determined as the average distance between the inner limiting membrane and the outer boundary of the RNFL, measured in micrometers. Trained technicians manually corrected automated layer segmentations if needed.¹⁴ For inclusion, OCT scans were required to have a quality score >15,¹⁵ with quality scores below this threshold considered as missing data for that particular visit. In instances where multiple scans were obtained on the same day, the author (BH) manually reviewed the scans and their associated timestamps to ensure the selection of the best quality scan. Participants underwent SAP using the Humphrey Field Analyzer II (HFA; Carl Zeiss Meditec Inc., Dublin, CA, USA), with the SITA Standard testing strategy and 24-2 test pattern. MD was calculated from the SAP data to provide a quantitative measure of overall visual field function. Because reliability indices from the HFA do not reflect test performance accurately,^16,17 reliability was instead assessed by the technicians who monitor fixation using the instrument's built-in camera and provide reminders as required. Fields were repeated if there were >15% false-positive results or >33% fixation losses, and the technician observed that this was due to response unreliability rather than, for example, inaccurate automated blind spot identification. Data at a given visit were retained only if acceptable quality data was available for RNFLT, SAP, and LSFG for that date.

Data Preparation

For the purpose of this analysis, the data was organized into six-month time intervals (with a ±3-month window). For example, the first visit occurring within the three- to nine-month period after the baseline visit was designated as Visit 2 (if there were multiple visits within the specified time frame, the first visit was selected for analysis). Then Visit 3 was defined as the first visit occurring three to nine months after Visit 2, and so on. If there were no visits within the three- to nine-month period after baseline, Visit 2 was defined to be a “missed visit,” and then Visit 3 was the first visit nine to 15 months after Visit 1. This approach allowed for the calculation of the rate of change between these designated visits: RNFLT Rate_n = (RNFLT_n+1 − RNFLT_n)/(Exam Date_n+1 − Exam Date_n). The main analysis was conducted on a time series of seven rates, using data from eight visits. A secondary analysis was performed using longer time series of 10 rates using data from 11 visits.

We chose the participant's longest continuous data series for our analysis. For instance, if a participant had recorded visits every six months from 2015 to 2020, then stopped for 2020 to 2021, and resumed with visits every six months from 2021 to 2022, we would only consider the data from 2015 to 2020 as the longest unbroken sequence for analysis. If a study visit was missed within the designated six-month time period, this was marked as missing data, and the next available exam was used (e.g., RNFLT Rate_n+1 was calculated using the formula: RNFLT Rate_n+1 = (RNFLT_n+2 − RNFLT_n)/(Exam Date_n+2 − Exam Date_n). This approach was applied for up to three consecutive time periods with missed visits.

SEMs

SEM provides a comprehensive framework for assessing and estimating connections between observed variables and latent constructs. SEMs delve into the interactions among these underlying constructs.¹⁸ It accommodates repeated measurements of variables with bidirectional causative relations, allowing for an exploration of how these variables evolve in relation to each other across multiple time points. Notably, SEM equips researchers with fit indexes that serve as valuable yardsticks to evaluate how well their proposed model aligns with observed data. This enables researchers to fine-tune and adapt their models based on fit indexes, ensuring a faithful representation of the underlying data structure. SEM has been previously used by the authors to demonstrate that changes in MD precede and predict changes in RNFLT.²

In this study, we wish to assess whether there is a significant time lag between rates of change of retinal blood flow (as measured by the average MBR in either vessels or tissue within the ONH), and rates of change of standard measures of disease severity (either MD from perimetry or RNFLT from OCT imaging). For each flow measurement and each standard measure of severity, we form four SEM models, which we will refer to as A–D:

Model A: Concurrent Severity Change ⇒ Blood Flow Change

$$\begin{array}{ccc}\hfill \mathrm{MBR}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}}& =& \mathrm{Intercep}{\mathrm{t}}_{\mathrm{MBR}}+\mathrm{True}\mathrm{MBR}\mathrm{Rate}\times \mathrm{n}+{\alpha }_{\mathrm{A}}\hfill \\ & & \times \mathrm{MBR}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}-1}+{\beta }_{\mathrm{A}}\times \mathrm{Severity}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}}+\mathrm{Error}\hfill \\ \hfill \mathrm{Severity}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}}& =& \mathrm{Intercep}{\mathrm{t}}_{\mathrm{Sev}}+\mathrm{True}\mathrm{Severity}\mathrm{Rate}\times \mathrm{n}+{\gamma }_{\mathrm{A}}\hfill \\ & & \times \mathrm{Severity}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}-1}+\mathrm{Error}\hfill \end{array}$$

Model B: Earlier Severity Change ⇒ Blood Flow Change

$$\begin{array}{ccc}\hfill \mathrm{MBR}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}}& =& \mathrm{Intercep}{\mathrm{t}}_{\mathrm{MBR}}+\mathrm{True}\mathrm{MBR}\mathrm{Rate}\times \mathrm{n}+{\alpha }_{\mathrm{B}}\hfill \\ & & \times \mathrm{MBR}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}-1}+{\beta }_{\mathrm{B}}\times \mathrm{Severity}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}-1}+\mathrm{Error}\hfill \\ \hfill \mathrm{Severity}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}}& =& \mathrm{Intercep}{\mathrm{t}}_{\mathrm{Sev}}+\mathrm{True}\mathrm{Severity}\mathrm{Rate}\times \mathrm{n}+{\gamma }_{\mathrm{B}}\hfill \\ & & \times \mathrm{Severity}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}-1}+\mathrm{Error}\hfill \end{array}$$

Model C: Concurrent Blood Flow Change ⇒ Severity Change

$$\begin{array}{ccc}\hfill \mathrm{MBR}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}}& =& \mathrm{Intercep}{\mathrm{t}}_{\mathrm{MBR}}+\mathrm{True}\mathrm{MBR}\mathrm{Rate}\times \mathrm{n}+{\alpha }_{\mathrm{C}}\hfill \\ & & \times \mathrm{MBR}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}-1}+\mathrm{Error}\hfill \\ \hfill \mathrm{Severity}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}}& =& \mathrm{Intercep}{\mathrm{t}}_{\mathrm{Sev}}+\mathrm{True}\mathrm{Severity}\mathrm{Rate}\times \mathrm{n}+{\gamma }_{\mathrm{C}}\hfill \\ & & \times \mathrm{Severity}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}-1}+{\beta }_{\mathrm{C}}\times \mathrm{MBR}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}}+\mathrm{Error}\hfill \end{array}$$

Model D: Earlier Blood Flow Change ⇒ Severity Change

$$\begin{array}{ccc}\hfill \mathrm{MBR}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}}& =& \mathrm{Intercep}{\mathrm{t}}_{\mathrm{MBR}}+\mathrm{True}\mathrm{MBR}\mathrm{Rate}\times \mathrm{n}+{\alpha }_{\mathrm{D}}\hfill \\ & & \times \mathrm{MBR}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}-1}+\mathrm{Error}\hfill \\ \hfill \mathrm{Severity}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}}& =& \mathrm{Intercep}{\mathrm{t}}_{\mathrm{Sev}}+\mathrm{True}\mathrm{Severity}\mathrm{Rate}\times \mathrm{n}+{\gamma }_{\mathrm{D}}\hfill \\ & & \times \mathrm{Severity}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}-1}+{\beta }_{\mathrm{C}}\times \mathrm{MBR}\mathrm{Rat}{\mathrm{e}}_{\mathrm{n}-1}+\mathrm{Error}\hfill \end{array}$$

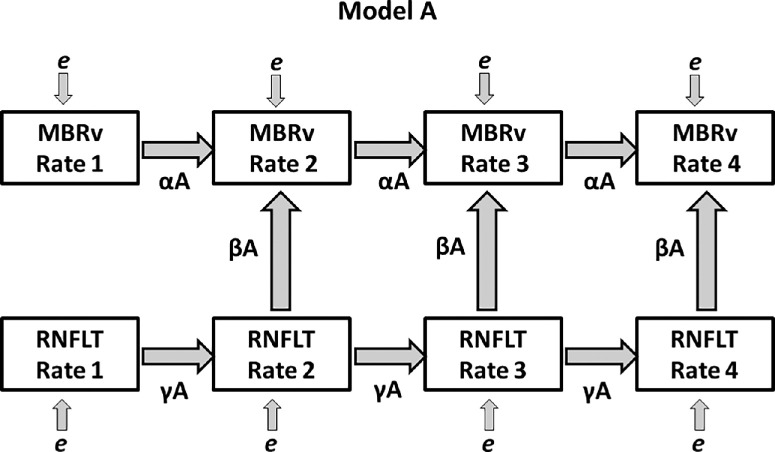
Figure 1 shows the path diagram for Model A. The underlying rate of change of MBR in each model in time interval n is given by (Intercept_MBR + True MBR Rate × n) and is treated as a latent variable to be estimated. Thus we are assuming that this rate changes linearly over time; this is reasonable because the time series featured in this analysis are relatively short (eight visits, typically less than four years). Similarly, the underlying rate of change of severity is given by (Intercept_Sev + True Severity Rate × n), and these underlying rates are constrained to be positively correlated with each other. The four models were fit independently of each other by maximum likelihood estimation. The goodness of fit of each model was assessed using the root mean square error of approximation (RMSEA, chosen as our primary measure of goodness of fit as it is an absolute fit index and gives 90% confidence intervals [CI]),¹⁹ the Tucker Lewis index (TLI),²⁰ and the comparative fit index (CFI), both examples of incremental fit indexes.²¹ RMSEA values closer to zero, and CFI and TLI values closer to one, represent a good fit. Analyses were performed using R statistical software, version 4.0.0, using the lavaan package.²²

Figure 1.

The path diagram for Model A, one of the four SEMs featured in this study. The observed variables RNFLT Rate_n and MBRv Rate_n (average MBR in vessels) are shown, representing the measured rates of change of the two modalities over period n (from visit n − 1 to visit n). Directional arrows indicate regressions, with labeled coefficients. Measurement errors are illustrated as e and are assumed to be Gaussian.

Our primary results are driven by the statistical significance of parameter β in each model:

• •βA is significant ⇒ knowing the rate of change of the severity measure (which could be either MD or RNFLT) improves predictions of the rate of change of MBR over that same time period, compared to only using the rate of change of MBR in the previous time period as a predictor.
• •βB is significant ⇒ the rate of change of the severity measure over the previous time period helps predict the rate of MBR change in the current period; that is, there is a time lag with the severity measure changing earlier than MBR.
• •βC is significant ⇒ the rate of change of MBR helps predict the concurrent rate of severity change, with no time lag.
• •βD is significant ⇒ the previous rate of MBR change predicts the current rate of severity change (i.e. there is a time lag with MBR changing earlier than the severity measure).

To allow for possible differences in the relation with disease stage, and possible non-monotonicity of MBR, secondary analyses were performed for eyes with average MD > −0.72 dB versus MD ≤ −0.72 dB; and RNFLT > 84 µm versus RNFLT ≤ 84 µm (the median values for RNFLT and MD).

Results

Study Population

A total of 345 eyes from 174 people were included in the study. Cohort demographics and clinical characteristics can be found in Tables 1 and 2³. Mean time difference between the first eight eligible visits was 204 days, which equates to 6.7 months (standard deviation ± 36 days; range 110–270 days).

Table 1.

Demographic Characteristics of n = 174 Participants

	Participants
Gender
Male	68 (39%)
Female	106 (61%)
Ethnicity
White	156 (90%)
Black	5 (3%)
Asian	6 (3%)
Mixed	2 (1%)
Native American	2 (1%)
Unknown	3 (2%)

Data sourced from self-report.

Table 2.

Baseline Characteristics and Rate of Change Across Seven Visits of n = 345 Eyes

	Mean	Standard Deviation	Range
Age (years)	69	7.85	47–88
Intraocular Pressure	16.43	4.0	4–30
Mean deviation (dB)	−1.37	3.69	−19.92 to 2.96
Retinal nerve fiber thickness (µm)	82.23	15.51	38.78 to 117.4
Average mean blur rate (vessels)	29.53	5.74	14.10 to 66.17
Average mean blur rate (tissue)	9.24	2.52	3.55 to 21.43
Rate of change across seven visits
MD (dB/y)	−0.32	1.87	−8.46 to 7.69
RNFLT (µm/y)	−0.08	5.57	−72.68 to 60.59
Average Mean Blur Rate (vessels)	−0.54	6.48	−43.71 to 50.03
Average Mean Blur Rate (tissue)	−0.02	2.08	−10.62 to 18.38
			No. Eyes
Glaucoma severity (MD [dB])
>−3dB			279 (81%)
≤−3dB, >−6dB			31 (9%)
≤−6dB, >−12dB			26 (7%)
≤−12dB			9 (3%)
Mean rate of change across seven visits (MD [dB/y])
<0			285 (82%)
<−0.5			92 (26%)
<−1			31 (9%)

Table 3.

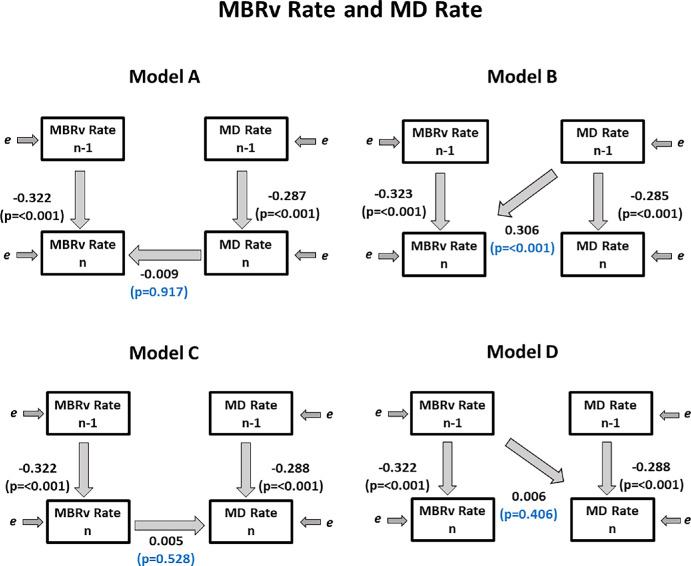
Coefficients and Goodness-of-Fit Measures for the Models Testing MBR in ONH Vessels and MD

	No. of Eyes	β	Coefficient	P	RMSEA	CFI	TLI
Model A	345	MD Raten predicting MBRv Raten	−0.009	0.917	0.083 (CI: 0.074, 0.093)	0.657	0.709
Model B	345	MD Raten−1 predicting MBRv Raten	0.306	<0.001 *	0.081 (CI: 0.072, 0.091)	0.674	0.723
Model C	345	MBRv Raten predicting MD Raten	0.005	0.528	0.083 (CI: 0.074, 0.093)	0.658	0.709
Model D	345	MBRv Raten−1 predicting MD Raten	0.006	0.406	0.083 (CI: 0.074, 0.093)	0.658	0.709

Full descriptions of the models are given in the Methods section; only coefficient β is reported here because that is the important relation for this study. A better fitting model will have RMSEA closer to 0; and both CFI and TLI closer to 1.

Bold value indicates P < 0.05.

^*Statistically significant after Holm-Bonferroni correction for multiple comparisons

Blood Flow in ONH Vessels Versus MD

As seen in Table 3 and Figure 2, in all four models, MBRv Rate_n−1 was a significant predictor of MBRv Rate_n and MD Rate_n−1 was a significant predictor of MD Rate_n, as expected. These coefficients (α and γ respectively) are negative, because they both have the measurement at visit n in common so Rate_n−1 is inversely correlated with Rate_n.

Figure 2.

Fitted coefficients for Models A–D used. Regression coefficients relating the observed variables are shown, showing the relations between the measured rates of change of MD (used as a metric of functional loss) and of MBRv (the blood flow in major vessels within the optic nerve head), over period n − 1 (from visit n − 2 to n − 1) and over period n (from visit n − 1 to visit n).

Using Model A, we found that coefficient β_A was not significant (P = 0.917), implying that knowing MD Rate_n did not improve predictions of MBRv Rate_n, compared to only using the rate of change of MBR in the previous time period as a predictor. Similarly using Model C, knowing MBRv Rate_n did not improve predictions of MD Rate_n. However, when using Model B, we found that MD Rate_n−1 was a significant predictor of MBRv Rate_n (P < 0.001), which means the previous rate of change of MD significantly predicts the current rate of change of MBRv. Therefore we found evidence that there is a clinically relevant time lag between MD and MBRv, whereby MD occurs before MBRv.

Similar models were created using linearized MD = 10^MD/10 instead of decibel scaled MD because this may be more linearly related to structural measures.²³ Results were essentially the same. When using Model B, linearized MD Rate n−1 was a significant predictor of MBRv Rate n (P = 0.001), which means the previous rate of change of linearized MD significantly predicts the current rate of change of MBRv.

Blood Flow in ONH Tissue Versus MD

We found the same trends in data for MBRt Rate as for MBRv Rate. As before, we found that coefficient β_B was significant (P = 0.043); MD Rate_n−1 was a significant predictor of MBRt Rate_n. Therefore we found evidence that there is a clinically relevant time lag between MD and MBRt, whereby changes in MD occur approximately one time period before changes in MBRt. See Table 4 and Figure 3 for details.

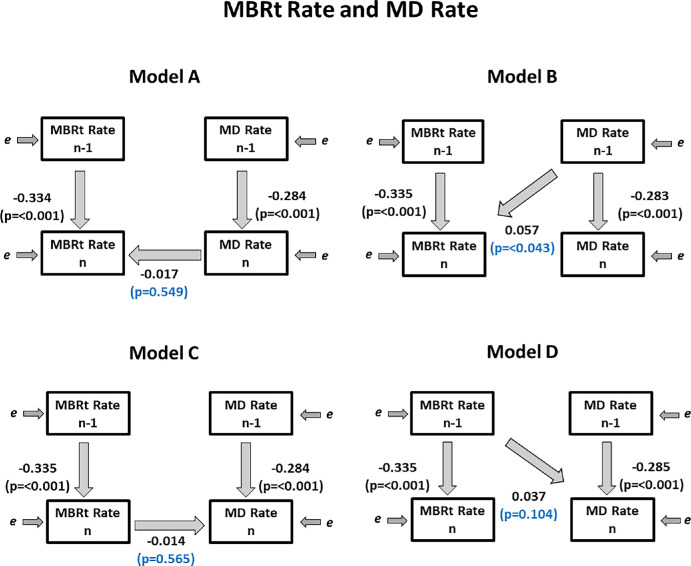
Table 4.

Coefficients and Goodness-of-Fit Measures for the Models Testing MBR in ONH Tissues and MD

	No. of Eyes	β	Coefficient	P	RMSEA	CFI	TLI
Model A	345	MD Raten predicting MBRt Raten	−0.017	0.549	0.079 (CI: 0.070, 0.089)	0.697	0.743
Model B	345	MD Raten−1 predicting MBRt Raten	0.057	0.043	0.078 (CI: 0.069, 0.088)	0.702	0.747
Model C	345	MBRt Raten predicting MD Raten	−0.014	0.565	0.079 (CI: 0.070, 0.089)	0.697	0.742
Model D	345	MBRt Raten−1 predicting MD Raten	0.037	0.104	0.079 (CI: 0.069, 0.088)	0.700	0.745

Bold value indicates P < 0.05.

Figure 3.

Fitted coefficients for Models A–D used. Regression coefficients relating the observed variables are shown, showing the relations between the measured rates of change of MD (used as a metric of functional loss) and of MBRt (the blood flow in major tissues within the optic nerve head), over period n − 1 (from visit n − 2 to n − 1) and over period n (from visit n − 1 to visit n).

Blood Flow in ONH Vessels Versus RNFLT

As seen in Table 5 and Figure 4, in all four models, MBRv Rate_n−1 was a significant predictor of MBRv Rate_n and RNFLT Rate_n−1 was a significant predictor of RNFLT Rate_n, as expected.

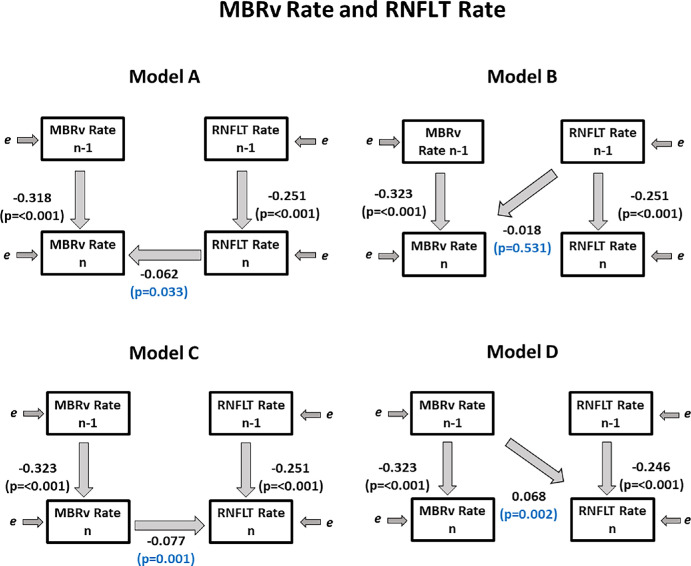
Table 5.

Coefficients and Goodness-of-Fit Measures for the Models Testing MBR in ONH Vessels and RNFLT

	No. of Eyes	β	Coefficient	P	RMSEA	CFI	TLI
Model A	345	RNFLT Raten predicting MBRv Raten	−0.062	0.033	0.090 (CI: 0.081, 0.100)	0.581	0.643
Model B	345	RNFLT Raten−1 predicting MBRv Raten	−0.018	0.531	0.078 (CI: 0.069, 0.088)	0.702	0.747
Model C	345	MBRv Raten predicting RNFLT Raten	−0.077	0.001 *	0.079 (CI: 0.070, 0.089)	0.697	0.742
Model D	345	MBRv Raten−1 predicting RNFLT Raten	0.068	0.002 *	0.091 (CI: 0.082, 0.100)	0.575	0.638

Bold value indicates P < 0.05.

^*Statistically significant after Holm-Bonferroni correction for multiple comparisons.

Figure 4.

Fitted coefficients for Models A–D used. Regression coefficients relating the observed variables are shown, showing the relations between the measured rates of change of RNFLT (used as a metric of structural loss) and of MBRv (the blood flow in major vessels within the optic nerve head), over period n − 1 (from visit n − 2 to n − 1) and over period n (from visit n − 1 to visit n).

Using Model A, we found that coefficient β_A was significant (P = 0.033), implying that knowing RNFLT Rate_n improved the prediction of the concurrent MBRv Rate_n, compared to only using the rate of change of MBR in the previous time period as a predictor. Similarly using Model C, knowing the concurrent MBRv Rate_n improved predictions of RNFLT Rate_n (P = 0.001). Coefficient β_B in Model B was not significant (P = 0.531). However, when using Model D, we found that MBRv Rate_n−1 was a significant predictor of RNFLT_n (P = 0.002), which means the previous rate of change of MBRv significantly predicts the current rate of change of RNFLT. Therefore we found evidence suggesting a clinically relevant time lag between MBRv and RNFLT, whereby MBRv occurs before RNFLT.

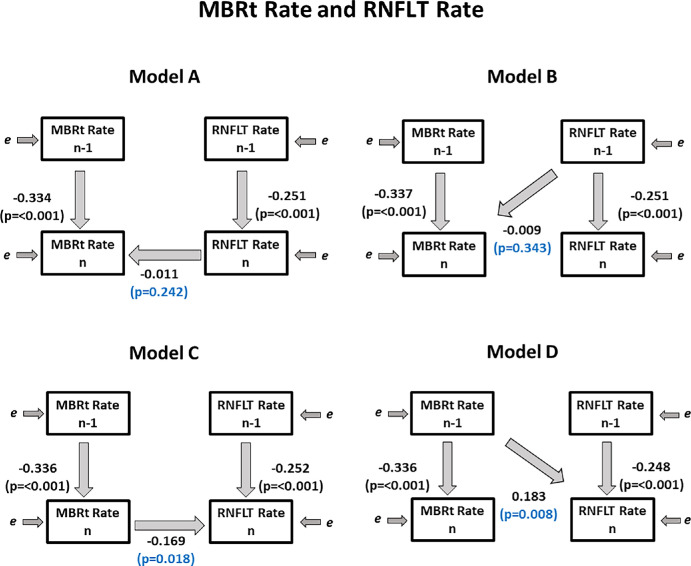
Blood Flow in ONH Tissue Versus RNFLT From OCT

We found similar trends in data for MBRt Rate as MBRv Rate. We did not find that coefficient β_A was significant (P = 0.242), implying that knowing RNFLT Rate_n did not improve the prediction of MBRt Rate_n. However, when using Model C, we did find that coefficient β_C was significant (P = 0.018), implying that knowing MBRt Rate_n improved the prediction of RNFLT Rate_n. As before, we found that coefficient β_B was not significant (P = 0.343); RNFLT Rate_n−1 was not a significant predictor of MBRt Rate_n. Yet, similar to MBRv, we found that MBRt Rate_n−1 was a significant predictor of RNFLT_n (P = 0.008), which means the previous rate of change of MBRt significantly predicts the current rate of change of RNFLT. Therefore we found evidence suggesting that there is a clinically relevant time lag between MBRt and RNFLT whereby MBRt occurs before RNFLT. See Table 6 and Figure 5 for details.

Table 6.

Coefficients and Goodness-of-Fit Measures for the Models Testing MBR in ONH Tissues and RNFLT

	No. of Eyes	β	Coefficient	P	RMSEA	CFI	TLI
Model A	345	RNFLT Raten predicting MBRt Raten	−0.011	0.242	0.090 (CI, 0.081, 0.100)	0.602	0.661
Model B	345	RNFLT Raten−1 predicting MBRt Raten	−0.009	0.343	0.090 (CI, 0.081, 0.100)	0.601	0.661
Model C	345	MBRt Raten predicting RNFLT Raten	−0.169	0.018	0.090 (CI, 0.081, 0.099)	0.607	0.666
Model D	345	MBRt Raten−1 predicting RNFLT Raten	0.183	0.008	0.090 (CI, 0.080, 0.099)	0.609	0.667

Bold value indicates P < 0.05.

Figure 5.

Fitted coefficients for Models A–D used. Regression coefficients relating the observed variables are shown, showing the relations between the measured rates of change of RNFLT (used as a metric of structural loss) and of MBRt (the blood flow in major tissues within the optic nerve head), over period n − 1 (from visit n − 2 to n − 1) and over period n (from visit n − 1 to visit n).

Secondary SEM Analysis

To assess the robustness of the SEMs, a secondary analysis was performed using longer time series of 10 rates using data from 11 visits. The models had similar RMSEA values overall, but values for CFI and TLI were noticeably poorer, meaning these models did not fit the data as well as the models featured in our main analysis possibly because of nonlinearities in the true course of progression over this longer period. On the whole, we found no notable changes in the coefficients and concluded that the models are robust. Details can be found in supplemental materials (Supplementary Tables S1, S2).

To assess the impact of nonlinearity, the data was split into subgroups based on the average MD and RNFLT within the series being above or below the median value for the cohort. Analyses were then repeated on these subgroups, as seen in Table 7. We found no changes in the sign of the coefficients between subgroups, suggesting that there were no problems from non-mononoticity. The time lagged coefficients remained significant, except for MD_n−1 predicting MBRt_n.

Table 7.

Coefficients for the Models of Interest^*

No. of Eyes	Subgroup	β	Coefficient	P
Model B
173	>−0.72 dB	MD Raten−1 predicting MBRv Raten	0.398	0.022
172	≤−0.72 dB	MD Raten−1 predicting MBRv Raten	0.261	0.01
173	>−0.72 dB	MD Raten−1 predicting MBRt Raten	0.001	0.990
172	≤−0.72 dB	MD Raten−1 predicting MBRt Raten	0.076	0.015
Model D
178	>84 µm	MBRv Raten−1 predicting RNFLT Raten	0.064	0.033
167	≤84 µm	MBRv Raten−1 predicting RNFLT Raten	0.087	0.009
178	>84 µm	MBRt Raten−1 predicting RNFLT Raten	0.202	0.027
167	≤84 µm	MBRt Raten−1 predicting RNFLT Raten	0.198	0.065

Bold value indicates P < 0.05.

^*Models of interest (i.e., Models B and D) assessing MBR in both ONH vessels and tissues, MD, and RNFL using subgroups of eyes with average MD ≤ −0.72 dB versus > −0.72dB; and subgroups of eyes with average RNFL > 84 µm versus ≤ 84 µm.

Discussion

In this study, we used SEMs to investigate whether there is a potential time lag between changes in MD and MBR, as well as between RNFLT and MBR. SEMs possess the capability to integrate latent variables into a time series, where the observed values depend on previous occurrences and serve as predictors for future values. This enables the examination of the effectiveness of time-lagged variables, allowing the identification of time lags between genuine rates of change. We observed that the rate of functional change, as measured by MD, in a specific time interval predicted the subsequent rate of blood flow change (MBR). This predictive relationship was not reciprocal; the rate of blood flow change did not predict subsequent functional changes. Additionally, our findings revealed that the rate of blood flow change in a given time interval predicted subsequent structural changes (RNFLT). Conversely, this predictive association was not observed in the reverse direction. These time lags imply that true functional change (as measured by MD) occurs earlier than blood flow changes, which in turn is precede change in RNFLT. Our findings align with previous research suggesting that a decrease in blood flow is associated with deteriorated visual function and structural damage in glaucoma.¹³ However, our study reveals a temporal sequence distinct from the established correlation.

The temporal precedence of MD compared to MBR implies that changes in function cannot be solely attributed to reduction in optic nerve head blood flow. Rather, it suggests the involvement of additional factors influencing the observed functional changes. For example, the mechanical theory of glaucoma, characterised by elevated intraocular pressure and increased cupping, which exerts a mechanical influence on the axons,²⁴ is likely a significant contributor to changes in visual field sensitivity. Furthermore, pathogenic mechanisms enabled by mechanical and vascular stress contribute to the neurodegenerative process associated with glaucoma, such as mitochondrial dysfunction, chronic oxidative stress, excitotoxicity, and neuroinflammation.²⁵ For example, oxidative stress, arising from the formation of multiple reactive oxygen species, is heightened in the aging retina. It is considered a key risk factor contributing to para-inflammation dysregulation in glaucoma,²⁶ resulting in cellular and tissue dysfunction and death. Thus our findings emphasize the intricate interplay of mechanical, vascular, and molecular factors influencing functional changes in the disease progression.

The RNFL primarily comprises axons of retinal ganglion cells, but also contains blood vessels and glial cells that contribute to its structural integrity. In glaucoma, the functionality of these axons likely ceases some time before the retinal ganglion cell undergoes cellular breakdown and the subsequent phagocytic processes, followed by reduction in the vascular and glial components. Thus RNFL thinning is likely to occur some time after axon loss,^27,28 consistent with our previous finding that functional changes precede RNFL thinning.² Our results suggest that the reduction in blood flow also precedes RNFL thinning. While we cannot yet be sure of the exact timing of the axon loss, our results are consistent with the order of changes being MD first, then MBR and axon loss almost concurrently, then RNFLT slightly later.

The time lag whereby MD changed earlier than MBRt was significant for the subgroup of eyes with MD < −0.72 dB, but not for MD > −0.72 dB. This finding could be driven by the fact that the magnitude of the coefficient for MBRt_n−1 predicting MBRt_n was greater for the MD > −0.72 dB subset (−0.347 vs. −0.312), suggesting that the rate of change of MBRt was more consistent between time periods; hence the additional information available from MD_n−1 did not improve predictions of MBRt_n. It is possible that the temporal relation between MD and MBRt does indeed vary with disease stage. However, the statistical significance of the time lags did not vary between those two subsets for MBRv; nor did it vary between subsets of RNFLT < 84 versus RNFL > 84. There are few patients in the cohort with severe or end-stage glaucoma, so we cannot conclude anything about the relation between ocular blood flow and functional and structural parameters at that stage of the disease.

The identification of time lags between ocular blood flow, functional and structural changes in glaucomatous eyes holds significant implications for the understanding and management of glaucoma. Our study reaffirms previous findings indicating that true functional change precedes structural changes in glaucoma,² notwithstanding the fact that RNFLT changes, being detectable earlier because of lower measurement variability, might serve as a more sensitive indicator. Although our investigation primarily focuses on temporal relations rather than detectability, clarifying whether blood flow changes serve as precursors to or concurrent with axon loss is crucial. It aids in establishing a more precise timeline of events in glaucoma pathogenesis, facilitating early detection and intervention, especially because all testing instruments used in this study are approved by the Food and Drug Administration and commercially available. Furthermore, this knowledge sheds light on the underlying mechanisms that drive glaucoma, offering a promising avenue for targeted approaches in the clinical management of glaucoma.

The use of SEMs in this study, as opposed to simpler statistical techniques, offers several strengths. SEMs allow for the simultaneous use of a variable as both an outcome and a predictor, essential for our comparative analysis. This framework is particularly advantageous for assessing time lags in longitudinal data because it handles missing data effectively, a crucial feature for longitudinal studies where missed visits are common. The availability of various model fit indexes in the lavaan package in R, used for building and testing SEMs, ensures the selection of the most accurate model that aligns with the observed data, enhancing the study's overall robustness. Importantly for this study, SEMs enable the incorporation of latent variables, further strengthening the analytical depth of this investigation.

This study is further strengthened by its use of high-quality, well-controlled longitudinal data sourced from the P3 study. Testing is conducted by a dedicated technician, alert to the main sources of error and variability, ensuring higher quality data than is often typical of clinical testing. There are some limitations to the LSFG device. For example, the device has a small field of view and so measurements can only be taken of the ONH. Furthermore, the resulting image is two-dimensional, not three-dimensional, so measurements cannot be localized to prelaminar versus lamina cribrosa versus postlaminar tissue. It is important to note that the LSFG software uses an auto-detection mechanism for pixels, categorizing them as either vessels or tissues. In reality, a pixel might contain information from both simultaneously when there is nonvascular tissue on top of or below a vessel. Despite this, our study revealed no significant difference between measurements obtained from tissue MBR and vessel MBR. It should be noted that phenylephrine drops have been found to decrease blood velocity in the ONH,²⁹ and future work should consider utilising tropicamide instead. Yet phenylephrine drops were used for all participants, so its use will not bias our conclusions. The P3 dataset lacks a substantial number of patients with late-stage glaucoma. Although our secondary analysis revealed no significant differences between subgroups of eyes with average RNFLT > 84 µm versus ≤ 84 µm and subgroups of eyes with average MD ≤ −0.72 dB versus > −0.72dB, it remains plausible that results may be different in severe glaucoma. We would also note that even if the average rates of change of MBR, MD, and RNFLT vary with severity, this would not necessarily cause any change in the time lag between them. Further investigation is warranted to explore potential differences in the rate of change in patients with advanced glaucoma. Another limitation of this study is the predominantly white cohort, potentially limiting the generalizability of findings. Ethnicity-based differences in glaucoma, which have been observed, might not be fully captured within this predominantly homogenous population. Normal-tension glaucoma is more prevalent in Asian populations, and it is possible that ocular blood flow may have a different or causative effect in that cohort or that there may be other populations in which blood flow reduction may precede axonal loss.³⁰

Conclusions

In a large cohort of people with glaucoma and glaucoma suspects, a clinically relevant time lag was determined between MD and MBR, and MBR and RNFLT, respectively. This time lag implies that true change for MD occurs earlier than blood flow changes, which in turn is predictive of subsequent change in RNFLT. These findings aid in establishing a more precise timeline of events in glaucoma pathogenesis and sheds light on the underlying mechanisms that drive glaucoma.