Statistical Evaluation of ERG Responses: A New Method to Validate Cycle-by-Cycle Recordings in Advanced Retinal Degenerations

Abstract

Purpose

To describe and evaluate a novel method to determine the validity of measurements made using cycle-by-cycle (CxC) recording techniques in patients with advanced retinal degenerations (RD) having low-amplitude flicker electroretinogram (ERG) responses.

Methods

The method extends the original CxC recording algorithm introduced by Sieving et al., retaining the original recording setup and the preliminary analysis of raw data. Novel features include extended use of spectrum analysis, reduction of errors due to known sources, and a comprehensive statistical assessment using three different tests. The method was applied to ERG recordings from seven patients with RD and two patients with CNGB3 achromatopsia.

Results

The method was implemented as a Windows application to processes raw data obtained from a commercial ERG system, and it features a computational toolkit for statistical assessment of ERG recordings with amplitudes as low as 1 µV, commonly found in advanced RD patients. When recorded using conditions specific for eliciting cone responses, none of the CNGB3 patients had a CxC validated response, indicating that no signal artifacts were present with our recording conditions. A comparison of the presented method with conventional 30 Hz ERG was performed. Bland–Altman plots indicated good agreement (mean difference, −0.045 µV; limits of agreement, 0.193 to −0.282 µV) between the resulting amplitudes. Within-session test–retest variability was 15%, comparing favorably to the variability of standard ERG amplitudes.

Conclusions

This novel method extracts highly reliable clinical recordings of low-amplitude flicker ERGs and effectively detects artifactual responses. It has potential value both as a cone outcome variable and planning tool in clinical trials on natural history and treatment of advanced RDs.

Electroretinography is a well-known technique for the assessment of retinal function. Since its inception more than 100 years ago,^1–3 the electroretinogram (ERG) has evolved into standard clinical practice with protocols delineated by the International Society for Clinical Electrophysiology of Vision (ISCEV). ERGs are typically elicited using a flash stimulation of variable frequency (0.05–33 Hz) and strength (0.01–25 cd·s/m²). The selection of the stimuli characteristics depends on the contribution of retinal elements (rod, cones, bipolar cells, amacrine cells) intended for study.⁴

In advanced retinal degenerations, full-field ERGs are regarded not only as a useful diagnostic tool but also as a prognostic aid.⁵ However, in advanced stages of degeneration, ERG responses can reach undetectable levels. Different approaches have been pursued to detect and quantify very small ERG amplitudes.^6–9 Most of these approaches make use of the flicker ERG, a retinal potential elicited by a train of evenly timed flashes or by a sinusoidally modulated light stimulus. When the stimulus frequency is in the range of 30 to 40 Hz, the resulting steady-state response is dominated by a sinusoidal component of photoreceptor/bipolar cell origin¹⁰ having the same temporal frequency as the stimulus.

In the study of advanced retinal degeneration, extremely low-voltage ERG responses need to be evaluated, and the use of Fourier analysis, based on an integral algorithm, is more reliable than a single-point measurement, such as peak-to-peak amplitude or implicit time.¹¹ Nonetheless, even the computation of Fourier components is affected by noise, which introduces a random variability in amplitude and phase measurements and possibly alters the response detection in the most severe cases. Therefore, a robust statistical assessment of results is needed.⁹

The aim of the present work is to describe and evaluate, in a clinical environment, a computational toolkit designed to determine the validity of measurements of very low-amplitude responses in patients with advanced retinal degeneration. The toolkit is applied to the method known as the cycle-by-cycle (CxC) recording⁹ and provides response measurements, as well as possible corrections to several common types of noise artifacts.

Methods

Experimental Settings and Subjects

ERGs were elicited using an ISCEV light-adapted flicker protocol⁴ with stimulus frequency of 32.26 Hz and stimulus strength of 3.0 cd·s/m². Potentials were obtained using corneal Burian–Allen electrodes (Hansen Ophthalmic Instruments, Iowa City, IA, USA). A commercial ERG system (Espion E2/ColorDome system; Diagnosys LLC, Lowell, MA, USA) provided both stimulus generation and signal recording. Settings included a total recording duration of 14.88 seconds (480 cycles), bandpass filter of 1 to 250 Hz, sampling rate of 2000 Hz, no automatic artifact rejection, and a dynamic range of 1.25 V. These settings were intended to produce a true steady-state, unaltered recording. A shorter 5-second section of optimum quality was selected for subsequent evaluation. The full recording output was exported as a text file to be processed offline with a separate software application featuring a statistical assessment toolkit. No trigger information was needed, as the system configuration guarantees a perfect synchronism between the processes of stimulus generation and signal sampling. The method was applied to ERG recordings from seven patients with advanced RD and two patients with CNGB3 achromatopsia. Subjects were light-adapted for 20 minutes at 30 cd/m² before each recording.

The study conformed to the tenets of the Declaration of Helsinki. Study subjects were enrolled under protocol 15-EI-0128, Genetics of Inherited Eye Disease (NCT02471287), approved by the Institutional Review Board of the National Eye Institute. The analysis of raw data coming from the acquisition system was divided into three steps: a preliminary analysis, a statistical evaluation including three tests, and a quality of signal assessment.

Preliminary Analysis of Raw Data

A preliminary analysis of the raw data file computes the sine and cosine components of the first harmonics (1Fs and 1Fc) for every cycle of the full recording (480 cycles) and searches for the 160-cycles section (4.96-second duration) having the lowest variance of the 1F components and no major artifacts (blinks). This low-noise section is used in the following analyses, starting with a fast Fourier transform (FFT) in the frequency range of 0 to 1000 Hz with 0.20 Hz resolution. The FFT components at the stimulation frequency (i.e., amplitude and phase) are the main result of the examination. All other data, consisting of the full frequency spectrum and the array of 160 cycle-by-cycle 1F values formerly computed, were used only for the statistical tests of significance described in the next paragraph. Here, it may be useful to remember that the 1F component given by the FFT of the 4.96-second time window coincides with that obtained by the FFT of the time-averaged signal cycles or by the vector average of the CxC components because of the linearity of the Fourier transform.

Statistical Evaluation

Following preliminary analysis, the toolkit performs three statistical tests based on the classical paradigm of hypothesis testing, where the null hypothesis is the absence of signal. All of the tests check against a confidence region calculated from continuous probability distributions, typically the Snedecor's F-distribution.

T1. CxC Test

This test is based on the analysis of the dispersion of the 1Fc and 1Fs components (cosine and sine) computed for each of the 160 individual cycles considered. On a Cartesian plot, these data appear as a widespread cloud of points (or vectors), whose mean is the outcome of the examination. Means of bivariate distributions are usually evaluated using Hotelling's T² test, the multivariate counterpart of Student's t-test. We tested the hypothesis that the vector mean is different from zero. Assuming zero covariance, as is the case for Fourier components of random noise,^12,13 the test statistic T² is simply

$$\begin{array}{c}\hfill T^2=\frac{x^2}{\frac{\sigma x^2}{n}}+\frac{y^2}{\frac{\sigma y^2}{n}}\end{array}$$

where x and y are the components of the 1F mean amplitude, σx² and σy² are the associated variances, and n is the number of points. If a normalized form of T² is used, the P value for the observed mean may be computed using pF, the cumulative probability distribution of F, as follows¹⁴:

$$\begin{array}{c}\hfill p=pF\left[T^2\frac{n-2}{2\left(n-1\right)},2,n-2\right]\end{array}$$

where pF is the cumulative probability distribution of F with 2 and n – 2 degrees of freedom.

A critical value for T may be computed for a 1 – α confidence level using qF, the inverse cumulative probability distribution:

$$Q=\sqrt{\frac{2\left(n-1\right)}{n-2}qF\left(1-\alpha ,2,n-2\right)}$$

Using the actual values (n = 160, α = 0.05), we obtain Q = 2.479, which is a close approximation of the limit value 2.448 obtained when n tends to infinity.

In the Cartesian plane, the equation T = Q defines an elliptical confidence region in canonical form, with semi-axes a and b given by

$$a=Q\frac{\sigma x}{\sqrt{n}}b=Q\frac{\sigma y}{\sqrt{n}}$$

where a and b depend on the standard error of the mean of cosine and sine components, as described previously.⁹ The test is passed if the test ratio T/Q is greater than 1, a condition having the geometrical meaning that the ellipse does not include the origin.

T2. Averages Test

This algorithm uses results obtained with the classical method of signal averaging, implemented in a specific form long used in our previous research work.^15,16 The signal is divided into four segments of 40 cycles, and the corresponding time averages are computed. The number of segments was chosen in order to have a sufficient number of samples to perform subsequent statistics while keeping the minimum segment length that is necessary to have independent spectral estimates.¹² The traces of partial and total averages are displayed, as in any clinical electrophysiology system. The Fourier analysis in this case produces only four vectors, whose mean is tested against the H₀ hypothesis using the T²_circ statistic,¹³ a method better suited than T² when only small samples are available. In this statistic, the variances of sine and cosine components are assumed to be equal, and the test statistic T² is defined as follows:

$$T^2=\frac{x^2+y^2}{\frac{\sigma x^2}{n}+\frac{\sigma y^2}{n}}$$

with the same meaning of symbols as in the former case. The P value is obtained by a direct application of the F cumulative distribution¹²:

$$p=pF\left[T^2,2,2n-2\right]$$

and the critical value for T is therefore

$$Q=\sqrt{qF\left(1-\alpha ,2,2n-2\right)}$$

In both formulas, the number of degrees of freedom of the denominator of F is doubled, giving the method a specific advantage when small samples are used. Using the actual values (n = 4, α = 0.05), we obtain Q = 2.268.

The equation T = Q now defines a circle of radius R in the x, y plane:

$$\sqrt{x^2+y^2}=R$$

where $R=Q\sqrt{\frac{\sigma x^2}{n}+\frac{\sigma y^2}{n}}$.

As $\sqrt{x^2+y^2}$ is nothing but the 1F amplitude, the value R may be regarded as an amplitude threshold for significance. A circle of confidence of radius R may also be traced and used as in the case of the ellipse.

T3. Noise Test (Periodogram)

This test reverses the point of view of the former ones. Instead of basing the calculations on the effect (that is, the observed variability of measurements), we focus on the cause, or the presence of additive random noise. In particular, it is considered that a noise component at the stimulation frequency may be interpreted as a response also in the absence of any physiological activity. The key idea of this test dates back to the classical work of Schuster on periodogram analysis,¹⁷ aimed at detecting a periodical signal hidden in noise. Afterward, it was adapted and improved in many ways, but in the present case, where the signal frequency is known a priori, the simplest form may be used. If we assume that the spectral power density of noise is constant in a small frequency band centered around the test frequency (a hypothesis that is usually well verified), then the amplitude of the Fourier sine and cosine components included in this band will have a normal distribution with equal variance and a mean of zero.¹² The test statistic T is obtained using this set of noise components plus the signal component, in the form of a signal-to-noise ratio, expressed in terms of power:

$$T^2=\frac{x^2+y^2}{\frac{1}{n}{\sum }_k\left[{\left(N{x}_k\right)}^2+{\left(N{y}_k\right)}^2\right]}$$

where Nx_k and Ny_k are the noise components at n frequency bins around the stimulation frequency, excluding it or its harmonics. As the numerator is the sum of two squared orthogonal components (sine and cosine) and likewise in the numerator there is a sum of 2N squared components, it follows from definitions that T² is distributed as F with 2 and 2n degrees of freedom in the numerator and denominator.¹⁸ The P value is therefore simply

$$p=pF\left[T^2,2,2n\right]$$

and the critical value for T is

$$Q=\sqrt{qF\left(1-\alpha ,2,2n\right)}$$

Using 20 noise measurements taken from the computed spectrum in the range of 30 to 34 Hz, we obtained a critical value Q = 1.798, given α = 0.05. A test ratio, T/Q, is then computed as for other tests, and T = Q now represents a signal-to-noise threshold (for power values).

A similar signal-to-noise statistic can also be calculated using signal amplitude 1Fa and the scalar average of noise amplitudes; that is, amplitudes are used instead of powers:

$$T=\frac{1Fa}{Navg}$$

The sum of noise amplitudes does not have the nice statistical features of the sum of noise powers, so the T ratio is now distributed in a very specific way. For N ≤ 2, it may be expressed by a closed formula,¹⁹ but for N > 2 no solution is available, to our knowledge. It is possible to use an approximate solution²⁰ and numerically calculate the critical value for a given confidence level. In this case, we obtain Q = 2.02 for the parameters previously used, and the extra material includes the algorithms used to compute approximate values of Q for n > 2.

This test has been verified to be in good agreement with the best known power version, and, apart from the difficulty in computing exact critical values, it has the advantage of using amplitudes, which are quantities of direct meaning to the user, readily plotted on the usual graphical representations. The noise components and the signal are shown both as an amplitude histogram and as a Cartesian vector plot. In the first case, T = Q defines a critical threshold for 1F amplitude traced as a line, and in the x,y plot a circular confidence region appears.

Methods Comparison

In order to compare the CxC protocol with the standard ISCEV examination, the seven RP subjects were studied with both protocols, and the results (1Fa) were compared using Bland–Altman analysis. The CxC protocol was repeated three times for every subject to assess its repeatability.

Quality of Signal and Corrections

Following the preliminary analysis and the statistical evaluation, the toolkit performs a series of seven additional tests (line interference, signal clipping, low-frequency noise, trend, in-band noise, noise components anomalies, and low signal-to-noise ratio) to detect the presence of common artifacts that could invalidate the results of the statistical tests. Each test has an associated warning, and a possible correction is proposed.

The presence of line interference is revealed using the power spectrum. In particular, the power at the line frequency and its harmonics is checked against the total power (“Line” warning). A possible correction consists of the use of a stop-band digital filter. The use of a sharp notch filter should be avoided because line interference usually is amplitude modulated, so that it spreads over a small frequency band. If the signal is “clipped” (i.e., it exceeds the available dynamic range), a light is activated (“Clip” warning). In this case, no corrections are possible, and the recording must be rejected.

A specific test indicates an abnormally high noise in the 0 to 20 Hz band (“LoFreq” warning). This condition has a counterpart in the time domain, showing itself as a wandering baseline or a definite trendline, that is also subject to a separate test (“Trend“ warning). The condition can be dealt with highpass digital filters or by the use of a detrend algorithm. The preferred correction is by linear filtering, as detrend may produce unreliable results due to the difficulty of dealing with the presence of isolated spikes. The toolkit features a programmable passband digital filter that can easily be used in this eventuality.

Another two tests are aimed at spotting noise spectrum anomalies. One computes the vector average of the noise in the vicinity of signal and checks for a value significantly greater than zero (“Nmed” warning), and the second checks for an abnormally high ratio of sine to cosine components (“Sine” warning). Both conditions indicate a departure from the assumed model of random noise equally distributed in power around the frequency of interest. In this case, a direct correction can be performed by the toolkit by subtracting the artifactual noise vector from the final result.

The last test is performed in case of a statistically significant response with very low signal-to-noise ratio. In this case, the toolkit searches for the presence of significant harmonics of higher order, in addition to the first one. This is a typical signature of an artifact caused by electromagnetic or photovoltaic interference. In this case, an “EMI” warning is raised, and the recording must be rejected.

The output of the toolkit, implemented as a Windows application, is a final report presenting T1, T2, and T3 results (P values of the tests, critical values, and test ratio T/Q); the associated confidence regions plot; and the recorded data in the time and frequency domains, as well as 1F and 2F harmonic amplitudes, noise amplitude, and signal-to-noise ratio (Figs. 1²–3)

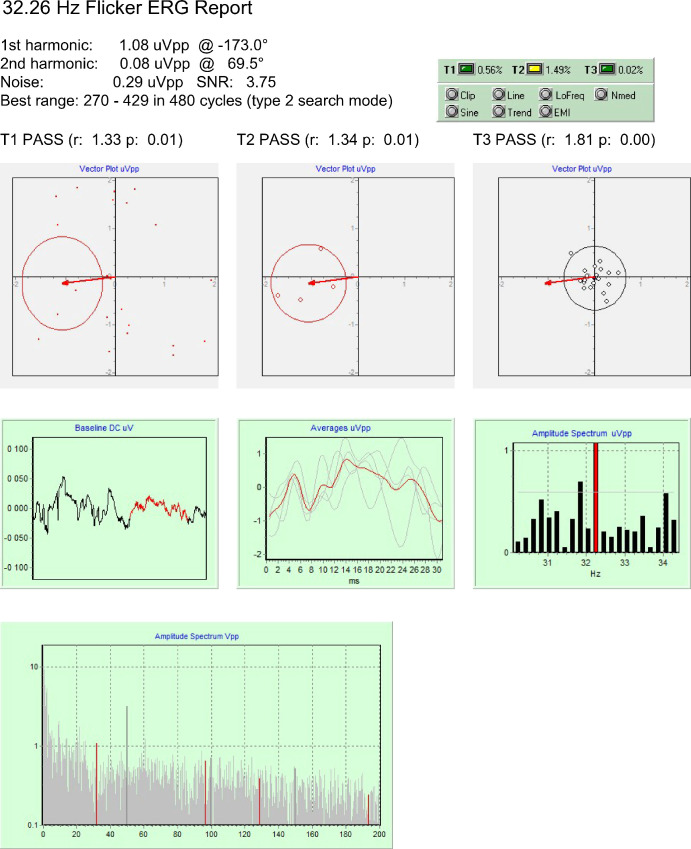
Figure 1.

Data obtained from a patient with severe function loss, where a microvolt-level response is fully validated.

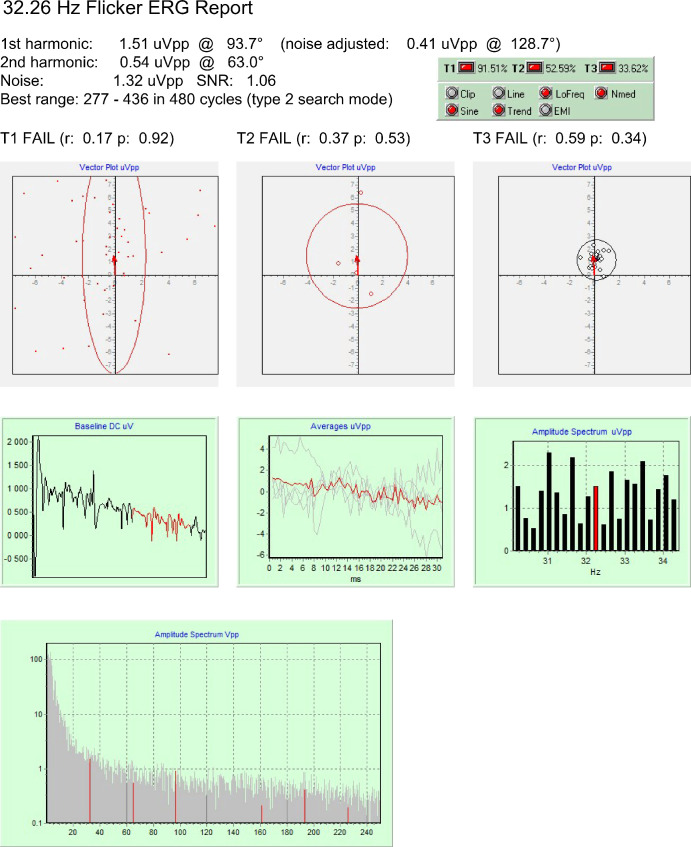
Figure 2.

Data obtained from one of the CNGB3 achromatopsia patients. Responses could not be validated, even when all warnings about signal quality were corrected (data not shown); hence, these recordings do not yield valid results.

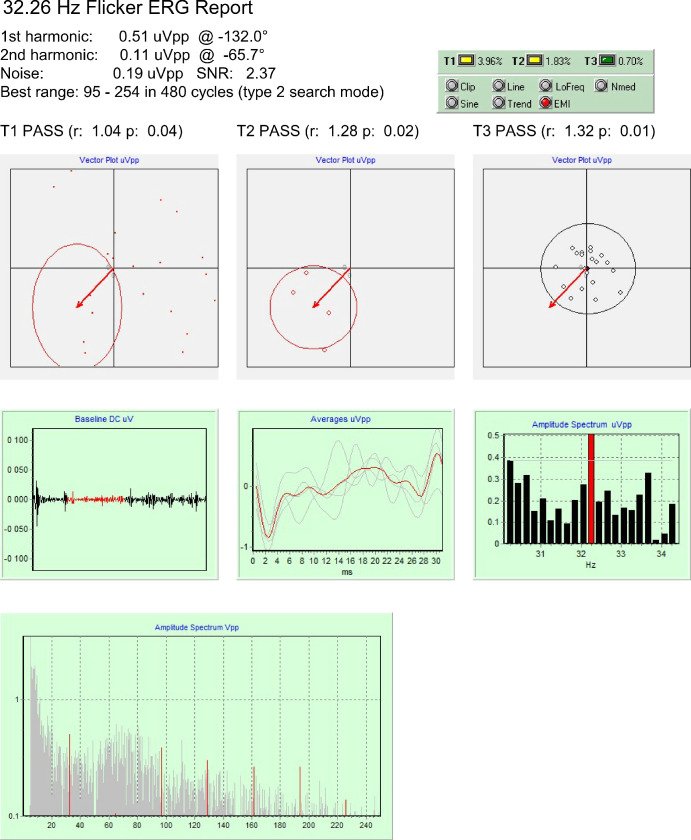
Figure 3.

Data obtained from a RP patient in the presence of electromagnetic interference. The statistical tests indicate a valid signal, but its artifactual origin is detected, as well (EMI warning signal).

Results

Validation on Patients

The method was primarily intended to study advanced stages of retinal diseases, where the amplitude response may be as low as 1 µV peak to peak, as in the case presented in Figure 1. These results show that all three statistical tests passed and no signal quality warning was on (Fig. 1, green box, upper right). A qualitative analysis of the graphs confirms that the noise spectrum has a typical distribution, the mean amplitude of noise is excellent, the baseline has no large trend, no blink artifacts are present, and sub-averages are consistent, so that no postprocessing is needed, and the 1.08-µVpp result may be accepted with confidence.

A different case is shown in Figure 2, obtained from a patient with absence of cone function. Here, all statistical tests failed, indicating that the measured amplitude, although not smaller than the former one, was not different from noise. The quality of the signal is also poor, and four warnings were raised. The toolkit detected the noise spectrum anomaly and processed the data to obtain an adjusted result (0.41 µVpp). Using the included digital filter with and highpass frequency of 12 Hz, it was possible to remove all warning signs but the result so obtained (0.35 µVpp) remained not significant (data not shown). None of the CNGB3 patients had a CxC validated response, indicating that no signal artifacts were present with our recording conditions.

The third case is that of a patient with a severe function loss in an experimental condition where a weak electromagnetic interference from the flash stimulator was also present. The analysis of original data (not shown) yielded only one valid test (T3) and EMI, LoFreq, and Nmed warnings. Application of a 5 to 250 Hz passband filter and of a line filter produced a valid signal (Fig. 3), but the EMI warning sign persisted. A visual inspection of the averaged waveform confirmed the artifactual origin of the response, which was eventually rejected.

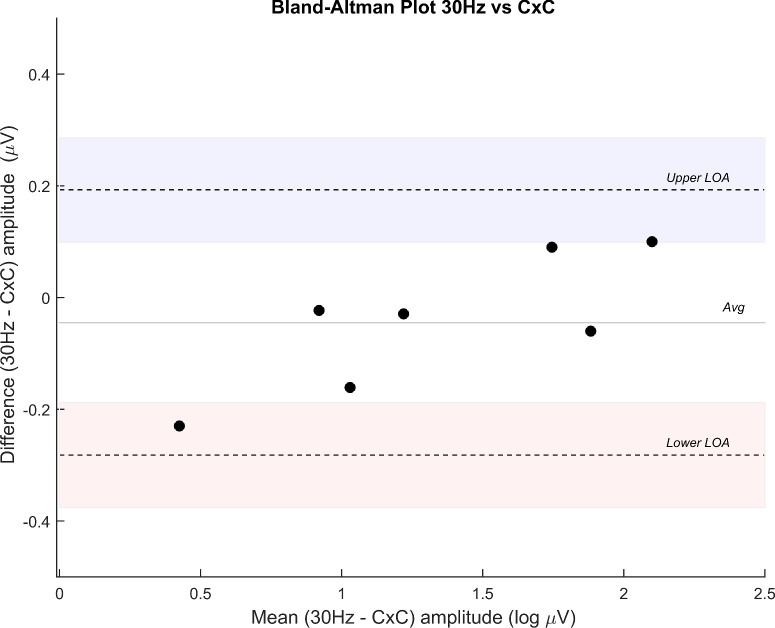
Finally, a group of seven RP subjects was studied with both the CxC protocol and the standard ISCEV examination. Results are summarized in a Bland–Altman plot (Fig. 4) that indicates a good agreement between the conventional 30 Hz ERG amplitude and CxC amplitude (mean difference, −0.045 µV; limits of agreement, 0.193 to −0.282 µV). The CxC protocol was repeated three times for every subject, and a coefficient of repeatability of 0.24 log µV was obtained. Within-session test–retest variability (average difference) of amplitude was 15%, a result comparable to variability for ISCEV ERG amplitudes.

Figure 4.

A Bland–Altman plot indicates good agreement between conventional 30 Hz ERG amplitude and CxC amplitude. Difference amplitude is expressed in log µV.

Discussion

The proposed method, in accordance with the original CxC algorithm, captures a true steady-state signal with no gaps, saturations, modulations, adaptation phenomena, or other anomalies. In addition, the sampling process is synchronized with the stimulus generation, and an integer number of cycles is collected, allowing for optimal use of Fourier analysis.¹⁹ The ideal model of a periodical signal hidden in random noise is then well matched, and a meaningful high-resolution spectrogram may be obtained from the recording. Moreover, the test–retest reliability is improved. The distinctive feature of our method is the use of a purposely designed statistical assessment toolkit that provides a comprehensive and contextual assessment of the quality of the recording and the reliability of the results.

The three tests presented are in principle strongly correlated and free of bias effects. It should therefore be possible, in given conditions, to assess their relative power and choose the one having the better performance. In less controlled conditions, the three tests frequently agree, but in case of discordance they give an indication of the origin of the problem, which in some cases may be corrected.

The CxC test has the advantage of having a larger sample dimension but may be altered by the presence of periodic interference at frequencies near the stimulus, typically coming from the 50 or 60 Hz mains. In a well-designed system, the stimulation frequency and the number of averaged cycles are adjusted to obtain a full cancellation of the interference from the final average. Nonetheless, the variance of the cycle components remains affected by the interference, and the resulting confidence region is abnormally extended.

The test based on partial averaging is the only part of the toolkit where traces of the averaged signal are shown, a feature that retains the utility of offering a qualitative check of the result to spot any evident anomaly of the examination. A specific problem appears in records where the variance of the sine component is significantly greater than that of the cosine component, typically the effect of low-frequency noise. This condition is in contrast with the assumption of equal variance made for the T²_circ test and may produce an altered statistic result.

The test based on the signal-to-noise ratio is affected by anomalies in noise spectrum distribution that usually are not an intrinsic feature of noise but are an artifact of the Fourier analysis, the well-known problem of spectral leakage. In the present context, the problem typically becomes important when the record has a large amplitude difference (VD) between the values of the first and last sample, a condition that is usually handled with the help of a window function. This VD may be the effect of a trend line, a low-frequency noise, or a combination of local features of the signal. In such a situation, the Fourier analysis, made without windowing, generates spurious components that generally spread all over the spectrum, starting as large ones at lower frequencies and decreasing in amplitude as frequency increases. In the vicinity of the frequency of interest, the disturbance generally becomes negligible, but, as the VD could be orders of magnitude greater than the response amplitude, significant spurious components may still appear. In a small frequency range nearby, the response frequency the amplitude of such artifactual components may be assumed to vary in a linear fashion, with the addition of true noise components having the normal random distribution. The average of these components may be therefore regarded as an unbiased estimator of the error component at the response frequency and used to correct the result. An effective correction may also be obtained using a detrend algorithm or a linear highpass filter on the signal before the Fourier analysis. The use of a window function such as the Hamming one is also appropriate and is commonly used in signal processing applications. This practice is not recommended in advanced RD because it further reduces the intrinsic signal-to-noise ratio, or process gain, and may impair the ability to detect the weakest responses.

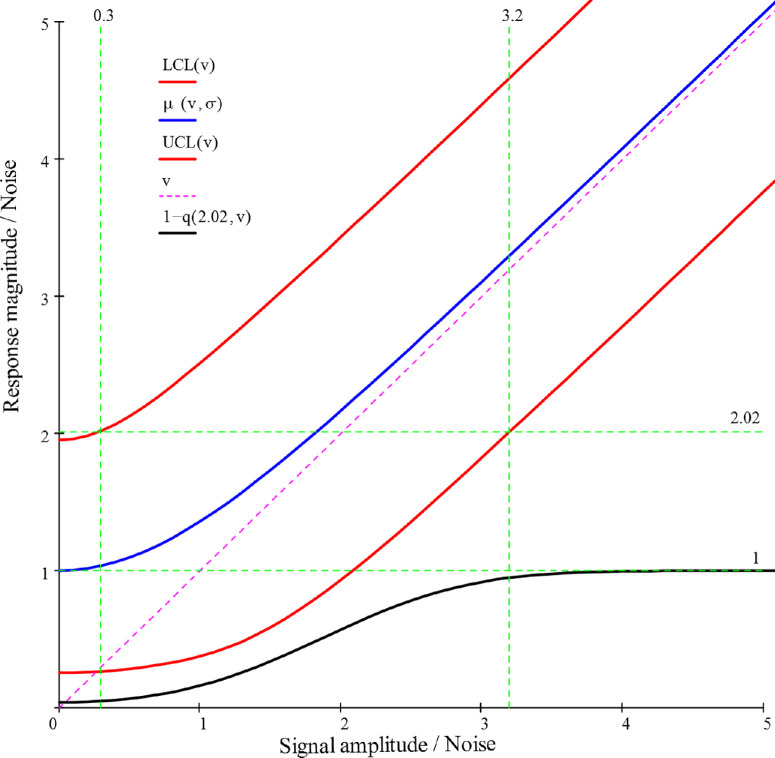
It is important to point out that the magnitude responses so far obtained result from the sum of the signal and noise amplitudes. This sum is a random variate that obeys the Rice distribution,²¹ and it is possible to compute the relationship between the underlying signal v and the observed response, as showed in Figure 5, where both signal and response are normalized to the noise amplitude. The mean response magnitude (central curve) was obtained from the analytic formulas of the moments of Rice's distribution and the confidence limits and the detection probability were obtained using the Marcum Q-function for the cumulative probability²² and the critical value Q = 2.02 previously described.

Figure 5.

Measured magnitude versus signal amplitude, both normalized to noise amplitude. The blue line is the mean magnitude, red lines are the 5% and 95% confidence limits, and the lower black line is the detection probability.

The chart may be used to raise many interesting considerations. First, it may be noted that the mean magnitude curve starts at a value of 1, due to the contribution of noise, and that the initial large positive bias over the “true” value v reduces itself as v increases, becoming negligible for v > 2.56 (bias error <5%). At the same time, the detection probability increases, attaining almost certainty (95% level) when v is greater than 3.2. Meanwhile, the spread range of the measured magnitudes reduces very little in absolute values, so that at the v = 3.2 level it is still +43.6% and −37.0%. of the mean. If an accuracy of ±20% is needed, the signal-to-noise ratio must be greater than 7.

Thanks to the noise data produced by the toolkit, it is possible to create a database useful to estimate the noise levels for different clinical or research settings. In this way the v values previously considered may be translated into actual voltages so that, using the chart in Figure 5, it is possible to forecast the detection probability and the average dispersion of the results for the cohort to be studied. This capacity may be of value for the rational planning of the clinical activity and the efficient design of clinical trials.

The dedicated software application made it possible to concentrate in a single tool a range of functions usually obtained with the help of different statistical and signal processing packages. The method provided reliable analysis of the validity of measurements made by ERG recordings of amplitude as low as 1 µV, as may be required for the study of advanced RD patients. Moreover, the method is of potential value both as an outcome variable and as a planning tool in clinical trials on natural history and treatment of advanced RDs. Future developments may include the use of correction schemes based on the analysis of the variance of the measured magnitude.