Abstract
Magnetic tunnel junctions (MTJs) are the core element of spintronic devices. Currently, the mainstream writing operation of MTJs is based on electric current with high energy dissipation, and it can be notably reduced if an electric field is used instead. In this regard, it is promising for electric field control of MTJ in the multiferroic heterostructure composed of MTJ and ferroelectrics via strain-mediated magnetoelectric coupling. However, there are only reports on MTJs with in-plane anisotropy so far. Here, we investigate electric field control of the resistance state of MgO-based perpendicular MTJs with easy-cone anisotropic free layers through strain-mediated magnetoelectric coupling in multiferroic heterostructures. A remarkable, nonvolatile, and reversible modulation of resistance at room temperature is demonstrated. Through local reciprocal space mapping under different electric fields for Pb(Mg1/3Nb2/3)0.7Ti0.3O3 beneath the MTJ pillar, the modulation mechanism is deduced. Our work represents a crucial step toward electric field control of spintronic devices with non–in-plane magnetic anisotropy.
Electric fields control resistance states in non–in-plane MTJs via magnetoelectric coupling.
INTRODUCTION
A magnetic tunnel junction (MTJ), which essentially consists of two ferromagnetic (FM) electrode layers separated by an ultrathin insulating tunnel barrier and has large tunnel magnetoresistance ratio at room temperature, is currently the core element of all magnetic random-access memory (MRAM) technology (1, 2). Because of the dominant attributes of non-volatility, virtually unlimited endurance, high speeds of read/write operations, high storage density, scalability to advanced (sub-20 nm) technology nodes, radiation hardness, and compatibility with complementary metal-oxide semiconductor (CMOS) processing (3), MRAM gradually becomes the most promising contender for the universal memory that combines the best attributes of static RAM (speed), dynamic RAM (density), and Flash (non-volatility) (4). However, the spin-transfer torque MRAM currently in use and spin-orbit torque MRAM with potential applications require high electric current density to realize a “writing” operation (5–11), which could lead to overheating in densely packed devices (12) and should be resolved especially beyond the 20-nm technological node (3). Therefore, extensive efforts have been focused on controlling MTJs via electric field instead of electric current (13–19) such as voltage-controlled magnetic anisotropy (VCMA) (14, 15, 17) and voltage-controlled exchange coupling (18, 19). However, these methods require a large voltage applied to the junction and the voltage is even close to the breakdown voltage (nearly 1 V) of the thin insulating barrier (2, 20), making the device easily damaged, in addition to the difficulty in simultaneous optimization of some key parameters of MTJ. Although some progress has been made (17, 21–24), the problem remains.
Recently, the development of multiferroic materials (25–28) provides an effective method for modulating magnetism via electric fields. Integrating ferroelectrics (FEs) and MTJs to realize electric field “writing” operation has become an important approach for energy-efficient spintronics. There are some reports using FE or multiferroic materials as the insulating layer of MTJs (29–32). Switching of the FE polarization induces changes in spin polarizations of FM layers at the interfaces, leading to manipulation of MTJ resistance (hereafter resistance for short) (31). However, low temperature is required to show the effect, which limits applications. Fortunately, electric field control of magnetism and resistance has been achieved in multiferroic heterostructures based on FEs and MTJs with in-plane magnetization at room temperature via strain-mediated magnetoelectric coupling (33–38), including experimental demonstration of volatile (33) and nonvolatile (34) resistance owing to electric field–induced magnetization rotation close to 90° of the free layer (FL) in MTJ with two electrodes (33, 34) and later on magnetization rotation close to 180° of the FL with multielectrodes (35). Nevertheless, only MTJs with in-plane magnetization, i.e., in-plane magnetic anisotropy, have been modulated by strain in MTJ/FE multiferroic heterostructures so far. There is still no report on strain-mediated modulation of resistance in MTJ with non–in-plane magnetic anisotropic FL in MTJ/FE, due to the following difficulties. For the case of in-plane magnetization (39–41), magnetic alloys without magnetocrystalline anisotropy and other magnetic anisotropies are used to achieve large modulations, as the magnetic moments of FM layers are almost free and exhibit good response to the electric field–induced in-plane anisotropic piezo strain and uniaxial magnetic anisotropy via minimizing magnetoelastic energy. However, for the case of non–in-plane magnetization, such as CoFeB/MgO (42) and Co/Pt (43, 44) structures with perpendicular magnetic anisotropy (PMA), the magnetic anisotropy or its equivalent magnetic field hinders the modulation of the magnetic moment. For example, Yu et al. (42) reported a strain-mediated modulation of PMA in the typical Ta/CoFeB/MgO structure, but the ferromagnetic resonance fields for different electric fields were barely altered. Nonetheless, the perpendicular MTJs (p-MTJs), compared with the in-plane MTJs, have advantages such as high density of information storage and have been commercialized (45, 46). Hence, it is of great importance to achieve strain-mediated modulation of resistance in p-MTJ/FE.
The p-MTJ with an easy-cone magnetic anisotropic FL is unique among MTJs with non–in-plane magnetic anisotropic FLs. The initial misalignment between the FL and the reference layer (RL) makes it deterministic for a spin-polarized current to transfer angular momentum (47). The threshold current for switching is reduced faster than the stability factor suggesting improvement of the overall performances of p-MTJ with the FL in the easy-cone regime (48). The improved switching speed makes the p-MTJ with an easy-cone anisotropic FL very useful in cryogenic and persistent memories that do not require too large thermal stability (47). Moreover, high-frequency zero-bias magnetic field precession in spin-torque oscillators (STOs) can be realized in a p-MTJ with an easy-cone anisotropic FL (49). Hence, electric field modulation of p-MTJ with an easy-cone magnetic anisotropic FL should be important for applications of cryogenic and persistent memories, as well as STOs with low power consumption.
Here, multiferroic heterostructures composed of MgO-based p-MTJs with easy-cone anisotropic FLs and Pb(Mg1/3Nb2/3)0.7Ti0.3O3 (PMN-PT) substrates were fabricated. Electric field–induced remarkable, nonvolatile, and reversible modulation of resistance at room temperature for p-MTJs is demonstrated. Through local reciprocal space mapping (LRSM) under different electric fields for PMN-PT beneath the MTJ pillar, the modulation of resistance can be ascribed to the magnetic anisotropy variation of the FL induced by the nonvolatile strain-mediated magnetoelectric coupling due to electric field–induced rhombohedral-orthorhombic (R-O) phase transition.
RESULTS
Magnetic properties of the FL and p-MTJ multilayer stacks
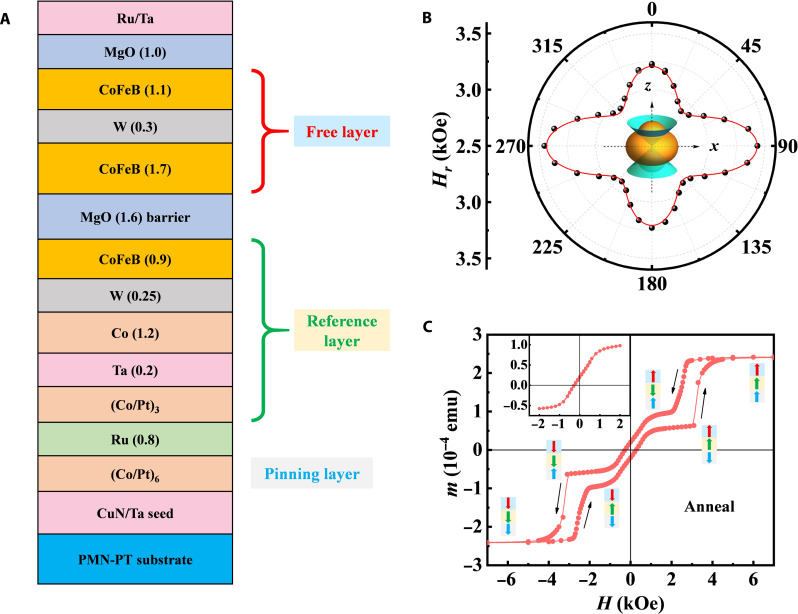
Figure 1A shows the schematic of detailed p-MTJ multilayer stacks consisting of Ta(25)/CuN(20)/Ta(3)/CuN(20)/Ta(0.7)/Pt(1.5)/[Co(0.5)/Pt(0.35)]6/Co(0.6)/Ru(0.8)/Co(0.6)/[Pt(0.35)/Co(0.5)]3/Pt(0.25)/Ta(0.2)/Co(1.2)/W(0.25)/CoFeB(0.9)/MgO(1.6)/CoFeB(1.7)/W(0.3)/CoFeB(1.1)/MgO(1)/Pt(1.5)/Ta(3)/CuN(5)/Ta(3)/Ru(5) (see Materials and Methods for details of sample preparation). Numbers in parentheses are the nominal thicknesses in nanometers and CoFeB denotes Co20Fe60B20. The CoFeB/W/CoFeB is used as the FL owing to the increased thermal stability factor (50–52) as well as the large tunability of magnetic anisotropy via changing the thickness of two CoFeB layers. The RL CoFeB, compensatory layer Co, and (Co/Pt)3 are ferromagnetically coupled via spacer layers W and Ta. A synthetic antiferromagnetic (SAF) pinning layer composed of (Co/Pt)6 and (Co/Pt)3 with a Ru spacer layer is used as the building block in MTJs for the effective reduction of stray fields. As shown in Fig. 1B, the easy-cone magnetic anisotropy of the FL is demonstrated by electron spin resonance (ESR) for a sample consisting of only the FL and barrier layer. The variation of resonance field with the angle between the external magnetic field and the normal direction of the sample is consistent with the easy-cone magnetic anisotropy and the easy-cone angle θ [the angle of the easy-cone state relative to the out-of-plane (OOP) direction] is about 40°. The magnetic moment versus OOP magnetic field hysteresis loop (m-H loop) is shown in Fig. 1C for the unpatterned MTJ multilayer stack. The magnetic moment directions of the FL (red), ferromagnetically coupled RL (green), and one part of the SAF pinning layer (Co/Pt)6 (blue) are shown for the different stages. Owing to the weak PMA of the FL, the magnetic moment changes slowly at low magnetic fields. The minor m-H loop is not symmetric with respect to the origin of m, which can be attributed to the incomplete reversal of magnetic moments (possibly CoFeB + Co) in the nonideal RL as shown later. The detailed analysis of the m-H loop and corresponding magnetic moment orientations is shown in text S1.
Fig. 1. Sample structure and magnetic properties.
(A) MTJ stack structure with CoFeB/W/CoFeB as FL (red), CoFeB/W/Co/Ta/(Co/Pt)3 as RL (green), and (Co/Pt)6 multilayers as synthetic antiferromagnetic pinning layer (blue). Numbers in parentheses are the nominal thicknesses in nanometers. (B) Variation of the electron spin resonance field of the FL with the angle between the external magnetic field and normal direction of the sample consisting of only the FL section in (A). The black circles are experimental results; the solid red line fits with the Kittel formula. (C) m-H loop and magnetic moment directions of different functional layers for the MTJ multilayer stack with an out-of-plane (OOP) magnetic field. The inset is the minor loop between +2000 and −2000 Oe after presetting at +7000 Oe. emu, electromagnetic unit.
Resistances for MTJs with the unpoled PMN-PT
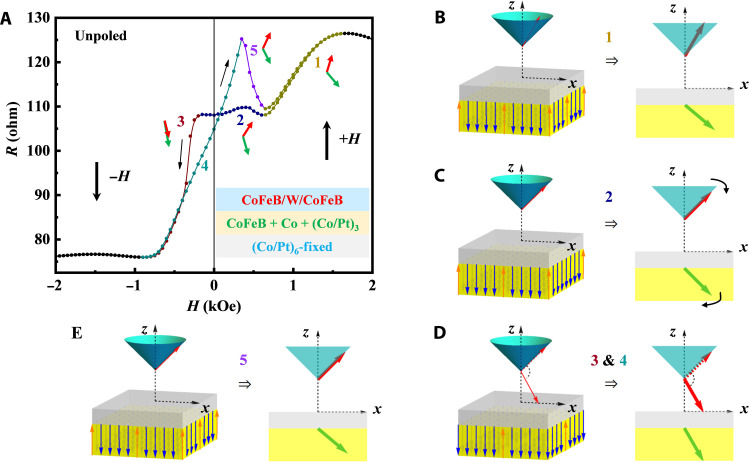
Figure 2A shows the resistance versus magnetic field (R-H) curve for the MTJ (10-μm diameter) with the unpoled PMN-PT between −2000 and +2000 Oe after presetting at +7000 Oe. The R-H curve shows some fine structures (peaks and dips), different from the behaviors of the in-plane MTJ and p-MTJ (with p-FL) (53), and can be understood by considering the variations of the FL and the nonideal RL with a magnetic field. Generally speaking, the magnetic moments of CoFeB + Co + (Co/Pt)3 should switch downward at about 2000 Oe (from +7000 to −7000 Oe; fig. S1A) and remain almost unchanged after that, however, the minor m-H loop for the sample with only the RL shows continuous change (fig. S2A) suggesting an incomplete reversal of magnetic moments of CoFeB + Co + (Co/Pt)3 (possibly CoFeB + Co), i.e., the magnetic moment directions are upward for some regions and downward for other regions (nonideal). There are also some reports on nonideal RL due to insufficient PMA in the conventional p-MTJ structures (single FL and SAF RL) (54, 55).
Fig. 2. Magnetoresistance measurements for MTJs under OOP magnetic field with unpoled PMN-PT.
(A) R-H curve for the MTJ pillar (10-μm diameter) between +2000 and −2000 Oe after presetting at +7000 Oe. The curve is highlighted in five sections with five colors numbered 1 to 5 as shown near the curve. The bottom inset is the structure of the MTJ stack, including FL (red), CoFeB+Co + (Co/Pt)3 in RL (green), and (Co/Pt)6 in RL (blue). (B to E) Left: The blue and orange arrows represent the nonideal magnetization directions that change with the sweeping of the magnetic field (detailed in fig. S2A). Right: The red and green arrows represent the equivalent moment directions of the FL and RL [also shown near the corresponding positions in (A)], respectively, corresponding to the five highlighted sections according to the resistance equivalent in tunneling.
To explain the unusual R-H curve, the inhomogeneous directions of magnetic moments in the RL are assumed to be equivalent to a single canted state [green arrows in Fig. 2, B to E; the canted angle is exaggerated to show its change with magnetic field] corresponding to an equivalent MTJ resistance, and the canted angle is determined by the relative portions of the regions with magnetic moment upward or downward (blue and orange arrows in Fig. 2, B to E). The structure of MTJ related to the FM films is shown in the inset of Fig. 2A with FL (red), CoFeB + Co + (Co/Pt)3 in RL (green), and (Co/Pt)6 in RL (blue). It should be mentioned that the magnetic moment directions of SAF composed of (Co/Pt)3 and (Co/Pt)6 are fixed during the minor R-H measurement because of the strong PMA. The resistance is determined by the angle between the moments of the FL and the equivalent moment of the RL with small angles favoring low resistance according to the Slonczewski model (56). From +1650 to −900 Oe, the magnetic moments of the FL first rotate to the easy cone of the FL, then rotate combined with a switch to the reverse direction for some magnetic moments, and lastly point downward for negative magnetic fields with large magnitudes. Meanwhile, for the equivalent moment of the RL, it rotates in the downward direction due to the reduction of regions with magnetic moment upward. The change of the FL leads to a reduction of resistance because it tends to decrease the angle between the magnetic moments of the FL and the equivalent moment of the RL. The change of the RL increases the angle, resulting in an increase in resistance. Therefore, the changes of the FL and RL compete for contribution to the resistance. As shown in Fig. 2A, from +1650 to +600 Oe (section 1) as well as from −200 to −900 Oe (section 3), resistance decreases remarkably suggesting the dominance of FL change. The equivalent canted states in the FL (red arrow) and RL (green arrow) are shown in Fig. 2 (B and D) (the dotted and solid red arrows represent the initial and final directions of magnetic moments of the FL in Fig. 2D, respectively). While from +600 to −200 Oe (Fig. 2A), the resistance changes slowly and nonmonotonically indicating dominance of strong competition between the changes of the FL and RL (Fig. 2C). From −900 to +1650 Oe, the magnetic moments of the FL first rotate to the easy cone of the FL, then rotate combined with switch to the reverse direction for some magnetic moments and lastly point upward for positive magnetic fields with large magnitudes. Meanwhile, for the equivalent moment of the RL, it rotates away from the downward direction due to the increase of regions with magnetic moment upward. The change of the FL leads to an increase in resistance because it tends to increase the angle between the magnetic moments of the FL and the equivalent moment of the RL. The change of the RL decreases the angle, resulting in a decrease in resistance. Again, the changes of the FL and RL compete for contribution to the resistance. As shown in Fig. 2A, from −900 to +350 Oe (section 4, the solid and dotted red arrows represent the initial and final directions of magnetic moments of the FL in Fig. 2D), the resistance increases and is even larger than that of section 2 which can be understood by considering the minor m-H loop of the RL (fig. S2A), suggesting the dominance of magnetic field–induced change of the FL. Above +350 Oe (section 5 in Fig. 2A), resistance decreases indicating the dominance of the change of the RL, consistent with the increased slope of the m-H curve for positive magnetic fields (fig. S2A).
Nonvolatile electric field control of MTJ resistance
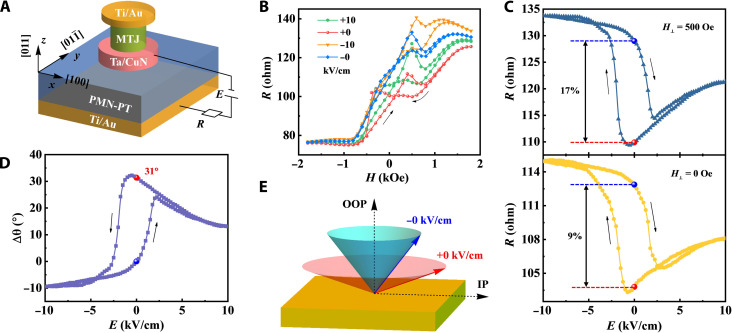
Figure 3A is the schematic of the MTJ configuration with the defined positive electric field. The electric field is applied to the PMN-PT through the buffer layer Ta/CuN (ground connection) and the Ti/Au electrode on the bottom of the PMN-PT. This is different from the VCMA method in which the electric field is directly applied to the MgO barrier through the two CoFeB layers adjacent to it and the electric field is close to the breakdown threshold of the MgO barrier (14, 20). Therefore, different from the VCMA method, our MTJ devices can avoid being damaged under electric fields. The R-H curves measured under different electric fields after presetting at +7000 Oe are shown in Fig. 3B. ±0 kV/cm corresponds to the electric field decreasing from ±10 kV/cm, respectively. The overall R-H behavior is similar to that measured without an electric field (Fig. 2A). Figure 3C shows the variation of resistance with an electric field (R-E curve), measured at +500 and + 0 Oe, respectively, after presetting at +2000 Oe. The resistance changes markedly at around ±2 kV/cm close to the coercive electric field of PMN-PT, suggesting its correlation with FE domain switching as discussed later. Two distinctive resistance states (red and blue circles in Fig. 3C) with a relative resistance change [defined as (R−0 – R+0)/R+0, ±0 correspond to ±0 kV/cm] of about 17% (H = +500 Oe) and 9% (H = +0 Oe) are realized at ±0 kV/cm. Therefore, room-temperature, nonvolatile, and reversible modulation of resistance is achieved in the MgO-based p-MTJs with easy-cone magnetic anisotropic FLs by electric fields. According to the Slonczewski model (56), as discussed in text S3, the change of the easy-cone angle Δθ with the electric field can be derived from the R-E curve (Fig. 3C, H = +500 Oe), and the calculated result is exhibited in Fig. 3D by selecting Δθ = 0° for −0 kV/cm (blue circle). The change of nonvolatile easy-cone angle is calculated to be about 31° at +0 kV/cm (red circle in Fig. 3D). Schematic illustration (Fig. 3E) also shows the modulation of easy-cone state of the FL under ±0 kV/cm (red and blue circular conical surfaces and arrows). It should be mentioned that some MTJs showed larger modulation by the electric field with a relative resistance change of about 33% at ±0 kV/cm and Δθ about 50° at +0 kV/cm (H = +600 Oe) (fig. S3, A to D). Unfortunately, these MTJs were damaged before more data were obtained (detailed in text S4). Therefore, it is promising that a much larger effect should be realized without a magnetic field if the design and processing of MTJ are optimized.
Fig. 3. Nonvolatile electric field control of MTJ resistance.
(A) Schematic of the MTJ configuration deposited and patterned on (011)-oriented PMN-PT. (B) R-H curves under different electric fields after presetting at +7000 Oe. The black arrows represent the sweeping direction of the magnetic field. (C) R-E curves measured at +500 and +0 Oe, respectively, after presetting at +2000 Oe. The black arrows represent the sweeping direction of the electric field. The nonvolatile modulations of resistance of about 17% (H = +500 Oe) and 9% (H = +0 Oe) are realized at ±0 kV/cm. (D) Variation of the easy-cone angle Δθ with the electric field by selecting Δθ = 0° for −0 kV/cm (blue circle). The value of Δθ at +0 kV/cm is indicated by the red circle. The black arrows represent the sweeping direction of the electric field. (E) Schematic illustrating the modulation of easy-cone state of the FL under ±0 kV/cm, respectively.
It should be mentioned that the strain-induced effective anisotropy field is about 120 Oe according to the previous report (34), which is very small compared to the pinning field [with field decreasing from 7000 Oe, the magnetic moment of the ferromagnetically coupled CoFeB + Co + (Co/Pt)3 layer switches above 2000 Oe; Fig. 1C] induced by the pinning layer on RL. Therefore, the strain does not affect the magnetization of RL (fig. S4) and we focus on the FL.
Nonvolatile electric field control of strain in PMN-PT
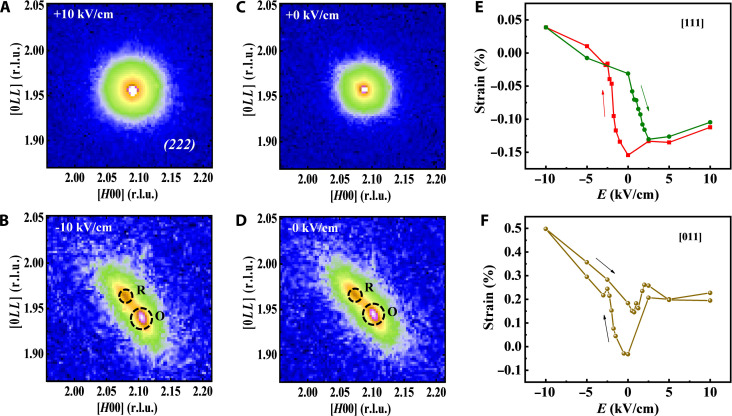
In principle, both strain- (39) and charge-based (57) magnetoelectric couplings are expected to achieve electric field control of magnetism in FM/FE multiferroic heterostructures. However, there exist dozens of nanometers of metal multilayers between PMN-PT and FL and the charge effect is effective only within one to two unit cells (58), so it can be neglected. The resistance changes sharply at about ±2 kV/cm (Fig. 3C), which is close to the coercive field of PMN-PT substrate (P-E loop in fig. S5). To understand the behavior of electric field control of resistance, it is essential and also challenging to characterize the strain of PMN-PT under the MTJ area. We performed an LRSM of PMN-PT beneath the MTJ pillar by choosing the (222) reflection with in situ electric fields through x-ray microdiffraction with a spot diameter of 10 μm, comparable to the junction size. Figure 4 (A to D) shows the LRSM results for E = +10, −10, +0, and −0 kV/cm, respectively. There only exists one diffraction spot under +10 and +0 kV/cm, while two spots under −10 and −0 kV/cm. According to the reports on RSM of PMN-PT (59, 60) and PZN-PT (FE phases similar to PMN-PT) (61), it can be deduced that the big spot in Fig. 4 (B and D) is related to the O phase of PMN-PT because of a larger [011] axis and smaller [100] axis compared with that of the R phase (Fig. 4, A and C), while the small spot in Fig. 4 (B and D) corresponds to the remanent R phase, which is perhaps due to the pinning of FE domains (62) of the R phase. Therefore, only the R phase exists under +10 and +0 kV/cm, while the R and O phases coexist under −10 and −0 kV/cm, resulting in the nonvolatile R-O phase transition. If the R phase converts to the O phase completely, then the LRSM for (222) reflection should have only one single circular spot with the O phase. It can be deduced that the OOP tensile strain and in-plane compressive strain would become larger in the complete O phase compared to the mix of R and O phases. This larger in-plane compressive strain will transfer to the FL, leading to larger in-plane compressive strain and larger OOP tensile strain in FL. As a result, more remarkable modulation of the MTJ resistance is expected in the complete O phase. Results with more electric fields are shown in fig. S6. The corresponding (222) interplanar spacings are calculated using the big and small spots, respectively (fig. S7A). According to the lattice parameters of the R phase of PMN-PT (63), the strain along the [111] crystal orientation was calculated using the big spot, and the result is shown in Fig. 4E (details of calculation method in text S8). As expected, it shows a loop-like behavior, similar to the R-E curve (Fig. 3C), indicating that strain can account for the nonvolatile resistance modulation. In addition to the aforementioned (222) interplanar spacings characterized by x-ray microdiffraction, x-ray diffraction (XRD) with in situ electric fields was also performed to characterize the evolution of (022) diffraction peak (lattice change along the OOP direction) of PMN-PT (fig. S8). There exists peak splitting under most electric fields, and the larger peak (reflecting the trend of lattice change) was selected to calculate the (022) interplanar spacing. Using a similar computing method in text S8, strain versus electric field curves along the [011] crystal orientation of PMN-PT were deduced (Fig. 4F), and the trend is also similar to the R-E curve with a nonvolatile and reversible modulation behavior.
Fig. 4. Nonvolatile strain behavior of PMN-PT (011).
(A to D) LRSM for (222) reflection of PMN-PT beneath the MTJ pillar performed with in situ electric fields +10, −10, +0, and −0 kV/cm, respectively, through x-ray microdiffraction. The intensity scale runs from blue (low) to white (high). Dashed circles show the big and small spots corresponding to the O and remanent R phase, respectively. (E) Strain versus electric field curve along the [111] crystal orientation of PMN-PT characterized by x-ray microdiffraction. The red and green arrows represent the sweeping directions of the electric field. (F) Strain versus electric field curve along the [011] crystal orientation of PMN-PT characterized by x-ray diffraction. r.l.u., reciprocal lattice units.
Therefore, we used LRSM with a synchrotron radiation source under different electric fields for PMN-PT just beneath the MTJ pillar (about 10 μm) to uncover what happened in PMN-PT below the MTJ pillar and found electric field–induced R-O phase transition which induced the modulation of MTJs. There has been no such report on the local (micro)structural characterization of FE material just beneath the micro-sized magnetic feature under electric fields and correlate it with the modulation of the magnetic feature above it for the magnetic/FE multiferroic heterostructure as we demonstrated here. This approach is very difficult in terms of both experiment and data analysis. It should be powerful for uncovering the mechanism of electric field control of magnetism in magnetic/FE multiferroic heterostructure with a mesoscopic scale. Moreover, local electric field–induced FE phase transition and its characterization as demonstrated in our work are also an interesting topic in terms of the electric field–induced phase transition in FE materials.
It should be mentioned that there has been some report on a crack in the (001) PMN-PT due to the application of electric fields (64). However, in our work, we used the (011) PMN-PT. Great care was taken in the experiment to avoid cracks, and scanning electron microscopy (SEM) was used to check the cracks (fig. S9).
Nonvolatile resistance induced by electric field pulses
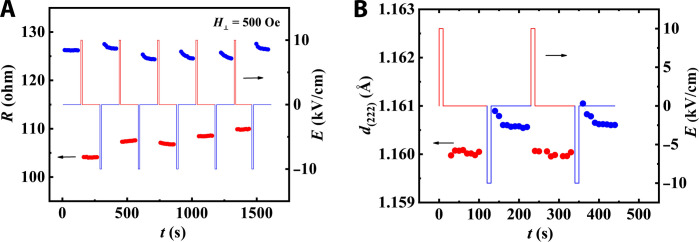
To further show the nonvolatile and reversible character of modulation, we also performed resistance modulation by pulses of electric fields of +10 and −10 kV/cm at +500 Oe, and repeatable bistable resistance states were achieved as shown in Fig. 5A. In our previous study, both the strain and MTJ resistance were measured thousands of times under different electric fields (34), demonstrating the stability and durability of the MTJ. The response time of the magnetization rotation is within 10 ns (33). A relaxation behavior appears after applying pulses of the negative electric field. Similar relaxation behavior was also reported in the literature (33, 34, 37) and has been attributed to the release process of the charges induced by FE polarization without experimental evidence. In our experiments, the (222) interplanar spacing under an electric field pulse, deduced from x-ray microdiffraction, exhibits obvious relaxation for the negative electric field pulses as shown in Fig. 5B, consistent with the resistance relaxation (Fig. 5A). This suggests that the resistance relaxation results from the relaxation of lattice/strain. This can be accounted for by the destabilization of small switched volumes by elastic interactions (65). For PMN-PT, only a very small region beneath the junction and nearby (Fig. 3A) is changed by pulses of electric field, resulting in strong elastic interactions between this region and its unchanged surroundings, especially for the pulses of negative electric field which induce remarkable change in the small region including R-O phase transition. As a result, the unchanged surroundings interact with the changed region to make it relax and reduce the elastic energy, leading to the relaxation of interplanar spacing (Fig. 5B) and resultant resistance relaxation. However, the relaxation is not very large, and a stable state is quickly reached with a remarkable difference from that of the electric pulse with reverse polarity. Moreover, it has been demonstrated that the relaxation related to local tuning of FE can be solved by using FE thin films with patterned structures (65).
Fig. 5. Nonvolatile resistance and lattice modulation with electric field pulses.
(A) Repeatable bistable resistance states (solid circles) switched by the pulsed electric fields of ±10 kV/cm (red and blue lines) at +500 Oe. (B) The deduced (222) interplanar spacing (solid circles) from x-ray microdiffraction with the pulses of electric fields of ±10 kV/cm (red and blue lines).
It is worth mentioning that the strain behavior of the PMN-PT (011) is different from the general case, which usually shows butterfly-like for bipolar electric fields (44, 66), i.e., volatile behavior in strain curve with the same strain state at ±0 kV/cm after applying bipolar electric fields. In contrast, our x-ray microdiffraction (Fig. 4E), XRD (Fig. 4F), and strain gauge measurements (fig. S10B) show nonvolatile strain behavior, which is very useful for applications. Similar behavior has also been reported in the literature (60, 67, 68). This unusual behavior should be related to the electric field–induced structural phase transition [our present work and (60)] and the detailed study is beyond the scope of this paper, so we only focus on the effects of the strain on the p-MTJs.
DISCUSSION
We report a room temperature, nonvolatile, and reversible manipulation of resistance of about 17% in MgO-based p-MTJs via electric fields in p-MTJ/PMN-PT multiferroic heterostructure. Through synchrotron radiation source x-ray microdiffraction characterization of the local strain of PMN-PT beneath the MTJ pillar, the modulation can be ascribed to the changes of FL easy-cone angle induced by the nonvolatile strain–mediated magnetoelectric coupling due to electric field–induced R-O phase transition in PMN-PT. This work represents a crucial step toward electric field control of spintronic devices with non–in-plane magnetic anisotropy including cryogenic and persistent memories that do not require too large thermal stability, as well as MTJ-based STOs, etc. In addition, the epitaxial PMN-PT thin film with superior piezoelectric properties grown on Si wafers has been reported (69), which is substantial for the resistance modulation by electric fields and can be integrated with the current CMOS processing for practical applications. Moreover, electric field control of magnetism has been realized in FM/FE multiferroic heterostructure composed of FM and freestanding PMN-PT membranes (70, 71), suggesting its promising applications. It has also been demonstrated by theoretical calculations that the energy dissipation of FE films per switching was about 0.85 fJ and the switching time was about 2.3 ns for FM/FE multiferroic heterostructure composed of FM and FE thin films (72), revealing ultralow power dissipation and fast writing operation.
MATERIALS AND METHODS
Sample preparation
The MTJ multilayer stacks consisting of, from the substrate side, Ta(25)/CuN(20)/Ta(3)/CuN(20)/Ta(0.7)/Pt(1.5)/[Co(0.5)/Pt(0.35)]6/Co(0.6)/Ru(0.8)/Co(0.6)/[Pt(0.35)/Co(0.5)]3/Pt(0.25)/Ta(0.2)/Co(1.2)/W(0.25)/CoFeB(0.9)/MgO(1.6)/CoFeB(1.7)/W(0.3)/CoFeB(1.1)/MgO(1)/Pt(1.5)/Ta(3)/CuN(5)/Ta(3)/Ru(5) were deposited on one-side–polished (011) oriented PMN-0.30PT substrates with sizes of 5 × 5 × 0.2 mm3 and 10 × 10 × 0.2 mm3 by a Singulus TIMARIS 200-mm magnetron sputtering machine at a base pressure of 3.75 × 10−9 torr. MgO deposition was performed by RF sputtering. To investigate the magnetic anisotropy of FL (Fig. 1B), the multilayer stack (FL section of MTJ) was also deposited as follows: Ta(25)/CuN(20)/Ta(3)/CuN(20)/W(5)/CoFeB(0.2)/MgO(1.6)/CoFeB(1.7)/W(0.3)/CoFeB(1.1)/MgO(1)/Pt(1.5)/Ta(3)/CuN(5)/Ta(3)/Ru(5). To investigate the RL switching properties with magnetic field (fig. S2), the multilayer stack without FL section was deposited as follows: Ta(25)/CuN(20)/Ta(3)/CuN(20)/Ta(0.7)/Pt(1.5)/[Co(0.5)/Pt(0.35)]6/Co(0.6)/Ru(0.8)/Co(0.6)/[Pt(0.35)/Co(0.5)]3/Pt(0.25)/Ta(0.2)/Co(1.2)/W(0.25)/CoFeB(0.9)/MgO(1.6)/Pt(1.5)/Ta(3)/CuN(5)/Ta(3)/Ru(5). Subsequently, all stacks were annealed in vacuum with the base pressure of 3.75 × 10−10 torr at 380°C for 1 hour. Electrodes with Ti(10)/Au(100) were sputtered on the bottom of PMN-PT. Numbers in parentheses are the nominal thicknesses in nanometers.
The MTJ multilayer stacks were fabricated into an array of MTJ pillars with 10-μm diameter by laser direct writing lithography and Ar ion beam etching. In addition, SiO2 surrounding the MTJ pillars was deposited by RF sputtering for insulation. After the liftoff procedure, bottom and top electrodes with Ti(10)/Au(100) were deposited to connect the MTJ pillars.
Magnetic and magnetotransport measurements
The magnetic moment versus magnetic field hysteresis loop (m-H loop) for the unpatterned MTJ sample was measured by a Quantum Design magnetic property measurement system with OOP magnetic fields. The magnetic anisotropy of the FL sample was investigated by ESR. The resistance and its modulations by magnetic and electric fields were performed by East Changing electromagnet using the four-probe method with Keithley 6221 current source, 2182A nanovoltmeter, and 2410 sourcemeter. All these measurements were performed at room temperature.
Strains of PMN-PT
The in-plane strain properties of PMN-PT were studied using the strain gauges. The lattice change along the [011] crystal orientation of PMN-PT was measured via a Rigaku SmartLab 3-kW x-ray diffractometer with Cu Kα radiation. The local strain of PMN-PT beneath the MTJ pillar was performed with in situ electric fields through x-ray microdiffraction with a spot diameter of ~10 μm as well as the extremely high beam energy of 1.1 × 1011 phs/s/μm2 in Shanghai Synchrotron Radiation Facility (beamline BL15U1).
Ferroelectricity of PMN-PT
The P-E loops of PMN-PT were measured using a Radiant Technologies Precision Premier II system.
Acknowledgments
This work was supported by the Shanghai Synchrotron Radiation Facility (x-ray microdiffraction at beamline BL15U1). We thank B. Xiang for some help in the measurement of MTJ property. We are grateful to J. Hu and M. Dai for the helpful discussion.
Funding: This work was supported by the Science Center of the National Natural Science Foundation of China (grant no. 52388201), National Key R&D Program of China (2023YFA1406400), National Natural Science Foundation of China (grant nos. 52172270, 51831005, and 12074429), and Programme of Guangdong Province, China (grant no. 2021B0301030003).
Author contributions: Y. Zhao, W.Z., W.S., and Y.Zhan. conceived the experiment plan. S.L. and K.C. grew all magnetic stacks. W.S. and Y.Zhan. performed the magnetic and magnetotransport measurements and data analysis. H.H., Y.L., W.S., Y.Zhan., S.Z., and C.F. performed the x-ray microdiffraction measurement and data analysis. W.S., W.L., Q.L., and S.M. performed the XRD measurement. W.S. and Q.L. performed the in-plane strain gauge measurements. W.S., Y.Zhan., and Y. Zhao wrote and discussed the original manuscript. W.S., Y.Zhan., W.Z., and Y. Zhao had discussions and outlines. All authors participated in the review and editing of the manuscript.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Supplementary Materials
This PDF file includes:
Supplementary Text S1 to S10
Figs. S1 to S10
References
REFERENCES AND NOTES
- 1.Tehrani S., Slaughter J. M., Deherrera M., Engel B. N., Rizzo N. D., Salter J., Durlam M., Dave R. W., Janesky J., Butcher B., Smith K., Grynkewich G., Magnetoresistive random access memory using magnetic tunnel junctions. Proc. IEEE 91, 703–714 (2003). [Google Scholar]
- 2.Chappert C., Fert A., Van Dau F. N., The emergence of spin electronics in data storage. Nat. Mater. 6, 813–823 (2007). [DOI] [PubMed] [Google Scholar]
- 3.B. Dieny, I. L. Prejbeanu, Magnetic random-access memory, in Introduction to Magnetic Random-Access Memory, B. Dieny, R. B. Goldfarb, K. J. Lee, Eds. (Wiley, 2017), chap. 5. [Google Scholar]
- 4.Åkerman J., Toward a universal memory. Science 308, 508–510 (2005). [DOI] [PubMed] [Google Scholar]
- 5.Brataas A., Kent A. D., Ohno H., Current-induced torques in magnetic materials. Nat. Mater. 11, 372–381 (2012). [DOI] [PubMed] [Google Scholar]
- 6.Ikeda S., Miura K., Yamamoto H., Mizunuma K., Gan H. D., Endo M., Kanai S., Hayakawa J., Matsukura F., Ohno H., A perpendicular-anisotropy CoFeB-MgO magnetic tunnel junction. Nat. Mater. 9, 721–724 (2010). [DOI] [PubMed] [Google Scholar]
- 7.Wang M. X., Cai W. L., Zhu D. Q., Wang Z. H., Kan J., Zhao Z. Y., Cao K. H., Wang Z. L., Zhang Y. G., Zhang T. R., Park C., Wang J. P., Fert A., Zhao W. S., Field-free switching of a perpendicular magnetic tunnel junction through the interplay of spin-orbit and spin-transfer torques. Nat. Electron. 1, 582–588 (2018). [Google Scholar]
- 8.Liu L. Q., Pai C. F., Li Y., Tseng H. W., Ralph D. C., Buhrman R. A., Spin-torque switching with the giant spin Hall effect of tantalum. Science 336, 555–558 (2012). [DOI] [PubMed] [Google Scholar]
- 9.Sato N., Xue F., White R. M., Bi C., Wang S. X., Two-terminal spin-orbit torque magnetoresistive random access memory. Nat. Electron. 1, 508–511 (2018). [Google Scholar]
- 10.Miron I. M., Garello K., Gaudin G., Zermatten P. J., Costache M. V., Auffret S., Bandiera S., Rodmacq B., Schuhl A., Gambardella P., Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 476, 189–193 (2011). [DOI] [PubMed] [Google Scholar]
- 11.Miron I. M., Gaudin G., Auffret S., Rodmacq B., Schuhl A., Pizzini S., Vogel J., Gambardella P., Current-driven spin torque induced by the Rashba effect in a ferromagnetic metal layer. Nat. Mater. 9, 230–234 (2010). [DOI] [PubMed] [Google Scholar]
- 12.Hu J. M., Nan C. W., Opportunities and challenges for magnetoelectric devices. APL Mater. 7, 080905 (2019). [Google Scholar]
- 13.Bibes M., Barthélémy A., Multiferroics: Towards a magnetoelectric memory. Nat. Mater. 7, 425–426 (2008). [DOI] [PubMed] [Google Scholar]
- 14.Wang W. G., Li M. G., Hageman S., Chien C. L., Electric-field-assisted switching in magnetic tunnel junctions. Nat. Mater. 11, 64–68 (2012). [DOI] [PubMed] [Google Scholar]
- 15.Shiota Y., Nozaki T., Bonell F., Murakami S., Shinjo T., Suzuki Y., Induction of coherent magnetization switching in a few atomic layers of FeCo using voltage pulses. Nat. Mater. 11, 39–43 (2012). [DOI] [PubMed] [Google Scholar]
- 16.Fusil S., Garcia V., Barthélémy A., Bibes M., Magnetoelectric devices for spintronics. Annu. Rev. Mat. Res. 44, 91–116 (2014). [Google Scholar]
- 17.Shao Y. X., Lopez-Dominguez V., Davila N., Sun Q. L., Kioussis N., Katine J. A., Amiri P. K., Sub-volt switching of nanoscale voltage-controlled perpendicular magnetic tunnel junctions. Commun. Mater. 3, 87 (2022). [Google Scholar]
- 18.Newhouse-Illige T., Liu Y. H., Xu M., Hickey D. R., Kundu A., Almasi H., Bi C., Wang X., Freeland J. W., Keavney D. J., Sun C. J., Xu Y. H., Rosales M., Cheng X. M., Zhang S. F., Mkhoyan K. A., Wang W. G., Voltage-controlled interlayer coupling in perpendicularly magnetized magnetic tunnel junctions. Nat. Commun. 8, 15232 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zhang D. L., Bapna M., Jiang W., Sousa D., Liao Y. C., Zhao Z. Y., Lv Y., Sahu P., Lyu D. Y., Naeemi A., Low T., Majetich S. A., Wang J. P., Bipolar electric-field switching of perpendicular magnetic tunnel junctions through voltage-controlled exchange coupling. Nano Lett. 22, 622–629 (2022). [DOI] [PubMed] [Google Scholar]
- 20.Khan A. A., Schmalhorst J., Thomas A., Schebaum O., Reiss G., Dielectric breakdown in Co-Fe-B/MgO/Co-Fe-B magnetic tunnel junction. J. Appl. Phys. 103, 123705 (2008). [Google Scholar]
- 21.Kato Y., Yoda H., Saito Y., Oikawa S., Fujii K., Yoshiki M., Koi K., Sugiyama H., Ishikawa M., Inokuchi T., Shimomura N., Shimizu M., Shirotori S., Altansargai B., Ohsawa Y., Ikegami K., Tiwari A., Kurobe A., Giant voltage-controlled magnetic anisotropy effect in a crystallographically strained CoFe system. Appl. Phys. Exp. 11, 053007 (2018). [Google Scholar]
- 22.Nozaki T., Kozioł-Rachwał A., Tsujikawa M., Shiota Y., Xu X. D., Ohkubo T., Tsukahara T., Miwa S., Suzuki M., Tamaru S., Kubota H., Fukushima A., Hono K., Shirai M., Suzuki Y., Yuasa S., Highly efficient voltage control of spin and enhanced interfacial perpendicular magnetic anisotropy in iridium-doped Fe/MgO magnetic tunnel junctions. NPG Asia Mater. 9, e451 (2017). [Google Scholar]
- 23.Nozaki T., Endo M., Tsujikawa M., Yamamoto T., Nozaki T., Konoto M., Ohmori H., Higo Y., Kubota H., Fukushima A., Hosomi M., Shirai M., Suzuki Y., Yuasa S., Voltage-controlled magnetic anisotropy in an ultrathin Ir-doped Fe layer with a CoFe termination layer. APL Mater. 8, 011108 (2020). [Google Scholar]
- 24.Nozaki T., Yamamoto T., Tamaru S., Kubota H., Fukushima A., Suzuki Y., Yuasa S., Enhancement in the interfacial perpendicular magnetic anisotropy and the voltage-controlled magnetic anisotropy by heavy metal doping at the Fe/MgO interface. APL Mater. 6, 026101 (2018). [Google Scholar]
- 25.Eerenstein W., Mathur N. D., Scott J. F., Multiferroic and magnetoelectric materials. Nature 442, 759–765 (2006). [DOI] [PubMed] [Google Scholar]
- 26.Fiebig M., Lottermoser T., Meier D., Trassin M., The evolution of multiferroics. Nat. Rev. Mater. 1, 16046 (2016). [Google Scholar]
- 27.Nan C. W., Bichurin M. I., Dong S. X., Viehland D., Srinivasan G., Multiferroic magnetoelectric composites: Historical perspective, status, and future directions. J. Appl. Phys. 103, 031101 (2008). [Google Scholar]
- 28.Fiebig M., Revival of the magnetoelectric effect. J. Phys. D Appl. Phys. 38, R123–R152 (2005). [Google Scholar]
- 29.Gajek M., Bibes M., Fusil S., Bouzehouane K., Fontcuberta J., Barthélémy A., Fert A., Tunnel junctions with multiferroic barriers. Nat. Mater. 6, 296–302 (2007). [DOI] [PubMed] [Google Scholar]
- 30.Garcia V., Bibes M., Bocher L., Valencia S., Kronast F., Crassous A., Moya X., Enouz-Vedrenne S., Gloter A., Imhoff D., Deranlot C., Mathur N. D., Fusil S., Bouzehouane K., Barthélémy A., Ferroelectric control of spin polarization. Science 327, 1106–1110 (2010). [DOI] [PubMed] [Google Scholar]
- 31.Pantel D., Goetze S., Hesse D., Alexe M., Reversible electrical switching of spin polarization in multiferroic tunnel junctions. Nat. Mater. 11, 289–293 (2012). [DOI] [PubMed] [Google Scholar]
- 32.Pawlak J., Skowroński W., Żywczak A., Przybylski M., Room-temperature multiferroicity and magnetization dynamics in Fe/BTO/LSMO tunnel junction. Adv. Electron. Mater. 8, 2100574 (2022). [Google Scholar]
- 33.Li P. S., Chen A. T., Li D. L., Zhao Y. G., Zhang S., Yang L. F., Liu Y., Zhu M. H., Zhang H. Y., Han X. F., Electric field manipulation of magnetization rotation and tunneling magnetoresistance of magnetic tunnel junctions at room temperature. Adv. Mater. 26, 4320–4325 (2014). [DOI] [PubMed] [Google Scholar]
- 34.Chen A. T., Wen Y., Fang B., Zhao Y. L., Zhang Q., Chang Y. S., Li P. S., Wu H., Huang H. L., Lu Y. L., Zeng Z. M., Cai J. W., Han X. F., Wu T., Zhang X. X., Zhao Y. G., Giant nonvolatile manipulation of magnetoresistance in magnetic tunnel junctions by electric fields via magnetoelectric coupling. Nat. Commun. 10, 243 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chen A. T., Zhao Y. L., Wen Y., Pan L., Li P. S., Zhang X. X., Full voltage manipulation of the resistance of a magnetic tunnel junction. Sci. Adv. 5, eaay5141 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Yang Y. J., Luo Z. L., Wang S. T., Huang W. Y., Wang G. L., Wang C. M., Yao Y. X., Li H. J., Wang Z. L., Zhou J. T., Dong Y. Q., Guan Y., Tian Y. C., Feng C., Zhao Y. G., Gao C., Xiao G., Electric-field-assisted non-volatile magnetic switching in a magnetoelectronic hybrid structure. iScience 24, 102734 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zhao Z. Y., Jamali M., D'Souza N., Zhang D. L., Bandyopadhyay S., Atulasimha J., Wang J. P., Giant voltage manipulation of MgO-based magnetic tunnel junctions via localized anisotropic strain: A potential pathway to ultra-energy-efficient memory technology. Appl. Phys. Lett. 109, 092403 (2016). [Google Scholar]
- 38.Chen A. T., Piao H. G., Ji M. H., Fang B., Wen Y., Ma Y., Li P., Zhang X.-X., Using dipole interaction to achieve nonvolatile voltage control of magnetism in multiferroic heterostructures. Adv. Mater. 33, e2105902 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zhang S., Zhao Y. G., Li P. S., Yang J. J., Rizwan S., Zhang J. X., Seidel J., Qu T. L., Yang Y. J., Luo Z. L., He Q., Zou T., Chen Q. P., Wang J. W., Yang L. F., Sun Y., Wu Y. Z., Xiao X., Jin X. F., Huang J., Gao C., Han X. F., Ramesh R., Electric-field control of nonvolatile magnetization in Co40Fe40B20/Pb(Mg1/3Nb2/3)0.7 Ti0.3O3 Structure at room temperature. Phys. Rev. Lett. 108, 137203 (2012). [DOI] [PubMed] [Google Scholar]
- 40.Wu T., Bur A., Zhao P., Mohanchandra K. P., Wong K., Wang K. L., Lynch C. S., Carman G. P., Giant electric-field-induced reversible and permanent magnetization reorientation on magnetoelectric Ni/(011) [Pb(Mg1/3Nb2/3)O3](1-x)-[PbTiO3]x heterostructure. Appl. Phys. Lett. 98, 012504 (2011). [Google Scholar]
- 41.Wang Z., Wang Y., Ge W., Li J., Viehland D., Volatile and nonvolatile magnetic easy-axis rotation in epitaxial ferromagnetic thin films on ferroelectric single crystal substrates. Appl. Phys. Lett. 103, 132909 (2013). [Google Scholar]
- 42.Yu G. Q., Wang Z. X., Abolfath-Beygi M., He C. L., Li X., Wong K. L., Nordeen P., Wu H., Carman G. P., Han X. F., Alhomoudi I. A., Amiri P. K., Wang K. L., Strain-induced modulation of perpendicular magnetic anisotropy in Ta/CoFeB/MgO structures investigated by ferromagnetic resonance. Appl. Phys. Lett. 106, 072402 (2015). [Google Scholar]
- 43.Peng B., Zhou Z. Y., Nan T. X., Dong G. H., Feng M. M., Yang Q., Wang X. J., Zhao S. S., Xian D., Jiang Z. D., Ren W., Ye Z. G., Sun N. X., Liu M., Deterministic switching of perpendicular magnetic anisotropy by voltage control of spin reorientation transition in (Co/Pt)3/Pb(Mg1/3Nb2/3)O3–PbTiO3 Multiferroic heterostructures. ACS Nano 11, 4337–4345 (2017). [DOI] [PubMed] [Google Scholar]
- 44.Sun Y., Ba Y., Chen A. T., He W., Wang W. B., Zheng X. L., Zou L. K., Zhang Y. J., Yang Q., Yan L. J., Feng C., Zhang Q. H., Cai J. W., Wu W. D., Liu M., Gu L., Cheng Z. H., Nan C. W., Qiu Z. Q., Wu Y. Z., Li J., Zhao Y. G., Electric-field modulation of interface magnetic anisotropy and spin reorientation transition in (Co/Pt)3/PMN-PT heterostructure. ACS Appl. Mater. Interfaces 9, 10855–10864 (2017). [DOI] [PubMed] [Google Scholar]
- 45.Bhatti S., Sbiaa R., Hirohata A., Ohno H., Fukami S., Piramanayagam S. N., Spintronics based random access memory: A review. Mater. Today 20, 530–548 (2017). [Google Scholar]
- 46.Dieny B., Prejbeanu I. L., Garello K., Gambardella P., Freitas P., Lehndorff R., Raberg W., Ebels U., Demokritov S. O., Akerman J., Deac A., Pirro P., Adelmann C., Anane A., Chumak A. V., Hirohata A., Mangin S., Valenzuela S. O., Onbaşlı M. C., d’Aquino M., Prenat G., Finocchio G., Lopez-Diaz L., Chantrell R., Chubykalo-Fesenko O., Bortolotti P., Opportunities and challenges for spintronics in the microelectronics industry. Nat. electron. 3, 446–459 (2020). [Google Scholar]
- 47.Teixeira B. M. S., Timopheev A. A., Caçoilo N., Auffret S., Sousa R. C., Dieny B., Sobolev N. A., Stabilization of the easy-cone magnetic state in free layers of magnetic tunnel junctions. Phys. Rev. B 100, 184405 (2019). [Google Scholar]
- 48.Timopheev A. A., Sousa R., Chshiev M., Nguyen H. T., Dieny B., Second order anisotropy contribution in perpendicular magnetic tunnel junctions. Sci. Rep. 6, 26877 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Atitoaie A., Firastrau I., Buda-Prejbeanu L. D., Ebels U., Volmer M., Macrospin analysis of RF excitations within fully perpendicular magnetic tunnel junctions with second order easy-axis magnetic anisotropy contribution. J. Appl. Phys. 124, 093902 (2018). [Google Scholar]
- 50.Sato H., Yamanouchi M., Ikeda S., Fukami S., Matsukura F., Ohno H., Perpendicular-anisotropy CoFeB-MgO magnetic tunnel junctions with a MgO/CoFeB/Ta/CoFeB/MgO recording structure. Appl. Phys. Lett. 101, 022414 (2012). [Google Scholar]
- 51.Wang M. X., Cai W. L., Cao K. H., Zhou J. Q., Wrona J., Peng S. Z., Yang H. W., Wei J. Q., Kang W., Zhang Y. G., Langer J., Ocker B., Fert A., Zhao W. S., Current-induced magnetization switching in atom-thick tungsten engineered perpendicular magnetic tunnel junctions with large tunnel magnetoresistance. Nat. Commun. 9, 671 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Khanal P., Zhou B. W., Andrade M., Dang Y. L., Davydov A., Habiboglu A., Saidian J., Laurie A., Wang J. P., Gopman D. B., Wang W. G., Perpendicular magnetic tunnel junctions with multi-interface free layer. Appl. Phys. Lett. 119, 242404 (2021). [Google Scholar]
- 53.Bultynck O., Manfrini M., Vaysset A., Swerts J., Wilson C. J., Sorée B., Heyns M., Mocuta D., Radu I. P., Devolder T., Instant-on spin torque in noncollinear magnetic tunnel junctions. Phys. Rev. Appl. 10, 054028 (2018). [Google Scholar]
- 54.Safranski C., Sun J. Z., Interface moment dynamics and its contribution to spin-transfer torque switching process in magnetic tunnel junctions. Phys. Rev. B 100, 014435 (2019). [Google Scholar]
- 55.Han G. C., Zhang K. Y., Yang X. L., Ai L. B., Wang M., Liu B., Magnetic switching behavior of each magnetic layer in perpendicular magnetic tunnel junctions. J. Magn. Magn. Mater. 527, 167789 (2021). [Google Scholar]
- 56.Slonczewski J. C., Conductance and exchange coupling of two ferromagnets separated by a tunneling barrier. Phys. Rev. B 39, 6995–7002 (1989). [DOI] [PubMed] [Google Scholar]
- 57.Molegraaf H. J. A., Hoffman J., Vaz C. A. F., Gariglio S., van der Marel D., Ahn C. H., Triscone J. M., Magnetoelectric effects in complex oxides with competing ground states. Adv. Mater. 21, 3470–3474 (2009). [Google Scholar]
- 58.Vaz C. A. F., Electric field control of magnetism in multiferroic heterostructures. J. Phys. Condens. Matter 24, 333201 (2012). [DOI] [PubMed] [Google Scholar]
- 59.Pesquera D., Khestanova E., Ghidini M., Zhang S., Rooney A. P., Maccherozzi F., Riego P., Farokhipoor S., Kim J., Moya X., Vickers M. E., Stelmashenko N. A., Haigh S. J., Dhesi S. S., Mathur N. D., Large magnetoelectric coupling in multiferroic oxide heterostructures assembled via epitaxial lift-off. Nat. Commun. 11, 3190 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Liang W. H., Hu F. X., Zhang J., Kuang H., Li J., Xiong J. F., Qiao K. M., Wang J., Sun J. R., Shen B. G., Anisotropic nonvolatile magnetization controlled by electric field in amorphous SmCo thin films grown on (011)-cut PMN-PT substrates. Nanoscale 11, 246–257 (2019). [DOI] [PubMed] [Google Scholar]
- 61.Liu M., Nan T. X., Hu J. M., Zhao S. S., Zhou Z. Y., Wang C. Y., Jiang Z. D., Ren W., Ye Z. G., Chen L. Q., Sun N. X., Electrically controlled non-volatile switching of magnetism in multiferroic heterostructures via engineered ferroelastic domain states. NPG Asia Mater. 8, e316 (2016). [Google Scholar]
- 62.Feng C., Liu Y., Huang H. L., Zhu Z. Z., Yang Y. J., Ba Y., Yan S. Y., Cai J. W., Lu Y. L., Zhang J. X., Zhang S., Zhao Y. G., Unusual behaviors of electric-field control of magnetism in multiferroic heterostructures via multifactor cooperation. ACS Appl. Mater. Interfaces 11, 25569–25577 (2019). [DOI] [PubMed] [Google Scholar]
- 63.Noheda B., Phase diagram of the ferroelectric relaxor (1−x)PbMg1/3Nb2/3O3−xPbTiO3. Phys. Rev. B 66, 054104 (2002). [Google Scholar]
- 64.Vinai G., Motti F., Bonanni V., Petrov A. Y., Benedetti S., Rinaldi C., Stella M., Cassese D., Prato S., Cantoni M., Rossi G., Panaccione G., Torelli P., Reversible modification of ferromagnetism through electrically controlled morphology. Adv. Electron. Mater. 5, 1900150 (2019). [Google Scholar]
- 65.Baek S. H., Jang H. W., Folkman C. M., Li Y. L., Winchester B., Zhang J. X., He Q., Chu Y. H., Nelson C. T., Rzchowski M. S., Pan X. Q., Ramesh R., Chen L. Q., Eom C. B., Ferroelastic switching for nanoscale non-volatile magnetoelectric devices. Nat. Mater. 9, 309–314 (2010). [DOI] [PubMed] [Google Scholar]
- 66.Liu M., Howe B. M., Grazulis L., Mahalingam K., Nan T. X., Sun N. X., Brown G. J., Voltage-impulse-induced non-volatile ferroelastic switching of ferromagnetic resonance for reconfigurable magnetoelectric microwave devices. Adv. Mater. 25, 4886–4892 (2013). [DOI] [PubMed] [Google Scholar]
- 67.Wang J., Pesquera D., Mansell R., van Dijken S., Cowburn R. P., Ghidini M., Mathu N. D., Giant non-volatile magnetoelectric effects via growth anisotropy in Co40Fe40B20 films on PMN-PT substrates. Appl. Phys. Lett. 114, 092401 (2019). [Google Scholar]
- 68.Wang P., Jin C., Wang Y. C., Liu S. S., Wang X. Y., Zheng D. X., Zheng W. C., Bai H. L., Differentiation of non-volatile strain and ferroelectric field effects in (011)- and (001)-La0.67Sr0.33MnO3/Pb(Mg1/3Nb2/3)0.7Ti0.3O3 heterostructures. J. Appl. Phys. 127, 244102 (2020). [Google Scholar]
- 69.Baek S. H., Park J., Kim D. M., Aksyuk V. A., Das R. R., Bu S. D., Felker D. A., Lettieri J., Vaithyanathan V., Bharadwaja S. S. N., Bassiri-Gharb N., Chen Y. B., Sun H. P., Folkman C. M., Jang H. W., Kreft D. J., Streiffer S. K., Ramesh R., Pan X. Q., Trolier-McKinstry S., Schlom D. G., Rzchowski M. S., Blick R. H., Eom C. B., Giant piezoelectricity on Si for hyperactive MEMS. Science 334, 958–961 (2011). [DOI] [PubMed] [Google Scholar]
- 70.Irwin J., Lindemann S., Maeng W., Wang J. J., Vaithyanathan V., Hu J. M., Chen L. Q., Schlom D. G., Eom C. B., Rzchowski M. S., Magnetoelectric coupling by piezoelectric tensor design. Sci. Rep. 9, 19158 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Lindemann S., Irwin J., Kim G. Y., Wang B., Eom K., Wang J. J., Hu J. M., Chen L. Q., Choi S. Y., Eom C. B., Rzchowski M. S., Low-voltage magnetoelectric coupling in membrane heterostructures. Sci. Adv. 7, eabh2294 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Peng R. C., Hu J. M., Momeni K., Wang J. J., Chen L. Q., Nan C. W., Fast 180° magnetization switching in a strain-mediated multiferroic heterostructure driven by a voltage. Sci. Rep. 6, 27561 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.N. Locatelli, V. Cros, Basic spintronic transport phenomena, in Introduction to Magnetic Random-Access Memory, B. Dieny, R. B. Goldfarb, K. J. Lee, Eds. (Wiley, 2017), chap. 1. [Google Scholar]
- 74.Yang L. F., Zhao Y. G., Zhang S., Li P. S., Gao Y., Yang Y. J., Huang H. L., Miao P. X., Liu Y., Chen A. T., Nan C. W., Gao C., Bipolar loop-like non-volatile strain in the (001)-oriented Pb(Mg1/3Nb2/3)O3-PbTiO3 single crystals. Sci. Rep. 4, 4591 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.M. Birkholz, “Principles of x-ray diffraction, in Thin Film Analysis by X-Ray Scattering, M. Birkholz, Ed. (Weinheim, 2006), chap. 1. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Text S1 to S10
Figs. S1 to S10
References