Abstract
Effective disease surveillance systems require large-scale epidemiological data to improve health outcomes and quality of care for the general population. As data may be limited within a single site, multi-site data (e.g., from a number of local/regional health systems) need to be considered. Leveraging distributed data across multiple sites for epidemiological analysis poses significant challenges. Due to the sensitive nature of epidemiological data, it is imperative to design distributed solutions that provide strong privacy protections. Current privacy solutions often assume a central site, which is responsible for aggregating the distributed data and applying privacy protection before sharing the results (e.g., aggregation via secure primitives and differential privacy for sharing aggregate results). However, identifying such a central site may be difficult in practice and relying on a central site may introduce potential vulnerabilities (e.g., single point of failure). Furthermore, to support clinical interventions and inform policy decisions in a timely manner, epidemiological analysis need to reflect dynamic changes in the data. Yet, existing distributed privacy-protecting approaches were largely designed for static data (e.g., one-time data sharing) and cannot fulfill dynamic data requirements. In this work, we propose a privacy-protecting approach that supports the sharing of dynamic epidemiological analysis and provides strong privacy protection in a decentralized manner. We apply our solution in continuous survival analysis using the Kaplan-Meier estimation model while providing differential privacy protection. Our evaluations on a real dataset containing COVID-19 cases show that our method provides highly usable results.
Keywords: Data Privacy, Survival Analysis, Distributed Data
I. Introduction
A growing number of research initiatives are collecting large epidemiological datasets to advance research and support knowledge sharing [1], [2], [3]. While these efforts are vital in enabling effective disease surveillance systems [4] (e.g., survival analysis), health data are often fragmented over multiple sites, and regulations and policies may limit the sharing of patient-level records across sites. To leverage these distributed data, a variety of privacy-protecting approaches have been recently proposed [5], [6]. Among them, the federated framework has emerged as a promising solution to addressing data privacy concerns [7], [8]. In the federated paradigm, institutions can jointly perform predictive analysis by sharing intermediate aggregate statistics, while the original patient-level data remain within the secure enclave of each local site, thus allowing institutions to comply with regulations and policies.
Several federated approaches have been proposed to perform epidemiological analysis. As examples, recent studies by Dai et al. [9] and Lu et al. [10] proposed to share intermediate statistics among sites to learn a collaborative Cox proportional hazards model. Despite promising results, these approaches may not adequately address the privacy risks. In fact, recent privacy studies have shown that the sharing of aggregate information (e.g., models, summary statistics, parameters) may lead to privacy breaches for individual data contributors (e.g., membership disclosure, attribute inference [11], [12], [13]). To mitigate these privacy risks, other approaches have employed a combination of privacy-enhancing techniques to protect both intermediate statistics and final results. Among them, cryptographic primitives (e.g., secure multiparty computation [14] and homomorphic encryption [15]) are often used to protect intermediate steps during distributed computation. Recent works have also proposed the use of differential privacy [16], which provides provable privacy protection against membership disclosure. In one relevant study, Froelicher et al. [17] have leveraged cryptographic primitives and discussed the use of differential privacy to provide strong privacy protection for the final survival results. In another study by Spath et al. [18], the intermediate statistics are first aggregated via secure primitives, and then perturbed by a third party to satisfy differential privacy.
While these approaches enable distributed survival analyses, there are significant limitations for their application in practice. Specifically, current differential privacy solutions [17], [18], [19] rely on a central server to perturb original aggregate results. However, it may be challenging to identify a trusted central server, as local sites may have different data privacy concerns. In worst-case scenarios, the server may fail to inject adequate perturbation noise to achieve differential privacy (e.g., single point of failure), thus potentially compromising the privacy of the overall data. Furthermore, in epidemiological studies, local data may change over time (e.g., new surge of local cases), requiring a continuous integration of the updated local data into collaborative analysis [20], [21]. However, current approaches mainly focus on static data settings. One simple solution is to apply existing methods repeatedly for each data update, but it may introduce significant computational burdens and increased privacy leakage [16], [22]. While incremental learning techniques have shown to be effective at addressing the computation burdens by incrementally training predictive models as data are updated [23], they do not provide protection against privacy breaches caused by model memorization of patient-level data [24].
In this work, we propose a new privacy-protecting framework for distributed Kaplan-Meier survival analysis, which supports dynamic data updates and provides privacy control to participating sites. To support privacy-protecting dynamic updates, we develop an adaptive technique that allows each site to control the privacy leakage in sharing longitudinal survival statistics. Specifically, each site can bound the overall privacy leakage by sharing only the most useful updates, which are dynamically determined by each site. To achieve differential privacy in a decentralized manner, we leverage distributed noise generation and secret sharing techniques. Specifically, our distributed noise generation approach decomposes the overall noise needed to achieve differential privacy into small, partial noises that will be injected in the statistics shared by local sites. Additionally, perturbed local statistics are protected and aggregated via a secret sharing protocol, eliminating the need for a trusted central server. Overall, our solution provides strong privacy protection while enabling accurate, continuous survival analysis.
The rest of the paper is organized as follows: Section II provides the preliminaries for this study as well as an overview of the proposed solution; Section III presents the technical details about proposed methods; Section IV describes the experimentation methodology and discusses empirical results; Section V discusses open challenges and considerations for future research; Section VI concludes the paper.
II. OVERVIEW
We consider patient-level time-to-event data for epidemiological analysis, which may comprise clinical, demographic, and temporal information about specific clinical events (e.g., hospital discharge, survival status, time and type of diagnosis). Data are distributed across multiple sites (e.g., hospitals), where local changes may occur over time (e.g., newly enrolled patients or a surge of cases). The overall goal is to perform collaborative survival analysis and enable a broad and continuous sharing of the overall results with external users (e.g., researchers, clinicians, policymakers).
A. Survival Analysis
We consider the Kaplan-Meier model [25] for survival analysis in epidemiological studies. The Kaplan-Meier model is a non-parametric model that describes the survival probability over time without requiring assumptions on the underlying data distribution. Note that when properties of the data are known (e.g., proportional relationship between the baseline hazard and the hazard attributes), more sophisticated models could be used (e.g., the Cox proportional hazards model [26]). In our application setting, we do not make any assumption on the prior data distribution. Therefore we adopt the Kaplan-Meier model to compute survival probabilities.
In deploying the Kaplan-Meier model in a distributed setting, the survival probability at any time need to be computed by aggregating the time-to-event data distributed across participating sites throughout the study duration. Specifically, let be a snapshot of the overall data at time , which are distributed across sites, where denotes the local data at the j-th site, for . Then, the survival probability up to time-to-event computed over the entire data can be expressed as a ratio between the aggregated partial counts of current events across sites, as follows:
| (1) |
| (2) |
where denotes the total number of events at time at the local site , and and represent the uncensored (i.e., individuals with the event of interest, such as diagnosis or death) and censored events (e.g., individuals who fail to follow up) up to time-to-event at the local site , respectively.
B. Privacy Model
Application Setting.
We consider multiple sites that participate in computing survival analysis collectively. Due to privacy concerns, only aggregate statistics can be shared. Below, we will discuss the privacy risk associated with the shared statistics. In our solution, we assume a third party (e.g., cloud service provider) that assembles the survival probability results by continuously aggregating the partial statistics shared by local sites. The third party in our setting may host a web-interface to enable external users to interact with the results. We do not require the third party to be trusted, as it has only access encrypted and privacy-enhanced results.
Adversary.
We aim at protecting patient privacy against an informed adversary who may learn information about participating individuals from the shared statistics. Compared to previous privacy studies in static settings [19], [11], here we consider an adversary who may leverage changes in the shared statistics over time as well as prior background knowledge to infer the participation of a target individual in a specific cohort of study (e.g., case group). The adversary’s background knowledge may include information inadvertently disclosed by individuals. As an example, recent studies have shown that patients may disclose their participation and time of their contribution to certain studies over online social networks [27], [28]. Additionally, an adversary may have access to data from other sites in the study, via data breaches or colluding parties. Under such adversarial assumptions, the attacker has a strong background knowledge about the data. The attacker may infer the presence of a target individual in a specific group in the study by observing how data are updated over time.
Differential Privacy.
In this work, we aim at developing a distributed data sharing approach to support accurate epidemiological studies while satisfying differential privacy. In brief, differential privacy guarantees that an adversary, who observes the output results, cannot determine whether any individual record was included in the input. This privacy model builds on the concept of indistinguishability, which ensures that any pair of datasets differing in at most a single record (i.e., neighboring datasets) should produce similar outputs. Formally, a randomized algorithm satisfies -differential privacy if for any two neighboring databases and any subset the following holds:
| (3) |
The privacy parameter , also known as the privacy budget, bounds the difference between output probabilities of neighboring databases, thus determining the level of indistinguishability. The parameter accounts for the probability of a privacy breach. In practice, and parameters help data curators control the information leakage and usability of the shared data. As an example, smaller values of and lead to stronger privacy protection but may reduce data usability. In our setting, we consider the privacy setting with , which is also referred to as -DP or pure DP. A variety of mechanisms have been proposed to achieve differential privacy [29]. In this work, we focus on the Laplace mechanism, in which the original data are perturbed with calibrated random noise sampled from a Laplace distribution prior to sharing.
Compared to previous studies, our problem setting poses novel privacy and usability challenges. First, the analytic tasks considered in this work are computed continuously as data at local sites are updated over time. From a differential privacy perspective, these continuous updates increase the privacy risk compared to the static setting, as an adversary may observe the contribution of an individual in the data over multiple releases. As a result, achieving privacy in this continuous data sharing scenario may inflict high utility loss, as shown in previous privacy studies over data streams [22], [30]. Second, in our distributed problem setting, we do not assume a central entity who collects the aggregate statistics and performs perturbation (e.g., injection of Laplace noise) to achieve differential privacy, as considered in previous studies [17], [18]. A simple application of the standard differential privacy at each local site may result in poor usability, as the data perturbation from all sites are accumulated in the final results. Protecting data from each site without a trusted aggregator requires a new solution that can strike the right balance between privacy and usability.
C. Protocol Overview
In this study, we propose to employ a binary tree structure for aggregating continuously updated local time-to-event data at multiple sites. Conceptually, the binary tree recursively decomposes the overall time-to-events into intervals; counts of time-to-events in those intervals can be perturbed to achieve differential privacy. In our previous work [19], we showed that input perturbation according to the binary tree can enable accurate Kaplan-Meier survival analysis in a static, centralized setting, and the noise magnitude grows only logarithmically with the length of the survival study instead of linearly. The noise grows linearly if applying Laplace mechanism to time-to-events at each time. In this work, we propose to maintain a binary tree at each site, and updates of the intervals will take place dynamically, as local data change over time. By incorporating the updated statistics from distributed intervals, we can effectively estimate the survival probabilities at any time. The main steps in our proposed protocol are summarized below.
Initialization. All sites agree on a binary tree decomposition of the overall study and initialize the tree locally. Given a study over a time range , we construct intervals of variable lengths that are placed at different heights of the binary tree. Specifically, intervals at height comprise time units, for . While the binary decomposition is common across all the sites, each site will populate tree intervals with counts of the local time-to-events that fall in each interval.
Local Updates. Each party maintains the updated event counts in the local binary decomposition. As local data may change (e.g., adding new patients), each site applies our proposed differentially private algorithm to adaptively determine which intervals need to be updated and shared. Those intervals are also perturbed with fresh random noise generated according to our distributed noise generation mechanism. Then, using a homomorphic secret sharing protocol, the updated noisy counts are shared and aggregated across sites. As an example shown in Figure 1, site 1 determines that and need to be updated. The original counts are perturbed with noise and , and then shared via a secret sharing protocol.
Aggregation and Survival Probability Estimation. The partial shares are aggregated from each site to obtain the updated counts in the overall data. With the distributed noise generation mechanism, the aggregate counts in each interval satisfies differential privacy. These counts are used to estimate the Kaplan-Meier survival probability in Equation (2). Continuing with the example in Figure 1, the total number of time-to-events for the first 6 time units, can be estimated via the perturbed counts of two intervals and aggregated via secure sum among all the sites as: . Finally, the overall differentially private survival results are shared with external users.
Fig. 1:
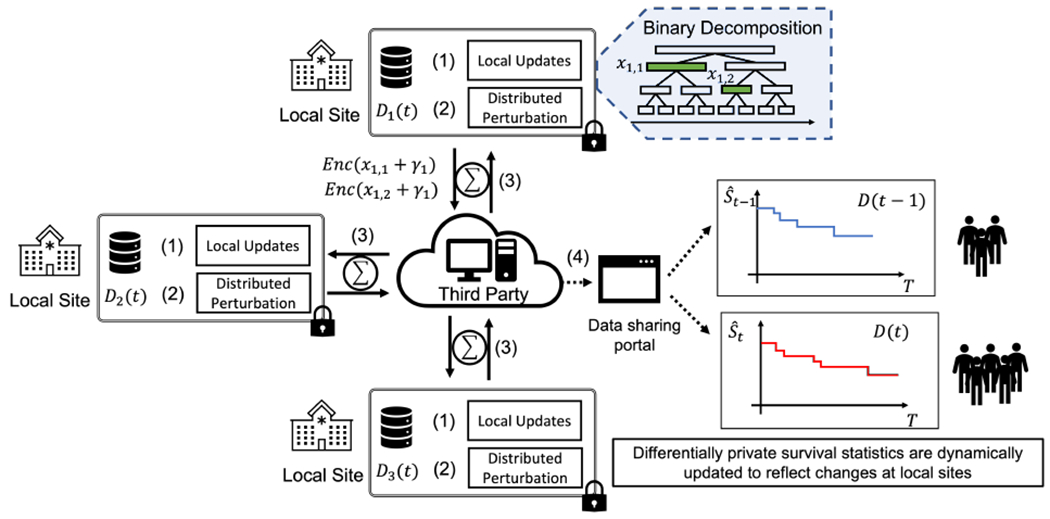
An illustrative example of our proposed framework. We define a binary decomposition of the study into intervals, which is shared across sites. During the iteration of the protocol each site populates the statistics in local representation with the counts of the site-specific time-to-events data. (1) As data may dynamically change, each site determines whether any count needs to be updated. For example, site 1 determines that local counts and need to be updated. (2) The original updated statistics are perturbed using a distributed noise generation mechanism (i.e., noise ). (3) Using a third party (not-necessarily trusted), for example a cloud service provider, the participating sites aggregate the perturbed results via a secure secret aggregation protocol and estimate the overall time-to-event counts across all sites in each interval. (4) The final results are shared (e.g., via a web portal), enabling external users to obtain updated statistics reflecting dynamic changes in the data (e.g., survival function updated with records from new enrolled individuals). During the entire process, the original patient-level data never leave the secure enclave of the local sites.
III. Methods
In this section, we present the proposed methods to support continuous survival analysis in distributed epidemiological applications while satisfying differential privacy.
A. Private Continuous Data Updates
In epidemiological applications, local data at each site may change throughout the study duration. As an example, new patients may contribute data to the study when there is a surge of infections. Therefore, participating sites may need to update the shared statistics to reflect those changes in the data. A naive differential privacy solution would require sites to perturb local statistics at every update, which may lead to overly-perturbed results when data updates are frequent.
To this end, we propose to apply the Sparse Vector Technique (SVT) for reporting local updates with better utility. Traditionally, the SVT method has been applied to improve the usability of differential privacy in sparse data streams [31], [30], [32], in which the total number of released statistics is controlled while bounding the overall privacy loss. In this work, we employ the SVT method in a distributed setting to control the privacy loss at each site while enabling the sharing of useful data updates. The SVT method is described in Algorithm 1. Each site at time runs the SVT procedure on the local binary decomposition to determine whether the event count for the -th interval released at time needs to be updated. To determine whether a count needs to be updated, we compare the updated count at time with the one at time and the algorithm shares the updated count if they are sufficiently different. Here, we use a threshold to decide whether the new count differs significantly from the previous one. In practice, each site could have different values and strategies for selecting (e.g., depending on the size of the intervals). As a rule of thumb, larger values of may reduce the number of shared updates, reducing the overall privacy risk but potentially diminishing the utility of the shared data. We set for all , following the privacy guidelines in previous studies on binning and thresholding [33], [34].
In addition, Algorithm 1 enables each site to control the total privacy leakage by limiting the number of shared updates (i.e., parameter c). As a result, our algorithm determines the most useful data updates by comparing the current statistics with those that have been previously released. Only updates that are sufficiently different from the previous release are shared with the addition of random noise to achieve overall differential privacy (the choice of which will be discussed in the next subsection).
B. Private Distributed Analysis
In the absence of a trusted central server, each site may directly perturb local statistics with the Laplace mechanism to achieve differential privacy. However, this simple solution may lead to poor usability, as multiple noises from participating sites are combined in the final results. Intuitively, the final noise magnitude grows with the number of participating sites. To improve data usability, we propose a new solution for distributed noise generation. The idea is that the noise required to achieve differential privacy globally can be derived by combining “small” noises generated locally at each site. In other words, each site can inject a partial noise in the shared statistics and once the partially perturbed results are aggregated across sites, the final results satisfy differential privacy. Distributed noise generation relies on the observation that the Laplace distribution enjoys infinite divisibility [35], in which a Laplace random variable can be obtained by summing independent and identically distributed (i.i.d.) gamma random variables [36]. In our protocol, noise generation is distributed across sites, where each site perturbs the current local statistics with prior to sharing, where and are two i.i.d. exponential random variables with parameter . When shared counts by sites are aggregated, the perturbed estimate of the global statistics satisfies -differential privacy.
Algorithm 1.
SVT for dynamically updating the interval count at site . The variable denotes the sensitivity of the query, which is 1 for count queries.
| Input Current count, Previous count, #update Number of updates shared | |
| Output Perturbed count | |
| 1: | procedure |
| 2: | |
| 3: | |
| 4: | |
| 5: | |
| 6: | if then |
| 7: | if #update then |
| 8: | Abort |
| 9: | else |
| 10: | |
| 11: | #update ← #update + 1 |
| 12: | end if |
| 13: | end if |
| 14: | end procedure |
Because the partial noise alone may not suffice to achieve differential privacy for the shared local updates from each site, we need to add an additional layer of protection. To this end, we will leverage secure aggregation described below to protect the partially perturbed local counts shared by participating sites. As a result, differential privacy can be achieved in a distributed setting without a trusted aggregator.
C. Secure Aggregation
To aggregate the partially perturbed statistics from local sites, we propose to leverage secure aggregation techniques to compute the summation of the private counts . Because some sites may be compromised or not following the protocol correctly, it is important to provide robust privacy protection to local sites. To this end, we adopt the homomorphic secret shares summation protocol proposed by Ranbaduge et al. [37] in our problem setting. Below, we summarize the main steps of the secure aggregation protocol with a running example for the sum of counts for the time-to-events associated with across all sites.
Each site creates a private and public key pair . The public keys are shared among all sites. The local perturbed count is decomposed into shares . The local site encrypts each of the shares with the public key of the other sites , while it keeps its own share (e.g., encrypting value 0 for its own share).
These shares are collected by a third party (e.g., cloud service provider), which performs a summation on the encrypted partial shares , and sends the encrypted partial sums to the corresponding site, i.e., site will receive .
Each site decrypts the partial shares received (using its private key) and adds the share that was set aside in step (1), . The partial sums of the -th shares from each site are shared with the third party, which aggregates them, computing the overall aggregated count .
Then, the final statistics are obtained by combining the shares. In this protocol, local statistics are aggregated without requiring a trusted third party. Furthermore, with the homomorphic secret sharing technique, data security is guaranteed even in the worst-case scenario. Specifically, based on the results in [37], neither the third party nor a set of sites would be able to reconstruct the partially perturbed counts of the non-colluding sites.
D. Overall Privacy Protection
In the privacy analysis, we break down the overall solution in two parts: (1) privacy analysis of Algorithm 1 and (2) privacy protection for the statistics aggregated from all sites.
Algorithm 1, which determines whether to update the local counts by comparing them with a threshold, satisfies -differential privacy. The privacy guarantee follows the proof of the original SVT approach in [32]. The protection for the aggregated statistics (2) is achieved by securely combining the noisy local statistics returned by Algorithm 1 via secure aggregation.
Theorem 1. Let be the aggregate sum of the perturbed counts of each site . If is computed using Algorithm 1, then .
Proof. is obtained by summing up all the estimates from the sites: . Then, applying the result in [35], we have that , and therefore .
Therefore, the overall proposed solution satisfies -differential privacy.
Discussion.
In our protocol, the original patient-level data are kept within the secure enclave of each site and only partial statistics are shared over time to reflect dynamic changes in local data. Compared to existing federated solutions for epidemiological studies, our method allows sites to control the overall privacy leakage over continuous updated releases. Furthermore, the perturbation for achieving differential privacy is fully decentralized with perturbed partial statistics that are aggregated via a secure protocol, thus the overall computation can be performed without the need for a trusted third party. Moreover, our protocol can be adapted to safeguard privacy in the event of multiple parties failing to perturb the local updates or leave the protocol. In fact, to ensure differential privacy in final results even when parties among fail to participate in the protocol, we can change the amount of partial noise injected by each site to [36], [38], [37]. Overall, our approach provides participating sites with strong privacy control over the shared data while preserving the usefulness of the final survival results.
IV. Results
In this section, we describe our evaluation methodology and present empirical results. We aim at simulating a disease surveillance setting, in which the Kaplan-Meier survival model is applied to estimate the probability of discharge for patients hospitalized with COVID-19 for different age groups. Our simulations consider dynamic data changes over the duration of the study (e.g., when new patients are hospitalized) and the overall data are distributed across multiple sites.
Data.
We use an epidemiological dataset for the COVID-19 outbreak [39], [40] collected from January 2020 to June 2020. While the dataset contains more than 2 million records, many of them have incomplete values. As a pre-processing step, we drop records with missing values for county, age, and gender, resulting in more than 550,000 records. Age may be represented as a range of values for some records, in those cases we replace the range with its mean. We further address the missing admission time values for conducting Kaplan-Meier analysis, by following the steps described in Nemati et al. [41], [42]. The obtained dataset results in roughly 186,000 patient records, divided into four cohorts according to their age: cohort 0 (0 ≤age≤ 35) with 60,160 patients, cohort 1 (35 <age≤ 46) with 17,711 patients, cohort 2 (47 <age 60) with 65,739 patients, and cohort 3 (age > 60) with 42,786 patients. The time-to-event in this dataset represents the patient length-of-stay in days. We vary the number of participating sites from 2 to 8. The default number of sites is 3, unless specified otherwise.
General Usability Measures.
To evaluate the usability of the Kaplan-Meir survival curves, we report the difference between the restricted mean survival time (RMST) between the curves generated by our distributed privacy-protecting method and those obtained with a centralized non-private approach (i.e., all data reside within a single site and no perturbation is performed) [43]. Lower values of RMST difference indicate that the computed curves are closer to the originals. Additionally, we report the mean absolute error (MAE) on the estimated number of reported cases during the duration of the study.
Approaches.
In our evaluations, we consider two distributed privacy-protecting approaches. First, we consider a baseline solution named Distributed Differential Privacy (DISTDP), in which each site perturbs the local data to satisfy differential privacy and shares it with a (untrusted) central site. The central site collects and aggregates the sanitized data from each site, and then shares the overall data with external users. To protect the local data, each site relies on the differentially private solution that we have previously developed [19]. As demonstrated in the original paper, our prior approach uses input perturbation and binary decomposition strategies, which significantly improve the usability of survival analyses compared to traditional output perturbation approaches (e.g., Laplace mechanism). Second, we consider the technique developed in this work, named Homomorphic Secret Sharing Differential Privacy (HSSDP), in which differential privacy is achieved in a distributed fashion and data are aggregated via a homomorphic secret shares protocol. Specifically, in this approach the overall noise required to achieve differential privacy is generated in a distributed fashion, enabling each site to introduce a smaller amount of noise locally while achieving full differential privacy protection once all the data are aggregated. Both solutions satisfy -differential privacy, where controls the level of privacy protection. Their results are compared with respect to a non-private centralized approach (i.e., single central site and survival statistics are shared without privacy protection).
A. Impact of the Number of Data Releases
We vary the number of data releases to simulate different frequency in data updates. Specifically, we consider survival statistics that are updated: every other day (2 days), weekly (7 days), bi-weekly (14 days), and monthly (31 days) over a period of 6 months. Figure 2a and Figure 2b show that our proposed solution achieves lower RMST difference and MAE compared to DISTDP. We observe that for frequent updates, the usability tends to slightly decrease (i.e., higher RMST and MAE). Relaxing the privacy protection (i.e., larger values of ), can help reduce the utility loss. Given a fixed differential privacy guarantee (i.e., fixed values of over the entire length of the study), more frequent updates may lead to larger perturbation for each update. Figure 2c illustrates the detailed MAE for each data release for both methods, with two different values of the privacy parameter. The results show that larger values of the privacy parameter (i.e., weaker protection) help reduce the error, leading to higher accuracy. We observe that our proposed approach may have a larger error than the baseline in the earlier data releases when data size is small (see Figure 2d). In later releases, the error for our approach quickly stabilizes, achieving significantly smaller error values than the baseline (i.e., 10x smaller error). Overall, these results show that our proposed approach outperforms the baseline when data updates are frequent and the adaptive updates may be fine-tuned by considering information about the data size.
Fig. 2:
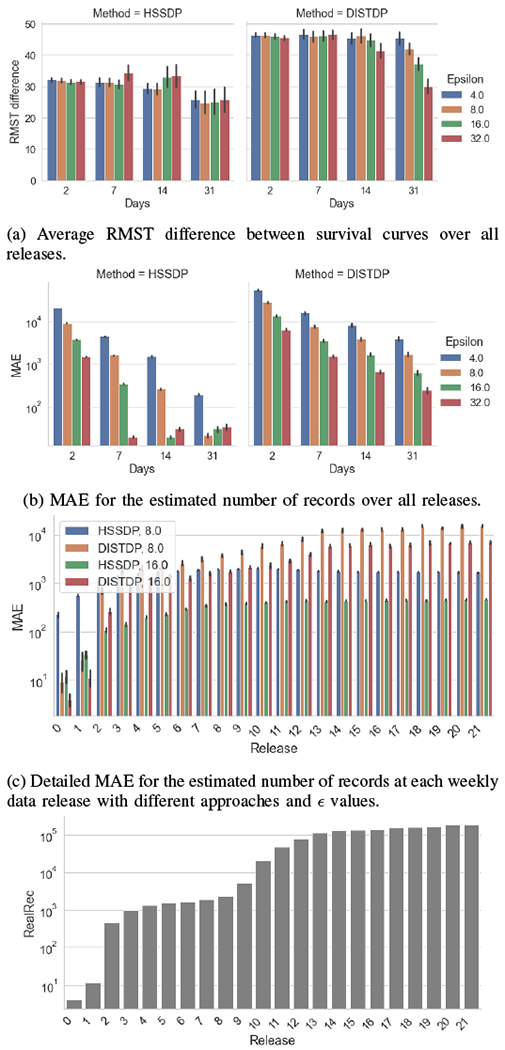
Usability of privacy-protecting survival curves with different frequencies of data releases and values of the privacy parameter. Results have been obtained with the overall data distributed across three sites.
B. Test Statistics for Kaplan-Meier Survival Curves
Table I and Table II report the log-rank test statistics for the final survival curves computed with different values of the privacy parameter against the non-private survival curves. Higher test statistics indicate higher dissimilarity with the ground truth. These results show that our proposed privacy solution significantly outperforms the baseline approach, enabling the computation of highly useful survival curves for each cohort. We observe that as privacy is relaxed (i.e., larger values of ), the performance of both privacy-protecting methods tend to improve. Also, less frequent releases can improve the accuracy of the privacy methods. Example survival curves obtained with non-private data and two privacy approaches are presented in Figure 3. Overall, we observe that our proposed method is able produce survival results that resemble the non-private results in most settings.
TABLE I:
Log-rank test results with different values of privacy parameters and weekly data releases.
| Test Statistics | Cohorts |
||||
|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | ||
| HSSDP | 8.10* | 6.82* | 0.01 | 0.18 | |
| 1.01 | 1.73 | 5.13e−7 | 1.29 | ||
| 0.22 | 2.22 | 0.17 | 0.46 | ||
| 0.51 | 1.03 | 0.81 | 1.34 | ||
|
| |||||
| DISTDP | 192.80* | 423.87* | 574.48* | 247.72* | |
| 313.29* | 394.14* | 141.87* | 93.50* | ||
| 110.40* | 84.66* | 75.56* | 21.33* | ||
| 55.70* | 12.70* | 68.37* | 42.56* | ||
p-value≤ 0.05
TABLE II:
Log-rank test results with different values of privacy parameters with bi-weekly data releases.
| Test Statistics | Cohorts |
||||
|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | ||
| HSSDP | 1.15 | 5.35* | 2.15e−4 | 0.49 | |
| 0.58 | 1.00 | 0.32 | 1.38 | ||
| 0.50 | 0.64 | 0.60 | 0.83 | ||
| 1.14 | 1.44 | 1.20 | 1.21 | ||
|
| |||||
| DISTDP | 13.03* | 211.44* | 283.18* | 239.32* | |
| 141.49* | 8.38* | 101.58* | 90.22* | ||
| 53.08* | 86.52* | 87.76* | 44.34* | ||
| 7.43* | 1.10 | 11.56* | 18.71* | ||
p-value≤ 0.05
Fig. 3:
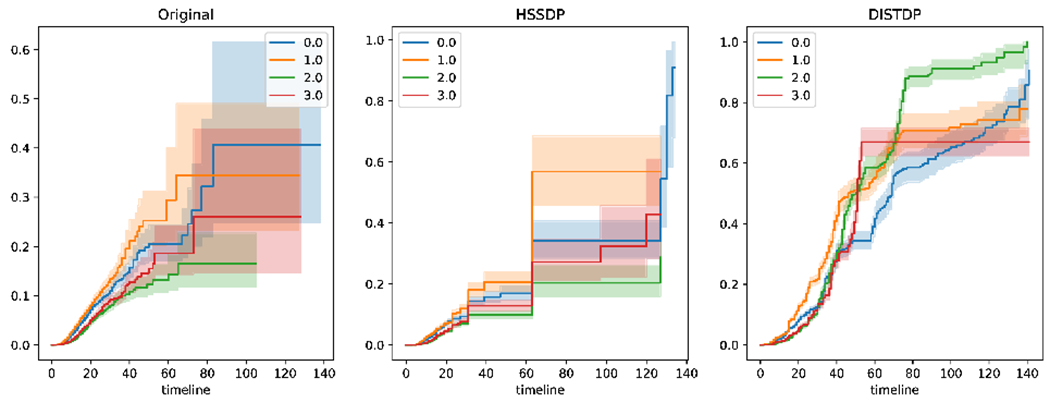
Example of the final survival curves obtained with bi-weekly releases and privacy parameter . From left to right the discharge curves computed: in a centralized non-private setting, using our privacy-protecting distributed approach (HSSDP), and using the aggregation of differentially private results from each site (DISTDP).
C. Varying the Number of Data Updates
In Figure 4, we report the results obtained with HSSDP when we bound the total number of updates allowed by a local site (i.e., in Algorithm 1). We express this value as a fraction over the study duration. As an example, we have at most 21 possible weekly updates for a period of roughly 6 months. As the number of maximum updates decreases, each site may share local data less frequently with other sites. Overall, we observe that the utility may not monotonically increase with more frequent updates. On one hand, a larger fraction of allowed updates enables sites to share more up-to-date statistics. On the other hand, increasing the number of updates may lead to higher perturbation noise to each update. As an example, Figure 4b shows that a good privacy-usability trade-off is achieved when the maximum number of allowed updates is 60%-80% of the overall periods (e.g., 12-16 weekly updates among 21 weeks). In practice, it may be challenging to find the best value for the maximum number of allowed updates, as the data dynamic may vary greatly across site.
Fig. 4:
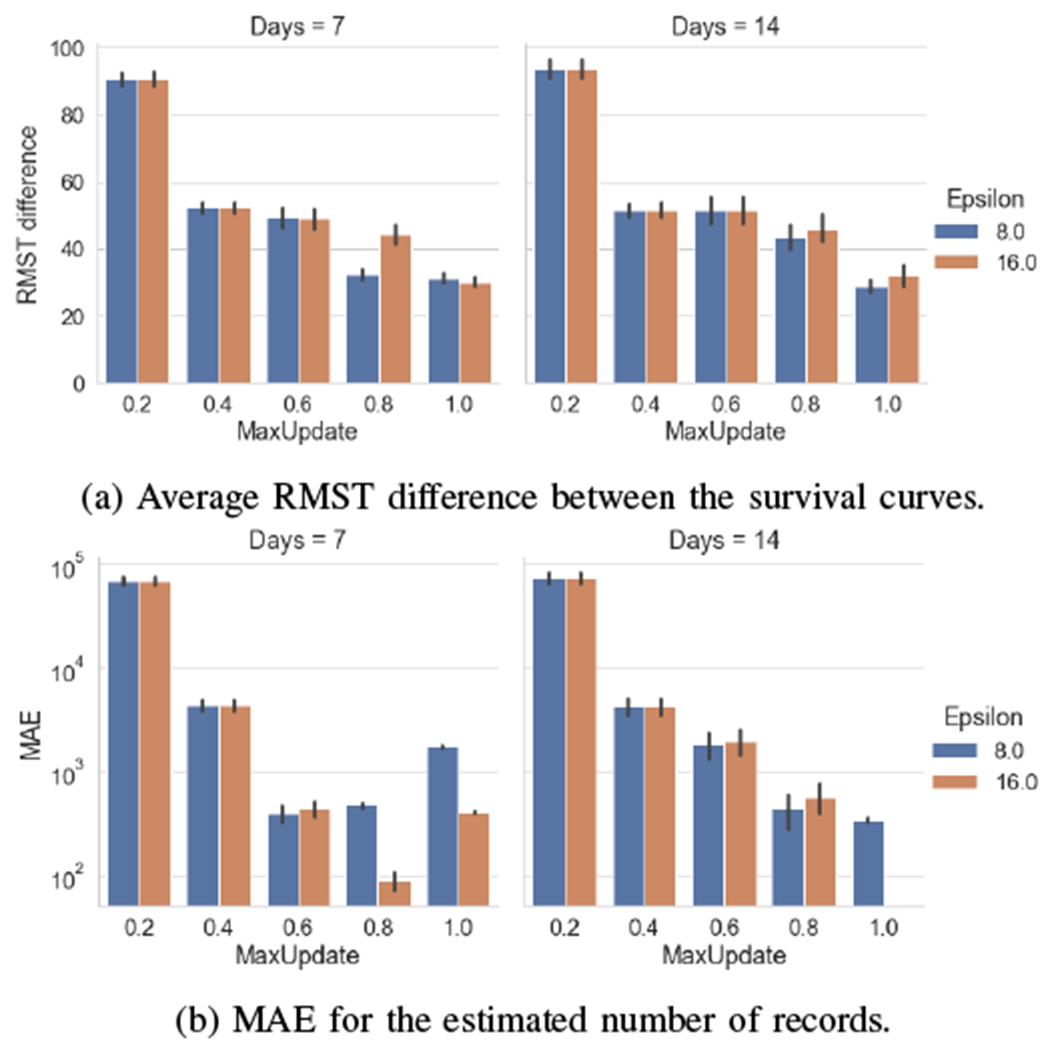
Usability of privacy-protecting survival curves obtained with our proposed method (HSSDP) with different maximum numbers of allowed data updates and values of the privacy parameter. We varied the fraction of maximum allowed updates from 20% to 100% of the possible weekly and bi-weekly updates of local sites.
D. Scalability
We evaluate the impact of the number of parties on the usability and scalability of our proposed approach. Figure 5 shows that our proposed approach is less sensitive to changes in the number of parties. Specifically, we observe that the distributed noise generation mechanism used in our HSSDP solution significantly improves the utility. This is because in HSSDP the required noise is distributed to multiple sites, while in DISTDP each site perturbs their data with the full noise, thus introducing a larger perturbation in the overall data, especially when the number of parties grows. Lastly, we notice in Figure 6 that despite the improvement in usability and privacy protection, HSSDP may inflict some run time overheads. While the secret sharing technique provides a safeguard against colluding malicious parties in the protocol, the running time increases with the number of parties in our HSSDP approach. For DISTDP, the running time is insensitive to the number of sites, as the overall data aggregation does not rely on communication rounds between parties.
Fig. 5:
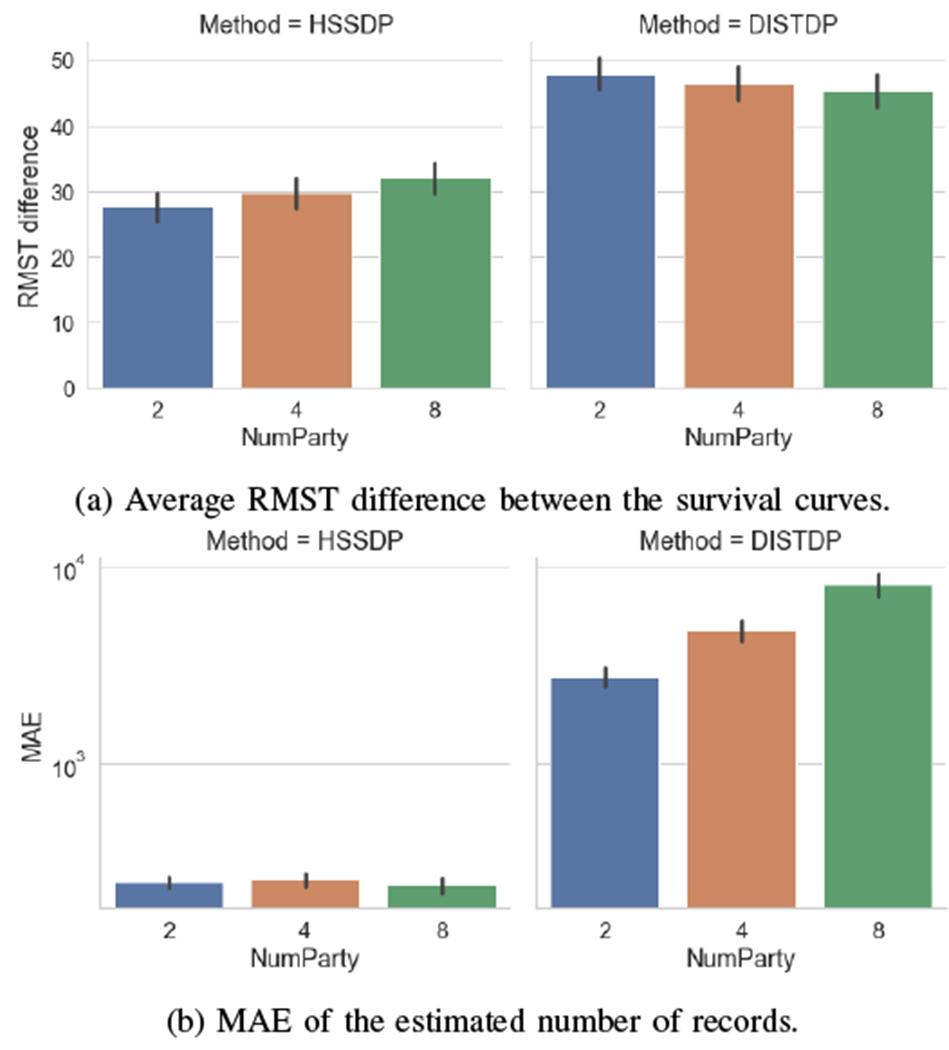
Impact of the number of parties on the usability of the proposed approach. Results have been obtained with bi-weekly data released and privacy parameter .
Fig. 6:
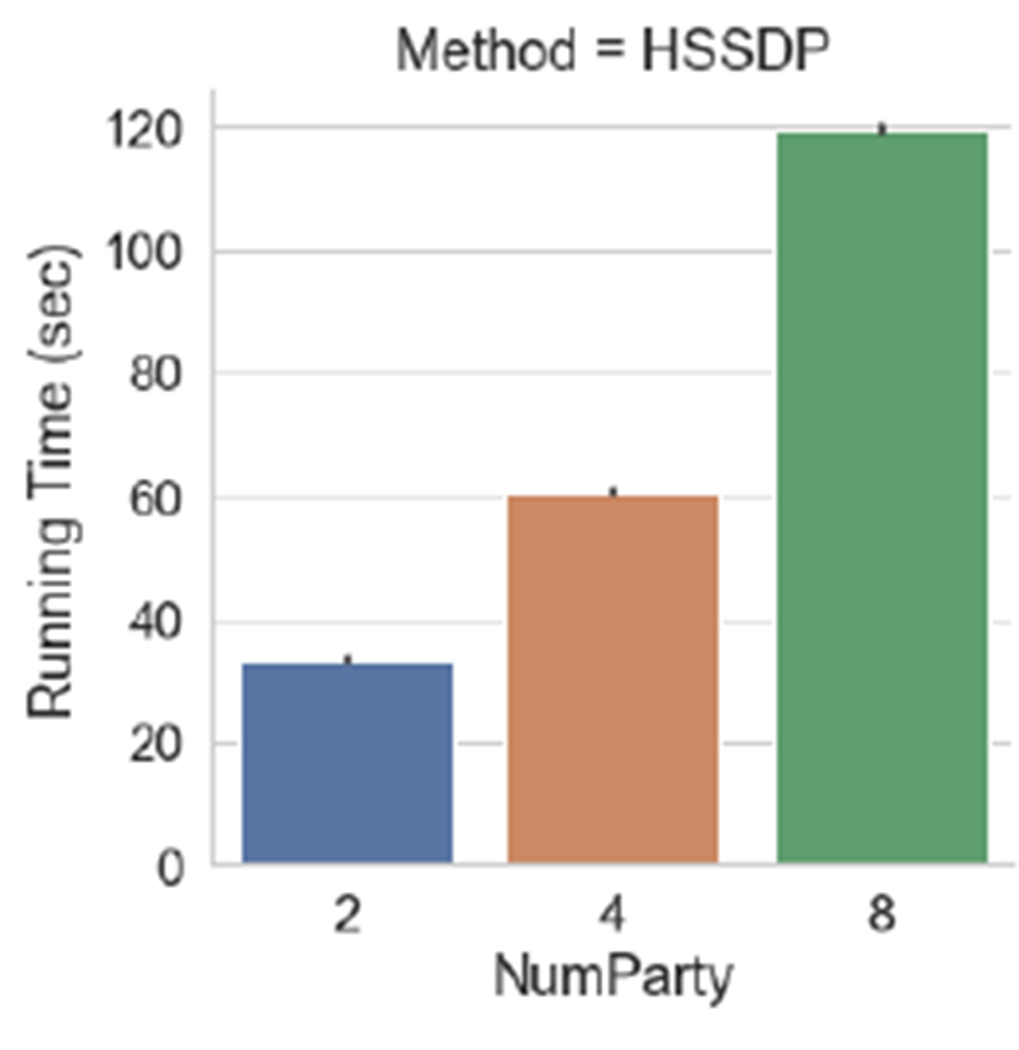
Average running time of the HSSDP protocol during each data update.
V. Discussion and Future Work
In this work, we focused on survival analysis for COVID-19 cases where our evaluations have been conducted on horizontally partitioned data. However, in some settings, epidemiological studies may be conducted on vertically distributed data, where covariates of the same patient are stored at different sites (e.g., genetic markers in one site and clinical data in another). Extending our proposed technique to those settings poses new challenges. Among them, it is not straight-forward to adapt the differential privacy model to address the privacy risks associated with data of the same patient across multiple sites. As a future work, we plan to investigate the applicability of generalized differential privacy models to provide provable privacy guarantees while improving usability [44].
In our proposed solution, we leverage cryptographic techniques to enable local sites to collectively compute accurate differential privacy results without relying on a trusted server. However, a strong adversarial model may inflict significant overheads due to the complexity of cryptographic primitives, as shown in run time results. One possible future research direction is to investigate more practical adversarial models. As an example, it may be helpful to consider realistic collaborative research settings where most participating sites will faithfully follow the protocol. Under such adversarial models, new privacy approaches could be designed to provide more usable privacy protection.
In recent years, we have witnessed a significant adoption of machine learning technology in health applications. As an example, emerging deep learning models for epidemiological studies can provide superior predictive performance compared to well established approaches [45], [46], including Kaplan-Meier and the Cox models. While there are benefits in the use of machine learning techniques, there have also been increased privacy concerns (e.g., membership disclosure of individuals in the training set) due to model memorization [47]. This work studied the privacy implications for Kaplan-Meier survival analysis. Despite the simplicity of the model, our results show that it is challenging to find the right balance between privacy and usability in practice. Overall, our findings provide important insights for future privacy research on advanced machine learning based survival models that could facilitate large-scale epidemiological applications.
VI. Conclusion
Effective disease surveillance systems rely on data that accurately reflect the evolving situation at each local site. In this work, we have proposed a new distributed privacy-protecting solution that facilitates the integration of such dynamic data from local sites to support collaborative epidemiological studies (i.e., Kaplan-Meier survival analysis). Compared to existing work, our solution enables continuous survival analysis and provides strong privacy control to participating sites while preserving data usability.
Acknowledgments
LB is supported in part by the National Human Genome Research Institute grant R00HG010493 and the National Library of Medicine grant R01LM013712. ML is supported in part by the National Science Foundation Research Experiences for Undergraduates (REU) grant 2050895. LF is supported in part by the National Science Foundation CNS-1951430 and CNS-2144684. The content is solely the responsibility of the authors and does not necessarily represent the official views of the funding agencies.
Contributor Information
Luca Bonomi, Dept. Biomedical Informatics, Vanderbilt University Medical Center, Nashville, TN.
Marilyn Lionts, Dept. Computer Science, Vanderbilt University, Nashville, TN.
Liyue Fan, College of Computing and Informatics, University of North Carolina, Charlotte, NC.
References
- [1].Lee B, Dupervil B, Deputy NP, Duck W, Soroka S, Bottichio L, Silk B, Price J, Sweeney P, Fuld J et al. , “Protecting privacy and transforming covid-19 case surveillance datasets for public use,” Public Health Reports, vol. 136, no. 5, pp. 554–561, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Haendel MA, Chute CG, Bennett TD, Eichmann DA, Guinney J, Kibbe WA, Payne PR, Pfaff ER, Robinson PN, Saltz JH et al. , “The national covid cohort collaborative (n3c): rationale, design, infrastructure, and deployment,” Journal of the American Medical Informatics Association, vol. 28, no. 3, pp. 427–443, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Datavant, “Covid-19 research database,” Accessed on 2022-11-21 from http://https://covid19researchdatabase.org, 2020. [Google Scholar]
- [4].Ibrahim NK, “Epidemiologic surveillance for controlling covid-19 pandemic: types, challenges and implications,” Journal of infection and public health, vol. 13, no. 11, pp. 1630–1638, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Wang S, Bonomi L, Dai W, Chen F, Cheung C, Bloss CS, Cheng S, and Jiang X, “Big data privacy in biomedical research,” IEEE Transactions on big Data, vol. 6, no. 2, pp. 296–308, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Malin BA, Emam KE, and O’Keefe CM, “Biomedical data privacy: problems, perspectives, and recent advances,” Journal of the American medical informatics association, vol. 20, no. 1, pp. 2–6, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Xu J, Glicksberg BS, Su C, Walker P, Bian J, and Wang F, “Federated learning for healthcare informatics,” Journal of Healthcare Informatics Research, vol. 5, no. 1, pp. 1–19, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Rieke N, Hancox J, Li W, Milletari F, Roth HR, Albarqouni S, Bakas S, Galtier MN, Landman BA, Maier-Hein K et al. , “The future of digital health with federated learning,” NPJ digital medicine, vol. 3, no. 1, pp. 1–7, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Dai W, Jiang X, Bonomi L, Li Y, Xiong H, and Ohno-Machado L, “Verticox: Vertically distributed cox proportional hazards model using the alternating direction method of multipliers,” IEEE Transactions on Knowledge and Data Engineering, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Lu C-L, Wang S, Ji Z, Wu Y, Xiong L, Jiang X, and Ohno-Machado L, “Webdisco: a web service for distributed cox model learning without patient-level data sharing,” Journal of the American Medical Informatics Association, vol. 22, no. 6, pp. 1212–1219, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Homer N, Szelinger S, Redman M, Duggan D, Tembe W, Muehling J, Pearson JV, Stephan DA, Nelson SF, and Craig DW, “Resolving individuals contributing trace amounts of dna to highly complex mixtures using high-density snp genotyping microarrays,” PLoS genetics, vol. 4, no. 8, p. e1000167, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Shokri R, Stronati M, Song C, and Shmatikov V, “Membership inference attacks against machine learning models,” in 2017 IEEE symposium on security and privacy (SP). IEEE, 2017, pp. 3–18. [Google Scholar]
- [13].Zhu L, Liu Z, and Han S, “Deep leakage from gradients,” Advances in neural information processing systems, vol. 32, 2019. [Google Scholar]
- [14].Goldreich O, “Secure multi-party computation,” Manuscript. Preliminary version, vol. 78, no. 110, 1998. [Google Scholar]
- [15].Gentry C, A fully homomorphic encryption scheme. Stanford university, 2009. [Google Scholar]
- [16].Dwork C, McSherry F, Nissim K, and Smith A, “Calibrating noise to sensitivity in private data analysis,” in Theory of cryptography conference. Springer, 2006, pp. 265–284. [Google Scholar]
- [17].Froelicher D, Troncoso-Pastoriza JR, Raisaro JL, Cuendet MA, Sousa JS, Cho H, Berger B, Fellay J, and Hubaux J-P, “Truly privacy-preserving federated analytics for precision medicine with multiparty homomorphic encryption,” Nature communications, vol. 12, no. 1, pp. 1–10,2021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Späth J, Matschinske J, Kamanu FK, Murphy SA, Zolotareva O, Bakhtiari M, Antman EM, Loscalzo J, Brauneck A, Schmalhorst L et al. , “Privacy-aware multi-institutional time-to-event studies,” PLOS Digital Health, vol. 1, no. 9, p. e0000101, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Bonomi L, Jiang X, and Ohno-Machado L, “Protecting patient privacy in survival analyses,” Journal of the American Medical Informatics Association, vol. 27, no. 3, pp. 366–375, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Lee C, Yoon J, and Van Der Schaar M, “Dynamic-deephit: A deep learning approach for dynamic survival analysis with competing risks based on longitudinal data,” IEEE Transactions on Biomedical Engineering, vol. 67, no. 1, pp. 122–133, 2019. [DOI] [PubMed] [Google Scholar]
- [21].Tomašev N, Harris N, Baur S, Mottram A, Glorot X, Rae JW, Zielinski M, Askham H, Saraiva A, Magliulo V et al. , “Use of deep learning to develop continuous-risk models for adverse event prediction from electronic health records,” Nature Protocols, vol. 16, no. 6, pp. 2765–2787, 2021. [DOI] [PubMed] [Google Scholar]
- [22].Chan THH, Li M, Shi E, and Xu W, “Differentially private continual monitoring of heavy hitters from distributed streams,” in Privacy Enhancing Technologies: 12th International Symposium, PETS 2012, Vigo, Spain, July 11-13, 2012. Proceedings 12. Springer, 2012, pp. 140–159. [Google Scholar]
- [23].Wu Y, Chen Y, Wang L, Ye Y, Liu Z, Guo Y, and Fu Y, “Large scale incremental learning,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019, pp. 374–382. [Google Scholar]
- [24].Bourtoule L, Chandrasekaran V, Choquette-Choo CA, Jia H, Travers A, Zhang B, Lie D, and Papernot N, “Machine unlearning,” in 2021 IEEE Symposium on Security and Privacy (SP). IEEE, 2021, pp. 141–159 . [Google Scholar]
- [25].Lee ET and Go OT, “Survival analysis in public health research,” Annual review of public health, vol. 18, no. 1, pp. 105–134, 1997. [DOI] [PubMed] [Google Scholar]
- [26].Cox DR, “Regression models and life-tables,” Journal of the Royal Statistical Society: Series B (Methodological), vol. 34, no. 2, pp. 187–202, 1972. [Google Scholar]
- [27].Liu Y, Yan C, Yin Z, Wan Z, Xia W, Kantarcioglu M, Vorobeychik Y, Clayton EW, and Malin BA, “Biomedical research cohort membership disclosure on social media,” in AMIA annual symposium proceedings, vol. 2019. American Medical Informatics Association, 2019, p. 607. [PMC free article] [PubMed] [Google Scholar]
- [28].Umar P, Akiti C, Squicciarini A, and Rajtmajer S, “Self-disclosure on twitter during the covid-19 pandemic: A network perspective,” in Machine Learning and Knowledge Discovery in Databases. Applied Data Science Track: European Conference, ECML PKDD 2021, Bilbao, Spain, September 13–17, 2021, Proceedings, Part IV 21. Springer, 2021, pp. 271–286. [Google Scholar]
- [29].Dwork C, Roth A et al. , “The algorithmic foundations of differential privacy,” Foundations and Trends® in Theoretical Computer Science, vol. 9, no. 3–4, pp. 211–407, 2014. [Google Scholar]
- [30].Dwork C, Naor M, Reingold O, Rothblum GN, and Vadhan S, “On the complexity of differentially private data release: efficient algorithms and hardness results,” in Proceedings of the forty-first annual ACM symposium on Theory of computing, 2009, pp. 381–390. [Google Scholar]
- [31].Cummings R, Krehbiel S, Lai KA, and Tantipongpipat U, “Differential privacy for growing databases,” Advances in Neural Information Processing Systems, vol. 31, 2018. [Google Scholar]
- [32].Lyu M, Su D, and Li N, “Understanding the sparse vector technique for differential privacy,” Proceedings of the VLDB Endowment, vol. 10, no. 6, 2017. [Google Scholar]
- [33].Lin Z, Hewett M, and Altman RB, “Using binning to maintain confidentiality of medical data.” in Proceedings of the AMIA Symposium. American Medical Informatics Association, 2002, p. 454. [PMC free article] [PubMed] [Google Scholar]
- [34].Brown JT, Yan C, Xia W, Yin Z, Wan Z, Gkoulalas-Divanis A, Kantarcioglu M, and Malin BA, “Dynamically adjusting case reporting policy to maximize privacy and public health utility in the face of a pandemic,” Journal of the American Medical Informatics Association, vol. 29, no. 5, pp. 853–863, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Kotz S, Kozubowski T, and Podgórski K, The Laplace distribution and generalizations: a revisit with applications to communications, economics, engineering, and finance. Springer Science & Business Media, 2001, no. 183. [Google Scholar]
- [36].Ács G and Castelluccia C, “I have a dream!(differentially private smart metering),” in International Workshop on Information Hiding. Springer, 2011, pp. 118–132. [Google Scholar]
- [37].Ranbaduge T, Vatsalan D, and Christen P, “Secure multi-party summation protocols: Are they secure enough under collusion?” Trans. Data Priv, vol. 13, no. 1, pp. 25–60, 2020. [Google Scholar]
- [38].Shi R, Chow R, and Chan THH, “Privacy-preserving aggregation of time-series data,” Oct. 8 2013, uS Patent 8,555,400. [Google Scholar]
- [39].Xu B, Gutierrez B, Mekaru S, Sewalk K, Goodwin L, Loskill A, Cohn E, Hswen Y, Hill SC, Cobo MM, Zarebski A, Li S, Wu CH, Hulland E, Morgan J, Wang L, O’Brien K, Scarpino SV, Brownstein JS, Pybus OG, Pigott DM, and Kraemer MUG, “Epidemiological data from the COVID-19 outbreak, real-time case information,” Scientific Data, vol. 7, no. 106, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].O. C.-. D. W. Group, “Detailed Epidemiological Data from the COVID-19 Outbreak,” Accessed on 2022-10-15 from http://virological.org/t/epidemiological-data-from-the-ncov-2019-outbreak-early-descriptions-from-publicly-available-data/337, 2020.
- [41].Nemati M, Ansary J, and Nemati N, “Machine-learning approaches in covid-19 survival analysis and discharge-time likelihood prediction using clinical data,” Patterns, vol. 1, no. 5, p. 100074, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Nemati M, “Machine-learning-approaches-in-covid-19-survival-analysis,” Accessed on 2022-11-21 from https://github.com/Mnemati/Machine-Learning-Approaches-in-COVID-19-Survival-Analysis, 2020. [DOI] [PMC free article] [PubMed]
- [43].Zhao L, Claggett B, Tian L, Uno H, Pfeffer MA, Solomon SD, Trippa L, and Wei L, “On the restricted mean survival time curve in survival analysis,” Biometrics, vol. 72, no. 1, pp. 215–221, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Bonomi L and Fan L, “Sharing time-to-event data with privacy protection,” in 2022 IEEE 10th International Conference on Healthcare Informatics (ICHI). IEEE, 2022, pp. 11–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Lee C, Zame W, Yoon J, and Van Der Schaar M, “Deephit: A deep learning approach to survival analysis with competing risks,” in Proceedings of the AAAI conference on artificial intelligence, vol. 32, no. 1, 2018. [Google Scholar]
- [46].Ranganath R, Perotte A, Elhadad N, and Blei D, “Deep survival analysis,” in Machine Learning for Healthcare Conference. PMLR, 2016, pp. 101–114. [Google Scholar]
- [47].Fan L and Bonomi L, “Mitigating membership inference in deep survival analyses with differential privacy,” in 2023 IEEE 11th International Conference on Healthcare Informatics (ICHI). IEEE, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]


