The electrochemistry of stable sulfur isotopes versus lithium

Significance

Elements of the third period and above usually show minor differences in physical properties among their stable isotopes. Here, we show that stable isotopes of the third-period elements, such as sulfur (³⁴S and ³²S), show notable differences in electrochemical properties for proceeding a Li–S reaction in a rechargeable battery. ³⁴S is more prone to react with Li than ³²S, and the soluble intermediates generated from Li–³⁴S reaction prefer staying at the cathode over shuttling to the anode. The isotopic effects of the S element offer opportunities to build a stable Li–S battery and to electrochemically split stable S isotopes at a high separation factor.

Abstract

Sulfur in nature consists of two abundant stable isotopes, with two more neutrons in the heavy one (³⁴S) than in the light one (³²S). The two isotopes show similar physicochemical properties and are usually considered an integral system for chemical research in various fields. In this work, a model study based on a Li–S battery was performed to reveal the variation between the electrochemical properties of the two S isotopes. Provided with the same octatomic ring structure, the cyclo-³⁴S₈ molecules form stronger S–S bonds than cyclo-³²S₈ and are more prone to react with Li. The soluble Li polysulfides generated by the Li–³⁴S conversion reaction show a stronger cation–solvent interaction yet a weaker cation–anion interaction than the ³²S-based counterparts, which facilitates quick solvation of polysulfides yet hinders their migration from the cathode to the anode. Consequently, the Li–³⁴S cell shows improved cathode reaction kinetics at the solid–liquid interface and inhibited shuttle of polysulfides through the electrolyte so that it demonstrates better cycling performance than the Li–³²S cell. Based on the varied shuttle kinetics of the isotopic-S-based polysulfides, an electrochemical separation method for ³⁴S/³²S isotope is proposed, which enables a notably higher separation factor than the conventional separation methods via chemical exchange or distillation and brings opportunities to low-cost manufacture, utilization, and research of heavy chalcogen isotopes.

As a crucial nonmetal element in the earth’s crust, sulfur has four stable natural isotopes (i.e., ³²S, ³³S, ³⁴S, and ³⁶S), with an identical valence electron configuration of 3s²3p⁴. Among them, ³²S and ³⁴S show much higher atomic abundance (³²S: 94.99 at.%; ³⁴S: 4.25 at.%, see SI Appendix, Fig. S1) (1). The stable S isotopes have been extensively studied and utilized in the fields of nuclear physics, agricultural science, organic and physical chemistry, physiology and medicine, astronomy, ecology, and geology (2). For example, through neutron-induced nuclear reactions, ³²S and ³⁴S can be used to prepare some important radioisotopes [e.g., ³²P prepared via the ³²S(n, p)³²P reaction and ³⁵S via the ³⁴S(n, γ)³⁵S reaction] (3–5). Stable S isotopes are also important tracers for monitoring the atmospheric S circulation in ecosystems so as to identify the possible pollution source and control the acidification of soils and water (6–10). By detecting the ³⁴S/³²S ratio in tissue samples, physicians are able to determine the etiology and intervene with the progression of cancer and other diseases in human bodies (11–13). Unlike the first/second-period elements (e.g., hydrogen and lithium), the relative mass differences between stable isotopes of the third-period elements become less significant. Therefore, some physical properties at a macroscopic level, such as density, vapor pressure, and melting/boiling/flashing points, do not vary evidently between ³²S and ³⁴S (SI Appendix, Table S1). However, for a single S molecule, the 1/16 mass difference between isotopic S atoms could account for varied intrinsic nuclear and energy-related properties.

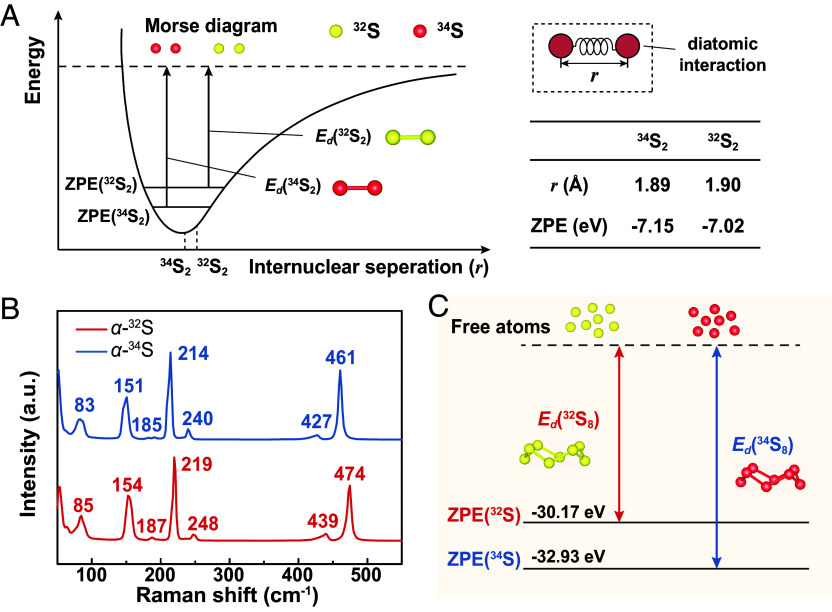
In the Morse potential curve that describes vibration of a diatomic amendatory harmonic oscillator (Fig. 1A and SI Appendix, Note S1), a ³⁴S₂ molecule, with a larger reduced mass ( ${\mu }_{{ }_{16}^{34}\text{s}}=17$   ) than a ³²S₂ molecule ( ${\mu }_{{ }_{16}^{32}\text{s}}=16$   ), shows a shorter S–S bond length (r), a lower zero-point energy (ZPE, defined as the vibrational energy at 0 K) and a higher dissociation energy (E_d, defined as the activation energy for homolysis of all S–S bonds) than a ³²S₂ molecule. The same principle could be applied to a cyclooctasulfur molecule (cyclo-S₈), the basic structural unit of crystalline rhombic sulfur (α-S) at ambient temperature and pressure. According to SI Appendix, Table S2, cyclo-³⁴S₈ and cyclo-³²S₈ show the same bond angle of 109.35°, yet cyclo-³⁴S₈ shows a shorter S–S bond length (2.04 Å) than cyclo-³²S₈ (2.06 Å), which indicates a more compact molecule structure. The vibrational information of isotopic cyclo-S₈ molecules calculated by the density functional theory (DFT) was compared in SI Appendix, Table S3. For all vibration modes, the cyclo-³⁴S₈ molecule shows much lower vibrational frequencies than the cyclo-³²S₈ molecule. Experimentally, Raman spectra were separately collected from the α-³²S and α-³⁴S powders to study the vibration and structures of the isotopic S molecules. According to Fig. 1B, both spectra indicate typical crown-like structure of cyclo-S₈ molecules with D_4d symmetry. For α-³²S (α-³⁴S), the peaks at 219 (214) and 474 (461) cm⁻¹, 85 (83) and 154 (151) cm⁻¹, 248 (240) and 439 (427) cm⁻¹ are assigned to the A₁, E₂, E₃ symmetry modes, respectively. The peak at 187 (182) cm⁻¹ could be assigned to the B₁ symmetry in violation of strict D_4d selection rules (14–16). Apparently, all Raman shifts of α-³⁴S are lower than those of α-³²S, which also indicate lower vibrational frequencies of cyclo-³⁴S₈. The vibrational energy of a molecule is positively correlated with its vibration frequency (SI Appendix, Note S1). Therefore, the cyclo-³⁴S₈ molecule shows a calculated ZPE much lower than the cyclo-³²S₈ molecule (−32.93 eV versus −30.17 eV, see Fig. 1C and SI Appendix, Table S2), so that it shows a higher E_d and is thermodynamically more stable.

Fig. 1.

Intramolecular interactions of S₂ and cyclo-S₈ molecules (in α-S) based on different S isotopes. (A) A Morse potential diagram that compares some intrinsic properties of the diatomic molecules, ³⁴S₂ and ³²S₂. (B) Raman spectra collected from α-³²S and α-³⁴S powders. (C) A schematic comparing ZPE and E_d of the cyclo-³²S₈ and cyclo-³⁴S₈ molecules.

In view of the varied intramolecular parameters and thermodynamic properties between cyclo-³⁴S₈ and cyclo-³²S₈, one could expect evident thermodynamic isotope effects in S-participated chemical reactions (17). A typical example would be the Li–S redox reaction (2Li + S = Li₂S), which has been extensively studied as a promising electrochemical reaction for designing the next-generation high-energy rechargeable batteries (18–20). The redox reaction in a Li–S cell can be spatially divided into two half-cell reactions, occurring separately on a S cathode and a Li–metal anode. For the S cathode prepared from conventional cyclo-S₈ molecules, it undergoes a stepwise conversion reaction at the S(solid)–electrolyte(liquid) interface, generating a series of chain-like Li polysulfides (LiPSs) intermediates before S is finally converted to Li₂S (21, 22). The electrochemical performance of a Li–S cell largely depends on the kinetics and thermodynamic stability of the cathode reaction. At the cathode–electrolyte interface, high-order LiPSs (Li₂S_n, 4≤n≤8) tend to dissolve and shuttle to the Li–metal anode (23–25). While the dissolution of LiPSs facilitates the kinetics of S conversion reaction at the solid–liquid interface, it also induces irreversible loss of active S and rapidly declined cathode capacity (unstable thermodynamics) (26–30). Therefore, insights into the LiPS “dissolution–shuttle” process at electrode–electrolyte interface could enrich the understandings about fundamental Li–S electrochemistry.

Results

In this work, we made an attempt to study the isotopic effect of S on the electrochemical reactions of a rechargeable Li–S battery. Isotopic S powder (³²S or ³⁴S) was mixed with an ordered mesoporous carbon (CMK-3) and heated to a temperature above the melting point of S to fill carbon pores by liquid S and to yield the S–C composites (³²S@CMK-3 or ³⁴S@CMK-3). Nitrogen adsorption–desorption isotherms were collected from the bare carbon. Referring to SI Appendix, Fig. S2, the CMK-3 carbon shows a type-IV isotherm with a hysteresis loop, indicating its mesoporous structure (31, 32). The pore size distribution calculated by the Barrett–Joyner–Halenda method indicates a dominated pore size at ca. 5 nm. At such a pore size, S exists in the forms of aggregates or nanoparticles and shows weak S–C interactions so that the pore structure does not notably affect the generation and migration of isotopic LiPSs. The carbon also shows a cumulative pore volume of 1.135 cm³/g, corresponding to a maximum S mass loading of 70.1 wt.% for ³²S and 69.9 wt.% for ³⁴S (SI Appendix, Table S4). Experimentally, the S mass loading in the S–C composites was controlled to be 60 wt.% for ³²S@CMK-3 and 61.5 wt.% for ³⁴S@CMK-3 (SI Appendix, Fig. S3), so that the composites share equal molar content of isotopic S. According to the X-ray diffraction (XRD) patterns in SI Appendix, Fig. S4, both ³²S@CMK-3 and ³⁴S@CMK-3 show an amorphous structure of S (instead of the rhombic crystal structure of pristine α-³²S and α-³⁴S). The ³²S and ³⁴S cathodes were separately prepared from the above S–C composites, and Li–S cells were assembled by pairing the cathode with a Li–metal anode. The galvanostatic discharge–charge (GDC) voltage profiles and cycling performance at 0.2C of the assembled Li–S cells were collected in SI Appendix, Fig. S5. Both the Li–³⁴S and Li–³²S cells show stepwise (dis)charge profiles (SI Appendix, Fig. S5 A and B) with two distinct plateaus that separately correspond to the conversion between cyclo-S₈ and high-order LiPSs, and the conversion between high-order LiPSs and low-order LiPSs (Li₂S_m, 2≤m<4, and Li₂S). As ³⁴S is 1/16 heavier (in relative atomic mass) than ³²S, it delivers a slightly lower theoretical specific capacity (1,576 mAh/g) than ³²S (1,675 mAh/g) via the same two-electron redox reaction with Li (SI Appendix, Note S2). Therefore, we adopted the Li uptake number of S (Li_xS, 0≤x≤2) to compare the depths of discharge of different isotopic S cathodes (i.e., the extent of Li–S reaction). The ³⁴S cathode delivers a slightly lower Li uptake number in the first cycle (x = 1.09 for ³⁴S and 1.10 for ³²S, corresponding to 859 mAh/g for ³⁴S and 925 mAh/g for ³²S, respectively) and a quicker capacity fade in the first few GDC cycles (SI Appendix, Fig. S5C). After 20 cycles, however, the ³⁴S cathode shows notably improved cycling stability compared with the ³²S cathode and is able to retain 81.7% of the initial capacity after 150 GDC cycles (which is higher than the ³²S cathode: 67.7%). The above results indicate that the ³⁴S cathode establishes, in a faster way, a stable S–electrolyte interface in Li–S battery than the ³²S cathode.

Discussion

From a thermodynamic point of view, building a stable ³⁴S–electrolyte interface would require faster conversion yet retarded migration of soluble LiPSs in the liquid electrolyte. To clarify this point, first-principle calculations were employed to study the LiPS formation process at two isotopic S cathodes. During the initial discharge of battery, Li₂S₈ (which usually shows the highest solubility in electrolyte among the LiPSs) generates from attack on a cyclo-S₈ molecule by Li, according to the following reaction:

$$2{\mathrm{Li}}^{+}+2{\mathrm{e}}^{-}+{\mathrm{S}}_8\left(\mathrm{ring}\right)\to {\mathrm{Li}}_2{\mathrm{S}}_8\left(\mathrm{chain}\right).$$ [1]

For the isotopic S cathodes, formation energy (E_f ) of Li₂³⁴S₈ and Li₂³²S₈ can be calculated by referring to the following equation (33):

$$E_f=E\left({\mathrm{Li}}_2{\mathrm{S}}_8\right)-2E\left(\mathrm{Li}\right)-E\left({\mathrm{S}}_8\right),$$ [2]

where E(Li₂S₈), E(Li), and E(S₈) denote the calculated energy of Li₂S₈, Li atom, and cyclo-S₈, respectively.

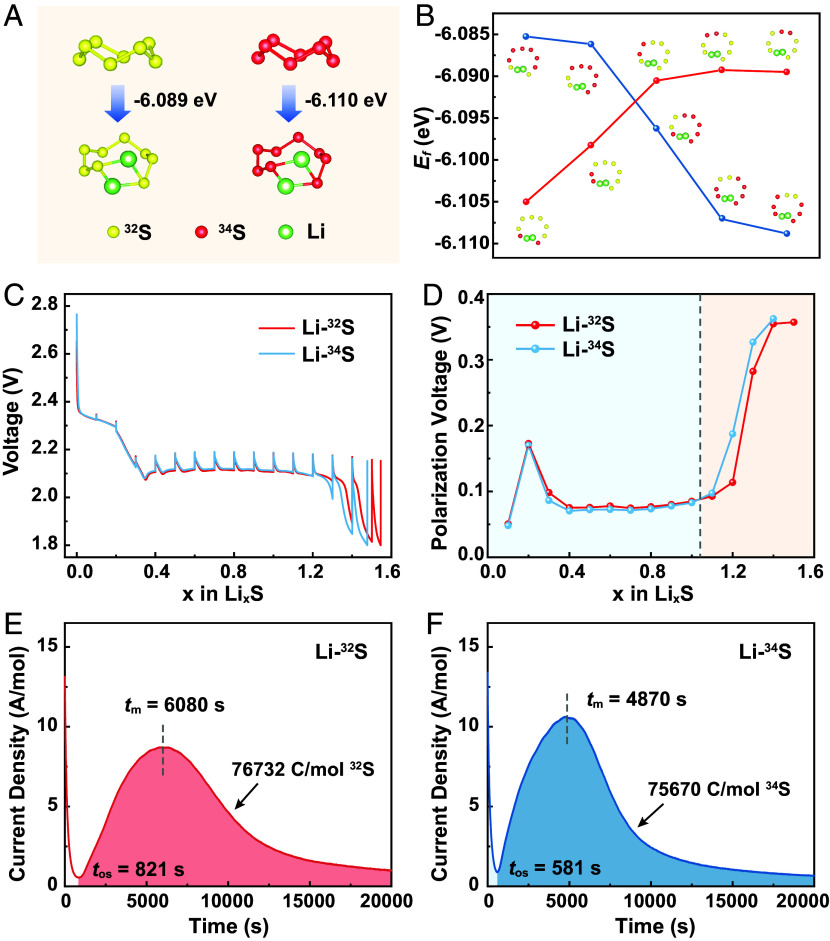
According to Fig. 2A, Li₂³⁴S₈ shows a lower formation energy (−6.110 eV) than Li₂³²S₈ (−6.089 eV). Therefore, formation of Li₂³⁴S₈ from initial Li uptake of cyclo-³⁴S₈ is thermodynamically more preferred. Note that the ³²S and ³⁴S cathode samples contain ≤5 wt.% of isotopic impurities (e.g., the ³²S cathode prepared from natural S that contains 4.25 at.% of ³⁴S), we also studied the site preference of Li attack on isotope-exchanged hetero-S₈ rings. Cyclo-³⁴S₂³²S₆ and cyclo-³²S₂³⁴S₆ molecules that contain two neighboring homo-isotopic S atoms were selected as the model. To calculate the formation energy of Li₂S₈ intermediates, two Li atoms were added onto the adjacent two S atoms. According to Fig. 2B, among the five configurations of Li₂³⁴S₂³²S₆, the one that bonds the Li atoms with the two ³⁴S atoms shows the lowest formation energy. In the case of Li₂³²S₂³⁴S₆, the configuration with two Li atoms bonding with the two neighboring ³⁴S atoms at the para-positions of ³²S shows the lowest formation energy. The notable site selectivity indicates stronger tendency for the Li atoms to react with the heavy S isotopes on a hetero-ring and could be applied to explain the reaction mechanism at different stages of the entire electrochemical separation process.

Fig. 2.

Insights into the electrochemistry of Li–³²S and Li–³⁴S cells. (A and B) Energy required to form Li₂S₈ intermediates from (A) cyclo-³²S₈ and cyclo-³⁴S₈ molecules and (B) cyclo-³²S₆³⁴S₂ and cyclo-³²S₂³⁴S₆ molecules. (C) GITT profiles collected during discharge of the Li–³²S and Li–³⁴S cells. (D) Polarization voltages of the above Li–S cells as a function of the Li uptake number at different SOCs. (E and F) i-t profiles recorded during potentiostatic discharge (E) of the Li–³²S cell and (F) of the Li–³⁴S cell at 2.09 V after initial galvanostatic discharge at 0.1 mA.

Galvanostatic intermittent titration technique (GITT) was employed to investigate the electrochemistry of Li–S batteries under the isotopic effect. Referring to Fig. 2C, the Li–³⁴S cell shows analogous GITT profiles to the Li–³²S cell, yet a lower Li uptake number at the end of discharge. The polarization voltages versus the Li uptake number at different states of charge (SOC) of the above Li–S cells were obtained from the GITT profiles and plotted in Fig. 2D (with voltage values collected in SI Appendix, Table S5). The Li–³⁴S cell shows a smaller polarization than the Li–³²S cell when x ≤ 1 and an opposite result when x > 1. Note that substantial nucleation and deposition of Li₂S₂/Li₂S (from soluble LiPSs) occurs at around x = 1, the above results indicate faster conversion from cyclo-³⁴S₈ to soluble LiPSs and more sluggish conversion from soluble LiPSs to insoluble Li₂³⁴S₂/Li₂³⁴S. An electrochemical precipitation experiment was performed to further study the electrochemical nucleation of Li₂S₂/Li₂S under the isotopic effects. Li–S cells were assembled and their current (i) versus time (t) was monitored during a potentiostatic discharge process at 2.09 V after initial galvanostatic discharge at 0.1 mA (Fig. 2 E and F) (34). An initial current drop is observed at 500 to 1,000 s, which is attributed to the reduction of long-chain polysulfides. The onset time (t_os) for Li₂S₂/Li₂S precipitation refers to the time of minimum current at the end of the current drop. As the nucleation of Li₂S₂/Li₂S occurs, the current quickly ascends and reaches a peak value, and the moment is termed as the time of current peak (t_m). After that, the adjacent nuclei start to overlap and quickly cover the active surface of electrode. In this way, the solution-mediated charge diffusion pathway almost vanishes and mobile charges have to diffuse along an insulated-Li₂S-mediated pathway, which accounts for continuous current decay (34, 35). In this way, a smaller t_m value would indicate faster surface coverage (and passivation) by insulated Li₂S₂/Li₂S deposits. While the Li–³²S cell shows a t_m value of 6,080 s, the Li–³⁴S cell shows a notably smaller t_m value of 4,870 s. Apparently, the ³⁴S cathode shows faster surface passivation as a consequence of Li₂S₂/Li₂S nucleation. Once the solid passivation layer covers the S particle surface, the charge transfer is impeded and the cathode shows sluggish conversion from low-order LiPSs to Li₂S. As a result, the Li–S cell shows a continuously declined current. By calculating the integral area between t_os (t₁) and time of experiment endpoint (t₂ = 20,000 s) of the i-t profile (SI Appendix, Note S3), a molar electron transfer number of 0.785 is obtained for Li₂S₂/Li₂S precipitation in a Li–³⁴S cell, which is smaller than the number for precipitation in a Li–³²S cell (0.797). By combining the calculation and experimental results, it becomes clear that ³⁴S facilitates formation and conversion of high-order LiPSs during initial discharge, but impedes the deep lithiation and low-order LiPSs conversion via charge transfer in a solid phase.

Migration of LiPSs (from cathode to anode) via electrochemical shuttle is considered another key factor that affects and even determines the performance of a Li–S cell (18, 36). At the anode side, the shuttled LiPSs tend to react with Li metal and be reduced to insoluble Li₂S₂/Li₂S, which are difficultly reactivated back to the S circulation, and therefore, inviting irreversible loss of active S and passivation of the anode surface. Consequently, it accounts for poor reversibility of Li–S electrochemistry and continuous capacity fade of battery (37, 38). Here, we studied the isotopic effects of S on LiPSs dissolution and shuttle. To eliminate the individual variations among different batteries, the study was performed in a single battery containing an equimolar ³²S/³⁴S mixture at the cathode. The mixture was prepared by melting and encapsulating the two S isotopes (in their liquid state) into the CMK-3 carbon, to yield cyclo-S₈-based, ³²S/³⁴S@CMK-3 composites after being cooled down to the room temperature (SI Appendix, Fig. S6A) (39). The melting temperature for the ³²S/³⁴S isotope mixture was controlled below the λ-transition temperature of S to avoid substantial isotope exchange among cyclo-S₈ molecules via ring opening and formation of macromolecular sulfur chains (SI Appendix, Fig. S6 B and C) (40–43). The ³²S/³⁴S@CMK-3 composites contain a total of ca. 40 wt.% S according to the thermogravimetric (TG) profile in SI Appendix, Fig. S7. XRD patterns in SI Appendix, Fig. S8, indicate a rhombic crystal structure of the ³²S/³⁴S mixture and an amorphous structure in the composites.

Images and elemental mapping data collected by scanning electron microscopy (SEM, see SI Appendix, Fig. S9) and transmission electron microscopy (TEM, see SI Appendix, Fig. S10) demonstrate uniform S-element distribution in the S@C composite both at a micron-scale and at a nanoscale (with clearly defined nanopores), free of any bulk S particles. The ³⁴S/³²S@CMK-3 composite was prepared into a S cathode (as shown in Fig. 3A) and characterized by time-of-flight secondary ion mass spectrometry (ToF-SIMS), a powerful tool for measurement of elements and isotopes, due to its low detection limit, high mass resolution, and sub-micron imaging resolution and depth profiling capabilities. Referring to the depth profile in Fig. 3B, both ³⁴S⁻ and ³²S⁻ fragments show equal intensity and fully consistent signal evolution by applying Cs⁺ sputtering along the vertical direction of the as-prepared cathode (before cycling). Both the two-dimensional planar and three-dimensional spatial distribution images (Fig. 3C and SI Appendix, Fig. S11A) show overlapped distribution of ³⁴S⁻ and ³²S⁻ fragments. The above results indicate homogeneous elemental distribution of an equimolar ³⁴S/³²S in the composites. A Li–S cell was assembled by pairing the ³⁴S/³²S@CMK-3 cathode with a Li–metal anode. A S-free electrolyte [LiClO₄ dissolved in an equivoluminal (v:v=1:1) mixture of 1,3-dioxolane (DOL) and 1,2-dimethyoxethane (DME)] was employed to exclude the interference with the cathode S species. The cell was applied with 10 full GDC cycles (SI Appendix, Fig. S12) for LiPSs shuttle and deposition onto the anode. The anode was then disassembled from the cycled cell and a ToF-SIMS depth profile of ³⁴S⁻/³²S⁻ was collected from the anode surface by applying continuous Cs⁺ sputtering (Fig. 3A). According to Fig. 3D, ³⁴S⁻ maintains a significantly lower intensity than ³²S⁻ at different sputtering times (depths), yielding a ³²S⁻/³⁴S⁻ intensity ratio of 1.6 to 2.0. Compared with the data obtained from the cathode, the above results demonstrate higher elemental abundance of ³²S than ³⁴S at the anode, which indicates much suppressed shuttle of ³⁴S-based LiPSs. The elemental distribution of ³⁴S/³²S at the anode, according to Fig. 3E and SI Appendix, Fig. S11B, shows no spatial preference and is highly consistent. The electrolyte was also extracted from the cycled cell and examined by an inductively coupled plasma mass spectrometer (ICP-MS, Fig. 3F). The results obtained from three parallel experiments indicate a higher content of ³²S than ³⁴S, with an average ³²S/³⁴S molar ratio of 1.81 (Fig. 3G and SI Appendix, Table S6). The above results prove low solubility of the ³⁴S-based LiPSs (than the ³²S-based LiPSs) in the electrolyte.

Fig. 3.

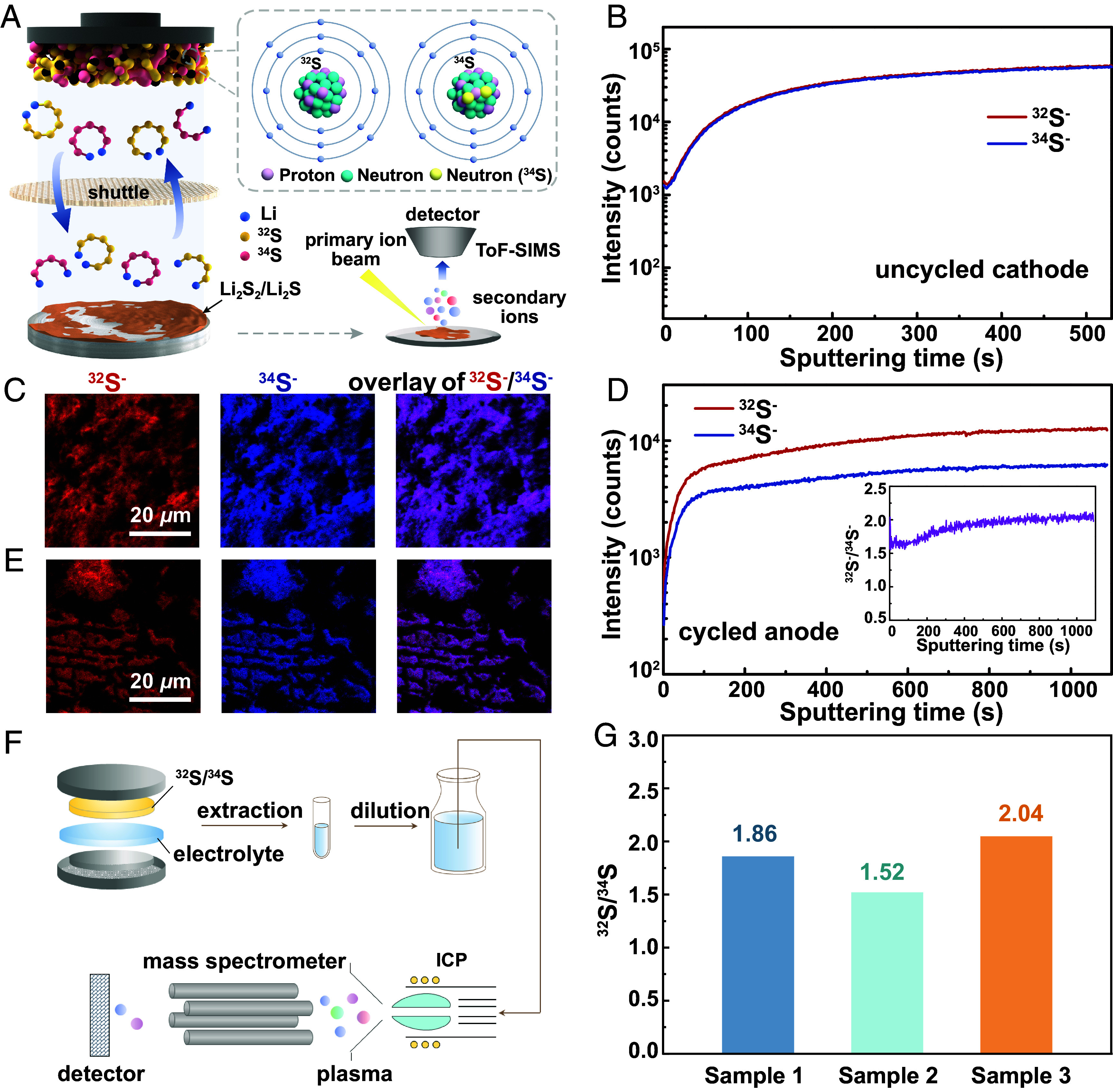
Spatial distribution and contents of S isotopes in the key components of a Li–S cell. (A) A schematic that illustrates the principle of the ToF-SIMS experiment. (B) Depth profile and (C) 2D planar images showing the distribution of isotopic S fragments at the uncycled ³⁴S/³²S@CMK-3 cathode. (D) Depth profile and (E) 2D planar images showing the distribution of isotopic S fragments at the cycled Li–metal anode; Inset of (D) shows the variation of ³²S/³⁴S (molar) ratio with sputtering time. (F) A schematic that illustrates the principle of the ICP-MS experiment. (G) Molar ratio of ³²S to ³⁴S in the cycled electrolyte.

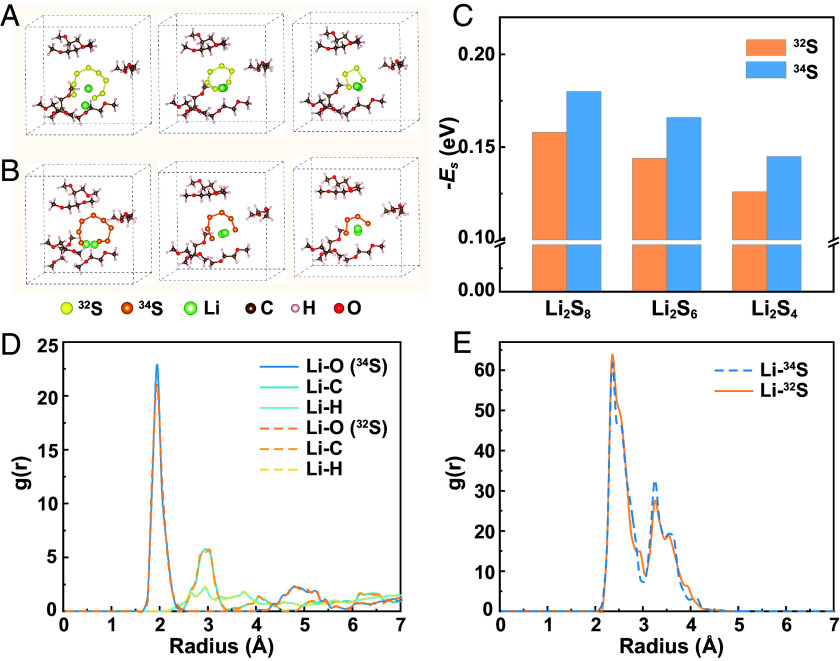
A model study that shows insights into the LiPS–solvent interaction is critical for comprehending the above results. To simplify the study, we focus on the LiPS–DME interaction (as DOL shows similar interaction with LiPSs, and the salt anion is barely involved in the inner cation solvation sheath once solvent-separated ion pairs form) (44, 45). Calculated results (Fig. 4 A–C and SI Appendix, Table S7) demonstrate that the ³⁴S-based soluble LiPSs, including Li₂³⁴S₈, Li₂³⁴S₆, and Li₂³⁴S₄, show higher solvation energy (E_s) with DME than the ³²S-based counterparts, though they share similar solvation structures. As such, dissolution of the ³⁴S-based LiPSs into the electrolyte appears to be thermodynamically more preferred than that of the ³²S-based LiPSs, which is contradictory to the experimental results that the ³⁴S-based LiPSs show inhibited shuttle and lower solubility in the electrolyte. To precisely depict the solvation process and the interaction of LiPSs with solvent molecules, ab initio molecular dynamics (AIMD) simulations were performed on a Li₂S₆–DME system (SI Appendix, Fig. S13). According to the radial distribution function (RDF) profiles (Fig. 4 D and E and SI Appendix, Fig. S14), both Li₂³⁴S₆–DME and Li₂³²S₆–DME show similar interatomic interactions, including Li–X (“X” represents C/H/O atoms of the solvent), Li–S, and S–X. Cation–solvent (Li⁺–DME) and cation–anion (Li⁺-S₆²⁻) interactions account for the main chemical interactions that build the solute-solvent pair, which are respectively formed through Li–O coordination and Li–S bond. Li₂³⁴S₆–DME shows a stronger cation–solvent interaction (via Li–O) than Li₂³²S₆–DME (Fig. 4D). Such a strong interaction promotes the Li₂S₆ dissociation by the ether solvent, and it reasonably explains the high E_s of ³⁴S-based LiPSs in the presence of DME. The cation–anion interaction via Li–S is competitive to the cation–solvent interaction via Li–O. Provided with a stronger cation–solvent interaction, the Li₂³⁴S₆–DME shows a weaker cation–anion (Li–S) interaction than Li₂³²S₆–DME (Fig. 4E). In another S₆²⁻ chain that contains three ³⁴S atoms and three ³²S atoms arranged in an alternant fashion, the ³⁴S atom also shows a weaker interaction with Li than the ³²S atom (SI Appendix, Fig. S15), where the force is contributed mainly by the terminal S. According to Kamphaus et al., the LiPSs barely exist in the form of S_n²⁻ anions but mostly in the form of neutral molecules when they migrate between cathode and anode, i.e., the shuttle of polysulfide anions awfully builds on their attachment to the Li⁺ cation (44). Therefore, a weak cation–anion interaction in Li₂³⁴S₆ may help to suppress LiPS shuttle in the ether electrolyte compared with Li₂³²S₆. With the above results, it becomes clear that the ³⁴S-based soluble LiPSs tend to quickly solvate yet slowly migrate in the ether electrolyte compared with the ³²S-based LiPSs. For Li–S cells, the unique electrochemical properties of ³⁴S would facilitate in situ formation and fixation of high-order LiPSs at the cathode–electrolyte interface, contributing to faster LiPS conversion kinetics via the solution-mediated pathway, as has been proven by the GITT and Li₂S precipitation experiments. Rapid Li–³⁴S conversion reaction at the cathode means improved conversion rate of high-order soluble LiPSs, which in turn contributes to their reduced solubility in the electrolyte and less low-order LiPS deposited at the anode. Consequently, the Li–³⁴S cell shows much improved cycling stability.

Fig. 4.

Chemical interactions between soluble LiPSs and ether solvent of electrolyte. (A and B) AIMD snapshots taken from DME-solvated structures of (A) Li₂³²S₈, Li₂³²S₆, and Li₂³²S₄ and of (B) Li₂³⁴S₈, Li₂³⁴S₆, and Li₂³⁴S₄. (C) E_s in DME of the above LiPSs. (D and E) RDF profiles that describe the interactions with DME of Li₂³²S₆ and Li₂³⁴S₆ via (D) Li–X and (E) Li–S.

To conclude, the (electro)chemical variations between stable S allotropes were studied and compared in a rechargeable Li–S battery. In the conventional form of cyclo-S₈, the S molecule based on heavy isotope (³⁴S) is thermodynamically more stable and shows stronger tendency to react with Li atom than the one based on light S (³²S). The soluble LiPSs formed by Li uptake of cyclo-³⁴S₈ show a stronger cation–solvent interaction yet a weaker cation–anion interaction than the ³²S-based counterparts, which accounts for quicker solvation yet more sluggish migration of LiPSs. Hence, the ³⁴S-based cathode enables faster Li–S conversion reaction at the solid–liquid interface and inhibited shuttle of LiPSs in the electrolyte. In this way, the Li–³⁴S cell simultaneously features improved cathode reaction kinetics and cycling stability compared with the Li–³²S cell. Though the ³⁴S cathode involves with retarded kinetics of solid-phase LiPS conversion, the issue could be addressed through applying a proper (dis)charge protocol that fits battery operation at different SOC [e.g., by applying a smaller (dis)charge rate at a low state of charge]. Another potential issue regarding the cathode use of heavy ³⁴S could be a reduced cell-level specific energy. According to SI Appendix, Table S8, a 10-Ah Li–S pouch cell could lose ~2.6% of cell energy by switching from the ³²S cathode to the ³⁴S cathode. However, since the ³⁴S cathode shows much inhibited LiPS shuttle and more stable cycling performance than the ³²S cathode, the gap between battery energy could be gradually closed after several (dis)charge cycles. Note that ³⁴S accounts for 1/25 to 1/20 of total S in nature, the heavy S isotope could claim a comparable mass abundance with the common metal elements in the earth’s crust such as copper or zinc (46), making it a promising material for battery and related industries.

Finally, the insights into the electrochemistry of S isotopes offer a perspective on heavy isotope separation, a key technology that enables large-scale manufacture and use of stable isotopes. Although stable S isotopes (mostly ³⁴S) can be separated from nature S via the conventional chemical exchange or distillation approaches (17), the separation technology usually involves a low separation factor (mostly <1.04), a long separation time and complicated procedures (2, 47, 48), which notably raise the manufacturing cost of the isotopes. By taking the advantage of electrochemical isotope effects of S, our simple demonstration on a Li–S battery shows promises to readily achieve a higher separation factor (α) of 1.1 to 1.2 after 1 (dis)charge cycle and 1.6 to 2.0 after 10 (dis)charge cycles (SI Appendix, Figs. S16 and S17 and Note S4). With properly designed electrolyte composition, cathode structure, and (dis)charge protocols, one could expect a magnified isotope effect that leads to a higher separation ratio of S isotopes. The other two stable S isotopes show relatively low abundances in natural S (³³S: 0.75 at.% and ³⁶S: 0.01 at.%), and it remains difficult to directly study their influence on Li–S electrochemistry in a coin cell. Use of a proper battery configuration, such as an Ah-level pouch cell with a high areal mass loading of S at the cathode, may help to magnify the isotope effects of ³³S/³⁶S and enrich the rare isotopes at different cell components. The current study could inspire interdisciplinary field of isotope electrochemistry that not only triggers science for existing electrochemical systems but also the development of isotope-related technology.

Materials and Methods

Preparation of ³²S@CMK-3 and ³⁴S@CMK-3.

In a typical synthesis, α-³²S (or natural S, Sigma-Aldrich, analytical reagent) powder was thoroughly mixed with the CMK-3 mesoporous carbon (Nanjing XFNANO Materials) at a mass ratio of m_S:m_C=60:40. In the control experiment, α-³⁴S (Cambridge Isotope Laboratories, Inc., 99.79%) powder was mixed with CMK-3 at a mass ratio of m_S:m_C=64:40. The mass ratio of natural S (and ³⁴S isotope) to CMK-3 on the cathode is precisely controlled so that both cathodes have an equal number of moles of total S isotopes. The above mixtures were sealed in an argon-prefilled container and maintained at 150 °C for 10 h. After being cooled down to room temperature, the ³²S@CMK-3 and ³⁴S@CMK-3 were prepared.

Preparation of ³⁴S/³²S@CMK-3.

In a typical synthesis, ³⁴S, ³²S, and CMK-3 were thoroughly mixed at a mass ratio of m_S-34:m_S-32:m_C=206:194:600. The mixture was sealed in the Ar-prefilled container and maintained at 150 °C for 10 h. After being cooled down to room temperature, the ³⁴S/³²S@CMK-3 was prepared.

Preparation of the S Electrodes.

To prepare the ³²S@CMK-3 and ³⁴S@CMK-3 electrodes, the as-prepared S–C composites, super-P conductive additives (Cabot) and poly(vinylidene fluoride) binder (Alfa Aesar) were mixed at a mass ratio of 8:1:1 in a 1-methyl-2-pyrolidone solvent (Alfa Aesar, 99.5%) to form a uniform slurry. The slurry was then casted onto a carbon-coated Al foil (Guangzhou Nanuo New Materials Technology Co., Ltd.) and dried at 60 °C for 24 h. The dried foil was cut into slices with a diameter of 10 mm and an areal S mass loading of 1.5 mg cm⁻². The preparation of the ³⁴S/³²S@CMK-3 electrode follows an almost identical procedure with the above ³²S@CMK-3 electrode, except for a reduced areal S mass loading of 0.5 mg cm⁻².

Preparation of the Li–S Cells.

CR2032-type coin cells were assembled in an Ar-filled glove box (Mikrouna, with H₂O and O₂ contents of <0.1 ppm). All experimental materials were dried at 60 °C for 2 h before battery assembly. To prepare the Li–³²S@CMK-3 (or Li–³⁴S@CMK-3) cell, the as-prepared S electrode (as the cathode) was paired with a 10-mm-in-diameter Li–metal disc (China Energy Lithium Co., Ltd. 99.9%) as the anode. A trilayer polypropylene/polyethylene/polypropylene composite polymer separator (Celgard, ~25 μm thick) was sandwiched between the two electrodes, which was filled by 50 μL of an ether electrolyte. The electrolyte consists of 1M bis(trifluoromethane)sulfonimide Li salt (LiTFSI, Sigma-Aldrich, 99.99%) in an equivoluminal mixture of DOL (Sigma-Aldrich, 99.8%) and DME (Sigma-Aldrich, 99.5%), with addition of 1 wt.% lithium nitrate (LiNO₃, Alfa, anhydrous, 99.98%). To prepare the Li–³⁴S/³²S@CMK-3 cell, a glass fiber (Whatman, ~650 μm thick) was sandwiched between the two electrodes, which was filled by 180 μL of an ether electrolyte consisting of 1M lithium perchlorate (LiClO₄, 99.99%, Sigma-Aldrich) in the equivoluminal DOL/DME mixture.

Material Characterization.

The morphology and elemental distribution of S–C composites were characterized by a SEM (JOEL JSM-6701F) operated at 10 kV and a TEM (JEM-2100F) coupled with an energy-dispersive X-ray spectrometer. The XRD patterns were collected using a Philips PW3710 (Rigaku D/max-2500 diffractometer) with filtered Cu Kα radiation (λ = 1.5418 Å) within a 2θ range of from 10° to 80° (scan rate: 5° min⁻¹). TG profiles were collected on a Netzsch thermal gravimetric analyzer (TG/DTA6300) from room temperature to 800 °C (heating rate: 10 °C min⁻¹) under the N₂ atmosphere. Raman spectra of α-³²S and α-³⁴S powders were collected on a HORIBA spectrometer (LabRAM HR Evolution) with a 532-nm excitation laser and a 100× long-distance objective. Differential scanning calorimetry (DSC) was performed on a Netzsch DSC 214 Polyma from room temperature to 210 °C (heating rate: 5 °C min⁻¹). N₂ absorption and desorption isotherms were obtained at 77.3 K with a Autosorb-iQ surface area pore size analyzer, and the ASIQ Win software (Quantachrome Instruments Version 11.04) was used to analyze the physisorption isotherms and determine the pore parameters.

Electrochemical Measurements.

The electrochemical measurements of Li–S cells were carried out on a NEWARE CT-4008 battery tester. For the Li–³²S@CMK-3 (or Li–³⁴S@CMK-3) cell, a voltage range of 1.8 to 2.8 V (versus Li⁺/Li) and a C-rate of 0.2C were employed, where 1C was defined as 1,675 mA/g for ³²S and 1,576 mA/g for ³⁴S. For the Li–³⁴S/³²S@CMK-3 cell, a voltage range of 1.5 to 2.8 V (versus Li⁺/Li) and a C-rate of 0.1C was employed, where 1C was defined as 1,624 mA/g. GITT was employed to study the cathode reaction kinetics in the Li–³²S@CMK-3 (or Li–³⁴S@CMK-3) cell, which was performed by applying a constant discharge current of 0.1C for 30 min, followed by a 10-h relaxation. Li₂S precipitation experiments were conducted on a Princeton electrochemical workstation by applying a potentiostatic process at 2.09 V on a Li–S cell after galvanostatic discharge from open-circuit voltage to 2.11 V at a current of 0.1 mA.

Characterization of S Isotopes.

Before the experiment, the Li–³⁴S/³²S@CMK-3 cell was applied with 10 discharge–charge cycles and was disassembled in the Ar-filled glovebox. The cycled Li–metal anode was taken out of the cell and dried in vacuum overnight. The electrolyte was extracted from the cycled cell and diluted with isopropanol (Acros, 99.5%) by 400 times. A ToF-SIMS instrument (ION-ToF GmbH, Münster, Germany) equipped with a 30-keV Bi₃⁺ primary ion gun and a 2-keV Cs⁺ sputter gun were employed to collect signals of ³⁴S⁻ and ³²S⁻ ions from both the uncycled ³⁴S/³²S@CMK-3 cathode and the cycled Li–metal anode. An electron flood gun was used for charge neutralization. The raster size of the image was 50 × 50 μm and the sputter area was 100 × 100 μm. The ³²S⁻/³⁴S⁻ ratio of the electrolyte was examined by an ICP-MS (Agilent 8900), where the uncycled electrolyte was employed as a blank sample.

Theoretical Calculation.

All calculations were performed using the plane wave-based periodic DFT method, which was implemented in the Vienna Ab Initio Simulation Package (49, 50). The electron–ion interaction was described with the projector augmented wave method (51, 52). The electron exchange and correlation energies were treated within the generalized gradient approximation in the Perdew–Burke–Ernzerhof functional (53). The plane wave basis was set up to 500 eV. AIMD was carried out to obtain configurations (54). The AIMD task was performed over 90,000 steps in the NVT ensembles at 300 K, using a small-time step of 0.1 fs due to the lightweight of H⁺.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix.