Multiple forces facilitate the aquatic acrobatics of grasshopper and bioinspired robot

Significance

Navigating diverse terrains is crucial for wild-operating robotics but remains a grand challenge. Research on Chinese rice grasshoppers reveals a surprising adaptation: Their ability to swim and leap off the water, challenging conventional notions of terrestrial animals’ limitations in aquatic environments and offering significant inspiration for advanced robotics. Investigating the grasshoppers’ aquatic acrobatics unveils a synergy between hydrostatics and limb-controlled hydrodynamics. Grasshopper-inspired robot emulates the aquatic prowess of animals, demonstrating the advantage of decoupling the challenge of aquatic locomotion by using combined static and dynamic hydro forces. This study will spark further research into the strategies employed by legged terrestrial animals in complex environments and further promote the integration of these principles into advanced robots, therefore facilitating cross-medium locomotion.

Abstract

Aquatic locomotion is challenging for land-dwelling creatures because of the high degree of fluidity with which the water yields to loads. We surprisingly found that the Chinese rice grasshopper Oxya chinensis, known for its terrestrial acrobatics, could swiftly launch itself off the water’s surface in around 25 ms and seamlessly transition into flight. Biological observations showed that jumping grasshoppers use their front and middle legs to tilt up bodies first and then lift off by propelling the water toward the lower back with hind legs at angular speeds of up to 18°/ms, whereas the swimming grasshoppers swing their front and middle legs in nearly horizontal planes and move hind legs less violently (~8°/ms). Force measurement and model analysis indicated that the weight support could be achieved by hydrostatics which are proportionate to the mass of the grasshoppers, while the propulsions for motion are derived from the controlled limb–water interactions (i.e., the hydrodynamics). After learning the structural and behavioral strategies of the grasshoppers, a robot was created and was capable of swimming and jumping on the water surface like the insects, further demonstrating the effectiveness of decoupling the challenges of aquatic locomotion by the combined use of the static and dynamic hydro forces. This work not only uncovered the combined mechanisms responsible for facilitating aquatic acrobatics in this species but also laid a foundation for developing bioinspired robots that can locomote across multiple media.

Locomotion constitutes a fundamental aspect for animals and robots, particularly in complex environments with diverse physicochemical properties (1, 2), including variations in physical states (3–6), shape (7–9), compliance (10–12), available contact points (13, 14), surface energy (15), and other parameters. Pushed by the evolutionary pressure, animals have evolved elaborate locomotor systems and spectacular capabilities (2) and have attracted much attention to the morphological intelligence of biological systems (16) and the animal–environment interactions (1), leading to discoveries on locomotion principles and novel propulsion mechanisms and therefore advancements in bio-inspired designs (17).

Terrestrial locomotion relies on the frictional and/or adhesive forces between the solid ground and animals’ locomotor appendages (1). In comparison, fluids like water are highly compliant and readily yield to loads, posing grand challenges to force generation and maneuvering in fluid media (1). We surprisingly found the aquatic acrobatics of a terrestrial species, the Chinese rice grasshopper Oxya chinensis (O. chinensis), which is widely spread in the rice-planting region, particularly along the Yangtze River. When they fall into water, the O. chinensis can easily escape from the water and fly away (Movie S1). So far, short-horned grasshoppers (including locusts) have been recognized as one of the best terrestrial jumpers, in addition to their locomotor skills of slow walking, intermediate speeds hopping, and flying, and therefore served as the animal model systems in the studies of insect attachment mechanisms (16, 18–20) and principles of terrestrial locomotion (11, 21–23), which further led to the development of jumping robotics (24). However, the aquatic locomotion capabilities of grasshoppers (especially aquatic jumping) have been largely unexplored, though some limited attention has been paid to the swimming of locusts for behavioral or ecological research (25–28).

Maneuvering on water surfaces presents animals with at least a dual challenge: preventing the body from sinking and accelerating against drags, contingent on effective force generation (29). The interplay of interfacial (30), aerodynamic, and hydrodynamic forces further heightened the complexity of force generation at the air–water interface. Consequently, research into locomotion dynamics in this particular context has been restricted to a limited selection of animal species (31–35). Previous studies indicated that the mechanisms with which the animals generate forces on the water surface vary broadly among species but could be roughly distinguished by comparing their characteristic dimension with the capillary length of water (29, 36). For instance, when the body is thinner than the capillary length, as in the case of a water strider’s leg (31), weight support principally benefits from the surface tension. Nonetheless, for bodies much larger than the capillary length, like the basilisk lizard (37), hydrodynamic forces take precedence (38). The recent work by Gwon et al. (36) further emphasized the connection between aquatic movement and the dynamical scale of creatures. As grasshoppers have intermediate sizes but use long and slender legs immersed in water for moving (Movie S2), they were supposed to utilize combined mechanisms to generate propulsions, but this remains unclear.

In this paper, we focused on the kinematics and dynamics of the O. chinensis when they leap off the water, compared this with the swimming locomotion mode, and then delved into the mechanisms used by the grasshoppers to generate forces that facilitate their aquatic acrobatics. Drawing inspiration from the grasshoppers, we built a robot with three pairs of distributedly controlled legs. Through further assimilating the locomotor strategies adopted by the insects, the robot exhibited the capability of locomoting on water like the insects, adding to our knowledge of biological locomotion, opening broad avenues for the integration of biomechanical insights into robotics, and therefore advancing the field’s potential applications across different environments.

Results and Discussion

Acrobatics of Grasshoppers on Water Surface.

Animals’ locomotor skills, anatomical features, and physical forms are intricately linked to their environment (39). The O. chinensis typically perch on aquatic vegetation like rice plants and is susceptible to falling into the water once disturbed, for example, by strong wind. Therefore, in addition to their terrestrial habits, they are expected to possess the ability to interact with water—a crucial adaptation for survival in the environment in the vicinity of water bodies. We experimented by deliberately dropping O. chinensis specimens into a river to validate our conjecture preliminarily. To our astonishment, the grasshoppers demonstrated a remarkable ability to swiftly and efficiently evade the water by employing leaping and soaring techniques (Movie S1). We further pursued a more controlled examination of the aquatic acrobatics of O. chinensis in the laboratory with high-speed video recordings.

The grasshoppers could either stay on the water surface without any action, waft with the tide passively, swim actively, or leap immediately once falling into a water tank. It has been found that aquatic arthropods of small dimensions, such as water striders (31), ants (40), and fishing spiders (32, 41), can effectively stand on the water surface using their legs. The unique microstructure seen in limbs, such as the setae (31), allows them to make the best of surface tension, therefore generating vertical force for weight support (29). While the larger vertebrates [e.g., geckos (34) and basilisk lizards (37) with a length over 10 cm] with the capability of aquatic locomotion are incapable of staying on the water surface without continuously flapping their feet (34, 37). As shown in Fig. 1 A and B and Movie S2, the intermediate-sized grasshoppers exhibited distinctly dissimilar postures while staying on the water surface. They did not keep their bodies entirely above the water level but instead made contact with the water using their abdomens; their legs penetrated the water’s surface but did not move.

Fig. 1.

The performance of jumping and swimming grasshoppers. (A and B) Lateral and dorsal views of the grasshoppers in motion; (C and D) The time sequences of the limbs of grasshoppers in jumping (C) and swimming (D); (E) The positions of the CoMs (center of mass) of jumping grasshoppers (orange lines) and swimming grasshoppers (blue lines); (F) The pitch angles of the jumping grasshoppers (orange curves) and swimming grasshoppers (blue curves). Figures (A and B) were adopted from Movie S2. In B, ① femur, ② tibia, ③ tarsus. In C and D, once the relative position change between a limb and the trunk was more significant than 2%, it was regarded as moving, and we gave it a color bar. The limb was considered motionless when its position relative to the trunk was less than 2%. Real-time T_real is the absolute time starting from the initiation of the front or middle limbs. The black bars indicate the SD of T_real. The percentage numbers indicated the sequences in relative time (T_rela: the ratio of current absolute time over the total time for acceleration). The lowercase letters in C and D indicate the statistical difference level: (a) P < 0.001; (d) P ≥ 0.05.

To leap off the water, grasshoppers first pushed the water toward the back lower place with their front and middle limbs, and then (Fig. 1 A and C, T_real ≈ 30 ms, T_rela ≈ 70%; T_real: the absolute time starting from the initiation of the front or middle limbs; T_rela: ratio of T_real to the total time for acceleration) ejected the trunks out of the water along an obliquely upward direction rapidly by vigorously beating the water with the long tibiae of hind limbs, resulting in trunks moved through a combination of rotation and translation (Fig. 1 A, E, and F). The action of the front and middle limbs first tilted the trunks up from 9.6 ± 1.2° to 16.3 ± 2.2° and thrust them in the horizontal directions for 0.06 ± 0.02 BL (BL: body length). After beating the water with the hind limb tibiae, the grasshoppers rapidly raised the pitching angles to 26.3 ± 4.1° (Fig. 1F, orange lines). The grasshoppers were almost entirely out of the water at surprisingly high velocities (horizontal 40.2 ± 9.2 BL/s, vertical 20.3 ± 5.8 BL/s) in 43.3 ± 5.6 ms (range: 32.5 to 55.0 ms). Alternatively, the grasshoppers could traverse the water surface by swimming (Fig. 1B and Movie S2). The tilts of the trunks of swimming grasshoppers were much reduced compared with jumping grasshoppers. As illustrated in Fig. 1F (blue lines), the pitching angles of the trunks were first increased from 7.5 ± 1.4° to 11.8 ± 1.9° as the grasshoppers swam for 0.42 ± 0.11 BL and then kept almost unchanged (12.4 ± 2.8°). After accelerations for 153.9 ± 29.4 ms, the swimming insects passed horizontal displacements for 0.8 ± 0.2 BL and obtained maximum horizontal speeds of 8.5 ± 3.3 BL/s (Fig. 1 B and D). Considering an average trunk length of 2.5 cm, the top speeds of jumping grasshoppers were ~110 cm/s on average (range: 82.8 to 215.5 cm/s), half of that in terrestrial jumping (42). Comparatively, the swimming grasshoppers demonstrated considerably lower speeds (~21 cm/s, mixed model with the individual as random effects, F_(1,12.48) = 522.15, P < 0.001, no strong individual independence P = 0.27), but still noticeably higher than the value observed in desert locusts [~13 cm/s (26)].

The Fig. 2 illustrates the limb actions of the grasshoppers (see Fig. 1 and SI Appendix, Fig. S1 for limb components identification). To initialize the water-jumping, the initially forward-pointing front limbs (279.7 ± 9.8°) swung backward. The angular speeds increased from 0.9 ± 0.5°/ms to ~3.5°/ms (T_rela ≈ 45%) gradually, then rapidly quadrupled (14.2 ± 4.9°/ms, T_rela ≈ 80%) before plunging, reducing the included angles to 49.0 ± 9.6° (solid pink line in Fig. 2 A and B). The middle limbs (144.5 ± 19.7°, T_rela = 0%) also swung backward with smaller angular velocities (dashed brown lines in Fig. 2A) and finally nearly stuck to the trunks of the grasshoppers (24.1 ± 6.3°) after turning for ~60° (for a single limb). While being swung backward, the front and middle limbs were also pushed downward, and their angular speeds in the vertical planes showed similar tendencies by increasing to ~2.5°/ms and then decreasing (solid pink line and dashed brown line in Fig. 2C). Consequently, the angles between the forelimbs and midlimbs and the water surface changed from ~9° above the water surface to 55.9 ± 9.7° and 36.6 ± 9.6° below the water surface (T_rela ≈ 85%), respectively (Fig. 2D, solid pink line and dashed brown line). Compared with the front and middle limbs, the hind legs remained almost motionless in the first two-thirds of the acceleration stage. As the relative time continued to ~71%, the femora clustered toward the body (dotted red line in Fig. 2D) while the tibiae struck the water powerfully with angular velocities of about 17°/ms (Fig. 2E, pink lines), extending the angles between the tibiae and the water surface from 18.5 ± 4.0° to 120.5 ± 9.3° in about 12 ms (Fig. 2F, pink lines). When the grasshoppers traversed the water by swimming, their limb behavior differed. They surprisingly clustered their front limbs toward the forward direction, with the angles between front limbs varying from 289.1 ± 12.0° to 337.2 ± 9.5° (Fig. 2B, solid navy line). The angles between the middle limbs and the angles between the hind femora were almost unchanged at the first one-fifth of the acceleration stage. They were then reduced (from 103.5 ± 20.1° to 32.9 ± 4.0° and 11.9 ± 6.6° to 0.7 ± 3.3°, respectively; Fig. 2B, blue and cyan lines) due to the slow backward clustering (Fig. 2A, blue and cyan lines). The front and middle limbs did not press the water downward while swinging in the coronal sections (Fig. 2 C and D, blue and cyan lines). At the latter half of the acceleration stage, the tibiae of hind limbs pushed the water to the back lower, increasing their angles to the water surface to ~116° in ~27 ms (Fig. 2F, green and cyan lines), with one starting at 74.4 ± 19.6 ms (T_rela = 48.8 ± 10.7%) while another started at 127.1 ± 26.6 ms (T_rela = 82.7 ± 3.7%). The angular speeds of the tibiae increased from nearly 0 to ~8°/ms when the extension angle reached the median and then decreased (Fig. 2E, green and cyan lines).

Fig. 2.

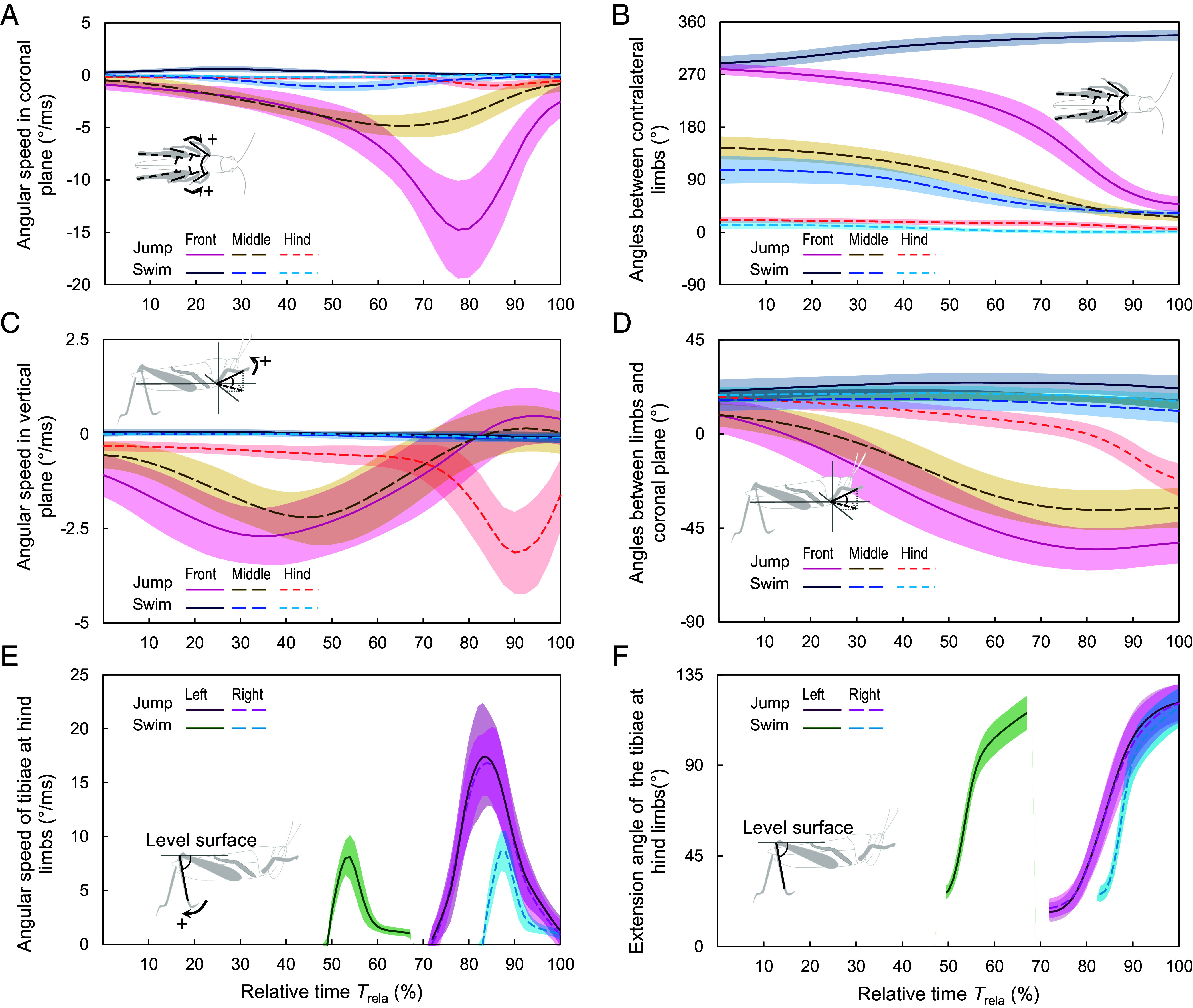
The kinetics of the limbs of the jumping (warm colors) and swimming (cold colors) grasshoppers. (A and B) The relative angular speeds (A) and angles (B) between contralateral limbs; (C and D) The angular speeds with which the limbs pushed down (C) and the angle changes (D); (E and F) The extension speeds of the tibiae at hind limbs (E) and their angle to the water surface (F). In E and F, the results of swimming grasshoppers were categorized into two groups according to the time during which the tibiae in the hind limbs extended. The other group shared the same pattern, except that the left and right hind tibias were in opposite phases. For the femur–tibia joints in the front and middle limbs were extended (Movie S2 and Fig. 1), we used lines that connect the trochanters and the terminals of tibiae to characterize the kinetics of the front and middle limbs. As to the hind limbs, the femur–tibia joints extended significantly, so we consider the femurs and tibiae, respectively. The lines represent average values, while shadows represent the SD.

The behavior of grasshoppers in jumping and swimming on the water surface showed some resemblances but more disparities. Upon readiness for movement, the tibiae at their front and middle limbs were extended, whereas the tibiae of the rear limbs were folded. However, the swimming grasshoppers had much lower included angles between their contralateral limbs than the jumping grasshoppers. In addition, the limbs of swimming grasshoppers exhibited greater inclinations relative to the water surface. Neurophysiological evidence has demonstrated that the grasshoppers’ locomotion is controlled by functional neuromodulation (43, 44), and the grasshoppers rely on visual input to decide their motion (45). Therefore, the aforementioned morphological and behavioral differences may lead to the conclusion that grasshoppers plan their motion well in advance. After the start, the jumping grasshoppers’ fore and middle limbs swing downward to lift their trunk, whereas the swimming grasshoppers’ fore and middle limbs are almost unchanged in the vertical plane, and so are their trunks. At the end of the acceleration phase, the jumping grasshoppers beat the water with both tibiae of their hind limbs almost simultaneously (F_(1,86.96) = 0.21, P = 0.65), whereas the swimming grasshoppers utilized them with a time difference of ~50 ms (after ln transformation, F_(1,99.11) = 153.79, P < 0.001). Though the angular variations of the tibiae were similar in both types of locomotion, jumping costs less time than swimming. Consequently, jumping grasshoppers are able to reach faster velocities in less time and over shorter distances, a crucial adaptation for predator escaping or initiating flight. These behavioral parallels and differences show that the water acrobatics of grasshoppers are closely related to the action of their limbs, from which the grasshoppers obtained reaction forces.

Among the organisms with the ability of aquatic locomotion, water striders (46), fishing spiders (47), and Pygmy mole crickets Xya capensis (48) were found to be able to move on or leap from the water surface, similar to grasshoppers. The water striders and fishing spiders typically traverse the water surface horizontally via rowing gaits, with the water striders predominantly employing their middle legs and the spiders relying on their frontmost three pairs of legs. In order to jump, water striders modify the impact angle of their driving stroke and push the water at an average angular speed of ~50 rad/s (i.e., ~2.9°/ms) (46). Fishing spiders flex their eight legs and simultaneously strike them downward (~3.4°/ms) to produce propulsions (47). Pygmy mole crickets achieve rapid propulsion out of the water by exerting force with their partially submerged hind legs at much faster speeds (~130°/ms according to ref. 48). Though the grasshoppers in our experiments exhibited the capability of traversing water as fast as the animals mentioned above (46, 48), the action strategies of their limbs are pretty different, indicating that the mechanisms the grasshoppers adopt to get beyond the challenges of aquatic locomotion are distinct.

Combined Mechanisms of Force Generation in Animals.

Static forces.

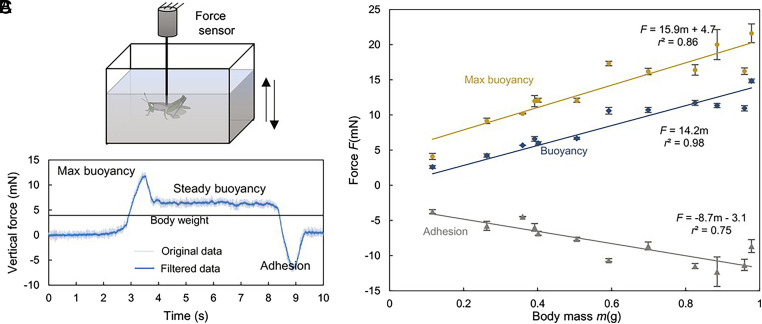
The floatation and wafting of grasshoppers demonstrated their ability to overcome the first challenge without using limb-controlled hydrodynamics. While the grasshoppers stayed on the water surface motionlessly, their legs were immersed in the water, and their attachment pads could release secretions containing water-soluble fractions with low contact angles (49). Therefore, the influence of surface tension appears to be less significant in grasshoppers compared to water striders and fishing spiders with superhydrophobic setae on feet (29). In order to understand how grasshoppers manage to stay afloat on the water surface, we measured the vertical forces using a force sensor while slowly immersing the grasshoppers in water (Fig. 3A). A representative force measurement, taken with a grasshopper weighing 0.40 g, is illustrated in Fig. 3B. The force began to rise upon the grasshopper touched the water with limbs and significantly increased as the grasshopper trunk touched the water, peaking at ~11.8 mN, but diminished to ~6.5 mN when the grasshopper was wholly submerged. Upon separating the grasshopper from the water, the vertical force decreased to a negative value (adhesion = −6.6 mN) and became immeasurable once the grasshopper was entirely out of the water.

Fig. 3.

Results of quasistatic measurement. (A) Experimental design; (B) A typical force measurement; (C) Maximum force, buoyancy, and adhesion depending on the animal mass. In A, the insects were immersed in water and pulled out slowly (~1.5 mm/s). In B, the thin purple line represents the original force data, while the thick magenta line represents the filtered data. In C, we averaged each individual’s max force, buoyancy, and adhesion and then performed linear regressions. The symbols indicate the average values, and the error bars indicate the SD for each individual.

When the animal was entirely immersed in water, the force measured here (i.e., the steady buoyancy in Fig. 3B) was the net buoyancy deduced by integrating the hydrostatic pressure over the body. Consequently, we were not surprised that the net buoyancy was proportional to the mass of grasshoppers, a function of the body volume (Fig. 3C, linear regression, F = 14.2, P < 0.001, r² = 0.98). The net buoyancy significantly exceeded the weight of the grasshopper, probably because of the air sacs and trachea situated in their body (50) and the porous structures in the cuticle (51). The maximum force (F_max) also exhibited a positive correlation with body mass, as indicated by the equation F_max = 15.9 m + 0.47 (P < 0.001, r² = 0.86). The maximum force was much larger than the net buoyancy, indicating that the surface tension also generated vertical force to prevent the grasshoppers from sinking. By subtracting the net buoyancy from the maximum force, the contribution of the surface tension could be roughly estimated as 1/3 of the weights of the grasshoppers, resulting in a Bond number of 1.57 ± 0.51, being in line with the conclusion by Bush and Hu (29). With the capability of generating ample buoyancy, the grasshoppers can quickly return to the water surface, even if they are deeply immersed due to the impact of high falls, avoiding suffocation due to the submergence of spiracles. The negative force shows the effects of the water resistance on the animal. In our quasistatic tests, the adhesion increased with the animal mass by F_adhesion = −8.7 m to 3.1 (P < 0.001, r² = 0.75).

The quasistatic measurement confirmed that the first challenge (i.e., weight support) is overcome by using hydrostatics. However, the overall resistance is even larger than the net buoyancy if the weight of the insects is also included. Thus, it can be concluded that grasshoppers have to rely on the hydrodynamic force generated through the interactions between their limbs to overcome the second challenge.

Limb-controlled hydrodynamics.

As the grasshoppers moved their limbs in water, the instantaneous reaction forces F_total might originate from different sources, including the drag force F_drag consisting of frictional drag and pressure drag, the added mass force F_mass arising from the accelerated fluid around the accelerating limbs, the buoyancy F_buo originating from hydrostatic pressure, and the surface tension F_sur (38), i.e.,

$$F_{\mathit{total}}=F_{\mathit{drag}}+F_{\mathit{mass}}+F_{\mathit{buo}}+F_{\mathit{sur}}.$$ [1]

The magnitudes of these components could be approximated using the parameters of legs (speed v, characteristic width w, characteristic area A, characteristic volume V, drag coefficient C_D, and added-mass coefficient α, SI Appendix, Tables S1 and S2), the parameters of water at 25 °C (density ρ = 997 kg/m³, surface tension coefficient σ = 0.072 N/m, and viscosity μ = 1.003e⁻³ kg/sm) as well as the volume of the water displaced by the limbs (V_water) (38, 52, 53):

$$F_{total} = \frac{1}{2}{\mathrm{C}}_D\rho V^{2}A+\alpha \rho V\dot{v}+\rho g{V}_{water}+\sigma \frac{A}{W}\mathit{.}$$ [2]

According to the kinetic data (Fig. 2) and geometric data (SI Appendix, Fig. S1), the Reynolds numbers of limbs ranged from several hundred and a few thousand in jumping and from dozens to several hundred in swimming. Therefore, we have chosen C_D = 1.2 as the drag coefficient, as recommended by Çengel (53). Referring to ref. 52, the added-mass coefficient α was set to 1.0. The Weber numbers of all limbs during jumping exhibited values significantly greater than 1. While swimming, the rear limbs had a substantially higher Weber number than the front and middle limbs, which had values below 1. The Bond number is also smaller than 1 (SI Appendix, Table S3). It, therefore, can be inferred that the limb–water interactions resulted in multiple forces, while the dynamic force is dominant, as confirmed by Fig. 4 and SI Appendix, Fig. S2.

Fig. 4.

The maximum forces and impulses of grasshoppers in jumping and swimming. (A and B) display the maximums of limb forces (see SI Appendix, Fig. S2 for details), while (C and D) display the impulses of each limb by integrating the forces over time. As the contralateral limbs moved almost simultaneously and symmetrically, this figure merely demonstrates the values of the left limbs. Also, we assumed they moved in vertical planes merely so that the lateral force was zero. The coordinate systems indicate the force directions. The lowercase letters demonstrate the statistic difference level: (a) P < 0.001; (b) 0.001 ≤ P < 0.01; (c) 0.01 ≤ P < 0.05; (d) P ≥ 0.05. The axes were broken to present the result more clearly; thus, some bars contain a white part. The error bars indicate the SD.

In water-jumping, a grasshopper’s front limb could obtain maximum forces of ~50 mN in the fore-aft (x) direction, ~100 mN laterally (y-direction), and ~10 mN vertically (z-direction) (Fig. 4A). While the forces generated at the middle limb were comparatively less (Fig. 4A). With a single tibia of the hind limb, the grasshopper could generate a forward force of ~250 mN and an upward force of ~100 mN. The hindlimb’s femur contributed an additional vertical force of around 25 mN (Fig. 4A). In swimming, the magnitudes of forces of the forelimb, the midlimb, and the femur of the hindlimb were smaller than 1 mN, whereas the forces generated at the tibiae of the hind limb were much larger (t ~ 48 mN in the horizontal direction and ~25 mN in the vertical direction), but still lower than those required for leaping locomotion mode (Fig. 4B). As the contralateral limbs move together, the fore-aft and vertical forces at the contralateral limbs will double while the lateral forces cancel. Notably, the limbs of the animals were not as round as assumed (SI Appendix, Fig. S1). For example, the cross-sections of the tibiae of the front and hind limbs become compressed in their distal parts. In the cross-sections, the tibiae of the hind limbs are triangular, especially in the distal part. The alteration in the cross-sectional form will increase drag coefficients (53). The neglected tarsi also contribute to the generated forces. In addition, the surfaces of the limbs exhibit roughness at both the micro and nano sizes due to the presence of surface structures. Several investigations have suggested that surface roughness might influence the magnitude of drag forces (53–55). Therefore, the real propulsions may exceed the estimates provided here.

The impulses were also derived by integrating the forces over time (Fig. 4 C and D). A jumping grasshopper could generate impulses of 0.61 ± 0.16 mN s, 0.75 ± 0.21 mN s, and 0.18 ± 0.05 mN s in x, y, and z direction correspondingly, using a front limb (Fig. 4C). Those of the middle limbs were not larger than 0.2 mN s (Fig. 4C). The femur of the hind limb merely provided impulses in the z-direction for ~0.2 mN s in jumping, whereas the tibiae generated ~3.2 mN s in the x-direction and ~1.3 mN s in the vertical direction (Fig. 4D). The impulses of each limb were much smaller in swimming. The hind limb tibiae were the most effective in generating propulsion, producing ~0.69 mN s in the x-direction and ~0.28 mN s in the z-direction (Fig. 4D). Consequently, jumping grasshoppers generated impulses of ~7.79 mN s and ~3.62 mN s in the horizontal and vertical directions, respectively, whereas swimming grasshoppers generated ~1.40 mN s (fore-aft) and 0.78 mN s (vertical). According to the former measurement (Figs. 1 and 3B), it was found that when the swimming grasshoppers attempted to exit the water surface completely, the maximum drag forces (resulting from water adhesion and body weight) in the vertical direction could exceed two mN s, which were significantly greater than the vertical impulses the swimming grasshoppers themselves could generate. That is why the grasshoppers could not leave the water surface in swimming. For grasshoppers that jumped, the resultant impulse (~7.86 mN s) can be estimated by deducting the resistant impulses (i.e., the integration of water adhesion and body weight over time, ~0.73 mN s) from the propulsive impulse ( $I_p \text{=} \sqrt{I_x^{\text{2}} \text{+} I_z^{\text{2}}} = \text{8.59} \text{mN} \mathrm{\text{s}}$ ). Their momentums were ~8.05 g cm/s according to the kinematics results (Fig. 1). Given that our calculation of limb forces may somewhat underestimate the real forces, this divergence is justifiable. Thus, it can be confirmed that the grasshoppers’ ability to jump is contingent upon the interaction between their legs and the water.

Multiple Forces Facilitate the Aquatic Acrobatics of Robot.

Compared with the surface tension-dominant aquatic locomotion and the hydrodynamic-dominant aquatic locomotion, the aquatic locomotion of the Chinese Rice Grasshoppers is advantageous due to the combined static and dynamic hydro forces. The two obstacles for locomotion on water surfaces are solved independently, facilitating the varied aquatic adaptations of insects. We developed a legged robot (Fig. 5 and SI Appendix, Fig. S3) to experimentally confirm biological findings by taking inspiration from nature. The robot possessing three pairs of legs was fabricated with carbon fiber boards with a water contact angle of ~90°. The legs were driven by springs. Biological observation indicates that the locomotor diversity of grasshoppers is strongly associated with the autonomous control of limb–water contacts, encompassing the sequencing and intensity of these interactions. We designed a mechanical trigger system to activate the release of each pair of legs chronologically. The trigger system was connected to the pneumatic linear actuator (SI Appendix, Fig. S3). As a result, the robot showed a maximum weight of ~22 g and a size of 135 mm × 75 mm × 60 mm (all limbs extended).

Fig. 5.

Aquatic locomotion of a bio-inspired robot. (A) The robot jumps out of the water in an oblique vertical direction; (B) The robot swims forward with two hind limbs working synchronously; (C) The robot swims forward with two hind limbs working sequentially; (D) The robot jumps almost vertically; (E) The traces of the robot’s head in the above motions; (F) The horizontal and vertical speeds of the robot’s head in the above motions. All limbs in A and D moved the water in the rear-down direction. The front and middle limbs swung rearward in B and C. The limbs, springs, and trigger timing in Fig. D were different from the others. (Scale bars in A–D are 20 mm.) The letters (A–D) in E indicate the trace results of corresponding experiments displayed in the Left panel. The letters (A–H, A–V, B–H, B–V, C–H, C–V, D–H, and D–V) in F indicate the speeds of corresponding experiments, with H representing horizontal and V representing vertical.

Initially, all springs were loaded and locked. A linkage mechanism connected the locking mechanisms to the linear actuator. Upon triggering, the forelimbs swiftly rotated rearward, increasing the included angle from 70° to 270°, and rotated downward by approximately 90° relative to the torso. The bilaterally located middle limbs also swung backward and downward by around 60° and 90°, respectively. The femora of the hind legs moved downward relative to the trunk, resulting in the tibiae rotating rearward relative to the femur, increasing the angle between them from 0° to 120°, while the angle between the hind legs remained constant at approximately 30°. By customizing the structure and speed of the trigger, we can adjust the temporal gaps between leg activations and even turn off the activations of limbs. Additionally, modifying the cross-sectional shape of the legs and the driving springs allows for alterations in their hydrodynamic characteristics.

To utilize hydrostatics like the grasshoppers, we connected a light form to the robot to achieve a relatively low equivalent density. The limbs interact with the water dynamically to generate hydrodynamics. We first explored the motion skills of the robot, as shown in Fig. 6 and Movie S3. In the first scenario, the front and middle limbs were successively triggered to create a backward fluttering motion combined with a downward fluttering. After a 2 to 4 ms delay following the activation of the front and middle limbs, both hind limbs were simultaneously activated, fluttering the water along a diagonally downward direction (Fig. 5A and Movie S3). After an acceleration of about 44 ms (Fig. 5 E and F), the robot leaped out of the water along an obliquely upward direction, like the insects do, possessing maximum speeds of ~1.7 m/s in the vertical direction and ~0.8 m/s in the horizontal direction (Fig. 5F, orange lines). Once we blocked the freedom of downward flapping, as shown in Fig. 5B, the robot could not leap out of the water body, though its head slightly rose during the locomotion (Fig. 6 B, E, and F, green lines). If we further let the two hind limbs interact with the water successively rather than synchronously (Fig. 5C), two accelerations were observed (Fig. 5F, cyan lines), resulting in a bit longer horizontal distance within the same periods (Fig. 5E, cyan lines). In all three motions mentioned above, the structures of the robot or the drive springs were the same. These results indicated that although the vertical force generated by the front and middle limbs during motion may be small compared to the hind limbs, splashing the water downward with the anterior limbs is crucial for animals and multilegged robots to leap from the water surface. We also examined the robot leg structure, spring force, and timing of triggering and were surprised to find that, in addition to the aforementioned leaping off the water surface in a diagonally upward direction or swimming forward, the robot was also able to jump vertically with much larger speeds (Fig. 5 D–F). In our experiments, the maximum vertical speed was as large as ~2.8 m/s (Fig. 5F purple lines). More interestingly, the robot can even jump in an upper rear direction by controlling the limb–water interactions (Movie S3). The aquatic locomotion of the bio-inspired robot further demonstrated the effectiveness of utilizing the hybrid hydro forces and decoupling the challenges for aquatic locomotion, as well as the possibility of achieving different modes of aquatic movement by controlling the limb–water interactions.

The robot was around five times the size and twenty times the mass of the insects but displayed similar water movement capabilities. A recently developed robot inspired by water striders (~28 mm) was ten times the original animal prototype in size (280 mm) and also demonstrated impressive leaping capabilities on the water surface (36). These distinctions and similarities between insect prototypes and robot prototypes demonstrated that the model and associated propulsive mechanism in aquatic locomotion are not solely governed by the absolute dimensions and mass of the system. Upon calculating the dimensionless numbers of the robot, we found that, like the jumping grasshoppers, the Weber number of the robot was much more significant than 1. The increase in size and mass also causes an increase in the Bond number, which indicates the ratio of buoyancy to surface tension (SI Appendix, Tables S2 and S3). However, the Bond number is still much smaller than the Weber number, suggesting that the robot also depends on the drag between the limbs and the water to generate propulsion that facilitates their aquatic locomotion. Simultaneously, it can be seen that the augmentation in body dimensions and weight has posed some challenges, such as the need for robots to possess more propulsive force, emphasizing the necessity of including dynamic scale in the development of water robots (36). By prioritizing the necessity of including dynamic scales that can be assessed by the dimensionless numbers (i.e., the Weber number, Reynolds number, Bond number, and so on), engineers are hopeful of surpassing the size and mass limitations proposed by the animal prototypes and create agile aquatic robotics with large sizes and masses the future.

In this work, we constructed a robot utilizing mechanical frames to validate the movement technique seen in Chinese rice grasshoppers. For future investigations, some novel structures and materials [e.g., bistable structures (56), shape memory alloys (36)] can be adopted to enhance the capabilities of our robotic prototype. Besides, some issues, such as fluid resistance, water adhesion, control methods, and limb retractions, were not adequately explored in the current version of the robot. The design of the robot could also improved, resulting in the robot remaining inferior to grasshoppers, leaving us many aspects to improve and will be our next step. For instance, reducing the wettability of the robot will decrease resistance, hence enhancing its performance. However, this prototype demonstrated aquatic mobility, which has never been observed in robots of similar configuration, as well as the benefits of decoupling the challenges for aquatic locomotion by leaning up the hybrid static and dynamic hydro forces, setting the groundwork for future research into robotics aimed at moving over varied mediums.

Bioinspiration.

Prior studies of locomotion involving water have mostly focused on two types: surface tension-dominant locomotion and limb dynamics-dominant locomotion (29, 38). Biomimetic design has evolved chiefly from these two primary areas of emphasis (36). The surface tension–dominant aquatic locomotion depends on superhydrophobic surfaces (29), which is not easy to accomplish for large robotics, while the limb dynamics-dominant aquatic locomotion involves frequent flapping of water by both animals and robots (37), leading to high energy consumption. This work reported the feat of water jumping of the grasshopper O. chinensis, a behavior that has not before been observed. The grasshoppers exhibited rather different mechanisms to facilitate their aquatic acrobatics by supporting their weight with static hydro forces and propelling their bodies with hydrodynamics. By controlling the limb–water interactions, the insects showed diverse aquatic acrobatics. The aquatic locomotion of the bio-inspired robot further demonstrated the effectiveness of utilizing the hybrid hydro forces and decoupling the challenges for aquatic locomotion. In addition to helping us to conclude that the use of multiple forces facilitates the water jump of the grasshopper, this work lays a foundation to develop robots that aim at locomoting across multiple media as well.

Materials and Methods

Observations of Aquatic Locomotion.

Within 2 h after being captured from the fields (Purple Mountain, Nanjing, China), fifteen grasshoppers O. chinensis (mass: 0.4 g to 1.0 g, BL: 2.2 to 3.4 cm) were set to move in a glass tank (300 mm × 200 mm × 200 mm) filled with water with a depth of 150 mm. As the grasshoppers swam on or jumped off a water tank, we filmed them with two orthogonally placed high-speed cameras (BFS-U3-16S2M-CS, 400 fps, FLIR Systems Inc., USA) from the top and the side. The experiments were performed at temperatures of about 25 °C.

The trials in which the insect thorax lost contact with the water were categorized as leaping, while the trials in which the grasshoppers stayed on the water surface were categorized as swimming. After eliminating the trials in which the insects partly left the water surface or rolled their body, we obtained 48 jumping trials from 8 individuals and 54 swimming trials from 8 individuals for analysis.

Behaviors and Kinetics.

Using MATLAB code (57), the time-dependent positions of the trunk and limbs were digitalized during the acceleration stages (the period from the beginning of the movement to the moment when the animals obtained their maximum speed). The other parameters, such as velocities and angular velocities, were subsequently computed from the position data. The results were presented in real-time (T_real) or relative time (T_rela). In particular, all jumping trials were calculated together as the movements of the contralateral limbs showed spatial symmetry and temporal consistency in jumping. As to the swimming trials, they were first categorized into two groups according to the time order of the motions of the left and right hindlimbs. However, if no statistical differences were found between the two groups, the trials were also processed together.

Force Estimation.

To estimate the contribution of the hydrostatic force, we carried out quasistatic measurements with insects. The animal was connected to a force sensor (same as the ones used in ref. 14) using a stiff, thin rod (0.8 mm in diameter) and then immersed in water slowly by vertically raising a water tank toward the animal at a speed of ~1.5 mm/s. Once the grasshopper was wholly immersed in the water, we kept the tank unmoved for ~4 s, and then moved the tank down. The force sensor recorded the interactional force between the grasshopper and the water. The force signals were collected through a DAQ module (NI SCXI 1000) at a sample rate of 500 Hz. Twelve grasshoppers whose mass ranged between 0.1 g to 1.0 g were tested.

Regarding the hydrodynamic force, it is generally impractical to measure in vivo or directly calculated as it is time dependent, geometry dependent, and motion dependent (38). In this paper, we estimated the hydrodynamics using an empirical formula referring to former studies. The geometry of the grasshopper was obtained from the µCT images (SkyScan1275, 40 kV, 50 μA, Bruker, US) of the grasshopper via RadiAnt DICOM Viewer (58). The other parameters were determined from the above experimental observation.

Calculation of Hydrodynamic Force.

To perform the force estimation, we neglected the tarsi containing adhesive pad claws and arolium (SI Appendix, Fig. S1) and made some simplifications. The front and middle limbs were simplified as rods consisting of a thick cylinder (diameter 1.1 mm, length 4.5 mm for the front, and diameter 1.1 mm, length 5 mm for the middle) and a thin cylinder (length 4.5 mm, diameter 0.6 mm for the front, and length 5.5 mm, diameter 0.6 mm for the middle). The femur of the hind limb was simplified as a rod with varying diameters along the length, whereas the tibia was simplified as a long, thin rod (diameter 0.6 mm, length 14.5 mm). The Reynolds numbers of limbs ranged from hundreds to a few thousand in jumping and from dozens to several hundred in swimming, we took 1.2 as the drag coefficient according to ref. 53. The added-mass coefficient was set to be 1.0 following ref. 52.

Bio-Inspired Robot.

Inspired by grasshoppers, we developed a six-legged robot using carbon fiber boards (water contact angle), springs, and a pneumatic linear actuator to conduct preliminary tests on the biological findings (SI Appendix, Fig. S3). The robot comprises four modules: the trunk, front and middle limbs, hind limbs, and trigger module. The trunk contains three carbon fiber sheets (~1 mm thick) connected by four 1.5-mm-diameter shafts (SI Appendix, Fig. S3C). The bottom and middle layers are spaced approximately 8 mm apart, while the middle and top layers are about 3 mm apart. The front and middle limbs share a similar structure (SI Appendix, Fig. S3D), comprising a base and two 120° beams with adjustable cross-sections for hydrodynamic properties. By setting this angle, the tibiae of the front and middle limbs will be aligned to the water surface in the preparation stage. While interacting with water, this angle could increase to 180°. The beams are able to rotate around the base vertically. The bases of these limbs connect to the above shafts, enabling fore-aft rotations. A pair of gears ensures synchronous motion. The hind limbs employ a double-rocker mechanism with rocker bars as the femur and an extending rod as the tibia (SI Appendix, Fig. S3E) attached to the trunk. The trigger module includes a pneumatic linear actuator, push rod, and hooks (SI Appendix, Fig. S3B). The hooks are located between the middle and top layers while the push rod is above the top layer (SI Appendix, Fig. S3A). To simulate the low density and floatation ability of insects, we added an ~8-mm-thick foam board to the robot’s abdomen for effortless flotation on water surfaces.

In the preparation stage, the forelimbs are aligned forward at a 70° angle, the middle limbs are symmetrically distributed at a 180° angle, and the hind leg segments are inclined at a 30° angle. All driving springs are locked by hooks. Triggering the pneumatic linear actuator releases the springs, causing the forelimbs to rotate rearward (increased included angle of 70° to 270°) and downward by ~90° relative to the trunk. The middle limbs swing backward and downward (~60° and ~90°, respectively). The femora of the hind legs move downward, rotating the tibiae rearward (~0° to 120°), while the angle between the hind legs remains constant (~30°). The vertical swinging of the front and middle limbs can be manually restricted to the horizontal plane.

Statistics.

Statistical analysis of the biological observations was performed in SPSS 19.0 (IBM, US). A mixed model with the individuals as random effects was applied to compare the differences between the two behaviors of grasshoppers. To interpret the static forces, we used regression analysis. In this work, the normality was confirmed when the kurtosis and skewness ranged from −1.5 to 1.5. When the normality and homogeneity were violated, the data were transformed to meet normality and homogeneity.

Supplementary Material

Appendix 01 (PDF)

Movie S1.

A Chinese Rice Grasshopper jumped out of the water and then flew away. The video was taken in a wild lake near Zijin Mountain by Gorb. In this preliminary test, the grasshopper was dropped into the water directly from a high place.

Movie S2.

The aquatic acrobatics (jumping and swimming) of the Chinese Rice Grasshopper. The video was taken in the lab using two orthogonally placed high-speed cameras (BFS-U3-16S2M-CS, 400 fps, FLIR Systems Inc., USA) from the top and the side.

Movie S3.

The aquatic locomotion of a six-legged robot inspired by the grasshopper. By adopting the mechanisms of using multiple forces shown by the insects, the robot is able to move on water like the grasshopper.

Data, Materials, and Software Availability

Necessary data have been supplied in the main text and supplementary information. Other supplementary data have been deposited in Figshare (https://doi.org/10.6084/m9.figshare.25256830.v1) (59).