Abstract
Protein–ligand interaction prediction presents a significant challenge in drug design. Numerous machine learning and deep learning (DL) models have been developed to accurately identify docking poses of ligands and active compounds against specific targets. However, current models often suffer from inadequate accuracy or lack practical physical significance in their scoring systems. In this research paper, we introduce IGModel, a novel approach that utilizes the geometric information of protein–ligand complexes as input for predicting the root mean square deviation of docking poses and the binding strength (pKd, the negative value of the logarithm of binding affinity) within the same prediction framework. This ensures that the output scores carry intuitive meaning. We extensively evaluate the performance of IGModel on various docking power test sets, including the CASF-2016 benchmark, PDBbind-CrossDocked-Core and DISCO set, consistently achieving state-of-the-art accuracies. Furthermore, we assess IGModel’s generalizability and robustness by evaluating it on unbiased test sets and sets containing target structures generated by AlphaFold2. The exceptional performance of IGModel on these sets demonstrates its efficacy. Additionally, we visualize the latent space of protein–ligand interactions encoded by IGModel and conduct interpretability analysis, providing valuable insights. This study presents a novel framework for DL-based prediction of protein–ligand interactions, contributing to the advancement of this field. The IGModel is available at GitHub repository https://github.com/zchwang/IGModel.
Keywords: protein–ligand interaction, scoring function, deep learning, graph neural network
INTRODUCTION
Understanding the precise binding poses of ligands within protein receptor structures is of immense significance in drug design [1–4]. Accurately predicting ligand binding poses provides valuable insights into the intricate mechanisms underlying drug–target interactions. This knowledge enables researchers to optimize binding affinity, selectivity and pharmacological properties, ultimately leading to the development of more potent and efficient therapeutic agents [5, 6].
However, experimental methods for determining the binding mode of small molecules within proteins are often inefficient and their accuracy is not always guaranteed [7, 8]. Experimental techniques, such as X-ray diffraction offers atomic insights into protein–ligand interactions but are often time-consuming and resource-intensive. They may also face challenges in obtaining high-resolution structures or capturing the dynamic aspects of the binding process [9, 10]. Furthermore, experimental approaches may be constrained by the availability of suitable protein samples and the complexity of the system under investigation. Therefore, relying solely on experimental techniques for determining ligand binding poses may not meet the demands of high-throughput drug discovery and design [11].
Computational methods, such as molecular docking, play a crucial role in this endeavor by offering efficient and accurate tools to explore the vast chemical space and guide rational drug design efforts [12–15]. Scoring functions (SFs) are developed to guide fast and accurate prediction of protein–ligand complex structures, particularly the ligand binding pattern when the protein structure is already known or determined [16, 17]. SFs calculate the binding energy or score associated with each pose, allowing for the ranking and selection of the most favorable binding configurations [9, 17]. These SFs consider various factors, including molecular shape complementarity, electrostatic interactions, van der Waals forces, hydrogen bonding and solvation effects [11], to estimate the overall binding affinity or likelihood of a ligand pose being biologically relevant. SFs facilitate the exploration of ligand conformational space by identifying potential binding modes and providing insights into the strength and specificity of ligand–receptor interactions [18]. They allow researchers to prioritize ligand poses for further analysis or optimization, thereby aiding in the rational design of drug candidates with enhanced binding affinity and selectivity [9, 19].
In the 1980s, rules were designed based on physical knowledge and expert experience, or by using force field parameters from bio-molecule simulation systems, which formed the early SFs [20]. However, traditional SFs, usually polynomials with few parameters and atom-type definitions, are not accurate enough to describe the conformational space of protein–ligand complexes [21]. Another category of SFs involves machine learning (ML)-based approaches, which have been developed since 2004 [22]. These SFs predict ligand binding affinity by extracting interaction features using various ML techniques [23, 24]. Notable SFs, such as RF-Score [25] (including its virtual screen version, RF-score-VS), NN-Score [26], AGL-Score [27], have achieved excellent performance (‘scoring power’; [28]) in PDBbind-related benchmarks. With the availability of public experimental data and advancements in deep learning (DL) algorithms, there has been a rising trend of utilizing DL models for predicting protein–ligand interactions [29–31]. Since 2017, various DL-based models have emerged for predicting protein–ligand affinity. AtomNet [32], K [33] and Pafnucy [34] have utilized 3D convolutional neural networks (CNNs) to correlate the three-dimensional mesh representation of a complex with its affinity. Additionally, our group has developed two models based on 2D convolution—OnionNet and OnionNet-2—which estimate protein–ligand affinity by tallying the number of contacts between ligand atoms and protein atoms/residues across various distance intervals [35, 36]. Nevertheless, recent studies indicate that ML or DL models trained solely on native structures tend to underperform in tasks related to docking and screening power, despite their robust performance in scoring power [37]. To make the models applicable to practical scenarios, researchers have designed predictors that can directly identify near-native poses of the ligand or screen active compounds. For instance, DeepBSP uses 3D CNN to predict the root mean square deviation (RMSD) of ligand docking poses [38]. DeepRMSD+Vina, previously proposed by our group, adopts modified formats of van der Waals and Coulombic terms used in traditional force fields as features and has been effective in docking power and docking pose optimization [39]. Additionally, DeepDock utilizes a graph neural network to learn the distance probability distribution between protein–ligand atoms rather than directly predicting the protein–ligand binding affinity or ligand pose RMSD. [40]. Building upon the idea of DeepDock, RTMScore introduces a novel graph representation and employs a graph transformer model to learn distance probability distributions, achieving state-of-the-art (SOTA) results across multiple virtual screening test sets and docking pose prediction tasks [41]. However, it has been observed that many DL SFs perform poorly for all evaluation metrics [28]. More researchers now recognize the importance of achieving balanced performance for both docking and screening tasks [42–44]. Among the numerous DL methods mentioned above, some provide affinity prediction or ligand pose prediction, but few can offer directly interpretable indicators with physical meanings, which is more intuitive for computational drug developers [28, 45]. Other methods lack robustness, especially when using predicted structures or cross-docked structures as protein templates. There are few approaches that can accurately predict the optimal ligand binding poses [46, 47].
[33] and Pafnucy [34] have utilized 3D convolutional neural networks (CNNs) to correlate the three-dimensional mesh representation of a complex with its affinity. Additionally, our group has developed two models based on 2D convolution—OnionNet and OnionNet-2—which estimate protein–ligand affinity by tallying the number of contacts between ligand atoms and protein atoms/residues across various distance intervals [35, 36]. Nevertheless, recent studies indicate that ML or DL models trained solely on native structures tend to underperform in tasks related to docking and screening power, despite their robust performance in scoring power [37]. To make the models applicable to practical scenarios, researchers have designed predictors that can directly identify near-native poses of the ligand or screen active compounds. For instance, DeepBSP uses 3D CNN to predict the root mean square deviation (RMSD) of ligand docking poses [38]. DeepRMSD+Vina, previously proposed by our group, adopts modified formats of van der Waals and Coulombic terms used in traditional force fields as features and has been effective in docking power and docking pose optimization [39]. Additionally, DeepDock utilizes a graph neural network to learn the distance probability distribution between protein–ligand atoms rather than directly predicting the protein–ligand binding affinity or ligand pose RMSD. [40]. Building upon the idea of DeepDock, RTMScore introduces a novel graph representation and employs a graph transformer model to learn distance probability distributions, achieving state-of-the-art (SOTA) results across multiple virtual screening test sets and docking pose prediction tasks [41]. However, it has been observed that many DL SFs perform poorly for all evaluation metrics [28]. More researchers now recognize the importance of achieving balanced performance for both docking and screening tasks [42–44]. Among the numerous DL methods mentioned above, some provide affinity prediction or ligand pose prediction, but few can offer directly interpretable indicators with physical meanings, which is more intuitive for computational drug developers [28, 45]. Other methods lack robustness, especially when using predicted structures or cross-docked structures as protein templates. There are few approaches that can accurately predict the optimal ligand binding poses [46, 47].
To address these limitations, we propose an SF based on the geometric graph neural network, IGModel, to enhance the prediction of protein–ligand interactions, especially the docking poses prediction. The input of IGModel consists of two graphs: one represents the protein binding pocket, and the other represents the protein–ligand atomic interactions. Unlike previous graph representations [48, 49], IGModel incorporates the distance and orientation between interacting atoms as geometric features of the complex, providing a more comprehensive description of the relative positions of the ligand within the binding pocket. We employ EdgeGAT layers proposed by Kamiński et al. [50] to encode protein–ligand interactions and derive a latent vector, which is subsequently decoded to yield the RMS) of the pose and the binding strength to the protein via two decoding modules. Hence, IGModel can be segmented into two sub-branches: IGModel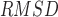 and IGModel
and IGModel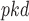 . In the CASF-2016 [28] test for docking power, IGModel
. In the CASF-2016 [28] test for docking power, IGModel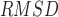 attained the highest Top1 docking success rate (97.5% with native poses included and 95.1% when excluded). Additionally, IGModel has shown commendable performance on cross-docking datasets such as the PDBbind-CrossDocked-Core set [51] and the DISCO [52], comparable to or even surpassing other baseline models. Additionally, IGModel demonstrates excellent performance on unbiased test sets and datasets containing target structures generated by AlphaFold2 [53], proving its outstanding generalizability and practicality for drug discovery. The model captures key charge-charge or hydrogen bond interactions, indicating potential robustness for protein–ligand interaction prediction and suggesting its potential use for lead optimization. Overall, we present a highly accurate ligand pose and binding affinity prediction model with enhanced drug design capability.
attained the highest Top1 docking success rate (97.5% with native poses included and 95.1% when excluded). Additionally, IGModel has shown commendable performance on cross-docking datasets such as the PDBbind-CrossDocked-Core set [51] and the DISCO [52], comparable to or even surpassing other baseline models. Additionally, IGModel demonstrates excellent performance on unbiased test sets and datasets containing target structures generated by AlphaFold2 [53], proving its outstanding generalizability and practicality for drug discovery. The model captures key charge-charge or hydrogen bond interactions, indicating potential robustness for protein–ligand interaction prediction and suggesting its potential use for lead optimization. Overall, we present a highly accurate ligand pose and binding affinity prediction model with enhanced drug design capability.
METHODS
Datasets
In this study, we utilized the native protein–ligand complexes from the PDBbind database (v.2019) [54] and their corresponding docking poses for training. To increase the diversity of ligand binding conformations, an average of 15 docking poses were generated for each native protein–ligand complex using AutoDock Vina [55] and ledock [56]. We excluded protein–ligand pairs from the CASF-2016 test set and those with peptide ligands, as well as any samples that could not be parsed by certain programs, such as rdkit [57]. The actual RMSD of the docking poses was calculated using the spyrmsd package [58]. The binding affinity (pKd) of the native protein–ligand complex is expressed as the negative logarithm of the dissociation constant (K ), the inhibition constant (K
), the inhibition constant (K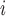 ) or the half-inhibitory concentration (IC50). The relationship between binding free energy and K
) or the half-inhibitory concentration (IC50). The relationship between binding free energy and K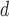 is
is  G = RTlnK
G = RTlnK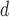 , where R is the gas constant and T is the temperature. At the room temperature, T = 298.15 K,
, where R is the gas constant and T is the temperature. At the room temperature, T = 298.15 K,  G = −1.3633 pKd. The division of the training and validation sets follows the same procedure as in previous work [39], wherein 1000 protein–ligand pairs were randomly selected from the refine set as the validation set, and all remaining samples from the general set were used as the training set. This ensures that there are no overlapping protein–ligand pairs in training, validation and test sets. The parameters used for molecular docking and the distributions of RMSD and pKd for docking poses are shown in Supplementary part 1.
G = −1.3633 pKd. The division of the training and validation sets follows the same procedure as in previous work [39], wherein 1000 protein–ligand pairs were randomly selected from the refine set as the validation set, and all remaining samples from the general set were used as the training set. This ensures that there are no overlapping protein–ligand pairs in training, validation and test sets. The parameters used for molecular docking and the distributions of RMSD and pKd for docking poses are shown in Supplementary part 1.
Graphical representation of protein–ligand complexes
Generally, the binding of a ligand within the pocket is governed by non-covalent interactions, and the potential energy surfaces associated with protein–ligand binding disclose preferred geometries among atoms. Therefore, to accurately describe the relative positions of atoms in the protein–ligand system, which is crucial for characterizing protein–ligand interactions, we construct a heterogeneous graph G . This graph consists of two types of nodes: protein atom nodes (V
. This graph consists of two types of nodes: protein atom nodes (V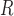 ) and ligand atom nodes (V
) and ligand atom nodes (V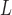 ). To conserve computational resources, only protein atoms within 8 Å of the ligand co-crystal structure are used for interaction modeling. There are four message-passing channels in G
). To conserve computational resources, only protein atoms within 8 Å of the ligand co-crystal structure are used for interaction modeling. There are four message-passing channels in G , namely E
, namely E (V
(V to V
to V ), E
), E (V
(V to V
to V ), E
), E (V
(V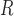 to V
to V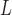 ) and E
) and E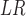 (V
(V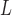 to V
to V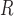 ).
).
Within the ligand subgraph G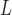 =(V
=(V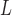 ,E
,E ), we define seven types of ligand atoms: C, N, O, P, S, Hal (representing halogen F, Cl, Br, and I), and DU (representing other element types). If a covalent bond exists between atoms i and j, an edge e
), we define seven types of ligand atoms: C, N, O, P, S, Hal (representing halogen F, Cl, Br, and I), and DU (representing other element types). If a covalent bond exists between atoms i and j, an edge e is defined between nodes v
is defined between nodes v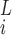 and v
and v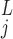 . The rdkit package enables the extraction of physical and chemical information pertaining to chemical bonds, which serves as the edge feature alongside bond length. For the protein subgraph G
. The rdkit package enables the extraction of physical and chemical information pertaining to chemical bonds, which serves as the edge feature alongside bond length. For the protein subgraph G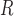 =(V
=(V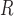 ,E
,E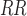 ), we redefine atom types based on the element type, the residue type to which they blong, and their location in either the main chain or the side chain. For example, ‘LYS-MC’ and ‘LYS-SC’ represent the carbon atom on the main chain and side chain of the lysine residue, respectively. The one-hot encoding of atom types, combined with aromaticity, charge, and distance to the
), we redefine atom types based on the element type, the residue type to which they blong, and their location in either the main chain or the side chain. For example, ‘LYS-MC’ and ‘LYS-SC’ represent the carbon atom on the main chain and side chain of the lysine residue, respectively. The one-hot encoding of atom types, combined with aromaticity, charge, and distance to the 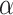 -C atom, are collectively used as node features for G
-C atom, are collectively used as node features for G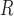 . When the distance between two nodes v
. When the distance between two nodes v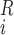 and v
and v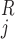 is less than 5 Å, an edge e
is less than 5 Å, an edge e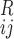 is established, and the edge length serves as the edge feature. If the distance between a protein node v
is established, and the edge length serves as the edge feature. If the distance between a protein node v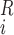 and a ligand node v
and a ligand node v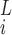 is less than 8 Å, directed edges e
is less than 8 Å, directed edges e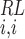 and e
and e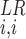 are created, where e
are created, where e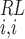 denotes the direction from v
denotes the direction from v to v
to v , and e
, and e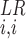 represents the direction from v
represents the direction from v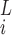 to v
to v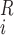 . This multilateral architecture facilitates the integration of node and edge information within the protein–ligand graph. To provide a more comprehensive description of the relative positions between protein–ligand atoms, in addition to considering the interatomic distance, we introduce a novel orientation feature. Specifically, we introduce a dihedral angle
. This multilateral architecture facilitates the integration of node and edge information within the protein–ligand graph. To provide a more comprehensive description of the relative positions between protein–ligand atoms, in addition to considering the interatomic distance, we introduce a novel orientation feature. Specifically, we introduce a dihedral angle 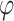 (formed by the geometric center of the pose, v
(formed by the geometric center of the pose, v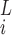 , v
, v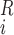 and
and 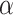 -C), as well as two angles
-C), as well as two angles  and
and 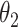 , as shown in Figure 1(B). In Figure 1(B), C
, as shown in Figure 1(B). In Figure 1(B), C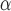 , R, L and P represent the C
, R, L and P represent the C of the residue, a specific atom within the residue, a specific atom within the ligand and the geometric center of the ligand, respectively.
of the residue, a specific atom within the residue, a specific atom within the ligand and the geometric center of the ligand, respectively. 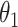 and
and 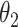 are the angles formed between the C
are the angles formed between the C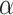 -R edge and the L-R edge, as well as the P-L edge and R-L edge, respectively. Finally,
-R edge and the L-R edge, as well as the P-L edge and R-L edge, respectively. Finally, 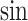 (
(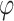 /2),
/2), 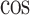 (
(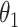 /2),
/2),  (
(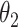 /2) and distance are used as features for the interaction edge. Table S1 summarizes all the node and edge features within this heterogeneous graph.
/2) and distance are used as features for the interaction edge. Table S1 summarizes all the node and edge features within this heterogeneous graph.
Figure 1.
Overview of IGModel. (A) Illustration of predicting RMSD and pKd from the protein–ligand complex structure. (B) The orientation information on the relative positions of protein–ligand atoms. C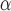 , R, L and P represent the C
, R, L and P represent the C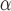 of the residue, a certain atom within the residue, a certain atom within the ligand and the geometric center of the ligand, respectively. The
of the residue, a certain atom within the residue, a certain atom within the ligand and the geometric center of the ligand, respectively. The 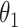 and
and 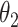 are the angles between C
are the angles between C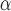 -R and L-R, and between P-L and R-L, respectively. The
-R and L-R, and between P-L and R-L, respectively. The 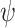 denotes the dihedral angle formed by C
denotes the dihedral angle formed by C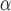 , R, L and P.
, R, L and P.
The physicochemical environment of the binding pocket is critical for ligand binding [59, 60]. However, macroscopic descriptions of binding pockets cannot be adequately represented solely by atomic-level interaction graphs. To overcome this challenge, we construct an undirected graph G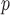 =(V
=(V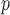 , E
, E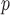 ) to characterize the residue states in the binding pocket. In a manner akin to RTMScore, we define the binding pocket as the residues within 8Å of the co-crystallized ligand. Each node v
) to characterize the residue states in the binding pocket. In a manner akin to RTMScore, we define the binding pocket as the residues within 8Å of the co-crystallized ligand. Each node v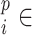 V
V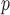 represents a residue within the binding pocket, and an edge e
represents a residue within the binding pocket, and an edge e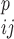 is established when the minimum distance between two residues is less than 10 Å. Node features primarily include the residue type, distance distribution between internal atoms, and the position relative to the pocket’s center. Meanwhile, edge features convey the distances between nodes associated with the main chain atoms. Table S2 provides a comprehensive summary of the detailed node and edge features of the binding pocket graph.
is established when the minimum distance between two residues is less than 10 Å. Node features primarily include the residue type, distance distribution between internal atoms, and the position relative to the pocket’s center. Meanwhile, edge features convey the distances between nodes associated with the main chain atoms. Table S2 provides a comprehensive summary of the detailed node and edge features of the binding pocket graph.
Architecture
IGModel comprises three main components: the interaction feature encoding module, the RMSD decoding module and the pKd decoding module.
The encoding portion of IGModel includes two branches that are tasked with processing the binding pocket graph and the protein–ligand interaction graph, respectively, with each branch featuring two EdgeGAT layers. When the binding pocket graph is input into the encoder, its node features h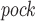 and edge features f
and edge features f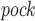 are updated as shown in Equation (1). The updated node features h
are updated as shown in Equation (1). The updated node features h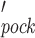 are converted into a vector of length 1024 to represent the binding pocket embedding:
are converted into a vector of length 1024 to represent the binding pocket embedding:
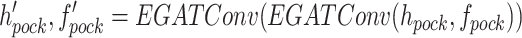 |
(1) |
For the protein–ligand interaction graph, the initial message-passing phase is shown in Equations (2)–(5). Following this phase, the nodes representing the protein and ligand atoms are updated. The revised nodes of the protein and ligand subgraphs, denoted as h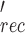 and h
and h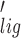 , are as shown in Equations (6)–(7). After undergoing two rounds of updates, the node features for both the protein and the ligand are converted into 1024-dimensional vectors, which acts as embeddings encapsulating details about the protein and ligand atoms. The amalgamation of these two embeddings, along with the binding pocket embedding, constitutes the final latent space that encapsulates the entirety of the protein–ligand interaction:
, are as shown in Equations (6)–(7). After undergoing two rounds of updates, the node features for both the protein and the ligand are converted into 1024-dimensional vectors, which acts as embeddings encapsulating details about the protein and ligand atoms. The amalgamation of these two embeddings, along with the binding pocket embedding, constitutes the final latent space that encapsulates the entirety of the protein–ligand interaction:
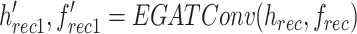 |
(2) |
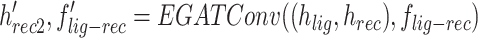 |
(3) |
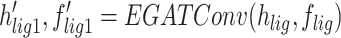 |
(4) |
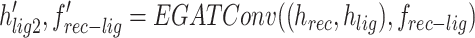 |
(5) |
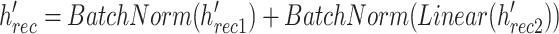 |
(6) |
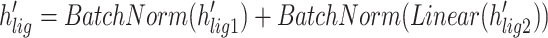 |
(7) |
Each learning module in the decoding part consists of a gMLP [61] layer and two linear layers. After passing through the two learning modules, the latent space is converted into two 128-dimensional vectors, V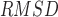 and V
and V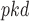 . To ensure that the predicted pKd considers the change in RMSD of the ligand pose, we map V
. To ensure that the predicted pKd considers the change in RMSD of the ligand pose, we map V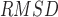 to a new vector V
to a new vector V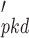 in the space of V
in the space of V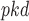 through a linear layer. This new vector is integrated with V
through a linear layer. This new vector is integrated with V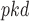 for decoding the pKd.
for decoding the pKd.
The training dataset encompasses both experimentally verified structures and virtual conformations produced through molecular docking. However, binding affinity data is solely available for native complexes. It is postulated that the binding strength of a given pose to its target is inversely proportional to its RMSD from the native conformation, with the native protein–ligand conformation processing the highest binding affinity. This study aims to decode the relationship between the RMSD of docking poses and their binding strength using DL. Additionally, the model is designed to predict a decay factor 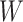 (illustrated in Figure 1A and defined in Equation 8) that ranges from of 0 to 1 within the pKd decoding segment, to portray the diminishing pKd value as the RMSD increases. Using
(illustrated in Figure 1A and defined in Equation 8) that ranges from of 0 to 1 within the pKd decoding segment, to portray the diminishing pKd value as the RMSD increases. Using  and the previous assumptions, the binding strength (pKd
and the previous assumptions, the binding strength (pKd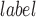 ) of the docking pose to the receptor can be deduced, which serves as the label for pKd (Equation 9):
) of the docking pose to the receptor can be deduced, which serves as the label for pKd (Equation 9):
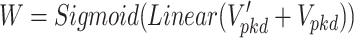 |
(8) |
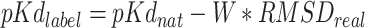 |
(9) |
In Equation (8), pKd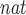 represents the binding affinity between the native conformation of the ligand and the receptor, and RMSD
represents the binding affinity between the native conformation of the ligand and the receptor, and RMSD is the real RMSD of the docking pose. When RMSD
is the real RMSD of the docking pose. When RMSD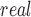 is close to 0, pKd
is close to 0, pKd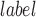 will be close to pKd
will be close to pKd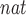 .
.
The loss function during training is defined as follows:
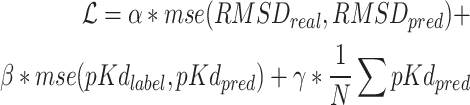 |
(10) |
where weights 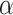 ,
, 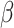 , and
, and 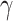 are used to sum up the components within the loss function, which are set as 1, 0.5 and 0.05 in this study. N is the number of samples in a mini-batch. According to our assumption, the binding strength between the ligand and the target exhibits a negative correlation with the RMSD of the ligand binding pose. The last term in the loss function is designed to ensure that IGModel fits pKd in a ‘descending’ direction, facilitating a negative correlation between the predicted pKd and the RMSD.
are used to sum up the components within the loss function, which are set as 1, 0.5 and 0.05 in this study. N is the number of samples in a mini-batch. According to our assumption, the binding strength between the ligand and the target exhibits a negative correlation with the RMSD of the ligand binding pose. The last term in the loss function is designed to ensure that IGModel fits pKd in a ‘descending’ direction, facilitating a negative correlation between the predicted pKd and the RMSD.
RESULTS
Evaluation on CASF-2016 benchmark
The performance of the SF is evaluated across four dimensions: scoring power, ranking power, docking power, and screening power, as defined by the CASF-2016 benchmark [28]. Previous research indicates that SFs with robust docking or screening power often exhibit weaker scoring and ranking power, such as DeepRMSD+Vina [39] and RTMScore [41]. Our model aims to achieve balanced performance across various tasks. Despite primarily focusing on identifying near-native conformations of the ligand (docking power), what is surprising is that IGModel also demonstrates a relatively balanced performance in other tasks (Figure 2 and Tables S3–S4). Firstly, for docking power, the top 1 success rate of IGModel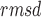 with native poses included in the test set is 97.5%, and the value remains as high as 95.1% when the native poses are excluded. At the same time, IGModel
with native poses included in the test set is 97.5%, and the value remains as high as 95.1% when the native poses are excluded. At the same time, IGModel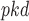 also achieves higher top 1 success rates compared to most models, which are 93.3 and 90.9
also achieves higher top 1 success rates compared to most models, which are 93.3 and 90.9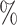 when crystal structures are included and excluded in the test set, respectively. The ablation experiments of IGModel on the validation set and the CASF-2016 docking power are detailed in Supplementary part 4. We also conducted a ‘binding funnel analysis’ by calculating the Spearman’s correlation coefficient (SCC) between the RMSD or pKd predicted by the IGModel and the actual RMSD for the decoy set of each protein–ligand pair, and then calculating the average SCC across different RMSD intervals. The result indicates that IGModel maintains a clear advantage across various RMSD ranges (Figure S2). However, the cocrystallized ligand may be unknown in actual virtual screening, thus we retrain the the IGModel (called IGModel
when crystal structures are included and excluded in the test set, respectively. The ablation experiments of IGModel on the validation set and the CASF-2016 docking power are detailed in Supplementary part 4. We also conducted a ‘binding funnel analysis’ by calculating the Spearman’s correlation coefficient (SCC) between the RMSD or pKd predicted by the IGModel and the actual RMSD for the decoy set of each protein–ligand pair, and then calculating the average SCC across different RMSD intervals. The result indicates that IGModel maintains a clear advantage across various RMSD ranges (Figure S2). However, the cocrystallized ligand may be unknown in actual virtual screening, thus we retrain the the IGModel (called IGModel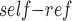 ) using the docking poses themselves as the reference to determine the binding pocket of the target. In this scenario, the performance of IGModel
) using the docking poses themselves as the reference to determine the binding pocket of the target. In this scenario, the performance of IGModel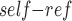 in the CASF-2016 docking power test significantly declined compared to the baseline version of IGModel (Table S3). Recently, AI-based protein–ligand blind docking algorithms have been significatly developed, such as DiffDock, a generative model based on the diffusion model [62]. We attempted to regenerate the binding poses of protein–ligand complex from the CASF-2016 test set using DiffDock. Subsequently, these binding poses were scored by IGModel, GatedCGN
in the CASF-2016 docking power test significantly declined compared to the baseline version of IGModel (Table S3). Recently, AI-based protein–ligand blind docking algorithms have been significatly developed, such as DiffDock, a generative model based on the diffusion model [62]. We attempted to regenerate the binding poses of protein–ligand complex from the CASF-2016 test set using DiffDock. Subsequently, these binding poses were scored by IGModel, GatedCGN ft
ft 1.0, GT
1.0, GT ft
ft 1.0 and Vina. By analyzing the PCC and SCC values obtained from these SFs, we further demonstrated the versatility of IGModel (see detail in Supplementary part 5).
1.0 and Vina. By analyzing the PCC and SCC values obtained from these SFs, we further demonstrated the versatility of IGModel (see detail in Supplementary part 5).
Figure 2.
Comparison of scoring, ranking, and docking power using the CASF-2016 benchmark against other SFs. (A) Scoring power measures the correlation between the scores of the model and experimental affinity, using the PCC as the metric. (B) Ranking power evaluates the ability of a SF to rank the known ligands for a certain target, with the Spearman’s correlation coefficient serving as the metric. (C) and (D) display the top 1 success rate when the crystal structures are included and excluded from the test set, respectively.
Additionally, screening power refers to the ability of the SFs to identify the true binders to a specific receptor among a large library of compounds. This is measured by two indicators: the first is the success rate of identifying the highest-affinity binder among the top 1, 5 or 10 of ranked ligands across all 57 target proteins in the test set; the second is the enrichment factor (EF), which is calculated by the average percentage of true binders among the top 1, 5 or 10
of ranked ligands across all 57 target proteins in the test set; the second is the enrichment factor (EF), which is calculated by the average percentage of true binders among the top 1, 5 or 10 of ranked candidates across all 57 targets. IGModel achieves a top 1% success rate of 66.7%, which is comparable to RTMScore [41], but slightly lower than GT
of ranked candidates across all 57 targets. IGModel achieves a top 1% success rate of 66.7%, which is comparable to RTMScore [41], but slightly lower than GT ft
ft 1.0 [43]. However, the EF achieved by IGModel
1.0 [43]. However, the EF achieved by IGModel is only 19.4, which is significantly lower than that of RTMScore and GT
is only 19.4, which is significantly lower than that of RTMScore and GT ft
ft 1.0, but still higher than most predictors, such as DeepDock [40]. In general, IGModel exhibits a relatively balanced performance across various metrics based on the CASF-2016 benchmark. Interestingly, for scoring power, IGModel
1.0, but still higher than most predictors, such as DeepDock [40]. In general, IGModel exhibits a relatively balanced performance across various metrics based on the CASF-2016 benchmark. Interestingly, for scoring power, IGModel achieved a Person correlation coefficient (PCC) of 0.831, very close to the 0.834 and 0.824 achieved by GatedCGN
achieved a Person correlation coefficient (PCC) of 0.831, very close to the 0.834 and 0.824 achieved by GatedCGN ft
ft 1.0 [43] and PLANET [42], respectively. The scatter plots of IGModel
1.0 [43] and PLANET [42], respectively. The scatter plots of IGModel on the validation set and CASF-2016 core set are shown in Figure S3. Finally, for the ranking power test, IGModel
on the validation set and CASF-2016 core set are shown in Figure S3. Finally, for the ranking power test, IGModel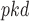 achieved a SCC of 0.723, higher than the 0.686 achieved by GatedCGN
achieved a SCC of 0.723, higher than the 0.686 achieved by GatedCGN ft
ft 1.0 (Table S4). To further assess the screening power of IGModel, the DUD-E and DUD-AD sets were utilizes as additional test sets. On the DUD-E set, RTMScore, GatedCGN
1.0 (Table S4). To further assess the screening power of IGModel, the DUD-E and DUD-AD sets were utilizes as additional test sets. On the DUD-E set, RTMScore, GatedCGN ft
ft 1.0 and GT
1.0 and GT ft
ft 1.0 demonstrate a significant advantage over IGModel, both in terms of EF and AUROC. On the unbiased DUD-AD set, RTMScore, GatedCGN
1.0 demonstrate a significant advantage over IGModel, both in terms of EF and AUROC. On the unbiased DUD-AD set, RTMScore, GatedCGN ft
ft 1.0 and GT
1.0 and GT ft
ft 1.0 still exhibited optimal EF, despite their AUROC being slight lower than that of IGModel. This indicates that there is still a gap between IGModel and SOTA SFs in screening tasks. The detailed results are presented in Figure 3 and Supplementary Part 6.
1.0 still exhibited optimal EF, despite their AUROC being slight lower than that of IGModel. This indicates that there is still a gap between IGModel and SOTA SFs in screening tasks. The detailed results are presented in Figure 3 and Supplementary Part 6.
Figure 3.
The performance of SFs on the DUD-E and DUD-AD sets. (A) and (C) show the EF (0.5, 1.05 and 5.0%) achieved by the SFs on the DUD-AD and DUD-E datasets, respectively. (B) and (D) present the AUROC of SFs on the DUD-AD and DUD-E datasets, respectively. The white circles in the boxplot denotes the mean value within each group of data. The boxplot for RTMScore and GenScore on DUD-E set can be found on the original papers.
Evaluation on the redocking and cross-docking test sets
Currently, in most molecular docking applications, the protein is treated as a rigid molecule, which deviates from the actual protein–ligand binding behavior observed in reality. This is because the binding pocket can accommodate different compounds with flexible side chains and, sometimes, even with adjustable backbones [63]. Redocking and cross-docking are two methods for evaluating molecular docking. Redocking involves reintroducing a ligand into its cognate receptor, while cross-docking pertains to docking a ligand into a non-cognate receptor within the original pocket [52]. To comprehensively assess the docking power of IGModel, various redocking and cross-docking benchmarks have been adopted.
The first test set we assessed is PDBbind-CrossDocked-Core [51], with all receptors and ligands derived from the PDBbind v2016 core set. Each ligand was extracted from 285 protein–ligand crystal structures, and then was redocked into the original protein or four other proteins belonging to the same target cluster using three docking software: Surflex-Dock, Glide SP and AutoDock Vina. IGModel was tested in these three groups of poses and compared with other SFs. The results are shown in Figure 4. For cross-docking, the top 1 success rates on poses generated by IGModel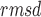 with Surflex, Glide and Vina are 0.662, 0.595 and 0.594, respectively, slightly better than GT
with Surflex, Glide and Vina are 0.662, 0.595 and 0.594, respectively, slightly better than GT ft
ft 1.0 and GatedGCN
1.0 and GatedGCN ft
ft 1.0, but outperformed most predictors. Meanwhile, IGModel
1.0, but outperformed most predictors. Meanwhile, IGModel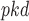 still performed well, comparable to GatedGCN
still performed well, comparable to GatedGCN ft
ft 1.0, although it is slightly worse than the IGModel
1.0, although it is slightly worse than the IGModel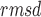 . For redocking tasks, the top 1 success rates of IGModel
. For redocking tasks, the top 1 success rates of IGModel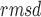 and IGModel
and IGModel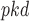 on poses generated by Surflex, Glide and Vina are 0.854 and 0.850, 0.786 and 0.779, as well as 0.761 and 0.754, respectively, demonstrating a significant advantage over other SFs. However, it must be acknowledged that only few proteins have known native binding ligands and predicting protein pockets through computational methods remains a challenge, and this will restrict the applicability of SFs such as RTMScore, GenScore and IGModel, which define pockets based on the co-crystal ligand. Therefore, grabbing pockets through docking pose itself is suitable for all application scenarios. The overall performance of
on poses generated by Surflex, Glide and Vina are 0.854 and 0.850, 0.786 and 0.779, as well as 0.761 and 0.754, respectively, demonstrating a significant advantage over other SFs. However, it must be acknowledged that only few proteins have known native binding ligands and predicting protein pockets through computational methods remains a challenge, and this will restrict the applicability of SFs such as RTMScore, GenScore and IGModel, which define pockets based on the co-crystal ligand. Therefore, grabbing pockets through docking pose itself is suitable for all application scenarios. The overall performance of 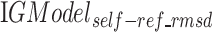 on the three cross-docking test sets is slightly superior to that of IGModel, although its performance on the redocking test sets is slightly worse than that of IGModel. This substantiates the practical application value of
on the three cross-docking test sets is slightly superior to that of IGModel, although its performance on the redocking test sets is slightly worse than that of IGModel. This substantiates the practical application value of  in real molecular docking scenarios.
in real molecular docking scenarios.
Figure 4.
Docking power of IGModel and other SFs on PDBbind-CrossDocked-Core set. (A), (B) and (C) show the top 1 success rate of SFs on poses generated by Surflex, GLide and AutoDock Vina, respectively. The results of SFs other than IGModel are cited from the reference.
Another cross-docking test set used in this study is DISCO, which contains 4399 crystal protein–ligand complexes across 95 protein targets [52]. The targets were derived from the DUD-E database [64], thereby encompassing a broad spectrum of protein families. Ligand poses were generated using AutoDock Vina [55], producing 20 poses per protein–ligand pair by default. For consistency with our prior research, we treated each target-ligand pair as an individual case when calculating the top 1 success rate, a method that differs from the integrated when tested on PDBbind-CrossDocked-Core set. The performance of IGModel in comparison to several baseline SFs on the DISCO set is depicted in Figure 5. It is evident that IGModel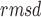 outperforms other baseline SFs, while IGModel
outperforms other baseline SFs, while IGModel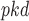 shows comparable results to GatedGCN
shows comparable results to GatedGCN ft
ft 1.0. The outstanding performance of IGModel in both redocking and cross-docking tasks underscores its significant practical value for applications.
1.0. The outstanding performance of IGModel in both redocking and cross-docking tasks underscores its significant practical value for applications.
Figure 5.

The top N success rate of IGModel and other baseline models on DISCO set.
Generalization assessment of IGModel
Recent studies have shown that the performance of DL models is susceptible to biases within the data set, such as protein sequence similarity [65]. In this paper, we assessed the generalizability of the IGModel from two additional perspectives. Firstly, most SFs do not rigorously eliminate redundancy in the training set, which may result in better performance on the test set than in actual scenarios. To address this, we introduced an unbiased test set (the unbias-v2019 set in this work) that we previously proposed. This set contains protein–ligand pairs with low similarity to those in the PDBbind database v2019, and the native conformation of the ligands was excluded [46]. The similarity is determined by the product of protein sequence similarity (calculated by NW-align, http://zhanglab.dcmb.med.umich.edu/NW-align) and the Tanimoto similarity of the ligand Morgan fingerprints calculated by rdkit [57]. Secondly, predicting the binding pose of a ligand becomes even more challenging when the native conformation of the target is unknown. Computational methods such as AlphaFold2 [53] provide solutions for rapidly obtaining high-precision protein structures. Based on these predicted protein structures, molecular docking was applied to generate poses of the ligands. In our previous study, CASF-2016 and the unbias-v2019 sets were used to construct the test sets for the AlphaFold2 version, namely CASF-2016-AF2 and unbias-2019-AF2, respectively [46].
We evaluated the docking performance of SFs on the three mentioned datasets. Table 1 presents the Pearson correlation coefficient (PCC) and Spearman correlation coefficient (SCC) between the scores of SFs and the true RMSD. It is evident that IGModel demonstrates significantly higher accuracy compared to other baseline SFs. Particularly, on the unbias-v2019-AF2 set, IGModel maintains robust performance. The top 1 success rate achieved by SFs with 2 and 3 Å as cutoffs is shown in Table 2, and, notably, IGModel outperforms other SFs by a significant margin. This effectively confirms the generalization ability and robustness of IGModel in different scenarios. However, for CASF2016-AF2 and unbias-v2019-AF2, two datasets based on structures predicted by AlphaFold2, the overall top 1 success rate is lower due to the larger RMSDs of the poses generated by molecular docking relative to the native poses.
Table 1.
Pearson correlation coefficient (PCC) and Spearman correlation coefficient (SCC) of IGModel and other SFs tested on the CASF2016-AF2, unbias-v2019 and unbias-v2019-AF2 datasets
| CASF2016-AF2 | unbias-v2019 | unbias-v2019-AF2 | ||||
|---|---|---|---|---|---|---|
| SFs | PCC | SCC | PCC | SCC | PCC | SCC |
| Vinaa | 0.035 | 0.071 | 0.364 | 0.356 | 0.209 | 0.192 |
| DeepBSPa | 0.401 | 0.375 | 0.543 | 0.507 | 0.451 | 0.418 |
| DeepRMSDa | 0.463 | 0.430 | 0.285 | 0.246 | 0.261 | 0.247 |
| DeepRMSD+Vinaa | 0.248 | 0.290 | 0.405 | 0.362 | 0.299 | 0.287 |
GT ft ft 1.0 1.0 |
0.503 | 0.455 | ||||
GatedGCN ft ft 1.0 1.0 |
0.560 | 0.524 | ||||
| zPoseScorea | 0.659 | 0.593 | 0.604 | 0.535 | 0.554 | 0.507 |
IGModel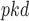
|
0.736 | 0.649 | 0.611 | 0.522 | 0.580 | 0.519 |
IGModel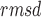
|
0.751 | 0.669 | 0.633 | 0.542 | 0.609 | 0.552 |
aThe results are cited from reference [46].
Table 2.
Top1 success rate of IGModel and other SFs tested on the CASF2016-AF2, unbias-v2019 and unbias-v2019-AF2 datasets
| CASF2016-AF2 | unbias-v2019 | unbias-v2019-AF2 | ||||
|---|---|---|---|---|---|---|
| SFs | 2Å | 3Å | 2Å | 3Å | 2Å | 3Å |
| Vinaa | 0.127 | 0.208 | 0.453 | 0.526 | 0.130 | 0.219 |
| DeepBSPa | 0.180 | 0.324 | 0.453 | 0.584 | 0.169 | 0.254 |
| DeepRMSDa | 0.269 | 0.425 | 0.210 | 0.324 | 0.089 | 0.185 |
| DeepRMSD+Vinaa | 0.261 | 0.416 | 0.441 | 0.534 | 0.144 | 0.253 |
GT ft ft 1.0 1.0 |
0.273 | 0.448 | ||||
GatedGCN ft ft 1.0 1.0 |
0.292 | 0.465 | ||||
| zPoseScorea | 0.339 | 0.506 | 0.599 | 0.700 | 0.185 | 0.274 |
IGModel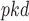
|
0.338 | 0.558 | 0.562 | 0.690 | 0.227 | 0.318 |
IGModel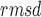
|
0.364 | 0.571 | 0.587 | 0.690 | 0.227 | 0.296 |
aThe results are cited from reference [46].
DISCUSSION
Different SFs have been developed using various training data for pKd or RMSD predictions, and a single score (either a traditional SF or an ML/DL-based SF) may effectively address the quality of docking poses for pose selection [44] and virtual screening [28]. RMSD reflects the difference between the docking pose and the native conformation, providing insight into ‘how it binds’. However, it does not represent the binding strength with the target protein. On the other hand, pKd represents the binding strength between the molecule and the target, addressing the ”how strong it binds’ problem, but it does not reflect the difference between the docking pose and the native pose [66].
Early ML- or DL-based SFs often directly predict protein–ligand binding affinity (pKd) using native protein–ligand complex structures [25, 34–36]. However, testing has shown that the scores of such models are challenging to distinguish correct binding poses generated by docking tools [28], and their accuracies in screening tasks are not satisfactory [37]. Subsequently, researchers began to directly predict the RMSD of docking poses (such as Gnina [67], DeepRMSD [39] and DeepBSP [38]), or use scores from other mathematical spaces (such as DeepDock [40], RTMScore [41] and GenScore [43]) trained with docking poses. The distance likelihood potential generated by DeepDock, RTMScore and Genscore, it is difficult to intuitively describe RMSD and the binding strength and could not provide an explicit and physical meaningful prediction for computational chemists. However, RMSD-corrected pKd is also used as a training target to construct ML models, which provides a direct estimate for both the pose binding pattern and the molecule’s binding strength with a single score [45, 68]. Some representative SFs are listed in Table S8.
In our work, we aim to address both questions of RMSD prediction for ‘how it binds’ and pKd prediction for ‘how strong it binds’ within an integrated framework. We achieve this by characterizing the protein–ligand interaction using two geometric graph modules: the pocket graph module and the protein–ligand atomic graph module. We then apply EdgeGAT layers [50] to encode the interaction features. Tests under different scenarios have demonstrated that IGModel performs well in predicting the RMSD of docking poses for redocking, cross-docking, and AF2-based docking tasks, indicating its excellent generalization ability and robustness for pose selection.
To visualize the protein–ligand interaction potential energy surface encoded by the graph neural network, we visualize the ligand embedding output by the last EdgeGAT layer in the protein–ligand graph branch, as well as the overall complex embedding. We have employed principal component analysis (PCA) to cluster the latent space and ligand embeddings of samples from the validation set, subsequently coloring them according to actual RMSD, predicted RMSD, pKd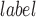 and predicted pKd. The resulting distributions of RMSD and pKd within the latent space are presented in Figure 6(A–D). These plots reveal that as RMSD and pKd vary, distinct stratification patterns become apparent. Analogous patterns are discernible in the ligand embedding plots (Figure 6E–H). A noteworthy observation is the broader coverage area in the latent space images compared to those of ligand embedding, suggesting a superior capacity of the latent space to differentiate between various clusters. This enhanced differentiation can likely be ascribed to the incorporation of protein pocket information into the latent space, thereby refining the depiction of protein–ligand interactions.
and predicted pKd. The resulting distributions of RMSD and pKd within the latent space are presented in Figure 6(A–D). These plots reveal that as RMSD and pKd vary, distinct stratification patterns become apparent. Analogous patterns are discernible in the ligand embedding plots (Figure 6E–H). A noteworthy observation is the broader coverage area in the latent space images compared to those of ligand embedding, suggesting a superior capacity of the latent space to differentiate between various clusters. This enhanced differentiation can likely be ascribed to the incorporation of protein pocket information into the latent space, thereby refining the depiction of protein–ligand interactions.
Figure 6.
Visualization of the complex embedding, ligand embedding and the decay factor W. (A)–(D) (E–H) show the visualization of the complex embedding (ligand embedding) of samples in the validation set after PCA clustering, colored according to real RMSD, predicted RMSD, pKd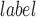 and predicted pKd, respectively. (I)–(K) present visualization of the decay weight of binding strength with respect to RMSD variations, organized according to pKd
and predicted pKd, respectively. (I)–(K) present visualization of the decay weight of binding strength with respect to RMSD variations, organized according to pKd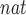 -real RMSD, pKd
-real RMSD, pKd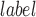 -real RMSD and predicted pKd-Predicted RMSD, respectively, where pKd
-real RMSD and predicted pKd-Predicted RMSD, respectively, where pKd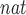 refers to the binding affinity of the native protein–ligand complex.
refers to the binding affinity of the native protein–ligand complex.
IGModel, as the first DL model capable of simultaneously predicting the RMSD of ligand docking poses relative to the native conformation and the binding strength to the target, is based on the assumption of a negative correlation between binding strength and RMSDs of docking poses. The relationship between the decay weight of binding strength and the RMSDs of docking poses remains uncertain. Past research has involved empirically setting functions to model the change in binding strength with RMSD [45, 68], but such manual interventions may introduce biases. We aim for the model to deduce appropriate decay weights autonomously for various protein–ligand complexes, as depicted in Figure 1. The decay weights are represented with respect to pKd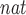 -real RMSD (Figure 6I), pKd
-real RMSD (Figure 6I), pKd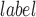 -real RMSD (Figure 6J) and predicted pKd-predicted RMSD (Figure 6K). A notable trend is that the decay weight W tends to increase with the rise in RMSD, confirming our initial hypothesis that poses closer to the native structure exhibit stronger binding.
-real RMSD (Figure 6J) and predicted pKd-predicted RMSD (Figure 6K). A notable trend is that the decay weight W tends to increase with the rise in RMSD, confirming our initial hypothesis that poses closer to the native structure exhibit stronger binding.
Moreover, we investigate the model’s proficiency in learning the physical aspects of protein–ligand interactions. It is widely accepted that protein–ligand binding predominantly involves non-bonded interactions [69], solvation [70] and entropic effects [71]. Specifically, short-range non-bonded interactions like hydrophobic contacts, cation- , salt bridges, hydrogen bonds and
, salt bridges, hydrogen bonds and 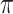 -
-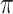 stacking are known to contribute favorably to the binding free energies of the complexes [69, 72, 73]. However, most current ML/DL-based SFs fail to explicitly or implicitly emphasize or highlight the direct non-bonded interactions between the protein and the ligand.
stacking are known to contribute favorably to the binding free energies of the complexes [69, 72, 73]. However, most current ML/DL-based SFs fail to explicitly or implicitly emphasize or highlight the direct non-bonded interactions between the protein and the ligand.
Considering atoms in different residue side chains and even those within the same residue display diverse physicochemical characteristics, it is crucial to account for various features such as residue type, element type, as well as polarity and aromaticity. This approach provides meaningful descriptors for protein atoms, enabling IGModel to identify essential non-bonded interactions like hydrogen bonds, as illustrated in Figure 7. We analyzed the attention values assigned by IGModel to each protein–ligand atom pair in the protein–ligand complexes from the CASF-2016 dataset to determine if the model effectively highlights the physical interactions. A protein atom’s importance is determined by the aggregated attention values from the interaction edges with the ligand atoms. We compiled the importance scores for all types of protein atoms and presented the top 20 in Figure 7. It is evident that among the most critical protein atoms, polar atoms are predominant, underscoring their vital role of polar interactions in protein–ligand binding [72] for binding strength and binding specificity. Moreover, certain non-polar atoms, such as ILE-CD1 and PHE-CZ, are also identified as significant contributors. This significance arises as alpha carbon atoms and aromatic rings are commonly involved in hydrophobic interactions, among the most prevalent in protein–ligand binding. Figure 7(B) illustrates that protein atoms engaged in hydrogen bonding receive higher importance scores, indicating that IGModel effectively recognizes hydrogen bonds and allocates increased attention to them. In Figure 7(C), the importance value is notably high for the edges of the benzene ring in phenylalanine when proximal to the ligand’s benzene ring, suggesting that IGModel can aptly detect 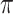 -
-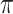 stacking interactions.
stacking interactions.
Figure 7.
Explainability and case study. (A) Ranking of importance of protein atoms at the binding pocket (only the top 20 protein atom types are shown). (B) and (C) show two cases (1QF1 and 2QE4) where IGModel identifies key interactions, including hydrogen bonding and  -
- stacking. In the two pictures located on the right, the distances between key atoms are shown (black), and the names and importance values of key atoms in the protein are colored in blue.
stacking. In the two pictures located on the right, the distances between key atoms are shown (black), and the names and importance values of key atoms in the protein are colored in blue.
CONCLUSION
In this study, we introduce IGModel, a novel scoring framework for predicting protein–ligand interactions, capable of concurrently predicting RMSD of ligand binding poses and binding strength to the target. The model employs the EdgeGAT layers to encode input graphs into a latent space that characterizes protein–ligand interactions, subsequently decoding this space into RMSD and pKd values using two separate decoders. IGModel has demonstrated SOTA performance across various docking power test sets. While designed to provide a holistic assessment of docking poses, IGModel also excels in scoring power and ranking power tests on the CASF-2016 benchmark, matching or surpassing other models. Additionally, it outperforms most baseline SFs in screening power. The robustness of IGModel is further validated on the challenging unbias-v2019 set and datasets containing targets predicted by AlphaFold2, showcasing its strong generalizability. Visualization of the latent space encoded by IGModel offers an intuitive depiction of the energy landscape that describes the RMSD and binding strength of docking poses. Case studies reveal IGModel’s adeptness in identifying key interactions like hydrogen bonding and  -
- stacking.
stacking.
It is acknowledged that no single SF can excel in all tasks, yet IGModel manages to achieve relatively balanced performance. Significantly, IGModel pioneers a novel approach in predicting protein–ligand interactions, moving beyond the traditional single-score output of SFs, to ensure outputs with clear physical interpretation. We posit that this framework holds substantial promise for molecular docking applications and the refinement and optimization of lead compounds in drug design. In conclusion, our research presents a new direction for the future design of SFs and opens up fresh challenges in the field.
Key Points
We introduce the first framework for simultaneously predicting the RMSD of the ligand docking pose and its binding strength to the target.
IGModel can effectively improve the accuracy of identifying the near-native binding poses of the ligands, and can still outperform most baseline models in scoring power, ranking power and screening power tasks.
IGModel is still ahead of other state-of-the-art models in the unbiased data set and the target structure predicted by AlphaFold2, proving its excellent generalization ability.
Latent space provided by IGModel learns the physical interactions, thus indicating the robustness of the model.
Supplementary Material
Author Biographies
Zechen Wang is a PhD candidate student at the School of Physics, Shandong University, China. He is working on protein-ligand interaction prediction and drug design.
Sheng Wang is the CEO (Chief Executive Officer) of Shanghai Zelixir Biotech Company Ltd. His research area is protein structure prediction and AI-based synthetic biology.
Yangyang Li is currently a professor at the School of Physics, Shandong University. His research interests focus on the investigation of novel physical (quantum) properties and functionalities of transition-metal-oxides with strongly correlated electrons.
Jingjing Guo is a professor at the Centre in Artificial Intelligence Driven Drug Discovery, Faculty of Applied Science, Macao Polytechnic University. Her research interests are computational biology and AI-drug discovery.
Yanjie Wei is the executive director of Center for High Performance Computing at Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences. His research area is bioinformatics and high performance computing.
Yuguang Mu is an associate professor at the School of Biological Sciences, Nanyang Technological University, Singapore. He is working on protein dynamics, molecular docking and drug discovery.
Liangzhen Zhen is a senior research scientist at Shanghai Zelixir Biotech Company Ltd. He is also an Associate Investigator at Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences. He is working on protein modeling and protein-ligand interaction modeling.
Weifeng Li is a full professor at the School of Physics, Shandong University. He is interested in multi-scale simulations of biological systems and drug development.
Contributor Information
Zechen Wang, School of Physics, Shandong University, South Shanda Road, 250100 Shandong, China.
Sheng Wang, Shanghai Zelixir Biotech, Xiangke Road, 200030, Shanghai, China.
Yangyang Li, School of Physics, Shandong University, South Shanda Road, 250100 Shandong, China.
Jingjing Guo, Centre in Artificial Intelligence Driven Drug Discovery, Faculty of Applied Sciences, Macao Polytechnic University, Rua de Luís Gonzaga Gomes, Macao, China.
Yanjie Wei, Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences, Xueyuan Road 1068, Shenzhen, 518055 Guang Dong, China.
Yuguang Mu, School of Biological Sciences, Nanyang Technological University, Singapore.
Liangzhen Zheng, Shanghai Zelixir Biotech, Xiangke Road, 200030, Shanghai, China; Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences, Xueyuan Road 1068, Shenzhen, 518055 Guang Dong, China.
Weifeng Li, School of Physics, Shandong University, South Shanda Road, 250100 Shandong, China.
FUNDING
This research is supported by National Key R&D Program of China (2023YFA0915500). This work is financially supported by the Natural Science Foundation of Shandong Province (ZR2020JQ04) and Local Science and Technology Development Fund Guided by the Central Government of Shandong Province (YDZX2022089). This work is partly supported by the Singapore Ministry of Education (MOE), tier 1 grants RG97/22 (M.Y.). This work was partly supported by the Key Research and Development Project of Guangdong Province under grant no. 2021B0101310002, National Science Foundation of China under grant no. 62272449, the Shenzhen Basic Research Fund under grant nos RCYX20200714114734194, KQTD20200820113106007, ZDSYS20220422103800001. We would also like to thank the funding support by the Youth Innovation Promotion Association(Y2021101), CAS to Yanjie Wei. The authors sincerely thank the support from Core Facility Sharing Platform of Shandong University and National Demonstration Center for Experimental Physics Education (Shandong University).
AUTHOR CONTRIBUTIONS STATEMENT
Z.W. designed research, performed research, analyzed data and wrote the paper; S.W., Y.L., J.G. and Y.W. analyzed data; Y.M. analyzed data and wrote the paper; L.Z. and W.L. designed research, analyzed data and wrote the paper.
References
- 1. Anderson AC. The process of structure-based drug design. Chem Biol 2003;10(9):787–97. [DOI] [PubMed] [Google Scholar]
- 2. Pinzi L, Rastelli G. Molecular docking: shifting paradigms in drug discovery. Int J Mol Sci 2019;20(18):4331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Grinter SZ, Zou X. Challenges, applications, and recent advances of protein-ligand docking in structure-based drug design. Molecules 2014;19(7):10150–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Prosser KE, Stokes RW, Cohen SM. Evaluation of 3-dimensionality in approved and experimental drug space. ACS Med Chem Lett 2020;11(6):1292–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Stephani Joy Y, Macalino VG, Hong S, Choi S. Role of computer-aided drug design in modern drug discovery. Arch Pharm Res 2015;38:1686–701. [DOI] [PubMed] [Google Scholar]
- 6. Guareschi R, Lukac I, Gilbert IH, Zuccotto F. SophosQM: accurate binding affinity prediction in compound optimization. ACS Omega 2023;8(17):15083–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Paul D, Sanap G, Shenoy S, et al. Artificial intelligence in drug discovery and development. Drug Discov Today 2021;26(1):80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Lane TJ. Protein structure prediction has reached the single-structure frontier. Nat Methods 2023;20(2):170–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Meli R, Morris GM, Biggin PC. Scoring functions for protein-ligand binding affinity prediction using structure-based deep learning: a review. Front Bioinform 2022;2:57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Yunta MJR. Docking and ligand binding affinity: uses and pitfalls. Am J Model Optim 2016;4(3):74–114. [Google Scholar]
- 11. Xing D, Li Y, Xia Y-L, et al. Insights into protein–ligand interactions: mechanisms, models, and methods. Int J Mol Sci 2016;17(2):144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Ferreira LG, Dos Santos RN, Oliva G, Andricopulo AD. Molecular docking and structure-based drug design strategies. Molecules 2015;20(7):13384–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Torres PHM, Sodero ACR, Jofily P, Silva-Jr FP. Key topics in molecular docking for drug design. Int J Mol Sci 2019;20(18):4574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Saikia S, Bordoloi M. Molecular docking: challenges, advances and its use in drug discovery perspective. Curr Drug Targets 2019;20(5):501–21. [DOI] [PubMed] [Google Scholar]
- 15. In Lam HY, Pincket R, Han H, et al. Application of variational graph encoders as an effective generalist algorithm in computer-aided drug design. Nat Mach Intell 2023;5(7):754–64. [Google Scholar]
- 16. Baig MH, Ahmad K, Roy S, et al. Computer aided drug design: success and limitations. Curr Pharm Des 2016;22(5):572–81. [DOI] [PubMed] [Google Scholar]
- 17. Dsouza S, Prema KV, Balaji S. Machine learning models for drug–target interactions: current knowledge and future directions. Drug Discov Today 2020;25(4):748–56. [DOI] [PubMed] [Google Scholar]
- 18. Li J, Ailing F, Zhang L. An overview of scoring functions used for protein–ligand interactions in molecular docking. Interdiscip Sci: Comput Life Sci 2019;11:320–8. [DOI] [PubMed] [Google Scholar]
- 19. Agamah FE, Mazandu GK, Hassan R, et al. Computational/in silico methods in drug target and lead prediction. Brief Bioinform 2020;21(5):1663–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. DesJarlais RL, Sheridan RP, Seibel GL, et al. Using shape complementarity as an initial screen in designing ligands for a receptor binding site of known three-dimensional structure. J Med Chem 1988;31(4):722–9. [DOI] [PubMed] [Google Scholar]
- 21. Huang S-Y, Grinter SZ, Zou X. Scoring functions and their evaluation methods for protein–ligand docking: recent advances and future directions. Phys Chem Chem Phys 2010;12(40):12899–908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Deng W, Breneman C, Embrechts MJ. Predicting protein-ligand binding affinities using novel geometrical descriptors and machine-learning methods. J Chem Inf Comput Sci 2004;44(2):699–703. [DOI] [PubMed] [Google Scholar]
- 23. Ain QU, Aleksandrova A, Roessler FD, Ballester PJ. Machine-learning scoring functions to improve structure-based binding affinity prediction and virtual screening. Wiley Interdiscip Rev: Comput Mol Sci 2015;5(6):405–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Lavecchia A. Machine-learning approaches in drug discovery: methods and applications. Drug Discov Today 2015;20(3):318–31. [DOI] [PubMed] [Google Scholar]
- 25. Ballester PJ, Mitchell JBO. A machine learning approach to predicting protein–ligand binding affinity with applications to molecular docking. Bioinformatics 2010;26(9):1169–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Durrant JD, Andrew McCammon J. Nnscore: a neural-network-based scoring function for the characterization of protein-ligand complexes. J Chem Inf Model 2010;50(10):1865–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Nguyen DD, Wei G-W. AGL-Score: algebraic graph learning score for protein–ligand binding scoring, ranking, docking, and screening. J Chem Inf Model 2019;59(7):3291–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Minyi S, Du Qifan Yang Y, Feng G, et al. Comparative assessment of scoring functions: the CASF-2016 update. J Chem Inf Model 2018;59(2):895–913. [DOI] [PubMed] [Google Scholar]
- 29. Chen H, Engkvist O, Wang Y, et al. The rise of deep learning in drug discovery. Drug Discov Today 2018;23(6):1241–50. [DOI] [PubMed] [Google Scholar]
- 30. Jing Y, Bian Y, Ziheng H, et al. Deep learning for drug design: an artificial intelligence paradigm for drug discovery in the big data era. AAPS J 2018;20:1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Meng Z, Xia K. Persistent spectral–based machine learning (perspect ml) for protein-ligand binding affinity prediction. Sci Adv 2021;7(19):eabc5329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Gomes J, Ramsundar B, Feinberg EN, Pande VS. Atomic convolutional networks for predicting protein-ligand binding affinity. arXiv preprint arXiv:1703.10603, 2017. [Google Scholar]
- 33. Jiménez J, Skalic M, Martinez-Rosell G, De Fabritiis G. KDEEP: protein–ligand absolute binding affinity prediction via 3d-convolutional neural networks. J Chem Inf Model 2018;58(2):287–96. [DOI] [PubMed] [Google Scholar]
- 34. Stepniewska-Dziubinska MM, Zielenkiewicz P, Siedlecki P. Development and evaluation of a deep learning model for protein–ligand binding affinity prediction. Bioinformatics 2018;34(21):3666–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Zheng L, Fan J, Yuguang M. OnionNet: a multiple-layer intermolecular-contact-based convolutional neural network for protein–ligand binding affinity prediction. ACS omega 2019;4(14):15956–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Wang Z, Zheng L, Liu Y, et al. OnionNet-2: a convolutional neural network model for predicting protein-ligand binding affinity based on residue-atom contacting shells. Front Chem 2021;9:753002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Shen C, Ye H, Wang Z, et al. Beware of the generic machine learning-based scoring functions in structure-based virtual screening. Brief Bioinform 2021;22(3):bbaa070. [DOI] [PubMed] [Google Scholar]
- 38. Bao J, He X, Zhang JZH. DeepBSP—a machine learning method for accurate prediction of protein–ligand docking structures. J Chem Inf Model 2021;61(5):2231–40. [DOI] [PubMed] [Google Scholar]
- 39. Wang Z, Zheng L, Wang S, et al. A fully differentiable ligand pose optimization framework guided by deep learning and a traditional scoring function. Brief Bioinform 2023;24(1):bbac520. [DOI] [PubMed] [Google Scholar]
- 40. Méndez-Lucio O, Ahmad M, Antonio E, et al. A geometric deep learning approach to predict binding conformations of bioactive molecules. Nat Mach Intell 2021;3(12):1033–9. [Google Scholar]
- 41. Shen C, Zhang X, Deng Y, et al. Boosting protein–ligand binding pose prediction and virtual screening based on residue–atom distance likelihood potential and graph transformer. J Med Chem 2022;65(15):10691–706. [DOI] [PubMed] [Google Scholar]
- 42. Zhang X, Gao H, Wang H, et al. Planet: a multi-objective graph neural network model for protein–ligand binding affinity prediction. J Chem Inf Model 2023. [DOI] [PubMed] [Google Scholar]
- 43. Shen C, Zhang X, Hsieh C-Y, et al. A generalized protein–ligand scoring framework with balanced scoring, docking, ranking and screening powers. Chem Sci 2023;14(30):8129–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Zheng L, Meng J, Jiang K, et al. Improving protein–ligand docking and screening accuracies by incorporating a scoring function correction term. Brief Bioinform 2022;23(3):bbac051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Yang C, Zhang Y. Delta machine learning to improve scoring-ranking-screening performances of protein–ligand scoring functions. J Chem Inf Model 2022;62(11):2696–712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Tao S, Fuxu L, Zechen W, et al. zPoseScore model for accurate and robust protein-ligand docking pose scoring in CASP15. Proteins 2023. [DOI] [PubMed] [Google Scholar]
- 47. Chatterjee A, Walters R, Shafi Z, et al. Improving the generalizability of protein-ligand binding predictions with AI-Bind. Nat Commun 2023;14(1):1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Jiang H, Wang J, Cong W, et al. Predicting protein–ligand docking structure with graph neural network. J Chem Inf Model 2022;62(12):2923–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Zhang Z, Chen L, Zhong F, et al. Graph neural network approaches for drug-target interactions. Curr Opin Struct Biol 2022;73:102327. [DOI] [PubMed] [Google Scholar]
- 50. Kamiński K, Ludwiczak J, Jasiński M, et al. Rossmann-toolbox: a deep learning-based protocol for the prediction and design of cofactor specificity in Rossmann fold proteins. Brief Bioinform 2022;23(1):bbab371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Shen C, Xueping H, Gao J, et al. The impact of cross-docked poses on performance of machine learning classifier for protein–ligand binding pose prediction. J Chem 2021;13(1):1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Wierbowski SD, Wingert BM, Zheng J, Camacho CJ. Cross-docking benchmark for automated pose and ranking prediction of ligand binding. Protein Sci 2020;29(1):298–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Jumper J, Evans R, Pritzel A, et al. Highly accurate protein structure prediction with alphafold. Nature 2021;596(7873):583–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Wang R, Fang X, Yipin L, Wang S. The pdbbind database: collection of binding affinities for protein- ligand complexes with known three-dimensional structures. J Med Chem 2004;47(12):2977–80. [DOI] [PubMed] [Google Scholar]
- 55. Trott O, Olson AJ. AutoDock Vina: improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J Comput Chem 2010;31(2):455–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Liu N, Xu Z. Using LeDock as a docking tool for computational drug design. In: IOP Conference Series: Earth and Environmental Science, Vol. 218, p. 012143. IOP Publishing, 2019. [Google Scholar]
- 57. Landrum G, et al. RDKit: open-source cheminformatics software. 2006. https://rdkit.org/docs/index.html.
- 58. Meli R, Biggin PC. SpyRMSD: symmetry-corrected RMSD calculations in Python. Journal of. J Chem 2020;12(1):1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. García-Sosa AT. Hydration properties of ligands and drugs in protein binding sites: tightly-bound, bridging water molecules and their effects and consequences on molecular design strategies. J Chem Inf Model 2013;53(6):1388–405. [DOI] [PubMed] [Google Scholar]
- 60. Spyrakis F, Ahmed MH, Bayden AS, et al. The roles of water in the protein matrix: a largely untapped resource for drug discovery. J Med Chem 2017;60(16):6781–827. [DOI] [PubMed] [Google Scholar]
- 61. Liu H, Dai Z, So D, Le QV. Pay attention to MLPs. Adv Neural Inf Process Syst 2021;34:9204–15. [Google Scholar]
- 62. Corso G, Stärk H, Jing B, et al. DiffDock: diffusion steps, twists, and turns for molecular docking. arXiv preprint arXiv:2210.01776, 2022.
- 63. Fan J, Ailing F, Zhang L. Progress in molecular docking. Quant Biol 2019;7:83–9. [Google Scholar]
- 64. Mysinger MM, Carchia M, Irwin JJ, Shoichet BK. Directory of useful decoys, enhanced (DUD-E): better ligands and decoys for better benchmarking. J Med Chem 2012;55(14):6582–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Kanakala GC, Aggarwal R, Nayar D, et al. Latent biases in machine learning models for predicting binding affinities using popular data sets. ACS Omega 2023;8(2):2389–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Ramírez D, Caballero J. Is it reliable to take the molecular docking top scoring position as the best solution without considering available structural data? Molecules 2018;23(5):1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. McNutt AT, Francoeur P, Aggarwal R, et al. GNINA 1.0: molecular docking with deep learning. J Chem 2021;13(1):1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Jianing L, Hou X, Wang C, Zhang Y. Incorporating explicit water molecules and ligand conformation stability in machine-learning scoring functions. J Chem Inf Model 2019;59(11):4540–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Černy J, Hobza P. Non-covalent interactions in biomacromolecules. Phys Chem Chem Phys 2007;9(39):5291–303. [DOI] [PubMed] [Google Scholar]
- 70. Amidon GL, Pearlman RS, Anik ST. The solvent contribution to the free energy of protein-ligand interactions. J Theor Biol 1979;77(1):161–70. [DOI] [PubMed] [Google Scholar]
- 71. Duan L, Liu X, Zhang JZH. Interaction entropy: a new paradigm for highly efficient and reliable computation of protein–ligand binding free energy. J Am Chem Soc 2016;138(17):5722–8. [DOI] [PubMed] [Google Scholar]
- 72. Frieden E. Non-covalent interactions: key to biological flexibility and specificity. J Chem Educ 1975;52(12):754. [DOI] [PubMed] [Google Scholar]
- 73. Wendler K, Thar J, Zahn S, Kirchner B. Estimating the hydrogen bond energy. Chem A Eur J 2010;114(35):9529–36. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.








