Abstract
From literature, majority of face recognition modules suffer performance challenges when presented with test images acquired under multiple constrained environments (occlusion and varying expressions). The performance of these models further deteriorates as the degree of degradation of the test images increases (relatively higher occlusion level). Deep learning-based face recognition models have attracted much attention in the research community as they are purported to outperform the classical PCA-based methods. Unfortunately their application to real-life problems is limited because of their intensive computational complexity and relatively longer run-times. This study proposes an enhancement of some PCA-based methods (with relatively lower computational complexity and run-time) to overcome the challenges posed to the recognition module in the presence of multiple constraints. The study compared the performance of enhanced classical PCA-based method (HE-GC-DWT-PCA/SVD) to FaceNet algorithm (deep learning method) using expression variant face images artificially occluded at 30% and 40%. The study leveraged on two statistical imputation methods of MissForest and Multiple Imputation by Chained Equations (MICE) for occlusion recovery. From the numerical evaluation results, although the two models achieved the same recognition rate (85.19%) at 30% level of occlusion, the enhanced PCA-based algorithm (HE-GC-DWT-PCA/SVD) outperformed the FaceNet model at 40% occlusion rate, with a recognition rate of 83.33%. Although both Missforest and MICE performed creditably well as de-occlusion mechanisms at higher levels of occlusion, MissForest outperforms the MICE imputation mechanism. MissForest imputation mechanism and the proposed HE-GC-DWT-PCA/SVD algorithm are recommended for occlusion recovery and recognition of multiple constrained test images respectively.
Keywords: Histogram equalisation, Gamma correction, Multiple imputation, Multiple constraints, Principal component analysis, FaceNet algorithm
1. Introduction
The sudden spike in the research and development of face recognition techniques and technologies can be attributed to the many advantages it provides especially when compared to other biometric techniques. The non-invasive characteristic of face recognition approaches largely accounts for its widespread use and acceptability [1]. The application areas include surveillance, voter identification, security and access control among others. For instance, face recognition is used to enforce access control in restricted areas, where any unauthorized person who breaches the entrance rule is identified and an alert is triggered.
The numerous advantages of face recognition account for the widespread interest of research in this field of biometrics. The drift is towards the development of an efficient and resilient recognition module to deal with the myriad of environmental constraints. Traditionally, the Principal Component Analysis (PCA) methods have been used extensively in the quest for a reliable recognition system. The main advantage of the PCA-based methods is that they are computationally efficient as they require relatively less samples for training. According to [2], single constraints such as aging, pose variation, varying expression, variable illumination and inter-person variability may hinder the performance of face recognition modules. The work of [3] further supports this claim, as they investigate the ability of the PCA-Eigenface method to identify human faces from a variety of databases that were obtained under constrained conditions, including low light levels, noticeably different expressions, and the use of accessories like glasses. They found that in each database, the mean recognition accuracy ranged from 100% to 67%. This situation becomes worse with the combined effect of more than one of the above-mentioned constraints (multiple constraints), such as occlusion and variable facial expression. According to [4], the factors which affect the performance of recognition algorithms in the real-world situations are normally coupled, but most research works are dedicated to dealing with them independently. The problem of multiple constraints in face recognition is far from being solved comprehensively.
Classical face recognition approaches based on Principal Component Analysis and Singular Value Decomposition (PCA/SVD) have been used copiously by various authors [5], [1], [6]. The PCA-based approaches have seen a lot of modifications and augmentations over the years since its proposal by [7], with the aim of improving their performance under different environmental constraints. [8], assessed the performance of Discrete Wavelet Transformation PCA/SVD algorithm (DWT-PCA/SVD) on angular constraints and found that, recognition distances increased substantially when the head tilt is beyond the angle of . They concluded that the performance of the DWT-PCA/SVD algorithm declines significantly beyond head tilt. [9] observed that the performance of most face recognition systems even with deep learning techniques degraded more than 10% from the frontal to the angular pose. The performance of the PCA-based techniques is not yet optimum, especially on different constraints. [10] also assessed the performance of DWT-PCA/SVD algorithm on the constraint of partially occluded images acquired with varying facial expressions. The study achieved recognition rates of 77.31% and 76.85%, corresponding to the left and right reconstructed face images with variable facial expressions. Although this result is appreciable, the error rates of 22.69% and 23.15% are too high for any efficient recognition system.
Deep learning techniques have attracted much attention in recent times, owing to its tremendous successes in diverse application areas like Biometrics [11], Healthcare and Medicine [12] and Face recognition [13]. Convolutional Neural Network (CNN) constitutes the most popular machine learning approach well-suited for face recognition and classification problems [14]. Transfer learning is a popular application of deep learning techniques. In transfer learning, pre-trained networks are used as a starting point in learning new tasks. [15] contend that fine-tuning a pre-trained network reduces the amount of time involved in training as opposed to developing a CNN from scratch. This is because it is computationally expensive as well as time consuming to train a CNN. There exist several research works in literature which make use of various transfer learning techniques such as AlexNet [16], GoogleNet [17], ResNet50 [18] and VGG-16 [19]. Developed by [20], FaceNet achieved a state-of-the-art recognition performance using benchmark image datasets such as the labeled faces in the wild (LFW). As a pre-trained deep neural network algorithm, FaceNet obtains an image and returns a vector of 128 numbers, termed as embeddings, which represent important image features. Classification of the embedding distances between a new image and a known image could be obtained with the K-NN, but this has proved to be computationally expensive and less efficient. Thus, the softmax classifier is popularly employed together with other classifiers like the random forest and support vector machine. Various researchers have reported on the performance of the FaceNet algorithm. [21] compared two deep learning algorithms; FaceNet and Openface, for employee presence using the support vector machine classifier and concluded that FaceNet obtained a 100% classification accuracy while Openface achieved 93.3%. After assessing the performance of FaceNet with three different classifiers; K-NN, SVM and Random Forest, [22], concluded that FaceNet with the multi-class SVM achieved the highest classification accuracy of 96.15%, while FaceNet with the Random Forest classifier had the lowest accuracy of 54.04%. In order to address the pose variations for face recognition, [23] presented a novel Deformable Face Net (DFN). The goal of the deformable convolution module is to simultaneously learn identity-preserving feature extraction and face recognition oriented alignment. It was discovered that the suggested DFN could manage pose invariant face recognition (PIFR) efficiently. Their research revealed that the suggested DFN works better than the most advanced techniques, particularly when applied to datasets with plenty of poses. [24], compared the face recognition performance of three pre-trained models; FaceNet, VGGFace2 and CASIA-WebFace, and concluded that the FaceNet model outperformed the others with an accuracy rate of 100% on YALE, JAFFE and AT & T face databases. According to [24], the FaceNet algorithm's training method necessitates intricate computation and extended computational duration. They accomplished a comparable training time with less computing complexity by combining the Tensorflow learning matching with the pre-trained model. In [25], the effectiveness of various statistical multiple imputation schemes on the FaceNet model's performance was evaluated, both with and without the use of train image data augmentation in situations where the number of images available for training per subject is constrained. Even though the average recognition rates of their proposed deep learning algorithm were appreciable at 85.19% and 79.5% at 30% and 40% occlusion levels, respectively, they suggested improving PCA-based methods instead, as they have been shown to have shorter run-times and lower computational complexity for accurately recognizing expression variant face images with higher levels of occlusion. The literature mentioned above clarifies that while deep learning techniques for face recognition have typically proven successful, they are computationally complex and take more time to process.
To address the challenge of multiple constraints, we provide a variation of the PCA-based approach in this study, which has been demonstrated to reduce computational complexity and provide quicker run-time. After that, to find an effective recognition algorithm with a comparatively higher average recognition rate, lower computational complexity, and shorter run-time, the performance of the improved PCA-based recognition module would be compared to the FaceNet (deep learning technique) under multiple constraints (expression-variant images acquired with relatively higher occlusion levels). From literature, various preprocessing mechanisms such as histogram equalization (HE), discrete wavelet transform (DWT), discrete cosine transform (DCT) and Fast Fourier Transform (FFT) have been recommended as suitable preprocessing and augmentation techniques to improve on the performance of the PCA-based techniques. In this study, we propose various variants and combinations such as histogram equalization and discrete wavelet transform (HE-DWT), histogram equalization and discrete cosine transform (HE-DCT), and 3-tier augmentation which combines histogram equalization, gamma correction and discrete wavelet transform (HE-GC-DWT) to improve the PCA/SVD recognition algorithm for recognizing multiple constrained face images.
The remaining sections of the paper are structured as follows: The procedures employed for the investigation and the data that was obtained are described in the Methods and Materials section. This part also outlines the reconstruction plans and augmentation strategies taken into account during the investigation. The upgraded PCA-based approach and the FaceNet algorithm's performance evaluation findings are shown in the results and discussion section. The summarized results are reported in the conclusion section, along with suggestions for further study.
2. Materials and methods
2.1. Data acquisition
Database: To evaluate the recognition methods, two databases were used: the AU-Coded Cohn-Kanade (CKFE) and the Japanese Female Facial Expression (JAFFE).
Train-Image Set: This includes twenty-six (26) and ten (10) neutral poses images from the Cohn-Kanade and JAFFE databases, respectively. The train dataset had thirty-six (36) participants in total. To expand the quantity of training sets for the FaceNet methodology, this set will be subjected to a variety of augmentation techniques. Sampled subjects captured in the train-image database are shown in Fig. 1. The sub-Figs. 1(a) and 1(b) contain neutral expressions of sampled individuals from JAFEE and CKFE databases respectively.
Figure 1.
Sampled individuals in the train-image database.
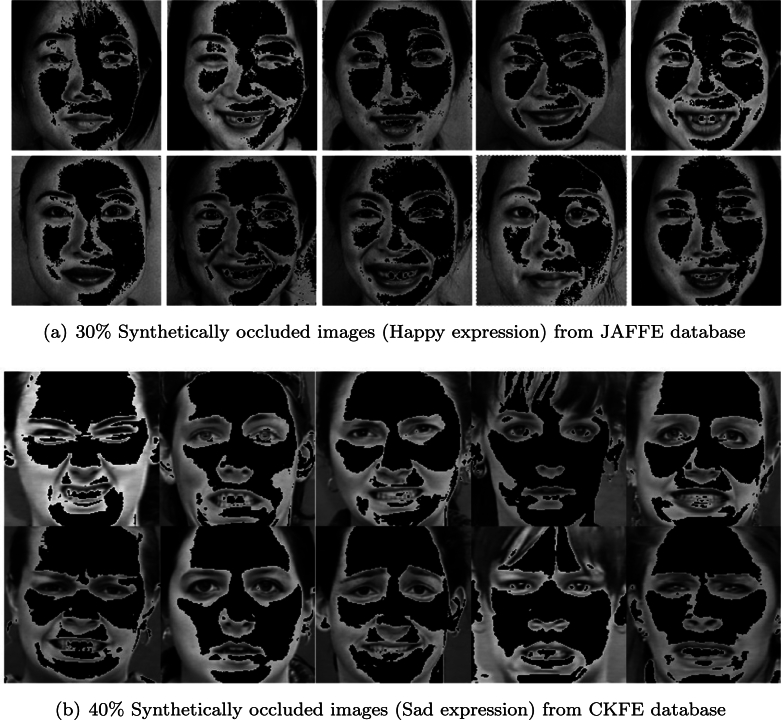
The test image set consisted of thirty-six (36) participants from the training set, whose six major expressions (angry, sad, disgust, fearful, joyful, and surprised) were artificially obscured to produce 30% and 40% missingness in the image pixels randomly. Occlusions and varying expressions are two characteristics of the images obtained from this process. In total, 216 face images were recorded in the test database (produced by multiplying the total number of photographs by the expression variations, or 36 × 6). A selection of occluded face image with varying expression that were utilized as the test set is displayed in Fig. 2. The sub-Figs. 2(a) and 2(b) contain 30% and 40% occluded face images with happy and sad expressions (multiple constrained images) from JAFEE and CKFE databases respectively.
Figure 2.
Sample of subjects in the test-image database.
2.2. Enhancement mechanisms
2.2.1. Histogram equalization
Normalization is a commonly used technique in image preprocessing. The most common noise acquired in face images is the gaussian noise. In this case, histogram equalization is employed to redistribute and stretch the original histogram with the whole range of discrete levels of the image, such that the contrast of the image is enhanced. Histogram equalization alters the histogram of the image into one which is constant for all the brightness values. Generally, this leads to brightness redistribution such that all values are equally likely. According to [26], histogram equalization has the advantage of being simple as well as producing image outputs with maximum entropy. However, [27] have suggested that histogram equalization is unable to improve all parts of the face image, stating that when the original image has irregular illumination, some details of the resulting image will still be too bright or dark. The primary reason for selecting Histogram Equalization (HE) over Contrast Limited Adaptive Histogram Equalization (CLAHE) in this study was its ease of usage. As previously mentioned, an effective approach with a comparatively lower computing complexity and run time was required.
While histogram equalization may make undesired image noises more visible (since it does not adjust to local contrast requirements, small contrast differences can go unnoticed when a given gray range has a large number of pixels), it is a straightforward and user-friendly method for evenly distributing the image's intensity levels [28], [29]. The CLAHE solves the noise issue by introducing a clip limit. Before calculating the Cumulative Distribution Function (CDF), the amplification is restricted by cutting the histogram at a predetermined value. Nevertheless, there is not a thorough process to determine its two crucial parameters (the clip limit and the number of tiles). Most users turn to heuristics, which, if not precisely calculated, would result in lower image quality than if the HE was used [28].
The histogram of pixel intensity in a given image f, having n pixels and g intensity levels, is given by equation (1).
| (1) |
where is the intensity level and represents the number of pixels having intensity level . , which represents the histogram equalized image of f is acquired by transforming (through the cumulative density function of f) each pixel with intensity to a new pixel which has intensity given in equation (2).
| (2) |
represents the probability density function of f.
2.2.2. Gamma intensity correction
Due to shortfalls of the linear histogram equalization method, non-linear contrast enhancement approaches have been advanced. [30] have asserted that non-linear contrast enhancement techniques are capable of enhancing the contrast, while moderating the average brightness to a desired level. To this, the gamma correction, which is aimed at brightness and contrast preservation comes in handy. The gamma correction is a gray-level transformation (non-linear) which is given by equation (3):
| (3) |
where p is the output image, q is the input image, k and γ are parameters greater than zero which controls the slope of the transformation and brightness function respectively. Gamma correction is used to correct the overall brightness of facial images to a predefined canonical form in a bid to weaken the effect of varying lighting. The local dynamic area of an image in shadowed or dark regions are enhanced while the bright regions are compressed. An image gets darker when the gamma value exceeds 1.0, and vice versa. According to [27], a good compromise is the range of values . A gamma value of 0.5 was used empirically for this investigation.
2.2.3. Discrete wavelet transform
The Discrete Wavelet Transform (DWT) is a technique which separates data into diverse frequency components, and learns each component with a resolution coupled with its scale [31]. The DWT is a pixel-based filtering mechanism which has been shown to be a viable technique for image denoising, while maintaining the key facial characteristics for face recognition. Transform domain denoising of noisy images involves a forward transformation using specified basis functions, a denoising process and an inverse transformation. The forward transformation process renders an output image showing the different frequency components of the noisy image or images showing different resolution form of an input image as in Discrete Wavelet Transforms [32]. [33] posited that the DWT presents a fast and easy way to filter facial images. [10] provides a thorough mathematical formulation of the DWT. This study examined the use of Haar wavelets to remove noise from a one-level, two-dimensional DWT. The Haar wavelet was chosen because of its computational simplicity and its orthogonal characteristic, which helps preserve distances after transformation [10]. A one-level DWT usually produces four sub-bands (LL, LH, HL, HH) of the image, where the LL sub-band denotes the approximate coefficients and the LH, HL and HH represents local information such as edges, noise, etc.
2.3. Reconstruction schemes
[34], argued that the various processes in the generation, transmission and retrieval of face images are met with external factors referred to as interference noise. According to [35], data missingness in the image matrix is as a result of occlusion in face images. Therefore, in a bid to improve the performance of recognition mechanisms, there is a need to enhance the image quality. There exist various statistical and machine learning-based techniques that have been suggested to reconstruct occluded images. The machine learning approaches try to reconstruct images by generation of data models, obtained from a dataset having missing values. These models are then used to churn out classifications which finds the missing values [36]. Although these methods are found to be computationally fast, they are known to have poor trade-offs for certain classes in terms of resolution and noise. On the contrary, the statistical methods iteratively find the missing values in degraded face images using statistical models [37].
2.3.1. Multiple imputation by chain equations
Multiple Imputation by Chain Equations (MICE) is a multiple imputation mechanism which works with the assumption that data is missing at random (MAR) and imputes missing data by specifying a model for each missing variable [38]. Thus, implementing MICE when data are not MAR could result in biased estimates [39]. It is a flexible parametric multiple imputation technique [40]. MICE can impute missing values in datasets containing continuous, binary, and categorical characteristics by using a distinct model to each attribute, according to [41]. Each feature is therefore modeled based on how it is distributed; that is, logistic regression is used to model binary or categorical variables, and linear regression is used to model continuous variables. Regression models designate the dependent variable as the modeled attribute and the independent variables as the remaining attributes.
Many researchers [42], [32] have employed MICE augmentation to reconstruct occluded face images, and recommended MICE as a suitable imputation technique for finding missing pixel values in occluded images.
2.3.2. MissForest
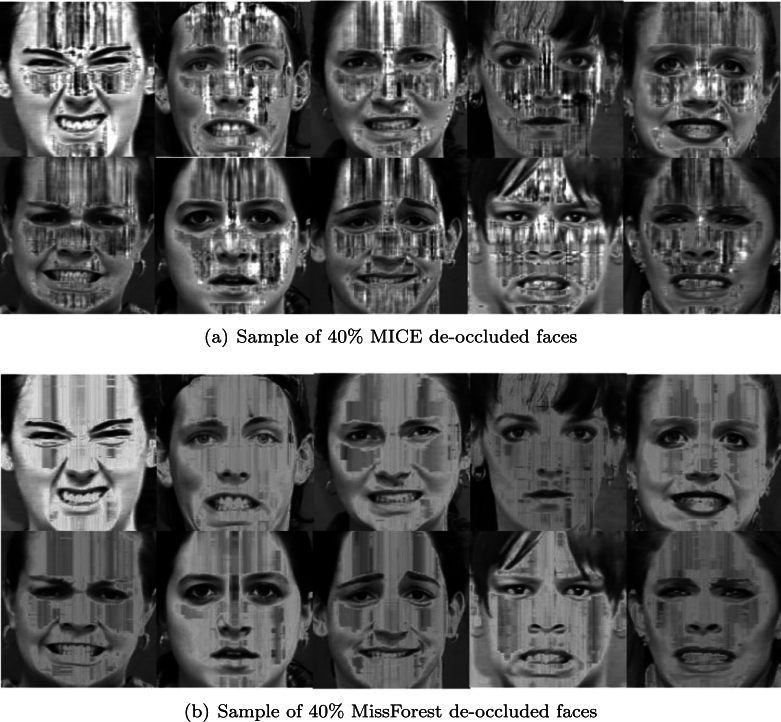
Random forest-based imputation techniques such as the MissForest have gained much acceptance and popularity in various research fields as posited by [43]. MissForest is a machine learning-based imputation technique capable of handling both categorical and continuous data types. As a non-parametric imputation mechanism, it is also able to deal with complex interactions in a given dataset without making any distributional assumptions [44]. MissForest starts by building a random forest model for all the variables, after which it employs the model iteratively to predict the missing values using the observed values. After assessing data from different biomedical fields having artificially introduced random missingness of up to 30%, [44] concluded that MissForest was found to be computationally efficient as compared with other imputation mechanisms such as the KNN and the MICE. Figure 3, Figure 4 display samples of the face images reconstructed at 30% and 40% rates of occlusion respectively. The sub-Figs. 3(a) and 3(b) in Fig. 3 contain samples of MICE and Missforest de-occluded images respectively with 30% level of missingness. Also the sub-Figs. 4(a) and 4(b) in Fig. 4 contain samples of MICE and Missforest de-occluded images respectively with 40% level of missingness.
Figure 3.
Sample of 30% de-occluded faces.
Figure 4.
Sample of 40% de-occluded faces.
2.4. Feature extraction
2.4.1. Principal component analysis
As a statistical procedure, the Principal Component Analysis (PCA) provides a way for sorting out the covariance structure of any given set of variables. Specifically, it helps in identifying the principal direction which results in data variation [45]. The PCA technique helps to convert the high dimensional face images in each of the two-dimensional images into a one-dimensional vector. From literature, it is evident that one of the most effective and simplest methods of feature extraction is the eigen face technique, which is normally based on PCA. This technique is capable of transforming images into smaller sets of face features, which contains the main parts of the original training set [46]. Given that the training sample is given by the matrix such that are the vectorized face images and m is the number of train images. The mean image is obtained using equation (4).
| (4) |
The mean centered image is obtained by subtracting from each image in X, to obtain equation (5).
| (5) |
The covariance matrix is obtained from equation (6) as
| (6) |
where is the mean-centered matrix.
A Singular Value Decomposition (SVD) is performed on the covariance matrix to derive the eigenvalues and eigen-vector as , where and are two orthogonal matrices whose entries are the eigen-vectors corresponding to the eigen-values in Σ, the diagonal matrix. The eigen-face of the train set is derived from equation (7) as
| (7) |
where is the column vector of G. Principal components of the training data were obtained using equation (8);
| (8) |
and .
The unique features of a new test image are extracted using equation (9);
| (9) |
and .
The city block distance was used as the classifier for recognition. This is obtained from equation (10);
| (10) |
For the purpose of classification, the minimum city block distance, and was used.
2.5. Classification
The last phase of the recognition process is the classification stage. At this level, the image embeddings acquired from the training set are compared (matched) with those from the test set with the use of a classifier. This study considered three different classifiers to assess the recognition rates.
2.5.1. Euclidean distance
Of all the distance metrics, the most common and widely used is the Euclidean distance. It is evident in literature that the main reason for the wide acceptability of the Euclidean distance as compared to the other distance metrics is due to the fact that it is simple and faster. The Euclidean distance between two given points is the straight-line distance, which is represented by square root of the squared differences between coordinates of the subjects. After obtaining the Euclidean distances, [47] assert that the most preferred is the minimum Euclidean distance classifier for normally distributed classes. Given that X is a train image feature vector and Y is a test image feature vector, the Euclidean distance is computed using equation (11):
| (11) |
2.5.2. Support vector machine
Support Vector Machine (SVM) has gained much attention in various classification tasks. The SVM is a strong supervised machine learning classification and regression technique which has the capability of analyzing the concealed consistency of various datasets. [6] have asserted that popular among the classification techniques employed in face recognition challenges is the support vector machine, stating that the SVM achieves a better generalization precision as compared with the other classifiers. One of the more important advantages of the SVM technique in dealing with classification problems is that of less prediction time. Support Vector Machine has been applied in diverse research fields such as face recognition [48], security [49], solid waste generation areas classification [50] and medicine [51]. SVM performs classification of the learned features by separating the various classes with the help of a hyperplane termed as the optimal separating hyperplane. SVM uses an n-dimensional feature space as the input data. The space is then divided into two sections by a dimensional hyperplane [52]. A hyperplane can be defined for linearly separable data by equation (12);
| (12) |
where is an n-dimensional vector and b is a scalar. The position of the hyperplane that completely separates the space has to obey the limits as shown in equation (13);
| (13) |
where represents the target variable in the training data with the different signs representing the two groups (correct match or wrong match). Other kernel functions which can be used to transform data and find hyperplanes are the polynomials, Sigmoid and Radial Basis Function.
2.5.3. City-block distance
The city-block distance, which is also known as the Manhattan distance measures the sum of the absolute difference between two vectors [5]. The city-block distance is particularly useful when dealing with discrete type of descriptions. According to [47], the city-block distance is a valid distance function as it responds to triangle inequality. Computationally, the city-block distance is depicted in equation (14):
| (14) |
2.6. Experimental setup
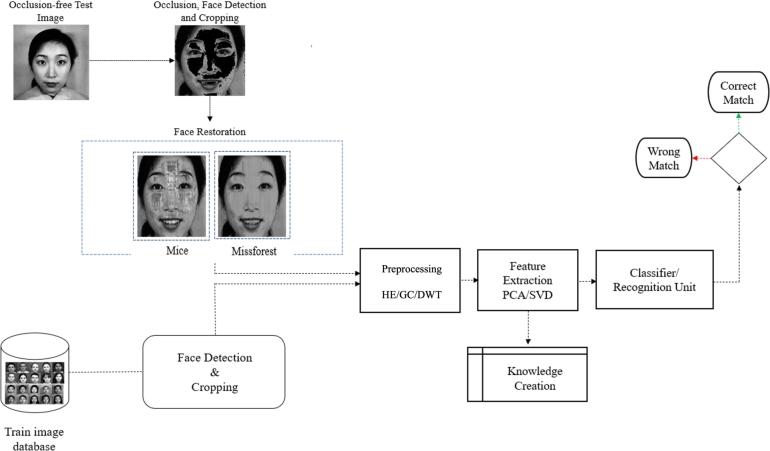
As previously mentioned, the recognition module was run over thirty-six (36) neutral pose images from the Cohn-Kanade and JAFFE databases to train or benchmark the recognition algorithm. Prior to matching, these images are pre-processed using DWT, Gamma Correction (GC), and HE. Their distinct features are then recorded as principal components in the classifier unit. In addition, 216 expression variation photos with artificial occlusion at 30% and 40% occlusion levels (6 major expressions of 36 people) are included in the test image collection. Initially, the test images are de-occluded using the utilization of MICE or Missforest imputation techniques. Each of these test images is run through the recognition module for pre-processing and feature extraction following the image restoration procedure. Additionally, their distinct qualities are retrieved and compared to those previously obtained. Using the SVM, City-block, and Euclidean distance classifiers, their distinct features are also collected and compared with those already stored from the training set. Fig. 5 shows the flow diagram of the enhanced PCA-based algorithm.
Figure 5.
Flow chart for the modified PCA-based Methods.
2.7. Data augmentation
Data augmentation refers to techniques performed to increase the number of training images especially when using deep learning. They consist of label-preserving transformations, which are generally applied to training datasets. It is a very difficult task to obtain a vast amount of labeled face data for training. According to [14], making use of additional synthetic data for training has proved to be very beneficial. Noise such as Poisson noise, gaussian, salt and pepper alter the pixel values of the face images, which can then be seen as different images to the training network, hence increasing the dataset. In this study, the augmentation methods used include minimal rotations, brightness adjustments, stretching, horizontal flipping and shearing.
2.7.1. FaceNet
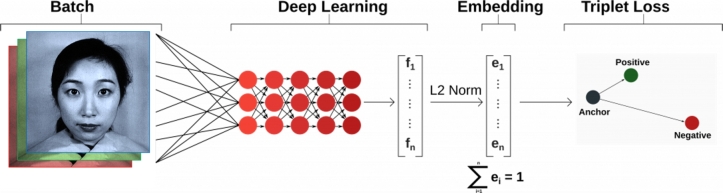
In general, the ultimate aim of feature extraction techniques is to obtain discriminative features of trained images in order to match against all other images (in the test database) to find a correct match. The FaceNet model learns a mapping from the input face image to an Euclidean space, such that the similarity between two faces is measured by the distance between their embeddings. [53] observed that the embeddings obtained show similarities and differences in face images, where similar images have smaller values while dissimilar images have larger values by the use of the triplet loss function. [21] also observed that the FaceNet feature extraction method produced high quality image embeddings (features) with a 128-dimensional vector. Fig. 6 shows the feature extraction process of the FaceNet architecture. The FaceNet method uses deep convolutional networks to optimize its embedding, compared to using intermediate bottleneck layers as a test of previous deep learning approaches [24]. The FaceNet network architecture consists of a batch input layer and a deep convolutional neural network which is then followed by L2 normalization, that provides the face embeddings. This process is followed by the triplet loss training [54].
Figure 6.
Feature extraction process of the FaceNet architecture.
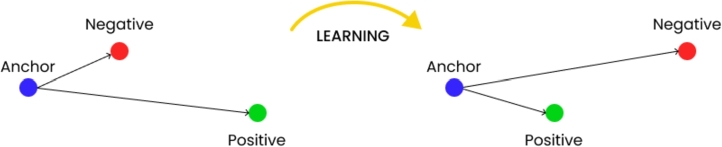
The triplet mining method consists of a collection of anchor images, where each image consists of positive and negative images [24]. This triplet loss works by minimizing the distance between anchors positively and maximizing the distance between anchors negatively.
As indicated by [25], the training procedure entails calculating a pair of Euclidean distances, denoted as and , correspondingly, between the anchor and the correct match (positive picture) and the wrong match (negative image). As far as feasible, the training approach aims to decrease and enhance . This will result in the creation of an embedding space where images with great differences will be located far apart and images with similarity will be located close to one another. That is, the distance between the anchor and the sample are minimized if the sample is positive and this signifies the same identity. Also, the distance between the anchor and negative sample, which signifies a different identity is maximized [54]. Fig. 7 shows the triple loss training.
Figure 7.
The Triplet Loss Training.
3. Results and discussion
Fig. 8 shows the results (matching decisions and recognition distances) of using the DWT-PCA/SVD, HE-DWT-PCA/SVD and a proposed unified (Histogram Equalization, Gamma Correction and Discrete Wavelet Transform) contrast-enhanced algorithm (HE-GC-DWT-PCA/SVD) for recognition for a sample of six (6) subjects at 30% de-occlusion rate. It can be observed that there was one (1) wrong match (MICE (0) and MissForest (1)) when the HE-GC-DWT-PCA/SVD algorithm was used for recognition. The number of wrong matches corresponding to the use of HE-DWT-PCA/SVD for recognition was two (2) (MissForest(1) and MICE(1)) and three (3) (MICE(1) and MissForest(2)) when DWT-PCA/SVD was used for recognition. It is worthy to note that the least number of wrong matches (at 30% de-occlusion rate) was attained when the MICE de-occluded expression faces were used as test faces and HE-GC-DWT-PCA/SVD algorithm was used for recognition.
Figure 8.
Recognition results for sample of 30% de-occluded face images.
The sub-Figs. 8(a) and 8(b) in Fig. 8 present the recognition results of MICE and Missforest de-occluded images (with 30% level of missingness) respectively subject to the DWT, HE/DWT and HE/GC/DWT preprocessing mechanisms. It is also evident from Fig. 8 that, the proposed HE-GC-DWT-PCA/SVD recognition module gave the lowest recognition distances for both MICE and Missforest de-occlusion mechanisms. The desired recognition distance (error) for any recognition problem is zero. This is practically not possible to achieve because the test images are usually captured under unconstrained environments. As earlier indicated, a recognition module that provides relatively lower recognition distances is desired as it signifies a closer matches.
3.1. Numerical evaluation:
The results for the improved PCA-based methods when the test set is occluded at relatively high levels (30% and 40% missing pixel values) and statistical multiple imputation methods (MICE and MissForest) are employed for de-occlusion under variable face expressions are detailed below.
Table 1 depicts the performance of FaceNet model after the various augmentations. At 30% de-occlusion, MissForest outperformed MICE imputation with respect to all the classifiers under consideration. More specifically, MissForest de-occlusion mechanism achieved the highest average recognition rate of 85.19% for both SVM and city block classifiers, while the highest recognition rate for MICE de-occlusion mechanism was 83.33%. It can also be observed that the least average recognition rate (84.26%) for MissForest de-occlusion mechanism was attained using the Euclidean distance classifier. This was greater than the highest average recognition rate obtained with MICE (83.33%). Similar results were obtained at 40% occlusion level, where MissForest outperformed MICE imputation across all the study classifiers. The obvious reduction in recognition rates for both imputation methods can be attributed to the relatively higher levels of occlusion which signifies increasing information/feature loss.
Table 1.
Performance of FaceNet model on de-occluded images.
| Occlusion Rate | Method | SVM | EUC | CB |
|---|---|---|---|---|
| 30% | MICE | 83.33% | 82.41% | 81.48% |
| MissForest | 85.19% | 84.26% | 85.19% | |
| 40% | MICE | 74.04% | 73.61% | 74.07% |
| MissForest | 79.52% | 78.13% | 79.52% |
The FaceNet recognition module attained its highest average recognition rates of 85.19% and 79.52% at 30% and 40% occlusion levels when Missforest de-occlusion mechanism was used along with either the City Block (CB) or Support Vector Machine (SVM) classifier. The average runtime of the FaceNet algorithm for the recognition of one test image was 0.98 second.
Table 2 presents the performance of the PCA-based method with various enhancement schemes.
Table 2.
Performance of enhanced PCA-based models on de-occluded images.
| Occlusion Rate | Method | DWT | DCT | HE-DWT | HE-DCT | HE-GC-DCT | HE-GC-DWT |
|---|---|---|---|---|---|---|---|
| 30% | MICE | 55.09% | 72.69% | 75.93% | 78.24% | 75.46% | 85.19% |
| MissForest | 47.69% | 72.69% | 76.85% | 78.24% | 75.46% | 84.26% | |
| 40% | MICE | 26.85% | 58.33% | 70.37% | 75.93% | 75.93% | 81.94% |
| MissForest | 39.81% | 64.81% | 67.81% | 68.98% | 75.46% | 83.33% |
At 30% occlusion rate, HE-GC-DWT PCA/SVD obtained the highest average recognition rate of 85.19% and 84.26% with the MICE and MissForest imputation mechanisms respectively. It is worthy to note that at 30% and 40% occlusion rates all the combined enhancement mechanisms (HE-DWT, HE-DCT, HE-GC-DCT, HE-GC-DWT) outperformed the individual enhancement mechanisms (DWT, DCT) across all imputation mechanisms. At 40% occlusion rate, HE-GC-DWT PCA/SVD achieved average recognition rates of 83.33% and 81.94% with MissForest and MICE de-occlusion mechanism respectively. It is evident from the Table 2 that, when occlusion rate increased from 30% to 40%, there was a marginal reduction in the average recognition rate under MissForest mechanism (from 84.26% to 83.33%) as compared to MICE mechanism (from 85.19% to 81.94%). It can be inferred from this finding that MissForest imputation mechanism is somewhat stable with relatively appreciable performance even at higher occlusion levels.
From Table 1, Table 2, the FaceNet with the city block classifier using MissForest de-occlusion mechanism achieves an average recognition rate of 85.19%, which is the same for the enhanced PCA-based method (HE-GC-DWT PCA/SVD) using MICE de-occlusion mechanism at 30% occlusion rate.
At 40% occlusion rate, the enhanced PCA-based method (HE-GC-DWT PCA/SVD) with MissForest de-occlusion mechanism had an average recognition rate of 83.33%, while the FaceNet with MissForest de-occlusion mechanism gave an average recognition rate of 79.52%. From the above findings, the enhanced PCA-based method (HE-GC-DWT PCA/SVD) is most preferred as opposed to the FaceNet algorithm, since the enhanced PCA-based method outperformed the FaceNet at relatively higher (40%) occlusion level.
The average runtime of the HE-GC-DWT-PCA/SVD for the recognition of one test image (occluded test image acquired with varying expression) was 0.2 seconds. This is less than the computational time of 0.98 seconds recorded for the FaceNet module. For this study, we used a system with the following specification: Core (TM) i7-9700 CPU @ 3.0GHZ (8 CPUs) with 32768 MB RAM and UHD Graphics 630. It is worthy to note that these computational times may vary depending on the specification of the system on which the experimental runs were conducted.
The enhanced PCA-based module (HE-GC-DWT-PCA/SVD) algorithm can be considered as a viable algorithm for recognition of frontal face images when occlusions of moderately high magnitudes (30% and 40%) and varying facial expressions are the underlying constraints. The performance of the enhanced PCA-based module algorithm is relatively less sensitive to the use of the MissForest imputation method for image reconstruction compared with the MICE multiple imputation method, considering its moderate decline in performance with increasing level or degree of occlusions (from 30% to 40%).
4. Conclusions and recommendations
The study sought to obtain an efficient recognition module for recognition of expression variant face images acquired with occlusion with relatively lower computational complexity and run-time.
To achieve this objective, the study proposed an enhanced PCA-based method (classical method) and compared its performance to the FaceNet recognition algorithm (deep learning technique), when test image datasets are obtained under multiple constraints (relatively high occlusion and varying facial expressions).
Two statistical multiple imputation mechanisms were used to recover the missing pixel in the occluded faces. The achieved average recognition rates (85.19% and 83.33% for 30% and 40% occlusion rates, respectively), show that the proposed enhancement (HE-GC-DWT) significantly boosts the PCA-based method's performance, outperforming the FaceNet algorithm (deep learning technique) presented by [25]. This result is in line with the findings of [34].
The performance of the enhanced PCA-based module (HE-GC-DWT PCA/SVD) was relatively consistent using the MissForest imputation method for image reconstruction compared with the MICE multiple imputation method, considering its moderate decline in performance with increasing levels or degrees of occlusion (from 30% to 40%). While the MICE imputation mechanism yielded quite impressive results (average recognition rates of 85.12% and 79.52% for 30% and 40% occlusion rates), the Missforest de-occlusion mechanism performs better at recovering missing portions of degraded face images acquired under expression variant constraint at moderately higher occlusion levels (40%). This result aligns with the findings of [25] and [10].
The study recommends the use of HE-GC-DWT PCA/SVD algorithm for recognition of face images acquired with multiple constraints (occlusion and varying expressions). An added advantage to the use of the classical PCA-based method is that they have relatively lower computational complexity and shorter run-times as compared to the deep learning techniques (0.2 seconds for recognition of an image for the PCA-based method and 0.98 seconds for the FaceNet module). The study further recommends the use of statistical multiple imputation techniques, especially MissForest, for restoration of degraded images with higher occlusion levels. Future work will assess the applicability of the HE-GC-DWT PCA/SVD on other multiple constraints such as occlusion and pose/head tilt variation. Furthermore, the relatively lower performance of the FaceNet algorithm will be investigated, especially with regards to the number of training samples per subject.
Ethics declaration
Review and/or approval by an ethics committee was not needed for this study because the databases used for the study are openly available from Labeled Faces in the Wild, a public benchmark for face verification.
CRediT authorship contribution statement
John K. Essel: Writing – original draft, Methodology, Formal analysis, Data curation, Conceptualization. Joseph A. Mensah: Writing – review & editing, Methodology, Formal analysis, Conceptualization. Eric Ocran: Writing – review & editing, Supervision, Formal analysis. Louis Asiedu: Writing – review & editing, Supervision, Methodology, Conceptualization.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Data availability
Upon request, the corresponding author will provide the data used to support the study's conclusions.
References
- 1.Barnouti N.H., Al-Dabbagh S.S.M., Matti W.E. Face recognition: a literature review. Int. J. Appl. Inf. Syst. 2016;11(4):21–31. [Google Scholar]
- 2.Hassaballah M., Aly S. Face recognition: challenges, achievements and future directions. IET Comput. Vis. 2015;9(4):614–626. [Google Scholar]
- 3.Mulyono I.U.W., Susanto A., Rachmawanto E.H., Fahmi A., et al. 2019 International Seminar on Application for Technology of Information and Communication (iSemantic) IEEE; 2019. Performance analysis of face recognition using eigenface approach; pp. 1–5. [Google Scholar]
- 4.Wei X. University of Warwick; 2014. Unconstrained face recognition with occlusions. Ph.D. thesis. [Google Scholar]
- 5.Abdullah M., Wazzan M., Bo-Saeed S. Optimizing face recognition using pca. 2012. arXiv:1206.1515 arXiv preprint.
- 6.Bhele S.G., Mankar V., et al. A review paper on face recognition techniques. Int. J. Adv. Res. Comput. Eng. Technol. (IJARCET) 2012;1(8):339–346. [Google Scholar]
- 7.Kirby M., Sirovich L. Application of the Karhunen-Loeve procedure for the characterization of human faces. IEEE Trans. Pattern Anal. Mach. Intell. 1990;12(1):103–108. [Google Scholar]
- 8.Asiedu L., Mettle F.O., Nortey E., Yeboah E.S. Recognition of face images under angular constraints using dwt-pca/svd algorithm. Far East J. Math. Sci. 2017;102(11):2809–2830. [Google Scholar]
- 9.Sengupta S., Chen J.C., Castillo C., Patel V.M., Chellapa R., Jacobs D.W. Proceedings of the 2016 IEEE Winter Conference on Application of Computer Vision (WASV) IEEE; Piscataway, NJ: 2016. Frontal to profile face verification in the wild; pp. 1–9. [Google Scholar]
- 10.Mensah J.A., Asiedu L., Mettle F.O., Iddi S. Assessing the performance of dwt-pca/svd face recognition algorithm under multiple constraints. J. Appl. Math. 2021;2021:1–12. [Google Scholar]
- 11.Sundararajan K., Woodard D.L. Deep learning for biometrics: a survey. ACM Comput. Surv. (CSUR) 2018;51(3):1–34. [Google Scholar]
- 12.Picciali F., Di Somma V., Giampaolo F., Cuomo S., Fortino G. A survey on deep learning in medicine: why, how and when? Inf. Fusion. 2021;66:111–137. [Google Scholar]
- 13.Pandey I.R., Mayank R., Kundan K.S., Mathew T., Padmini M.S. Face recognition using machine learning. Int. J. Res. Eng. Technol. (IRJET) 2019;6(4) [Google Scholar]
- 14.Guo G., Zhang N. A survey on deep learning-based face recognition. Comput. Vis. Image Underst. 2019;189 [Google Scholar]
- 15.Maheen Z., Syed F., Khan J., Khurshid K. 2019 International Conference on Emerging Trends in Computing and Communication Engineering (ICETCCE) 2019. Deep face recognition for biometric authentication. [DOI] [Google Scholar]
- 16.Krizhevsky A., Sutskever I., Hinton G.E. Advances in Neural Information Processing Systems. 2012. Imagenet classification with deep convolutional neural networks; pp. 1097–1105. [Google Scholar]
- 17.Szegedy C., Liu W., Jia Y., Sermanet P., Reed S., Anguelov D., Erhan D., Vanhoucke V., Rabinovich A. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2015. Going deeper with convolutions; pp. 1–9. [Google Scholar]
- 18.He L., Li H., Zhang Q., Sun Z., He Z. 2016 IEEE 8th International Conference on Biometrics Theory, Applications and Systems (BTAS) IEEE; 2016. Multiscale representation for partial face recognition under near infrared illumination; pp. 1–7. [Google Scholar]
- 19.Prakash D., Madusanka N., Bhattacharjee S., Park H.-G., Kim C.-H., Choi H.-K. A comparative study of Alzheimer's disease classification using multiple transfer learning models. J. Multimed. Inf. Syst. 2019;6:209–216. [Google Scholar]
- 20.Schroff F., Kalenichenko D., Philbin J. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. 2015. Facenet: a unified embedding for face recognition and clustering; pp. 815–823. [Google Scholar]
- 21.Cahyono F., Wirawan W., Rachmadi R. 2020 4th International Conference on Vocational Education and Training (ICOVET) IEEE; 2020. Face recognition system using facenet algorithm for employee presence; pp. 57–62. [Google Scholar]
- 22.Adhinata F.D., Rakhmadani D.P., Wijayanto D. Fatigue detection on face image using facenet algorithm and k-nearest neighbor classifier. J. Inf. Syst. Eng. Bus. Intell. 2021;7(1):22–30. doi: 10.20473/jisebi.7.1.22-30. [DOI] [Google Scholar]
- 23.He M., Zhang J., Shan S., Kan M., Chen X. Deformable face net for pose invariant face recognition. Pattern Recognit. 2020;100 [Google Scholar]
- 24.William I., Rachmawanto E.H., Santoso H.A., Sari C.A., et al. 2019 Fourth International Conference on Informatics and Computing (ICIC) IEEE; 2019. Face recognition using facenet (survey, performance test, and comparison) pp. 1–6. [Google Scholar]
- 25.Mensah J.A., Appati J.K., Boateng E.K., Ocran E., Asiedu L. Facenet recognition algorithm subject to multiple constraints: assessment of the performance. Sci. Afr. 2024;23 [Google Scholar]
- 26.Longkumer N., Kumar M., Jaiswal A.K., Saxena R. Contrast enhancement using various statistical operations and neighborhood processing. Signal Image Process. 2014;5(2):51. [Google Scholar]
- 27.Anila S., Devarajan N. Preprocessing technique for face recognition applications under varying illumination conditions. Glob. J. Comput. Sci. Technol. 2012;12 (11-F) [Google Scholar]
- 28.Musa P., Al Rafi F., Lamsani M. 2018 Third International Conference on Informatics and Computing (ICIC) IEEE; 2018. A review: contrast-limited adaptive histogram equalization (clahe) methods to help the application of face recognition; pp. 1–6. [Google Scholar]
- 29.Kuran U., Kuran E.C. Parameter selection for clahe using multi-objective cuckoo search algorithm for image contrast enhancement. Int. Syst. Appl. 2021;12 [Google Scholar]
- 30.Gonzalez R.C., Woods R.E. 2nd edition. Prentice Hall; Upper Saddle River: 2002. Digital Image Processing. [Google Scholar]
- 31.Kociolek M., Materka A., Strzelecki M., Szczypin'ski P. Discrete wavelet transform-derived features for digital image texture analysis. International Conference on Signals and Electronic Systems; Lodz, Poland; 2001. pp. 99–104. [Google Scholar]
- 32.Asiedu L., Mensah J.A., Ayiah-Mensah F., Mettle F.O. Assessing the effect of data augmentation on occluded frontal faces using dwt-pca/svd recognition algorithm. Adv. Multimed. 2021:1–11. [Google Scholar]
- 33.Chang S.G., Yu B., Vetterli M. Adaptive wavelet thresholding for image denoising and compression. IEEE Trans. Image Process. 2000;9(9):1532–1546. doi: 10.1109/83.862633. [DOI] [PubMed] [Google Scholar]
- 34.Mairal J., Jenatton R., Obozinski G., Bach F. 2010. Vision, perception and multimedia understanding. [Google Scholar]
- 35.Gonzalez-Sosa E., Vera-Rodriguez R., Fierrez J., Ortega-Garcia J. Proceedings of the 2016 IEEE International Carnahan Conference on Security Technology (ICCST) 2016. Dealing with occlusions in face recognition by region-based fusion; pp. 1–6. [DOI] [Google Scholar]
- 36.Pain C.D., Egan G.F., Chen Z. Deep learning-based image reconstruction and post-processing methods in positron emission tomography for low-dose imaging and resolution enhancement. Eur. J. Nucl. Med. Mol. Imaging. 2022;49(9):3098–3118. doi: 10.1007/s00259-022-05746-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Fessler J.A. Model-based image reconstruction for mri. IEEE Signal Process. Mag. 2010;27(4):81–89. doi: 10.1109/MSP.2010.936726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Van Buuren S. CRC Press; Boca Raton, FL, USA: 2018. Flexible Imputation of Missing Data. [Google Scholar]
- 39.Azur M.J., Stuart E.A., Frangakis C., Leaf P.J. Multiple imputation by chained equations: what is it and how does it work? Int. J. Methods Psychiatr. Res. 2011;20(1):40–49. doi: 10.1002/mpr.329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Slade E., Naylor M.G. A fair comparison of tree-based and parametric methods in multiple imputation by chained equations. Stat. Med. 2020;39(8):1156–1166. doi: 10.1002/sim.8468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mera-Gaona M., Neumann U., Vargas-Canas R., López D.M. Evaluating the impact of multivariate imputation by mice in feature selection. PLoS ONE. 2021;16(7) doi: 10.1371/journal.pone.0254720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ayiah-Mensah F., Asiedu L., Mettle F.O., Minkah R. Recognition of augmented frontal face images using fft-pca/svd algorithm. Appl. Comput. Intell. Soft Comput. 2021;2021 [Google Scholar]
- 43.Hong S., Lynn H.S. Accuracy of random-forest-based imputation of missing data in the presence of non-normality, non-linearity, and interaction. BMC Med. Res. Methodol. 2020;20(1):1–12. doi: 10.1186/s12874-020-01080-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Stekhoven D.J., Bühlmann P. Missforest–non-parametric missing value imputation for mixed-type data. Bioinformatics. 2012;28(1):112–118. doi: 10.1093/bioinformatics/btr597. [DOI] [PubMed] [Google Scholar]
- 45.Fodor I.K. Livermore National Laboratory; Livermore, CA, USA: 2002. A survey of dimension reduction techniques.http://www.llnl.gov/CASC/sapphire/pubs/148494-pdf Tech. Rep., LLNL Technical Report, Lawrence. [Google Scholar]
- 46.Nguyen H.V., Bai L., Shen L. Local Gabor binary pattern whitened pca: a novel approach for face recognition from single image per person. Advances in Biometrics: Third International Conference, ICB 2009; ICB 2009, Alghero, Italy, June 2-5, 2009. Proceedings 3; 2009. pp. 269–278. [Google Scholar]
- 47.Kapoor S., Khanna S., Bhatia R. Facial gesture recognition using correlation and Mahalanobis distance. 2010. arXiv:1003.1819 arXiv preprint.
- 48.Jonsson K., Kittler J., Li Y.P., Matas J. Support vector machines for face authentication. Image Vis. Comput. 2002;20(5–6):369–375. [Google Scholar]
- 49.Mukkamala S., Janoski G., Sung A. Proceedings of the 2002 International Joint Conference on Neural Networks (IJCNN'02) 2002. Intrusion detection using neural networks and support vector machines; pp. 1702–1707. [DOI] [Google Scholar]
- 50.Chapman-Wardy C., Ocran E., Iddi S., Asiedu L. Classification of solid waste generation areas in the greater accra region using machine learning algorithms. Model Assist. Stat. Appl. 2023;18(4):359–371. [Google Scholar]
- 51.Tibshirani R., Hastie T., Narasimhan B., Chu G. Diagnosis of multiple cancer types by shrunken centroids of gene expression. Proc. Natl. Acad. Sci. 2002;99(10):6567–6572. doi: 10.1073/pnas.082099299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Alkan A., Günay M. Identification of emg signals using discriminant analysis and svm classifier. Expert Syst. Appl. 2012;39(1):44–47. [Google Scholar]
- 53.Sun J.J., Zhao J., Chen L.-C., Schroff F., Adam H., Liu T. View-invariant probabilistic embedding for human pose. Computer Vision–ECCV 2020: 16th European Conference; Glasgow, UK, August 23–28, 2020, Proceedings, Part V 16; Springer; 2020. pp. 53–70. [Google Scholar]
- 54.Jose E., Greeshma M., Haridas M.T., Supriya M. 2019 5th International Conference on Advanced Computing & Communication Systems (ICACCS) IEEE; 2019. Face recognition based surveillance system using facenet and mtcnn on jetson tx2; pp. 608–613. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Upon request, the corresponding author will provide the data used to support the study's conclusions.