Effects of boosting and waning in highly exposed populations on dengue epidemic dynamics

Abstract

Sequential infection with multiple dengue virus (DENV) serotypes is thought to induce enduring protection against dengue disease. However, long-term antibody waning has been observed after repeated DENV infection. Here, we provide evidence that highly immune Nicaraguan children and adults (n=4478) experience boosting and waning of antibodies during and after major Zika and dengue epidemics. We develop a susceptible-infected-recovered-susceptible (SIRS-type) model that tracks immunity by titer rather than number of infections to show that boosts in highly immune individuals can contribute to herd immunity, delaying their susceptibility to transmissible infection. In contrast, our model of lifelong immunity in highly immune individuals as previously assumed results in complete disease eradication after introduction. Periodic epidemics under this scenario can only be sustained with a constant influx of infected individuals into the population or high basic reproductive number. We also find that ZIKV infection can boost DENV immunity and produce delays and then surges in dengue epidemics as observed with real epidemiological data. This work provides insight into factors shaping periodicity in dengue incidence and may inform vaccine efforts to maintain population immunity.

One Sentence Summary:

Using a mathematical model and serological data collected longitudinally on children and adults, we show that antibody boosting and decay in highly immune individuals shape dengue epidemics.

INTRODUCTION:

Dengue virus (DENV) is the leading mosquito-borne viral agent, infecting up to 390 million people annually worldwide, 25% of whom suffer from clinical disease (1). Zika virus (ZIKV), a close relative of DENV also spread by Aedes mosquito vectors, was introduced into Latin America in 2013–2014 and spread in geographic areas where the four DENV serotypes (DENV1–4) were already endemic (2, 3). DENV infection, and possibly ZIKV infection, are thought to confer lifelong immunity against reinfection with that virus/serotype as well as cross-reactive antibodies that transiently protect but then wane. Such antibodies can facilitate viral infection and disease during secondary heterotypic infection by a mechanism called antibody-dependent enhancement (ADE) (4–7). Following secondary infection with a different DENV serotype, individuals are at reduced risk of future severe disease even from unexposed serotypes (8). Whether protection is maintained because immunity is long-lived or whether re-exposure helps maintain protection in those with multiple prior DENV infections, like adults, remains unexplored, with important implications for dengue vaccination.

In general, most dengue-endemic countries report cyclic and sometimes chaotic dengue epidemic dynamics with huge peaks and low to no troughs (9, 10). Compartmental susceptible- infected-recovered (SIR) models have been developed to understand these dynamics, encompassing single- or multi-serotype DENV transmission models where the mosquito population is explicitly tracked or accounted for indirectly using seasonal forcing (9–18). Dengue, like other infectious diseases, shows periodicity in incidence due to several potential causes, including temporal variation in transmission rates, stochasticity and nonlinear incidence due to mosquito ecology, host age-structure, human population size, and geography (16). ADE has also been modeled by assuming higher infectivity of secondary infected individuals and/or susceptibility enhancement, where first exposure increases susceptibility to heterologous infection (9, 11, 14–16, 19–21). However, epidemic patterns generated solely by ADE or heterogeneity in virus virulence are not consistent with the characteristic signatures observed in dengue case data, and a combination of seasonal variation in vector demography and, crucially, short-lived cross-immunity is sufficient to produce periodic dengue epidemics (11). Thus, the persistence or eradication of dengue depends on complex interaction mechanisms resulting from the host’s immunological response and efficiency of virus transmission by mosquitoes (22).

While most compartmental models of dengue have assumed that after two (or in some instances four) infections with distinct serotypes, individuals have life-long protection against all four serotypes (9, 16, 17, 19, 21, 23), recent immunological studies question this assumption, suggesting alternative model frameworks may be informative. First, homologous DENV reinfections do occur (22, 24, 25). Waggoner et al. reported detectable and high viremia in the homotypic reinfections (e.g. approximately 10⁷ RNA copies/mL of plasma) (24), which is a level expected to contribute to transmission (26), although further studies exploring the transmission competency of these infections are required. Second, anti-DENV binding antibodies wane for many years after secondary DENV infection, sometimes to the titers observed following first DENV infection, suggesting immunity after two infections may not persist (4, 27). One hypothesis is that frequent exposure to DENV may lead to infections that ‘boost’ the immune response and reduce future risk of DENV infection but without causing enough viremia to transmit (28). Boosts may be caused by homotypic re-exposure or exposure to a novel serotype when immunity is high, and are distinct from transmissible infections, which may be inapparent or symptomatic (29–31). In a study where individuals were vaccinated with a live attenuated tetravalent DENV vaccine and challenged 6 months later with DENV2, none of the individuals had detectable viremia (32). However, though transient, 43% of the participants had a ≥4-fold rise in antibody titer, demonstrating homotypic boosting (13, 14). A few transmission models have explored the role of boosting in general (33) and in protection against symptomatic and severe dengue (13, 14). Alexander et al. built two- and four-serotype models including immune waning, with and without boosting, and varying cross-protection to explain the fluctuations in the inapparent/symptomatic ratio in DENV infections documented worldwide (13). They found that homotypic and heterotypic boosts result in “primary” and secondary transmissible infections that are more likely to be inapparent than symptomatic (13). However, to our knowledge, existing dengue models were not designed to evaluate whether long-term waning of immunity and boosting in adults who are likely already exposed to multiple serotypes contribute to dengue epidemic periodicity. This is in part because measuring re-exposure to DENV in highly immune individuals is difficult because the force of infection of DENV in any given year is generally low. Further, individuals with multiple prior DENV infections often have high antibody titers that protect against infection and disease (27, 34), reducing the probability of detecting a rise in antibodies following exposure.

Here, we draw on concepts from theoretical models (13, 33, 35–37) to build a susceptible-infected-recovered-susceptible (SIRS-type) model that that tracks immunity by titer rather than number of prior infections to examine the effect of re-exposure on dengue epidemic dynamics. Our model was simulated to predict dengue incidence using estimates from the DENV binding antibody titers measured annually in children and adults in Nicaragua after the Zika pandemic and a major DENV2 epidemic, enabling more accurate estimates of boosting. The impact of some of the model assumptions on epidemic dynamics were also examined. Finally, we evaluate how well our model fits pediatric case data from Nicaragua compared to models with traditional assumptions about flavivirus interactions and immunity.

RESULTS:

Antibodies wane and boost in highly immune individuals after the Zika epidemic and a subsequent dengue epidemic.

The documented natural history of flavivirus epidemics in Nicaragua provides a unique opportunity to investigate the effect of immunological boosting across ages (38). Of note, the force of infection of dengue was very high (>50% of susceptible individuals infected per year) in the 1990s in Nicaragua as each serotype was being introduced to the Americas; thus, most adults by 2017 in Nicaragua had been previously infected with two or more serotypes (38–40). We analyzed anti-DENV binding antibodies measured by the DENV inhibition enzyme-linked immunosorbent assay (iELISA), which measures antibodies that bind cross-reactive epitopes on DENV1–4 virions (4, 34). The iELISA is associated with protection against dengue and Zika disease at high titers and with enhancement of dengue disease severity at low to intermediate titers. We analyzed the iELISA titers in two cohorts (n=4478 total participants) from 2017–2021, spanning the Zika pandemic in 2016 and a large DENV2 epidemic in 2019, with minimal flavivirus transmission in inter-epidemic years (Fig. 1A). The Nicaraguan Pediatric Dengue Cohort Study (PDCS) has followed approximately 10,000 participants ages 2–17 years since 2004. The Household Influenza Cohort Study (HICS) includes approximately 1000 adolescent and adult participants ranging in age from 11–84 who have been followed annually since 2017–2021 for anti-flavivirus antibodies. Across both cohorts during the Zika epidemic, 41% of children ages 2–14 were infected and 56% of adults ages 15–80 were infected (41, 42). In children, ZIKV infection strongly boosted cross-reactive antibodies to DENV measured by the iELISA that later waned over time (4).

Fig. 1. Cases and anti-DENV iELISA titers among participants in the Nicaraguan Household Influenza Cohort Study (HICS) and the Nicaraguan Pediatric Dengue Cohort Study (PDCS).

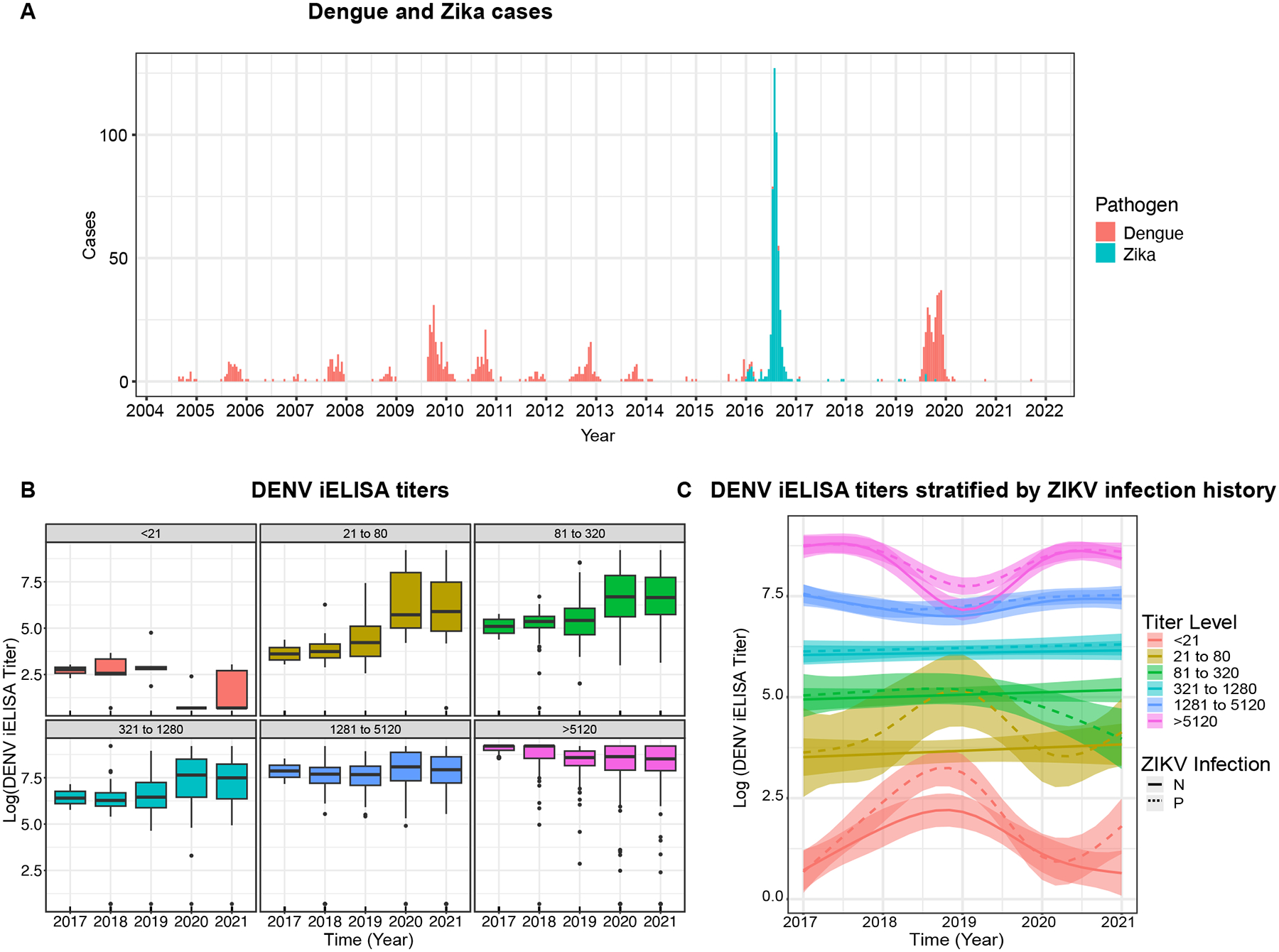
A. Weekly confirmed dengue and Zika cases in the PDCS, 2004 to 2021. B. Combined DENV iELISA titers over 5 years (2017–2021) in children and adults. Boxplots show means and interquartile ranges. C. Anti-DENV iELISA titer kinetics modeled by GAMM in children and adults, stratified by ZIKV blockade-of-binding (BOB) assay positivity measured in 2017 to confirm prior ZIKV infection. Estimated kinetics (colored lines) with 95% confidence intervals (shared regions) are shown. N and P denote ZIKV seronegative and positive by ZIKV BOB assay, respectively.

We first stratified individuals based on DENV iELISA titers following the 2016 Zika epidemic into antibody groups of 4-fold increments. In the highest titer groups (1280–5120 and >5120) we observed a constant decline in antibody titers from 2017 to 2019. Adults make up 53% of these groups. Unexpectedly, we observed a strong increase in titers across high-titer groups in 2019–2020 during the DENV2 epidemic, with 12% experiencing a ≥4-fold rise in antibodies, with a later decline from 2020 to 2021 (Fig. 1B). When we considered only adults (age≥18), a similar trend was observed, with 13% in the high-titer group experiencing a ≥4-fold rise following the DENV2 epidemic. Similar trends across all groups were observed when individuals were stratified by their 2016 ZIKV infection status (Fig. 1C). These findings suggest boosting and waning occurred following major Zika and dengue outbreaks in highly exposed Nicaraguan populations including adults.

Consistent with our previous findings that antibody kinetics are mostly stable after primary DENV infection (4), the lower titer groups (<1280) had stable antibody titers between epidemics (Fig. 1B). Notably, individuals in the low titer groups (<320), especially those with a documented ZIKV infection, had DENV iELISA titers that increased for multiple years before the dengue epidemic, as previously observed following primary ZIKV infection (4) (Fig. 1C). Across groups, DENV iELISA titers increased after 2019–2020 dengue epidemic, consistent with a high infection rate in these populations, with 13% of the naïve children seroconverting to DENV in 2019–2020.

We modeled the continuous trend in antibody titers over time using generalized additive mixed model (GAMM) to obtain the breakpoints in kinetics and then used piece-wise linear mixed models (LMM) to estimate the antibody half-lives for each of these periods. Both models include individual and group level effects to account for heterogeneity in the individuals’ antibody magnitude and kinetics (Fig. S1). In this analysis, we re-classified titer groups following the 2019 epidemic. A gradual decline in antibodies was observed in those with intermediate titers (1281–5120) following the 2016 Zika epidemic (${\text{t}}_{1/2}$:4.7 years, 95% confidence interval: 3.4 to 7.8) and 2019 dengue epidemic (${\text{t}}_{1/2}$:5.2 years, 2.7 to 127), while the highest titer group (>5120) had the shortest half-life (after Zika epidemic: ${\text{t}}_{1/2}$:2.2 years, 1.9 to 2.4; after dengue epidemic, ${\text{t}}_{1/2}:$ 2.9 years, 2.2 to 4.2). DENV iELISA titers were stable in the group with baseline titers between 320 and 1280 (${\text{t}}_{1/2}$:17 years (−26 to 6)). Conversely, individuals with low preexisting titers (<320), had a steady increase in titers following ZIKV infection, which stabilized after the dengue epidemic.

Thus, we found that antibody waning and boosting occurs even in highly exposed adults who either were already assumed to have been infected with DENV2 and/or to have broadly protective antibodies and immunity.

Antibody boosting and waning in the highly exposed individuals help drive dengue epidemic dynamics.

Based on these observations, we hypothesized that both homologous and heterologous DENV exposure may boost immunity when individuals have high enough titers to protect against disease. However, if titers wane below protective levels, regardless of number of prior exposures, individuals would be at risk of sustained infection that may lead to onward transmission and/or disease. To evaluate whether boosting due to re-exposure maintains herd immunity and modulates epidemic dynamics, we developed and analyzed a stochastic immunity-structured SIRS-like model (Fig. 2). Our model incorporates primary and secondary DENV infections but does not explicitly model distinct serotypes, and considers individual antibody waning and boosting between infections, as well as ADE. Our system ignores some complexities inherent in natural vector-host transmission and disease dynamics. However, we make reasonable assumptions on the population structure, dengue epidemiology, and transmission dynamics, such as a constant homogenously mixing population, direct between- host transmission and negligible disease-induced mortality, as supported by previous modelling studies (21, 43). Fully naïve individuals are born into the susceptible compartment $S_1$ and become infected at a rate defined by the force of infection, $\lambda \left(t\right)$. They recover into one of three immune compartments: $R_L,R_M$ and $R_H$. $R_L$ represents individuals with low antibody titers, who undergo an initial period of antibody cross-protection of ~6 months, based on previous estimates from the same cohort (Table S1) (4), then wane into a non-naïve susceptible compartment, $S_2$. However, a fraction of individuals experiencing primary infection end up with intermediate ($R_M$) or high ($R_H$) titers, consistent with observations that some individuals have higher titers even after a single DENV exposure. Previous models have evaluated the effect of ADE on transmission dynamics by assuming either an increased infectiousness with secondary infection or increased susceptibility to infection after primary infection (11, 21, 43–46). Since our model does not explicitly track the secondary infected group, and previous studies have found both ways of modeling ADE produce similar results, we assume ADE results in an increased susceptibility. Therefore, individuals in the $S_2$ compartment become infected at an enhanced rate, $\epsilon \lambda \left(t\right)$, representing ADE due to prior DENV immunity, and recover into the $R_L,R_M$ or $R_H$ compartments. Individuals move from high to low immune compartments by antibody waning. $R_H$ and $R_M$ waning parameters are assumed to be constants and are estimated from the high (>5120) and medium (1281–5120) DENV iELISA titer groups described above. Individuals move to higher immune compartments by boosting, which is proportional to the force of infection, $\lambda \left(t\right)$. The equations accompanying our model framework and the approach to calibrate our model parameters are described in the Method section. Based on our model calibration to dengue incidence data in Nicaragua (Fig. 3A), the full model’s 95% prediction interval contained the observed case counts. Other models (described below, Fig. 3B–D) did not capture case data within their 95% prediction intervals and had slightly higher Akaike Information Criterion (AIC) values.

Fig. 2. Susceptible-infected-recovered-susceptible compartmental DENV transmission model.

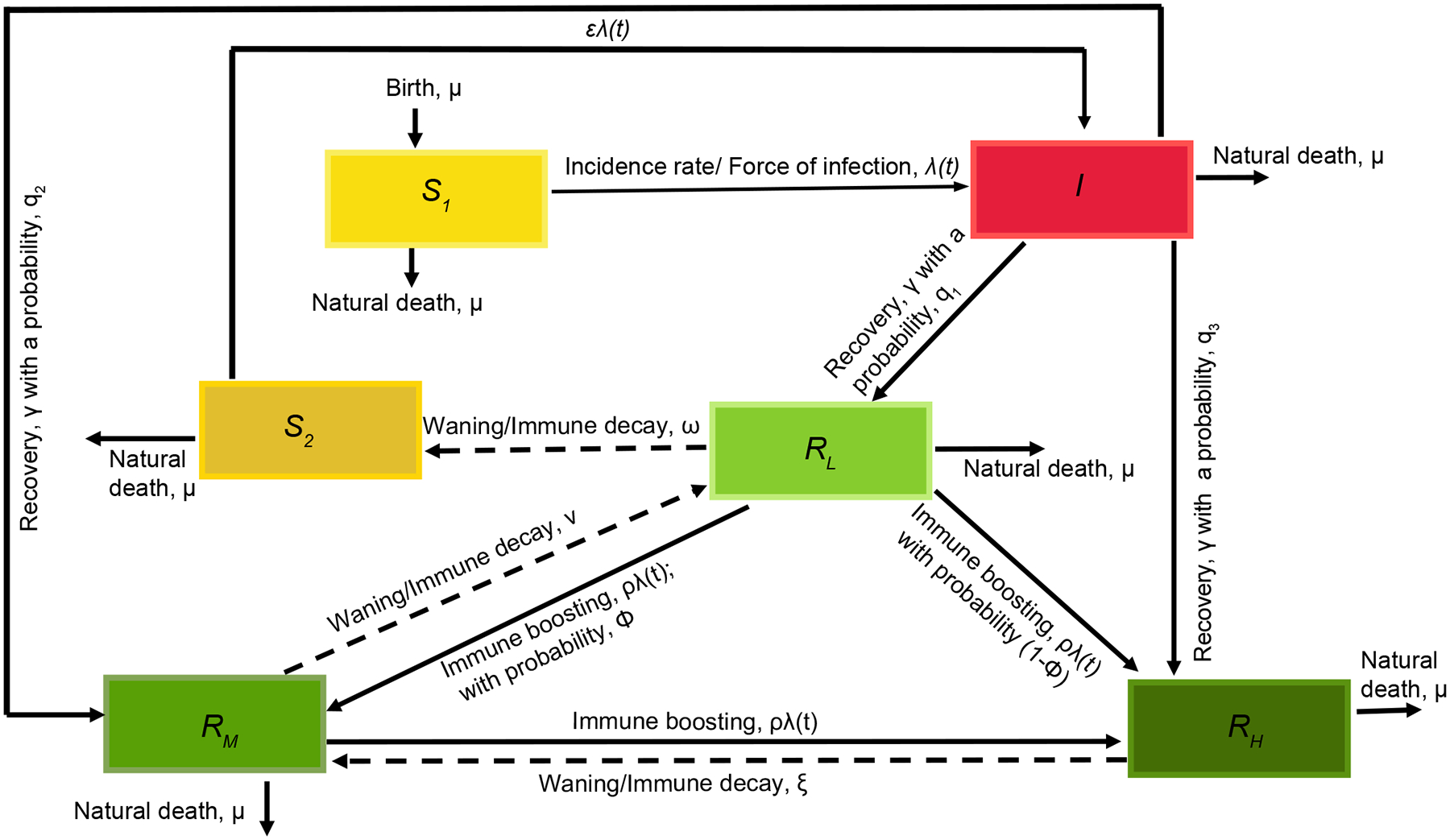
The broken arrows represent waning back to lower immune compartments and to the susceptible compartment.

Fig. 3. Model calibration to the dengue case data.

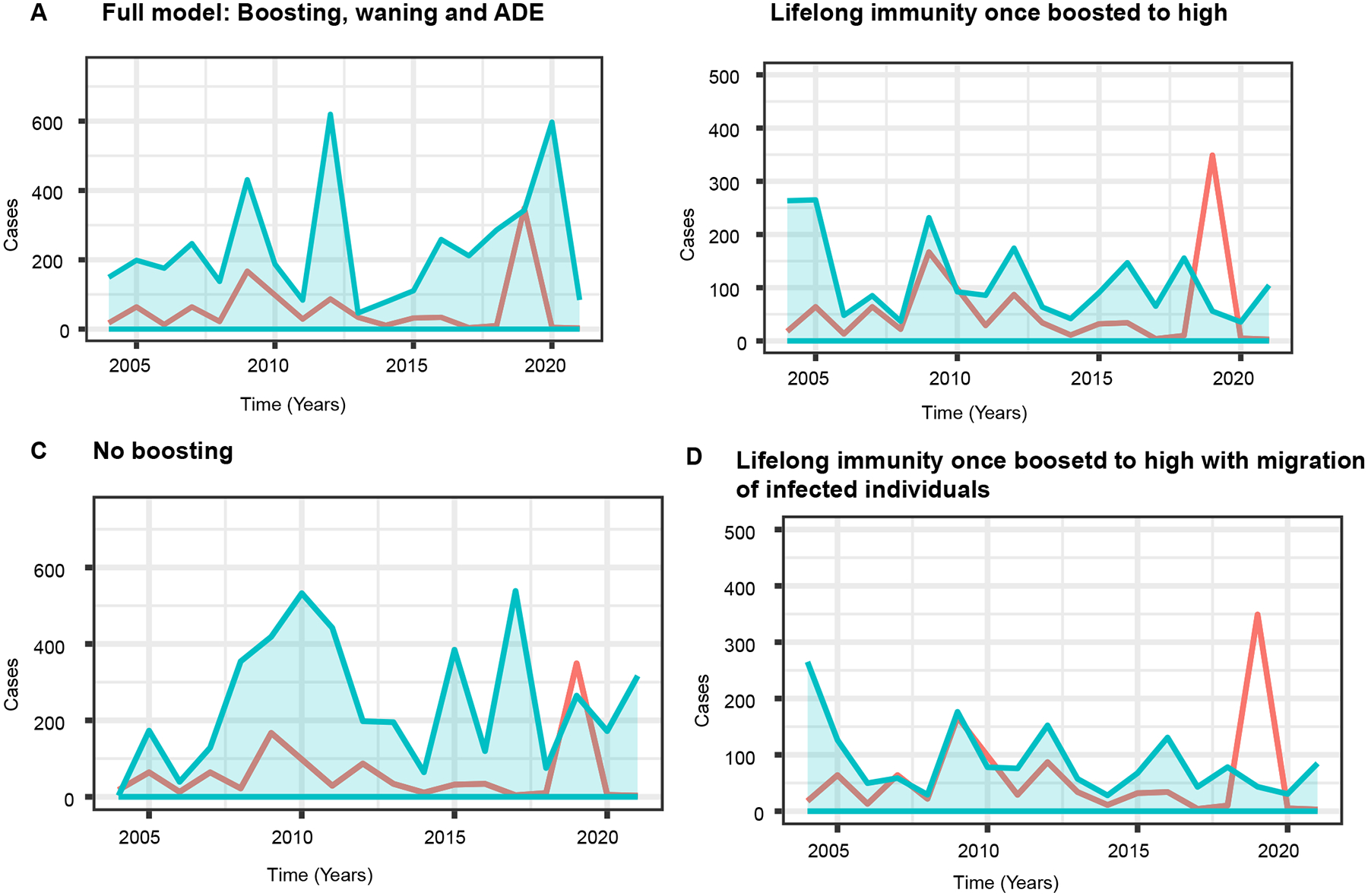
The red line denotes the Nicaraguan dengue case data in Fig. 1A, and the light-blue shaded region is the 95% prediction interval from the 50 model simulations using the maximum likelihood estimated parameters for fits to the case data. A. The full model assuming boosting, waning, and ADE (AIC=315.62; $\sigma =0.012$). B. Lifelong immunity once boosted to the high levels (${\text{R}}_{\text{H}}$) (AIC=316.53; $\sigma =0.015$). C. A model with transient immunity and no boosting (AIC=317.99 $\sigma =0.016$). D. Life-long immunity once boosted to the high levels with constant introduction of infection (immigration of infected individuals) into the population (AIC=316.50 $\sigma =0.014$).

We simulated our model to predict dengue dynamics over the next 30 years. We observe periods of close to no dengue cases and huge epidemics occurring periodically, consistent with our observed epidemic dynamics (Fig. 4A & B). We performed spectral analysis (wavelet power spectrum) of our simulated time-series of dengue case data to detect and quantify the cycles and synchrony of epidemics. The Morlet wavelet power spectrum slides Gaussian-shaped wavelets of different periodicities across the time-series to identify the cycles that best describes the data (i.e. “similarities” between the signal and the wavelet), with high power indicating a strong interepidemic signal (Fig. 4C). We then plot the time-averaged power spectrum to estimate the most prominent epidemic cycles observed across the time-series (Fig. 4D). Our analyses show that our time-series data is relatively complex with several significant modes of oscillations. Nevertheless, we see a prominent oscillating interepidemic cycle at 1–3 years during the whole simulation period (Fig. 4C & D). During periods following large epidemics, most of the population have higher levels of immunity. It then takes approximately 1–3 years for the population to become sufficiently susceptible to support a subsequent epidemic (Fig. 4B). The delay in susceptible build-up occurs because if a large proportion of the population have high immunity there are few chances for exposure or transmission and consequently for immune boosting. This would lead to waning of immunity in this population during the low transmission period and subsequent build-up of the susceptible individuals. For low-immune individuals, there are sufficient new births into the susceptible population to cause the low peaks observed in between the large epidemics. Interestingly, a second pattern occurring every about 10–12 years is also evident (Fig. 4C & D). We also observed a signal for an 18-year period; however, given the length of our time-series, this may not be generalizable. For comparison, we performed wavelet analysis of the observed Nicaraguan case data and found that it contained similar trends to the model predictions (Fig. 4E & F). Notably, we observed major peaks of dengue epidemics at 1 and 3-year periods (Fig. 4E). Similarly, a modest interepidemic pattern oscillating every 10 years is also observed, which might coincide with serotype-specific dengue outbreaks observed in the region and in the pediatric cohort (Fig. S2) (47–49) or regional climactic effects (50) (Fig. 4E & F).

Fig. 4. Full model assuming immune boosting, waning, and ADE.

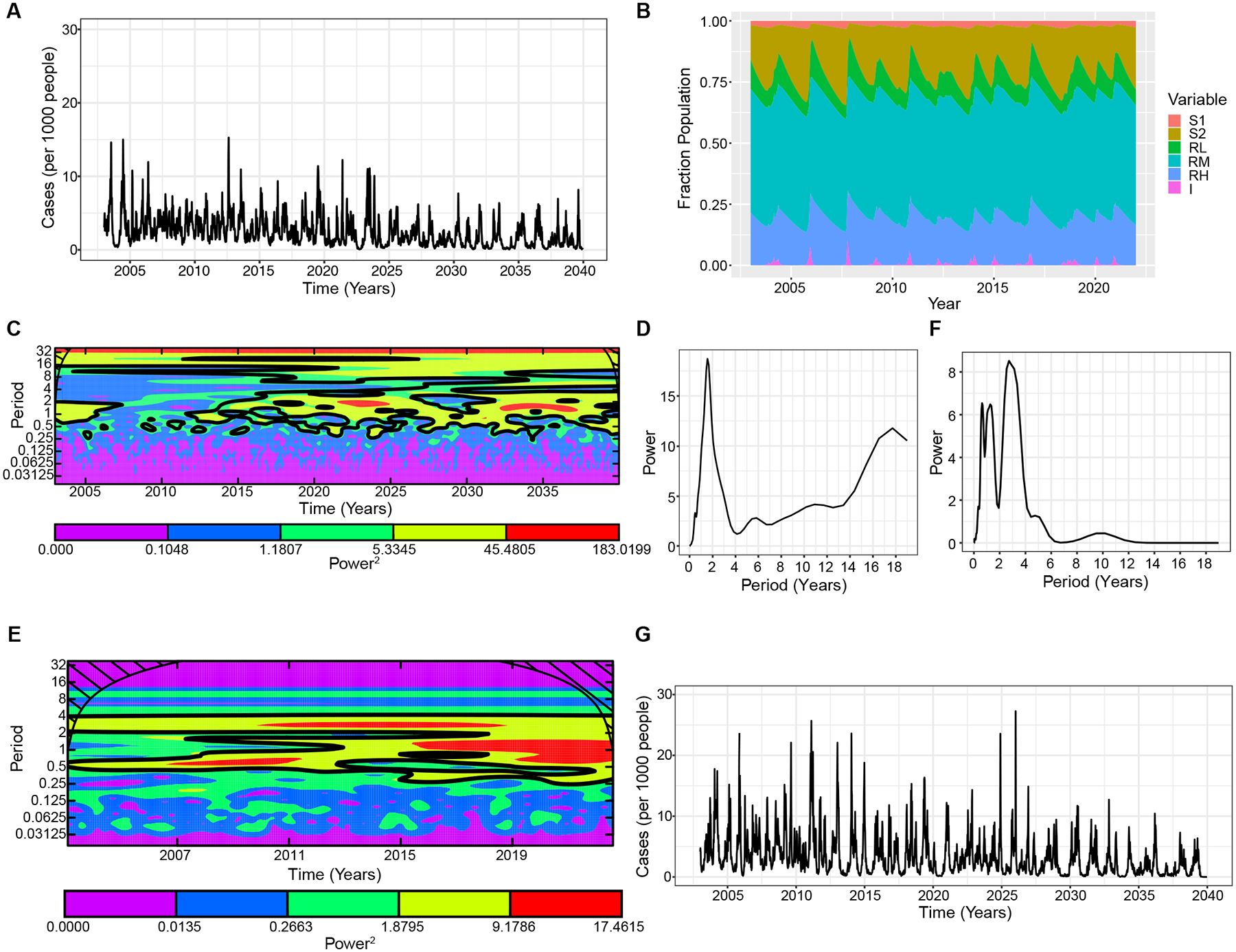
A. Simulated weekly dengue incidence in a population of 10 million, where the DENV reproduction number was set to 5 and individuals with previous DENV exposure experience 20% of the force of infection that a fully susceptible individual would. Simulation results are the mean of 10 realizations. B. Population distribution of each model compartment over time. C. Wavelet power spectrum (Morlet) of the time-series of log-transformed simulated weekly dengue incidence. The colors code for power values ranging from purple, low values, to red, high values. The black contours (outline) indicate the regions of greater than 95% confidence for the power values, indicating the most probable estimate of the interepidemic period. The cone of influence (black hashed lines) indicates where the power spectrum can be accurately estimated and is not influenced by effects of the edges of the time-series. D. Wavelet power spectrum for Fig. 4C averaged over the time course. E. Wavelet power spectrum of the observed Nicaraguan case data, and F. averaged over the time course. G. Simulated weekly dengue incidence for the full model as in Fig. 4A, but with seasonal forcing where $\lambda \left(t\right)=\beta I\left(t\right)/N\left(t\right)$ and $\beta ={\beta }_0(1+{\beta }_1\text{cos }2\pi t)$. ${\beta }_0=110$ is the baseline transmission rate, ${\beta }_1=0.15$ is the amplitude of seasonality. See Table S1 for other parameters used.

Seasonal effects can be explained by immune dynamics, and not just temporal variation in vector distributions.

Previous dengue transmission models have incorporated random variation in the transmission rate, as reported here, as well as seasonal forcing to account for the strong seasonal fluctuations in transmission observed in temperate regions throughout the world. To include the seasonal effect in the model, previous studies have assumed the average transmission rate varies sinusoidally. Without such seasonal forcing, dengue is often driven to extinction in model simulations or settles to a constant fraction of the population (9, 19), where stochastic extinction may occur due to low disease incidence (Fig. S3). However, in many regions, dengue incidence is high year-round, calling into question the assumption of such a strong seasonal forcing effect (51). Interestingly, in our full waning and boosting model, realistic dengue epidemic patterns were observed with a frequency-dependent transmission subject only to a relatively small degree of stochasticity representing environmental effects. Hence, antibody titers and seropositivity rates are sufficient to explain the reoccurrence of dengue epidemics, contrary to previous studies finding that synchronization of epidemics to a particular time is due to seasonal forcing. To evaluate if our results changed by incorporating seasonal forcing, we employed a similar approach to previous models and included a seasonal effect in our force of infection. We simulated our modified model and the results showed similar trends, but with higher absolute incidence compared to the models with only random variation in the transmission rate (Fig. 4G).

Model assuming lifelong immunity once individuals boost to the high immune group shows long inter-epidemic periods with constant influx of infected individuals into the population.

To test how our waning and boosting model compares to existing dengue transmission models, we developed a null model where we assume that low to intermediate immunity is temporary and wanes to titers where reinfection is possible. However, highly immune individuals ($R_H$) do not wane back to lower immune levels ($\xi =0$) and are permanently protected against reinfection, analogous to dengue models assuming that after secondary DENV infection, individuals are protected and no longer contribute to transmission. Surprisingly, our results show that the interaction of immune boosting and waning of the low and intermediate immune levels is not enough to sustain realistic dengue epidemic dynamics (Fig. 5A), even with seasonal forcing, as included in most dengue models (Fig. S4A). The epidemic dynamics are characterized by sharp epidemic spikes interspersed by intervals of extremely low (or no) dengue incidence, and we observe complete eradication of disease soon after introduction. However, if we assume a constant influx of infected individuals through immigration into the population, subsequent periodic epidemics are sustained with longer interepidemic periods (3-year periods) (Fig. 5 B–D). Here, we also observe peaks occurring at around a 12-year period.

Fig. 5. Comparison of simulated weekly dengue incidence for two distinct models of life-long immunity.

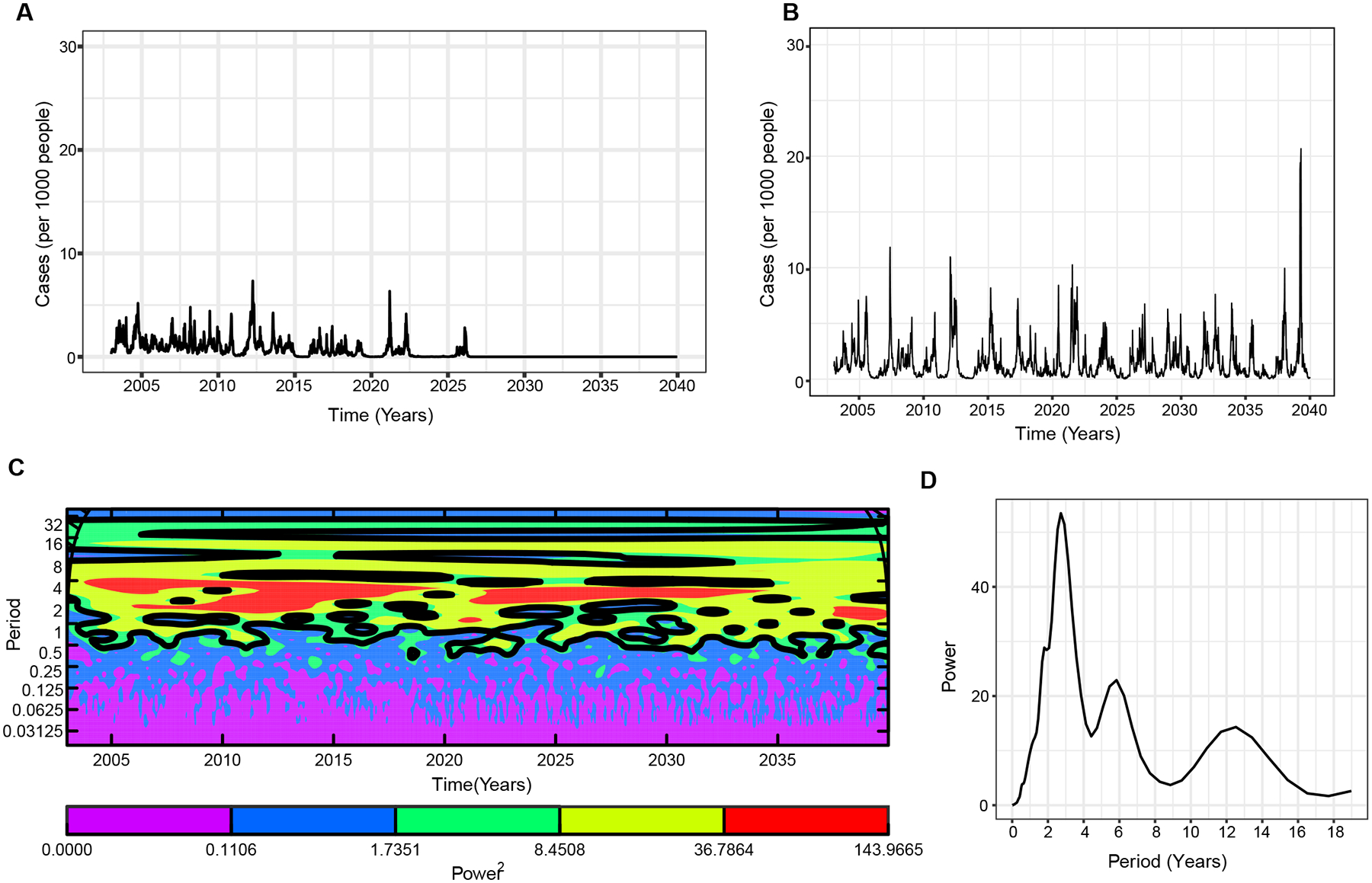
A. Life-long immunity once individuals are boosted to the high immune group, assuming zero waning rate in the $R_H$ compartment. B. Same as A, but with constant influx of infections incorporated in the force of infection as $\lambda \left(t\right)=(\iota +\beta I\left(t\right))/N\left(t\right)$; where $\iota =10$. Simulation results of the mean of 10 realizations. C. Wavelet power spectrum (Morlet) of the time-series of the log-transformed weekly dengue incidence in B, and D. averaged over the time course. The black contours in C (outline) indicate the regions of greater than 95% confidence for the power values. See Table S1 for other parameters used.

Previous studies have highlighted other parameters that result in disease extinction or persistence over inter-epidemic periods in endemic regions. Host’s infectious period (52), population size/critical community size (53), spatial structure (54), stochasticity/seasonality (55), transmission rate/route (56) and viral pathogenicity captured in our model through ADE have been shown to impact the epidemic dynamics observed in diseases conferring some life-long immunity (16, 57). Furthermore, Teissier et al. showed a long-term circulation of DENV for decades across French Polynesia in regions where the estimated critical community size of 175,000 (a population size much lower than Managua, Nicaragua (47)) was only attained in the early 2000 (53), further suggesting other important sources of DENV transmission in small and large communities. To further investigate other phenomena that may affect the periodic cycles in immune population, we also simulated our lifelong immunity model assuming a relatively high basic reproduction number $R_0=5$ as seen in highly pathogenic organisms such as measles (57–59). We found an oscillatory dynamic marked by low and high incidences (Fig. S4B). Similarly, increasing the host’s infectious period to 20 days results in oscillatory disease persistence though at low levels which might result in stochastic extinction (Fig. S4C). Despite observing realistic dynamics with a high basic reproduction number, $R_0=5$ is relatively high for dengue, especially in Managua region. Overall, similar to the model analyzed by Ferguson et al. (43) where introduction of new infections into the population of moderate size preserved cyclic epidemic behavior in a life-long strain-specific immunity model, we show here the effect of this modification in recovering the cycles observed in endemic regions.

A model Without Boosting Cannot Explain Large Periods Observed Between Dengue Epidemics.

We next consider a version of our full model, but without boosting in the immune compartments or seasonal forcing. We observe large epidemics occurring annually, albeit of varying amplitude (Fig. 6A–C), contrary to the pattern observed in the Nicaraguan cohort case data (Fig. 1A). As such, this model demonstrates why models incorporating other interacting immunological mechanisms like boosting help explain observed epidemic dynamics.

Fig. 6. Model with waning and ADE, but without boosting.

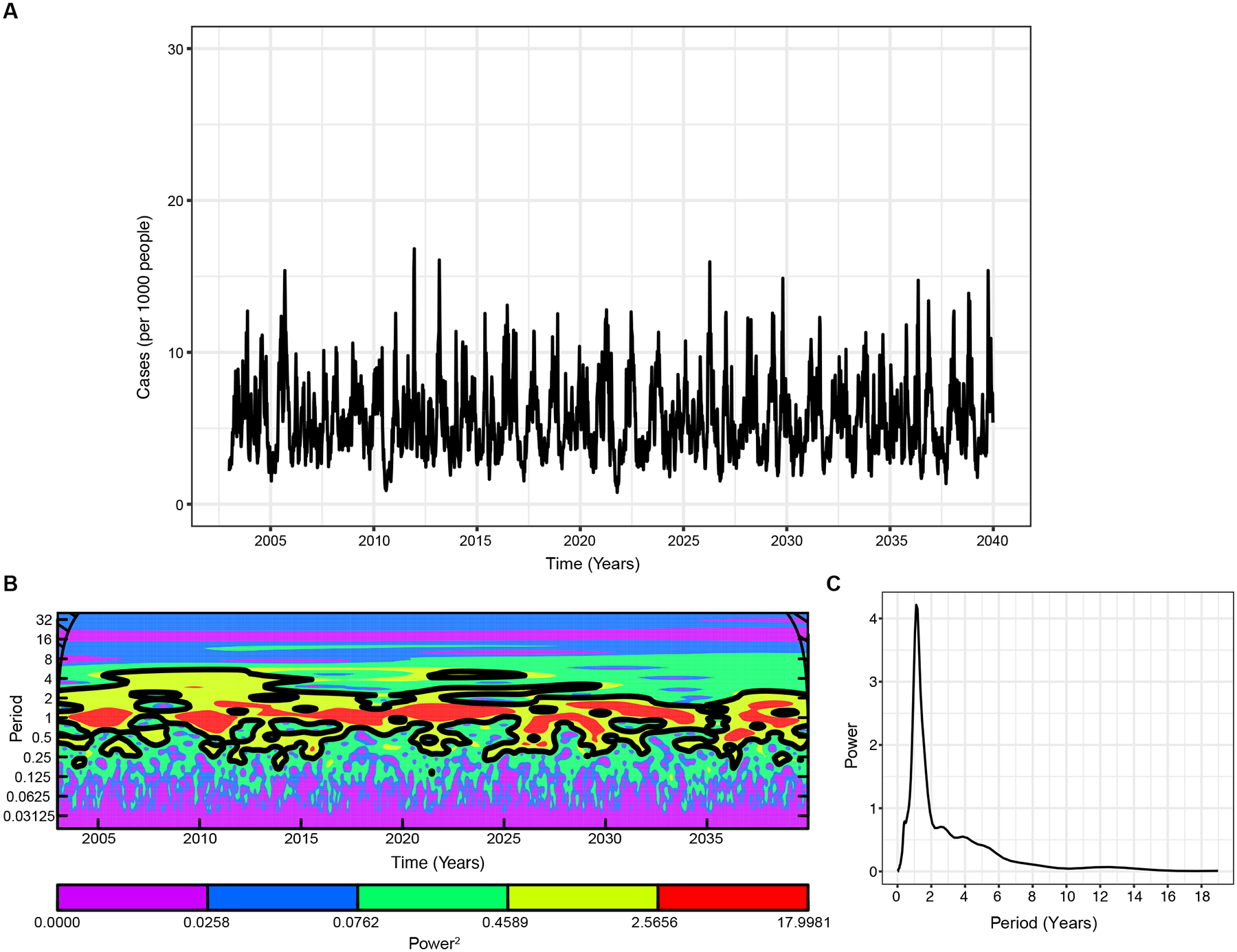
A. The simulated weekly dengue incidence. B. The Morlet wavelet power spectrum of the time-series of log-transformed weekly dengue incidence. The black contours (outline) indicate the regions of greater than 95% confidence for the power values C. The wavelet power spectrum averaged over the time course. Here boosting strength, $\rho =0$.

ZIKV infection modulates dengue immunity and subsequent dengue epidemics.

The introduction of ZIKV between 2013 and 2017 caused a pandemic across the Americas, followed by a continent-wide period of low arbovirus incidence and then a dengue outbreak in 2019 (60, 61). We previously observed that anti-DENV antibody titers either increased or remained constant after ZIKV infection in naïve individuals but were initially boosted and then declined in individuals with histories of DENV infection, in both instances to titers that can enhance future risk of dengue disease (4, 62). We modified our DENV transmission model (Supplementary Fig. S5) to investigate the effects of ZIKV exposure on an individual’s anti-DENV immune status and in turn its effect on dengue epidemic dynamics. Together with the parameters estimated from our simple Zika epidemic model (see Supplementary Fig. S6), we used our serological data to measure the probability of DENV boost by the DENV iELISA following exposure to ZIKV, which was detected using the highly specific ZIKV NS1 BOB assay (63). We performed simulations where ZIKV was introduced to a population with DENV immunity in 2016, reflecting the observed detection of ZIKV in Nicaragua. Consistent with observed incidence, in simulations where ZIKV infection boosts immunity across the immune groups and moves naïve individuals to ${\text{R}}_{\text{L}}$, we observed low dengue incidence during the large Zika epidemic, followed by low dengue transmission until dengue caused a large epidemic three years later (Fig. 7A). However, assuming ZIKV infection only boosts immunity in the immune groups, we observe a period of cross-immunity with low dengue cases in the year of the Zika epidemic and possibly the succeeding years (Fig. 7B). These observations suggest ZIKV infection may have affected the DENV-immune population and help explain the low dengue during and after the Zika pandemic (61), while ZIKV infection mediating ADE in otherwise naïve individuals may have contributed to the resurgence of dengue.

Fig. 7.

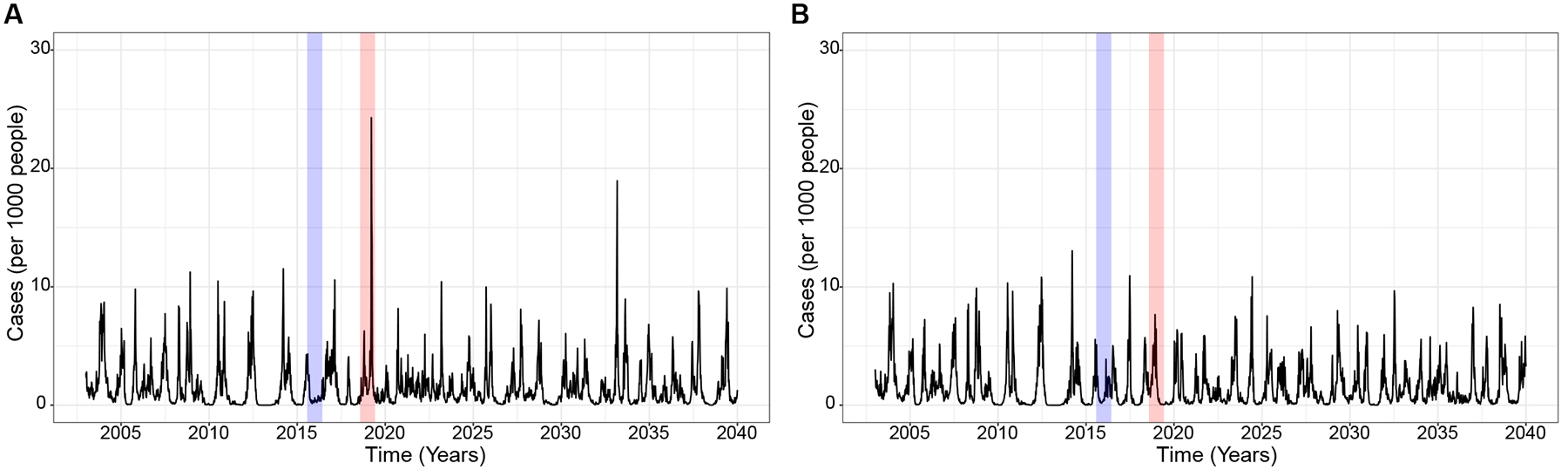
Simulated weekly dengue incidence incorporating immune-mediated interactions between DENV and ZIKV. The Zika introduction in 2016 (blue) and dengue epidemic in 2019 (red) are highlighted. Models assume ZIKV infection boosts immune groups and either A. moves naïve individuals to the ${\text{R}}_{\text{L}}$ compartment or B. does not. All the parameters used here are in Table S1. Additionally, we estimated parameters associated with the Zika effect from our cohort described above. We report the proportion of individuals who were infected with ZIKV in 2016 (infection probability following ZIKV exposure, $d=0.4$) and following ZIKV infection, the proportion of naïve, $S_1$, lower immune group ${,R}_L$ and intermediate immune group, $R_M$ that experienced a ≥4-fold rise in cross-reactive antibodies (boosting) were, $k_1=0.4,k_2=0.7$ and $k_3=0.7$, respectively.

DISCUSSION:

In this study, we developed a model framework with immune boosting, waning, and ADE to elucidate the mechanisms underlying dengue epidemic patterns. Using antibody titers to DENV and ZIKV measured annually in Nicaraguan household and pediatric cohorts, we show that boosting and waning occur following major Zika and dengue epidemics in highly exposed Nicaraguan populations, including adults. Surprisingly, our analyses suggest epidemic dynamics are best explained when antibodies wane and are boosted by re-exposure in highly immune individuals.

Previous dengue modeling studies with two or four serotypes have shown that periodicity in dengue incidence can be explained by enhancement between serotypes, transient cross-protective immunity, as well as vector distribution, human population size, geography, and seasonality (9, 11, 16, 17, 21, 23). As we find in our study, loss of temporary cross-protective immunity creates a time delay that can cause fluctuations in disease dynamics, as also shown in a Mumps epidemic dynamics study (64). A recent model also showed that boosting can increase temporary cross-protective immunity and explain fluctuations in the annual symptomatic to inapparent DENV infection ratio (13, 65, 66). However, previous dengue models have assumed complete protection against prior infecting serotypes, and most models have assumed complete protection against all serotypes after two sequential infections, in contrast with recent findings that anti-DENV antibodies wane for many years after secondary DENV infection (4, 27). Our unique model framework tracks immunity by titer rather than number of prior infections or disease outcome, and our key result demonstrates that the interaction between boosting and waning drives dengue epidemics. We found that low dengue case counts, as observed in Nicaragua and other regions, coincided with periods when population-level susceptibility to dengue is building up as immunity wanes in the highly immune individuals until high susceptibility helps fuel large dengue epidemics in upcoming seasons. Moreover, continued transmission during these low dengue periods is sustained mostly by new births and the transient immune compartment individuals that wane back to the enhanced susceptible compartment. Our model behavior is likely related to the complex periodicity and chaotic oscillations that boosting and waning generate in the system, exacerbated by the inherent oscillations introduced by the random variation in the transmission rate.

Our results show that the interaction of immune boosting and waning without the seasonal forcing similarly produces realistic dengue epidemic dynamics seen in the Nicaraguan cohort with huge epidemics occurring periodically, suggesting that immune-mediated mechanisms could explain the reoccurrence of dengue epidemics. Interestingly, boosting of immunity has also been reported to prolong the period of protection and subsequently maintain oscillations in pertussis disease prevalence (67) and together with vaccination, immune waning and boosting was found sufficient for resurgence of pertussis in a pertussis disease dynamics model (68). Separately, a COVID-19 modelling study found a reduction in infections with an increase in vaccination of the young adults in addition to the older population highlighting the importance of immune boosting in the population and overall epidemic dynamics (69).

Our study has several limitations. First, we use binding antibody titers as a proxy for immunity. Other immune components, such as specific populations of neutralizing antibodies and CD4⁺ and CD8⁺ T cell responses, likely contribute to protective immunity against dengue and Zika and may not correlate with binding antibodies (70–73). Our modeling framework is designed to understand the role of immune kinetics on disease transmission and epidemic dynamics and thus can be extended as the dengue field collects richer data on other aspects of immunity at the population level. Second, despite the complex patterns of mixing among individuals, our model assumes homogenous mixing, and does not account for demographic transition (equal birth and death rates). However, we did explore demographic effects by considering immigration of infected individuals, and we were able to approximate realistic dengue epidemics, despite lifelong protection in the highly exposed individuals. Further, our model was only simulated and calibrated for the dengue epidemics observed in Nicaragua. Our model framework is generalizable and could be adapted to examine factors shaping periodicity in incidence for many infectious diseases such as influenza, pertussis, and coronaviruses that induce imperfect immunity that is only partially protective, can wane over time, and has complicated interactions due to immune boosting. This model framework could also inform vaccine efforts to maintain population immunity.

Overall, we find that boosting and waning due to flavivirus exposure of immune adults shape dengue epidemics in our model. This finding has implications for future control of dengue. While ideal dengue vaccines would provide full, lifelong protection against all four serotypes, some vaccines enhance dengue in naïve individuals (74). Further, waning vaccine protection, even in previously DENV exposed individuals, is seen over time, suggesting boosters may be required (75, 76). Our model suggests that even if a dengue vaccine were equivalent to natural DENV infection, boosters may still be required both in children and adults to maintain sufficient levels of protective immunity and suppress epidemics. Our model also provides evidence that ZIKV infection modulated DENV herd immunity and delayed and then amplifies dengue epidemics, consistent with epidemiological observations. This finding suggests ZIKV infections and potentially ZIKV vaccines may modulate dengue epidemics. Our modeling study draws on new immunological insights into anti-DENV immunity and helps explain mechanisms driving dengue epidemics, informing vaccine and non-pharmaceutical efforts to maintain broad immunity over several decades.

MATERIALS AND METHODS:

Study Design

The objective of this study was to quantify the contributions of re-exposure on anti-DENV antibody kinetics and subsequent dengue epidemics dynamics. To do this, we used serological data collected as part of two longitudinal observational cohort studies in Nicaragua, following the guidelines in the Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) checklist. In this study, we used antibody titers to DENV measured by the inhibition ELISA and ZIKV measured by the NS1 blockade-of-binding assay on samples collected annually from participants in the Nicaraguan Pediatric Dengue Cohort Study (PDCS) and Household Influenza Cohort Study (HICS) (n=4478 total participants) from 2017–2021. The antibody titers were measured in the annual samples collected in March, during the low arbovirus transmission season, and 5 to 8 months after peak transmission season. We have previously shown that there are dramatic changes in antibody titers in the first 4 months after infection in this population, but by 6 to 8 months, antibody kinetics are stabilizing or reaching their long-term rate of decay. All measured titers were included in the analyses. The study design and sample size for the initial and subsequent PDCS and HICS cohorts have been described previously (4, 38, 41, 77, 78).

Ethics Statement

The PDCS was reviewed and approved by the institutional review boards of the University of California, Berkeley (2010-09-2245), the University of Michigan (HUM00091606), and the Nicaraguan Ministry of Health (CIRE-09/03/07–008). The HICS was approved by the institutional review boards at the University of Michigan (HUM00119145) and the Nicaraguan Ministry of Health (CIRE05/04/12–080). Participants in the HICS study were approached to participate in an arbovirus study, and those that consented were asked to complete an arbovirus survey every March/April. Parents or legal guardians of all pediatric subjects provided written informed consent. Participants aged 6 to 14 years of age provided oral assent, and participants aged 15 to 17 provided written assent. Participants 18 years of age and older provided written informed consent.

Statistical Analyses

All statistical and model analyses were performed using R Statistical Software (v4.2.1; R Development Core Team 2022) (79). We assumed antibody titers kinetics follow a non-linear function of time and modeled the kinetics using generalized additive mixed model (GAM, non-parametric model). The GAM model accounts for clustering at the individual level by incorporating random effects. We assume subject-specific slope and intercept which accounts for the difference in individuals’ starting titers and antibody rates. The GAM approximates the points of inflection. Antibody half-lives were then estimated by modeling each phase of decay or rise using multiphasic linear mixed models.

Mathematical Model

Using the serological data described above, we model DENV transmission in Nicaragua. We develop a SIRS-like immune-structured model considering a closed and homogeneously mixing population with the constant population size $\text{N}$ divided into three main parts: susceptible, infected, and recovered populations. Our model extends from the theoretical model frameworks by Barbarossa et al. (33, 35, 80). Here, we categorize the recovered population into three compartments tracking immunity by titer: $R_L$, from individuals with transient immunity, $R_M$, from individuals with intermediate immunity, and $R_H$, from those with high immunity. Fig. 2 shows the population movement between compartments.

We define $\mu$ as the birth (and death) rate for a constant population. We assume that the death rate is equal for members of all six compartments, and because of the nature of dengue disease, we assume disease-related death is negligible. Susceptible individuals become infected at a rate $\lambda \left(\text{t}\right)$, a frequency-dependent transmission, which assumes the rate of infection is independent of population density upon contact with the infected individuals. The Nicaraguan cohort studied here is well-mixed hence, the assumption that a person’s contacts are randomly distributed among all others in the population (homogeneous mixing) implying that all the infected cases equally contribute to subsequent infection. Infected individuals recover at a rate $\gamma >0$ that is, $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\gamma $}\right.$ is the infectious period (infection duration).

Because our main aim is to study the influence of immune boosting on the dynamics of dengue epidemics, we first consider a scenario where stochasticity was solely due to the white noise in the external environment. Therefore, we assume the $\lambda \left(\text{t}\right)=\beta I\left(t\right)/N\left(t\right)$ representing the average transmission rate in the stochastic setting in our system is subject to some random environmental effects. We then evaluate the effect of introducing seasonal effects in DENV transmission, employing a similar approach to previous studies, and have assumed the average transmission rate $\stackrel{-}{\beta }$ varies sinusoidally according to the formula $\stackrel{-}{\beta }={\beta }_0(1+{\beta }_1\text{cos }2\pi t)$.

Our full model is governed by the following equations, where $S_1$ denotes naïve individuals and $S_2$ susceptible individuals with enhanced susceptibility. $I$ is the infected population. $R$, the recovered individuals, are further divided into three compartments described hereafter.

$$\frac{d{S}_1}{dt}=\mu N-\lambda \left(t\right)S_1-\mu S_1,$$

$$\frac{d{S}_2}{dt}=-\epsilon \lambda \left(t\right)S_2-\mu S_2+\Psi$$

$$\frac{dI}{dt}=\lambda \left(t\right)S_1+\rho \lambda \left(t\right)S_2-\left(\gamma +\mu \right)I,$$

In general, for the immune population (total recovered population), we let $r\left(t,a\right)$ denote the density of immune individuals at time $t$ with antibody level $a\in \left[a_{min},a_{max}\right],0<a_{min}<a_{max}<\infty$. Thus, $R\left(t\right)={\int }_{a_{min}}^{a_{max}}r\left(t,a\right)da$ gives the total recovered population. We assume that individuals who recover at time $t$ enter the immune compartment (R) with a level of immunity ${{\stackrel{-}{a},a}_{min}<\stackrel{-}{a}<a}_{max}$. We further divide the recovered population into three categories, $R_L\left(t\right)≔r\left(t,a_L\right)$, recovered individuals with transient levels of antibodies at time $t$. Following re-exposure (dependent on force of infection), individuals have a probability, $\varphi$ of boosting to intermediate levels and $\left(1-\varphi \right)$ of boosting to higher antibody levels. In the absence of boosting, antibodies decay at a rate $\omega ≔g\left(a_L\right)=\frac{d}{dt}{a}_L\left(t\right)>0$, and at a minimal value $a_{min}$, the host becomes susceptible with an increased risk. This is captured by increasing susceptibility to infection per contact by a factor $\epsilon (\epsilon >1)$. On the other hand, $R_M\left(t\right)≔r\left(t,a_M\right)$ tracks the recovered individuals with intermediate levels of antibodies at time $t$. These individuals can boost and move to $R_H$, and their antibodies decay at rate $\nu ≔g\left(a_M\right)>0$. Lastly we have, $R_H\left(t\right)≔r\left(t,a_H\right)$, the recovered individuals with high level of antibodies at time $t$ having immune decay at a rate $\xi ≔g\left(a_H\right)>0$. The highest immune group, $R_H\left(t\right)$ experience immune boost to maximal level. However, we consider a scenario where the immune boost by highest immune group is negligible given the high antibody levels in these individuals. Therefore, we have the following ODEs for the susceptible and infected compartments coupled with PDEs of the immune populations structured by their level of immunity expressing the rate of change in the density of recovered individuals according to immune level due to natural waning, mortality, and boosting. In the population-structured model that follows, the transition occurs in both directions, that is, there is increase and decrease in the population. The population is governed by transport process with decay of immunity and boosting to any higher immune level. $\Psi$ is given by the number $g\left(a_L\right)r\left(t,a_L\right)$ of immune hosts who reach the minimal level of immunity. Also, we consider recovery to either of the three immune compartments $R_L,R_M$ and $R_H$ with probabilities $q_1,q_2$ and $q_3$ respectively.

$$\frac{d{S}_1}{dt}=\mu N\left(t\right)-\lambda \left(t\right)S_1\left(t\right)-\mu S_1\left(t\right),\frac{d{S}_2}{dt}=-\epsilon \lambda \left(t\right)S_2\left(t\right)-\mu S_2\left(t\right)+\Psi ,$$

$$\frac{dI}{dt}=\lambda \left(t\right)S_1\left(t\right)+\epsilon \lambda \left(t\right)S_2\left(t\right)-\left(\gamma +\mu \right)I\left(t\right),$$

$$\frac{\partial }{\partial t}r\left(t,a_L\right)-\frac{\partial }{\partial a}\left(g\left(a_L\right)r\left(t,a_L\right)\right)=-\mu r\left(t,a_L\right)-\rho \lambda \left(t\right)r\left(t,a_L\right)+g\left(a_M\right)r\left(t,a_M\right)+q_1\gamma I\left(t\right)$$

$$\frac{\partial }{\partial t}r\left(t,a_M\right)-\frac{\partial }{\partial a}\left(g\left(a_M\right)r\left(t,a_M\right)\right)=-\mu r\left(t,a_M\right)+q_2\gamma I\left(t\right)+\rho \lambda \left(t\right)\left({\int }_{a_L}^{a_M}p\left(a_M,\stackrel{-}{a}\right)r\left(t,\stackrel{-}{a}\right)d\stackrel{-}{a}-r\left(t,a_M\right)\right)+g\left(a_H\right)r\left(t,a_H\right)$$

$$\frac{\partial }{\partial t}r\left(t,a_H\right)-\frac{\partial }{\partial a}\left(g\left(a_H\right)r\left(t,a_H\right)\right)=-\mu r\left(t,a_H\right)+q_3\gamma I\left(t\right)+\rho \lambda \left(t\right)\left({\int }_{a_L}^{a_H}p\left(a_H,\stackrel{-}{a}\right)r\left(t,\stackrel{-}{a}\right)d\stackrel{-}{a}+r\left(t,a_M\right)\right)$$

for $t>0$ and $a\in [a_{min},a_{max}]$ with boundary condition

$$R_{a_{max}}\left(t\right)≔r\left(t,a_{max}\right)g\left(a_{max}\right)=\rho \lambda \left(t\right){\int }_{a_H}^{a_{max}}p\left(a_{max},\stackrel{-}{a}\right)r\left(t,\stackrel{-}{a}\right)d\stackrel{-}{a}=\rho \lambda \left(t\right)R_H\left(t\right).$$

Since $S_1,S_2,$ and $I$ do not depend on $a$ but only time, the general initial conditions are $S_1\left(0,a\right)=S_1\left(0\right)>0,S_2\left(0,a\right)=S_2\left(0\right)=0,I\left(0,a\right)=I\left(0\right)\ge 0,$ and a non-negative initial condition/distribution for each immune compartment $r\left(0,a\right)=\phi \left(a\right),a\in [a_{min},a_{max}]$.

We specify boosting probability $p\left(a,\stackrel{-}{a}\right)$ with $a\in [a_{min},a_{max}]$ as

$$p\left(a,\stackrel{-}{a}\right)=\left\{\begin{array}{c}\varphi if \stackrel{-}{a}= a_L and a= a_M\\ \left(1-\varphi \right) if \stackrel{-}{a}= a_L and a= a_H\\ 1 if \stackrel{-}{a}= a_M and a=a_H\\ 0 \mathit{\text{otherwise}}\end{array}\right.$$

Recovered individuals have a reduced rate of boosting according to a factor $\rho$ (partial susceptibility factor). This partial immunity reduces the hazard of non-transmissible ‘infection’ by the parameter $\rho$.

We use the method of lines to approximate the PDE dynamics. Forward approximation for the a-derivative of the immune compartments is used to obtain a system in which a system of ODEs replaces the original PDE for the immune population. It is worth noting that the ODE system is a rough approximation of the PDE in our general model. All the numerical analyses (or integration) and model calibration presented herein were performed on the nonlinear ODE system below, using numerical solvers incorporated into the R package pomp (Partially observed Markov process) (81, 82).

$$\frac{d{S}_1}{dt}=\mu N\left(t\right)-\lambda \left(t\right)S_1\left(t\right)-\mu S_1\left(t\right),\frac{d{S}_2}{dt}=-\epsilon \lambda \left(t\right)S_2\left(t\right)-\mu S_2\left(t\right)+\omega R_L,$$

$$\frac{dI}{dt}=\lambda \left(t\right)S_1\left(t\right)+\epsilon \lambda \left(t\right)S_2\left(t\right)-\left(q_1\gamma +\mu \right)I\left(t\right)$$

$$\frac{d{R}_L}{dt}=q_1\gamma I\left(t\right)-\omega R_L-\rho \lambda \left(t\right)R_L\left(t\right)-\mu R_L\left(t\right)+\nu R_M,$$

$$\frac{d{R}_M}{dt}=-\nu R_M-\mu R_M\left(t\right)+q_2\gamma I\left(t\right)+\rho \lambda \left(t\right){(\theta R}_L\left(t\right)-R_M\left(t\right))+\xi R_H,$$

$$\frac{d{R}_H}{dt}=-\xi R_H-\mu R_H\left(t\right)+q_3\gamma I\left(t\right)+\rho \lambda \left(t\right){\left(\right(1-\theta )R}_L\left(t\right)+R_M\left(t\right)),$$

where $S_1\left(t\right),S_2\left(t\right),I\left(t\right),R_L\left(t\right),R_M\left(t\right),R_H\left(t\right)$ is the density of susceptible (naive), susceptible with enhanced susceptibility, infected, recovered with transient levels of antibodies, recovered with intermediate levels of antibodies and recovered with high levels of antibodies population at time $t$ respectively. $\lambda \left(t\right)=\beta I\left(t\right)/N\left(t\right)$, where $N\left(t\right)$ is the density of the total population at time $t$, and $N\left(t\right)=S_1\left(t\right),+S_2\left(t\right)+I\left(t\right)+R_L\left(t\right)+R_M\left(t\right)+R_H\left(t\right)$.

Model Simulations

We performed simulation for each of the models presented here using parameters estimated from our serological data and some previously estimated parameters (Supplementary Material; Table S1). We used the antibody titer data to estimate the antibody decay/waning parameters using generalized additive model and linear mixed models as described above. The boosting probability of the immune group is calculated by estimating the seroprevalence of the adults relative to children (naïve individuals). To simulate the dynamic of the dengue disease, we evaluate our stochastic nonlinear ODE transmission model, using ODE integrators incorporated in the R package pomp (Partially observed Markov process) (81, 82).

Model Calibration

We calibrated each stochastic model to the Nicaraguan case data to draw inference on the parameters that determine the dynamic of the dengue disease and compared resulting fits by Akaike Information Criterion values and 95% prediction intervals. The models were calibrated using Iterated filtering (maximum likelihood inference), implemented in mif2 function in the R package pomp (Partially observed Markov process) (81, 82). Iterated filtering performs a stepwise resampling which updates the estimate of the parameters and state of the system (that is, the values of the state variables that are unmeasured) with the data up to the current time point. Thus, the resampling of particles (or ‘particle filtering’) over time is used to update the estimated initial states of the system for forward simulation (82). We use particle filtering, a sequential Monte Carlo together with the outer loop (‘iterated filtering’), which allows for the estimates of the parameters to be updated by the data.

To calibrate each model, we first used a Sobol design sampling algorithm (82) to draw 200 combinations of the model parameters. We then used Iterated filtering which explores the parameter space, approximating the likelihood of the perturbed model at each iteration by evaluating the particle filter.

Here, we perform series of successive 50-iteration maximum likelihood via iterated filtering (MIF) searches from 100 starting values, with the output of each search serving as the initial conditions for the subsequent search. We use 1,000 particles for each MIF search. The likelihood of the output for each search is calculated by averaging the likelihood from 10 runs through the particle filter, each using 1,000 particles. It is important to note that the parameters estimated include waning of the $R_L,R_M,$ and $R_H$, that is, $\omega ,\nu$ and $\xi$ respectively, fractions of the infected population that recover to the $R_L,R_M$ and $R_H$ compartments ($q_1,q_2$ and $q_2$ respectively), the boosting probability ($\rho$), the case reporting efficiency, $\phi$, the reporting overdispersion, $\tau$, the intensity of the Gamma white noise process, $\sigma$, and the initial conditions of the state variables. Importantly, in the Sobol design sampling, we fixed the lower and upper limits to the estimated waning ($\omega ,\nu$ and $\xi$) and boosting ($\rho$) confidence intervals estimated from our serological data (see Model Simulations above) to maximize the sampling space and reduce uncertainty in our estimates.

Data and Material availability:

The data and code needed for producing the analyses in this manuscript are available publicly on Zenodo (doi: 10.5281/zenodo.8336603). Requests for individual-level data may be shared following UC Berkeley and University of Michigan IRB approval. Please contact E.H. (eharris@berkeley.edu) and A.G. (gordonal@umich.edu). The materials and data used in this study are covered by standard data and material transfer agreements.