Fairness-Aware Class Imbalanced Learning on Multiple Subgroups

Abstract

We present a novel Bayesian-based optimization framework that addresses the challenge of generalization in overparameterized models when dealing with imbalanced subgroups and limited samples per subgroup. Our proposed tri-level optimization framework utilizes local predictors, which are trained on a small amount of data, as well as a fair and class-balanced predictor at the middle and lower levels. To effectively overcome saddle points for minority classes, our lower-level formulation incorporates sharpness-aware minimization. Meanwhile, at the upper level, the framework dynamically adjusts the loss function based on validation loss, ensuring a close alignment between the global predictor and local predictors. Theoretical analysis demonstrates the framework’s ability to enhance classification and fairness generalization, potentially resulting in improvements in the generalization bound. Empirical results validate the superior performance of our tri-level framework compared to existing state-of-the-art approaches. The source code can be found at https://github.com/PennShenLab/FACIMS.

1. INTRODUCTION

Machine learning has achieved exceptional performance through overparameterization and advanced techniques. This progress is supported by high-quality datasets with sufficient samples for each data class and subgroup. However, real-world datasets frequently exhibit imbalances of different types and magnitudes, reflecting the significance and diversity of the underlying domains [Barocas et al., 2023]. Two common imbalances are observed in label-imbalanced and group-sensitive classification scenarios.

Label-imbalanced classification (LIC) suffers from a significant discrepancy in the number of examples across classes, requiring the use of balanced accuracy as a more suitable metric than conventional misclassification error. To improve model performance and balanced accuracy, various methods have been developed, including [Buda et al., 2018] and loss re-weighting [He and Garcia, 2009]. Weighted cross-entropy (wCE) loss, a classical approach, amplifies the contribution of minority examples in proportion to the imbalance level. However, wCE may not effectively handle the imbalance in overparameterized models [Cao et al., 2019], which can result in poor generalization. Recent studies propose alternative loss functions, such as logit-adjusted loss [Menon et al., 2020, Cao et al., 2019], class-dependent temperature loss [Ye et al., 2020], and vector-scaling loss [Kini et al., 2021], aiming to address the challenges associated with overparameterization. Nonetheless, there is still a risk of overfitting on minority class samples despite these advancements [Rangwani et al., 2022].

In group-sensitive classification (GSC), the goal is to ensure fairness concerning protected attributes like gender or race, addressing the issue of stereotyping where certain target labels are more frequently associated with specific groups [Mehrabi et al., 2021]. For instance, the occupation of “nurse” being commonly associated with females. While there is no universal fairness metric [Kleinberg et al., 2016], one suggestion is group sufficiency, which aims to maintain identical conditional expectations of the ground-truth label $(𝔼[Y\mid f(X),A])$ across different subgroups $A\in 𝒜$ given the predictor’s output $f(X)$. However, in overparameterized models with limited samples per subgroup, this control of group sufficiency may not always hold, despite its effectiveness under certain assumptions in unconstrained learning [Liu et al., 2019a, Shui et al., 2022c].

Given the aforementioned challenges regarding the performance of LIC and GSC in overparameterized models, we pose the following question:

Q: How can a classifier be designed to effectively generalize on imbalanced subgroups with limited samples?

To address $\mathbf{Q}$, we establish a link between LIC and GSC and propose a novel Bayesian framework that maintains informative predictions for imbalanced data while minimizing generalization error. Our contributions can be summarized as follows.

• We design a Bayesian-based tri-level optimization framework called Fairness-Aware Class Imbalanced Learning on Multiple Subgroups (FACIMS). In FACIMS, local predictors are learned using a small amount of training data and a fair, class-balanced predictor. The lower-level formulation utilizes the sharpness-aware minimization [Foret et al., 2020] to encourage convergence to a flat minimum and effectively avoid saddle points for minority classes. The upper-level problem dynamically adjusts the loss function by monitoring the validation loss, following a similar approach to [Li et al., 2021], and updates the global predictor to align with all subgroup-specific predictors.

• We establish the $𝒪(1/\sqrt{T})$ convergence rate of our proposed three-level optimization framework, corresponding to a $𝒪\left({ϵ}^{-2}\right)$ sample complexity with a fixed number of samples used per iteration.

• We quantify the generalization performance of the models trained using our proposed tri-level FACIMS approach. The generalization bound analysis demonstrates that our method can achieve superior generalization performance compared to bilevel variants, such as [Rangwani et al., 2022], for fair learning on multiple subgroups.

• We conduct experiments on synthetic and real-world datasets to evaluate the balanced accuracy, demographic parity, equalized odds, and group sufficiency. The results showcase the effectiveness of our proposed method.

2. PRELIMINARIES

We consider a joint random variable $(X,Y,A)$ that follows an underlying distribution $𝒫(X,Y,A)$, where $X\in 𝒳$ represents the input, $Y\in 𝒴=\{1,\dots ,K\}$ represents the label, $A\in 𝒜$ is a scalar discrete random variable that denotes the sensitive attribute or subgroup index. For instance, $A$ could represent gender or race. Throughout, $𝔼[Y\mid X]$ denotes the conditional expectation of $Y$, which can be seen as a function of $X.{𝔼}_{A,X}[\cdot ]$ represents the expectation over the marginal distribution of $𝒫(A,X)$.

Suppose we have a dataset $𝒮={\left({\mathbf{x}}_i,y_i\right)}_{i=1}^n$ sampled i.i.d. from a distribution $𝒫$ with input space $𝒳$ and $K$ classes. Let $f:𝒳\to {ℝ}^K$ be a model that outputs a distribution over classes and let $h_f(\mathbf{x})=\arg {\max }_{i\in [K]}f(\mathbf{x})$. The standard classification error is denoted by $\mathrm{ACC}={\mathbb{P}}_{𝒮}\left[y\ne {\hat{y}}_f(\mathbf{x})\right]$. For a loss function $\ell (y,\hat{y})$, we similarly denote

$$\text{Population risk:}ℒ(f;𝒫):={𝔼}_{𝒫}[\ell (y,{\widehat{y}}_f(x))],$$ (1a)

$$\text{Empirical risk:}ℒ(f;𝒮):=\frac{1}{n}{\sum }_{i=1}^n\ell (y_i,{\widehat{y}}_f(x_i)).$$ (1b)

We denote the frequency of the $k$’th class via ${\pi }_k={\mathbb{P}}_{(\mathbf{x},y)\sim 𝒫}(y=k)$. Label/class-imbalance occurs when the class frequencies differ substantially, i.e., ${\max }_{i\in [K]}{\pi }_i>>{\min }_{i\in [K]}{\pi }_i$. We define

$$\text{Class-conditional risk:}{f}_k:={𝔼}_{{𝒫}_k}[\ell (y,{\widehat{y}}_f(x))],$$ (2a)

$$\text{Balanced risk: BACC}(f):=\frac{1}{K}{\sum }_{k=1}^K{f}_k.$$ (2b)

2.1. PARAMETRIC LOSSES

We review some of the SOTA re-weighting methods for training on imbalanced data with distribution shifts.

Label-Distribution-Aware Margin (LDAM) [Cao et al., 2019] determines optimal margins for each class by minimizing errors using a generalization bound. It utilizes ${\mathrm{\Delta }}_j$ as the margin for each class, defined as follows:

$$\begin{gathered} {\ell }_{\text{Δ}}(f;x,y)=-\text{log}\frac{e^{f{(x)}_y-{\text{Δ}}_y}}{e^{f{(x)}_y-{\text{Δ}}_y}+{\sum }_{j\ne y}{e}^{f{(x)}_j}}, \\ \text{where}{\text{Δ}}_j=\frac{C}{n_j^{1/4}}\text{for}j\in \{1,\dots ,K\}. \end{gathered}$$ (LDAM)

LDAM prioritizes classes with low sample sizes $\left(n_j\right)$ over those with high frequencies. Deferred Re-Weighting (DRW) [Cao et al., 2019] involves training the model with an average loss until a certain epoch, then applying weights proportional to the inverse of the sample size to the loss term for each class. The loss function for DRW is as follows:

$$\begin{gathered} {\ell }_u(f;x,y)=-u_y\text{log}\frac{e^{f{(x)}_y}}{{\sum }_{j=1}^K{e}^{f{(x)}_y}}, \\ \text{where}{u}_j=\frac{1}{1+(n_j-1){𝟙}_{\text{epoch}\ge K}}. \end{gathered}$$ (DRW)

This way of re-weighting has been shown to be effective for improving generalization performance when combined with various losses.

Vector Scaling (VS) [Kini et al., 2021] loss is a recently proposed loss function that unifies the idea of multiplicative shift [Ye et al., 2020], additive shift [Menon et al., 2020], and loss re-weighting. It has the following form:

$$\ell (f,v;x,y)=-u_y\text{log}\frac{e^{{\gamma }_{y}f{(x)}_y+{\text{Δ}}_y}}{{\sum }_{j=1}^k{e}^{{\gamma }_{j}f{(x)}_j+{\text{Δ}}_j}}.$$ (VS)

Here, $\mathbf{v}:=\left[{\mathbf{v}}_1,\dots ,{\mathbf{v}}_K\right]$, where ${\mathbf{v}}_j:=\left(u_j,{\mathrm{\Delta }}_j,{\gamma }_j\right)$ are some hyperparameters.

Throughout, our main focus is on VS loss, but our framework can also accommodate other loss functions.

2.2. FAIRNESS NOTIONS

Next, we discuss fairness notions and their gaps.

Definition 1. Let f be a score function that maps the random variable X to a real number.

• Group Sufficiency (GS): We say that f is sufficient with respect to attribute A if $𝔼[Y\mid f(X)]=𝔼[Y\mid f(X),A]$.

• Demographic Parity (DP): f satisfies demographic parity with respect to A if $𝔼[f(X)]=𝔼[f(X)\mid A]$.

• Equalized Odds (EO): f satisfies equalized odds with respect to A if $𝔼[f(X)\mid Y]=𝔼[f(X)\mid Y,A]$.

GS means that the score function f captures all the information about the label Y that is relevant for prediction, regardless of the attribute A. DP ensures that the expected score $f(X)$ remains constant, regardless of the attribute A. This principle guarantees that the distribution of scores remains unaffected by the sensitive attribute, thereby promoting fairness in the decision-making process. EO dictates that the expected score $f(X)$ remains consistent across all combinations of labels Y and attributes A. It ensures that individuals sharing the same label but differing attributes are treated equally in terms of their predicted scores, irrespective of the sensitive attribute.

The impossibility theorem of fairness asserts that, in general cases, it is impossible to simultaneously achieve all common and intuitive definitions of fairness. Notably, [Barocas et al., 2019, Chouldechova, 2017] demonstrate that if $A\cancel{\perp }Y$, it is not feasible to achieve both group sufficiency and demographic parity. Moreover, [Barocas et al., 2019, Pleiss et al., 2017] reveal that when $𝒫(X,Y,A)>0$ and $A\cancel{\perp }Y$, it is not possible for both group sufficiency and demographic parity to hold simultaneously.

Definition 1 leads to a notion of the group sufficiency gap, demographic parity gap, and equalized odds gap defined, respectively, as:

$${\mathbf{SGap}}_f(A)=𝔼[|𝔼[Y\mid f(X)]-𝔼[Y\mid f(X),A]|],$$ (3a)

$${\mathbf{PGap}}_f(A)=𝔼[𝔼[f(X)]-𝔼[f(X)\mid A]],$$ (3b)

$${\mathbf{OGap}}_f(A)=𝔼[𝔼[f(X)\mid Y]-𝔼[f(X)\mid Y,A]].$$ (3c)

${\mathbf{SGap}}_f$ measures the extent of group sufficiency violation, induced by the predictor f, which is taken by the expectation over $(X,A)$. Hence, ${\mathbf{SGap}}_f=0$ suggests that f satisfies group sufficiency and vice versa. For completeness, we also discuss computing these gaps in Appendix.

To conclude this section, we provide Group A-Bayes predictor and an upper bound for ${\mathbf{SGap}}_f$ from [Shui et al., 2022c]. These findings serve as the foundation for our Bayesian-based tri-level optimization framework.

Definition 2 (A-group Bayes predictor). The A-group Bayes predictor $f^{A,\mathit{Bayes}}$ associated with distribution $𝒫(X,Y,A)$ is defined as: $f^{A,\mathit{Bayes}}(X)=𝔼[Y\mid X,A]$.

The following Theorem provides the upper bound of group sufficiency gap w.r.t. any predictor f:

Theorem 3. If A takes finite value, i.e. $|𝒜|<+\mathrm{\infty }$ and follows uniform distribution with $p(A=a)=1/|𝒜|$, then

$${\mathit{SGap}}_f(A)\le \frac{4}{\left|𝒜\right|}\sum _{a\in 𝒜}{𝔼}_X\left[|f-f^{A,\mathit{Bayes}}|\mid A=a\right].$$ (4)

Hence, $\mathbf{SGap}f(A)$ depends on the discrepancy between the predictor f and the A-group Bayes predictor $f^{A,\text{Bayes}}$. In other words, when considering different subgroups $A=a$, the optimal predictor f should closely align with all the group Bayes predictors $f^{A=a,\text{Bayes}}$, for all $a\in 𝒜$.

3. PROPOSED FRAMEWORK

In this section, we present the formulation of FACIMS, which is a framework designed to promote both classification accuracy and fairness through a randomized algorithm. FACIMS achieves this by learning a predictive distribution $\mathbf{Z}$, which assigns higher scores to predictors that are favorable based on the available data. In the context of the Bayes framework, the predictor is sampled from the posterior distribution, represented as $\tilde{f}\sim \mathbf{Z}$. During the inference stage, the predictor’s output is computed as the expectation of the learned predictive distribution $\mathbf{Z}:f(X)={𝔼}_{\tilde{f}\sim \mathbf{Z}}\tilde{f}(X)$.

In practical scenarios, it is infeasible to optimize over the entire space of possible distributions. Therefore, we constrain the predictive distribution $𝒵$ to a specific distribution family $\mathbf{Z}\in 𝒵$, such as the Gaussian distribution. Additionally, we denote ${\mathbf{Z}}^{a,\star }\in 𝒵$ as the optimal prediction distribution with respect to the subgroup $A=a$ within the family $𝒵$:

$$Z^{a,*}=\text{arg}\underset{Z^a\in 𝒵}{\text{min}}{𝔼}_{{\tilde{f}}^a\sim Z^a}ℒ({\tilde{f}}^a,v;{𝒮}^a).$$

In general, ${\mathbf{Z}}^{a,\star }\ne {\tilde{f}}^{a,\text{Bayes}}$, since the distribution family $𝒵$ is only the subset of all possible distributions.

Corollary 4 (Shui et al. [2022c]). The group sufficiency gap in a randomized algorithm w.r.t. the learned predictive distribution $\mathbf{Z}$ is bounded as follows:

$${\mathit{SGap}}_f\le 𝒪(\mathit{Optim}+\mathit{Approx}),$$ (5)

where

$$\begin{gathered} \mathit{Optim}:=\frac{1}{\left|𝒜\right|}\sum _a\sqrt{KL(Z^{a,\star }\parallel Z)}, \\ \mathit{Approx}:=\frac{1}{\left|𝒜\right|}\sum _a\sqrt{KL(Z^{a,\star }\parallel 𝒫(Y\mid X,A=a))}. \end{gathered}$$

Minimizing the Optim term ensures that the learned distribution $\mathbf{Z}$ is both fair and informative for making predictions. On the other hand, the Approx term represents the KL divergence between the optimal distribution ${\mathbf{Z}}^{a,\star }$ and $𝒫$. If the distribution family $𝒵$ has a rich expressive power, like that of a deep neural network, the Approx term will be small. See Figure 1 for a visual representation.

Figure 1:

An illustration of the FACIMS model defined in (7). $f^a$ and $f^b$ maximize the margin for minority classes for groups $a$ and $b$ in (7b). In the upper level problem (7a), FACIMS finds $\mathbf{Z}\in 𝒵$ to achieve a small balanced accuracy while minimizing the discrepancy between $\left({\mathbf{Z}}^{a,\star },{\mathbf{Z}}^{b,\star }\right)$. The approximation term $\mathrm{KL}\left({\mathbf{Z}}^{a,\star }\mid \mathbf{Z}\right)$ is based on the distribution family $𝒵$ (orange region). If the predefined $𝒵$ has good expressive power, the approximation is treated as a small constant.

Now, we provide a framework for fairness-aware class imbalanced learning on multiple sub-groups with potentially improved generalization bound and ${\mathrm{SGap}}_f$. We begin with formulating the loss function design as a bilevel optimization over hyperparameters $\mathbf{v}$ and a distribution $𝒵$. Assume each group $a\in 𝒜$ has a fine-tuning training set ${𝒯}^a={\cup }_{i=1}^n\left\{\left(x_i^a,y_i^a\right)\right\}$ and a separate validation set ${𝒱}^a={\cup }_{i=1}^n\left\{\left(x_i^a,y_i^a\right)\right\}$, where data are independently and identically distributed (i.i.d.) and drawn from the per-task data distribution ${𝒫}^a$. Following [Li et al., 2021], define the empirical risk and the balanced empirical risk over a finite-sample dataset $𝒮$ as ${ℒ}_{\mathrm{vs}}(\tilde{f},\mathbf{v};𝒮):=1/n{\sum }_{i=1}^n\ell \left(\tilde{f},\mathbf{v};{\mathbf{x}}_i,y_i\right)$ and ${ℒ}_{\text{bal}}(\tilde{f};𝒮):=1/n{\sum }_{i=1}^n\ell \left(\tilde{f},\overline{\mathbf{v}};{\mathbf{x}}_i,y_i\right)$. Here, $\overline{\mathbf{v}}$ can be manually adjusted using (DRW), (LDAM), and (VS).

Let $\mathbf{Z}$ stand for both fair and informative prediction. Building on [Kini et al., 2021, Li et al., 2021, Shui et al., 2022c], we design the following objective:

$$\underset{Z\sim 𝒵,v}{\text{min}}\sum _{a\in 𝒜}{\alpha }^{\text{up}}\text{KL}(Z^{a,*}\Vert Z)+{𝔼}_{\tilde{f}\sim Z}{ℒ}_{\text{bal}}(\tilde{f};{𝒱}^a),$$ (6a)

$$\text{s.t.}{Z}^{a,*}=\text{arg}\underset{Z^a\in 𝒵}{\text{min}}{\alpha }^{\text{low}}\text{KL}(Z^a\Vert Z)+{𝔼}_{{\tilde{f}}^a\sim Z^a}{ℒ}_{\text{vs}}({\tilde{f}}^a,v;{𝒯}^a),\forall a\in 𝒜.$$ (6b)

Here, the lower-level problem (6b) includes a regularization term $\mathrm{KL}\left({\mathbf{Z}}^a\mid \mathbf{Z}\right)$ as an informative prior for learning local predictor ${\mathbf{Z}}^{a,\star }$ with a fixed predictive distribution $\mathbf{Z}$. This optimization reduces the upper bound of the group-specific generalization error.

In the upper-level problem (6a), we update $\mathbf{Z}$ by minimizing the average KL-divergence between different ${\mathbf{Z}}^{a,\star }$, controlling the upper bound of ${\mathbf{SGap}}_f$ according to (5), as well as the balanced empirical risk. However, directly minimizing (6b) in a single-level approach does not work well in our setting due to the limited number of samples in each subgroup. This leads to overfitting and large generalization error for each subgroup. To address this, we consider additional assumptions, such as the similarity in the data generation distribution $𝒫[Y\mid X,A]$ for each subgroup. With these assumptions, we can learn shared and fair models that are informative and sufficient for a large number of subgroups.

3.1. PARAMETRIC MODELS AND FACIMS

In this section, we propose a practical learning algorithm applicable to various differentiable and parametric models, including neural networks.

We utilize the Isotropic Gaussian distribution as $𝒵$ to learn global informative $\mathbf{Z}$ with parameters $(\mathit{\theta },\mathit{\sigma })$. For each subgroup $A=a$, we also learn group-specific parameters $\left({\mathit{\theta }}^a,{\mathit{\sigma }}^a\right)$ for ${\mathbf{Z}}^a$ in $𝒵$. The Isotropic Gaussian distribution is selected for computational efficiency in optimization, but other differentiable distributions can also be used for parameter density functions.

Given a training set, we learn ${\tilde{f}}_{\mathbf{w}}:𝒳\mapsto 𝒴$ parameterized by $\mathbf{w}\in {ℝ}^d$. Then ${\tilde{f}}_{\mathbf{w}}\sim \mathbf{Z}$ is equivalent to sampling the model parameter $\mathbf{w}$ from the predictive-distribution $\mathbf{Z}$. Hence, learning the distribution $\mathbf{Z}$ is equivalent to learning parameter $(\mathit{\theta },\mathit{\sigma })$. Note that for each subgroup $A=a$, ${\tilde{f}}_{\mathbf{w}}^a\sim {\mathbf{Z}}^a$ can be modeled similarly. Both procedures can be formulated as follows:

$$w\sim 𝒩(\mathit{\theta },\mathit{\sigma })=\prod _{i=1}^d𝒩(\mathit{\theta }[i],\mathit{\sigma }[i]),$$

$$w^a\sim 𝒩({\mathit{\theta }}^a,{\mathit{\sigma }}^a)=\prod _{i=1}^d𝒩({\mathit{\theta }}^a[i],{\mathit{\sigma }}^a[i]),\forall a\in 𝒜.$$

To enhance the convergence to a flat minimum and effectively avoid saddle points for minority classes, we integrate the sharpness-aware minimization (SAM) algorithm [Foret et al., 2020] into (6b). SAM is a recently introduced technique that improves generalization performance by jointly minimizing the loss value and the loss sharpness, leveraging the geometry of the loss landscape. Given a perturbation parameter $\beta >0$ and the empirical risk $ℒ\left({\tilde{f}}_{\mathbf{w}};𝒮\right)$, the goal of training is to choose $\mathbf{w}$ having low population loss

$$\underset{v,Z\sim 𝒵}{\text{min}}\sum _{a\in 𝒜}{\alpha }^{\text{up}}\text{KL}(Z^{a,*}\Vert Z)+{𝔼}_{w\sim Z}{ℒ}_{\text{bal}}({\tilde{f}}_w;{𝒱}^a),$$ (7a)

$$\text{s.t.}{Z}^{a,*}\in \underset{Z^a\in 𝒵}{\text{arg min}}\underset{\Vert {\mathit{ϵ}}^a\Vert \le {\beta }^a}{\text{max}}{\alpha }^{\text{low}}\text{KL}(Z^a\parallel Z)+{𝔼}_{w^a\sim Z^a}{ℒ}_{\text{vs}}({\tilde{f}}_{w^a+{\mathit{ϵ}}^a},v;{𝒯}^a),\forall a\in 𝒜.$$ (7b)

Algorithm 1.

An Alternating Stochastic Gradient Method for FACIMS

1:	Input: VS loss hyperparameters $v_0$; distribution parameters $({\theta }_0,{\sigma }_0)$ and $({\theta }_0^a,{\sigma }_0^a)$ for all $a\in 𝒜$; regularization parameters $({\alpha }^{\text{low}},{\alpha }^{\text{up}})$; sharpness parameters ${\{{\beta }^a\}}_a$; and stepsizes $({\gamma }^{\text{up}},{\gamma }^{\text{low}})$.
2:	for $t=0\dots T-1$ do
3:	Sample dataset $S_t^a=({𝒯}_t^a,{𝒱}_t^a)$, where $a\in {𝒜}^{\prime }\subseteq 𝒜$.
4:	for $a\in 𝒜$ do
5:	Update ${\mathit{ϵ}}^a$ in the lower level:          $${\mathit{ϵ}}_{t+1}^a\leftarrow \underset{\Vert {\mathit{ϵ}}^a\Vert \le {\beta }^a}{\arg \max }{\alpha }^{\text{low}}\text{KL}({\mathbf{Z}}_t^a\Vert {\mathbf{Z}}_t)+{𝔼}_{{\mathbf{w}}^a\sim {\mathbf{Z}}_t^a}{ℒ}_{\text{vs}}({\tilde{f}}_{{\mathbf{w}}^a+{\mathit{ϵ}}^a},v_t;{𝒯}_t^a).$$ (8)
6:	Update $Z^a=𝒩({\mathit{\theta }}^a,{\mathit{\sigma }}^a)$ using SGD (with step size ${\gamma }^{\text{low}}$) in the middle level:        $$Z_{t+1}^a\leftarrow \underset{Z^a\in 𝒵}{\arg \min }{\alpha }^{\text{low}}\text{KL}(Z^a\Vert Z_t)+{𝔼}_{{\mathbf{w}}^a\sim {\mathbf{z}}^a}{ℒ}_{\text{vs}}({\tilde{f}}_{{\mathbf{w}}^a+{\mathit{ϵ}}_{t+1}^a},v_t;{𝒯}_t^a).$$ (9)
7:	end for
8:	Update $Z=𝒩(\mathit{\theta },\mathit{\sigma })$ and $\mathbf{v}$ using SGD (with step size ${\gamma }^{\text{up}}$) in the upper level:        $$(Z_{t+1},v_{t+1})\leftarrow \underset{Z\sim 𝒵,\mathbf{v}}{\arg \min }\sum _{a\in 𝒜}{\alpha }^{\text{up}}\text{KL}(Z_{t+1}^a\Vert Z)+{𝔼}_{\mathbf{w}\sim \mathbf{Z}}{ℒ}_{\text{bal}}({\tilde{f}}_{\mathbf{w}};{𝒱}_t^a).$$ (10)
9:	end for
10:	Return: $({\mathbf{v}}_T,{\mathit{\theta }}_T,{\mathit{\sigma }}_T)$.

$ℒ\left({\tilde{f}}_{\mathbf{w}};𝒫\right)$. SAM achieves this via the problem

$$\underset{{\tilde{f}}_w}{\text{min}}\underset{\Vert ϵ\Vert \le \beta }{\text{max}}ℒ({\tilde{f}}_{w+\mathit{ϵ}};𝒮).$$ (SAM)

Given $\mathbf{w}$, the maximization in (SAM) seeks to find the weight perturbation $\mathit{ϵ}$ in the Euclidean ball that maximizes the empirical loss. If we define the sharpness as

$$\underset{\Vert ϵ\Vert \le \beta }{\text{max}}\left[ℒ({\tilde{f}}_{w+\mathit{ϵ}};𝒮)-ℒ({\tilde{f}}_w;𝒮)\right]$$

then (SAM) essentially minimizes the sum of the sharpness and the empirical loss $ℒ\left({\tilde{f}}_{\mathbf{w}};𝒮\right)$.

We incorporate (SAM) into (6b) and propose (7) by introducing a set of positive constants ${\left\{{\beta }^a\right\}}_{a\in 𝒜}$. The FACIMS framework, combined with SAM, promotes convergence to a flat minimum and aids in escaping saddle points for minority classes [Rangwani et al., 2022]. We empirically demonstrate the superiority of integrating SAM into FACIMS over popular baselines and provide theoretical evidence suggesting improved generalization bounds. Despite the tri-level problem formulation in (7), our algorithm design efficiently approximates the maximization step, making the computational cost comparable to that of (6).

Based on the analysis and (7), we provide an alternating optimization algorithm for solving (7) in Algorithm 1. Line 3 provides a partial group setting, i.e., for many subgroups, we can randomly sample a subset ${𝒜}^{\prime }$ such that $\left|{𝒜}^{\prime }\right|<<|𝒜|$ for memory saving.

4. THEORETICAL ANALYSIS OF FACIMS

Next, we analyze the performance of the FACIMS method.

To simplify, we assume ${\beta }^a=\beta$ for all $a\in 𝒜$ and combine ${ℒ}_{\text{bal}}$ and ${ℒ}_{\mathrm{vs}}$ into a single notation $ℒ$. We represent the stochastic gradients of $ℒ$ as $\tilde{\nabla }ℒ$. Let $\mathbf{\Theta }:=(\mathit{\theta },\mathit{\sigma },\mathbf{v})\in {ℝ}^p$ and $F$ be the objective of (7a).

Assumption A (Lipschitz continuity). Assume that $ℒ\left(\cdot ;{𝒱}^a\right)$, $\nabla ℒ\left(\cdot ;{𝒯}^a\right)$, $\nabla ℒ\left(\cdot ;{𝒱}^a\right)$, ${\nabla }^2ℒ\left(\cdot ;{𝒯}^a\right)$, $\forall a\in 𝒜$ are Lipschitz continuous with constant ${\ell }_0$, ${\ell }_1$, ${\ell }_1$, ${\ell }_2$.

Assumption B (Stochastic derivatives). Assume that $\tilde{\nabla }ℒ\left(\cdot ;{𝒯}^a\right)$, ${\tilde{\nabla }}^2ℒ\left(\cdot ;{𝒯}^a\right)$, $\tilde{\nabla }ℒ\left(\cdot ;{𝒱}^a\right)$ are unbiased estimator of $\nabla ℒ\left(\cdot ;{𝒯}^a\right)$, ${\nabla }^2ℒ\left(\cdot ;{𝒯}^a\right)$, $\nabla ℒ\left(\cdot ;{𝒱}^a\right)$ respectively and their variances are bounded by ${\sigma }^2$.

Assumptions A–B also appear similarly in the convergence analysis of and bilevel optimization [Chen et al., 2021, Tarzanagh et al., 2022, Abbas et al., 2022]. With the above assumptions, we get the following theorem. The proof is deferred in Appendix.

Theorem 5. Under Assumptions $A-B$, and choosing step-sizes ${\gamma }^{\text{up}}={\gamma }^{\text{low}}=𝒪(1/\sqrt{T})$ and sharpness parameter $\beta =𝒪(1)$, with some proper constants, we can get that the iterates ${\left\{\left({\mathit{\theta }}_t,{\mathit{\sigma }}_t,{\mathbf{v}}_t\right)\right\}}_t$ generated by Algorithm 1 satisfy

$$\frac{1}{T}\sum _{t=1}^T𝔼\left[{\Vert \nabla F({\mathit{\theta }}_t,{\mathit{\sigma }}_t,v_t)\Vert }^2\right]=𝒪\left(\frac{1}{\sqrt{T}}\right).$$ (11)

Theorem 5 implies that under some standard assumption, Algorithm 1 can find $ϵ$ stationary points for FACIMS objective (7) with $𝒪\left({ϵ}^{-2}\right)$ iterations and $𝒪\left({ϵ}^{-2}\right)$ samples.

Next, we establish the generalization performance.

Theorem 6. Assume the function $ℒ(\cdot )$ is bounded for any $𝒮$. Let $F(\cdot ;𝒫)={𝔼}_{𝒮\sim 𝒫}[F(\cdot ;𝒮)]$. Assume $F(\hat{\mathit{\theta }},\hat{\mathit{\sigma }},\hat{\mathbf{v}};𝒫)\le {𝔼}_{ϵ\sim 𝒩\left(0,{\beta }^2𝕀\right)}[F(\hat{\mathit{\theta }}+ϵ,\hat{\mathit{\sigma }}+ϵ,\hat{\mathbf{v}};𝒫)]$ at the stationary point of (7) denoted by $(\hat{\mathit{\theta }},\hat{\mathit{\sigma }},\hat{\mathbf{v}})$. Then, with probability $1-\delta$ over the choice of the training set $𝒮\sim 𝒫$, with $|𝒮|=n|𝒜|$, we have

$$\begin{gathered} F(\widehat{\Theta };𝒫)\le \underset{\parallel ϵ\parallel \le \beta }{\text{max}}{𝔼}_{ϵ\sim 𝒩(0,{\beta }^2𝕀)}[F(\widehat{\mathit{\theta }}+ϵ,\widehat{\mathit{\sigma }}+ϵ,\widehat{v};𝒮)] \\ \le 𝒪\left({\left(\frac{p\text{ln}{A}_{\beta }+\text{ln}\frac{1}{\delta }+\text{ln}(n|𝒜|)}{n\left|𝒜\right|}\right)}^{\frac{1}{2}}\right). \end{gathered}$$ (12)

Here, $A_{\beta }:=1+\frac{{\Vert \widehat{\Theta }\Vert }_2^2}{{\beta }^2}{\left(1+\sqrt{\frac{\text{ln}(n|𝒜|)}{p}}\right)}^2$.

Theorem 6 shows that the difference between the population loss and the empirical loss of FACIMS is bounded by $\widetilde{𝒪}(p/n|𝒜|)$. Note that the bound in (12) is a function of $\beta$. Hence, for a choice of $\beta \to 0$, the bound (12) is not optimal. This suggests that tri-level FACIMS can have better generalization performance than that from bilevel variants such as [Li et al., 2021, Shui et al., 2022c].

5. EXPERIMENTS

5.1. EXPERIMENTAL SETUP

Datasets.

We applied our model to the Alzheimer’s disease (AD), credit card and drug consumption datasets, and the data information is summarized in Table 1.

Table 1:

Statistical summary of the datasets including class and sensitive feature information.

Dataset	#Instance	#Features	Class	Class Distr.	Sensitive Feature	Sensitive Feature Distr.
Alzheimer’s Disease	5137	17	AD / MCI	21% / 79%	Race	93.75% / 3.20% / 1.88% / 1.17%
Credit Card	30,000	22	Credible / Not Credible	22% / 77%	Education Level	46.77% / 35.28% / 16.39% / 0.93% / 0.41% / 0.17% / 0.05%
Drug Consumption	1885	9	Never used / Not used in the past year / Used in the past year / Used in the past day	1.81% / 5.41% / 65.98% / 26.80%	Education Level	6.74% / 6.90% / 26.86% / 14.28% / 25.48% / 15.02% / 4.72%

Alzheimer’s Disease dataset¹ were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database [Weiner et al., 2017, Shen et al., 2014]. We included 5137 instances, including 4080 mild cognitive impairment (MCI, a prodromal stage of AD) and 1057 AD instances, to conduct the binary classification. Moreover, we chose race as the sensitive feature and divided the participants into four subgroups, where white subjects exceeding 90%. Our features included 17 AD-related biomarkers, including cognitive scores, volumes of brain regions extracted from the magnetic resonance imaging (MRI) scans, amyloid and tau measurements from positron emission tomography (PET) scans and cerebrospinal fluid (CSF), and risk factors like APOE4 carriers and age.

Credit Card dataset² contains 22 attributes like clients’ basic information, history of payments, and bill statement amount to classify whether the clients are credible or not. We included 30000 instances with 6636 credible and 23365 not credible clients. We chose the education level as the sensitive feature where we observed more clients who graduated from university than other six levels.

Drug Consumption dataset³ contains demographic information such as age, gender, and education level, as well as measures of personality traits thought to influence drug use for 1885 respondents. The task is to predict alcohol use with $\mathrm{K}=4$ categories (never used, not used in the past year, used in the past year, and used in the past day) for multi-class outcomes. The sensitive feature is education level (Left school before or at 16, Left school at 17-18, Some college, Certificate diploma, University degree, Masters, Doctorate ). The data information is summarized in Table 1 below. As can be seen, the class distribution shows that the dataset suffers from heavy label imbalance.

Baselines

To validate the effectiveness of our method, FACIMS, we compare it with seven baseline methods.

• EIIL [Creager et al., 2021]: An Invariant Risk Minimization (IRM) based approach that promotes group sufficiency.

• FSCS [Lee et al., 2021]: An approach that adopts the conditional mutual information constraint to improve group sufficiency.

• FAMS [Shui et al., 2022c]: A bilevel framework that considers maintaining both the accuracy and group sufficiency gap for multiple subgroups.

• ERM: Empirical Risk Minimization using a four-layer fully connected neural network trained with cross-entropy loss.

• BERM: ERM with a balanced cross-entropy loss, incorporating class proportions as weights similar to [Cao et al., 2019].

• FACIMS ($\beta =0$, $\mathbf{v}=\overline{\mathbf{v}}$): Our method without the lower level. Besides, in the upper level, we manually adjust the logits using the proportion of class [Menon et al., 2020, Kini et al., 2021] instead of learning the hyperparameter for logits adjustment.

• FACIMS $(\beta =0)$: Our method without the lower level which aims to flatten the sharp landscape of the objective in the middle level.

We set ${\alpha }^{\text{up}}$ and ${\alpha }^{\text{low}}$ to be 0.7. We use the grid of [0.1, 0.01, 0.001] to search the learning rate for global model and local models and report the results over five independent repeats.

5.2. EXPERIMENTAL RESULTS

In this section, we analyze Alzheimer’s disease and credit card datasets. The numerical results of the multi-class dataset drug consumption are included in the appendix due to page limits.

Balanced Accuracy and Sufficiency Gap

We primarily focus on balanced accuracy and group sufficiency gap as our main goals. Table 2 shows that on the Alzheimer’s disease dataset, our method FACIMS outperforms EIIL, FSCS, FAMS, and ERM in terms of balanced accuracy, with improvements of 2.6%, 4.0%, 5.3%, and 2.1% respectively. While BERM addresses the class imbalance issue and demonstrates a significant improvement over ERM by nearly 2%, our method still achieves a higher balanced accuracy than BERM. Our method significantly improves the group sufficiency gap by 6.5% and 4.0% respectively, compared to ERM and BERM which do not address this issue. Although EIIL, FSCS, and FAMS specifically target the group sufficiency problem and achieve lower sufficiency gaps than ERM and BERM, our method still outperforms these three baseline methods by improving the sufficiency gap by 1.4%, 2.0%, and 2.8% respectively.

Table 2:

Numerical results (mean ± standard deviation) for 5 repeats of different methods on Alzheimer’s disease (AD) and Credit Card (CC) datasets regarding six measurements. Time is in the format of “hours:minutes:seconds”. FACIMS-I means FACIMS $(\beta =0)$, and FACIMS-II means FACIMS $(\beta =0,v=\overline{v})$. “$\uparrow$” indicates the larger the better while “$\downarrow$” indicates the smaller the better. The best one in each column is bold.

Data	Method	Balanced Accuracy ↑	Demographic Parity ↓	Equalized Odds ↓	Sufficiency Gap ↓	Recall 0 ↑	Recall 1 ↑	Time ↓
AD	EIIL	.8639±.0199	.0764±.0176	.1015±.0529	.1193±.0206	.9288±.0119	.7991±.0409	0:03:32
	FSCS	.8498±.0485	.0711±.0287	.1650±.1008	.1254±.0528	.9504±.0426	.7493±.1018	0:08:05
	FAMS	.8369±.0136	.0431±.0210	.1444±.0435	.1328±.0273	.7624±.0077	.9114±.0096	0:09:51
	ERM	.8687±.0136	.0550±.0196	.1143±.0390	.1701±.0387	.9883±.0053	.7491±.0430	0:00:51
	BERM	.8886±.0042	.0869±.0204	.0813±.0129	.1456±.0330	.9854±.0043	.7918±.0520	0:02:24
	FACIMS-II	.8839±.0079	.0747±.0182	.0868±.0130	.1167±.0139	.8456±.0148	.9222±.0043	0:09:58
	FACIMS-I	.8887±.0066	.0893±.0080	.0450±.0049	.1059±.0060	.8780±.0104	.8994±.0148	0:13:38
	FACIMS	.8897±.0098	.0765±.0208	.0616±.0142	.1052±.0197	.8832±.0072	.8962±.0054	0:15:26
CC	EIIL	.6357±.0267	.0834±.0200	.1723±.0515	.1266±.023	.7897±.0176	.4817±.0448	0:03:30
	FSCS	.5976±.0277	.0850±.0137	.2000±.0456	.2007±.0039	.8953±.0130	.3000±.0685	0:42:10
	FAMS	.6542±.0098	.0746±.0066	.1859±.0368	.1352±.0106	.8194±.0374	.4890±.0270	0:10:21
	ERM	.6104±.0111	.0599±.0173	.1577±.0175	.2760±.0710	.9919±.0233	.2289±.0820	0:02:07
	BERM	.6570±.0106	.1060±.0125	.1631±.0304	.2315±.0623	.8717±.0191	.4423±.0146	0:02:09
	FACIMS-II	.6446±.0163	.0707±.0073	.1973±.0358	.1340±.0147	.8002±.0374	.4890±.0270	0:10:03
	FACIMS-I	.6768±.0040	.0750±.0105	.1951±.0524	.1396±.0081	.8081±.0114	.5455±.0098	0:14:07
	FACIMS	.6799±.0374	.0593±.0070	.1567±.0230	.1264±.0145	.8136±.0054	.5462±.0017	0:14:18

Removing the lower level $(\beta =0)$ leads to a slight decrease in balanced accuracy and group sufficiency gap as the objective landscape is not flattened in the middle level. Additionally, manually adjusting the logits instead of learning the hyperparameters (as in [Menon et al., 2020]) further decreases the balanced accuracy and group sufficiency gap. However, our bilevel structure for addressing fairness ensures that the group sufficiency gap remains good despite these drops.

On credit card dataset, we have similar results. As for balanced accuracy, our method FACIMS improves the performance by 4.4%, 8.2%, 2.6%, 7.0%, and 2.3% comapred to EIIL, FSCS, FAMS, ERM and BERM. When it comes to the group sufficiency gap, the performance of our method is improved by 0.2%, 7.4%, 0.8%, 15%, and 11% comapred to the same baseline methods as metioned above. The performances of FACIMS $(\beta =0)$ and FACIMS ($\beta =0$, $\mathbf{v}=\overline{\mathbf{v}}$) drop slightly regarding both measurements.

To provide a more intuitive visualization of the results, we present boxplots in Figure 2. Each axis represents a measurement, where the mean value is represented by the middle of the box and the box width corresponds to twice the length of the standard deviation. The model’s performance is reflected by the position of the box, with improved performance observed towards the bottom right corner, indicating higher balanced accuracy and lower group sufficiency gap. For clarity, we have excluded two variants of our method from Figure 2. The complete figures can be found in the appendix. Figure 2 highlights that our method is positioned towards the bottom right corner, indicating improved performance compared to other methods.

Figure 2:

Boxplot comparing balanced accuracy and group sufficiency gap for three real datasets with 5 repeats. The mean is represented by the middle of each box, while the box width represents twice the standard deviation. Better performance is indicated by boxes located towards the bottom right (higher balanced accuracy and lower group sufficiency). Two FACIMS variants are excluded for clarity, with complete results available in the appendix.

Results on Other Metrics

In addition to the result analysis on balanced accuracy and group sufficiency, we also report demographic parity, equalized odds, recall, and time in Table 2. The results show that our method achieves competitive results despite not outperforming all baselines in terms of demographic parity and equalized odds gaps. We emphasize that our method primarily addresses the group sufficiency gap for fairness, and it is challenging to optimize all three fairness measurements simultaneously, as discussed in Section 2. When assessing a classifier’s performance, it is important to achieve a high recall for each class. However, the average recall across all classes determines the balanced accuracy, highlighting the need for a balanced recall quantity across all classes. Our approach and its variations demonstrate a more balanced recall for each class, as illustrated in Table 2.

Comparing the time aspect, despite employing a complex tri-level optimization framework for training our model, the total runtime is not significantly longer than other fairness baselines. Indeed, utilizing differentiable bilevel methods in the large hyperparameter search provides substantial cost reduction and speedup compared to traditional approaches like grid search or random search. For instance, the first variant of our method, FACIMS ($\beta =0$, $v=\overline{v}$), runs in approximately 13 minutes. However, employing grid search or random search to tune the parametric loss would require significantly more time. For example, if we perform a search with five different settings to enhance the accuracy of FACIMS ($\beta =0$, $v=\overline{v}$), the total time would be $13\min \times 5=65\min$, which is around four times longer than our differentiable tri-level FACIMS approach.

Influence of ${\alpha }^{\text{low}}$

In the middle level, the parameter ${\alpha }^{\text{low}}$ determines the attention given to $\mathrm{KL}\left({\mathbf{Z}}^a\mid \mathbf{Z}\right)$. A higher value of ${\alpha }^{\text{low}}$ brings the local model closer to the global model, leading to improved group sufficiency gap but potentially worse balanced accuracy. We experimented with four different values of ${\alpha }^{\text{low}}:0.01,0.1,0.2,\text{and}1$. Figure 3 illustrates the Accuracy-${\mathbf{SGap}}_f$ curve under varying ${\alpha }^{\text{low}}$ on the Alzheimer’s disease dataset. The figure demonstrates a clear trend: as ${\alpha }^{\text{low}}$ increases, both the balanced accuracy and group sufficiency gap decrease, aligning with our expectations. This analysis provides insight into how the KL divergence in the middle level influences the group sufficiency gap and balanced accuracy, enhancing our understanding of the framework’s mechanism.

Figure 3:

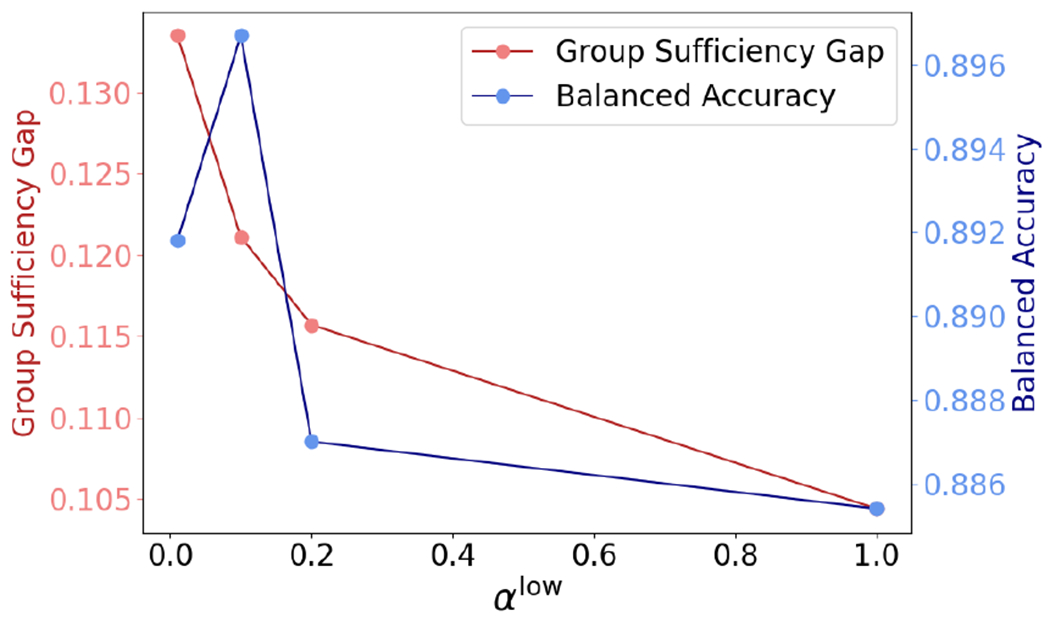
Accuracy-SGap_f curve under different ${\alpha }^{\text{low}}$ in Alzheimer’s disease dataset.

6. RELATED WORK

6.1. LONG-TAILED LEARNING

Re-sampling [Buda et al., 2018] and Re-weighting [He and Garcia, 2009] are commonly used methods for training on imbalanced datasets. Recent studies focus on optimizing loss landscapes for class-imbalanced datasets [Khan et al., 2017, Cao et al., 2019, Menon et al., 2020, Ye et al., 2020, Li et al., 2021, Kini et al., 2021, Behnia et al., 2023, Thrampoulidis et al., 2022]. Our work is related to the long-tail learning literature [Cao et al., 2019, Menon et al., 2020, Ye et al., 2020, Kini et al., 2021], where authors propose refined class-balanced loss functions that better adapt to training data. These include the logit-adjusted loss [Menon et al., 2020, Cao et al., 2019], the class-dependent temperature loss [Ye et al., 2020], and the VS loss [Kini et al., 2021], which unifies the concepts of multiplicative shift, additive shift, and loss re-weighting.

6.2. NESTED OPTIMZIATION

Nested optimization involves solving hierarchical problems with multiple levels of optimization [Colson et al., 2007, Tarzanagh et al., 2022, Chen et al., 2021, Ji et al., 2021, Tarzanagh and Balzano, 2022]. Min-max nested optimization is commonly used to learn fair representations in the context of demographic parity or equalized odds [Zemel et al., 2013, Song et al., 2019, Zhao et al., 2019]. Bi-level optimization and meta-learning algorithms have also been explored in the context of fair learning and classification [Shui et al., 2022b, Abbas et al., 2022]. Recent advancements in differentiable algorithms have led to faster bilevel algorithms for learning hyperparameters and classification [Li et al., 2021, Lorraine et al., 2020, Tarzanagh et al., 2022, Chen et al., 2021, Ji et al., 2021]. Building on [Li et al., 2021, Abbas et al., 2022], we propose a theoretically justified tri-level optimization perspective to control the group sufficiency gap and improve generalization performance across multiple subgroups with limited samples.

6.3. FAIRNESS

Group-sensitive learning aims to ensure fairness in the presence of under-represented groups [Lin et al., 2023, Zafar et al., 2017, Tarzanagh et al., 2021, Chierichetti et al., 2017]. Our work mainly focuses on the fair notion of group sufficiency. This notion has recently been studied in the health of populations [Obermeyer et al., 2019] and crime prediction [Chouldechova, 2017, Pleiss et al., 2017]. Liu et al. [2019b] show that under some assumptions, the group sufficiency can be controlled in unconstraint learning. On the other hand, Obermeyer et al. [2019], Shui et al. [2022a], Koh et al. [2021] claim that this conclusion may not always hold in the overparameterized models with limited samples per group. Subramanian et al. [2021] provided a method for fair and class-imbalanced learning.Lee et al. [2021] proposed a bilevel objective approach to achieve fairness in predictive models across all groups. In contrast, our tri-level algorithm incorporates a Bayesian framework for imbalanced learning, considering both class imbalance and subgroup distribution within each class, while also employing a nested optimization akin to SAM to overcome saddle points for minority classes.

7. CONCLUSIONS

We studied fairness-aware class imbalanced learning on multiple subgroups (FACIMS) using a Bayesian-based optimization framework. Through extensive empirical and theoretical analysis, we demonstrated that FACIMS enhances the generalization performance of overparameterized models when dealing with limited samples per subgroup.