Exploration of uncertainty of PRx time trends

Abstract

Introduction

PRx can be used as surrogate measure of Cerebral Autoregulation (CA) in traumatic brain injury (TBI) patients. PRx can provide means for individualising cerebral perfusion pressure (CPP) targets, such as CPPopt. However, a recent Delphi consensus of clinicians concluded that consensus could not be reached on the accuracy, reliability, and validation of any current CA assessment method.

Research question

We aimed to quantify the short-term uncertainty of PRx time-trends and to relate this to other physiological measurements.

Material and methods

Intracranial pressure (ICP), arterial blood pressure (ABP), end-tidal CO₂ (EtCO₂) high-resolution recordings of 911 TBI patients were processed with ICM + software. Hourly values of metrics that describe the variability within modalities derived from ABP, ICP and EtCO₂, were calculated for the first 24h of neuromonitoring. Generalized additive models were used to describe the time trend of the variability in PRx. Linear correlations were studied for describing the relationship between PRx variability and the other physiological modalities.

Results

The time profile of variability of PRx decreases over the first 12h and was higher for average PRx ∼0. Increased variability of PRx was not linearly linked with average ABP, ICP, or CPP. For coherence between slow waves of ABP and ICP >0.7, the variability in PRx decreased (R = −0.47, p < 0.001).

Discussion and conclusion

PRx is a highly variable parameter. PRx short-term dispersion was not related to average ICP, ABP or CPP. The determinants of uncertainty of PRx should be investigated to improve reliability of individualised CA assessment in TBI patients.

Highlights

• •The Pressure reactivity index PRx is highly variable.
• •Variability in PRx may be physiological or derive form methodological errors.
• •Short-term variability in PRx seems not to be (linearly) associated with CPP, ICP, ABP.

Abbreviations

PRx –

pressure reactivity index

TBI –

traumatic brain injury

CA –

cerebral autoregulation

CPP –

cerebral perfusion pressure

CPPopt –

Optimal cerebral perfusion pressure

ICP –

intracranial pressure

ABP –

arterial blood pressure

EtCO₂ –

end-tidal carbon dioxide

EVD –

extra ventricular drain

ABP_slow

power of slow waves in ABP

ICP_slow-

power of slow waves in ICP

EtCO_2slow -

power of slow waves in EtCO₂

GAM –

generalized additive models

PRx_iqr –

hourly interquartile range of PRx

CBFV –

cerebral blood flow velocity

1. Introduction

The pressure reactivity index (PRx) has been developed as a surrogate measure of cerebral autoregulation (CA) in traumatic brain injury patients (TBI) (Czosnyka et al., 1997). PRx can be monitored at the bedside in a semi-continuous fashion (Fig. 1), and high PRx is associated with worse outcome in TBI patients (Czosnyka et al., 1997; Zeiler et al., 2019). PRx can provide means for individualising cerebral perfusion pressure (CPP) targets, such as the optimal cerebral perfusion pressure (CPPopt) (Aries et al., 2012; Beqiri et al., 2023a; Liu et al., 2017b; Steiner et al., 2002) or the lower limit of pressure reactivity (Beqiri et al., 2023b; Donnelly et al., 2017). The results of the phase II trial (COGiTATE) proved safety and feasibility of targeting CPP at the PRx-derived CPPopt (J et al., 2021; Optimal cerebral perfusion pressure, 2023). However, a recent Delphi consensus of clinicians concluded that consensus could not be reached on the accuracy, reliability, and validation of any current CA assessment method (Depreitere et al., 2021).

Fig. 1.

PRx monitored at the bedside.

The neuromonitoring software ICM+ (schematically represented as a red square in the figure) allows to: 1) retrieve high resolution, waveform level, data of intracranial pressure (ICP) and arterial blood pressure (ABP); 2) apply advanced signal processing techniques and calculate in real time derived indices such as pressure reactivity index (PRx) and optimal cerebral perfusion pressure (CPPopt); 3) display time trends, risk charts, error bar charts and histograms, updated in a semi-continuous manner, on a laptop at the bedside. The Σ symbol denotes computational algorithms within ICM+.

The lack of reliability and reproducibility of cerebral autoregulation indices may depend on the CA physiological variability itself or on the methods used to infer CA (Panerai, 2014). The indices used for continuous monitoring of dynamic CA at the bedside, rely on spontaneous waves. Signal processing techniques are used to filter the information carried by the vasogenic slow waves and are based on correlation between waves of different sources (Brassard et al., 2021; Panerai, 2014). These indices do not measure CA, but they infer the CA behaviour.

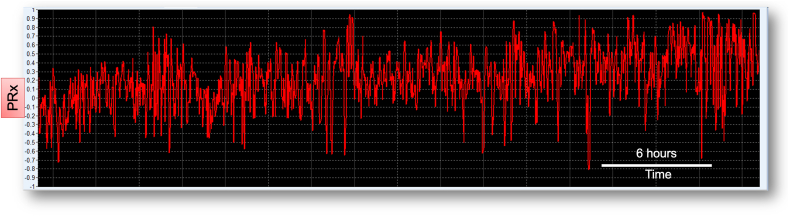
What is the reason for the lack of accuracy and reliability of PRx? The index is calculated as a moving Pearson correlation coefficient of 30 consecutive 10-s averages of arterial blood pressure (ABP) and intracranial pressure (ICP), updated every minute (Czosnyka et al., 1997). Pitfalls in PRx methodology have been identified (Czosnyka et al., 2017). Firstly, PRx is based on volume variations and not flow variations (Klein et al., 2021). It relies on adequate transmission of blood volume changes in ICP and may not be reliable when compliance is high (such in decompressive craniectomy). PRx also relies on the assumption that ICP variability is only driven by an extra-cranial source (ABP). Furthermore, PRx is a global index, and it may not adequately reflect regional changes in autoregulation. As a result, time trends of minute-by-minute PRx at the bedside are very noisy (Fig. 2), and it is unlikely that this kind of variability reflects the pathophysiological variability in CA. While this may not pose a significant problem for statistical associations performed on per-patient average values, it is likely to introduce errors for any short-term PRx-based metrics, as in the CA-oriented pressure management. Averaging PRx over 30 min or longer periods has been suggested as method for dealing with the ‘noise’ in the metric. This approach does not solve the problem because of the unknown nature of the ‘noise’, and may still lead to erroneous assessment of vascular reactivity, particularly when long periods of unreliable values are averaged out together. Additional metric of uncertainty, or quality, could help in selective smoothing potentially improving robustness of the PRx time trends.

Fig. 2.

Time trends of PRx at the bedside

Example of PRx time trends as displayed with ICM + at the bedside for a TBI patient. The time trends of PRx assessed at the bedside and displayed as minute-by-minute values can look very noisy. It is unlikely that this kind of variability is related to physiological variability in cerebral autoregulation. PRx, pressure reactivity index.

We hypothesise that the lack of reliability of PRx is related to the violation of assumptions of the PRx methodology. As a first step in the path of improving the reliability of PRx at the bedside, we aimed to quantify the short-term uncertainty of PRx time-trends and to relate the uncertainty of PRx to other physiological measurements.

2. Material and Methods

911 de-identified high-resolution arterial blood pressure (ABP), intracranial pressure (ICP) and end-tidal carbon dioxide (EtCO₂) recordings of TBI patients admitted in the neurocritical care unit of the Addenbrookes Hospital (Cambridge, UK) between 2002 and 2021, were accessed from the Brain Physics Lab research database (REC 23/YH/0085). Each recording corresponded to one single patient. Monitoring of brain modalities was conducted as a part of the standard patient care (Donnelly et al., 2019; Menon and Ercole, 2017). ICP was monitored with an intraparenchymal micro-sensor inserted into the frontal cortex (Codman ICPMicroSensor, Codman&Shurtleff, Raynham, Massachusetts) or via an extra ventricular drain (EVD). ABP was monitored in the radial or femoral artery (Baxter Healthcare, Deerfield, Illinois) with a zero calibration at the level of the right atrium (2002–2015) and at the foramen of Monro (2015–2022). Data of ICP, ABP and EtCO₂ from the vital monitor were streamed in real-time into the ICM + software (Cambridge Enterprise, University of Cambridge, UK) [https://icmplus.neurosurg.cam.ac.uk] (Smielewski et al., 2012), which provided data integration and storage at sampling rate from 50 Hz to 250 Hz, and de-identification for the Brain Physics Lab research database. For basic cohort description, binned age, sex and GCS at the presentation were retrieved form the Brain Physics Lab research database when possible.

2.1. Data processing

ICM + software was used for data processing. The data were first curated manually for large artefacts. Further, automated artefact markup was applied. EtCO₂ values below 20 mmHg or above 70 mmHg were rejected. EtCO₂ was available for 283 records. Arterial blood pressure (ABP) artefacts were removed automatically in case of absence of detected pulse, or when diastolic (and systolic) values fell to below (and above) unphysiological thresholds (15 mmHg and 300 mmHg respectively). Automatic intracranial pressure (ICP) artefacts removal used low pulse amplitude values (<0.04 mmHg) to reject artefactual periods which corresponded to either noise or short recording periods during which EVD was kept open (for those recordings where ICP was measured via EVD). Spectral edge frequency 95% above 10 Hz was used to reject periods of non-physiological measurements of ICP. All recorded signals were subsequently down-sampled to 0.1 Hz by coarse graining using 10 s, non-overlapping averages.

2.2. Measurements

ICM + software was further used to process the 10 s data and derive minute by minute time trends of various metrics used in the analysis.

PRx was calculated as moving 5 min window correlation coefficients between 30 consecutive 10 s averages of ABP and ICP, with moving lag of 1 min. PRx values were Fisher-transformed prior to any statistical analysis to address the <-1; +1> hard constrain of those indices.

We selected eight physiological modalities that we could explore and relate to the variability of PRx: ABP, ICP, pulse amplitude of ICP (AMP), EtCO₂, cerebral perfusion pressure (CPP), power of slow waves in ABP (ABP_slow), ICP (ICP_slow) and EtCO₂ (EtCO_2slow). For each of these, and for combinations of these, we extracted metrics of short-term variability. The full list of modalities explored is available in Table 1. The full list of summary metrics retrieved for each modality is available in Table 2. These metrics were calculated as hourly summaries for the first 24 h of recording. Each hour represented one epoch and they were considered independently.

Table 1.

Modalities considered in the analysis.

Variable	Description	calculation window (seconds)	update window (seconds)
ABP	mean ABP	60	60
ABP_dt	detrended ABP. An infinite response DC-filter with a frequency cut-off of 0.001 Hz was applied to 10sec averages of ABP	10	10
ABPslow	the power of slow waves in ABP was estimated with the Standard deviation of 10sec averages of ABP	600	60
ABPslow_entropy	entropy of the power of the power spectrum of ABP in the range 0–0.05 Hz.	3600	60
sdABP	single difference between consecutive data points of 10sec average ABP	10	10
SDsdABP_1h	standard deviation of the single difference of ABP	3600	60
ICP	mean ICP	60	60
ICP_dt	detrended ICP. An infinite response DC-filter with a frequency cut-off of 0.001 Hz was applied to 10sec averages of ICP	10	10
Coh_ABP_ICP	mean modulus coherence between ABP and ICP, in the frequency range 0–0.05 Hz, calculated with cross-spectral analysis (Hamming window, 5 segments, 50% overlap)	300	60
ICPslow	the power of slow waves in ABP was estimated with the Standard deviation of 10sec averages of ICP	600	60
ICPslow_entropy	entropy of the power of the power spectrum of ICP in the range 0–0.05 Hz.	3600	60
sdICP	single difference between consecutive data points of 10sec average ICP	10	10
SDsdICP_1h	standard deviation of the single difference of ICP	3600	60
CPP	(mean ABP) – (mean ICP)	10	10
sdCPP	single difference between consecutive data points of 10sec average CPP	10	10
SDsdCPP_1h	standard deviation of the single difference of CPP	3600	60
AMP	amplitude of the fundamental harmonic within the frequency range of 40–180 b/min using Fast Fourier Transform. This analysis was performed on full resolution, waveform level, data of ICP	10	10
sdAMP	single difference between consecutive data points of 10sec average AMP	10	10
SDsdAMP_1h	standard deviation of the single difference of AMP	3600	60
etco2	mean EtCO2	10	10
Etco2slow	the power of slow waves in ABP was estimated with the Standard deviation of 10sec averages of EtCO2	600	60
Etco2slow_entropy	entropy of the power of the power spectrum of etco2 in the range 0–0.05 Hz.	3600	60

All variables were further down sampled to 0.0167 Hz by coarse graining using 60 s, non-overlapping averages.

Table 2.

List of the summary metrics used in the analysis.

List of metrics used for the assessment of uncertainty and variability
minimum value (min)
first quartile (q1)
mean
median
third quartile (q3)
standard deviation (STdDev)
maximum value (max)
range (max - min)
interquartile range (iqr)
valid count (n of valid data points within the buffer)

2.3. Statistical analysis

The statistical analysis was performed with R software, version 4.0 (R2021 (2021) R Core Team, 2021). A p value of 0.05 was adopted for statistical significance. Correction for multiple comparison was not applied in this analysis.

2.3.1. PRx variability

The uncertainty of PRx was quantified with summary values of descriptive statistics of the metrics that describe the variability of PRx. The short-term uncertainty of PRx time trends were explored with generalized additive models (GAM) with cubic spline. GAM models allow to capture the shape of the relationship between two variables without pre-judging the issue by choosing a particular parametric form. Hence, they can reveal non-linear patterns. In the models, the explanatory variable was Time (hour number) and the response variable was the hourly interquartile range of PRx. Values of the interquartile range of PRx were either considered all together, or grouped depending on the corresponding average value of PRx: between −0.3 and + 0.3, below −0.3, above 0.3. We used cubic splines as a basis for the models’ explorations.

2.3.2. Correlations with other physiological modalities

Pearson correlations between metrics for PRx variability and other physiological measurements were performed and visualised with correlograms and R² was evaluated. All summary metrics for all physiological modalities were considered at this stage.

Further, to count for the fact that the variability metrics would be related to each other, we selected the following three descriptors for each modality: valid data count, median value, and range. To select the variables that have more influence on the variability of PRx we used an ordered bar plot of the t-statistics (absolute values) for the respective correlation coefficients and aimed to identify an elbow in the graph. Each epoch was treated as independent for the correlations analysis.

3. Results

The TBI patients included in this analysis were on average 45 years old, the majority were male and with GCS <9 at the presentation (Table 3). Of note, there is a considerable amount of missing data in the demographic information.

Table 3.

Basic demographics.

Variable	median (q1:q3) or n (%)	data availability, n (%)
Age	45 (25:55)	698 (76.6)
Sex (female)	121 (13.3)	558 (61.3)
Severity		578 (63.4)
GCS 3-8	408 (44.8)
GCS 9-13	132 (14.5)
GCS 14-15	38 (4.2)

GCS: Glasgow Coma Scale; q1: first quartile; q3: third quartile.

The amount of monitoring data remaining after data cleaning within the 24h considered for this analysis was in median (q1:q3) of 1355 (1147:1424) minutes for ICP, 1061.5 (66.5:1388) minutes for ABP, and 1338 (1064.5:1436) for EtCO₂.

3.1. Descriptive statistics of variability of PRx

A total n of 18262 epochs were analysed. Similar behaviour was observed for all metrics that describe PRx variability (Table 4). The hourly interquartile range of PRx (PRx_iqr) was chosen for further explorations.

Table 4.

Descriptive statistics of metrics that describe variability of PRx.

Variability of PRx metrics	min	max	median	q1	q3	iqr	mean	sd
PRx_iqr	0.000	1.809	0.361	0.273	0.489	0.216	0.398	0.185
PRx_mean	−0.952	0.992	0.029	−0.145	0.225	0.370	0.056	0.289
PRx_median	−0.952	0.995	0.024	−0.166	0.243	0.409	0.057	0.319
PRx_range	0.000	1.976	1.164	0.901	1.416	0.515	1.151	0.355
PRx_StdDev	0.000	0.880	0.276	0.213	0.351	0.138	0.286	0.101
sdPRx_mean	−0.450	0.383	0.000	−0.005	0.005	0.011	0.000	0.020
sdPRx_StdDev	0.000	0.637	0.190	0.150	0.235	0.085	0.195	0.064

q1, first quartile; q3, third quartile; iqr, interquartile range; sd, standard deviation; sdPRx, single difference between consecutive data points of minute-by-minute PRx.

3.2. Time profile of short-term PRx interquartile range

Fig. 3 shows the time profile of PRx variability (PRx_iqr) over the first 24h of neuromonitoring. The time profile of variability of PRx seems to decrease slightly over the first 12 h (Fig. 3A). Fig. 3B shows how the variability is overall higher for levels of PRx between −0.3 and + 0.3 (yellow line in the plot), as opposed to variability of PRx when PRx levels are below −0.3 (green, denoting preserved pressure reactivity), or above 0.3 (red, impaired pressure reactivity).

Fig. 3.

Time profile of PRx variability

The plots show the GAM models fit (with cubic spline) for PRx_iqr vs time (in hours from the start of neuromonitoring). The grey shaded area represents the standard error. In plot An all hourly PRx_iqr values are considered. In plot B, the values are grouped depending on the corresponding average value of PRx: between −0.3 and + 0.3 (yellow line), below −0.3 (green line), above 0.3 (red line). IQR: interquartile range.

3.3. Relationship with other physiological variables

Linear correlations with the modalities selected (see Table 1, Table 2 for the list of modalities) showed that mean values of ABP, ICP, CPP and EtCO₂ were not related to the variability of PRx (p > 0.05). When the modulus coherence between slow waves of ABP and ICP was above 0.7, there was a negative relationship between coherence and variability in PRx (R = −0.47, p < 0.001).

A total n of 67 variables were considered in the second exploration that aimed to select the variables that have more influence on the variability of PRx. For each variable, the correlation between the variable and PRx_iqr was computed. t-statistics absolute values were plotted (Fig. 4) and, after a visual inspection, an elbow in the plot was identified (red arrow). Variables on the left side of the elbow are listed here: 1) CPP range (R² = 0.14); 2) ABP range (R² = 0.13); 3) Range of Slow waves in ABP (R² = 0.12); 4) ICP range (R² = 0.11); 5) Range of coherence between slow waves in ABP and in ICP (R² = 0.09); 6) ABP detrended range (R² = 0.09); 7) ICP detrended range (R² = 0.08); 8) Range of Slow waves in ICP (R² = 0.08).

Fig. 4.

Bar plot of t-statistics

Absolute values of t-statistics of the linear correlation coefficients between each variable and the hourly interquartile range of PRx. The arrow indicates the elbow that we visually identified to select the variables with higher influence on the variability of PRx.

4. Discussion

In this work, we explored means for quantifying the uncertainty of PRx time trends within the first 24 h of neuromonitoring in TBI patients. Our results suggest that higher variability is related to periods with PRx around “0”. In our cohort, short-term variability of PRx was not significantly linearly related to any of average ICP, ABP, or CPP. The variability in CPP explained only 14 % of the variability in PRx. High coherence between slow waves in ABP and ICP were associated with lower uncertainty in PRx time trends.

How should we quantify the uncertainty of PRx time trends? Methods for quantifying uncertainty and reliability of indices of cerebral autoregulation (CA) have been suggested outside the realm of traumatic brain injury (Bryant et al., 2021; Gommer et al., 2010; Mitsis et al., 2002; O'Keeffe and Mahdi, 2018; Olsen et al., 2022; Panerai, 2014). For example, Bryant et al. (2021) implemented a parametric bootstrap approach that could estimate the confidence intervals for estimates of average phase obtained from transfer function analysis between ABP and cerebral blood flow velocity (CBFV), under the assumption of additive random noise in the output signal CBFV. They validated the method in a small cohort of young adults for identifying confidence intervals of phase estimates in individual short recordings. O'Keeffe et al. (O'Keeffe and Mahdi, 2018) used Bayesian parameter inference to estimate the error in the Autoregulation Index ‘ARI’ outputs. In both these examples, the data were represented by short recordings of non-invasive ABP and CBFV of healthy young subjects and were underpinned by a concrete physiological model-derived theoretical relationship between the analysed variables. PRx, on the other hand, is an entirely non-parametric index which does not lend itself to such approaches. Therefore, in our work we explored general, short-term variability metrics, such as interquartile range and standard deviation, that could quantify uncertainty over 1 h of data of minute-by-minute PRx. While this represented an initial step in this field, further methodological explorations are warranted in identifying suitable metrics for quantifying the uncertainty of PRx time trends in TBI.

How did the variability of PRx behave in the first 24 h of neuromonitoring in TBI patients? In this first exploration we could appreciate that the maximum values of the hourly interquartile range and range of PRx were very close to 2. Given that PRx can range from −1 to +1, this would mean that PRx would fluctuate from one extreme to the other within 1 h of time. This kind of variability seems unlikely to reflect physiological variability of CA in TBI patients admitted in intensive care unit. We noticed that the variability of PRx slightly decreased over the first 12 h (Fig. 3A), as the interquartile range decreased from 0.43 to 0.38. Whether this is a significant decrease and the reasons for it should be investigated in future studies. Importantly, the variability was higher and significantly different for epochs where the average PRx was around 0. Similarly, Sorrentino et al. looked at the critical thresholds for PRx and described values between 0 and 0.3 as a ‘grey zone’ in terms of relationship with outcome (Sorrentino et al., 2012). Values of PRx close to ‘0’ may reflect either working vascular reactivity, or incoherent variability in ICP and ABP. Our GAM models seem to support the latter and this has important clinical implications, suggesting that PRx values in this ‘0’ region should not be fully trusted as representing intact reactivity.

What is the uncertainty and variability of PRx related to? It is desirable that the variability in PRx captures the physiological variability of the autoregulatory mechanism. The main determinant of the autoregulatory mechanism, monitored by PRx, is CPP (Brassard et al., 2021). Hence, one would expect that the variability of PRx would be related to the variability of mean CPP. However, the short-term variability of PRx was not linearly related to average CPP in our cohort and the hourly range of CPP only explained 14% of the variability in PRx as expressed by R². This may be explained by the fact that non-linear relationships should be explored instead (Marmarelis et al., 2012; Mitsis and Marmarelis, 2004) or by the fact that CPP influences PRx on longer time periods. On the other hand, our result might suggest that other factors (methodological or physiological) are involved in explaining the variability of PRx. Physiological factors may be related to metabolic or neurovascular effects on ICP, hence multivariate models could help in describing vascular reactivity in a more reliable way. High coherence between slow waves in ABP and ICP was related to lower variability in PRx. This result was reassuring as it reflects the assumption of PRx for which the variability of ICP is driven by variability in ABP. This result also supports the idea of using wavelet methods for improving the stability of PRx calculations, as previously explored by our group (Liu et al., 2017a, 2018). Ideally a threshold for coherence, above which PRx can be computed, could be identified. For low coherence values though, the problem of detangling the source of uncertainty in PRx remains. In the attempt of identifying the variables that influence the short-term variability in PRx, we singled out a reasonable number of modalities that could be explored further in future studies (see paragraph 3.4).

Real-time availability of uncertainty metrics at the bedside along with the time-trend of PRx, could inform about reliability of the individualised CA assessment in TBI patients. The uncertainty metrics of PRx would serve to either reassure the clinician on the validity of the assessment of vascular reactivity or warn about the possible invalidity of the assessments. This would allow a more informed decision-making process at the bedside and help the clinician to select the patients and the scenarios when the CA assessment could be reasonably implemented, as well as provide reliability weighting in downstream algorithms, like CPPopt.

We speculate that the information of the determinants of uncertainty could also potentially aid in the evaluation of the status of CA. High uncertainty of the index would at least warn about the low confidence that the clinician should have on the assessment of CA and on the derived CPP targets, such as CPPopt. If such uncertainty was associated, for example, with high variability in EtCO₂, and the assessment of CA was considered relevant for the clinical management, then stabilizing the ventilation (if clinically feasible) could be a means for lowering the uncertainty of PRx and hence achieving a reliable assessment of CA and derived CPP targets. If the uncertainty was associated with low coherence between slow waves in ABP and ICP, then a brief period of induced oscillatory waves with the ventilator sigh function (provided this was clinically feasible) could provide with a period of high signal-to-noise for PRx (Tas et al., 2022). On the other hand, low uncertainty of the estimation of CA would provide high confidence in utilizing PRx and the derived CPP targets for the clinical decision-making process. We speculate that this will pave the path to reaching consensus among the clinical community on accuracy, reliability, and operationalization of PRx at the bedside.

With this first exploration we set out a research agenda for achieving the goal of providing real-time availability of uncertainty metrics at the bedside along with the time-trend of PRx, and so informing about reliability of the individualised CA assessment in TBI patients. First of all, methods for quantifying uncertainty of within patient short-term PRx should be explored. Next, factors that are related to high uncertainty should be identified. Further, nonlinearity of the autoregulatory mechanism should be considered in estimation of CA in those data that are considered reliable for assessment of autoregulation in TBI patients admitted in intensive care.

Our study has several limitations. Our cohort included all TBI patients with ICP monitoring admitted in Addenbrookes hospital that had ICM + monitoring data stored in the Brain Physics Lab research database. The availability of ICM + monitoring data depended on researchers’ availability. We do not hold a screening log and thus we cannot describe how many TBI patients were monitored out of all those that were admitted. We did not address the selection bias in our analysis. We only considered the first 24 h of neuromonitoring, and we did not reslice the data to the time of injury, but to the neuromonitoring start time, which makes our discussion of the time profiles less insightful. Each hourly epoch was considered as independent, and we did not count for repeated measures per patient. It is likely that both time and patient dependence would be relevant in the assessment of uncertainty of PRx. Clinical presentation, demographic variables, and injury severity scores were not considered in this analysis. Hence, in this cohort are included patients with EVD and patients that underwent decompressive craniectomy. The validity of PRx is questionable in both cases, however we attempted to address this issue with careful signal processing. Further, the possible demographic indicators of PRx variability were not explored. Lastly, the type of modalities that we explored were dictated by the data availability.

5. Conclusion

PRx is a highly variable parameter, and its short-term dispersion does not seem to be linearly related to mean values of ICP, ABP or CPP. Variability in CPP explained only 14% of the variability in PRx. High coherence between slow waves of ABP and ICP were associated with lower uncertainty of PRx. Real-time availability of uncertainty metrics along with the time-trend of PRx could inform the reliability of the individualised CA assessment in TBI patients.

Funding

Erta Beqiri is supported by the Medical Research Council (grant no.: MR N013433-1) and by the Gates Cambridge Scholarship. Giada Cucciolini is supported by a research grant from University of Pisa. Claudia A. Smith is supported by the Skye Cambridge International Patrick & Margaret Flanagan Scholarship. Michal M. Placek was supported by REVERT project within EC Interreg programme.

Declaration of competing interest

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests:

Peter Smielewski, Marek Czosnyka has patent with royalties paid to Cambridge Enterprise Ltd, University of Cambridge, Cambridge.

Handling Editor: Dr W Peul