Transporting a Prediction Model for Use in a New Target Population

Abstract

We considered methods for transporting a prediction model for use in a new target population, both when outcome and covariate data for model development are available from a source population that has a different covariate distribution compared with the target population and when covariate data (but not outcome data) are available from the target population. We discuss how to tailor the prediction model to account for differences in the data distribution between the source population and the target population. We also discuss how to assess the model’s performance (e.g., by estimating the mean squared prediction error) in the target population. We provide identifiability results for measures of model performance in the target population for a potentially misspecified prediction model under a sampling design where the source and the target population samples are obtained separately. We introduce the concept of prediction error modifiers that can be used to reason about tailoring measures of model performance to the target population. We illustrate the methods in simulated data and apply them to transport a prediction model for lung cancer diagnosis from the National Lung Screening Trial to the nationally representative target population of trial-eligible individuals in the National Health and Nutrition Examination Survey.

Abbreviations

MSE

mean squared error

NHANES

National Health and Nutrition Examination Survey

NLST

National Lung Screening Trial

OLS

ordinary least squares

WLS

weighted least squares

Users of prediction models typically want to apply the models in a specific target population of substantive interest. For example, a health-care system may want to deploy a clinical prediction model to identify individuals at high risk for adverse outcomes among all patients receiving care. Prediction models are often built using data from source populations sampled in prospective epidemiologic cohorts, confirmatory randomized trials (1), or administrative databases (2). In most cases, the sample of observations from the source population that is used for developing the prediction model is not a random sample from the target population where the model will be deployed, and the two populations have different data distributions (e.g., a different “case-mix” (3)). Consequently, a model developed using the data from the source population may not be applicable to the target population and model performance estimated using data from the source population may not reflect performance in the target population.

Ideally, we would use both covariate and outcome data from a sample of the target population in order to develop and evaluate prediction models. In many cases, however, only covariate data are available from the target population, and outcome data, alongside covariate data, are available only from a source population with a different data distribution. For example, when developing a prediction model, covariate data are often available in administrative databases representative of the target population, but outcome data may be unavailable (e.g., when outcome ascertainment requires specialized assessments) or inadequate (e.g., when the number of outcome events is small due to incomplete follow-up). In this setup, the lack of outcome information from the target population precludes the development or the assessment of prediction models using exclusively target population data. Thus, using covariate and outcome data from the source population may be an attractive alternative, provided we can adjust for differences in the data distributions of the two populations. More specifically, we are faced with two transportability tasks: 1) tailoring a prediction model for use in the target population when outcome data are only available from the source population; and 2) assessing the performance of the model in the target population from which outcome data are unavailable.

These transportability tasks have received attention in the computer science literature on covariate shift and domain adaptation (4–12). Related ideas have also appeared in the extensive epidemiologic literature on addressing updating, refitting, recalibrating, or extending a prediction model to a target population, but this literature has typically assumed that outcome and covariate information is available from both the source and target population (3, 13–17). Furthermore, the tasks of prediction model transportability are related to the problem of transporting inferences about treatment effects to a new target population (18–21), but there are important differences between transportability analyses for causal effects and those for prediction models, in terms of target parameters, assumptions, and estimation methods.

Here, we examine the conditions that allow transporting prediction models from the source population to the target population, using covariate and outcome data from the source population and only covariate data from the target population. Specifically, we tailor a prediction model for use in the target population and show that measures of model performance in the target population can be identified and estimated, under different sampling designs, even when the prediction model is misspecified. To aid reasoning about transportability of measures of model performance to the target population, we introduce the concept of prediction error modifiers. Last, we illustrate the methods using simulated data and apply them to transport a prediction model for lung cancer diagnosis from the National Lung Screening Trial (NLST) (22) to the nationally representative target population of trial-eligible individuals in the National Health and Nutrition Examination Survey (NHANES).

SAMPLING DESIGN AND IDENTIFIABILITY CONDITIONS

Let Y be the outcome of interest and X a covariate vector. We assume that outcome and covariate information is obtained from a simple random sample from the source population 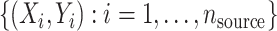. Furthermore, covariate information is obtained from a simple random sample from the target population, 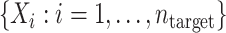; no outcome information is collected from the target population. This “non-nested” sampling design (23, 24), where the samples from the target and source population are obtained separately, is the one most commonly used in studies examining the performance of a prediction model in a new target population. For that reason, we discuss results for non-nested designs in some detail below (and provide technical details in Web Appendix 1, available at https://doi.org/10.1093/aje/kwac128). Nested sampling designs are an alternative approach where the sample from the source population is embedded, by prospective design or via record linkage, within a cohort representing the target population (21, 24, 25) (we provide results for nested designs in Web Appendix 2).

Let S be an indicator for the population from which data are obtained, with 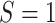for the source population and 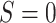for the target population. We use 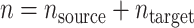to denote the number of observations in the composite data set consisting of the data from the source and target population samples. This composite data set is randomly split into a training set and a test set. The training set is used to build a prediction model for the expectation of the outcome conditional on covariates in the source population, 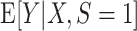, and then, the test set is used to evaluate model performance. We use 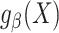to denote the posited parametric model, indexed by the parameter 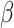, and 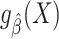to denote the “fitted” model with estimated parameter 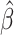. We use 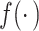to generically denote densities.

We assume the following identifiability conditions, A1 and A2:

A1: Independence of the outcome Y and the population S, conditional on covariates. For every x with positive density in the target population, ,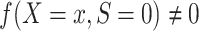

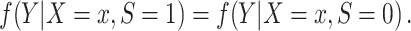Condition A1 connects the source and target populations; in applications, it will typically be a fairly strong assumption. Informally, it requires the relationship between Y and X to be common across populations, allowing us to learn about the target population even when outcome data are available only from the source population. Condition A1 implies conditional mean exchangeability over S: For every x such that 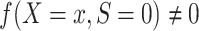, 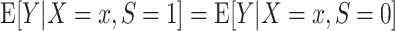. For nonbinary outcomes, however, the converse is not true: Conditional mean exchangeability over S does not imply condition A1.

We note that condition A1 is not testable without outcome information from the target population sample and thus needs to be evaluated on a case-by-case basis in view of background knowledge about the relationship between the source and target population. Developing sensitivity analysis methods (26) for examining the impact of violations of this condition may be the subject of future work. Furthermore, if outcome data can be collected from the target population sample, condition A1 becomes testable and can potentially be relaxed, allowing the combination of information on the covariate-outcome association from both the source and target population (this is what various previously proposed methods for updating or refitting models focus on (15, 13, 3, 16)).

A2: Positivity. 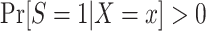, for every x such that .

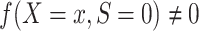Informally, condition A2 means that every pattern of the covariates needed to satisfy condition A1 can occur in the source data. This condition is in principle testable, but formal evaluation may be challenging in practice, particularly when the covariates are high-dimensional (27).

As we discuss next, conditions A1 and A2 will allow us to tailor the prediction model and assess its performance for use in the target population.

TAILORING THE MODEL TO THE TARGET POPULATION

Recall that 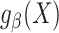is a model for 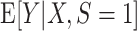. Suppose that the parameter 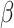takes values in the space 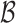. We say that the model is correctly specified if there exists 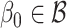such that 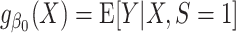(28). The approach for tailoring the fitted model 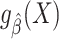for use in the target population depends on whether the posited model 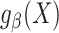is correctly specified. Throughout this paper we focus on maximum likelihood estimators of 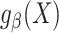, but many of the ideas generalize to more general M-estimators (29).

Correctly specified model

Suppose that the model 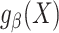is correctly specified and thus we can construct a model-based estimator 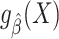that is consistent for 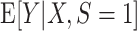. Under condition A1, a consistent estimator for 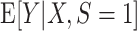is also consistent for 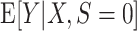(because the two expectations are equal). Moreover, when the model for the conditional expectation is parametric and the parameter 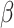is estimated using maximum likelihood methods, then the unweighted maximum likelihood estimator 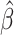that uses only training-set data from the source population is optimal in terms of having the smallest asymptotic variance (30, 31).

Misspecified model

Now, suppose that the model 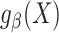is misspecified, as we would expect to be the case in most practical applications. Then, the maximum likelihood estimator that uses only data from the source population is inconsistent for 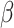; in fact, as the sample size goes to infinity, the limiting value of the estimator of the misspecified model does not minimize the Kullback-Leibler divergence between the estimated and true conditional density of the outcome given covariates (31). Instead, the Kullback-Leibler divergence is minimized by using a weighted maximum likelihood estimator with weights set equal to the ratio of the densities in the target and source populations, that is, .

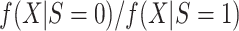In applied work, the density ratio is typically unknown and needs to be estimated using the data, but direct estimation of density ratios is challenging, particularly when X is high-dimensional (32). Instead, we can use the fact that the density ratio is, up to a proportionality constant, equal to the inverse of the odds of being from the source population,

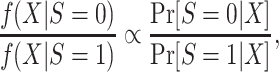to replace density ratio weights with inverse-odds weights and obtain an estimator of the model tailored for use in the target population. The inverse-odds weights can be obtained by estimating the probability of membership in the source population conditional on covariates—a task for which many practical methods are available for high-dimensional data (33). Thus, a reasonable approach for tailoring a potentially misspecified prediction model for use in the target population would proceed in three steps. First, estimate the probability of membership in the source population, using training data from the source population and target population. Second, use the estimated probabilities to construct inverse-odds weights for observations in the training set from the source population. Third, apply the weights from the second step to estimate the prediction model using all observations in the training set from the source population.

An apparent difficulty with the above procedure is that, in non-nested designs, the samples from the source population and target populations are obtained separately, with sampling fractions from the corresponding underlying populations that are unknown by the investigators. When that is the case, the probabilities 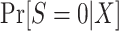and 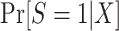in the inverse-odds weights are not identifiable from the observed data (and cannot be estimated using the observed data) (24, 34). Although the inverse-odds weights are not identifiable, in Web Appendix 1 we show that, up to an unknown proportionality constant, they are equal to the inverse-odds weights in the training set,

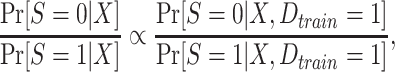(1)

where 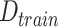is an indicator of whether data from an observation is in the training set. It follows that we can use inverse-odds weights estimated in the training set, when estimating 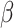with the weighted maximum likelihood estimator (in the second step of the procedure described above).

ASSESSING MODEL PERFORMANCE IN THE TARGET POPULATION

We now turn our attention to assessing model performance in the target population. For concreteness, we focus on model assessment using the squared error loss function and on identifying and estimating its expectation, the mean squared error (MSE), in the target population. The squared error loss 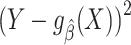quantifies the discrepancy between the (observable) outcome Y and the model-derived prediction 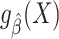in terms of the square of their difference. The MSE in the target population is defined as

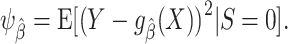Although we focus on the MSE in the main text of this paper, our results readily extend to other measures of performance; in Web Appendix 1 we give identifiability results for general loss function-based measures.

Prediction error modifiers

To help explain why measures of model performance need to be tailored for use in the target population, we introduce the notion of “prediction error modifiers” to describe covariates that, for a given prediction model, are associated with prediction error as assessed with some specific measure of model performance. Slightly more formally, and using the squared error loss as an example, we say that X is a prediction error modifier for the model 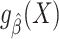, with respect to the squared error loss function in the source population, if the conditional expectation 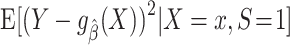varies as a function of x. Several parametric or nonparametric methods are available to examine whether 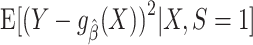is constant (i.e., does not vary over different values of X). If condition A1 holds and X is a prediction error modifier in the source population for values of X that belong in the common support of the source and target populations, then X is also a prediction error modifier in the target population. When the distribution of prediction error modifiers differs between the source and target populations, measures of model performance estimated using data from the source population are unlikely to be applicable in the target population, in the sense that the performance of the model in the source data may be very different (either better or worse) compared with performance of the same model in the target population. Potentially large differences in performance measures between the source and target population can occur even if the true outcome model in the two populations is the same (i.e., even if condition A1 holds) because most common measures of model performance average (marginalize) prediction errors over the covariate distribution of the target population (as is the case, e.g., for MSE), and the covariate distribution of the target population can be different from the distribution in the source population.

Figure 1 shows an example of a prediction error modifier that has a different distribution between the source and target population, resulting in a “true” MSE in the target population that is higher than the MSE in the source population. In Figure 1B we plot the inverse-odds weights as a function of the prediction error modifier X; in Figure 1C we plot the expectation of the squared errors (from the “true” model of the outcome expectation) as a function of X (i.e., the true conditional MSE function). Because both the expectation of the squared errors and the inverse-odds weights (and therefore the probability of membership in the target population) increase as X increases, the target population MSE (which is equal to the expectation of the conditional MSE over the target population distribution of X) is larger than the source population MSE. Hence, directly using the source population MSE in the context of the target population would lead to over-optimism about model performance.

Figure 1.

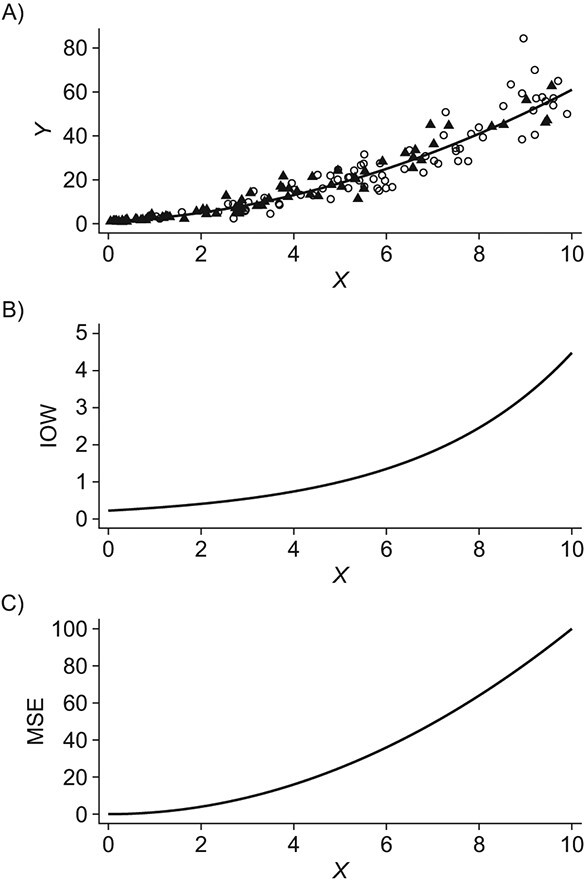
An example of a prediction error modifier, X. A) A scatter-plot of the simulated data, including the unmeasured target population outcomes. Data from the source population are depicted by black triangles; data from the target population are depicted as white circles. The solid black line is the true conditional expectation function 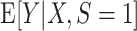. B) The inverse-odds weights (IOW) as a function of X; C) the conditional expectation of the squared deviations of the observations from the true model as a function of X (informally, this can be thought of as the “true” conditional mean-squared-error (MSE) function for the correctly specified model). In these data, larger values of X correspond to higher probability of membership in the target population, 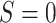(corresponding to lower odds of being from the source population and higher inverse-odds weights), and higher MSE. Hence, X is a prediction error modifier that is differentially distributed between the source and the target population. This leads to the target population MSE being larger than the source population MSE. Panel (A) was created from a single draw from the simulation model described under “Illustration using simulated data” by sampling a random subset of observations.

Assessing model performance in the target population

In our setup, where outcome information is only available from the sample of the source population, we need to account for differences in the data distribution between the source population and the target population to assess model performance in the target population. Proposition 1 in Web Appendix 1 shows that, under the setup described previously and conditions A1 and A2, 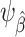is identifiable by the following functional of the source and target population data distribution:

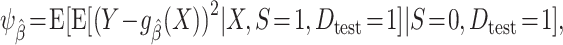(2)

or equivalently using an inverse-odds weighting expression

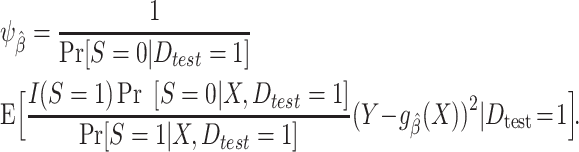(3)

Here, 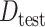is an indicator for whether an observation is in the test data (from either the target or the source population). Importantly, the components of the above expressions can be identified from the observed data and do not require outcome information to be available from the target population.

The identifiability result in expression 3 suggests the following weighting estimator (35, 31) for the target population MSE:

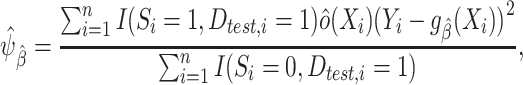(4)

where 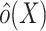is an estimator for the inverse-odds weights in the test set, 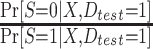. Typically, 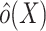will be obtained by specifying a model for the probability of membership in the source population conditional on covariates (among observations in the test set), 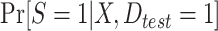. Provided that this model is correctly specified, the estimator 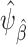is consistent for 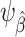. To ensure independence between the data used to train the model and the data used to evaluate the model, we propose to use inverse-odds weights estimated using the training set for model building and inverse-odds weights estimated using the test set for estimating model performance. As is often the case when using weighting methods, empirical near-violations of the positivity condition A2 can lead to high variability of the inverse-odds weighting estimator and we recommend careful examination of the distribution of the estimated weights in applications (27, 36, 20).

An important feature of our results is that they do not require the prediction model to be correctly specified. In other words, we do not assume that 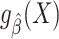converges to the true conditional expectation of the outcome in the source population, 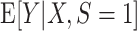. This implies that measures of model performance in the target population are identifiable and estimable, both for misspecified and correctly specified models, provided conditions A1 and A2 hold. Informally, our identifiability results require the existence of a common underlying model for the source and target population, and overlap of their respective covariate distributions, but they do not require the much less plausible assumption that investigators can correctly specify that model.

Our results pertain to applications where the prediction model is built using the training data and is evaluated using the test data, and where the entire composite data set is split into a test and a training set that are used for model estimation and assessment. In some cases, an established model is available, and the goal of the analysis is limited to assessing model performance in the target population. In that case, no data from the source or target population need to be used for model development, and all available data can be used to evaluate model performance and treated as a part of the “test set.”

Furthermore, we have proceeded as if the source population data in the training set are used to estimate parameters of a prespecified parametric model, without employing any form of model selection (e.g., variable choice or other specification search) or tuning parameter selection. But, when developing prediction models, analysts often consider multiple models, and statistical learning algorithms usually have one or more tuning parameters. Model and tuning parameter selection is commonly done by minimizing a measure of prediction error. In Web Appendix 3, we discuss how to tailor data-driven model and tuning parameter selection to the target population.

Last, note that provided the prediction model is correctly specified, conditional mean exchangeability over S, that is (rather than condition A1), is sufficient for the parameter 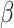to be identifiable using data from the source population alone. For nonbinary Y, however, conditional mean exchangeability is not in general sufficient for transporting measures of model performance, such as the MSE. To illustrate, in Web Appendix 4 and Web Figure 1 we give an example where mean exchangeability holds but is not sufficient to identify the target population MSE (because assumption A1 is violated).

ILLUSTRATION USING SIMULATED DATA

We used simulated data to illustrate 1) the performance of correctly and incorrectly specified prediction models when used with or without inverse-odds weights; 2) the potential for reaching incorrect conclusions about model performance in the target population when using a naive (unweighted) MSE estimator that uses only the source population outcome data to estimate the target population MSE (i.e., naively applying the MSE from the source population data to the target population); and 3) the ability to adjust for this bias using the inverse-odds weighting MSE estimator.

Data generation

We simulated outcomes using the linear model 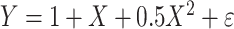, where 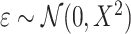and 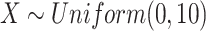. Under this model, the errors are heteroscedastic because the error variance directly depends on the covariate X. We simulated membership in the source population using a logistic regression model 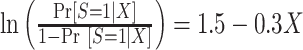. We set the total sample size to 1,000 and split the source and target population data randomly, with a 1:1 ratio, into the training and test sets.

With this data-generating mechanism, the true target population MSE is larger than the true source population MSE, and both conditions A1 and A2 are satisfied. We considered two prediction models, a correctly specified linear regression model that included main effects of X and 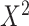and a misspecified linear regression model that included only the main effect of X. We also considered two approaches for estimating the parameters of each posited prediction model: ordinary least squares (OLS) regression (unweighted) and weighted least squares (WLS) regression where the weights were equal to the inverse of estimated odds of being in the source-data training set. We estimated the inverse-odds of membership in the training set, 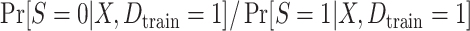, using a correctly specified logistic regression model for 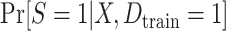. Figure 2 highlights the relationship between the correctly specified outcome model, and the large-sample limits of the weighted and unweighted estimators of the misspecified outcome model. For the inverse-odds weighting estimator 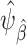, we estimated the odds weights 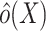by fitting a correctly specified logistic regression model for 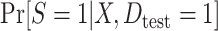using the test set data.

Figure 2.

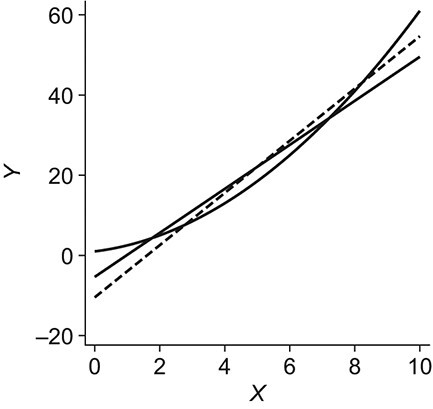
An example using simulated data to illustrate transportability of prediction models. The solid curved line depicts the “true” conditional expectation function 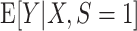(which for this data-generating distribution is equal to 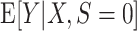); the solid straight line is the large-sample limit of the misspecified regression model estimated using source population data without using weighting; and the dotted line is the large-sample limit of the misspecified regression model estimated using source population data with inverse-odds weights. The weighted estimation gives more influence to observations with higher values of X, compared with unweighted estimation, because higher values of X are associated with higher odds of a sampled observation being from the target population (i.e., lower odds of being from the source population, corresponding to higher inverse-odds weights). This is seen in the figure as for high values of X the weighted model better approximates 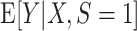compared with the unweighted model, but the opposite is true for smaller values of X. This figure reflects the data-generating mechanism described under “Illustration using simulated data” (the population limits of misspecified models were obtained by simulating a large number of observations from the true model and fitting misspecified models, with and without weighting).

Simulation results

The results from 10,000 runs of the simulation are presented in Table 1. For both OLS and WLS estimation of the prediction model, the correctly specified model resulted in smaller average estimated target population and source population MSE compared with the misspecified model. When examining different approaches for estimating the prediction model for use in the target population, OLS performed slightly better than WLS when the model was correctly specified (average MSE of 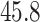vs. 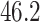). In contrast, OLS performed worse than WLS (average MSE of 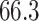vs. 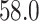) when the prediction model was incorrectly specified. The last column in the table shows that the average of the inverse-odds weighting MSE estimator across the simulations was very close to the true target population MSE (obtained via numerical methods) for all combinations of outcome model specification (correct or incorrect) and estimation approach (OLS or WLS). In all scenarios of this simulation, the average of the estimator for the source population MSE was biased for the target population MSE. Hence, naively using the estimated source population MSE as an estimator for the target population MSE would lead to substantial underestimation (i.e., showing model performance to be better than it is in the context of the target population). In contrast, the inverse-odds weighting estimator would give an accurate assessment of model performance in the target population.

Table 1.

Target Population Mean Squared Error, Average of the Source Data Mean-Squared-Error Estimators, and Average of the Weighted Estimators for the Target Population Mean Squared Error From a Prediction Model Simulation

Model Specification, Estimation Approach a	True Target Population MSE	Average of Unweighted MSE Estimator	Average of Weighted MSE Estimator b
Correctly specified, OLS	45.8	22.5	45.8
Incorrectly specified, OLS	66.3	34.5	66.3
Correctly specified, WLS	46.2	22.8	46.2
Incorrectly specified, WLS	58.0	43.6	57.9

Abbreviations: MSE, mean squared error; OLS, ordinary least squares; WLS, weighted least squares.

^a Correctly specified and incorrectly specified refer to the specification of the posited prediction model.

^b Weighted MSE estimator results were obtained using the estimator in equation 4. OLS regression was unweighted; WLS regression was with weights equal to the inverse of the odds of being from the source population

A PREDICTION MODEL FOR LUNG CANCER DIAGNOSIS

We applied the methods to tailor a prediction model for lung cancer diagnosis to the general US population of trial-eligible individuals, using outcome information from a large clinical trial. Specifically, we obtained source population data from the computed-tomography arm of the NLST (37), a large randomized trial comparing the effect of computed tomography versus chest radiography screening for individuals at high risk for lung cancer (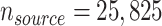 after removing 897 observations with missing data). The results of the study helped inform national policy for lung cancer screening (38, 39). The outcome we focused on is whether a participant was diagnosed with lung cancer within 6 years from study enrollment. Because computed-tomography screening for lung cancer is implemented nationally, a natural target population is everyone in the United States who is eligible for screening. We obtained target population data from the NHANES, which was designed to obtain a representative sample of the noninstitutionalized US population. We used the subset of NHANES participants who provided information to a smoking substudy conducted between 2003 and 2004 and met the NLST eligibility criteria, which are very similar to the criteria used for recommending lung cancer screening in the United States (39, 38) (unweighted 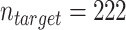after removing 3 observations with missing data). NHANES is a cross-sectional study so no follow-up information on lung cancer diagnosis was available from the target population. Web Appendix 5 provides additional information on the two data sets and describes how we handled the NHANES sampling weights in the analysis.

The prediction model for lung cancer diagnosis was estimated using inverse-odds weighted logistic regression for the conditional probability of lung cancer diagnosis with main effects of the following variables as predictors: age, body mass index, race/ethnicity (Black, White, Hispanic, other), education (less than high school, high-school graduate, associate’s degree/some college, college graduate), personal history of cancer, smoking status, smoking intensity, duration of smoking, and smoking quit time.

The coefficients and 95% confidence intervals for the prediction model parameters are presented in Web Table 1 in Web Appendix 5. Using the weighted MSE estimator given above, the estimated Brier score in the target population (which is equivalent to the target population MSE for binary outcomes) for the inverse-odds weighted prediction model was 0.053. For comparison, when applying the same model (estimated using inverse-odds weights) to the source population without using weights in the MSE estimator, the estimated Brier score was 0.035. The difference in the two MSE estimates highlights that using inverse-odds weights when assessing model performance (e.g., estimating the Brier score) is necessary in addition to using inverse-odds weights for tailoring the model to the target population.

DISCUSSION

We considered transporting prediction models to a target population that is different from the source population providing data for model development, when outcome and covariate data are available on a simple random sample from the source population, and covariate data—but not outcome data—are available on a simple random sample from the target population. Specifically, we discussed how to tailor the prediction model to the target population and how to calculate measures of model performance in the context of the target population, without requiring the prediction model to be correctly specified. A key insight is that most measures of model performance average over the covariate distribution, and as a result, estimators of these measures obtained in data from the source population will typically be biased for the corresponding measures in the target population, when the covariate distribution differs between the two populations. Prospective external validation using a random sample of covariates and outcomes from the target population would be the ideal way to evaluate model performance in the target population. But when such evaluation is infeasible (e.g., due to cost or when long-term follow-up is needed to obtain outcome information from the target population), the methods proposed here can be an appealing alternative.

An important aspect of our approach is the explicit consideration of the target population where the prediction model will be applied and the use of covariate information from a sample of that population. In practice, lack of access to data from the target population could limit the applicability of the methods we described (40). Over time, however, we expect that this limitation will be mitigated by the increasing availability of routinely collected data (e.g., electronic health records and medical claims) and survey data from relevant target populations.

For simplicity, we assumed that the covariates needed to satisfy the conditional independence condition A1 are the same as the covariates used in the prediction model. In practice, the set of covariates needed to satisfy condition A1 may be much larger than the set of covariates that are practically useful to include in the prediction model. Our identifiability results can be easily modified to allow for the two sets of covariates to be different. Furthermore, to maintain focus on transportability methods, we did not address important practical issues such as missing data and measurement error. Nevertheless, the methods we describe can be combined with standard methods for addressing these issues (e.g., weighting methods for missing data (41) can be combined with the inverse-odds estimators we describe).

Future research could consider the statistical properties of transportability methods in the presence of missing data, as well as extensions to address censoring (e.g., failure-time outcomes) and measurement error. Future research could also consider data-driven approaches to identify prediction error modifiers or subgroups of participants with differential prediction accuracy, the development of more efficient and robust estimators than the inverse-odds weighting estimator given above (42), and methods for combining samples from the source and target population when both contain outcome information.