Potential energy functions for atomic-level simulations of water and organic and biomolecular systems

Abstract

An overview is provided on the development and status of potential energy functions that are used in atomic-level statistical mechanics and molecular dynamics simulations of water and of organic and biomolecular systems. Some topics that are considered are the form of force fields, their parameterization and performance, simulations of organic liquids, computation of free energies of hydration, universal extension for organic molecules, and choice of atomic charges. The discussion of water models covers some history, performance issues, and special topics such as nuclear quantum effects.

The last 30 years have witnessed remarkable progress in condensed-phase theory. Before that time, atomic-level computer simulations of fluids were largely restricted to atomic and diatomic systems. The first simulation of liquid water was not reported until 1969 and was a Monte Carlo (MC) effort (1), which was followed by the molecular dynamics (MD) studies of Rahman and Stillinger (2, 3) in the early 1970s. The state-of-the-art simulations of water in 1974 were performed for 216 molecules for <10 ps (3). Even by 1990, there had been almost no MD simulations for a protein in aqueous solution covering 100 ps (4), whereas today MD simulations for a protein with ≈10,000 water molecules for many nanoseconds or mixed quantum and molecular mechanics (QM/MM) simulations for an enzymatic reaction are not problematic. Of course, performing longer simulations for larger systems does not guarantee the production of useful results. Key underlying issues for accuracy are adequate configurational sampling and the quality of the description of the intramolecular and intermolecular energetics. Progress on the former issue has been aided greatly by massive increases in computing power, although the substantial technical developments in the latter area are the focus of this overview. The topic also has received attention in comprehensive, recent reviews for the treatment of water (5) and biomolecular systems (6–10) that go far beyond the present page limitations. So, the presentation here will be more condensed with a focus on force-field development, water, and aqueous solutions and with some emphasis on our personal experiences and viewpoint.

Force Fields

A force field consists of classical potential energy expressions and the associated adjustable parameters. The large majority of condensed-phase simulations have invoked pairwise additivity such that the total potential energy for a collection of molecules and/or ions (components) with coordinates 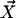is given by the sum of the intermolecular interaction energies between all components plus the sum of the intramolecular energies of the components (Eq. 1).

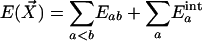[1]

The intramolecular potential energy is typically represented by harmonic terms for bond stretching and angle bending, a Fourier series for each torsional angle, and Coulomb and Lennard–Jones interactions between atoms separated by three or more bonds (Eqs. 2–5). The latter “nonbonded” interactions also are evaluated between intermolecular atom pairs to yield the intermolecular energy (Eq. 6). For the charges q_i and Lennard–Jones terms, an interaction site is normally placed on each atom to yield all-atom (AA) models. These models have superceded earlier united atom models, which collapsed aliphatic hydrogens on to their carbons. Commonly used force fields for organic and biomolecular systems such as AMBER, CHARMM, and optimized potentials for liquid simulations (OPLS)-AA follow this format with minor variations (11–13).

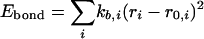[2]

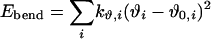[3]

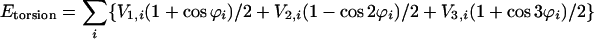[4]

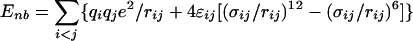[5]

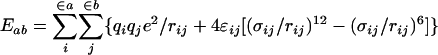[6]

These functional forms provide a minimalist rendition of molecular energetics that has been adopted as a compromise between speed and accuracy. More complex force fields have been developed that add, for example, cubic and quartic terms to Eqs. 2 and 3 to reflect anharmonicity, and stretch-bend cross-terms, or that replace the Lennard-Jones function with more flexible Buckingham (exp-6) or Morse potentials. Such force fields, including MM4 and MMFF (14, 15), were developed primarily to yield highly accurate structures, conformational energetics, and vibrational frequencies for isolated molecules and have not been used significantly in more computer-time-demanding fluid simulations.

The other major simplification in the minimalist model is that the atomic charges are fixed, and there is no explicit treatment of polarization, which exceeds the pairwise additivity of Eq. 1. This approximation is well known to be problematic for interactions with charge-concentrated atomic ions and for interactions of ions with π -electron systems, including aromatic rings (16–18). However, it can also be problematic for less obvious cases such as polar solutes in low-dielectric media (19). Although there has been great interest in the development of polarizable force fields for water (ref. 5; for recent examples, see also refs. 20 and 21) and biomolecular systems (22–25), generally accepted models have not emerged, and several alternatives for the treatment of polarizability, including use of inducible dipoles, fluctuating charges, and Drude oscillators, remain under active consideration (26). An ancillary problem is the increased computational costs over the fixed-charge models, although significant advances have been made to reduce the increase to below a factor of two through use of extended Lagrangian methodology (27).

Overall, it is easy to anticipate that there will be continued development and increased use of polarizable force fields. It is clear that electronic structure depends on environment, so there are inaccuracies when, for example, the same fixed-charge water model is used to describe liquid water at 25°C and 1 atm (1 atm = 101.3 kPa) and water molecules near a hydrophobic surface or an ion. There will be reduced effort devoted to development of nonpolarizable force fields. Nevertheless, their use will remain high because they do work well in many contexts that are consistent with their range of parameterization, and they will provide an important reference point for the improvements that are available by progressing to more complex models.

Parameterization

Development of a comprehensive force field is a major undertaking that goes beyond the resources and patience of most research groups in computational chemistry. As with the development of quantum mechanical methods, force-field development has been predominantly the province of academic groups. Collaboration is the likely road to success for future efforts. Before the mid-1980s, force fields were primarily tested on reproduction of experimental or ab initio quantum mechanical results for molecular geometries in the gas phase and in crystals, vibrational frequencies for small molecules, conformational energetics, and hydrogen bonding. Even though use in fluid simulations was envisaged, the available computer resources were inadequate for extensive testing in MC or MD simulations of liquids. Reproduction of experimental densities and heats of vaporization for pure organic liquids can be identified as particularly important because these are key properties representative of molecular size and intermolecular interactions. However, the limited simulations that were performed in the early days were predominantly in the NVE (constant number of particles, volume, and energy; MD) or NVT (constant number of particles, volume, and temperature; MC) ensembles, which masked density errors that become strikingly evident in the more desirable and now common NPT (constant number of particles, temperature, and pressure) simulations.

For example, the historically significant MCY potential, which was developed by fitting to accurate ab initio results for the water dimer energy surface (28), produced an OO radial distribution function (rdf) for liquid water in NVT-MC simulations at 1 g·cm^–3 in excellent agreement with x-ray diffraction findings. However, it turned out to yield a 24% error in the density of liquid water, when an NPT-MC simulation was run (29). Serious density errors also are expected and found for other potential functions in the absence of optimization for this important property, which is sensitive to the choice of short-range (e.g., Lennard–Jones) parameters (30, 31). The failure of an accurate dimer potential such as the MCY model to fare well in simulations of the liquid emphasizes the importance of the missing many-body effects in Eq. 1. Thus, today's successful, nonpolarizable force fields all represent effective pair potentials that incorporate the many-body effects in an average sense, e.g., through the use of charges that yield enhanced dipole moments.

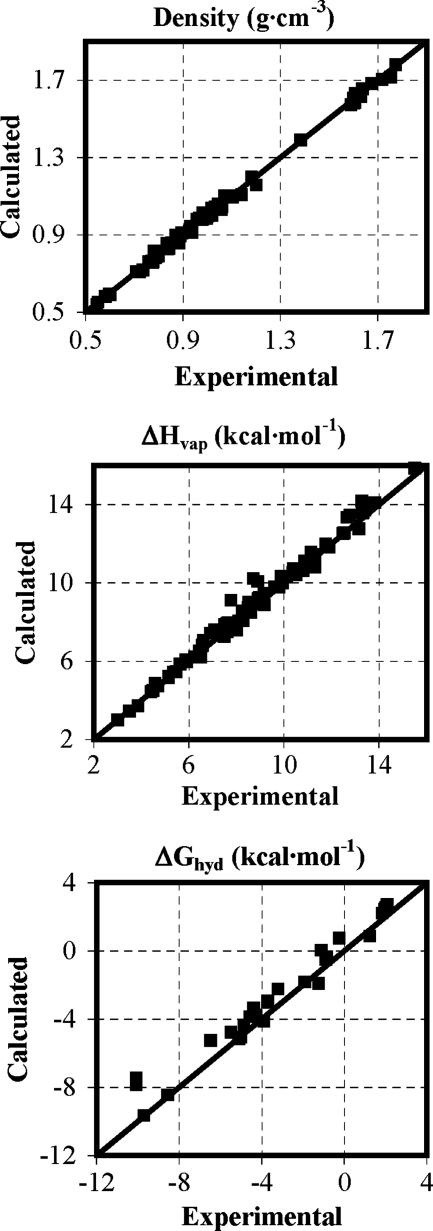
The extensive use of simulations of pure organic liquids as part of the parameterization process for a comprehensive force field began with the development of the OPLS model (32, 33). The importance of reproducing liquid properties is now well recognized, and the current generation of force fields has been developed, including testing for densities and heats of vaporization (11–13, 34). The success in the case of the OPLS-AA force field is illustrated in Fig. 1. In the process, much has been learned about the structure and properties of a wide range of organic liquids (35). Early work included topics such conformational shifts in liquids vs. the gas phase (36), effects of pressure on hydrogen bonding (37), and even effects of pressure on mixing enantiomeric liquids (38). Avant garde topics for simulations of organic liquids include examination of phase equilibria with grand canonical MC methods (39).

Fig. 1.

Computed (OPLS-AA) and experimental results for liquid densities (Top), heats of vaporization (Middle), and free energies of hydration (Bottom) at 25°C and 1 atm.

Thus, there has been much improvement in the quality of biomolecular force fields through more rigorous testing on reproduction of a wide range of experimental data for fluids. Additional notable enhancement has come from using accurate quantum mechanical results for conformational energetics and hydrogen bonding in the parameterization. Such information was used in the development of the AMBER and OPLS force fields from their earliest versions and is now standard practice (11–13, 15, 23). Friesner and coworkers (40–42) have been particularly active in providing accurate results as a basis for improving torsional energetics, especially for protein backbones and side chains. The OPLS-AA force field performed relatively well in these and other comparisons for conformational energetics of peptides (41, 43), whereas problems with the treatment of helical conformers with the AMBER and CHARMM force fields are being addressed (43–45). A general impediment for force-field optimization in this area is lack of precise knowledge of the ϕ, ψ map for prototypical systems such as the alanine dipeptide in water. Instead, problems often only become apparent after repeated observation of aberrant tendencies in long simulations. Nevertheless, improvements are being made for conformational energetics that will benefit biomolecular simulations in general and especially polypeptide structure prediction.

The ab initio LMP2/cc-pVTZ(–f) findings from the Friesner group for water-amine hydrogen bonding also identified inadequacies in force fields that led to incorrect orderings of free energies of hydration for amines (46). The problem, which had been conjectured to arise from polarization effects, could, in fact, be resolved through parameterization of a nonpolarizable force field to reproduce the correct pattern of hydrogen-bond strengths (47).

Free Energies of Hydration

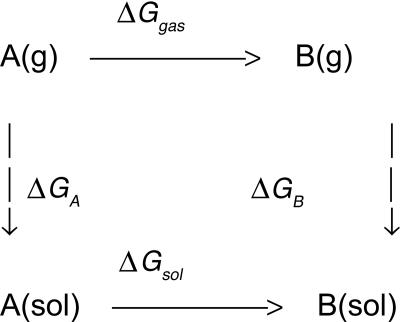
Free energies of hydration are another obvious testing ground because accurate experimental data are available, and the relevance for simulations of biomolecular systems is clear. Simulation results for proteins and polynucleotides can be expected to be erroneous if the balance of intramolecular and solute–water interactions is not correct. However, it was not known how to compute free energies of solvation with acceptable precision until 1985 (48–50). At that time, it was shown that the difference in free energy of hydration for two organic molecules could be computed to a precision of at least ±0.2 kcal/mol by using statistical perturbation theory (48). The computation of ΔΔG_hyd involves the thermodynamic cycle in Scheme 1 and the gradual perturbation (mutation) of A to B, through a series of intermediate steps. The free energies of transfer from the gas phase to solution then are related to ΔΔG_hyd by Eq. 7. MC or MD simulations are used to perform the conversions of A to B in the gas phase and in solution to obtain ΔG_gas and ΔG_sol. If the solutes are rigid, i.e., no internal degrees of freedom are sampled, then ΔG_gas = 0, and only the solution-phase conversion is needed. This simplification was the case for the original methanol to ethane conversion (48), although the calculations today generally use flexible solutes. Alternative free-energy approaches including thermodynamic integration are also now popular (49, 50). Once free-energy differences for mutation of one molecule to another in solution can be performed with good precision, thermodynamic cycles could be set up to obtain free-energy changes for many important processes (49, 50).

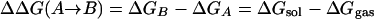[7]

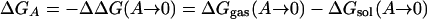[8]

Scheme 1.

In fact, the absolute free energy of solvation of A, ΔG_A, can be obtained by taking B as a null particle and making A disappear in two simulations (Eq. 8). Then, once one absolute ΔG_hyd is known, others are readily obtained by perturbing to this reference molecule. The Gibbs free energy of water itself was obtained in this way by disappearing one water molecule in the liquid (51, 52); for TIP4P water, the result of –6.1 ± 0.3 kcal/mol agrees with the experimental value of –6.3 kcal/mol (52). Other early applications included computation of the absolute free energies of hydration of methane and chloride ion in TIP4P water (52), and, for example, many studies of the hydration of hydrocarbons have been performed to yield insights on hydrophobic effects, as summarized elsewhere (53, 54).

Despite these developments, the free-energy calculations are sufficiently intensive that they have only recently become an integral part of force-field development rather than an after-the-fact test. Again, current force fields are expected to perform well in this arena. In a recent independent test, the OPLS-AA force field performed the best among several alternatives with an average error of 0.85 kcal/mol for 15 molecules (55). With larger, more diverse data sets, the average error with OPLS-AA is 0.7 kcal/mol (56), as illustrated in Fig. 1. It can be expected that improvements will be made in the future to reduce the average errors to <0.5 kcal/mol (34, 56, 57).

Universal Force Fields

Although there are many other issues with force-field development (6, 7), generalization to the treatment of any organic molecule is a particular challenge (15, 56–58). The advent of combinatorial chemistry and the variety of heterocycles that are used in medicinal chemistry stress the need. For some nonpolarizable force fields such as MMFF and OPLS-AA, parameters have been explicitly developed for many organic functional groups, and through the use of synonym procedures and extrapolations, missing bond stretching, angle bending, and torsional parameters can usually be well estimated. If the precedents are inadequate, it is important that the modeling software provides alerts to the condition, and then it is typically necessary to perform some ab initio or density functional theory calculations on appropriate model systems to fill the voids.

Default Lennard–Jones parameters are also available for all common atom types found in organic and biomolecular systems, so the principal remaining problem resides in the assignment of partial atomic charges, q_i in Eqs. 5 and 6. The dominant route has been to perform a QM calculation and to fit the charges to reproduce electronic properties, especially dipole moments and electrostatic potentials (59). This method has led to several common alternatives, such as CHELPG and RESP charges that are usually derived from ab initio wave functions (59), and faster approaches by using, for example, semiempirical QM charges with bond-charge corrections (57). Our own preference has been for the charge model (CM) charges of Cramer, Truhlar, and coworkers, which are derived from AM1 or PM3 semiempirical calculations (60, 61). Their rapid procedures, which yield highly accurate dipole moments, are incorporated directly into our software for computing charges for arbitrary organic molecules for both force-field and QM/MM calculations (62, 63). The different CM alternatives have been tested in computations of free energies of hydration in TIP4P water by using OPLS-AA parameters except for the charges (56). The best results come from the AM1-based CM1A charges scaled by 1.14 for neutral molecules. They yield an average error of 1.0 kcal/mol for 25 diverse organic molecules, whereas the error is 0.7 kcal/mol with OPLS-AA charges. These results and further testing for solvent effects on reaction rates and conformational and tautomeric equilibria (62, 63) demonstrate that the resulting general force field, OPLS/CM1A, performs well in many contexts. Some degradation for conformational energetics is expected, although the differences are generally tolerable, as reflected by the results in Table 1.

Table 1. Representative conformational energy differences.

Molecule	Conformers	ΔE OPLS-AA	ΔE OPLS/CM1A*	ΔE Exptl.†
Butane	Gauche—anti	0.80	0.44	0.75
1,2-Dichloroethane	Gauche—anti	1.11	1.08	1.20
Ethyl methyl ether	Gauche—anti	1.47	1.20	1.50
Propylamine	Gauche—anti	0.54	0.26	0.42
N-methylpiperidine	Axial—equat.	3.60	3.24	3.15
N-methylacetamide	E—Z	2.30	1.50	2.30
Glyoxylic acid	s-trans E—Z	1.25	2.05	1.20
2-Methoxy-THP	Equat.—axial	1.34	2.37	1.05

Values are in kcal/mol. Exptl., experimental; equat., equatonial.

^*Using charges computed for the lower-energy conformer.

^†See ref. 40.

Water Models

MD and MC simulations of aqueous solutions with explicit representation of the water molecules depend critically on the availability of water models that provide an accurate representation of the liquid, can be rapidly evaluated, and are compatible with the force field for the solutes. Simulations of water through 1982 largely used the BNS, MCY, and ST2 potential functions, as reviewed by Beveridge et al. (64). The TIP3P and TIP4P models were introduced in 1983 (65) and, along with the SPC model (66), remain the most commonly used water models despite a continual stream of proposed alternatives (5). The TIP3P and SPC models follow the minimalist TIPS (transferable intermolecular potentials) form (67) of having just three interaction sites centered on the nuclei. Each site has a partial charge for computing the intermolecular Coulomb energy, and the only additional term is a Lennard–Jones interaction between oxygens (Eq. 9). For the TIP4P model, the site of negative charge is moved off the oxygen to a point 0.15 Å along the bisector of the HOH angle, as in the earlier Bernal–Fowler and MCY models, which improves the quadrupole moment and computed liquid structure and properties (65).

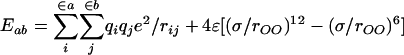[9]

Evaluation of an intermolecular interaction requires computation of 9 or 10 intermolecular distances. Thus, these models all require essentially the same amount of computer time. An important component of the popularity of the TIP3P, TIP4P, and SPC models and a restriction in their development was that their functional form (Eq. 9) was kept compatible with the common nonpolarizable force fields (Eq. 6). Most simulations of biomolecular systems with the AMBER, CHARMM, and OPLS-AA force fields use TIP3P or TIP4P water. The geometry of the water molecule is fixed in these simple water models, so there is no bond stretching or angle bending. Although flexible models have been explored (5), classical treatment of the high-frequency vibrations for water is not physically sound.

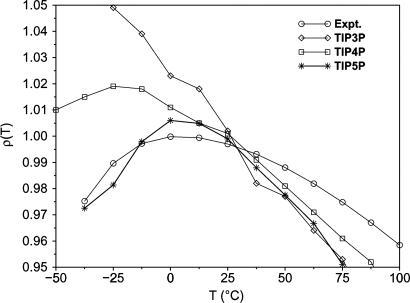
The parameterization of the TIP3P, TIP4P, and SPC models and most subsequent water models has emphasized reproduction of the experimental energy, density, and rdfs for liquid water near 25°C and 1 atm. However, a lingering problem had been poor reproduction of liquid water's unusually flat density vs. temperature profile at 1 atm including the temperature of maximum density (TMD) at 4°C. Basically, the three-site models do not yield TMDs, the five-site ST2 model has an overly sharp TMD at 30–40°C, and the best results were for TIP4P with a TMD near –15°C (5, 68–70). In response, the TIP5P model (71) was introduced in 2000 and solved the problem well in the –40 to 60°C range (Fig. 2). A hindrance to earlier pursuit of this challenge was the extremely long simulations that are necessary to obtain converged densities at temperatures in the supercooled regime. TIP5P still adheres to Eq. 9, although there are now partial charges on the hydrogens and two lone-pair sites. The model also gives excellent results for diffusion (72) and dielectric (71) constants for water, which are often additional problematic properties (Table 2).

Fig. 2.

Computed and experimental results for the density (g·cm^–3) of liquid water vs. temperature at a pressure of 1 atm.

Table 2. Computed properties for liquid water at 25°C and 1 atm.

Model	ρ, g/cm3	ΔHvap, kcal/mol	Cp, cal/mol·deg	106 κ, atm-1	105 α, deg-1	ε	105D, cm2/s
SPC	0.985	10.74	20	60 ± 4	106 ± 8	60 ± 10	3.9
TIP3P	1.002	10.41	20	64 ± 5	92 ± 8	88 ± 6	5.1
TIP4P	1.001	10.65	20	60 ± 5	44 ± 8	60 ± 10	3.3
TIP5P	0.999	10.46	29	41 ± 2	63 ± 6	82 ± 2	2.6
Exptl.	0.997	10.51	18.0	45.8	25.7	78.3	2.30

See refs. 70-72. Values are ± SD. Exptl., experimental.

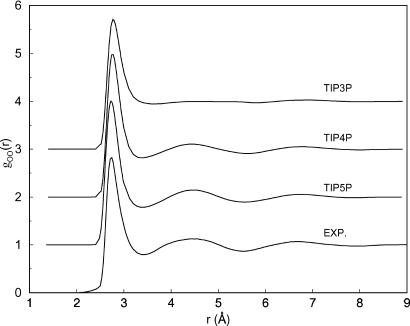
Strikingly, the TIP5P model improved the second peak in the OO rdf; however, the results for the first-peak position and amplitude differed noticeably from the then-reigning diffraction results of Soper and Phillips (73). However, the experimental g_OO subsequently was revised through the x-ray analyses of Head-Gordon and coworkers (74, 75) with the following conclusion:”The agreement of the TIP5P simulation with the ALS [advanced light source] data are remarkable, and as far as g_OO is concerned is a noteworthy improvement over TIP4P“(74). These latest experimental results and the TIPnP predictions for g_OO at 25°C and 1 atm are illustrated in Fig. 3. This finding represents a significant success for water modeling, particularly in view of the lone reviewer's analysis in December 1999: “From figure 4 [of ref. 71] I gather that the TIP5P potential performs much worse than TIP4P (and presumably than many other models) in reproducing the first maximum of the oxygen–oxygen radial distribution function, failing one of the most crucial experimental tests of water models... The paper cannot be published in its current form.” Although this review delayed publication, we persisted because it seemed unlikely that TIP5P could get so much right about liquid water, including the density profile and OH and HH rdfs, but err for the OO rdf. We also were aware of the history of revisions to the experimental g_OO and the associated uncertainties in extracting it from the diffraction data (75).

Fig. 3.

Computed and experimental (74) oxygen–oxygen rdfs for liquid water at 25°C and 1 atm.

Scope, Cutoffs, and Quantum Effects

The fixed-charge water models are not expected to perform well for computing, for example, virial coefficients for gaseous water or, in general, for handling water at low or very high density. Nevertheless, despite warnings to this effect (71), they have been widely applied over the entire phase diagram and criticized for predicted failings. Overall, the TIP4P model holds up notably well and does provide a qualitatively correct description of the phase diagram (76, 77), whereas both TIP4P and TIP5P are popular for studies of the supercooled liquid, ice nucleation or melting, and ice collision dynamics (78–82). In this context, another pleasing feature of the TIP5P model is that TIP5P ice has a melting point of 268 ± 6 K at 1 atm; TIP4P ice melts at 229 ± 9 K (81).

The simulations of liquid water in the development of the ST2, TIPnP, and SPC models were all carried out with spherical truncation and, sometimes, feathering of the intermolecular interactions at an OO distance of ≈9 Å. These are effective pair potentials, and spherical cutoffs are part of the models. Fortunately, most results from fixed-charge water models, e.g., density, energy, and structure, have been known for many years to show little variation for systems sizes above ≈125 molecules and cutoffs beyond ≈8 Å (83, 84). However, one can invoke specific procedures such as reaction field and Ewald methods to estimate the effects of neglected interactions beyond the cutoff. Again, the effects on density and energy have been demonstrated to be at the ≈1% level for pure water (85, 86), whereas the position of the TMD is sensitive to the treatment of long-range interactions (71) owing to the flatness of the density profile (Fig. 2). Nevertheless, slightly modified parameterizations have been reported for use of SPC and TIP4P with a reaction field (86) and of TIP4P and TIP5P with Ewald sums (87, 88) to yield similar quality as the original models. The Ewald approach is widely adopted for simulations of periodic systems and, in particular, improves the description of systems containing ions. However, periodic systems are not the subject of MD or MC simulations in many situations, such as molecular clusters, interfacial systems, and the majority of biomolecular studies. Instead, solvent droplets (caps) are the norm, for example, in simulations of protein–ligand complexes or QM/MM studies of enzymatic reactions (6–10). In these cases, spherical truncation of the potential functions is the norm by using “residue-based cutoffs,” e.g., if any interatomic distance between atoms in two residues is below the cutoff, the entire residue–residue interaction is included.

An issue that warrants greater interest, but is comparatively inconvenient, is quantum effects on the atomic positions for water molecules in the liquid (89, 90). This issue has been explored for TIP5P water by using path integral (PI) MC simulations (91); the effects in this case are substantial, yielding a much less structured liquid and a large shift in the TMD to too low of a temperature. The damage is readily repaired by a small increase in the partial charges to yield the TIP5P(PIMC) quantum model (91). The PIMC calculations also allow the examination of isotope effects, and accord is found between theory and experiment that D₂O is more structured and has a higher TMD than H₂O (91). Although physically more advanced, PIMC calculations are uncommon, owing to their relative technical complexity and the computational costs associated with discretization of each quantum particle into 5–10 classical beads.

Ab initio path integral MD calculations are an alternative for incorporating the nuclear quantum as well as polarization effects (92). This fully (electronic and nuclear) quantum simulation of liquid water is an exciting development, although the computational demands are such as to place the system sizes and times back to the ST2 days (3). The non-PI version of ab initio MD or Car–Parinello MD, has been gaining in popularity for liquid simulations; however, the dependence of the results for water on technical details has been a matter of some recent discord (93–95). Some of the problems result from the small system sizes, mostly 32 and 64 molecules, and short run lengths; e.g., state-of-the-art simulations for 216 water molecules cover 5 ps (95). The electronic structure part of the calculations features density functional theory with plane wave basis sets, which are sometimes augmented with Gaussian functions. The results for liquid water depend on the chosen density functionals; the current alternatives yield overly structured rdfs and diffusion constants that are a factor of 10 too low. Improvement for the treatment of dispersion forces with plane-wave density functional theory is under active investigation (96). Thus, it will be quite a while before the ab initio approaches can rival the empirical models for accuracy and for the range of properties that can be studied because some, e.g., the TMD and melting point, require very long simulations. Nevertheless, on-the-fly QM coupled with MD has the potential to provide valuable computational solutions for many complex chemical problems involving, for example, excited electronic states, transition-metal complexes, and reactions with changes in covalent bonding (97).

Summary and Outlook

In this perspective, we have touched on the fundamental advances and testing that have led to the current generation of force fields, which are used in MC and MD simulations of water and biomolecular systems. The progress has been substantial with all leading force fields now providing reasonable results for a wide range of properties of isolated molecules, pure liquids, and aqueous solutions. The advances have resulted from greatly increased computing power, methodological and software developments, and much hard work in many research groups. The near future will certainly feature continued refinement, expansion, and use of fixed-charge force fields, and increased activity with polarizable force fields and ab initio MD. A vast range of applications will also be explored including, to name a few, biomolecular structure prediction, protein and catalyst design, mechanisms of enzymatic reactions, protein–ligand binding, structure-based drug design, and transport through membranes and ion channels.