Abstract
Proton translocation in the D-pathway of cytochrome c oxidase has been studied by a combination of classical molecular dynamics and the multistate empirical valence bond methodology. This approach allows for explicit Grotthuss proton hopping between water molecules. According to mutagenesis experiments, the role of proton donor/acceptor along the D-pathway is carried by the highly conserved residue Glu-242. The present multistate empirical valence bond simulations indicate that the protonation/deprotonation state of Glu-242 is strongly coupled to the distance of proton propagation in the D-pathway. The proton was seen to travel the full length of the D-pathway when Glu-242 was deprotonated; however, it was trapped halfway along the path when Glu-242 was protonated. Further investigation in terms of both proton dynamical properties and free energy calculations for the pathway of proton transport provides evidence for a two-step proton transport mechanism in the D-pathway.
Keywords: molecular dynamics
Cellular respiration, a process of oxidizing nutrient molecules to carbon dioxide and water, involves the transfer of electrons through a series of membrane protein complexes. This process is coupled with generation of an electrochemical gradient across the membrane, which can be used to drive the synthesis of ATP. Cytochrome c oxidase (CcO), the terminal enzyme of the respiratory chain, catalyzes the reduction of dioxygen to water as follows: O2 + 4H+ + 4e– → 2H2O. The transfer of four electrons from cytochrome c to dioxygen is accompanied by the translocation of eight protons, four being consumed internally in the reduction of oxygen and the other four being pumped across the membrane (1).
In CcO, two proton-conducting pathways have been identified on the basis of results from site-directed mutagenesis experiments (2–8) and from an inspection of the available crystal structures (9–13). The K-pathway leads from the N-side of the membrane toward the catalytic site via Lys-319. (All amino acid positions are numbered here according to the bovine sequence.) The other pathway, called the D-pathway, leads from the proton uptake side approximately halfway into the membrane via a solvent-filled cavity and ends at the well conserved Glu-242. The key residue for the proton uptake is Asp-91, being situated at the entrance of the D-pathway close to the N-side of the membrane. Beyond Glu-242, there is no obvious proton connectivity. The transient water chains may connect Glu-242 either to the catalytic site of the enzyme or to the heme a3 propionate group (14–16).
The proton translocation in both bacterial and mitochondrial CcO has been investigated by using standard molecular dynamics (MD) methodology in the past few years (14–19). However, the molecular properties and detailed mechanisms governing the explicit proton translocation in the protein have remained elusive. Notably, all of the previously conducted computational studies have attempted to infer the mechanisms of proton translocation by examining the characteristics of the hydrogen-bonded (H-bonded) water networks inside protein. In particular, the explicit simulation of an excess proton in the system has remained a challenge.
According to the well-known “Grotthuss mechanism” (20, 21), the transport of an excess proton through water-filled protein channels occurs by means of the O-H covalent bond breaking in one protonated water molecule and reforming in an adjacent water molecule as the excess proton is exchanged between the two. This process can continue, involving numerous protons in the water chain; hence, the phrase “proton shuttling” is often invoked. Because of this specialized nature of the proton transport (PT) process, the MD modeling of PT is not possible using conventional MD force fields. Ab initio MD simulations can instead be used to describe processes involving bond dissociation. However, extension of these methods to study large biological systems over long (multinanosecond) time scales will require the introduction of additional approximations not yet in hand.
To meet the challenge of the explicit MD simulation of PT, we have developed the multistate empirical valence bond (MS-EVB) model (22–25), including its second generation MS-EVB2 version (25). We have successfully incorporated this model into a classical MD simulation framework and applied it to study PT in several different aqueous (24–26) and biological (27–30) systems. The MS-EVB model allows the proton to explicitly diffuse along the H-bonded network of water molecules. The MS-EVB potential has been found to describe various important features of the proton translocation progress, in good agreement with both experimental (24, 25, 31) and ab initio MD (32) results. This model is much more computationally efficient compared with the ab initio MD simulations, yet it is of comparable or better accuracy for well-defined test cases. It is thus ideal for use in simulating realistic biological systems. For a complete description of this model, as well as a discussion of its relationship to other attempts to develop MD models with similar properties, see the introduction of ref. 25.
The aim of this work is to study the PT in CcO by means of classical MD simulations using the MS-EVB2 model. With this approach, one can in principle consider both structural and dynamical properties of the excess proton propagating through the channel to provide a detailed mechanistic picture of proton translocation in CcO. The present work reports MS-EVB2 simulations of PT in the D-pathway between Asp-91 and Glu-242.
This work is organized as follows. first, the MS-EVB model and the related concepts will be briefly introduced, followed by the details of the MD simulations. Structural and dynamical properties of the excess proton in the D-pathway then will be presented and discussed, along with the consideration of the approximations of our simulations. Conclusions that may be drawn from this work and several future directions will be given in the final section.
Methods
Simulations of the proton translocation in the D-pathway were performed by using a combination of classical MD and MS-EVB2 approaches, which are described in detail in refs. 22–31. In the present work, the excess proton was only allowed to transfer between water molecules, whereas the proton hopping between water and amino acids, such as Glu-242, was not explicitly allowed.
Because of the delocalized nature of the excess proton, one can define a suitable coordinate to describe the position of the “excess proton” at each step, given by the “center of excess charge” (CEC) (33):
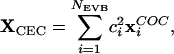 |
[1] |
where c2i is the amplitude for MS-EVB state i, and xCOCi is the vectorial location of the center of charge of the hydronium in the ith MS-EVB state. There is a total of NEVB possible MS-EVB states, and it should be noted that the coefficients ci are functions of all system coordinates according to the MS-EVB algorithm (22–25). This CEC coordinate can be used to describe the excess proton diffusion through the channel (26–30).
Initial MD Simulation. The starting MD configuration for the fully oxidized CcO from bovine heart mitochondria at 1.8-Å resolution was taken from the Protein Data Bank (ID code 1V54). To make the simulation reasonable, but computationally less demanding, a reduced system was used consisting of subunit I, 375 crystal water molecules, and 960 added bulk water molecules, resulting in ≈12,000 atoms. To avoid deformation of the structure due to the missing neighboring subunits and membrane, the α carbon (Cα) atoms whose distances to all of the water molecules in the D-pathway are >5 Å were tethered to the x-ray crystal coordinates by using a harmonic potential with a force constant of 1 kcal/mol per Å2. The absence of tethering along the proton conduction pathway allows for minor structural reorganization of protein side chains. All bonds were constrained by using the SHAKE algorithm (34) with a tolerance of 10–5, allowing for the integration of Newton's equations of motion by using a 2.0-fs time step. Water molecules were described by using the TIP3P model (35). Simulations were performed at constant temperature (300 K) and constant volume, with periodic boundary condition applied in all three directions. Temperature was controlled by using the Nose–Hoover thermostat (36) with a relaxation constant of 0.2 ps. The box size was adjusted to make sure that the periodic images of the protein do not overlap with the protein in the real cell. Electrostatic interactions were calculated by using the Smooth Particle Mesh Ewald summation technique (37) with a tolerance of 10–5. The cutoff radii for both Lennard–Jones interactions and the real-space Coulomb interactions were 10 Å. The system was then run for a 1.6-ns constant number/volume/temperature (NVT) equilibrium simulation by using the methods just described.
To make the water chain in the D-pathway continuous, we simulated the addition of water in the equilibrated system by placing a water molecule in the hydrophobic cavity between Ser-157 and Glu-242, equilibrating it, and running MD simulation at 300 K. At the end of the 250-ps run, a new water molecule was placed in this region. This procedure was repeated until no obvious space was left in the cavity, and the H-bonded water chain remained stable.
All classical MD simulations reported here were performed by using the program dl_poly (38) with the AMBER99 force field.
MS-EVB Simulations of PT in CcO. The final configuration from the MD simulations described above then was used to construct the initial structure for the MS-EVB simulations. An excess proton was placed at the bottom of the D-pathway by replacing a pore water molecule with a hydronium. (Because the primary goal of the present simulations is to study the PT inside the channel environment, the question of how the proton enters the channel was not investigated in this work.) An equilibration run (100 ps) then was performed by restricting the proton solvation shell to zero (PT was not allowed). This run was conducted to relax the protein structure and pore water around the inserted hydronium molecule. In the subsequent production run, the excess proton then was allowed to transfer between water molecules according to the MS-EVB algorithm. The MD time step was 1.0 fs, and the electrostatic interactions were calculated by using the Ewald summation technique with a tolerance of 10–5. All of the other simulation conditions were the same as in the equilibrium classical MD simulations.
To evaluate how the protonation/deprotonation state of Glu-242 affects the mobility of the excess proton, the calculations were repeated with and without a proton on the carboxylic acid group of Glu-242 (GluH or Glu–). A Cl– ion, if needed, was added into the bulk water region to maintain the charge neutrality of the system.
In this work, we also examined the PT in a mutant. A double mutant was prepared by replacing both Ser-156 and Ser-157 with the hydrophobic amino acid Ala, followed by at least 500-ps equilibration. The MS-EVB2 simulations in the double mutant then were performed in the same way as previously described for the wild-type protein.
Potential of Mean Force (PMF) Calculations. The umbrella sampling technique was used to compute the PMF, i.e., free energy profile, along the PT pathway in the system with deprotonated Glu-242. Details regarding the application of umbrella sampling in free energy calculations can be found in refs. 39 and 40. The CEC of the system (Eq. 1) was biased with a harmonic potential, k(XCEC – Xi)2/2, centered on successive values of Xi, where k is the restraining harmonic force constant. The force constants in the multiple-window simulations, executed on the CEC, were chosen to homogenously sample in each window. The conformational sampling was performed with MS-EVB2 MD simulations; trajectories of 700 ps were generated for 53 windows each, centered on an equidistant grid from–10.7 to 2.3 Å in the D-pathway. Each window was equilibrated for 100 ps starting from the final configuration of the previous window. The self-consistent set of equations was iterated by using the WHAM algorithm (39) until the convergence tolerance was <10–4 kcal/mol.
MS-EVB simulations and PMF calculations were performed in parallel on the National Center for Supercomputing Applications TeraGrid cluster at the University of Illinois at Urbana-Champaign. Eighty-five picoseconds of simulation took 24 h of central processing unit time on eight 1.5-GHz Intel Itanium 2 processors.
Results and Discussion
Before proceeding with more detailed analysis, it is important to assess the stability of the system. For this purpose, we analyzed the root-mean-square (rms) deviation of the backbone atoms as a function of time for the classical MD trajectory. Because most of the Cα atoms were restrained during the simulation, the rms deviation leveled off rapidly after an initial increase and remained stable over most of the 1.6-ns simulation. No strong drift was observed. Second, fluctuations in structure can be evaluated in terms of the rms fluctuations as a function of residue number. With the tethering, for the transmembrane helices the backbone rms fluctuations were ≈0.5 Å, which is smaller in comparison with previously published data obtained from MD simulation of a larger system without constraints (19), where a rms fluctuations of ≈0.7 Å was reported. However, one should bear in mind that the different force fields and simulation conditions also may contribute to such a difference. The extramembrane domain exhibited greater fluctuations than the α-helical regions.
Water Molecules in the Pathway. In the crystal structure, there are 10 water molecules confined in the course of the D-pathway between Asp-91 and Ser-157. Yet, there are no water molecules resolved in the hydrophobic cavity between Ser-157 and Glu-242. Thus, the question arises as to how protons are transferred through these hydrophobic regions. As is evident from the experimental studies (9), electron density for several water molecules at H-bonded distances are visible leading away from Ser-157 to Glu-242. Results from computer modeling also have suggested that three well-defined water molecules connect Ser-157 to Glu-242 by H-bonding (18).
In this work, up to five water molecules were added to the hydrophobic cavity in the manner described in Methods. In the MD run, two molecules were expelled into the bulk, and three remained in the cavity. The number of solvent molecules in the D-pathway leading from Asp-91 to Ser-157 remained constant at 10, i.e., the same number as seen in the crystal structure. The overall structure of the H-bonded water chain remained stable connecting Asp-91 all the way to Glu-242 and persisting for the duration of the simulations (800 ps), thus providing a proton-conducting pathway that involves both the water and amino acid side chains.
Glu-242: Protonation or Deprotonation. The D-pathway involves the highly conserved Asp-91 and Glu-242 besides a number of polar residues. Glu-242, one of the most conserved residues, plays an essential role in the proton translocation mechanism of CcO. The role of Glu-242 has been affirmed by the fact that mutations at this locus have resulted in significant alteration of the proton conductance behavior (5, 6, 11, 17, 41). For example, mutating Glu-242 with Ala, Gln, or Cys completely abolishes the channel function; replacement with Tyr also results in significantly reduced activity, whereas with Asp in the 242 locus, the enzyme was found to have normal proton translocation, suggesting that the acidic function of Glu-242 is critical for its mechanism. Because the D-pathway is used for uptake of both the chemical protons and the pumped protons, there must be a branching point within the pathway. Results from previous studies (14–16, 42) suggest that this branching point is located at Glu-242. The consecutive deprotonation and reprotonation of Glu-242 in the catalytic cycle illustrates the role of this residue as a proton shuttle (43). That is, it may explicitly participate in the PT pathway and play a role of proton donor/acceptor rather than being a mere proton conductor.
To further investigate the role of protonation/deprotonation of Glu-242 on the PT in the D-pathway, simulations of the wild-type enzyme using the MS-EVB2 methodology were performed with and without the protonation of the carboxylic acid group of Glu-242. In the first simulation, with Glu-242 unprotonated, the excess proton traveled the full length of the path within 30 ps to a position within a H-bonding distance of the carboxylic acid group of Glu-242. The same initial configuration was used as a starting point in the second simulation, i.e., where Glu-242 was protonated. Interestingly, the excess proton in the second simulation only diffused halfway along the channel direction within 100 ps and became relatively immobilized. Simulations with different initial configurations were also performed to ensure that the observed behavior is not an artifact of the initial configurations (data not shown).
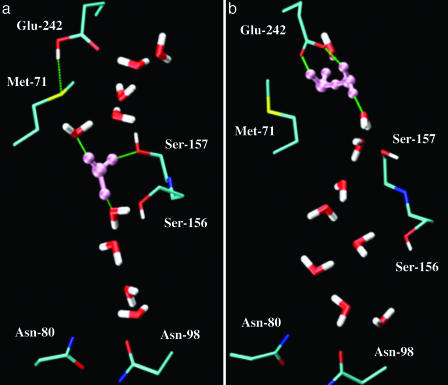
According to these simulations, there seems to be a link between the protonation state of Glu-242 and the motion of the proton in the proton-conducting pathway; e.g., the protonation state of Glu-242 evidently determines how far the proton can propagate along the channel axis. This connection is of particular interest given that Glu-242 was postulated to have a central shuttle function in the proton translocation mechanism. This behavior therefore was further examined by comparing two representative structures of the channel environment taken from the end of the MS-EVB2 simulations. In the case of protonated Glu-242, as shown in Fig. 1a, one can see that the hydronium (colored in pink) is H-bonded with two water molecules and the side chain of Ser-157, a distance 6–7 Å away from Glu-242. The hydroxyl group of Ser-157 exhibits a strong H-bonding interaction with the proton donor hydronium, and hence may contribute to the anchor of the excess proton. As can be seen from the MS-EVB2 simulation trajectories, rather than forming a typical Zundel (H5O2+) or Eigen (H9O4+) cation as in the bulk, the proton can freely shuttle between the donor water and two other acceptor water molecules, demonstrating the complexity of the solvation of an excess proton in the polar channel environment. Evidently, this structure is rather stable and to some degree prevents the diffusion of an excess proton further along the pathway.
Fig. 1.
The hydration structures of the excess proton in the D-pathway, formed at the end of the MD simulations. (a) The case where Glu-242 is protonated. (b) The case where Glu-242 is deprotonated. The solvated excess proton is colored in pink. The H-bond is represented as the dashed line in green. The pictures were generated with the vmd software (www.ks.uiuc.edu/Research/vmd).
In the case of the protonated Glu-242, the COOH group of that residue appears to be positioned according to the crystal structure, forming a H bond with the sulfa of Met-71 and not directly participating in the PT pathway. In contrast, once Glu-242 was deprotonated, as shown in Fig. 1b, the carboxylic acid group reorients itself by pointing toward to the extended water chain from the D-pathway and actively interacts with these water molecules. In fact, upon startup there was a rapid movement of the carboxylic acid group, relative to its initial structure, to a point lower down, in the orientation of Fig. 1b. The protonation state of Glu-242 could be responsible for the orientation change. This conformational change of Glu– versus GluH and its intimate association with H-bonded water molecules has been intensively studied on the basis of potential mean force calculations and standard MD simulations (14, 44, 45). In accordance with previous findings, a comparison of the two snapshots in Fig. 1 also demonstrated that the conformational isomerization of the Glu-242 side chain, although small in its scale of motion, is accompanied by displacement in the positions of H-bonded water molecules in the region between Ser-157 and Glu-242. This local structural fluctuation of protein and bound water molecules may have a large contribution to the observed behavior of the excess proton in the channel.
In addition, the enhanced activity of the excess proton in the channel also can be understood from the electrostatic interactions of negatively charged Glu-242 with the positively charged hydronium. Note that in switching from GluH to Glu–, the charge on the side group of Glu-242 has been changed from –0.0907 on COOH to –0.8322 on COO–. It therefore is not surprising that an altered proton affinity at Glu-242 could occur upon the change of its protonation state. Furthermore, an experimental investigation (46) of the pH dependence of the rate of the internal PT from Glu-242 to the binuclear center showed that the pKa of Glu-242 is 9.4, much higher than the ambient physiological pH condition, suggesting that the protonated form of Glu-242 is highly favorable over the deprotonated form. As inferred from experiments, the Glu-242 only becomes transiently deprotonated to release the proton and spends most of its time as GluH (47). It is therefore reasonable to assume that the deprotonation/protonation reaction at the Glu-242 locus is the significant driving force for the translocation of the channel proton. With this driving force to protonate Glu–, the excess proton in the channel can easily escape from a local H-bonded network instead of being trapped inside the channel. Note that in Fig. 1b the excess proton is solvated as a Zundel complex, shared between two individual water molecules; the Zundel complex is in turn stabilized by H-bonding with the carboxyl group of Glu-242.
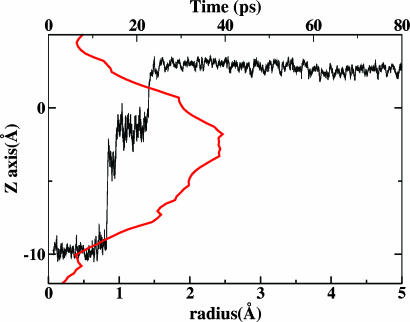
PT in the D-Pathway: A Two-Step Mechanism. To characterize the dynamic behavior of an excess proton in the D-pathway, one can consider the time evolution of the CEC (Eq. 1). In Fig. 2, we present the CEC along the z axis as a function of time in the simulation with deprotonated Glu-242 (black line). A value of ZCEC of approximately –10Å corresponds to the bottom of the channel where the initial PT event began. As Fig. 2 depicts, although the proton proceeded through the channel (≈13 Å) very quickly, the proton diffusion rates varied significantly. The mobility of the excess proton seemed strongly reduced as the excess proton approached the midway in the channel and then increased again as the proton moved closer to Glu-242. Results obtained from a visual inspection of simulation trajectories are quite similar: the proton spent ≈10 ps residing at the bottom of the channel, waiting for the reorganization of the H-bond network between water molecules inside the pore and the polar groups lining the pore. Once the proton translocation processes initiated, the excess proton moved quickly across a significant length of the channel (≈10 Å) to the channel midpoint, where it became relatively immobile for a short 10-ps interval. The subsequent step comprised another fast transfer of the proton between consecutive water molecules from the channel midpoint to Glu-242. The PT thus appeared to exhibit a biphasic process. These results support the notion that the proton diffusion is highly sensitive to a channel interior region, which is ≈7 Å away from Glu-242. This region, which significantly inhibits the proton propagation along the path, defines what we shall refer to as a “proton trap.” As Fig. 2 infers, this trap may divide the PT in the D-pathway into two steps.
Fig. 2.
Time evolution of the CEC along the z axis in the simulation with deprotonated Glu-242 (black line), along with the pore radii as a function of channel axis (red line) (see text for details).
In Fig. 2, we also plot the average pore radius profiles as a function of the z axis for CcO/water system with a hydronium in the channel (red line). The method for estimating the pore size is the hole program (48). The pore is apparently nonuniform; its radius rises to a maximum at ZCEC of approximately –3 Å and then drops down for positive ZCEC values. An interesting and important feature of this plot is that the wide channel region, with a pore radius of 2.5 Å, corresponds to the position where the excess proton is more stable. Consistent with our recent study (28), which concluded that ≥2.5-Å-radius wide channel has a higher preference for a well-solvated structure, this 2.5-Å-radius channel region in the D-pathway, as seen from the lower regions of Fig. 1a, has sufficient space for the threefold water solvation of the hydronium to form the Eigen cation H9O4+. As a result, the distribution of directions along which PT can occur in that region becomes more isotropic. The PT there may no longer be exclusively along the channel direction, and Grotthuss-type PT becomes more inhibited in this region.
Proton mobility in narrow channels, however, has been found to increase by more than an order of magnitude (26) under certain conditions. This behavior can be ascribed to the formation of a continuous 1D chain (i.e., “proton wire”) as the pore radius decreases. In CcO this feature may provide a rationale for our observations shown in Fig. 2: In the narrow channel region, the proton hops successively between adjacent water molecules; whereas in the 2.5-Å-radius wide channel region, the excess proton remains stabilized as an Eigen cation complex for a short interval. It also is interesting to note that the interconversion between successive proton hopping and Eigen cation formation is to some degree correlated with the symmetric shape of channel pore radius. The 2.5-Å-radius wide channel region hence behaves as some sort of dynamical “gate” in the proton-conducting pathway and appears to temporarily trap the excess proton.
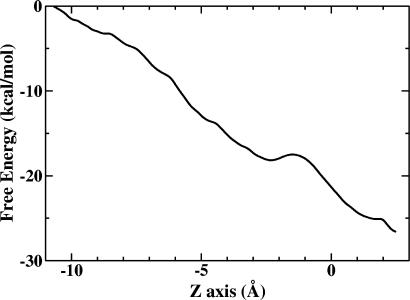
To characterize the free energy profile associated with the PT through the D-pathway, umbrella sampling was carried out as described in Methods for the case of deprotonated Glu-242, and the result is plotted in Fig. 3. The CEC is initially at ZCEC of approximately –10.7 Å. In general, the free energy along the reaction goes downhill. This result therefore quantitatively proves that there is a strong affinity for the proton to move toward Glu-242 at ZCEC ≈ 2.5 Å, which allows the proton to transfer spontaneously without the assistance of any external potential. This strong affinity as we mentioned above may be attributed to the highly preferred protonation state of Glu-242, owing to its high pKa value.
Fig. 3.
PMF for proton translocation along the z axis of the CcO D-pathway with Glu-242 in its deprotonated state.
One of the characteristic features of the free energy curve as the proton approaches Glu-242 in going from z = –10.7 to 2.5 Å is that the PMF exhibits a slight shoulder, spanning from ZCEC of approximately –3 to approximately –1 Å. The shoulder, as might be expected, corresponds to the location of the proton trap and the wide channel region (Fig. 2). It should be noted, however, that the PMF is a free energy profile and may not reflect transient dynamical effects in the PT process.
The results discussed above from the dynamical, geometric, and free energy (PMF) perspectives provide some evidence for a two-step mechanism of PT to Glu-242 through the D-pathway: The proton trap, primarily ascribed to the wide pore, may divide the D-pathway between Asp-91 and Glu-242 into two short H-bonded proton wires that may form independently of one another. The proton first transfers from Asp-91 at the beginning of the D-pathway to the proton trap region at the top of the first proton wire by a Grotthuss-type mechanism through a continuous H-bonded water chain. The second proton wire facilitates another fast transfer of the excess proton via a hydrophobic cavity where the transient water chain can be formed by recruitment of water molecules to establish a functional PT connection between the proton trap and Glu-242. Although the existence of a successively H-bonded proton wire is essential for the proton translocation, the driving force for the second step PT is likely primarily attributed to the protonation state of Glu-242. This behavior also explains our observations that when Glu-242 is protonated the second PT step becomes impeded.
Role of the Conserved Serines in the D-Pathway. The Ser-156 and Ser-157 groups, two conserved hydrophilic residues in the channel, also are noted to be within the H-bonded proton-conducting pathway. The stabilizing H-bond interaction between the protonation complex and the polar groups on the channel wall may have the effect of retarding the PT, thus aiding in the proton trapping or gating behavior. To explore the possible role of the conserved Sers in proton translocation, an examination was carried out by using comparisons between simulations of wild-type CcO and its double mutant (S156A/S157A). As in the wild type, the MS-EVB2 simulations were repeated with Glu-242 in the two different protonation states. The mutations revealed no dramatic effect on the transport properties of the excess proton in the channel. In agreement with site-directed mutagenesis experiments (49), the mutations of two Sers into hydrophobic amino acid Ala result in an enzyme still capable of transferring protons, suggesting these two Sers are not as critical for the PT as Glu-242. In the mutant, a water molecule coming from the water chain occupied the spatial position of the OH groups of Sers, and provided a H-bond to the hydronium. The functional role of Ser was compensated in the mutant by conformational adjustment of the internal water molecules. However, although the proton in the mutant traveled the same amount of distance as in the wild type, it took a significantly longer time (120 ps) to reach its destination. This difference became more pronounced when Glu-242 was protonated. The reason for this difference is that during the course of the diffusion the H-bonded water chain was observed to break several times, then to rearrange itself to adapt to the absence of two Ser OH groups, finally allowing the proton translocation to occur. Such behavior is also compatible with the experimental observation of the decreased enzymatic activity in the mutant (49).
Analysis of Approximations. For simplicity and reduced computational cost, we have used in this work a reduced system represented only by subunit I and water molecules. Because of the missing CcO subunits and the lipid bilayer, the protein has been treated by tethering most of the Cα atoms to the x-ray coordinates to maintain its structural integrity. The approximation associated with the reduced model is based on the rationale that the D-pathway is buried inside the protein, and the immediate channel environment is more relevant for the PT properties than the influence from the other surrounding subunits and the lipid bilayers. Nevertheless, this special treatment may introduce some artifacts. For example, because the tethering force constant has been arbitrarily selected in all of the reported simulations, minor motions of the channel might be inhibited by the position restraints. However, we have examined these possible effects by performing the same MS-EVB2 simulations with different tethering force constant. Support for our reduced approach can be drawn from these simulations (data not shown), which showed that with a significantly larger force constant (20 kcal/mol per Å2) the proton is still able to diffuse the channel in approximately the same amount of time. The PT even takes place with all of the Cα atoms fixed in the space. These results also suggest that the efficient PT in the D-pathway may not require any concerted changes of channel conformations, which may be attributed to the extensive water network in the D-pathway.
Conclusions
The MS-EVB2 simulations reported in this work have provided insights into the detailed proton translocation mechanism in the D-pathway of CcO. Our results indicate that the protonation/deprotonation state of Glu-242, a residue that has been repeatedly implicated as contributing to the proton translocation, is strongly coupled to how far the proton can propagate along the D-pathway. The proton was seen to travel the full length of the D-pathway when Glu-242 is deprotonated; however, it was trapped halfway along the path when Glu-242 is protonated. Glu-242 may therefore “reserve” this proton for the moment when it becomes deprotonated perhaps due to an increased negative charge of the binuclear center (42). As a consequence, the re-protonation of Glu-242 could occur sufficiently rapidly to be consistent with its high pKa value; the PT in the D-pathway thus becoming continuous and more efficient.
It is also well known that Glu-242 is the switching point in the proton-conducting path across the membrane (14–16). Indeed, the D-pathway itself may also be connected via several independent proton wires. Based on the results presented in this work, we can suggest a two-step PT mechanism to Glu-242 through the D-pathway: The proton first transfers from the channel entry to the proton trap region, located at a wide channel section, by a Grotthuss-type mechanism through a continuous 1D H-bonded water chain. A second transiently formed proton wire then facilitates another fast transfer of proton between the proton trap and Glu-242. Whether or not the secondary PT step will take place is primarily determined by the protonation state of Glu-242, as was observed in our MS-EVB2 simulations.
The fate of the proton after leaving the D-pathway has not been discussed in the present paper. One possibility is that the protonated Glu-242 side chain can flip upward and deliver its proton either to the binuclear center or to a heme a3 propionate group as originally proposed by Iwata et al. (9). Future research in our group will be concerned with the aspects of PT beyond Glu-242, as well as the role of the reduction of heme groups in the proton translocation process.
Acknowledgments
We thank Yujie Wu and Dr. Boaz Ilan for stimulating discussions. This work was supported by National Institutes of Health Grant R01 GM053148. The computations were carried out with generous allocations of computer time from the National Center for Supercomputing Applications and the Utah Center for High Performance Computing.
Author contributions: J.X. and G.A.V. performed research and wrote the paper.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: CcO, cytochrome c oxidase; CEC, center of excess charge; MD, molecular dynamics; MS-EVB, multistate empirical valence bond; PMF, potential of mean force; PT, proton transport.
References
- 1.Wikstrom, M. K. (1977) Nature 266, 271–273. [DOI] [PubMed] [Google Scholar]
- 2.Thomas, J. W., Lemieux, L. J., Alben, J. O. & Gennis, R. B. (1993) Biochemistry 32, 11173–11180. [DOI] [PubMed] [Google Scholar]
- 3.Thomas, J. W., Puustinen, A., Alben, J. O., Gennis, R. B. & Wikstrom, M. (1993) Biochemistry 32, 10923–10928. [DOI] [PubMed] [Google Scholar]
- 4.Fetter, J. R., Qian, J., Shapleigh, J., Thomas, J. W., Garcia-Horsman, A., Schmidt, E., Hosler, J., Babcock, G. T., Gennis, R. B. & Ferguson-Miller, S. (1995) Proc. Natl. Acad. Sci. USA 92, 1604–1608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hosler, J. P., Ferguson-Miller, S., Calhoun, M. W., Thomas, J. W., Hill, J., Lemieux, L., Ma, J., Georgiou, C., Fetter, J., Shapleigh, J., et al. (1993) J. Bioenerg. Biomembr. 25, 121–136. [DOI] [PubMed] [Google Scholar]
- 6.Verkhovskaya, M. L., Garcia-Horsman, A., Puustinen, A., Rigaud, J. L., Morgan, J. E., Verkhovsky, M. I. & Wikstrom, M. (1997) Proc. Natl. Acad. Sci. USA 94, 10128–10131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pfitzner, U., Odenwald, A., Ostermann, T., Weingard, L., Ludwig, B. & Richter, O. M. (1998) J. Bioenerg. Biomembr. 30, 89–97. [DOI] [PubMed] [Google Scholar]
- 8.Gennis, R. B. (1998) Biochim. Biophys. Acta 1365, 241–248. [DOI] [PubMed] [Google Scholar]
- 9.Iwata, S., Ostermeier, C., Ludwig, B. & Michel, H. (1995) Nature 376, 660–669. [DOI] [PubMed] [Google Scholar]
- 10.Tsukihara, T., Aoyama, H., Yamashita, E., Tomizaki, T., Yamaguchi, H., Shinzawa-Itoh, K., Nakashima, R., Yaono, R. & Yoshikawa, S. (1996) Science 272, 1136–1144. [DOI] [PubMed] [Google Scholar]
- 11.Svensson-Ek, M., Abramson, J., Larsson, G., Tornroth, S., Brzezinski, P. & Iwata, S. (2002) J. Mol. Biol. 321, 329–339. [DOI] [PubMed] [Google Scholar]
- 12.Abramson, J., Larsson, G., Byrne, B., Puustinen, A., Garcia-Horsman, A. & Iwata, S. (2000) Acta Crystallogr. D 56, 1076–1078. [DOI] [PubMed] [Google Scholar]
- 13.Ostermeier, C., Harrenga, A., Ermler, U. & Michel, H. (1997) Proc. Natl. Acad. Sci. USA 94, 10547–10553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hofacker, I. & Schulten, K. (1998) Proteins 30, 100–107. [PubMed] [Google Scholar]
- 15.Wikstrom, M., Verkhovsky, M. I. & Hummer, G. (2003) Biochim. Biophys. Acta 1604, 61–65. [DOI] [PubMed] [Google Scholar]
- 16.Zheng, X., Medvedev, D. M., Swanson, J. & Stuchebrukhov, A. A. (2003) Biochim. Biophys. Acta 1557, 99–107. [DOI] [PubMed] [Google Scholar]
- 17.Backgren, C., Hummer, G., Wikstrom, M. & Puustinen, A. (2000) Biochemistry 39, 7863–7867. [DOI] [PubMed] [Google Scholar]
- 18.Riistama, S., Hummer, G., Puustinen, A., Dyer, R. B., Woodruff, W. H. & Wikstrom, M. (1997) FEBS Lett. 414, 275–280. [DOI] [PubMed] [Google Scholar]
- 19.Olkhova, E., Hutter, M. C., Lill, M. A., Helms, V. & Michel, H. (2004) Biophys. J. 86, 1873–1889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nagle, J. F. & Morowitz, H. J. (1978) Proc. Natl. Acad. Sci. USA 75, 298–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Argmon, N. (1995) Chem. Phys. Lett. 244, 456–462. [Google Scholar]
- 22.Schmitt, U. W. & Voth, G. A. (1998) J. Phys. Chem. B 102, 5547–5551. [Google Scholar]
- 23.Schmitt, U. W. & Voth, G. A. (1999) Isr. J. Chem. 39, 483–492. [Google Scholar]
- 24.Schmitt, U. W. & Voth, G. A. (1999) J. Chem. Phys. 111, 9361–9381. [Google Scholar]
- 25.Day, T. J. F., Soudackov, A. V., Cuma, M., Schmitt, U. W. & Voth, G. A. (2002) J. Chem. Phys. 117, 5839–5849. [Google Scholar]
- 26.Brewer, M. L., Schmitt, U. W. & Voth, G. A. (2001) Biophys. J. 80, 1691–1702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ilan, B., Tajkhorshid, E., Schulten, K. & Voth, G. A. (2004) Proteins 55, 223–228. [DOI] [PubMed] [Google Scholar]
- 28.Wu, Y. & Voth, G. A. (2003) Biophys. J. 85, 864–875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Smondyrev, A. M. & Voth, G. A. (2002) Biophys. J. 82, 1460–1468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Smondyrev, A. M. & Voth, G. A. (2002) Biophys. J. 83, 1987–1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kim, J., Schmitt, U. W., Gruetamacher, J. A., Voth, G. A. & Scherer, N. E. (2002) J. Chem. Phys. 116, 737–746. [Google Scholar]
- 32.Marx, D., Tuckerman, M. E., Hutter, J. & Parrinello, M. (1999) Nature 397, 601–604. [Google Scholar]
- 33.Cuma, M., Schmitt, U. W. & Voth, G. A. (2001) J. Phys. Chem. A 105, 2814–2823. [Google Scholar]
- 34.Ryckaert, W. E., Ciccotti, G. & Berendsen, H. J. C. (1977) J. Comput. Phys. 23, 327–341. [Google Scholar]
- 35.Jorgensen, W. L., Chandrasekhar, J., Madura, J. D., Impey, R. W. & Klein, M. L. (1983) J. Chem. Phys. 79, 926–935. [Google Scholar]
- 36.Hoover, W. G. (1985) Phys. Rev. A 31, 1695–1697. [DOI] [PubMed] [Google Scholar]
- 37.Essmann, U., Perera, L., Berkowitz, M. L., Darden, T., Lee, H. & Pedersen, L. G. (1995) J. Chem. Phys. 103, 8577–8593. [Google Scholar]
- 38.Smith, W. & Forester, R. T. dl_poly (Daresbury Lab., Daresbury, Warrington, U.K.).
- 39.Roux, B. (1995) Comput. Phys. Commun. 91, 275–282. [Google Scholar]
- 40.Torrie, M. G. & Valleau, P. J. (1974) Chem. Phys. Lett. 28, 578–581. [Google Scholar]
- 41.Pfitzner, U., Hoffmeier, K., Harrenga, A., Kannt, A., Michel, H., Bamberg, E., Richter, O. M. & Ludwig, B. (2000) Biochemistry 39, 6756–6762. [DOI] [PubMed] [Google Scholar]
- 42.Popovic, D. M. & Stuchebrukhov, A. A. (2004) FEBS Lett. 566, 126–130. [DOI] [PubMed] [Google Scholar]
- 43.Nyquist, R. M., Heitbrink, D., Bolwien, C., Gennis, R. B. & Heberle, J. (2003) Proc. Natl. Acad. Sci. USA 100, 8715–8720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Cukier, R. I. (2004) Biochim. Biophys. Acta 1656, 189–202. [DOI] [PubMed] [Google Scholar]
- 45.Pomes, R., Hummer, G. & Wikstrom, M. (1998) Biochim. Biophys. Acta 1365, 255–260. [Google Scholar]
- 46.Namslauer, A., Aagaard, A., Katsonouri, A. & Brzezinski, P. (2003) Biochemistry 42, 1488–1498. [DOI] [PubMed] [Google Scholar]
- 47.Puustinen, A., Bailey, J. A., Dyer, R. B., Mecklenburg, S. L., Wikstrom, M. & Woodruff, W. H. (1997) Biochemistry 36, 13195–13200. [DOI] [PubMed] [Google Scholar]
- 48.Smart, O. S., Breed, J., Smith, G. R. & Sansom, M. S. P. (1997) Biophys. J. 72, 1109–1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Mitchell, D. M., Fetter, J. R., Mills, D. A., Adelroth, P., Pressler, M. A., Kim, Y., Aasa, R., Brzezinski, P., Malmstrom, B. G., Alben, J. O., et al. (1996) Biochemistry 35, 13089–13093. [DOI] [PubMed] [Google Scholar]