Simulations of the pressure and temperature unfolding of an α-helical peptide

Abstract

We study by molecular simulations the reversible folding/unfolding equilibrium as a function of density and temperature of a solvated α-helical peptide. We use an extension of the replica exchange molecular dynamics method that allows for density and temperature Monte Carlo exchange moves. We studied 360 thermodynamic states, covering a density range from 0.96 to 1.14 g·cm^–3 and a temperature range from 300 to 547.6 K. We simulated 10 ns per replica for a total simulation time of 3.6 μs. We characterize the structural, thermodynamic, and hydration changes as a function of temperature and pressure. We also calculate the compressibility and expansivity of unfolding. We find that pressure does not affect the helix–coil equilibrium significantly and that the volume change upon pressure unfolding is small and negative (–2.3 ml/mol). However, we find significant changes in the coordination of water molecules to the backbone carbonyls. This finding predicts that changes in the chemical shifts and IR spectra with pressure can be due to changes in coordination and not only changes in the helical content. A simulation of the IR spectrum shows that water coordination effects on frequency shifts are larger than changes due to elastic structural changes in the peptide.

Enhanced sampling methods enable the sampling of the configurational space of proteins and peptides in an efficient way, overcoming sampling limitations due to the multiple time scales involved in protein folding (1). Umbrella sampling (2), replica exchange molecular dynamics (REMD) (3–5) [which can be derived as an umbrella sampling technique (6)], and multicanonical ensemble methods (7, 8) are efficient methods for modeling thermodynamic equilibrium at the cost of kinetic information. With the development of equilibrium-enhanced sampling methods, we are able to validate (or invalidate) and modify semiempirical force fields and to explore the free-energy landscape of proteins and peptides (9, 10). The REMD method has been used to describe the energy landscape of peptides (9, 11–15), proteins (16), and protein membrane systems (17). For recent reviews, see refs. 1 and 6.

In this work, we use an extension of REMD to describe pressure effects on the equilibrium helix–coil transition of an α-helical peptide. Similar to temperature exchanges, we can devise exchange rules for systems with different intensive thermodynamic parameters like density and its conjugate variable, pressure (18). Pressure effects on proteins are of interest in biotechnology and biology (19). Pressure effects are also of interest in the physical chemistry of proteins, because pressure provides a way of shifting equilibrium of protein configurations without increasing thermal fluctuations or changing the system composition (e.g., chemical unfolding) (20–22). Proteins undergo unfolding upon addition of pressures of >200 MPa (2 kbars; 1 bar = 100 kPa). High pressures also are able to dissociate protein complexes. In addition, pressure may affect the dynamics and function of proteins; as shown in myoglobin, which is mainly an α-helical protein, pressure can shift the equilibrium of conformational substates (23, 24). Water plays a crucial role in the effect of pressure in protein unfolding (25). Structural studies of the ensemble of conformations of the pressure-unfolded state of proteins suggest that dominant conformations are not the same as the temperature (T) unfolded state (26–28).

At high pressures (100–200 MPa), the volume of proteins upon unfolding decreases. This finding seemed at odds with the model that assumes that protein unfolding is equivalent to the transfer of hydrophobic group from the protein interior to the aqueous solvent, because the volume change upon transfer of hydrophobic groups to water is positive. Hummer et al. (29) proposed a model in which pressure unfolding of proteins is modeled as the transfer of water into the protein hydrophobic core with increasing pressure. The transfer of water molecules into protein interior becomes key to the pressure-unfolding process, leading to the dissociation of close hydrophobic contacts and subsequent swelling of the hydrophobic protein interior through insertions of water molecules (29). The characteristic features of water-mediated interactions between hydrophobic solutes in water are found to be pressure-dependent. In particular, with increasing pressure the solvent-separated configurations in the solute–solute potential of mean force are stabilized with respect to the contact configurations. In addition, the desolvation barrier increases monotonically with respect to both contact and solvent-separated configurations. The locations of the minima and the barrier move toward shorter separations, and pressure effects are considerably amplified for larger hydrophobic solutes (30–32).

Pressure also changes the entropy/enthalpy balance of the hydrophobic interactions. Ghosh et al. (31) found that the contact minimum is dominated by entropy, whereas the solvent-separated minimum is stabilized by favorable enthalpy of association. Both the entropy and enthalpy at the contact minimum change negligibly with increasing pressure, leading to the relative pressure insensitivity of the contact minimum configurations. In contrast, the solvent-separated configurations are increasingly stabilized at higher pressures by enthalpic contributions that prevail over the slightly unfavorable entropic contributions to the free energy. The desolvation barrier is dominated by unfavorable enthalpy of maintaining a dry volume between methanes. However, the increasing height of the desolvation barrier with increasing pressures results from entropy changes at the barrier configurations.

The effect of pressure on the protein secondary structure is complex (33). It is clear that the stability of α-helices and β-sheets in proteins is strongly affected by the nature of the environment provided by the protein core. In some instances, it has been suggested that β-sheets in ubiquitin convert into α-helices at high pressures (34), while the native α-helices are maintained. In other instances, α-helices may be stabilized by a hydrophobic core, and, upon increases in pressure, the helices unfold (35). Overall, high pressures will favor lower-volume configurations of the system. High-pressure studies of α-helical peptides suggest that α-helices preserve the helical structure at pressures up to 300 MPa (36). These experiments have motivated us to explore the pressure effects on the stability and hydration of peptides. For this purpose, we use an extension of the REMD approach where replicas sample a range of volumes and temperatures, which we call the VTREMD (volume–temperature REMD) approach (18). In a previous study, we determined the reversible folding/unfolding of the C-terminal (41–56) fragment of protein G (GB1) as a function of density and temperature. By using the rms deviation from the folded structure as a quantitative measure, we were able to obtain the fraction of folded states and established the free-energy difference between the folded and unfolded states of the protein fragment as a function of temperature and pressure. For the pressure unfolding, the weakening of the hydrophobic interaction between the bulky side chains is found to be crucial at lower temperatures, leading to an apparent destabilization of the folded backbone structure at elevated pressures. In these calculations, we did not find a significant population of the α-helical conformation at high pressures.

Here, we describe the temperature–pressure helix coil stability diagram of a predominantly α-helical peptide, the AK-peptide, consisting of 20-aa residues, with sequence AcAA(AAKAA)₃AAY-Nme. The thermodynamic stability of this peptide as a function of temperature has been studied by linear IR (37), nonlinear IR (38), and vibrational circular dichroism (39) experiments, as well as theoretically (13). The local information within this peptide also has been characterized by using isotope labeling (37, 40). We will show that the α-helical content of the peptide is largely insensitive to pressure and that the helical content depends mostly on temperature. However, although the helical content does not change, we find that the hydration of the peptide changes significantly with pressure. We will show that the shielding of carbonyl atoms by the lysine side chains observed in previous calculations disappears at high pressures. We will characterize the hydration, size, and volume changes as a function of temperature and pressure. To make direct contact with IR measurements on the AK peptide, we also simulate the IR spectra of the peptide.

Simulation Methods

The VTREMD (18) simulations reported here were conducted by using a grid of 360 different (V,T)-states, each state characterized by its volume V and temperature T. Starting from the total partition function of the extended ensemble, we have derived the acceptance rule for state-swapping moves between two states i and j as being according to the acceptance probability

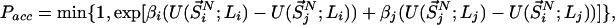with β_i = 1/k_BT_i, corresponding to the average temperature characterizing the state i (18). Here, 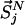represents the set of scaled coordinates 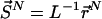the entire N-particle system belonging to state j. 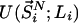denotes the potential energy of configuration 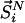at volume 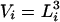, whereas 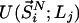represents the configurational energy belonging to 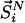at volume V_j. The volume change is performed in such a way gthat only intermolecular distances are changing. Because we obtain the pressure routinely during the simulation, and given that we consider only small volume changes, we approximate the energies as

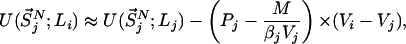and

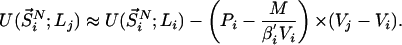where M represents the number of molecules in the simulation box, P_i and P_j denote the pressures of states i and j, and β′ represents the instantaneous temperature. To fulfill the detailed balance condition, the decision whether a state-swapping move or a molecular dynamics move is executed is made at random.

The AK-peptide was represented by 259 interaction sites employing the amber94 force field (41) as modified by Garcia and Sanbonmatsu (9). Here, we used the amber default values for the 1–4 interactions. The solvent phase was represented by 2,660 three-center transferable intermolecular potential 3 point (TIP3P) water molecules (42). Each replica represents a molecular dynamics simulation in the NVT ensemble (constant number of particles, volume, and temperature) by using the Nose–Hoover thermostat (43, 44) with coupling times τ_T = 0.5 ps. The electrostatic interactions are treated by the smooth particle mesh Ewald summation (45) with a real space cutoff of 0.9 nm and a 38 × 38 × 38 mesh with fourth-order interpolation for the reciprocal lattice contribution. The Ewald convergence factor α wassetto3.38nm^–1. Proper Lennard–Jones cutoff corrections for energy and pressure were taken into account. A 2-fs time step was used for all simulations. For all bonds within the protein, constraints were applied by using shake (46), whereas the water constraints were solved by using the effective settle procedure (47).

All simulations reported here were carried out by using the gromacs 3.2 program (www.gromacs.org), modified by us to allow for V,T-state-swapping moves. Either temperature- or volume-exchange moves were performed. In addition, only neighboring states were considered for exchange. The temperature tiling was chosen to maintain an acceptance ratio of ≈0.2. For this purpose, a preceding series of NVT simulations of exactly the same system, as used later, in the VTREMD simulations, was performed. From these simulations, the first and second moments of the potential energy distributions 〈E〉, 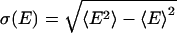, were obtained as a function of temperature and fitted to fourth-order polynomials. Based on this model parameterization, exchange rates between neighboring states were obtained numerically by a Monte Carlo procedure. The final temperature tiling was chosen in such a way to maintain an acceptance ratio of 20% over the entire temperature range, while ensuring a mostly constant overlap of the energy-distribution functions for neighboring temperatures and densities. Because the width of the pressure distribution is only weakly density-dependent, a constant increment for the density of 0.02 g·cm^–3 was used. In addition, to keep balance between temperature and volume swaps, the probability to pick a volume exchange was reduced by a factor of 10. The simulated state-points are represented by the temperatures 300.0, 304.5, 309.0, 313.7, 318.5, 323.3, 328.3, 333.4, 338.7, 344.0, 349.5, 355.2, 361.0, 366.9, 373.0, 379.3, 385.7, 392.3, 399.1, 406.0, 413.2, 420.6, 428.2, 435.9, 444.0, 452.2, 460.6, 469.3, 478.3, 487.4, 496.9, 506.5, 516.4, 526.6, 537.0, and 547.6 K at the densities 0.96, 0.98, 1.00, 1.02, 1.04, 1.06, 1.08, 1.10, 1.12, and 1.14 g·cm^–3. The method has been checked extensively, providing identical results for simulations carried out with and without replica exchange. The second momenta of the energy distributions σ_E obtained for the configurational energies from the VTREMD exchange simulations was found to obey the relation 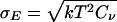, with C_ν being the isochoric heat capacity according to the temperature dependence of the energy E(T) obtained from the same set of simulations.

The system was prepared by placing the initial folded peptide structure into a transferable intermolecular potential 3 point solvent configuration at a density close to 0.98 g·cm^–3. Subsequently, the system densities were changed to the values indicated above. To provide a broad distribution of different initial peptide configurations as a starting point for the VTREMD simulations, each of the 10 systems with different density was simulated for 1 ns at temperatures at ≈650 K. Thus, a broad distribution of unfolded configurations was obtained for each density and then used as a start-configuration for the successive VTREMD simulation. Starting from this ensemble of states, the VTREMD simulation was conducted (as outlined above) for 10 ns. The average time interval between two successful exchanges was obtained to be ≈3 ps. During the course of the simulation, each replica visited each of the state points at least once and crossed the whole temperature and density interval roughly three times.

After an initial equilibration period of 5 ns, the general pattern revealing the helical content as a function of temperature and pressure emerged and persisted during the entire course of the simulation. Consequently, all data presented here were obtained from the final 5 ns of the simulation run.

Results

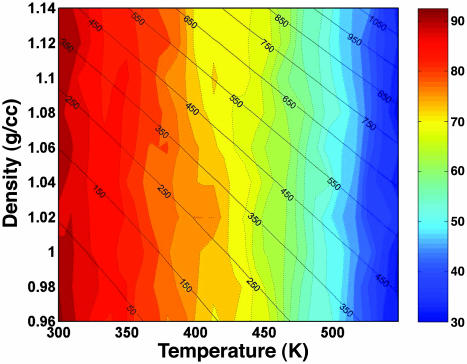
Fig. 1 shows the calculated helical content as a function of the density and temperature. The plot also shows contour of the equal pressure lines obtained in the simulation. The average pressure in the VTREMD simulations ranges from –53 to 411 MPa at 300 K, from 69 to 613 MPa at 373 K, and from 404 to 1,136 MPa at 547.6 K, the highest simulated temperature. We see that the helical content decreases as T increases, but it remains almost constant at fixed T, for the whole P range sampled. The helical content is higher than measured due to inadequacies in the force field (13). The large insensitivity of the α-helical conformation to pressure suggests small volume changes upon unfolding. We can estimate the free energy of unfolding by using a van't Hoff two-state model, with ΔG_u(P, T) = –RT log[(1 – f_helical)/f_helical], where R is the gas constant, and f_helical is the fractional helical content. To second order in pressure, the Gibbs free energy of unfolding is

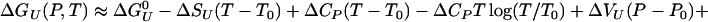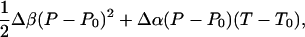where ΔC_p is the heat capacity, ΔS_U is the entropy of unfolding, 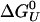is the Gibbs free energy of unfolding at the reference temperature T₀, Δβ is the compressibility change, ΔV_U is the volume change upon unfolding, and Δα is the temperature independent expansivity change upon unfolding (48). We take the reference pressure, P₀ = 0 MPa, and the reference temperature, T₀ = 300 K. A van't Hoff analysis of ΔG_u(P), using the lowest three temperatures, gives ΔV_U =–2.3 ml/mol; Δβ = 1.2 × 10^–3 ml/mol·bar, and 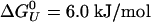. The volume change is significantly lower (a factor of four) than the volume change obtained for the GB1 β-hairpin (–10 ml/mol). The change in compressibility is also smaller than for the GB1 hairpin (18). A van't Hoff analysis for T < 400 K, and for all P < 100 MPa gives an enthalpy of ΔH_U = 11 kJ/mol and an entropy of ΔS_U = 0.14 kJ/mol·K, assuming ΔC_p ≈ 0. If we allow for nonzero ΔC_p in the fittings, we get a small ΔC_p = 0.12 kJ/mol·K, in agreement with thermodynamic measurements on α-helices by Lopez et al. (49). A fit of the free energy, based on the helical content, over the whole [〈P〉, T (where 〈P〉 is the averaged pressure)] range sampled in the simulations gives very similar results, with ΔC_p = 0.094 kJ/mol·K, 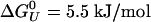but smaller values for ΔV⁰ =–0.6 ml/mol, and Δβ = 1.6 × 10^–4 ml/mol·bar. In this fit, we obtained the expansivity, Δα = –0.9 × 10^–3 ml/mol·K, which is the same order of magnitude as the measured values for a short non-α-helical peptide, but with opposite sign (50).

Fig. 1.

Helical content of AK peptide as a function of temperature and density. The color contours with dashed lines show the helical content increments of 2.5%. The color gradient from red to blue represents high to low helical content. The average pressure at the corresponding temperature and density is marked on the contour plot with solid lines.

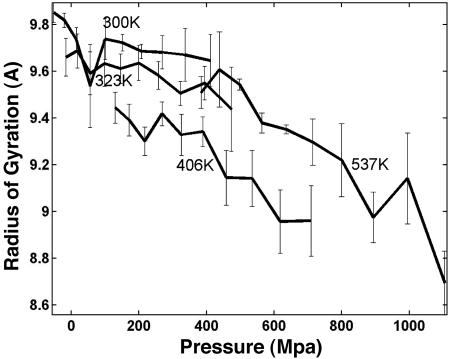
The changes in size of the α-helix are elastic; that is, they occur without changing significantly the α-helical structure (36, 51). To explore size changes, we monitored the radius of gyration, R_g, and the end-to-end distance, d_end, of the peptide as a function of pressure. Fig. 2 shows the profile of R_g as a function of pressure at low and high temperatures. At low pressure and temperature, R_g is the largest (≈9.8 A), corresponding predominantly to a helical AK peptide. The R_g exhibit a slight decrease, on the order of 0.2 A with increasing pressure. At higher T, there is a clear reduction in R_g as pressure increases, suggesting that the unfolded state is more compressible than the α-helical state. The reduction in R_g is more marked at P ≈ 400 MPa. Contrary to the observations for the GB1 β-peptide, we do not see an increase in R_g at low temperatures. The increase of R_g with pressure (at low T) has been taken as an indication of the insertion of water molecules into the hydrophobic protein core. However, for the α-helical peptides there is no hydrophobic core for water to penetrate. We evaluated d_end and found a small reduction at low temperatures. At 300 K, the calculated compressibility, measured as the fractional linear extension with pressure (Δd_end/d_end), is 6 × 10^–4 per MPa, in agreement with the values measured by NMR on melittin in alcohol (36). At higher T, when the system is partially disordered, Δd_end/d_end ≈ 30 × 10^–4 per MPa, showing that the disordered peptide is more sensitive to pressure than the α-helix.

Fig. 2.

Radius of gyration as a function of pressure is shown at four representative temperatures (300, 323, 406, and 537 K). The error bar shows SEM obtained from 1-ns block analysis.

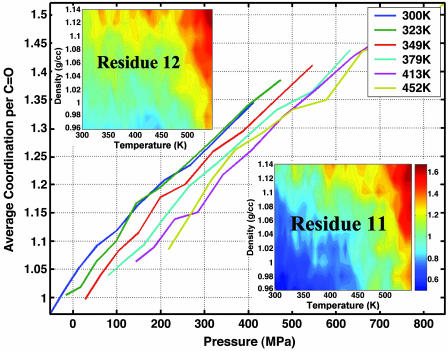
The effect of pressure in proteins depends on the interaction of the protein with the solvent. Fig. 3 shows the average coordination number of water to the backbone carbonyls. The coordination of water molecules to carbonyls increases linearly with pressure. The rate of increase in the average number of coordinated water is 0.06 per MPa at 300 K. This rate does not depend strongly on temperature. Previous simulations on the thermal unfolding of this peptide found that the number of coordinated waters is not uniform and specific carbonyls were shielded from water by the lysine side chains (13). Fig. 3 Insets show contour plots of the water coordination number with respect to temperature and density for two specific carbonyls: one is unshielded (residue 12) and the other is shielded (residue 11). A comparison of the two contour plots shows that the coordination number of the shielded residue is reduced by half the value of the unshielded carbonyl at low temperature and pressure. By increasing the pressure, the shielding effect disappears, and the carbonyls are exposed to water. With increasing pressure, the rate of change of coordination number is the same for the shielded and unshielded carbonyls. Therefore, even though increased pressure solvates the shielded carbonyls, the coordination does not reach the same level as that of an unshielded carbonyl at lower T. At higher T, however, the effect of shielding is minimal, and both shielded and unshielded carbonyls achieve a similar level of water coordination with increasing pressure.

Fig. 3.

Pressure-dependence of the average coordination number of water to the backbone carbonyl oxygen. Insets show the average water coordination number as a function of density and temperature to the carbonyls of two specific residues: residues 11 and 12, which are positions where the carbonyl is shielded and unshielded from water, respectively, by the lysine side chain. The color schemes are the same in both contours where increase in coordination corresponds to color gradient from blue to red.

The interplay between mode coupling and backbone hydrogen-bonding results in the amide-I spectrum that provides information about the overall secondary structural components of the protein system (13, 52, 53). The helix–coil transition for the AK peptide was studied by means of the temperature dependence of its IR spectra in the amide-I region (40). Here, we compute effects of peptide carbonyl (C = O) hydrogen-bonding to HN group of peptide linkage (internal) and water (external) and the coupling between amide-I modes on the amide-I frequency as a function of temperature and pressure. The amide-I band is calculated by using an excitonic model that takes into account the above effects. Details on the simulation of the amide-I band are described in ref. 13.

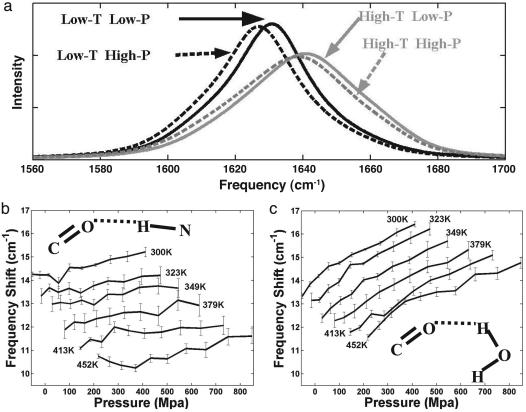
The simulated amide-I band spectrum, shown in Fig. 4a, displays a characteristic behavior upon thermal unfolding seen in other helical peptides. That is, at lower temperatures the amide I band is narrower with higher peak intensity. With increasing temperatures, it shifts to higher frequency and broadens. The loss of peak intensity is generally associated with the loss in helical content. In a recent study on the same peptide using REMD simulations, we provided a microscopic reasoning for this behavior of the amide-I band (13). Upon thermal unfolding of the peptide, the amide-I band shifts to higher frequency because the increase in solvent hydrogen-bonding fails to compensate for the loss in internal (helical) hydrogen bonds. The loss of uniformity of the mode coupling along the helix at higher T accounts for the well known thermal broadening of the amide IR spectrum.

Fig. 4.

Temperature and pressure dependence of the amide-I band of the AK peptide. (a) The simulated amide-I band at four values of pressure and temperature (low T, low-P; low T, high P; high T, low P; and high T, high P). The dark and gray lines show pressure dependence at low (300 K) and high (547 K) temperatures. The solid and dashed lines correspond to low (ρ = 1.0 g·cm^–3) and high (ρ = 1.14 g·cm^–3) densities. (b and c) Plots correspond to the contribution from the internal (helical) (b) and external (solvent) (c) hydrogen bonding to the amide-I frequency. These contributions will lower the amide-I frequency of the individual carbonyls by the frequency shift given in cm^–1.

We can now provide a description of the pressure effects on the amide-I spectra of α-helices. Fig. 4a shows that the band shifts slightly (4 cm^–1) toward lower frequency and has no significant broadening at low temperatures. The magnitude of this shift decreases at higher temperatures. The direction and magnitude of the calculated frequency shift are comparable with the experimental observations of the “red shift” in the amide-I band in the elastic region (34, 51, 54).

A microscopic reasoning for the behavior of amide-I band in elastic regime can now be gained by considering the pressure effects on internal (helical) and external (solvent) hydrogen-bonding and mode-coupling. The coupling between amide-I does not change with increasing pressure, and consequently no significant broadening is caused by an increase in pressure. However, the hydrogen-bonding of backbone carbonyls changes with pressure. Even though internal (Fig. 4b) and external (Fig. 4c) hydrogen-bonding cause similar shift of the amide-I frequency, their dependencies on pressure are quite different. In the elastic regime, the solvent hydrogen-bonding shows a high rate of red shift (0.65 cm^–1/kbar at 300 K), whereas the helical hydrogen-bonding shows a smaller rate of red shift (0.25 cm^–1/kbar). Although we observed shorter helical hydrogen-bonding distance due to compression of helix as suggested from experiments (36), the major component that contributes to the observed red shift of the amide-I band is the increase in strength of solvent hydrogen bonding to the peptide carbonyls. This strong dependence of external hydrogen bonding on the pressure-denatured peptide will shift amide-I band to lower frequency when compared with shift of the temperature-denatured peptide.

Conclusions

We have used an extension of the REMD enhanced sampling approach to model the temperature and pressure stability diagram of an α-helical peptide. We calculated the α-helical content of the AK peptide over a broad range of temperatures and pressures. We found that the helical content does not change with pressure. We characterized the thermodynamic of the (T,P) helical content diagram. We found that the unfolding transition is characterized by a negative volume change of –2.3 ml/mol. This volume change is small but of the same order of magnitude as volume changes measured in protein unfolding. We also found that the helix unfolding is characterized by a small change in compressibility. The value for an α-helix is smaller than what we found for a β-hairpin, and both are of the same order of magnitude as the measured values for proteins. Interestingly, the α-helical structure and hydration change with pressure, even though the helical content was pressure-insensitive. We found that the helix size decreases with pressure. The radius of gyration and the end-to-end distance decrease with increasing pressure. Our calculations predict that the red shift in the amide-I band with pressure is due mostly to changes in hydration than to changes in the intramolecular hydrogen-bond length. Our calculations also suggest that α-helical peptides could be used as models to calibrate the changes in amide-I band in proteins. In many instances, the protein secondary structure as a function of pressure is deconvoluted from the IR spectrum (34). However, changes in the frequency due to solvation have not been quantified.

Enhanced sampling methods, together with large-scale, parallel computations, have enabled the study of the pressure–temperature stability diagram for an α-helix. The atomistic nature of the calculation allows for a microscopic understanding of the competing forces that determine the stability and the vibrational spectra of proteins.