Origin of the long-range attraction between surfactant-coated surfaces

Abstract

We compare the “long-range hydrophobic forces” measured (i) in the “symmetric” system between two mica surfaces that had been rendered hydrophobic by the adsorption of a double-chained cationic surfactant, and (ii) between one such hydrophobic surface and a hydrophilic surface of bare mica (“asymmetric” case). In both cases, the forces were purely attractive, stronger than van der Waals, and of long-range, as previously reported, with those of the asymmetric, hydrophobic–hydrophilic system being even stronger and of longer range. Atomic force microscopy images of these surfaces show that the monolayers transform into patchy bilayers when the surfaces are immersed in water, and that the resulting surfaces contain large micrometer-sized regions of positive charges (bilayer) and negative charges (bare mica) while remaining overall neutral. The natural alignment of oppositely charged domains as two such surfaces approach would result in a long-range electrostatic attraction in water, but the short-range, “truly hydrophobic” interaction is not explained by these results.

The hydrophobic interaction is among the most important nonspecific interactions in biological and many colloidal systems. The significant role of the hydrophobic interaction has led to a great deal of study and yet, over 20 years since the first direct measurement of the attraction between two nominally hydrophobic surfaces (1, 2), no single theory is able to account for all observed experimental behavior. One source of confusion in determining the origins of the long-range hydrophobic interaction is the apparent existence of two different force regimes. It has been suggested (3–6) that the measured force between hydrophobic surfaces is in fact a combination of a “truly hydrophobic” short-range force (D < 10 nm) and a longer-ranged force (D > 10 nm) due to a mechanism unrelated or only indirectly related to the hydrophobicity of the surfaces. Suggested mechanisms for the long-range attraction include electrostatic charge or correlated dipole–dipole interactions (7–13), water structure (2, 14), phase metastability (15, 16), and preexisting submicroscopic bubbles that bridge the surfaces (17–19). Although there is convincing evidence of bridging nanobubbles between some types of surfaces (18, 20), it has become clear that none of these models can explain all of the forces observed between the many different surfaces studied so far.

Langmuir–Blodgett (LB)-deposited monolayers of cationic surfactants such as dimethyl-dioctadecyl-ammonium bromide (DODAB) have been used often in the past 25 years to study the hydrophobic interaction (3, 15, 16, 21–23), but the data presented in this article indicate that the long-range attraction between such surfaces may not be directly related to their hydrophobicity. In this article, surface forces apparatus (SFA) force measurements and atomic force microscopy (AFM) imaging are combined. Both symmetric (hydrophobic–hydrophobic) and asymmetric (hydrophobic–hydrophilic) systems were studied and compared. Previous studies of asymmetric systems (9, 24) found the force to be slightly stronger and of longer range than that in the symmetric system of two similar hydrophobic surfaces, but a satisfactory explanation for this phenomenon has yet to be provided. Results in both systems are discussed in the context of new AFM images, and a possible explanation is presented for the long-range attraction between surfaces that have been rendered hydrophobic by physisorbed surfactant monolayers.

Materials and Methods

The hydrophobic surfaces were prepared by LB-deposition of DODAB (deposition pressure 25 mN/m). This double 18-carbon chain surfactant forms bilayer vesicles in solution and has a chain transition temperature of 44°C (10). Hydrophobic and bare (untreated) mica surfaces were mounted into the SFA, which was subsequently filled with water purified by a Milli-Q A-10 water purification system (Millipore). Forces were measured by using a Mark III SFA (SurForce, Santa Barbara, CA) as described in ref. 25, employing the dynamic force measurement method of Chan et al. (26), where the separation between two attracting surfaces approaching at a constant rate is measured as a function of time, from which the force–distance function is deduced. The results were reproducible from run to run and from experiment to experiment.

AFM imaging was carried out by using standard tapping mode AFM (Nanoscope IV, Digital Instruments, Santa Barbara, CA), equipped with silicon cantilevers (Tap 300, NanoDevices) and bioprobes (Olympus). Images were recorded in air and in clean (Milli-Q) water at room temperature, at a scan rate of 1 Hz.

Results

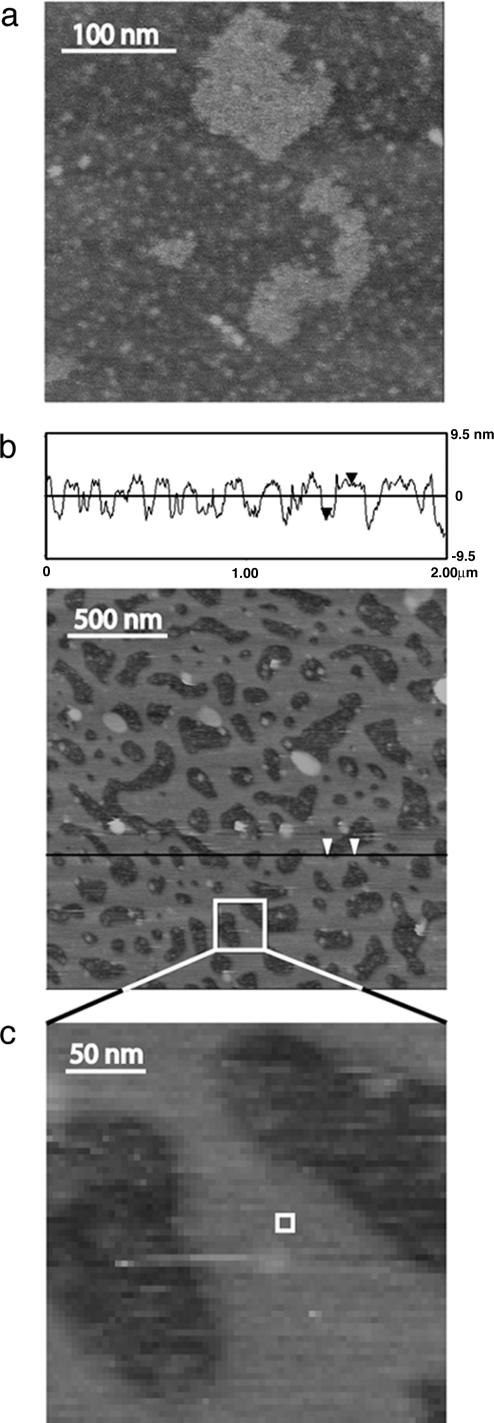
LB-deposited monolayers of DODA on mica imaged with AFM are presented here. AFM images of DODA-coated mica surfaces are shown in Fig. 1. The images in air (Fig. 1a) show a smooth monolayer, with roughness on the order of 3 Å. The images under water (Figs. 1 b and c), however, are considerably different: Within 90 min of immersion in water, the smooth monolayer becomes a patchy bilayer. The bilayers occupy an area that is ≈60% of the total, a number consistent with calculations for a stressed bilayer.

Fig. 1.

AFM images. (a) AFM image in air. (b) AFM image under water. The roughness in air is ≈3 Å, whereas the holes that appear under water are ≈60 Å deep, the thickness of a DODA bilayer. A portion of the underwater image is enlarged in c, and an area the size of that imaged by Tsao et al. (10) is depicted by the white box.

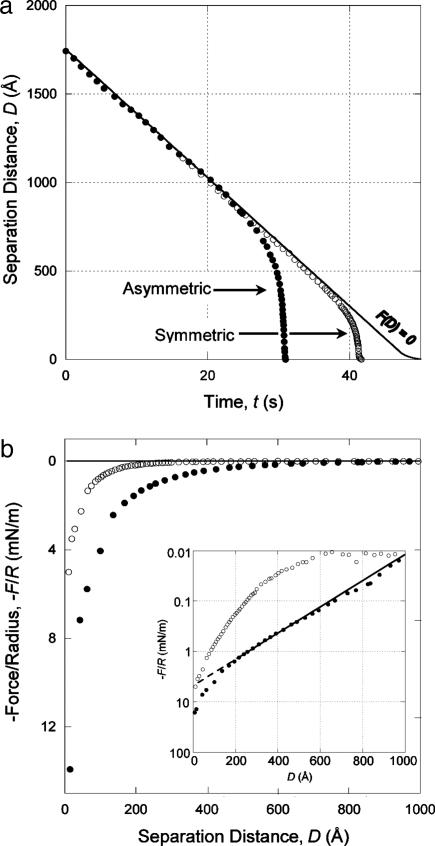
Data acquired in symmetric experiments were presented in refs. 6 and 27 and will be discussed here only for comparison and in the context of these AFM results. Representative data for the forces in the symmetric and asymmetric systems are shown in Fig. 2. The solid curve in Fig. 2a represents the path the data would follow in the absence of surface forces [F(D) = 0]. In the case of the asymmetric system (Fig. 2a), distance vs. time data show that the surfaces accelerate away from the F(D) = 0 curve at a separation distance of >1,000 Å and jump into adhesive contact from a distance of ≈600 Å, indicating a considerably stronger, longer-ranged attraction than in the symmetric case. Normalized force vs. distance data (Fig. 2b) show the same trend, with the force increasing at a separation distance of 1,000 Å in the asymmetric case and 450 Å in the symmetric case. Fig. 2b Inset shows that the attractive force in the asymmetric case is well approximated by the exponential function

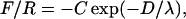[1]

where D is the separation between the two original monolayers, with C ≈ 5 mN/m and λ ≈ 175 Å at separations from 1,000 Å down to 200 Å, below which the force becomes considerably stronger.

Fig. 2.

Representative data are shown for distance vs. time (a) and normalized force vs. distance (b) curves for a DODA monolayer-coated mica surface and a bare mica surface (•) and for two DODA monolayer-coated mica surfaces (○) approaching at constant driving velocity in water. The solid curve in a represents the path the trajectory would be expected to take in the absence of any molecular intersurface forces. A spring constant of K = 160 N/m was used in both cases. b Inset shows the force curves on a log-linear scale.

Discussion

These data on the behavior of LB-deposited DODA monolayers under water has important implications for understanding the “long-range hydrophobic forces” measured here and previously between physisorbed surfactant surfaces (3, 15, 16, 21–23, 27, 28). We begin by discussing the symmetric case. The most common mechanism presented for the origin of the long-range attraction in this system has been a model based on the metastability of the intervening fluid (15, 16). With the system near a liquid–vapor critical point, small density fluctuations could lead to an attraction of sufficient range to explain experimental results. Although there is no evidence to directly dispute (or support) this model, AFM images of patchy bilayers under water (Fig. 1 b and c) suggest an alternative model based on electrostatics.

A conventional electrostatic mechanism has been ruled out as the origin of the long-range attraction in this system in previous publications on the basis of studies carried out in electrolyte solution (21, 22, 28). Effects of electrolytes, both in these publications and in our own unpublished results, are seen to be considerably more complex than could be accounted for by pure double-layer forces. Indeed, DODA-coated surfaces have been shown to be “unstable” in salt solution (29), and one should not necessarily expect the effects of salt to be limited to electrostatic screening. Chistenson et al. (28), for example, ascribed the effects of salt on this system to surface effects such as electrolyte adsorbing to the hydrophobic surfaces rather than to the presence of electrolytes in the solution. Another indication of the instability of these surfaces is the measured contact angle hysteresis, with θ_a = 110° and θ_r = 60° (30). Such a hysteresis is an indication of molecular rearrangement of the surface. It has in fact been shown that there is a correlation between the lack of stability of a surface, as indicated by contact angle hysteresis, and the presence of the long-range attraction discussed here (5).

Tsao et al. (8–10) studied a system of DODA adsorbed from cyclohexane solution and attributed the long-range attraction to electrical fields originating from domains of correlated in-plane dipoles that result from the ordering of the hydrocarbon chains. Yoon and Ravishankar (7) arrived at a similar conclusion by studying mica surfaces in equilibrium with dodecylamine hydrochloride. Rabinovich et al. (11) determined chain order parameters for DODA monolayers LB-deposited on a silicon attenuated total reflectance crystal and found their results to be in agreement with the conclusions of Tsao et al. All of these articles discussed the effects of patches in a monolayer resulting in correlated charges or dipoles. It should be noted that AFM imaging carried out on DODA monolayers adsorbed from cyclohexane showed only a slight change when immersed in water (10). However, the area imaged was ≈9 nm × 9 nm, an area considerably smaller than any features we observe in our own images (represented by the white box in Fig. 1c). Even if patchy bilayers had been present in this system, they may have gone undetected by imaging areas of this size.

Electrostatic interactions are among the only interactions capable of giving rise to a force of the measured range of the hydrophobic interaction, yet no consensus has been reached as to why such an interaction would take place between hydrophobic surfaces. Several models for the long-range attraction between hydrophobic surfaces involving correlated charges or dipoles have also been presented in recent years (7–12). Miklavic et al. (12) showed that theory predicts that the interaction between two nonuniform, net neutral surfaces with charges that are free to migrate will always be attractive, regardless of the nature of the surfaces, with the magnitude of the attraction on order of or greater than the van der Waals attraction. The authors suggested that this result should be considered in the context of mica surfaces modified to measure hydrophobic effects.

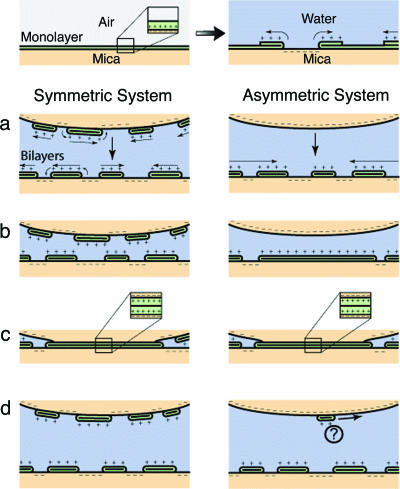
In light of the AFM images presented here, a model related to the findings of Miklavic et al. (12) for mobile charges on net neutral surfaces is suggested for the long-range attraction between LB-deposited hydrophobic monolayers in aqueous solution. After formation of the patchy bilayer, the surfaces remain net neutral, but now with distinct but mobile patches of both positive (DODA headgroups) and negative (bare mica) charge. Some indication of the extent of the mobility of these patches can be seen by considering the free diffusion rates of lipids in bilayers (31), which are consistent with movement by distances of ≈300 nm in 1 sec. The molecules in the bilayer also experience a force due to the charge of the approaching surface, so that sufficiently rapid movement of these patches via a “rolling” mechanism (see Fig. 3) is within reasonable physical parameters. As the surfaces approach, these patches migrate to reduce the interaction free energy, thus creating a system in which patches of opposite charge face one another. A schematic is shown in Fig. 3. The result is a system that exhibits a long-range attraction, exponential in form until a considerably stronger force takes over at much smaller separations (27). It remains unclear whether the surfaces return to their original monolayer states just before contact, thus returning the surfaces to a hydrophobic state, to account for this increased attraction. Even if this is not the case, the electrostatic attraction at short distances would remain considerably stronger than any hydration repulsion between the surfaces.

Fig. 3.

Schematic of the initial overturning of the DODA monolayer upon immersion in water (Upper), and schematic diagrams (Lower) of the symmetric (Left) and asymmetric (Right) systems at large separation (a), at smaller separation (b), in contact (c), and after separation (d).

The model presented here also immediately offers an explanation for the strong attraction in asymmetric systems. The interaction between a hydrophilic mica surface and a hydrophobized mica surface has been studied only twice before. Claesson et al. (24) studied the force between a bare mica surface and a surface coated with an LB-deposited DODA monolayer, similar to what we have presented in this article. The measured force, stronger than that of the symmetric system, was attributed to a positive charge on the hydrophobized mica surface interacting with the negatively charged bare mica. Tsao et al. (9) studied an asymmetric system of a bare mica surface and a mica surface hydrophobized by surfactant adsorption from cyclohexane solution. The authors questioned the interpretation of Claesson et al. (24), citing measurements showing that, when charged, the hydrophobic surfaces acquire a negative charge. Tsao et al. (9) claimed that the force had the same origin as that in the symmetric system: that the hydrophobic surface remains uncharged but generates dipoles through hydrocarbon chain ordering.

Taking the AFM images into account, it would appear that the mechanism presented by Claesson et al. (24), that of a positively charged hydrophobized surface interacting with the negatively charged bare mica surface, may have been correct, although the suggested origin of the positive charge was not. Due to the presence of a reservoir of positively charged patches of bilayer, these positively charged patches can migrate into the contact area as the surfaces approach, thus lowering the interaction free energy. The result is a fully negatively charged mica surface opposite what has now become a fully positively charged bilayer, as shown schematically in Fig. 3. The resulting force would be stronger than that in the case of oppositely charged patches on net neutral surfaces, as observed.

The state of the system following separation from contact remains unclear at this point (Fig. 3d). Force runs are entirely reproducible between initial and subsequent approaches in both the symmetric and the asymmetric systems, indicating that each system returns to its original, large separation state within seconds after separation from contact. This situation could result from more than one scenario: In the symmetric case, separation from contact may result directly in bilayer patches on each surface, or in a monolayer remaining on each surface that then returns to a patchy bilayer at large separations. Similarly, in the asymmetric system, patches of monolayer or bilayer may be pulled off by the bare mica surface but would then migrate into the reservoir, thus returning the system to its initial equilibrium state.

The results presented here are likely to have implications for colloidal and biological systems where surfactants, lipids, and other hydrophobic or amphiphilic molecules are involved. In particular, they indicate that surfactants can be mobile under the action of weak colloidal forces, even when in a nominally frozen state, and that amphiphiles will move to “close” any hydrophobic patch that opens up to water, even when this requires the breaking of (hydrated) ionic bonds. Such effects may occur in the adhesion, and especially fusion, of micelles, microemulsions, lipid bilayers, and biological macromolecules (32).

Conclusions

The AFM images presented here offer an interpretation for the long-range attraction between LB-deposited DODA surfaces. Although this system has been used for many years to study the hydrophobic interaction (3, 15, 16, 21–23, 27, 28), we see that the observed long-range attraction may in fact be due to an interaction between patchy bilayers, rather than an interaction between hydrophobic monolayers. Just as preexisting nanobubbles appear to be responsible for the long-range attraction between surfaces hydrophobized by certain methods (33), we see here another example of a long-range force between hydrophobized surfaces that is only indirectly related to the hydrophobicity of the surfaces. As studies of the hydrophobic interaction continue, it becomes increasingly likely that the long-range attraction observed in so many experiments is not in fact due to any direct hydrophobic attraction at all. Experiments to elucidate the origin of the shorter-range force between “truly hydrophobic” surfaces must continue before we can hope to fully understand this fundamentally important interaction.