Abstract
Growing interest in quantum computing for practical applications has led to a surge in the availability of programmable machines for executing quantum algorithms1,2. Present-day photonic quantum computers3–7 have been limited either to non-deterministic operation, low photon numbers and rates, or fixed random gate sequences. Here we introduce a full-stack hardware−software system for executing many-photon quantum circuit operations using integrated nanophotonics: a programmable chip, operating at room temperature and interfaced with a fully automated control system. The system enables remote users to execute quantum algorithms that require up to eight modes of strongly squeezed vacuum initialized as two-mode squeezed states in single temporal modes, a fully general and programmable four-mode interferometer, and photon number-resolving readout on all outputs. Detection of multi-photon events with photon numbers and rates exceeding any previous programmable quantum optical demonstration is made possible by strong squeezing and high sampling rates. We verify the non-classicality of the device output, and use the platform to carry out proof-of-principle demonstrations of three quantum algorithms: Gaussian boson sampling, molecular vibronic spectra and graph similarity8. These demonstrations validate the platform as a launchpad for scaling photonic technologies for quantum information processing.
The past decade has seen remarkable progress in quantum computation and simulation. Breakthroughs across a range of platforms have enabled the construction of programmable machines delivering the automation, stability and repeatability demanded by increasingly sophisticated quantum algorithms. Rigorous benchmarks have been carried out on an 11-qubit trapped ion system1,9, and a 53-qubit super-conducting system has been used to generate random samples from a probability distribution at a rate exceeding what is reasonably achievable using classical hardware2,10. Similar machines can now be remotely accessed and loaded with algorithms written in high-level programming languages by users having little knowledge of the low-level quantum hardware details of the apparatus. These capabilities have accelerated application development for near-term quantum computers11–13.
Such hardware has primarily been designed to access problems in the qubit model, where computation is carried out by initializing a quantum state in a space spanned by a product of binary-valued basis states, followed by a sequence of gates selected from a typically discrete set of operations14. Present-day machines are limited to dozens of noisy qubits, restricting their applicability to quantum algorithms compatible with this scale15. Other algorithms are more efficiently expressed in a model where each independent quantum system is described by a state in an infinite-dimensional Hilbert space. Examples include those implementing bosonic error correction codes16,17, a wide class of Gaussian boson sampling (GBS) applications8,18–23, and bespoke algorithms exploiting the structure of infinite-dimensional Hilbert spaces24,25.
A promising platform for the large-scale implementation of bosonic quantum algorithms is offered by photonic hardware. A number of groundbreaking demonstrations of photonic quantum information processing have recently been completed. Two-dimensional cluster states with tens of thousands of entangled nodes have been deterministically generated using bulk-optical components3,4, and photonic experiments have been constructed to sample from the photon number distribution of multi-mode Gaussian states6,7. Combined with advances in photonic chip fabrication26, such demonstrations coincide with new optimism towards photonics as a platform for quantum computation27.
Despite these advances, much work remains in developing photonic systems for practical use in quantum computation. Photonic cluster state demonstrations3,4 were limited to all-Gaussian states, gates and measurements, rendering them efficiently simulatable at any scale by classical computers. Single-photon-based experiments on integrated platforms5 suffer from non-deterministic state preparation and gate implementation, hindering their scalability. This deficit can be evaded in photonic experiments by using deterministically prepared squeezed states and linear optics, with non-Gaussian operations provided by photon-counting detectors. In such experiments, and in the machine we present, squeezed state inputs have the role of qubits as the basic independently accessible quantum systems. But demonstrations of such squeezing-based photonic machines6,7 lacked programmability, with each accessing only a fixed, randomized quantum state. Furthermore, these demonstrations were limited to small numbers of detected photons.
To date, no photonic machine has been demonstrated that is simultaneously (1) dynamically programmable, (2) readily scalable to hundreds of modes and photons, and (3) able to access a class of quantum circuits that could not, when the system size is scaled, be efficiently simulated by classical hardware. Here we report results from a device based on a programmable nanophotonic chip that includes all of these capabilities in a single scalable and unified machine. We describe the performance of the components designed for initial state preparation, gate sequence implementation, and readout, and verify the non-classicality of the device output. We then use the machine to carry out proof-of-principle demonstrations of the execution of three types of quantum algorithms: GBS28, molecular vibronic spectra18 and graph similarity22. Although our device, at its current scale, can readily be simulated by a classical computer, the architecture and platform developed can potentially enable future generations of such machines to exit this regime and perform tasks that are not practically simulatable by classical systems.
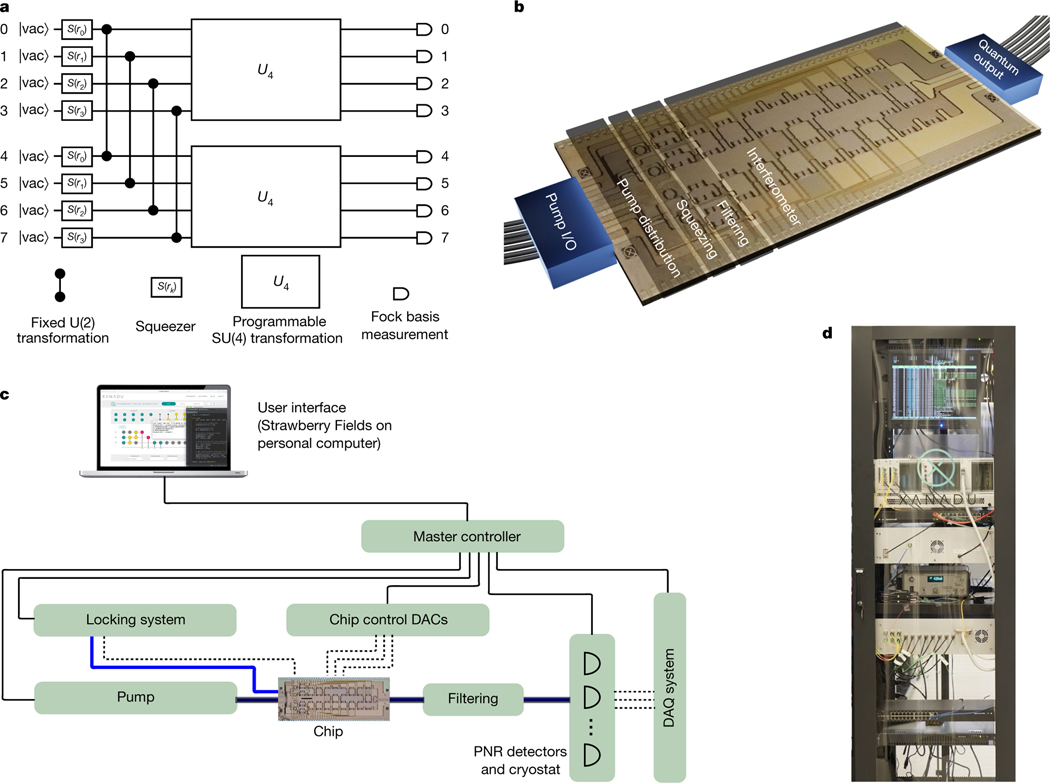
The core of our device is a 10 mm × 4 mm photonic chip. It generates squeezed light29 in up to eight optical modes, with a fixed initialization into four independent two-mode squeezed vacuum states. The squeezing is generated between bichromatic mode pairs, with each such pair populating one of four spatially separated waveguide modes. An interferometer, based on a network of beam splitters and phase shifters, implements a user-programmable gate sequence corresponding to an SU(4) transformation (with SU(n) the special unitary group of degree n) applied to the spatial modes. The resulting eight-mode Gaussian state synthesized by the chip is then measured in the Fock basis using eight independent photon-number-resolving detectors. An equivalent quantum circuit diagram for the machine is illustrated in Fig. 1a.
Fig. 1 |. Overview of apparatus.
a, Equivalent quantum circuit diagram illustrating the functionality of the photonic hardware. Up to eight modes initialized as vacuum are squeezed with squeezing parameters and entangled (via the fixed two-mode unitary transformation U(2) equivalent to a 50/50 beam splitter with the relative input phase set to produce two-mode squeezing at the output) to form two-mode squeezed vacuum states. Programmable four-mode rotation gates (SU(4) transformation, represented by the large boxes labelled ) are applied to each four-mode subspace. All eight modes are individually read out by measurements in the Fock basis. b, Rendering of the chip (based on a micrograph of the actual device) showing fibre optical inputs and outputs, and on-chip modules for coherent pump power distribution, squeezing, pump filtering and programmable linear optical transformations. c, Schematic of full apparatus and control system. Solid (dashed) black lines indicate digital (analogue) electronic signals; blue lines indicate optical signals. DAC, digital-to-analogue converter; DAQ, data acquisition; PNR, photon number resolving. d, Photograph of entire system (except for photon-number-resolving detector hardware), which has been fitted into a standard server rack.
The chip itself (Fig. 1b) is based on silicon nitride waveguides and thermo-optic phase shifters, fabricated using a commercially available service offered by Ligentec SA. The die contains modules for coherent distribution of pump light, generation of squeezed states, filters to separate pump light from generated quantum signals, and programmable linear-optical transformations. Four squeezers based on microring resonators30 are integrated, each generating a bichromatic two-mode squeezed state in a nearly single temporal mode when pumped with a pulsed laser; that is, each squeezer generates an entangled-mode pair in its respective waveguide output. The modes in these pairs are distinguished by wavelength; we refer to them as the ‘signal’ and ‘idler’. Four wavelength filters separate the pump light from the generated squeezed states, directing the squeezed light into the programmable interferometer and the pump light out of the chip. The interferometer implements an arbitrary programmable four-mode linear optical transformation on both the signal and idler subspaces of the squeezed light. The use of two-mode squeezers doubles the total number of modes available for detection per spatial mode, at the cost of restricting the space of eight-mode Gaussian states accessible from the chip. The synthesized Gaussian state is then coupled out of the chip for photon counting. More detail is provided in Methods.
To operate the apparatus, a control system was developed to autonomously actuate all required control signals, monitor system status and acquire data. An overview diagram of the full system is shown in Fig. 1c. A master controller (conventional server computer) running custom-developed control software coordinates the operation of the chip and all other hardware required. The system is accessed by a high-level application programming interface: a classical computer providing the quantum programs for the photonic chip, using the Strawberry Fields Python library31. This enables users with no knowledge of the hardware details to run quantum algorithms remotely on the device. Apart from the photon-counting system, the entire machine is contained in a standard server rack (Fig. 1d); the chip itself is optically and electronically packaged, forming a mechanically stable solid-state system. The full apparatus is alignment-free and indefinitely stable for continuous operation, except for the cryogenic detection system, which requires 2 h of downtime every 24 h for its automated cycling process to complete.
In contrast with demonstrations of earlier photonic devices6,7, our machine features non-classical light sources designed to generate squeezed light in single temporal modes with high average photon number (squeezing parameter , mean photon number at the sources). In addition, detection is carried out using transition-edge sensors, yielding true photon-number resolution at the readout stage32. This enables execution of quantum algorithms involving multi-photon contributions, a key requirement for implementing many squeezing-based photonic quantum applications. For example, large-photon-number contributions are essential for accessing higher-energy transitions when using a photonic device for vibronic spectrum simulations18. Large is also crucial for achieving a quantum advantage33. Our device readily achieves large-photon-number event rates exceeding all previous demonstrations of programmable photonic devices: with all squeezers activated, four-photon detection events occur at an average rate of 10,000 events per second, ten-photon events at an average rate of 270 events per second, and nineteen-photon events at an average rate of 0.3 events per second.
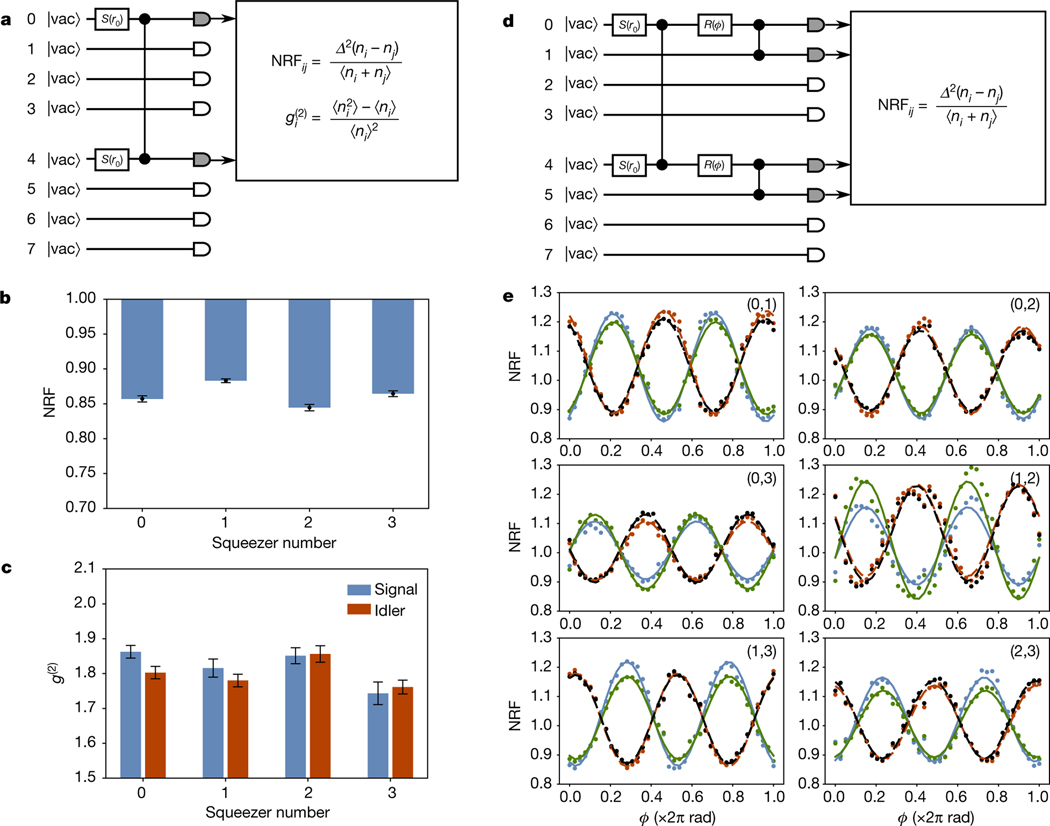
We characterize the component-level system performance by operating the interferometer in fixed simple configurations and computing relevant statistics on the event data acquired. As shown in Fig. 2a, the interferometer is first set to the identity transformation and each squeezer individually turned on. The two-mode cross-correlation is then measured, where is the combined total mean photon number in the ith signal/idler mode pair and is the variance of the photon number difference between the ith signal/idler mode pair. This quantity is termed the noise reduction factor (NRF) and is a measure of non-classicality34. For two-mode Gaussian states indicates an ideal two-mode squeezed state, and indicates a classical coherent state. As evident in Fig. 2b, the measured NRF for each signal/idler mode pair is well below unity, averaging 0.86(1). This value is limited primarily by losses, which degrade the measurable correlations in an otherwise ideal two-mode squeezed state as , with the total transmission efficiency experienced by mode pair (assuming balanced losses between the signal and idler pair). Our estimated system efficiency of approximately 15%, inferred both from direct measurements of components using classical light and from fitting the photon-number statistics to a general theoretical model, is consistent with measured NRFs. From this, we estimate the effective input squeezing in each mode (that is, the squeezing produced by each squeezer in the circuit representation of Fig. 1a, in the absence of losses) to be approximately 8 dB.
Fig. 2 |. Component statistics.
a, Schematic of the circuit used to measure NRFs and second-order correlation statistics for individual squeezers, here illustrated for squeezer 0. The unitary is set to the identity transformation, and each squeezer is turned on individually. Photon samples collected from the corresponding signal and idler outputs are collected and used to calculate the relevant quantities. b, Raw NRF for each of the squeezers. Each is well below unity, indicating non-classicality. Error bars represent one standard deviation over eight batches of 105 samples. c, Raw measured unheralded second-order correlation statistic of the signal and idler for each squeezer. Each is close to , indicating nearly single-temporal-mode operation. Error bars represent one standard deviation over eight batches of 105 samples. d, Schematic of the circuit used to measure quantum interference between pairs of squeezers. Here the circuit for the (0,1) pair is illustrated: two squeezers are turned on, and the interferometer is used to interfere their outputs on an effective 50/50 beam splitter with relative input phase , implemented by the single-mode rotation . The NRFs are then calculated from the photon-number samples. e, Interference traces between pairs of squeezers. The six panels each correspond to a different squeezer pair . Within each panel, four NRFs are plotted as function of the relative phase : [signal 1 – idler 1] (blue), [signal 2 – idler 2] (green), [signal 1 – idler 2] (red), [signal 2 – idler 1] (black). Points correspond to raw, uncorrected measured data; solid and dashed lines are best fits (least squares) to a model that incorporates no imperfections except photon loss.
Next, we characterize the temporal mode structure of the squeezers. This can be quantified by the Schmidt numbers (refs. 30,35) of our sources, or, equivalently, the unheralded second-order correlation statistic , where is the photon number measured in the signal (idler) from the ith squeezer. This statistic is independent of the NRF of the sources, as it pertains not to the degree of photon-number correlation between the mode pairs, but to the temporal mode structure of each generated squeezed state. Ideally, for all squeezers, indicating a single-mode thermal state populating a single temporal mode, as is expected from each half of a two-mode squeezed state. The raw measured second-order correlation statistics for each of the eight measured modes is plotted in Fig. 2c; the average over all eight modes is 1.81(4), indicating that our squeezers are working close to single-temporal-mode operation. From this and the inferred level of background noise, we estimate that over 85% of detected photons come from squeezing in the dominant Schmidt mode across all squeezers.
An even more stringent requirement than single-temporal-mode operation is uniformity of the squeezed light sources: for high-visibility quantum interference to occur, the temporal modes populated by each squeezer must be nearly identical. To verify that genuine multi-source quantum interference is accessible in our device, we configure the interferometer to selectively interfere pairs of squeezed sources, and measure the phase-dependent response of four NRFs between all six possible pairs of squeezers. A representative quantum circuit is shown in Fig. 2e. The 24 resulting traces are plotted in Fig. 2e alongside fits to a theoretical model of this interference that includes only optical loss as an imperfection. The pronounced phase-dependent response of the photon statistics, consistent with the theoretical model, demonstrates multi-photon quantum interference between all four sources. We emphasize that, in contrast to the typical presentation of data from experiments based on heralded single-photon sources, no post-selection or other post-processing was applied to the data exhibited in Fig. 2e.
Finally, we show that the output distribution of the device cannot be efficiently simulated with small error by approximating the output state with a classical Gaussian state, that is, a state with a positive Glauber−Sudarshan P-function36,37. This condition is necessary but not sufficient to demonstrate the inability to classically simulate the device.
We characterize the chip using a model with a single Schmidt mode per squeezer, non-uniform loss, and excess noise from residual photons not blocked by the filtering system38. Using to denote the experimental photon number distribution, and for the fitted model distribution, we find the sampling error, defined as , where is the total variation distance, to be .
A device is deemed classical, meaning it can be efficiently simulated up to error by sampling from classical states, if the following condition is satisfied33:
| (1) |
where , is the transmission efficiency of mode , is the single-mode squeezing level, is the probability of detecting one excess photon and is the number of modes. Setting equal to the modelling error and substituting the model parameters, we obtain 2.5 × 10−3 for the right-hand side and 1.0 × 10−2 for the left-hand side in equation (1), meaning that the inequality is not satisfied and the device passes the non-classicality test. The minimum error satisfying the inequality can be interpreted as a measure of non-classicality; large indicates a highly non-classical device. We find . This can be compared to previous four-mode experimental results6 for which can be inferred33. Thus our device samples from a distribution that is quantifiably more non-classical, which originates from the improved level of squeezing and transmission efficiency.
We now showcase the programmability, high sampling rate and photon-number-resolving capabilities of the machine by demonstrating proof-of-principle implementations of photonic quantum algorithms. The device is programmed remotely using Strawberry Fields31. Theoretical predictions are performed with respect to a model of the device involving two Schmidt modes per squeezer, non-uniform loss and excess noise.
GBS
Sampling from the distribution induced by a Fock basis measurement on Gaussian states is believed to require exponential time using classical computers28,39. This model is known as GBS and it is a leading platform for demonstrating a quantum advantage using photonic hardware.
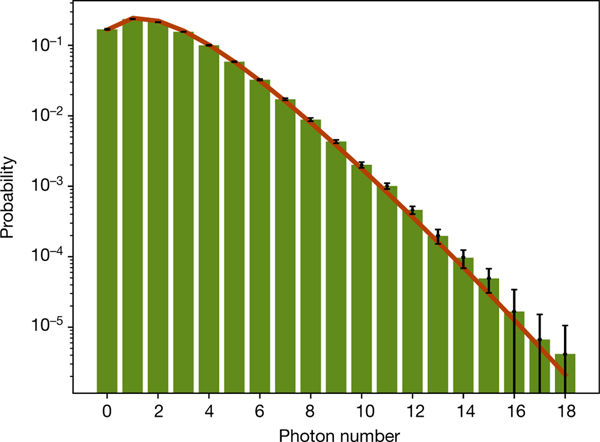
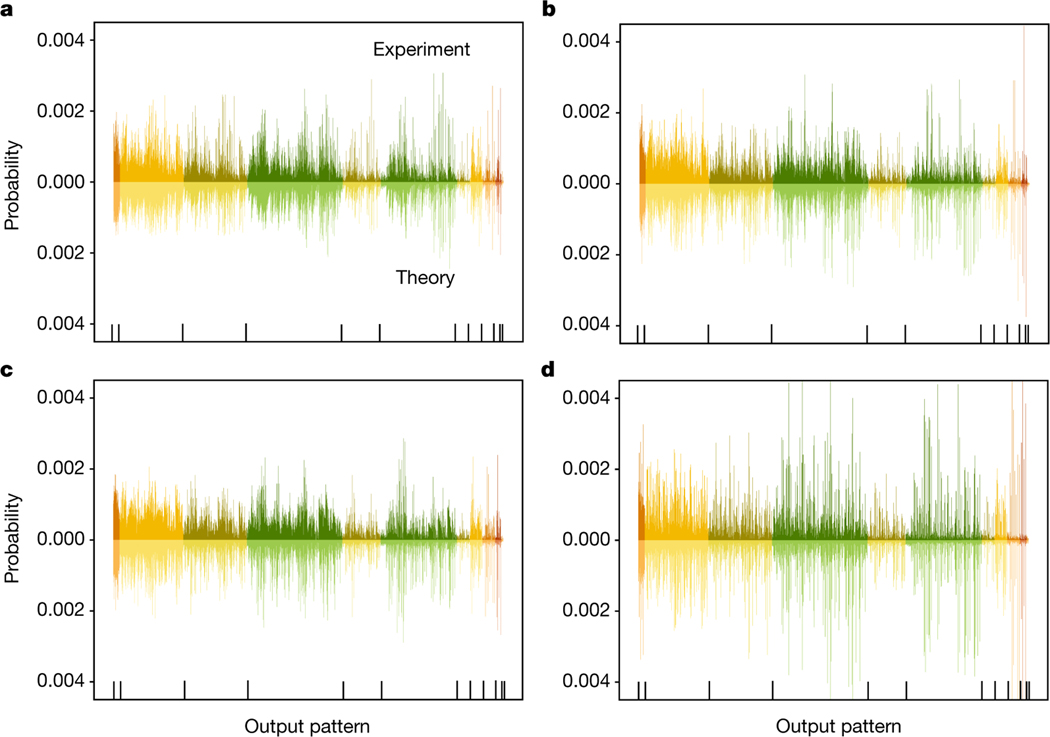
Owing to strong on-chip squeezing in the device, a large number of photons can be generated. This is illustrated in Fig. 3, which shows the probability distribution for the total number of photons measured. In the implementation, the device is configured according to three different interferometers randomly selected from the Haar measure, generating 1.2 × 106 samples for each. Sampling is repeated for an interferometer set to the identity. The results are shown in Fig. 4, where we plot the full distribution of six-photon output patterns compared to their theoretical predictions based on the detailed model described above. The average total variation distance between experimental and theoretical distributions is 0.09(1).
Fig. 3 |. Total photon-number distribution.
All squeezers are turned on and the interferometer is set to the identity. Estimates of the probabilities obtained from experimental samples are shown as bars. The theoretical prediction appears as a continuous line. Error bars denote one standard deviation taken over 12 runs of 105 samples. For large photon numbers, error bars are comparable to the probabilities.
Fig. 4 |. GBS experiment.
In each figure, the top bar plot depicts experimental probabilities estimated from chip samples and the bottom plots show the theoretical values. Output patterns are organized by orbits, separated by different colours as well as vertical bars in the bottom of the plots. Starting from the left, the orbits are [1,1,1,1,1,1], [2,1,1,1,1], [3,1,1,1], [2,2,1,1], [4,1,1], [3,2,1], [5,1], [2,2,2], [4,2], [3,3] and [6]. Panels a to c show the distributions for Haar-random interferometers, and panel d is the identity.
Vibronic spectra
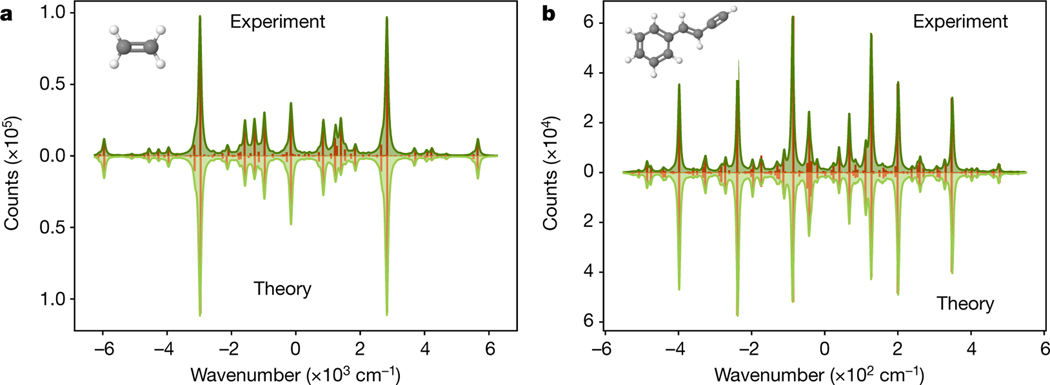
The vibronic spectrum of a molecule specifies the frequencies and intensities of light absorbed when the molecule undergoes a transition between different vibrational and electronic states. In the photonic algorithm, optical modes represent the vibrational normal modes and the device is programmed in terms of squeezing, displacement and linear interferometers to generate Franck−Condon profiles efficiently18,40. We program the chip interferometer according to the Duschinsky matrices that represent mixing between four normal coordinates in ethylene (C2H4) and (E)-phenylvinylacetylene (C10H8). Displacements are not included and squeezing is only present in the first mode, so the resulting profiles do not correspond to the true vibronic spectra of these molecules. Nevertheless they can be used as proof-of-principle benchmarks with respect to the theoretical model of the device6. Results are shown in Fig. 5, obtained by generating 1.2 × 106 samples for each molecule.
Fig. 5 |. Vibronic spectra experiment.
Franck−Condon profiles are obtained from chip distributions programmed according to the vibronic transitions of ethylene (a, with structure shown in the inset) and (E)-phenylvinylacetylene (b, with structure shown in the inset). The red bar graphs depict the histogram of energies, whereas green continuous lines show a Lorentzian broadening of the bars. Counts refer to the number of times the corresponding energy was observed. Wavenumbers correspond to the energy differences between initial and final energy levels. Vacuum outputs are omitted.
Graph similarity
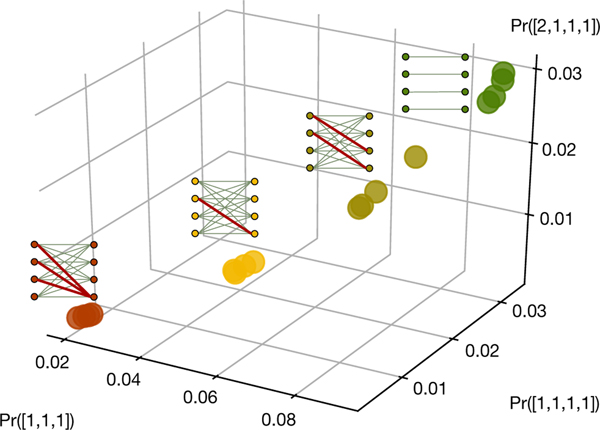
A graph can be encoded in a photonic circuit through a correspondence between the graph’s adjacency matrix and the combination of a linear optical interferometer with squeezed light21. The statistics of detected photon patterns can be used to estimate orbit probabilities and collect them in m-tuples called feature vectors22,41. The distance between feature vectors is used to quantify the similarity of the corresponding graphs. We demonstrate this algorithm by encoding bipartite graphs on eight vertices. Four graphs are considered, with their corresponding adjacency matrices shown in the Supplementary Information. Feature vectors are estimated using 20 million samples for each graph. The results are illustrated in Fig. 6, showing that these graphs result in separate feature vectors, which are invariant to mode permutations. To showcase this property, three random permutations were selected and each of the four graphs was permuted accordingly, resulting in clusters of isomorphic graphs. These results are the first demonstration of graph similarity on a quantum device.
Fig. 6 |. Graph similarity experiment.
Feature vectors corresponding to four different graphs, which are drawn next to their corresponding feature vectors. Negative-weighted edges are highlighted by thick red lines. The components of the vectors are probabilities for the orbits [1,1,1], [1,1,1,1] and [2,1,1,1], respectively. Feature vectors are also calculated for three random permutations of the graph. These appear as clusters of permutationally invariant graphs.
Discussion
We have presented a nanophotonic device pioneering several record capabilities: high sampling rates, large on-chip squeezing, nearly ideal second-order correlation statistics, and considerably more detected photons than previously reported in similar devices. The hardware is programmable and can be remotely configured via a custom application programming interface, which enables deployment for cloud access. We have further showcased the capabilities of the nanophotonic chip with example demonstrations.
As the first of its generation, our device constitutes an initial step in scaling nanophotonic chips to a larger number of modes, eventually reaching the regime of quantum advantage. The greatest challenge in scaling is maintaining acceptably low losses. Designs for integrated beamsplitters and phase shifters, requiring more precise (but available) chip fabrication tools, could achieve an order-of-magnitude improvement in the loss per layer. This would enable a 100-mode device to be realized with less than 3 dB of loss in the interferometer. The inclusion of tunable single-mode squeezing42 and displacement will constitute a substantial upgrade, permitting the generation of arbitrary Gaussian states and unlocking the capability of implementing quantum algorithms. Such scaling and upgrades are natural next steps for near-term photonic quantum information processing demonstrations.
Online content
Any methods, additional references, Nature Research reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at https://doi.org/10.1038/s41586-021-03202-1.
Methods
Programming a nanophotonic chip
The device can be programmed remotely using the Strawberry Fields Python library31. A user with valid credentials can specify the settings of the device using a few lines of code and subsequently request samples. The example Python code shown in the Supplementary Information, from version 0.14.0 of Strawberry Fields, shows a typical workflow where 4 × 105 samples are requested from a device. All squeezers are turned on and the interferometer is programmed according to a unitary transformation drawn randomly from the Haar measure.
Apparatus details
As described in the main text and in Fig. 1, the full apparatus consists of:
A custom modulated pump laser source producing a regular pulse train (100 kHz repetition rate) of 1.5-ns-duration rectangular pulses,
An electrically and optically packaged chip that synthesizes a programmable eight-mode Gaussian state with temporal-mode characteristics appropriate for photon-number resolving readout,
A locking system which serves to align and stabilize the resonance wavelengths of the on-chip squeezer resonators,
An array of DACs for programming phase shifter voltages on the chip,
An array of low-loss (off-chip) wavelength filters to suppress unwanted light, passing only wavelengths close to the signal and idler for detection,
A detection system, which consists of an array of eight transition-edge sensor detectors for photon-number-resolving readout, and the auxiliary equipment, including an adiabatic demagnetization refrigerator, required to operate and acquire data from them, and
A master controller consisting of a conventional server computer running custom software to coordinate the continuous and automated operation of all subsystems, and receive and process jobs sent to the machine.
In the following sections we provide more detail on these subsystems and the techniques used to characterize them.
Pump system
The pump laser is a compact continuous-wave tunable laser assembly, tuned to a wavelength of 1,554.9 nm. The laser is connected to a 10-GHz-bandwidth fibre-integrated intensity modulator which is used to define a regular train of 1.5-ns-wide optical pulses with a 100 kHz repetition rate. The output of the modulator is coupled to a 99/1 fibre splitter, with the 1% tap directed to a photodiode used to lock the modulator bias voltage. Bias voltage locking in continuous operation is performed by a modular field programmable gate array (FPGA)/DAC board. The other 99% is directed to a fibre polarizer, before being sent to an erbium doped fibre amplifier (EDFA). After the EDFA, the pump is spectrally filtered using low-loss fibre bandpass filters and directed to the chip subsystem. All of the components of the pump are controlled remotely and do not require human intervention for operation.
Integrated components
The chip layout is illustrated in Fig. 1b. Pump light is edge-coupled from fibre to the chip through a single waveguide input. This waveguide enters a binary tree of 50/50 beam splitters based on multimode interferometer (MMI) devices, which distributes the pump light equally among four spatial modes. Each of these four waveguides is coupled to a separate squeezer. The chip was fabricated using a photolithographic process on a dedicated wafer run through a commercial service offered by Ligentec SA.
The squeezers are based on a microring resonator design that uses strongly pumped spontaneous four-wave mixing to generate bichromatic two-mode squeezing. This design is described in full detail by ref. 30; here we summarize the operation and details specific to the squeezers on the eight-mode chip. The waveguide cross-section of the rings is 1,500 nm × 800 nm, and their radius is chosen to be 113 μm, corresponding to a free spectral range of 200 GHz. The loaded quality factors of the resonances used were approximately 7 × 105, corresponding to a full-width at half-maximum linewidth of 275 MHz, and varying less than 5% across all four rings. The escape efficiencies for these resonances are approximately 75%, that is, the probability of a photon generated in a ring being lost before it can be collected by the bus waveguide is approximately 25%. This makes up 1.2 dB of the loss within the overall 8 dB system efficiency.
To produce single-temporal-mode squeezed light, it is sufficient to employ pump pulses with duration comparable to the resonator dwelling time; the exact pulse shape is unimportant. In our case, 1.5-ns square pulses yielded nearly single-temporal-mode operation, as quantified by the second-order correlation data exhibited in Fig. 2c. Shorter pulses can be used, but they do not appreciably improve the temporal-mode structure, and they compromise the generation efficiency as the pulse bandwidth exceeds the resonator linewidth. The exact pulse energy used is difficult to measure precisely, owing to the extremely low duty cycle of the pulse train, but we estimate this quantity to be of the order of 0.5 nJ. This was chosen to yield a mean photon number of about one per mode at the sources, and could be increased by using more pump power or designing better resonators with higher escape efficiencies and quality factors. This value of 8 dB for effective input squeezing cannot easily be directly measured, but serves as a guideline for theoretical modelling of our device.
No excess noise from unwanted processes occurring within the ring was measured. As discussed below, the dominant source of photon noise in the squeezing band is from Raman scattering in the fibre components carrying pump power to the chip. This can be managed in future versions by better pump filtering before the squeezers.
Each resonator output mode is directed to a separate asymmetric Mach−Zehnder interferometer (AMZI) device, which acts as a pump rejection filter. This ensures that very little nonlinear light generation occurs in the interferometer portion of the chip, and also allows the rejected pump to be collected and used as a signal for locking the ring resonances to the pump laser wavelength. The bright outputs of the AMZI filters are directed back to the input facet and coupled out of the chip for detection. The free spectral ranges of the AMZIs and rings are carefully matched to be compatible with the standard telecom dense wavelength division multiplexing spacing of 100 GHz, and to allow the signal and idler to pass to the interferometer when the AMZI is tuned to reject the pump. The signal and idler resonances are each separated in frequency from the pump by three ring free spectral ranges (approximately 600 GHz).
The interferometer is composed of a network of MMIs and phase shifters in a rectangular configuration43. The user must specify twelve independent real parameters to program this transformation, with the remaining three free parameters of the SU(4) transformation corresponding to irrelevant output phases. This transformation implements the gate sequence on both four-mode subspaces distinguished by their optical wavelength. This configuration contains a sequence of six SU(2) transformations that enable arbitrary programmability of the interferometer by controlling the thermo-optic phase shifters integrated within the chip. The splitting ratio of the MMIs is constant to within 1% over the range of wavelengths used. This control is accomplished using a multi-channel DAC system. Light is coupled out of the chip via edge couplers to a fibre array, and then directed to a fibre-based low-loss filter stack that separates the signal and idler photons and directs them to separate photon-number-resolving detectors. The total pump rejection ratio is well in excess of 100 dB. In addition, the filter stack rejects photons from unwanted resonator modes, and any residual pump light and broadband generated photons from in-fibre Raman scattering. The total remaining number of noise photons per pulse from all sources (pump leakage and Raman scattering) incident on the transition-edge sensor detectors is approximately 0.02 or lower for each channel. Overall, about 5% of the photons detected in our experiments arise from noise photons generated by Raman scattering in fibre components before the chip, and 10% from unwanted temporal modes populated by the squeezers. These figures can be improved by implementing better wavelength filtering on the pump input to the chip to eliminate noise, and by engineering the squeezers to permit more broadband pump pulses to be used. The residual pump light rejected by the filter stack is directed to a photodiode array, and was used for the calibration of the interferometer. The filter stack comprises approximately 2 dB of the overall 8 dB of loss in the system.
The chip is both electrically and optically packaged to ensure stable operation. The chip is glued to a copper sub-mount using a thermally conductive die adhesive. The submount is mounted on top of a thermo-electric cooler used to actively stabilize the temperature of the chip. Connectorized printed circuit boards are affixed to the sub-mount and the chip is wirebonded to these boards. Cables carry the electronic signals responsible for programming the unitary transformation and locking the rings to a secondary printed circuit board that interfaces with custom control circuitry and the interferometer DAC. V-groove arrays of ultrahigh numerical aperture (UHNA7) fibre are aligned to each edge facet of the chip using loop-back waveguide structures placed on the chip. These fibre arrays are fixed in place using an optical adhesive, resulting in an average coupling efficiency of approximately 70%.
Operating procedure
Quantum programs are written by users with the Strawberry Fields Python library31. These programs are sent to the master controller as ‘jobs’, that is, scripts specifying squeezing parameters and interferometer phases. Upon receipt of a job, the information is compiled into a set of hardware instructions. The control system then implements the following control sequence:
Voltages of the interferometer that correspond to the requested unitary operation are set,
The chip is allowed to equilibrate thermally,
The ring resonance wavelengths are swept to calibrate the squeezer control circuitry, followed by locking of the rings to the pump wavelength,
Checks are performed to ensure that the interferometer and squeezers are in the desired state,
The requested number of samples are acquired from the detectors,
Checks are performed to ensure the interferometer and squeezers are still in their desired state, that is, that the chip has not drifted out of the specified state during data acquisition,
The sample and job data are returned to the user, and finally
The chip is re-initialized to its default state.
Chip calibration
To set the interferometer to a user-specified state, the on-chip thermo-optic phase shifters must first be calibrated to determine the voltage-to-phase relationship for each phase shifter. The thermal nature of the phase shifter implies (and tests confirm) that to a high degree of accuracy, the relationship between phase and voltage can be described by
| (2) |
The goal of the calibration process is to determine and . Then, when a specific phase is requested, the phase-to-voltage can be inverted to produce the required voltage. The calibration is accomplished by injecting classical light into a single mode of the interferometer at a time by injecting pump light into the second input of the filter AMZI for that mode. A standard telecom fibre switch enables control of which mode the calibration light is injected into. The transmission of the interferometer is detected using classical light detectors connected to the pump rejection channel of the output filter stack. Employing optimization algorithms, it is possible to learn the voltage-to-phase relationship for each thermo-optic phase shifter in sequence.
It is challenging, however, to learn the input phases of the interferometer using classical light, since these phases will depend on properties of the squeezers themselves. Instead, to calibrate these three relevant phases, two-squeezer interference is used. Each pair of neighbouring squeezers is locked to the pump laser, and the input phase shifters in modes 0, 1 and 2 are swept. Mode 3 has no input phase shifter because only the relative phase between the inputs is physically relevant. The NRF is monitored between the pair of interfering modes and the relevant phase-to-voltage relationship is extracted.
Photon detection system
Each of our transition-edge-sensor-based detectors has quantum efficiency above 95% and produces an analogue voltage pulse every 10 μs, synchronized with the incident optical pulse train, with a shape that depends on the number of incident photons. These voltage signals are digitized by analogue-to-digital converters, resulting in time series referred to here as voltage traces. Thus, determining photon numbers amounts to being able to associate a photon number to each trace. This is typically accomplished for sets of a few hundred thousand traces, by first ordering them according to a feature such as their maximum or their overlap with some reference trace. Reasonable points are then determined, in terms of this feature, by which to organize the traces into photon-number bins44,45. In previous work on measuring photon-number difference squeezing from nanophotonic sources30, a principal component analysis was performed on sets of 8 × 105 traces. These traces were then ordered with respect to their overlap with their first principal component, and a sum of Gaussians fitted to the resulting histogram, solving for the points of intersection between adjacent Gaussians to determine photon-number bin edges.
That approach suffers from two drawbacks, which make it less appropriate for a more complex system like the one described in this work. The first is that it relies on a global comparison of each trace to the full set of traces acquired during the corresponding experimental run, and so cannot associate a photon number with a single trace in real time after it is generated given that the principal component analysis depends on all traces in the dataset. This limits the speed of the trace-to-photon number discrimination in our system. Second, and of more concern, the maximum assignable photon number —that is, the value at which actual -photon events (with ) will be identified as -photon events—could be different for each dataset, because each dataset may identify a different number of photon-number bins. Both of these drawbacks were eliminated in our system.
Before activating the full system, we first calibrate each detector, allowing each subsequent voltage trace to immediately be assigned, in real time, to a photon number up to the determined by the calibration. This calibration involves two steps: (1) identification of a standard trace for calculating overlaps, and (2) determination of photon-number bin edges associated with the standard trace. Each calibration uses a set of 107 voltage traces. To obtain a standard trace, we perform principal component analysis and histogram fitting to identify all of the two-photon traces in the set, and calculate the resulting average trace. We use the set of two-photon traces as opposed to one-, three- or four- photon traces in an effort to balance the tradeoff between capturing some detector nonlinearity and having enough events to obtain a representative average trace. Using sets of higher-photon-number traces in principle allows us to extend . However, as we calibrate using one arm of a two-mode squeezed vacuum state we always expect to have more -than -photon traces. Next, we calculate the overlap of each trace in the full set of 107 traces with the standard trace, generate a histogram, fit to it a sum of Gaussians, and determine photon-number bin edges. The resultant for each of our eight detectors ranges between five and seven.
NRF
To assess the degree of photon number correlations between the signal and idler for each individual squeezer, the NRF was measured. For a single two-mode squeezed vacuum source, we define this as
| (3) |
where and are the photon number observables for the signal and idler, respectively, and refers to the variance of the photon number difference. An ideal measurement of a perfect source would yield NRF = 0, since the photon number of the signal and idler are perfectly correlated for a two-mode squeezed vacuum state. On the other hand, a pair of coherent states would yield NRF = 1. In our system, the dominant imperfection that degrades the correlation is loss: a total photon transmission efficiency of yields an NRF of
| (4) |
for two-mode squeezed vacuum30.
The NRF values reported in Fig. 2b were obtained by setting the interferometer to the identity transformation, activating only one squeezer at a time, and collecting 8 × 105 samples. These samples were divided into eight batches of 1 × 105, and the NRF was calculated for each batch. The mean and standard deviation of these eight NRF values correspond respectively to the data points and uncertainties reported.
Second-order correlation
For faithful execution of quantum circuits according to the idealized functionality illustrated in Fig. 1a, it is important that no additional co-propagating modes are substantially populated with photons apart from those that carry the desired Gaussian state; because the photon detectors cannot distinguish between overlapping temporal modes, they would show up as an effective noise contribution to the collected samples. It is therefore vital to assess the temporal-mode structure of the individual squeezer outputs: the squeezed states should as closely as possible populate only a single temporal mode.
To verify that each squeezer is substantially populating only one temporal mode, the unheralded second-order correlation statistic was measured for the signal and idler of each squeezer30. For any output channel of the device described by photon number operator , this statistic is defined as
| (5) |
This statistic provides a loss-insensitive measure of the temporal-mode structure of a two-mode squeezed vacuum source. In the absence of noise, the Schmidt number is related to via35
| (6) |
An ideal single-temporal-mode two-mode squeezed vacuum source would yield for the signal and idler, whereas coherent states or highly multi-mode squeezed light would yield .
The values reported in Fig. 2c were obtained, like the NRF values, by setting the interferometer to the identity transformation, activating only one squeezer at a time, and collecting 8 × 105 samples. These samples were divided into eight batches of 1 × 105, and the was calculated for each batch. The mean and standard deviation of these eight values correspond respectively to the data points and uncertainties reported. The values reported are raw and uncorrected for noise, which tends to lower the measured towards unity. Noise from unwanted Raman scattering is the dominant factor affecting the measured in our system, and therefore the values reported are in fact lower bounds for this quantity.
Two-squeezer interference
Here we provide a simple model to explain the behaviour of the NRF as a function of the phases of the interferometer used in our chip. We consider two identical squeezing sources, labelled 1 and 2, that each produce photons in their idler arms , and in their signal arms and . We write the NRF between an arbitrary pair of modes , as
| (7) |
Since we are considering Gaussian states (two-mode squeezed states with squeezing parameter ) undergoing Gaussian operations (a beam splitter with unitary matrix and loss quantified by transmission efficiency ), and assuming the losses to be homogeneous and the squeezing identical in both sources, it can be shown that the variance and mean photon number of all the modes are the same and given by
| (8) |
Now we need to evaluate only
| (9) |
where Wick’s theorem46 was used to write the fourth-order expectation values in terms of second-order ones. For our system, the same interferometer acts on both the signal modes and the idler modes (as in Fig. 1a), and that interferometer transformation can be expressed according to . With this, we find that
| (10) |
where we parameterized the interferometer in terms of the unitary matrix
| (11) |
The data exhibited in each panel of Fig. 2e were obtained as follows: the corresponding pair of squeezers were activated, with the others turned off. The unitary transformation was set to interfere the two squeezers with , corresponding to an effective 50/50 beam splitter with relative input phase . A batch of 4 × 105 photon number samples was then acquired for each of 40 different settings of between 0 and . The four NRF combinations (signal 1 – idler 1, signal 2 – idler 2, signal 1 – idler 2, signal 2 – idler 1) were then computed from these samples, and the results plotted alongside least-squares fits to the model of equation (10) (with a free offset phase included to account for calibration offsets in ).
The interference can be quantified by the amplitude of the oscillations in these traces. The NRFs between modes from separate squeezers, made to interfere according to the circuit of Fig. 2d, obey an oscillatory dependence on the relative phase , with an amplitude proportional to the sum of the mean photon number (after losses) and total system transmissivity. The amplitudes extracted from the fits in Fig. 2e are consistent to within 40% of the independently estimated values for these quantities; imperfections apart from loss, including squeezer distinguishability, need to be accounted for in the model to obtain better agreement. In future, more general modelling of the device can be used to extract an estimate for the overlap between the temporal modes populated by different squeezers, informing the path to optimizing two-source interference of these devices.
We note that if the sources were completely distinguishable, that is, if the temporal modes populated by different squeezers were very different, then the visibility of the interference would be zero: interferometer would not be able to interfere the modes and there would be no oscillating phase dependence with amplitude in equation (10). The extracted fit parameters for the curves, averaged over all traces, are and . The extracted transmission efficiency is consistent with independent estimates, whereas the extracted mean photon number is about 40% smaller than independent estimates. The interference visibility is thus measurably affected by imperfections other than loss, including unitary transformation infidelity (the effective 50/50 beam splitter has approximately 18 dB extinction), noise, temporal multi-modedness, and potentially some squeezer distinguishability.
Scalability
An important factor in assessing the viability of the platform presented is the scalability of this approach. What improvements to the platform and design are required in order to scale the system size to a level where quantum advantage could potentially be achieved? To answer this, we fix a target of 100 modes, which in our architecture would require: 50 squeezers operating with squeezing factors of , a universal 50-spatial-mode interferometer, and 100 photon-number-resolving detector channels. We also stipulate, as a rough estimate, that such a machine should incur no more than 3 dB of loss in the interferometer; this criterion is especially demanding, since the interferometer loss scales with the number of modes. Events with hundreds of photons would be detectable with such a machine.
At present, the total system loss is approximately 8 dB, of which about 3 dB is incurred in the four-spatial-mode interferometer. This is dominated by losses in the MMI-based beam splitters (0.2 to 0.4 dB per layer) and in the bent segments of the waveguide coils used in the interferometer phase shifters (0.35 to 0.55 dB per layer). MMIs are employed for their fabrication tolerance, as they reliably achieve close to 50:50 splitting ratio across large chip areas even with imperfect lithography and wafer uniformity. The waveguide coils are designed to achieve a longer phase shifter propagation length, increasing thermal efficiency. For both of these components, the dominant source of loss is not directly related to the fundamental straight-waveguide propagation loss of 0.2 dB cm–1 associated with their lengths.
Optimization of the design and fabrication process can greatly reduce these losses. By moving to a fabrication line offering more precise lithography, less fabrication-tolerant directional couplers can replace MMIs as the beam splitting element. These can achieve length-limited loss, contributing approximately 200 μm of length per layer, which would correspond to about 0.008 dB of loss per layer. Upgrading the microheaters used in the phase shifters to a more specialized material can lower the required number of bends and shorten the propagation length of the two waveguide coils to 3 mm per layer, contributing 0.06 dB per layer. These coils can also achieve length-limited performance by designing more adiabatic transitions between straight and bent segments. Combined, these changes would yield an interferometer loss of approximately 0.068 dB per layer. For a 50-spatial-mode interferometer, this would result in a total of 3.4 dB of loss. A modest improvement in waveguide propagation loss to 0.17 dB cm–1 would then suppress interferometer losses to below 3 dB. Considering silicon nitride waveguides have been demonstrated in a similar platform with losses as low as 0.055 dB cm–1 (ref. 47), we believe this is a demanding but realistic pathway to controlling losses as the system size scales.
Other challenges associated with scaling the interferometer arise from the power dissipated by the thermo-optic phase shifters. Currently, the interferometer in our device dissipates approximately 1 W of power for a typical unitary setting, in a chip area of 0.4 cm2. A 50-spatial-mode interferometer would require 2,450 phase shifters, dissipating a total of about 120 W across a chip area of about 21 cm2 (corresponding to three reticle write-fields of a standard lithography tool), when each is tuned to achieve a phase shift. The thermal load density (power dissipated per unit chip area) would therefore approximately double, despite the number of phase shifters increasing by two orders of magnitude. For comparison, a modern microprocessor dissipates between 100 W and 200 W under full load in a die area of about 1 cm2. With proper thermal management, we do not anticipate power dissipation posing a barrier to scaling.
Model parameters
A theoretical model of the chip distribution is used for benchmarking purposes in the experimental demonstrations. To estimate the model parameters quoted in the tables below, we construct a two-dimensional photon-number histogram for each signal and idler mode in a two-mode squeezed vacuum state generated by a single squeezer, keeping all other squeezers off. We model this data as a pair of two-mode squeezed vacua (two Schmidt modes each with squeezing parameter ) hitting the detectors after undergoing loss (with transmissivity ). The squeezing parameter is related to the two-mode squeezing operator by . To represent noise in the detectors, we add an extra model with Poisson statistics (mean value ) that accounts for the measured counts when all the squeezers are off. With these physical parameters it is possible to calculate a two-dimensional histogram using the methods from ref. 38. After this we simply use the well known Levenberg–Marquardt algorithm to solve the inverse problem and retrieve the physical parameters from the measured photon number histograms. It is important to note that these parameters are not the directly measured values of squeezing and losses; they are the values that best approximate the behaviour of the chip given the simplified model we consider. All parameter values are reported in the Supplementary Information.
Sampling from non-classical light
A non-classicality test for photonic devices has been formulated by ref. 33. The results there presented are valid for a simple noise model that includes uniform single Schmidt mode squeezers, uniform loss and threshold detectors with dark counts. Therefore, we also consider a model with a single Schmidt mode and coarse-grain the output distribution as if obtained with threshold detectors. We furthermore generalize the formula in ref. 33 to include non-uniform squeezing and losses. Numerically, we find a modelling error of averaged over 15 random unitary transformations and calculations are made by considering a cutoff of 14 photons per mode. Since the coarse-graining procedure can only decrease the total variation distance, we can use the value of quoted above.
We briefly present the derivation of equation (1), which generalizes the results of ref. 33. Assuming the aforementioned noise model, the output quantum state of the device is given by , where are the lossy squeezed states in each mode. In ref. 48, the authors studied the problem of exact sampling from an M-mode quantum state of the form , where is an arbitrary ()-classical Gaussian state, that is, a state with positive -ordered phase-space quasiprobability distribution48. We denote the distribution obtained by sampling from this classical state by , which is calculated using The Walrus49. It can be shown that sampling from by using noisy threshold detector with excess photon rate can be simulated exactly in classical polynomial time if (ref.48).
Therefore, when the mixed input state is close to some classical Gaussian state , the corresponding noisy GBS experiment can be efficiently simulated with small error. Since any such state leads to an efficient classical simulation, it is necessary to minimize the distance to over all possible choices of . This intuition is made precise in ref. 33. Following a similar procedure, it is straightforward to derive that we have whenever . Here is the quantum fidelity between and . From ref. 33, the maximal fidelity optimized over all possible is given by sech . By setting , we obtain the sufficient condition of the efficient simulation of noisy GBS given in equation (1).
GBS
It has been shown28 that for a Gaussian state prepared using only squeezing followed by linear interferometry, the probability of observing an output , where denotes the number of photons detected in the ith mode, is given by
| (12) |
where , , , and is the covariance matrix of the state in the creation/annihilation operator basis. The submatrix is specified by the output pattern (sample) of detected photons: if , the rows and columns and are deleted from and, if , the corresponding rows and columns are repeated times. When the Gaussian state is pure, the matrix can be written as , with an symmetric matrix. In this case, the output probability distribution is given by
| (13) |
where the submatrix is defined with respect to rows and columns , not . The matrix function is the Hafnian50, defined as
| (14) |
where are the entries of and PMP is the set of perfect matching permutations. Computing the Hafnian is a #P-hard problem, a fact that has been leveraged to argue that, unless the polynomial hierarchy collapses to third level, it is not possible to efficiently simulate GBS using classical computers28,39. These complexity proofs are valid when the squeezing levels are equal in all modes and the interferometer unitary transformation is chosen randomly from the Haar measure.
In the architecture of our device, a Gaussian state is prepared using two-mode squeezing operations and an interferometer acts equally on both halves of the modes. This is similar to the scattershot boson sampling proposal of ref. 51, with a notable difference: both pairs of modes are affected by the interferometer and no post-selection is necessary. The GBS distribution is also given by equation (14), but in this case the matrix satisfies
| (15) |
| (16) |
where is the squeezing parameter on the ith pair of modes. The resulting distribution can be expressed directly in terms of the matrix . Using the identity
| (17) |
we can express the GBS distribution as:
| (18) |
where Per denotes the permanent of a matrix and where we use to denote a sample across 2m modes. The notation corresponds to a submatrix obtained as follows: if , the ith row of is removed. If , it is instead repeated times. Similarly, if , the ith column of is removed and if , it is repeated times. This architecture can be interpreted as a combination of boson sampling and GBS: the number of photons is not fixed and probabilities are given by permanents, but of a symmetric matrix . This suggests that hardness proofs for boson sampling may be readily ported to this setting.
These hardness proofs show that ideal boson sampling cannot be efficiently simulated classically, even approximately, unless the polynomial hierarchy collapses, modulo the validity of two well established conjectures39. Because these proofs apply to approximate classical sampling, they imply that imperfect GBS is also hard to simulate classically, provided the imperfections are sufficiently small. This raises the question of how much loss can be tolerated to ensure hardness.
Ideally, a sufficient condition would be formulated. This remains a challenge. Several studies have been performed providing necessary conditions for hardness, for example ref. 52. in the context of boson sampling. For GBS, ref. 33 provides the condition that is used in this work as a benchmark of non-classicality. These studies place stringent restrictions on the amount of tolerable loss, which set a bar for experiments. Conversely, any experiment that is able to satisfy all known necessary conditions while also outperforming the best known classical simulation algorithms will provide strong evidence for having achieved a quantum advantage. It is possible this will require detection of 100 photons in 100 modes.
In the demonstration described in the main text, three unitary transformations were generated and implemented in the device, which are reported in the Supplementary Information.
Vibronic spectra
According to the Franck−Condon approximation53, the probability of a given vibronic transition is given by the Franck−Condon factor, defined as
| (19) |
Where is the Doktorov operator, is the vacuum state of all modes in the initial electronic state, and is the state with phonons in the ith vibrational mode of the excited electronic state. The Franck−Condon profile determines the probability of generating a transition at a given vibrational frequency . For finite-temperature vibronic transitions it is defined as
| (20) |
| (21) |
where is the vibrational Fock state of the electronic ground state, is its initial thermal distribution at temperature , is the frequency of the kth vibrational mode of the initial electronic state, and is the frequency of the kth vibrational mode of the final electronic state.
A photonic algorithm for computing Franck−Condon profiles was introduced by ref. 18. The main insight of this algorithm is that a quantum device can be programmed to sample from a distribution that naturally assigns high probability to outputs with large Franck−Condon factors, without actually having to compute these factors. Sampling from the distribution can then be used to generate outputs with large Franck−Condon factors, which show up as peaks in the spectra.
In the algorithm, optical photons correspond to vibrational phonons, and the Doktorov operator can be decomposed in terms of multi-mode displacement, squeezing and linear interferometer operations, each determined by the transformation between the normal coordinates of the initial and final electronic states. In particular, the interferometer is configured as follows. The diagonal matrices and are constructed respectively from the ground and excited electronic state frequencies:
| (22) |
| (23) |
The Duschinsky matrix is obtained from the normal mode coordinates of the ground and excited electronic states, and respectively, as , where is a displacement vector related to the structural changes of the molecule upon vibronic excitation. From the matrix, a singular value decomposition is performed:, where and are the left and right unitary matrices. For the specific case of zero-temperature vibronic spectra, it is sufficient to set the interferometer according to the unitary transformation . This is done in the experiments reported in the main text.
When sampling from the resulting distribution, each output photon pattern is assigned a frequency
| (24) |
and the collection of output frequencies is used to create a histogram that represents the Franck−Condon profile.
There is no known efficient classical algorithm for computing molecular vibronic spectra. Methods for computing approximate spectra exist, but these can still be challenging to employ for large molecules. Therefore, the quantum algorithm tackles a problem that is known to be hard, but it faces the challenge of providing better approximations than classical methods, even in the presence of imperfections. Additionally, the algorithm requires tunable squeezing and displacements, which are additional technological challenges in the construction of photonic devices. There is optimism that a quantum advantage can be obtained for this problem, for example as expressed in ref. 54, but more work remains to further support this.
In the proof-of-principle demonstration, a single mode is squeezed and there are no displacements. The interferometer is configured as described above according to the Duschinksy rotations and normal-mode frequencies of two molecules: ethylene (C2H4) (ref. 55) and (E)-phenylvinylacetylene (C10H8) (ref. 56). This chemical information is reported in the Supplementary Information.
Graph similarity
An undirected weighted graph can be represented in terms of its symmetric adjacency matrix . The entries denote the weight of the edge connecting nodes and . Symmetric matrices can be encoded in a GBS distribution following equation (13). For the nanophotonic chip implementing the class of quantum circuits illustrated in Fig. 1a, it is possible to encode bipartite graphs on eight vertices that are compatible with the architecture of the device. For a given bipartite graph with adjacency matrix , the circuit is constructed by finding the eigendecomposition of : the eigenvectors determine the unitary transformation of the linear interferometer and the eigenvalues are used to set the squeezing parameters8.
Once the graph is encoded in the device, feature vectors are constructed by estimating orbit probabilities. An orbit is a set of click patterns that are equivalent under permutation. It can be represented as a sorting of a pattern in non-increasing order with the trailing zeros removed. For example, a click pattern belongs to the orbit [2,1,1]. Similarly, the orbit [2,1,1] consists of all patterns with four photons where two photons are detected in only one mode, and a single photon is observed in exactly two modes. For a given orbit , the probability of observing a sample belonging to the orbit is given by
| (25) |
Since there is a combinatorially large number of samples in an orbit, the probability is sufficiently high that it can be estimated without the need for a prohibitive number of samples. By choosing suitable orbits, a feature vector is defined as .
It is currently unclear whether this GBS algorithm can provide a quantum advantage for graph similarity problems. The strongest evidence is the study performed in ref. 22, where an exact computation of GBS feature vectors outperformed existing classical methods for some graph classification tasks. However, there are several challenges. No study of the effect of losses has been conducted, so there is a possibility that there is insufficient loss tolerance for this approach. Additionally, graph similarity problems are amenable to a wide array of heuristic approaches that work very well in practice and are therefore challenging to outperform.
For the demonstration reported in the main text, these orbits were chosen to be , and , which allows the feature vectors to be displayed in a three-dimensional plot. We focus on these orbits because they strike a balance between a sufficiently large number of photons and a high probability of observing outputs in the orbit. Four bipartite weighted graphs were encoded into the device. Their adjacency matrices through are reported in the Supplementary Information. Each graph was then permuted three times to create clusters of isomorphic graphs. Using one-line notation, the permutations are , , .
Supplementary Material
Acknowledgements
Certain commercial equipment, instruments, or materials are identified in this paper to foster understanding. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the materials or equipment identified are necessarily the best available for the purpose.
Footnotes
Code availability
Codes used for data analysis in this work are available upon request from the authors. The Supplementary Information contains example Strawberry Fields code, parameters of the theoretical model, and interferometer unitaries used in the demonstrations.
Additional information
Supplementary information The online version contains supplementary material available at https://doi.org/10.1038/s41586-021-03202-1.
Peer review information Nature thanks the anonymous reviewer(s) for their contribution to the peer review of this work.
Competing interests The authors declare no competing interests.
Data availability
All data underlying the findings of this work are available upon request from the authors.
References
- 1.Clements WR, Humphreys PC, Metcalf BJ, Kolthammer WS & Walmsley IA Optimal design for universal multiport interferometers. Optica 3, 1460–1465 (2016). [Google Scholar]
- 2.Levine ZH et al. Algorithm for finding clusters with a known distribution and its application to photon-number resolution using a superconducting transition-edge sensor. J. Opt. Soc. Am. B 29, 2066–2073 (2012). [Google Scholar]
- 3.Humphreys PC et al. Tomography of photon-number resolving continuous-output detectors. New J. Phys 17, 103044 (2015). [Google Scholar]
- 4.Vignat C. A generalized Isserlis theorem for location mixtures of Gaussian random vectors. Stat. Probab. Lett. 82, 67–71 (2012). [Google Scholar]
- 5.Pfeiffer MHP et al. Photonic damascene process for low-loss, high-confinement silicon nitride waveguides. IEEE J. Sel. Top. Quant. Electron 24, 1–11 (2018). [Google Scholar]
- 6.Rahimi-Keshari S, Ralph TC & Caves CM Sufficient conditions for efficient classical simulation of quantum optics. Phys. Rev. X 6, 021039 (2016). [Google Scholar]
- 7.Gupt B, Izaac J. & Quesada N. The Walrus: a library for the calculation of hafnians, Hermite polynomials and Gaussian boson sampling. J. Open Source Softw 4, 1705 (2019). [Google Scholar]
- 8.Caianiello ER On quantum field theory–I: explicit solution of Dyson’s equation in electrodynamics without use of Feynman graphs. Il Nuovo Cimento 10, 1634–1652, (1953). [Google Scholar]
- 9.Lund AP et al. Boson sampling from a gaussian state. Phys. Rev. Lett. 113, 100502 (2014). [DOI] [PubMed] [Google Scholar]
- 10.Brod DJ & Oszmaniec M. Classical simulation of linear optics subject to nonuniform losses. Quantum 4, 267 (2020). [Google Scholar]
- 11.Sharp T. & Rosenstock H. Franck–Condon factors for polyatomic molecules. J. Chem. Phys 41, 3453–3463 (1964). [Google Scholar]
- 12.Sawaya NP., Paesani F. & Tabor DP. Near-and long-term quantum algorithmic approaches for vibrational spectroscopy. Preprint at https://arxiv.org/abs/2009.05066 (2020). [Google Scholar]
- 13.Mebel A, Hayashi M, Liang K. & Lin S. Ab initio calculations of vibronic spectra and dynamics for small polyatomic molecules: Role of duschinsky effect. J. Phys. Chem. A 103, 10674–10690 (1999). [Google Scholar]
- 14.Müller CW, Newby JJ, Liu C-P, Rodrigo CP & Zwier TS Duschinsky mixing between four non-totally symmetric normal coordinates in the s 1–s 0 vibronic structure of (E)-phenylvinylacetylene: a quantitative analysis. Phys. Chem. Chem. Phys 12, 2331–2343 (2010). [DOI] [PubMed] [Google Scholar]
- 15.Wright K. et al. Benchmarking an 11-qubit quantum computer. Nat. Commun 10, 5464 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Arute F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019). [DOI] [PubMed] [Google Scholar]
- 17.Larsen MV, Guo X, Breum CR, Neergaard-Nielsen JS & Andersen UL Deterministic generation of a two-dimensional cluster state. Science 366, 369–372 (2019). [DOI] [PubMed] [Google Scholar]
- 18.Asavanant W. et al. Generation of time-domain-multiplexed two-dimensional cluster state. Science 366, 373–376 (2019). [DOI] [PubMed] [Google Scholar]
- 19.Qiang X. et al. Large-scale silicon quantum photonics implementing arbitrary two-qubit processing. Nat. Photon 12, 534–539 (2018). [Google Scholar]
- 20.Paesani S. et al. Generation and sampling of quantum states of light in a silicon chip. Nat. Phys 15, 925–929 (2019). [Google Scholar]
- 21.Zhong H-S et al. Experimental Gaussian boson sampling. Sci. Bull 64, 511–515 (2019). [DOI] [PubMed] [Google Scholar]
- 22.Bromley TR et al. Applications of near-term photonic quantum computers: Software and algorithms. Quant. Sci. Technol 5, 034010 (2020). [Google Scholar]
- 23.Kielpinski D, Monroe C. & Wineland DJ Architecture for a large-scale ion-trap quantum computer. Nature 417, 709–711 (2002). [DOI] [PubMed] [Google Scholar]
- 24.Clarke J. & Wilhelm FK Superconducting quantum bits. Nature 453, 1031–1042 (2008). [DOI] [PubMed] [Google Scholar]
- 25.Wootton JR & Loss D. Repetition code of 15 qubits. Phys. Rev. A 97, 052313 (2018). [Google Scholar]
- 26.Dumitrescu EF et al. Cloud quantum computing of an atomic nucleus. Phys. Rev. Lett 120, 210501 (2018). [DOI] [PubMed] [Google Scholar]
- 27.Anschuetz E, Olson J, Aspuru-Guzik A. & Cao Y. Variational quantum factoring. In Int. Worksh. on Quantum Technology and Optimization Problems 74–85 (Springer, 2019). [Google Scholar]
- 28.Nielsen MA & Chuang I. Quantum Computation And Quantum Information (Cambridge: Univ. Press, 2010). [Google Scholar]
- 29.Preskill J. Quantum computing in the NISQ era and beyond. Quantum 2, 79 (2018). [Google Scholar]
- 30.Gottesman D, Kitaev A. & Preskill J. Encoding a qubit in an oscillator. Phys. Rev. A 64, 012310 (2001). [Google Scholar]
- 31.Flühmann C. et al. Encoding a qubit in a trapped-ion mechanical oscillator. Nature 566, 513–517 (2019). [DOI] [PubMed] [Google Scholar]
- 32.Huh J, Guerreschi GG, Peropadre B, McClean JR & Aspuru-Guzik A. Boson sampling for molecular vibronic spectra. Nat. Photon 9, 615 (2015). [Google Scholar]
- 33.Arrazola JM & Bromley TR Using Gaussian boson sampling to find dense subgraphs. Phys. Rev. Lett 121, 030503 (2018). [DOI] [PubMed] [Google Scholar]
- 34.Brádler K, Friedland S, Izaac ,J, Killoran N. & Su D. Graph isomorphism and gaussian boson sampling. Preprint at https://arxiv.org/abs/1810.10644 (2018). [Google Scholar]
- 35.Brádler K, Dallaire-Demers P-L, Rebentrost P, Su D. & Weedbrook C. Gaussian boson sampling for perfect matchings of arbitrary graphs. Phys. Rev. A 98, 032310 (2018). [Google Scholar]
- 36.Schuld M, Brádler K, Israel R, Su D. & Gupt B. Measuring the similarity of graphs with a Gaussian boson sampler. Phys. Rev. A 101, 032314 (2020). [Google Scholar]
- 37.Banchi L, Fingerhuth M, Babej T, Ing C. & Arrazola JM Molecular docking with Gaussian boson sampling. Sci. Adv 6, eaax1950 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Killoran N. et al. Continuous-variable quantum neural networks. Phys. Rev. Res 1, 033063 (2019). [Google Scholar]
- 39.Arrazola JM, Kalajdzievski T, Weedbrook C. & Lloyd S. Quantum algorithm for nonhomogeneous linear partial differential equations. Phys. Rev. A 100, 032306 (2019). [Google Scholar]
- 40.Wang J, Sciarrino F, Laing A. & Thompson MG Integrated photonic quantum technologies. Nat. Photon 14, 273–284 (2019). [Google Scholar]
- 41.Rudolph T. Why I am optimistic about the silicon-photonic route to quantum computing. APL Photon. 2, 030901 (2017). [Google Scholar]
- 42.Hamilton CS et al. Gaussian boson sampling. Phys. Rev. Lett 119, 170501 (2017). [DOI] [PubMed] [Google Scholar]
- 43.Lvovsky A. Squeezed light. In Photonics Vol. 1 Fundamentals of Photonics and Physics 121–164 (Wiley, 2015) [Google Scholar]
- 44.Vaidya VD et al. Broadband quadrature-squeezed vacuum and nonclassical photon number correlations from a nanophotonic device. Sci. Adv 6, eaba9186 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Killoran N. et al. Strawberry Fields: a software platform for photonic quantum computing. Quantum 3, 129 (2019). [Google Scholar]
- 46.Rosenberg D, Lita AE, Miller AJ & Nam SW Noise-free high-efficiency photon-number-resolving detectors. Phys. Rev. A 71, 061803 (2005). [Google Scholar]
- 47.Qi H, Brod DJ, Quesada N. & García-Patrón R. Regimes of classical simulability for noisy Gaussian boson sampling. Phys. Rev. Lett 124, 100502 (2020). [DOI] [PubMed] [Google Scholar]
- 48.Aytür O. & Kumar P. Pulsed twin beams of light. Phys. Rev. Lett 65, 1551 (1990). [DOI] [PubMed] [Google Scholar]
- 49.Christ A, Laiho K, Eckstein A, Cassemiro KN & Silberhorn C. Probing multimode squeezing with correlation functions. New J. Phys 13, 033027 (2011). [Google Scholar]
- 50.Glauber RJ Coherent and incoherent states of the radiation field. Phys. Rev 131, 2766 (1963). [Google Scholar]
- 51.Sudarshan E. Equivalence of semiclassical and quantum mechanical descriptions of statistical light beams. Phys. Rev. Lett 10, 277 (1963). [Google Scholar]
- 52.Burenkov IA et al. Full statistical mode reconstruction of a light field via a photon-number-resolved measurement. Phys. Rev. A 95, 053806 (2017). [Google Scholar]
- 53.Aaronson S. & Arkhipov A. The computational complexity of linear optics. Theor. Comput 9, 143–252 (2013). [Google Scholar]
- 54.Quesada N. Franck-Condon factors by counting perfect matchings of graphs with loops. J. Chem. Phys 150, 164113 (2019). [DOI] [PubMed] [Google Scholar]
- 55.Brádler K, Israel R, Schuld M. & Su D. A duality at the heart of gaussian boson sampling. Preprint at https://arxiv.org/abs/1910.04022 (2019). [Google Scholar]
- 56.Vernon Z. et al. Scalable squeezed-light source for continuous-variable quantum sampling. Phys. Rev. Appl 12, 064024 (2019). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data underlying the findings of this work are available upon request from the authors.